²H and ²⁷Al Solid-State NMR Study of the Local Environments in Al-Doped 2-Line Ferrihydrite, Goethite, and Lepidocrocite

Abstract

Although substitution of aluminum into iron oxides and oxyhydroxides has been extensively studied, it is difficult to obtain accurate incorporation levels. Assessing the distribution of dopants within these materials has proven especially challenging because bulk analytical techniques cannot typically determine whether dopants are substituted directly into the bulk iron oxide or oxyhydroxide phase or if they form separate, minor phase impurities. These differences have important implications for the chemistry of these iron-containing materials, which are ubiquitous in the environment. In this work, ²⁷Al and ²H NMR experiments are performed on series of Al-substituted goethite, lepidocrocite, and 2-line ferrihydrite in order to develop an NMR method to track Al substitution. The extent of Al substitution into the structural frameworks of each compound is quantified by comparing quantitative ²⁷Al MAS NMR results with those from elemental analysis. Magnetic measurements are performed for the goethite series to compare with NMR measurements. Static ²⁷Al spin–echo mapping experiments are used to probe the local environments around the Al substituents, providing clear evidence that they are incorporated into the bulk iron phases. Predictions of the ²H and ²⁷Al NMR hyperfine contact shifts in Al-doped goethite and lepidocrocite, obtained from a combined first-principles and empirical magnetic scaling approach, give further insight into the distribution of the dopants within these phases.

1. Introduction

Aluminum substitution into the structural frameworks of iron oxides/oxyhydroxides such as ferrihydrite, goethite (α-FeOOH), and lepidocrocite (γ-FeOOH) has been studied extensively since Al-substituted compounds are prevalent in soil, particularly in weathering environments.¹ A significant number of studies have focused on establishing the limit of solid solutions and local environments of Al in these materials,¹⁻⁸ using techniques such as elemental analysis,¹ thermal analysis,¹ Mössbauer spectroscopy,²⁻⁵ and X-ray powder diffraction (XRD).^4,6,7 However, the extent of Al substitution is difficult to determine unambiguously since the materials are not always single phase and are typically nanosized, with poorly crystalline aluminum oxide/hydroxide precipitates often being present in addition to the Al-substituted iron containing phases. Furthermore, Al substitution generally decreases the crystallinity of the iron containing phases. Both these factors impede accurate analysis by XRD methods. Elemental and thermal analyses do not provide direct evidence for Al incorporation, because they cannot quantify the fraction of Al present in aluminum precipitates and Mössbauer spectroscopy is an indirect technique since it probes the Fe.

In principle, solid-state NMR (ssNMR) spectroscopy can provide direct evidence for Al substitution into the iron oxyhydroxides, because it is sensitive to the local environment of the Al nucleus. However, studies are hindered significantly by the magnetic properties of these compounds (generally either paramagnetism, antiferromagnetism, or superparamagnetism). The dominant mechanism that leads to NMR shifts in these systems is the hyperfine or Fermi contact shift, which is a short-range, through-bond interaction caused by the delocalization of unpaired electron density over local bond pathways (here, the Fe–O–Al or Fe–O–H bond pathways). A finite amount of spin density in the s-orbitals of the NMR nucleus alters the effective magnetic field felt by the nuclear spin under investigation and causes large isotropic hyperfine shifts often the order of 10–10,000 ppm.⁹ The resultant signals can be extremely broad and difficult to detect and are sometimes termed “invisible”.

The strength and short-range nature of the hyperfine contact shift can be advantageous, providing a contrast by which to distinguish species that are spatially separated from the source of the unpaired electrons [Fe(II) or Fe(III) in this case]. This contrast has been exploited in recent studies of Al-substituted ferrihydrite, where the observable ²⁷Al NMR signal could be unambiguously assigned to diamagnetic Al impurities and quantified to give the total amount of Al in these diamagnetic impurity phases.^10,11 Comparing this amount with the total dopant concentration from elemental analysis then gave an estimate of the amount of ²⁷Al that is in other phases that are “invisible” to the NMR (i.e., not detected in a standard ²⁷Al high resolution NMR measurement) and therefore expected to be directly incorporated into the superparamagnetic ferrihydrite structure. However, there have also been a number of studies in which NMR signals have been detected directly from species in paramagnetic phases. In iron oxyhydroxides these studies have focused on surface or adsorbed species,¹²⁻¹⁵ but there has also been much work concentrating on paramagnetic energy storage materials, where spectra have been acquired for NMR active nuclei in the bulk.^9,16−20 The development of methods by which to predict and assign the NMR resonances in these spectra has been pivotal in the success of these studies. These methods began by rationalizing the magnitude and sign of the hyperfine contact shift using insight from the bonding geometry to assess the nature of the atomic orbital overlap and therefore the extent of the electron delocalization to the NMR-active nucleus.^18,19,21 Recent advances have made this approach more robust and quantifiable by combining evaluations of the delocalized unpaired electron spin density from first-principles calculations with magnetic scaling models based on empirical magnetic susceptibility measurements.¹⁶ The idea of this approach is that the first-principles calculations estimate the hyperfine shifts in the 0 K, ferromagnetic state of the system and the magnetic model provides a way to scale the results to the paramagnetic, finite-temperature regime of the NMR experiment. This approach has been successfully applied to a range of systems,^9,16,17,22 and novel modifications to it have even allowed the shift contributions from individual structurally distinct bond pathways to be assessed.²² We use these methods to study Al substitution in the work presented in this paper.

The structures and magnetic properties of the three minerals investigated in this study are briefly reviewed in the next paragraphs.

Goethite (α-FeOOH) is the most common iron oxyhydroxide in soils. Its structure is reported to be orthorhombic with space group Pbnm(1) and is isostructural with the aluminum oxyhydroxide, diaspore (α-AlOOH). It consists of chains of paired, edge-sharing FeO₃(OH)₃ octahedra that corner-share to form tunnels along the b axis that are bordered by 2 × 1 octahedra (see Figure 1a). Two hydrogen atoms are asymmetrically bonded to two oxygen atoms across these tunnels. Goethite typically shows an antiferromagnetic ordering at approximately 403 K.¹

Figure 1.

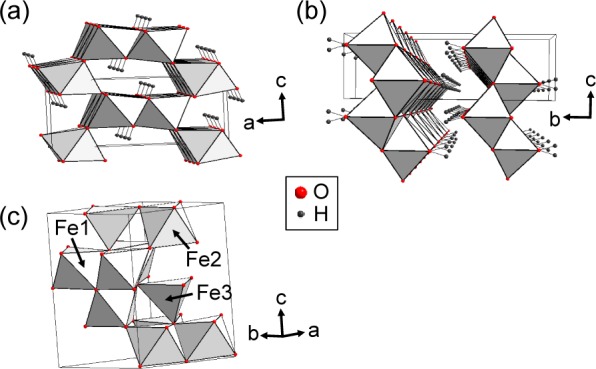
Crystal structures of (a) goethite,¹ (b) lepidocrocite,²³ and (c) 2-line ferrihydrite²⁴ drawn with the reported crystallographic parameters. The unique octahedral (Fe1, Fe2) and tetrahedral (Fe3) Fe environments are labeled for 2-line ferrihydrite.

Lepidocrocite (γ-FeOOH) also has an orthorhombic structure with space group Cmcm (Figure 1b) and is isostructural with boehmite (γ-AlOOH).²³ It consists of corrugated layers of FeO₃(OH)₃ octahedra that are held together by hydrogen bonding, forming stacked sheets.¹ It has a Néel temperature, T_N, of 77 K.¹

Ferrihydrite is ubiquitous in surface environments and plays a role in many environmental, biological, and chemical processes. Its chemical formula and crystal structure have been the subject of considerable debate due to difficulties in characterization caused by its small particle size (<10 nm). So far, two structural models have been proposed: single²⁴ and multiphase.²⁵⁻²⁹ The single phase model has the hexagonal space group P6₃mc (a = 5.95 and c = 9.06 Å) with a chemical formula of Fe₁₀O₁₄(OH)₂.²⁴ This model was proposed to have a significant amount of tetrahedrally coordinated iron (FeO₄), accounting for a total of approximately 20% of the total iron content in the structure (Figure 1c). The other is a multiphase model with a preliminary chemical formula of Fe₅O₈H·H₂O³⁰ and a proposed structure comprising three components:²⁵⁻²⁹ a defect-free component with hexagonal unit-cell parameters a = 2.9514 and c = 9.4149 Å in space group P1c; a defective component with hexagonal unit-cell parameters a = 5.126 Å in space group P3; and an ultradispersed hematite component (α-Fe₂O₃). However, the presence of hematite is still controversial. It is also worth noting that this multiphase model does not contain any tetrahedral iron sites.³¹ Ferrihydrite is typically antiferromagnetic at room temperature but also displays superparamagnetism due to its small particle size.^1,32 Studies of its magnetic properties at higher temperatures are complicated by its metastability,³² but the Neel transition temperature has been estimated at 350 K.³³

In this work, we report an ²⁷Al and ²H NMR spectroscopy investigation of Al-substituted 2-line ferrihydrite, goethite, and lepidocrocite and use these methods to probe the extent of Al incorporation and its distribution within the three iron oxyhydroxide frameworks. We are able to detect NMR signals for these nuclei in both diamagnetic and Fe-containing (paramagnetic) majority phases, allowing us to definitively prove that Al is incorporated into the Fe structures in each case, as well as providing an estimation of the incorporation levels. Furthermore, we use first-principles calculations with the recently developed magnetic scaling model described above¹⁶ to predict the expected hyperfine contact shifts for a variety of doped goethite and lepidocrocite structural models. Experimental magnetic susceptibility measurements for Al-doped goethite samples have been performed to support this analysis and to help understand the impact of doping upon the magnetism of these materials.

2. Experimental Section

2.1. Sample Preparation

Al-Doped Goethite

Two sets of samples were prepared, labeled sets A and B, which differ in the temperature used in their syntheses. Set A, 70 °C synthesis: to synthesize a series of goethite with 0, 6, 13, and 27 mol % Al substitution (labeled GA0, GA6, GA13 and GA27, respectively) a 0.3125 M aluminate solution was prepared by adding 25 mL of 0.5 M Al(NO₃)₃·9H₂O solution to 15 mL of a 5 M KOH solution.³⁴ 0, 2, 5, and 12 mL aliquots of this aluminate solution were added to four polypropylene bottles, followed by 18.0, 17.8, 17.4, and 16.5 mL of a 5 M KOH solution, respectively. Ten mL of 1 M Fe(NO₃)₃·9H₂O solution was then added to each bottle, and the four solutions were made up to 200 mL using distilled water under vigorous stirring, before being placed in an oven at 70 °C for approximately 14 days. A yellow colored precipitate was formed, which was separated by centrifugation, washed with distilled water several times, and then dried at room temperature. Deuterated samples were synthesized in H₂O/D₂O (1:1) using the same procedure as described above. Set B; 48 °C synthesis: 0, 5, and 7 mol % Al-doped samples (labeled GB0, GB5, and GB7, respectively) were prepared by slowly adding 4.64 mL of 3 M NaOH solution, while stirring, to 30.94 mL of 0.16 M Fe(NO₃)₃·9H₂O contained in three separate 125 mL polyethylene bottles.³⁵ After 15 min, 16.78, 17.00, and 17.00 mL of 3 M NaOH solution were added into GB0, GB5, and GB7, respectively. The solutions were stored at room temperature for 3 h, during which time a mixture of 0.928 mL of 0.5 M Al(NO₃)₃·9H₂O and 1.160 mL of 3 M NaOH solution was added to GB5. For GB7, a mixed solution of 4.641 mL of the Al(NO₃)₃·9H₂O solution and 6.807 mL of the NaOH solution was added. The three solutions, GB0, GB5, and GB7, were sealed, shaken, and stored at 48 °C for 5, 17, and 19 days, respectively. The yellow precipitate that formed was separated by centrifugation and dried at room temperature. Deuterated samples were prepared by suspending the as-synthesized goethite in D₂O (98%, Cambridge Isotope Laboratories) for 1 week, after which they were freeze-dried.

Al-Doped Lepidocrocite

A series of Al-doped lepidocrocite samples was synthesized as described previously:⁷ a 1 M NaOH solution was added dropwise to a 0.1 M mixed solution of FeCl₂·4H₂O and Al(NO₃)₃·9H₂O under stirring. When the pH was close to 8.0, air was bubbled through the solution to allow an oxidation reaction. The solution was maintained at pH 8.0 by adding NaOH solution during this time. When a pale brown colored precipitate was formed, the solution was filtered and dried at room temperature. The molar ratio of Al(NO₃)₃·9H₂O and FeCl₂·4H₂O was adjusted to make 0, 1, 4, 8, and 12% mole Al-doped samples, labeled as L0, L1, L4, L8, and L12. Deuterated samples were prepared by suspending as-synthesized lepidocrocite into D₂O (98%, Cambridge Isotope Laboratories) for 1 week, after which the samples were freeze-dried.

Al-Doped Ferrihydrite

A series of 0.2 M mixed solutions of Al(NO₃)₃·9H₂O and Fe(NO₃)₃·9H₂O were prepared to synthesize Al-doped 2-line ferrihydrite samples. The Al/Fe molar ratios of the solutions were adjusted to 0, 10, 30, 50, 70, 90, and 100 mol % Al (labeled as Fh0, Fh10, Fh30, Fh50, Fh70, Fh90, and Fh100). Ferrihydrite was precipitated from these solutions with a 0.1 M KOH solution at pH 7.0; the slurries were then centrifuged, and the solids were dried at 80 °C.

2.2. X-ray Diffraction (XRD) and Elemental Analysis

XRD patterns of the synthesized samples were collected on a Rigaku Miniflex benchtop X-ray diffractometer (Cr Kα radiation). The measured XRD patterns were converted to 2Θ values corresponding to Cu Kα radiation. All diffraction patterns of the synthesized samples were compared with the corresponding Joint Committee on Powder Diffraction Standards (JCPDS) files. The aluminum content of the Al-doped samples was analyzed by XRD and by using atomic absorption spectroscopy, with an MCC-TOX-100 analyzer (Galbraith Laboratories).

2.3. Magnetic Susceptibility Measurements

The magnetic properties of goethite were studied using a Quantum Design SQUID magnetometer (MPMS XL-5). The temperature dependences of the DC susceptibility (χ = M/H), where M is the magnetization of the sample and H is the applied constant magnetic field) were measured while cooling the sample from 400 or 350 to 2 K in a magnetic field of 1000 Oe. High-temperature magnetic susceptibility data was measured using a MPMS system with a high-temperature oven at Quantum Design Inc., heating the sample from 300 to 480 K in a magnetic field of 1000 Oe.

2.4. Solid-State NMR

²⁷Al MAS NMR spectra were acquired at a Larmor frequency of 93.85 MHz with a 15 kHz spinning rate on an Infinity-360 equipped with a Chemagnetics 4 mm MAS probe. A 1 M Al₂(SO₄)₃ solution was used as a reference at 0 ppm. A rotor-synchronized, spin–echo pulse sequence was used with a pulse delay of 0.05 s and a pulse width of 1.5 μs for all of the Al-doped samples. Fh100 spectra were measured with a pulse delay of 1 s.

Static ²⁷Al spin–echo mapping experiments were performed at a Larmor frequency of 52.10 MHz on a CMX-200 spectrometer equipped with a 5 mm Chemagnetics static probe. A spin–echo pulse sequence, 90°_x-τ-180°_y-τ-acquire, was employed with an evolution period, τ, of 20 μs. A pulse delay of 0.01 s and a pulse width of 6 μs were used. The pulse delay was chosen so that it was >6 times the spin–lattice relaxation time (T₁ ≈ 0.43 ms), determined for sample G7 using an inversion–recovery pulse sequence. The irradiation frequency in the spin mapping experiment was varied with a step size of 0.04 MHz below and above the Larmor frequency, where the step size was chosen to be less than ω₁.³⁶ Spectra collected at each irradiation frequency were phased and then summed, after the addition of the appropriate offset-frequency, to yield the full spectrum. The spin–echo mapping spectra of Al-substituted goethite samples were obtained at 433 K, while the Al-substituted lepidocrocite samples were measured at room temperature. Spin–echo mapping experiments were not undertaken on the ferrihydrite samples because of their challenging (superparagmagnetic) magnetic properties that made it difficult to observe the Fermi contact-shifted peaks.

Quantifiable ²⁷Al MAS NMR experiments were performed to estimate the amount of diamagnetic aluminum impurities; these are considered to comprise Al atoms that do not contain iron in their first cation coordination shell and may be present either as Al clusters in the iron oxyhydroxide phases or as separate Al phases. A direct estimate of the amount of Al in these diamagnetic phases can be obtained from ²⁷Al MAS NMR, as the resonances of these nuclei will be approximately unaffected by the hyperfine interactions. Meanwhile, elemental analysis gives the total amount of Al in the samples. Therefore, the amount of Al in the paramagnetic environments (i.e., Al with Fe³⁺ in its first cation coordination shell) can be estimated by subtracting the amount of diamagnetic Al, as estimated from the NMR, from the total amount of Al, as determined by elemental analysis.

To convert the integrated intensities of ²⁷Al signals in the MAS spectra to approximate masses of Al present, they were compared to the integrated signal from the Fh100 sample, which contained a known amount of Al, and no iron. Signal integration was performed over all of the spinning sidebands (SSBs) in the spectra, and the intensities were further normalized by the sample mass, number of scans, and the transverse relaxation times (T₂) of the samples; these were obtained using a spin–echo pulse sequence with variable evolution times. The value of T₂ = 0.63 ms for Fh50 was used for all Al-doped samples, and a value of 0.99 ms was used for Fh100. When quantifying spectra of quadrupolar nuclei with a half-integer spin, such as ²⁷Al, signal acquired from satellite transitions should be corrected for. These effects are difficult to quantify in the broadened spectra of paramagnetic systems, although they are expected to be very small.¹⁰ Furthermore, the normalization of all of the signals to the Fh100 standard, which will have a similar relative proportion of signal from satellite transitions as the rest of the spectra, minimizes the overall quantification error associated with these effects.

²H MAS NMR spectra were acquired at a Larmor frequency of 55.27 MHz on an Infinity-360 spectrometer. The goethite samples were acquired at 433 K with a 15 kHz spinning speed and a Chemagnetics 4 mm MAS probe. The Al-substituted lepidocrocite samples were measured at room temperature with a Samoson 1.3 mm MAS probe and a MAS spinning speed of 53 kHz. ²H NMR spectra were referenced to D₂O at 4.8 ppm. A rotor-synchronized, spin–echo pulse sequence was used with a pulse delay of 0.15 s.

All NMR spectra were normalized by the sample mass and the number of averaging scans used to acquire the signal, allowing for a direct comparison between the absolute intensities of each series of spectra acquired under the same conditions. The position of the isotropic peaks in the MAS experiments were confirmed by repeating experiments with a 12 kHz spinning speed.

2.5. First-Principles Calculation of ²H and ²⁷Al Hyperfine Contact Shifts in Goethite and Lepidocrocite

Spin polarized, periodic first-principles calculations were performed following the method of refs (9,16, and 22) using the CRYSTAL09 linear combinations of atomic orbitals (LCAO) code.³⁷ Hybrid Becke-LYP functionals including weights 20% and 35% of Hartree–Fock (HF) exchange were used, where the 20% corresponds to the usual B3LYP functional; it has been demonstrated that hybrid functionals within this range of HF exchange can accurately model the electronic properties of transitional metal compounds,³⁸ as well as predicting hyperfine shifts in agreement with experiment in systems similar to those studied here.^9,16,22 Results provided in the main text use 20% HF exchange, while the data from the 35% HF exchange calculations are presented in Table S1 and Figure S1.

The modified IGLO-III³⁹ (H and O) and DZP⁴⁰ (Fe) basis sets successfully adopted for the calculation of ³¹P and ⁷Li hyperfine shifts in a series of iron phosphates are also used here.¹⁶ We follow a similar approach in adapting a basis set for Al that is suitable for periodic calculations, removing the most diffuse s- and p-shells from the standard IGLO-III set and increasing the exponent of the next most diffuse shell, yielding a (11s7p2d)/[7s6p2d] basis set where the values in parentheses denote the number of Gaussian primitives used and those in square brackets, the contraction scheme.

For both goethite and lepidocrocite, calculations were performed on the pure, undoped unit cells, as well as on Al-doped supercells comprising four unit cells for both systems, constructed in each case from 2 × 1 × 2 expansions of the unit cells along the a, b, c directions, respectively. Two types of doped configurations were considered: (a) a single Al dopant substituted for Fe, resulting in cell compositions of AlFe₁₅O₁₆(OH)₁₆ and (b) doubly substituted cells in which the Al dopants occupy first, second, and third nearest neighbor positions (Al–O–Al) with respect to each other, with cell compositions of Al₂Fe₁₄O₁₆(OH)₁₆. In both goethite and lepidocrocite, the three doubly substituted cells (labeled 1NN, 2NN, and 3NN in each system, in order of increasing Al–Al distance) constitute all of the unique configurations in which the Al dopants occupy the noted nearest-neighbor (Al–O–Al) positions, as discussed in more detail later. All structures were geometry optimized (atomic positions and lattice vectors) prior to the calculation of NMR parameters.

The first-principles calculations yield the unpaired electron densities at each nuclear position in the cell, which are then used directly to calculate the expected hyperfine contact shifts of each nucleus of interest, following the methods outlined previously.¹⁶ The shifts are scaled from the perfectly ferromagnetic zero-temperature regime representative of the DFT calculations to the finite temperature, paramagnetic regime accessed by the NMR experiments. This scaling is done using a linear Curie–Weiss magnetic scaling model, in which the Weiss constant is scaled so that the calculated susceptibility of the DFT cell matches the experimental value at the temperature of the NMR experiments,^16,41 using the spin-only value of the Fe³⁺ effective magnetic moment. The empirical magnetic mass susceptibilities, χ_m, used were 110 × 10^–6 emu/(g Oe) for lepidocrocite at 293 K⁴² and 26.7 × 10^–6 emu/(g Oe) for goethite at 433 K, as obtained in the current work (extracted from the experimental data collected as part of this study) . The same susceptibilities were used for both the pure and doped cells in each system. Figure S2 justifies this approximation, showing that the susceptibilities for the differently doped goethite compounds converge near T_N and remain similar at temperatures above it.

3. Results and Discussion

3.1. Powder X-ray Diffraction (XRD) and Elemental Analysis

The XRD patterns of GA0, GA6, GA13, and GA27 (i.e., the samples prepared at 70 °C) are consistent with that of goethite (Figure 2a), and no impurities, such as hematite, are observed. A shift of all peak positions to larger 2θ values is observed with increasing Al substitution due to the difference in the ionic radii of the Fe and Al cations (the Al³⁺ ion is 17% smaller than Fe³⁺),⁴³ indicating that Al is incorporated into the structure of goethite.^34,35 No significant line broadening of the XRD reflections is observed.

Figure 2.

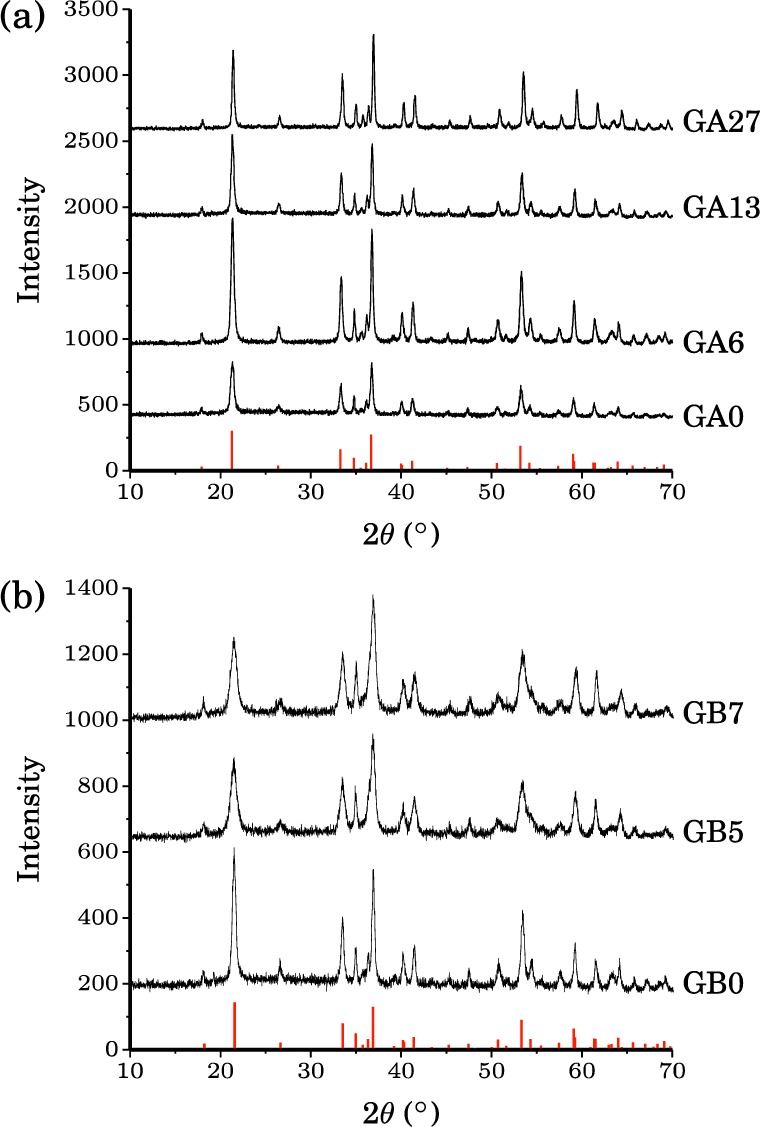
X-ray powder diffraction patterns for (a) the GA series and (b) the GB series. Red vertical lines show the XRD pattern from the JCPDS file for pure goethite.

The XRD patterns of GB0, GB5, and GB7 (i.e., the samples prepared at 48 °C) show that these samples are also phase-pure goethite (Figure 2b). However, here there is an increase in the XRD peak line widths as the nominal Al content increases along the sample series: this increase in width is a clear indication that the particle size and/or crystallinity is decreasing from GB0 to GB5 and GB7. As in the GA series, the peaks shift to higher 2θ values as the Al doping increases across the series, confirming that increasing amounts of Al are incorporated into the goethite structure.

The XRD patterns of unsubstituted (L0) and Al-substituted lepidocrocite samples (L1–12) match with that of the JCPDS file of lepidocrocite (Figure 3). However, the presence of maghemite (γ-Fe₂O₃) or magnetite (Fe₃O₄) impurity phases become apparent when Al contents exceeding 8 mol % are used in the synthesis solutions. This is consistent with previous reports indicating that lepidocrocite forms a solid solution up to a limit of about 10% Al substitution; maghemite formation at lower Al concentrations has been ascribed to local pH fluctuations during synthesis, higher pH favoring maghemite formation.^3,4,34 However, lepidocrocite remains the major component of these samples. In addition, the XRD powder patterns show that the crystallinity of the Al-substituted lepidocrocite samples decreases with increasing Al content. This decrease is particularly noticeable in the powder pattern of L12, which shows very broad XRD reflections shifted to higher 2θ values (Figure 3). The shifts and broadening of XRD reflections with increasing Al concentration in the synthetic solutions are in good agreement with previously reported indicators of Al incorporation.⁴ Since the XRD reflections are too broad to obtain accurate 2θ values, it is difficult to quantify the fraction of Al atoms incorporated into the structures on the basis of the observed shifts.

Figure 3.

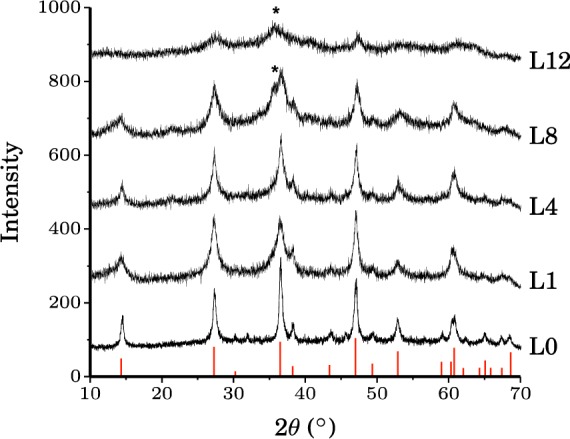
X-ray powder diffraction patterns for the lepidocrocite series. Red vertical lines show the XRD pattern from the JCPDS file for lepidocrocite. (*) denotes reflections due to maghemite (γ-Fe₂O₃) or magnetite (Fe₃O₄) impurities.

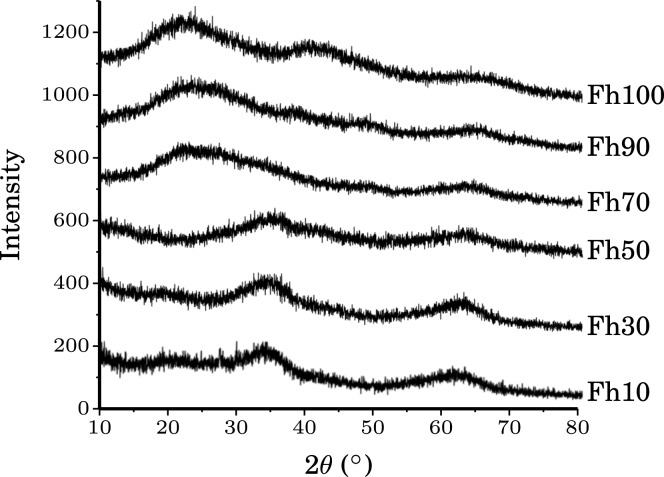
The XRD powder patterns of the Fh10, 30, and 50 samples show two very broad reflections at approximately 2θ ≈ 33 and 64° (Figure 4), matching the previously reported XRD pattern of 2-line ferrihydrite. However, the Fh70, 90, and 100 samples show very different XRD patterns from that of 2-line ferrihydrite, indicating that their structures are dissimilar, although they do show similarly broadened reflections due to their low crystallinities.

Figure 4.

X-ray powder diffraction patterns for the ferrihydrite series. The two broad reflections visible in Fh10-50 are consistent with the previously reported XRD patterns for 2-line ferrihydrite.^10,32

3.2. Elemental Analysis and Quantification of Al Content in the Oxide/Oxyhydroxide Structural Frameworks via ²⁷Al MAS NMR Spectroscopy

Elemental Analysis

Results from the elemental analyses of all of the samples studied are shown in Table 1. The GA6, GA13, and GA27 samples have Al:Fe ratios that are noticeably lower than those of the solutions used in their syntheses. In contrast, those of the GAB series are similar to, if not slightly higher than, the original Al:Fe ratios. This is in agreement with previous reports, which found that an increase in synthesis temperature from 25 to 70 °C speeds up crystal growth and reduces Al incorporation levels.¹ The levels of total Al incorporation in lepidocrocite and ferrihydrite are similar to those of the original synthesis solutions, consistent with their syntheses at close to room temperature.

Table 1. Summary of Al mol % Incorporated into the Al-Substituted Fe Samples.

	Al mol % in synthesis solution	Al mol % by elemental analysis	substituted structural Al nearby Fe atoms from SSNMR (mol %)a
GA6	5.9	3.3	3
GA13	13.5	4.9	5
GA27	27.3	19.2	20
GB5	5.0	5.3	5
GB7	7.0	8.9	9
L1	1.0	1.1	1
L4	4.0	4.8	5
L8	8.0	7.9	8
L12	12.0	12.4	10
Fh10	10.0	10.5	10
Fh30	30.0	30.5	30
Fh50	50.0	52.6	30
Fh70	70.0	67.6	30
Fh90	90.0	90.9	10

^aNMR data is quoted to one significant figure to account for error in the measurement.

²⁷Al MAS NMR Spectroscopy

The room temperature ²⁷Al MAS NMR spectra acquired when the carrier frequency used to excited the ²⁷Al spins is set close to 0 ppm (the diamagnetic region) are first investigated for all three minerals so as to help determine the concentration of Al³⁺ ions that have not been incorporated into the iron-oxyhydroxide phases.

Goethite

The Al-doped goethite samples GA6, 13, and 27 and GB5 and 7, all show a broad signal with a peak maximum at about 800–1000 ppm and a sharp, weak isotropic resonance at −5 ppm (Figure 5). The peak at approximately −5 ppm is assigned to Al in a diamagnetic environment: occurring either as large Al clusters within the goethite framework or, more likely, as an Al phase either present in too low an amount or lacking sufficient crystallinity to be detected by XRD measurements. The intensity of the broad signal centered at approximately 1000 ppm increases with Al substitution level, the broad resonance being ascribed to Al atoms that are in close proximity to Fe³⁺ ions and therefore incorporated into the iron oxyhydroxide phase.

Figure 5.

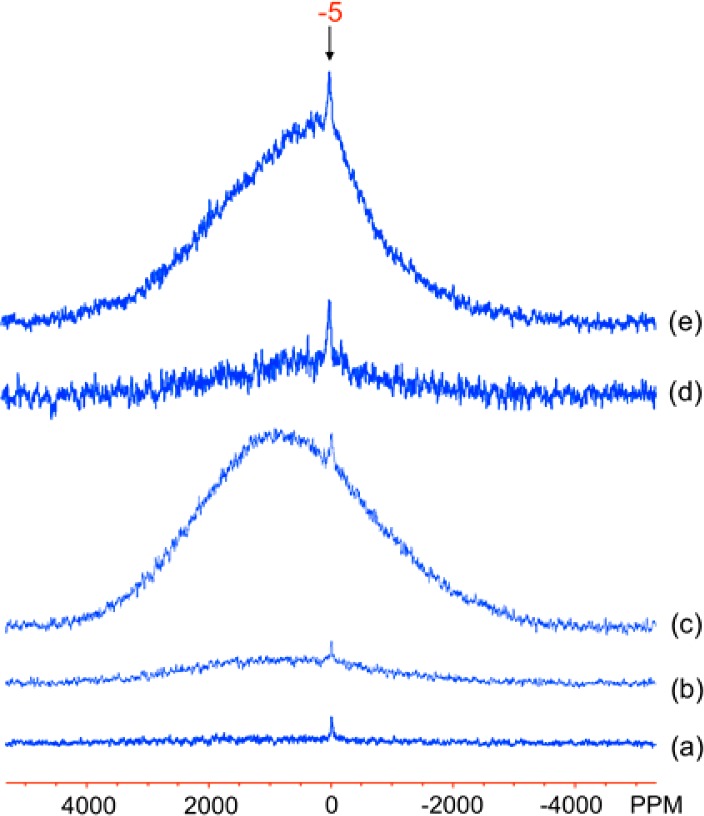
²⁷Al MAS NMR spectra of the Al-doped goethite samples: (a) GA6, (b) GA13, (c) GA27, (d) GB5, and (e) GB7. The spectra were acquired on a 360 MHz magnet, on-resonance for the diamagnetic species (i.e., close to 0 ppm), at room temperature. The isotropic resonance of the diamagnetic component is labeled in (e).

Lepidocrocite

The ²⁷Al MAS NMR spectra of the Al-doped lepidocrocite samples, shown in Figure 6, consist of two components: a highly shifted broad peak and a relatively sharp peak at −6 ppm with an associated spinning sideband manifold. As in the goethite data, the −6 ppm peak is assigned to diamagnetic Al phases or large diamagnetic Al clusters within the structural framework of lepidocrocite. The SSBs are thought to originate in part from the quadrupolar interactions of the spin-5/2 ²⁷Al nucleus, with a second contribution from bulk magnetic susceptibility (BMS) effects that are caused by long-range electron–nuclear dipolar coupling to nearby paramagnetic particles/domains.^10,44 That no SSBs are apparent in the goethite series (Figure 5) is most likely due to the reduced intensity of the diamagnetic peak in those spectra. Indeed, in the lepidocrocite series they are only visible in the L12 and possibly L8 samples, which contain the most diamagnetic Al impurities. The size of the SSB manifolds will also be affected by the sizes of the diamagnetic clusters/particles and their spatial proximity to the paramagnetic phases. The broad signal is ascribed to a subset of Al atoms in close proximity to Fe sites.

Figure 6.

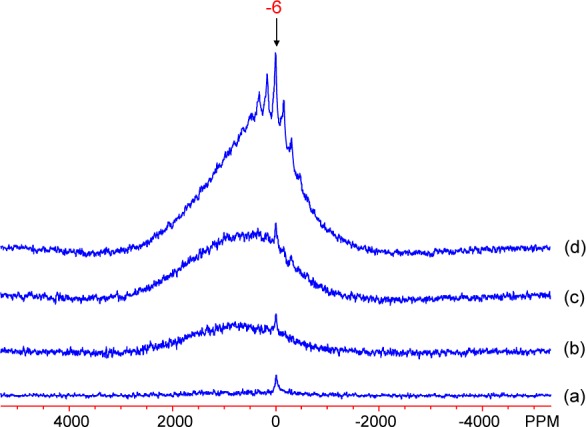
²⁷Al MAS NMR spectra of Al-doped lepidocrocite samples: (a) L1, (b) L4, (c) L8, and (d) L12. The spectra were obtained at room temperature, with the carrier frequency on-resonance for the diamagnetic species. The isotropic resonance of the diamagnetic component is labeled in (d).

Ferrihydrite

²⁷Al MAS NMR spectra of Al-doped ferrihydrite samples, displayed in Figure 7, show an isotropic resonance at approximately 4 ppm for the 10–70 mol % samples, with an associated SSB pattern originating from quadrupolar interactions and BMS effects. The Fh 90 sample shows three additional resonances with isotropic shifts at approximately 4, 32, and 64 ppm, assigned to 6-, 5-, and 4-fold coordinated Al sites, respectively.⁴⁵ These sites are likely within diamagnetic Al phases that must also be amorphous, as the XRD patterns in Figure 4 show no significant crystalline phases at any level of doping. Despite the similarity of the Fh70 XRD pattern to that of Fh90 and 100 (Figure 4), its ²⁷Al NMR spectrum shows few or no 5- or 4-fold coordinated Al sites.

Figure 7.

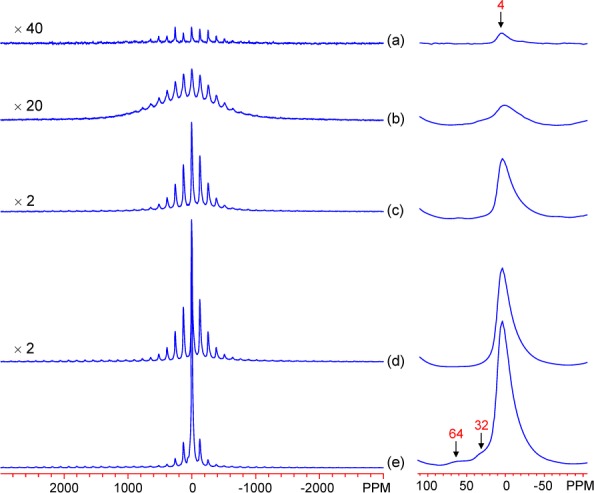
²⁷Al MAS NMR spectra of Al-doped ferrihydrite samples: (a) Fh10, (b) Fh30, (c) Fh50, (d) Fh70, and (e) Fh90. The spectra were obtained with the carrier frequency on-resonance with the diamagnetic components. Isotropic resonances are labeled. Right side: expansion of the diamagnetic region.

Determination of Al Incorporation

Estimates of the total mass of Al in diamagnetic impurities were obtained by integrating the NMR signals for the diamagnetic Al impurities in the three systems and normalizing by the relaxation times, sample mass, and number of scans. The differences between these values and the total Al contents derived by the elemental analyses then provide direct estimates of the Al fraction that is incorporated directly into the Fe sublattices, as shown in the last column of Table 1. The data reveal that, in goethite and lepidocrocite, only very small amounts of Al impurities exist and that almost all (greater than 95% in every case) of the Al is doped directly into the Fe sublattice in environments that are in close proximity to Fe.

In the ferrihydrite series the dopant range is much higher, and a limit of 30% Al incorporation is reached, in agreement with a recent study in which a limit of 20–30% was found.¹⁰ Significant concentrations of diamagnetic impurities are formed under synthesis conditions with larger proportions of Al, as opposed to the Al being incorporated into the structural framework of 2-line ferrihydrite. This result implies that it is difficult to increase the Al doping level of ferrihydrite without the formation of a significant amount of diamagnetic impurity phases. The Fh70 and 90 data reveal that 30 and 10%, respectively, of the total amount of Al in the samples is substituted into the Fe structural framework, leading to Al sites in close proximity to Fe ions. These values are similar to those of Fh30 and 10.

These solubilities show some qualitative agreement with the ab initio energetics of Al substitution predicted from ab initio methods by Pinney and Morgan.⁸ They found that the lowest Al dilute heats of solution are for goethite, lepidocrocite, and the Fe1 sites in ferrihydrite (the Michel et al. model is used for ferrihydrite).²⁴ These energies are consistent with the successful Al substitution in goethite and lepidocrocite and the partial Al substitution in ferrihydrite. However, the Fe1 sites make up 60% of the Fe sites in the bulk ferrihydrite assuming a perfect (no defects) periodic version of the Michel model,²⁴ so filling these sites would incorporate significantly more Al than observed in the present work. The origin of this discrepancy is not clear but may be explained by different site energetics in nanoparticles due to many sites being at or near the surface or structural inaccuracies of the idealized Michel model.

Given the findings above, the challenge is now to determine the manner in which the Al ions are incorporated into the structure, since small Al impurity phases or Al clusters within or at the surface of the iron oxyhydroxide particles will not be detected by the XRD experiments described earlier.

3.3. Magnetic Properties of Goethite

We now examine the magnetic properties of goethite, since its Néel transition temperature, T_N, is in the same temperature regime as the temperatures used in the NMR study. T_N is highly correlated to the sample composition, with higher Al-doping levels in both the GA and GB series, generally leading to lower transition temperatures (Figure 8a). Noticeably lower T_N values are observed for the GB series, in comparison to the GA series, for the same Al content (Figure 8a). A reduced T_N is commonly observed in all Al-doped iron oxides and is likely a consequence of two effects. First, the diamagnetic impurities disrupt the exchange-coupling network of the unpaired electrons present at the Fe sites. Second, it has been observed previously that T_N shows some dependency on particle size: in goethite in particular, a drastic reduction in T_N has been seen upon moving from micro- to nanosized systems.⁴⁶ It seems likely that both of these mechanisms are of importance here, where the differences in the magnetic behaviors of the GA and GB series most likely arise due to the decreasing particle sizes in the GB series, as supported by the broadening in the XRD patterns of the latter materials. Figure 8 shows the high temperature magnetization curve for GB7, illustrating that at the temperature of the NMR experiments (433 K) the magnetic susceptibility is in the Curie–Weiss regime. This will be discussed further in the context of the empirical scaling of the calculated hyperfine shifts.

Figure 8.

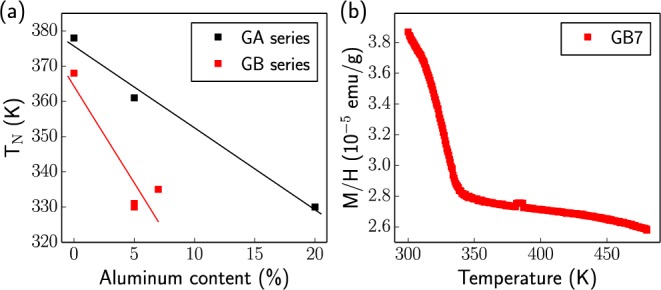
(a) Comparison of the measured Néel transition temperatures for the Al-doped goethite series. The plotted Al content is that determined from the NMR and elemental analysis results (final column of Table 1). The full magnetization curves from which these values were estimated are shown in Figure S2. (b) High temperature magnetization curve for the GB7 sample.

3.4. Solid-State NMR and Structural Assignment using First-Principles Calculations

²⁷Al NMR

The magnetic data for both the GA and GB series (Figure 8a) clearly show that the room temperature ²⁷Al MAS NMR spectra shown in Figure 5 were acquired below the Néel transition temperatures of all the samples (all ≥320 K). The spectrum of GB7 was therefore reacquired at 433 K, well above its Néel temperature (350 K) (Figure 9b). The ²⁷Al resonance at close to 0 ppm is largely unchanged, but the broad resonance has now shifted noticeably to positive frequencies. This large shift is consistent with Al³⁺ ions nearby Fe³⁺ ions in the paramagnetic state. At temperatures below T_N, Figure 9a, the strong antiferromagnetic ordering in these materials is expected to result in a noticeable reduction of the hyperfine shift. The broadening of the spectrum, even in the antiferromagnetic state, is ascribed to the disorder in the material, which will result in a distribution of magnetic couplings and large local fields. Furthermore, the unpaired electrons are essentially unscaled in the antiferromagnetically ordered state, and so the contact shifts and the inhomogeneous broadening due to their variation across the particles in the powder sample are greatly magnified in comparison to those observed for the paramagnetic state. The small positive shift of the center of gravity of this broad resonance suggests that there might be regions with a depressed T_N (most likely in domains rich in Al³⁺) where the ²⁷Al nuclei are nearby residual Fe³⁺ ions in the paramagnetic state.

Figure 9.

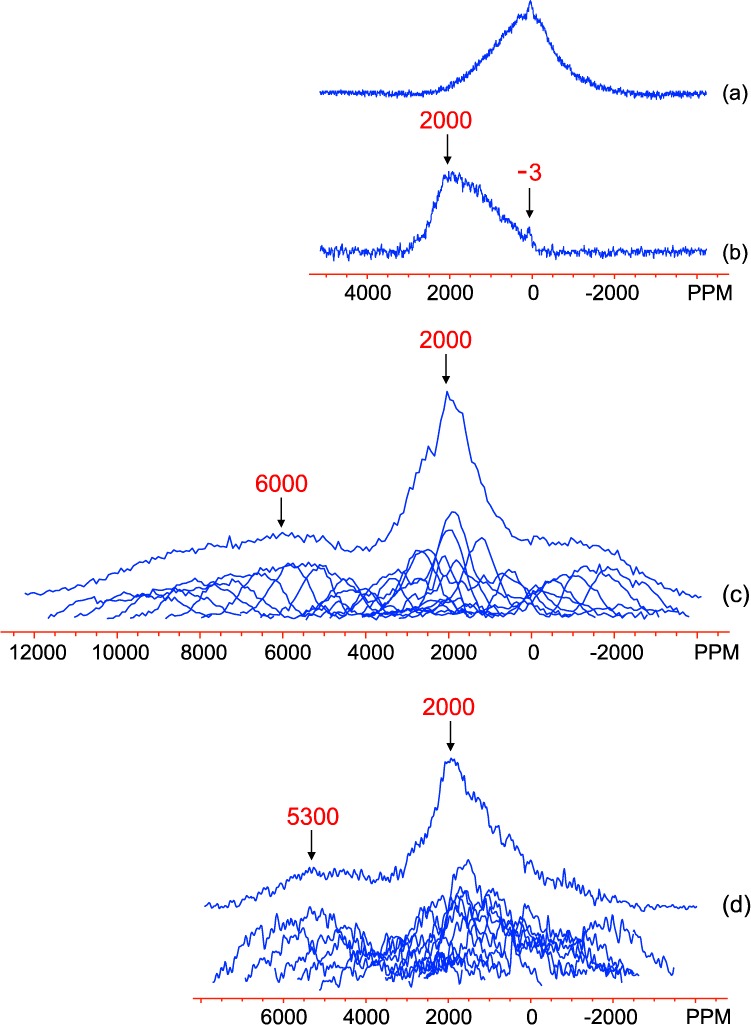
²⁷Al NMR spectra of GB7: (a) MAS spectrum at room temperature, (b) MAS spectrum at 433 K, (c) static spin–echo mapping spectra (individual and summed) at 433 K, and (d) static spin–echo mapping spectra (individual and summed) for GA27 at 433 K. The spectra were obtained on a 200 MHz magnet. MAS spectra were acquired on-resonance with the diamagnetic peak. The MAS spectra (a,b) are plotted on a different scale to the spin–echo mapping spectra (c,d).

Although the MAS NMR results confirm the presence of Al in paramagnetic regimes within the samples, they do not provide the full ²⁷Al signal in these phases because of the limited excitation profile of the pulses employed (approximately 80 kHz, or 900 ppm). More accurate representations are obtained from the static spin–echo mapping experiments, which are shown in Figure 9c,d for samples GB7 and GA27 at 433 K. The two spectra show similar features: an extremely broad set of shifts covering the region from 7000 to −2000 ppm in GA27 and 10000 to −3000 ppm in GB7 (although it is possible that the spectra cover a wider range than the mapped region in both cases) and a much narrower distribution of resonances centered at approximately 2000 ppm in both samples. This shift range and distribution provides unambiguous evidence that the Al is doped into the goethite structure and that the amount of Al in this phase far outweighs that occupying diamagnetic environments in these samples. However, obtaining further insight into the relationship between the local Al environment in the doped structures and the ²⁷Al hyperfine shifts is difficult on the basis of the NMR spectra alone.

A static spin–echo mapping experiment was similarly performed on the L4 sample (Figure 10). Two very broad signals centered at approximately 2000 and 5300 ppm are identified, along with an extra split peak centered at about 0 ppm. The latter split peak is assigned to diamagnetic ²⁷Al environments, the peak splitting being tentatively ascribed to the quadrupolar interaction of the ²⁷Al quadrupolar nuclei, resulting in a second-order line shape, possibly broadened further by the dipolar coupling between the nuclear and electron spins. It is unclear why this effect is not also seen in the goethite spectra, where the quadrupole coupling constants should be similar. Most likely, the broadened lineshapes are not intense enough to be resolved due possibly to the slightly lower Al³⁺ diamagnetic impurity levels in the goethite samples. It is also possible that the splitting is caused by Fe³⁺ ions in more distant coordination shells. The large observed shifts at 2000 and 5300 ppm are again attributed to short-ranged Fermi-contact shift interactions between the unpaired electron spins at the Fe³⁺ sites and the ²⁷Al nuclei under observation, confirming Al substitution into bulk lepidocrocite.

Figure 10.

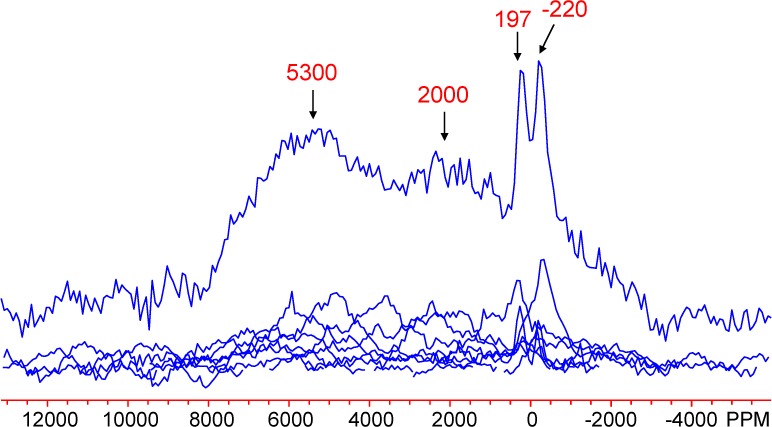
Static ²⁷Al spin–echo mapping spectrum of L4. Two broad peak maxima and two sharper ones are labeled.

Calculated ²⁷Al Hyperfine Contact Shifts

The calculated, scaled ²⁷Al hyperfine shifts, and unscaled (0 K) values, for goethite and lepidocrocite are given in Table 2. Shifts of 1070 and 6960 ppm are observed when one isolated Al³⁺ ion is substituted into the goethite and lepidocrocite structures, respectively, the larger shift for lepidocrocite resulting from both a larger 0 K hyperfine shift (originating from structural effects) and the larger scaling factor (due to magnetic properties). We then considered the effect of a second Al³⁺ ion substituted in the first coordination shell of a central Al³⁺ ion, labeled 1NN, 2NN, and 3NN for the three distinct environments in each system, as illustrated in Figure 11. Atom 1 in Table 2 refers to the original Al³⁺ and atom 2, the second substituted Al³⁺ ion. The geometries of each nearest neighbor pair are given in Figure 11.

Table 2. Calculated ²⁷Al Unscaled and Scaled Hyperfine Shifts for Al-Doped Goethite and Lepidocrocite Configurations^a.

	unscaled 27Al shifts/105 ppm		scaled 27Al shifts/ppm
configuration	Al atom 1	Al atom 2	Al atom 1	Al atom 2
goethite
single	4.88		1070
1NN	2.93	2.93	643	643
2NN	5.64	5.64	1240	1240
3NN	4.10	4.29	900	942
lepidocrocite
single	7.71		6960
1NN	7.24	7.25	6530	6540
2NN	7.52	7.59	6790	6840
3NN	3.44	3.44	3110	3100

^aAtom 1 and 2 refer to values observed when two ions are substituted into the goethite/lepidocrocite lattice.

Figure 11.

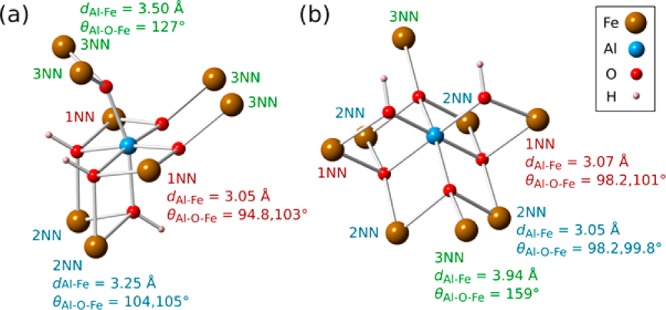
Local environment around a single Al dopant in (a) goethite and (b) lepidocrocite. The nearest neighbor designations and their geometries are indicated. Bond angles and lengths are taken from the geometry optimized, singly doped cells, although the cells doped with two Al atoms do not deviate from these values by more than 2–3%.

The behavior of the shifts in both systems is more complex than the notionally simplest case where the hyperfine shift is straightforwardly proportional to the number of nearest-neighbor Fe contacts. Indeed the largest shift in goethite occurs when two Als are substituted into the cell in 2NN positions. The enhancement from Al 2NNs indicates that the 2NN pathway contributes negative electron density and therefore a negative hyperfine shift, so that when the Fe³⁺ is substituted with Al, the shifts actually increase. There are two, almost identical Al–O–Fe bond pathways linking the 2NN pair (Figure 11a), with 104 and 105° bond angles and the oxygen atoms on each pathway protonated. The pathways have similar geometry as for the 1NN pair (94.8 and 103° bond angles, only one oxygen protonated) that has a positive shift contribution, so the negative shift contribution is likely related to the protonation of the oxygen atoms in the bond pathways (or possibly to incremental changes in the long-range structure that come about when Al substitutes into the 2NN position).

The range of calculated shifts for lepidocrocite agrees reasonably well with the experimental results and suggests that the broad resonance at 5300 ppm can be assigned to either single Al³⁺ ions or Al³⁺ pairs in the 1NN and 2NN environments. The weaker 2000 ppm resonance is assigned to the 3NN environment. In contrast, the magnitudes of the calculated goethite shifts appear to be significantly underestimated. The cause of this discrepancy most likely lies in an inaccurate model of the magnetic properties of goethite. The ferromagnetic-to-paramagnetic scaling factors used in the calculations are based upon the Curie–Weiss model and so assume that the thermally averaged Fe³⁺ magnetic moments vary with temperature T as 1/(T–Θ), where Θ is the Weiss constant. The high temperature magnetic susceptibility measurements for GB7 (Figure 8b) appear to validate this model, showing that the NMR experiments are performed in the Curie–Weiss regime and sufficiently far above the depressed Néel transition temperatures of the doped samples. However, magnetic susceptibility is a bulk property, while NMR probes the local environment around the Al dopants, where there may exist residual magnetic couplings even in the Curie–Weiss regime. This could feasibly lead to enhanced Fe³⁺ magnetic moments around the dopants and therefore to larger Fermi contact shifts than predicted in the paramagnetic regime. This may not occur in lepidocrocite because the NMR experiments are performed at temperatures significantly further away from the undoped Néel transition temperature (T_N = 77 K,¹ experiments performed at 300 K) than for goethite (T_N ≈ 400 K,¹ experiments performed at 433 K). Performing NMR experiments at significantly higher temperatures is not feasible for goethite because it undergoes dehydroxylation at temperatures above 530 K.¹ Note, however, that this dehydroxylation temperature is sensitive to sample composition, and we have observed mass loss at 470 K in TGA measurements, signaling the start of dehydroxylation.

It is expected that the major contribution to the line broadening observed in the static spin–echo mapping spectra is due to the electron–nuclear dipolar interaction between the ²⁷Al nuclei and the unpaired Fe³⁺ electrons. Simple calculations identical to those described in the literature⁴⁴ provide an estimate of the magnitude (approximated as the anisotropy of the dipolar coupling tensor) of these interactions to be 400 ppm in goethite and 2400 ppm in lepidocrocite. Together with the distribution in the calculated Fermi contact shifts, this broadening can account for the overall appearance of the lepidocrocite spectra. However, this is not the case for goethite, where the experimental shift distribution is much broader (>10000 ppm in Figure 9c for GB7) than this estimate of the electron–nuclear dipolar coupling. The Fe³⁺ magnetic moments used in these calculations are scaled using the same factor as employed for the hyperfine shift calculations on goethite and lepidocrocite and are therefore based on the empirical magnetic susceptibility of the samples. Therefore, the discrepancy noted above for the calculated Fermi contact shifts of goethite also holds for the calculated electron–nuclear dipolar interaction, which will be underestimated. Models beyond the present mean field Curie–Weiss approach are currently being developed to account for this larger range of structural configurations and the corresponding changes in the microscopic magnetic properties, with the hope of assigning the full ²⁷Al lineshapes in the spin–echo mapping spectra.

²H MAS Solid-State NMR of Al-Doped Goethite and Lepidocrocite

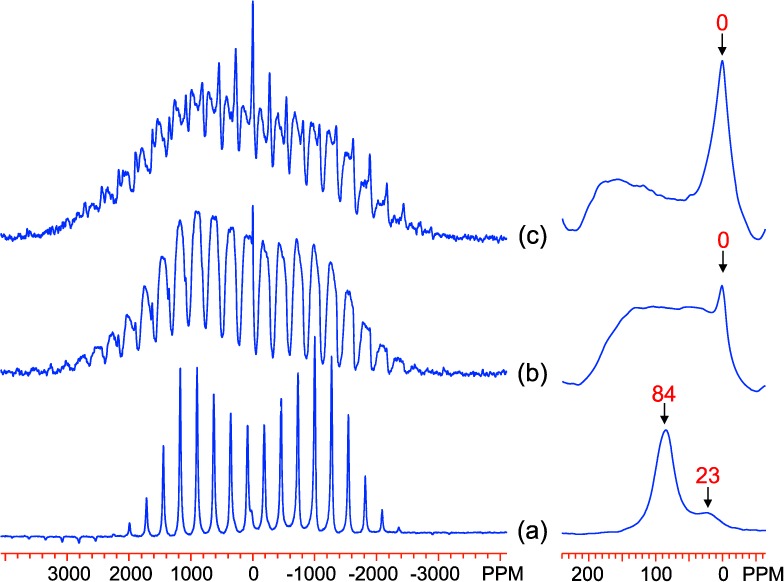
The ²H MAS NMR spectra of GA0 and GB0, shown in Figure 12a and Figure 13a, respectively, show isotropic resonances at 23 and 84–90 ppm. The peak at 84–90 ppm has a sideband pattern resembling that of a Pake doublet and is very similar to that observed previously for bulk (micron-sized) goethite;¹² it is therefore assigned to bulk Fe₃OD groups inside the 2 × 1 tunnels of goethite. The second resonance at 23 ppm has a shift approximately one-third as large, and the shape of the spinning sideband manifold resembles that of a deuterium atom in a water molecule undergoing 180° flips; this peak is therefore assigned to deuterium in mobile D₂O molecules coordinated to a single Fe³⁺ ion, most likely at the particle surface, but possibly in defect (Fe³⁺ vacancy) sites within the lattice, three protons charge-compensating for one Fe³⁺ vacancy, as found in hydrogarnet and manganese(IV) oxides, where they are termed Ruetschi defects.^47,48 The only significant difference between the spectra of GA0 and GB0 lies in the relative intensities of the two peaks, and this is ascribed to both the different methods used for synthesis and deuteration of the samples: the GA series was directly synthesized using a D₂O solvent and so the bulk deuterium species dominates, while the GB series were suspended in D₂O postsynthesis and so a more significant fraction occupies the surface sites. The lower temperature synthesis of GB0 (48 vs 70 °C) may also promote more vacancy formation.

Figure 12.

²H MAS NMR spectra of Al-doped goethite samples, (a) GA0, (b) GA13, and (c) GA27, acquired at 433 K with a 15 kHz spinning rate at a Larmor frequency of 55.27 MHz. The isotropic resonances are labeled. Right side: expansion of the spectra near 0 ppm.

Figure 13.

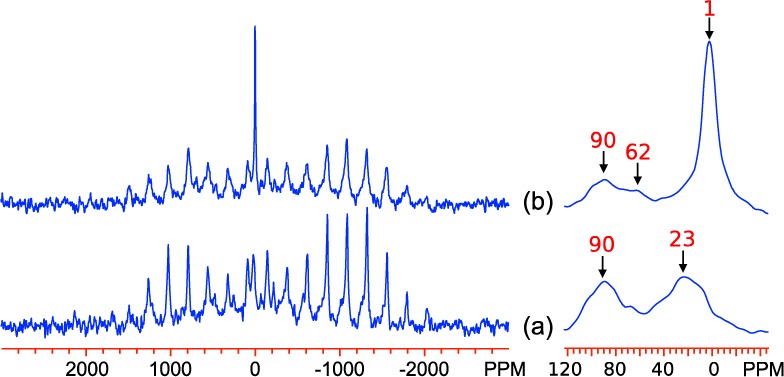
²H MAS NMR spectra of Al-doped goethite samples, (a) GB0 and (b) GB7, acquired at 433 K with a 15 kHz spinning rate at a Larmor frequency of 55.27 MHz. The isotropic resonances are labeled. Right side: expansions showing the isotropic resonances.

Al-doping in the GA series leads to considerable variations in the ²H MAS NMR spectra. In the GA13 spectrum a strong peak at 0 ppm emerges, assigned to a purely diamagnetic environment that is most likely water attached to a single Al ion at the particle surface. Meanwhile, the peak at 84 ppm appears to shift and split, with the resulting environments spread over a large shift range between approximately −10 and 150 ppm. The substantial chemical shifts indicate that all of these environments remain paramagnetic, suggesting a solid-solution model for the Al incorporation into the Fe sites, rather than Al clustering. The introduction of Al atoms into the structure seems to have the simultaneous effect of increasing the shifts of some ²H environments while reducing the shifts of others. In GA27, the peak at 0 ppm appears to have an increased intensity, while the broader set of resonances moves to even higher chemical shifts. These ideas are discussed further below, in light of observations from the ²H chemical shift calculations.

The spectra of the B-series (Figure 13) are very different and exhibit variations with Al-doping varying markedly from those observed in the GA series. This effect must be at least partly due to the different deuteration methods discussed above. As in the GA series, the most significant change in the spectra with doping is the development of the peak near 1 ppm, which is again assigned to rotating D₂O molecules at the particle surface attached to a single Al ion. However, there is very little change in the remaining shifts upon Al doping, despite the fact that the T_N values decrease significantly (Figure 8a), and the shifts are generally clustered close to the value for GA27.

The ²H MAS NMR spectra of Al-doped lepidocrocite samples are shown in Figure 14. The spectrum of L1 shows two main isotropic peaks, at 4 and 172 ppm: the peak at 172 ppm is ascribed to bulk Fe₂OD groups, as previously reported,¹³ while the 4 ppm peak is assigned to adsorbed surface water (Fe-OD₂). The latter assignment is confirmed by comparison of the spectra for sample L12 in Figure 14 (d, 150 ms pulse delay) and (e, 50 ms pulse delay); as there is no increase in the intensity of the resonance when a longer pulse delay is used, the magnetization cannot be saturated by the shorter delays and therefore must have a T₁ much shorter than is typical of species in diamagnetic phases. As the doping level increases, the intensity of the peak at 172 ppm reduces, and a peak at around 84 ppm becomes more pronounced. This is tentatively assigned to a FeAlOD group. There is also an increase in intensities in the region above 172 ppm, with a shoulder developing around 250 ppm. This is similar to the effect doping has on the goethite ²H spectra and the GA series in particular, where the high frequency peak seemingly splits and becomes distributed at higher and lower shifts.

Figure 14.

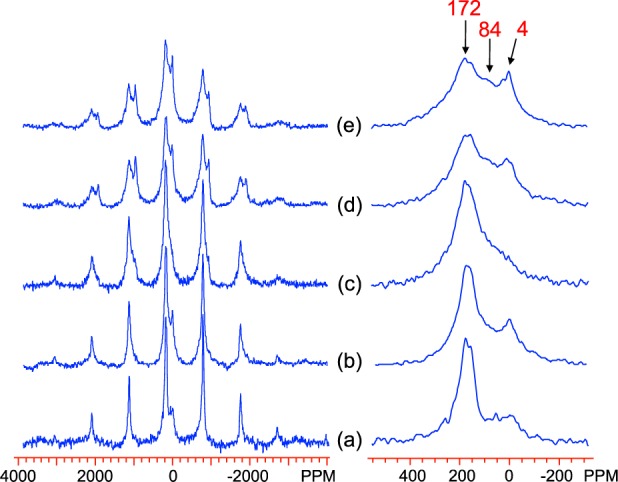
²H MAS NMR spectra of Al-doped lepidocrocite samples, (a) L1, (b) L4, (c) L8, (d) L12, and (e) L12 (with shorter pulse delay of 50 ms), acquired at room temperature with a 53 kHz spinning rate at a Larmor frequency of 55.27 MHz. The isotropic resonances are labeled. The spectra of (a)–(d) were obtained with a pulse delay of 150 ms. Right side: expansions showing the isotropic resonances.

Calculated ²H Hyperfine Contact Shifts

Only one unique ²H environment arises in the goethite and lepidocrocite bulk phases, leading to only one resonance in each phase, which the DFT calculations place at 60 ppm (unscaled shift = 1.66 × 10⁴ ppm) and 450 ppm (unscaled shift = 3.05 × 10⁴ ppm), respectively. Contrary to the behavior of the computed Al shifts, the goethite shift agrees quite well with the experimental value of 84 ppm for bulk Fe₃OD groups, while the lepidocrocite shift differs more significantly from the experimental value of 172 ppm for bulk Fe₂OD groups. As discussed previously, the calculated shifts are expected to be inaccurate in goethite due to the difficulties modeling the magnetic properties, and so it seems that other uncertainties introduced in the ²H calculations are compensating for the inherent errors due to the magnetism. In lepidocrocite, where T_N is much lower than the experimental temperature, these additional errors alone are responsible for the deviation from the experimental values. This error is likely associated with the uncertainty in the position of the light ²H nucleus, and the effect of dynamic changes in the hydrogen bonding configurations that are not accounted for in the calculations. These effects are expected to be slightly different in goethite, where the ²H nuclei occupy positions inside the 2 × 1 tunnels, than in lepidocrocite, where the ²H are sited between H-bonded layers of Fe octahedra whose spacing has been shown to be more sensitive to the details of the calculations.⁴⁹ In light of these significant errors, the absolute values of the calculated shifts are ignored, and only the general trends in the ²H shifts upon Al doping are considered.

Figure 15 shows the effect that replacing one bulk Fe site by Al has on the shifts of the local ²H nuclei. In both systems, the local deuterons take one of two distinct types of interaction with the metal sites: the first is a conventional supertransferred (i.e., involving an intervening lattice site) Fermi contact interaction via a directly bonded M–O–²H pathway involving the hydrogen bond donor O site, while the second type proceeds via a hydrogen bond, i.e. a M–O···²H pathway involving the hydrogen bond acceptor O site. Upon Al substitution, deuterons in the supertransfer pathways all drastically reduce in shift (these sites are labeled in blue in the spectra and the schematics on the right-hand side of Figure 15). Meanwhile, the deuterons in the hydrogen-bonded pathways increase in shift (sites/shifts labeled in red on the right of Figure 15) on Al doping. A further splitting arises in goethite because there are two types of each of the supertransfer and hydrogen-bonded pathways, while in lepidocrocite there is only one of each. The increase in shift upon Al substitution for the H-bonded pathways indicates that their hyperfine shift contribution is negative, and hence that these types of pathways contribute a negative unpaired electron density at the ²H nucleus.

Figure 15.

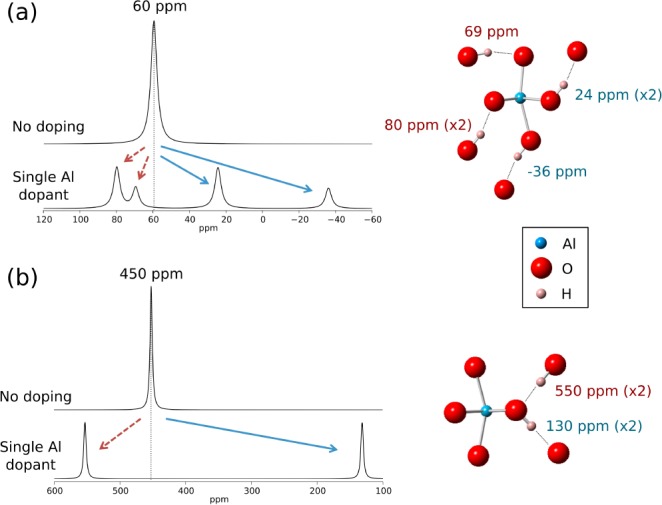
Results from the first-principles calculation of the ²H hyperfine shifts around a single metal site in (a) goethite and (b) lepidocrocite. Simulated spectra are constructed from a sum of Lorentzian lines of width 4 ppm centered at the calculated shifts of the ²H nuclei around a single metal site when it is occupied by Fe (top of pair) or Al (bottom of pair). The local geometry and individual ²H shifts for the Al-doped case are shown on the right.

The predictions from the ²H shift calculations agree particularly well with results from the GA series in Figure 12, where the peak at 84 ppm in the pure compound is lost on doping, while new environments appear at lower and higher shifts. The peaks at approximately 93 and 45 ppm in GA13 and 101 and 29 ppm in GA27 are tentatively assigned to environments such as Fe₂AlOD and FeAl₂OD, respectively, while the higher frequency resonances are assigned to environments such as Fe₃OD, the higher frequency shoulders originating from hydrogen bonding to an O^2– anion coordinated to Al³⁺. That this phenomenon is apparent in the experimental spectra serves as strong evidence that Al is doped directly into the bulk of the FeOOH structure because the increased shifts are associated with ²H that shares at least one supertransfer pathway to Fe and a hydrogen bonded pathway to a substituted Al. Such an environment cannot exist at the particle surface. The fact that these effects are much less pronounced in the GB and L series provides further evidence for this assertion, as the postsynthesis deuteration used in these samples will preferentially deuterate surface sites over those in the bulk.

The general increase in shift is also, at least in part, ascribed to reductions in short- and long-range antiferromagnetic couplings between Fe³⁺ ions caused by the Al³⁺ substitution, again consistent with uniform doping. Changes in the magnetic structure do not, however, affect the NMR spectra in a consistent manner. For example, little shift is seen for the Fe₃OD resonance between GB0 and GB7, and yet T_N is depressed by 35K. Furthermore, both GB7 and GA27 show similar depressions of T_N, yet the effect of this on the Fe₃OD is very different. In GA27 the depression in T_N can now be ascribed to uniform Al³⁺ substitution throughout the lattice. In GB7, with its lower Al³⁺ substitutions, this must also be due to Fe³⁺ vacancies and also particle size, both consistent with the ²H peak at 23 ppm. Interestingly the local magnetic interactions with the goethite particle remain largely unchanged from GB0 to GB7 (as probed by NMR), perhaps suggesting that either Al³⁺ substitution is both not high enough and sufficiently uniform to affect the local interactions and/or that the particle size plays a role in controlling T_N.

4. Conclusions

The present study demonstrates how solid-state NMR spectroscopy can be applied to study Al substitution in systems that are poorly crystalline and disordered. Structural substitution of Al into the lepidocrocite and goethite framework was investigated via ²H MAS NMR and ²⁷Al MAS and spin–echo mapping NMR spectroscopy. A comparison of the elemental analysis and ²⁷Al MAS experiments quantifies the Al present in diamagnetic impurities and has allowed us to indirectly determine the extent of Al incorporation into the Fe sublattices of the majority oxide/oxyhydroxide phases across a broad range of Al contents in goethite, lepidocrocite, and 2-line ferrihydrite. The results suggest that the levels of incorporation are very high in goethite and lepidocrocite at the dopant concentrations explored (up to 12% for lepidocrocite and 27% for goethite), with less than <5% of the introduced Al forming diamagnetic phases. Similarly high levels are observed in ferrihydrite at low dopant concentrations, although the overall Al-incorporation level is limited to ∼30%, consistent with previous observations.¹⁰

The observation of signals with large associated hyperfine shifts in the ²⁷Al spin–echo mapping NMR experiments confirms that Al substitution occurs into sites neighboring paramagnetic Fe³⁺ cations. Changes in the ²H MAS NMR spectra upon Al³⁺ substitution further support this, with the trends from the DFT hyperfine shift calculations showing that Al³⁺ substitution can both reduce (by Fe³⁺ for Al³⁺ substitution in directly bonded H–O–Fe/Al pathways) and increase (by H-bonding to an oxygen ion coordinated to Al³⁺) the size of the ²H hyperfine shift. Indeed, the combination of experiment and the ²H and ²⁷Al contact shift calculations seems to be a promising approach in the present and related systems, although further development is needed to model the shifts more accurately by accounting for the local variation in the magnetic properties that is caused by the doping of diamagnetic species and by residual magnetic correlations at temperatures only slightly above T_N.

Supporting Information Available

Results from calculations using 35% Hartree–Fock exchange and full magnetization curves for Al-doped goethite. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemmater.5b00856.

The authors declare no competing financial interest.