Visualizing Transient Watson-Crick Like Mispairs in DNA and RNA Duplexes

Abstract

Rare tautomeric and anionic nucleobases are believed to play fundamental biological roles but their prevalence and functional importance has remained elusive because they exist transiently, in low-abundance, and involve subtle movements of protons that are difficult to visualize. Using NMR relaxation dispersion, we show that wobble dG•dT and rG•rU mispairs in DNA and RNA duplexes exist in dynamic equilibrium with short-lived, low-populated Watson-Crick like mispairs that are stabilized by rare enolic or anionic bases. These mispairs can evade Watson-Crick fidelity checkpoints and form with probabilities (10⁻³-10⁻⁵) that strongly imply a universal role in replication and translation errors. Our results indicate that rare tautomeric and anionic bases are widespread in nucleic acids, expanding their structural and functional complexity beyond that attainable with canonical bases.

Nucleic acid bases exist predominantly in one neutral tautomeric form. This in turn gives rise to the strict Watson-Crick (WC) pairing rules (Fig. 1a) that govern how genetic information is replicated, transcribed, and translated. However, if bases adopt alternative energetically disfavored tautomeric or anionic forms (Fig. 1a), pairing rules can be violated and new functions can emerge. For example, although rarely observed, minor tautomeric and anionic bases can form WC-like dG•dT^1-3, dA•dC⁴, and rG•rU^5,6 mispairs that are believed to contribute to spontaneous mutations^1,7-9 and translational errors¹⁰. Chemical modifications that stabilize or lock bases in their anionic or enol-like forms can be mutagenic^11,12 or expand the decoding capacity of tRNAs^13,14. In addition, anionic and tautomeric forms of the bases are believed to play crucial roles in nucleic acid catalysis^15,16, RNA-ligand recognition^17,18, and in the therapeutic mechanisms of nucleic acid base analogues¹⁹.

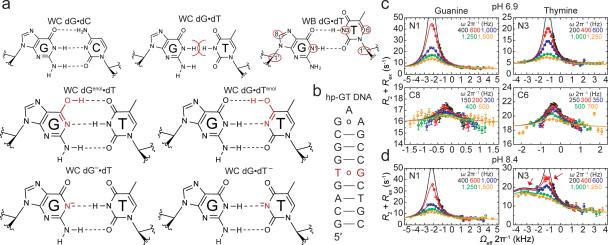
Figure 1. Chemical exchange in dG•dT mispairs.

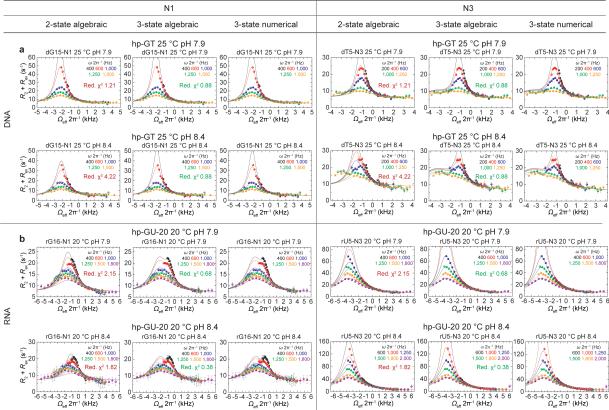
a, WC dG•dC, sterically prohibited WC dG•dT, and WB dG•dT (R_1ρ measured nuclei highlighted in red ovals). Below are four WC-like tautomeric and anionic (implied charge delocalization) bps. b, DNA duplex with a ¹³C/¹⁵N site-labeled dG•dT mispair. c, RD profiles for dG•dT (25 °C and pH 6.9) showing R₂+R_ex as a function of the spin lock offset (Ω_eff 2π⁻¹) and power (ω_SL 2π⁻¹, in insets) with global fits to dG-N1, dG-C8, dT-N3, and dT-C6. Error bars represent experimental uncertainty (one s.d., see Methods). d, RD profiles showing 3-state exchange (25 °C and pH 8.4) and global 3-state fit to dG-N1 and dT-N3.

Despite growing evidence that rare tautomeric and anionic bases play important roles in nucleic acids, their occurrence, stabilities, and biological significance has remained elusive. Characterizing rare tautomeric and anionic bases in polynucleotides is a longstanding problem because such energetically unfavorable species typically exist in low abundance, for short periods of time, and involve movements of protons that are difficult to visualize at the atomic level. NMR relaxation dispersion (RD) techniques^20-22 are making it possible to characterize low-populated (populations of 0.1%-10%) transient (lifetimes of micro-to-milliseconds) states of nucleic acids^23-25 that are often referred to as ‘excited states’ (ES). Here, we use NMR RD to characterize transient WC-like dG•dT and rG•rU mispairs in DNA and RNA that are stabilized by rare tautomeric and anionic bases and obtain evidence that they play universal roles in misincorporation during replication and translation.

Transient WC-like dG•dT tautomer mispair

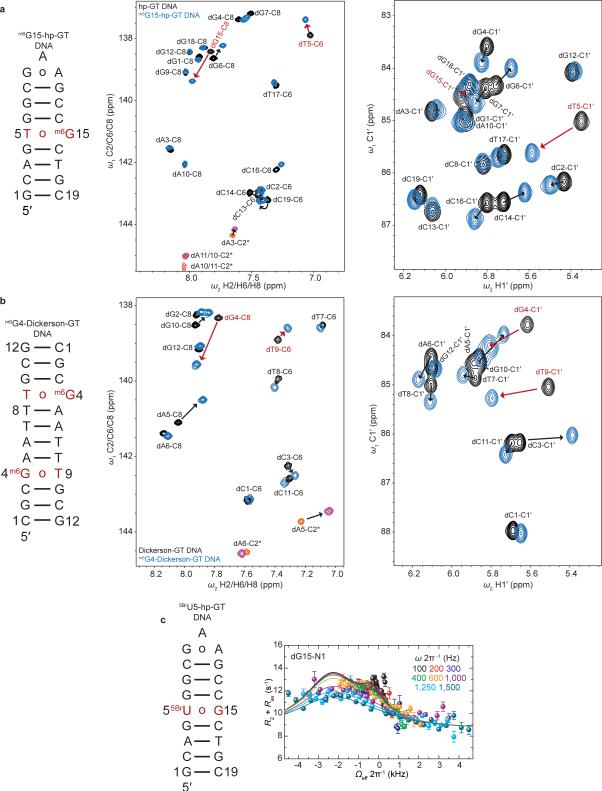
dG•dT mispairs generally adopt a distinct ‘wobble’ (WB) geometry (Fig. 1a) since a WC geometry results in a steric clash between imino protons (Fig. 1a). However, enol tautomers of dG or dT, or their anionic form, can alleviate this steric clash, and allow formation of WC-like dG•dT mispairs (Fig. 1a). Soon after the discovery of the DNA double helix, Watson and Crick hypothesized that such WC-like mispairs could provide a basis for spontaneous mutations⁷. We used NMR rotating frame spin relaxation (R_1ρ) RD^20,26,27 to examine whether wobble dG•dT mispairs can transiently morph into such WC-like dG•dT mispairs in canonical DNA duplexes. For these studies we used a hairpin DNA duplex (hp-GT DNA) containing a site-specifically ¹³C/¹⁵N-labeled dG•dT wobble mispair (Fig. 1b and Extended Data Fig. 1). Exchange between WB and WC dG•dT mispairs entails deprotonation of either dG-N1 or dT-N3 via tautomerization (neutral) or ionization (charged), both of which would induce large changes in N1/3 chemical shifts (CSs) and therefore give rise to significant ¹⁵N RD. In contrast, because a WB-to-WC transition preserves an anti base and C2′-endo sugar pucker, it is expected to induce smaller changes in the sugar (dG-C1′ and dT-C1′) and base (dG-C8 and dT-C6) carbon CSs and therefore induce more limited ¹³C RD. Indeed, we observed very significant ¹⁵N RD at base imino dG-N1 and to a lesser extent at dT-N3, much less significant ¹³C RD at base dG-C8 and dT-C6, and essentially no ¹³C RD at sugar dG-C1′ and dT-C1′ at pH 6.9 and 25 °C (Fig. 1c and Extended Data Fig. 2-3). This unique pattern of RD is consistent with exchange directed toward a transient WC-like mispair (Fig 1a). It is inconsistent with exchange directed toward other base pair (bp) geometries such as Hoogsteen²⁴ or base opened states (Supplementary Discussion 1 and Extended Data Fig. 4). A second exchange process was apparent at pH 8.4 (Fig. 1d) and this will be discussed further below. Similar RD profiles were observed in a different DNA duplex (Extended Data Fig. 1-2), indicating that the observed dG•dT exchange occurs robustly in DNA duplexes.

Figure 2. Characterizing WC-like transient states.

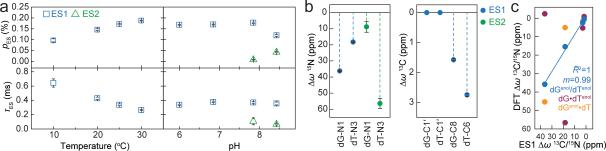
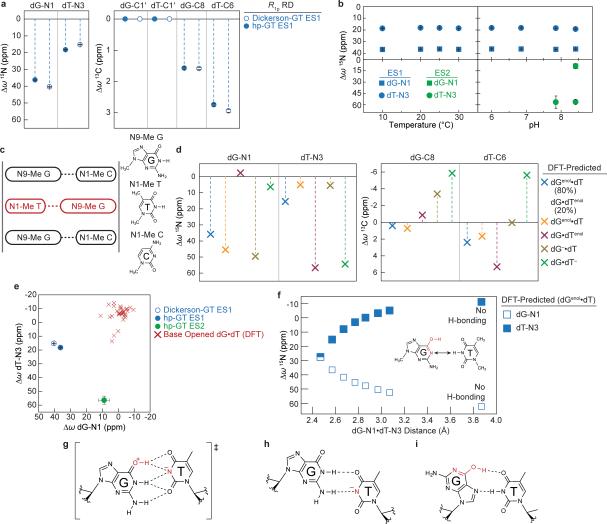
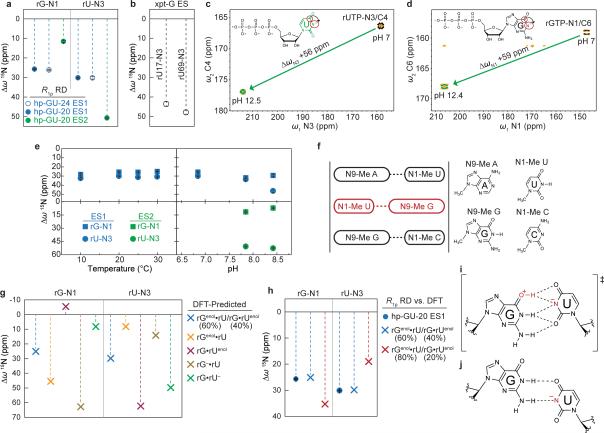
a, Population and lifetime of dG•dT ES1/ES2 measured in hp-GT DNA as a function of temperature (at pH 6.9) and pH (at 25 °C). Errors in fitted parameters denote s.e. from the weighted global fit. b, Differences between the GS (referenced to 0 ppm) and ES CSs (Δω=ω_ES-ω_GS) for hp-GT DNA. c, Measured CSs for ES1 are plotted against DFT-predicted values.

The RD data measured at dG-N1, dT-N3, dG-C8 and dT-C6 could be globally fitted (Supplementary Table 1 and Extended Data Fig. 2-3) to a single exchange process directed toward an excited state (ES1) that has a population (p_ES1) of ~0.17% and a lifetime (t_ES1) of ~0.38 ms (Fig. 2a). ES1 is characterized by ¹⁵N CSs that are significantly downfield shifted for dG-N1 (Δω_N1 +36 ppm) and to a lesser extent dT-N3 (Δω_N3 +18 ppm)(Fig. 2b, Extended Data Fig. 4). The downfield shifted imino nitrogen CSs are unprecedented for nucleic acids, and are directed toward the CSs of bases (dG and dT) that have been deprotonated due to ionization or modifications that lock an enol-like form (Δω ~50-60 ppm)(Extended Data Fig. 5)^28-30. On the other hand, ES1 features much smaller changes in carbon CSs (Fig. 2b), consistent with a WB-to-WC transition.

Figure 3. Mutate-and-CS fingerprinting ES1 and ES2.

a, Multi-state equilibrium between WB and WC-like dG•dT mispairs. ES1/ES2 populations and weights are shown (25 °C and pH 6.9). p_ES2 estimated based on the observed apparent pK_a. b, CS fingerprinting dG•dT ES1/ES2 using chemical modifications and structure-based DFT predictions of CSs. ES1 DFT CSs are given for 80:20 dG^enol•dT:dG•dT^enol weighting. c, ^m6dG•dT structure^12,30. d, dG•^5BrdU^– ES2 stabilized relative to dG•dT^– ES2. Populations and weights (10 °C and pH 6.9) are shown.

It would be highly energetically disfavored to simultaneously deprotonate dG-N1 and dT-N3 when forming ES1. Moreover, though the magnitude of the ES1 N1/N3 downfield CSs strongly suggests deprotonation, it is not as far downfield shifted as expected based on deprotonation of nucleotides in free solution (Extended Data Fig. 5). Therefore, the strongly but incompletely downfield shifted dG-N1 and dT-N3 CSs suggest that ES1 consists of at least two WC-like species in rapid exchange on the NMR timescale in which either dG-N1 (dG^enol•dT or dG^–•dT) or dT-N3 (dG•dT^enol or dG•dT^–) is deprotonated (Fig. 1a). The ES1 population and CSs are largely independent of pH within the pH range of 6.0-7.9 (Fig. 2a and Supplementary Discussion 2). This is inconsistent with exchange directed toward ionic dG^–•dT and dG•dT^– (Extended Data Fig. 5). Rather, the population of ES1 increases with temperature (Fig. 2a) as expected for tautomeric species dG^enol•dT and dG•dT^enol.

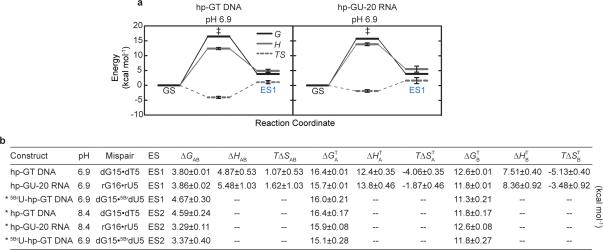
Based on the measured p_ES1 and t_ES1, the free energy difference (ΔG) between GS and ES1 is ~3.8 kcal/mol and the forward free energy barrier (ΔG^‡) is ~16.4 kcal/mol (Extended Data Fig. 6). These values are in good agreement with computationally predicted parameters (2.8-5.6 kcal/mol³¹ and ~17-21 kcal/mol^31,32, respectively) for dG•dT WB-to-WC tautomer transitions.

These computational studies also predict that dG^enol•dT likely exists in fast exchange on the NMR timescale (free energy barrier ~5-6 kcal/mol³¹) with a minor dG•dT^enol (20%) species (Fig. 1a and Supplementary Discussion 3-4). Under these conditions, the measured ES1 CSs would represent a population-weighted average of the two tautomeric states (Methods). We find that all ES1 CSs (dG-N1, dT-N3, dG-C8 and dT-C6) are in quantitative agreement with values predicted by density functional theory (DFT)³³ calculations for a weighted dG^enol•dT(80%)⇌dG•dT^enol(20%) equilibrium (Fig. 2c, 3a).

Transient WC-like dG•dT^– anionic mispair

Interestingly, upon increasing the pH to 8.4, we observed evidence for a second excited state (ES2), which is seen as a second peak in the off-resonance RD profile of dT-N3 (Fig. 1d). Global fitting of this RD data (Extended Data Fig. 2-3) revealed two excited states (ES1 and ES2) that are most likely arranged in a linear topology (ES1⇌dG•dT⇌ES2).

Compared to ES1, ES2 (ΔG^‡ 16.4 and ΔG 4.59 kcal/mol) has a considerably lower population (p_ES2 ~0.04%) and lifetime (t_ES2 ~70 μs) at pH 8.4 (Fig. 2a). The dG-N1 and dT-N3 ES2 CSs are not only ‘swapped’ relative to ES1 such that dT-N3 experiences the larger downfield shift (Δω_N3 +56 ppm) while dG-N1 experiences a smaller downfield shift (Δω_N1 +9 ppm)(Fig. 2b); they are also more asymmetric in favor of a deprotonated dT species. In addition, unlike p_ES1, p_ES2 increases significantly with pH, consistent with ionization and the formation of dG•dT^– (Fig. 3a). The ES2 CSs are in excellent agreement with values computed using DFT assuming a WC-like dG•dT^– (100%) species (Fig. 3a-b). However, we cannot rule out that dG•dT^– is in rapid equilibrium with a WC-like dG^–•dT or an inverted wobble (iWB) geometry^3,34,35 (Extended Data Fig. 4 and Supplementary Discussion 1) that falls outside detection limits (Fig. 3a).

Fingerprinting the dG•dT excited states

We adapted a mutate-and-CS fingerprint strategy^24,25 to test the proposed ES1 and ES2 (Fig. 3a). Here, chemical modifications are used to trap an ES, or induce specific perturbations to the GS⇌ES equilibrium. We trapped ES1 (dG^enol•dT) using the mutagenic base O⁶-methyl-2′-deoxyguanosine (^m6dG)(Fig. 3c and Extended Data Fig. 7) which is known to adopt a distorted WC dG^enol•dT-like mispair^12,30. Relative to the WB, this modification resulted in negligible changes in dG-C1′ (Δω_C1′ −0.1 ppm) and dT-C1′ (Δω_C1′ +0.7 ppm) CSs, and a small downfield shift in dG-C8 (Δω_C8 +1 ppm), consistent with the RD-derived ES1 CSs (Fig. 3b and Extended Data Fig. 7). The modification induced a small upfield shift in dT-C6 (Δω_C6 −0.5 ppm) that is inconsistent with the downfield dT-C6 CS (Fig. 3b) observed by RD. However, such a deviation is expected based on DFT calculations (Δω_C6 −2.3 ppm for dT-C6 in the ^m6dG•T pair)(Supplementary Discussion 5) and can be attributed to minor deviations from an ideal dG^enol•dT WC-like mispair geometry (Fig. 3c)^12,30. Severe line broadening did not permit measurement of the dT-N3 CSs in these non-isotopically enriched samples.

To test the proposed dG•dT^– ES2, we measured the difference in dT-N3 CS between neutral and anionic dTTP (Δω_N3 +55 ppm) and found them to be in excellent agreement with the dT-N3 CS differences measured by RD (Δω_N3 +56 ppm)(Fig. 3b and Extended Data Fig. 5). In addition, we used the mutagenic thymidine-analogue, 5-bromo-2′-deoxyuridine (^5BrdU) to push the equilibrium toward dG•^5BrdU^– (Fig. 3d). This modification lowers the pK_a of ^5BrdU-N3 (~8.6) and favors a WC-like dG•^5BrdU^– geometry at high pH¹¹. This modification increased the population of ES2 (ΔG^‡ 15.1 and ΔG 3.37 kcal/mol) by over two orders of magnitude at the expense of ES1 (ΔG^‡ 16.0 and ΔG 4.67 kcal/mol) while minimally affecting the ES1 and ES2 CSs (Fig. 3b). The consistencies in ES2 CSs between dG•dT^– and dG•^5BrdU^– mispairs further support a dominant WC-like ES2, rather than an iWB bp, in naked DNA. The unaffected ES1 CSs indicate that ^5BrdU does not significantly impact the dG^enol•^5BrdU⇌dG•^5BrdU^enol equilibrium (Fig. 3d) relative to dG•dT (Fig. 3a), consistent with prior computational studies^31,36.

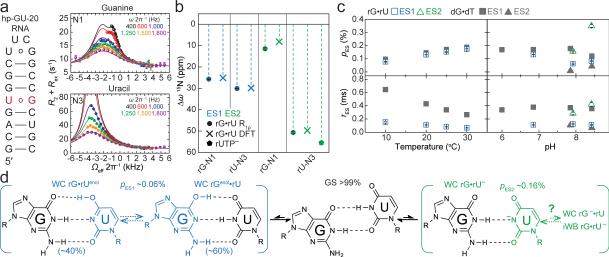
Transient WC-like rG•rU mispairs in RNA

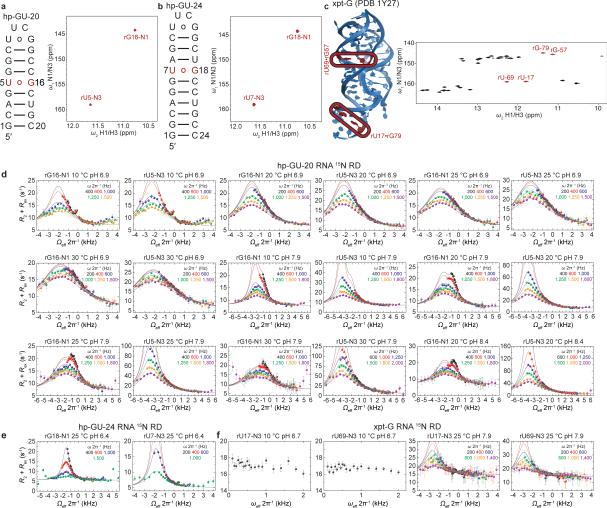
If the observed ESs correspond to WC-like dG•dT mispairs, one would predict that similar ESs should arise in rG•rU mispairs in RNA where WC bps are also readily accommodated within the A-form helix. To test this hypothesis, we carried out analogous pH- and temperature-dependent RD measurements on two RNA duplexes. RD profiles measured for rG•rU in A-form RNA (Fig. 4a and Extended Data Fig. 8) are very similar to those measured for dG•dT in B-form DNA (Fig. 1c-d). Global analyses of the RD data (Supplementary Table 1) revealed an apparent 3-state exchange process at pH ≥7.9 (Extended Data Fig. 3). The RD-derived CSs (Fig. 4b and Extended Data Fig. 9), together with the pH and temperature dependence of the populations and lifetimes (Fig. 4c), are consistent with rG•rU^enol⇌rG^enol•rU as ES1 and rG•rU^– as ES2 (Fig. 4d) as observed in DNA. The rG•rU ES1 forward free energy barrier (ΔG^‡ 15.7 and ΔG 3.86 kcal/mol) is consistent with barriers measured for dG•dT ES1 (16.4 kcal/mol) and computationally predicted barriers for G•U tautomerization (17.1 kcal/mol)³².

Figure 4. Transient tautomeric and anionic WC-like mispairs in A-form RNA.

a, RNA duplex and R_1ρ RD profiles with 3-state global fits to rG-N1 and rU-N3 (20 °C and pH 7.9). b, CSs for rG•rU ES1/ES2 compared to structure-based DFT predictions and rUTP ionization. c, Population and lifetime of rG•rU ES1/ES2 measured as a function of temperature (at pH 6.9) and pH (at 20 °C). dG•dT ES1 and ES2 shown (in grey) for comparison. d, Multi-state equilibrium between WB and WC-like rG•rU mispairs (20 °C and pH 7.9).

Computational studies³⁶ show that dG•dU^enol is stabilized relative to dG•dT^enol. This is predicted to tilt the rapid rG^enol•rU⇌rG•rU^enol equilibrium in favor of rG•rU^enol (40%) in RNA as compared to dG•dT^enol (20%) in DNA (Methods). We find that in RNA, the ES1 rU-N3 CSs are slightly more downfield shifted (Δω_N3 +30 ppm) than rG-N1 (Δω_N1 +26 ppm)(Fig. 4b). Reweighting the DFT-predicted CSs assuming 60:40 ratios of rG^enol•rU:rG•rU^enol gives an excellent fit to RD-derived values (Fig. 4b), and are in better agreement than 80:20 rG^enol•rU:rG•rU^enol (Extended Data Fig. 9). We note that we observe changes in the ES1 CSs at higher pH that suggest a potentially more complex exchange process (Supplementary Discussion 6). As with dG•dT^–, the WC-like rG•rU^– may exist in equilibrium with both a WC-like rG^–•rU and/or an iWB rG•rU^– (Fig. 4d).

rG•rU wobbles are widespread in RNA where they play important structural and functional roles³⁷. We therefore examined whether the ESs observed here would occur in more complex RNA structural contexts. Indeed, the rU-N3 ¹⁵N RD profiles measured for two wobble rG•rU mispairs in a 69-nt Bacillus subtilis guanine riboswitch (Extended Data Fig. 8) provide initial evidence (Δω_N3 +44-47 ppm and p_ES ~0.04% at pH 7.9) for WC-like rG•rU^– mispairs in more complex RNA structures (Extended Data Fig. 9 and Supplementary Discussion 7). Therefore, we can expect that transient WC-like rG•rU mispairs exist robustly across the RNA transcriptome.

Biological implications

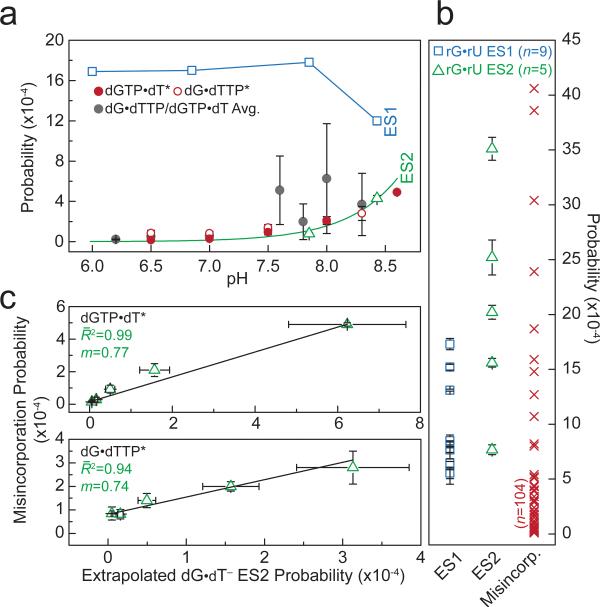
Initial selection of NTPs during replication, and tRNAs during translation, strongly relies on WC stereochemical geometry as a means of discriminating against mispairs^38,39. The low error rate (10⁻³-10⁻⁶) during initial selection accounts for most of the overall fidelity of replication (~10⁻⁶-10⁻¹⁰)^40-42 and translation (~10⁻³-10⁻⁵)^43-45. By stereochemically mimicking the WC geometry, the ES WC-like dG•dT and rG•rU mispairs observed here can provide a mechanism for evading WC fidelity checks during initial substrate selection^1,8,10. The intrinsic probabilities with which WC-like mispairs form have long been suspected as important determinants of substitution mutation probability^8,10. By carrying out the first measurements of the intrinsic probabilities with which WC-like dG•dT and rG•rU mispairs form in native DNA/RNA systems, we are able to obtain unique insights into the mechanisms of misincorporation and the potential roles of ES1/ES2.

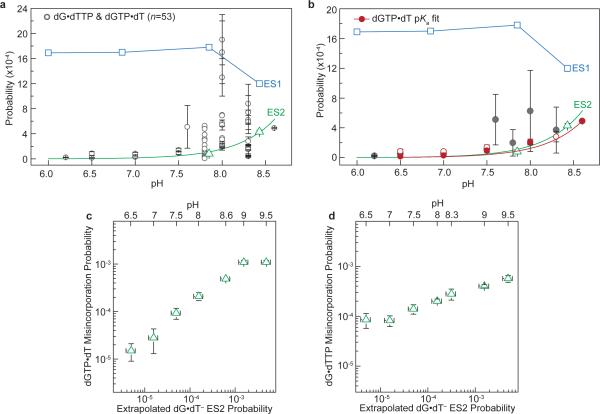
We find that the probabilities with which WC-like dG•dT ES1 and ES2 form in duplex DNA (10⁻³-10⁻⁵) span the dGTP•dT/dG•dTTP misincorporation and base substitution probabilities seen during replication using high-fidelity polymerases with little/no proof-reading capabilities (Fig. 5a, Extended Data Fig. 10 and Supplementary Discussion 8)^46-48. Similarly, the WC-like rG•rU ES1 and ES2 probabilities (10⁻³-10⁻⁴) span the majority of amino acid misincorporation probabilities arising specifically due to rG•rU pairing at any codon position (10⁻³-10⁻⁵)^43,44 (Fig. 5b and Supplementary Discussion 8). Note that some of the amino acid misincorporation probabilities (10⁻⁵) are lower than the measured rG•rU ES2 probability, which could be due to translational proofreading⁴⁵ and/or lower pH conditions that destabilize ES2. These results, together with previous structural studies showing that WB and WC-like mispairs can exist within polymerase^1-3 and ribosome^5,6,13 active sites, strongly suggest that energetic competition between WB and WC-like mispairs is robust and is a key determinant of misincorporation probability during replication and translation (Supplementary Discussion 9). However, additional studies are needed to determine the probabilities with which WC-like mispairs form within the unique environment of polymerases and ribosomes. A recent MD study found that rG^enol•rU tautomers can be stabilized in a ribosome context, but challenges their involvement in decoding errors based on predicted tRNA binding energies⁴⁹.

Figure 5. Correlation between WC-like bps and misincorporation probabilities.

a, dG•dT ES1 (blue square) and ES2 (green triangle) probabilities. pH-dependent dGTP•dT*/dG•dTTP* misincorporation probabilities (errors as published)⁴⁷. Averaged dGTP•dT/dG•dTTP misincorporation and base substitution probabilities; error bars reflect the s.d. (Supplementary Discussion 8). ES2 fit to Henderson-Hasselbalch equation shown as green line (see Methods). A blue line connects ES1 points for visualization purposes. b, rG•rU ES1 (blue square) and ES2 (green triangle) probabilities measured at varied conditions (Supplementary Table 1), and amino acid misincorporation probabilities (red ‘X’) due to rG•rU mispairs (Zhang et al.⁴⁴). c, The probabilities of dGTP•dT/dG•dTTP misincorporation (error as given) by AMV RT (Yu et al.⁴⁷) versus the pK_a-predicted probability (s.e.) of forming a WC-like dG•dT^– mispair as a function of pH.

The pH-dependent dG•dT misincorporation probability^47,48,50 points to the involvement of an anionic species in misincorporation¹. Our results strongly suggest that this species is most likely ES2 dG•dT^– and not the energetically disfavored dG^–•dT. We observe excellent agreement between the pK_a-predicted probability of forming ES2 dG•dT^– and pH-dependent dGTP•dT/dG•dTTP misincorporation probabilities measured for a reverse transcriptase⁴⁷ which lacks any proofreading ability (Fig. 5c and Extended Data Fig. 10). We note that the correlation is reduced at more extreme pH, near the pK_as of other ionizable groups in proteins and DNAs (Extended Data Fig. 10 and Supplementary Discussion 10). We also find that dG•^5BrdU^– enhances the probability of forming a WC-like ES2 (Fig. 3d) and correspondingly results in an ~8-fold increase dG•^5BrdU misincorporation⁴⁷. These data suggest that for this polymerase, misincorporation proceeds predominantly via a WC-like dG•dT^–. It is very likely that parameters such as polymerase types, DNA sequence, and the chemical environment can affect the relative stabilities and lifetimes of the anionic, tautomeric, and WB mispairs³. Therefore we can expect this to affect the flux through distinct misincorporation pathways involving different WC and WB conformations, which may help to explain the broad range of misincorporation probabilities.

Our findings suggest that unconventional enol tautomeric and anionic bases exist robustly in genomes. We anticipate these rare tautomeric and anionic bases play unique roles in DNA damage induction and repair, nucleic acid recognition, chemical modifications of nucleic acids, and catalysis. The NMR methods outlined here can immediately be applied to characterize tautomeric and anionic species, which we believe will not be restricted to dG•dT and rG•rU mispairs, but rather will be widespread across diverse nucleic acid motifs.

METHODS

Sample Preparation

NMR buffer

All duplex DNA and RNA samples were buffer exchanged using a centrifugal concentrator (EMD Millipore) into a solution containing 25 mM sodium chloride (100 mM sodium chloride for Dickerson-GT DNA), 15 mM sodium phosphate, 0.1 mM EDTA, and 10% D₂O with variable pH (6.0, 6.4, 6.8, 6.9, 7.9). pH values of 8.4 were obtained for hp-GT DNA and hp-GU-20 RNA samples by direct titration of pH 7.9 samples with filtered 0.5 M NaOH solution. Monovalent ion concentration subsequently increased by a small amount proportional to the NaOH titrated in but did not affect DNA/RNA conformation as confirmed by NMR. Natural isotopic abundance oligonucleotide sample concentrations ranged from 2-3.5 mM. ¹³C/¹⁵N-labeled oligonucleotide sample concentrations ranged from 0.7-3.5 mM. xpt-G riboswitch sample was diluted to ~30 μM in a solution containing saturated guanine, denatured, and annealed on ice. Sample was buffer exchanged against either potassium acetate (pH 6.7) or sodium phosphate (pH 7.9) buffer and concentrated to 0.7-1.7 mM. Mg²⁺ was titrated in until total concentration was ~5 mM.

Site-specifically ¹³C/¹⁵N-labeled DNA samples

Selectively ¹³C/¹⁵N-labeled DNA samples (hp-GT DNA, ^5BrU5-hp-GT and ^8BrG15-hp-GT DNA) were purchased from the Yale Keck Oligonucleotide Synthesis Facility and were synthesized using commercially available 2′-deoxyguanosine DMT-phosphoramidite (98% ¹³C10, 98% ¹⁵N5) and 2′-deoxythymidine phosphoramidite (98% ¹³C10, 98% ¹⁵N2) purchased from Cambridge Isotope Labs. hp-GT DNA was selectively ¹³C/¹⁵N-labeled at dT5 and dG15, ^5BrU5-hp-GT DNA was ¹³C/¹⁵N-labeled at dG15, and ^8BrG15-hp-GT was ¹³C/¹⁵N-labeled at dT5. Samples were purified using RP-HPLC prior to buffer exchange. NMR experiments were used to confirm native folding of hp-GT, ^5BrU5-hp-GT, and ^8BrG15-hp-GT DNA constructs.

Enzymatic synthesis of ¹³C/¹⁵N-labeled DNA samples

The Dickerson-GT DNA sample was synthesized in vitro using uniformly enriched ¹³C/¹⁵N dGTP and dTTP (Silantes GmbH) as previously described⁵¹. Reaction mixture was centrifuged and filtered to remove excess pyrophosphate and concentrated down to 1 mL in a 3 kDa molecular weight cut-off centrifugal concentrator (EMD Millipore). Sample was mixed with 1 mL of a formamide-based denaturing loading dye, denatured at 95 °C for 5 min, and loaded onto a 33×102 cm sequencing gel (20% polyacrylamide/8M urea) and run for 12 hours to resolve target oligonucleotide from template and other nucleic acid species. Target band was shadowed briefly using a UV hand-lamp and excised prior to gel electroelution (Whatman, GE Healthcare), followed by ethanol precipitation. Sample purity was confirmed using gel electrophoresis (20% polyacrylamide/8M urea) stained with SybrGOLD prior to buffer exchange.

Enzymatic synthesis of ¹³C/¹⁵N-labeled RNA samples

The hp-GU-20, hp-GU-24 and xpt-G riboswitch RNA samples were prepared using in vitro transcription as previously described²⁵ using uniformly enriched ¹³C/¹⁵N ribonucleotide triphosphates (hp-GU-20 RNA: rGTP & rUTP only, hp-GU-24: All and xpt-G: All). Purification was carried out as described above for ¹³C/¹⁵N-labeled DNA construct.

Unlabeled and unlabeled-modified DNA samples

hp-GT and Dickerson-GT DNA constructs at natural isotopic abundance were purchased from Integrated DNA Technologies. The O⁶-Methyl-2′-deoxyguanosine mismatch constructs (^m6G15-hp-GT and ^m6G4-Dickerson-GT DNA) were purchased from the Yale Keck Oligonucleotide Synthesis Facility. hp-GT and Dickerson-GT DNA constructs were desalted prior to buffer exchange. Unlabeled-modified samples were purified using RP-HPLC prior to buffer exchange.

Isotopically enriched dNTP and rNTP samples

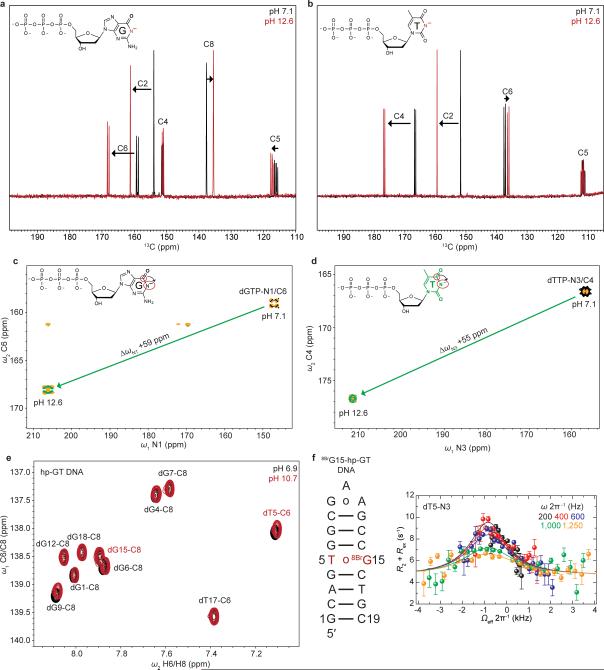
Uniformly ¹³C/¹⁵N enriched dGTP, dTTP, rGTP and rUTP samples were purchased (Silantes GmbH) and added to an NMR buffer (25 mM sodium chloride, 15 mM sodium phosphate, 0.1 mM EDTA and 10% D₂O at pH 6.9). Sample was adjusted to pH ~12.5 directly using 5 M NaOH.

NMR experiments

Resonance assignment

The CS assignment for DNA and RNA constructs were obtained using aromatic [¹³C, ¹H], aliphatic [¹³C, ¹H], imino [¹⁵N, ¹H] heteronuclear and [¹H, ¹H] NOESY homonuclear correlation experiments. The data for all DNA constructs were acquired on an 18.8T Agilent spectrometer equipped with a triple resonance HCN cryogenic probe, for the uniformly ¹³C/¹⁵N-labeled hp-GU-24 RNA construct on a 14.1T Bruker Avance spectrometer equipped with a triple-resonance HCN cryogenic probe, and for the xpt-G RNA riboswitch on a 14.1T Agilent spectrometer equipped with a Bruker HCPN cryogenic probe. All data were processed and analyzed using the software NMRpipe⁵² and SPARKY (T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco), respectively. Resonance assignment for exchangeable and non-exchangeable ¹H was performed using the 2D [¹H, ¹H] WATERGATE NOESY experiment⁵³ (mixing time 250 ms) as described previously^27,54, and their covalently bonded ¹³C/¹⁵N nuclei were assigned using heteronuclear single/multiple quantum coherence correlation experiments (HSQC or HMQC). For the labeled RNA constructs conventional HSQC experiments⁵³ were acquired for all spins, while for unlabeled DNA constructs conventional HSQC was used for the aliphatic C1′ spins and SOFAST-HMQC^55,56 were employed for the imino and aromatic spins.

¹⁵N R_1ρ relaxation dispersion

1D ¹⁵N R_1ρ RD experiments^27,57 targeting imino nitrogen resonances of interest were carried out at 14.1T (hp-GT, ^5BrU5-hp-GT, Dickerson-GTDNA and hp-GU-24 RNA) and 16.4T (hp-GU-20 RNA) as previously described⁵⁷. Raw data were processed using NMRpipe⁵² to generate a series of peak intensities. On- and off-resonance R_1ρ RD profiles were recorded using spinlock powers (ω_SL 2π⁻¹) ranging from 100-2000 Hz, with the absolute offset frequencies (Ω 2π⁻¹ Hz) ranging from 0-3.5× the applied spinlock power (Supplementary Table 1). Offset frequencies greater than 3.5× the given spinlock power were not used owing to significant R₁ relaxation contributions²⁷. Magnetization of the spins of interest was allowed to relax under an applied spinlock for the following durations: [0 – 120 ms] for N1/N3 of hp-GT, ^5BrU5-hp-GT, Dickerson-GT DNA and hp-GU-24 RNA and [0 – 100 ms] for N1/N3 of hp-GU-20 RNA, and [0 – 80 ms], [0 – 74 ms], [0 – 68 ms] for N3 of the xpt-G riboswitch.

¹³C R_1ρ relaxation dispersion

¹³C R_1ρ RD experiments targeting carbon resonances of interest were carried out at 14.1T as previously described^24,27. On- and off-resonance R_1ρ RD profiles were measured using spinlock powers (ω_SL) ranging from 150-3500 Hz, with the absolute offset frequencies (Ω 2π⁻¹, Hz) ranging from 0-3.5× the applied spinlock power (Supplementary Table 1). Magnetization of the spins of interest were allowed to relax under an applied spinlock for the following durations: [0 – 60 ms] for C1′/C6/C8 of hp-GT DNA and C1′ of Dickerson-GT, [0 – 50 ms] for C6/C8 Dickerson-GT DNA.

¹³C/¹⁵N CSs of ionized dNTPs and rNTPs

Carbon and nitrogen CSs of neutral and deprotonated dNTPs and rNTPs were collected at 25 °C and pH ~6.9 and ~12.5 using a 2D [¹⁵N, ¹³C] HMQC experiment on a 14.1T Agilent spectrometer equipped with a Bruker HNCP cryoprobe.

Analysis of R_1ρ data

Fitting of ¹³C and ¹⁵N R_1ρ data

R_1ρ values were calculated by fitting the decay of peak intensity versus relaxation delay to a monoexponential⁵⁸. Errors in R_1ρ were estimated using spectral noise and duplicate R_1ρ data points using a suite of Mathematica notebooks⁵⁸. Measured on- and off-resonance R_1ρ data were globally fit to algebraic equations describing N-site chemical exchange using a Levenberg-Marquardt method, weighted to the experimental error in the R_1ρ data. For 2-state exchange, data was fit to the Laguerre equation (1)⁵⁹ under the valid assumption that the populations are highly asymmetric, such that p_GS >> p_ES where p_ES < 0.3. For the 3-state chemical exchange model where k_BC = k_CB = 0, data was fit to both the 3-state Laguerre equation (2) as well as the general 3-state equation (3)⁵⁹, where p_GS >> p_ES and p_ES < 0.1. Fitted parameters derived from Eqn. 2 and Eqn. 3 are in excellent agreement with one another (Supplementary Table 1). Statistical tests, F-Test and Akaike information criterion (AIC), were used to select the best-fit N-state exchange model²⁴ (Extended Data Fig. 3). ¹³C and ¹⁵N RD data from the dG•dT or rG•rU mispair resonances for each construct, at each temperature and pH condition were fitted globally (where k_ex and p_B are the shared-parameters) when possible. In the cases where ¹⁵N RD data was available but ¹³C RD data showed no chemical exchange, did not exhibit 3-state exchange, or was not collected, the ¹⁵N N1/N3 RD data were globally fitted as described above. Bloch-McConnell⁶⁰ (B-M) numerical simulations were used to validate the algebraic approximations’ for 2- and 3-state exchange scenarios.

• (1)
  2-state Laguerre equation^59,61:

  $$R_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +\frac{{\sin }^2\theta p_{GS}{p}_{ES1}\Delta {\omega }_{ES1}^2{k}_{ex1}}{\left\{{\omega }_{GS}^2{\omega }_{ES1}^2∕{\omega }_{eff}^2+k_{ex1}^2-{\sin }^2\theta p_{GS}{p}_{ES1}\Delta {\omega }_{ES1}^2\left(1+\frac{2k_{ex1}^2\left(p_{GS}{\omega }_{GS}^2+p_{ES1}{\omega }_{ES1}^2\right)}{{\omega }_{GS}^2{\omega }_{ES1}^2+{\omega }_{eff}^2{k}_{ex1}^2}\right)\right\}}$$
• (2)
  3-state Laguerre equation with no minor exchange²⁵:

  $$R_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +{\sin }^2\theta \left(\frac{p_{GS}{p}_{ES1}\Delta {\omega }_{ES1}^2{k}_{ex1}}{\left\{{\omega }_{GS}^2{\omega }_{ES1}^2∕{\omega }_{eff}^2+k_{ex1}^2-{\sin }^2\theta p_{GS}{p}_{ES1}\Delta {\omega }_{ES1}^2\left(1+\frac{2k_{ex1}^2\left(p_{GS}{\omega }_{GS}^2+p_{ES1}{\omega }_{ES1}^2\right)}{{\omega }_{GS}^2{\omega }_{ES1}^2+{\omega }_{eff}^2{k}_{ex1}^2}\right)\right\}}+\frac{p_{GS}{p}_{ES2}\Delta {\omega }_{ES2}^2{k}_{ex2}}{\left\{{\omega }_{GS}^2{\omega }_{ES2}^2∕{\omega }_{eff}^2+k_{ex2}^2-{\sin }^2\theta p_{GS}{p}_{ES2}\Delta {\omega }_{ES2}^2\left(1+\frac{2k_{ex2}^2\left(p_{GS}{\omega }_{GS}^2+p_{ES2}{\omega }_{ES2}^2\right)}{{\omega }_{GS}^2{\omega }_{ES2}^2+{\omega }_{eff}^2{k}_{ex2}^2}\right)\right\}}\right)$$
• (3)
  3-state general equation with no minor exchange^59,62:

  $$R_{1\rho }=R_1{\cos }^2\theta +R_2{\sin }^2\theta +{\sin }^2\theta \left(\frac{k_{\mathrm{GS}\to \mathrm{ES}1}\Delta {\omega }_{ES1}^2}{{\Omega }_{ES1}^2+{\omega }_{SL}^2+k_{\mathrm{ES}1\to \mathrm{GS}}^2}+\frac{k_{\mathrm{GS}\to \mathrm{ES}2}\Delta {\omega }_{ES2}^2}{{\Omega }_{ES2}^2+{\omega }_{SL}^2+k_{\mathrm{ES}2\to \mathrm{GS}}^2}\right)$$

in which R₁ and R₂ are the intrinsic longitudinal and transverse relaxation rates (s⁻¹). The exchange rates are defined as k_exi = k_GS→ESi + k_ESi→GS, where k_GS→ESi = p_ESik_exi and k_ESi→GS = p_GSk_exi and where i = 1 or 2. The CS difference between the GS and ESs is given by Δω_ESi = Ω_ESi - Ω_GS, where Ω = Ω_obs - ω_rf defines the resonance offset from the carrier frequency (ω_rf), Ω_obs = (Ω_GSp_GS + Ω_ES1p_ES1) or Ω_obs = (Ω_GSp_GS + Ω_ES1p_ES1 + Ω_ES2p_ES2), and where Ω_obs ≈ Ω_GS when p_GS >> p_ESi, as is the case in the ESs measured. The average effective spinlock field in the rotating frame is given by ω²_eff = Ω² + ω²_SL and ω²_GS = (Ω_GS – ω_rf)² + ω²_SL, ω²_ESi = (Ω_ESi – ω_rf)² + ω²_SL and ω_SL is the spinlock power. The tilt angle in the rotating frame is given by θ = arctan(ω_SL/Ω).

Analysis of the 3-state exchange model

We repeated measurements of RD profiles for hp-GT dG-N1 and dT-N3 at pH 8.4 and 25 °C on a different spectrometer and also obtained data that is consistent with 3-state exchange (Extended Data Fig. 2 and Supplementary Table 1). In addition, we collected one additional spinlock power (800 Hz) for both resonances, and find that the inclusion of this extra spinlock power has negligible effect on the fitted exchange parameters indicating that they are robustly determined by the measured data. We note that differences in the RD profiles and fitted parameters between spectrometers are largely within error, with minor differences likely arising due to small differences in temperature and/or spinlock calibrations.

The dT-N3 resonance of hp-GT DNA at 25 °C and pH 7.9 was also individually refit assuming both 2-state and 3-state exchange. The individual dT-N3 3-state fit gave very similar fitted parameters as the dT-N3 in the 3-state global fit with dG-N1. The F-test (at 0.05 significance level) favored the 3-state individual fit model over the 2-state individual fit model. AIC also favored the 3-state model, estimating the 3-state model to be 3.1×10¹⁵ times more likely to be the correct model than the 2-state model. The individual 2-state and 3-state fits to dG-N1 RD profiles give similar agreement (reduced χ² ~0.83) when the ES2 CS is fixed based on the globally fitted value; however, statistical tests slightly favor the simpler model (AIC favors 2-state by approximately two-fold).

The 3-state model is supported by statistical tests (F-test and AIC favor the 3-state over 2-state exchange model) and also by B-M simulations (data not shown) for the hp-GT dG-N1 and dT-N3 data at pH 7.9. Here, R_1ρ values were simulated, noise corrupted, and evaluated for the ability to report on the 3-state exchange following the procedure reported in Bothe et al.⁶³.

Bloch-McConnell 3-state numerical simulations

Parameters derived from the algebraic 3-state fits, along with the ω_rf and ω_SL, were used to simulate numerical solutions to the 3-state B-M equations⁶⁰ (Extended Data Fig. 3). The B-M simulations were carried out using a procedure similar to that described recently for 2-state exchange⁶³. Simulations were carried out assuming a 0.25 second relaxation delay under the applied ω_SL.

Thermodynamic analysis of R_1ρ RD-derived parameters

Temperature-dependent analysis of forward and reverse exchange rates in the site-labeled (dG15•dT5 ¹³C/¹⁵N) hp-GT DNA and G/U labeled hp-GU-20 RNA samples were carried out as previously described²⁴. This analysis employed the ES populations and exchange rates obtained based on 2-state global fitting of dG15-N1 and dT5-N3 RD data measured in hp-GT DNA at 10, 20, 25 and 30 °C. For hp-GU-20 RNA, the analysis employed populations and exchange rates obtained based on 2-state and 3-state global fitting of rG16-N1 and rU5-N3 RD data measured at 10, 20, 25 and 30 °C at pH 6.9. Errors in the fitted thermodynamic parameters are given by weighted fits of the modified van't Hoff equation²⁴ to the RD-derived forward and reverse exchange rates and their errors. The NMR sample temperature was calibrated using 99.8% methanol-d₄ (Cambridge Isotope Laboratories) using the equation T = −16.7467(Δδ)² – 52.5130(Δδ) + 419.1381, where Δδ is the difference in CS (ppm) between the hydroxyl and methyl proton⁶⁴.

Density functional theory geometry optimizations and CS calculations

All DFT calculations³³ were performed using Gaussian 09c (Gaussian, Inc.)⁶⁵ and carried out on the University of Michigan's Advanced Research Computing HPC cluster, Flux, as previously described²⁴ with minor modifications to DFT method and basis set used. Geometry optimizations were carried out using the empirical exchange-correlation functional, M06-2X⁶⁶, with the 6-31+G(d,p) basis-set. The ¹³C and ¹⁵N isotropic magnetic shielding (σ_13C and σ_15N) were calculated using the GIAO method with M06-2X/6-31+G(d,p). CSs of the nucleobases (δ_13C and δ_15N) were calculated by δ_13C/15N = σ_13C/15N – σ_TMS/NH3, where σ_TMS and σ_NH3 are the isotropic magnetic shieldings calculated for the reference compounds trimethylsilane (¹³C) and NH₃ (¹⁵N), respectively.

Input structures for DFT calculations

We generated idealized B-/A-form helices corresponding to our sequence contexts (hp-GT DNA and hp-GU-24 RNA) using make-NA (J. Stroud, make-NA, http://structure.usc.edu/make-na/server.html 2011). The duplexes were truncated to the trinucleotide step centered on the target mispair (GTG/CGC for hp-GT DNA and GUA/UGC for hp-GU-24 RNA). The sugar and phosphate moieties were removed and replaced with a methyl for i (dG•dT or rG•rU mispair), i+1, and i−1 base pairs to save on computational time. Although the structures lack a 2′-deoxyribose or ribose sugar moieties, they will be denoted as dG•dT or rG•rU to avoid confusion. All heavy atoms were frozen for the i+1 and i−1 base pairs while geometry optimizations were carried out for protons and heavy atoms of the central dG•dT or rG•rU base pair as well as the protons of the i+1/i−1 pairs. We performed full geometry optimizations on: dG•dT and rG•rU GS WB pairs, dG^enol•dT, dG•dT^enol, rG^enol•rU, rG•rU^enol, and dG^–•dT and rG^–•rU ES WC-like pairs. All converged to the expected WB or WC-like geometries. In the instance where the geometry optimizations of dG•dT^– and rG•rU^– starting states failed to converge to a stable WC-like dG•dT^–/rG•rU^– geometry (and instead converged to an iWB geometry, in vacuum), the WC-like dG•dT^enol/rG•rU^enol states were converted to dG•dT^–/rG•rU^– and geometry optimizations were carried out on the protons only. CSs for each state were calculated and later used in calculating population weighted CSs assuming different populations of these mispair species. In addition, while the sugar moieties were truncated to methyl groups to save on computation time, it should be noted that previous DFT studies of nucleotides have shown that tautomerization, primarily of pyrimidines, can have an affect on the sugar conformation⁶⁷. However, we can rule out large changes in sugar pucker arising in ES1 based on the negligibly small chemical exchange contributions to both dG-C1′ and dT-C1′ (see Extended Data Fig. 2) and only very small changes in dG-C1′ and dT-C1′ CSs upon locking the enol-like form with ^m6dG•dT (|Δω_C1′| ≤ 0.7 ppm, see Fig. 3b and Extended Data Fig. 7). Finally, while the CSs of the anionic pairs are predicted assuming planar pair geometry, prior computational studies of G•T^– and G^–•T nucleobase pairs in isolation have shown that they can favor non-planar and non-WC geometry³⁵.

dG^enol•dT distance dependent DFT calculations

We carried out distance dependent DFT calculations⁶⁸ on a pair of WC-like dG^enol•dT N1/N9-methyl nucleobases in vacuum using the M06-2X method and 6-31+G(d,p) basis-set, as described above. The geometry of a dG•dT wobble pair and dG^enol•dT WC-like pair was optimized with no constraints prior to CS calculations. The ideal N1-N3 distance of the dG^enol•dT WC-like mispair was then manually varied from 2.44Å to 3.8Å in increments of 0.1Å from 2.44-3.04Å and then to 3.8Å (Extended Data Fig. 4). At every increment the proton positions alone were optimized and CSs were calculated relative to an optimized dG•dT wobble base pair.

Population-weighted average DFT-predicted CS calculations

Based on the computationally predicted energetic differences between interconverting dG^enol•dT and dG•dT^enol base mispairs in water (ΔG 0.7-0.8 kcal/mol)³¹ and in a weakly polar medium (ΔG 0.99 kcal/mol)⁶⁹, we can predict that the dG•dT ES1 CSs represent a population weighted average between interconverting dG^enol•dT(~80%)⇌dG•dT^enol(~20%) states. Thus, the DFT-predicted CSs for dG^enol•dT and dG•dT^enol were summed in a population-weighted manner. It is noted that the computationally predicted energetic stabilities of the tautomeric states differ when calculated in water versus vacuum, or a weakly polar medium, with the values predicted in water giving the greatest agreement with our experimental results.

In the case of rG•rU ES1, computational studies have shown that dG•dU^enol is ~1 kcal/mol more stable than dG•dT^enol in a DNA fragment³⁶, suggesting that an rG^enol•rU⇌rG•rU^enol equilibrium should be titled slightly more towards rG•rU^enol than dG•dT^enol in DNA. We can qualitatively estimate the relative stability between rG^enol•rU and rG•rU^enol to be 60:40 based on a best fit to the RD-derived CSs.

pK_a fitting and probability estimation

The apparent pK_as for hp-GT ES2, ^5BrU-hp-GT ES2, and dGTP•dT misincorporation (pH 6.5-8.6) were fit to the Henderson-Hasselbalch equation using a Monte-Carlo (MC) approach. Here, 10⁶ p_Bs at pH 7.9 and/or 8.4 were selected from a Gaussian distribution with mean p_B value and standard deviation representing the uncertainty in p_B based on fitting of the RD data. 10⁶ fits to Eqn. 4 were then carried out assuming these p_B values to generate 10⁶ pK_as.

$$p_B=\left(\frac{{10}^{pH-pKa}}{1+{10}^{pH-pKa}}\right)$$ (4)

Where p_B is the probability of forming ES2 or dGTP•dT misincorporation probability at a given pH. The resulting fitted pK_a values were fitted to a Gaussian distribution. The mean value of the Gaussian distribution is the reported pK_a value and the standard deviation is assumed to be the error. An analogous approach was used to back-calculate predicted p_Bs at a given pH using the pK_a derived by the above method.

Extended Data

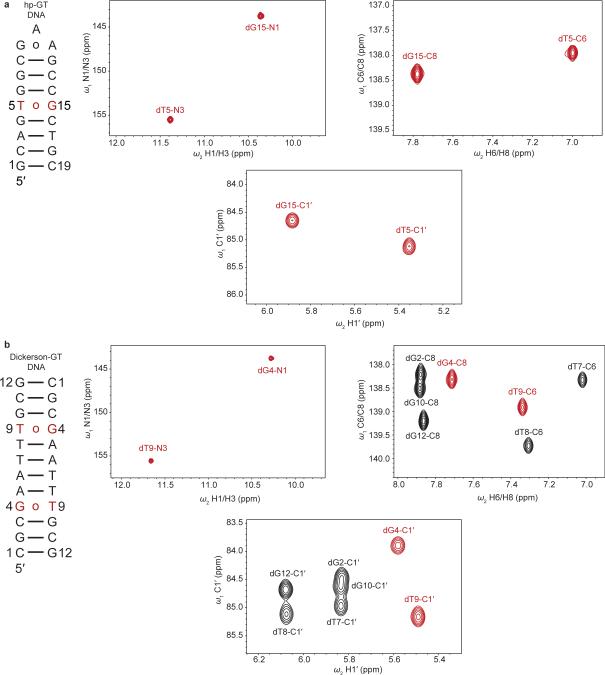
Extended Data Figure 1. NMR spectra of site- and selectively-labeled dG•dT mispair DNA constructs.

a-b Shown are the a, hp-GT DNA and b, Dickerson-GT constructs with ¹³C/¹⁵N labeled dG•dT mispairs highlighted in red along with 2D imino [¹⁵N, ¹H] HSQC, 2D aromatic [¹³C, ¹H] HSQC and 2D C1′ [¹³C, ¹H] HSQC spectra (pH 6.9, 25 °C).

Extended Data Figure 2. Rotating frame relaxation dispersion profiles of dG•dT mispairs in hp-GT and Dickerson-GT DNA constructs.

RD profiles showing chemical exchange (R₂+R_ex) in the dG•dT mispair as a function of the spin lock offset (Ω_eff 2π⁻¹) and spin lock power (ω_SL 2π⁻¹, color coded in insets). Shown are a, ¹⁵N and b, ¹³C RD profiles in hp-GT DNA in hp-GT. On-resonance profiles showing solid and dashed black lines indicate fits assuming no chemical exchange (solid) and simplified 2-state exchange process (dash). The hp-GT dG15-N1 and dT5-N3 in brackets denote duplicate profiles (with an additional 800 Hz spinlock power for each) collected at pH 8.4 and 25 °C collected on a different spectrometer from the preceding profiles. c, ¹⁵N and ¹³C RD profiles for Dickerson-GT. Sample conditions are indicated on each profile. Error bars represent experimental uncertainty (one s.d., see Methods).

Extended Data Figure 3. Multiple site exchange comparison and numerical solutions.

Global fitting of a, hp-GT DNA and b, hp-GU-20 RNA N1 and N3 RD profiles to 2-state algebraic equation (Eqn. 1, fit reduced χ² shown in inset) and 3-state algebraic equation (Eqn. 2, fit reduced χ² shown in inset). Numerical solutions to the Bloch-McConnell 3-state equations assuming no minor exchange and input exchange parameters obtained based on the 3-state algebraic fit are also shown to establish the validity of the 3-state expression under these exchange scenarios (Eqn. 2, see Methods). Sample conditions are indicated on each profile. Error bars represent experimental uncertainty (one s.d., see Methods).

Extended Data Figure 4. Chemical shift fingerprinting dG•dT excited states.

a, RD-derived dG15-N1 and dT5-N3 CSs (CSs) (referenced to GS WB) for ES1 (25 °C and pH 6.9) and ES2 (25 °C and pH 8.4) of hp-GT and ES1 of Dickerson-GT (25 °C and pH 6.9) are shown. Errors in all RD-derived fitted parameters (eg. Δω) denote s.e. from the weighted global fit (see Methods). b, RD-derived hp-GT dG•dT ES1 (blue) and ES2 (green) ¹⁵N CSs are shown as a function of temperature and pH for both dG15-N1 (square) and dT5-N3 (circle). c, Scheme used to calculate CSs using DFT (see Methods). Shown is a schematic representation of scenario used to for calculating CSs using DFT. Idealized B-form DNA helix is generated to give a central dG•dT mispair (red) that is flanked by canonical dG•dC pairs, analogous to the hp-GT construct. Residues are trimmed to 1-/9-methyl bases and i+1/i−1 pairs are frozen in place for subsequent geometry optimizations and NMR CS calculations. d, DFT-calculated CSs (referenced to an energy optimized WB geometry) are shown for various tautomeric and anionic configurations, where dG^enol•dT/dG•dT^enol represents population weighted average over dG^enol•dT (80%) and dG•dT^enol (20%). e, RD-derived ES1 and ES2 CSs are plotted against DFT-calculated CSs of base opened dG•dT mispairs, taken from X-ray structures and pruned to 1-/9-methyl bases. f, DFT-calculated CSs (referenced to an energy optimized WB geometry) are plotted as a function of dG-N1- -dT-N3 inter-atomic distance for a WC-like dG^enol•dT tautomeric pair. g, Computational studies^31,32,70 predict that the tautomeric pathway proceeds via a planar dG⁺•dT⁻ ion pair (charge delocalization is implied) that is highlighted by a network of five H-bonds. h, Predicted pair geometry of an anionic dG•dT^– inverted wobble. Deprotonated dT-N3 is highlighted in red (charge delocalization is implied). i, Predicted pair geometry of a dG^enol•dT Hoogsteen mispair.

Extended Data Figure 5. Attempts to trap anionic dG.

a, 1D ¹³C spectra (without ¹³C-¹³C homonuclear decoupling) of the aromatic carbon region of protonated dGTP (black) and anionic dGTP (red) showing CS perturbations induced upon deprotonation of dGTP-N1. b, ¹³C spectra (without ¹³C-¹³C homonuclear decoupling) of the aromatic carbon region of protonated dTTP (black) and anionic dTTP (red) showing CS perturbations induced upon deprotonation of dTTP-N3. c, 2D [¹⁵N, ¹³C] HMQC spectra of dGTP showing CS of dGTP-N1 induced upon deprotonation. The spectra is rotated by 90°, to depict ¹⁵N CS along x-axis for visualization purposes. Red circles on inset structure highlight measured resonances (C6 and N1). d, 2D [¹⁵N, ¹³C] HMQC spectra of dTTP showing CS perturbation of dTTP-N3 induced upon deprotonation. The spectra is rotated by 90°, to depict ¹⁵N CS along x-axis for visualization purposes. Red circles on inset structure highlight measured resonances (C4 and N3). e, hp-GT DNA spectra of the dG/dT aromatic carbons upon increase in pH from 6.9 (black) to 10.7 (red). Minor upfield CSs are observed for dT5-C6 and dG9-C8, but not dG15-C8, indicating the dT5 in the dG•dT mispair is likely undergoing deprotonation and not the paired dG15. f, ^8BrG15-hp-GT DNA construct bearing a ¹³C/¹⁵N site-labeled dT5 paired with a 8-bromo-2′-deoxyguanosine is shown (left) along with the ¹⁵N RD profile for the paired dT5-N3. Error bars represent experimental uncertainty (one s.d., see Methods).

Extended Data Figure 6. Kinetic-thermodynamic plots and parameters.

a, Kinetic-thermodynamic diagram for exchange between GS and ES1 via a transition state for hp-GT DNA ES1 (left) and hp-GU-20 RNA ES1 (right), showing activation (G^‡) and net free energy (G), enthalpy (H), and entropy (TS) changes (referenced to 0). b, Kinetic-thermodynamic parameters derived from RD data. Asterisk denotes parameters calculated using only a single temperature (see Methods), wherein enthalpic and entropic parameters cannot be derived. Here, dG15•dT5 ES2 values were calculated at 25.05 °C, rG16•rU5 ES2 values were calculated at 20.05 °C, and dG15•^5BrdU5 ES1 and ES2 values were calculated at 10.05 °C. Error is given by the s.e. of the weighted global fits of the corresponding RD profiles. Error is propagated using the respective uncertainties in k_ex and p_ES.

Extended Data Figure 7. Trapping or stabilizing dG•dT ES1 and ES2.

a, ^m6G15-hp-GT DNA construct is shown (left) where dG15 is methylated at the O⁶ position to trap a near-WC “dG^enol•dT”-like geometry (Fig. 3c). CS perturbations induced in the aromatic (center) and sugar (right) resonances upon O⁶-methylation (blue) with the hp-GT DNA spectra (black) with the resonances for the dG•dT mispair from hp-GT DNA in red. ^m6dG•dT mispair and CSs are highlighted in red. b, Similarly, ^m6G4-Dickerson-GT DNA construct is shown (left) where dG4 is O⁶-methylated to trap a WC-like state, with similar color scheme as a. c, ^5BrU5-hp-GT DNA construct bearing a ¹³C/¹⁵N site-labeled dG15 paired with a 5-bromo-2′-deoxythymidine is shown (left) along with the ¹⁵N RD profile for the paired dG15-N1. Error bars represent experimental uncertainty (one s.d., see Methods).

Extended Data Figure 8. Rotating frame relaxation dispersion profiles for rG•rU mispairs in hp-GU-20, hp-GU-24 and xpt-G RNA constructs.

a-b RNA constructs and the imino [¹⁵N, ¹H] HSQC zoomed into the rG•rU wobble region of the spectra for hp-GU-20 and hp-GU-24. rG•rU mispair resonances are shown in red. c, The Bacillus subtilis guanine binding riboswitch (xpt-G RNA)⁷¹ construct and full imino [¹⁵N, ¹H] HSQC of folded and guanine ligand-bound riboswitch. rG•rU mispair resonances are shown in red. d-f, ¹⁵N RD profiles for d, hp-GU-20 e, hp-GU-24 and f, xpt-G riboswitch RNA. Error bars represent experimental uncertainty (one s.d., see Methods).

Extended Data Figure 9. CS fingerprinting rG•rU excited states.

a, RD-derived rG16-N1 and rU5-N3 CSs (referenced to GS WB) are shown for ES1 (20 °C and pH 6.9) and ES2 of hp-GU-20 (20 °C and pH 7.9) and ES1 rG18-N1 and rU7-N3 CSs of hp-GU-24 (25 °C and pH 6.9). Errors in all RD-derived fitted parameters (eg. Δω) denote s.e. from the weighted global fit (see Methods). b, RD-derived CSs (referenced to GS WB) are shown for the ES of xpt-G riboswitch (rU17-N3 and rU69-N3) at 25 °C and pH 7.9. c, 2D [¹⁵N, ¹³C] HMQC spectra of rUTP showing CS of rUTP-N3 induced upon deprotonation. The spectra is rotated by 90°, to depict ¹⁵N CS along x-axis for visualization purposes. Red circles on inset structure highlight measured resonances (C4 and N3). d, 2D [¹⁵N, ¹³C] HMQC spectra of rGTP showing CS of rGTP-N1 induced upon deprotonation. The spectra is rotated by 90°, to depict ¹⁵N CS along x-axis for visualization purposes. Red circles on inset structure highlight measured resonances (C6 and N1). e, RD-derived hp-GU-20 rG•rU ES1 (blue) and ES2 (green) CSs are shown as a function of temperature and pH for both rG16-N1 (square) and rU5-N3 (circle). f, Scheme used to calculate CSs using DFT. Idealized A-form RNA helix is generated to give a central rG•rU mispair (red) that is flanked by canonical rG•rC and rA•rU pairs, analogous to the hp-GU-24 construct. Residues are trimmed to 1-/9-methyl bases and i+1/i−1 pairs are frozen in place for subsequent geometry optimizations and CS calculations (see Methods). g, DFT-predicted CSs (referenced to an energy optimized WB geometry) are shown for various tautomeric and anionic configurations, where rG^enol•rU/rG•rU^enol represents population weighted average CSs of rG^enol•rU (60%) and rG•rU^enol (40%). h, ¹⁵N rG-N1 and rU-N3 CS comparison between RD-derived ES1 CSs and population weighted DFT-predicted CSs (60:40 vs. 80:20). i, Computational studies³² predict that the tautomeric pathway for a rG•rU pair can proceed via a planar rG⁺•rU⁻ ion pair (charge delocalization is implied) that is highlighted by a network of five H-bonds. j, Pair geometry of an anionic rG•rU^– inverted wobble. Deprotonated rU-N3 is highlighted in red (charge delocalization is implied).

Extended Data Figure 10. dG•dT Misincorporation probabilities and correlation to WC-like excited states.

a, Explicit dGTP•dT and dG•dTTP kinetic misincorporation and base substitution probabilities (n=53) and associated errors^46-48,72-77 (see Supplementary Discussion 8) are plotted against hp-GT dG•dT ES1 (blue squares) and ES2 (green triangles). The pK_a fit of ES2 probabilities to the Henderson-Hasselbalch equation (Eqn. 4, see Methods) is shown as the green trend line. b, Red trend line shows the pK_a fit to dGTP•dT misincorporation probabilities⁴⁷ from pH 6.5-8.6 to the Henderson-Hasselbalch equation. The fit was weighted using reported experimental errors and gave a reduced χ² of 3.56. c-d, Extrapolated dG•dT^– ES2 probability (s.e. from the weighted global fit) is plotted against dGTP•dT (left) and dG•dTTP (right) misincorporation probabilities (errors as given)⁴⁷ from pH 6.5–9.5.