Predicting reintubation, prolonged mechanical ventilation and death in post-coronary artery bypass graft surgery: a comparison between artificial neural networks and logistic regression models

Abstract

Introduction

In coronary artery bypass (CABG) surgery, the common complications are the need for reintubation, prolonged mechanical ventilation (PMV) and death. Thus, a reliable model for the prognostic evaluation of those particular outcomes is a worthwhile pursuit. The existence of such a system would lead to better resource planning, cost reductions and an increased ability to guide preventive strategies. The aim of this study was to compare different methods – logistic regression (LR) and artificial neural networks (ANNs) – in accomplishing this goal.

Material and methods

Subjects undergoing CABG (n = 1315) were divided into training (n = 1053) and validation (n = 262) groups. The set of independent variables consisted of age, gender, weight, height, body mass index, diabetes, creatinine level, cardiopulmonary bypass, presence of preserved ventricular function, moderate and severe ventricular dysfunction and total number of grafts. The PMV was also an input for the prediction of death. The ability of ANN to discriminate outcomes was assessed using receiver-operating characteristic (ROC) analysis and the results were compared using a multivariate LR.

Results

The ROC curve areas for LR and ANN models, respectively, were: for reintubation 0.62 (CI: 0.50–0.75) and 0.65 (CI: 0.53–0.77); for PMV 0.67 (CI: 0.57–0.78) and 0.72 (CI: 0.64–0.81); and for death 0.86 (CI: 0.79–0.93) and 0.85 (CI: 0.80–0.91). No differences were observed between models.

Conclusions

The ANN has similar discriminating power in predicting reintubation, PMV and death outcomes. Thus, both models may be applicable as a predictor for these outcomes in subjects undergoing CABG.

Introduction

Coronary artery bypass graft (CABG) surgery is a proven and effective mode of treatment for coronary artery disease. It relieves symptoms, reduces myocardial ischemia and increases overall survival. However, complications associated with CABG lead to increased morbidity and mortality [1]. Some complications in this context include the need for prolonged mechanical ventilation (PMV), need for reintubation and death [1–3].

These complications are known to result in higher morbidity (sepsis, pneumonia, mediastinitis) and higher mortality, which are associated with an increased length of stay in intensive care units, decreased hospital bed availability, and increased overall costs associated with hospitalization [4]. Recently, some authors have shown that late extubation of patients after CABG surgery also increases the incidence of postoperative atrial fibrillation [5]. Predicting the risk for post-CABG complications is thus of major interest in order to improve not only resource allocation and management, but to enhance the patients’ recovery by guiding mainly preventive physiotherapy and medical strategies.

Logistic regression (LR) modeling is a powerful and well-established method both in statistics and biomedical fields with straightforward interpretability and ubiquitous availability in traditional statistical analysis packages. The LR is a generalized linear model and, as such, assumes the outcome variable to be a linear combination of input variables applied to a non-linear link function. Although LR is widely used, true linear relationships rarely exist in epidemiology; this can be interpreted as either a blessing (as it allows for easier interpretation of the model) or as a curse (as many important problems cannot be appropriately solved using linear predictions) [6–9].

Artificial neural networks (ANNs), on the other hand, are not limited to linear predictive rules. These models have the ability to “learn” complex relationships between input and output variables, and have been regarded as universal function approximations. However, they have traditionally been seen as black-box models which are often difficult to interpret. As their name implies, ANNs have been created in an effort to model the workings of the human brain. In reality however, ANNs can be seen as simple parametric mathematical functions, which have to be estimated from data or other sources just as any other popular statistical models [10, 11].

Previous studies suggest that ANNs are superior to traditional regression methods for outcome prediction [12] while other author suggests ANNs are not superior to LR analysis [13]. However, to our knowledge no previous studies have compared these models to predict PMV, reintubation and death following CABG. Thus, the purpose of this study was to compare the performance of ANNs and LR models for prediction of PMV, reintubation and death post-CABG surgery. We hypothesized that ANNs would be a better predictive instrument for identifying subjects at increased risk for adverse outcomes post-CABG compared with LR.

Material and methods

Subjects and data collection

Subjects in this study were gathered through a joint partnership between the Federal University of São Carlos and the Hospital de Base of São José do Rio Preto, Brazil. The data set contains measurements from 1315 subjects who underwent CABG surgery. Subjects were specifically asked to participate in the study and expressed their willingness through informed written consent. Standard preoperative and postoperative management was performed in all subjects. A human subject's investigation committee approved the study protocol (197/2005). On-pump or off-pump CABG was performed through a median sternotomy. Anesthesia, body temperature and cardioplegia during the procedure were standardized.

Inclusion was based on the availability of all the following possible predictive pre-operative variables: age, gender, weight, height, body mass index, diabetes, creatinine, preserved (left ventricular ejection fraction – LVEF ≥ 50%), moderate (LVEF 31–49%) and significant ventricular dysfunction (LVEF ≤ 30%) and operative variables: cardiopulmonary bypass and total number of grafts. The need for PMV was also considered as an input for the prediction of death. Variables were collected by research assistants and maintained in a computer database.

Outcome measurements

Three dichotomous (binary) variables were chosen as outcomes: PMV, reintubation and death after CABG. The PMV was defined as any mechanical ventilation of more than 24 h and the duration of mechanical ventilation was standardized as the time from arrival at the intensive critical unit to the time of extubation [14]. The outcome reintubation was defined as the need to reinstitute the artificial airway after extubation. Death occurring within 30 days of CABG was considered an event.

The decision to extubate was made on a patient-by-patient basis and was a joint decision made between the physician and physiotherapist of the coronary unit. Criteria for extubation included: 1) awake subjects (with minimal or no sedative agents), 2) hemodynamically stable with mean arterial pressure ≥ 60 mm Hg (without vasopressors or with minimum vasopressor support, e.g. ≤ 5 µg/kg/min), 3) no evidence of excessive bleeding or fever, 4) partial pressure of oxygen ≥ 60 mm Hg, with a fraction of inspired oxygen ≤ 0.40, partial pressure of carbon dioxide < 50 mm Hg, pH > 7.30 and a respiratory rate < 30 breaths/min.

The decision to reintubate was also a joint decision between the treating physician and physiotherapist. Criteria included signs of distress during spontaneous breathing, defined as heart rate > 140 bpm or 20% heart rate increase, systolic blood pressure > 180 mm Hg, signs of increased respiratory work, oxygen saturation < 90%, fraction of inspired oxygen > 0.40, respiratory rate > 35 breaths/min, somnolence, anxiety, agitation and increased sweating.

For documentation of death we also considered the need for PMV (death considering PMV). We considered the presence of this variable as important in assessing the likelihood of a possible death.

Data analysis

Two classes of prediction models were created, LR and ANNs. For each outcome we created an LR and several ANNs with a varying number of hidden neurons. We computed ROC areas to compare predicted values against the truth. The predictive pre-operative and intra-operative data presented in Table I were used as the independent variables and the outcomes PMV, reintubation and death post-CABG surgery were the dependent variables. Gender, diabetes, ventricular dysfunction and cardiopulmonary bypass use were dichotomous variables.

Table I.

Comparison of clinical features between training and validation groups

Variable	Training set (n = 1053)	Validation set (n = 262)
Age [years]	60.4 (9.6)	61.1 (9.8)
Gender male	715 (67.9%)	183 (69.8%)
Weight [kg]	73.5 (13.8)	73.7 (14.4)
Height [m]	1.64 (0.08)	1.64 (0.09)
Body mass index [kg/m2]	27.0 (4.2)	27.1 (4.5)
Creatinine [mg/dl]	1.22 (0.6)	1.22 (0.7)
Total number of grafts	2.48 (0.8)	2.5 (0.8)
Cardiopulmonary bypass	786 (74.6%)	196 (74.8%)
Diabetes mellitus	353 (33.5%)	72 (27.5%)
Preserved ventricular function	814 (77.3%)	192 (73.2%)
Moderate ventricular dysfunction	147 (13.9%)	48 (18.3%)
Severe ventricular dysfunction	91 (8.6%)	22 (8.4%)

Data are mean (SD) or numbers (%), LVEF – left ventricular ejection fraction; preserved ventricular function: left ventricular ejection fraction (LVEF) ≥ 50%; moderate ventricular dysfunction: LVEF 31–49%; severe ventricular dysfunction: LVEF ≤ 30%.

The outcomes PMV, reintubation and death after CABG were dichotomous variables expressed as 1 and 0 for presence and absence, respectively. From the whole dataset, 80% of the data were randomly assigned to the training group for developing the ANN and LR models, and the remaining 20% were randomly assigned to a testing group. Thus, 1053 subjects were used for training, and 262 were used for validation of both models (Table I).

Modeling tools

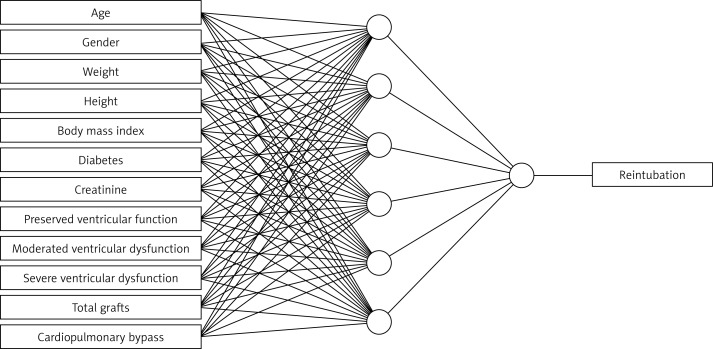
A feed-forward multi-layer neural network was trained using the Levenberg-Marquardt learning algorithm with the aid of Bayesian regularization. All networks were created using a single hidden layer with a varying number of hidden neurons and a single output neuron, trained until convergence of the error function. In a study by Souza et al. [15], the complexity of the networks was controlled using early stopping. Early stopping can be considered a form of regularization of complexity control. In this study, instead of controlling complexity through early stopping, we controlled complexity by determining a suitable number of hidden neurons. The use of Bayesian regularization also permitted the networks to automatically adjust their number of free parameters, further avoiding over-fitting and allowing for increased generalization.

Prior to training, all inputs were scaled into the centered unit interval, with training data balanced among the target classes. The final model can be seen in Figure 1.

Figure 1.

Schematic representation of artificial neural network (ANN) for reintubation outcome

The LR is a generalized linear model. As such, it is based on a link function to produce non-linear outputs from an otherwise linear combination of its inputs. The LR model can be written as: y = g (θ · x), in which θ is a parameter vector, x is the input vector and is the logistic sigmoid function given by g (z) = 1/1 + e^–z.

All computations were performed using the Accord.NET Framework 2.8.2 for scientific computing, a tool used in computer vision [16, 17], data-mining [18] and in the medical sciences.

Statistical analysis

Data are expressed as mean ± SD or as a percentage. The ANNs and LR analyses were compared by receiver operating characteristic (ROC) curve and the common measures of discrimination sensitivity, specificity and accuracy. The sensitivity of a clinical test refers to the ability of the test to correctly identify the patients with the disease whereas the specificity refers to the ability to correctly identify the patients without the disease. Accuracy is the proportion of true results, either true positive or true negative, in a population. The area under the ROC curve (AUC) was calculated as an overall measure of the discrimination abilities of the prediction models and represents the probability that the model predicted for a randomly chosen positive case will exceed the result for a randomly chosen negative case [19, 20]. The ROC curve was obtained by plotting sensitivity against 1-specificity for all possible cut-off points.

The AUC can be considered the probability that a subject randomly selected from the morbidity group will have a diagnostic marker indicating greater risk than a randomly selected subject from the normal course group [21]. According to the AUC ROC values, discrimination was categorized as “perfect” (AUC, 1), “good” (AUC, > 0.8), “moderate” (AUC, 0.6–0.8), or “poor” (AUC, < 0.6) [22]. The comparison of the ROC curves was performed using the method of DeLong. This is one of the most commonly used nonparametric methods for comparing correlated ROC curves which is also able to account for correlation among the studied variables [23].

Results

The clinical features between training and validation groups are summarized in Table I. The event rates for the study population (n = 1315) were 8.6%, 8.6% and 8.3% for reintubation, PMV and death, respectively. The reintubation, PMV and death rates in the training set (n = 1053) were 8.6%, 9.8%, 8.3% and in the validation set (n = 262) were 8.4%, 9.5% and 8.3%, respectively. Table II summarizes predictive accuracy, sensitivity, and specificity using ANN and LR models for predicting reintubation, PMV and death. Table III shows the area under the ROC curve analyses for the diagnostic performance of ANN and LR for outcomes, and the statistical significance of the difference comparing two ROC curves is also presented. Table IV indicates the odds ratio and confidence interval of independent variables in LR for reintubation, prolonged mechanical ventilation and death models.

Table II.

Performance comparison of artificial neural network and logistic regression models for predicting reintubation, prolonged mechanical ventilation and death

Outcomes	Accuracy	Sensitivity	Specificity	AUC	AUC p-value
Reintubation:
Artificial neural network	0.63	0.64	0.63	0.65 (0.53–0.77)	0.013
Logistic regression	0.60	0.64	0.60	0.62 (0.50–0.75)	0.049
Prolonged mechanical ventilation:
Artificial neural network	0.63	0.76	0.62	0.72 (0.64–0.81)	7.11 × 10–7
Logistic regression	0.63	0.64	0.63	0.67 (0.57–0.78)	0.0016
Death (considering PMV):
Artificial neural network	0.77	0.91	0.76	0.85 (0.80–0.91)	0
Logistic regression	0.77	0.82	0.77	0.86 (0.79–0.93)	0

AUC – area under the receiver operating characteristic (ROC) curve, PMV – prolonged mechanical ventilation

Table III.

Pairwise comparison of area under the receiver operating characteristic curves (AUC) analysis between artificial neural network and logistic regression model for predicting prolonged mechanical ventilation, reintubation and death

Variable	Difference between AUCs	Standard error	95% CI		Value of p
			Lower	Upper
Reintubation	–0.028	0.022	–0.073	0.016	0.21
Prolonged mechanical ventilation	–0.049	0.037	–0.122	0.023	0.18
Death (considering PMV)	0.003	0.0221	–0.039	0.047	0.87

AUC – area under the receiver operating characteristic curve, CI – confidence interval

Table IV.

Odds ratio and confidence interval of independent variables in logistic regression for reintubation, prolonged mechanical ventilation and death models

Independent variable	Reintubation		PMV		Death
	OR	95% CI	OR	95% CI	OR	95% CI
Age [years]	1.06	1.05–1.08	1.06	1.05–1.07	1.05	1.03–1.06
Gender male	1.15	0.83–1.61	0.16	0.60–1.11	2.69	1.84–3.95
Weight [kg]	1.11	1.01–1.23	0.04	1.02–1.19	1.02	0.92–1.14
Height [m]	8.92 × 10–7	1.39 × 10–10–0.005	3.56	4.47 × 10–8–0.05	3.09 × 10–5	1.32 × 10–9–0.72
Body mass index [kg/m2]	0.72	0.55–0.93	0.10	0.64–0.97	0.89	0.67–1.20
Creatinine [mg/dl]	2.56	2.07–3.17	0.11	2.11–3.27	2.31	1.90–2.80
Total number of grafts	1.29	1.11–1.50	0.07	0.95–1.24	1.15	0.98–1.35
Diabetes mellitus	1.56	1.22–1.98	0.11	1.35–2.01	1.04	0.80–1.35
Preserved VE function	3.26	2.29–4.62	0.15	1.80–3.20	3.74	2.53–5.53
PMV	–	–	–	–	22.3	15.67–31.67

CI – confidence interval, OR – odds ratio, PMV – prolonged mechanical ventilation, VE – ventricular

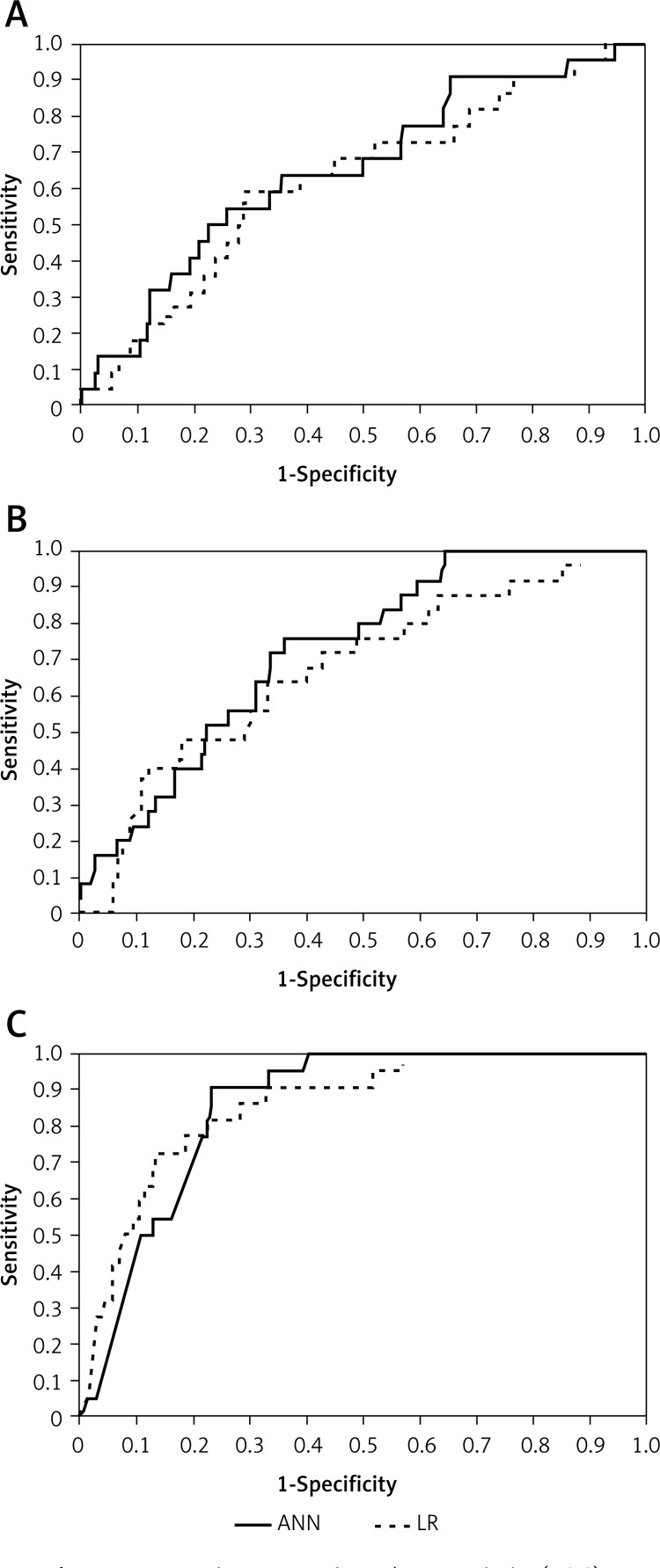
For the validation group, Figure 2 shows the ROC curves for the outcomes constructed using LR and ANN models. The LR versus ANN model provided the following ROC curve values: 62% vs. 65%, 67% vs. 72% and 86% vs. 85% for reintubation, PMV and death, respectively.

Figure 2.

Receiver-operating characteristic (ROC) curves for the artificial neural network (ANN) and logistic regression (LR) model for predicting reintubation (A), prolonged mechanical ventilation (B) and death (C). The difference was not significant. Area under the ROC (AUC) for (A) LR model = 0.62, ANN model = 0.65; (B) LR model = 0.67, ANN model = 0.72; and (C) LR model = 0.86, ANN model = 0.85

Discussion

The present study was undertaken to compare the performance of ANNs and LR models for three important outcomes: reintubation, PMV and death prediction post-CABG surgery on the same predictor dataset. The results obtained show that both the LR and ANN prognostic models demonstrate comparable accuracy for prediction of reintubation, PMV and death in subjects undergoing CABG. Although risk stratification following cardiac surgery has gained increasing importance in recent years, to our knowledge there are currently no data comparing ANN and LR for prediction of CABG-related outcomes. Previous prognostic studies involving cardiac surgery have evaluated outcomes such as prolonged length of stay in the intensive care unit [24], mortality and general complications [25, 26].

Reintubation and PMV increase are associate with airway and lung trauma increased morbidity (ventilator-associated pneumonia, intensive care unit length of stay, resource utilization and health care costs) and mortality [14, 15, 27]. In this context, the greatest difficulty for health care professionals is to predict the risk for adverse events early in the process. Thus, improved prognostic models may result in more efficient strategies to optimize clinical management of these subjects with better resource allocation.

The ANN modeling is a technique that is gaining increasing application in clinical research. An advantage over traditional LR modeling is the ability of ANNs to use information from data records that are incomplete. Given the fact that incomplete data in clinical practice are common, the ability to incorporate and use more information allows ANNs to create models that more accurately represent the clinical scenario under investigation [6]. However, in our study, prognostic performance was similar between the LR and ANN models and did not include subjects with missing data because of the nature of the comparison. In a clinical context, another advantage of ANNs should be emphasized. The ANNs have the capacity to train themselves without human intervention. Once trained, ANNs could reside in the background of clinical information systems and could be continuously improved as more patients are accumulated [26].

Although we highlight some advantages of ANNs, our results demonstrate similar performance between ANN and LR prediction models. This could be explained in part by the class imbalance (for instance, high imbalance between the numbers of subjects that were reintubated in comparison with those that were not) and the absence of complex relationships in the dataset. Moreover, because of the direct relationship between single neuron ANNs and the LR, what we have found is that simpler models (as in ANNs with low neuron counts) can learn the data better than complex models, which are more prone to overfitting. This is an issue because the data we are most interested in (post-surgery complications) only represent a relatively small fraction of the dataset. Thus, more complex models would not have sufficient data to learn the problem well, and may not lead to good generalization.

Orr [28], Tu et al. [29] and Lippmann and Shahian [30] showed that an ANN could be used to predict cardiac surgical mortality, and according to our results the performance was equivalent to that of LR. The latter authors also attribute their results to the absence of a complex nonlinear relationship among the independent variables.

It is noteworthy that in contrast to other studies, variable selection was performed without stepwise testing in the present study. The variables included in the present models have previously been applied in other studies [4, 27, 31]. We used age, gender, weight, height, body mass index, diabetes, creatinine level, cardiopulmonary bypass, status of left ventricular function (i.e. preserved or moderate to severely impaired) and the total number of grafts as independent variables. These variables have previously been documented as predictors of these outcomes, and are readily available in subjects undergoing cardiac surgery. Thus similar models could be applied in many surgical centers. However, the number of variables optimally included in risk models following cardiac surgery has not been adequately explored.

Given that respiratory complications are common in these subjects, we felt that it was important to consider PMV as an additional independent factor that could influence death as an endpoint. The incidence of PMV at our institution is comparable to that in previous reports. Kern et al. [32] reported an incidence of PMV of 9.0%. Légaré et al. [14] studied a series of 1829 subjects and reported a PMV rate of 8.6%, which was associated with significantly higher mortality as compared to subjects who did not require ventilation > 24 h. The current and previous findings suggest that PMV identifies subjects at increased risk of morbidity and mortality following CABG.

The definition of PMV should be mentioned. As in other studies [6, 33], we defined PMV as greater than 24 h, established as the time from arrival at the intensive care unit to the time of extubation. However, no consensus exists in terms of a standardized definition and cutoff points selected, potentially leading to conflicting results. In addition, patients are currently extubated within 6 h after cardiovascular surgery due to the respiratory and cardiovascular benefits of such an approach [34]. We opted for 24 h based on the concept that this time is sufficient for hemodynamic stabilization and to offset the deleterious effects of surgery and cardiopulmonary bypass if used [33].

The authors would like to emphasize that in this study, specifically for models that considered PMV as one of the independent variables, we found a higher occurrence of multicollinearity. However, since one can note that multicollinearity does not adversely affect the regression model when the goal is to predict the outcome of the dependent variable, we chose not to exclude those variables from our model in order to provide direct and complete comparisons between the LR and the ANN models.

For mortality, our study demonstrated higher rates (approximately 8%) when compared to the literature (approximately 3%) [35]. However, we did not evaluate mortality alone but took into consideration the coexistence of prolonged mechanical ventilation in patients who died, which may explain the difference in our results.

It is worth mentioning that the bootstrapping technique is indeed very useful to compare different prediction models. However, neural networks often do not scale very well with the bootstrapping method, as both neural networks and the bootstrapping method are quite expensive to compute. The use of neural networks also involves a non-convex learning process which can require several weight re-initializations, increasing the computational effort even further. In order to provide a trade-off between comparison accuracy and efficiency, we chose to stick with a split-set validation based on development and testing sets for the neural networks. In order to keep results between neural networks and the logistic model comparable, the logistic models were also created following this same methodology.

There are some limitations to the current study. The database was drawn from one center only. Data sets collected from multiple centers would provide more general information for risk stratification in subjects undergoing CABG. Thus, the model developed herein requires prospective validation, preferably at multiple centers. In addition, only variables that already existed in the database were applied in the models. Other variables that may be associated with reintubation, PMV and death (such as diagnosis of COPD and neurological complications) were not evaluated.

In conclusion, these results suggest that an ANN had similar discriminating power in predicting reintubation, PMV and death as conventional LR among subjects undergoing CABG. Thus, both models may be applicable for predicting outcomes following CABG.

Conflict of interest

The authors declare no conflict of interest.