Thyroid Dose Estimates for a Cohort of Belarusian Children Exposed to ¹³¹I from the Chernobyl Accident: Assessment of Uncertainties

Abstract

Deterministic thyroid radiation doses due to iodine-131 (¹³¹I) intake were reconstructed in a previous article for 11,732 participants of the Belarusian–American cohort study of thyroid cancer and other thyroid diseases in individuals exposed during childhood or adolescence to fallout from the Chernobyl accident. The current article describes an assessment of uncertainties in reconstructed thyroid doses that accounts for the shared and unshared errors. Using a Monte Carlo simulation procedure, 1,000 sets of cohort thyroid doses due to ¹³¹I intake were calculated. The arithmetic mean of the stochastic thyroid doses for the entire cohort was 0.68 Gy. For two-thirds of the cohort the arithmetic mean of individual stochastic thyroid doses was less than 0.5 Gy. The geometric standard deviation of stochastic doses varied among cohort members from 1.33 to 5.12 with an arithmetic mean of 1.76 and a geometric mean of 1.73. The uncertainties in thyroid dose were driven by the unshared errors associated with the estimates of values of thyroid mass and of the ¹³¹I activity in the thyroid of the subject; the contribution of shared errors to the overall uncertainty was small. These multiple sets of cohort thyroid doses will be used to evaluate the radiation risks of thyroid cancer and non-cancer thyroid diseases, taking into account the structure of the errors in the dose estimates.

INTRODUCTION

Correct accounting for uncertainty in dose estimates is a well recognized concern in radiation epidemiology studies (1–4). The uncertainties arise from, among other sources, stochastic variability of parameters used in exposure assessment, lack of knowledge about true values and low reliability of data on individual behavior during radiation exposures that occurred a long time ago. The current state-of-the-art approach in dosimetry is to document sources and quality of all input data, to establish a dosimetry error structure and to characterize each parameter used in dose calculations as a source of shared or unshared error (5, 6). These data may then be used in a probabilistic dose calculation to generate multiple sets of dose estimates for the entire study population, so that dose-response analyses can be performed using multiple sets of doses (7–9).

The U.S. National Cancer Institute, in collaboration with the Belarusian Ministry of Health, has been conducting a study of thyroid cancer and other thyroid diseases in a cohort of 11,732 persons who were exposed in childhood and adolescence to fallout from the Chernobyl accident that occurred on April 26, 1986 (10–12). To evaluate the radiation risk of thyroid diseases, deterministic thyroid doses were reconstructed for the study subjects based on estimated ¹³¹I activity in the thyroid derived from direct thyroid measurements of each cohort member and responses to interviews of all subjects on residential history, consumption of milk, milk products and leafy vegetables and administration of stable iodine (13). It is clear that there are uncertainties associated with these dose estimates since it is impossible to obtain precise and complete data for exposure assessment. The major sources of uncertainties were: 1. Errors in the ¹³¹I activities in the thyroids derived from the direct thyroid measurements; 2. Errors in assigning of individual thyroid-mass value; 3. The uncertainties attached to the parameters of the ecological and biokinetic models; and 4. The uncertainties attached to the information obtained during personal interviews on relocation history and individual diet at the time of the Chernobyl accident in 1986.

Here we report on the estimation of uncertainty in individual estimates of thyroid doses due to ¹³¹I intake, which was the predominant exposure of the thyroid for the majority of study participants, and on average, contributed about 92% to the total thyroid radiation dose. Other exposure pathways, such as intake of short-lived ¹³²Te, ¹³²I and ¹³³I, external irradiation and ingestion of ¹³⁴Cs and ¹³⁷Cs, are not considered in this study.

MATERIALS AND METHODS

The study was reviewed and approved by the institutional review boards of the participating organizations in Belarus and the United States, and all study subjects or their guardians (for subjects who were 16 years or younger at screening) signed informed consent.

Thyroid Dose Calculation

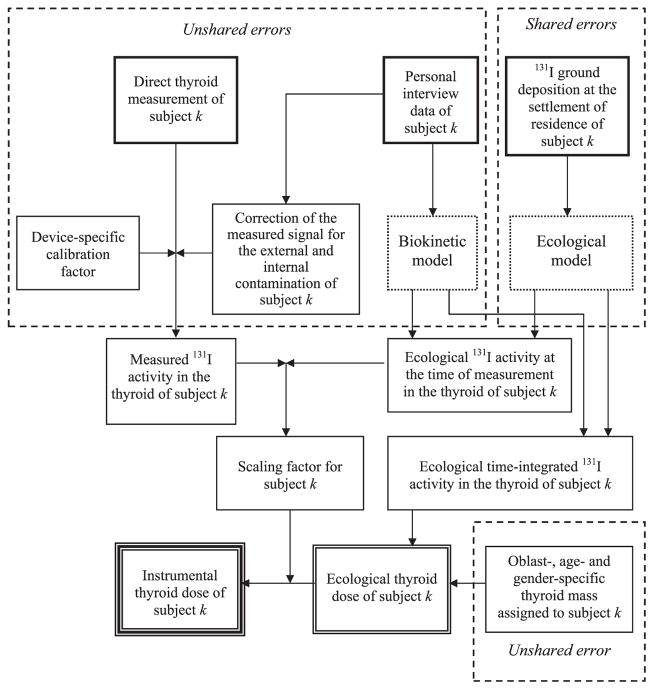
Figure 1 shows the scheme of thyroid dose calculation for the Belarusian cohort members. The thyroid doses were estimated using input data specific to each cohort member (direct thyroid measurement and personal interview) and ecological data (e.g., ¹³¹I ground deposition in the settlements where any of the cohort members resided). Ecological and biokinetic models were used to reconstruct the transport of ¹³¹I from the ground deposition to the child’s thyroid via the activity intake with contaminated air and foodstuffs calculated using personal interview data on individual behavior and consumption rates of foodstuffs. For each study subject k, two estimates of thyroid dose, differing in the manner in which the activity of ¹³¹I in the thyroid was assessed, were calculated: 1. an “instrumental” thyroid dose, D_k, based on the measured ¹³¹I activity in the thyroid at time t_m after the accident, $Q_k^{\mathit{meas}}(t_m)$, which is derived from the direct thyroid measurement; and 2. an “ecological” thyroid dose, in which the ¹³¹I activity in the thyroid; $Q_k^{\mathit{ecol}}(t)$, is calculated for any time t after the accident using ecological and biokinetic models, together with personal interview data on individual behavior and consumption rates of foodstuffs. The “instrumental” thyroid dose estimate, being based on a dose-related measurement performed on each study subject, is better than the “ecological” dose estimate and is recommended for use in the assessment of radiation risks. The main purpose of the “ecological” dose estimate is to provide an evaluation of the reliability of the “instrumental” thyroid dose estimate. The “ecological” thyroid dose (D_k^ecol, mGy) for subject k is calculated as follows:

$$D_k^{\mathit{ecol}}=\frac{U_c·E_{th}}{m_k}·\underset{0}{\overset{T}{\int }}{Q}_k^{\mathit{ecol}}(t)dt;$$ (1)

where: U_c is a unit conversion factor of 13.82 (Bq kBq⁻¹ g kg⁻¹ J MeV⁻¹ s d⁻¹ mGy Gy⁻¹); m_k is the subject-specific mass of the thyroid (g); E_th is the mean energy absorbed in the thyroid per decay of ¹³¹I in the thyroid (MeV decay⁻¹); $Q_k^{\mathit{ecol}}(t)$ is the “ecological” activity of ¹³¹I in the thyroid of study subject k at time t (kBq). The period of integration is from the time of the accident on 26 April 1986 (t = 0) until 30 June 1986 (t = T = 66 days).

FIG. 1.

Scheme of thyroid dose calculation for the Belarusian cohort members [adapted from ref. (13)].

To calculate the “instrumental” thyroid dose (D_k, mGy), the calculated “ecological” ¹³¹I activity in the thyroid at time t_m, $Q_k^{\mathit{ecol}}(t_m)$, is replaced in Eq. (1) with the measured activity, $Q_k^{\mathit{meas}}(t_m)$, and it is assumed that the relative shape of the variation of $Q_k^{\mathit{ecol}}(t)$ with time is correct, so that the adjustment at time t_m also applies to any other time after the accident. Under those conditions, one obtains:

$$D_k=\frac{Q_k^{\mathit{meas}}(t_m)}{Q_k^{\mathit{ecol}}(t_m)}·D_k^{\mathit{ecol}}$$ (2)

A more detailed description of the methodology used to calculate the “instrumental” thyroid doses for all members of the cohort of Belarusian children can be found elsewhere (13).

Estimation of Uncertainties: General Approach

Using Monte Carlo simulation to estimate the uncertainties in instrumental thyroid doses, we calculated 1,000 sets of cohort instrumental thyroid doses, which take into account classification of errors as shared or unshared. This procedure is similar to and generally consistent with the 2-dimensional Monte Carlo method (14). For a specific dose realization some of the model parameter values were in common among members of subgroups, i.e., shared among subjects of those groups, implying that any error made on this parameter was shared by all subjects to whom it applied. Twenty subject-independent or shared, parameters were identified in the dose calculation procedures used in our study. They are parameters of the ecological model that describe the temporal variation of the ground, air and foodstuff contamination with ¹³¹I and ¹³¹I activity in the thyroid gland. Other uncertainties were considered to be subject-dependent or unshared. Twenty-eight parameters used for dose calculations were considered to be unshared errors related to measurements of ¹³¹I activity in thyroid (7 parameters), thyroid mass (1 parameter), biokinetic models of iodine in human body (4 parameters) and imprecise responses to questions administered during the personal interview (16 parameters). Eleven parameters of the dose calculation procedures were considered to be known precisely. These include the radioactive decay constant of ¹³¹I, energy per decay of ¹³¹I absorbed in thyroid, fraction of ingested ¹³¹I transferred to blood and delay between milking and consumption of seven types of milk and milk products as well as between harvesting and consumption of leafy vegetables.

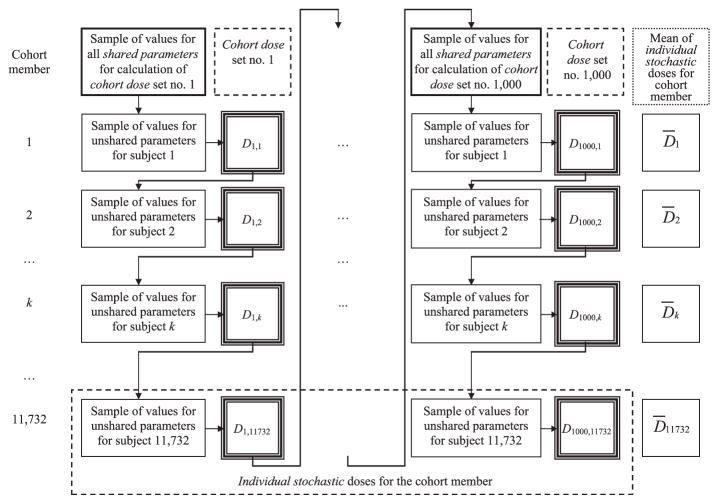
Figure 2 shows the scheme of calculation of 1,000 sets of cohort thyroid doses. At the beginning of calculation of each dose set for the entire cohort, we sampled values for all shared parameters from their probability distributions. To calculate one dose set for the entire cohort, the same value for each shared parameter was used for all cohort members for whom this parameter was considered to be shared. This step intentionally introduced correlations in each simulated dose set between individual dose estimates of the study subjects who shared parameter values. In the process of dose set simulation, we sampled values of unshared parameters for each cohort member from their distributions and calculated one dose realization for cohort member k, D_i,k. A set of doses from D_i,1 to D_i,11732 represents set number i of cohort thyroid doses (Fig. 2). The thousand realizations of dose, from D_i,k to D_1000,k, for cohort member k, represent the individual stochastic thyroid doses of that cohort member (Fig. 2).

FIG. 2.

Scheme of calculation of multiple sets of cohort doses with account of shared and unshared errors.

A detailed description of the evaluation of the errors associated with the parameters used for calculation of thyroid doses is presented in the following sections.

Shared Errors Associated with the Parameters of the Ecological Model

The errors attached to the parameters of the ecological model were considered to be shared, that is, subject independent. The parameters of the ecological model and their distributions are listed in Table 1. Some errors were assigned to be shared among all study subjects, while others were shared among specific subgroups. For example, the error in the ¹³¹I deposition in a settlement was considered to be shared among subjects who resided in that settlement. In other words, in the process of calculating a dose set for the entire cohort, the same value of ¹³¹I deposition density was applied for all persons who resided in that location.

TABLE 1.

Parameters of Ecological Model Considered to be Shared (Subject Independent)

Parameter			Central valuea (arithmetic mean)	Distribution	Shared among subjects	Reference(s)
Description	Symbol	Unit
Daily deposition of 131I	GDS	kBq m−2 d−1	0–209,000	TLN(0.9 × AMb, 1.6, 0.4 × GM, 2.6 × GM)c	In the same settlement	(15)
Deposition velocity of 131I	Vg	m d−1	600	TLN(455, 2.1, 105, 2,000)	All	(15)
Removal rate of 131I from grass	λgrass	d−1	0.15	TR(0.13, 0.15, 0.17)d	All	(16)
Pasture grass yield	Ygrass	kg m−2	0.23–0.33	TR(0.5 × AM, AM, 1.5 × AM)	Living in the same oblast	Averin (2008)e
Coefficient of 131I interception by grass	b1,s	Unitless	Calculated	TLN(0.94 × AM, 1.4, 0.5 × GM, 2 × GM), but b1,s ≤ 0.85	In the same settlement	Averin (2008)
Daily grass consumption by cow	Ip	kg d−1	45	U(30, 60)f	All	Averin (2008)
Daily soil intake by cow	Isoil	kg d−1	0.35	U(0.2, 0.5)	All	Averin (2008)
Soil per unit of ground	Ysoil	kg m−2	1.0	TR(0.3, 1.0, 1.5)	All	(17)
Rate of 131I elimination from milk	λbm	d−1	1.0	TR(0.5, 1.0, 1.74)	All	(18)
Feed-to-cow’s milk transfer factor of 131I	fm	d L−1	0.004	TLN(0.003, 2.1, 0.0007, 0.013)	All	Averin (2008), (19)
Ratio of 131I content in goat’s to cow’s milk	Rg	Unitless	8	TLN(6.3, 2, 1.6, 25)	All	(20)
Ratio of 131I content in mother’s to cow’s milk	Rm	Unitless	0.32	TLN(0.3, 1.4, 0.15, 0.6)	All breastfed	Adapted from (21)
Culinary factor for:
Leafy vegetables	PF1	Unitless	0.8	U(0.6, 1.0)	All	(18, 22)
Milk in soup	PF5	Unitless	0.5	U(0.3, 0.7)	All
Sour milk	PF6	Unitless	0.7	U(0.5, 0.9)	All
Sour cream	PF7	Unitless	0.7	U(0.5, 0.9)	All
Soft cottage cheese	PF8	Unitless	0.6	U(0.4, 0.8)	All
Kefir	PF9	Unitless	0.7	U(0.5, 0.9)	All
Reduction factor of 131I uptake by the thyroid after stable iodine administration	RFKI(t)	Unitless	0.07–0.95	TR(0.8 × AM, AM, 1.2 × AM), but RFKI(t) ≤ 1.0	With stable iodine prophylaxis	Expert judgment
Assigned date of measurement	tm		April 30–June 17, 1986	DU(AM − 2, AM − 1, AM, AM + 1, AM + 2)g	With assigned given date of measurement	Expert judgment

^aOr range of values among cohort members.

^b $GM=AM·(\sqrt{exp({(ln\mathit{GSD})}^2)})$ [derived from (23); GM: geometric mean; AM: arithmetic mean; GSD: geometric standard deviation].

^cTLN(GM, GSD, min, max): truncated lognormal distribution with the following parameters: geometric mean (GM), geometric standard deviation (GSD), minimal value (min), maximal value (max).

^dTR(min, mode, max): triangular distribution with the following parameters: minimal value (min), mode of distribution (mode), maximal value (max).

^eV. Averin, personal communication, Minsk; January 2008.

^fU(min, max): uniform distribution with the following parameters: minimal value (min), maximal value (max).

^gDU(a₁, a₂, …, a_n): discrete uniform distribution that returns a₁, a₂, …, a_n with equal probability of n⁻¹.

Date of measurement

For 5,097 of the 11,732 study subjects, the date of measurement was either not correctly recorded in the notebook because of clerical errors or was not recorded at all. In those instances, the date of measurement was assigned, based on dates of measurements available in the same notebook for other measured persons, or using information on dates when measurements were performed at the same location. If the date of measurement was assigned, its uncertainty was subjectively assessed to be ±2 days around the assigned date. Uncertainty in the assigned date of measurement was considered to be shared among study subjects who were assigned a given date of measurement.

Unshared Errors Associated with the Estimates of ¹³¹I Activity in the Thyroid

Correct accounting for errors in the estimates of ¹³¹I activity in the thyroid derived from individual direct thyroid measurements is important because the measured activity is key to the instrumental dose calculated for the study subject. Evaluation of the net exposure rate near the thyroid was the first step in the estimation of the ¹³¹I activity in the thyroid, which was calculated as a difference between the exposure rate measured near the thyroid gland and the background radiation level in the room:

$$P_{\mathit{net}}(t_m)=P_m(t_m)-P_{bg}(t_m),$$ (3)

where P_m(t_m) is the exposure rate measured near the thyroid gland (mR h⁻¹); P_bg(t_m) is the radiation background (mR h⁻¹) in the room where the measurements were performed on day of measurement, t_m; and P_net(t_m) is the net exposure rate (mR h⁻¹).

Often, the radiation background, in the room where the measurements were performed, was not measured. In those instances, the method used to estimate P_bg(t_m) depended on the availability of outdoor exposure rates (13).

The next step was to account for the contribution of the external and internal contamination of the subject to the exposure rate measured near the thyroid, by means of a correction factor as:

$$P_{\mathit{net},\mathit{corr}}(t_m)=P_{\mathit{net}}(t_m)·v_{\mathit{corr}}(t_m),$$ (4)

where P_net,corr(t_m) is the net exposure rate (mR h⁻¹) measured near the thyroid that was corrected to take into account the external and internal contamination of the body; ν_corr(t_m) is the correction factor, specific to device, age, region, scenario of deposition and behavior, which represents the contribution of the ¹³¹I activity in the thyroid to the measured signal (unitless).

The corrected net exposure rate, which is only due to the ¹³¹I activity in the individual’s thyroid at the time of the measurement, was used to calculate the ¹³¹I activity in the thyroid:

$$Q_k^{\mathit{meas}}(t_m)=P_{\mathit{net},\mathit{corr}}(t_m)·{CF}_{\mathit{dev}},$$ (5)

where $Q_k^{\mathit{meas}}(t_m)$ is the activity of ¹³¹I measured in the thyroid of study subject k (kBq); and CF_dev is the device-specific calibration factor (kBq mR⁻¹ h).

Taking into account the steps described above, errors in the estimates of ¹³¹I activity in the thyroid arose from:

• Measurement error of the thyroid detectors;

• Uncertainties in the evaluation of the correction factor that was used in Belarus to account for the contribution of the external and internal contamination of the human body to the signal recorded by the thyroid detector; and

• Uncertainties in the estimates of the calibration factor for the thyroid detectors.

Measurement error of thyroid detectors

Three detector types, DP-5, SRP-68-01 and DRG3-02, were used to measure both the exposure rate near the thyroid gland and the radiation background in the room where the measurements were performed on the day of measurement.³ The net exposure rate, which was used to derive the ¹³¹I activity in the thyroid, represents the difference between these two measurements. Therefore, uncertainty in net exposure rate, σ_i,P_net, was calculated as:

$${\mathrm{\sigma }}_{i,P_{\mathit{net}}}=\sqrt{2}·{\mathrm{\sigma }}_{i,\mathit{device}},$$ (6)

where σ_i,device is the error in a measurement made by the device. The typical relative error for measurement made with each device is: 0.3 (DP-5), 0.13 (SRP-68-01) and 0.15 (DRG3-02).

As mentioned above, in some instances, the room background was calculated from measurements of outdoor exposure rate or from a known mix of radionuclides of Chernobyl origin deposited on the ground. It was assumed that the uncertainty of the calculated background on a relative basis did not exceed the measurement error of the thyroid detectors.

Lower limit of exposure rate

If the measured exposure rate was recorded in the notebook as zero or “background” or was recorded to be less than the minimal indication of the DP-5 device (0.05 mR h⁻¹), or less than the radiation background in the room where the measurements were performed, it was replaced with a “lower limit of exposure rate” (LLE). Values of LLE assigned to 1,156 cohort members varied from 0.001 to 0.071 mR h⁻¹ and depended on the type of thyroid detector and radiation background in the room where the measurements were performed. The uncertainty range was assumed to be from essentially 0–2 times the assigned LLE value.

Correction factor

A correction factor was used to eliminate the contribution to the exposure rate measured near the thyroid gland from external and internal contamination of the body. This factor was specific to device, age, region, scenario of deposition, behavior, date of relocation and date of measurement, and was established for each subject and entered into the database. Values of correction factor, which were assigned to 11,556 cohort members measured in Belarus, are spread in 1,510 potentially shared subgroups with numbers of subjects in each subgroup varying from 2 (656 subgroups) to 246 (1 subgroup). Therefore the interindividual correlation associated with some degree of shared uncertainty across the entire cohort was expected to be weak. Due to the complexity and the time-consuming nature of the task, the uncertainty in the correction factor was not evaluated for each subject, but was subjectively assessed to be 40% around the central value for most individuals.

Calibration factor of the thyroid detector

The calibration factors for the thyroid detectors and their uncertainties due to variability of the device characteristics, variability in thyroid mass, and statistical uncertainty were calculated using a Monte Carlo method of numerical simulation of radiation transport (Table 2). A detailed description of the evaluation of the calibration factor for the SRP-68-01 device and its uncertainties can be found elsewhere (24). Similar work was done for the DP-5 and DRG3-02 instruments.

TABLE 2.

Calibration Factors of the Thyroid Detectors: Arithmetic Means (AM) and Standard Deviations (SD), kBq per mR h⁻¹

Age group (years)	DP-5		SPR-68-01		DRG3-02
	AM	SD	AM	SD	AM	SD
Newborn	190	29	98	8	66	7
1	185	28	100	6	70	6
5	200	20	110	10	84	9
10	285	29	126	13	126	14
15	390	50	147	15	175	19
20 (adult)	450	68	167	15	233	23

The parameters used to derive the ¹³¹I activity in the thyroid from the direct thyroid measurements are listed in Table 3. All errors associated with estimates of ¹³¹I activity in the thyroid were considered to be unshared.

TABLE 5.

Thyroid Mass and Parameters of Biokinetic Models Considered to be Unshared (Subject-Dependent)

Parameter			Central value (arithmetic mean)	Distribution	Reference(s)
Description	Symbol	Unit
Thyroid mass	mth	g	Table 4	TLN(GM, GSD, GSD−2 × GM, GSD2 × GM)a	(27)
Ventilation rate	r1	m3 d−1	Table A1.3 (13)	TLN(0.94 × AM, 1.4, 0.5 × GM, 2 × GM)	(29, 30)
Fraction of inhaled iodine transferred to blood	winh	Unitless	0.66	TR(0.5, 0.66, 0.82)b	(31)
Fraction of iodine uptake by thyroid	wth	Unitless	0.3	TR(0.2, 0.3, 0.4)	(32)
Biological half-time of iodine removal from thyroid	Tb	d	Table A1.3 (13)	TR(0.85 × AM, AM, 1.15 × AM)	(32)

^aTLN(GM, GSD, min, max): truncated lognormal distribution with the following parameters: geometric mean (GM), geometric standard deviation (GSD), minimal value (min), maximal value (max).

^bTR(min, mode, max): triangular distribution with the following parameters: minimal value (min), mode of distribution (mode), maximal value (max).

Thyroid Masses

Thyroid volumes from about 56,000 Belarusian children and adolescents from Gomel and Mogilev Oblasts aged from 5 to 16 years were measured by ultrasound by Sasakawa Memorial Health Foundation (SMHF) in 1991–1996 (26). The database with the results of ultrasound measurements was cleaned and revised to derive representative age-, gender- and oblast-specific thyroid-mass values (27). Thyroid masses were calculated from these measurements using a physical density of the thyroid gland of 1.05 g cm⁻³ (28). The probability density distributions of thyroid-mass values were found to be lognormal and characterized by geometric standard deviations (GSDs) from 1.25 to 1.40 (Table 4). In subgroups of children under 5 years old and adolescents over 16 years old for whom thyroid measurements were scarce or not done at all, the variability of thyroid volume among those subjects was subjectively assigned to be characterized with a GSD of 1.4. Probability density distributions of thyroid-mass values derived for children and adolescents, who were not part of the cohort, from measurements done in 1991–1996 were assigned to define the thyroid-mass values of the cohort members in 1986.

TABLE 3.

Unshared Errors Associated with the Estimates of ¹³¹I Activity in the Thyroid

Parameter			Central valuea (arithmetic mean)	Distribution	Reference(s)
Description	Symbol	Unit
Net exposure rate near the thyroid gland after subtraction of background radiation in the room measured by:	Pnet(tm)	mR h−1			DB information
DP-5			0.005–4.3	TN(AM, 0.42 × AM, 0.16 × AM, 1.84 × AM)b	Kutsen (2011)c
SRP-68-01			0.001–3.2	TN(AM, 0.18 × AM, 0.64 × AM, 1.36 × AM)	SRP-68 (1986)d
DRG3-02			0.03–7.9	TN(AM, 0.21 × AM, 0.58 × AM, 1.42 × AM)	Kutsen (2011)
Correction factor that takes into account external and internal contamination of human body	vcorr(tm)	unitless	0.024–0.94	TR(0.6 × AM, AM, 1.4 × AM)e, but vcorr(tm) ≤ 1.0	DB information
Exposure rate near the thyroid calculated as lower limit of exposure rate	PLLE(tm)	mR h−1	0.001–0.071	U(~0, 2 × AM)f	(25)
Calibration factor of the thyroid detectors	CF(dev)	kBq per mR h−1	Table 2	TN(AM, SD, AM − 2 × SD, AM + 2 × SD). (For SD, see Table 2)	(24)
Activity measured by the RFT-20046 gamma spectrometer in Sankt-Petersburg	$Q_{\mathit{meas}}^k(t_m)$	kBq	0.19–37	TN(AM, SD, 0.8 × AM, 1.2 × AM)	Konstantinov (2008)g

^aOr range of values among cohort members.

^bTN(AM, SD, min, max): truncated normal distribution with the following parameters: arithmetic mean (AM), standard deviation (SD), minimal value (min), maximal value (max).

^cS. Kutsen, personal communication, 2011, Minsk.

^dGeological scintillation device SRP-68: technical description and user manual; 1986 (in Russian).

^eTR(min, mode, max): triangular distribution with the following parameters: minimal value (min), mode of distribution (mode), maximal value (max).

^fU(min, max): uniform distribution with the following parameters: minimal value (min), maximal value (max).

^gY. Konstantinov, personal communication, 2008, Minsk.

In the implementation of the Monte Carlo calculations, a thyroid-mass value for each cohort member of a particular age, gender and oblast of residence was independently sampled and imputed by randomly selecting a value from the appropriate age-, gender- and oblast-specific distribution. Although the same distribution was used for all cohort members of a given age, gender and oblast of residence, there is some degree of shared uncertainty in the central values of the thyroid mass because of the extrapolation process, as the distributions of the thyroid mass for the study subjects were taken to be the same as those measured on different individuals at different times (1991–1996 instead of 1986) and also at different locations (Minsk Oblast instead of Gomel Oblast). However, because the thyroid-mass values were estimated with high precision from measurements in individuals classified into 52 age-, gender- and oblast-specific categories, the interindividual correlation associated with some degree of shared uncertainty across the entire cohort is expected to be weak. Therefore, the error associated with the thyroid mass was considered to be unshared.

Unshared Errors Associated with the Parameters of the Biokinetic Model

We considered the parameters of the biokinetic model (namely, the ventilation rate, the fraction of inhaled iodine transferred to blood, the thyroid uptake and the half-time of residence of ¹³¹I in the thyroid) to be sources of unshared errors because of their biological variability between individuals, and we assigned values using an individual imputation process. In the case of half-time of residence of ¹³¹I in the thyroid, the specification of error as shared or unshared is almost irrelevant, because the kinetics of ¹³¹I are influenced by the fact that the radioactive half-life of ¹³¹I is much shorter than the biological half-life of stable iodine in the human body. Table 5 contains a list of the parameters for the biokinetic model and their distributions.

TABLE 4.

Values of Age- and Gender-Dependent Thyroid Masses [Arithmetic Mean and Geometric Standard Deviation (GSD) [based on ref. (27)]

Age (years)	Gomel Oblast and othersa				Mogilev Oblast
	Thyroid mass (g)		GSD		Thyroid mass (g)		GSD
	Girls	Boys	Girls	Boys	Girls	Boys	Girls	Boys
0–0.9	1.3		1.40		1.3		1.40
1.0–1.9	2.0		1.40		2.3		1.40
2.0–2.9	2.7		1.40		3.1		1.40
3.0–3.9	3.4		1.40		3.9		1.40
4.0–4.9	4.1		1.40		4.7		1.40
5.0–5.9	4.7		1.39		5.4		1.28
6.0–6.9	5.4		1.31		6.0		1.27
7.0–7.9	6.1		1.29		6.3		1.29
8.0–8.9	6.6		1.36		6.9		1.29
9.0–9.9	7.2		1.31		7.6		1.30
10.0–10.9	8.4	7.8	1.38	1.30	8.5	8.3	1.33	1.31
11.0–11.9	9.5	8.5	1.39	1.31	9.8	9.2	1.32	1.32
12.0–12.9	11.0	9.5	1.40	1.34	11.6	10.4	1.34	1.30
13.0–13.9	12.6	10.8	1.40	1.25	12.5	11.6	1.34	1.32
14.0–14.9	12.9	12.2	1.40	1.38	13.4	13.2	1.33	1.33
15.0–15.9	13.2	13.5	1.37	1.36	14.3	14.6	1.32	1.33
16.0–16.9	14.2	14.7	1.34	1.29	14.7	15.3	1.33	1.31
17.0–17.9	14.9	16.0	1.40		15.5	16.6	1.40

^aExcept Mogilev Oblast.

Unshared Errors Associated with Information from Questionnaire

Personal interviews of cohort members were conducted in 2001–2007 to collect information on residential history, foodstuff consumption and administration of stable iodine during the first two months after the Chernobyl accident. The questionnaires that were administered to all 11,732 cohort members resulted in about 355,000 responses. Some of the respondents experienced difficulties recalling the foodstuff consumption or the dates related to change of residence, modification of dietary habits or stable iodine administration. Some responses were either devoid of information (e.g., “I do not remember”) or imprecise (inability to provide, for example, the exact date of cessation of milk consumption). Unshared errors associated with the responses during the personal interview are described below and summarized in Table 6.

TABLE 6.

Unshared Errors that are Associated with Information Obtained from Personal Interviews

Parameter			Central value (arithmetic mean)	Distribution
Description	Symbol	Unit
Imprecise date of relocation, change of consumption habits or administration of stable iodine
Answer: “End of April”			28 April	DU(27, 28, 29, 30 April)a
Answer: “Beginning of May”			5 May	DU(1, 2, 3, 4, 5, 6, 7, 8, 9, 10 May)
Answer: “Middle of May”			15 May	DU(11, 12, 13, 14, 15, 16, 17, 18, 19, 20 May)
Answer: “End of May”			25 May	DU(21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 May)
Answer: “June”			15 June	DU(1–30 June by 1 day)
Date of stable iodine administration	-	-	Questionnaire	B(0.5)b
Consumption rate
Consumption rate of cow milk, milk from shop, milk products (milk in soup, sour milk, sour cream, soft cottage cheese, kefir), and leafy vegetables reported during personal interview	ri	L d−1 (kg d−1)	Questionnaire	TR(0.75 × AM, AM, 1.25 × AM)c
Imprecise consumption rate
Response: “I did consume (foodstuff), but I do not remember how much (foodstuff) I consumed”	ri	L d−1 (kg d−1)	Table 7	TLN(GM, GSD, GSD−2 × GM, GSD2 × GM)d
Response: “I do not remember if I consumed (foodstuff)”	ri	L d−1 (kg d−1)	Pcons × AM (Table 7)	TLN(GM, GSD, GSD−2 × GM, GSD2 × GM) with probability of B(Pcons)

^aDU(a₁, a₂, … , a_n): discrete uniform distribution that returns a₁, a₂, … , a_n with equal probability of n⁻¹.

^bB(p): Bernoulli distribution that returns “1” with probability (p) and returns “0” with probability (1 – p).

^cTR(min, mode, max): triangular distribution with the following parameters: minimal value (min), mode of distribution (mode), maximal value (max).

^dTLN(GM, GSD, min, max): truncated lognormal distribution with the following parameters: geometric mean (GM), geometric standard deviation (GSD), minimal value (min), maximal value (max).

Imprecise responses about dates

About 37,000 responses related to dates of relocation, change of consumption habits or administration of stable iodine were imprecise. A set of rules was developed to impute imprecise responses and to attach uncertainties to them. If a respondent did not recall the exact date of relocation, change of consumption habits or stable iodine administration, he or she was prompted to estimate the period of time during which the event occurred, such as “end of April (1986)”, “beginning of May”, “middle of May”, “end of May” or “June”. In the stochastic dose calculation process, these imprecise responses were replaced by the time intervals of 26–30 April, 1–10 May, 11–20 May, 21–31 May or 1–30 June, respectively, and the date was sampled uniformly, for each subject, from this interval.

For imprecise dates of stable iodine administration another rule was applied. If the respondent was not sure about the date of stable iodine administration, it was assumed that stable iodine was either administered or not on this day according to a Bernoulli distribution with equal relative probability of 0.5. This rule was applied to every day in an interval when the study subject may have taken stable iodine.

Imprecise responses about foodstuff consumption rates

The remainder of the imprecise responses (~11,500) related to lack or absence of information about consumption of foodstuffs, such as “I do not remember”. For the answer “I did consume cow milk, but I do not remember how much milk I consumed”, the milk consumption rate was imputed from the age-, gender- and type of settlement-specific distribution of cow milk consumption rates that was obtained from quantitative responses provided by the cohort members during personal interview (Table 7). For the answer “I do not remember if I consumed cow milk”, it was assumed that the respondent consumed cow milk with probability equal to the fraction of cow milk consumers in the cohort (Table 7), and the milk consumption rate was imputed as described above. The same rules were applied for consumption of milk products and leafy vegetables.

TABLE 7.

Fraction of Consumers (P_cons), Arithmetic Mean (AM), Geometric Mean (GM) and Geometric Standard Deviation (GSD) of Consumption Rates of Foodstuff Used for Imputation of Imprecise Responses Provided during the Personal Interviews

Age (years)	Boys				Girls
	Pcons	Consumption rate		GSD	Pcons	Consumption rate		GSD
		L d−1 (kg d−1)				L d−1 (kg d−1)
		AM	GM			AM	GM
Rural settlements: private cow milk
0–0.9	0.61	0.55	0.45	2.0	0.59	0.53	0.40	2.3
1–1.9	0.89	0.58	0.49	1.9	0.89	0.53	0.44	2.0
2–6.9	0.93	0.58	0.47	2.0	0.92	0.49	0.39	2.2
7–11.9	0.96	0.67	0.53	2.1	0.90	0.50	0.39	2.2
12–16.9	0.92	0.81	0.61	2.2	0.88	0.53	0.41	2.3
17–17.9	0.89	0.82	0.63	2.2	0.81	0.51	0.40	2.1
Urban settlements: milk from shop
0–0.9	0.48	0.40	0.34	1.9	0.59	0.43	0.32	2.4
1–1.9	0.87	0.40	0.30	2.4	0.83	0.34	0.25	2.5
2–6.9	0.90	0.34	0.25	2.3	0.90	0.28	0.20	2.3
7–11.9	0.91	0.36	0.25	2.5	0.88	0.30	0.21	2.4
12–16.9	0.91	0.41	0.28	2.5	0.85	0.32	0.21	2.7
17–17.9	0.88	0.45	0.28	2.9	0.82	0.31	0.19	2.9
Rural settlements: milk products
0–0.9	0.73	0.23	0.15	2.7	0.74	0.21	0.16	2.2
1–1.9	0.94	0.25	0.19	2.2	0.92	0.19	0.14	2.4
2–6.9	0.93	0.17	0.12	2.5	0.94	0.15	0.10	2.6
7–11.9	0.96	0.18	0.12	2.6	0.95	0.15	0.11	2.6
12–16.9	0.94	0.22	0.14	2.9	0.96	0.16	0.10	2.8
17–17.9	0.91	0.22	0.15	2.6	0.93	0.18	0.12	2.7
Urban settlements: milk products
0–0.9	0.82	0.23	0.15	2.4	0.85	0.22	0.15	2.4
1–1.9	0.95	0.19	0.15	2.1	0.97	0.19	0.14	2.3
2–6.9	0.95	0.19	0.13	2.5	0.96	0.18	0.13	2.4
7–11.9	0.96	0.25	0.16	2.7	0.97	0.18	0.13	2.6
12–16.9	0.95	0.28	0.18	2.7	0.97	0.21	0.15	2.7
17–17.9	0.95	0.29	0.20	2.7	0.98	0.21	0.13	2.9
Rural settlements: leafy vegetables
0–0.9	0.14	0.005	0.003	2.8	0.13	0.010	0.006	2.8
1–1.9	0.42	0.015	0.010	2.4	0.47	0.014	0.009	2.5
2–6.9	0.62	0.027	0.018	2.5	0.65	0.030	0.021	2.4
7–11.9	0.69	0.051	0.033	2.5	0.70	0.050	0.032	2.6
12–16.9	0.75	0.055	0.036	2.5	0.80	0.057	0.038	2.5
17–17.9	0.89	0.065	0.046	2.3	0.87	0.051	0.035	2.4
Urban settlements: leafy vegetables
0–0.9	0.13	0.006	0.003	3.0	0.10	0.009	0.006	2.6
1–1.9	0.35	0.013	0.009	2.4	0.44	0.016	0.008	3.3
2–6.9	0.57	0.022	0.012	2.9	0.58	0.023	0.014	2.7
7–11.9	0.65	0.042	0.025	2.8	0.66	0.040	0.024	2.8
12–16.9	0.76	0.046	0.029	2.6	0.72	0.044	0.027	2.7
17–17.9	0.79	0.039	0.022	2.9	0.72	0.040	0.024	2.8

Sensitivity Analysis

To assess the sensitivity of the dose calculation model to parameters that where “shared” compared to those that were “unshared”, a sensitivity analysis was performed. The sensitivity index was calculated for each parameter as follows (33):

$${SI}_k(p)=\left|1-\frac{D_k^{min}(p)}{D_k^{max}(p)}\right|,$$ (7)

where SI_k(p) is the sensitivity index (unitless) for parameter p and subject k; $D_k^{min}(p)$ is the instrumental thyroid dose estimate (mGy) obtained when parameter p has a minimal value; $D_k^{max}(p)$ is the instrumental thyroid dose estimate (mGy) obtained when parameter p has a maximal value. In sensitivity index calculations, the central values (see Tables 1–6) were assigned to the other parameters.

The value of the sensitivity index varies within the range {0, +1}, and the closer the value is to “1”, the more sensitive the model is to this parameter. Due to the time-consuming nature of the task, the sensitivity index was not calculated for all 11,732 Belarusian cohort members but for 10% randomly selected from the entire cohort, i.e., for 1,174 study subjects.

RESULTS

Summary Statistics of Thyroid Doses

One thousand sets of instrumental thyroid doses from ¹³¹I intake were calculated for the cohort of the 11,732 Belarusian persons. Table 8 shows the distribution of arithmetic means of individual stochastic thyroid doses for the Belarusian cohort. The global arithmetic mean of individual mean thyroid doses for the entire cohort was 0.68 Gy. For two thirds of the cohort members the arithmetic mean of their individual stochastic thyroid doses was less than 0.5 Gy. The highest individual arithmetic mean of stochastic doses among the study subjects was 39 Gy.

TABLE 8.

Distribution of the Means of Individual Stochastic Thyroid Doses from ¹³¹I Intakes for the 11,732 Belarusian Cohort Members

Interval of the means of stochastic thyroid doses (Gy)	N	Percentage (%)	Mean dose in interval (Gy)
<0.05	1,982	16.9	0.023
0.05–0.19	3,005	25.6	0.11
0.2–0.49	2,819	24.0	0.33
0.5–1.9	3,083	26.3	0.98
2–4.9	643	5.5	3.0
5–9.9	149	1.3	6.6
≥10	51	0.4	15
Entire cohort	11,732	100.0	0.68

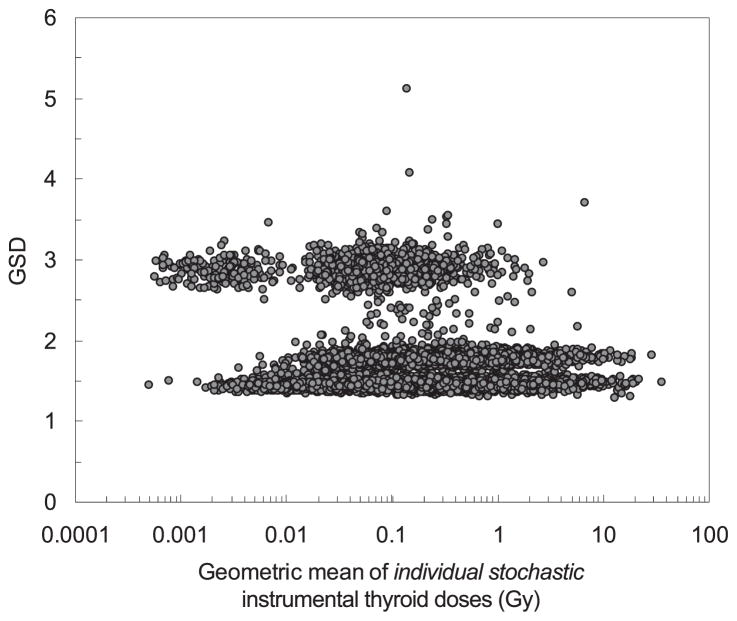
The fitted distribution of individual stochastic doses for each subject was found to be approximately lognormal and the GSD of that distribution was used to characterize the overall uncertainty for each individual. The GSD over all subjects varied from 1.33 to 5.12 with an arithmetic mean of 1.76 and a geometric mean of 1.73. Table 9 shows the distribution of the GSDs attached to the individual stochastic thyroid doses for Belarusian cohort members. For more than half of the cohort, the GSD ranged from 1.5 to 2.0. The largest GSDs were associated with small ¹³¹I activity in the thyroid and were defined by measurement uncertainties attached mainly to the calculated LLE.

TABLE 9.

Distribution of the GSDs Attached to the Individual Stochastic Thyroid Doses

GSD interval	N	Percentage (%)	Mean dose in interval (Gy)
<1.5	4,015	34.2	0.67
1.5–1.9	6,477	55.2	0.78
2–2.9	1015	8.7	0.20
≥3	225	1.9	0.29
Entire cohort	11,732	100.0	0.68

Figure 3 shows the subject-specific uncertainties (GSD) of the individual stochastic instrumental doses plotted against the geometric means of the individual stochastic instrumental doses. As can be seen in Fig. 3, there are three groups of GSDs, which correspond to three groups of subjects with different characteristics of measured ¹³¹I activity: 1. The points in the lower area correspond to the subjects with activity in thyroid measured with SRP-68-01, DRG3-02 or RFT-20046 instruments; 2. The points in the middle area correspond to the subjects with activity in thyroid measured with the DP-5 device; and 3. The points in the upper area correspond to the subjects with activity calculated from the LLE with an assigned error of 100% for the SRP-68-01 device (left side) and DP-5 device (right side).

FIG. 3.

Subject-specific uncertainty (GSD) of individual stochastic instrumental doses as a function of geometric mean of individual stochastic instrumental doses.

Sensitivity Analysis

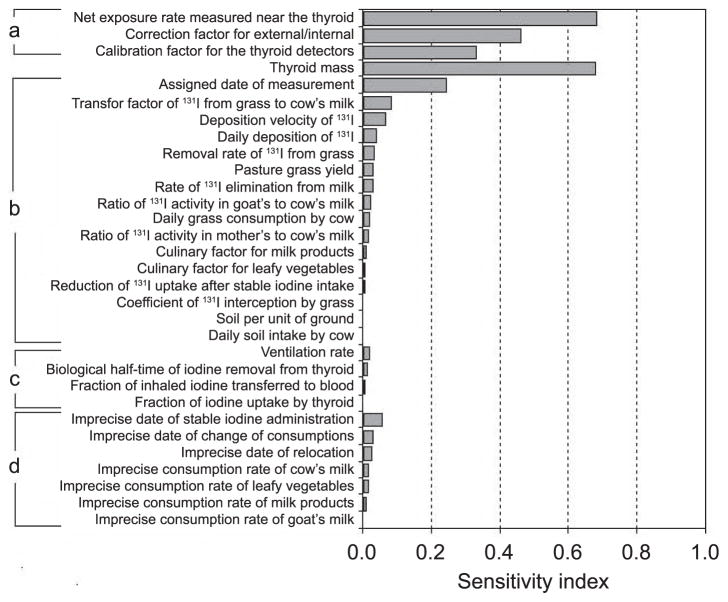
Figure 4 shows the rank of the parameters according to sensitivity index, i.e., their relative contribution to the overall uncertainty in the thyroid dose estimate. For a given parameter, the geometric means of sensitivity index is shown only for those study subjects for whom uncertainty in the parameter was considered. For example, the sensitivity index for thyroid mass was estimated based on calculations done for the entire sample of 1,174 study subjects, while the sensitivity index for the date of measurement was calculated for 514 study subjects for whom date of measurement was assigned.

FIG. 4.

Ranking of the model parameters according to their contribution to uncertainty in dose estimates. Section a: Errors associated with estimates of ¹³¹I activity in the thyroid. Thyroid mass. Section b: Shared errors associated with ecological model. Section c: Unshared errors associated with biokinetic models. Section d: Unshared errors associated with information from personal interviews.

The sensitivity analysis (Fig. 4) shows that sources of unshared errors associated with estimates of ¹³¹I activity in the thyroid (i.e., net exposure rate, correction factor for external and internal contamination of human body, calibration factor for the thyroid detector) as well as thyroid mass are the major contributors to overall uncertainty in thyroid dose estimates. It should be noted that the highest value of the sensitivity index (0.99, not shown on Fig. 4) was found for LLE that was assigned to 117–1,174 subjects for whom sensitivity index was calculated.

Unshared errors associated with parameters of biokinetic models and imprecise answers from personal interviews were found to be small contributors to the overall uncertainty. Among shared errors associated with parameters of the ecological model, only the contribution of assigned date of measurement to uncertainty is similar to that for parameters used to estimate the ¹³¹I activity in the thyroid. However, error in assigned date of measurement is shared not among all study subjects, but among those for whom results of measurements were recorded in the same notebook. Since these data are spread out over 363 notebooks with numbers of subjects recorded in the notebooks ranging from 1 to 91, interindividual correlation associated with this source of shared error across the entire cohort is weak.

Table 10 provides the statistical distributions of parameters of the thyroid dose among the 1,000 sets of cohort dose realizations. The columns show the cohort distribution of the arithmetic mean thyroid dose and of three quantiles of the cohort distribution, i.e., the 2.5 percentile, the median and the 97.5 percentile. As can be seen from the table, the mean, median and 95% uncertainty range exhibit very small variations between the 1,000 cohort dose realizations, indicating that the shared sources of uncertainty in the estimated instrumental doses are quite small.

TABLE 10.

Statistical Distributions of Parameters of the Instrumental Thyroid Dose among 1,000 Sets of Cohort Dose Realizations

Parameter	1,000 sets of cohort dose realizations (Gy)
	2.5%	Median	Mean	97.5%
Minimum	0.005	0.21	0.64	3.7
Maximum	0.007	0.27	0.80	4.9
Median	0.006	0.23	0.68	4.1
Mean	0.006	0.23	0.68	4.1
SD	0.0003	0.008	0.024	0.16

DISCUSSION AND CONCLUSIONS

Comparison with Deterministic Dose Estimates

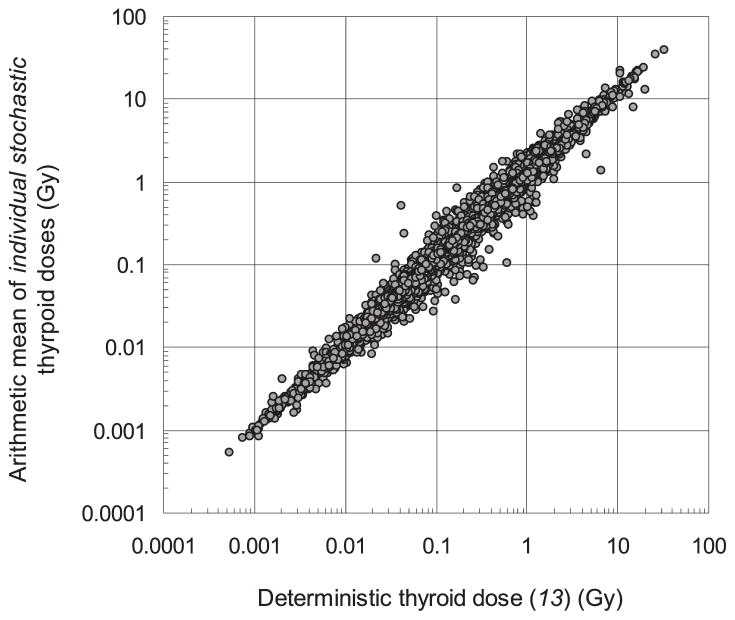
We compared the arithmetic means of stochastic thyroid doses calculated in this study with the deterministic doses estimated previously (13) for the same cohort (Fig. 5). The global arithmetic mean of simulated individual mean doses in this study is 0.68 Gy compared to the mean of deterministic estimates of 0.58 Gy. The geometric mean of the arithmetic means of stochastic doses among all cohort members is 0.27 Gy compared to the geometric mean of the deterministic estimates of 0.23 Gy. The differences between the stochastic and deterministic dose estimates (Fig. 5) are mainly due to the asymmetric nature of the lognormal distribution of individual stochastic doses, as well as other factors, such as:

FIG. 5.

Relationship between the arithmetic mean of stochastic thyroid doses and deterministic thyroid dose for Belarusian cohort members.

• The revision of values of correction factor used to account for contribution of external and internal contamination of human body to the signal recorded by the thyroid detector;

• The uncertainty assigned to the date of measurement, which influences the ecological activity of ¹³¹I in the thyroid at the time of measurement and consequently, the ratio of measured to ecological ¹³¹I activity that defines the instrumental thyroid dose [eq. (2)]; and

• The imputation of foodstuff consumption rates with probability of Bernoulli distribution (see section, Unshared Errors Associated with Information from Questionnaire).

Thyroid Masses

To verify if the thyroid-mass values used in this study, which were derived from thyroid volume ultrasound measurements performed in 1991–1996 in individuals who were not part of the cohort, provide a plausible characterization of the age-dependent thyroid masses in the cohort at the time of the Chernobyl accident, we compared the values for Gomel Oblast that were used in this study (see Table 4) with: 1. thyroid-mass values in children aged 8–16 years derived from measurements done in 1998–2002 by Sasakawa Memorial Health Foundation;⁴ and 2. values measured in 1996–2003 during the 1st screening cycle of Belarusian-American cohort study (10). Age-specific mean values of thyroid mass in boys and girls for 1998–2002 and 1996–2003 are shown in Table 11. On average, age-specific thyroid masses measured in 1998–2001 and in 1996–2003 were, respectively, 17 and 23% lower than those measured in 1991–1996 and used in this study (Table 4), both for boys and girls.

TABLE 11.

Values of Age-Dependent Thyroid Masses [Arithmetic Mean and Geometric Standard Deviation (GSD)] in Children of Gomel Oblast Derived from Ultrasound Measurements of Thyroid Volumes Done in 1998–2001 and 1996–2003

Age (years)	Girls				Boys
	1998–2001		1996–2003		1998–2001		1996–2003
	Thyroid mass (g)	GSD	Thyroid mass (g)	GSD	Thyroid mass (g)	GSD	Thyroid mass (g)	GSD
8.0–8.9	5.0	1.30	-	-	5.0	1.30	-	-
9.0–9.9	5.6	1.30	-	-	5.6	1.30	-	-
10.0–10.9	6.6	1.33	-	-	6.4	1.30	-	-
11.0–11.9	7.9	1.33	7.4	1.34	7.1	1.30	6.1	1.48
12.0–12.9	9.1	1.34	7.3	1.40	8.0	1.31	7.3	1.48
13.0–13.9	10.2	1.32	9.3	1.40	9.2	1.33	8.2	1.39
14.0–14.9	11.2	1.35	10.1	1.35	10.8	1.32	9.7	1.34
15.0–15.9	11.7	1.31	10.4	1.35	12.2	1.31	11.2	1.38
16.0–16.9	12.7	1.28	11.3	1.41	13.5	1.29	11.8	1.34

The values of the thyroid mass are determined by several factors, with iodine sufficiency in the area of residence playing an important role. To show evidence that the gender- and age-specific thyroid masses used in our study are the best approximation of thyroid masses in children at the time of the Chernobyl accident, we performed a literature review to clarify the situation with respect to stable iodine supplementation in Belarus before and after the Chernobyl accident. A program of stable iodine supplementation had been implemented in Belarus by the beginning of the 1980s resulting in a significant reduction in endemic goiter rates (34–36). By the mid-1980s, the work on iodine supplementation was discontinued even though the results of a geochemical study at that time showed low iodine content in soil and water, with subsequent low absorption of iodine in the plants. Medical attention to preventing endemic goiter was reduced with many specialized antigoiter dispensaries being closed. By the time of the Chernobyl accident, there were no systematic efforts or a national program on stable iodine supplementation in the country, and substantial increase of goiter incidence was observed in 1990 in all regions of Belarus (34). Measurements of urinary iodine and thyroid volume performed in 1995–1998 among 11,562 children 6–18 years old selected from 30 schools across Belarus showed moderate iodine deficiency in all oblasts in Belarus, with the exception of Gomel (37). In Gomel Oblast the iodine deficiency was classified as mild because of some efforts on iodine prophylaxis after the Chernobyl accident (37). The nationwide stable iodine supplementation program started in Belarus in 2001.

Because of higher rates of iodine turnover and lower inventory of iodine in the thyroid of children compared to adults, it is plausible that children may be more sensitive to fluctuations in dietary iodine availability, with signs of iodine deficiency appearing sooner than in adults. Signs of thyroid dysfunction in children aged 6–16 years became apparent 14 months after the discontinuation of the iodine supplementation program (38). Twelve months after the beginning of the iodine supplementation program, positive changes in thyroid function, including reduction of thyroid volume, could already be observed in 6–16 year old children (38).

Based on the available information, we concluded that thyroid volume measurements performed in children in 1991–1996 are a good approximation of thyroid volumes in children at the time of the Chernobyl accident. Measurements performed in later years, i.e., 1998–2002 and 1996–2003, could be more biased as a result of the stable iodine supplementation activity that took place in Gomel Oblast and made evident by the mild degree of iodine deficiency in 1995–1998.

Comparison with Other Studies

The stochastic thyroid dose estimates from ¹³¹I intakes that have been obtained in our study were compared with those from a study that was conducted in a Ukrainian cohort of 13,204 subjects using similar methodology (6). The results are similar in terms of the overall mean stochastic thyroid dose for the cohort (0.68 Gy in our study and 0.65 Gy in Ukraine) and geometric mean (0.27 Gy in our study and 0.19 Gy in Ukraine). The stochastic doses estimated in this study are characterized by a larger uncertainty with an arithmetic mean GSD of 1.76 (compared to 1.55 in Ukraine), a geometric mean GSD of 1.73 (compared to 1.47 in Ukraine) and a higher fraction of stochastic thyroid doses with a GSD greater than 2.0 (11% in this study and 3.8% in Ukraine). Higher uncertainty in doses estimated in this study is mainly a result of larger uncertainties in the estimates of ¹³¹I activity in the thyroid and due to uncertainty of assigned dates of measurements. In the Ukrainian cohort, exact dates were available for all measurements.

Uncertainties in thyroid dose estimates in our study are lower than those reported for studies where thyroid doses, in the absence of thyroid measurements, were estimated using only modeling. In post-Chernobyl case-control studies of thyroid cancer, the estimated GSDs of the thyroid doses were in range from 1.7 to 4.0 in a study of 1,615 Belarusian and Russian children (39) and from 1.8 to 3.5 in a study of 198 Russian children (40); the median GSD in both studies was 2.2. A mean GSD of 2.2 (range 1.6–5.4) was reported by Kopecky et al. (41) for thyroid doses reconstructed for the participants of the Hanford thyroid disease study. The GSDs varied from about 1.5–8.5 with a majority of values lying in a range from 2 to 3 for thyroid doses reconstructed in the Utah thyroid cohort study (42) as a consequence of radioactive fallout from atmospheric nuclear weapons tests.

Although our study has significant strengths, it also has limitations. In the calculation of the instrumental thyroid dose [see Eqs. (1) and (2)], the assumption is made that the relative shape of the variation of $Q_k^{\mathit{ecol}}(t)$ with time is correct, so that the adjustment at time t_m, which replaces the calculated ¹³¹I thyroid activity at time t_m with the measured value, also applies to any other time after the accident. It is also implicitly assumed that: 1. The measured ¹³¹I thyroid activity is correct, i.e., it is not associated with a clerical error that cannot be readily accounted for in an uncertainty analysis; and 2. The responses provided by the study subject during the personal interview are reliable.

The first assumption is reasonable as long as the scaling factor, which is defined as the ratio of the measured and calculated ¹³¹I activities in the thyroid at time t_m (see Fig. 1), is relatively close to 1 (i.e., between 0.1 and 10). This is because the variation with time of the ¹³¹I thyroidal activity resulting from the consumption of each of the main foodstuffs contributing to the thyroid dose (milk, milk product and leafy vegetables) is, to a good approximation, proportional to the same function of time; therefore, the shape in time of their sum does not change much with errors in the proportions represented by the different foodstuffs. The additional contribution to the thyroid dose from inhalation of airborne radioiodine, as opposed to dietary intake, is typically small, of the order of a few percentages. This is evident by the relative insensitivity of the calculated activity in the thyroid to the parameters for ventilation rate and fraction of inhaled radioiodine that is transferred to blood (Fig. 4). Therefore, under conditions of continuous residence in the same settlement during the two months after the accident and daily consumption of foodstuffs from the same sources, scaling factors relatively close to 1 presumably arise from biases in the estimated ¹³¹I ground deposition density, interception coefficient of ¹³¹I by vegetation, transfer coefficient of ¹³¹I from pasture intake to cow milk, daily consumption of ¹³¹I-contaminated foodstuffs, or other parameter values that have a multiplicative effect on the calculated dose. Thus the assumption, that the relative shape of the variation of $Q_k^{\mathit{ecol}}(t)$ with time is correct, appears to be valid and we are justified in considering it a small source of uncertainty compared to those related to the thyroid mass or to the derivation of the ¹³¹I thyroidal activity from the direct thyroid measurement. For some study subjects, the scaling factor was found to be very high (i.e., greater than 100) or very low (i.e., less than 0.01), and biases in the parameter values of the ecological model are not sufficient to explain these extreme values. Case examples of such study subjects were presented and analyzed in previous work (13). The results indicate that biases in parameter values cannot fully explain the discrepancies between the instrumental doses and in the ecological doses when the scaling factors are either very high or very low. Possible reasons for those discrepancies are that the person interviewed was not the study subject with the assigned direct thyroid measurement, or that experimental or clerical errors were made during the direct thyroid measurement or its processing. It is acknowledged that in those cases the uncertainty associated with the instrumental thyroid dose value may have been grossly underestimated. However, to assess the doses to all study subjects in the same manner, it was assumed that the direct thyroid measurement was correctly performed and processed. There are a number of study subjects with scaling factors in the intermediate ranges (i.e., from 10 to 100 and 0.01 to 0.1). Although the main reasons for these intermediate values are usually not clear, it is believed that they are due to a combination of factors, including biases in parameter values, complex residential histories and difficulties in processing the direct thyroid measurements. Here again, it is acknowledged that the uncertainties are somewhat underestimated.

The second assumption is also reasonable if a good agreement between the instrumental dose and the ecological dose is observed. However, unreliable responses provided during the interviews may result in the scaling factor to be very high or very low (13). Reliability of questionnaire-based doses is limited by memory recall of the respondent. Further work is underway to evaluate reliability of responses provided by the study subject during the personal interview and their influences on uncertainty in the dose estimates, both ecological and instrumental.

Another possible limitation of our study deals with the approach when the uncertainties in the parameters used to calculate thyroid doses were either assigned to be shared or unshared. For example, we considered thyroid mass to be a source of unshared error and used the mean and the variability of the thyroid-mass values derived from measurements to characterize the distribution of this parameter. As the number of measurements in each age-, gender- and oblast-specific category was close to or more than 1,000, the mean and variability of thyroid-mass values were estimated with high precision and it was not deemed necessary to consider shared uncertainty in the mean and GSD of the distributions of thyroid-mass values.

Finally, it is recognized that the sensitivity analysis that was performed for the purposes of this study is rather simplistic. However, because the results that were obtained are entirely consistent with what was expected based on the input data and on the dose assessment method, it was deemed unnecessary to perform a more sophisticated sensitivity analysis.

In summary, in this study the 1,000 sets of instrumental thyroid doses due to ¹³¹I intake have been calculated for the cohort of Belarusian children. Uncertainties in estimated thyroid doses are driven by unshared errors associated with estimates of ¹³¹I activity in the thyroid, thyroid masses and, to a lesser degree, imprecise dates of direct thyroid measurements that are shared among multiple subgroups of the study subjects. The contribution of other shared errors (parameters of ecological model) and of unshared errors (parameters of the biokinetic model and with information from personal interviews) is small. The small degree of shared uncertainty in the estimated thyroid doses is shown in Table 10, which provides information on the distribution of the 1,000 alternative cohort dose realizations. These multiple sets of cohort doses will be used to evaluate radiation risks of thyroid cancer and other thyroid diseases taking into account the structure of dosimetry errors.