Highly-accelerated chemical exchange saturation transfer (CEST) measurements with linear algebraic modeling

Abstract

Purpose

In clinical studies compartmental average CEST measurements rather than high-resolution CEST images may suffice for evaluating its diagnostic value. A recently-developed method—spectroscopy with linear algebraic modeling or SLAM—could directly provide compartmental measures with dramatically reduced scan time and optimal signal-to-noise ratios. Here, we test whether SLAM can be adapted to significantly accelerate CEST acquisitions.

Methods

Conventional anatomical images and raw CEST image k-space data were acquired from 7 brain tumor patients. SLAM was applied to the CEST data using acceleration factors of R=1-45, after segmenting compartments from co-registered images. SLAM-CEST measures were compared with average values from the identical compartments obtained by conventional Fourier transform (FT) CEST.

Results

SLAM generated compartment average CEST z-spectra that were indistinguishable from conventional FT-CEST for R≤5. SLAM-CEST z-spectra at ±3.5 ppm were highly correlated with FT-CEST measures (r²≥0.98 for R≤9; r≥0.995 for R≤45). The average error of SLAM-CEST vs. FT-CEST measures was ≤10% for R≤45, in acquisitions requiring as few as a single k-space phase-encoding step.

Conclusion

Applied to patients with brain tumors, SLAM-CEST can yield results that are quantitatively equivalent to conventional CEST up to 45 times faster, which could prove enabling in clinical settings where scan time is limiting.

INTRODUCTION

Chemical exchange saturation transfer (CEST) (1) is an emerging MRI contrast mechanism. The technique can indirectly detect low-concentration exogenous (2-7) and endogenous (8-11) molecular pools via their saturation transfer effect on the bulk water signal with which they exchange (12-14). CEST imaging may have a useful role in the assessment of many human diseases, including cancer (15-18), stroke (19,20) and Parkinson’s disease (21).

However, CEST imaging is much slower than routine MRI because saturation images need to be acquired repetitively at multiple saturation frequencies. This can become prohibitive when whole brain coverage is required and/or when three-dimensional (3D) acquisition is used (22). Even longer scan times are needed to acquire whole z-spectra at a high spectral resolution over a wide range of offset frequencies. Recently, several z-spectral fitting methods (23-27) used for quantifying pure CEST effects and resolving confounding nuclear Overhauser effects (NOE) (9), have placed further burdens on scan-time. Meanwhile, ultrafast CEST (28-31) and other acceleration techniques (32) do offer some respite through increased efficiency. Nevertheless, in clinical studies, CEST images are typically evaluated by averaging individual voxel indices over multiple voxels or compartments, which makes the proportionate fraction of time spent on fine spatial-encoding for CEST, unnecessary. Examples employing compartment average CEST measurements include those in gadolinium-enhancing areas of tumor for grading them (17,18), and in the substantia nigra in Parkinson’s disease (21). Therefore arguably, the ability to generate the end-product–a compartmental average CEST index–has practical value, both in terms of speed and potential clinical utility.

Recently, spectroscopy with linear algebraic modeling (SLAM) (33,34) was introduced as a method for accelerating acquisitions that generates near optimal compartment signal-to-noise ratios (SNR) per unit time. The central idea of SLAM is to group voxels defined by scout MRI into compartments, and reduce the number of phase-encoding gradient steps to a small subset of the original ones, chosen from central k-space, which maximizes SNR. The reduction in phase-encodes is possible because the number of unknowns is significantly reduced from the number of voxels, to the number of compartments. The compartmental spectra are solved by incorporating the compartment segmentation information into the standard Fourier Transform (FT) reconstruction model. SLAM has been applied to human cardiac ³¹P spectroscopy (33) and brain ¹H spectroscopy (34), achieving 8- to 120-fold acceleration factors compared to conventional patient acquisitions; or up to a 3-fold higher SNR in heart or tumor compartments as compared to summing the constituent MRS voxels if scan-time is held constant.

Here, the SLAM method is adapted to accelerate CEST acquisitions by reconstructing compartmental average CEST indices directly. The SLAM formulae are updated to be compatible with imaging (MRI) localization models which, unlike spectroscopy, include both phase-encoding and frequency-encoding terms. The main magnetic field (B₀) inhomogeneity correction, crucial for CEST, is incorporated into SLAM in a manner equivalent to standard CEST processing procedures. Furthermore, the SLAM formula is modified to account for z-spectrum normalization. Finally, the feasibility of SLAM CEST is demonstrated on eight brain tumor data sets yielding effective acceleration factors of up to 45-fold.

THEORY

Imaging localization with SLAM

In accordance with the conventions used in Ref. (34), the image reconstruction problem involves solving the linear equation,

$${\mathbf{s}}_{M^{\prime }}={\mathbf{E}}_{M^{\prime \ast }M}\times {\rho }_M,$$ (1)

for the image-space data, ρ, where s is the vectorized k-space raw data, E is the combined encoding matrix, M′ is the total number of known k-space data and M is the number of unknown image space voxels. M′ is the product of the number of phase-encoding steps times the number of frequency-encoding steps, times the number of coil elements used for sensitivity encoding (Nc).

For multi-receive acquisition (Nc > 1), E can be constructed as,

$$\mathbf{E}=\left[\begin{array}{c}\hfill {\left(\mathbf{PE}\otimes \mathbf{FE}\right)}_{M^{″\ast }M}\times {\mathbf{SE}}_{M^{\ast }M}^1\hfill \\ \hfill {\left(\mathbf{PE}\otimes \mathbf{FE}\right)}_{M^{″\ast }M}\times {\mathbf{SE}}_{M^{\ast }M}^2\hfill \\ \hfill ⋮\hfill \\ \hfill {\left(\mathbf{PE}\otimes \mathbf{FE}\right)}_{M^{″\ast }M}\times {\mathbf{SE}}_{M^{\ast }M}^{\mathit{Nc}}\hfill \end{array}\right],$$ (2)

where PE is the phase-encoding operator, FE is the frequency-encoding operator which now corresponds to the read-out gradient, SE is the sensitivity encoding matrix for each coil element (1, …, Nc), ⊗ is the Kronecker operator (35), and M″ (= M′/Nc) is the product of the number of phase-encoding steps and the number of frequency-encoded points.

Because the frequency-encoding dimension is typically fully-sampled and two-dimensional (2D) Fourier transformation (FT) is separable in both phase- and frequency-encoding dimensions, a first FT is applied in the frequency-encoding (read-out) dimension before constructing Eqs. [1-2]. FE in Eq. [2] is then replaced by an identity matrix, and s is replaced by a hybrid k-space vector of the FT of the raw data in the frequency-encoding dimension. Furthermore, a noise covariance matrix can be included in both the s hybrid matrix and the E operator using a pre-whitening strategy (36). For simplicity, the same notations are used after these preprocessing steps. Thus, for a single-channel receiver acquisition (Nc = 1), E is simply (PE⊗FE)_M′*M, where FE is an identity matrix and s is the FT of k-space raw data in the frequency-encoding dimension.

The SLAM method incorporates compartment segmentation and correction information (34) into Eq. [1] as:

$${\mathbf{s}}_{M^{\prime }}={\mathbf{E}}_{M^{\prime \ast }M}\times {\mathbf{A}}_{M^{\ast }M}^{-1}\times {\mathbf{b}}_{M^{\ast }M}^{-1}\times {\mathbf{b}}_{M^{\ast }M}\times {\mathbf{A}}_{M^{\ast }M}\times {\rho }_M.$$ (3)

Here the auxiliary b matrix contains the spatial localization information relating to the segmented compartments (33,34), and A is a correction matrix accounting for spatial and temporal B₀ and B₁ inhomogeneity. As described in those references, dimensionality reduction is performed whereby only the compartmental average values of the signal are retained, leading to,

$${\mathbf{s}}_{M^{\prime }}={\mathbf{E}}_{M^{\prime \ast }M}\times {\mathbf{A}}_{M^{\ast }M}^{-1}\times {\mathbf{b}}_{M^{\ast }C}^r\times {\rho }_C^r,$$ (4)

where b^r preserves the C columns in b⁻¹ corresponding to the C compartmental average values in ρ^r. Two possible solutions to Eq. [4] follow:

$${\rho }_C^r={({\mathbf{E}}_{M^{\prime \ast }M}\times {\mathbf{A}}_{M^{\ast }M}^{-1}\times {\mathbf{b}}_{M^{\ast }C}^r)}^{+}\times {\mathbf{s}}_{M^{\prime }}$$ (5)

$$\text{and}{\rho }_C^r={\left({\mathbf{b}}_{M^{\ast }C}^r\right)}^{+}\times {\mathbf{A}}_{M^{\ast }M}\times {\left({\mathbf{E}}_{M^{\prime \ast }M}\right)}^{+}\times {\mathbf{s}}_{M^{\prime }},$$ (6)

where “+” denotes the Moore-Penrose pseudo-inverse. A truncated singular value decomposition (TSVD) (37) strategy is used for computing the pseudo-inverses by discarding singular values less than 2% of maximum ones. The second solution, Eq. [6], was shown to be more compatible with SENSE than Eq. [5] (34), and thus is chosen here. M′ for SLAM can be much smaller than that used for conventional SENSE MRI (38) involving FT followed by SENSE unfolding, because only the C unknown compartmental values are solved.

Adaption of SLAM to CEST

For CEST MRI, images are typically acquired repetitively at different saturation frequencies. Correcting the nominal saturation frequency offset for B₀ inhomogeneity is crucial for generating meaningful CEST maps or z-spectra in the saturation frequency offset domain (39,40). In conventional CEST MRI, z-spectra in image space are first linearly interpolated to a finer resolution along the saturation frequency offset dimension and then shifted based on a separately acquired B₀ map on a voxel-by-voxel basis (17).

To accommodate the correction for SLAM which operates in k-space instead of image space, two steps are performed. First, a linear interpolation is applied to the CEST k-space raw data along the saturation frequency offset dimension. This is equivalent to interpolation in image space in the frequency offset domain, as illustrated in Appendix A. Second, B₀ correction is implemented by incorporating the B₀ map, into the A term in Eq. [6], after stacking the ${\rho }_C^r$ solutions for all offset frequencies. The FT of the stack in the offset dimension is then performed, yielding

$${\rho }_{C^{\ast }N}^f={\left({\mathbf{b}}_{M^{\ast }C}^r\right)}^{+}\times {\mathbf{A}}_{M^{\ast }M}\times {\left({\mathbf{E}}_{M^{\prime \ast }M}\right)}^{+}\times {\mathbf{s}}_{M^{\prime \ast }N}^f,$$ (7)

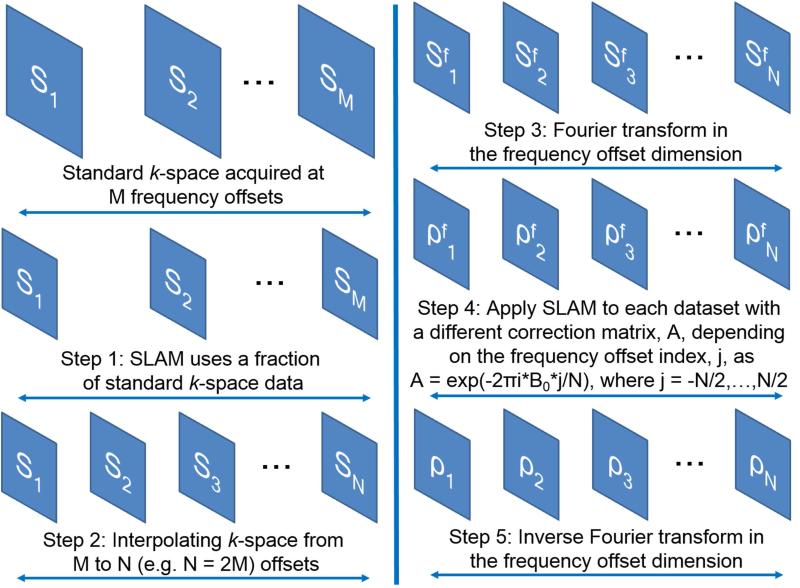
where ${\mathbf{s}}_{M^{\prime \ast }N}^f$ is the FT of stacked s_M′*N in the frequency offset dimension; N is the number of interpolated frequency offsets; and ${\rho }_{C^{\ast }N}^f$ is the FT of stacked ${\rho }_{C^{\ast }N}^r$ in the offset dimension. In Eq. [7], A = e^{−i2π*B₀*j/N} is different for each frequency offset index, j, with −N/2 ≤ j ≤ N/2), and B₀(x,y,z) is the standard B₀ spatial correction map. Finally, an inverse FT of ${\rho }_{C^{\ast }N}^f$ leads to the compartmental-average z-spectrum in image space, ${\rho }_{C^{\ast }N}^r$. Schematic steps for incorporating interpolation and shifting into SLAM are shown in Fig. 1.

Figure 1.

Schematic steps of incorporating linear interpolation and B₀ correction into SLAM. s₁…s_M denote standard k-space raw data acquired at M saturation frequencies. ${\mathbf{s}}_1^f$ … ${\mathbf{s}}_N^f$ refer to interpolated SLAM hybrid k-space data after FT in the saturation frequency dimension, corresponding to ${\mathbf{s}}_{M^{\prime \ast }N}^f$ in Eq. [7]. ${\rho }_1^f$ … ${\rho }_N^f$ represent intermediate SLAM results after B0 correction, corresponding to ${\rho }_{C^{\ast }N}^f$ in Eq. [7]. ${\rho }_{C^{\ast }N}^r$ is the inverse FT of ${\rho }_{C^{\ast }N}^f$ in the saturation frequency offset dimension and gives the SLAM compartmental z-spectra.

Another important adaption neglected by Eq. [7] is the normalization of z-spectra, wherein the saturated image is divided by the unsaturated control image. The unsaturated control image, without a nominal saturation frequency, is not subjected to any interpolation or shifting operations. To accommodate normalization, Eq. [7] can be modified to:

$${\rho }_{C^{\ast }N}^f={\left({\mathbf{b}}_{M^{\ast }C}^r\right)}^{+}\times {\mathbf{A}}_{M^{\ast }M}\times \left\{\right[{\left({\mathbf{E}}_{M^{\prime \ast }M}\right)}^{+}\times {\mathbf{s}}_{M^{\prime \ast }N}^f].∕[{\left({\mathbf{E}}_{M^{\prime \ast }M}\right)}^{+}\times {\mathbf{s}}_{M^{\prime \ast }N}^0\left]\right\}.$$ (8)

Here ./ denotes element-wise division of two matrices, and ${\mathbf{s}}_{M^{\prime \ast }N}^0$ is the stacked k-space data from the unsaturated scan obtained by replicating acquired raw data, ${\mathbf{s}}_{M^{\prime }}^0$, N times in the frequency offset domain. All other processing steps are the same as shown in Fig. 1.

METHODS

MRI experiments

All studies were performed on a 3T Philips Achieva MRI system (Best, Netherlands) with a 32-element head coil. Human studies were approved by the Johns Hopkins Institutional Review Board. Seven patients with pathology-confirmed brain tumors were recruited and provided written, informed consent for the study. All processing and analyses were done with in-house Matlab (Mathworks, Natick, MA) programs on a personal laptop computer (quad-core, 2.7 GHz).

CEST imaging was performed using four 200-ms, 2 μT B₁-amplitude block saturation pulses with a 10 ms inter-pulse gap (22). Saturation offset frequencies were from −14 ppm to +14 ppm with respect to water at 0.5 ppm steps. Eight data sets were acquired (two different slices were acquired for one patient), using a 2D turbo spin-echo (TSE) readout (echo time, TE = 6.4 ms; repetition time, TR = 3 s; field-of-view, FOV = 212×186 mm; acquisition resolution = 2.2×2.2 mm; slice thickness, ST = 4.4 mm; SENSE factor = 2 resulting a 96×45 acquisition matrix size; turbo factor = 45). A separate 2D TSE WASSR (40) sequence, with two 200-ms block saturation pulses and a 10 ms inter-pulse delay at 0.5 μT, was employed for determining B₀ inhomogeneity corrections. WASSR offset frequencies were from −1.5 ppm to +1.5 ppm stepped at 0.125 ppm. Except for setting TR = 1.3 s, the WASSR sequence used the same TSE readout parameters as CEST. Lipid suppression by the “spectral presaturation with inversion recovery” (SPIR) method was used for both CEST and WASSR sequences. The k-space raw data from the CEST scan and from the vendor’s preset SENSE reference scan, were saved for offline in-house reconstruction.

Anatomical images were acquired with conventional T₂-weighted (T₂w), fluid-attenuated inversion recovery (FLAIR) (41), and T₁-weighted (T₁w) MRI sequences. The T₂w scan was a dual-echo multi-slice TSE sequence with TE = 10/80 ms, TR = 2772 ms, FOV = 212×190×131 mm, resolution = 1.1×1.2×2.2 mm, SENSE factor = 2 and duration = 2.4 min. The FLAIR sequence used an inversion recovery multi-slice TSE strategy with TE = 120 ms, TR = 11 s, inversion-recovery delay (TI) = 2.8 s, FOV = 212×189×32 mm, resolution = 0.8×1.1×2.2 mm, SENSE factor = 1.5, for a scan-time of 3.9 min. The T₁w scan was a 3D MP-RAGE (42) sequence with TE = 3.7 ms, TR = 8 ms, FOV = 212×172×165 mm, resolution = 1×1×1.1 mm, TI = 803.5 ms, flip angle = 8°, SENSE factor = 2, and a 4.4 min scan-time. The T₁w sequences were performed before and after intravenous gadolinium contrast injection.

Image reconstruction and analysis

For the conventional “FT” CEST MRI reconstruction, the raw k-space CEST data were first Fourier transformed and then unfolded in the phase-encoding direction with the SENSE (38) algorithm using sensitivity maps computed from the SENSE reference scan. Reconstructed images were interpolated in the frequency offset dimension to 1 Hz (1/128 ppm) resolution between −14.5 ppm and +14.5 ppm. Thereafter, for each voxel, the interpolated z-spectrum was Fourier transformed, a B₀-based linear phase correction applied, and the result inverse transformed, similar to the process detailed for Eq. [7] above. The z-spectrum was down-sampled back to the 0.5 ppm resolution after B₀ correction. The B₀ map was obtained from the vendor’s reconstruction of the WASSR images. A 12^th-order polynomial fitting was applied to the WASSR z-spectrum of each voxel (39). Then, the fitted polynomial coefficients were used to form a new z-spectrum spanning a range of −1.5 ppm and +1.5 ppm, stepped at 1/128 ppm. The difference between the lowest point of the newly-formed z-spectrum and the nominal 0-ppm point was stored as the B₀ map.

The “SLAM CEST” data were reconstructed as follows.

1. The CEST slice was co-registered with an anatomical image based on the off-center distances since both CEST and anatomical images were acquired with the same angulations.

2. The registered anatomical image was segmented into different compartments (Figs. 2a and 3a). Segmentation was primarily based on post-contrast T₁w images after considering all the other T₂w, FLAIR, and pre-contrast T₁w images. Regions of interest were drawn manually by an experienced neuro-radiologist (S.J.). Specifically for high-grade gliomas, a region identified as hyper-enhancing on MP-RAGE images post-contrast was assigned as the tumor compartment. A contralateral compartment was defined by reflecting the tumor compartment about the brain midline using in-house programs. The contralateral compartment typically consists of a mixture of gray and white matter, which shows little amide proton transfer (APT) signal difference between each other at 3T (17). However, cerebrospinal fluid filled ventricular regions were excluded from the contralateral SLAM CEST segmentation. Three other compartments were also defined, “rest of the brain”, scalp and background. The definition of all compartments conformed to the unsmoothed spatial resolution of the conventional CEST acquisition.

3. A subset of phase-encoding lines (fully-sampled in the frequency-encoding direction) were retroactively chosen for 12 different acceleration factors of R = 1 – 7, 9, 11, 15, 23, 45. The subsets of phase encoding steps were always chosen from those closest to central k-space to maximize SNR (33), for example, R = 2 using phase-encoding steps from −11 to 11 (compared to R = 1 using all −22 to 22 phase-encoding steps).

4. Compartmental average z-spectra were directly reconstructed from the chosen subsets of k-space data using Eq. [8] and the segmentation information included in b, with the interpolation and B₀ correction incorporated as depicted in Fig. 1.

Figure 2.

Anatomical image, and SLAM overlaid with conventional FT z-spectra for a patient with a low-grade oligodendroglioma. a: Segmentation of the gadolinium-enhanced T₁w image showing tumor (1), contralateral brain (2), “rest of the brain” (3), scalp (4) and background (5) compartments. b-d: SLAM z-spectra (red) overlaid onto conventional FT (blue) z-spectra for acceleration factors R = 4 (top), 9 (middle) and 45 (bottom) for the tumor (b), contralateral brain (c), and “rest of the brain” compartments (d). The horizontal axis indicates saturation frequency offsets and the vertical axis indicates the saturated CEST signal intensity normalized by the unsaturated signal intensity expressed as a percentage. Zoomed MTR asymmetry spectra can be seen in the online Supporting Information.

Figure 3.

Anatomical image, and SLAM overlaid with conventional FT z-spectra for a patient with a high-grade anaplastic astrocytoma. a: Segmentation of the corresponding gadolinium-enhanced T₁w anatomical image showing tumor (1), contralateral brain (2), “rest of the brain” (3), scalp (4) and background (5). b-d: SLAM z-spectra (red) overlaid onto conventional FT (blue) z-spectra for acceleration factors, R, of 4 (top), 9 (middle) and 45 (bottom), for the tumor (b), the contralateral brain (c), and the “rest of the brain” compartments (d). The horizontal axis indicates saturation frequency offsets and the vertical axis indicates the saturated CEST signal intensity normalized by the unsaturated signal intensity expressed as a percentage. Zoomed MTR asymmetry spectra can be seen in the online Supporting Information.

Conventional FT z-spectra from the individual CEST image voxels comprising the same compartments segmented for SLAM, were averaged to produce reference compartment z-spectra for comparison with SLAM. Asymmetric magnetization transfer ratios (MTRasym) (43) were also calculated to evaluate differences between SLAM and conventional FT CEST. For visual comparison, the FT and SLAM MTRasym values determined at 3.5 ppm, which correspond to the APT-weighted (APTw) image intensities (8), were assigned to all of the voxels in the segmented compartment regions, to form color-coded APTw maps of each compartment. Quantitative comparisons of conventional FT metrics with those from SLAM CEST, were performed using coefficients of determination (r²), Bland-Altman analysis (44) and Pearson’s correlation coefficients (r).

RESULTS

Fig. 2 compares SLAM z-spectra (red) with conventional FT z-spectra (blue) in a patient with a low-grade oligodendroglioma, at three acceleration factors (top to bottom: R = 4, 9, and 45). SLAM z-spectra from the tumor (Fig. 2b), contralateral (Fig. 2c) and “rest of the brain” (Fig. 2d) compartments are essentially coincident with the conventional spectra. Note that with R = 45, SLAM used only a single phase-encoding k-space line. Fig. 3 compares SLAM with conventional FT z-spectra for another patient who had a high-grade anaplastic astrocytoma. Again the z-spectra from the three compartments are highly coincident, especially with an R = 4 (top) acceleration factor.

Fig. 4 shows a quantitative comparison of the conventional FT and SLAM z-spectral intensities measured at 3.5 ppm pooled from the three brain compartments (tumor, contralateral brain, “rest of the brain”) in the eight patient data sets, and reconstructed with six different acceleration factors (R = 2-45). Close alignment to the identity line and high coefficients of determination (r² ≥ 0.98 for R ≤ 9; r² ≥ 0.69 for R ≤ 45) attests to the reliability with which SLAM can track and reproduce conventional FT CEST measurements of APTw signals at 3.5 ppm. For all brain compartments and data sets, the mean error of the SLAM vs. FT (calculated as 1-SLAM/FT) signal at 3.5 ppm was ≤ 3.1% and the standard deviation (SD) of the error was ≤ 7.2% for all 12 acceleration factors.

Figure 4.

Quantitative comparison of z-spectral intensities of SLAM (vertical axes) vs. conventional FT (horizontal axes) measured at 3.5 ppm (APT) for acceleration factors of R = 2 (a), 4 (b), 6 (c), 9 (d), 15 (e) and 45 (f). r² is the coefficient of determination.

Fig. 5 plots the SLAM z-spectrum intensities at the control frequency on the opposite side of water at −3.5 ppm attributed to NOE, as compared to those from the conventional FT z-spectrum. For the six acceleration factors, the SLAM measurements correlate with the conventional FT results with r² ≥ 0.98 for R ≤ 9, deteriorating to r² = 0.89 and 0.69 for R = 15 and 45, respectively. For all brain compartments, data sets and all 12 acceleration factors, the mean error of SLAM vs. conventional FT at −3.5 ppm was ≤ 3.0% ± 7.6% (SD).

Figure 5.

Quantitative comparison of z-spectral intensities of SLAM (vertical axes) vs. conventional FT (horizontal axes) measured at −3.5 ppm (NOE location) for acceleration factors, R = 2 (a), 4 (b), 6 (c), 9 (d), 15 (e) and 45 (f). r² is the coefficient of determination.

Fig. 6 plots the error and Pearson’s correlation coefficients (r) for the entire z-spectra obtained from SLAM in all subjects, as compared to those from conventional FT. The percentage error (Fig. 6a) increases as the acceleration factor grows, with a mean value of ≤ 3.0% and SD of ≤ 8.3%, comparable to those measured at frequency offsets of ±3.5 ppm. The Pearson’s correlation coefficients remain high for all R, dropping to 0.9995 ± 0.0009% (mean ± SD) at R = 45, reflecting the high coincidence of the SLAM and conventional FT z-spectra overall (Figs. 2, 3).

Figure 6.

Error analysis of SLAM vs. conventional FT z-spectra at all frequency offsets. a: Mean ± SD of error percentage (SLAM/FT - 1) for all brain compartments from all subjects, with 12 different accelerations factors (R, horizontal axes). b: Pearson’s correlation coefficients (mean ± standard deviation) comparing SLAM with conventional FT spectra for all brain compartments, data sets and acceleration factors.

Fig. 7 presents Bland-Altman plots for SLAM APTw signals vs. conventional FT APTw signals at different acceleration factors. No significant systemic bias is seen at any acceleration factor. The difference between SLAM and FT increases with acceleration factors: the SD of the differences are 0.029%, 0.077%, 0.085%, 0.17%, 0.25%, and 0.49% for R = 2, 4, 6, 9, 15 and 45, respectively. At least for R≤9, these are much smaller than the mean APTw signal of ~1%.

Figure 7.

Bland-Altman plots of APTw (MTR asymmetry at 3.5 ppm) signals measured by SLAM with different acceleration factors, R = 2 (a), 4 (b), 6 (c), 9 (d), 15 (e) and 45 (f), compared to those by FT. The horizontal axes is the mean of SLAM and conventional FT, and the vertical axes are the difference between SLAM and FT. The solid line is the mean of the difference and the dotted lines bracket ±1.96 times the SDs of the means.

Fig. 8 shows color-coded APTw maps alongside anatomical images of the patient data shown in Figs. 2 and 3. For both patients, little difference can be seen between their compartment-average APTw images obtained by conventional FT (f, h) and SLAM (i and k for R = 4; j and l for R = 9). For the patient from Fig. 2, APTw contrast between the tumor region and the normal brain compartment is negligible (Figs. 8f, 8i and 8j), consistent with the low-grade tumor in this case. The APTw signal from the tumor compartment is 1.4%. This value is consistent with the 95% confidence interval of 0.54%–1.53% (mean, 1.09%) for APTw values in low-grade gliomas reported in the literature under the same experimental conditions (17). For the patient from Fig. 3, the tumor compartment is hyper-intense in the APTw images relative to the normal brain region (Figs. 8h, 8k and 8l). The tumor APTw signal is 2.8%, consistent with reported values of 2.50% (95% confidence interval: 2.04%–2.96%) (17) for high-grade tumors.

Figure 8.

Color-coded APTw maps (e-l) and anatomical images (a-d) for the two patients shown in Fig. 2 (a, b, e, f, i, j) and Fig. 3 (c, d, g, h, k, l). Anatomical MRIs are FLAIR (a, c) and post-contrast T₁w (b, d), with shaded red regions designating the segmented tumor compartments. The color-coded APTw images show the brain maps overlaid on the registered post-contrast patient T₁w images obtained by conventional voxel-by-voxel FT (e, g), compartmentally-averaged FT (f, h) and by SLAM with R = 4 (i, k) and R = 9 (j, l).

DISCUSSION

As the CEST technique moves into clinical settings, incorporating it into existing clinical protocols that include a plethora of other essential MRI techniques, necessitates its implementation with maximum speed and efficiency. Here we have demonstrated that application of the SLAM method can achieve dramatic acceleration factors of up to 45-fold (Figs. 2-8) for providing relevant compartmental average CEST indices. SLAM CEST spectra are based on segmented co-registered anatomical images, which are incorporated into the standard FT model. Although information about the intra-compartmental variation of CEST indices–which may be important in certain applications (45)–is traded for the order-of-magnitude speed-up provided by SLAM, there are many clinical applications, including tumor grading (17,18), Parkinson’s disease (21), creatine kinetics (11) and pediatric brain development (46), where compartmental indices could suffice for diagnosis or assessment, especially when the time required for conventional CEST would preclude any measurement at all. This is of particular concern for pediatric cases (46).

In the present study, SLAM CEST was validated on 8 brain tumor datasets, generating compartmental results that were quantitatively (Figs. 4-7) indistinguishable from conventional FT CEST. The SLAM CEST results can be visualized (Fig. 8) in a similar color-coded manner as conventional FT CEST maps (17) to facilitate interpretation, in practice. In situations where pathological lesions are not apparent on conventional anatomic MRI, different test regions could be defined post-acquisition and compartmental average CEST measurements reconstructed with SLAM CEST to test for MRI-occult CEST abnormalities. We have shown with SLAM MRS that the user is free to arbitrarily define compartment boundaries post-acquisition, the only limitation being to the total number of compartments, which must be chosen scanner-side (34).

Various acceleration factors from 2 to 45 were demonstrated here. The agreement between SLAM and conventional FT CEST deteriorated as the acceleration factors were increased (Figs. 4-7). The choice of the SLAM acceleration factor that can be tolerated depends in part on the magnitude of the CEST effect anticipated in the study. For example, given MTR asymmetry values of 2.50% and 1.09% for high-grade and low-grade gliomas at ±3.5 ppm noted above (17), SLAM acceleration factors of up to R=9 should suffice for differentiating tumor grades with an error of ≤0.17% compared to a conventional FT CEST experiment (Fig. 7). Total scan times of about 11 min have been reported elsewhere for conventional APT brain tumor studies (17): SLAM could reduce these to about 1 min.

The accuracy of whole z-spectra appears to be less sensitive to high acceleration factors than MTR asymmetry at ±3.5 ppm. As shown in Fig. 6, the average errors are within ~4% (mean ≤ 0.6%, standard deviation ≤ 3.1%) for R=6~9; or ~10% (mean ≤ 3.0%, standard deviation ≤ 8.3%) for R=45. Also, the correlation coefficients are greater than 0.995 for all acceleration factors up to 45. This implies that SLAM might be used for whole z-spectral acquisition methods (23-26) to achieve even higher acceleration factors than for applications involving MTR asymmetry. Note that SLAM can achieve acceleration factors higher than 45 for 3D imaging: here we were limited to R=45 because this corresponded to just one frame from central k-space—the minimum possible. A 2D 45-fold acceleration is not possible by any other acceleration technique (32).

Although SLAM CEST was tested here over a wide frequency range of ±14 ppm, SLAM is readily applicable to acquisitions involving more limited ranges of z-spectra, e.g. the “6-offset” case (39). This is because shifting the z-spectrum via a linear phasing in the Fourier domain is independent of the number of z-spectrum points. Also, Eq. [8] is not the only strategy for incorporating z-spectrum normalization into SLAM. For example, Eq. [7] can be applied serially for saturated and unsaturated frequency offsets, then the compartmental results for unsaturated data used for normalization. We have seen comparable but slightly worse results from such a strategy. The formulae (Eqs. 1-6) might also prove useful for obtaining compartmental average measurements from whole organs or lesions of other NMR or MRI parameters, such as relaxation times, for example.

Conclusions

SLAM is a viable strategy for accelerating CEST image acquisitions many-fold. If compartment-average indices can suffice, SLAM can speed-up CEST studies by at least up to 45-fold and generate quantitatively equivalent results as the conventional FT method. SLAM’s ability to yield CEST measures within a scan time of one minute or so, should facilitate its application in many clinical settings where scan time is limiting.

APPENDIX A

Equivalence of interpolation in image space and k-space

Suppose there are three generic FT pairs, A =F{a}, B = F{b} and C = F{c}, where a, b and c are in original space, and A, B and C are in Fourier space. Assume c is a weighted sum of a and b, as c = w₁ × a + w₂ × b, where w₁ and w₂ are linear weighting coefficients. Then: C = w₁ × A + w₂ × B due to the linearity of the FT. This means that linear weighting in one space leads to the equivalent linear weighting in the other space. New data points are created from existing closest data independent of the values being interpolated, so linear interpolation can be performed in either image space or k-space.