A Note on Income Effects and Health Care Cost Growth in Medicare

Abstract

This paper sets out a model of technical change and health care cost growth for a representative Medicare beneficiary facing a budget constraint. Derivation of an explicit expression for health care cost growth shows how technological change and preferences, including income effects, affect cost growth. The analysis highlights the role of the 76% percent subsidy from current taxpayers to Medicare beneficiaries for purchase of health insurance. This subsidy insulates beneficiaries from the income effects of cost growth by shifting the costs and income effects to taxpayers. Simulations show that over the next 10-20 years, income effects will have little effect on cost growth in Medicare.

1. Introduction

Accurate projection of health care cost growth, particularly for Medicare, is critical for formulation of public policy, even in the short run, as decisions about financing and organization of health care can be hard to change and can have significant, potentially costly, long-term consequences. It is generally acknowledged that technological change, with both value and cost consequences, sustains cost growth (Chernew and Newhouse, 2012; Newhouse, 1992). It is also generally acknowledged that “things cannot continue as they are” with health care accounting for a steadily increasing share of national income (Orszag, 2008). At some point, budget constraints, and before that, income effects, should come into play, dampening health care cost growth. When the irresistible force, technological change, meets the immovable object, the budget constraint, what gives?

This note sets out a simple model of technical change, demand and health care cost growth for a representative consumer facing a budget constraint. The consumer is a Medicare beneficiary enjoying subsidies for health insurance from general revenues. The analysis exposes the role of Medicare program design in Medicare cost growth. The subsidy from current taxpayers to Medicare beneficiaries for purchase of health insurance insulates beneficiaries from part of the costs (and therefore the income effects) of increasing health care costs, accelerating Medicare cost growth. Of the $15,374 average spending on Medicare beneficiaries for 2009, the beneficiary paid $2,084 (13.5% of the total) in cost sharing and $1,517 (10% of the total) in premiums, leaving a subsidy from taxpayers at 76.5% of spending.¹ The 76% subsidy estimate is distinct from figuring the full incidence of Medicare which would take account of a beneficiary's tax payments during his or her working life, including the contribution to the Medicare payroll tax (McClellan and Skinner, 2006).² The concern here is not with “who pays” for Medicare but rather in the effect of the subsidy on income effects and cost growth.

The role of trends in income and health care costs is attracting more notice as health care costs approach 20 percent of national income. Hall and Jones (2007) argue that health care spending extends life and that it is reasonable to expect the marginal value of spending on more years of life to decline less rapidly than non-health consumption during a year. If so, health care spending should grow faster than national income.³ The empirical literature does not, however, yield a consensus estimate of the income elasticity of health care demand, though it is at least clear that the income effect is positive.⁴

Medicare financing implies that younger taxpayers bear most of the income effects of Medicare cost growth, and it is their health care use, not Medicare beneficiaries,’ that will be slowed by income effects. The subsidy to Medicare insulates beneficiaries from the income effects of cost growth by shifting the costs and income effects to taxpayers. Simulations show that over the next 10-20 years, income effects will have little effect on cost growth in Medicare. The current pattern of Medicare financing implies a steady redistribution of health care resources from the young to the old.

2. A Model of Health Care Cost Growth

This section derives an expression for health care cost growth in terms of parameters of technological change, utility, and Medicare program design.

2.1 Technological change

Technological change is exogenous and affects cost growth in two ways. First, technological change enhances the value of medical care. Let the marginal benefits from health care (measured in dollars) be λ^tb(q) where q is quantity of medical care, t is time, b > 0, b’ < 0, and λ ≥ 1. The marginal benefit function shifts upward at rate ln(λ). Increasing benefits from medical services increase demand and total costs.

Second, technological change affects costs of production. Let the marginal cost of medical care be γ^t. If technological change reduces unit costs, γ < 1. The opposite case, where γ ≥ 1, is more likely in medical care. Medical care is a service industry, subject to Baumol's cost disease.⁵ Moreover, value-enhancing change (from λ) comes at increased costs. The per-unit cost curve shifts upward at rate ln(γ).⁶ Unit cost increases have countervailing effects. Costs increase because of per unit cost growth. But, demand response to increasing cost constrains growth.⁷

Technological change increases welfare if the rate of increase in benefits exceeds the rate of increase in cost per unit, λ > γ, the natural case to consider.

2.2 Utility and demand with income effects and subsidized insurance

Measure utility in dollars and let utility be

$$\mathrm{U}=\mathrm{B}\left(\mathrm{q}\right)+\mathrm{V}\left(\mathrm{x}\right),$$

where B(q) is the total benefit of health care (such that the marginal benefit is λ^t b(q)) and V(x) is the benefit from consumption of other goods, with V’ ≡ v(x), v > 0, v’< 0. Note that v’< 0 (the fall in the marginal benefit of consumption as consumption increases) introduces income effects.

The budget constraint is:

$$\mathrm{c}{\gamma }^{\mathrm{t}}\mathrm{q}+\mathrm{x}+\mathrm{p}\le \mathrm{y},$$

where c is the fixed coinsurance, p is the premium the consumer pays for health insurance, and y is income, also assumed to be constant.⁸ Actuarial balance requires p = γ^t(1-c)q, but the consumer may not pay the full premium (as is the case in Medicare). Suppose that the consumer only pays a share of the premium, s, so p = s γ^t(1-c)q, with s < 1. Furthermore, the consumer does not take into account the effect of purchase of q on p (moral hazard).

Using the budget constraint to solve for x in terms of parameters and q, substituting it into utility, and taking the derivative with respect to q (the only remaining decision variable), we have the demand equation for q:

$${\lambda }^{\mathrm{t}}\mathrm{b}=\mathrm{c}{\gamma }^{\mathrm{t}}\mathrm{v}=0$$ (1)

Totally differentiating (1) to find dq/dt:

$$\left[{\lambda }^{\mathrm{t}}{\mathrm{b}}^{\prime }+\mathrm{c}{\gamma }^{2\mathrm{t}}{\mathrm{v}}^{\mathrm{t}}\left(\mathrm{c}+\mathrm{s}\left(1-\mathrm{c}\right)\right)\right]\mathrm{dq}=-\left\{\ln \left(\lambda \right)\mathrm{b}{\lambda }^{\mathrm{t}}-\mathrm{c}\left[\mathrm{v}\ln \left(\gamma \right){\gamma }^{\mathrm{t}}-{\gamma }^{\mathrm{t}}{\mathrm{v}}^{\prime }\left(\mathrm{c}+\mathrm{s}\left(1-\mathrm{c}\right)\right)\mathrm{q}\ln \left(\gamma \right){\gamma }^{\mathrm{t}}\right]\right\}\mathrm{dt}$$

After dividing through by λ^tb’:

$$\frac{\mathrm{dq}}{\mathrm{dt}}=\frac{-\ln \left(\lambda \right)\left(\frac{\mathrm{b}}{{\mathrm{b}}^{\prime }}\right)+\left(\frac{\mathrm{c}}{{\mathrm{b}}^{\prime }}\right)\ln \left(\gamma \right){\left(\frac{\gamma }{\lambda }\right)}^{\mathrm{t}}\left(\mathrm{v}-{\gamma }^{\mathrm{t}}{\mathrm{v}}^{\prime }\left(\mathrm{c}+\mathrm{s}\left(1-\mathrm{c}\right)\right)\mathrm{q}\right)}{1+\left(\frac{{\mathrm{v}}^{\prime }}{{\mathrm{b}}^{\prime }}\right){\left(\frac{{\gamma }^2}{\lambda }\right)}^{\mathrm{t}}\mathrm{c}\left(\mathrm{c}+\mathrm{s}\left(1-\mathrm{c}\right)\right)}$$

We make a number of substitutions into the expression for dq/dt. Use (1) to substitute for c in the numerator and denominator. Define the compensated (or Hicksian) price elasticity of demand for medical care,⁹ ${\epsilon }_{\mathrm{q}}=\frac{\mathrm{b}}{{\mathrm{b}}^{\prime }\mathrm{q}}$, and the elasticity of the marginal benefit of consumption, ${\epsilon }_{\mathrm{x}}=\frac{{\mathrm{xv}}^{\prime }}{\mathrm{v}}$. Also, define the ratio of health care costs to other consumption to be $\mathrm{r}=\frac{\mathrm{q}{\gamma }^t}{\mathrm{x}}$ and the share of health care cost paid by Medicare beneficiaries σ = c + s(1-c). (Earlier, we estimated σ to be about .24) With these substitutions, we can then rewrite the expression for dq/dt as follows:

$$\frac{\mathrm{dq}}{\mathrm{dt}}=\frac{{\epsilon }_{\mathrm{q}}\mathrm{q}\left[-\ln \left(\lambda \right)+\ln \left(\gamma \right)(1-{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})\right]}{1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r}}$$ (2)

2.3 Cost growth

The rate of cost growth is g(t):

$$\mathrm{g}\left(\mathrm{t}\right)\equiv \frac{\mathrm{d}\left(\mathrm{q}\left(\mathrm{t}\right)\left({\gamma }^{\mathrm{t}}\right)\right)∕\mathrm{dt}}{\mathrm{q}\left(\mathrm{t}\right){\gamma }^{\mathrm{t}}}$$

Using (2) we have:¹⁰

$$\begin{array}{cc}\hfill \mathrm{g}\left(\mathrm{t}\right)=& \frac{\mathrm{q}\ln \left(\gamma \right){\gamma }^{\mathrm{t}}+\frac{{\epsilon }_{\mathrm{q}}\mathrm{q}\left[-\ln \left(\lambda \right)+\ln \left(\gamma \right)(1-{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})\right]{\gamma }^{\mathrm{t}}}{1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r}}}{\mathrm{q}{\gamma }^{\mathrm{t}}}\hfill \\ \hfill \mathrm{g}\left(\mathrm{t}\right)=& \ln \left(\gamma \right)+\frac{{\epsilon }_{\mathrm{q}}\left[-\ln \left(\lambda \right)+\ln \left(\gamma \right)(1-{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})\right]}{1-{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r}}\hfill \end{array}$$ (3)

3. Analysis

In general, as (3) shows, health care cost growth, g(t), depends on the effect of technological change on the rate of growth of marginal benefits from health care ln(λ), the rate of growth of unit costs ln(γ), elasticity of demand ε_q, elasticity of the marginal utility of other consumption, ε_x, the consumer's share of health care costs paid through by the coinsurance or premium, σ, and on the present ratio of health care costs relative to other consumption, r. All of these pieces in (3) are parameters with the exception of r, which depends on t. As health care costs grow, r will be increasing, magnifying the impact of income effects. Before analyzing the general case, we examine some special cases of (3).

3.1 No demand elasticity (ε_q = 0)

The simplest case is when ε_q = 0. Recall that ε_q is defined as the compensated elasticity of demand. When the compensated demand elasticity is zero, the uncompensated demand elasticity will also be equal to zero. With no demand elasticity, growth is simply the rate of growth of unit costs, ln(γ). There is no quantity response to increasing costs.¹¹

3.2 No income effects (ε_x = 0)

With some demand elasticity, but no income effects, (3) simplifies to:

$$\mathrm{g}\left(\mathrm{t}\right)=\ln \left(\gamma \right)+{\epsilon }_{\mathrm{q}}[-\ln \left(\lambda \right)+\ln \left(\gamma \right)].$$

In the case in which technological change enhances value (ln(λ)) at the same rate as unit costs (ln(γ)), health care costs simply grow at that rate of growth (ln(λ) or ln(γ)). Visually, the marginal benefit and marginal cost schedule are shifting upward at the same rate, and the intersection point at q, is constant.¹²

With demand elasticity, the rate of health care cost growth is constant, as no terms on the rhs of (3’) involve time.¹³ In the normal case in which the rate of value-enhancing change exceeds the unit-cost increasing change, the rate of growth exceeds ln(γ). Visually, the marginal benefit curve is shifting up faster than the unit cost curve, and the utility maximizing q is increasing; demand elasticity determines by how much.¹⁴

Of course, any positive rate of cost growth is ultimately unsustainable with a fixed income. As health care costs increase, the increasing marginal utility of other goods – the income effect – will moderate cost growth.

3.3 Income effects (ε_x < 0) and the role of Medicare subsidy

The most interesting and relevant case is when there are income effects, represented in (3) by the elasticity of the marginal utility of consumption, which will be negative. As an elasticity, we might expect this parameter to take on values around −1. Income effects are greater if ε_x is larger in absolute value. We can see analytically that an increase in this elasticity, corresponding to ε_x becoming more negative, decreases cost growth. From (3), an increase in the income effect is –dg(t)/d(ε_x):

$$\begin{array}{cc}\hfill \frac{-\mathrm{d}\left(\mathrm{g}\left(\mathrm{t}\right)\right)}{\mathrm{d}{\epsilon }_{\mathrm{x}}}=& \frac{{\epsilon }_{\mathrm{q}}\left[-\ln \left(\lambda \right)+\ln \left(\gamma \right)\right]{\epsilon }_{\mathrm{q}}\sigma \mathrm{r}}{{(1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})}^2}+\frac{(1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})\ln \left(\gamma \right){\epsilon }_{\mathrm{q}}\sigma \mathrm{r}-\ln \left(\gamma \right){\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r}{\epsilon }_{\mathrm{q}}\sigma \mathrm{r}}{{(1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})}^2}\hfill \\ \hfill \frac{-\mathrm{d}\left(\mathrm{g}\left(\mathrm{t}\right)\right)}{\mathrm{d}{\epsilon }_{\mathrm{x}}}=& \frac{{\epsilon }_{\mathrm{q}}\left[-\ln \left(\lambda \right)+\ln \left(\gamma \right)\right]{\epsilon }_{\mathrm{q}}\sigma \mathrm{r}}{{(1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})}^2}+\frac{\ln \left(\gamma \right){\epsilon }_{\mathrm{q}}\sigma \mathrm{r}}{{(1+{\epsilon }_{\mathrm{q}}{\epsilon }_{\mathrm{x}}\sigma \mathrm{r})}^2}\hfill \end{array}$$ (4)

Both the first and second terms in (4) are negative when technological change is on net beneficial, and λ > γ.

Returning to (3), we can see that income effects work through the ε_xσr term, the product of the elasticity of the marginal utility of consumption, the share of Medicare costs paid for by beneficiaries, and the ratio of health care costs to other consumption. ε_x derives from preferences, σ is a policy variable, and r is a state of the economy at any point in time. The term ε_xσr will grow over time as health care costs grow in relation to other consumption. A low σ, as we currently have in Medicare, undermines income effects and their dampening effect on growth, directly in proportion to the degree of taxpayer-to-beneficiary subsidy.

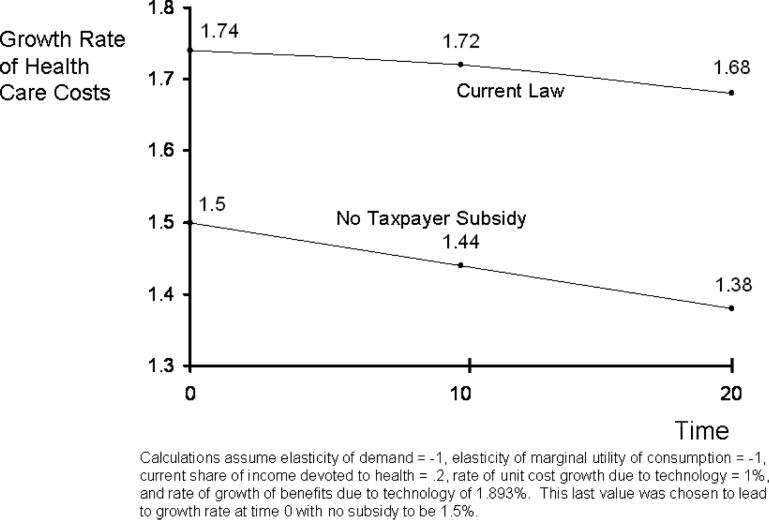
Simulations using (3) illustrate the quantitative importance of the subsidy from taxpayers in terms of health care cost growth. Figure 1 uses as a base case, values for technological change and elasticities such that at a health share of national income of 20%, the rate of growth of health would be 1.5% if there were no subsidies from taxpayers to Medicare beneficiaries.¹⁵ Income effects depress cost growth modestly over time, bringing growth down to 1.38 after 20 years. Income effects become more powerful over time because of the increasing share of income going to health care. (In 20 years, the share in the base case grows to 26.6% of national income.)

Figure 1.

Health Care Cost Growth in Medicare

Growth rates of costs are markedly higher with the subsidy in current Medicare policy. With beneficiaries paying only 30% of their health care costs (a conservative estimate based on the discussion in Section 1), the growth in health care costs is 1.74% per year instead of 1.5% (a 16% increase) due to the weakening of the income effect. Furthermore, growth rates fall more slowly as well – by year 20, they are only down to only 1.68% per year (increasing the gap to 22% in comparison to no subsidy). Under the “current law” simulations, health care costs would have risen to 28.1% of income in 20 years. Running the simulations forward, with the current subsidy, it takes 50 years to bring the rate of cost growth down to 1.5%.

The simulations depicted in Figure 1 make the two main points of the paper. First, income effects bring down cost growth, but at reasonable parameter values, this effect is modest over intermediate time horizons. Second, the subsidy from taxpayers to Medicare beneficiaries has large effect on growth rates, and the impact grows over time.

4. Discussion

Within a comprehensive model of demand for health care, this paper highlights the role of the large subsidy to Medicare beneficiaries from taxpayers in moderating any income-effect brake on health care cost growth in Medicare. An explicit model of utility, technology, financing, and health care cost growth may be useful to researchers forecasting health care costs. The simple model constructed here may be grafted on to multiple-sector or microsimulation models of health care costs over time. The analysis provides a benchmark for quantifying the expected magnitude of income effects on cost growth in terms of the underlying factors determining the force of these effects.

Two major sets of considerations are not included in the analysis. The first has to do with any feedback from Medicare subsidies and cost growth to the rate and direction of technological change in health care. Weisbrod (1991) called attention to the connection between payment systems in health care, primarily the distinction between reimbursing providers for cost or paying them prospectively, and incentives for cost-saving or value-enhancing technical change in health care. Although clearly important, the empirical basis for connecting the form of insurance and payment systems to technological change is weak.

A second missing element is analysis of the non-Medicare sector. One way to approach this would be to incorporate the entire health care sector within an overlapping generations framework. The advantage of this would be to recognize that higher health care costs paid when a consumer is working (to subsidize the current elderly) reduce the wealth the consumer carries forward into retirement.

Another way would be to construct a two-sector model with shared technology. With this approach, the subsidy coming from taxpayers to pay for around 75 percent of Medicare beneficiaries’ health care costs dilutes the income effect on Medicare cost growth, but exacerbates the income effect of health care cost growth on this other sector. Assuming technology's exogenous contribution to cost growth affects both the Medicare and non-Medicare sector equally, members of the other sector bear the burden of increasing health care costs for themselves and for most of Medicare. Income effects of health care cost growth – from their own health care and from the income effects shifted from Medicare beneficiaries -- will hit this group doubly hard, depressing demand for all goods, including health care outside of Medicare.¹⁶ Although I have not formally modeled two-sector health care demand, it can be expected that the two effects would roughly offset one another, assuming other utility and coverage parameters were about the same between the two groups. In other words, the subsidy from taxpayers to Medicare increases health care cost growth in Medicare but compensates by decreasing cost growth for taxpayers. Income effects coupled with current financing imply that over time, even with no changes in preferences, Medicare beneficiaries will get a larger and larger share of health care resources.

Is the subsidy from taxpayers to workers a good or bad thing? From the standpoint of utility-based economic efficiency, an income transfer does not create a welfare loss. Transfer of purchasing power from taxpayers to beneficiaries of the kind modeled here would need to be judged on fairness grounds. One could introduce efficiency criteria that were not utility-based (such as cost-effectiveness) and the transfer of health care resources from younger to older groups could be judged on those grounds as well.¹⁷ Current Medicare beneficiaries are of course former worker so some of this transfer (though not all) is over time to the same people.

Subsidizing premiums for Medicare beneficiaries can cause inefficiencies in a conventional welfare economics framework if the premium subsidy has substitution as well as income effects. A substitution effect of the subsidy would be present if beneficiaries chose more generous insurance coverage because they were paying only a small share of the premium.

Broadly speaking, the subsidy does not appear to cause Medicare beneficiaries to buy too much insurance.¹⁸ Medicare Part A (hospital services) is automatic (no choice). Part B is virtually automatic, partly because of the subsidy, of course, but the coverage involves considerable cost sharing, and, by itself, is unlikely to represent “overinsurance.” Part D (drugs) is also optional but Medicare's subsidy is voucher-like and does not apply at the margin. Part C, an alternative to traditional Medicare, also has no subsidy at the margin in the sense that if a Part C plan offers extra benefits, the cost of these are added to the premium.¹⁹

It is worth noting that Medicare beneficiary “demand” for health insurance is expressed in the voting booth as well as the market. Even if beneficiaries cannot buy a more generous Part A or B subsidized by taxpayers, in the political sphere, beneficiaries’ self-interest is tilted towards more a generous program (for example through higher provider payment rates) because of the 76% subsidy.