Correlations Between the Morphology of Sonic Hedgehog Expression Domains and Embryonic Craniofacial Shape

Abstract

Quantitative analysis of gene expression domains and investigation of relationships between gene expression and developmental and phenotypic outcomes are central to advancing our understanding of the genotype-phenotype map. Gene expression domains typically have smooth but irregular shapes lacking homologous landmarks, making it difficult to analyze shape variation with the tools of landmark-based geometric morphometrics. In addition, 3D image acquisition and processing introduce many artifacts that further exacerbate the problem. To overcome these difficulties, this paper presents a method that combines optical projection tomography scanning, a shape regularization technique and a landmark-free approach to quantify variation in the morphology of Sonic hedgehog expression domains in the frontonasal ectodermal zone (FEZ) of avians and investigate relationships with embryonic craniofacial shape. The model reveals axes in FEZ and embryonic-head morphospaces along which variation exhibits a sharp linear relationship at high statistical significance. The technique should be applicable to analyses of other 3D biological structures that can be modeled as smooth surfaces and have ill-defined shape.

1 Introduction

A current line of thought is that the process of embryonic development acts to structure and modulate genetic and phenotypic variation in ways that influence how natural selection can act on that variation to produce morphological change. However, it is unclear how various developmental processes generate and structure variation (Hendrikseet al. 2007; Wagner et al. 2006; Houle et al. 2010, Hallgrimsson et al. 2009). Developmental processes can be identified and characterized by specific gene expression patterns and are often visualized through mRNA or protein localization. To uncover relationships between developmental processes and phenotypic variation, spatial patterns of protein and mRNA expression are being systematically recorded over a range of spatial and temporal scales in several animal systems (Kudoh et al. 2001; Myasnikova et al. 2001; Visel et al. 2004; Lein et al. 2007; Tassy et al. 2010; Wong et al. 2013). However, quantitative studies have focused primarily on building atlases for studies of variation of gene expression level and relationships between different genes (Lein et al. 2007; Fowlkes et al. 2008; Fisher et al. 2008). This paper focuses on methodology for investigation of a different facet of this problem, how variation in the morphology of gene expression domains relates to developmental and phenotypic outcomes. Here, we develop a morphometric method to quantify 3D shape variation in Sonic hedgehog (Shh) mRNA expression domains in avians (chickens and ducks) and explore relationships with embryonic facial shape. The focus here is on methods and a more thorough discussion of the experimental model and its biological context appears elsewhere (Hu et al. 2015).

Signaling by Sonic hedgehog plays an essential role in the development of the vertebrate upper jaw (Hu et al. 2003; Marcucio et al. 2005; Hu and Marcucio 2009; Young et al. 2010). In amniotes, including mice and avians, Shh is first expressed in the forebrain prior to outgrowth of the facial prominences. As neural crest cells migrate into the midface, Shh expression is activated in the frontonasal ectodermal zone (FEZ), which acts as a signaling center that controls growth of the upper jaw (Marcucio et al. 2005). Hu and Marcucio (2009) demonstrate empirically that spatial organization of the FEZ regulates morphological variation in the developing upper jaw. The methods of this paper let us uncover quantitative relationships between the morphology of Shh mRNA expression in the FEZ and embryonic facial shape.

Quantification of shape variation in gene expression domains poses particularly challenging problems, as these domains typically have no clearly defined forms, often appearing seemingly amorphous, as illustrated in Figs. 1C and 1D. In particular, 3D morphometrics based on landmarks (Kendall 1984; Kendall et al. 1999) is not easily applicable to this problem, severely limiting the effectiveness of some existing methods of statistical shape analysis (Le and Kendall 1993; Dryden and Mardia 1998). Another layer of difficulty is related to image acquisition. The geometric 3D meshes representing gene expression domains tend to be noisy and contain multiple local topological and geometrical defects such as holes and irregularities that are not really present in the tissues. For these reasons, our approach has two key components:

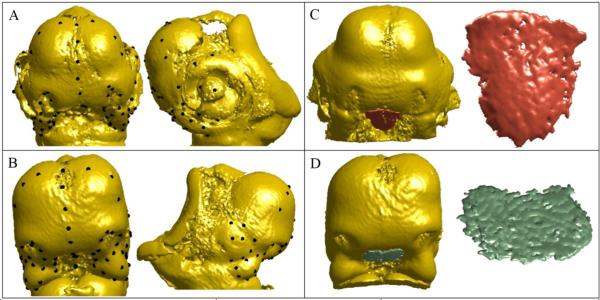
Fig. 1.

Frontal and side views of 67 landmarks on the embryonic head of (A) a chicken and (B) a duck, covering the face, mouth, eyes, and forebrain; embryonic head and close-up view of the Shh expression domain in the FEZ of (C) a chicken and (D) a duck.

(i) A Shape Regularization Technique

The FEZ is a thin, surface-like structure. A difficulty in fitting a smooth surface model to a 3D FEZ image is that FEZes among organisms lack homologous landmarks. If landmarks were available, we could construct a smooth template and morph the template to fit the image using the landmarks as guides. Dense template morphing can be done with such techniques as thin-plate spline (TPS) interpolation (Duchon 1977; Meinguet 1979). Section 2 describes a method that combines TPS interpolation with probability density estimation to bypass landmarks and obtain smooth FEZ models that remove noise and enhance shape.

(ii) FEZ Topography Vectors

Lack of well-defined form makes it difficult to develop statistical FEZ shape models using standard techniques. To obtain an informative model of shape variation, we exploit the relative position of the FEZ as a structure embedded in the embryonic face. Thus, implicit in our approach is the homology of the position of the FEZ as a whole in the embryonic face, despite the fact that FEZes lack local homologies. We introduce FEZ topography vectors that let us construct effective shape summaries that retain the most salient morphological features and filter out confounding details. A topography vector essentially describes how the FEZ width varies across its extension. The choice of these particular shape signatures was largely determined by the specific FEZ analysis problem at hand.

Using optical projection tomography scans of 17 specimens (7 chickens and 10 ducks), the shape regularization method and FEZ topography vectors, we show that there is a strong linear association between particular characteristics of FEZ morphology and embryonic craniofacial shape. Variation in craniofacial shape is quantified using geometric morphometrics based on 67 landmarks, covering the face, mouth, eyes, and forebrain. The landmarks are depicted in Figs. 1A and 1B. Analysis of Shh expression in the FEZ guided the development of the landmark-free morphometric technique, but the method should be useful in other settings, particularly in the analysis of smooth structures devoid of landmarks and well-defined form. This is discussed further in Section 4.

2 Methods

2.1 In Situ Hybridization and Optical Projection Tomography (OPT) Imaging

Shh expression in the avian embryos was detected by standard in situ hybridization resulting in the domain of interest being stained dark blue (Hu et al. 2015; Chong et al. 2012). 3D data of both this domain, as well as exterior surface of the avian embryo were acquired on Bioptonics 3000 OPT system (Sky Scan, Germany). OPT has the advantage over more conventional imaging methods that it can generate 3D surface data of 1-3 cm³ objects as well as detect colorimetric or fluorescent signals. It therefore, allows the correlation of multiple data types (Quintana and Sharpe 2011; Sharpe 2002). Embryos were imaged on the OPT system as previously published (Quintana and Sharpe 2011). Briefly, embryos were embedded in 1% low melt agarose (Invitrogen), which was then cut into a hexagonal block, mounted onto a magnetic chuck dehydrated for 48 hours in methanol and cleared in BABB (2 parts Benzyl Benzoate: 1 part Benzyl Alcohol). Embryos were imaged in the UV range on the GFP channel (~480 nm) and in the visual light range. The NRecon software package (SkyScan, Germany) was used to align the stacks and reconstruct the images. Image stacks were imported into Amira (Version 5.0, FEI, Hillsboro OR, USA) for landmark placement and segmenting of the Shh FEZ domain. Sixty-seven landmarks were registered on each embryo, as shown in Figs. 1A and 1B.

2.2 Quantitative Methods

In this section we develop (i) a shape regularization technique that is used to construct smooth surface models of Shh expression domains in the FEZ and (ii) FEZ topography vectors that capture the most salient morphological characteristics of Shh expression and yet are robust to uninformative details. Henceforth, we refer to an expression domain in the FEZ simply as FEZ.

2.2.1 Shape Regularization

As illustrated in Figs. 1C and 1D, FEZ data acquired through 3D imaging are very irregular with numerous artifacts, whereas the FEZ itself resembles a smooth surface. To remove these irregularities and make the meshes more tractable, we build smooth surface models from imaging data. We approximate a FEZ mesh K by the graph of a smooth function f defined over a (bounded) plane region D with smooth boundary, as indicated in Fig. 2A. We begin with the construction of a plane P that contains D and then proceed to the estimation of D and construction of f.

Fig. 2.

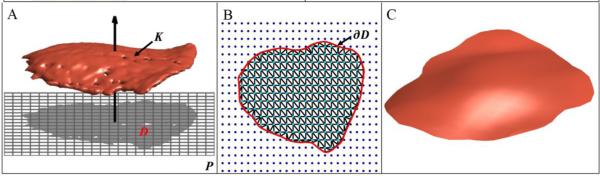
FEZ regularization process: (A) original FEZ mesh K and projection onto a plane P based on the first two PC scores that delineate a region D in P; (B) estimation of the interpolation domain D whose bounday ∂Dis highlighted in red; (C) regularized FEZ.

Viewing the vertices v₁, ..., v_n of the mesh K as n data points in 3D space, we use principal component analysis (PCA) to construct a plane P parallel to the first two principal directions, as indicated in Fig. 2A. The usual practice is to choose P containing the mean v̄ = (v₁ + ... + v_n)/n, but for the present purposes the plane may be translated off the mean. This is done primarily to facilitate visualization. We use PCA because the first two principal directions define a suitable basis plane for the function f. Orthogonal projection of v₁, ..., v_n onto P gives a point cloud p₁, ..., p_n that delineates a region D in the plane P, as shown in Fig. 2A. We now describe a procedure to estimate the domain D from these points.

We model the distribution of the projected points by the Gaussian density estimator (Rosenbaltt 1956; Parzen 1962)

$$\varphi \left(p\right)=\frac{1}{n2\pi {\sigma }^2}\sum _{i=1}^n\exp \left(-\frac{{\Vert p-p_i\Vert }^2}{2{\sigma }^2}\right).$$

ϕ is the uniform mixture of isotropic Gaussians of width σ centered at the points p_i. For a discussion of selection of the bandwidth parameter σ, one may consult, for example, (Silverman 1998). A key observation is that ϕ is large within the domain D relative to the values it attains outside D because only the interior of D is well populated by (projected) data points. Thus, the contour ∂D of the region D comprises points where a transition occurs. This suggests that we estimate ∂D as an isocontour of ϕ; that is, D = {p ∈ P:ϕ(p) = ε}, where ε > 0 is a fixed small value learned from data. If the isocontour has multiple components, we take the component that encloses the most points since holes or outliers produce the small components. Fig. 2B shows an example of a contour obtained with this technique.

The final step in the mesh regularization process is the construction of a smooth function f on the domain D whose graph interpolates the points v₁, ..., v_n. We introduce a coordinate system, where becomes P the x − y plane and the z− axis is orthogonal to P, as indicated in Fig. 2A. Let v_i = (a_i, b_i, c_i) be the coordinates of the vertex v_i, so that the (x, y) − coordinates of its projection p_i are (a_i, b_i). The goal is to construct a smooth function f(x, y) such that f(a_i, b_i ≈ c_i) , which ensures that the graph of f smoothly interpolates the data points. We use thin-plate spline (TPS) interpolation to construct such a function. TPS interpolation is a technique widely used in data analysis, including geometric morphometrics (Bookstein 1996). In simple terms, a TPS interpolation balances out minimization of the average residual ${\sum }_i{\mid f(a_i,b_i)-c_i\mid }^2∕n$ and the smoothness of f. One may consult (Wahba 1990) for further details. The TPS interpolant f is defined over the entire plane P, but the part of the graph over the domain D gives the desired smooth FEZ model. Next, we describe a method to discretize the smooth surface model, as discrete representations will be useful for algorithmic analyses of the FEZ. We use the Delaunay triangulation (Guibas and Stolfi 1985; Fortune 1987) τ of the bounded region D associated with the points p₁, ..., p_n . We map the vertices of τ to 3D space via the TPS interpolant f, maintaining the mesh structure of τ. Fig. 2C shows a discrete FEZ model constructed with this method.

2.2.2 FEZ Topography Vectors

We develop a quantitative representation, termed FEZ topography vector, which summarizes the most salient morphological properties of the FEZ and to a large extent is blind to confounding details. This yields a representation that is robust to the large variability observed in local and regional FEZ morphology. Although the lack of homologous landmarks makes it difficult to find point correspondences between FEZ meshes for different specimens, a relaxed notion of shape correspondence that exploits the position of the FEZ in the embryonic head is implicit in topography vectors. In spite of lacking specific local homologies, we assume the homology of the relative position of the FEZ as a whole structure embedded in the embryonic head.

Using 67 landmarks, depicted in Figs. 1A and 1B, covering the face, mouth, eyes, and forebrain, we normalize centroid size and employ Procrustes superimposition to standardize position and spatial orientation of an embryonic head by aligning it to a template. In particular, this fixes a scale and orientation for the FEZ. We construct a sagittal plane, as shown in Fig. 3A, and use parallel translates of this plane to slice up the FEZ along a series of curves. These curves carry rich information about the structure of the FEZ surface, cf. (Mio et al, 2007), and are used in the construction of the FEZ topography vector. To estimate the sagittal plane, we exploit the following facts: (i) the head landmarks are nearly symmetrical about the sagittal section and (ii) the dominant spatial spread of the head landmarks occurs in a direction perpendicular to the sagittal plane. Thus, PCA on the landmarks gives a simple way of estimating the sagittal plane as the plane through the centroid of the landmarks that is parallel to the second and third principal directions since we expect the first principal direction to be orthogonal to the sagittal plane. Sweeping the FEZ from left to right with parallel translates of the sagittal plane yields a continuous family of sections of the FEZ by spatial curves, as illustrated in Figs. 3B and 3C. As the shape of these spatial curves is still sensitive to the high variability of the FEZ across specimens, we only use their lengths to describe FEZ morphology. (This simplification is mainly based on this particular use of the smooth FEZ model and the correlations that will result between FEZ morphology and head shape.) In this manner, we obtain FEZ shape descriptors that may be viewed as encoding how the topography of the FEZ varies as we sweep it from left to right. As the variation of the length of the sagittal sections is gradual, in practice, it suffices to consider a discrete, sparse family comprising k (equally spaced) sections across the width of the FEZ. Denoting the length of the th section by h_i, FEZ shape is summarized in a FEZ topography vector h, the k – dimensional vector whose coordinates are h_i, 1 ≤ i ≤ k.

Fig. 3.

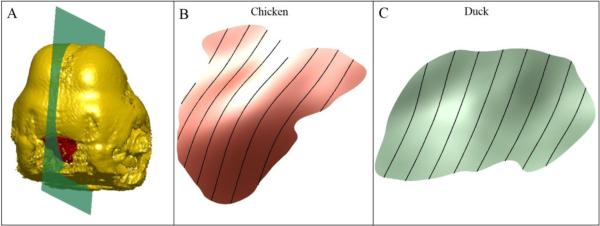
Sectioning the FEZ: (A) sagittal section of an embryonic head; (B) and (C) FEZ sections (black curves) by translates of the sagittal plane.

3 Correlations between FEZ Morphology and Craniofacial Shape

We employed FEZ regularization and topography vectors to model variation in FEZ morphology and to study correlations with embryonic craniofacial shape. The analysis was based on optical projection tomography scans of the embryonic heads of 7 chickens and 10 ducks. FEZ meshes were smoothed with the regularization technique of Section 2.2.1 and FEZ shape variation was quantified using topography vectors. Head shape variation was modeled with standard techniques of geometric morphometrics using sixty-seven manually placed landmarks described above.

As topographical variation across a smooth FEZ model is gradual, the lengths of the sagittal sections exhibit multiple correlations. Thus, it is natural to expect that a rather low-dimensional topography vector (k small) should suffice for encoding topographical variation across the FEZ. We employed topography vectors of dimension k = 8 because our experiments with different values of k indicated that little additional information about relationships between FEZ morphology and embryonic head shape is revealed with denser samplings. The method used is described in more detail below. Figs. 3B and 3C show examples of FEZ sections used in the construction of topography vectors for a chicken and a duck.

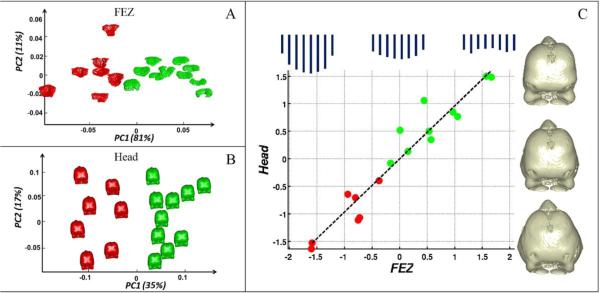
Principal component analysis showed that PC1 and PC2 explain 81% and 11%, respectively, of FEZ topographical variation. Fig. 4A shows a plot of the PC scores and indicates that they discriminate chickens from ducks sharply. An examination of the PC loadings revealed that PC1 is primarily about FEZ width at its center and PC2 about width gradient from the center to the left and right ends. To quantify variation in head shape, we standardized centroid size and used Procrustes superimposition to spatially align all head meshes to the mean head of the entire group. The mean was calculated with a fast converging fixed-point algorithm developed by Liu et al. (2008). PC1-PC6 explained approximately 78% of the shape variation and the individual PCs explained 35%, 17%, 11%, 6%, 5% and 4% of the variation, respectively. Fig. 4B shows a plot of the first two PC scores for head shape. PC1 sharply discriminates chickens from ducks and reflects the fact that embryonic duck faces are deeper and narrower than chicken faces.

Fig. 4.

(A) Plot of PC1 and PC2 scores for FEZ topography that clearly separate chickens (red) from ducks (green). (B) PC1 and PC2 scores for head shape, with PC1 explaining 35% of the total shape variation and sharply discriminating chickens from ducks. (C) First pair of canonical directions in the FEZ and head morphospaces. The plot shows a clear separation of chickens from ducks, as well as a strong correlation (ρ = 0.96) between FEZ morphology and head shape. The plot includes a schematic illustration of the variation of the FEZ topography vectors and 3D head shape changes along the first pair of canonical directions.

To explore relationships between FEZ morphology and embryonic facial shape, we used canonical correlation analysis (CCA) (Hotelling 1936; Krzanowski 1988; Seber 1984) on the FEZ morphospace determined by the first two PC scores and head shape space determined by the first six PC scores. CCA uncovers a pair of directions and in the FEZ and head morphospaces, respectively, such that the data projected onto these axes have maximal correlation coefficient. CCA produced a pair of axes along which the correlation coefficient is ρ = 0.96 at high statistical significance. Under the null hypothesis that the projected data are uncorrelated, a permutation test yielded a p-value < 10⁻⁵ . Fig. 4C shows a plot of the scores along these axes, the regression line of head shape over FEZ topography, as well as illustrations of shape variation along these directions. The sets of eight bars, across the top of Fig. 4C, give a schematic illustration of the variation of the FEZ topography vectors. The length of each bar corresponds to an entry of the topography vector. The first canonical direction in the FEZ morphospace nearly coincides with the anti-diagonal direction in the PC1-PC2 plane, whereas the axis in the head morphospace captures primarily the fact that the heads of ducks are narrower and deeper than the heads of chickens. This suggests that the correlation between FEZ morphology and head shape involves complex cranial features and is not dominated by landmarks surrounding the FEZ. To produce further quantitative evidence for this, we repeated the experiment replacing the original 67 head landmarks with a subset of 20 randomly selected landmarks. The average correlation coefficient over 100 such experiments was 0.95, strongly indicating that the method uncovered head shape features that are highly correlated to FEZ morphology and are not localized to a region near the FEZ. It is also worth noting that the scores of the data along the first pair of canonical directions sharply discriminate chickens from ducks. For the second pair of canonical directions, the correlation coefficient dropped to ρ = 0.5, revealing no additional statistically significant correlations between FEZ topography and head shape.

4 Discussion

Understanding how genetic variation acts through developmental processes to produce the amazing variation in complex morphologies in nature both within and among species remains one of the greatest and most difficult challenges in modern biology. Addressing this challenge will require both conceptual and methodological advances that result in coherent and quantitative explanations of relationships among events across the genotype-phenotype map (Hallgrimsson and Hall 2011). This paper presents one such methodological advance – the quantification of the morphology of gene expression domains and its relationship to phenotypic variation. We show how the combination of optical projection tomography, geometric morphometrics and landmark-free shape analysis can result in coherent quantification of the relationship between gene expression and the morphology of the structure influenced by that gene expression. The landmark-free approach quantifies variation in shape of seemingly amorphous gene expression domains, enhancing their most salient morphological characteristics and being robust to uninformative local shape variation and artifacts associated with image acquisition. A key strength of the method stems from the fact that it is difficult, if not impossible, to quantify such variation with the usual methods of geometric morphometrics because gene expression domains typically lack homologous landmarks and well-defined forms.

We modeled variation in the morphology of Sonic hedgehog expression in the FEZ of embryonic chickens and ducks and uncovered relationships between morphology of Shh expression and craniofacial shape. The FEZ is a signaling center located within the single layer sheet of epithelium that comprises the surface cephalic ectoderm. Shh is an important mediator of FEZ activity (Marcucio et al, 2011), but how the shape of the Shh expression domain affects morphogenesis is largely unknown. While slight variations in Shh expression levels may exist within individual epithelial cells, the net effect of FEZ function results from activation of the Hh pathway in the adjacent mesenchymal cells. Hence, the shape of the Shh expression domain appears directly related to the mesenchyme that is affected by FEZ activity. Differences in intensity of Shh expression in the epithelium should be averaged as the FEZ signals to the adjacent tissues. A key next step in our work is to develop methods to quantify the shape of the responding mesenchymal cells. However, this is more difficult than quantifying the shape of the FEZ, because the FEZ is a sheet of epithelium and can be modeled as a surface rather than a 3-dimensional object required of the mesenchymal tissues. Our model revealed axes in Shh expression and craniofacial morphospaces along which variation exhibits a strong linear relationship at high statistical significance. Although this paper only illustrates the method, we believe that it has tremendous potential for advancing quantitative integration across the genotype-phenotype map for complex morphologies. The method should be particularly useful in quantitative analyses of 3D smooth, surface-like structures that have ill-defined shape. A potential limitation of the method is that shape signatures such as FEZ topography vectors derived from the method overlook local shape emphasizing morphological properties that are observable at larger scales. On the other hand, this is precisely what enables the method to reveal important patterns of morphological variation even in the presence of localized unstructured variation.

Shape regularization, as presented in this paper, should be useful in a broad variety of applications, as it can be used for fitting smooth surface models to noisy points clouds provided that the surface can be represented as the graph of a smooth function over a bounded domain contained in a plane. However, variants may be developed for fitting a more complex surface, such as the contour of a solid in 3D space, provided that it can be represented as a smooth section of the normal bundle of a given compact, smooth surface embedded in 3D space such as a sphere. In contrast, the use of topography vectors is more specific to the present application to FEZ and craniofacial shape analysis. Other morphological signatures of the fitted surfaces may be used for shape analysis with the choice depending on the application.

5 Software Accessibility

Matlab code for the shape regularization method developed in this paper is available for free use at https://github.com/qx0731/Mesh-Regularization-/