Model-Updated Image Guidance: A Statistical Approach to Gravity-Induced Brain Shift

Abstract

Compensating for intraoperative brain shift using computational models has been used with promising results. Since computational time is an important factor during neurosurgery, a prior knowledge of a patient’s orientation and changes in tissue buoyancy force would be valuable information to aid in predicting shift due to gravitational forces. Since the latter is difficult to quantify intraoperatively, a statistical model for predicting intraoperative brain deformations due to gravity is reported. This statistical model builds on a computational model developed earlier. For a given set of patient’s orientation and amount of CSF drainage, the intraoperative brain shift is calculated using the computational model. These displacements are then validated against measured displacements to predict the intraoperative brain shift. Though initial results are promising, further study is needed before the statistical model can be used for model-updated image-guided surgery.

1 Introduction

In the past several years, the importance to account for intraoperative brain shift during image-guided neurosurgical procedures has been well documented. Also known as post imaging brain distortion or brain deformation, the shift can be caused by a variety of factors such as surgical manipulation, gravitational forces, clinical presentation of the patient, pharmacological responses, etc. Systematic studies have demonstrated that the fidelity of image-guided systems can be seriously compromised by brain deformations if left unchecked [1, 2]. One important statistically significant finding common to these studies is that the direction of brain shift has a predisposition to move in the direction of gravity [1, 2].

To correct for deformations, various imaging techniques such as computed tomography (CT), magnetic resonance imaging (MRI), and ultrasound (US) have been used for intraoperative image-guided surgery, and each imaging procedure has its inherent advantages and disadvantages [3-5]. While CT and MR procedures have been labeled cumbersome and have been questioned for their cost-effectiveness, US lacks the image clarity that CT and MR scans produce.

As a cost-effective and an efficient method, computational modeling is a procedure that can translate complex surgical events into accurate estimates of tissue response and thereby compensate for intraoperative brain shift. Various computational models based on different physical and biomechanical principles have been developed [6, 7]. The biphasic model used by Miga et al. has been shown to compensate for 70–80% of the intraoperative brain shift. In a study on gravity induced brain deformations [7], Miga et al. report a reduction of error from 6mm to 1mm. However the amount of intraoperative CSF drainage (which determines the gravitational force in the biphasic model) and the patient’s orientation in the OR with respect to gravity cannot be ascertained. Although the preoperative surgical plan can provide an estimate of the patient’s orientation a priori, estimates for the degree of change in buoyancy forces acting on the brain are somewhat more elusive. Since computational time is an important factor in model updated image-guided surgery, prior knowledge of a patient’s orientation and amount of CSF drainage would increase the effectiveness of model updated image-guided surgery.

The work presented here attempts to remove the uncertainties by combining a simple statistical model with that of the biphasic model reported in [7]. Although limited, the use of statistical models to compensate for tissue motion does have some precedent. Davatzikos et al. [8] report a framework for modeling and predicting anatomical deformations with an emphasis on tumor induced deformations. Their statistical models were based on analyzing the principal modes of covariation between deformed and undeformed anatomy within the context of two separate methods: (1) a shape-based estimation (SBE) and, (2) a force-based estimation using a biomechanical model. The results from these studies suggested that statistical models could be used to represent deformations from positional changes and tumor growth.

In this paper, a computational model is used to generate displacement data sets for a range of patient orientations and CSF drainage states. The statistical model combines these displacements using a nonlinear least squares approach. The rationale for this approach is provided by recent work reported by Miga et al. [9]. In this study, a high-resolution laser-range scanner (LRS) was used to spatially characterize the patient’s exposed cortical surface during neurosurgery. As a result, information regarding the nature of deformations during neurosurgery are derived and could be used as input for the statistical model reported in this paper. In addition, the statistically reconstructed displacement values are compared against independently measured displacements to assess accuracy. Simulations are also provided which are more closely related to data acquired by the LRS system used in [9].

2 Methods

2.1 Computational Model

This section briefly discusses the computational model used in this study. Equations (1) and (2) were originally developed by Biot [10] to represent biphasic soil consolidation, but were later used by Nagashima et al. [11] and Paulsen et al. [12] to model the deformation behavior of brain tissue. The last term on the left-hand-side in equation (1) represents the effect of gravitational forces acting on the brain. Intraoperative CSF drainage reduces the buoyancy forces which serve to counteract gravity forces thus causing gravitational forces to deform the brain. The effect of gravitational forces on the brain can be modeled as a difference in density between tissue and surrounding fluid. Figure 1 demonstrates the deformation effects of CSF drainage on the brain as modeled by equations

$$\nabla •G\nabla u+\nabla \frac{G}{1-2v}\left(\nabla •u\right)-\alpha \nabla p+\left({\rho }_t-{\rho }_f\right)g=0$$ (1)

$$\alpha \frac{\partial }{\partial t}\left(\nabla •u\right)+\frac{1}{S}\frac{\partial p}{\partial t}-\nabla •k\nabla p=0$$ (2)

where

G	shear modulus
υ	Poisson’s ratio
u	displacement vector
p	pore fluid pressure
α	ratio of fluid volume extracted to volume change of the tissue under compression
k	hydraulic conductivity
1/S	amount of fluid, which can be forced into the tissue under constant volume
ρt	density of tissue
ρf	density of surrounding fluid
g	acceleration due to gravity

The partial differential equations can be solved numerically using the Galerkin weighted residual method. Finite element treatment of these equations coupled with a weighted time stepping scheme results in an equation of the form

$$\left[A\right]\left\{U^{n+1}\right\}=\left[B\right]\left\{U^n\right\}+\left\{C^{n+\theta }\right\}$$ (3)

where [A] and [B] represent the stiffness matrices for the n+1 and n^th time step, respectively and {C} represents integrations of boundary integral expressions associated with the traditional “weak” forms of the weighted residual expression. The detailed development of the equations can be found in previous publications [12] [7].

Fig. 1.

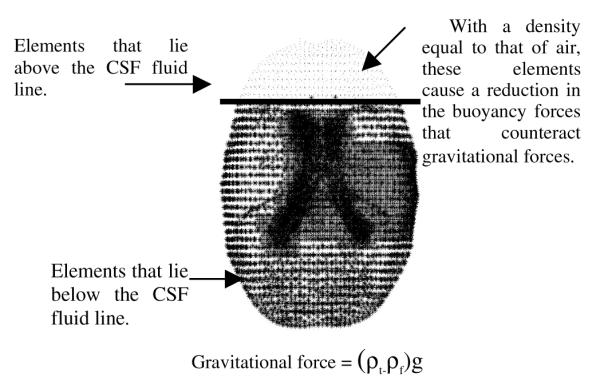
Effect of Gravitational forces on the brain

The boundary conditions used in the model are illustrated in Figure 2. Although the actual boundary conditions are patient specific, the highest elevations in the brain are stress-free and allow drainage to the surface; the mid elevations slide along the cranial wall and can experience partial drainage and the lowest elevations allow movement along the cranial wall but do not allow fluid drainage. The assumed level of intracranial CSF determines the fluid drainage boundary condition for the highest and mid elevations in the brain.

Fig. 2.

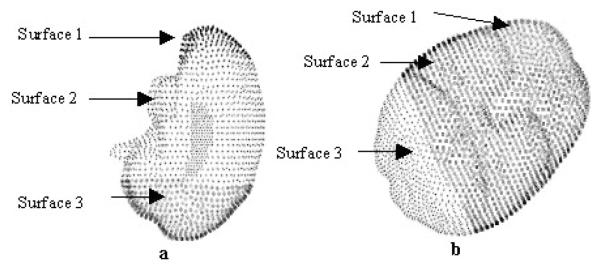
Boundary Condition template for (a) neutral head orientation and (b) patient’s head turned 60° in the OR. Surface 1 is stress-free at atmospheric pressure; surface 2 slides along the cranail wall but not along the normal direction and surface 3 is fixed at atmospheric pressure. The amount of intraoperative CSF drainage determines the drainage boundary condition.

2.2 Statistical Model

As discussed above, the amount of intraoperative CSF drainage and patient’s orientation in the OR (determines orientation of gravitational acceleration vector in equation (1)) are two important variables in predicting intraoperative brain shift. A statistical based model has been developed to compensate for these uncertainties. As shown in Figure 3, the model begins by building a statistical atlas based on the patient’s preoperative MR images. Equations (1) and (2) are solved assuming a range of patient orientations and degrees of intraoperative CSF drainage based on preoperative surgical planning. This series of model solutions serves as a statistical data set that can be used to characterize intraoperative deformations under varying surgical presentations. Having built the statistical atlas, a least squares regression analysis is performed with non-negativity constraint s (provided by MATLAB (Mathworks Inc.)) using the objective function below:

$$\text{Minimize}\mid \mid \mathit{Ex}-f\mid \mid \text{subject to}x\ge 0$$ (4)

where f is a vector of n measured displacements, E is a matrix where E_ij is the displacement value for i^th nodal position on the surface at the j^th orientation and CSF drainage level. x also contains a requirement that the regression coefficients must add to unity. The unknown coefficients associated with the regression analysis are x and they are used to calculate the intraoperative brain shift as shown below.

$$\mathrm{Intraoperative}\mathrm{brain}\mathrm{shift}=X_1{}^{\ast }x$$ (5)

where X₁ is the matrix containing the displacement field vectors for all points in the brain at the various orientations/CSF drainage levels and x is a vector of coefficients obtained from solving equation (4).

Fig. 3.

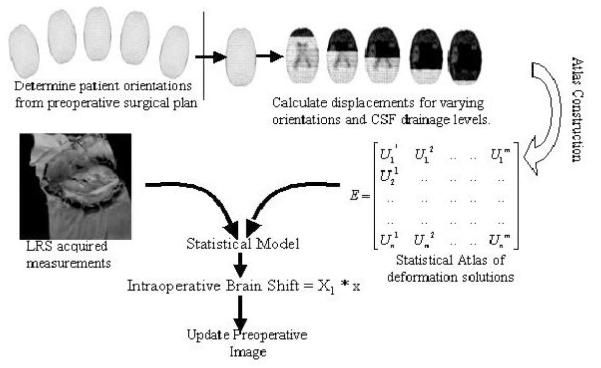
Statistical Model

The findings of Miga et al. [7] were used to validate the combined statistical and biphasic model. The values reported in Table 1, columns 1-4 are reproduced from their work published in IEEE Transactions of Medical Imaging, Vol. 18, No. 16, 1999. In their paper, they simulate the intraoperative brain shift for four different human cases using the computational model and also measure the intraoperative brain shift for four points on the cortical surface in the direction of gravity. These measured displacements are used in equation (4) as the basis for determining the regression coefficients. After calculating the coefficients, results from the statistical model are compared to measured data and performance is reported in Table 1.

Table 1.

Comparison between measured shift, computational model and statistical model based shift with respect to gravity

Subject	Point #	Measured Displ. (mm)	Computational model Displ. (mm)	Statistical Model Displ. (mm)
PATIENT	1	6.7	4.9	4.7
1	2	4.6	5.4	5.1
	3	4.2	5.8	5.4
	4	3.5	3.4	3.6
PATIENT	1	10.4	5.7	7.4
2	2	6.2	6.3	7.2
	3	5.9	6.2	7.8
PATIENT	1	6.1	5.2	4.8
3	2	5.0	6.5	6.2
	3	-	-	-
	4	7.5	6.1	5.9
PATIENT	1	4.4	4.8	4.5
4	2	3.5	3.8	3.4
	3	-	-	-

Although the above intraoperative data is sparse, a laser range scanner significantly improves the number of measured data points and hence should constrain and aid the statistical model. To simulate this, for each patient, a specific orientation and CSF level were selected which were not to be part of the statistical solution set. In all cases, the computational model was executed for a range of patient orientations and CSF drainage states. The coefficients were then calculated using the statistical model and intraoperative brain shift was compared to the model solution not included within the statistical set. The results are presented in the following section.

3 Results

3.1 Comparison of Statistical Model with Measured Displacements Reported by Miga et al

The results of the statistical model are compared with the measured displacements in Table 1. The values in column 3 and column 4 are based on the findings of Miga et al. [7]. Column 5 shows the statistical model prediction on a point-by-point basis. Point 3 in Patients 3 and 4 was on bone and hence experienced no shift.

Averaging over all points in the four human cases, the statistical model produces an absolute error of 1.1 ± 0.9mm. For the computational model, Miga et al report an average error of 1.2 ± 1.3 mm. The statistical model predicts approximately 75-80% of the intraoperative brain shift.

3.2 Comparison of Statistical Model with the Simulated Intraoperative Data Acquisition Case

The results of the statistical model for the simulation are shown in Table 2. The values in column 2 report the maximum difference between the measured intraoperative displacements and those predicted by the statistical model. In a similar fashion the values in column 3 represent the mean error. Averaging over all points in the four human cases, the statistical model produces an absolute maximum error of 0.7 ± 0.8mm and a mean error of 0.1mm ± 0.08mm. Relative to the average cortical displacement of 2.4 mm, the statistical model predicts an average error of 0.1 mm, indicating that it recaptured 96% of the simulated intraoperative brain shift.

Table 2.

Maximum and mean errors generated by the statistical model for the simulated intraoperative data acquisition

Subject	Max. Error (mm)	Mean Error (mm)
PATIENT 1	1.9	0.2
PATIENT 2	0.3	0.06
PATIENT 3	0.4	0.07
PATIENT 4	0.3	0.07

4 Discussion

The statistical model performed comparably to published results and was able to compensate for 75-80% of brain deformation. To increase the accuracy, simulations suggest that dense intraoperative cortical shift measurements may be appropriate. In the simulation case reported, the statistical model results in an average error of 0.1 mm displacement error and predicts approximately 96% of the intraoperative brain shift. With the advent of cheap and efficient intraoperative data acquisition techniques such as laser range scanning [9], the statistical model can prove to be a useful tool for model updated image guidance. Furthermore, the statistical model should significantly reduce intraoperative computational time since perturbations of patient orientation and the state of CSF drainage can be precomputed.

5 Conclusions

A statistical based approach has been outlined for image-guided surgery. The statistical model was compared with measured intraoperative data and with a simulated intraoperative case. These simulations showed a good match between the brain shifts predicted by the computational model and that predicted by the statistical model. Given the prominent role that gravity takes in the development of brain shift, it is encouraging that a relatively simple statistical model increases the model-updating speed by providing a framework to pre-compute the early stages of brain shift and can also be used to compensate for this motion.