Abstract
We consider estimation and variable selection in high-dimensional Cox regression when a prior knowledge of the relationships among the covariates, described by a network or graph, is available. A limitation of the existing methodology for survival analysis with high-dimensional genomic data is that a wealth of structural information about many biological processes, such as regulatory networks and pathways, has often been ignored. In order to incorporate such prior network information into the analysis of genomic data, we propose a network-based regularization method for high-dimensional Cox regression; it uses an ℓ1-penalty to induce sparsity of the regression coefficients and a quadratic Laplacian penalty to encourage smoothness between the coefficients of neighboring variables on a given network. The proposed method is implemented by an efficient coordinate descent algorithm. In the setting where the dimensionality p can grow exponentially fast with the sample size n, we establish model selection consistency and estimation bounds for the proposed estimators. The theoretical results provide insights into the gain from taking into account the network structural information. Extensive simulation studies indicate that our method outperforms Lasso and elastic net in terms of variable selection accuracy and stability. We apply our method to a breast cancer gene expression study and identify several biologically plausible subnetworks and pathways that are associated with breast cancer distant metastasis.
Key words and phrases: Laplacian penalty, network analysis, regularization, sparsity, survival data, variable selection, weak oracle property
1. Introduction
With advances in high-throughput technology, gene expression profiling is extensively used to discover new markers, pathways, and new therapeutic targets. This technique measures the expression levels of tens of thousands of genes. In cancer genomics, gene expression levels provide important molecular signatures for cancers, which in turn can be very predictive for cancer recurrence or survival. To link high-dimensional genomic data to censored survival outcomes, Cox’s proportional hazards model (Cox (1972)) is most commonly used; it specifies that the hazard function of a failure time T, conditional on a p-dimensional vector of genomic measurements X, takes the form
| (1.1) |
where λ0(·) is an unspecified baseline hazard function and β0 is a p-vector of regression coefficients. A key feature of genomic data is that the dimensionality p can be much larger than the sample size n, so that traditional methodology cannot be directly applied. To make inferences for the high-dimensional Cox model (1.1), a variety of regularization approaches have been proposed. Of particular interest is the Lasso method (Tibshirani (1996, 1997); Gui and Li (2005)), that can perform estimation and variable selection simultaneously by shrinking some estimates to exactly zero. Alternative methods that exploit sparsity include the SCAD (Fan and Li (2001, 2002)), adaptive Lasso (Zou (2006); Zhang and Lu (2007)), and Dantzig selector (Candes and Tao (2007); Antoniadis, Fryzlewicz and Letué (2010)), among others. All these methods can lead to the parsimonious models that are crucial for achieving good prediction performance and easy interpretation with high dimensionality.
Although the Lasso-type regularization methods have been demonstrated to be useful in high-dimensional failure time regression, two major drawbacks remain. First, in the linear regression context, the Lasso has been shown to be model selection consistent only under an irrepresentable condition (Zhao and Yu (2006)) that is quite stringent and may not be satisfied in high dimensions because of multicollinearity. Recent developments have also confirmed that similar restrictions exist for survival models (Bradic, Fan and Jiang (2011); Lin and Lv (2013)). Second, these procedures lack a built-in mechanism to incorporate the prior structural information about the covariates that is often available in scientific applications. For instance, in genomic studies, a wealth of knowledge about genes that are functionally similar or belong to the same pathways has accumulated over the years and can be obtained through several publicly available databases. It is expected that taking into account such biological knowledge would help to identify important genes that are functionally related and produce more reliable and biologically more interpretable results.
Several efforts have been made to overcome these drawbacks. The elastic net (Zou and Hastie (2005)) has been applied to high-dimensional Cox regression (Engler and Li (2009); Wu (2012)) to achieve some grouping effects. This method, still, does not utilize any prior information on the graphical structure among the covariates. Wang et al. (2009) proposed hierarchically penalized Cox regression when the variables can be naturally grouped. However, their method is not intended for incorporating any graphical or network structure and, more importantly, their penalty function is nonconvex, which may be a potential issue for efficient computation.
The complexity of genomic data and the aforementioned considerations have motivated us to propose a network-based regularization method for high-dimensional Cox regression. We aim to incorporate prior gene regulatory network information, as represented by an undirected graph, into the analysis of genomic data and censored survival outcomes. Specifically, our method uses an ℓ1-penalty to enforce sparsity of the regression coefficients, and a quadratic Laplacian penalty to encourage smoothness between the coefficients of neighboring variables on a given network. The resulting optimization problem is convex and allows for an efficient implementation by coordinate descent optimization. Our method extends the work of Li and Li (2010), where only linear regression models were considered. The extension, however, is nontrivial in that new techniques are required for theoretical development under the Cox model. Owing to the semiparametric nature of survival models, high-dimensional analysis of regularization methods for survival data is much more challenging than for (generalized) linear models, and results of this kind are rare. In fact, even in the special case of ℓ1-penalized Cox regression, our theoretical results are novel and substantially different from the few available in the literature (e.g., Bradic, Fan and Jiang (2011); Huang et al. (2013); Kong and Nan (2012)). Moreover, our theoretical results provide insights into the gain from taking into account the covariate graphical structure information. We demonstrate through extensive simulation studies and a data example that our method outperforms Lasso and elastic net, which do not utilize any prior network information, in terms of variable selection and biological interpretability.
The rest of this paper is organized as follows. In Section 2, we introduce a network-based regularization method for high-dimensional Cox regression and describe a coordinate descent algorithm for implementation. We provide in Section 3, theoretical results in the setting where the dimensionality p can grow exponentially fast with the sample size n, and discuss their consequences and implications. Simulation studies and real data analysis are presented in Sections 4 and 5, respectively. We conclude with a brief discussion in Section 6. Proofs and additional simulation results are relegated to the Appendix and Supplementary Material.
2. Methodology
2.1. Network-regularized Cox regression
We begin by introducing some notation. Let T be the failure time and C the censoring time. Denote by T̃ = T∧C the censored failure time and Δ = I(T ≤ C) the failure indicator, where I(·) is the indicator function. Let X = (X1, …, Xp) be a vector of covariates and assume that T and C are conditionally independent given X. The observed data consist of the triples (T̃i, Δi, Xi), i = 1, …, n, which are independent copies of (T̃, Δ, X). Moreover, we assume that the relationships among the covariates are specified by a network (weighted graph) G = (V, E, W), where V = {1, …, p} is the set of vertices corresponding to the p covariates, an element (i, j) in the edge set E ⊂ V × V indicates a link between vertices i and j, and W = (wij), (i, j) ∈ E is the set of weights associated with the edges. For simplicity, we assume that G contains no loops or multiple edges. In practice, the weight of an edge can be used to measure the strength or uncertainty of the link between two vertices. For instance, in a gene regulatory network constructed from data, the weight may indicate the probability that two genes are functionally related. Further, denote by di = Σj:(i, j)∈E wij the degree of vertex i, and define the normalized Laplacian matrix L = (lij) of the graph G by
In the low-dimensional setting, estimation of β0 in model (1.1) is based on maximizing the partial likelihood
where Ri is the index set for the subjects that are at risk just before time T̃i. In the high-dimensional setting where the dimensionality p is comparable to or much larger than the sample size n, however, some form of regularization is required. We assume that β0 is sparse in the sense that only a small portion of the components of β0 are nonzero. We are interested in identifying the nonzero components of β0 as well as accurate estimation and prediction.
In the context of linear regression, to obtain a sparse estimate that approximately retains the structure of a given network, Li and Li (2010) introduced a network-constrained penalty,
| (2.1) |
where β = (β1, …, βp)T and λ1, λ2 ≥ 0 are two regularization parameters. The penalty (2.1) consists of two parts. The first term is an ℓ1 part that penalizes the regression coefficients individually and is the key to achieving sparsity and performing variable selection. The second term is a quadratic Laplacian penalty that penalizes on the differences of scaled coefficients between neighboring variables on a given network, thus promoting local smoothness over the network and encouraging simultaneous selection of related variables. The scaling of coefficients by the (square root of) degrees is preferable for two reasons. First, the penalty on each linked pair suggests that the scaling should allow variables with a larger degree to achieve a more dramatic effect. This is often desirable in practice; for example, in genomic studies, genes that are highly connected to others, such as the hub genes, are believed to play a fundamental role in biological processes (Lehner et al. (2006)). Second, in addition to the bias caused by the ℓ1 part, the quadratic penalty induces extra estimation bias and, without scaling or normalization, a highly connected variable would be overpenalized and hence subject to unendurable bias. In fact, the normalized Laplacian matrix has eigenvalues between 0 and 2 (Chung (1997)), leading to a more numerically stable procedure.
Using the penalty at (2.1), we propose to estimate β0 in the high-dimensional model (1.1) by the penalized partial likelihood estimator
| (2.2) |
where ℓ(β) is the log partial likelihood
| (2.3) |
2.2. Accounting for different signs of coefficients
As pointed out by Li and Li (2010), the penalty (2.1) may not perform well when neighboring variables have opposite signs of regression coefficients, which is reasonable in, e.g., network-based analysis of gene expression data. To address this issue, they proposed a modified version of (2.1),
| (2.4) |
| (2.5) |
where L̃ = (l̃ij) = STLS with S = diag(sgn (β̃1), …, sgn (β̃p)) and β̃ = (β̃1, …, β̃p) is obtained from a preliminary regression analysis.
Here we motive the penalty (2.5) from another point of view. To account for regression coefficients with opposite signs, consider the penalty
| (2.6) |
where |β| = (|β1|, …, |βp|)T. Similar to (2.1), this explicitly uses the Laplacian matrix as a differential operator, distinguishing it from other network-based penalties, such as those considered in Pan, Xie, and Shen (2010). To emphasize this unique feature, we refer to (2.1) and (2.6) as the Laplacian net and absolute Laplacian net, respectively. The latter penalty is in general nonconvex, posing challenges for efficient implementation and theoretical analysis. In the spirit of Zou and Li (2008), we propose to use the approximation
in the second term of (2.6), which gives rise to (2.5). Therefore, the penalty (2.5) can be viewed as an adaptive, convex approximation to (2.6) and should inherit the performance of the latter provided a reasonably good initial estimate β̃ can be obtained. We call the penalty (2.5) the adaptive Laplacian net.
We propose to estimate β0 by the adaptively penalized partial likelihood estimator
| (2.7) |
where ℓ(β) and p*(β; β̃, λ1, λ2) are defined in (2.3) and (2.5), respectively. Since an ordinary least squares estimator does not perform well, or can even fail when p grows fast with n, whereas the Lasso and elastic net produce sparse estimates that can prevent many edges on a given network from being active, we recommend that the initial estimate β̃ be computed from a ridge regression for model (1.1),
where λ ≥ 0 is a regularization parameter. The ridge method does not shrink any coefficient to exactly zero and thus helps to preserve and utilize all the information contained in the network. We demonstrate in our simulation studies and data analysis that this modified approach can effectively adapt to the different signs of the coefficients and yield encouraging results. Note that the optimization problem (2.2) is a special case of (2.7) with sgn (β̃i) = sgn (β̃j) ≠ 0 for all (i, j) ∈ E; to avoid redundancy, we present implementation details and theoretical properties only for the latter.
2.3. Implementation
Since the objective function in (2.7) is convex, the optimization problem can be solved by many commonly used algorithms for convex optimization. We describe an implementation by coordinate descent, a method that is especially appealing for large-scale sparse problems (Friedman et al. (2007); Wu and Lange (2008)). We adapt the coordinate descent algorithm to network-regularized high-dimensional Cox regression, which turns out to be quite efficient.
Let γ = (γ1, …, γn)T = (βTX1, …, βTXn)T. Following Simon et al. (2011), we approximate ℓ(β) by
where and yi(γ) = γi − (∂ℓ(β)/∂γi)/ui(γ). A simple calculation as in Li and Li (2010) yields that the univariate optimization problem
has the exact solution
| (2.8) |
where
and Xij is the jth component of Xi. We then obtain an algorithm for computing the solution to the optimization problem (2.7) for a given pair of regularization parameters (λ1, λ2).
Step 1. Initialize β̂ = 0 and γ̂ = (β̂TX1, …, β̂TXn)T.
Step 2. Compute ui(γ̂) and yi(γ̂) for i = 1, …, n.
Step 3. Update β̂j by (2.8) cyclically for j = 1, …, p until convergence.
Step 4. Update γ̂ = (β̂TX1, …, β̂TXn)T and repeat Steps 2 and 3 until convergence.
To select the tuning parameters λ1 and λ2, it is convenient to reparameterize them as λ1 = λa and λ2 = λ(1 − a), where λ ≥ 0 and 0 ≤ a ≤ 1. We first set a to a sufficiently fine grid of values on [0, 1]. For each fixed a, set , which ensures that β̂ = 0, and let λmin = ελmax for some small ε ∈ (0, 1). We then compute the solution path for a decreasing sequence of λ from λmax to λmin, at each step using the solution from the previous position as a warm start. Finally, we use K-fold cross-validation to choose the optimal pair (λ, a) that minimizes the cross-validation error
where β̂(−k)(λ, a) is the estimate obtained from excluding the kth part of the data with a given pair of values of (λ, a), and ℓ(−k)(·) is the log partial likelihood without the kth part of the data.
3. Theoretical Properties
We adopt the usual counting process notation. For subject i, denote by Ni(t) = I(T̃i ≤ t, Δi = 1) the counting process for the observed failure and by Yi(t) = I(T̃i ≥ t) the at-risk indicator, and let N(t) and Y(t) be the generic processes. For convenience, we write v⊗0 = 1, v⊗1 = v, and v⊗2 = vvT, for any vector v. Let , s(k)(β, t) = E{Y(t)X⊗k exp(βTX)}, k = 0, 1, 2, X̄(β, t) = S(1)(β, t)/S(0)(β, t), and e(β, t) = s(1)(β, t)/s(0)(β, t). The partial likelihood score function can then be written as
where τ is the maximum follow-up time. The performance of the penalized partial likelihood estimators depends critically on the covariance structure reflected by the empirical information matrix
and its population counterpart
Also, denote the augmented empirical and population information matrices by
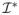 (β, λ2) =
(β, λ2) =
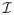 (β) + λ2L̃ and Σ*(β, λ2) = Σ(β) + λ2L̃, respectively. Note that L̃, and hence Σ*(β, λ2), depends on the initial estimator β̃ through the signs of the coefficients in β̃.
(β) + λ2L̃ and Σ*(β, λ2) = Σ(β) + λ2L̃, respectively. Note that L̃, and hence Σ*(β, λ2), depends on the initial estimator β̃ through the signs of the coefficients in β̃.
Further, define the active set A = {j : β0j ≠ 0} and estimated active set  = {j : β̂j ≠ 0}, where β0j and β̂j are the jth components of β0 and β̂, respectively. Let s = |A| be the number of nonzero coefficients in β0, and denote the complement of a set B by Bc. We use sets to index vectors and matrices; for example, β0A is the subvector formed by β0j with j ∈ A, and
is the submatrix formed by the (i, j)th entries of Σ*(β, λ2) with i ∈ Ac and j ∈ A. Finally, let d be a signal threshold such that minj∈A |β0j| ≥ d, and let
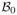 be the hypercube {β ∈ ℝp : ||βA − β0A||∞ ≤ d, βAc = 0}, where ||·||∞ is the supremum norm. All these quantities can depend on the sample size n and, in particular, we allow the dimensions s and p to grow with n.
be the hypercube {β ∈ ℝp : ||βA − β0A||∞ ≤ d, βAc = 0}, where ||·||∞ is the supremum norm. All these quantities can depend on the sample size n and, in particular, we allow the dimensions s and p to grow with n.
We need to impose conditions.
(C1) and P{Y(τ) = 1} > 0.
(C2) The covariates Xj, j = 1, …, p, are bounded and there exists a constant M > 0 such that Σj∈A |Xj| ≤ M.
-
(C3) There exists a constant Cmin > 0 such that
where Λmin(·) denotes the minimum eigenvalue.
-
There exists a constant α ∈ (0, 1] such that
where ||·||∞ is the matrix ∞-norm.
Condition (C1) is standard in the asymptotic theory for the Cox model (Andersen and Gill (1982)). The boundedness assumptions in (C2) are convenient for technical derivations, but are not essential and can be weakened to tail bound conditions as in Lin and Lv (2013). Conditions (C3) and (C4) are the main assumptions for obtaining strong performance guarantees. The former reflects the intuition that the relevant covariates cannot be overly dependent, which is required for estimating the nonzero effects with diverging dimensionality; the latter formalizes the intuition that the set of relevant covariates and the set of irrelevant covariates cannot be overly correlated, needed for distinguishing between these sets of variables and achieving model selection consistency. In the special case of ℓ1 regularization, these conditions parallel those in Wainwright (2009) that concern linear regression models, and are also related to those in Bradic, Fan and Jiang (2011) for the Cox model.
Two new messages are conveyed by these conditions. First, since (C3) and (C4) are imposed on submatrices of the augmented matrix Σ* (β, λ2), a proper choice of λ2 and L̃ can substantially relax the conditions. Specifically, Weyl’s inequality (Horn and Johnson (1985)) and the fact that L̃ is positive semidefinite entail that . Hence, the Laplacian net method tends to improve on the condition number of the sparse information matrix ΣAA(β0) and weaken the restriction imposed by (C3); that is, it has the conditioning effect. On the other hand, nonzero entries in the matrix Σ(β) indicate that the contributions of the corresponding covariates in the partial likelihood score equation are correlated, which are shrunk toward zero by the entries of λ2L̃ provided that the choice of L̃ correctly captures this relationship; that is, the Laplacian net has the correlation shrinkage effect, which helps to relax the restrictions in both (C3) and (C4). It is worth pointing out that the elastic net, with an identity matrix in place of L̃, does not have the latter effect. Note also that the (approximate) sign consistency of the initial estimator β̃ plays a helpful, but not essential, role in achieving these effects through the matrix L̃.
Second, in a different nature from the conditions in Bradic, Fan and Jiang (2011), (C4) shows that restrictions on the population information matrix, rather than its empirical counterpart, are sufficient, which can then be viewed as a high-dimensional extension of the classical asymptotic regularity conditions. Such an extension is highly nontrivial and is achieved by a detailed characterization of the uniform convergence of the empirical information matrix.
Proposition 1 (Concentration of empirical matrices)
Under (C1)−(C4), if s = O(n1/3), then there exist constants D,K > 0 such that
| (3.1) |
| (3.2) |
The proof of Proposition 1 is given in the Appendix. This result says that with high probability, the empirical matrices satisfy almost the same conditions as those imposed on their population counterparts.
Our main result is that, under suitable conditions, the proposed estimators correctly identify the sparse model and are uniformly consistent in estimating the nonzero effects, the weak oracle property in the sense of Lv and Fan (2009).
Theorem 1 (Weak oracle property)
Suppose (C1)−(C4) hold, that
| (3.3) |
and the regularization parameters λ1 and λ2 are chosen to satisfy
| (3.4) |
where L̃ ·,A is the submatrix formed by the columns of L̃ with index j ∈ A. Then there exist constants D,K > 0 such that, with probability at least , (2.7) has a unique solution that satisfies
(Sparsity) β̂Ac = 0.
(ℓ∞-loss) .
The dimension condition (3.3) there allows both s and p to grow with n, at the rates s = o(n1/4) and log p = o(n), respectively. This is especially relevant in genomic studies, where the number of features usually far exceeds the sample size and is usefully modeled as exponentially growing with the latter, while the number of relevant features can also grow slightly as more are included in the analysis. The second condition in (3.4) requires λ2 to be within a certain proportion of λ1, depending on the matrix L̃ and the signal β0A. This is reasonable because the bias induced by the quadratic Laplacian penalty needs to be controlled so as not to prevent consistent variable selection; see a related discussion in Hebiri and van de Geer (2011) for linear regression models.
In view of the last condition in (3.4), parts (a) and (b) in Theorem 1 together imply sign consistency (Zhao and Yu (2006)), which is in fact stronger than model selection consistency. The benefit of the Laplacian net method in estimation can be clearly seen from the upper bound in part (b); with appropriately chosen λ2 and L̃, one obtains a larger constant Cmin in Condition (C3) and hence a smaller estimation loss.
4. Simulation Studies
We conducted simulation studies to evaluate the finite-sample performance of the proposed Laplacian net (Lnet) and adaptive Laplacian net (AdaLnet) methods, and compared them with the Lasso and elastic net (Enet). We also made comparisons with the Cox regression method with the network-based penalty considered in Pan, Xie, and Shen (2010), a sum of grouped penalties, each in the form of the ℓγ-norm of the two coefficients for a pair of neighboring nodes on a given network (GLγ). We considered scenarios that are likely to be encountered in genomic studies, with different settings of the strengths and directions of genetic effects.
We simulated gene expression data within an assumed network. Each network consisted of 100 disjoint regulatory modules, each with one transcription factor gene (TF) and ten regulated genes, resulting in a total of p =1,100 genes. We took di = 10 for the TFs and di = 1 for the regulated genes, and wij = 1 between the TFs and their regulated genes and 0 otherwise. The expression value of each TF was generated from a standard normal distribution, and the expression values of the ten regulated genes were generated from a conditional normal distribution with a correlation of ρ between the expressions of these genes and that of the corresponding TF. We set ρ = 0.7 for five regulated genes and ρ = −0.7 for the other five. This mimics the fact that the TF can either activate or repress the regulated genes. We then generated failure times from the Cox model
that includes only the s = 44 relevant genes. The baseline hazard function λ0(t) was specified by a Weibull distribution with shape parameter 5 and scale parameter 2, and censoring times were generated from U(2, 15), resulting in a censoring rate of about 30%. In each setting, the sample size was fixed at n = 200 and the simulations were replicated 50 times. We applied fivefold cross-validation to choose the optimal tuning parameters.
We considered six models. In Model 1, all genes within the same module have the same directions in their effects on the survival outcome. The coefficients βj , j = 1, …, 22, which correspond to the genes in the first two modules, were generated from U(0.1, 1), while βj , j = 23, …, 44, were generated from U(−1, −0.1). In Model 2, we assigned a random set of three regulated genes different signs of regression coefficients from the other regulated genes within the same module, while keeping their absolute values the same as in Model 1.
We considered models where the TFs have stronger effects than the regulated genes, as typically observed in practice. In Model 3, we set the regression coefficients of the four TFs to (2, −2, 4, −4), and those of the regulated genes to , where βTF is the coefficient of the corresponding TF. In Model 4, we changed the signs of regression coefficients of three genes in each module as in Model 2. In Model 5, we allowed the ten regulated genes within each module to have different effect sizes, with regression coefficients for j = 1, …, 10. In Model 6, we changed the signs of regression coefficients of three genes in each module from Model 5. Finally, Models 7 and 8 were the same as Models 5 and 6, except that the coefficients of two randomly selected genes in each module were set to zero. Only Model 3 assumes that the neighboring genes have the same degree-scaled coefficients.
The variable selection performance of each method is summarized by sensitivity, specificity, and the Matthews correlation coefficient
where TP, TN, FP, and FN denote the numbers of true positives, true negatives, false positives, and false negatives, respectively. The MCC is an overall measure of variable selection accuracy, and a larger MCC indicates a better variable selection performance.
Simulation results for Models 1 and 2 are reported in Table 1. We observed that, in general, AdaLnet and Enet gave the best overall variable selection performance, while Lasso tended to select too many variables with high false positive rates. In contrast, GLγ tended to select the smallest number of genes and resulted in the lowest sensitivities. Since the majority of the genes were irrelevant and all methods resulted in sparse models, specificity in all cases was much higher than sensitivity and was comparable among all methods. Enet selected a slightly higher proportion of irrelevant genes and hence had slightly lower specificity compared with AdaLnet. Comparisons of the results for Models 1 and 2 suggest the additional benefit of accounting for different directions of the genetic effects from AdaLnet. In Model 1, since all genes within the same module have equal directions in their effects, Lnet and AdaLnet had similar performance, although AdaLnet showed slightly higher sensitivity because the expression levels of these relevant genes were not always positively correlated. In Model 2, where linked genes may affect the survival outcome in opposite directions, AdaLnet exhibited consistent improvement over Lnet in terms of sensitivity and MCC. All methods had similar estimation performance in terms of mean squared error (MSE). Lasso had a lightly smaller MSE than the other methods at the price of a much worse variable selection performance.
Table 1.
Simulation results for Models 1–4. (n, p, s) = (200, 1100, 44). Sensitivity, specificity, MCC, number of selected genes, number of false positives (FPs), and mean squared error (MSE) were averaged over 50 replicates. Lnet: Laplcian net; AdaLnet: adaptive Laplacian net; Lasso: ℓ1-penalty; Enet: elastic net; GL: group ℓγ-penalty. Standard errors are given in the Supplementary Material.
| Method | Sensitivity | Specificity | MCC | # of genes | # of FPs | MSE |
|---|---|---|---|---|---|---|
| Model 1 | ||||||
| Lnet | 0.346 | 0.997 | 0.524 | 18.84 | 3.60 | 0.016 |
| AdaLnet | 0.395 | 0.996 | 0.559 | 21.47 | 4.09 | 0.016 |
| Lasso | 0.435 | 0.950 | 0.310 | 72.25 | 53.13 | 0.012 |
| Enet | 0.407 | 0.995 | 0.561 | 22.77 | 4.88 | 0.016 |
| GLγ | 0.233 | 0.998 | 0.431 | 12.66 | 2.42 | 0.015 |
| Model 2 | ||||||
| Lnet | 0.442 | 0.996 | 0.600 | 23.54 | 4.09 | 0.015 |
| AdaLnet | 0.557 | 0.996 | 0.682 | 28.79 | 4.23 | 0.015 |
| Lasso | 0.465 | 0.958 | 0.362 | 64.32 | 43.88 | 0.011 |
| Enet | 0.616 | 0.991 | 0.675 | 36.68 | 9.58 | 0.015 |
| GLγ | 0.434 | 0.996 | 0.594 | 22.99 | 3.91 | 0.014 |
| Model 3 | ||||||
| Lnet | 0.526 | 0.987 | 0.591 | 37.06 | 13.91 | 0.070 |
| AdaLnet | 0.624 | 0.995 | 0.715 | 33.24 | 5.77 | 0.071 |
| Lasso | 0.363 | 0.975 | 0.346 | 42.67 | 26.71 | 0.067 |
| Enet | 0.684 | 0.986 | 0.682 | 44.90 | 14.79 | 0.072 |
| GLγ | 0.437 | 0.999 | 0.633 | 20.26 | 1.05 | 0.070 |
| Model 4 | ||||||
| Lnet | 0.446 | 0.996 | 0.601 | 24.34 | 4.71 | 0.070 |
| AdaLnet | 0.633 | 0.995 | 0.728 | 32.62 | 4.76 | 0.070 |
| Lasso | 0.407 | 0.974 | 0.376 | 45.66 | 27.76 | 0.063 |
| Enet | 0.661 | 0.988 | 0.684 | 41.96 | 12.88 | 0.072 |
| GLγ | 0.541 | 0.999 | 0.703 | 25.22 | 1.40 | 0.070 |
Simulation results for Models 3–8 are summarized in the rest of Table 1 and in Table 2, indicating essentially the same trends as for Models 1 and 2. In these settings, where the TFs and regulated genes had different strengths of effects, the improvement of Lnet and AdaLnet over Lasso and Enet was more dramatic, because the difference in effect sizes was taken into account by our methods. In addition, AdaLnet always resulted in the highest MCC among the four models considered. GLγ gave the smallest number of false positives; however, it also had, in general, lower sensitivity and MCC compared to AdaLnet. Lasso and Enet resulted in large numbers of false positives. The Supplementary Material contains some additional simulation settings where the weights wij were generated by sample correlation coefficients of gene expressions, yielding very similar results.
Table 2.
Simulation results for Models 5–8. (n, p, s) = (200, 1100, 44). Sensitivity, specificity, MCC, number of selected genes, number of false positives (FPs), and mean squared error (MSE) were averaged over 50 replicates. Lnet: Laplcian net; AdaLnet: adaptive Laplacian net; Lasso: ℓ1-penalty; Enet: elastic net; GLγ: group ℓγ-penalty. Standard errors are given in the Supplementary Material.
| Method | Sensitivity | Specificity | MCC | # of genes | # of FPs | MSE |
|---|---|---|---|---|---|---|
| Model 5 | ||||||
| Lnet | 0.491 | 0.989 | 0.575 | 10.65 | 12.08 | 0.077 |
| AdaLnet | 0.567 | 0.996 | 0.687 | 29.55 | 4.62 | 0.077 |
| Lasso | 0.339 | 0.977 | 0.337 | 39.61 | 24.71 | 0.073 |
| Enet | 0.649 | 0.985 | 0.651 | 44.83 | 16.28 | 0.078 |
| GLγ | 0.377 | 0.999 | 0.586 | 17.46 | 0.88 | 0.076 |
| Model 6 | ||||||
| Lnet | 0.439 | 0.996 | 0.600 | 23.52 | 4.22 | 0.076 |
| AdaLnet | 0.642 | 0.996 | 0.732 | 31.43 | 3.98 | 0.076 |
| Lasso | 0.404 | 0.973 | 0.369 | 46.74 | 28.98 | 0.069 |
| Enet | 0.650 | 0.988 | 0.675 | 41.61 | 13.00 | 0.078 |
| GLγ | 0.523 | 0.998 | 0.686 | 24.78 | 1.75 | 0.076 |
| Model 7 | ||||||
| Lnet | 0.518 | 0.985 | 0.553 | 35.06 | 16.43 | 0.067 |
| AdaLnet | 0.587 | 0.992 | 0.639 | 29.61 | 8.48 | 0.067 |
| Lasso | 0.424 | 0.969 | 0.349 | 47.99 | 32.73 | 0.061 |
| Enet | 0.656 | 0.983 | 0.610 | 42.05 | 18.42 | 0.069 |
| GLγ | 0.507 | 0.994 | 0.606 | 24.87 | 6.62 | 0.066 |
| Model 8 | ||||||
| Lnet | 0.483 | 0.993 | 0.582 | 24.83 | 7.45 | 0.067 |
| AdaLnet | 0.641 | 0.992 | 0.673 | 31.84 | 8.76 | 0.067 |
| Lasso | 0.458 | 0.969 | 0.373 | 49.22 | 32.74 | 0.059 |
| Enet | 0.676 | 0.984 | 0.632 | 41.10 | 16.78 | 0.069 |
| GLγ | 0.564 | 0.994 | 0.647 | 26.41 | 6.10 | 0.067 |
Our algorithm is very fast: the average computation time for obtaining a single solution path over a grid of 50 points in our simulation setting with (n, p) = (200, 1100) was about 0.7 second, only slightly above the average computation time for the Lasso from the R package glmnet.
5. Application to a Breast Cancer Gene Expression Study
We illustrate the proposed method by application to analyzing a gene expression data set for patients with lymph-node-negative primary breast cancer, as reported by Wang et al. (2005). These 286 patients were treated between 1980 and 1995 and did not receive adjuvant systemic therapy, of which 107 (37.4%) developed distant metastases in a median follow-up time of 7.2 years. Gene expression profiles were measured on these patients using Affymetrix HG-U133A arrays. To perform a network-based analysis, we focused our analysis on the genes that can be mapped to the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways (Kanehisa and Goto (2000)). After merging the gene expression data with the KEGG pathways, we obtained a network consisting of 2563 genes and 15,028 edges. Based on this KEGG network, the edge weight was wij = 1 if genes i and j are linked and 0 otherwise, and the node degree di was the number of genes that link to gene i. The focus of our analysis was to identify the genes and pathways on the KEGG network that are related to cancer survival.
5.1. Regression coefficients of linked genes on the KEGG network
We first demonstrate that the regression coefficients of linked genes on the KEGG network are closer to each other than randomly selected gene pairs. We have a total of p = 2, 554 genes with 15,028 edges after removing all isolated genes and loops. For each of these genes, we first obtained the estimated regression coefficient from fitting the Cox model with the expression level of this gene as a covariate. Denote the estimated coefficient for gene i as β̂i. We define the difference between the absolute values of scaled coefficients of two linked genes by
where di is the total number of genes linked to gene i. The sum of absolute differences of all linked genes is given by DE = Σ(i,j)∈E |Dij |, where E is the edge set of all linked genes on the KEGG network.
We obtained DE = 2.8645 for the 15,028 edges of the KEGG network. We then performed a randomization test to see if the regression coefficients of the linked genes are likely to be similar. Specifically, we generated an edge set consisting of randomly selected 15,028 gene pairs out of the total p(p−1)/2 = 3, 260, 181 pairs and calculated DE0 using the same node degrees as in calculating DE. With 50,000 random edge sets, we obtained the empirical distribution of DE0 as shown in Figure 1. It is clear that the observed DE is far away from the empirical distribution for randomly selected edge sets, where the range of DE0 is between 10.28 and 15.05. We also observe that the coefficient difference of the linked genes on the KEGG network is much smaller than any of the randomly selected gene pairs, which indicates that the regression coefficients of two linked genes in this data set are more similar than randomly selected gene pairs. This partially supports our biological intuition that genes connected in the KEGG network should have similar regression coefficients in the Cox model.
Figure 1.
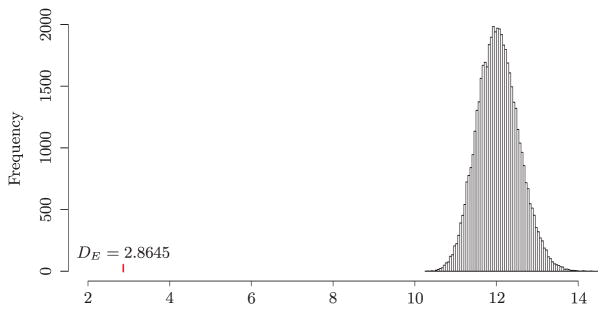
Analysis of breast cancer gene expression data: histogram of the sum of scaled differences between two Cox regression coefficients for 15,028 randomly selected gene pairs based on 50,000 permutations. The vertical bar represents the sum of scaled differences between two Cox regression coefficients for the 15,028 genes pairs on the KEGG network.
5.2. Genes and subnetworks selected
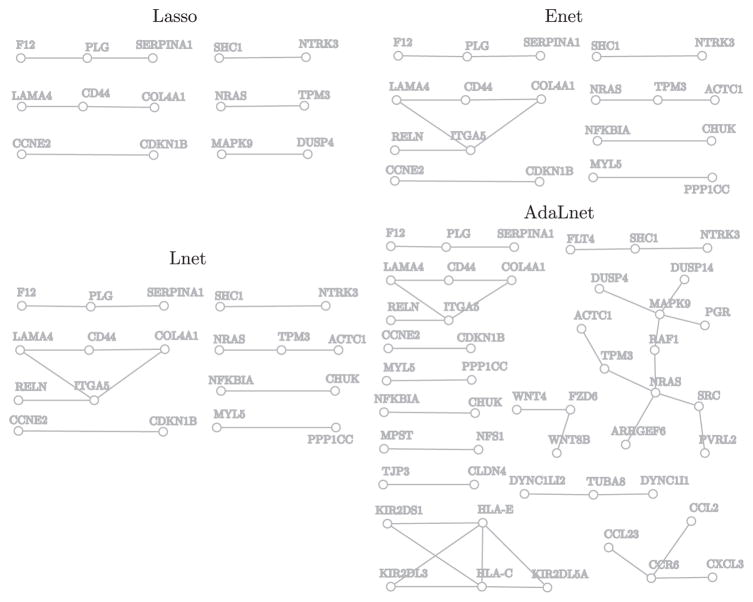
We applied the Lnet, AdaLnet, Lasso, and Enet methods to the data set and used tenfold cross-validation to choose the optimal tuning parameters. Lnet, AdaLnet, Lasso, and Enet selected 98, 140, 62, and 87 genes, respectively. AdaLnet identified many more genes and edges on the KEGG network than Lasso, Enet, and Lnet.
Figure 2 shows the non-isolated genes and associated subnetworks that were identified by these four methods. We observe that AdaLnet selected 47 nonisolated genes, many more than Lasso (14), Enet (19), and Lnet (27). The largest connected component on the subnetwork identified by AdaLnet includes 11 genes, most of which are involved in the mitogen-activated protein kinase (MAPK) pathway. The MAPK pathway participates in fundamental cellular processes such as proliferation, differentiation, migration, and apoptosis, and plays a key role in the development and progression of cancer (Dhillon et al. (2007)). Of particular interest is the well-known oncogene SRC; it has recently been revealed that Src pathway activity is critical for the survival of disseminated breast cancer cells in the bone marrow microenvironment, leading to an extended period for latent metastasis in breast cancer (Zhang et al. (2009)). This connected subnetwork also includes DUSP4/DUSP14 genes, which negatively regulate members of the mitogen-activated protein (MAP) kinase superfamily (MAPK/ERK) and are associated with cellular proliferation and differentiation (Guan and Butch (1995)). In contrast, although Lasso and Enet identified some links in this subnetwork (e.g., NRAS-TMP3, MAPK9-DUSP4 and NRAS-TPM3-ACTC1), the results from these analyses did not provide strong evidence indicating the involvement of the MAPK pathway in distant metastases of breast cancer.
Figure 2.
Subnetworks of the KEGG network identified by four different methods applied to the breast cancer gene expression data set. Only nonisolated genes are shown.
A second largest component includes two human leukocyte antigen (HLA) class I molecules and three killer immunoglobulin-like receptors (KIRs). It has been known that altered expression of classical (e.g., HLA-C) and nonclassical (e.g., HLA-E) HLA class I molecules is among the immune escape routes most widely taken by tumor cells (Algarra et al. (2004)). The clinical impact of tumor expression of classical and nonclassical HLAs, as well as their interactions, have been confirmed in a study of 677 early breast cancer patients (de Kruijf et al. (2010)). Another second largest component includes CD44 and integrin α5 (ITGA5), which have been identified as target genes of microRNAs miR-373/520c and miR-31, respectively, in mediating breast cancer metastasis (Valastyan et al. (2009)). It is interesting to note that SRC was not selected by Lasso, Enet, or Lnet, HLA-C and HLA-E were not selected by Lasso or Enet, and ITGA5 was not selected by Lasso.
The fourth subnetwork identified by AdaLnet involves the inflammatory chemokines CCL2 and CCL23 and its receptor CCR6. A causal role was recently attributed to inflammation in many malignant diseases, including breast cancer. The different inflammatory mediators that are involved in this disease include cells, cytokines, and chemokines, and many studies have addressed the involvement and roles of the inflammatory chemokine CCL2 (MCP-1) in breast malignancy and progression (Soria and Ben-Baruch (2008)). Another subnetwork identified by AdaLnet only includes genes in the Wnt signaling pathway (WNT4, WNT8B, and FZD6), which is also implicated in breast cancer metastasis (Matsuda et al. (2009)).
5.3. Stability selection
We saw that AdaLnet selected more genes than the other methods, and we now demonstrate that the genes selected are also quite stable. Following Meinshausen and Bühlmann (2010), let Sk be the kth random subsample of {1, …, n} of size ⌊n/2⌋ without replacement, where ⌊x⌋ is the largest integer not greater than x. To balance the censored observations, we sampled half of the censored subjects and half of the uncensored subjects. For a given pair of tuning parameters (λ, α), the selection probability of gene j is defined as
where is the estimate of βj using a regularization procedure based on the j subsample Sk given the tuning parameters (λ, α), and K is the number of resampling replicates. We used K = 100 as suggested by Meinshausen and Bühlmann (2010). A measurement of stability of gene j is then given by maxλ,α Pr(λ,α)(j). Table 3 summarizes the stability measurements of the genes selected by each of the four methods. We see Lnet resulted in the highest variable selection stability, followed by AdaLnet and Enet. It is interesting that the selected genes that are linked on the KEGG network had in general higher stability than those isolated genes. By encouraging connectivity of the solution, genes that are highly connected in the graph tend to be more often selected, improving stability of the solution.
Table 3.
Summary of stability measurements of the genes selected by four different methods. The minimum (Min), first quantile (Q1), median, mean, third quantile (Q3), and maximum (Max) are shown.
| Method | # of genes | Min | Q1 | Median | Mean | Q3 | Max |
|---|---|---|---|---|---|---|---|
| All selected genes | |||||||
| Lasso | 6̃2 | 0.06 | 0.21 | 0.30 | 0.31 | 0.40 | 0.65 |
| Enet | 8̃7 | 0.35 | 0.65 | 0.79 | 0.76 | 0.87 | 0.99 |
| Lnet | 9̃8 | 0.46 | 0.71 | 0.82 | 0.80 | 0.91 | 1.00 |
| AdaLnet | 140 | 0.34 | 0.60 | 0.75 | 0.73 | 0.87 | 0.99 |
| Selected genes that are linked on the KEGG network | |||||||
| Lasso | 1̃4 | 0.12 | 0.22 | 0.40 | 0.37 | 0.47 | 0.65 |
| Enet | 1̃9 | 0.44 | 0.69 | 0.80 | 0.78 | 0.91 | 0.99 |
| Lnet | 2̃7 | 0.56 | 0.71 | 0.84 | 0.81 | 0.94 | 1.00 |
| AdaLnet | 4̃7 | 0.39 | 0.68 | 0.80 | 0.78 | 0.92 | 0.99 |
6. Discussion
We have proposed a network-based regularization method for high-dimensional Cox regression, as a means to incorporate prior network structural information about the covariates. In genomic studies, regularization methods that ignore current biological knowledge often result in selection of isolated genes, rendering interpretation of the results difficult. In contrast, network-based methods can identify many more functionally related genes and help to bridge the gap between genomic data analysis and understanding of biological mechanisms.
A practical issue in the application of the proposed methodology is to decide which existing biological network to use and how to account for its uncertainty. Choice of the network to use with measured gene expression data depends on the scientific questions asked and whether the network interactions can be reflected at the transcriptional levels. In our analysis of the breast cancer gene expression data, we chose the KEGG pathways and aimed to identify which KEGG subnetworks were associated with distant metastasis. Alternatively, we could focus on the known cancer-related pathways or the large-scale protein-protein interaction network. Instead of using the prior network information, one can build a gene co-expression network from the data and use it to determine the gene neighbors; see Section 3 of Huang et al. (2011) for a discussion of adjacency measures that can be used for the construction of such networks. If the prior network structure is inaccurate or uninformative, we expect the tuning parameter λ2 to be small and therefore the Laplacian penalty to have little effect on variable selection and estimation. Incorporating the uncertainty of the network structure directly into our methodology and theory is a worthwhile research direction.
We have used the convex ℓ1-penalty to induce sparsity of the regression coefficients to facilitate theoretical analysis and fast computation of a global solution. It would be interesting to explore several nonconvex extensions, as in Huang et al. (2011) for linear regression models. If one replaces the ℓ1-penalty in our method by SCAD or MCP, our arguments could be adapted to establish the oracle property of the modified method, under stronger conditions than those required by the weak oracle property. It is worth noting that the concentration inequalities we established reflect some intrinsic properties of the Cox model in high dimensions and do not depend on any specific penalty function; they will play a role in the theoretical development of such nonconvex extensions.
We have demonstrated in Section 5.1 that local smoothness of regression coefficients over a gene network may be a biologically plausible assumption. One can consider alternatively the weaker assumption that two neighboring variables are either both important or both unimportant. This would be more reasonable and likely to be satisfied in broader contexts. Network-based regularization under this assumption could be achieved by a modification of the Laplacian penalty. The discrete nature of the weaker assumption, however, makes the choice of a penalty that allows for efficient implementation much more challenging. These are interesting topics but are beyond the present scope.
Supplementary Material
Acknowledgments
This research was supported in part by NIH grants CA127334, GM097505, and GM088566. Hokeun Sun and Wei Lin contributed equally to this work. We thank Professor Wei Pan for sharing his computer code and helpful discussions. We are also grateful to the Co-Editor, an associate editor, and two referees for constructive comments that have led to substantial improvement in the presentation of the paper.
Appendix: Proofs
A few lemmas are essential to the proofs of our main results; their proofs can be found in the Supplementary Material. The constants in our proofs may vary from line to line.
Lemma A.1 (Optimality conditions)
A vector β̂ ∈ ℝp is a unique solution to (2.7) if
| (A.1) |
| (A.2) |
and is positive definite, where L̃Â,· and L̃Âc,· are the submatrices formed by the jth rows of L̃ with j ∈ Â and j ∈ Âc, respectively.
Lemma A.2 (Concentration of U(β0))
Under (C1) and (C2), there exist constants C, D, K > 0 such that
for all x > 0 and j = 1, …, p, where Uj(β0) is the jth component of U(β0).
Lemma A.3 (Concentration of
 (·))
(·))
Under (C1) and (C2), there exist constants C, D, K > 0 such that
for all x > 0 and i, j = 1, …, p, where
 (·) and σij(·) are the (i, j)th entries of
(·) and σij(·) are the (i, j)th entries of
 (·) and Σ(·), respectively.
(·) and Σ(·), respectively.
Proof of Proposition 1
By the Hoffman-Wielandt inequality (Horn and Johnson (1985)), we have
where Λ(j)(·) denotes the jth smallest eigenvalue and ||·||F is the Frobenius norm. It then follows from Lemma A.3 and the union bound that
which, together with (C2), implies (3.1).
To show (3.2), we write
Consider the term T1. By Lemma A.3 and the union bound, we have
| (A.3) |
Since , (3.1) implies that
| (A.4) |
Hence, we have
Consider the term T2. Similar to (A.3), we have
This, together with (C3) and (A.4), leads to
Combining the bounds for T1 and T2 gives
which, along with (C3), implies (3.2). This completes the proof.
Proof of Theorem 1
We first define an “ideal” event that occurs with high probability, then analyze the behavior of the penalized estimator β̂ conditional on that event by using deterministic arguments based on Lemma A.1.
By Lemma A.2 and the union bound, we have
This, along with (3.1) and (3.2), implies that, with probability at least ,
| (A.5) |
| (A.6) |
We condition on the event that these inequalities hold. It suffices to find a β̂ ∈ ℝp that satisfies all the optimality conditions in Lemma A.1 and the desired properties. With β̂Ac = 0, we determine β̂A by condition (A.1). A Taylor expansion of UA(β̂) gives UA(β̂) = UA(β0) −
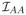 (β̄)(β̂A − β0A), where β̄ lies between β0 and β̂. Also, we have L̃A,·
β̂ = L̃AAβ0A + L̃AA(β̂A − β0A). Substituting into the equation UA(β̂) − λ1sgn (β̂A) − λ2L̃A,·
β̂ = 0 and rearranging yields
(β̄)(β̂A − β0A), where β̄ lies between β0 and β̂. Also, we have L̃A,·
β̂ = L̃AAβ0A + L̃AA(β̂A − β0A). Substituting into the equation UA(β̂) − λ1sgn (β̂A) − λ2L̃A,·
β̂ = 0 and rearranging yields
| (A.7) |
Define f: ℝs → ℝs by f(θ) = β0A+
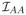 (θ̄, λ2)−1{UA(β0) − λ1sgn (θ) − λ2L̃AAβ0A}, where θ̄Ac = 0 and θ̄A lies between β0A and θ. Let
(θ̄, λ2)−1{UA(β0) − λ1sgn (θ) − λ2L̃AAβ0A}, where θ̄Ac = 0 and θ̄A lies between β0A and θ. Let
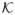 denote the hypercube {
}. Then, by (A.4), (A.5), and the assumption that (λ2/λ1)||L̃·,Aβ0A||∞ < α/8, we have, for θ ∈
denote the hypercube {
}. Then, by (A.4), (A.5), and the assumption that (λ2/λ1)||L̃·,Aβ0A||∞ < α/8, we have, for θ ∈
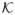 ,
,
or f(
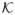 ) ⊂
) ⊂
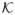 . The assumption
entails sgn (θ) = sgn (β0A); hence, f is a continuous function on the convex, compact set
. The assumption
entails sgn (θ) = sgn (β0A); hence, f is a continuous function on the convex, compact set
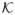 . An application of Brouwer’s Fixed Point Theorem yields that (A.7) has a solution β̂A in
. An application of Brouwer’s Fixed Point Theorem yields that (A.7) has a solution β̂A in
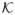 . Moreover, sgn (β̂A) = sgn (β0A) and hence  = A. Thus, we have found a β̂ ∈ ℝp that satisfies (A.1) and the desired properties. Moreover, (A.5) implies that
is positive definite.
. Moreover, sgn (β̂A) = sgn (β0A) and hence  = A. Thus, we have found a β̂ ∈ ℝp that satisfies (A.1) and the desired properties. Moreover, (A.5) implies that
is positive definite.
It remains to verify that β̂ satisfies (A.2). A Taylor expansion of UAc (β̂) and substituting (A.7) gives
Then, by (A.5), (A.6), and the assumption that (λ2/λ1)||L̃·,Aβ0A||∞ < α/8, we
which verifies (A.2) and concludes the proof.
References
- Algarra I, García-Lora A, Cabrera T, Ruiz-Cabello F, Garrido F. The selection of tumor variants with altered expression of classical and nonclassical MHC class I molecules: Implications for tumor immune escape. Cancer Immunol Immunother. 2004;53:904–910. doi: 10.1007/s00262-004-0517-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersen PK, Gill RD. Cox’s regression model for counting processes: A large sample study. Ann Statist. 1982;10:1100–1120. [Google Scholar]
- Antoniadis A, Fryzlewicz P, Letué F. The Dantzig selector in Cox’s proportional hazards model. Scand J Statist. 2010;37:531–552. [Google Scholar]
- Bradic J, Fan J, Jiang J. Regularization for Cox’s proportional hazards model with NP-dimensionality. Ann Statist. 2011;39:3092–3120. doi: 10.1214/11-AOS911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candes E, Tao T. The Dantzig selector: Statistical estimation when p is much larger than n (with discussion) Ann Statist. 2007;35:2313–2404. [Google Scholar]
- Chung FRK. Spectral Graph Theory. Amer. Math. Soc; Providence, RI: 1997. [Google Scholar]
- Cox DR. Regression models and life-tables (with discussion) J Roy Statist Soc Ser B. 1972;34:187–220. [Google Scholar]
- de Kruijf EM, Sajet A, van Nes JGH, Natanov R, Putter H, Smit VTHBM, Liefers GJ, van den Elsen PJ, van de Velde CJH, Kuppen PJK. HLA-E and HLA-G expression in classical HLA class I-negative tumors is of prognostic value for clinical outcome of early breast cancer patients. J Immunol. 2010;185:7452–7459. doi: 10.4049/jimmunol.1002629. [DOI] [PubMed] [Google Scholar]
- Dhillon AS, Hagan S, Rath O, Kolch W. MAP kinase signalling pathways in cancer. Oncogene. 2007;26:3279–3290. doi: 10.1038/sj.onc.1210421. [DOI] [PubMed] [Google Scholar]
- Engler D, Li Y. Survival analysis with high-dimensional covariates: An application in microarray studies. Stat Appl Genet Mol Biol. 2009;8:Article 14. doi: 10.2202/1544-6115.1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. J Amer Statist Assoc. 2001;96:1348–1360. [Google Scholar]
- Fan J, Li R. Variable selection for Cox’s proportional hazards model and frailty model. Ann Statist. 2002;30:74–99. [Google Scholar]
- Friedman J, Hastie T, Höfling H, Tibshirani R. Pathwise coordinate optimization. Ann Appl Stat. 2007;1:302–332. [Google Scholar]
- Guan KL, Butch E. Isolation and characterization of a novel dual specific phosphatase, HVH2, which selectively dephosphorylates the mitogen-activated protein kinase. J Biol Chem. 1995;270:7197–9203. doi: 10.1074/jbc.270.13.7197. [DOI] [PubMed] [Google Scholar]
- Gui J, Li H. Penalized Cox regression analysis in the high-dimensional and low-sample size settings, with applications to microarray gene expression data. Bioinformatics. 2005;21:3001–3008. doi: 10.1093/bioinformatics/bti422. [DOI] [PubMed] [Google Scholar]
- Hebiri M, van de Geer S. The Smooth-Lasso and other ℓ1 +ℓ2-penalized methods. Electron J Stat. 2011;5:1184–1226. [Google Scholar]
- Horn RA, Johnson CR. Matrix Analysis. Cambridge Univ. Press; New York: 1985. [Google Scholar]
- Huang J, Ma S, Li H, Zhang CH. The sparse Laplacian shrinkage estimator for high-dimensional regression. Ann Statist. 2011;39:2021–2046. doi: 10.1214/11-aos897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Sun T, Ying Z, Yu Y, Zhang CH. Oracle inequalities for the lasso in the Cox model. Ann Statist. 2013;41:1142–1165. doi: 10.1214/13-AOS1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong S, Nan B. Non-asymptotic oracle inequalities for the high-dimensional Cox regression via lasso. Statist Sinica. 2012 doi: 10.5705/ss.2012.240. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehner B, Crombie C, Tischler J, Fortunato A, Fraser AG. Systematic mapping of genetic interactions in Caenorhabditis elegans identifies common modifiers of diverse signaling pathways. Nat Genet. 2006;38:896–903. doi: 10.1038/ng1844. [DOI] [PubMed] [Google Scholar]
- Li C, Li H. Variable selection and regression analysis for graph-structured covariates with an application to genomics. Ann Appl Stat. 2010;4:1498–1516. doi: 10.1214/10-AOAS332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin W, Lv J. High-dimensional sparse additive hazards regression. J Amer Statist Assoc. 2013;108:247–264. [Google Scholar]
- Lv J, Fan Y. A unified approach to model selection and sparse recovery using regularized least squares. Ann Statist. 2009;37:3498–3528. [Google Scholar]
- Matsuda Y, Schlange T, Oakeley EJ, Boulay A, Hynes NE. WNT signaling enhances breast cancer cell motility and blockade of the WNT pathway by sFRP1 suppresses MDA-MB-231 xenograft growth. Breast Cancer Res. 2009;11:R32. doi: 10.1186/bcr2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N, Bühlmann P. Stability selection (with discussion) J Roy Statist Soc Ser B. 2010;72:417–473. [Google Scholar]
- Pan W, Xie B, Shen X. Incorporating predictor network in penalized regression with application to microarray data. Biometrics. 2010;66:474–484. doi: 10.1111/j.1541-0420.2009.01296.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon N, Friedman J, Hastie T, Tibshirani R. Regularization paths for Cox’s proportional hazards model via coordinate descent. J Statist Software. 2011;39:1–13. doi: 10.18637/jss.v039.i05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soria G, Ben-Baruch A. The inflammatory chemokines CCL2 and CCL5 in breast cancer. Cancer Lett. 2008;267:271–285. doi: 10.1016/j.canlet.2008.03.018. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J Roy Statist Soc Ser B. 1996;58:267–288. [Google Scholar]
- Tibshirani R. The lasso method for variable selection in the Cox model. Stat Med. 1997;16:385–395. doi: 10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Valastyan S, Reinhardt F, Benaich N, Calogrias D, Szász AM, Wang ZC, Brock JE, Richardson AL, Weinberg RA. A pleiotropically acting microRNA, miR-31, inhibits breast cancer metastasis. Cell. 2009;137:1032–1046. doi: 10.1016/j.cell.2009.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Wainwright MJ. Sharp thresholds for high-dimensional and noisy sparsity recovery using ℓ1-constrained quadratic programming (Lasso) IEEE Trans Inform Theory. 2009;55:2183–2202. [Google Scholar]
- Wang S, Nan B, Zhou N, Zhu J. Hierarchically penalized Cox regression with grouped variables. Biometrika. 2009;96:307–322. [Google Scholar]
- Wang Y, Klijn JGM, Zhang Y, Sieuwerts AM, Look MP, Yang F, Talantov D, Timmermans M, Meijer-van Gelder ME, Yu J, Jatkoe T, Berns EMJJ, Atkins D, Foekens JA. Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. Lancet. 2005;365:671–679. doi: 10.1016/S0140-6736(05)17947-1. [DOI] [PubMed] [Google Scholar]
- Wu TT, Lange K. Coordinate descent algorithms for lasso penalized regression. Ann Appl Stat. 2008;2:224–244. doi: 10.1214/10-AOAS388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y. Elastic net for Cox’s proportional hazards model with a solution path algorithm. Statist Sinica. 2012;22:271–294. doi: 10.5705/ss.2010.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang HH, Lu W. Adaptive Lasso for Cox’s proportional hazards model. Biometrika. 2007;94:691–703. [Google Scholar]
- Zhang XHF, Wang Q, Gerald W, Hudis CA, Norton L, Smid M, Foekens JA, Massagué J. Latent bone metastasis in breast cancer tied to Src-dependent survival signals. Cancer Cell. 2009;16:67–78. doi: 10.1016/j.ccr.2009.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao P, Yu B. On model selection consistency of Lasso. J Mach Learn Res. 2006;7:2541–2563. [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. J Amer Statist Assoc. 2006;101:1418–1429. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J Roy Statist Soc Ser B. 2005;67:301–320. [Google Scholar]
- Zou H, Li R. One-step sparse estimates in nonconcave penalized likelihood models (with discussion) Ann Statist. 2008;36:1509–1566. doi: 10.1214/009053607000000802. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.