Dealing with inter-expert variability in Retinopathy of Prematurity: a machine learning approach

Abstract

Background and Objective

Understanding the causes of disagreement among experts in clinical decision making has been a challenge for decades. In particular, a high amount of variability exists in diagnosis of retinopathy of prematurity (ROP), which is a disease affecting low birthweight infants and a major cause of childhood blindness. A possible cause of variability, that has been mostly neglected in the literature, is related to discrepancies in the sets of important features considered by different experts. In this paper we propose a methodology which makes use of machine learning techniques to understand the underlying causes of inter-expert variability.

Methods

The experiments are carried out on a dataset consisting of 34 retinal images, each with diagnoses provided by 22 independent experts. Feature selection techniques are applied to discover the most important features considered by a given expert. Those features selected by each expert are then compared to the features selected by other experts by applying similarity measures. Finally, an automated diagnosis system is built in order to check if this approach can be helpful in solving the problem of understanding high inter-rater variability.

Results

The experimental results reveal that some features are mostly selected by the feature selection methods regardless the considered expert. Moreover, for pairs of experts with high percentage agreement among them, the feature selection algorithms also select similar features. By using the relevant selected features, the classification performance of the automatic system was improved or maintained.

Conclusions

The proposed methodology provides a handy framework to identify important features for experts and check whether the selected features reflect the pairwise agreements/disagreements. These findings may lead to improved diagnostic accuracy and standardization among clinicians, and pave the way for the application of this methodology to other problems which present inter-expert variability.

1. Introduction

Retinopathy of prematurity (ROP) is a disease affecting low-birth weight infants, in which blood vessels in the retina of the eye develop abnormally and cause potential blindness. ROP is diagnosed from dilated retinal examination by an ophthalmologist, and may be successfully treated by laser photocoagulation if detected appropriately [1]. Despite these advances, ROP continues to be a major cause of childhood blindness in the United States and throughout the world [2]. This is becoming increasingly significant in middle-income countries in Latin America, Eastern Europe and Asia because these countries are expanding neonatal care, yet have limited expertise in ROP. In addition, the number of infants at risk for ROP throughout the world is increasing dramatically because of improved survival rates for premature infants [3], while the availability of adequately-trained ophthalmologists to perform ROP screening and treatment is decreasing [4].

An international classification system was developed during the 1980s, and revised in 2005, to standardize clinical ROP diagnosis [5]. One key parameter of this classification system is called “plus disease”, and is characterized by tortuosity of the arteries and dilation of the veins in the posterior retina. Plus disease is a boolean parameter (present or absent), and is the most critical parameter for identifying severe ROP. Numerous clinical studies have shown that infants with ROP who have plus disease require treatment to prevent blindness, whereas those without plus disease may be monitored without treatment. Therefore, it is essential to diagnose plus disease accurately and consistently.

However, high levels of inconsistency among experts when diagnosing ROP have been demonstrated [6, 7]. Inter-expert variability in clinical decision making is an important problem which has been widely studied in the literature for several decades [8]. Much of this previous work has examined inter-expert variability in the interpretation of ophthalmic images [9, 6, 10, 11]. There are also studies which focus on the variability in diagnosis of acute diseases such as prostate cancer [12], breast cancer [13], melanoma [14], papillary carcinoma [15], and polycystic ovary disease [16]. Although there is a broad range of studies on analysis of inter-expert variability, few of them focus on investigating its underlying causes [17, 18, 19, 20].

Understanding the causes of disagreement among experts is a challenging problem. In the cognitive process during clinical diagnosis, some features may be considered more important by certain experts than by others. If two experts consider different sets of features during diagnosis, then we might expect to see a strong disagreement between them. Hence, such a feature-observer analysis enables us to understand the underlying causes of inter-expert variability.

In this work, we propose a methodology for investigating the important features for the experts when diagnosing ROP, with the final aim of building automated diagnosis systems. The proposed system makes use of feature selection, which is a machine learning technique employed to detect the most important features for a given classification task [21]. After selecting the useful features for each expert, we carry out a similarity analysis to see if the selected features can reflect the disagreement among experts. Finally, we propose an approach to build automated diagnosis tools applying machine learning techniques. The contributions of this paper are, (i) use and comparison of various feature selection algorithms to understand the underlying causes of inter-expert disagreement, (ii) a similarity analysis to validate whether feature selection results are consistent with the disagreement among experts, and (iii) the construction of an automatic diagnosis system that makes use of the feature selection results and similarity analysis findings.

In our previous work [20], we proposed a method to investigate whether there are groups of observers who decide consistently with each other and if there exist important features these experts mainly focus on. The previous approach involved a hierarchical clustering of the experts using a pair-wise similarity based on mutual information between the diagnostic decisions. Next, we performed an analysis to see the dependence between experts' decisions and image-based features which enabled us to qualitatively assess whether there are popular features for the group of observers obtained through clustering. Different than our previous study, in this work (i) we provide an in-depth analysis to find important features for each expert using various feature selection algorithms, (ii) we validate the feature selection results performing a quantitative similarity analysis between the selected features and the experts' agreement (i.e. we expect to select the same features for expert pairs with a high degree of agreement), and (iii) we build an automated classification system considering the analysis results and compare different classification algorithms.

The remainder of this paper is organized as follows: Section 2 explains the research methodology, and Section 3 details the problematics of ROP diagnosis. Finally, Section 4 reports the experimental results, and Section 5 describes the discussion of the main findings and conclusions.

2. Research methodology

In order to develop automatic systems that can support clinicians in the diagnosis of ROP, it is necessary to extract the knowledge from the medical experts. However, as discussed before, there is a high degree of disagreement among experts, and the reasons behind this disagreement are not clear. This paper proposes a methodology to understand the causes of inter-expert variability in ROP diagnosis, as a step toward extracting the necessary knowledge to build an automatic diagnosis tool.

A four-step methodology is thus applied, as illustrated in Figure 1. First, the problem needs to be analyzed to check if disagreement among experts exists. Second, several feature selection methods are applied to discover which features are the most important to each individual expert. Third, a similarity analysis is performed to check if, for experts with a high ratio of agreement, the feature selection methods also select similar features. Finally, the classification performance is calculated in order to see whether the selected features are sufficient for a correct classification of the given samples. We explain each step in the following subsections. A more detailed description of the employed methods is available in Appendix A.

Figure 1. Steps of the research methodology.

2.1. Assessment of experts' agreement

Bearing in mind that the objective of this work is to evaluate the causes of disagreement among experts, it is necessary to use measures that are able to calculate the amount of disagreement. These measures can be divided into two main groups: pairs' tests and group tests. The former involve a comparison between two reference criteria (for example, a pair of experts or a human expert and a computer-aided diagnosis system). Pairs' tests include contingency tables, percentage agreement methods and the Kappa statistic. Group tests, on the other hand, offer an overall view of the set of experts by locating each expert in relation to the others. Examples of group tests include the Williams' index.

Table 1 shows the interpretation given by Landis and Koch [22] for different ranges of values for the Kappa statistic and Williams' index. The Kappa measure must be used with caution, however, particularly in cases where few classification categories exist, or where the validation examples are concentrated in a single category. In these cases, a low Kappa value does not necessarily indicate disagreement between observers but could be due, in fact, to an unbalanced distribution among the classes [23].

Table 1. Interpretation of Kappa statistic and Williams' index.

Statistic	Value	Interpretation
Kappa	1.00	Total agreement
	0.75-1.00	Excellent level of agreement
	0.40-0.75	Fairly good to good level of agreement
	0.00-0.40	Poor level of agreement, which could be considered due to chance
	0.00	Agreement entirely due to chance
	<0.00	Agreement even lower than that expected by chance
Williams'	> 1.00	Agreement between isolated expert and group of experts is greater than agreement among members of group
	1.00	Agreement between isolated expert and group of experts is equal to agreement among members of group
	0.00-1.00	Agreement between isolated expert and group is less than agreement among members of group

2.2. Feature selection

After studying the degree of disagreement between experts for ROP diagnosis, the second and third steps of this methodology aim to understand if the causes of the disagreement are related with the features which are relevant for each expert, since the features extracted from the retinal blood vessels play an important role in the subsequent detection of the disease [24, 25]. Therefore, feature selection methods are applied trying to find out the important features for each expert.

Feature selection is a well-known machine learning technique which aims to identify the relevant features for a problem and discarding the irrelevant ones, in some cases even achieving an improvement in the performance of automatic classifiers compared to classification systems using all features [21]. Feature selection methods can be divided into two approaches: individual evaluation and subset evaluation [26]. Individual evaluation is also known as feature ranking and assesses individual features by assigning them weights according to their degrees of relevance. On the other hand, subset evaluation produces candidate feature subsets based on a certain search strategy. Each candidate subset is evaluated by a certain evaluation measure and compared with the previous best one with respect to this measure. While the individual evaluation is incapable of removing redundant features because redundant features are likely to have similar rankings, the subset evaluation approach can handle feature redundancy with feature relevance. However, methods in this framework can suffer from an inevitable problem caused by searching through all the feature subsets required in the subset generation step, and thus, both approaches are worth to be studied. Among the broad suite of feature selection methods available in the literature, we employ correlation-based feature selection (CFS) [27], consistency-based filter [28], INTERACT [29], Information Gain [30], ReliefF [31] and Recursive Feature Elimination for Support Vector Machines (SVM-RFE) [32], since they are widely used and based on different metrics ensuring some variability in our comparative analysis. It has to be noted that three of these methods return a subset of optimal features (CFS, INTERACT and Consistency-based) whilst the remaining three return a ranking of all the features (Information Gain, ReliefF and SVM-RFE).

2.3. Similarity analysis

Once we have determined the degree of variability among experts and the important features for each expert, we are interested in studying if, for those experts with a high degree of agreement among them, the selected features are also similar. Thus, we use similarity measures, which evaluate the sensitivity of the result given by a feature selection algorithm to variations in the training set (in this case, to variations in the class label). It is expected that, for those experts which show a reasonable amount of agreement in their labels, the features returned by the feature selection methods would be similar. We employ three different measures: (i) Jaccard index, (ii) Spearman correlation coefficient, and (iii) Kendall Index. While using these measures, we consider whether the feature selection method returns a subset of optimal features (Jaccard) or a ranking of features (Spearman and Kendall).

2.4. Classification

After studying the causes of inter-expert variability through the application of feature selection techniques, the last step of the proposed methodology is devoted to checking if the features selected as relevant for each expert are enough for building an automatic system able to classify new images in “plus”, “pre-plus” or “neither”. In addition to this, entrusting the task of distinguishing between class labels to an automatic classification system can be helpful to solve the problem of the high variability among experts, since this type of systems are objective and rely on the characteristics of the data. In the proposed methodology, we use four popular classifiers, C4.5 [33], naive Bayes [34], k nearest neighbors, and Support Vector Machine (SVM) [35], which are described in detail in Appendix A.

3. Retinopathy of Prematurity

This paper proposes a methodology trying to analyze the causes of variability between observers in ROP diagnosis by applying feature selection methods. The experiments will be performed on a set of 34 images that had been previously rated by 22 experts [6, 36]. In the original study, Chiang et al. recruited 22 eligible experts who were defined as “practicing pediatric ophthalmologists or retina specialists who met at least 1 of the following 3 criteria: having been a study center principal investigator for one of the two major NIH-funded multi-center randomized controlled trials involving ROP treatment [1, 37], having been a certified investigator for either of those studies, or having coauthored at least 5 peer-reviewed ROP manuscripts”. These experts, utilizing a secure website to review a set of retinal images, were asked to classify each of the 34 retinal posterior pole images as either “plus”, “pre-plus”, “neither”, or “cannot determine”. In a previous work [19], a total of 66 features have been extracted, some of which were curve-based and others of which were tree-based.

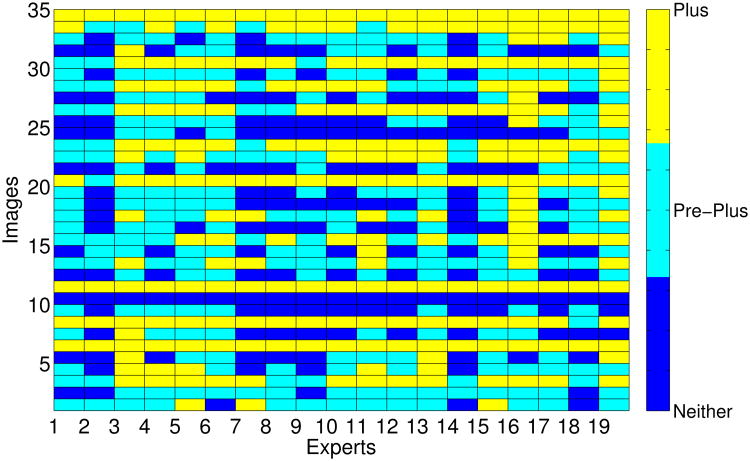
For data analysis, “cannot determine” decisions were excluded since there were few observers who decided “cannot determine” for at least one sample. In particular, three of the 22 experts decided “cannot determine” for at least one sample. The number of samples each expert decided as “cannot determine” was 1, 6 and 11 respectively. Figure 2 shows the different diagnoses given by the different experts for each image whereas Table 2 shows the percentage of images that were labeled as each one of the three categories. Note that there are some images in which all the 19 experts agreed (such as images 6, 10, 11 or 34) while there are other images in which the experts did not coincide in their diagnoses (such as images 5, 14, 16 or 25).

Figure 2. Labels given by experts.

Table 2. Absolute agreement in plus disease diagnosis among 19 experts labeling 34 images (number of images and percentage).

Image		Neither		Pre-Plus		Plus
1	3	15.79%	13	68.42%	3	15.79%
2	4	21.05%	15	78.95%	0	0.00%
3	0	0.00%	6	31.58%	13	68.42%
4	4	21.05%	10	52.63%	5	26.32%
5	9	47.37%	7	36.84%	3	15.79%
6	0	0.00%	0	0.00%	19	100.00%
7	10	52.63%	8	42.11%	1	5.26%
8	0	0.00%	1	5.26%	18	94.74%
9	11	57.89%	8	42.11%	0	0.00%
10	19	100.00%	0	0.00%	0	0.00%
11	0	0.00%	0	0.00%	19	100.00%
12	10	52.63%	9	47.37%	0	0.00%
13	0	0.00%	13	68.42%	6	31.58%
14	8	42.11%	9	47.37%	2	10.53%
15	0	0.00%	8	42.11%	11	57.89%
16	10	52.63%	8	42.11%	1	5.26%
17	2	10.53%	10	52.63%	7	36.84%
18	9	47.37%	9	47.37%	1	5.26%
19	5	26.32%	12	63.16%	2	10.53%
20	0	0.00%	1	5.26%	18	94.74%
21	12	63.16%	7	36.84%	0	0.00%
22	0	0.00%	9	47.37%	10	52.63%
23	0	0.00%	4	21.05%	15	78.95%
24	14	73.68%	5	26.32%	0	0.00%
25	9	47.37%	8	42.11%	2	10.53%
26	0	0.00%	5	26.32%	14	73.68%
27	11	57.89%	7	36.84%	1	5.26%
28	0	0.00%	7	36.84%	12	63.16%
29	5	26.32%	13	68.42%	1	5.26%
30	0	0.00%	3	15.79%	16	84.21%
31	11	57.89%	7	36.84%	1	5.26%
32	4	21.05%	12	63.16%	3	15.79%
33	0	0.00%	5	26.32%	14	73.68%
34	0	0.00%	0	0.00%	19	100.00%

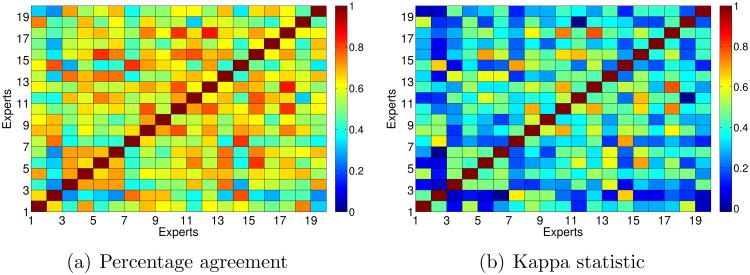
For a better understanding, Figure 3 shows the percentage of agreement and the Kappa statistic between each pair of experts. As can be seen, the Kappa statistic is more conservative than the percentage agreement. In any case, the maximum agreement between experts is reported between experts 12 and 17, and there are four pairs of experts which show high level of agreement. In general, the experts who obtained the highest percentage agreement and Kappa statistic with other experts were 8, 10, 12 and 17. On the contrary, the experts who achieved the lowest ratios of agreement with the remaining experts were 2, 7 and 11.

Figure 3. Agreement among experts considering three classes: plus, pre-plus, neither.

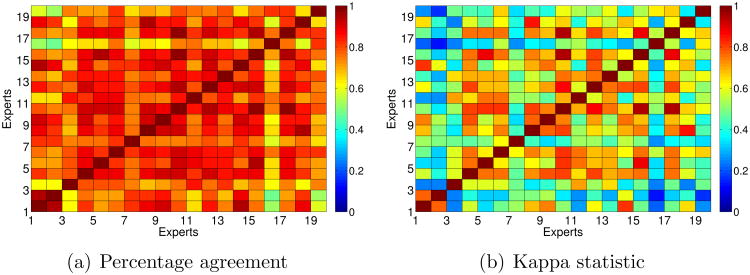
If we simplify the problem to a binary problem and we only consider the diagnosis of “plus” versus “not plus”, the ratios of agreement increase, as can be seen in Figure 4. In this case, the maximum percentage of agreement is over 97% and the Kappa statistic is over 93%, which confirm the fact that multiclass problems are much more difficult than binary ones.

Figure 4. Agreement among experts considering two classes: plus, not plus.

4. Experimental results

In this section we will report the results obtained after applying the methodology explained in Section 2 to the problem of ROP diagnosis.

4.1. Feature selection

First, we will analyze the results obtained with subset filters (CFS, Consistency-based and INTERACT) and then we will analyze the results achieved by ranker methods (Information Gain, ReliefF and SVM-RFE).

4.1.1. Subset methods

Figure 5 shows the number of times that a feature was selected for the label given by each expert according to the selection obtained by CFS, INTERACT and Consistency-based. As can be seen, there are some features that are mostly selected by these filters, as it is summarized in Table 3. Notice that, in the description of the features, it is indicated if they belong to a vein (v) or to an artery (a).

Figure 5. Features selected by CFS, INTERACT and Consistency-based feature selection methods.

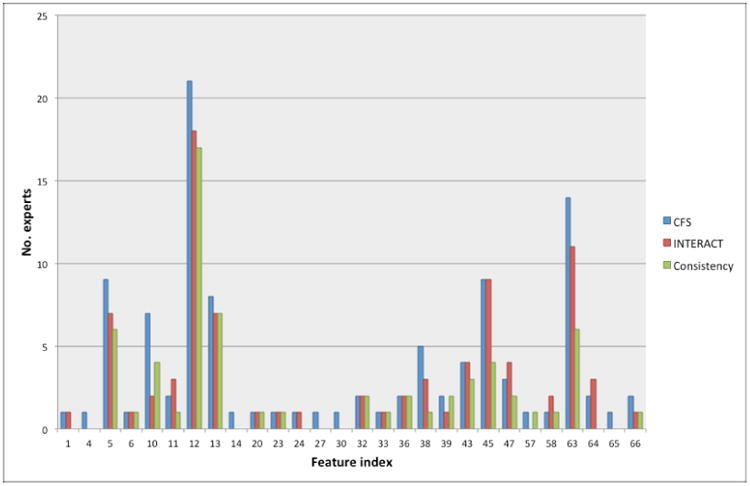
Table 3. Summary of features mostly selected by subset filters.

Feature Index	Description	No. of times selected
		CFS	Cons	INT
5	Mean Acc (v)	42%	26%	32%
12	Mean TI (v)	100%	19%	84%
13	CM2 TI (v)	42%	32%	32%
45	Mean TI (a)	47%	21%	47%
63	Max MBLF (a)	68%	32%	53%

In light of the results visualized in Table 3, the most important feature seems to be the mean of the tortuosity index in veins, followed by the same feature in arteries, mean acceleration and CM2 of tortuosity index in veins, and maximum of MBLF in arteries.

4.1.2. Ranker filters

In this case, each ranker method (Information Gain, ReliefF and SVM-RFE) returned an ordered ranking of all the features. In order to analyze these results, we have calculated a combination of all the rankings for each method, using the SVM-Rank technique [38]. In Tables 4, 5 and 6, we can see the top 10 features ranked by Information Gain, ReliefF and SVM-RFE, respectively (after combining the 19 rankings with SVM-rank). It is interesting to note that the feature that is ranked in the first position for the three ranker methods is, again, the mean of the tortuosity index in veins, confirming its crucial importance.

Table 4. Top 10 features ranked by Information Gain.

Feature Index	Description
12	Mean TI (v)
13	CM2 TI (v)
63	Max MBLF (a)
5	Mean Acc (v)
21	CM3 Diameter (v)
22	Min DDC (v)
27	CM2 DDC (v)
20	CM2 Diameter (v)
19	Mean Diameter (v)
23	2nd Min DCC (v)

Table 5. Top 10 features ranked by ReliefF.

Feature Index	Description
12	Mean TI (v)
5	Mean Acc (v)
63	Max MBLF (a)
45	Mean TI (a)
6	CM2 Acc (v)
13	CM2 TI (v)
37	Max Acc (a)
46	CM2 TI (a)
10	2nd Max TI (v)
36	2nd Min Acc (v)

Table 6. Top 10 features ranked by SVM-RFE.

Feature Index	Description
12	Mean TI (v)
63	Max MBLF (a)
5	Mean Acc (v)
23	2nd Min DCC (v)
25	Max DDC (v)
24	2nd Max DDC (v)
29	Min MBLF (v)
20	CM2 Diameter (v)
32	CM2 MBLF (v)
21	CM3 Diameter (v)

4.2. Similarity

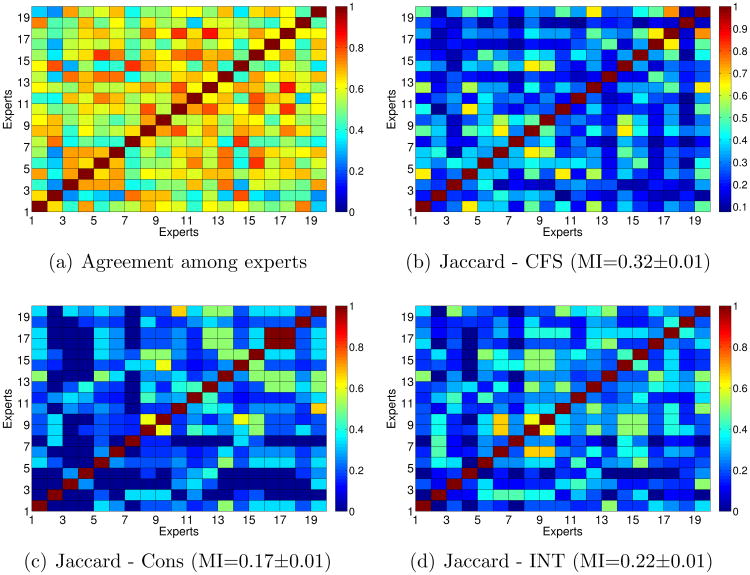
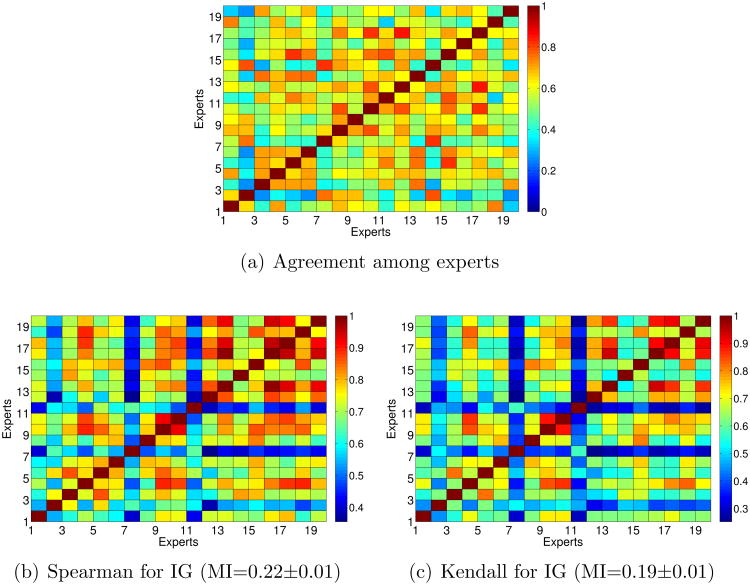
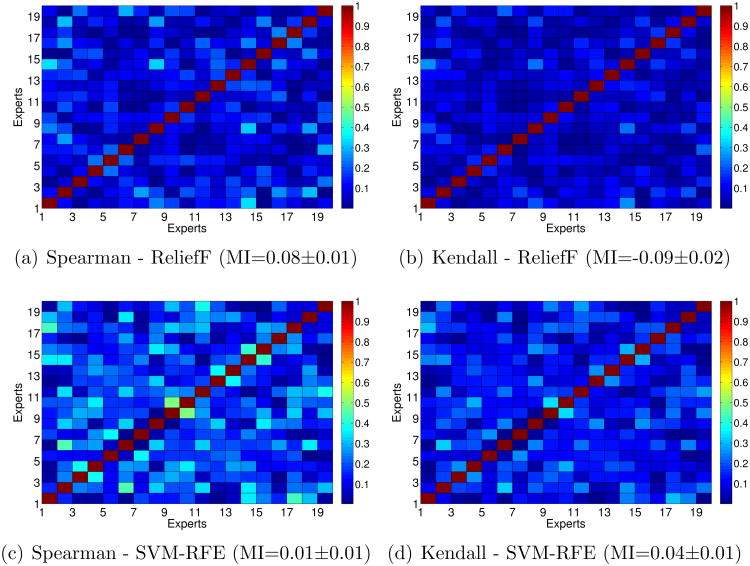
In this section we try to check if, for experts with a high ratio of agreement, the feature selection methods also selected similar features. For the subset filters (CFS, Consistency-based and INTERACT) we have calculated the Jaccard-index. Figures 6(b), 6(c) and 6(d) show the Jaccard-index for each pair of experts for the subsets of features selected by CFS, consistency-based and INTERACT, respectively, in which the higher the value, the higher the similarity. For a visual comparison, we have included the percentage agreement among experts at the first panel. In order to quantify the dependency between similarity index and the percentage agreement, we compute the Mutual Information (MI) between the index and the percentage agreement by utilizing Kernel Density Estimation. MI estimates are reported at the caption of each figure. MI values tell how much is known about percentage agreement given the similarity index. Hence, a higher MI value shows that a corresponding feature selection algorithm gives more consistent features with the percentage agreement. Note that these estimates only provide a relative comparison between methods.

Figure 6. Jaccard-index for subset filters.

In general, the similarity between subsets is low, as it is expected because feature selection methods tend to be very sensible to variations in the data. It is interesting to note that, for the three subset methods, some of the experts with a low ratio of agreement (see Figure 3) also obtained low similarities regarding their optimal subsets of features. For example, this happens with experts 2 and 11. On the other hand, the similarity between the features selected by experts 12 and 17 (who obtained high percentage agreement and Kappa statistic) and the remaining experts is quite high. In terms of MI, the stability of the features selected by CFS seem to be more consistent with the percentage of agreement than the remaining subset methods.

Figures 7 and 8 show the Spearman correlation coefficient and Kendall-index for each pair of experts for the rankings of features obtained by Information Gain, ReliefF and SVM-RFE as well as the agreement between experts for comparisons. Again, the higher the value, the higher the similarity between rankings.

Figure 7. Spearman correlation coefficient and Kendall-index for rankings of features (I).

Figure 8. Spearman correlation coefficient and Kendall-index for rankings of features (II).

It is easy to see that the rankings obtained by Information Gain are much more similar to the percentage agreement than those obtained by ReliefF and SVM-RFE. This happens because Information Gain is a univariate method (each feature is considered independently) whereas ReliefF and SVM-RFE are multivariate methods (they consider relationships between features). So, univariate filters such as Information Gain tend to obtain more stable rankings than multivariate methods. This fact is also reflected if one focuses on the MI values.

Regarding the results achieved with the filter Information Gain, in Figures 7(b) and 7(c) one can see that the rankings for the experts 2, 7 and 11 are very dissimilar compared with the rankings obtained by the remaining experts, since these experts had not achieved high rates of agreement with other experts. On the contrary, the similarities between the rankings achieved by experts 12 and 17 are again fairly high.

4.3. Classification

In order to check if the features selected by the different methods are sufficient for a correct classification of the data, we performed some classification experiments. Since we have the data labeled by 19 different experts, we have opted for determining the class label by majority vote. Information about more sophisticated methods for aggregation of opinions from multiple experts can be found in [39], although this kind of techniques are out of the scope of this paper.

We have chosen four well-known different classifiers available in the Weka tool [40], with default values for their parameters: C4.5, naive Bayes, k-NN and SVM. The three former filters can directly deal with multiclass datasets but, in the case of SVM, it is necessary to employ a one-versus-rest approach. As validation technique, we have chosen leave-one-out cross-validation, which is a common choice when the number of available samples is small [41]. This technique is an extreme case of k-fold cross-validation, where the dataset is divided into as many parts as there are instances, each instance effectively forming a test set of one. If k is the number of instances, then k classifiers are generated, each from k – 1 instances, and each is used to classify a single test instance. The estimated classification error is the total number of incorrectly classified instances divided by the total number of instances.

As for the feature selection stage, for the subset filters (CFS, consistency-based and INTERACT) we have used the union of all the subsets of features selected for all the experts. For the ranker methods (Information Gain, ReliefF and SVM-RFE) we have used the ranking obtained by SVM-rank after combining the rankings for all the experts. Since for ranker methods we need to establish a threshold, we have opted for classifying with top 50% of the ranked features.

In Table 7 we can see the average test classification results for all classifiers and feature selection methods. We also trained a classifier using all features (i.e. without feature selection (FS)) as displayed in the first row of the table. Notice that the best result was achieved using feature selection (SVM-RFE + NB) and that, for all classifiers, feature selection is able to improve the classification error, which demonstrates that this problem contains irrelevant features that can hinder the process of classification.

Table 7. Average classification error (%) using leave one out cross validation.

Method	C4.5	NB	k-NN	SVM
No FS	58.82	38.24	64.71	44.12
CFS	52.94	35.29	44.11	38.24
Cons	70.59	32.35	44.12	38.24
INT	70.59	32.35	44.11	38.24
InfoGain	41.18	41.18	50.00	35.29
ReliefF	70.59	35.29	58.82	41.18
SVM-RFE	52.94	20.59	47.06	32.35

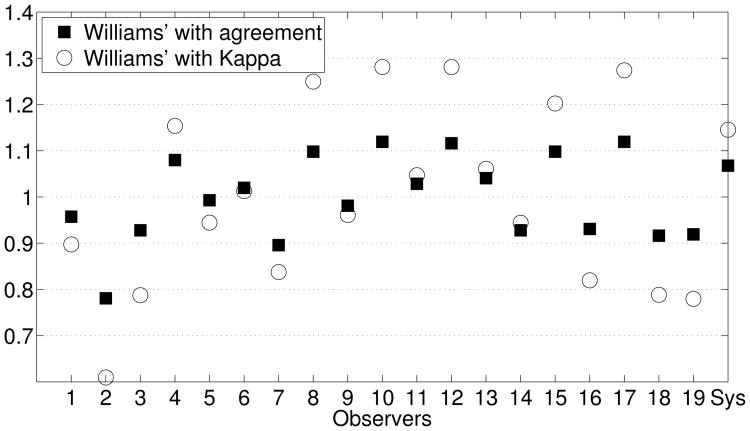
To assess the automatic system globally, group tests were applied to the results obtained from the complete analysis of the 19 experts plus the system (in this case, the best option was SVM-RFE + NB in Table 7). Figure 9 shows the Williams' indices obtained using both the percentage agreement and the Kappa value measures. From among the Williams' indices obtained, the highest indices correspond to expert 10, which means that this expert exhibits the highest agreement with the remaining experts. For the system, the indices obtained are greater than 1, from which it can be deduced that (a) the agreement between the system and the group of experts is greater than the agreement among experts; and (b) the influence of chance is practically null, as is to be expected from an automatic computer-based system. Therefore, results indicate that the system can be asserted to behave in a similar manner to the experienced experts.

Figure 9.

Williams' index calculated utilizing percentage agreement and the Kappa statistic as agreement measurements.

In order to simplify the task, we have converted the multiclass problem into a binary problem, i.e., we are only interested in distinguishing between plus disease and not plus disease. In Table 8 we show the average test classification results for all classifiers and feature selection methods. As can be seen, the results have improved as a consequence of simplifying the classification task. For all classifiers tested, adding a feature selection stage results in improving or maintaining the test error, so this demonstrates the adequacy of feature selection techniques for this problem.

Table 8. Average test classification error results (%) on binary dataset using leave one out.

Method	C4.5	NB	k-NN	SVM
No FS	29.41	11.76	38.24	20.59
CFS	35.29	14.71	26.47	20.59
Cons	32.35	14.71	32.35	20.59
INT	32.35	14.71	26.47	17.65
InfoGain	29.41	20.59	29.41	17.65
ReliefF	35.29	11.76	35.29	11.76
SVM-RFE	29.41	14.71	26.47	17.65

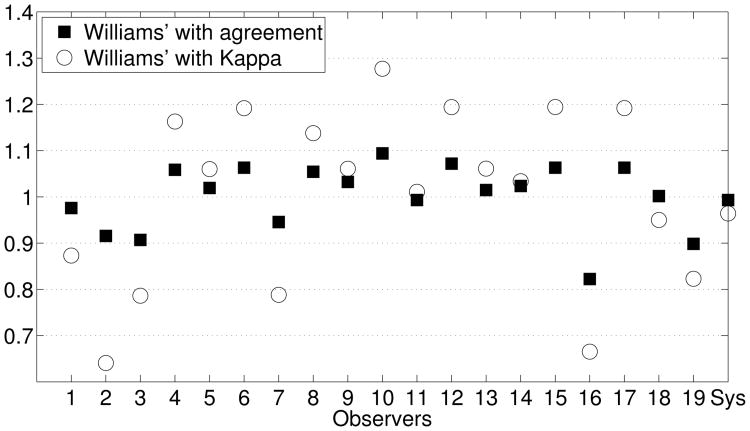
Again, we applied group test to assess the performance of the system (in this case, we have chosen the combination of ReliefF + naive Bayes in Table 8). Figure 10 shows the Williams indices obtained using both percentage agreement and the Kappa value as measures of agreement. As in the multi-class case, the highest indices correspond to expert 10. For the system, the indices obtained are quite close to 1, which means that the agreement between the system and the group of experts is similar to the agreement among experts and the influence of chance is practically null.

Figure 10.

Williams' index calculated utilizing percentage agreement and the Kappa statistic as agreement measurements in the binary case.

5. Discussion and conclusion

Retinopathy of prematurity is an important public health problem which affects a high number of infants in the world. One key parameter of the diagnosis of ROP is called plus disease, and is characterized by tortuosity of the arteries and dilation of the veins in the posterior retina. Plus disease is a boolean parameter (present or absent), and the most critical for identifying severe ROP. Numerous clinical studies have shown that infants with ROP who have plus disease require treatment to prevent blindness, whereas those without plus disease may be monitored without treatment. Therefore, it is essential to diagnose plus disease accurately and consistently. However, even when having sophisticated image analysis programs, a critical factor for ROP diagnosis is the inconsistency among experts.

In order to solve this problem, in this paper we have proposed a methodology to discover the underlying causes of variability among experts when diagnosing plus disease and to check if an automatic system could overcome this limitation. The proposed methodology consists of applying feature selection techniques to discover the features which are more important for a given expert. After that, the features selected for each expert are compared in order to see if experts showing a high level of agreement are also focusing on the same features. Finally, an automatic system is built with the mostly selected features, using machine learning techniques, to check if the use of this type of systems could help in solving the problem of the high inter-rater variability.

The experiments were carried out on a dataset of 34 retinal images diagnosed by 22 experts, in which a high level of disagreement among experts was found. After applying different feature selection methods, based on different metrics, we have found that some features were mostly selected, regardless of the feature selection algorithm. The top selected features are the mean of venous and arterial tortuosity (#12 and #45), the mean of venous acceleration (#5) and the maximum main branch leaf node factor (MBLF) in arteries (#63). This is surprising because the standard definitions for the diagnosis of severe ROP with “plus disease” are based on arterial tortuosity and venous dilation, although some experts anecdotally mention other factors such as arterial dilation, venous tortuosity, vascular branching pattern and peripheral retina features [42, 43]. In light of the obtained results, it seems that although it is expected that the great majority of experts focus on the representative features (according to the standard), they are also paying attention to other features, maybe being this the cause of their disagreement.

After obtaining the features most relevant for each expert, we have calculated if the experts who agree in their diagnosis also share relevant features (according to the feature selection algorithms applied). With this aim, we have computed several measures of similarity, depending on if the feature selection method returned a subset of optimal features or an ordered ranking of all the features. The experimental results revealed that, in fact, groups of experts with high percentage agreement among them also selected similar features.

Finally, we have built an automatic system using machine learning techniques and the features mostly selected by the feature selection algorithms, in order to see if they were enough for a correct classification of the problem and to check if an automatic system is able to classify with a similar performance to the experts. We have applied several classifiers to assess the multiclass problem (“plus”, “pre-plus” or “neither”) and also the binary problem (“plus” vs. “neither”). By using feature selection, the classification performance was improved or maintained, confirming the adequacy of focusing on the relevant features for the problem in hand. For evaluating the system, we have also calculated group tests. The high Williams' indices obtained by it reinforced the idea that the system demonstrates a behavior similar to that of expert clinicians. This, together with the fact that its agreement with the experts is greater or similar to agreement between the experts themselves, permit our system to be considered at least as skillful as the experts.

Although the behavior of the automatic system was satisfactory, it was hard to come up with a “golden standard” to train the model. A common practice is to train only with those images in which the whole set of experts agree. However, this was not possible for our case study due to the high level of disagreement among experts. So we opted for computing the golden standard as majority vote among all the labels given by the experts. Note that acquisition of a golden standard in ROP diagnosis is extremely difficult. One major difficulty is that agreement for diagnosis, even among national and international experts, has been shown to be imperfect in numerous studies [6, 44, 7, 45]. One possible approach would be to define a gold standard based on long-term follow-up of subjects to determine clinical outcomes. However, that approach would probably be impractical in the real world because infants who are felt to have severe disease during clinical examination are always treated to prevent blindness.

In summary, our study findings suggest that disagreement among experts can be produced by the fact that the experts' decisions are based on the examination of different features. This can be due to the fact that the standard for diagnosing ROP considers only a couple of features, but they might be not enough for a correct detection of the problem (at least for an automatic system). These study findings have implications that may lead to improved diagnostic accuracy and standardization among clinicians, and for development of computer-based decision support tools that model expert behavior. Moreover, we leave as future work the application of the proposed methodology to other real problems in which variability among experts is present.

Highlights.

• Inter-expert variability in clinical decision making is an important problem.

• Retinopathy of prematurity is a disease that suffers from inter-expert variability.

• We propose a methodology for understanding the causes of disagreement.

• The methodology provides a framework to identify important features for experts.

• An automatic system was also developed to deal with this problem.

Appendix A. Methods

This appendix shows the description of the methods used in the four-step methodology described in Section 2.

Appendix A.1. Measures to assess experts' agreement

Appendix A.1.1. Contingency tables

A contingency table juxtaposes two elements of opinion for each of the classes under consideration. Usually, it is considered that one of these elements provides the correct classification (reference system) and the other provides a prediction respecting this classification (classification system); in other words, the second opinion is evaluated in terms of the first one. Correct predictions will be located on the diagonal of the matrix and all the other cells of the table will correspond to misclassifications. Contingency tables are particularly useful in the detection of systematic errors committed by the system undergoing validation; they are also valuable in analysing low levels of agreement between confronted pairs.

Appendix A.1.2. Percentage agreement and the Kappa statistic

The percentage agreement method is a straightforward measurement in which an index of agreement between two observers is calculated as

$$p_0=\frac{{\sum }_{i=1}^k{n}_{ii}}{N}$$ (A.1)

where k represents the number of classification categories; n_ii is the number of cases where both observers agree to classify as category i and N represents the total number of cases considered.

The Kappa statistic [46] is also a measure of agreement between pairs of experts but introduces a correction factor that eliminates those agreements that can be attributed to chance. The Kappa statistic is defined as

$$\kappa =\frac{p_0-p_c}{1-p_c},$$ (A.2)

where p₀ is the observed proportion of agreements (Eq. (A.1)); p_c is the agreement by chance, calculated as

$$p_c=\sum _{i=1,j=1,i=j}^k{p}_i{p}_j,$$ (A.3)

with p_i and p_j being the marginal probabilities calculated, respectively, for each i^th row and j^th column of the k × k contingency table that confronts a pair of experts.

Appendix A.1.3. Williams' measurements

Williams' measurements [47] provide a method for determining the level of agreement between an isolated expert and a group of reference experts, and defined as an index I_n as follows:

$$I_n=\frac{q_0}{q_n},$$ (A.4)

with

$$q_0=\frac{{\sum }_{a=1}^{n}P(0,a)}{n},q_0\in [0,1]$$ (A.5)

and

$$q_n=\frac{2{\sum }_{a=1}^{n-1}{\sum }_{b=a+1}^{n}P(a,b)}{n(n-1)},q_n\in [0,1]$$ (A.6)

where P(a, b) represents the percentage agreement between expert a and expert b; n is the number of experts (excluding the isolated expert); and 0 is the isolated expert.

Appendix A.2. Feature selection

Appendix A.2.1. Correlation-based Feature Selection, CFS

This is a simple filter algorithm that ranks feature subsets according to a correlation based heuristic evaluation function [27]. The bias of the evaluation function is toward subsets that contain features that are highly correlated with the class and uncorrelated with each other. Irrelevant features should be ignored because they will have low correlation with the class. Redundant features should be screened out as they will be highly correlated with one or more of the remaining features. The acceptance of a feature will depend on the extent to which it predicts classes in areas of the instance space not already predicted by other features. CFS's feature subset evaluation function is

$$M_S=k\overline{r_{cf}}/\sqrt{k+k(k-1)\overline{r_{ff}}},$$ (A.7)

where M_S is the heuristic ‘merit’ of a feature subset S containing k features, $\overline{r_{cf}}$ is the mean feature-class correlation (f ∈ S) and $\overline{r_{ff}}$ is the average feature-feature intercorrelation. The numerator of this equation accounts for how predictive of the class a set of features is; and the denominator accounts for amount of redundancy among the features.

Appendix A.2.2. Consistency-based Filter

The filter based on consistency [28] evaluates the worth of a subset of features by the level of consistency in the class values when the training instances are projected onto the subset of attributes. From the space of features, the algorithm generates a random subset S in each iteration. If S contains fewer features than the current best subset, the inconsistency index of the data described by S is compared with the index of inconsistency in the best subset. If S is as consistent or more than the best subset, S becomes the best subset. The criterion of inconsistency, which is the key to success of this algorithm, specify how large can be the reduction of dimension in the data. If the rate of consistency of the data described by selected characteristics is smaller than a set threshold, it means that the reduction in size is acceptable. Notice that this method is multivariate.

Appendix A.2.3. INTERACT

The INTERACT algorithm [48] is based on symmetrical uncertainty (SU) [29], which is defined as the ratio between the information gain (IG) and the entropy (H) of two features, x and y:

$$\mathit{\text{SU}}(x,y)=2\mathit{\text{IG}}(x|y)/[H(x)+H(y)],$$ (A.8)

where the information gain is defined as IG(x|y) = H(y) + H(x) – H(x, y), being H(x) and H(x,y) the entropy and joint entropy, respectively.

Beside SU, INTERACT also includes the consistency contribution (c-contribution). C-contribution of a feature is an indicator about how significantly the elimination of that feature will affect consistency. The algorithm consists of two major parts. In the first part, the features are ranked in descending order based on their SU values. In the second part, features are evaluated one by one starting from the end of the ranked feature list. If c-contribution of a feature is less than an established threshold, the feature is removed, otherwise it is selected.

Appendix A.2.4. Information Gain

The Information Gain filter [30] is one of the most common univariate methods of evaluation attributes. This filter evaluates the features according to their information gain and considers a single feature at a time. It provides a ranking for all the features, and then a threshold is required to select a certain number of them according to the order obtained.

Appendix A.2.5. ReliefF

The filter ReliefF [31] is an extension of the original Relief algorithm [49]. This extension is not limited to two class problems, is more robust, and can deal with incomplete and noisy data. As the original ReliefF algorithm, ReliefF randomly selects an instance R_i, but then searches for k of its nearest neighbors from the same class, nearest hits H_j, and also k nearest neighbors from each one of the different classes, nearest misses M_j(C). It updates the quality estimation W[A] for all attributes A depending on their values for R_i, hits H_j and misses M_j(C). If instances R_i and H_j have different values of the attribute A, then this attribute separates instances of the same class, which clearly is not desirable, and thus the quality estimation W[A] has to be decreased. On the contrary, if instances R_i and M_j have different values of the attribute A for a class then the attribute A separates two instances with different class values which is desirable so the quality estimation W[A] is increased. Since ReliefF considers multiclass problems, the contribution of all the hits and all the misses is averaged. Besides, the contribution for each class of the misses is weighted with the prior probability of that class P(C) (estimated from the training set). The whole process is repeated m times where m is a user-defined parameter (See Algorithm 1).

Algorithm 1: Pseudo-code of ReliefF algorithm

Data: training set D, iterations m, attributes a

Result: the vector W of estimations of the qualities of attributes

The function diff(A, I₁, I₂) calculates the difference between the values of the attribute A for two instances, I₁ and I₂.

Appendix A.2.6. Recursive Feature Elimination for Support Vector Machines, SVM-RFE

This embedded method [32] carries out feature selection by iteratively training a SVM classifier with the current set of features and removing the least important feature indicated by the weights in the SVM solution.

Appendix A.3. Similarity measures

Appendix A.3.1. Jaccard-index

The Jaccard-index (J) is a metric which measures dissimilarity between sets of samples (in this case, sets of features). It is defined as the cardinality of the intersection divided by the cardinality of the union of the sets A and B.

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

Appendix A.3.2. Spearman correlation coefficient

The Spearman correlation coefficient (ρ) is a metric which measures similarity between rankings of features. It is defined as the Pearson correlation coefficient between the ranked variables. In this measure, A and B are rankings, d is the distance between the same elements in both rankings and #feats is the total number of features in the sets A and B.

$$\rho (A,B)=(1-\frac{6\sum d_i^2}{\#\mathit{\text{feats}}(\#{\mathit{\text{feats}}}^2-1)})$$

Appendix A.3.3. Kendall-index

The Kendall-index (K) is a metric that counts the number of pairwise disagreements between two ranking lists A and B. The larger the index, the more similar the two lists are.

$$K(A,B)={\sum }_{\{i,j\}\in P}{\overline{K}}_{i,j}(A,B)$$

where

P is the set of unordered pairs of distinct elements in A and B

K̄_i,j(A,B) = 1 if i and j are in the same order in A and B

K̄_i,j(A,B) = 0 if i and j are in the opposite order in A and B

Appendix A.4.1. C4.5

C4.5 is a classifier developed by [33], as an extension of the ID3 algorithm (Iterative Dicotomiser 3). Both algorithms are based on decision trees. A decision tree classifies a pattern doing a descending filtering of it until finding a leaf, that points to the corresponding classification. One of the improvements of C4.5 with respect to ID3 is that it can deal with both numerical and symbolic data. In order to handle continuous attributes, C4.5 creates a threshold and depending on the value that takes the attribute, the set of instances is divided.

Appendix A.4.2. naive Bayes, NB

A naive Bayes classifier [34] is a simple probabilistic classifier based on applying Bayes' theorem with strong (naive) independence assumptions. This classifier assumes that the presence or absence of a particular feature is irrelevant to the presence or absence of any other feature, given the class variable. A naive Bayes classifier considers each of the features to contribute independently to the probability that a sample belongs to a given class, regardless of the presence or absence of the other features. Despite their naive design and apparently oversimplified assumptions, naive Bayes classifiers have worked quite well in many complex real-world situations. In fact, naive Bayes classifiers are simple, efficient and robust to noise and irrelevant attributes.

Appendix A.4.3. k-nearest neighbors, k-NN

K-Nearest neighbor [50] is a classification strategy that is an example of a “lazy learner”. An object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (where k is some user specified constant). If k = 1 (as it is the case in this paper), then the object is simply assigned to the class of that single nearest neighbor.

Appendix A.4.4. Support Vector Machine, SVM

A Support Vector Machine [35] is a learning algorithm typically used for classification problems (text categorization, handwritten character recognition, image classification, etc.). More formally, a support vector machine constructs a hyperplane or set of hyperplanes in a high- or infinite-dimensional space, which can be used for classification, regression, or other tasks. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training data point of any class (so-called functional margin), since in general the larger the margin the lower the generalization error of the classifier.

Appendix B. Extracted features for diagnosing ROP

Table B.9 reveals the description of the 66 extracted features from the retinal images for ROP diagnosis. Several structured features are considered for both veins (first column) and arteries (second column). Curve-based features account for the dilation and tortuosity of the vessels, whilst tree-based features are related to branching in vessel junction points [20].

Table B.9. Description of features extracted for ROP diagnosis.

Index veins	Index arteries	Description
1	34	Minimum acceleration
2	35	2nd minimum acceleration
3	36	2nd maximum acceleration
4	37	Maximum acceleration
5	38	Mean acceleration
6	39	CM2 acceleration
7	40	CM3 acceleration
8	41	Minimum tortuosity
9	42	2nd minimum tortuosity
10	43	2nd maximum tortuosity
11	44	Maximum tortuosity
12	45	Mean tortuosity
13	46	CM2 tortuosity
14	47	CM3 tortuosity
15	48	Minimum diameter
16	49	2nd minimum diameter
17	50	2nd maximum diameter
18	51	Maximum diameter
19	52	Mean diameter
20	53	CM2 diameter
21	54	CM3 diameter
22	55	Minimum distance to disc center (DDC)
23	56	2nd minimum DDC
24	57	2nd maximum DDC
25	58	Maximum DDC
26	59	Mean DDC
27	60	CM2 DDC
28	61	CM3 DDC
29	62	Minimum branching factor
30	63	Maximum branching factor
31	64	Mean branching factor
32	65	CM2 branching factor
33	66	CM3 branching factor