Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Aug 26;5:13382. doi: 10.1038/srep13382

Edge state magnetism in zigzag-interfaced graphene via spin susceptibility measurements

T L Makarova 1,2,a, A L Shelankov 2, A A Zyrianova 2, A I Veinger 2, T V Tisnek 2, E Lähderanta 1, A I Shames 3, A V Okotrub 4, L G Bulusheva 4, G N Chekhova 4, D V Pinakov 4, I P Asanov 4, Ž Šljivančanin 5
PMCID: PMC4549622  PMID: 26307529

Abstract

Development of graphene spintronic devices relies on transforming it into a material with a spin order. Attempts to make graphene magnetic by introducing zigzag edge states have failed due to energetically unstable structure of torn zigzag edges. Here, we report on the formation of nanoridges, i.e., stable crystallographically oriented fluorine monoatomic chains, and provide experimental evidence for strongly coupled magnetic states at the graphene-fluorographene interfaces. From the first principle calculations, the spins at the localized edge states are ferromagnetically ordered within each of the zigzag interface whereas the spin interaction across a nanoridge is antiferromagnetic. Magnetic susceptibility data agree with this physical picture and exhibit behaviour typical of quantum spin-ladder system with ferromagnetic legs and antiferromagnetic rungs. The exchange coupling constant along the rungs is measured to be 450 K. The coupling is strong enough to consider graphene with fluorine nanoridges as a candidate for a room temperature spintronics material.

The search for evidence of the magnetic ordering in graphene has been an active field of research for many years and has focused primarily on point and line defects as the most promising candidates for engineering magnetism in graphene1. Recent experiments have indicated that point defects, acting as paramagnetic centres are unlikely to lead to magnetic ordering because their density appears to be limited to one Bohr magneton per approximately 1000 carbon atoms2. Theoretical predictions of one-dimensional (1D) ferromagnetism in graphene nanoribbons3,4 have triggered an extensive search for magnetism in graphene nanostructures with reduced dimensionality. Despite the remarkable progress achieved in the detection5,6,7 of localized electronic states at zigzag edges of graphene8, a wide and discouraging gap still exists between the theoretical anticipation of edge spin ferromagnetism and its experimental realisation. Magnetic order on the zigzag graphene edges was deduced from the transport and scanning tunnelling microscopy data6,9, but since all these measurements were done using charge-based instead of spin-based techniques, they could be a subject to various interpretations. Fortunately, a torn edge is not a prerequisite for such edge magnetism: the edges of graphene nanoribbons (GNRs) embedded in a functionalized C-sp3 layer possess essentially the same electronic properties as those of a freestanding GNR. Theory suggests that spin ordering can be induced along the interfaces10 and within relatively small 1-D and 2-D graphene nanosegments in the interior of functionalized graphene11. Here, we show experimentally that a dense network of fluorine chains effectively transforms an extended honeycomb lattice of sp2-carbon atoms into nanosegments of pristine graphene framed by C-sp2/C-sp3 interfaces. In these confined geometries, with a large interface-to-area ratio, we observe magnetic effects consistent with theories that treat edge-inherited magnetism as an essentially 1D quantum phenomenon and predict a spin-gapped ground state with an antiferromagnetic inter-edge superexchange interaction1,12,13,14,15,16. The observed magnetism is preserved up to the fluorine detachment temperature (520 K), at which the samples irreversibly collapse into a diamagnetic state.

The functionalization of graphene with fluorine transforms carbon atoms from C-sp2 to CF-sp3 hybridized states. By virtue of its favourable characteristics, the room-temperature fluorination of intercalated graphite has emerged as an efficient method of creating crystallographically selective patterns at decoupled carbon planes17,18. First, because of the enlarged interlayer spacing, both sides of the graphene layers are available to the fluorinating agent. Second, over an extended period (on the scale of several months) at room temperature, the fluorine adatoms relax into an energetically preferable configuration on the basal planes. Fluorine adsorbates tend to align in a chain sequence in which F adatoms are located on alternating sides of a graphene plane11,19. Simultaneous F adsorption at multiple sites results in the seeding of the chains in a random distribution across the graphene planes. A nuclear magnetic resonance study has indicated homogeneous fluorination and a planar configuration of the graphene sheets18, and angle-resolved X-ray absorption spectroscopy has provided evidence of the sequential attachment of fluorine atoms to opposite sides of a sheet17. Adjacent CF chains are well separated, thus creating a low-dimensional π-electron system between them.

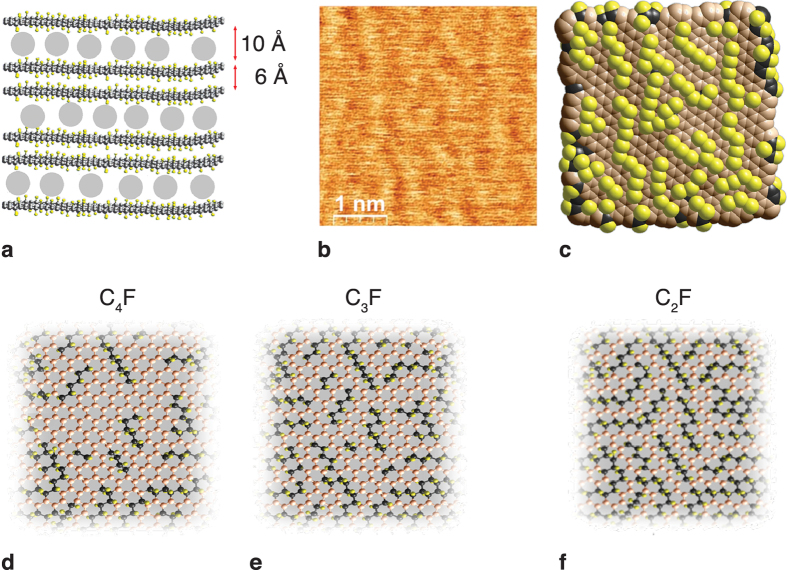
We investigated samples with C4F, C3F and C2F stoichiometries; the various types of samples are detailed in Table S1 of the Supplementary Material together with their exact compositions and the intercalating molecules (guests). CnF compounds represent stacks of fluorinated graphene bilayers separated by guests, which are weakly diamagnetic and otherwise magnetically inert (Fig. 1a). Experimental data were collected from more than 50 samples that differ in both fluorine content and the properties of the guest molecules: small and large, polar and non-polar, organic and inorganic. Measurements of the magnetic susceptibilities demonstrated that the chemical composition of the guests does not affect the magnetism. Here, we restrict ourselves to bilayer graphenes prepared from the 2nd stage graphite intercalated compounds with dichloromethane, dichloroethane, acetonitrile, acetone, and n-hexane. We have similar magnetic results on single-layer graphenes prepared from the 1st stage graphite intercalated compounds, which will be reported elsewhere. The presence of guest molecules increases the distance between planes by up to ~1 nm, excluding any significant hybridisation between electronic states at different planes. Thus, the guests convert graphite to graphenes and effectively reduce the dimensionality of the electronic system from three to two. The fluorine chain patterns further reduce the effective dimensionality of the electron gas to one. Atomic force microscopy (Fig. 1b) revealed bright and dark strips that correspond to the fluorine chains and pristine graphene regions, respectively (Fig. 1c). The observed relative orientation of the strips implies that both zigzag and armchair fluorine chains are present. Using a set of spectroscopic data17,18, we determined that the chains are monatomic, and the chain length typically comprise 6–8 fluorine atoms. These crystallographically oriented fluorine chains divide the basal plane into a dense, non-periodic array of π-electron nanofragments: narrow GNR and nanosegments in the case of a low-fluorination matrix (Fig. 1d,e) and carbon polyacetylene-like nanochains when the stoichiometry approaches C2F (Fig. 1f).

Figure 1. Structure of the CnF compounds.

Figure 1

Open in a new tab

(a) Side view. The bilayers of fluorinated graphenes are separated by intercalating guest molecules (grey circles). (b) Atomic force microscopy (AFM) topographical image of a basal plane of a C3F sample. (c) Atomistic reconstruction of the AFM image. (d–f) Basal-plane structures of samples with continual C-sp2 nanosegments in C4F (d) and in C3F (e) and isolated C-sp2 nanochains (C2F) (f) plotted according to a set of spectroscopic data17,18.

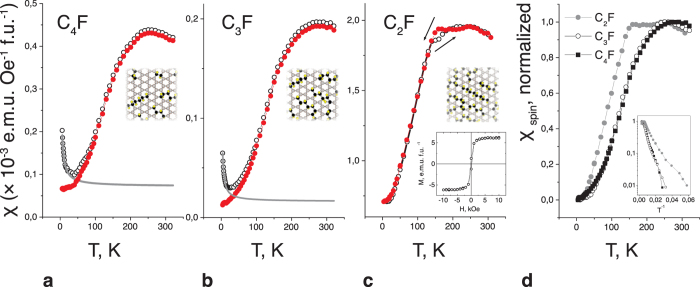
Magnetic measurements revealed strong magnetism in these purely organic graphene-based structures. We begin by presenting results for the samples with lower fluorine contents, i.e., C4F and C3F (Fig. 2a,b). These samples exhibit a reversible magnetic response and a linear magnetic susceptibility

Figure 2. Magnetic susceptibility of the CnF samples.

Figure 2

Open in a new tab

(a,b) Raw data from the C4F (a) and C3F (b) samples measured at an applied magnetic field of 100 Oe upon being heating after zero-field cooling (open circles); the same curves with the Curie contribution (grey) subtracted are represented by filled red circles. (c) Raw data from a C2F sample measured upon heating (filled circles) and upon cooling (open circles); inset: room-temperature M(H) loop. (d) Normalized spin susceptibilities for C4F, C3F and C2F samples; inset: spin susceptibility vs reciprocal temperature for these samples.

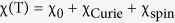graphic file with name srep13382-m1.jpg

that can be split into a temperature-independent term χ0, a small Curie-like component χCurie (identified by the low-T upturn), and a strong non-Curie paramagnetic spin susceptibility χspin. When the first two terms of Eq. 1 are subtracted, a broad maximum at 250 K followed by a low-temperature exponential decrease is revealed in χspin(T), reflecting the low-dimensional nature of the spin system. The major characteristics of the thermomagnetic curves are reminiscent of molecule-based magnets20, particularly organic radical crystals21 in which interactions are constrained to act in fewer than three spatial dimensions.

The behaviour of the C3F samples is similar to the C4F samples. The results obtained for the C2F samples in which the C-sp2-islands shrink into the C-sp2-chains, highlight the critical role played by the fluorine patterns in the observed magnetism (Fig. 2c). An exponential trend in susceptibility is observed below a kink at T ≈ 150 K; near the kink, thermal hysteresis is observed, with a temperature difference of T ≈ 20 K between the heating and cooling traces. Curie paramagnetism is undetectable suggesting the near absence of isolated spins in the dense CF network, whereas the magnetic response contains a small irreversible contribution (Fig. 2c, inset) which depends weakly on temperature.

Figure 2d presents a comparison of the normalized spin-susceptibility curves for the three stoichiometries. The logarithmic plots of χspin vs 1/T (Fig. 2d, inset) clearly demonstrate exponentially activated susceptibility (χspin ~ exp (−Δ/T)) and thus reveal an energy gap Δ — the so-called spin gap — in the spin excitation spectrum. The existence of the spin gap is an unequivocal manifestation of spin-spin interaction. However, long-range antiferromagnetic spin ordering is very unlikely in our samples: the absence of sharp features in χ(T) suggests that, if we are encountering a cooperative phenomenon, only a few atoms are correlated. The spin gap and the absence of classical spin ordering are purely quantum phenomena, which are relatively common at low dimensions, where quantum and/or thermal fluctuations suppress magnetic order. The simplest model of an activated magnetic susceptibility is the scenario in which the spins are antiferromagnetically coupled pairwise as dimers22. For our description of the magnetism in fluorinated graphene, we will rely on the more sophisticated spin-ladder model23 for which spin dimers and linear chains are the limiting cases.

Fluorination is well known to be an effective method of introducing localized spin centres into graphene2. Obviously, the magnetism observed in our experiments originates from structures more complex than monatomic adsorbates, and we will demonstrate that the fluorine chains provide conditions that favour spontaneous spin alignment. The model of the magnetism, as described below and in the Supplementary Material, is based on the fact that carbon atoms that are covalently bonded to fluorines lack π-electrons; i.e., the fluorine chain is seen by the graphene π-electron network as a high-energy barrier — a “nanoridge” extending the length of the chain. Thus, the fluorine chain serves as chemical scissors that cut the graphene plane in the sense that the lattice sites that are occupied by CF groups become unavailable to the π-electron system. This “cut” creates two edges that are separated by a nearly impenetrable CF-nanoridge. Graphene bipartite lattice consists of inequivalent α and β sublattices. In the case of a zigzag chain, one expects a set of localized spin states in sublattice α on one side of the nanoridge and sublattice β on the other side.

In the simplest model, we adopt a picture of Ns spins ½ localized on each side of the ridge, where Ns is of the order of the number of fluorines in the chain. Because of the ferromagnetic intra-edge exchange interaction1, the two sets of edge spins behave as collective spins, |S1,2| = ½Ns. The small but finite penetrability of the nanoridge allows a superexchange antiferromagnetic interaction across the edges, which favours an antiparallel orientation of the edge spins, S1 = −S2, or, more precisely, a gapped singlet ground state. The existence of the spin gap in the energy spectrum of the nanoridge is a common feature of a system with a spontaneously broken symmetry at infinite volume, where the broken symmetry is restored by quantum fluctuations at finite size24,25.

This interaction resembles the exchange couplings between the zigzag edge-inherited states in GNRs, which were described using a spin-ladder model shortly after their theoretical discovery12. The difference between the nanoridge model and the GNR model lies in the microscopic origins of the interactions: the antiferromagnetic-like interaction originates not from the bulk tails of the edge states26 but from the overlapping of the edge states on the nanoridge separating the two edges.

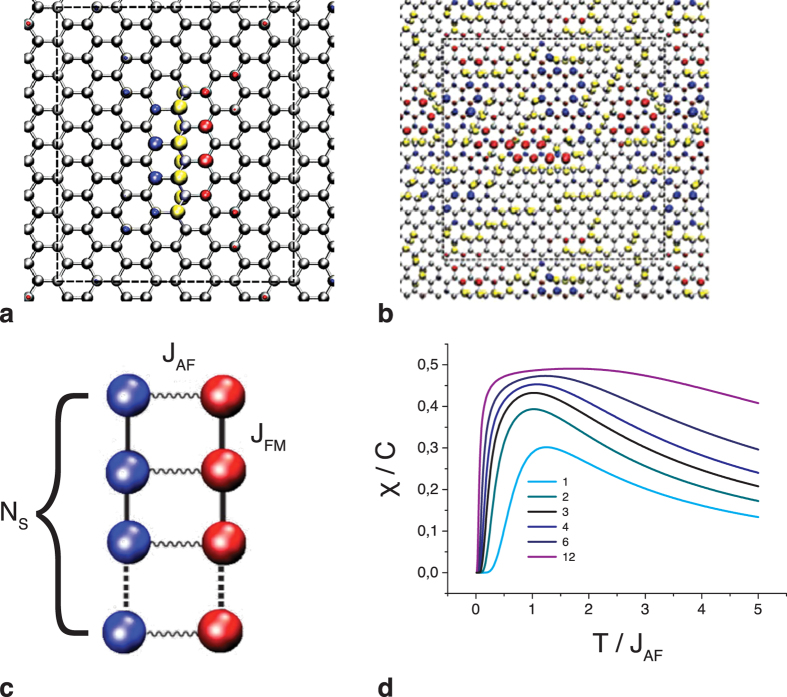
To verify this qualitative picture of the magnetism in fluorinated graphene, we performed density functional theory (DFT) calculations using GPAW computer code27. First, we applied DFT to illuminate the origin of the magnetism in graphene functionalized with fluorine, guided by the experimental evidence that monatomic chains of fewer than 10 F atoms on graphene, are dominant structural motifs17,18. The DFT calculations for well-separated F lines and chains of four to ten atoms clearly revealed the emergence of magnetism in fluorinated graphene, as demonstrated in Fig. 3a, where we plot the spin density in the vicinity of a zigzag chain with eight F atoms. The calculated complex magnetic configuration combines the strong ferromagnetic interaction between the local magnetic moments of C atoms on the same side of the chain with the antiferromagnetic coupling between the magnetic moments of C atoms located on different sides of the CF chain. According to our calculations, no similar magnetic effects occur in isolated armchair chains of F atoms. After we confirmed that distant zigzag F chains induce magnetism in graphene, we investigated a realistic model of fluorinated graphene, assuming a random network of the interacting F chains that were observed in the AFM images presented in Fig. 1. The results obtained for the structure shown in Fig. 3b demonstrate that magnetic sites near a single zigzag chain are preserved in disordered networks of densely packed nanoridges. Non-magnetic solution is as much as 582 meV per unit cell less favourable compared to the magnetic configuration in Fig. 3a

Figure 3. Magnetic units and exchange interactions for the fluorine chains on the graphene basal plane.

Figure 3

Open in a new tab

(a) A zigzag chain of fluorine on graphene, with isocontour plots of the spin density obtained from the DFT calculations. Regions with opposite spin orientations are painted in red and blue. C and F atoms are represented by grey and yellow spheres, respectively. (b) The calculated spin density for a random network of both zigzag and armchair chains. (c) A model of a spin ladder of length Ns with an infinitely strong ferromagnetic intra-leg interaction JFM and an antiferromagnetic inter-leg coupling JAF. (d) A plot of the magnetic susceptibility χ(T,N)/C for the finite size spin ladder vs the reduced temperature T/JAF. The numbers near the curves correspond to Ns; the scaling constant is C = (g μB)2/3JAF, where g is the electron gyromagnetic ratio and μB is the Bohr magneton.

The atomic-scale description of the magnetism, as established through ab initio calculations, enables us to quantify the experimental results in terms of the spin-coupling strength and the concentration of coupled spins by applying the quantum spin-ladder model in the limit of a strong intra-edge ferromagnetic interaction. The quantum numbers of the ladder eigenstates are the total spin S = 0, 1, …, Smax (where Smax = Ns is the largest possible value of the total spin of 2Ns spin-½ particles) and its z-projection M, where ±M = 0, 1, …, S. The corresponding eigenenergy (see the Supplementary Material) is as follows

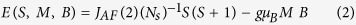graphic file with name srep13382-m2.jpg

where JAF is the effective inter-leg coupling constant per spin pair, g is the electron gyromagnetic ratio, and B is an external magnetic field.

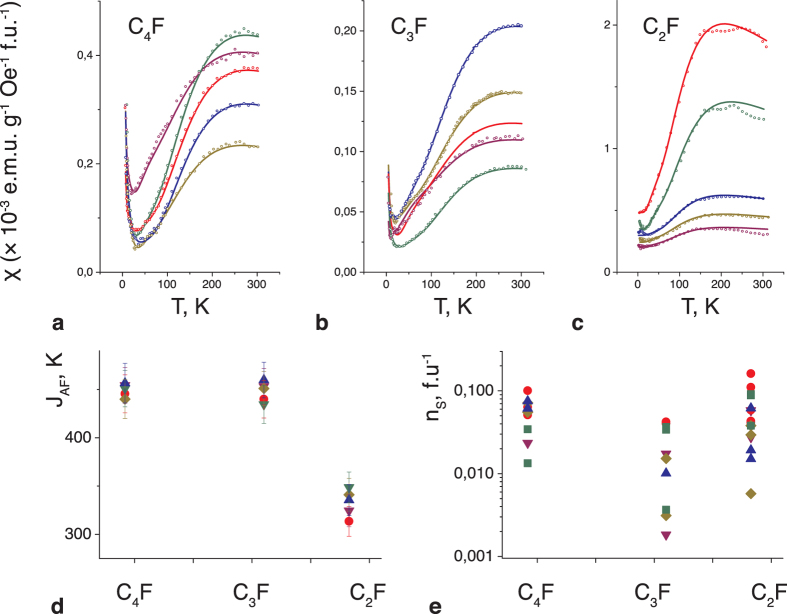
The calculations of the magnetic susceptibility χ are provided in the Supplementary Material, and the resulting temperature dependencies of the susceptibility are depicted in Fig. 3d. As expected for a disordered chain network, none of the single curves derived from Eq. 2 satisfactorily describes the experiment, whereas a combination of two structural descriptions (Ns = 1 and Ns = 3) with the same JAF value provides a perfect fit to the experimental data (Fig. 4a,b). The Ns = 1 contribution originates from imperfect chains, e.g., the T-junctions of the chains. The presence of a positive χ0 term in Eq. 1 indicates that longer chains are also present in the samples, enhancing the paramagnetic background. The magnetic model of the C2F stoichiometry is more complicated because of the denser network of fluorine chains on the basal plane, resulting in a 1D-like π-electron system. We speculate that the kink in the temperature curves (Fig. 4c) may be a manifestation of a Peierls-instability-type mechanism, which has been predicted for quasi-one-dimensional even-numbered carbon chains generated in sp3-functionalized graphene28,29. The ferromagnetic-like non-linear component may originate from sublattice imbalance30, most likely from odd-numbered π-electron chains29. A parallel can be drawn between our results and the persistent reports of room-temperature ferromagnetism in graphene-based samples achieved through the functionalisation31,32,33.

Figure 4. Magnetic susceptibility of the CnF structures and the extracted values of the parameters of the spin system.

Figure 4

Open in a new tab

(a–c) Temperature dependence of the magnetic susceptibility for samples of three different stoichiometries, as indicated in each panel. The scattered points represent the experimental data, and the lines represent calculations of χ (T, JAF, NS) using Eq. 2. Different colours correspond to different guest molecules between the graphene planes: red for dichloromethane, blue for dichloroethane, green for acetonitrile, yellow for acetone, and violet for n-hexane. (d) Exchange-coupling values JAF. (e) Concentration ns of interacting spins per formula unit vs the basal-plane stoichiometry.

By extracting the strength of the interaction from the χ(T) data and estimating the number of interacting spins, we draw the following quantitative conclusions: (i) the JAF value for the C3F and C4F stoichiometries is approximately 450 K (Fig. 4d), and that for C2F is approximately 330 K; (ii) the concentration of coupled spins is particularly large, in the range ns ≈ 1020–1021 g−1, which corresponds to 1 spin per several CF units (Fig. 4e). This value is 2–3 orders of magnitude greater than previously reported2,34; besides, the magnetic states induced within the C-sp2 nanosegments are strongly correlated and magnetic susceptibility is characteristic of thermal excitation from a nonmagnetic ground state with a spin gap.

Based on various characterisation techniques, thermomagnetic measurements and ab initio calculations, a picture emerges in which the quantum confinement of the electronic states, induced by the presence of the fluorine interfaces, enhances the Coulomb interactions and strengthens electron-electron correlations. The 1D nature of these correlated states suppresses long-range order and, in accordance with the theories that account for the quantum nature of edge magnetism, gives rise to magnetic behaviour that is typical of low-dimensional quantum spin systems. The apparent connection between a spin gap and superconductivity has been a source of motivation to search for quasi-one-dimensional ladder materials35. Calculations performed for similar but hypothetical structures indicate that, upon either electrical or chemical doping, on/off switching between nonmagnetic and magnetic states might be achieved; such functionality is a prerequisite for spintronics applications14. Our results provide the first practical step towards the fabrication of theoretically constructed spin valves16 and spin filters36 that exploit the differences between the ground and excited states when toggled by the gate bias. Stacked fluorographene can be easily delaminated in organic solvents, which will be a beneficial property for its integration into electronic devices.

Methods

Synthesis of CnF graphenes

The CnF structures were synthesized via the intercalation and fluorination of crystalline graphite. Here, we restrict ourselves to bilayer graphenes prepared from the 2nd stage graphite intercalated compounds. We have similar magnetic results on single-layer graphenes prepared from the 1st stage graphite intercalated compounds. However, due to technological constraints, the single layer graphenes have less perfect structure, leading to 3D graphite-like magnetism which is outside the scope of this paper. During the first stage of synthesis, the graphite platelets were placed in a Teflon flask with a perforated wall; the flask was sealed with a lid and placed in a hermetic reactor containing liquid bromine. After 2 days of exposure of the graphite to Br2 vapour at room temperature, an intercalation compound with a composition of C8Br was formed. The C8Br compound was subsequently transferred to another Teflon flask and placed over a solution of BrF3 in Br2. The fluorination proceeded at room temperature. The next stage included a subsequent exchange of guest components from the fluorination media to pure Br2. The resultant product consisted of fluorinated graphene layers separated by intercalated bromine molecules. During the final stage, Br2 was exchanged with other guest molecules. The sample thus obtained was dried under nitrogen flow until a constant mass was achieved, which resulted in uniformly fluorinated graphene bilayers with the CnF stoichiometry. Immediately after synthesis, all samples were diamagnetic with a small Curie paramagnetic component. As is known from structural studies, long-term relaxation processes on the scale of approximately one year affect the structures of CnF samples. We observed the emergence of both a non-Curie component and an irreversible magnetic response after one to three months of storage under an inert atmosphere. During one year of storage, the non-Curie paramagnetism manifesting spin-ladder magnetism of the samples gradually developed and finally stabilised.

Characterization methods

A topographic image of the C3F surface was obtained using a Nanoscope III atomic force microscope (Digital Instruments, Veeco, Santa Barbara, CA, USA) in a semi-tapping mode under ambient conditions. Magnetic measurements were performed using an MPMS-XL1 superconducting quantum interference device (SQUID)-based magnetic property measurement system manufactured by Quantum Design; the measurements were performed in magnetic fields of −10 kOe to 10 kOe, and the data were collected in the 1.76–300 K range using the ZFC (zero-field cooling), FC (field-cooled cooling) and FCW (field-cooled warming) protocols in the applied fields 10–100 Oe. Data were obtained from samples with a mass of ~0.02 g comprising randomly oriented sub-millimeter flakes (0.4 × 0.3 × 0.02 mm3). The samples were maintained under an inert atmosphere to ensure the absence of magnetic effects originating from oxygen.

Computational Details

All density functional theory (DFT) calculations were performed using the GPAW computer code, based on real space grid implementation of the projector augmented wave (PAW) method. The electronic exchange and correlation effects were described by the Perdew-Burke-Ernzerhof (PBE) functional. An isolated F chain and the network of chains were modelled using unit cells with 128 and 448 carbon atoms, respectively, and a grid spacing of 0.15 Å. Two-dimensional periodic boundary conditions were imposed across the honeycomb sheet. In the direction perpendicular to the surface, we employed open boundary conditions with 9 Å of vacuum separating the graphene layer from the cell boundaries The k-point sampling was restricted to Γ-point. The positions of all atoms were optimized using the BFGS algorithm.

Additional Information

How to cite this article: Makarova, T. L. et al. Edge state magnetism in zigzag-interfaced graphene via spin susceptibility measurements. Sci. Rep. 5, 13382; doi: 10.1038/srep13382 (2015).

Supplementary Material

Supplementary Information
srep13382-s1.pdf (401.3KB, pdf)

Acknowledgments

This work was supported by European FP7 IRSES projects 295180 MagNonMag and 269138 NanoGuard, Russian RFBR 13-02-00360 and RNF 14-13-00813, and the Serbian Ministry of Education and Science Grant No. 171033.

Footnotes

Author Contributions T.L.M. planned the project, designed and carried out the experiments. Z.S. and A.L.S. performed theoretical modelling. Data analysis and interpretation of the results was made by T.L.M., A.L.S. and Z.S. with important contributions from A.I.S., A.I.V. and E.L. Samples were prepared by G.N.C. and D.V.P., whereas A.V.O., L.G.B. and I.P.A. provided structural characterisation. T.V.T. and A.A.Z. contributed to the magnetic measurements. T.L.M. wrote the manuscript with the contributions from A.L.S. and Z.S. All authors discussed the results.

References

  1. Enoki T. in Graphene: Synthesis, Properties, and Phenomena. (eds. Rao C. N. R. & Sood A. K. ) 151–157 (Wiley-VCH, 2013). [Google Scholar]
  2. Nair R. R. et al. Spin-half paramagnetism in graphene induced by point defects. Nat. Phys. 8, 199–202 (2012). [Google Scholar]
  3. Nakada K., Fujita M., Dresselhaus G. & Dresselhaus M. S. Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys. Rev. B 54, 17954–17961 (1996). [DOI] [PubMed] [Google Scholar]
  4. Son Y. W., Cohen M. L. & Louie S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006). [DOI] [PubMed] [Google Scholar]
  5. Joly V. L. J. et al. Observation of magnetic edge state in graphene nanoribbons. Phys. Rev. B 81, 245428 (2010). [Google Scholar]
  6. Tao C. et al. Spatially resolving edge states of chiral graphene nanoribbons. Nat. Phys. 7, 616–620 (2011). [Google Scholar]
  7. Pan M. H. et al. Topographic and Spectroscopic Characterization of Electronic Edge States in CVD Grown Graphene Nanoribbons. Nano Lett. 12, 1928–1933 (2012). [DOI] [PubMed] [Google Scholar]
  8. Fujita M., Wakabayashi K., Nakada K. & Kusakabe K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920–1923 (1996). [Google Scholar]
  9. Magda G. Z. et al. Room-temperature magnetic order on zigzag edges of narrow graphene nanoribbons”. Nature 514, 608–611 (2014). [DOI] [PubMed] [Google Scholar]
  10. Okada S. & Oshiyama A. Magnetic ordering in hexagonally bonded sheets with first-row elements. Phys. Rev. Lett. 87, 146803 (2001). [DOI] [PubMed] [Google Scholar]
  11. Ribas M. A., Singh A. K., Sorokin P. B. & Yakobson B. I. Patterning nanoroads and quantum dots on fluorinated graphene. Nano Res. 4, 143–152 (2011). [Google Scholar]
  12. Wakabayashi K., Sigrist M. & Fujita M. Spin wave mode of edge-localized magnetic states in nanographite zigzag ribbons. J. Phys. Soc. Jpn. 67, 2089 (1998). [Google Scholar]
  13. M. Golor M., Wessel S., Schmidt M. J. Quantum nature of edge magnetism in graphene. Phys. Rev. Lett. 112, 046601 (2014). [DOI] [PubMed] [Google Scholar]
  14. Alexandre S. S., Lucio A. D., Castro Neto A. H. & Nunes R. W. Correlated magnetic states in extended one-dimensional defects in graphene. Nano Lett. 12, 5097–5102 (2012). [DOI] [PubMed] [Google Scholar]
  15. Yazyev O. V., Katsnelson M. I. Magnetic correlations at graphene edges: basis for novel spintronics devices. Phys. Rev. Lett. 100, 047209 (2008). [DOI] [PubMed] [Google Scholar]
  16. Dutta S. & Wakabayashi K. Tuning charge and spin excitations in zigzag edge nanographene ribbons. Sci. Rep. 2, 519 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Asanov I. P. et al. Graphene nanochains and nanoislands in the layers of toom-temperature fluorinated graphite. Carbon 59, 518–529 (2013). [Google Scholar]
  18. Vyalikh A. et al. Fluorine patterning in room-temperature fluorinated graphite determined by solid-state NMR and DFT. J. Phys. Chem. C 117, 7940/7948 (2013). [Google Scholar]
  19. Ewels C. P., Van Lier G., Charlier J.-C., Heggie M. I. & Briddon. P. R. Pattern formation on carbon nanotube surface. Phys. Rev. Lett. 96, 216103 (2006). [DOI] [PubMed] [Google Scholar]
  20. Lahti P. M. (ed.), Magnetic Properties of Organic Materials (Marcel Dekker, New York, 1999). [Google Scholar]
  21. Makarova T. & Palacio F. (eds) Carbon-Based Magnetism – An overview of the magnetism of metal free carbon-based compounds and materials. (Elsevier, Amsterdam, 2006). [Google Scholar]
  22. Bleaney B. & Bowers K. D. Anomalous paramagnetism of copper acetate. Proc. R. Soc. London A 214, 451–465 (1952). [Google Scholar]
  23. Dagotto E. & Rice T. M. Surprises on the way from one- to two- dimensional quantum magnets: The ladder materials. Science. 271, 618–623 (1996). [Google Scholar]
  24. Neuberger H. & Ziman T. Finite-size effects in Heisenberg antiferromagnets. Phys. Rev. B 39, 2608–2618 (1989). [DOI] [PubMed] [Google Scholar]
  25. Koma T. & Tasaki H. Symmetry breaking and finite-size effects in quantum many-body systems. J. Statist. Phys. 76, 745–803 (1994). [Google Scholar]
  26. Lee H., Son Y.-W., Park N., Han S. & Yu J. Magnetic ordering at the edges of graphitic fragments: Magnetic tail interactions between the edge-localized states. Phys. Rev. B 72, 174431 (2005). [Google Scholar]
  27. Enkovaara J. et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys. Cond. Mat. 22, 253202 (2010). [DOI] [PubMed] [Google Scholar]
  28. Tozzini V. & Pellegrini V. Electronic structure and Peierls instability in graphene nanoribbons sculpted in graphane. Phys. Rev. B. 81, 113404 (2010). [Google Scholar]
  29. Kim H. J., Oh S. & Cho J. H. Peierls instability and ferrimagnetic ordering of quasi-one-dimensional carbon chains generated in H-passivated graphene. Phys. Rev. B 83, 235408 (2011). [Google Scholar]
  30. Vozmediano M. A. H., López-Sancho M. P., Stauber T. & Guinea F. Local defects and ferromagnetism in graphene layers. Phys. Rev. B 72, 155121 (2005). [Google Scholar]
  31. Garnica M. et al. Long-range magnetic order in a purely organic 2D layer adsorbed on epitaxial graphene. Nat. Phys. 9, 368–374 (2013). [Google Scholar]
  32. Hong J., Bekyarova E., Liang P., de Heer W. A., Haddon R. C. & Khirsoev S. Room-temperature magnetic ordering in functionalized graphene. Sci. Rep. 2, 624 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Giesbers A. J. M. et al. Interface induced room-temperature ferromagnetism in hydrogenated epitaxial graphene. Phys. Rev. Lett. 111, 166101 (2013). [DOI] [PubMed] [Google Scholar]
  34. Feng Q. et al. Obtaining high localized spin magnetic moments by fluorination of reduced graphene oxide. ACS Nano. 7, 6729–6734 (2013). [DOI] [PubMed] [Google Scholar]
  35. Dagotto E., Riera J. & Scalapino D. Superconductivity in ladders and coupled planes. Phys. Rev. B 45, 5744–5747 (1992). [DOI] [PubMed] [Google Scholar]
  36. Li L. et al. Functionalized Graphene for High-Performance Two-Dimensional Spintronics Devices, ACS Nano 5, 2601–2610 (2011). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep13382-s1.pdf (401.3KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES