Physical Parameters, Modeling, and Methodological Details in Using IR Laser Pulses to Warm Frozen or Vitrified Cells Ultra-Rapidly

Abstract

We report additional details of the thermal modeling, selection of the laser, and construction of the Cryo Jig used for our ultra-rapid warming studies of mouse oocytes (B Jin, FW Kleinhans, Peter Mazur, Cryobiology 68 (2014) 419–430). A Nd:YAG laser operating at 1064 nm was selected to deliver short 1 msec pulses of sufficient power to produce a warming rate of 1 × 10⁷ °C/min from –190°C to 0°C. A special Cryo Jig was designed and built to rapidly remove the sample from LN₂ and expose it to the laser pulse. India ink carbon black particles were required to increase the laser energy absorption of the sample. The thermal model reported here is more general than that previously reported. The modeling reveals that the maximum warming rate achievable via external warming across the cell membrane is proportional to (1/R²) where R is the cell radius.

Introduction

We report here further details of the use of an IR laser pulse to produce ultra-rapid warming of vitrified or frozen cell systems in Jin, Kleinhans, and Mazur [6]. By ultra-rapid warming, we mean rates up to 1 × 10⁷ °C/min for 0.1 µl samples, some 100 times faster than that resulting from the abrupt transfer of a Cryotop from liquid nitrogen (LN₂) into a buffer at ^~23°C. Our lab has been using a mouse oocyte model to investigate fundamental cryobiological questions. Recent work from our laboratory has shown that the survival of mouse oocytes subjected to a matrix of cooling and warming rates is much more dependent on the warming rate than on the cooling rate, The higher the warming rate, the better [12,16,17,18]. Mazur and Seki [12] have demonstrated that ultra-rapid warming can greatly increase the survival of cells previously subjected to rapid cooling.. This has recently been confirmed in our report showing that ultra-rapid warming of mouse oocytes yields high survivals even for diluted vitrification solutions [6]. The basic premise is that ultra-rapid warming avoids recrystallization during warming and it is this recrystallization which is lethal [2,3,15].

We need to warm the cell sample from LN₂ temperatures to near 0 °C, melt the ice present, and continue warming to room temperature (RT). The critical warming range is that where recrystallization occurs, say in the range from −100 to ^~ −30 °C [16]. Thus it is this latter range where we desire to have ‘fast’ warming.

The use of a laser pulse to achieve ultra-rapid warming of living frozen or vitrified cells is novel. We will detail several aspects of our work including: (i) Choice of laser wavelength, (ii) Laser requirements; especially pulse duration and energy, (iii) Energy absorbing medium (India ink), (iv) Cryo Jig design and construction, (v) Practical problems, (vi) MS Excel model for estimation of warming rates, (vii) Maximum warming rate vs sample size.

Lasers

Wavelength

The choice of an optimal laser wavelength for cell heating poses some interesting questions. Our initial interest was in Nd:Yag lasers operating at 1064 nm because of local expertise and their common availability. Biological cells are relatively transparent to this wave length [14]. It is because of this high transparency at this wave length that most optical tweezers use Nd:YAG lasers. Optical tweezers use intense light beams to literally hold and move cells [13,21]. Eventually we decided that the cell transparency at 1064 nm was desirable. By not heating the cell directly, we completely avoid the problem of localized regions in the cell being strong absorbers and experiencing localized, lethal, overheating. The optical tweezers studies demonstrated that cells can tolerate very high light intensities at 1064 nm. Typically, with tweezers, intense laser light is directed ‘backwards’ though a high numerical aperture microscope objective (e.g. NA = 1.3) and onto the target cell. This yields a spot size in the cell focal plane of ^~ 0.8 um; smaller than many cells. Concentration of the laser light to such a very small spot size leads to very high intensities and thus provides a very stringent test of the ability of cells to withstand 1064 nm radiation. Numerous studies have found minimal to no cell damage in E. coli, yeast, protozoa, RBC, Chinese Hamster Ovary cells, sperm, and other cell types at intensities in excess of 100,000 W/mm² for durations of tens of seconds [1,8,10,13,14,21]. In contrast our exposures are less than 2,500 W/mm² for milliseconds, but to the entire cell and not just a small spot (see calculations, below). Laser tweezers studies do report damage at the highest intensities and longest exposure times. It is suspected that this is thermal damage [10,14]. Because our laser intensity is low and our exposure time is three orders of magnitude less than used for laser tweezers, we are confident, and our results demonstrate, that mouse oocytes experience no laser damage in our ultra-rapid warming system.

However, a serious drawback would appear to be that because of the high transparency of aqueous systems to 1064 nm wavelengths, the energy absorption would be too low to warm the samples at anywhere near the desired rate. This dilemma was solved by adding particles of carbon in the form of India ink at ^~0.275% (V/V) to the vitrification solution in which the cells are located. These particles absorb the incident laser energy because they approximate black bodies. Another feature of importance is that these particles are too large to cross plasma membranes.

An important consequence of this indirect cell heating is the limitation on warming rate. It takes time for heat to flow from the ink particles to the oocytes. At high enough warming rates, the cell center reaches a limiting rate and simply can warm no faster. In this case, the very concept of a ‘warming rate’, applicable to the entire cell, becomes meaningless. This is what drives the necessity to thermally model the system and determine just what the fastest possible rate is for a given cell size and experimental configuration.

Laser Power- Energy Requirements

Fast warming requires small sample sizes. For our studies with mouse oocytes and early embryos, our samples have consisted of 5 cells in a 0.1 µl droplet. This droplet is placed on the tip of a polypropylene Cryotop [9]. To determine the requirements for the laser, we needed to determine both the energy needed to warm and melt the frozen/vitrified sample and the power (energy/time) of the pulse required to achieve ultra-high warming rates. The relationship is:

$$E_L={P_L}^{*}\Delta t$$ (1)

where E_L, P_L, and Δt are the laser energy in one pulse, the laser power for the duration of the pulse, and the duration or width of the laser pulse, respectively. The MKS units of E, P, and t are joules, watts, and seconds. As a practical matter, all three parameters are important when selecting a laser. It is entirely possible to find a laser that ‘apparently’ has appropriate values for two of the parameters, but not the third. We will first calculate the energy to warm the sample. The pulse energy can be calculated from the requirement that the laser pulse has to contain enough energy to warm the sample droplet of interest as well as warming the tip of the Cryotop stick. Thus:

$$E_w=E_{wd}+E_{wct}={f_i}^{*}EL$$ (2)

where E_wd is the energy required to warm the droplet and E_wct is the energy required to warm the Cryotop tip, and E_w the sum. The fraction of the laser beam that is intercepted by the droplet is given by f_i. The terms are easily estimated. For the simplest case, consider the droplet to be water (ice) and assume it is to be warmed from ^~ −180 to ^~ 0 °C (ΔT = 180 °C). (The choice of an 180 °C range is justified later.) Then

$$E_{wd}={m_d}^{*}{C_p}^{*}\Delta T=\mathit{0.027}J,$$ (3)

where m_d is the mass of the droplet, c_p is the specific heat capacity of the droplet (taken to be ice), and ΔT is the warming range. Inserting appropriate values for 0.1 µl (0.l mg) of ice yields a value of ^~ 0.027 J. The thickness of the Cryotop is 0.1 mm and the width is 0.7 mm. We assume that 1.5 mm of its length is warmed by the laser pulse. This is an over estimate, just to be on the conservative side in calculating energy requirements. The Cryotop density and heat capacity are 0.92 g/cm³ and 1.05 J/g/K, respectively [5]. Then, E_wct = m*c_p* ΔT = 0.018 J and the total energy required to warm, E_w is 0.027 + 0.018 = 0.045 J.

Finally, we need to estimate f_i, the fraction of laser energy intercepted and absorbed by the droplet. It is determined by two factors: the droplet area vs the laser beam area and the droplet absorption characteristics:

$$f_i={(\text{Droplet Area}/\text{Beam Area})}^{*}\text{Droplet absorption}$$ (4)

Our 0.1 µl droplets are ^~ 0.6 by 0.6 mm, square, yielding a droplet area of 0.36 mm². The cross sectional area of the circular laser beam needs to be sufficiently larger than that to allow the droplet to be easily aligned in its path. The laser we chose has a maximum beam cross section of 2 mm diameter so we use that for the calculation. The use of a beam that is too large wastes laser energy which in turn would require a more powerful and more expensive laser.

The final factor is the absorption characteristics of the droplet. As discussed in some detail in our previous report, Jin et. al. 2014 [6], the droplet transparency needs to be relatively high so that the back edge of the droplet sees a beam intensity comparable to that on the front edge, in order to attain relatively uniform deposition of laser energy. Theoretically we would prefer a droplet transparency of ^~ 90%. Empirically we found that ^~ 80% worked better. Thus the droplet absorption factor is 0.2 and f_i = 0.02 (Dr. Jin discovered that our 2014 paper [6] erroneously reported the value to be 0.04.)

Combining all these factors, we come up with

$${\mathrm{E}}_{\mathrm{L}}={\mathrm{E}}_{\mathrm{w}}/{\mathrm{f}}_{\mathrm{i}}=0.045\mathrm{J}/0.02=2.2\mathrm{J}$$ (5)

where E_L is the required energy in a single laser pulse required to warm a 0.1 µl droplet sitting on a Cryotop stick from –180°C to ^~ –0°C.

Laser pulse duration and warming rates

We would like the range of laser pulse durations to be such as to produce warming rates ranging from 100,000°C/min to 10,000,000°C/min. The former is the rate of warming achieved when a Cryotop blade plus droplet is abruptly transferred from LN₂ to a water bath at 23°C in the absence of a laser pulse. The latter is two orders of magnitude higher.

The relationship between the laser pulse and the warming rate is given by:

$$WR=\Delta T/\Delta t$$ (6)

where WR, ΔT, and Δt are the droplet warming rate, temperature range over which warming occurs, and the time over which it occurs. Delta t is, of course, just the laser pulse width or duration. We note some important assumptions and caveats: To speak of a ‘WR’, we need it to be reasonably constant; i.e., the droplet temperature should be a linear function of time. Typically, lasers put out a constant power during a laser pulse. This will produce a constant rate of warming if the heat capacity of the sample is reasonably constant with temperature. In fact, the heat capacity of ice varies by a factor of 2 ½ between − 180 and 0 °C [4]. However, as previously noted, the important recrystallization range is approximately −100 to − 30 °C. In this range the heat capacity of ice only varies by 10’s of percent. Thus in principle we could hold the warming rate constant to a few 10’s of percent. Finally, we note that some lasers have the capability to temporally ‘shape’ the pulse and this would allow the power to be adjusted during the pulse to maintain a constant warming rate. Indeed, the laser we eventually chose has this capability, but the time resolution is too low to be useful for the short pulse durations we used in our mouse work.

But, we have ignored a critical fact to this point. The sample is not, in fact, pure water (ice) but an aqueous solution containing 2 molal or more concentrations of cryoprotective solutes. (We ignore the contributions of the ^~5 oocytes in the droplet as they only represent 1/50 th of its volume.) This affects the situation in two ways. First, the melting point of a 2 molal solution is ^~−3.6°C- not 0 °C. This is too small to introduce complications. However, the second effect does introduce complications. This second effect is that a solution begins to melt when warmed above its eutectic point (approx −60°C for EAFS [6], and progressively melts as the temperature rises further. The consequence of this is that between −60°C and −3.5°C, the absorbed laser energy goes both to warm the droplet and to melt ice. Moreover, the higher the temperature the more the laser energy is shifted from the former to the latter.

At this juncture, we note an important experimental consideration. The only physical end point of the droplet immediately post laser warming, which we can reliably observe, is complete or nearly complete droplet melting. Occasionally (^~20% of the time), we find small arcs of ice around the edge of the droplet. We attribute these to the droplet being slightly off center from the laser beam. Furthermore, as discussed more fully later, the energy required to achieve this must be empirically determined. The use of a fully melted droplet as an endpoint gave good results in our mouse studies, so for now, we have adopted it as our standard end point of the laser pulse. In principle, one could empirically find the laser energy necessary to fully melt and then reduce this energy by say 10%, so that the droplet is warmed through the critical range (−100 to − 30 °C) but not fully melted.

We must now add the energy to melt the droplet to that already determined for warming. This is easily approximated for a pure water droplet as E_m = m_d*L_f where E_m, m_d, and L_f are the energy to melt, droplet mass, and heat of fusion of water, respectively. Inserting appropriate values for our 0.1 µl droplet yields E_m = 0.033 J, comparable to the energy required to warm the droplet and Cryotop tip from - 180 to near 0 °C. Adding this melting energy to the warming energy already determined yields a required laser pulse power from Eq. 5 of:

$$E_L=(E_w+E_m)/f_i=(0.045+0.033\mathrm{J})/0.02=0.078\mathrm{J}/0.02=4\mathrm{J}$$ (7)

We believe that this value of 4J is subject to some uncertainty, perhaps ± 25%, because of a number of experimental variables, known and unknown. But this is not a serious problem experimentally, because the required energy settings on the laser are determined experimentally for each day’s run (see below). Finally we note that the energy to warm and melt is independent of warming rate, as long as that rate is fast compared to the warming rate in air.

We return now to the problem of determining the warming rate (WR). During the time Δt, we apply a constant input of laser energy sufficient to warm and melt the sample to a temperature slightly below 0 °C (below because of freezing point depression). During the time prior to melting, all of the deposited laser energy goes to heating the sample (and Cryotop tip) and none to melting. When the sample starts to melt, some laser energy goes to warming and some to melting. The greater the degree of melting, the less energy is available for warming. Thus in general terms we expect our droplet to begin rapid warming at – 180 °C and then undergo slower warming when the temperature climbs above the eutectic temperate and melting begins. Thus the warming rate is higher below the eutectic temperature and lower above it. Our WR is just the average of these differing rates.

To get a sense of how this affects the warming rate, consider an ‘ideal’ droplet of pure water (ice). Upon application of the laser pulse, a fixed rate of warming will commence and continue until the droplet reaches – 0 °C at which point warming stops abruptly and all the remainder of the laser pulse is used to melt the sample. For the numerical example above, the warming energy, 0.045 J, is 58 % of the total needed to warm and melt. To simplify the argument, round this to 50 %; half. Thus all the warming occurs during the first half of Δt, all melting during the second half, and the true warming rate is WR_t = ΔT/(0.5*Δt) = ^~ 2*WR. Of course our real droplet is more complex; it contains cryoprotectants and thus begins melting at the eutectic temperature, well below zero. As a consequence the warming and melting occur simultaneously over part of the warming range and the factor of two in the warming rate will be reduced. To evaluate the effect more fully will require modeling that accounts for the actual phase and thermal properties of the cryoprotectant solution. But again, the details are likely not so important. With the laser, we are achieving warming rates up to 100 times higher than those achievable by conventional means. A factor of 2 is not significant.

(Note: This factor of ^~2 increase in WR, discussed above, depends on the length of the Cryotop tip which is assumed to be in thermal equilibrium with the droplet. We have variously estimated this as 1 to 1.5 mm. The lower estimate leads to a WR factor of 2, reported by Jin et al., 2014 [6], the larger to a factor of 1.7; the precise result here.)

We are now ready to calculate the necessary laser pulse widths to achieve the desired warming rates. Table 1 gives some typical values of WR and Δt.

Table 1.

Warming Rate (WR) of a sample droplet as a function of the applied laser pulse duration, Δt, where WR ^~ ΔT/Δt and ΔT = 180 °C. Also shown is the necessary instantaneous laser power: P_L = E_L/Δt using E_L = 4J (Eq. 7).

WR (°C/min)	1.1 × 105	3.6 × 105	1.1 × 106	3.6 × 106	1.1 × 107	3.6 × 107
Δt (msec)	100	30	10	3	1	0.3
PL (watts)	40	133	400	1,330	4,000	13,300

In order to compare laser warming with conventional warming of Cryotops at 1.2 × 10⁵ °C/min it would be desirable to have a laser pulse width of 100 msec.

Finally, we note that a suitable laser has to have a sufficient power output in addition to possessing the appropriate pulse duration and pulse energy. In theory, knowing the first two, we can calculate the third. In practice laser specifications can be misleading. Table 1 shows the required instantaneous laser power for the various pulse durations. Note that achieving the desired warming rate of 1 × 10⁷ °C/min requires an instantaneous laser power of 4,000 watts–Not a trivial value!

Finding a suitable laser

The discussion in the previous section was concerned with two items. First was determining how much energy the laser beam has to provide to warm the droplet containing the oocytes from –180°C to 0°C and melt it, plus the energy required to warm the affected portion of the Cryotop. Second it was concerned with what the duration of the laser pulse has to be to obtain the desired ultra-rapid warming. The current section, on the other hand, is concerned with the specifications the laser machine has to possess to deliver these energies in the required time.

There are three categories of Nd:YAG lasers: Research, medical, and industrial. Research lasers are typically designed to produce very short pulse widths on the order of nanoseconds. They are expensive and totally unsuited for our purposes. Some medical lasers might be suitable but it is hard to find ‘useful’ specifications and there will of necessity be a hefty premium in price for all the regulatory approvals and “turn-key” packaging. That leaves industrial lasers and particularly, welding lasers. In our search we identified the LaserStar 990 Series iWeld jewelry welding laser as the best choice (LaserStar Technologies, Riverside, RI, USA). These lasers have specifications which are nearly perfect for our application and have numerous safety features to protect both the laser and the operator. Additionally, they were the least expensive laser found. It should be noted that lasers of the required power are Class IV; the most dangerous. Even momentary eye exposure to the beam would surely lead to severe eye damage. The iWeld series has a downward directed beam, which provides the first level of protection; a second level is provided by various protective devices on the microscope and viewing window. Thirdly, we wear protective googles which allow for good working vision while heavily filtering 1064 nm radiation. We found the iWeld lasers very user friendly. Briefly, the laser ‘chamber’ allows convenient and safe access to the beam, several microscope options are available for viewing the target, the laser is easily triggered by an external switch closure, the control panel provides for easy laser control, and the laser operates from a standard 120 VAC, 15 A source.

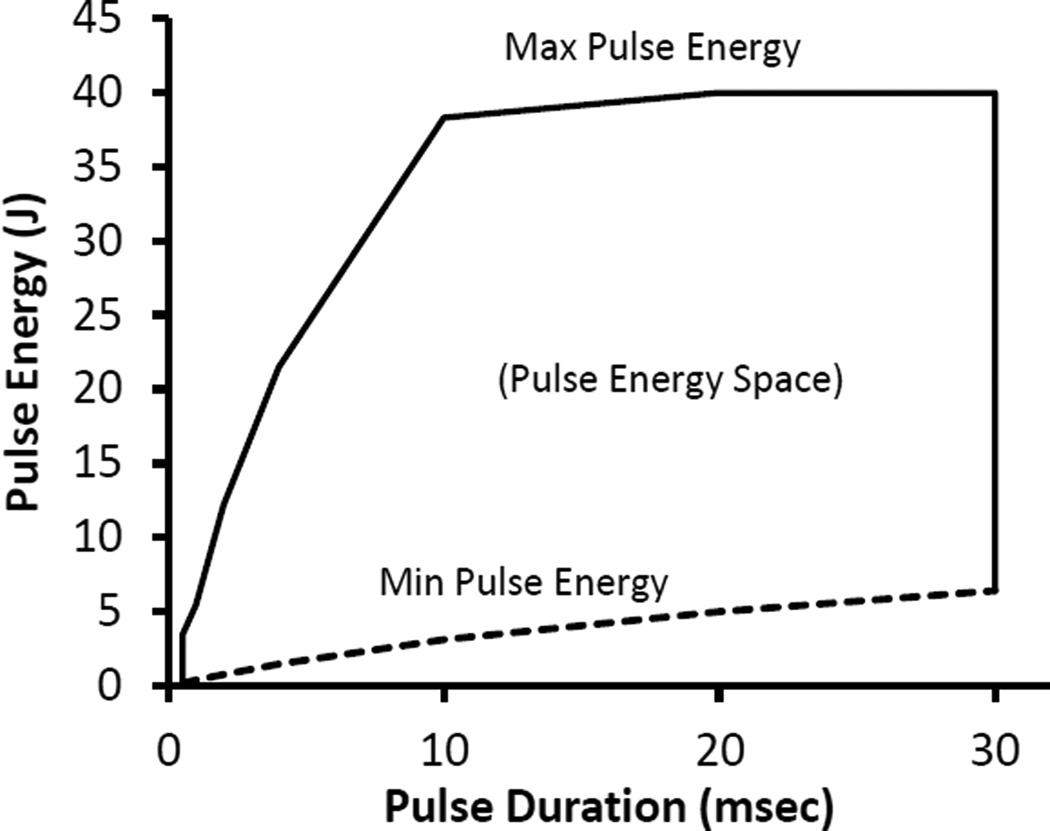
The two most important laser parameters are the available pulse durations and power or energy. The iWeld laser is available in 40 to 100 Joule/pulse versions. Our experiments have been done with the 40 Joule model. Nominally the spec sheet reports pulse energies of 0.1 to 40 Joules and pulse durations of 0.5 to 30 msec. A thirty msec pulse duration is short of our desired 100 msec duration but otherwise the specs meet our requirements. But the devil is in the details. Fig 1 is an energy- space plot of the available energy vs. the pulse duration (based on our interpolation and extrapolation of the engineering data provided by LaserStar). Note that when pulse durations are shorter than 10 msec, the maximum energy per pulse is no longer constant. For long pulse durations, we see that the minimum energy exceeds our 4.4 J requirement (Eq 7) and thus some additional attenuation of the beam may be necessary. For 1 msec pulses (the shortest we have used) the energy in the pulse (^~4 J) is just about equal to that required to warm and melt our 0.1 µl samples (Eq. 7). Samples significantly larger than 0.1 µl might benefit from one of the more powerful LaserStar iWeld lasers.

Fig 1.

Available energy space plot for the LaserStar iWeld 990 40 Joule Laser. Only pulse durations and energies inside the polygonal figure are available. Note the drop in available pulse energy for short pulse durations. Determined from unpublished LaserStar data.

We note here a few additional key factors in selecting a laser. The beam diameter must be appropriate to the droplet size. The iWeld 990 is adjustable from 0.05 to 2 mm. Some small increase to, say, 2.5 mm is possible by placing the target above the laser focal point. This proved impractical however, as the viewing system is designed to come into focus only in the laser focal plane. Alternatively it might be possible to place a negative lens in the beam to expand its diameter. Lenses with coatings designed for 1064 nm light are available; e.g. Edmund Optics (Barrington, NJ, USA).

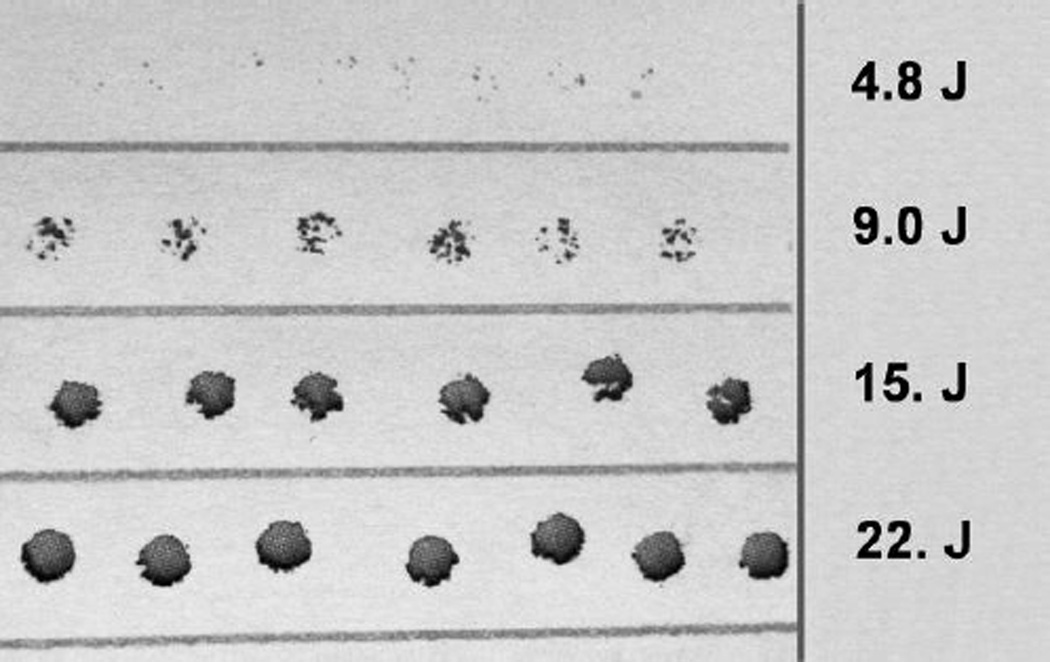
A second requirement is that the beam energy be uniformly distributed across the spatial profile of the beam. Typically, most lasers produce a spatial beam profile that is Gaussian. Thus the energy would be concentrated to the center of the beam and fall off rapidly towards the edge of the beam. This would lead to uneven heating of the 0.1 µl droplet with attendant complications. LaserStar offers a ‘SoftTouch’ option that produces a more uniform spatial energy distribution. This is a substantial improvement over a Gaussian profile. It is not, however, entirely uniform. Fig 2 displays burn holes in paper for a range of laser pulse power settings. It is obvious that there are hot spots in the beam (see the second row, Fig 2) which are not reproducible from one shot to the next. This highlights again, the advantage of depositing the laser energy into a droplet and then having this energy transferred to the cells by conduction. If the cells were heated directly, this small inhomogeneity of spatial beam energy would lead to different warming rates for different cells and/or cell sub structures.

Fig 2.

Burn holes in paper depicting the spatial uniformity of our laser pulse energy. There are 4 rows, each containing 6 to 7 burn holes obtained using the pulse energy shown to the right. It is apparent from the second row that it is not possible to make the beam energy profile entirely uniform. The pulse duration is 7 msec and the burn holes are ^~ 2 mm in diameter. The paper was positioned by hand; consequently the slight scatter in the position of the holes has no significance.

Laser Pulse Energy Calibration

Several paragraphs above, we estimated the energy needed to warm and melt a droplet. This is the starting point for experiments. However the iWeld (and probably most lasers) do not have a ‘dial’ calibrated in pulse energy. The iWeld controls the duration and voltage applied to the flash tube which pumps the laser. The iWeld is designed for welding and the user manual and literature contain information for this purpose. Because of our special needs, LaserStar provided us with an engineering sheet listing ‘typical’ pulse energy values for various pulse durations and voltage settings. These we cross checked with our own calibrations to make sure we understood the LaserStar data and that our laser was operating normally. We used two calibration methods. A crude calibration can be made by setting the laser up for repetitive pulses and firing them into a cuvette of water and India ink containing a thermocouple. The input energy is computed from the temperature rise of the water. We obtained better results with a commercial version of essentially the same concept. We recommend the Analog Laser Power Probe (#P50Y) for ^~$400 from Macken Instruments (Santa Rosa, CA, USA). The probe has a stated accuracy of ± 5%, presumably of the full scale range. For pulse durations in the range of 1 to 5 msec, where our mouse work was done, the LaserStar engineering data agreed with the power probe to within 10 to 20%. However, for longer pulse durations, up to 30 msec, the discrepancy is much larger. The essential point for our purposes is that once we had empirically determined the melting energy (voltage) for a given droplet size, composition, and ink concentration, we could reproducibly melt repetitive droplet preparations.

India Ink

We chose India ink as the absorbing medium in our target droplets; specifically Higgins #44201 Waterproof Black India Drawing Ink in 1 oz bottles, which is basically a suspension of carbon black. The scheme is to load the medium bathing the cells with India ink; the ink absorbs the laser energy which heats the bathing medium which in turn heats the cells to be warmed. Electron micrographs of India ink show that the carbon black particles range in size from 0.1 to 1 µm [11]. This is large enough to exclude the ink from the mouse embryo proper and from the perivitelline space inside the zona pellucida. Additionally, India ink is a strong absorber at 1064 nm. Our Higgins Ink has an absorptivity of ^~ 1*(%*mm)⁻¹ when diluted on order of 1000 × in phosphate buffered saline (PBS). Note that for a Beer -Lambert obeying solution, the absorptivity is independent of the solute concentration. Ink concentrations of ^~ 0.2 to 0.5% (V/V) were used, as detailed below. India ink also includes a binder, typically gelatin or shellac [20]. Preliminary toxicity tests on mouse embryos at an ink concentration of 0.1% revealed no toxicity (data not shown). Moreover, Jin et al. 2014 [6], obtained survivals of over 90% for mouse oocytes subjected to vitrification and laser warming with India ink.

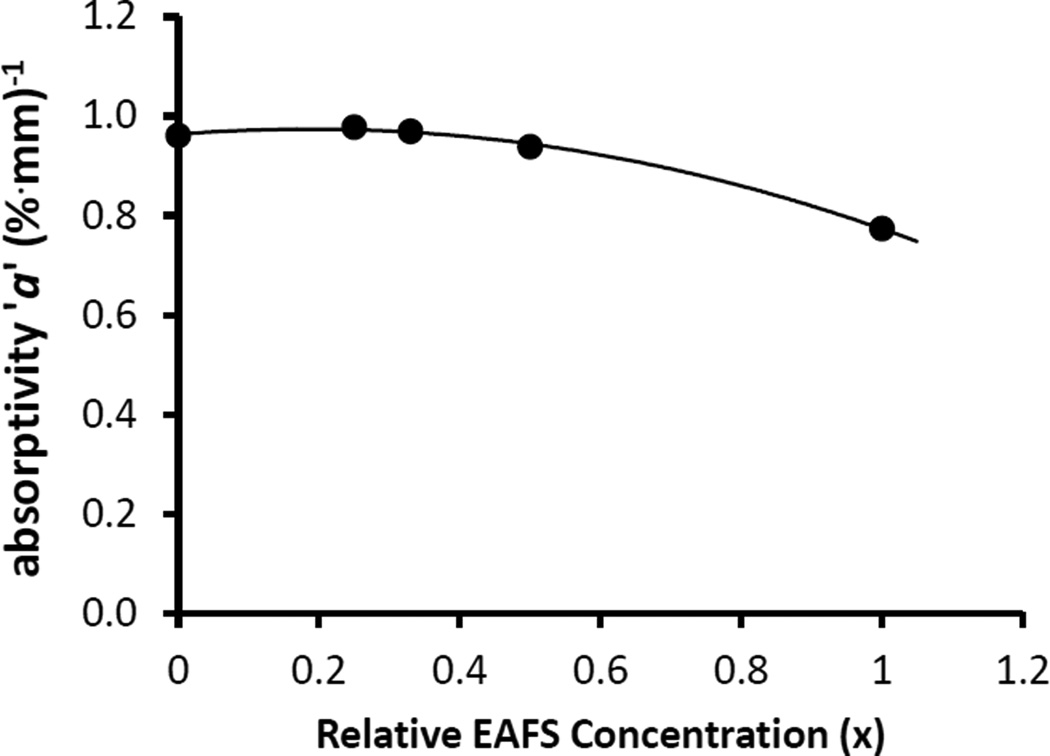
We note several practical considerations. First, India ink is not a reagent. There are significant bottle to bottle variations of, say, 40% around the mean absorptivity ‘a’ of ^~1*(%*mm)⁻¹. The ink tends to clump over time. Shaking and sonification may be helpful at minimizing this. Also the absorptivity depends on the suspending medium. Changing the cryoprotectant or its concentration will change ‘a’. Fig 3 illustrates this for differing concentrations of the EAFS solution used in our mouse work (EAFS = ethylene glycol, acetamide, ficol, and sucrose; [6]). As the EAFS concentration increases from 0 to 100%, the absorptivity decreases by ^~ 20%. This change is readily visible to the naked eye.

Fig 3.

Dependence of India ink absorptivity, ‘a’, on EAFS concentration. EAFS contains ethylene glycol, acetamide, ficol, and sucrose as detailed in Jin et al. 2014 [6]. 1× is the standard concentration, 0.33 is the typical concentration used in our mouse studies. The ink, itself, is diluted to 0.275% (V/V) in the EAFS. These data are for samples from the same ink bottle.

In our hands, India ink is an ideal absorber and follows the Beer - Lambert Law well in the range we have worked with; transmission % = ^~ 25 to 98 %. To illustrate, we compute the required ink concentration for a typical experiment using a 0.1 µl droplet of 0.33× EAFS. Beer- Lambert states:

$$A=a^{*}{b}^{*}c$$ (8)

where A is the sample absorbance (≡ optical density), a is the absorptivity, b is the optical path length, and c is the concentration. The sample light transmission % is related to A by:

$$T_{\%}={\mathit{100}\%}^{*}{\mathit{10}}^{-A}$$ (9)

Note that a, A, and T_% are all wavelength dependent. Our 0.1 µl droplets are 0.3 mm thick; thus b = 0.3 mm. We desire they have a T_% of ^~ 80% (see Laser section above). From Eq. 9 this gives an A of 0.1. From Fig 3, a is 0.97*(%*mm)⁻¹. Solving Eq. 8 for the concentration yields c = 0.34 % (V/V) for ink from this same bottle. It is perhaps useful to note that the use of percentage solution concentrations necessitates a corresponding adjustment to the absorptivity, a. Since concentrations, c, are multiplied by 100%, it is necessary to divide a in units of mm⁻¹ by 100% yielding an a with units of (%*mm)⁻¹ and numerically 100 times smaller.

Measurements of ‘a’ were made on a Thermo Scientific Genesys 10 Spectrophotometer (Fisher Scientific, USA) and a Bausch and Lomb Spectronic 710 Spectrophotometer using ink dilutions of approximately 1000 ×. The dilution factor is chosen to optimize the measurement accuracy of the spectrophotometer; not too opaque, not too transparent. The B&L 710, like many spectrophotometers, only extends to a wavelength of 1000 nm. However India ink has a smooth, featureless spectrum and measurements at 1000 nm can easily stand in for the correct 1064 nm wavelength of the laser. From published spectra and our own measurements, we estimate that Higgins India ink is ^~ 3.5 % more transparent at 1064 nm than at 1000 nm.

Cryo Jig

The operation of our Cryo Jig, Fig 4, and sample handling for removing samples from LN₂ and irradiating them with a laser pulse have been previously described in detail by Jin et al. 2014 [6]. Briefly when warming is to be initiated, the wood block (3) is tipped, flipping the Cryotop sample out of the LN₂ reservoir and firing the laser. Here we consider some of the design and construction details. We have previously determined that a 0.1 µl droplet on a Cryotop transferred from LN₂ to RT air warms at 7,850 °C/min or 130 °C/s [12]. Thus the Cryo Jig has to fire the laser in a fraction of a second, otherwise the droplet will air warm before the laser fires.

Fig 4.

The Cryo Jig used to move samples from LN₂ to air and laser warm/melt them. Note the use of ‘common’ materials in the construction. The labeling used here is the same as that in (Jin et al 2014). However, note that this picture shows the Jig in its loaded or cocked position (but without LN₂ in the reservoir). (1) Droplet position on the clear Cryotop tip. (2) Cryotop. (3) Cryotop holder block/trigger block. (4) Alignment ruler. (5) Styrofoam LN₂ reservoir. (6) LN₂ cover slide to protect droplet from being cooled by LN₂ vapor after the laser fires and warms the droplet. (7) Spring to pull cover slide. (8) Trigger tab mechanism for releasing the cover slide when the trigger shaft is rotated. (9) Micro-switch to fire laser on closure. (10) Trigger shaft which rotates when the holding block is depressed. (11) Tab to close micro-switch. (12) Sliding base. (13) Velcro friction tab to hold the trigger block and Cryotop steady after Jig firing. For scale, the Styrofoam reservoir has internal dimensions of 90 × 50 × 30 mm (LxHxW).

It is the first author’s experience that attempting to design a complex device from scratch (in a finite length of time) and have it constructed by the machine shop would likely lead to a pretty but non-functioning device. Thus the decision was made to construct the Jig in the lab using commonly available tools and materials. Materials were obtained, literally, by walking the local hardware stores and buying everything which looked promising. The principal construction materials were small pieces of wood, aluminum (flat and angle ‘iron’), and steel rods. Electrical parts were obtained from Radio Shack (USA). The disadvantage of this method is that the Jig is more subject to ‘wear and tear’ and requires occasional adjustment.

The Jig was designed and built step by step, rather than by executing the full design first and building second. This had the advantage that problems could be solved one at a time. And when a sub-assembly design did not work, it could be altered repeatedly until it did work before proceeding. The only decisions made initially were: (1) the laser beam would not be redirected from vertical to horizontal with a mirror and (2) the Cryotop would be removed from the LN₂ rather than the other way around. Loctite Super Glue Ultra Liquid Control glue (Loctite, Westlake, OH, USA) was used for assembly. This is a pressure setting glue which sets in 15 sec. It proved ideal. The bonds were strong enough to hold parts together during normal Jig operation and weak enough to break when mistakes were made or adjustments were needed. Once a section of the Jig was working right, the parts were epoxied for permanence.

We will only point out a few especially pertinent details here. Further details can be obtained from the first author (FWK). The starting point for the Jig is a small LN₂ bath. This proved vexing. We were unable to find any rigid foam material locally or online which was LN₂ leak proof. Eventually we were forced to use Styrofoam from an empty, cold shipping container. This had insufficient thickness but we were able to glue two pieces together with GE Premium Waterproof Silicone purchased in a standard calking gun cartridge. Were we to build a new bath, we would make it a little wider.

In an experiment, everything is initiated by pressing on the back of the holding block (3) which flips the Cryotop out of the LN₂ bath. The most difficult part of the design was transferring this motion to the right side of the Jig to release the cover slide (6) and fire the laser. Part of the mechanism is hidden in the picture. The trigger rod, (10), has a tab on the left which sits under the holding block. When the holding block is depressed, it presses this tab down, rotating the trigger rod. This rotation causes the tab (8a), affixed to the trigger rod to rotate, releasing the tab (8b), affixed to the cover slide (6). When the cover slide slides home, tab (11) depresses and closes the micro-switch (9) firing the laser. The micro switch is chosen to require very little force to close. We used a Radio Shack NTE54–417 switch (www.radioshack.com). The iWeld laser has an electrical plug for an external trigger which LaserStar uses for their foot switch but will sense any switch closure. I.e. just short the trigger leads. Finally, we note that the numerous unidentified parts in the vicinity of the trigger rod (10) serve only to stabilize the rod and hold it in place.

The Cryotops have a square shaped handle. We did not have a ‘square’ drill in our kit, so made a square holding hole in the holding block as follows: A Cryotop handle was coated with a thin layer of oil followed with grease and then a round oversized hole was drilled in the block. This was filled with epoxy glue, quickly followed by the coated Cryotop handle. Some means must be used to hold the Cryotop in position while the glue sets. After the glue sets, and if you are lucky, the Cryotop can be pulled back out leaving a perfect square shaped hole.

Figure 4 shows a plywood base (12) which slides across a second piece of plywood on the floor of the laser chamber. This proved unsatisfactory and both were replaced with flat pieces of ceramic floor tile with thin felt pads between. Thus the Jig is slid around by hand inside the laser chamber to position it under the beam (as determined by the cross hair eyepiece in the viewing microscope). The laser chamber has arm hole ports on both sides so that one’s hands can be inside the chamber, one holding the Jig and one pressing on the holding/trigger block to initiate the rapid warming process.

Since the mouse work reported in Jin et al. 2014 [6] and Jin and Mazur, 2015 [7], we have upgraded our Cryo Jig by mounting it on an X–Y stage. We recommend the Thorlabs (Newton, NJ, USA) DT25 stages. These are 20 mm thick and provide 25 mm of adjustment. Two, at right angles, are stacked to yield an X–Y stage. Because of the tight fit in the laser chamber it was necessary to make a new LN₂ bath with a height of only 36 mm.

Warming Range ΔT

Calculation of the estimated warming rate, WR, and the estimated energy needed for warming and melting requires specifying the temperature range ΔT over which the laser pulse warming occurs. The sample droplet starts out at LN₂ temperature, - 196 °C. Upon removal from the LN₂ bath, we estimate it takes ^~ 1/10 sec for the residual ‘wetting’ LN₂ to boil off the droplet. Then air warming begins at 130 °C/s [12]. Video imagery at 30 frames/s shows that 0.15 sec elapses between the time the Cryotop and its adhering droplet are withdrawn from the LN₂ bath and firing of the laser pulse. The exact time interval depends on the tension in the spring system, (7) in Fig 4. In summary then, the droplet leaves the LN₂, residual LN₂ boils off in 0.1 sec, and then air warming occurs for 0.05 sec, warming the droplet by 6.5 C to ^~ −190 °C, and then the laser fires. The laser warming ends when the droplet melts at about −3.5 C for 0.33× EAFS. Thus ΔT ^~ 186.5 °C. Previously, we estimated the starting point of laser warming at ^~ −180 °C [6], yielding a ΔT of ^~ 176.5 °C. These are just estimates and we deliberately have made a slightly different estimate in these two papers to stress that these small ΔT differences are unimportant. The laser energy to melt is empirically determined as stressed in the next section. The calculated WR’s only differs by 6% for these two ΔT estimates, inconsequential when we are concerned about the effect of differences in WR of 200%, 1000% or 10,000% on survival.

Empirical Reality

We have calculated the theoretical energy required to warm and melt a droplet. However, this only provides the initial settings for the laser. We have always had to empirically find the exact energy (voltage) settings necessary to warm at the desired rates for experiments on a single day. There are several reasons why the theoretical calculations may not be as precise as desired. First we have approximated the droplet as water/ice, but it is actually an aqueous solution/ice. Secondly, and perhaps most importantly, the absorption characteristics of the sample are based on measurements of unfrozen cryoprotectant medium plus India ink in a flat sided cuvette at room temperature. We do not know how good an estimate this is of the absorption characteristics of the India ink when it is embedded in a frozen cryoprotectant droplet on a Cryotop tip. Also we do not have the means to precisely calibrate the laser energy output and/or verify that our LaserStar ‘generic’ laser energy data accurately characterize our specific laser. Fortunately, variability in the droplet volume is not a problem for largely transparent droplets. If a droplet is a little larger than normal, it contains a little more India ink than normal and absorbs a little more energy than normal. Everything balances out and undersized, normal, and oversized droplets all warm and melt with the same laser settings. There are other interesting factors worth noting too. Different experimentalists will lay down droplets of slightly different dimensions and thickness. This is not a problem as far as energy absorption is concerned (for relatively transparent droplets) but may have other unexpected consequences.

Nominally (given the uncertainties in laser pulse energy calibration) we find that the theoretical and experimental energies to warm and melt mouse droplets agree and are independent of the pulse duration, as expected.

Modeling

Finite element analysis

We have previously described a model of the warming profile induced by the laser heating of the droplet with India ink particles and mouse oocytes [6]. The analysis depends on a finite element analysis of Fourier heat conduction in the sample droplet implemented in Microsoft Excel. The objective is to determine how quickly energy from the carbon black heated medium (droplet) is transferred to the bio sample; in our case mouse oocytes. The speed of this transfer determines the maximum oocyte warming rate that can be attained. We have since made improvements in this model which we report here. For completeness we briefly reproduce the model in its entirety. Additionally, we note that an analytical solution probably exists; but we have not found it.

We assume a spherical droplet of 0.1 µl volume. This assumption of spherical symmetry makes this model relatively tractable. This droplet has a radius of 288 µm, which we round off to 290 µm. It contains the India ink particles. These particles can not penetrate the outer non-living membrane of the oocyte, the zona pellucida (ZP). The radius of the ZP is 47.5 µm, which is rounded to 48 µm. As long as the oocyte is far from the edge of the droplet, it is the droplet’s volume that is important, rather than its shape which we know to be more of a flattened rectangular box. We can break the droplet into finite elements of spherical shells. Shells exterior to the zona pellucida (ZP) contain India ink and are directly warmed by the laser pulse. Shells interior to the ZP are ink free and can only be warmed by heat conduction from the India ink regions. We ignore the small percentage of the incident laser energy that is absorbed by the oocytes although it could be easily incorporated if desired. Previously we limited ourselves to the oocyte and a volume out to 100 µm radius and assumed that the included India ink volume was large enough so that the following boundary condition was satisfied. Namely, the outermost shell tracked the laser pulse warming ramp exactly, without lag. Our more complete modeling, here, shows that this was a valid approximation.

We extend our model to the full droplet dimensions as follows. In the vicinity of the oocyte we desire good spatial resolution and thus use shell thicknesses of 2 µm from r = 0 to 90 µm, well beyond the ZP. From 90 µm to 290 µm radius we use shells of 10 µm thickness. Thus there are a 45 plus 20 shells for a total of 65. We have examined the modeled T vs r profile in the vicinity of the transition from 2 to 10 µm shells and find it smooth and thus believe the model robust for the task at hand.

Three factors affect the change in temperature of a shell: (i) the amount of laser energy absorbed directly by the India ink particles, (ii) heat flow from the next ‘outer’ shell, and (iii) heat flow to the next ‘inner’ shell. With this preamble, the change in temperature of a shell element during one time step, δt, is given by:

$$T’=To+\delta T=To+C{\mathit{1}}^{*}W{R}^{*}\delta t+(\mathit{1}/(c{p}^{*}g))[(k^{*}\delta t/\delta r)(A{U}^{*}\delta TU-A{L}^{*}\delta TL)]$$ (10)

where:

• T’ and To are the new and old element temperatures of the element being evaluated,

• WR is the warming rate,

• δt is the time step and in our current model we break the laser pulse into 12,000 time steps (i.e. 12,000 rows in Excel). This is more than needed for most cases,

• C1 is a scale factor = (Total Droplet Volume)/(Portion of Vol. containing India ink); see below,

• C1*WR*δt is the laser component of temperature change in the shell,

• cp and k are the specific heat capacity and thermal conductivity of ice, taken to be: cp = 1.67 J/g/K and k = 3.0 W/m/K, chosen at ^~ −70 °C, the middle of the temperature range of prime interest between −100 and −30 °C, [19],

• g is the mass of the spherical shell in question and δr is the finite element step size, 2 or 10 µm,

• AU and AL are the upper (r greater) and lower (r lesser) surface areas of the adjacent shells to the one being evaluated,

• δTU and δTL are the differences in temperature between the upper shell and shell in question and similarly for δTL

Then, depending on the shell(s) in question, certain of the terms are dropped from the equation. The outer most shell at r = 280 – 290 µm has no shell above it. The inner most shell at r = 0 – 2 µm has no shell inside it. The shells inside the ZP have no ink and thus the laser warming term C1*WR* δt is dropped for these shells. In Excel, our model is 65 columns (=shells) wide and 14,000 rows (time intervals) deep which includes the 12,000 time steps for the laser pulse and an additional 2,000 steps to follow the thermal equilibration of the droplet, post pulse.

Finally an explanation of the constant, C1: Because the oocyte absorbs no laser energy, enough laser energy has to be deposited into the surrounding India ink solution to warm and melt it and the oocyte. The scaling factor C1 accounts for this. An alternative way to view C1 is as follows: If the warming rate is slow, the entire droplet remains thermally equilibrated and the bio sample and ink regions experience the same warming rate, WR. However, if the WR is very high, the warming of the ink solution gets ‘ahead’ of the bio sample and experiences a WR increased by the factor C1. As a consequence, at the end of the laser pulse, the outer regions of the droplet will be warmer than – 3.5 °C (the chosen end point) in order to hold the energy necessary to warm and melt the oocyte(s). For a sample such as a zebrafish embryo in an only slightly larger droplet volume, the term C1 becomes significant. For example, if the biological sample is half the volume of the droplet, C1 will be two. On the other hand, in the limit of cells small relative to the droplet, C1 goes to the limit of 1.

We have redone the calculations in our mouse oocyte report [6] and find that our previous modeling results are essentially identical with those of this more complete model, Fig 5. That is because in this case, the cells occupy only a small fraction of the droplet (^~ 2%). If the cells become large relative to the droplet, e.g. a zebrafish embryo in a droplet, then this more complete model is required.

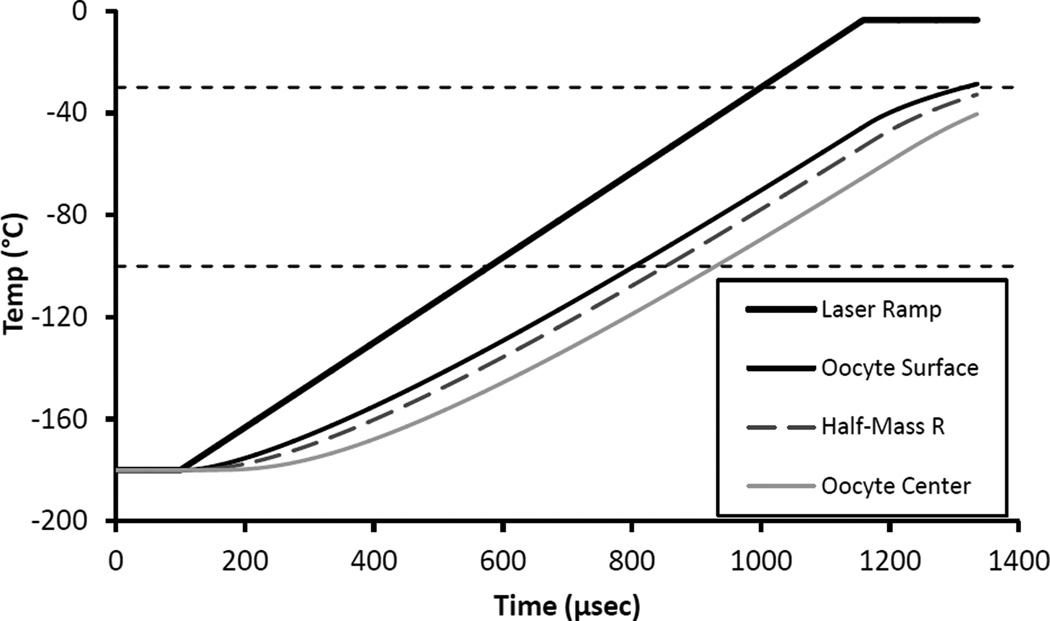
Fig 5.

Thermal response of IR transparent oocytes immersed in IR absorbing India ink when subjected to a laser-induced warming pulse of 1 × 10⁷ °C/min. Calculated in Excel using a finite element analysis model. The top bold curve is the desired warming ramp. The remaining three curves show the response temperature at the surface of the oocyte proper (r = 37.5 um), at the half mass radius (r=29.8 um), and at the center of the oocyte (r=0). These results are essentially identical to our previous results (Jin et. al. 2014; [6]) that used the original more approximate model. There is noticeable thermal lag, but the WR, i.e. the slope of the curve for the oocyte half mass radius, is only slightly less than that of the applied ramp.

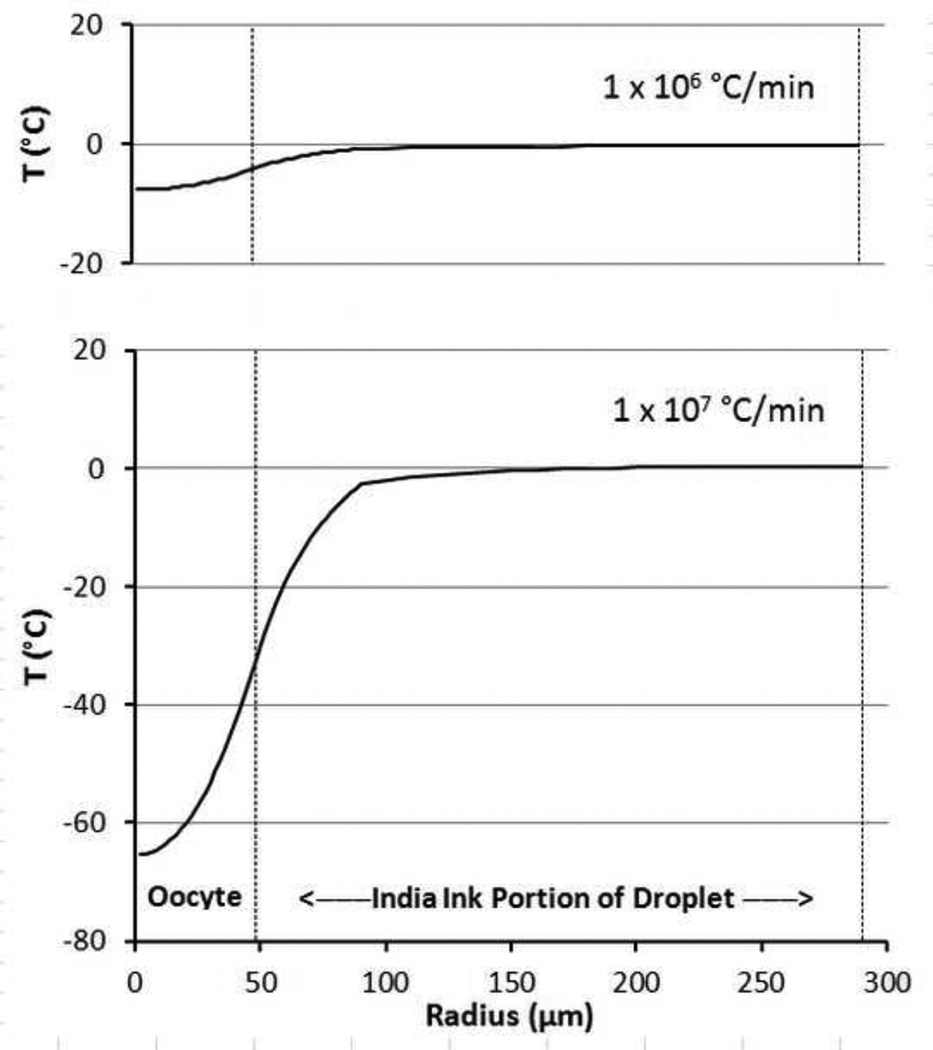
A different way to visualize the model results is to examine the temperature as a function of the radius from the center of the oocyte at a given time, say the end of a warming pulse. Figure 6 is just such a plot for two cases: a warming ramp pulse of 1 × 10⁶ and of 1 × 10⁷ °C/min. The large thermal lag between the center and surface of the oocyte at higher warming rates is readily apparent. It takes another several tens of msec for the oocyte to reach – 3.5 °C.

Fig 6.

Modeled temperature response vs radius of an oocyte and surrounding India ink shell at the end of a laser pulse yielding warming rates of 1× 10⁶ and 1 × 10⁷ °C/min. The radius is measured from the center of the oocyte to the edge of the droplet at 290 um. The outer edge of the zona pellucida at 48 um is denoted by the vertical dotted line and marks the division between the inner, ink free region and outer ink containing region which absorbs the laser IR energy.

Finally we note, as discussed in our previous report, that the preparation of the oocytes in EAFS prior to vitrification or freezing results in their osmotically shrinking to about half their original volume and typically in a non spherical fashion. This violates our assumption of spherical shape, but the shrunken size means that our embryos will actually exhibit faster warming and less thermal lag when subjected to a given laser pulse.

Maximum Warming Rate vs the Size of the cell or tissue

In our previous report [6] we suggest that the maximum warming rate WR_max scales as (1/R) where R is the radius of the cell(s) to be warmed. We now find that to be in error. Our thinking was that the volume to be heated, V_R scales as R³ and the area across which thermal energy must pass, A_R, scales as R² so that together, the scaling goes as A_R/V_R = (1/R). It is possible to test this with our modeling software and that has now been done. First, it is subjective to decide how much lag can be tolerated between the applied laser pulse ramp and the cell response, as the WR is increased. Fig 7B of our previous paper [6] illustrates a reasonable choice. Using Fig 7B as a ‘template’ for how much thermal lag is permissible, we estimated WR_max for a range of cell radii from 5 to 1000 um. Plotting the data quickly reveals that WR_max is not linear in (1/R); i.e. (1/cell size). In fact we find that:

$$W{R}_{\mathit{\text{max}}}\propto (\mathit{1}/R^{\mathit{2}})$$ (11)

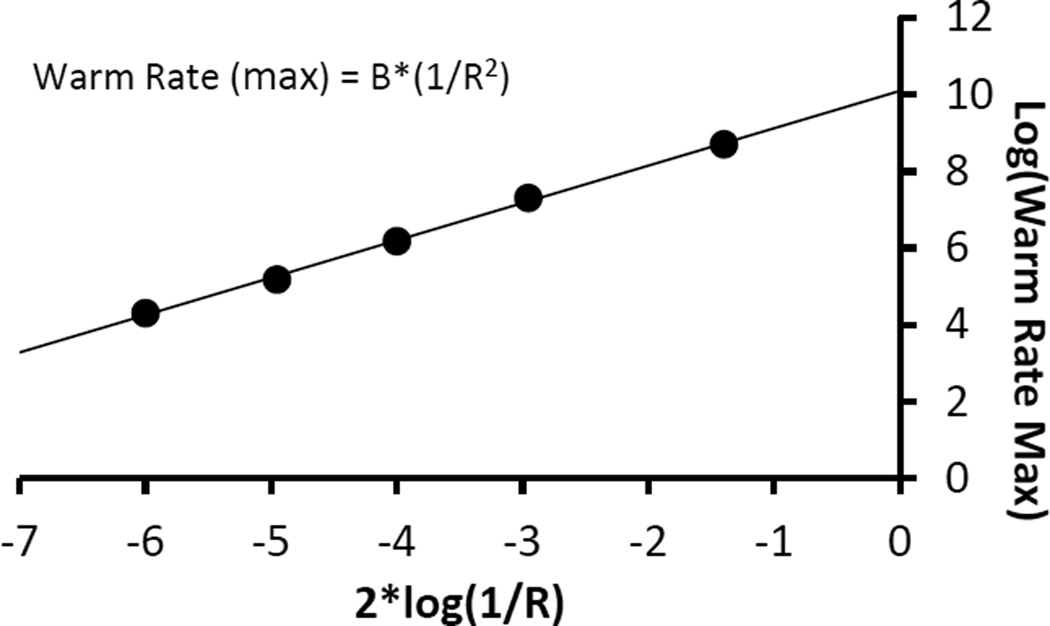
Fig 7.

Plot of maximum laser driven warming rate, WR_max, as a function of cell radius in the range of 5 to 1000 µm when the cell is warmed from the outside by a laser heated India ink solution. The WR_max is estimated from modeling of the different sized systems (see text). The plot is linear, with slope 1, in log(WR_max) vs 2*log(1/R), demonstrating that WR_max ∝ (1/R²). B = 10^10.09 (°C*µm²/min).

This can be demonstrated from the data as follows: Assume WR_max = B*(1/R²) where B is a constant. Taking the log of both sides yields log(WR_max) = log(B) + 2*log(1/R). Then plotting log(WR_max) vs 2*log(1/R) will yield a straight line (with slope 1). Fig 7 shows the results for our modeling data of WR_max. If it seems remarkable that a ‘visual’, subjective estimate of WR_max should yield such a good fit straight line, remember that it is the log that is plotted here. The extra factor of R in the WR_max formula may be due to the greater distance that heat has to travel in a larger sample.

But unfortunately this inverse square dependence makes it more difficult to attain ultra-high warming rates with large cell systems such as a zebrafish embryo. At about 8× the size of a mouse oocyte, its WR_max will be (1/8²) times slower than attainable for the mouse with the present laser system and procedure; I.e. ^~ 1×10⁷/64 ^~ 1.5 × 10⁵ °C/min.

Summary

We have tried to point out the factors we consider important in using a laser to achieve ultra-rapid warming of living frozen or vitrified cells. An important feature is that the warming of the cells results from the absorption of laser energy by India ink particles in the extracellular medium and the flow of that heat to the cells. There are advantages and disadvantages to this indirect warming method. By warming indirectly, we greatly reduce the chance of cell damage as a result of sub structures in the cell being over heated by the laser radiation. On the other hand, we are limited in how rapidly a cell can be warmed, especially a large cell(s). We have discussed the meaning of warming rate, WR = ΔT/Δt, and pointed out two circumstances in which caution is required. (i) Because the eutectic melting point of cryo solutions is usually significantly below zero, it is not possible to achieve a constant warming rate independent of temperature if constant laser power is applied. (ii) For sufficiently fast warming rates, a gradient develops across the cell and the inner portions of the cell warm at a lower rate than the outer portions. This gradient may become so large as to become damaging. Finally, we would be happy to help others in replicating our Cryo Jig or in applying our Excel modeling software.