Abstract
We employ state-of-the-art pair and three-body potentials with path-integral Monte Carlo (PIMC) methods to calculate the third density virial coefficient C(T) for helium. The uncertainties are much smaller than those of the best experimental results, and approximately one-fourth the uncertainty of our previous work. We have extended our results in temperature down to 2.6 K, incorporating the effect of spin statistics that become important below approximately 7 K. Results are given for both the 3He and 4He isotopes. We have also performed PIMC calculations of the third acoustic virial coefficient γa; our calculated values compare well with the limited experimental data available. A correlating equation for C(T) of 4He is presented; differentiation of this equation provides a reliable and simpler way of calculating γa.
Keywords: coustic virial coefficients, calibration, density, helium, metrology, thermodynamic properties, virial coefficients
1. Introduction
Accurate knowledge of the thermophysical properties of helium is desirable for many applications in metrology [1–3]. At low and moderate densities, thermodynamic properties are well described by the virial expansion, which gives a rigorous series of corrections to ideal-gas behavior:
| (1) |
In Eq. (1)p is the pressure, ρ the molar density, R the molar gas constant, and T the absolute temperature. The second virial coefficient B(T) depends only on interactions between pairs of molecules, while the third virial coefficient C(T) depends on interactions among three molecules.
In 2009, two of us reported [4] path-integral Monte Carlo (PIMC) calculations of the third virial coefficient C(T) for 4He at temperatures from 24.5661 K (corresponding to the triple point of neon) to 10 000 K. The values of C(T) reported in Ref. [4] were based on a representation of the pair potential [5] and a three-body potential [6] that were state-of-the-art (or nearly so) at the time the work was performed.
The uncertainties obtained in Ref. [4] were smaller than those of the best experimental results by approximately an order of magnitude, with the majority of the uncertainty coming from the three-body potential. Further improvement is desirable—for example, in a proposed pressure standard based on capacitance measurement at 273.16 K, the uncertainty in C is still the largest contributor to the uncertainty budget between approximately 8 MPa and 20 MPa [7]. It is also desirable to extend the results to lower temperatures, where helium plays an important role in temperature metrology.
Recently, a state-of-the-art pair potential for helium has been developed [8, 9]. The new potential incorporates not only extremely accurate results for the potential energy in the Born-Oppenheimer (BO) approximation [10], but also accurate calculations for the most important post-BO effects (adiabatic, relativistic, and quantum electrodynamics). The claimed uncertainty of the new pair potential is at least one order of magnitude smaller than that of the potential we used in Ref. [4]. This pair potential has been used to obtain highly accurate values for the second virial coefficient B(T) and for the low-density limits of the viscosity and thermal conductivity [9]. In addition, a new three-body potential has been developed at the full-configuration-interaction (FCI) level [11], reducing the uncertainty of the three-body potential by approximately a factor of five compared to that used in Ref. [4].
In this work, we take advantage of the availability of these better potentials, and of increased computing capabilities and algorithmic improvements, to recalculate C(T) with lower uncertainty than could be obtained in Ref. [4] and to extend our calculations to lower temperatures. We also extend our work to the third acoustic virial coefficient, and give some results for the 3He isotope. In this paper, we will focus on aspects that differ from Ref. [4], such as the calculation of acoustic virials and the low-temperature results. The reader is referred to Ref. [4] for further background, a literature review, and details of the uncertainty analysis. Some additional details of the PIMC calculations, especially at low temperatures where spin statistics become important, are discussed in Ref. [12].
2. Intermolecular Potentials
For the pair potential, we use the potential first presented by Przybytek et al. [8] and described in more detail by Cencek et al. [9]. A function for the uncertainty of this potential is given in the Supplemental Material for Ref. [8], so that upper- and lower-bound potentials can be obtained by adding or subtracting the uncertainty function from the recommended pair potential. While Przybytek et al. do not attach a rigorous statistical interpretation to their “uncertainty,” we believe that it is reasonable to treat it as an expanded uncertainty with coverage factor k = 2, which corresponds to a 95 % confidence limit. For calculations with 3He, a small adjustment (negligible in the context of this work) was made to scale the adiabatic correction to the pair potential [9] to account for the different mass.
For the nonadditive three-body potential of helium, we use the FCI potential of Cencek et al. [11]. This potential is stated to have a relative uncertainty of 2 %, which again we interpret as an expanded uncertainty at the k = 2 level. For our uncertainty analysis, we construct perturbed three-body potentials FCI− (obtained by multiplying the corresponding potential by 1.02 where it is negative and by 0.98 where it is positive) and FCI+ (multiplying by 0.98 where it is negative and by 1.02 where it is positive).
3. Calculation Methods
3.1 Third Density Virial Coefficient
It has been shown in Refs. [4] and [12] that the second virial coefficient B(T) and the third virial coefficient C(T) for a quantum system obeying Boltzmann statistics can be written as
| (2) |
| (3) |
where NA is Avogadro’s constant, β = 1/kBT, and the effective two-body and three-body potentials and are given by the following path-integral expressions:
| (4) |
| (5) |
where U2(r) and V3(r1,r2,r3) are the two-body and three-body potential energies, respectively, and m is the particle mass. In Eq. (5), the position of particle 3 in the τ = 0 imaginary-time slice has been fixed at the origin of the coordinate system, due to the translational invariance of the integrand. The variables r1 and r2 reduce to the position of particles 1 and 2, respectively, in the classical limit, that is, when T is so high that the paths xk(τ) (k = 1, 2, 3) contributing most to the path integrals shrink to a point. A similar procedure was followed for Eq. (4), where we used the translational invariance of the integrand to fix the position of particle 2 in the τ = 0 imaginary-time slice at the origin. The variable r in Eq. (4) denotes the position of particle 1 in the classical limit.
The three-body potential energy is given by
| (6) |
where U3(r1, r2, r3) denotes the non-additive part of the three-body potential energy and U2(r) is the pair potential. In Eqs. (4) and (5), the path integrals are performed over all closed paths that have the origin as endpoints, that is, paths x(τ) fulfilling the conditions x(0) = x(βħ) = 0. The path integrals are normalized in such a way that their discretized form reads [12]
| (7) |
where x(P+1) = x(1) = 0 and is the de Broglie wavelength of a particle with mass m. The integrand of the middle expression in Eq. (7) can be interpreted as the probability of having a ring polymer with P beads in the positions given by the coordinates x(1),…,x(P) [13]. In the following subsection, this quantity will be denoted as Fring.
At low temperatures where Boltzmann statistics is no longer a good approximation, the above equations must be extended to incorporate Bose-Einstein or Fermi-Dirac statistics. The details of this extension are given in Ref. [12], where it was shown that the incorporation of spin statistics is necessary for both isotopes of helium at temperatures below approximately 7 K.
The number of beads P was chosen as a function of temperature according to P = 7 + (1200 K)/T for 4He and P = 7 + (1800 K)/T for 3He, with the resulting P rounded to the nearest integer. Preliminary calculations showed that these choices for P provide converged results (well within the statistical uncertainty of the calculation) for C(T) throughout the range of temperatures spanned by the present work. The ring polymers were generated as described in Ref. [4]. As in Ref. [4], we used the VEGAS algorithm [14] for the numerical integration of Eq. (7). We averaged 256 independent calculations, each with 106 integration points, in order to obtain the final result and its statistical uncertainty. For low temperatures where spin statistics are significant, the additional non-Boltzmann terms required were calculated as described in Ref. [12] with 128 independent integrations.
3.2 Third Acoustic Virial Coefficient
The square of the speed of sound in a gas as a function of pressure on isotherms has the low-density expansion:
| (8) |
Here, u is the speed of sound; βa, γa, and δa are the temperature-dependent second, third, and fourth acoustic virial coefficients; M is the molar mass; and γ0 ≡ Cp/Cv is the ratio of the constant-pressure heat capacity to the constant-volume heat capacity in the ideal-gas state, which is exactly 5/3 for a monatomic gas. [The ideal-gas heat-capacity ratio γ0 should not be confused with the acoustic virial coefficient γa.] Insofar as γa is a second-order correction for non-ideality, it is analogous to the third density virial coefficient C. We choose to discuss RTγa instead of γa because RTγa has both the units and the order of magnitude of the more familiar third density virial coefficient C. Exact thermodynamic relations connect γa to the density virial coefficients B and C and their first two temperature derivatives [15]. These relations are:
| (9) |
where βa is related to the second density virial coefficient B(T) and its temperature derivatives by
| (10) |
and
| (11) |
| (12) |
For PIMC calculation of the acoustic virial coefficients, it is necessary to derive path-integral expressions for the temperature derivatives of the density virial coefficients. For this purpose, we use the derivatives of Eqs. (2) and (3) with respect to β = 1/kBT, together with the identities
| (13) |
| (14) |
In Eqs. (2) and (3), the second and third density virial coefficients are given as a sum of terms that involve the integral of products of ring-polymer probability distributions with Boltzmann factors of the interaction potential averaged along the path. Making use of the fact that , the derivatives of the ring-polymer probability distribution can be written as
| (15) |
where the last equality defines the quantity a. The Boltzmann factors of the potential along the paths quite generally have the form
| (16) |
whose β derivative is given by
| (17) |
where the last equality defines the quantity b.
Path-integral expressions for the temperature derivatives of B(T) and C(T) can then be derived with the use of Eqs. (15) and (17). For example, the first temperature derivative of B(T) can be written as
| (18) |
where Fring(1) is the probability distribution for the configurations of the first ring polymer, with a corresponding definition for the second, and a1 and a2 are the quantity a defined in Eq. (15) for the first and second ring polymer, respectively.
In the case of C(T), Eq. (18) can be modified to calculate the temperature derivatives of the terms appearing in Eq. (3), taking into account the fact that the potential in the definition of W is actually a three-body potential and that three ring polymers must be considered. As a consequence, there is another distribution probability Fring(3) for the third particle, as well as an integration over these ring-polymer configurations (that is,an additional factor in the integration measure). Moreover, a1 + a2 must be replaced by a1 + a2 + a3, and the integral over dr in Eq. (18) becomes an integration over dr1dr2 when calculating dC/dT.
To calculate the second temperature derivatives of the virial coefficients, we use Eq. (14) together with the relations
| (19) |
| (20) |
The final result for the second derivative of B(T) is
| (21) |
The second derivative of C(T) is given by a similar expression, after performing on Eq. (21) the same substitutions described above for the first derivative, together with replacing the term 3(P − 1) by 9(P − 1)/2.
The temperature derivatives of C(T) were used to calculate L(T) according to Eq. (11). The same PIMC methodology was used as described in Sec. 3.1; the values were obtained from 256 independent calculations with 106 integration steps each.
4. Results
4.1 Third Virial Coefficients
Table 1 shows our calculated C(T) for 4He. In addition to all the temperatures given in Ref. [4], Table 1 includes lower temperatures (including some corresponding to fixed points on the ITS-90 temperature scale) and a few additional intermediate temperatures. Spin statistics significantly affect C(T) below about 7 K; this is discussed in detail in Ref. [12], where we describe the method of incorporating these effects and show the size of the various exchange contributions at low temperatures for both 3He and 4He.
Table 1.
Third virial coefficients C(T) for 4He calculated in this work and our estimates (see Sec. 4.3) of their expanded (k = 2) uncertainties U(C)
|
T (K) |
C (cm6 · mol−2) |
U(C) (cm6 · mol−2) |
|---|---|---|
| 2.6 | 292. | 53. |
| 2.8 | 616. | 45. |
| 3 | 826. | 35. |
| 3.2 | 950. | 30. |
| 3.5 | 1050. | 24. |
| 3.7 | 1070. | 21. |
| 4.0 | 1086. | 17. |
| 4.2 | 1075. | 15. |
| 4.5 | 1047. | 13. |
| 5 | 987. | 10. |
| 6 | 854.8 | 6.2 |
| 7 | 744.5 | 4.2 |
| 8.5 | 620.7 | 3.2 |
| 10 | 530.1 | 2.3 |
| 12 | 449.9 | 1.5 |
| 13.8033 | 399.8 | 1.1 |
| 15 | 373.8 | 1.0 |
| 17 | 341.91 | 0.82 |
| 18.689 | 319.86 | 0.70 |
| 20 | 307.24 | 0.64 |
| 24.5561 | 273.84 | 0.47 |
| 30 | 248.75 | 0.37 |
| 35 | 233.56 | 0.31 |
| 40 | 222.08 | 0.27 |
| 50 | 205.75 | 0.21 |
| 63.15 | 190.87 | 0.17 |
| 75 | 180.81 | 0.15 |
| 83.806 | 174.59 | 0.14 |
| 100 | 164.84 | 0.12 |
| 120 | 155.06 | 0.10 |
| 140 | 146.846 | 0.092 |
| 170 | 136.791 | 0.082 |
| 200 | 128.427 | 0.074 |
| 223.152 | 122.916 | 0.070 |
| 235 | 120.266 | 0.068 |
| 250 | 117.223 | 0.067 |
| 273.16 | 112.847 | 0.064 |
| 293.15 | 109.426 | 0.062 |
| 302.915 | 107.822 | 0.062 |
| 325 | 104.493 | 0.060 |
| 350 | 100.997 | 0.058 |
| 375 | 97.793 | 0.057 |
| 400 | 94.837 | 0.056 |
| 429.75 | 91.598 | 0.055 |
| 450 | 89.552 | 0.054 |
| 500 | 84.934 | 0.053 |
| 550 | 80.885 | 0.051 |
| 600 | 77.285 | 0.050 |
| 650 | 74.039 | 0.050 |
| 700 | 71.104 | 0.049 |
| 750 | 68.427 | 0.048 |
| 800 | 65.994 | 0.048 |
| 900 | 61.661 | 0.047 |
| 1000 | 57.949 | 0.047 |
| 1200 | 51.857 | 0.046 |
| 1400 | 47.039 | 0.045 |
| 1600 | 43.114 | 0.045 |
| 1800 | 39.842 | 0.044 |
| 2000 | 37.063 | 0.044 |
| 2500 | 31.615 | 0.043 |
| 3000 | 27.610 | 0.042 |
| 4000 | 22.039 | 0.041 |
| 5000 | 18.317 | 0.039 |
| 7500 | 12.765 | 0.036 |
| 10000 | 9.664 | 0.034 |
The low-temperature values in Table 1 differ slightly from those given in Ref. [12]; we discovered a small error in our earlier implementation of the three-body potential and the values in Table 1 supersede those in Ref. [12]. These differences are smaller than the uncertainties of the calculated C(T), and the conclusions of Ref. [12] are not affected.
4.2 Third Acoustic Virial Coefficients
In Table 2, we show results for the third acoustic virial coefficient γa. Because the quantity actually calculated by PIMC is L (see Sec. 3.2 and Eqs. (9) and (11)), and because of the variation of the magnitude of γa with temperature, we tabulate the quantity RTγa (and its expanded uncertainty as discussed below). Calculation of RTγa via Eq. (9) requires values of B and βa, which we obtain from the work of Cencek et al. [9] and which have such small uncertainties that they can be considered exact in the context of these calculations of γa.
Table 2.
Third acoustic virial coefficients expressed as RTγa for 4He calculated by PIMC and our estimates of their expanded (k = 2) uncertainties U(C). Also shown are values calculated from the C(T) correlation Eq. (22)
| T (K) | RTγa (PIMC) (cm6 · mol−2) | U(RTγa) (cm6 · mol−2) | RTγa (Eq. 22) (cm6 · mol−2) |
|---|---|---|---|
| 3 | – | – | −13335. |
| 4 | – | – | −5250. |
| 5 | – | – | −2124. |
| 6 | – | – | −681. |
| 7 | – | – | 57. |
| 8 | – | – | 458. |
| 9 | – | – | 682. |
| 10 | – | – | 807 |
| 12 | – | – | 906. |
| 14 | – | – | 914. |
| 16 | – | – | 885. |
| 18 | – | – | 843. |
| 20 | 736. | 83. | 796. |
| 24.5561 | 715. | 51. | 695. |
| 30 | 590. | 34. | 592. |
| 40 | 455. | 18. | 454. |
| 50 | 366. | 12. | 360. |
| 63.15 | 269.9 | 7.8 | 276.4 |
| 75 | 222.9 | 6.0 | 223.9 |
| 83.806 | 192.9 | 4.8 | 193.9 |
| 100 | 152.7 | 3.3 | 151.9 |
| 120 | 113.4 | 2.8 | 115.4 |
| 140 | 88.0 | 2.2 | 89.3 |
| 170 | 62.4 | 1.8 | 61.9 |
| 200 | 42.8 | 1.4 | 43.1 |
| 223.152 | 32.3 | 1.2 | 32.3 |
| 235 | 27.8 | 1.1 | 27.6 |
| 250 | 22.5 | 1.1 | 22.4 |
| 273.16 | 15.82 | 0.88 | 15.61 |
| 293.15 | 10.18 | 0.93 | 10.71 |
| 302.915 | 8.18 | 0.79 | 8.59 |
| 325 | 3.90 | 0.75 | 4.32 |
| 350 | 0.07 | 0.73 | 0.25 |
| 375 | −3.90 | 0.65 | −3.19 |
| 400 | −6.03 | 0.57 | −6.12 |
| 429.75 | −9.27 | 0.52 | −9.06 |
| 450 | −11.39 | 0.50 | −10.79 |
| 500 | −14.19 | 0.46 | −14.31 |
| 550 | −17.65 | 0.40 | −17.02 |
| 600 | −19.31 | 0.43 | −19.12 |
| 650 | −20.90 | 0.36 | −20.79 |
| 700 | −21.93 | 0.34 | −22.11 |
| 750 | −22.93 | 0.32 | −23.17 |
| 800 | −23.98 | 0.32 | −24.02 |
| 900 | −25.27 | 0.26 | −25.26 |
| 1000 | −26.28 | 0.25 | −26.07 |
| 1200 | −26.99 | 0.23 | −26.87 |
| 1400 | −27.13 | 0.21 | −27.07 |
| 1600 | −27.13 | 0.19 | −26.96 |
| 1800 | −26.77 | 0.18 | −26.68 |
| 2000 | −26.40 | 0.17 | −26.30 |
| 2500 | −25.24 | 0.14 | −25.19 |
| 5000 | −20.27 | 0.11 | −20.25 |
| 10000 | −14.58 | 0.09 | −14.72 |
The uncertainty in the path-integral calculation of γa becomes quite large at low temperatures, which is why PIMC values at lower temperatures are not reported in Table 2. This is due to the statistical uncertainty of the Monte Carlo integration for L; the convergence behavior of this integration is much worse than that for C(T). The reason for this difference is not completely clear, but it may be due to the fact that the quantity a that is averaged in the calculation of dC/dT [see Eq. (15)] is the so-called thermodynamic estimator of the kinetic energy. This estimator is known to be characterized by a large variance, and therefore long computations are needed to evaluate its average value with small uncertainty [16]. Moreover, the second temperature derivative needed for calculation of the acoustic virial coefficients might add further statistical noise to the calculation.
It is also possible to calculate γa from a correlation of C(T), as given in Sec. 4.4, by differentiating the correlation to produce dC/dT and d2C/dT2 as required in Eq. (11). The quantities involving B can again be obtained from the work of Cencek et al. [9]. Values of RTγa calculated in this manner are also shown in Table 2. They are consistent with the values calculated directly by PIMC.
4.3 Uncertainty Analysis
The analysis of uncertainty in C(T) was similar but not identical to that described in Ref. [4]. The contributing factors are the uncertainty in the pair potential, the uncertainty in the three-body potential, and the uncertainty in the convergence of the PIMC calculation.
The standard uncertainty due to PIMC convergence was estimated as the standard deviation of the mean from the 256 independent Monte Carlo runs.
The contributions due to the uncertainties in the potentials were evaluated by calculating C(T) with perturbed upper- and lower-bound versions of the potentials as described in Sec. 2. In order to avoid noise introduced by the PIMC convergence uncertainty, these calculations were performed with the semiclassical method described in Sec. 3.1 of Ref. [4], which was shown to be fairly accurate down to about 50 K. This approach to estimating uncertainty is adequate even at lower temperatures where the semiclassical values of C(T) are no longer very accurate, since the needed quantity is not C(T) itself but rather the difference between C(T) calculated from the upper perturbed potential and C(T) calculated from the lower perturbed potential.
Below 20 K, the semiclassical results deviate sufficiently from reality that we no longer trust them for uncertainty analysis. Instead, we observe that the uncertainty due to the potentials increases slowly and smoothly as the temperature is reduced, while the statistical uncertainty of the PIMC calculation increases more quickly. Because of these trends, the contribution of the potential uncertainty, which is our largest uncertainty component above 40 K, is roughly 60 % as large as the PIMC convergence component at 20 K. It is reasonable to assume that this trend continues, so that the uncertainty from the potentials will be less than 60 % of that from the PIMC convergence at lower temperatures. Therefore, we make the conservative estimate that the potential component of the uncertainty is 60 % of that from the PIMC convergence at all temperatures below 20 K.
The last column of Table 1 shows the resulting expanded uncertainties U(C) with coverage factor k = 2. For purposes of illustration, we summarize the uncertainty calculation for the point at 273.16 K. The standard uncertainty of the PIMC integration is 0.0069 cm6 · mol−2. The standard uncertainty due to the uncertainty of the two-body potential is 0.0042 cm6 · mol−2 (1/4 of the difference between C(T) calculated semiclassically with the upper- and lower-bound pair potentials, with the three-body potential of Ref. [11] used in each case). The standard uncertainty due to the three-body potential, computed analogously with perturbed three-body potentials, is 0.0311 cm6 · mol−2. These are combined in quadrature to yield a standard uncertainty u(C) = 0.0321 cm6 · mol−2, which when multiplied by two yields an expanded uncertainty U(C) of 0.064 cm6 · mol−2.
The uncertainty in the acoustic third virial coefficient, shown in Table 2, is computed analogously. In this case, the analysis is less rigorous because the perturbed potentials do not necessarily define upper and lower bounds for the temperature derivatives of C that contribute to γa. However, at all but the highest temperatures (above 2000 K), the uncertainty in γa is dominated by the convergence uncertainty in the PIMC calculations, so the expanded uncertainties shown in Table 2 should be good estimates.
4.4 Correlation for Results
We correlated the results for C(T) in Table 1 as a function of temperature:
| (22) |
where T* = T/(100 K) and the parameters ai and bi are given in Table 3. Equation (22) reproduces the values in Table 1 within tolerances smaller than their expanded uncertainties U(C); the fit is much closer than U(C) at high temperatures where the uncertainty is dominated by the Type B contribution from the uncertainty of the potentials. It covers the entire range from 2.6 K to 10 000 K, but should not be extrapolated outside this range. It may be differentiated to obtain dC/dT and d2C/dT 2, which can be used for calculation of acoustic virial coefficients as discussed in Sec. 4.2.
Table 3.
Coefficients for Eq. (22) for the third virial coefficient of helium
| i | ai | bi |
|---|---|---|
| 1 | 177.98 | −0.15 |
| 2 | −494.87 | −0.25 |
| 3 | 849.84 | −0.50 |
| 4 | −1003.30 | −0.95 |
| 5 | 635.18 | −1.07 |
| 6 | −0.035 012 | −3.15 |
It is also convenient to have a continuous function for the expanded uncertainty U (C). This will naturally be approximate, as there is significant noise in the uncertainties given in Table 1. U(C) can be represented reasonably well as a function of temperature over the entire range of Table 1 by
| (23) |
where τ = log10(T/K).
4.5 Comparison With Experiment for C(T)
Extensive comparisons with experimental C(T) data were given in Ref. [4], demonstrating that the uncertainties of calculated C(T) were much smaller than those obtained from experiment. Since our new values are within the expanded uncertainties of those calculated previously, we do not repeat all the comparisons because the figures would look nearly identical to those in Ref. [4]. Instead, we limit our comparisons to the important range near room temperature and to the low-temperature range that was not covered in Ref. [4].
In Fig. 1, our results are compared to those from the two most widely used experimental sources for C(T) [17,18] at temperatures from 250 K to 325 K. The error bars on the experimental points represent expanded uncertainties with coverage factor k = 2, while the expanded uncertainties on our calculated points (see Table 1) are smaller than the size of the symbols. Our calculations are fully consistent with the experimental data, but have smaller uncertainties by factors of approximately 50.
Fig. 1.
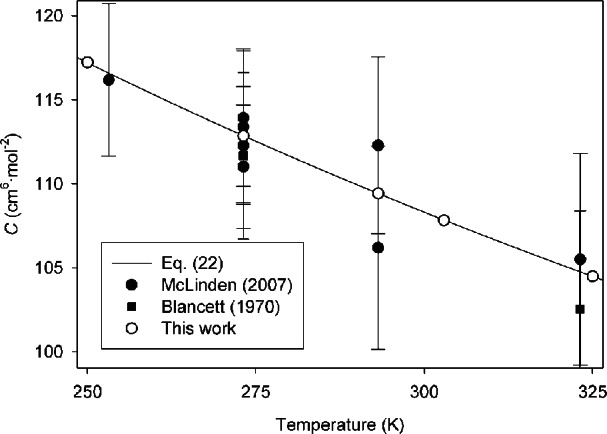
Comparison of C(T) for 4He calculated in this work with experimental values at near-ambient temperatures. Error bars on experimental points represent expanded uncertainties with coverage factor k = 2; uncertainties for this work (see Table 1) are not shown because the error bars would be smaller than the symbols.
In Fig. 2, we compare our calculated C(T) with the available experimental data below 40 K [19–24]. Error bars drawn on the points from this work represent expanded uncertainties U(C) from Table 1; they are not drawn above 5 K because they would be smaller than the size of the symbols. For clarity, we do not draw error bars for the experimental points; in some sources [19,20] these were not reported and in the others they were usually quite large (on the order of hundreds of cm6 · mol−2), often extending off the scale of Fig. 2. Gaiser et al. [24] described their data obtained by dielectric-constant gas thermometry from 3.7 K to 36 K with a smooth function for C(T), which we show as a dashed line on Fig. 2. From a figure in Ref. [24], it appears that their expanded (k = 2) uncertainties would be on the order of 20 cm6 · mol−2 over most of this range, becoming somewhat larger at the lowest temperatures.
Fig. 2.
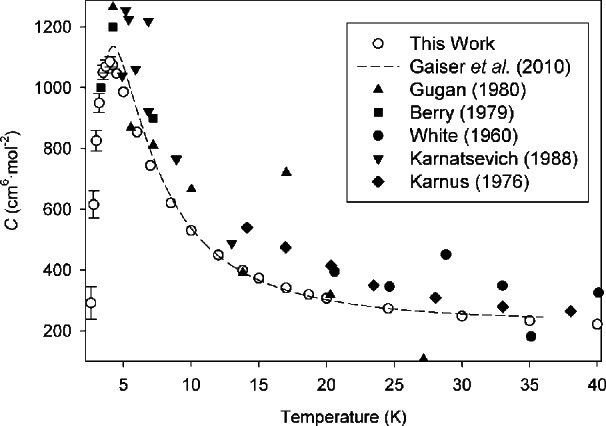
Comparison of C(T) for 4He calculated in this work with experimental values at low temperatures. Error bars on calculated points represent expanded uncertainties with coverage factor k = 2 (see Table 1), and are not shown when they would be smaller than the symbol size. Uncertainties for experimental points are not shown for clarity (see text).
Our results are generally consistent with the older experimental sources [19–23] within their scatter and uncertainties. We are for the most part in good agreement with the recent results of Gaiser et al. [24], with moderate disagreement at the low end of their temperature range. To examine this more closely, in Fig. 3 we plot the difference between the function of Gaiser et al. and our results as correlated by Eq. (22); Fig. 3 also shows our calculated PIMC points to demonstrate that Eq. (22) reproduces our results within their uncertainties. Our results agree with Gaiser et al. within mutual expanded uncertainties except between approximately 4 K and 8 K. It is possible that the functional form assumed for C(T) by Gaiser et al. [24] is not the right shape to represent this system.
Fig. 3.
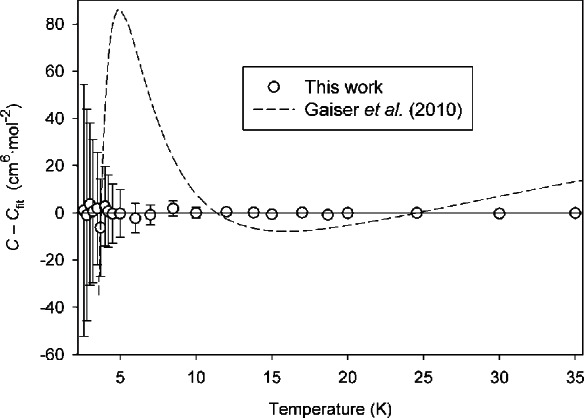
Deviation of PIMC results and of low-temperature C(T) data of Gaiser et al. [24] from fitted C(T) as given by Eq. (22).
4.6 Comparison With Experiment for γa
In this section, we compare our results for RTγa with measurements spanning the temperature range 3 K to 423 K. In this range, RTγa has a strong temperature dependence; it increases from approximately −13 000 cm6 · mol−2 at 3 K to approximately 900 cm6 · mol−2 near 14 K and then decreases to −9 cm6 · mol−2 at 423 K. Throughout most of this range, the uncertainty of our PIMC values of RTγa is on the order of 0.5 % to 3 %. Because of the wide range and precision required, we do not compare our results with measurements on a conventional graph. Instead, we have plotted the quantity 10−3(T/K)1.5 × RTγa, where the exponent 1.5 was chosen so that the range of the product 10−3(T/K)1.5 × RTγa in the interval from 3 K to 423 K is much smaller than the range of RTγa (see Fig. 4).
Fig. 4.
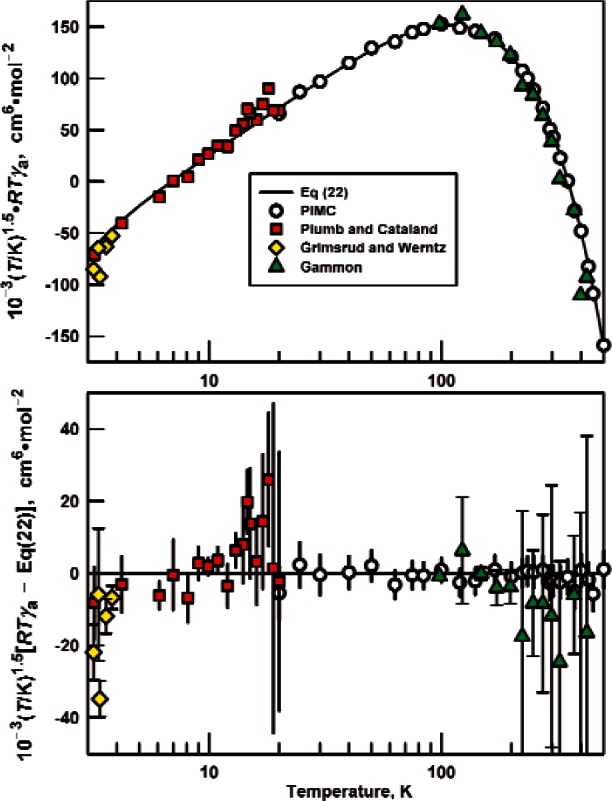
Comparison with experimental results of third acoustic virial coefficients γa for 4He calculated in this work both directly with path-integral Monte Carlo (PIMC), and with γa calculated with the use of derivatives of the C(T) correlation Eq. (22).
We examined the speed-of-sound data for 4He published in archival journals and found three publications from which we could determine accurate values of γa [25–27]. Remarkably, the most recent of these publications is 35 years old. Thus, these studies did not benefit from the dramatic reduction in the uncertainty of speed-of-sound measurements that acoustic thermometry has achieved during the past 20 years [3, 28–30].
Gammon [25] measured the speed of sound of 4He on 14 isotherms spanning the temperature range 98 K to 423 K at intervals of 25 K and spanning the pressure range 10 atm to 150 atm at intervals of 10 atm (1 atm = 0.101 325 MPa). Gammon correlated his data using a classical model He-He pair potential. From his correlation, he identified the isotherm at 348 K and 10 other isolated measurements as outliers. We ignored Gammon’s isolated outliers and fit the remaining data on each isotherm, including 348 K, with the function
| (24) |
In Eq. (24), we define Za ≡ Mu2/(γ0RTlab) as the square of the speed of sound divided by its ideal-gas value, and we calculated it from Gammon’s tabulated values of u2. The values of Za have the narrow range 1 to 1.38; therefore, we weighted every data point on each isotherm equally. We took βa from Cencek et al. [9], and we fitted the parameters T/Tlab, γa/(RTlab), and, when they are statistically unequal to zero, δa/(RTlab) and εa/(RTlab). [Here, T is the thermodynamic temperature of each isotherm and Tlab is the temperature reported by Gammon after adjustment for the changes in the internationally accepted temperature scale. The parameter T/Tlab also accounts for possible changes in M/γ0 that would occur if there were impurities in the helium.] Seven of Gammon’s 14 isotherms (98 K, 148 K, 173 K, 198 K, 248 K, 273 K, and 373 K) were very well behaved; that is, the deviations from a fit with an appropriate number of terms had no obvious pressure dependence. The standard deviation of Za − βap/(RTlab) from the fits, averaged over these isotherms, was 0.000 014. For the remaining isotherms, the deviations from the fits are neither random nor have single, outlying points. Therefore, we are unable to rigorously estimate the uncertainties of γa/RT. [We confirmed Gammon’s identification of the 348 K isotherm as anomalous because a satisfactory fit required the term δap3/(RTlab) even though the adjacent isotherms (323 K and 373 K) did not.] For the 13 isotherms (excluding 348 K), we estimated the standard uncertainty u(γa/RT) by multiplying the result of the fitting routine by (χ 2/N)1/2, where N is the number of degrees of freedom and χ 2 is the sum of the squares of the deviations of the data from the function fitted to it. All of the tabulated (Table 4) uncertainties reflect multiplication of u(RTγa) by an additional factor of two to approximate a 95 % confidence limit.
Table 4.
Third acoustic virial coefficient for 4He and its expanded (k = 2) uncertainty from the data of Gammon [25], excluding the isotherm at 348 K. Asterisks indicate fits including additional terms, as discussed in the text
|
T K |
RTγa cm6·mol−2 |
U(RTγa) cm6·mol−2 |
(RTγa)* cm6·mol−2 |
[U(RTγa)]* cm6·mol−2 |
|---|---|---|---|---|
| 98.15 | 153.2a | 1.0 | 155.1b | 2.5 |
| 123.16 | 106.0a,c | 6.3 | 115.3b | 10.5 |
| 148.16 | 77.5a | 1.0 | 80.7b | 2.5 |
| 173.16 | 57.8a | 2.1 | 57.9b | 8.0 |
| 198.16 | 32.4 | 4.1 | 42.8a | 1.6 |
| 223.16 | 22.4 | 2.3 | 27.0a | 10.2 |
| 248.16 | 17.1 | 0.9 | 20.9a | 3.7 |
| 273.15 | 8.2 | 1.3 | 13.8a | 5.3 |
| 298.15 | 7.3 | 6.9 | 21.2a | 27.4 |
| 323.13 | 0.4 | 4.7 | ||
| 373.13 | −3.8 | 11.9 | ||
| 398.15 | −13.5 | 40.5 | ||
| 423.15 | −10.4 | 26.0 |
Fit included the term δap3 / (RTlab).
Fit included the terms δap3 / (RTlab) and εap4 / (RTlab).
Not recommended.
The values of RTγa and their expanded uncertainties U(RTγa) resulting from fitting Gammon’s data are displayed in Fig. 4 and Table 4. Our calculations and Gammon's data agree within combined uncertainties, even though Gammon’s values of RTγa are more negative than our calculated values near the upper end of his temperature range. The uncertainties from fitting acoustic data will be underestimated if they do not account for the bias introduced by truncating the virial expansion. We crudely estimate the effect of truncation by comparing the 2nd and 4th columns in Table 4. For Gammon’s isotherms at 98 K, 123 K, 148 K, and 173 K, Table 4 compares RTγa obtained with and without the term εap4/(RTlab) in Eq. (24). The two values of RTγa agree within combined uncertainties. Table 4 also compares values of RTγa obtained with and without the term δap3/(RTlab) on the isotherms 198 K through 298 K. Except at 298 K, the two values of RTγa on each isotherm are mutually consistent. Above 298 K, δa was zero, within its uncertainty; however, the values of RTγa could be influenced by contributions from δa. We verified that the uncertainties of the values of a βa from Cencek et al. [9] did not contribute significantly to the uncertainty of γa.
Plumb and Cataland [27] measured the speed of sound in 4He on 21 isotherms from 2.3 K to 20 K for the purpose of determining the thermodynamic temperature T. As is often done in acoustic thermometry, Plumb and Cataland deliberately restricted their data to low densities; therefore, they were unable to determine meaningful values of γa. Because we have βa from Cencek et al. [9], we were able to determine values of γa on all of the isotherms except those at 5 K, 2.8 K, and 2.3 K. For each isotherm, the values of δa and εa in Eq. (24) were set equal to zero, and the data were weighted equally. The results are displayed on Fig. 4 and in Table 5.
Table 5.
Third acoustic virial coefficient for 4He and its expanded (k = 2) uncertainty from the data of Grimsrud and Werntz [26] and from Plumb and Cataland [27]
|
T K |
RTγa cm6·mol−2 |
U(RTγa) cm6·mol−2 |
|---|---|---|
| Grimsrud and Werntz [26] | ||
| 3.816 | −7100 | 440 |
| 3.595 | −9300 | 700 |
| 3.379 | −14800 | 790 |
| 3.337 | −10600 | 3000 |
| 3.182 | −15000 | 1400 |
| 2.978 | −16400 | 1300 |
| 2.671 | −19500 | 4300 |
| 2.13 | −46000 | 7500 |
| Plumb and Cataland [27] | ||
| 20 | 770 | 400 |
| 18.9 | 840 | 560 |
| 18 | 1180 | 240 |
| 17 | 1070 | 270 |
| 16 | 940 | 190 |
| 15 | 1140 | 260 |
| 14.6 | 1260 | 160 |
| 14 | 1070 | 210 |
| 13 | 1050 | 100 |
| 12 | 820 | 140 |
| 10.9 | 970 | 110 |
| 9.9 | 854 | 75 |
| 9 | 780 | 170 |
| 8.1 | 190 | 300 |
| 7 | 30 | 530 |
| 6.1 | −990 | 260 |
| 4.2 | −4740 | 910 |
| 3.2 | −12400 | 1800 |
| 5 | 1400 | 5100 |
Grimsrud and Werntz [26] measured the speed of sound in 4He on eight isotherms from 2.13 K to 3.816 K. They fitted their data by, in effect, adjusting T/Tlab, βa, and γa. When analyzing their data, we weighted each measurement using the uncertainties that they tabulated. Because we fixed values of βa from Cencek et al. [9], we were able to determine values of γa with roughly 1/5 the uncertainty achieved by Grimsrud and Werntz. These values are also shown in Table 5 and on Fig. 4. The values of RTγa from Grimsrud and Werntz are systematically more negative than our calculated values, particularly at the lowest temperatures where, for reasons discussed in the next section, the measurements may be more accurate than our calculations.
In the narrow region of overlap, the data of Grimsrud and Werntz [26] are consistent with the data of Plumb and Cataland [27]. As the temperature decreases, both sets of data tend towards values of RTγa smaller than those derived from our Eq. (22).
Additional values for γa derived from acoustic experiments between 2.3 K and 34 K were reported in a conference proceeding by Plumb [31]. Unfortunately, the actual measured data were never reported, so we were not able to apply new high-accuracy values of βa [9] to obtain values of γa consistent with the best current knowledge, as we did for Refs. [25–27]. We therefore do not show the data from Ref. [31] in Fig. 4, but we note that the reported values of γa are generally consistent with our calculated values within the reported uncertainties of Ref. [31]. Our calculated values are also consistent within mutual uncertainties with a recent experimental result for γa at 273.16 K by Gavioso et al. [32].
4.7 Results for 3He
While the primary focus of this work was on the common isotope 4He, the same methods can be used for 3He, which is of interest for cryogenic temperature metrology. Table 6 presents values of C(T) for 3He, along with their expanded uncertainties. More extensive discussion of the 3He calculations at low temperatures, along with comparison with the limited experimental data, is given in Ref. [12]. We note that, in addition to the data sources below 10 K examined in Ref. [12], values of C(T) for 3He between 14 K and 60 K were reported by Karnus [20]; these seem to be systematically high below about 30 K, similar to the data for 4He from the same study shown in Fig. 2.
Table 6.
Third virial coefficients C(T) for 3He calculated in this work and our estimates (see Sec. 4.3) of their expanded (k = 2) uncertainties U(C)
|
T K |
C cm6·mol−2 |
U(C) cm6·mol−2 |
|---|---|---|
| 2.6 | 1343. | 62. |
| 2.8 | 1436. | 46. |
| 3 | 1464. | 41. |
| 3.2 | 1462. | 36. |
| 3.5 | 1418. | 29. |
| 3.7 | 1366. | 27. |
| 4.0 | 1298. | 22. |
| 4.2 | 1257. | 19. |
| 4.5 | 1175 | 16. |
| 5 | 1071. | 12. |
| 6 | 895.0 | 9.1 |
| 7 | 775.6 | 6.6 |
| 8.5 | 644.9 | 4.4 |
| 10 | 553.7 | 3.4 |
| 12 | 475.3 | 2.4 |
| 13.8033 | 426.5 | 1.7 |
| 15 | 401.8 | 1.6 |
| 17 | 367.6 | 1.3 |
| 18.689 | 346.9 | 1.0 |
| 20 | 333.53 | 0.87 |
| 24.5561 | 296.76 | 0.67 |
| 30 | 268.91 | 0.52 |
| 35 | 251.22 | 0.41 |
| 50 | 218.56 | 0.26 |
| 100 | 170.63 | 0.13 |
| 150 | 146.71 | 0.10 |
| 200 | 130.762 | 0.081 |
| 273.16 | 114.365 | 0.068 |
| 300 | 109.627 | 0.065 |
| 400 | 95.707 | 0.058 |
| 500 | 85.563 | 0.054 |
| 750 | 68.758 | 0.049 |
| 1000 | 58.168 | 0.047 |
| 1500 | 45.083 | 0.045 |
| 2000 | 37.130 | 0.044 |
For the same reason discussed for 4He in Sec. 4.1, the values in Table 6 differ slightly from those reported in Ref. [12], and the new values in Table 6 should be preferred.
4.8 Accuracy of Semiclassical Calculations
In Ref. [4], we assessed the accuracy of a first-order semiclassical calculation of C(T), concluding that the semiclassical results were adequate (in the sense of reproducing the fully quantum C(T) from PIMC calculations within their expanded uncertainties at the k = 2 level) at temperatures above about 120 K. That conclusion can be reassessed in light of the reduced uncertainties achieved in this work. The semiclassical C(T) deviates from our new PIMC results by more than the expanded uncertainty of our new results at temperatures below about 280 K. For example, at 273.16 K, the semiclassical calculation yields 112.939 cm6 · mol−2, which exceeds the PIMC value by slightly more than the expanded uncertainty given in Table 1.
5. Discussion
The availability of new, state-of-the-art pair and three-body potentials has allowed us to calculate C(T) for helium with uncertainties approximately one-fourth that of our previous work [4]. In addition, we have extended the temperature range of our results, which previously had a lower bound of 24.5661 K, to 2.6 K. We also calculated C(T) for the 3He isotope. The incorporation of exchange effects (non-Boltzmann statistics) was necessary to achieve accurate results for both isotopes below about 7 K.
Within the temperature range covered in our previous work [4], our new results given in Table 1 are consistent with our previous results. The present C(T) are somewhat higher than those calculated previously, typically by an amount near one-half of the expanded (k = 2) uncertainties of the results in Ref. [4]. This change is primarily due to the more accurate three-body potential used here [11], and is consistent with a few preliminary calculations using the potential of Ref. [11] that were reported in Ref. [4].
We extended the PIMC method to calculate the third acoustic virial coefficient γa; our results are consistent with values of γa obtained from experimental acoustic data, and have smaller uncertainties above 18 K. However, the statistical uncertainty in the PIMC calculation of γa becomes quite large at lower temperatures. We believe more reliable values are obtained by differentiating Eq. (22) to obtain the temperature derivatives of C and then using those values in Eq. (11). Values derived in that way are consistent with experimental results for γa in the entire range of our C(T) correlation, with the possible exception of the lowest temperatures (below 4 K), where the experimental data lie slightly below our results. One might expect this approach to be less reliable at the low end of the temperature range of Eq. (22), where the uncertainty in the points to which the C(T) function was fitted is larger and dC/dT and d2C/dT2 derived from Eq. (22) would have relatively large uncertainties.
At low temperatures, the uncertainty of the present results for C(T) is dominated by the statistical uncertainty of the PIMC integration. This could, of course, be improved somewhat simply by applying more computing resources. Above about 35 K, the uncertainty from the three-body potential becomes the largest contribution. Therefore, for metrology near room temperature, further improvement in the three-body potential would be desirable; a reduction in by a factor of two in the uncertainty of the three-body potential would produce a reduction by almost that factor in the uncertainty of C(T) at room temperature.
The present results could also be extended to lower temperatures at the expense of more computer time. This could have some application in primary thermometry at these temperatures.
One could perform similar calculations for the “cross” third virial coefficients that characterize isotopic mixtures; these would be C334(T), representing interactions among two 3He atoms and one 4He atom, and the similarly defined C344(T). Because the natural abundance of 3He is tiny, contributions from these coefficients would be insignificant for experiments with naturally occurring helium. We are not aware of any situation in metrology where these mixture coefficients would be useful, but, if needed, the extension of the methods used here to the mixture coefficients would be straightforward.
Another quantity of interest is the fourth virial coefficient D(T), whose calculation would be a straightforward extension of our methods. With the reduction in the uncertainty of C(T) achieved in the present work, D(T) will become the largest uncertainty in some situations in metrology [7]. In principle, calculating D(T) requires not only pair and three-body potentials but also the nonadditive four-body potential. Such a potential would be difficult to develop, but the relatively small size of the three-body effects in helium suggests that one might be able to assume the nonadditive four-body effects were negligible. It should be possible to test that assumption by performing a few high-level ab initio calculations for simple assemblies of four helium atoms (such as tetrahedrons or squares). The calculation for D(T) would require major computing resources because of the increased dimensionality of the integral, but such a calculation may at least be feasible near room temperature where the number of beads in the ring polymers in the PIMC procedure would be relatively small.
Acknowledgments
We thank K. Szalewicz and J. B. Mehl for providing information (in some cases prior to publication) on the helium pair potential and properties calculated from it, C. Gaiser for advice on helium C(T) data at low temperatures, K. R. Shaul and D. A. Kofke for performing classical calculations that helped us discover a small error in our previous work, and E. W. Lemmon for fitting Eq. (22). The path-integral Monte Carlo calculations were performed on the computing cluster KORE at Fondazione Bruno Kessler.
Biography
About the authors: Giovanni Garberoglio is a physicist and a member of the Interdisciplinary Laboratory for Computational Science (LISC), a collaboration between Fondazione Bruno Kessler and the University of Trento, Italy. Michael Moldover is a physicist and a NIST Fellow; he is the Leader of the Fluid Metrology Group in the Temperature, Pressure, and Flow Metrology Division of the NIST Physical Measurement Laboratory. Allan Harvey is a chemical engineer in the Theory and Modeling of Fluids Group in the Thermophysical Properties Division of the NIST Material Measurement Laboratory. The National Institute of Standards and Technology is an agency of the U.S. Department of Commerce.
Contributor Information
Giovanni Garberoglio, Email: garberoglio@fbk.eu.
Michael R. Moldover, Email: michael.moldover@nist.gov.
Allan H. Harvey, Email: allan.harvey@nist.gov.
6. References
- [1].Schmidt JW, Gavioso RM, May EF, Moldover MR. Polarizability of Helium and Gas Metrology. Phys Rev Lett. 2007;98:254504. doi: 10.1103/PhysRevLett.98.254504. [DOI] [PubMed] [Google Scholar]
- [2].Fellmuth B, Gaiser Ch, Fischer J. Determination of the Boltzmann Constant—Status and Prospects. Meas Sci Technol. 2006;17:R145. [Google Scholar]
- [3].Pitre L, Moldover MR, Tew WL. Acoustic thermometry: new results from 273 K to 77 K and progress towards 4 K. Metrologia. 2006;43:142. [Google Scholar]
- [4].Garberoglio G, Harvey AH. First-Principles Calculation of the Third Virial Coefficient of Helium. Res Natl Inst Stand Technol. 2009;114:249. doi: 10.6028/jres.114.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Hurly JJ, Mehl JB. 4He Thermophysical Properties: New Ab Initio Calculations. J Res Natl Inst Stand Technol. 2007;112:75. doi: 10.6028/jres.112.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Cencek W, Jeziorska M, Akin-Ojo O, Szalewicz K. Three-Body Contribution to the Helium Interaction Potential. J Phys Chem A. 2007;111:11311. doi: 10.1021/jp072106n. [DOI] [PubMed] [Google Scholar]
- [7].Moldover MR, McLinden MO. Using Ab Initio “Data” to Accurately Determine the Fourth Density Virial Coefficient of Helium. J Chem Thermodyn. 2010;42:1193. [Google Scholar]
- [8].Przybytek M, Cencek W, Komasa J, Łach G, Jeziorski B, Szalewicz K. Relativistic and Quantum Electrodynamics Effects in the Helium Pair Potential. Phys Rev Lett. 2010;104:183003. doi: 10.1103/PhysRevLett.104.183003. [DOI] [PubMed] [Google Scholar]
- [9].Cencek W, Przybytek M, Komasa J, Mehl JB, Jeziorski B, Szalewicz K. Effects of adiabatic, relativistic, and quantum electrodynamics interactions in helium dimer on thermophysical properties of helium. J Chem Phys. 2011 doi: 10.1063/1.4712218. to be submitted. [DOI] [PubMed] [Google Scholar]
- [10].Jeziorska M, Cencek W, Patkowski K, Jeziorski B, Szalewicz K. Pair potential for helium from symmetry-adapted perturbation theory calculations and from supermolecular data. J Chem Phys. 2007;127:124303. doi: 10.1063/1.2770721. [DOI] [PubMed] [Google Scholar]
- [11].Cencek W, Patkowski K, Szalewicz K. Full-configuration-interaction calculation of three-body nonadditive contribution to helium interaction potential. J Chem Phys. 2009;131:064105. doi: 10.1063/1.3204319. [DOI] [PubMed] [Google Scholar]
- [12].Garberoglio G, Harvey AH. Path-integral calculation of the third virial coefficient of quantum gases at low temperatures. J Chem Phys. 2011;134:134106. doi: 10.1063/1.3573564. [DOI] [PubMed] [Google Scholar]
- [13].Garberoglio G. Boltzmann bias grand canonical Monte Carlo. J Chem Phys. 2008;128:134109. doi: 10.1063/1.2883683. [DOI] [PubMed] [Google Scholar]
- [14].Galassi M, Davies J, Theiler J, Gough B, Jungman G, Booth M, Rossi F. GNU Scientific Library Reference Manual, Network Theory. (2nd edition) 2006 revised. http://www.gnu.org/software/gsl.
- [15].Gillis KA, Moldover MR. Practical Determination of Gas Densities from the Speed of Sound Using Square-Well Potentials. Int J Thermophys. 1996;17:1305. [Google Scholar]
- [16].Herman MF, Bruskin EJ, Berne BJ. On path integral Monte Carlo simulations. J Chem Phys. 1982;76:5150. [Google Scholar]
- [17].Blancett AL, Hall KR, Canfield FB. Isotherms for the He-Ar System at 50 °C, 0 °C and 50 °C up to 700 Atm. Physica. 1970;47:75. [Google Scholar]
- [18].McLinden MO, Lösch-Will C. Apparatus for wide-ranging, high-accuracy fluid (p,ρ,T) measurements based on a compact two-sinker densimeter. J Chem Thermodyn. 2007;39:507. [Google Scholar]
- [19].White D, Rubin T, Camky P, Johnston HL. The virial coefficients of helium from 20 to 300 °K. J Phys Chem. 1960;64:1607. [Google Scholar]
- [20].Karnus AI. Virial Coefficients and some Thermodynamic Quantities of the Helium Isotopes in Low Temperature Range. Ukr Fiz Zh. 1976;21:1179. [Google Scholar]
- [21].Berry KH. Measurements of the second and third virial coefficients of 4He in the range 2.6–27.1 K. Mol Phys. 1979;37:317. [Google Scholar]
- [22].Gugan D, Michel GW. Measurements of the polarizability and of the second and third virial coefficients of 4He in the range 4.2–27.1 K. Mol Phys. 1980;39:783. [Google Scholar]
- [23].Karnatsevich LV, Bogoyavlenskii IV, Titar LP. Virial coefficients of helium isotopes at low temperatures. Sov J Low Temp Phys. 1988;14:1. [Google Scholar]
- [24].Gaiser C, Fellmuth B, Haft N. Dielectric-Constant Gas-Thermometry Scale from 2.5 K to 36 K Applying 3He, 4He, and Neon in Different Temperature Ranges. Int J Thermophys. 2010;31:1428. [Google Scholar]
- [25].Gammon BE. The velocity of sound with derived state properties in helium at −175 to 150 °C with pressure to 150 atm. J Chem Phys. 1976;64:2556. [Google Scholar]
- [26].Grimsrud DT, Werntz JH. Measurements of the Velocity of Sound in He3 and He4 Gas at Low Temperatures with Implications for the Temperature Scale. Phys Rev. 1967;157:181. [Google Scholar]
- [27].Plumb H, Cataland G. Acoustical Thermometer and the National Bureau of Standards Provisional Temperature Scale 2–20 (1965) Metrologia. 1966;2:127. [Google Scholar]
- [28].Estrada-Alexanders AF, Trusler JPM. The speed of sound in gaseous argon at temperatures between 110 K and 450 K and at pressures up to 19 MPa. J Chem Thermodyn. 1995;27:1075. [Google Scholar]
- [29].Benedetto G, Gavioso RM, Spagnolo R, Marcarino P, Merlone A. Acoustic measurements of the thermodynamic temperature between the triple point of mercury and 380 K. Metrologia. 2004;41:74. [Google Scholar]
- [30].Ripple DC, Strouse GF, Moldover MR. Acoustic Thermometry Results from 271 K to 552 K. Int J Thermophys. 2007;28:1789. [Google Scholar]
- [31].Plumb HH. 4He second and third virial coefficients from acoustical isotherms: The Helmholtz-Kirchhoff correction at temperatures below 35 K. In: Schooley JF, editor. Temperature: Its Measurement and Control in Science and Industry. Vol. 5. American Institute of Physics; New York: 1982. pp. 77–88. Part 1. [Google Scholar]
- [32].Gavioso RM, Benedetto G, MadonnaRipa D, Giuliano Albo PA, Guianvarc’h C, Merlone A, Pitre L, Truong D, Moro F, Cuccaro R. Progress in INRiM Experiment for the Determination of the Boltzmann Constant with a Quasi-Spherical Resonator. Int J Thermophys. doi: 10.1007/s10765-011-1032-9. in press. [DOI] [Google Scholar]


