A Spatial Model of Fluid Recycling in the Airways of the Lung

Abstract

The genetic disease cystic fibrosis (CF) is a mutation in the cystic fibrosis transmembrane conductance regulator (CFTR) gene, and results in viscous mucus and impaired mucociliary clearance leading to chronic recurring pulmonary infections. Although extensive experimental research has been conducted over the last few decades, CF lung pathophysiology remains controversial. There are two competing explanations for the observed depletion of periciliary liquid (PCL) in CF lungs. The low volume hypothesis assumes fluid hyperabsorption through surface epithelia due to an over-active Epithelial Na⁺ Channel (ENaC), and the low secretion hypothesis assumes inspissated mucins secreted from glands due to lack of serous fluid secreted from gland acini.

We present a spatial mathematical model that reflects in vivo fluid recycling via submucosal gland (SMG) secretion, and absorption through surface epithelia. We then test the model in CF conditions by increasing ENaC open probability and decreasing SMG flux while simultaneously reducing CFTR open probability. Increasing ENaC activity only results in increased fluid absorption across surface epithelia, as seen in in vitro experiments. However, combining potential CF mechanisms results in markedly less fluid absorbed while providing the largest reduction in PCL volume, suggesting that a compromise in gland fluid secretion dominates over increased ENaC activity to decrease the amount of fluid transported transcellularly in CF lungs in vivo. Model results also indicate that a spatial model is necessary for an accurate calculation of total fluid transport, as the effects of spatial gradients can be severe, particularly in close proximity to the SMGs.

Introduction

The genetic disease cystic fibrosis (CF) results in an accumulation of mucus in many major organs, with more than 90% of mortality arising from lung complications (Quinton, 1990). A monolayer of predominantly ciliated epithelia line the inside of the lungs from the trachea to bronchioles, and are located underneath the Airway Surface Liquid (ASL); two mostly distinct layers consisting of serosal fluid from the cell surface to the tips of the cilia (the periciliary liquid or PCL) and above it, a layer of varying thickness consisting of a gel of mucins. The ASL has antimicrobial and antibacterial properties (J. J. Smith et al., 1996; Bals et al., 1998), and is maintained at an optimal volume through a balance of ion/water transport to maintain healthy hydration of the airways. Lung surface epithelia allow passive transport of fluid through leaky membranes and osmotic gradients, and active/passive ion transport through channels, exchangers and transporters located on cell membranes.

The mucus layer is a tangled macromolecular mesh comprising 90% gel-forming mucins such as MUC5AC and MUC5B secreted by goblet surface epithelia and cells from the gland mucous tubule (Button et al., 2012). The other 10% of the mesh consists primarily of tethered mucins MUC1, MUC4 and MUC16 that are attached to surface cells, and therefore densely pack the negatively-charged PCL fluid (Sheehan et al., 2007).

CF is a mutation in the gene for the protein cystic fibrosis transmembrane conductance regulator (CFTR). In healthy lungs, the CFTR transports Cl⁻ through cell membranes and is associated with water secretion that replenishes the ASL. CFTR dysfunction results in compromised mucociliary clearance which causes mucus accumulation and disrupts the natural innate defense molecules inherent in healthy serosal fluid. The mechanisms which increase mucus from a healthy volume are still unclear, and two main hypotheses attempt to explain this phenomenon.

In the low volume hypothesis, it is assumed that normal CFTR function inhibits the ENaC tonically, whereby the malfunction results in the hyper-absorption of PCL Na⁺ and water by the cell layer, thus depleting PCL fluid (Tarran et al., 2001, 2006; Matsui et al., 2000, 1998). Depleted or inspissated PCL causes cilia to become stuck, disrupting healthy mucociliary clearance mechanisms. The low secretion hypothesis assumes CFTR function is highest in serous acini located at the distal end of submucosal glands (SMG), where a defective CFTR results in reduced secretion of fluid (Shen et al., 1994; Wu et al., 2007; Salinas et al., 2005). This is due to compromised Cl⁻ secretion from the acini where Na⁺ generally follows via electroneutrality and subsequently fluid is secreted via osmosis.

The PCL is predominantly hydrated by fluid secreted from SMGs (Wu et al., 2007), which are found approximately once per 1 mm² (10⁶ μm²) of tracheal surface (Tos, 1970). Therefore, we have constructed a model to analyse how this spatial arrangement of fluid-secreting glands affects water fluxes and cellular/PCL ion concentrations, and to test the validity of the two hypotheses for CF conditions. As the amount of fluid above the cell distribution is paramount to maintaining healthy lung hydration, we have also constructed the model to predict PCL volume. We contend that fluid recycling is the important factor in considering CF lung epithelia, where fluid is secreted from the glands and reabsorbed across the cell layer. This assumption is derived from the facts that surface epithelia are primarily absorptive in basal conditions due to large amounts of fluid secreted from the glands into the ASL (≈ 1.5 L/d) (Kilburn, 1968; Widdicombe et al., 1997) and PCL evaporation rates are comparatively low (4.34 × 10⁻⁸L/m².s, estimated by Novotny & Jakobsson, 1996). Essentially, we demonstrate that the balance between the secretion and absorption of ions and water effectively controls airway hydration, and use this to predict cellular behaviour in vivo.

Previous mathematical models have thus far focused on time-dependent solutions and transepithelial water flux through singular, primarily water-secreting cells, all identical in nature. No spatial model has been constructed to our knowledge, and no model contains transport of the PCL as a whole. Although Warren et al. (2010) published a spatio-temporal model focused on the balance between fluid secretion from epithelia and evaporation from the airways, the epithelia in their model are secretory and model predictions indicate a dehydrated PCL without a significant contribution of fluid from either the glands or from some other source.

Model Construction

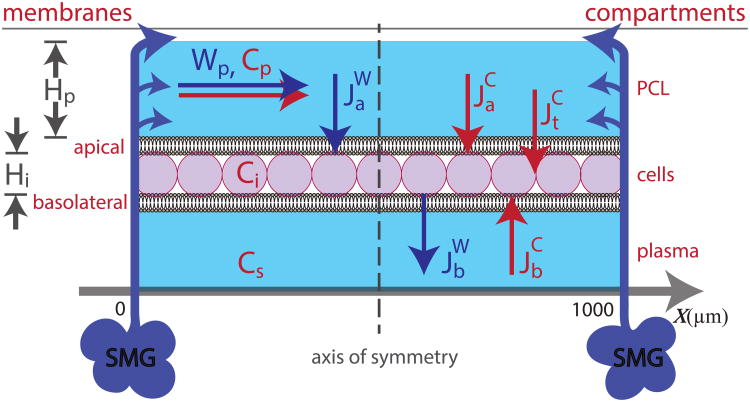
We consider a continuous distribution of absorptive epithelial cells between neighbouring submucosal glands in a one dimensional, three compartmental model. In order to model the effects of fluid secretion from the glands, we have included a term for lateral water movement in the PCL layer, W_p, as a volumetric flux. If we assume the area is square, we have a domain of 1000×1000 μm², indicating a linear boundary of x ∈ [0, 1000]. Water is secreted from the glands into the PCL, where it is translated into PCL water flux at the boundaries x = 0, 1000 μm, and renders boundary conditions for W_p. Fig. 1 shows water secreted from the glands entering the domain at the two boundaries, as indicated by the arrows. We assume secretions from the glands will push water inwards, forcing the flux to be zero in the middle of the domain due to symmetry. This effectively cuts our domain in half, creating a new boundary condition W_p(500 μm) = 0 μm/s, and therefore it is only necessary to solve the system numerically to x ∈ [0, 500].

Figure 1.

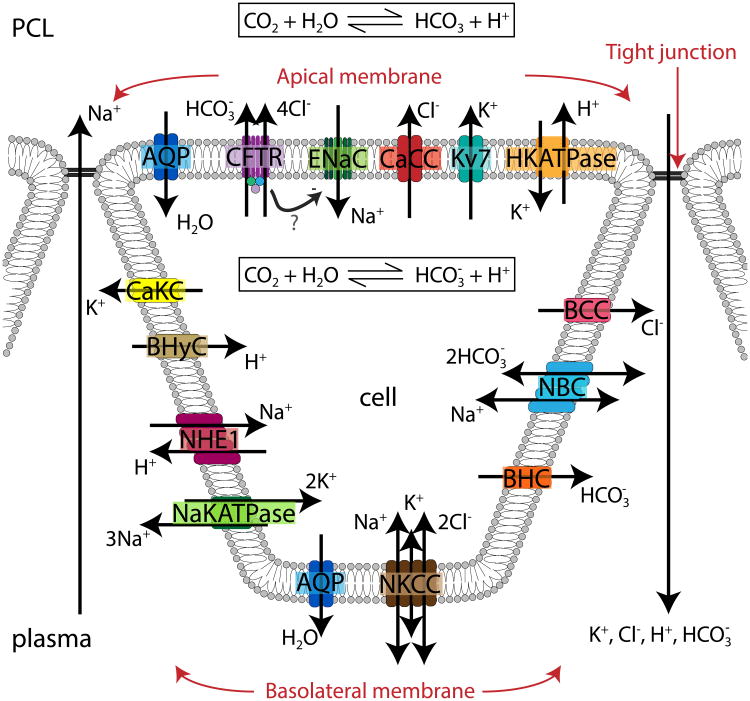
Schematic of full compartmental model with ionic and water fluxes over a distribution of ‘continuous’ cells in between secretions from submucosal glands (SMGs) at x = 0, 1000 μm. The glands secrete fluid at the boundaries of the domain and push the PCL inwards, which is then transported transcellularly. Ions flow into the cell via the apical or basolateral membrane and from the PCL directly to plasma via the tight junctions. W_p - PCL water flux, c_p - PCL ion concentration, c_i - cellular ion concentration, c_s - plasma ion concentration, H_p - PCL height, H_i - cellular height, $J_a^w$ - water flux through apical membrane, $J_b^w$ - water flux through basolateral membrane, $J_a^d$ - ionic flux through apical membrane, $J_b^d$ - ionic flux through basolateral membrane, $J_t^d$ - ionic flux through tight junction. Arrows denote positive flux direction, and we assume negligible thickness of cellular membrane.

The three compartments represent the PCL, cell and underlying serous bath (plasma) which are denoted by subscripts p, i and s, respectively. Water is driven across both apical and basolateral membranes due to osmotic gradients, which gives rise to changes in cell volume. The plasma located underneath the cell layer is considered to be an infinite bath, preserving constant ionic concentrations. Cellular and PCL compartments are assumed well stirred in the y-z direction.

Model Equations

Compartmental Volume

As we assume PCL water and cell volume are homogenous in the y-z direction, we therefore describe the PCL and cell ‘volume’ as one-dimensional heights. We assume H_p is constant over the spatial domain and although it may not be a good approximation, we do so for simplicity. If we assume otherwise, the time-dependent fluid layer could be modelled only with the equations of fluid mechanics (as well as constitutive equations for the flow of the viscous fluid in response to gradients in height), which is a model that is orders of magnitude more difficult and complex than the one presented here. Differential equations describing PCL height (H_p) and cell height (H_i) are derived using conservation of water mass and incompressibility:

$$\frac{\partial H_p}{\partial t}=-H_p\frac{\partial W_p}{\partial x}-J_a^w,$$ (1)

$$\frac{\partial H_i}{\partial t}=J_a^w-J_b^w,$$ (2)

where W_p is the PCL water flux (in units of μm/s) and measures the volume of water transported laterally above the epithelia, as shown in Fig. 1. Volumetric fluxes of water through the apical and basolateral cell membranes are represented by $J_a^w$ and $J_b^w$ (in units of μm.mM/s), respectively. The partial differential equation governing H_i represents the change in cellular height over the spatial distribution.

Ions

The change in ionic species concentration in PCL ( $c_p^j$) or cellular compartment ( $c_i^j$), is derived from conserving the number of ions, and in generic form is given by:

$$\frac{\partial }{\partial t}(H_p{c}_p^j)=H_p{\mathcal{D}}_{c_j}\frac{{\partial }^2{c}_p^j}{\partial x^2}-H_p\frac{\partial }{\partial x}(c_p^j{W}_p)-J_a^{c_j}-J_t^{c_j},$$ (3)

$$\frac{\partial }{\partial t}(H_i{c}_i^j)=J_a^{c_j}+J_b^{c_j},$$ (4)

where we have assumed the lateral velocity of ions in the PCL is equivalent to that of the water. The species included in this model are the ions Na⁺, K⁺, Cl⁻, ${\text{HCO}}_3^{-}$, H⁺, and the molecule CO₂. Ionic fluxes through the apical, basolateral, and tight junctional membranes are represented by $J_a^{c_j}$, $J_b^{c_j}$ and $J_t^{c_j}$ for ion species c_j. The diffusion coefficient is _cj for each ionic species. We assume that intercellular diffusion and advection of ions or water between cells via tight junctions contribute negligibly to PCL hydration, and thus are not included in model equations.

Membrane Potential

Each cell membrane is divided into apical and basolateral regions, and at each position along the epithelia, membrane potentials are described by Kirchoff's current law for a simple RC circuit with linear IV relationship:

$$A_a{C}_a\frac{d{V}_a}{\mathit{\text{dt}}}=-\sum _{j=1}^n{z}_j(I_a^{c_j}+I_t^{c_j}),$$ (5)

$$A_b{C}_b\frac{d{V}_b}{\mathit{\text{dt}}}=-\sum _{j=1}^n{z}_j(I_b^{c_j}-I_t^{c_j}),$$ (6)

$$V_t=V_a-V_b,$$ (7)

where the right-hand side of the differential equations represents the sum of the currents for each ionic species through respective cell membranes, multiplied by its valency. Currents through the tight junction ( $I_t^{c_j}$), contribute to changes in both membrane potentials. Apical and basolateral membrane areas are represented by A_a and A_b, respectively, and capacitances (C_a, C_b) are in units of capacitance per unit area. V_t is the transepithelial potential. Membrane potentials are measured from outside the cell to inside the cytoplasm, with the sign convention that positive current drives negative ions into the cell or from PCL to plasma.

Water Fluxes

Water is driven by the osmotic gradient between neighbouring compartments through aquaporins (AQP); water-specific membrane channel proteins. Evidence for apical AQP4 and basolateral AQP5 on membranes of ciliated epithelia is given in Fischbarg (2010). We assume negligible hydrostatic pressure:

$$J_a^w=L_a{V}_w({[{\text{Na}}^{+}]}_i+{[{\mathrm{K}}^{+}]}_i+{[{\text{Cl}}^{-}]}_i+{[{\text{HCO}}_3^{-}]}_i+{[{\mathrm{H}}^{+}]}_i+{[{\text{CO}}_2]}_i+\frac{X_i}{{\omega }_i}-{[{\text{Na}}^{+}]}_p-{[{\mathrm{K}}^{+}]}_p-{[{\text{Cl}}^{-}]}_p-{[{\text{HCO}}_3^{-}]}_p-{[{\mathrm{H}}^{+}]}_p-{[{\text{CO}}_2]}_p-\frac{X_p}{{\omega }_p}),$$ (8)

$$J_b^w=L_b{V}_w({[{\text{Na}}^{+}]}_s+{[{\mathrm{K}}^{+}]}_s+{[{\text{Cl}}^{-}]}_s+{[{\text{HCO}}_3^{-}]}_s+{[{\mathrm{H}}^{+}]}_s+{[{\text{CO}}_2]}_s+X_s-{[{\text{Na}}^{+}]}_i-{[{\mathrm{K}}^{+}]}_i-{[{\text{Cl}}^{-}]}_i-{[{\text{HCO}}_3^{-}]}_i-{[{\mathrm{H}}^{+}]}_i-{[{\text{CO}}_2]}_i-\frac{X_i}{{\omega }_i}),$$ (9)

where ω_p = H_pA_a and ${\omega }_i=H_i\left(\frac{A_a+A_b}{2}\right)$ are the volumes of the PCL and cell, respectively. L_a and L_b are the water permeabilities of the apical and basolateral membranes. We have included terms for impermeable ions in the PCL (X_p), cell (X_i) and plasma (X_s); all values are found by assuming electroneutrality. As plasma volume remains unchanged, X_s is in the same units as ionic concentrations, mM. V_w is the partial molal volume of water, and we have assumed the contribution of the partial molal volume of ions is negligible.

Nernst Potentials

All membrane ionic fluxes are denoted positive when directed towards the cell, and tight junctional fluxes are positive when directed towards plasma.

The Nernst potentials across the apical and basolateral membranes and transepithelia are denoted by

$$\begin{array}{c}{V}_a^c=\frac{\mathit{\text{RT}}}{z_{c}F}ln\left(\frac{c_p}{c_i}\right),\\ V_b^c=\frac{\mathit{\text{RT}}}{z_{c}F}ln\left(\frac{c_s}{c_i}\right),\\ V_t^c=\frac{\mathit{\text{RT}}}{z_{c}F}ln\left(\frac{c_p}{c_s}\right),\end{array}$$

where c denotes an ion concentration.

Ion Channels - Apical Membrane

Cystic Fibrosis Transmembrane Conductance Regulator - CFTR

The CFTR is permeable to Cl⁻ and ${\text{HCO}}_3^{-}$ with a permeability ratio of 4:1 (Poulsen et al,. 1994), and generally secretes Cl⁻. Patch-clamp techniques used on CFTR-deficient nasal epithelia reveal an increase in apical Na⁺ flux by approximately 60% from normal cells due to an increase in membrane permeability, where applying cAMP only increases Na⁺ absorption further (R. C. Boucher et al., 1986; Kunzelmann et al., 1995; Willumsen & Boucher, 1991). Normal CFTR function is therefore linked to apical membrane Na⁺ permeability inhibition.

Poulsen et al. (1994) showed a linear current-voltage (IV) relationship for the apical membrane potential between -100mV and 100mV, and therefore the CFTR is modelled using the Ohmic current equation, defined separately for Cl⁻ and ${\text{HCO}}_3^{-}$:

$$J_{\text{CFTR}}^{\text{Cl}}=\frac{0.8P_{\text{CFTR}}{G}_{\text{CFTR}}}{F}(V_a+V_a^{\text{Cl}}),$$ (10)

$$J_{\text{CFTR}}^{{\text{HCO}}_3}=\frac{0.2P_{\text{CFTR}}{G}_{\text{CFTR}}}{F}(V_a+V_a^{{\text{HCO}}_3}),$$ (11)

where P_n and G_n represent the open probability and maximum conductance of channel n, and $V_a^{c_j}$ represents the Nernst potential of ion c_j (the same notation is used further on).

Although high levels of PCL [H⁺] are known to markedly enhance apical Cl⁻ flux (Matsuda et al., 2010), we do not include any pH-sensitivity on any apical Cl⁻ channel, and leave this up for future extensions of our work.

Epithelial Na⁺ Channel - ENaC

The ENaC is highly Na⁺ selective, and is thought to be critical in fluid absorption, and therefore important in cell volume regulation (Caci et al., 2009; Cao, 2005). It is inhibited by Phospholipase C (PLC) (Huang et al., 2004) and is sensitive to amiloride (Fischer & Widdicombe, 2006; Sariban-Sohraby & Benos, 1986). The ENaC and CFTR are actually colocalised in many tissues, including the airways, sweat ducts, salivary ducts and others (Kunzelmann, 1999). The channel is known to have a linear IV relationship (Cao, 2005), and is therefore modelled using a linear IV model:

$$J_{\text{ENaC}}=-\frac{P_{\text{ENaC}}{G}_{\text{ENaC}}}{F}(V_a-V_a^{\text{Na}}).$$ (12)

Ca²⁺-Activated Cl⁻ Channel - CaCC

The CaCC is activated at low intracellular Ca²⁺ levels by membrane depolarisation and when Ca²⁺ reaches micromolar concentrations (Frizzell & Hanrahan, 2012). It is known as the only membrane protein to secrete Cl⁻ under CF conditions for lung epithelia (Paradiso et al., 2001). Intracellular Ca²⁺ concentration remains at 50 nM for most numerical results, therefore the open probability is constant and we believe a linear IV relation for ion flux through the CaCC is sufficient for the model:

$$J_{\text{CaCC}}=\frac{P_{\text{CaCC}}{G}_{\text{CaCC}}}{F}(V_a+V_a^{\text{Cl}}).$$ (13)

Outwardly-Rectifying K⁺ Channel - Kv7

Apical Kv7s are highly K⁺-selective, with channel activity found in Calu-3 cells, intact airways and lung alveoli using immunocytochemistry, Ussing chamber and patch-clamp techniques by applying specific channel blockers (Moser et al., 2008; Namkung et al., 2009; Sakuma et al., 1998). Some large-conductance Ca²⁺-activated K⁺ (BK) channels are expressed apically in freshly isolated nasal airway epithelia and human bronchial epithelia using patch-clamp and Ussing chamber techniques (Manzanares et al., 2011). We have amalgamated the BK channel into the Kv7 to help with fluid regulation, with channel flux modelled using the Ohmic current equation due to speculated small ranges of membrane potential:

$$J_{\text{Kv}7}=-\frac{P_{\text{kv}7}{G}_{\text{Kv}7}}{F}(V_a-V_a^{\mathrm{K}}).$$ (14)

H⁺-K⁺ ATPase Pump - HKATPase

This protein pumps one cellular proton and one PCL K⁺ against their osmotic gradient, via the binding of ATP, and is localised to the apical membrane of lung epithelia (Coakley et al., 2003). The HKATPase pump provides basal proton secretion and K⁺ absorption across the apical membrane in airway epithelia (Fischer, 2012; Fischer et al., 2002; J. H. Poulsen & Machen, 1996; J. J. Smith & Welsh, 1993). Brzezinski et al. (1988) constructed a 10 state reaction model for a gastric HKATPase that was then adapted by Weinstein in 1998 by changing the stoichiometry of 1:1 and extending the model for renal HKATPase. We have simplified Weinstein's gastric model to the following equation (see Fig. 3):

Figure 3.

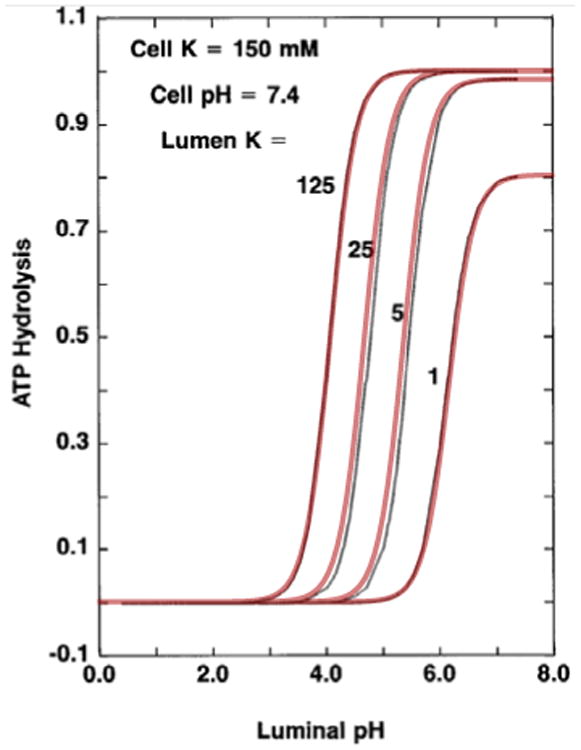
Simplified model for the HKATPase superimposed onto results from Weinstein's model, Weinstein (1998), Fig. 3, showing the relationship between luminal pH levels and ATP hydrolysis for specific [K⁺]_p values utilising Eq. (15)

$$J_{\text{HK}}=G_{\text{HK}}\left(\frac{1}{b_1+b_2{({[{\mathrm{K}}^{+}]}_p)}^{-\beta }}\right)\left(\frac{1}{1+{\mathrm{e}}^{(\frac{b_3}{{({[{\mathrm{K}}^{+}]}_p)}^{\gamma }}+\eta {log}_{10}({[{\mathrm{H}}^{+}]}_p))}}\right),$$ (15)

with constants listed in Table 1.

Table 1. Constants for new HKATPase model.

b1 = 0.999612	s/Ωmmol	β = 1.662
b2 = 0.24474	s/pΩ.mmol.mM	γ = 0.085
b3 = 27.675	mM	η = 4.5

Ion Channels - Basolateral Membrane

Ca²⁺-Activated K⁺ Channel - CaKC

The CaKC is voltage-gated, Ca²⁺-modulated as found by inducing [Ca²⁺]_i increase via cAMP, activated by isoprotenerol and inhibited by clotrimazole (Vergara et al., 1998). The protein is generally considered to be a BK channel, localised to the basolateral membrane in airway epithelia (Fernández-Fernández et al., 2002; Manzanares et al., 2011). An intermediate conductance channel is however seen in the Calu-3 cell line and Xenopus oocytes, and a small conductance, inwardly-rectifying CaKC is found in primary cultures of canine tracheal epithelia (Ishii et al., 1997; Ito et al., 2004; McCann et al., 1990). Assuming the IV relationship is linear as found by (Grissmer et al., 1993), our model predicts a large maximum single channel conductance, indicating the possibility of a BK channel in lung airways in vivo. The equation for the flux is given as:

$$J_{\text{CaKC}}=-\frac{P_{\text{CaKC}}{G}_{\text{CaKC}}}{F}(V_b-V_b^{\mathrm{K}}).$$ (16)

Na⁺-Hydrogen Exchanger - NHE1

The NHE1 exchanges one cellular proton for an extracellular Na ion and is known to be a major intracellular pH-regulator (Noel et al., 1996; Dudeja et al., 1999) and volume regulator (Putney et al., 2002) and is expressed ubiquitously in basolateral membranes of airway epithelia (Al-Bazzaz et al., 2001; Paradiso, 1997). The mathematical representation of the flux is based on the model presented by Falkenberg et al. (2010), and membrane potential is not included as a term for the NHE1 flux, as the exchanger is known to be voltage independent (Demaurex et al., 1995):

$$J_{\text{NHE}1}=G_{\text{NHE}1}{\left(\frac{{[{\mathrm{H}}^{+}]}_i}{{[{\mathrm{H}}^{+}]}_i+K_H}\right)}^2\left(\frac{{[{\text{Na}}^{+}]}_p}{{[{\text{Na}}^{+}]}_p+K_{\text{Na}}}\right)\left(\frac{K{p}_N}{K{p}_N+{[{\mathrm{H}}^{+}]}_i}\right).$$ (17)

Na⁺-K⁺-ATPase Pump - NaKAPase

The electrogenic NaKATPase is an endogenous enzyme that converts the energy released by the hydrolysis of intracellular ATP into electrochemical gradients, to exchange three intracellular Na ions for two extracellular K ions. The pump results in a net outwards current, considered a product of the reaction (Glitsch & Tappe, 1995). This pump could be the main driver for decreased PCL volume via the hyperabsorption of [Na⁺]_p, as NaKATPase activity doubles in human CF tracheal epithelia (Peckham et al., 1997). We use a simplified model by Palk et al. (2010), which was based on Smith & Crampin:

$$J_{\text{NaK}}={\alpha }_b^{\text{NaK}}\frac{r{[{\mathrm{K}}^{+}]}_s^2{[{\text{Na}}^{+}]}_i^3}{{[{\mathrm{K}}^{+}]}_s^2+\alpha {[{\text{Na}}^{+}]}_i^3}.$$ (18)

Basolateral Cl⁻ Channel - BCC

BCCs are localised to the basolateral membrane in airway epithelia, and are known to be quantitatively the most important contributor to basolateral Cl⁻ current (Fischer et al., 2007). The channel is expected to support transcellular Cl absorption, and/or limit transcellular Cl secretion, and is regulated by the CFTR (Szkotak et al., 2003). The current voltage relationship is found to be nearly linear (Itani et al., 2007), thus we model the flux as:

$$J_{\text{BCC}}=\frac{P_{\text{BCC}}{G}_{\text{BCC}}}{F}(V_b+V_b^{\text{Cl}}).$$ (19)

Na⁺-Bicarbonate Cotransporter - NBC

The NBC transports ${\text{HCO}}_3^{-}$ and Na⁺ across the basolateral membrane and has been found in the Calu-3 cell line and lung tissue (Devor et al., 1999; Kreindler et al., 2006; Romero et al., 1998). The stoichiometry can vary between cell types, where 3:1 reflects NBC-mediated ${\text{HCO}}_3^{-}$ and 2:1 ${\text{HCO}}_3^{-}$ exit (Boron et al., 1997). As it is unclear of the appropriate stoichiometry for airway epithelia, we have used the ratio 2:1, and opt for a simple linear IV relationship and flux equation based upon the model by Gross & Hopfer (1996):

$$J_{\text{NBC}}=\frac{P_{\text{NBC}}{G}_{\text{NBC}}}{F}[V_b-\frac{RT}{F}ln(\frac{{[{\text{HCO}}_3^{-}]}_s^2{[{\text{Na}}^{+}]}_s}{{[{\text{HCO}}_3^{-}]}_i^2{[{\text{Na}}^{+}]}_i}\left)\right].$$ (20)

Na⁺-K⁺-2Cl⁻ Cotransporter - NKCC

The NKCC transports one Na⁺, one K⁺ and two Cl⁻ ions electroneutrally across the basolateral membrane simultaneously, thus resulting in zero contribution to current. We use a model constructed by Palk et al. (2010), which is a simplified version of the one presented in Benjamin & Johnson, and its flux is given as:

$$J_{\text{NKCC}}={\alpha }_b^{\text{NKCC}}\frac{{\alpha }_1-{\alpha }_2{[{\text{Na}}^{+}]}_i{[{\mathrm{K}}^{+}]}_i{[{\text{Cl}}^{-}]}_i^2}{{\alpha }_3+{\alpha }_4{[{\text{Na}}^{+}]}_i{[{\mathrm{K}}^{+}]}_i{[{\text{Cl}}^{-}]}_i^2}.$$ (21)

Basolateral Bicarbonate Channel - BHC and Basolateral Hydrogen Channel - BHyC

There are many inherent sources/sinks of protons in airway epithelia not considered in the model, as we have included only a simple pH regulation model. For example, sulphuric acid is formed during the breakdown of amino acids containing sulphur, and phosphoric acid is formed during the breakdown of glucose phosphate structures by nucleic acids (Thorpe, 2009). We found it necessary to include pathways for ${\text{HCO}}_3^{-}$ and H⁺ to enter the cell, as intracellular generation of these ions via the dissolution of CO₂ is not sufficient to stabilise cellular volume. Although there is no evidence for the expression of these channels in airway epithelia, their addition becomes particularly important when considering a CFTR knockout simulation, as there is no ${\text{HCO}}_3^{-}$ efflux from the apical membrane and so ${\text{HCO}}_3^{-}$ influx through the NBC must be balanced. Due to their electrochemical gradient, these fluxes are best localised to the basolateral membrane. We assume a simple linear IV relationship, given by:

$$J_{\text{BHC}}=\frac{P_{\text{BHC}}{G}_{\text{BHC}}}{F}(V_b+V_b^{\text{HCO}3}),$$ (22)

$$J_{\text{BHyC}}=-\frac{P_{\text{BHyC}}{G}_{\text{BHyC}}}{F}(V_b-V_b^H).$$ (23)

Tight Junction

Airway epithelia contain leaky paracellular pathways, and therefore could contribute to PCL modulation through ion and water transport (Coakley et al., 2003; Frizzell & Hanrahan, 2012; Miller, 1992). However, tight junctional fluid equations are not included in the model, as significant expression of AQP4 and AQP5 exist in bronchial epithelium (Kreda et al., 2001). Studies have shown that the tight junction is either anion selective (Poulsen et al., 2006) or cation selective (Flynn et al., 2009; Miller, 1992). As experiments have provided inconclusive results, we have assumed the tight junctions are permeable to all ions, and the equations representing the ionic fluxes for these ions are given by linear IV relationships of the form:

$$J_t^c=-\frac{G_t^c{P}_t^c}{z_{c}F}(V_t-V_t^d),$$ (24)

where c denotes the ion species and z_c is the valence of that species.

Impermeable Ions

We assume the number of impermeable ions in the PCL remains constant over the domain. In order to ensure approximately isotonic fluid flow as found by Boucher et al. (1994), we estimate the number of impermeable ions to adjust the osmolarity to 0.2% isosmolarity for the bulk of the cells. Additionally, we ensure a hypotonic PCL as found by Cowley et al. (1997), Zabner et al. (1998) and McCray et al. (1999), which provides a net osmotic fluid absorption.

Impermeable molecules such as large proteins or mucins are secreted from the glands in vivo, and can degrade via catabolism or be transported away with the net PCL movement. For simplification, we assume the impermeable molecules do not break down and are immobile, and hence no differential equation is necessary. Due to this assumption we impose a model constraint; that these impermeable molecules must be considered as having no net charge in this simple model, and therefore do not contribute to electroneutrality. We therefore refer to them as impermeable osmolytes as they still contribute to the overall osmolarity of the PCL. This is an important model aspect that is examined in more detail in Appendix 1.

The number of impermeable ions in the cells and the concentration of impermeable ions in plasma remain constant and have a negative charge, due to the principle of electroneutrality.

CO₂ Transport

CO₂ diffuses into plasma and red blood cells via its concentration gradient and dissolves in water, producing carbonic acid (Keener & Sneyd, 2008). Carbonic acid then rapidly dissociates into ${\text{HCO}}_3^{-}$ and H⁺ in the following chemical reaction:

$${\text{CO}}_2+{\mathrm{H}}_2\mathrm{O}\underset{k_1^{-}}{\overset{k_1^{+}}{\rightleftharpoons }}{\text{HCO}}_3^{-}+{\mathrm{H}}^{+}.$$

According to the law of mass action, and assuming chemical equilibrium, we have the following relationship for both PCL and cellular compartments:

$${[{\text{CO}}_2]}_p=\frac{k_1^{-}}{k_1^{+}}{[{\text{HCO}}_3^{-}]}_p{[{\mathrm{H}}^{+}]}_p,$$ (25)

$${[{\text{CO}}_2]}_i=\frac{k_1^{-}}{k_1^{+}}{[{\text{HCO}}_3^{-}]}_i{[{\mathrm{H}}^{+}]}_i,$$ (26)

with constants taken from Smith & Crampin (2006). As we now have an analytical equation for CO₂, we therefore do not need a differential equation to govern CO₂ concentration in either the PCL or cellular compartment.

The apical and basolateral membranes are also permeable to carbon dioxide, so CO₂ can diffuse across the membrane. We have included the diffusion across both membranes as linear terms:

$$J_{\text{CO}2\mathrm{a}}=P_{\text{CO}2}({[{\text{CO}}_2]}_p-{[{\text{CO}}_2]}_i),$$ (27)

$$J_{\text{CO}2\mathrm{b}}=P_{\text{CO}2}({[{\text{CO}}_2]}_s-{[{\text{CO}}_2]}_i),$$ (28)

where P_CO2 is the membrane permeability to carbon dioxide which is considered the same for both membranes.

System of Time-Dependent Equations

We assume that ion transport via advection and membrane channels/exchangers dominate over diffusive effects; thus diffusion is neglected from our state equations. We have the following system of equations:

$$\frac{\partial H_p}{\partial t}=-H_p\frac{\partial W_p}{\partial x}-J_a^w,$$ (29)

$$\frac{\partial }{\partial t}({[{\text{Na}}^{+}]}_p{H}_p)=-H_p\frac{\partial }{\partial x}({[{\text{Na}}^{+}]}_p{W}_p)-J_{\text{ENaC}}-J_t^{\text{Na}},$$ (30)

$$\frac{\partial }{\partial t}({[{\mathrm{K}}^{+}]}_p{H}_p)=-H_p\frac{\partial }{\partial x}({[{\mathrm{K}}^{+}]}_p{W}_p)-J_{\text{Kv}7}+J_{\text{HK}}-J_t^{\mathrm{K}},$$ (31)

$$\frac{\partial }{\partial t}({[{\text{Cl}}^{-}]}_p{H}_p)=-H_p\frac{\partial }{\partial x}({[{\text{Cl}}^{-}]}_p{W}_p)-J_{\text{CaCC}}-J_{\text{CFTR}}^{\text{Cl}}-J_t^{\text{Cl}},$$ (32)

$$\frac{\partial }{\partial t}({[{\text{HCO}}_3^{-}]}_p{H}_p)=-H_p\frac{\partial }{\partial x}({[{\text{HCO}}_3^{-}]}_p{W}_p)+Z_1,$$ (33)

$$\frac{\partial }{\partial t}({[{\mathrm{H}}^{+}]}_p{H}_p)=-H_p\frac{\partial }{\partial x}({[{\mathrm{H}}^{+}]}_p{W}_p)+Z_2,$$ (34)

$$\frac{\partial H_i}{\partial t}=J_a^w-J_b^w,$$ (35)

$$\frac{\partial }{\partial t}({[{\text{Na}}^{+}]}_i{H}_i)=J_{\text{ENaC}}+J_{\text{NHE}1}-3J_{\text{NaK}}+J_{\text{NBC}}+J_{\text{NKCC}},$$ (36)

$$\frac{\partial }{\partial t}({[{\mathrm{K}}^{+}]}_i{H}_i)=J_{\text{Kv}7}+J_{\text{CaKC}}+2J_{\text{NaK}}+J_{\text{NKCC}},$$ (37)

$$\frac{\partial }{\partial t}({[{\text{Cl}}^{-}]}_i{H}_i)=J_{\text{CaCC}}+J_{\text{CFTR}}^{\text{Cl}}+J_{\text{BCC}}+2J_{\text{NKCC}},$$ (38)

$$\frac{\partial }{\partial t}({[{\text{HCO}}_3^{-}]}_i{H}_i)=J_{\text{CFTR}}^{{\text{HCO}}_3}+J_{\text{NBC}}+J_{\text{BHC}},$$ (39)

$$\frac{\partial }{\partial t}({[{\mathrm{H}}^{+}]}_i{H}_i)=-J_{\text{NHE}1}+J_{\text{BHyC}},$$ (40)

$$A_a{C}_a\frac{d{V}_a}{\mathit{\text{dt}}}=J_a^{\text{Na}}+J_a^{\mathrm{K}}+J_a^{\text{Hy}}-J_a^{\text{Cl}}-J_a^{{\text{HCO}}_3},$$ (41)

$$A_b{C}_b\frac{d{V}_b}{\mathit{\text{dt}}}=J_b^{\text{Na}}+J_b^{\mathrm{K}}+J_b^{\text{Hy}}-J_b^{\text{Cl}}-J_b^{{\text{HCO}}_3},$$ (42)

for the functions Z₁, Z₂ in Eqs. (33) and (34), see Appendix 2.

The model comprises 13 first order differential equations and one algebraic expression; a system of 14 equations in total. However, we have 15 variables. Therefore in order to solve the time-dependent system, we need another differential equation governing the PCL water flux. We do this by finding a simplified expression for a time-dependent equation governing PCL height that ensures a symmetric boundary condition. Integrating Eq. (1) over the spatial domain (x ∈ [0, L]), gives us:

$${\int }_0^L\frac{\partial H_p}{\partial t}\mathit{\text{dx}}=-{\int }_0^L(H_p\frac{\partial W_p}{\partial x}+J_a^w)\mathit{\text{dx}}.$$

We have assumed H_p is constant over x, resulting in ${\int }_0^L{H}_p\mathit{\text{dx}}=L{H}_p$, where L is the length of the interval of integration, giving us:

$$\frac{d{H}_p}{\mathit{\text{dt}}}=\frac{H_p(W_p(0)-W_p(L))}{L}-\frac{1}{L}{\int }_0^L{J}_a^w\mathit{\text{dx}}.$$

With the symmetric boundary condition ensuring W_p(L) = 0, we have the following time-dependent integro-differential equation for PCL height:

$$\frac{d{H}_p}{\mathit{\text{dt}}}=\frac{H_p{W}_p(0)}{L}-\frac{1}{L}{\int }_0^L{J}_a^w\mathit{\text{dx}},$$ (43)

Equating the right-hand side of Eq (1) to Eq (43), we have the following time-dependent integro-differential equation for PCL water velocity:

$$\begin{array}{c}-H_p\frac{\partial W_p}{\partial x}-J_a^w=\frac{H_p{W}_p(0)}{L}-\frac{1}{L}{\int }_0^L{J}_a^w\mathit{\text{dx}},\\ \frac{\partial W_p}{\partial x}=\frac{W_p(0)}{L}+\frac{J_a^w}{H_p}-\frac{1}{L{H}_p}{\int }_0^L{J}_a^w\mathit{\text{dx}}.\end{array}$$ (44)

We therefore replace Eq. (29) with Eq. (43) and add Eq. (44) to the system of equations.

To solve the time-dependent system, we first obtain an initial profile for all variables by solving the steady-state system for H_p = 5 μm. Then we change the system to a new state, for example by increasing W_p by 10% (from 1.92 to 2.12 μm/s), as discussed in the Results section. We then integrate H_p in time using the following finite difference expression:

$$\begin{array}{c}\frac{{H_p}^{i+1}-{H_p}^i}{\mathrm{\Delta }t}=\frac{{H_p}^i{W}_p(0)}{L}-\frac{1}{L}{\int }_0^L{J}_a^w\mathit{\text{dx}},\\ {H_p}^{i+1}=\frac{\mathrm{\Delta }t{H_p}^i{W}_p(0)}{L}-\frac{\mathrm{\Delta }t}{L}{\int }_0^L{J}_a^w\mathit{\text{dx}}+{H_p}^i,\end{array}$$

where we estimate the integral of apical water flux over the spatial domain ( ${\int }_0^L{J}_a^w\mathit{\text{dx}}$) by the value obtained in the previous time step. This value represents the total amount of water absorbed by the cells over the whole spatial domain, and we expect to see the value converge to H_pW_p(0) as t → ∞. This procedure is repeated until a tolerance of $|H_p^{i+1}-H_p^i|<1^{-10}$ is reached, updating the value for ${\int }_0^L{J}_a^w\mathit{\text{dx}}$ after each spatial integration.

System of Steady State Equations

To find steady state equations, we set all time derivatives (Eqs. (29)-(41)) to zero. Therefore, we have a system of differential algebraic equations (DAEs), given by the following:

$$H_p\frac{d{W}_p}{\mathit{\text{dx}}}=-J_a^w,$$ (45)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{Na}}^{+}]}_p{W}_p)=-J_{\text{ENaC}}-J_t^{\text{Na}},$$ (46)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\mathrm{K}}^{+}]}_p{W}_p)=-J_{\text{Kv}7}+J_{\text{HK}}-J_t^{\mathrm{K}},$$ (47)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{Cl}}^{-}]}_p{W}_p)=-J_{\text{CaCC}}-J_{\text{CFTR}}^{\text{Cl}}-J_t^{\text{Cl}}$$ (48)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{HCO}}_3^{-}]}_p{W}_p)=Z_1,$$ (49)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\mathrm{H}}^{+}]}_p{W}_p)=Z_2,$$ (50)

$$0=J_a^w-J_b^w,$$ (51)

$$0=J_{\text{ENaC}}+J_{\text{NHE}1}-3J_{\text{NaK}}+J_{\text{NBC}}+J_{\text{NKCC}},$$ (52)

$$0=J_{\text{KV}7}+J_{\text{CaKC}}+2J_{\text{NaK}}+J_{\text{NKCC}},$$ (53)

$$0=J_{\text{CaCC}}+J_{\text{CFTR}}^{\text{Cl}}+J_{\text{BCC}}+2J_{\text{NKCC}},$$ (54)

$$0=J_{\text{CFTR}}^{{\text{HCO}}_3}+J_{\text{NBC}}+J_{\text{BHC}},$$ (55)

$$0=-J_{\text{NHE}1}+J_{\text{BHyC}},$$ (56)

$$0=J_a^{\text{Na}}+J_a^{\mathrm{K}}+J_a^{\text{Hy}}-J_a^{\text{Cl}}-J_a^{{\text{HCO}}_3},$$ (57)

$$0=J_b^{\text{Na}}+J_b^{\mathrm{K}}+J_b^{\text{Hy}}-J_b^{\text{Cl}}-J_b^{{\text{HCO}}_3},$$ (58)

again, for the functions Z₁, Z₂ in Eqs. (49) and (50), see Appendix 2.

The sum of the currents across the apical membrane is always zero according to Eqs. (57) and (58), where $J_a^n$ and $J_b^n$ represent the combination of apical and tight junctional basolateral and tight junctional currents for ion n, which contribute to the membrane potential according to the cable equation. Eqs. (57) and (58) ensure the assumption that the membrane potential moves instantly to its steady state value for each new set of variables. Due to Kirchoffs loop and node laws, there will be no charge accumulation in the cell. Cell height can vary over the spatial domain according to Eq. (51), where H_i is adjusted to satisfy this equation.

We therefore require 6 boundary conditions and 8 consistency conditions, which are dictated by values at x = 0 μm. PCL compartmental boundary conditions represent the velocity of water or concentration of ions secreted from the glands, with typical values given by Jayaraman, Joo et al. (2001) and Wine & Joo (2001). ${\text{HCO}}_3^{-}$ is calculated using the principle of electroneutrality. Consistency conditions for all other variables represent values in the cell located just above the glands. Cellular concentrations, height and basolateral membrane potential consistency values are found by ensuring Eqs. (52)-(58) are zero, given PCL boundary values. The boundary and consistency conditions are given in Table 2, with the extra boundary condition W_p(500) = 0 μ/s.

Table 2. Boundary and Consistency Conditions.

Variable	Unit	Variable	Unit
[Na+]p(0) = 94	mM	[Na+]i(0) = 21.8	mM
[K+]p(0) = 13	mM	[K+]i(0) = 103.7	mM
[Cl−]p(0) = 92	mM	[Cl−]i(0) = 45.7	mM
${[{\text{HCO}}_3^{-}]}_p(0)=15$	mM	${[{\text{HCO}}_3^{-}]}_i(0)=12.4$	mM
pHp(0) = 6.81		pHi(0) = 6.94
[CO2]p(0) = 3.8	mM	[CO2]i(0) = 3.9	mM
Va(0) = -29	mV	Vb(0) = -34.1	mV
Wp(0) = 1.92	μm/s	Hi(0) = 35.9	μm

Assuming the solution is symmetric imposes a zero condition for PCL water flux velocity, namely, W_p(x = 500) = 0 μm/s. As this is a superfluous condition, we now have an over-constrained system where a system parameter becomes our eigenvalue, signifying a numerical solution exists for one particular parameter value that will satisfy the symmetric boundary condition. To solve the system numerically, we use the shooting method with H_p as the unknown shooting parameter. Thus, the height of the PCL emerges as an eigenvalue of the model equations. Other eigenvalues are also possible, and used when appropriate. For example, if the height of the PCL is considered known, then the amount of fluid produced by the SMGs can be adjusted to give the correct boundary condition at x = 500 μm, in which case the flux from the gland becomes the eigenvalue.

Electroneutrality

We must ensure that both PCL and cellular compartments are electroneutral, due to the principal of electroneutrality, meaning the number of positive charges must equal the number of negative charges:

$${[{\text{Na}}^{+}]}_p+{[{\mathrm{K}}^{+}]}_p-{[{\text{Cl}}^{-}]}_p-{[{\text{HCO}}_3^{-}]}_p+{[{\mathrm{H}}^{+}]}_p=0$$ (59)

$${[{\text{Na}}^{+}]}_i+{[{\mathrm{K}}^{+}]}_i-{[{\text{Cl}}^{-}]}_i-{[{\text{HCO}}_3^{-}]}_i+{[{\mathrm{H}}^{+}]}_i-\frac{X_i}{{\omega }_i}=0.$$ (60)

If we add the following equations:

$$0=\text{Eq}.(52)+\text{Eq}.(53)-\text{Eq}.(54)-\text{Eq}.(55)+\text{Eq}.(56)=(J_a^{\text{Na}}+J_a^{\mathrm{K}}+J_a^{\text{Hy}}-J_a^{\text{Cl}}-J_a^{{\text{HCO}}_3})+(J_b^{\text{Na}}+J_b^{\mathrm{K}}+J_b^{\text{Hy}}-J_b^{\text{Cl}}-J_b^{{\text{HCO}}_3}),$$

which means, if Eq. (57) is satisfied, Eq. (58) is always true, and therefore redundant. We replace Eq. (58) with the electroneutrality condition, Eq. (60).

Appendix 1 shows how electroneutrality is maintained in the PCL.

Parameters

Ionic concentrations and membrane potentials have been measured under basal conditions in many cell types, and specific ion channel conductances have been recorded when possible. Our model assumption of symmetrical solution profiles forces the value and the gradient of the variables at the end of the domain to match. This results in the necessary condition that the gradient must be zero at the end of the spatial domain, allowing us to calculate unknown transport parameters. Therefore, tight junctional, HKATPase, NBC and CaKC maximum channel conductances and NaKATPAse and NKCC maximum channel densities were determined by setting Eqs. (46)-(50) to zero at equilibrium values (where the gradient is zero) and are listed in Table 5. A list of known parameters and equilibrium values used in the model are given in Tables 3 and 4. Parameters estimated from the model are listed in Table 6.

Table 5. Parameters determined from model.

Variable	Unit	Description
La = 1490	μm/s	apical membrane water permeability
Lb = 790	μm/s	basolateral membrane water permeability
$G_t^{\text{Na}}=32$	pS/μm2	maximum conductance of paracellular Na+ per unit areac,d
$G_t^{\mathrm{K}}=0.4$	pS/μm2	maximum conductance of paracellular K+ per unit aread
$G_t^{\text{Cl}}=80$	pS/μm2	maximum conductance of paracellular Cl− per unit areac,d
$G_t^{{\text{HCO}}_3}=0.8$	pS/μm2	$\text{maximum conductance of paracellular}{\text{HCO}}_3^{-}\text{per unit}{\text{area}}^{\mathrm{d}}$
$G_t^{\mathrm{H}}=1.85$	pS/μm2	maximum conductance of paracellular H+ per unit aread
GHK = 0.68	fS/μm2	maximum conductance of apical HKATPase per unit aread
GNBC = 4.54	pS/μm2	maximum conductance of NBC per unit aread
GCaKC = 313	pS/μm2	maximum conductance for CaKC per unit area
αNaK = 1.42	fmol/μm2.cycle	density of NaKATPase on basolateral membrane
αNKCC = 4.34	fmol/μm2.cycle	density of NKCC co-transporter on basolateral membrane

^cValues found to be in good comparison with predicted model values published in Warren et al. (2009).

Table 3. List of Parameters: Known Parameters, from literature.

Variable	Unit	Description	Reference
Vw = 18.05×10−6	mM−1	partial molal volume of water	Morillon et al. (2001)
Aa = 38.9	μm2	apical membrane areaa
Ab = 58.9	μm2	basolateral membrane areaa
Aa:Ab = 1:1.51		ratio of apical to basolateral membrane areas	Griffiths et al. (1993)
PENaC = 0.15		open probability of ENaC	Chinet et al. (1994)
GENaC = 21.4	pS	maximum conductance of ENaC	Chinet et al. (1994)
PKv7 = 0.55		open probability of Kv7 channel	Wu et al. (2004)
GKv7 = 2.2	pS	maximum conductance of Kv7 channel	Wu et al. (2004)
PCFTR = 0.34		open probability of CFTR channel	Krouse & Wine (2001)
GCFTR = 6.1	pS	maximum conductance of CFTR channel	Krouse & Wine (2001)
PCaCC = 0.066		open probability of CaCC for [Ca2+]i = 50nM	Tarran et al. (2000)
GCaCC = 3	pS	maximum conductance of CaCC	Takahashi (1987)
PBCC = 0.56		open probability of BCC	Fischer et al. (2007)
GBCC = 9.5	pS/μm2	maximum conductance of BCC per area	Fischer et al. (2007)
PCaKC = 0.045		open probability of CaKC for [Ca2+]i = 50nM	Ishii et al. (1997)
[Na+]s = 134.9	mM	plasma Na+ concentration	Mangos et al. (1973)
[K+]s = 5.3	mM	plasma K+ concentration	Mangos et al. (1973)
[Cl−]s = 102.6	mM	plasma Cl− concentration	Mangos et al. (1973)
${[{\text{HCO}}_3^{-}]}_s=21$	mM	${\text{plasma HCO}}_3^{-}\text{concentration}$	Fischer et al. (2006)
[H+]s = 3.89×10−5	mM	plasma H+ concentration	Lewis (2013)
KpN = 0.9977		half maximal H+ flux constant	Falkenberg & Jakobsson (2010)
T = 310	K	temperature of the human body
R = 8.314	J/mol.K	universal gas constant
F = 96.485	kC/mol	Faraday's constant

^aMembrane areas were calculated using the ratio of membrane surface areas, using equilibrium values for cell volume and cell height listed in Table 4∷

$${\omega }_i=H_i\frac{A_a+A_b}{2},$$

where A_a = 1.51A_b. This gives values A_a = 38.9 μm, A_b = 58.7 μm. Mercer et al. (1994) estimate an apical membrane of 60.3 μm in human bronchioles, in good comparison with model predictions. Although basolateral membrane areas for bronchial columnar cells may exceed this ratio, we could find no current literature that presented results on measurements for both membranes.

Table 4. Equilibrium values.

Variable	Unit	Description	Reference
ωi = 1400	μm	cell volume	Matsui et al. (2000)
Hi = 28.7	μm	cell height	Matsui et al. 2000
[Na+]p = 103	mM	PCL Na+ concentration	Jayaraman, Song et al. (2001)
[K+]p = 20.8	mM	PCL K+ concentration	Namkung et al. (2009)
[Cl−]p = 92	mM	PCL Cl− concentration	Jayaraman, Song et al. (2001)
[H+]p = 1.55×10−4	mM	PCL H+ concentration	Jayaraman, Joo et al. (2001)
${[{\text{HCO}}_3^{-}]}_p=31.8$	mM	${\text{PCL HCO}}_3^{-}\text{concentration}$	determined from modelb
[CO2]p = 11.6	mM	PCL CO2 concentration	determined from Eq. (25)
[Na+]i = 22	mM	intracellular Na+ concentration	Willumsen & Boucher (1991)
[K+]i = 117	mM	intracellular K+ concentration	Treharne et al. (2006)
[Cl−]i = 42.7	mM	intracellular Cl− concentration	Willumsen et al. (1989)
[H+]i = 1.23×10−4	mM	intracellular H+ concentration	Stewart et al. (2001)
${[{\text{HCO}}_3^{-}]}_i=12$	mM	${\text{intracellular HCO}}_3^{-}\text{concentration}$	Smith & Crampin (2006)
[CO2]i = 3.5	mM	intracellular CO2 concentration	determined from Eq. (26)
Va = -29	mV	apical membrane potential	Cotten et al. (1987)
Vb = -36.2	mV	basolateral membrane potential	Willumsen et al. (1989)
U0 = 1.92	μm/s	submucosal gland secretory flux	determined from model

^bThe equilibrium PCL ${\text{HCO}}_3^{-}$ concentration was found using the electroneutrality condition:

$$\begin{array}{c}{[{\text{HCO}}_3^{-}]}_p={[{\text{Na}}^{+}]}_p+{[{\mathrm{K}}^{+}]}_p-{[{\text{Cl}}^{-}]}_p-{[{\mathrm{H}}^{+}]}_p,\\ =31.8\text{mM}.\end{array}$$

Table 6. Estimated Parameters.

Variable	Unit	Description
Xi = 118	fmol	number of impermeable ions in the cell, set by electroneutralitye
Xp = 4.21	fmol	number of impermeable ions in the PCL, to 0.2% isosmolaritye
Xs = 16.6	mM	concentration of impermeable ions in plasma, set by electroneutralitye
GBHyC = 10	fS/μm2	$\text{maximum conductance of basolateral}{\text{HCO}}_3^{-}\text{channel per unit}{\text{area}}^{\mathrm{d}}$
GBHC = 50	fS/μm2	maximum conductance of basolateral H+ channel per until aread
GNHE1 = 0.1	fM.μm/s	maximum conductance of basolateral NHE1d

^dAssuming an open probability of one,

^eequilibrium values were used for setting electroneutrality and isosmolarity conditions. Compartmental osmolarity is found to be ≈ 281 mOsm; slightly less that 331 ± mOsm found in normal and CF nasal epithelia by Zabner et al. (1998). The concentration of impermeable ions at equilibrium in the PCL is ≈ 22 mM, in good comparison to an estimate by Tarran et al. (2001) to be around 40-50 mM.

Results

Time-Dependent Model Solutions

Some dynamical models have predicted oscillating steady state solutions, such as the one presented by Novotny & Jakobsson (1996a, 1996b), where oscillating solutions were seen with a set of in vivo parameters in both secreting and non-secreting states. In order to perform useful analysis on steady state data, we must exclude the possibility of oscillating solutions in time, and show that the time-dependent solutions converge to our steady state profiles for all variables.

As explained previously, we create an initial profile for the time-dependent system by solving the steady state equations. PCL height is fixed at H_p = 5 μm (volume contribution from cilia not included), as found by Tarran et al. (2006) for normal bronchial epithelia (NBE). Our steady state system eigenvalue is submucosal gland secretion, predicted to give W_p(0) = 1.92 μm/s.

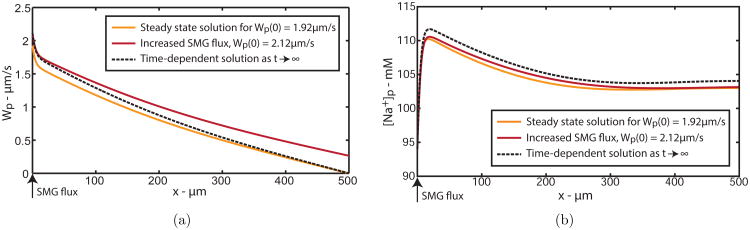
After increasing W_p(0) by 10% to 2.12 μm/s on the first time step, we see the spatial solutions move as time increases. Fig. 4(a) shows the spatial profile for PCL water velocity, W_p. The grey curve is the initial profile for the time integration, and the black curve is the solution after the first time step, where we can see the boundary condition has increased. As time increases, the black curve converges to the dashed curve, which is exactly the profile predicted by our steady state solution, where the symmetric boundary condition W_p(500) = 0 μm is satisfied.

Figure 4.

Spatial solution for PCL (a) water velocity and (b) PCL sodium concentration, W_p and [Na⁺]_p, as time increases. Steady state solution for H_p = 5 μm (grey solid line) when t = 0; Increased SMG flux by 10% (black solid line) when t = 1s; Solution as t → ∞ (dashed line).

We confirm the solutions to all other variables converge to predicted steady state profiles, and have included the solution for PCL Na⁺, shown in Fig. 4(b). The spatial solution converges to the predicted steady state profile (dashed solution), with no discernible oscillations. As all variables behave much the same way, we thus validate our steady state solution profiles.

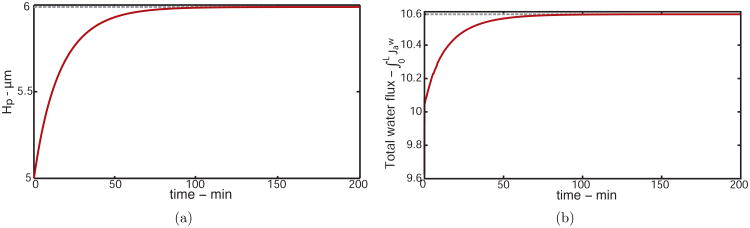
We now show how the height of the PCL changes over time to verify the predicted value used in our steady state model. Integrating H_p over time shows a solution that reached a steady state value of H_p ≈ 5.99 μm, as shown in Fig. 5(a), with no discernible oscillations. This value is exactly the eigenvalue predicted by the steady state model, indicating our time-independent model predicts valid PCL height values.

Figure 5.

(a) PCL height as a function of time reaching a steady state of 5.99 μm, exactly the value predicted from our steady state model from increasing SMG flux by 10% from W_p(0) = 1.92 μm/s where H_p = 5 μm, to W_p(0) = 2.12 μm/s. (b) Total water flux as a function of time reaching a steady state of 10.62 μm²/s, a value also predicted by our steady state model.

The total water flux as a function of time is shown in Fig. 5(b). The initial steep gradient is due to the numerical approximation of the total water flux, which eventually converges to the value predicted by the steady state model, H_pW_p(0) = 10.62 μm²/s.

Steady State Model Solutions

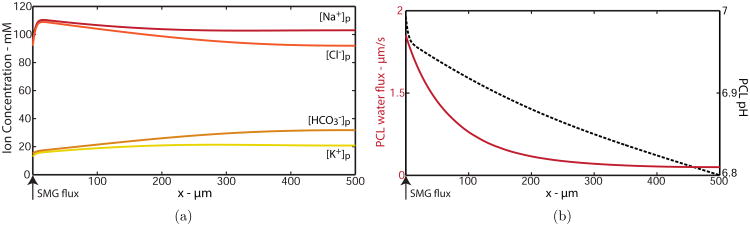
As we have found no oscillating steady state profiles, and thus validated our steady state analysis, we now focus on steady-state solutions. First we show the standard solution to the boundary value problem that represents the left half of a symmetric solution and satisfies W_p(500) = 0 μm/s for H_p = 5 μm. Fig. 6(a) shows solutions for PCL ion concentrations of Na⁺, Cl⁻, ${\text{HCO}}_3^{-}$, and K⁺.

Figure 6.

(a) Solutions for PCL ion concentrations. (b) Solutions for PCL pH (solid line) and water flux (dashed line) for a distribution of normal bronchial epithelia at H_p = 5 μm, representing the left half of a symmetric solution.

We implement PCL boundary conditions as ionic concentrations secreted from the gland and water velocity. As gland secretions are hypotonic (Widdicombe, 1989; Wine & Joo, 2004), an increase in PCL ion concentrations is seen from the boundary x = 0 μm where the gland is found.

The steepest solution gradients are located near x = 0 μm, demonstrating the cells closest to the gland are likely the most important for driving ion/fluid transport to maintain constant PCL height. All concentrations approach their ‘equilibrium’ state by x ≈ 400 μm, where the solutions have reached zero gradient, as expected due to our symmetric condition. This indicates that the cells near the end of the domain (in between the glands) are in homeostasis. The term ‘equilibrium’ will be used further on to refer to these values, which represent those of the bulk cells/PCL. All system variables in the standard solution reach equilibrium values listed in Table 4. Similar solution trends are found for intracellular concentrations and membrane potentials.

Fig. 6(b) shows solutions for PCL pH levels (solid line) and PCL water flux velocity (dashed line). The solution for W_p reaches zero at x = 500 μm, as is satisfied by H_p = 5 μm. PCL pH decreases by approximately 3% from the gland and reaches equilibrium by x = 400 μm.

Model Validation

Biological experiments are not generally constructed towards gathering spatially-dependent data over a distribution of epithelial cells. Therefore for model validation, we compare the trends of time-dependent experiments where possible, with the bulk of parameters found in published literature on human airway epithelia.

Application of Amiloride

We are firstly interested in comparing model predictions to experimental data by the simulation of amiloride application, which blocks Na⁺ transport through the ENaC. Smith et al. (1994) applied 30 μM of amiloride to nasal epithelial monolayers, and found that both ENaC activity and fluid absorption were inhibited in normal (NL) cells; indicating active Na⁺ transport drives fluid absorption. Sodium transport was reduced but not abolished in CF cells. Likewise, Jiang et al. (1993) applied 100 μM of amiloride to human tracheal epithelia, which reduced fluid absorption by 75% in NL cells and 80% in CF cells.

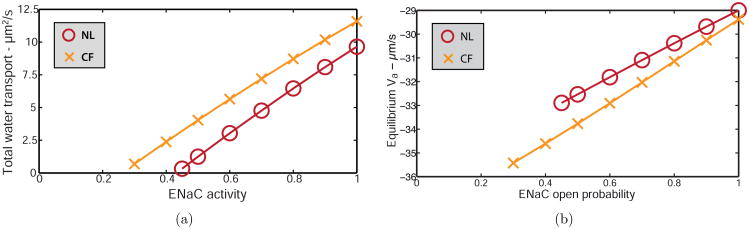
We simulate the application of amiloride by multiplying the ENaC open probability (P_ENaC) by a constant, as it is unknown how much amiloride blocks ENaC completely. We examine the effects on the total amount of water transported through the cell layer and the equilibrium apical membrane potential. We wish to isolate the relationship between Na⁺ transport and fluid flow without compensating for changes in PCL height, hence we fix PCL height at H_p = 5μm. The water flux at the left boundary W_p(0) becomes our eigenvalue, adjusted for each simulation to satisfy the symmetric boundary condition. Fig. 7 shows model solutions for total water flux (positive values denote absorption) and apical membrane potential for NL (○) and CF (×) epithelia with simulated amiloride application. Cystic fibrosis simulations were conducted by decreasing CFTR open probability to zero, which is experimentally equivalent to CFTR knockout.

Figure 7.

Simulating the application of amiloride by decreasing the activity of the ENaC for (a) total water transport across the domain, where positive values denote absorption, and (b) apical membrane equilibrium potential for NL (○) and CF (×) cells at H_p = 5 μm; where the open probability of the CFTR is zero for CF simulations.

As ENaC activity is decreased, less Na⁺ is absorbed through the cell layer. Fig. 7(a) shows that as ENaC activity decreases, fluid absorption decreases for both NL and CF cells, indicating less fluid is needed from the SMGs to maintain a constant PCL volume. Extrapolating the linear solution curve to find the intersection with the x-axis, we see fluid absorption is completely inhibited by reducing ENaC activity to approximately 0.42 in NL epithelia, and absorption is abolished by reducing EnaC activity to approximately 0.24 in CF. Simulated results indicate transepithelial Na⁺ absorption drives fluid absorption, and only a partial reduction in ENaC function is required to completely inhibit transepithelial water transport. Only half of ENaC activity in CF compared to NL is required to inhibit total transepithelial fluid flow, as CFTR knockout increases the amount of water absorbed.

Fig. 7(b) shows that reducing ENaC activity in the model hyperpolarises the apical membrane by 18% for NL and 24% for CF cells. Boucher et al. (1988) experimented on cultured nasal epithelia and showed the application of 100 μM amiloride hyperpolarised the apical membrane potential by 24% in NL cells, in good agreement with model predictions, and 79% in CF cells. The larger hyperpolarisation recorded experimentally in CF cells could be due to other amiloride-sensitive apical membrane channels not accounted for in the simulations, for example, some classes of the NHE are found to be inhibited by amiloride (Putney et al., 2002). Discrepancies between model and experimental results could also be due to a difference in PCL height, which was not measured by Boucher et al. (1988).

Simulations in Cystic Fibrosis Conditions

Two principal hypotheses regarding the consequences of CFTR malfunction in cystic fibrosis lungs are 1) increased ENaC activity and 2) reduced gland secretory flux. These theories are based on experiments performed by Chinet et al. (1994) on nasal epithelial cell cultures where the open probability of the ENaC doubled in CF cultures, and by Salinas et al. (2005) who found a 2.7-fold reduction in CF nasal biopsy gland fluid secretion compared with normal biopsies. We investigate quantitatively the effects of decreasing CFTR function while implementing individual and combined theories to determine their relative contribution to the overall effect on PCL salt concentration, height, equilibrium water transport and PCL pH levels. To simulate both theories, we decrease the water flux from the SMG by up to 2.7 and increase ENaC activity by up to a factor of 2, while simultaneously decreasing CFTR activity to 0. Both theories predict a compromise in PCL volume, therefore PCL height becomes an important parameter in estimating healthy airway hydration. Thus we choose H_p as our eigenvalue.

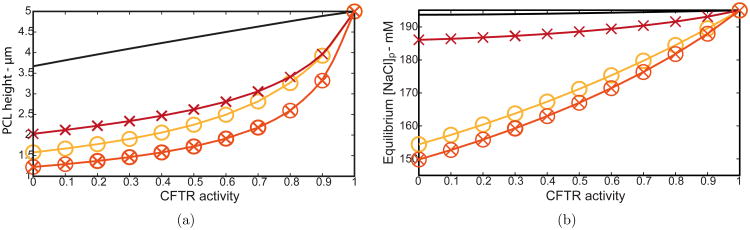
PCL height

We firstly investigated how PCL height changes with CFTR activity in four different cases; (i) normal cells (solid line) (ii) decreased SMG flux (×), (iii) doubled ENaC activity (○), and (iv) combined decreased SMG flux and doubled ENaC (⊗). Fig. 8(a) shows that decreasing CFTR activity significantly reduced PCL volume for all cases. The most drastic reduction of 75% corresponding to a value of H_p = 1.23 μm occurred for combined CF theories (increased ENaC activity plus reduced SMG flux) and complete CFTR inhibition. Tarran et al. (2006) found H_p ≈ 1 μm in CF bronchial PCL above in vitro cell cultures. Our model also predicts a severe depletion of PCL height even without considering reduced gland flux in CF conditions, indicating either reduced gland flux or increased ENaC activity or a combination is responsible for a reduction in PCL volume in vivo.

Figure 8.

(a) PCL height and (b) equilibrium [NaCl]_p values as a function of CFTR activity. (Solid line) decrease in CFTR only, (×) reducing SMG flux from 1.92 to 0.71 μm/s, (○) doubling ENaC activity, (⊗) reducing SMG flux and doubling ENaC activity.

PCL salt

Experiments on human airway epithelia show an increase (Smith et al., 1994; Joris et al., 1993) or no change (Matsui et al., 1998) in PCL salt concentration, so we investigated how PCL equilibrium salt concentration varies with CFTR activity. Results are shown in Fig. 8(b), where we plot equilibrium [NaCl]_p (salt concentration above cells at x ≈ 500 μm), and PCL height as a function of CFTR activity for the four cases mentioned. Our simulations reveal that PCL salt concentration is not significantly affected by decreasing CFTR with or without decreasing SMG flux for normal cells, as shown in Fig. 8(b) (solid line, ×). However, increasing ENaC activity with and without decreased SMG flux shows a significant decrease in PLC salt levels (○, ⊗); a predictable result as the ENaC absorbs Na ions in basal conditions. These results indicate that if salt levels in CF lungs remain comparable to those in healthy lungs in vivo, ENaC activity is likely to be unaffected by the genetic mutation or any secondary effect of CF.

pH levels

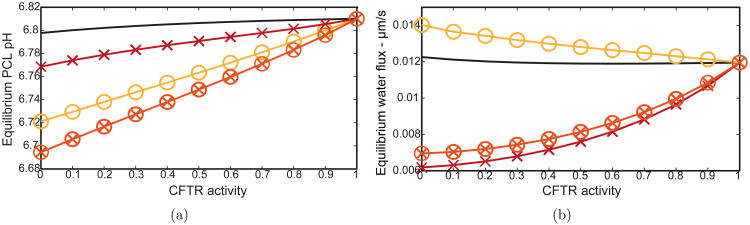
Defective ${\text{HCO}}_3^{-}$ secretion has been thought to contribute to the pathophysiology of CF by acidifying the PCL (Smith & Welsh, 1992), which reduces the strength of antibacterial and antimicrobial combatants in this fluid layer. Additionally, antibacterial activity is best expressed in near neutral pH levels (Selsted et al., 1984). Coakley et al. (2003) measured ASL pH above human bronchial epithelia and found a consistent 4% decrease from NL to CF cultures over a prolonged period after potassium bromide application. In a recent study by Pezzulo et al. (2012), PCL pH was measured in porcine CF tracheal surfaces in vivo. The authors showed ASL pH to decrease by approximately 3%, and adding staphylococcus aureus showed a decrease in dead bacteria colonies by over 50% in CF airways, persisting even after stimulating gland secretion with methacholine. These experimental results indicate that even a small decrease in PCL pH levels could compromise the antibacterial properties inherent in airways.

Fig. 9(a) shows PCL pH equilibrium levels for our four CF cases. While decreasing CFTR alone results in a minimal pH decrease only (solid line), the combination of both CF theories results in a 2% reduction in PCL pH for complete CFTR knockout (⊗). These results suggest that a combination of reduced SMG flux and increased ENaC activity are most likely responsible for PCL acidification seen in CF lungs.

Figure 9.

(a) PCL pH levels and (b) equilibrium water flux as functions of CFTR activity. (Solid line) decrease in CFTR activity only, (×) reducing SMG flux from 1.92 to 0.71 μm/s, (○) doubling ENaC activity, (⊗) reducing SMG flux and doubling ENaC activity.

Fluid transport

We investigated how much fluid is absorbed across the epithelia in between the glands, implementing individual and combined CF hypotheses. Fig. 9(b) shows that solely decreasing CFTR (solid line) results in no significant change, suggesting CFTR is not solely responsible for transepithelial fluid transport. Doubling ENaC activity with no CFTR function (○) results in a 15% increase in fluid absorbed across the epithelia, despite a 70% decrease in PCL volume (see Fig. 8(a)). However, reducing the SMG flux exclusively (×) or in combination with an increase in ENaC activity (⊗) results in markedly less fluid absorbed across the bulk of the cells in between the glands (to ≈ 50%), as is found in newborn porcine airway epithelia in vivo (Chen et al., 2010). Additionally, Chen et al. (2010) measured liquid absorption at a rate of approximately 0.022 μm/s, in good agreement with our basal fluid flux of 0.012 μm/s at equilibrium. Although experiments performed by Jiang et al. (1993) on nasal and tracheal cultures reveal a 40% increase in fluid absorption across surface epithelia, the cultures were not in their natural environment where SMG secretions contribute to the recycling of fluid. These results indicate that although Na⁺ absorption drives fluid absorption across surface epithelia, a compromise in gland fluid secretion will dominate in CF conditions and result in less fluid absorption than normal epithelia in vivo.

We are also interested in whether a spatial variation is necessary when considering the total amount of water absorbed across surface epithelia, or if one cell could be a good representation of a distribution. Could the measurement of fluid absorbed at x = 500 μm multiplied by the length of the domain be sufficient to determine the total water transport across the entire length of the epithelial cells?

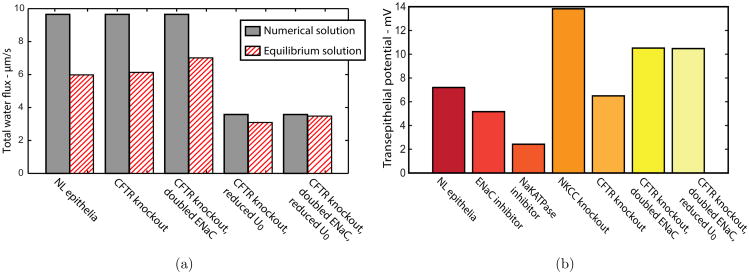
In our model, the total water flux across the epithelia multiplied by PCL height is exactly the integral of the PCL water velocity, given by the conservation Eq. (1). As we decrease gland fluid secretion, we decrease the amount of fluid transported through the epithelia, and force cells near the glands to secrete water to adequately hydrate the PCL. Fig. 10(a) shows the total amount of water transported through the whole line of epithelia (grey bars) versus the total amount calculated by assuming all epithelia transport the same amount of water as the cells in equilibrium (striped bars), hence we coin the term equilibrium approximation. In decreasing SMG flux (U₀), the grey bars reduce by 67%, whereas the striped bars only reduce by ≈ 40%, showing that an in vivo reduction in gland flux needs to be represented by a spatial model, as the equilibrium water flux is not a good representation of the total water absorbed by the monolayer.

Figure 10.

(a) Total water flux through epithelia over whole spatial domain. Numerical solution (grey bars) and equilibrium approximation (striped bars). (b) Model predictions for transepithelial potential.

Transepithelial Potential

Garcia et al. (2013) published a comprehensive solute-fluid transport model based on experiments in nasal epithelia, with a systematic parameter estimation approach to quantify ion membrane permeabilities and maximum NaKATPase and NKCC fluxes. The application of amiloride decreased the transepithelial potential (V_t) from -12 to -5 mV (measured inside to outside) over 40min, a trend replicated in their mathematical model. Our model predicts a decrease in equilibrium V_t from 7.2 to 5.2 mV (measured outside to inside), which is in good agreement with their experimental values, see Fig. 10(b). Reducing ENaC activity in conjunction with SMG flux reduction plus CFTR knockout shows the same quantitative behaviour as seen in newborn porcine CF airways where ENaC is shown not to increase in CF conditions (Chen et al., 2010). The application of ouabain decreased V_t from -12 to -1 mV and in our model inhibiting NaKATPase activity decreased V_t from 7.2 to 2.4 mV, again in good agreement. The application of bumetanide which inhibits basolateral NKCC is known to cause cell shrinkage, is shown to not affect bioelectrical properties. In our model, simulating the application of bumetanide by reducing NKCC activity, shrinks equilibrium cell height by 33% but also increases V_t from 7.2 to 13.8 mV. The reason why NKCC knockout affects model bioelectrics remains unclear and requires further investigation.

PCL Rehydration in CF Conditions

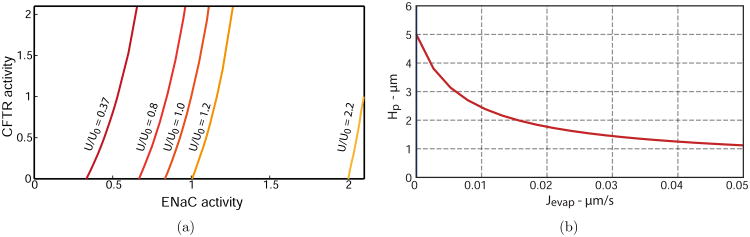
In both doubled ENaC activity and decreased SMG flux CF theories, the important mechanism being compromised is a depleted PCL. Therefore we are interested in exploring the relationship between ENaC and CFTR activity as the amount of secreted fluid from the glands changes, preserving a healthy PCL volume. Fig. 11(a) shows values of CFTR and ENaC activities that solve the BVP while varying the amount of fluid secreted from the glands and maintaining a constant PCL height of 5 μm. The steep gradients of all curves indicate a system with a greater sensitivity to ENaC than CFTR changes, which signifies larger changes in CFTR activity are required to rehydrate the PCL to normal volume. When the gland flux is decreased by a factor of 2.7 (U/U₀ = 0.37), a decrease in ENaC activity to 0.33 will result in the restoration of PCL volume to normal levels when CFTR activity is zero. Fig. 11(a) also demonstrates that approximately doubling the gland flux while ENaC activity is doubled will increase the depleted volume back to 5 μm when CFTR activity is zero.

Figure 11.

(a) Iso-H curves of CFTR activity vs ENaC activity for H_p = 5 μm, (b) plot of PCL height versus evaporation constant, J_evap.

Evaporation

We are interested in how evaporation rates could affect predicted values of PCL height in basal conditions, and therefore subtract a constant term J_evap from Eq. (45). Novotny & Jakobsson calculated ASL evaporation rates to be 4.34 × 10⁻⁸ L/m².s (4.34×10⁻⁵ μm/s), from measured daily water loss from the lung and estimated lung surface area, (Novotny & Jakobsson, 1996a). Therefore we solve the system using H_p as the eigenvalue, varying J_evap.

Fig. 11(b) shows a that increasing PCL evaporation decreases PCL height from a basal value of H_p = 5 μm, as expected. The function is non-linear, suggesting that evaporation becomes less important for smaller H_p values. We also see that for J_evap = 4.34 × 10⁻⁵ μm/s, our model predicts a nominal decrease in PCL height, namely to H_p = 4.99 μm. These results indicate that in basal conditions, PCL evaporation rates may be insignificant. Further studies will be required to test how evaporation affects PCL hydration in CF conditions.

Discussion

In this paper we have presented a theoretical model of fluid recycling through secretion via submucosal glands and absorption through ciliated epithelia that line the lungs. We focus on predicting important factors that influence fluid transport and PCL height, salt concentration and pH levels in cystic fibrosis conditions, implementing two current major theories. We have demonstrated that a combination of increased ENaC activity and decreased SMG flux is mostly likely responsible for depleted PCL volume and acidified PCL seen in CF conditions. We have also shown that it is likely the glands dominate over ENaC activity to decrease the amount of transepithelial fluid transported in CF, while still depleting PCL volume. Additionally, spatial variation is necessary to fully capture the details of fluid flow across a line of epithelial cells.

This model is fundamentally based on a three compartment model introduced by Curran & Solomon in 1957 and further developed in 1962, who demonstrated the correlation between the concentration of luminal salt and the rate of volume flow in isolated rat small intestines. This was accounted for by passive water transport via active solute transport by the basolateral NaKATPase and NKCC cotransporter. A number of mathematical models of airway epithelia have been similarly constructed (Hartmann & Verkman, 1990; Duszyk & French, 1991; Novotny & Jakobsson, 1996a; Warren et al., 2009; Falkenberg & Jakobsson, 2010; Garcia et al., 2013). However, most have focused on airway epithelia secreting fluid rather than absorbing, therefore fluid recycling methods rely solely on evaporative fluxes. Many include the possibility of paracellular transport only for particular ions (Warren et al., 2009; Novotny & Jakobsson, 1996a; Palk et al., 2010; Falkenberg & Jakobsson, 2010; Whitcomb & Ermentrout, 2004). We have assumed all ions can travel paracellularly as there is no definitive evidence for the affinity of the tight junction (Poulsen et al., 2006, Flynn et al., 2009, Miller, 1992). Additionally, we have not included fluid flow through the tight junctions, as paracellular water transport is almost nil in ‘leaky’ epithelia such as renal proximal tubules in AQP1 knockout mice and canine kidney cells (Kovbasnjuk et al., 1998; Schnermann et al., 1998).

Unlike previous models, our model predicts the water permeability of both membranes. We calculate the apical membrane permeability by setting the apical water flux equation at equilibrium to $J_a^w=0.0119\mathrm{\mu }\mathrm{m}/\mathrm{s}$, as found by Jiang et al. (1993) in tracheal cultures, which predicts a value of L_a = 1490 μm/s. Then we solve for the basolateral membrane permeability by equating apical water flux to basolateral water flux, and predict a value of L_b = 790 μm/s, almost half of that across the apical membrane. This indicates the basolateral membrane permeability is much less than the apical, as found in bronchial and tracheal cell cultures (Farinas et al., 1997; Matsui et al., 2000). Although past models have used values between 22-360 μm/s, in vivo values have been estimated to be much higher in airways due to the large volume of transcellular water transport and unstirred layer effects (Folkesson et al., 1994; Matsui et al., 2000).

The novel aspect of this model contribution to current airway epithelial cell transport models is its spatial aspect, coupling SMG fluid secretion to absorptive epithelia. We track PCL movement and implement an extra symmetric boundary condition which is satisfied by adjusting a particular system parameter. We estimated the volumetric water flux secreted from the glands to be 1.92 μm/s in basal conditions for H_p = 5 μm. For one gland per 1 mm² of tracheal surface area, the volumetric flow rate becomes 1.92 × 10⁶ μm³/s. The secretory rate of fluid from submucosal glands has been measured in various airway epithelia from human trachea to porcine bronchi and has been estimated between 2.2×10⁵ to 1.1 ×10⁴ μm³/s in volumetric flow rates assuming one gland per 1 mm² (Choi et al., 2009; Jiang et al., 1997; Salinas et al., 2005; N. S. Joo et al., 2001; Ballard et al., 1999; N. Joo et al., 2009; Wine & Joo, 2004). We believe that our predicted value may be overestimated due to the fixed value of fluid absorption across the cells at equilibrium as mentioned in the previous paragraph. If we had used an absorption rate of 0.0025 μm/s as found by Fang et al. (2005), the gland flux value (and potentially the membrane water permeabilities) may have been an order of magnitude smaller.

Some experiments show that the root cause of CF pathogenesis starts from abnormally tethered mucins secreted from glands (Hoegger et al., 2014; Stoltz et al., 2010) and that newborn porcine airways show no initial infection. Thus the authors concluded that mucociliary defects are secondary to tethered mucins that negatively charge the PCL and increase the viscosity. In our model, we assume mucin volume remains constant as a constituent for impermeable osmolytes in the PCL, and leave variable volume contribution as future extensions of our work.

We do not include second messengers such as Ca²⁺ or cAMP as Warren et al. (2009) and Hartmann & Verkman (1990), instead we opt for constant open channel probabilities, some of which were predicted from the steady state model and are listed in Table 3. These were found by setting Eqs. (46)-(50) to zero at equilibrium and solving Eqs. (51)-(58). An extension to our model would be to incorporate intracellular Ca²⁺ dynamics to explore the influence on PCL volume, as we include ‘theoretical’ Ca²⁺-activated channels.

Our steady state model contains a number of limitations. For example, there can be no net transepithelial ion or water transport, as flux into the cell must equal to the flux out of the cell. We have assumed that the SMGs are the dominant contribution of fluid to PCL volume, therefore we cannot model the effects of zero SMG fluid flux. However, we can predict behaviour in vivo with vastly reduced flux (≈ 97%), where the PCL will almost completely deplete, and some epithelia will switch to secreting fluid to rehydrate the PCL. In distal airways with no glands, current theories regarding fluid recycling are based on continuous epithelia that alternate between secreting and absorbing in a spatial pattern (Shamsuddin & Quinton, 2012). We therefore know these surface epithelia can switch direction of water flow depending on the need for PCL hydration.

Although there is no experimental evidence for basolateral voltage-sensitive ${\text{HCO}}_3^{-}$ and H⁺ channels, it was necessary to include them to balance ${\text{HCO}}_3^{-}$ and H⁺ fluxes. This becomes of particular importance when simulating CFTR knockout, as we have no alternate ${\text{HCO}}_3^{-}$ efflux from the apical membrane and so ${\text{HCO}}_3^{-}$ influx through the basolateral NBC must be balanced. Previous models did not require such channels, as steady state spatial behaviour was not a focus.

To attempt to account for the extreme hyperpolarisation of the apical membrane seen in experiments performed by Boucher et al. (1998) in CF cultures with amiloride, we added an apical NHE1 and simulated the application of amiloride by decreasing the activity of both apical and basolateral NHE1s and the ENaC in CF conditions. We found that the absence of the exchangers coupled with reduced ENaC activity still hyperpolarised the apical membrane at equilibrium, but not to the same extent as our previous simulations shown in Fig. 7(b). Therefore the NHE1 is most likely not responsible for the severe hyperpolarisation of the apical membrane. We are unsure what mechanism could cause this behaviour and could not reconcile this in our model.

Known ion fluxes and electrochemical driving forces under resting conditions have been recorded in primary cultures of human airway epithelia by Willumsen & Boucher (1991). Our model predicts an equilibrium sodium absorptive flux across the apical membrane of 6.0 amol/μm².s and electrochemical driving force of 70 mV, close to those found by Willumsen & Boucher of 3.28 ± 1 amol/μm².s and 63.1 mV. Additionally, the maximum chloride secretory flux across the apical membrane is found to be -1.5 ± 0.8 amol/μm².s in rabbit nasal epithelium by Röpke et al. (1996), close to our model prediction of -2.46 amol/μm².s at equilibrium. Comparable model and experimental values indicate physiologically relevant NaCl fluxes through the bulk of the cell membranes.

Model predictions in CF conditions were simulated by decreasing CFTR activity independently and with increasing ENaC activity and/or decreasing SMG secretion flux. Although doubling ENaC activity increased equilibrium water flux, combining this theory with reduced SMG flux shows a vast reduction in water flux, indicating less fluid is absorbed in vivo in CF conditions. We showed that increasing ENaC activity decreases equilibrium PCL salt in vivo, implying that the ENaC is responsible for any disruption in PCL natural innate defense molecules in CF via salt imbalance. PCL height is shown to decrease with reduced CFTR activity, to a maximum of 1.23 μm with combined theories, signifying that a depleted PCL height is caused by a compromise in both ENaC activity and SMG flux. We determined that the total amount of fluid absorbed through surface epithelia differs significantly when comparing the amount absorbed calculated via a full numerical solution to an equilibrium approximation. Therefore we conclude that a spatial model is necessary to represent total water flux through epithelia, as the equilibrium approximation is not a good representation of the total amount of fluid absorbed.

We focus on modelling the effects of dehydration of the PCL only, as we believe the gel surrounding the cilia may be the most important factor in CF and we are not trying to construct a complete model of fluid recycling. Additionally, we assume that the cilia beat back and forth and provide no net PCL movement. To account for net movement, we would add (subtract) a constant term from Eq. (1), which would decrease (increase) the absorption of water across the cells, and therefore would require less (more) secretion from the glands to satisfy the symmetric boundary condition.

Conclusions

The greatest spatial gradient occurs at x = 0 μm in the numerical solutions for all system variables under basal conditions (apart from PCL water velocity). These results indicate the importance of cells in close proximity to the glands in regulating PCL height through ion/fluid transport mechanisms. Model results show the cells closest to the gland will start secreting fluid to replenish the PCL with elevated ENaC activity, indicating the importance of a spatial model with reference to fluid transport. Additionally, these results indicate the importance of examining the influence of gland secretion in CF more closely, and perhaps should be more of a focus for procuring experimental data in CF research.

The most important mechanism being compromised in CF is PCL height, according to the volume and secretion hypothesis. Our model results were able to demonstrate a higher sensitivity to changes in ENaC over CFTR activity whilst varying SMG flux secretion, indicating that restoring ENaC (rather than CFTR) function, may be more beneficial to CF patients to restore a healthy PCL volume.

Figure 2.

Schematic representation of a single cell with ion channels included in the model. AQP aquaporins, CFTR cystic fibrosis transmembrane conductance regulator, ENaC epithelial Na⁺ channel, CaCC Ca²⁺-activated Cl⁻ channel, Kv7 K⁺ voltage-gated channel, HKATPase - H⁺-K⁺ ATPase pump, BCC basolateral Cl⁻ channel, Functional and molecular characterisation of an anion exchanger in airway serous epithelial cells ${\text{Na}}^{+}{\text{HCO}}_3^{-}$ cotransporter, BHC basolateral ${\text{HCO}}_3^{-}$ channel, NKCC Na⁺-K⁺-2Cl⁻ cotransporter, NaKATPase Na⁺-K⁺ pump, NHE1 Na⁺-H⁺ exchanger, BHyC basolateral H⁺ channel, CaKC Ca²⁺-activated K⁺ channel.

Appendix 1: Impermeable Osmolytes in the PCL

For simplicity, we assume impermeable osmolytes do not degrade or are transported away with net PCL movement, which forces the particles to be defined as uncharged or electroneutral. Assuming electrogenic impermeable ions results in including them into the electroneutrality condition, so we have:

$${[{\text{Na}}^{+}]}_p+{[{\mathrm{K}}^{+}]}_p+{[{\mathrm{H}}^{+}]}_p-{[{\text{Cl}}^{-}]}_p-{[{\text{HCO}}_3^{-}]}_p-\frac{X_p}{A_a{H}_p}=0,$$

where the impermeable ions have a negative charge. Taking the differential with respect to x at steady state:

$$\begin{array}{c}\frac{d}{\mathit{\text{dx}}}{[{\text{Na}}^{+}]}_p+\frac{d}{\mathit{\text{dx}}}{[{\mathrm{K}}^{+}]}_p+\frac{d}{\mathit{\text{dx}}}{[{\mathrm{H}}^{+}]}_p-\frac{d}{\mathit{\text{dx}}}{[{\text{Cl}}^{-}]}_p-\frac{d}{\mathit{\text{dx}}}{[{\text{HCO}}_3^{-}]}_p-\frac{d}{\mathit{\text{dx}}}\frac{X_p}{A_a{H}_p}=0,\\ -J_{\text{Na}}-J_{\mathrm{K}}-J_{\text{Hy}}+J_{\text{Cl}}+J_{{\text{HCO}}_3}+{[{\text{Na}}^{+}]}_p{J}_a^w+{[{\mathrm{K}}^{+}]}_p{J}_a^w+{[{\mathrm{H}}^{+}]}_p{J}_a^w-{[{\text{Cl}}^{-}]}_p{J}_a^w-{[{\text{HCO}}_3^{-}]}_p{J}_a^w-\frac{W_p}{A_p}\frac{d{X}_p}{\mathit{\text{dx}}}=0.\end{array}$$

We know from Eq. (57):

$$J_a^w({[{\text{Na}}^{+}]}_p+{[{\mathrm{K}}^{+}]}_p+{[{\mathrm{H}}^{+}]}_p-{[{\text{Cl}}^{-}]}_p-{[{\text{HCO}}_3^{-}]}_p-\frac{W_p}{A_p{J}_a^w}\frac{d{X}_p}{\mathit{\text{dx}}})=0,$$

and from our electroneutrality condition, we see that:

$$\frac{d{X}_p}{\mathit{\text{dx}}}=\frac{J_a^w}{W_p{H}_p}{X}_p.$$

We now replace the apical flux $J_a^w$ with the relationship $H_p\frac{d}{\mathit{\text{dx}}}{W}_p=-J_a^w$, giving us the following separable equation:

$$\begin{array}{c}\frac{d{X}_p}{\mathit{\text{dx}}}=\frac{d{W}_p}{\mathit{\text{dx}}}\frac{1}{W_p}{X}_p,\\ W_p\frac{d{X}_p}{\mathit{\text{dx}}}+X_p\frac{d{W}_p}{\mathit{\text{dx}}}=0,\\ \frac{d}{\mathit{\text{dx}}}(W_p{X}_p)=0.\end{array}$$

Now we integrate both sides with respect to x and find the expression:

$$X_p{W}_p=C.$$

Implementing the boundary condition W_p(L) = 0 indicates C = 0. We know that W_p changes over x, so therefore the only valid solution is that the number of charged ions in the PCL is zero. We therefore contend that X_p governs impermeable osmolytes that are electroneutral, and do not contribute to the electroneutrality of the PCL.

Appendix 2: Bicarbonate Buffer System

We have the following differential equations for ${\text{HCO}}_3^{-}$, H⁺ and carbon dioxide in the PCL at steady state:

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{HCO}}_3^{-}]}_p{W}_p)=J_{\mathrm{H}\mathrm{p}}-J_{\text{CFTR}}^{\text{HCO}3}-J_t^{\text{HCO}3},$$ (61)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{CO}}_2]}_p{W}_p)=-J_{\mathrm{H}\mathrm{p}}-J_{\text{CO}2\mathrm{a}},$$ (62)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\mathrm{H}}^{+}]}_p{W}_p)=J_{\mathrm{H}\mathrm{p}}-J_{\text{Hk}}-J_t^{\mathrm{H}},$$ (63)

Where $J_{\mathrm{H}\mathrm{p}}=k^{+}{[{\text{CO}}_2]}_p-k^{-}{[{\mathrm{H}}^{+}]}_p{[{\text{HCO}}_3^{-}]}_p$, due to the law of mass action. By adding Eq. (62) to Eqs. (61) and (63), we find:

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{HCO}}_3^{-}]}_p{W}_p)+H_p\frac{d}{\mathit{\text{dx}}}({[{\text{CO}}_2]}_p{W}_p)=-J_{\text{CFTR}}^{\text{HCO}3}-J_t^{\text{HCO}3}-J_{\text{CO}2\mathrm{a}},$$ (64)

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\mathrm{H}}^{+}]}_p{W}_p)+H_p\frac{d}{\mathit{\text{dx}}}({[{\text{CO}}_2]}_p{W}_p)=-J_{\text{HK}}-J_t^{\mathrm{H}-}-J_{\text{CO}2\mathrm{a}}.$$ (65)

Giving us the following equations:

$$\frac{d}{\mathit{\text{dx}}}({[{\text{HCO}}_3^{-}]}_p{W}_p)=\frac{X_1-K{[{\text{HCO}}_3^{-}]}_p{W}_p(\frac{d}{\mathit{\text{dx}}}{[{\mathrm{H}}^{+}]}_p)}{H_p{K}_H},$$ (66)

$$\frac{d}{\mathit{\text{dx}}}({[{\mathrm{H}}^{+}]}_p{W}_p)=\frac{X_2-K{[{\mathrm{H}}^{+}]}_p{W}_p(\frac{d}{\mathit{\text{dx}}}{[{\text{HCO}}_3^{-}]}_p)}{H_p{K}_{\text{HC}}},$$ (67)

where

$$\begin{array}{c}{X}_1=-J_{\text{CFTR}}^{\text{HCO}3}-J_t^{\text{HCO}3}-J_{\text{CO}2\mathrm{a}},\\ X_2=-J_{\text{HK}}-J_t^{\mathrm{H}}-J_{\text{CO}2\mathrm{a}},\\ K_H=1+\frac{k^{-}}{k^{+}}{[{\mathrm{H}}^{+}]}_p,\\ K_{\text{HC}}=1+\frac{k^{-}}{k^{+}}{[{\text{HCO}}_3^{-}]}_p.\end{array}$$

Rearranging Eq. (66) and substituting into Eq. (67), we get an expression for ${[{\mathrm{H}}^{+}]}_p^{\prime }$:

$$\frac{d}{\mathit{\text{dx}}}{[{\mathrm{H}}^{+}]}_p=\frac{K_H(X_2+{[{\mathrm{H}}^{+}]}_p{J}_a^w(1+2K{[{\text{HCO}}_3^{-}]}_p))-K{[{\mathrm{H}}^{+}]}_p{X}_1}{W_p(K_{\text{HC}}{K}_H+K^2{[{\text{HCO}}_3^{-}]}_p{[{\mathrm{H}}^{+}]}_p)}.$$ (68)

Substituting this expression into Eq. (47), we get the following:

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\text{HCO}}_3^{-}]}_p{W}_p)=Z_1=\frac{X_1}{K_H}-\frac{K{[{\text{HCO}}_3^{-}]}_p}{K_H}\frac{K_H(X_2+{[{\mathrm{H}}^{+}]}_p{J}_a^w(1+2K{[{\text{HCO}}_3^{-}]}_p))-K{[{\mathrm{H}}^{+}]}_p{X}_1}{(K_{\text{HC}}{K}_H+K^2{[{\text{HCO}}_3^{-}]}_p{[{\mathrm{H}}^{+}]}_p)}.$$ (69)

Similarly, we get an expression for ([H⁺]_pW_p)′:

$$H_p\frac{d}{\mathit{\text{dx}}}({[{\mathrm{H}}^{+}]}_p{W}_p)=Z_2=\frac{X_2}{K_{\text{HC}}}-\frac{K{[{\mathrm{H}}^{+}]}_p}{K_{\text{HC}}}\frac{K_{\text{HC}}(X_1+{[{\text{HCO}}_3^{-}]}_p{J}_a^w(1+2K{[{\mathrm{H}}^{+}]}_p))-K{[{\text{HCO}}_3^{-}]}_p{X}_2}{(K_H{K}_{\text{HC}}+K^2{[{\text{HCO}}_3^{-}]}_p{[{\mathrm{H}}^{+}]}_p)}.$$ (70)