Probabilistic approach to lysozyme crystal nucleation kinetics

Abstract

Nucleation of lysozyme crystals in quiescent solutions at a regime of progressive nucleation is investigated under an optical microscope at conditions of constant supersaturation. A method based on the stochastic nature of crystal nucleation and using discrete time sampling of small solution volumes for the presence or absence of detectable crystals is developed. It allows probabilities for crystal detection to be experimentally estimated. One hundred single samplings were used for each probability determination for 18 time intervals and six lysozyme concentrations. Fitting of a particular probability function to experimentally obtained data made possible the direct evaluation of stationary rates for lysozyme crystal nucleation, the time for growth of supernuclei to a detectable size and probability distribution of nucleation times. Obtained stationary nucleation rates were then used for the calculation of other nucleation parameters, such as the kinetic nucleation factor, nucleus size, work for nucleus formation and effective specific surface energy of the nucleus. The experimental method itself is simple and adaptable and can be used for crystal nucleation studies of arbitrary soluble substances with known solubility at particular solution conditions.

Introduction

Crystallization of proteins is an important issue in a number of contemporary science fields and related industrial sectors, e.g., molecular biology, bionanotechnology, pharmacy, etc. Nucleation of crystals is crucial for overall crystallization behavior and outcome. It is a stochastic process and is characterized by the formation of nanoscopic clusters of a new phase called nuclei, which are in labile equilibrium with the old phase of the substance they are made of [1]. Further attachment of growth units to the nuclei drastically reduces the probability for their decomposition and such clusters grow to macroscopic size. The knowledge of protein crystal nucleation and growth is of particular importance. On the one hand, X-ray diffraction of single crystals is the most recognized and reliable method for protein molecular structure determination so far. It requires large and defect-free crystals, which can be obtained by appropriate control over crystal nucleation and growth. On the other hand, there are routine industrial processes involving crystal nucleation and growth phenomena, which require a number of specific solutions, especially in the pharmaceutical industry.

In the present paper, we consider an approach for experimental determination of nucleation probabilities in quiescent lysozyme crystallization solutions and quantify important parameters of crystal nucleation. Relevant probabilistic approaches have already been used in nucleation studies of water [2], tin [3], electrocrystallization of mercury [4], amino acids [5], and isonicotinamide [5, 6] in stirred solutions.

The proposed experimental method provides the possibility for profound analysis of crystal nucleation and could serve as a good prognostic and control tool on a laboratory or large crystallization scale.

Theoretical basis

As nuclei appear randomly in time, the probability P to form at least one supernucleus until time t is given by [2–4, 7]:

$$P\left(t\right)=1-e^{-N\left(t\right)}$$ 1

where N is the mean number of supernuclei. When nucleation occurs at stationary nucleation rate J in a system of volume V, N increases linearly with t (t ≥ t_g) according to [7]:

$$N\left(t\right)=JV\left(t-t_g\right)$$ 2

where t_g is the time taken by the supernucleus to grow to a given detectable size. For t < t_g we have N (t) = 0, because the nuclei have not yet exceeded the detectable size. Combining Eqs. (1) and (2) yields, for (t ≥ t_g):

$$P\left(t\right)=1-e^{-JV\left(t-t_g\right)}$$ 3

According to the classical nucleation theory (CNT), the stationary nucleation rate is given by [1, 7]:

$$J\left(s\right)=A{e}^{\left(s-B/s^2\right)}$$ 4

where s = ln (C/C_e) is the supersaturation, with C and C_e being the actual solute concentration and solubility, respectively, A is a practically s-independent kinetic factor and for spherical nuclei the thermodynamic parameter B is expressed as [1]:

$$B=16\pi {v_m}^2{{\gamma }_{ef}}^3/3{\left(k_{B}T\right)}^3$$ 5

where v_m is the molecular volume, γ_ef is the effective specific surface energy, k_B is the Boltzmann constant and T is absolute temperature.

Finally, for isothermal nucleation from a low-density old phase, the size of the crystal nucleus n^* is related to experimentally obtainable J (s) according to [1, 8]:

$$n^{*}=d\left(lnJ\right)/ds-1$$ 6

Experimental section

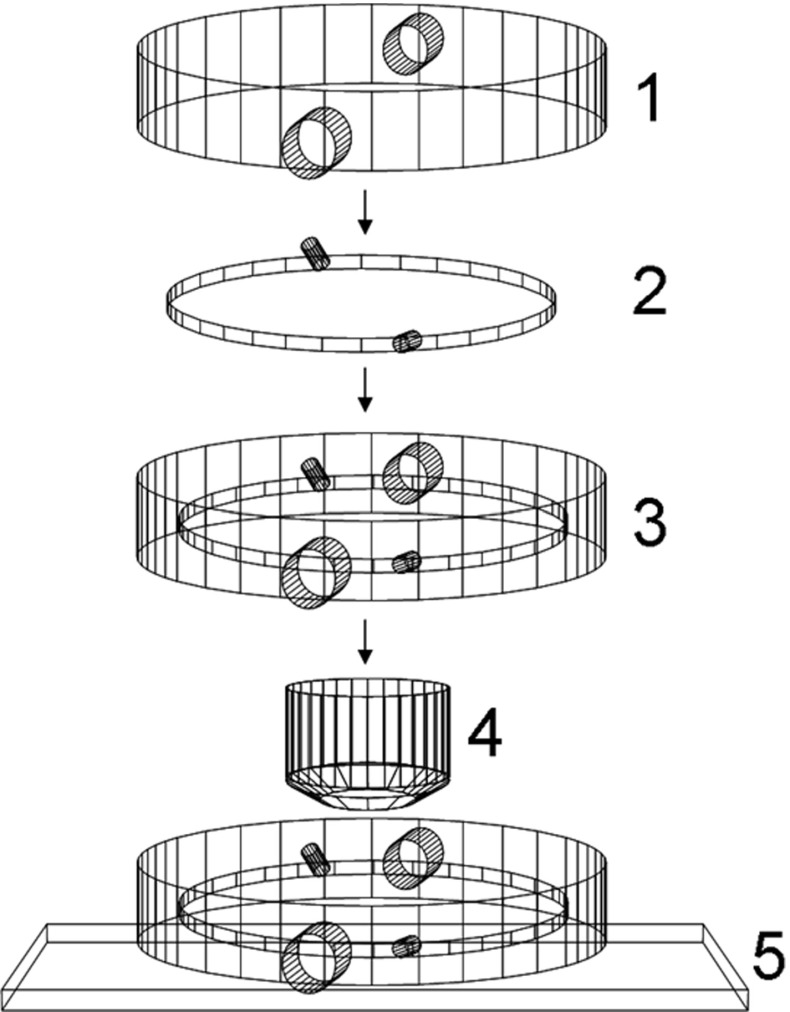
All experiments were performed in a closed transparent crystallization cell in a batch crystallization setup. The construction of the cell is shown in Fig. 1. Chicken egg white lysozyme (Sigma, 3x crystallized) was used at six different concentrations, defining a particular supersaturation under the following other conditions: sodium chloride 5% (w/v), 0.1 M sodium acetate buffer, pH 4.0, temperature of 22 °C. At these conditions the lysozyme solubility is reported to be 2.12 mg/ml, determined with an accuracy of ±0.1 mg/ml or better [9]. The experimental setup contains the following elements:

1. Glass jacket with water inlet and outlet.

2. Quasi-two-dimensional cell made of two optically flat glass circular plates fused at the periphery in a parallel position, closing in a small void volume. The distance between the plates is 100 μm.

3. The cell integrated in the glass jacket.

4. Microscope objective.

5. Microscope stage.

Fig. 1.

Crystallization cell

Lysozyme powder was dissolved in the buffer and the solution was left to equilibrate at 22 °C for 15 min. The precipitant solution (sodium chloride 5% (w/v)) was equilibrated separately. The two solutions were than mixed thoroughly at 22 °C and immediately injected into the crystallization cell at that temperature. The crystallization system was sealed with two Teflon caps to prevent evaporation. The cell was inspected repeatedly for detectable crystals in a number of fixed crystallization volumes under a light microscope and detection size was 1 μm (which is the minimum size of an inhomogeneous object that could be detected under the used magnification (100x)). The experimental setup allowed us to keep track of the object size evolution with time and to clearly state if it was a crystal or not. Both inner surfaces of the crystallization cell were inspected for crystals.

All individual experiments to determine P offer two mutually exclusive outcomes, namely absence of detectable crystals or presence of at least one detectable crystal. Then, for any given t, the probability P is calculated from the expression:

$$P=N^{+}/\left(N^{+}+N^{-}\right)$$ 7

where N⁺ and N⁻ denote the number of positive and negative outcomes at time t, respectively.

In order to collect more data from the single crystallization setup we used a grid system that fixed 25 single crystallization volumes. The single crystallization volume V inspected in the present study was 3.14 × 10⁻¹⁰ m³. Time intervals t were deliberately chosen as 18 discrete time intervals, the detection event being recorded at the end of each one.

Results

Nucleation parameters

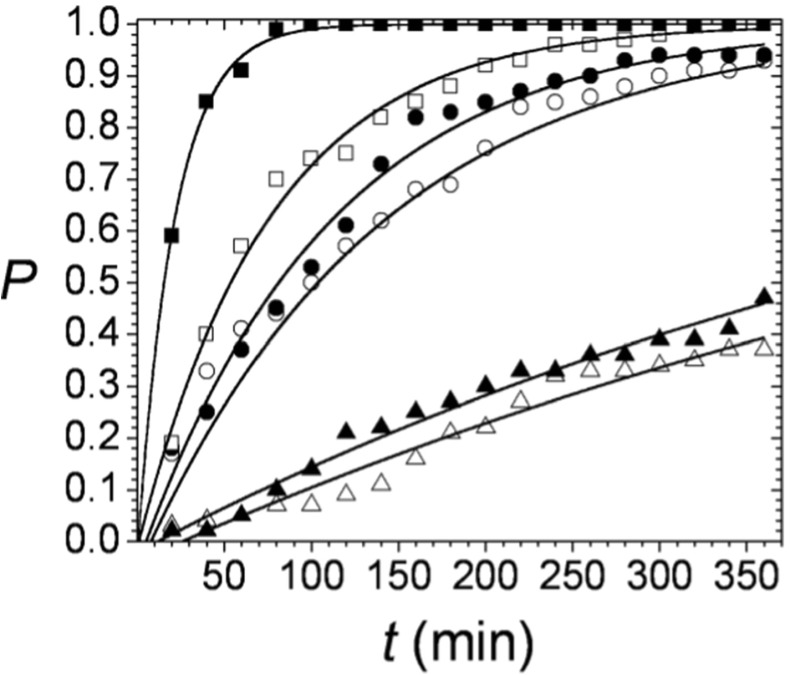
One hundred separate sample crystallization volumes were inspected for P determination at each t according to Eq. (7). The calculated probabilities for six different protein concentrations are plotted vs. time in Fig. 2.

Fig. 2.

Time dependence of the probability to form at least one detectable lysozyme crystal. Each value is a result of 100 single sample volume inspections. The solid lines represent fits of Eq. (3). to the experimental data. Lysozyme concentrations: △ - 8.66 mg/ml; ▲ - 9.66 mg/ml; ○ - 10.66 mg/ml; ● - 11.66 mg/ml; □ - 12.66 mg/ml; ■ - 15.33 mg/ml

Solid lines in Fig. 2 represent fits of Eq. (3). to the experimental data, with two free parameters, JV and t_g. The obtained values for J and t_g for the six lysozyme concentrations are given in Table 1.

Table 1.

J and t _g for six lysozyme concentrations^a

C (mg/ml)	J (m−3 sec−1)	t g (min)
8.66	(0.79 ± 0.04) × 105	26.8 ± 8.9
9.66	(0.94 ± 0.04) × 105	12.6 ± 6.5
10.66	(3.84 ± 0.23) × 105	8.2 ± 5.7
11.66	(4.84 ± 0.21) × 105	5.4 ± 3.4
12.66	(6.96 ± 0.27) × 105	1.2 ± 2.4
15.33	(2.47 ± 0.11) × 106	0.8 ± 1.1

^aThe standard errors of the fitting parameters of Eq. (3). are represented by ± values

Equation (4) allows us to plot the experimental data in J-vs.-s coordinates and fit them to the experimental data, with two free parameters, A and B. In turn, with the help of Eq. (5), we can calculate the effective specific surface energy γ_ef at the nucleus/solution interface. In case of homogeneous nucleation, γ_ef = γ. For a spherical nucleus it is expressed as [1, 5]:

$$\gamma =\left(0.514k_{B}T/{v_m}^{2/3}\right)ln\left(1/v_m{C}_e\right)$$ 8

where C_e is the lysozyme solubility in molecules m⁻³. In case of heterogeneous nucleation, γ_ef = ψ × γ. The activity factor 0 < ψ < 1 accounts for heterogeneous nucleation and is responsible for the fact that the heterogeneously formed nucleus requires less work W^* for its formation [1]:

$$W^{*}=16\pi {v_m}^2{{\gamma }_{ef}}^3/3{\left(k_{B}T\right)}^2{s}^2$$ 9

The estimation of γ_ef makes also possible the calculation of the number of lysozyme molecules in a heterogeneously formed crystal nucleus, through the Gibbs-Thomson equation for the nucleus size [1]:

$$n^{*}=32\pi {v_m}^2{{\gamma }_{ef}}^3/3{\left(k_{B}T\right)}^3{s}^3$$ 10

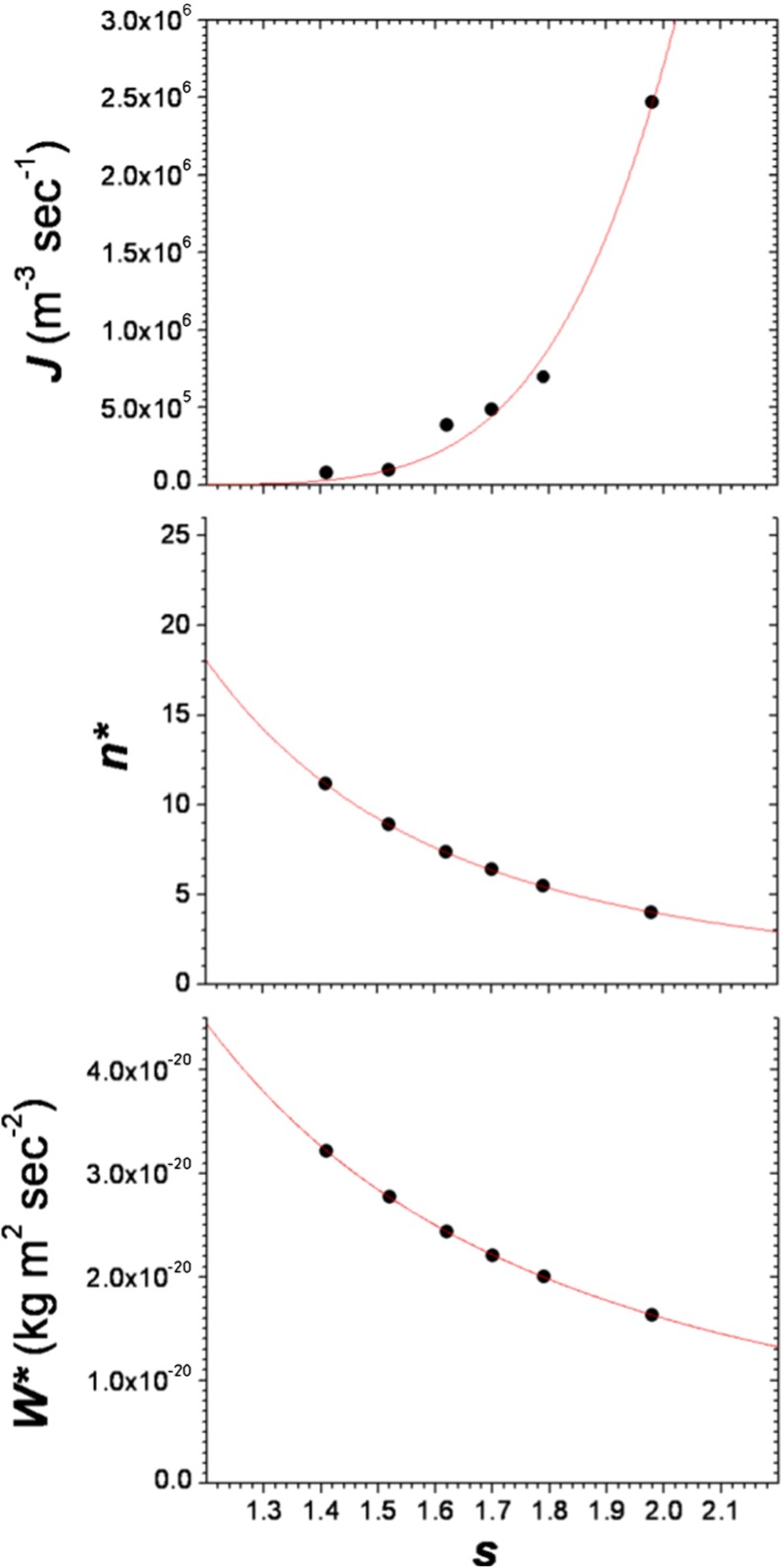
As v_m for lysozyme (tetragonal crystal form, 1 atm) we used the value [10] of 1.5669 × 10⁻²⁶ m³ and C_e (22 °C) = 8.92 × 10²² m⁻³. Plots of J (s) and n^*(s) and W^*(s) are given in Fig. 3. The calculated nucleation parameters are listed in Table 2.

Fig. 3.

Plots of J vs. s, n ^* vs. s and W ^*vs.s. Upper solid line represents the fit of Eq. (4) to the experimental data. The middle solid line represents the fit of Eq. (11). to the data obtained via Eq. (10). The bottom solid line represents the fit of Bk _B T/s ² to the data obtained via Eq. (9)

Table 2.

Kinetic factor A, thermodynamic parameter B, effective specific surface energy γ _ef, specific surface energy γ and activity factor ψ

A (m−3 sec−1)	B	γ ef (mJ m−2)	γ (mJ m−2)	ψ
1.83 × 107	15.65	0.64	2.19	0.29

An important application of the nucleation theorem [1, 8] is that the experimentally determined quantity J (s) can be used for evaluation of the number of lysozyme molecules in the crystal nucleus. Accounting for the significant difference between the lysozyme apparent solution density and crystal density [11], the brief CNT expression [12, 13] for n^* (Eq. 10) can be obtained via differentiating the logarithmic form of Eq. (4) with respect to s and substituting the result into Eq. (6).:

$$n^{*}=2B/s^3$$ 11

Thus if B is determined from the fitting of Eq. (4) to the data, the number of molecules in the crystal nucleus is known.

Mean crystal number

The small crystallization volumes used for the determination of P were examined again when crystal nucleation had already stopped. The grown lysozyme crystals were counted. Results for three different lysozyme concentrations are shown in Fig. 4.

Fig. 4.

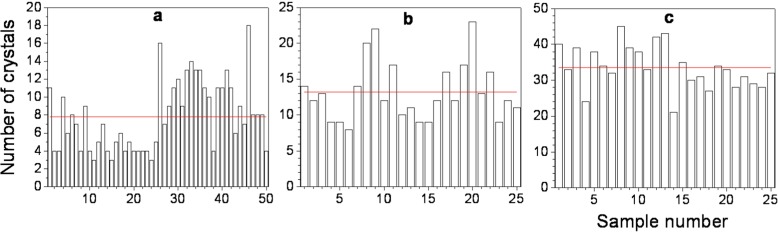
Number of lysozyme crystals per single solution volume at a condition of no further crystal nucleation. a 50 single volumes examined after 21 h for 10.66 mg/ml lysozyme solution; b 25 single volumes examined after 48 h for 12.66 mg/ml lysozyme solution; c 25 single volumes examined after 5 h for 15.33 mg/ml lysozyme solution. Solid lines denote the mean crystal number value

The relative standard deviations for 10.66, 12.66, and 15.33 mg/ml lysozyme are respectively 48.5, 31.2, and 17.61%. This is a reasonable result as lower supersaturations imply poorer crystallization reproducibility.

Crystal growth

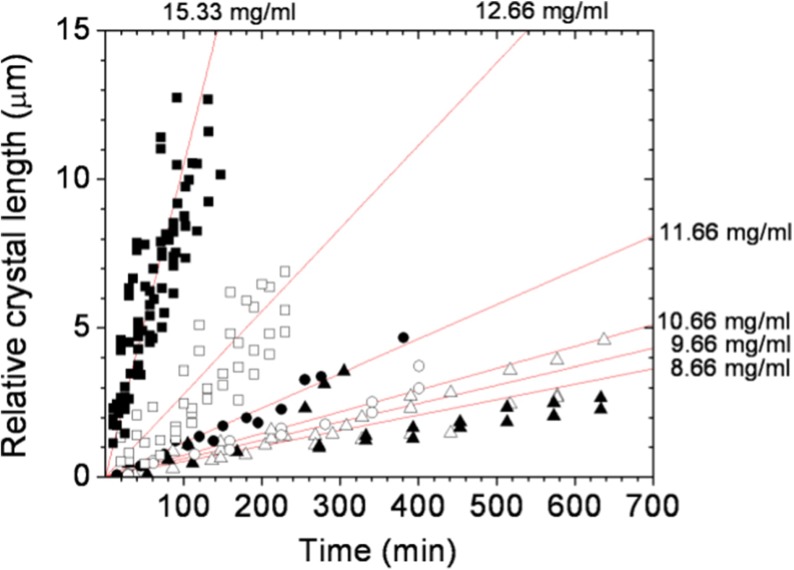
The crystal growth rates for tetragonal lysozyme were estimated to be around 0.002 μm sec⁻¹ for prismatic {110} faces, with a supersaturation ratio of 10 (22 °C, pH 4.0, 0.1 M NaAC) and were observed to drop drastically below a supersaturation ratio of 7.5 (22 °C, pH 4.0, 0.1 M NaAC) [14]. At these conditions, the growth rates of pyramidal {101} faces were alike [15], in spite of the large scatter of the data [16] reported for pH 4.0. However, lysozyme crystallization behavior may often differ even among different batches of the same commercial protein. This is why we performed a supporting crystal growth study with the same lysozyme samples used for the estimation of crystal detection probabilities. The experimental setup (Fig. 1) was significantly modified in order to allow higher microscope magnifications for better image resolution. Disposable glass crystallization cells were used as well. The overall growth rates of tetragonal lysozyme crystals at the early growth stages were determined through image analysis of the time evolution of a single crystal surface area, for all six lysozyme concentrations. The measured areas were then represented as average crystal lengths (Fig. 5). The growth time t_g for the detectable crystal size (1 μm) was then estimated from linear fits to the data, through the relation t_g = m⁻¹, where m is the slope of the linear function (Table 3).

Fig. 5.

Time dependence of the relative crystal length at the early stage of crystal growth. Each solid line represents the averaged linear fit over growth rates of several individual lysozyme crystals. Lysozyme concentrations: △ - 8.66 mg/ml; ▲ - 9.66 mg/ml; ○ - 10.66 mg/ml; ● - 11.66 mg/ml; □ - 12.66 mg/ml; ■ - 15.33 mg/ml

Table 3.

Slopes of the linear curves (shown in Fig. 5) and the respective t _g for six lysozyme concentrations

C (mg/ml)	m	t g (min)
8.66	0.0052 ± 0.00024	192 ± 8.86
9.66	0.0062 ± 0.00022	161 ± 5.71
10.66	0.0073 ± 0.00037	137 ± 6.94
11.66	0.012 ± 0.00041	83 ± 2.84
12.66	0.028 ± 0.0011	36 ± 1.41
15.33	0.11 ± 0.0045	9 ± 0.37

Discussion

Constant supersaturation

The maintenance of constant supersaturation is an obligatory requirement for probability data reproducibility. For all the experimental series and for the entire time interval investigated, we detected one to a few lysozyme crystals per single volume for the least supersaturated solutions (8.66 mg/ml) and up to several crystals at the highest supersaturated solutions (15.33 mg/ml). This was probably the best expected crystallization outcome, as it simultaneously met the requirement for the presence of at least one detectable crystal and the formation of very small total crystalline volume during experimental runs (far below 1% of that volume, which was observed a day or two later). Equation (2) can now be used to check how reasonable is the probability distribution shown in Fig. 2 through the obtained stationary nucleation rates (Table 1). As we are about to consider fairly long time periods, we assume t_g = 0. For example, the mean number of crystals at 360 min (the end of the experimental run) for solutions of 10.66 mg/ml lysozyme is N = 2.6 and for 12.66 mg/ml  N = 4.7 crystals. These values represent accurately the number of experimentally observed detectable crystals. For longer time intervals, N = 9.1 for 10.66 mg/ml (21 h) vs. N = 7.8 (Fig. 4a). This is an expected result as the requirement for constant supersaturation will no longer be valid for longer periods of time, when a considerable amount of lysozyme will be in crystalline form. For 12.66 mg/ml lysozyme (48 h) we get N = 37.8 and N = 13.2 (Fig. 4b), for the predicted and experimentally observed crystals, respectively. This trend is similar to that for 10.66 mg/ml lysozyme and it is reasonable to expect a larger difference for a more supersaturated solution as dissolved lysozyme is being converted to the crystalline phase faster. In solutions of 15.33 mg/ml lysozyme, however, for 5 h it was predicted N = 14 vs. N = 33.6 (Fig. 4c). This result appears to reflect a limitation of the present experimental setup, which will be considered below.

Probability for nucleation

Bearing in mind the probability definition (Eq. 3) and the experimental setup used in this study (Fig. 1), it is obvious that there will be such lysozyme concentrations (or respective experimental times) beyond which we will practically always get the probability values of 0 and 1. Such values (e.g., Fig. 2, concentration of 15.33 mg/ml lysozyme, times ≥ 100 min) could affect the fit quality of the probability function and would eliminate the possibility of recalculating probabilities for an arbitrary nucleation volume, V_a. The probability P(V_a) at constant J, t and t_g can be estimated by dividing Eq. (3). solved for V_a, by the solution for V:

$$P_{\left(V_a\right)}=1-{\left(1-P_{\left(V\right)}\right)}^{V_a/V}$$ 12

where V is the used nucleation volume. For example, if we measured P(V) = 0.75 in a volume of 5 μl, for 15 μl we would obtain a probability of 0.98 and for a volume of 1 μl, a probability of 0.24. It is obvious that this equation will not work with the probabilities of zero and unity. So we suggest a criterion for an adjustment of the experimental volume that would improve the measured probability:

$$1-{\left(1-P_{\left(V\right)}\right)}^{V_{a*}/V}=0.5$$ 13.1

and

$$V_{a*}=-\frac{0.69V}{ln\left(1-P_{\left(V\right)}\right)}$$ 13.2

where V_a* is the adjusted volume, where the probability for detection of at least one crystal and the probability for detection of no crystals are equal. For example, if we measured P(V) = 0.9 in a volume of 5 μl, we should use a new volume of 1.5 μl. This will amend the accuracy of the measured probability and explain the odd results for the mean crystal number at 15.33 mg/ml lysozyme discussed above. The adjusted volumes have to be different not just for different lysozyme concentrations but also for different crystallization times. This, however, would require quite a sophisticated and dynamic experimental setup. Note that the suggested criterion will basically only lower the chance of having zero and unity probabilities. As there is generally at least one measured probability value between 0 and 1, Eq. (13.2) can be used as a good optimization tool for a single crystallization volume. This will result in the absence of zero and unity values of the measured probabilities in quite a large number of experimental trials, times and concentrations. Normally, the measured probability will improve with the number of detections.

As mentioned in the experimental section, the (cylindrical) detection volumes were only 100 μm in height. Therefore, the sedimentation of bulk nucleated crystals should be taken into account as well, because of a possible impact on the probability measurement accuracy. The terminal velocity, U, of a spherical particle falling vertically in a fluid is given by [17]:

$$U=\frac{2g{r}^2}{9\eta }\left({\rho }_p-{\rho }_f\right)$$ 14

where g is the acceleration due to gravity, r is the radius of the particle, η is the fluid absolute viscosity and ρ_p and ρ_f are the particle and fluid densities, respectively. With g ≈ 9.81 m sec⁻², η ≈ 1.09 mP sec [18], ρ_p ≈ 1.24 g cm⁻³, ρ_f ≈ 1.036 g cm⁻³ [11], we obtain a maximum settling time of about 16 min for a crystal of size 1 μm. That time is comparable to the length of the detection interval (20 min) and the settling of bulk crystals will generally have a negligible effect on the probability measurement accuracy. Finally, the inspection of all crystallization volumes in a single setup took a few minutes for every t.

Considering the relatively small concentration variations in our experimental series and the presumable drawbacks discussed above, Fig. 2 represents an acceptable probability distribution of nucleation times, based on 100 individual detections for every single P(t) determination. Refitting the probability data with one free parameter function (Eq. 3, fixed t_g), we obtained parameters JV that fell in the standard errors of parameters JV of the initial two free parameters fit, except for the 10.66 mg/ml lysozyme data in the upper range of t_g.

As expected, the obtained values for t_g (Table 1) show inverse dependence on lysozyme concentration. More important, however, are the large deviations in t_g and the relatively low values of t_g, especially at highest lysozyme concentrations. First of all, this could be attributed to the intrinsic impurity content of protein solutions, especially in the considered case, where a variety of aggregates are expected to be present, which are likely to distort nucleation kinetics [19]. The second reason might be in the method of solution preparation. Here, we used direct mixing of protein and precipitant solution at the nucleation temperature. This could lead to spurious nucleation upon mixing, which would be generally manifested by a few non-zero measured probabilities at the initial times, with a greater effect at lower lysozyme concentrations (Fig. 2). A common practice to overcome this effect is an incubation of protein crystallization solutions at a temperature significantly higher than the temperature of the solubility limit. However, this would result in a more complicated interpretation of the nucleation events, considering the possible solution processes accompanying cooling to the desired supersaturation and leading to less reproducible nucleation [6], or irreversible lysozyme conformational changes upon heating [20]. Reasonably, the independent crystal growth measurement study (Fig. 5) led to the obtaining of t_g values one order of magnitude higher (Table 1 vs. Table 3), implying that the processes involved in the supernucleus formation might be different from those involved in the early crystal growth stage.

Nucleation parameters

The calculated stationary nucleation rates are similar to lysozyme crystal nucleation rates obtained by other methods [21–24], although there could be a strong dependence on the particular crystallization system composition and the type of nucleation (homogeneous or heterogeneous). The effective specific surface energies provided by these authors are quite close (generally, below 1 mJ m⁻²) to the one evaluated here (Table 2, γ_ef). The activity factor (Table 2, ψ) suggests predominant heterogeneous nucleation, which is in good agreement with the expected natural presence of a variety of impurities in solution samples of commercial lysozyme [19]. The walls of the crystallization solution container have a minor contribution to heterogeneous nucleation, even at a high ratio of wall surface to solution volume [25]. The obtained kinetic parameter (Table 2, A) is similar to that obtained for lysozyme nucleation at relevant crystallization conditions [13]. Values in the order of 10⁷–10⁹ m⁻³ sec⁻¹ are relatively low. This parameter is proportional to the concentration of heterogeneous nucleation sites and the crystal growth-unit attachment frequency [1]. The attachment frequency could be the term appearing to determine the relatively low value of A, as proteins possess highly heterogeneous molecular surfaces [26] and because of this the proper molecular orientation becomes very important [27]. The calculated lysozyme crystal nucleus size (Fig. 3, n^*(s)) is on the same order of magnitude as calculated elsewhere [13].

Conclusions

A method for the investigation of protein crystal nucleation in small volumes of a quiescent solution was presented. It relied on the stochastic nature of crystal nucleation. The developed approach is based on the sampling of equal crystallization solution microliter volumes, simply for presence or absence of detectable crystals at arbitrary discrete time intervals. The experimental setup was adaptable and easily tunable to the crystallization conditions, duration of experimental trials and sampling volumes and could be used in an automation strategy for a better estimation of the crystal detection probabilities. Possible applications may include crystallization screening protocols, crystal growth optimization procedures and control over crystallization on a laboratory or industrial scale. The presented approach allowed direct or indirect calculation of basic crystal nucleation parameters, such as the stationary nucleation rate, nucleus size, nucleation work and specific nucleus surface energy. It demonstrated a good capacity for the prediction of the overall crystallization behavior and as such could be successfully used, e.g., for particular modification of crystalline suspensions for pharmaceutical formulations. Valuable information for the type of crystal nucleation (heterogeneous or homogeneous) could also be obtained. Finally, the dependence n^*(s) (Fig. 3) might be used for the exploration of supersaturations at which spinodal decomposition could eventually occur (i.e., supersaturations where n^* is expected to be of growth-unit size).