Stochastic predictors from the DXA scans of human lumbar vertebrae are correlated with the microarchitecture parameters of trabecular bone

Abstract

The purpose of this study was to provide a novel stochastic assessment of inhomogeneous distribution of bone mineral density (BMD) from the Dual-energy X-ray Absorptiometry (DXA) scans of human lumbar vertebrae and identify the stochastic predictors that were correlated with the microarchitecture parameters of trabecular bone.

Eighteen human lumbar vertebrae with intact posterior elements from 5 cadaveric spines were scanned in the posterior-anterior projection using a Hologic densitometer. The BMD map of human vertebrae was obtained from the raw data of DXA scans by directly operating on the transmission measurements of low- and high-energy X-ray beams. Stochastic predictors were calculated by fitting theoretical models onto the experimental variogram of the BMD map, rather than grayscale images, from DXA scans. In addition, microarchitecture parameters of trabecular bone were measured from the 3D images of human vertebrae acquired using a Micro-CT scanner.

Significant correlations were observed between stochastic predictors and microarchitecture parameters. The sill variance, representing the standard deviation of the BMD map to some extent, had significantly positive correlations with bone volume, trabecular thickness, trabecular number and connectivity density. The sill variance was also negatively associated with bone surface to volume ratio and trabecular separation.

This study demonstrates that the stochastic assessment of the inhomogeneous distribution of BMD from DXA scans of human lumbar vertebrae can reveal microarchitecture information of trabecular bone. However, future studies are needed to examine the potential of stochastic predictors from routine clinical DXA scans in providing bone fragility information complementary to BMD.

1. Introduction

Clinical evaluation of areal bone mineral density (BMD) in the central skeleton by Dual-energy X-ray Absorptiometry (DXA) has proven its efficacy in predicting the risk of osteoporotic fractures in the spine (WHO, 2003). However, BMD measurements from DXA have limitations (Genant et al., 1996) and cannot account for other factors associated with fracture risks (Hui et al., 1988; Marshall et al., 1996). For example, the distribution of BMD within the human vertebrae is not homogeneous (Banse et al., 2001; Briggs et al., 2006). The standard deviation of regional bone mineral density in human vertebrae has been shown to strongly correlate with the fracture load of the vertebral bodies (Cody et al., 1991; Kim et al., 2007). In a previous study (Dong et al., 2013), we have used a novel stochastic approach to assess the inhomogeneity of 2D projection images generated from 3D Micro-CT scans of trabecular bone. Significant relationships were found between the sill variance, one of stochastic predictors, and biomechanical properties and microarchitecture parameters of trabecular bone (Dong et al., 2013). The objective of this study was to extend the stochastic method to assess the inhomogeneity of BMD from DXA scans of human lumbar vertebrae. The hypothesis for this study was that the sill variance of bone mineral density from DXA scans of human lumbar vertebrae was significantly correlated with the microarchitecture parameters of trabecular bone within the vertebral body.

2. Materials and Methods

2.1 Specimen Preparation

Eighteen fresh lumbar vertebrae were obtained from cadaver spines of five tissue donors (4 males and 1 female; Age: 70±10 years old; range: 57 to 81 years old). Detailed descriptive statistics of the tissue donors are available in the Table 1. The cadaver spines were acquired from National Disease Research Interchange (Philadelphia, PA) and screened for known bone diseases. In order to identify human vertebrae with fractures, Vertebral Fracture Assessment (VFA) was performed on the cadaver spines using a Hologic densitometer (QDR Discovery W, Bedford, MA). No pre-existing vertebral fractures were observed by a radiologist. After the human vertebrae with intact posterior elements were dissected from the cadaver spine, the vertebral specimens were wrapped with gauze and stored at −25°C until further examination.

Table 1.

Descriptive statistics of tissue donors.

Subject	Age	Gender	Cause of Death	Vertebrae
1	57	M	Respiratory Failure	L1, L2, L3, L4, L5
2	81	M	Alzheimer’s Disease	L1, L2, L3, L4, L5
3	79	M	Subarachnoid Hemorrhage	L4
4	76	F	Respiratory arrest	L1, L2, L3
5	63	M	Melanoma	L1, L2, L3, L4

2.2 DXA Scans of Human Vertebrae

Human vertebrae with intact posterior elements were scanned in the posterior-anterior (PA) projection (Fig.1a) using the Hologic densitometer. Posterior elements were retained in the vertebral specimen to simulate the in vivo situation for clinical DXA scans. Prior to scanning, an anthropometric spine phantom supplied by the manufacturer was scanned to monitor scanner precision. During the scan, the vertebral specimens were fully submerged under water in a plastic container to mimic the soft tissue in the human body (Ebbesen et al., 1998; Perilli et al., 2012). The human vertebrae were scanned using the Express mode by choosing the default settings of “AP Lumbar Spine” scans in the Hologic densitometer. Analysis of the scan in the PA projection was performed by following the standard lumbar spine protocol described by Hologic (Hologic, 2010). Bone mineral density (BMD, g/cm²), bone mineral content (BMC, g), and projected bone area (cm²) were reported by the Hologic densitometer for each vertebra.

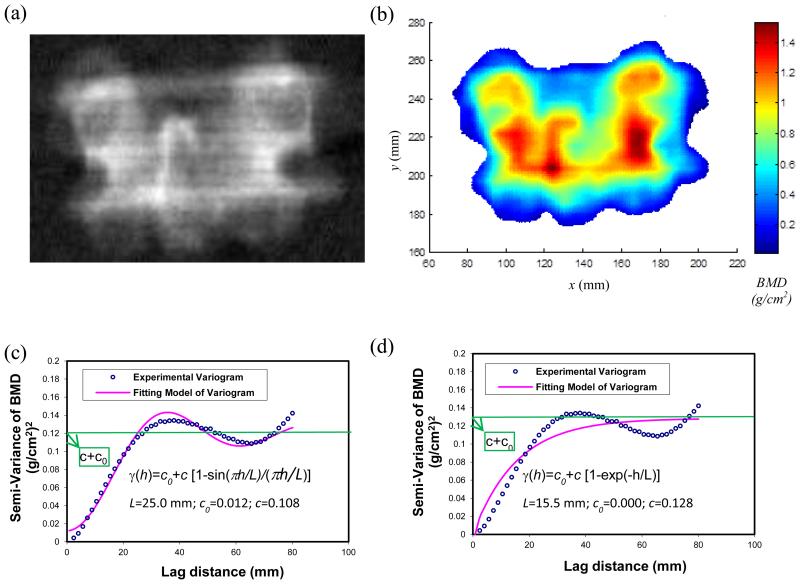
Figure 1.

Calculation of stochastic predictors from the BMD map of human vertebrae. (a) A DXA image of a human vertebra in the PA projection from Hologic densitometers; (b) A typical BMD map obtained from the raw data of DXA scans of human vertebrae; (c) A hole-effect fitting model of the experimental variogram of the BMD map. The stochastic predictors, correlation length (L), sill variance (c) and nugget variance (c₀), were extracted from the hole-effect model; and (d) An exponential fitting model of the experimental variogram of the BMD map.

In addition, the values of T-score for human vertebral specimens were reported from the DXA scan of the cadaver spine, rather than the DXA scan of the individual vertebrae. The DXA scan of the whole cadaver spine was close to the clinical conditions in which the T-score was normally used.

2.3 Extraction of the BMD map from DXA scans

The BMD map of human vertebrae (Fig.1b) in this study was obtained from the raw data (i.e., R files in Hologic densitometers) of DXA scans by directly operating on the transmission measurements of low-energy and high-energy X-ray beams (Stein, 1989; Blake et al., 1992; Blake and Fogelman, 1997; Blake et al., 1999). There were two reasons for extracting the BMD map straightly from the raw data, rather than using the DXA image (Fig.1a) provided by the densitometer. First, grayscale values in the DXA image were not the exact value of bone mineral density of human vertebrae. Second, grayscale values in DXA images could be easily affected by varying the brightness and the contrast of these DXA images.

Details of obtaining the BMD map from the raw data of DXA scans are available in the literature (Stein, 1989; Blake et al., 1992; Blake and Fogelman, 1997; Blake et al., 1999). One of major challenges in extracting the BMD map was to understand the use of an internal reference system in Hologic densitometers to accommodate the drift in the X-ray tube, the effect of beam hardening, and the differences in patient thickness (Stein, 1989). An important feature of the internal reference system was its ability to calculate the mass attenuation coefficients of soft tissue and bone on every scan line and provide continuous calibration of the densitometer (Stein, 1989; Blake and Fogelman, 1997). The current method of extracting the BMD map from the raw data of DXA scans was validated in another study (Dong et al., 2015). The BMD map was obtained from a software package developed by the authors (Dong et al., 2015). The software package is available for research use upon request.

2.4 Stochastic assessment of inhomogeneity in the BMD map

The spatial variation of the BMD map (Fig.1b) from DXA scans of human vertebrae was described by an experimental variogram (Fig.1c). The concept of experimental variograms was described in the previous studies (Dong et al., 2010; Dong et al., 2013; Dong et al., 2015) and is also available in the Appendix 1. A hole-effect model (Ma and Jones, 2001; Webster and Oliver, 2001) was used to characterize the trend in the experimental variogram (Fig.1c) in which the semi-variance decreased from its maximum to a local minimum and then increased again. Additionally, an exponential model (Fig.1d) was used to compare with the hole-effect model.

The stochastic predictors, correlation length (L), sill variance (c) and nugget variance (c₀), were obtained from both hole-effect and exponential models. The correlation length was a distance parameter defining the spatial extent of the model. The nugget variance was the positive intercept on the axis of semi-variance (Fig.1c). The sill variance was a priori variance of the random field when the nugget variance was not present. The experimental variogram may reach its sill variance asymptotically (Fig.1d). When the nugget variance was present, the sill variance became a partial sill (Fig.1c). The sum of sill variance and nugget variance was the converging value of variance when the lag distance approached infinity (i.e. the global variance in the BMD map), which gave rise to a measure of magnitude of spatial variation of BMD map.

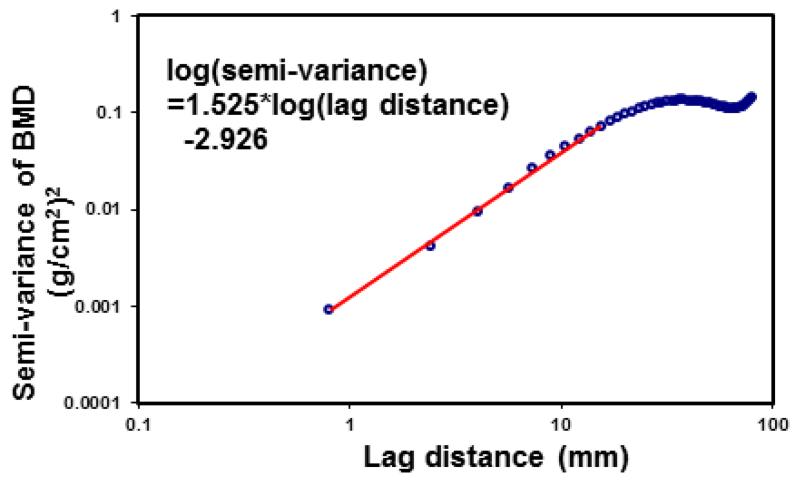
2.5 The slope of the experimental variogram of the BMD map

In order to compare with the Trabecular Bone Score (TBS), a parameter determined from the grayscale analysis of DXA images (Pothuaud et al., 2008; Pothuaud et al., 2009; Hans et al., 2011; Winzenrieth et al., 2013; Silva et al., 2014), the slope at the origin of the log-log representation of experimental variograms of the BMD maps was calculated using the linear least squares fitting technique (Fig.2). The slope represented the initial trend of the experiment variogram. On the other hand, stochastic predictors, correlation length, sill variance and nugget variance, were derived from theoretical models of random fields that captured the underlying mechanisms of the experimental variogram.

Figure 2.

The slope at the origin of the log-log representation of the experimental variogram was calculated using the linear least squares fitting technique. The slope of the experimental variogram is a parameter similar to the earliest description of Trabecular Bone Score (TBS) (Pothuaud et al., 2008; Pothuaud et al., 2009).

2.6 Microarchitecture parameters from 3D Micro-CT images of trabecular bone

3D images of human vertebrae with intact posterior elements were acquired using a Micro-CT scanner (GE eXplore Locus, GE Healthcare, London, ON, Canada) with a resolution of 93μm. Scans were performed with an X-ray tube voltage 80 kVp, current 450μA, number of views 200, and exposure time 90 milliseconds. Three consecutive scans were performed to cover the whole vertebra with intact posterior elements. A single volume of Micro-CT image was then created by stitching three scans together.

A volume of interest (VOI) was chosen to include only trabecular bone within the vertebral body. A global thresholding method was used to segment Micro-CT images with the threshold value automatically determined inside the volume of interest. Microarchitecture parameters of trabecular bone within the vertebral body were obtained through the Advanced Bone Analysis tool of the software package from the Micro-CT manufacturer (Microview 2.0, GE Healthcare, London, ON, Canada). The following microarchitecture parameters were obtained: bone volume fraction (BV/TV), bone surface to volume ratio (BS/BV), trabecular thickness (Tb.Th), trabecular number (Tb.N), trabecular separation (Tb.Sp) and the connectivity density (Con.Den). The units of these microarchitecture parameters followed a report from the ASBMR histomorphometry nomenclature committee (Parfitt et al., 1987).

2.6 Statistical analyses

Statistical analyses were performed with SPSS (Version 20, IBM, Armonk, NY) with a significance level at p<0.05. Pearson correlation analyses were performed to study the relationships among DXA measurements of human lumbar vertebrae, stochastic predictors from the BMD map and microarchitecture parameters of trabecular bone. Before the Pearson correlation analysis, Shapiro-Wilk tests were used to examine the normality of these parameters. Additionally, paired Student’s t-tests were conducted to compare the stochastic predictors from the hole-effect model with the exponential model. Next, we tested whether stochastic predictors were correlated with the microarchitecture parameters of trabecular bone after the removal of the effect of BMD using a statistical procedure called a partial correlation. Finally, multiple regression analysis was performed with the stochastic predictor as the response variable, and the microarchitecture parameters as the exploratory variables.

3. Results

Descriptive data derived from the DXA measurements of human vertebrae, stochastic predictors from DXA scans of human vertebrae and microarchitecture parameters of trabecular bone within the vertebral body were summarized in Table 2. The normality of these variables was evaluated with Shapiro-Wilk tests and all variables had normal distribution (Table 2).

Table 2.

Descriptive statistics of DXA measurements of human vertebrae, stochastic predictors from the BMD map of human vertebrae, and microarchitecture parameters of trabecular bone within the vertebral body.

	Avg.±S.D.	Range	p-value
DXA parameters
BMD (g/cm2)	0.941±0.084	0.749~1.089	0.108(a)
BMC (g)	16.95±2.25	12.540~20.570	0.776(a)
Area (cm2)	18.06±2.16	14.64~21.33	0.411(a)
T-score	−0.6±0.8	−2.4~0.5	0.435(a)
Stochastic predictors
Hole-effect model
Correlation length (mm)	27.6±4.9	17.7~35.3	0.469(a)
Sill variance (g/cm2)2	0.115±0.021	0.075~0.150	0.623(a)
Nugget variance (g/cm2)2	0.017±0.012	0~0.041	0.293(a)
Exponential model
Correlation length (mm)	17.3±2.6	13.1~21.2	0.408(a)
Sill variance (g/cm2)2	0.151±0.032	0.08~0.21	0.797(a)
Nugget variance (g/cm2)2	0.000±0.00	0.000~0.000	(b)
Paired differences between hole-effect and exponential models
Correlation length (mm)	10.3±5.0	−3.21~15.2	0.000(c)
Sill variance (g/cm2)2	−0.036±0.015	−0.0673~−0.00699	0.000(c)
Nugget variance (g/cm2)2	0.017±0.012	0.00568~0.0408	0.000(c)
Slope of experimental variograms
Slope	1.510±0.038	1.447~1.606	0.469(a)
Microarchitecture parameters
BV/TV (%)	21.6±4.5	14.6~28.5	0.198(a)
BS/BV (mm2/mm3)	8.857±0.809	7.415~10.037	0.517(a)
Tb.Th (mm)	0.228±0.021	0.199~0.270	0.446(a)
Tb.N (1/mm)	0.941±0.133	0.733~1.158	0.456(a)
Tb.Sp (mm)	0.856±0.170	0.622~1.165	0.300(a)
Con.Den (1/mm3)	0.922±0.232	0.580~1.340	0.393(a)

^(a)The significance value of a Shaprio-Wilk test indicates whether the data are normal distribution. A p-value of less than 0.05 means the deviation away from the normal distribution.

^(b)The significance value of a Shaprio-Wilk test cannot be computed because at least of one of the variables is constant.

^(c)The significance values from the Student’s t-tests for paired samples.

3.1 T-score of human vertebrae

Only the T-score values of L1-L4 vertebrae were available in the DXA scan of cadaver spines using the Hologic densitometer. Therefore, two L5 vertebrae were excluded from the results and only the T-score values of sixteen human vertebrae were reported. Overall, the human vertebrae in this study were normal since the average value of T-score was −0.6 (Table 2). Specifically, there were eleven normal vertebrae (T-score was greater than −1.0); there were five vertebrae with osteopenia (T-score was between −2.5 and −1.0). None of these human vertebrae were osteoporotic.

3.2 Stochastic predictors from the hole-effect model and the exponential model

Paired Student’s t-tests indicated that significant differences of stochastic predictors were observed between the hole-effect model and exponential model (Table 2). The correlation length and the nugget variance from the hole-effect model was significantly (p<0.001) greater than those from the exponential model (Table 2). The sill variance from the hole-effect model was significantly (p<0.001) less than that from the exponential model (Table 2).

The sill variance from the hole-effect model was strongly (r=0.925, p<0.001) correlated with the sill variance from the exponential model. However, neither the correlation length (r=0.240, p=0.338) nor the nugget variance (r=−0.057, p=0.822) from the hole-effect model had significant relationships with those from the exponential model.

3.3 Stochastic predictors vs. microarchitecture parameters

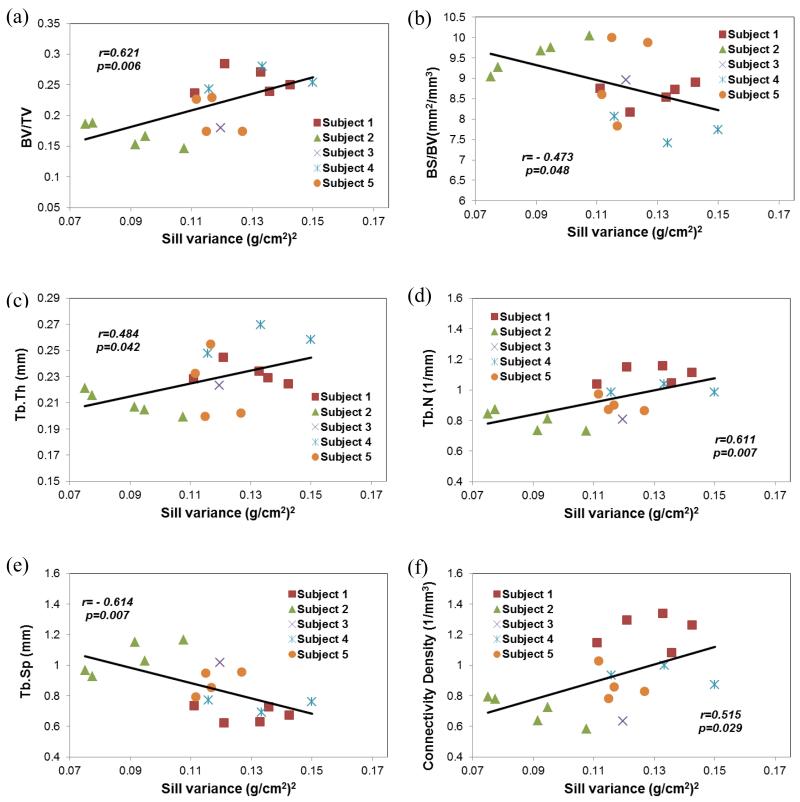
For the hole-effect model, significant correlations were found between the sill variance and the microarchitecture parameters of vertebral trabecular bone (Table 3, Figure 3). The sill variance had significantly positive correlations with the bone volume fraction (r=0.621, p<0.01), trabecular thickness (r=0.484, p<0.05), trabecular number (r=0.611, p<0.01) and connectivity density (r=0.515, p<0.05). The sill variance was also negatively correlated with the bone surface to volume ratio (r=−0.473, p<0.05) and trabecular separation (r=−0.614, p<0.01). The correlation length and the nugget variance from the BMD map were not significantly correlated with microarchitecture parameters of trabecular bone (Table 3).

Table 3.

Correlations of microarchitectural parameters with stochastic predictors and DXA parameters.

		BV/TV	BS/BV	Tb. Th	Tb. N	Tb. Sp	Con.Den
Hole-effect model
L	r (a)	.044	.043	−.005	.048	−.067	−0.017
	p-value (b)	.863	.865	.984	.851	.792	0.945
c	r (a)	.621**	−.473*	.484*	.611**	−.614**	0.515*
	p-value (b)	.006	.048	.042	.007	.007	0.029
c0	r (a)	.051	−.063	.116	−.026	−.021	−0.133
	p-value (b)	.840	.804	.646	.919	.934	0.598
Exponential model
L	r (a)	.284	−.211	.225	.281	−.322	0.190
	p-value (b)	.254	.401	.370	.259	.192	0.449
c	r (a)	.596**	−.440	.459	.586**	−.600**	0.469*
	p-value (b)	.009	.068	.055	.011	.009	0.049
c0	r (a)	(c)	(c)	(c)	(c)	(c)	(c)
	p-value (b)
Slope of experimental variograms
Slope	r (a)	−.006	−.153	.165	−.111	.064	−.124
	p-value (b)	.982	.544	.514	.661	.802	.624
DXA parameters
BMD	r (a)	.325	−.203	.233	.333	−.333	.271
	p-value (b)	.188	.420	.353	.176	.176	.277
BMC	r (a)	−.263	.371	−.359	−.147	.203	−.064
	p-value (b)	.291	.129	.143	.562	.419	.801
Area	r (a)	−.532*	.548*	−.556*	−.418	.478*	−.280
	p-value (b)	.023	.019	.017	.085	.045	.260

^(a)Pearson correlation coefficient

^(b)The significance value (p-value) from the Pearson correlation analysis

^(c)The significance value (p-value) cannot be computed because at least one of the variables is constant

^**Correlation is significant at the 0.01 level.

^*Correlation is significant at the 0.05 level.

Figure 3.

Sill variance of the BMD map from DXA scans of human vertebrae had significant relationships with the microarchitecture parameters of trabecular bone within the vertebral body. (a) bone volume fraction (BV/TV); (b) bone surface-to-volume ratio (BS/BV); (c) trabecular thickness (Tb.Th); (d) trabecular number (Tb.N); (e) trabecular separation (Tb.Sp); and (f) connectivity density.

Similar results were observed for the exponential model (Table 3). Significant correlations were observed between the sill variance and bone volume fraction, trabecular number, trabecular separation and connectivity density. The correlations between the sill variance and bone surface to volume fraction (r=−0.440, p=0.068) and trabecular thickness (r=0.459, p=0.055) were marginally significant. The correlation length and nugget variance had no significant (p>=0.192) relationships with microarchitecture parameters of trabecular bone.

3.4 Slope of experimental variogram vs. microarchitecture parameters

The slope from the experimental variogram had weak positive Pearson correlation coefficients with the trabecular thickness and the trabecular separation, and weak negative Pearson correlation coefficients with the bone volume fraction, the bone surface to volume ratio, trabecular number and connectivity density (Table 3). However, none of these correlations were statistically significant (p>=0.514).

3.5 DXA measurements vs. microarchitecture parameters

BMD and BMC from the PA projection of human vertebrae with intact posterior elements had no significant relationships (p>=0.143) with microarchitecture parameters of trabecular bone within the vertebral body (Table 3).

However, the area from the PA projection had correlations with bone volume fraction (r=−0.532, p=0.023), bone surface to volume ratio (r=0.548, p=0.019), trabecular thickness (r=−0.556, p=0.017), and trabecular separation (r=0.478, p=0.045). The area in the PA projection had marginally significant correlation (r=−0.418, p=0.085) with trabecular number. The area in the PA projection had no significant correlation (r=−0.280, p=0.260) with connectivity density.

3.6 DXA measurements vs. stochastic predictors

BMD from the PA projection of human vertebrae had significantly positive correlation (r=0.820, p<0.001) with the sill variance from the hole-effect model (Table 4). No other significant relationships were observed between DXA measurements and stochastic predictors (Table 4).

Table 4.

Correlations between DXA measurements and stochastic predictors from DXA scans of human vertebrae based on hole-effect model.

		L	c	c0
BMD	r (a)	.042	.820**	.307
	p-value (b)	.868	.000	.216
BMC	r (a)	−.081	.307	−.009
	p-value (b)	.750	.216	.973
Area	r (a)	−.118	−.280	−.240
	p-value (b)	.640	.260	.338

^(a)Pearson correlation coefficient

^(b)The significance value (p-value) from the Pearson correlation analysis

^**Correlation is significant at the 0.01 level.

3.7 Partial correlation analysis

The partial correlation analysis indicated that the sill variance remained significantly correlated with the bone volume fraction (r=0.655, p=0.004), bone surface to volume ratio (r=−0.546, p=0.023), trabecular thickness (r=0.527, p=0.030), trabecular number (r=0.625, p=0.007), trabecular separation (r=−0.631, p=0.007), and connectivity density (r=0.531, p=0.028) after controlling the association of BMD.

3.8 Multiple regression analysis

The multiple regression analysis provided further information about the relationship between the sill variance from DXA scans and the microarchitecture parameters of trabecular bone (Table 5).

Table 5.

Multiple regression analysis between the sill variance (c) and microarchitecture parameters. The regression model was c ~ constant+BV/TV+BS/BV+Tb.N+Tb.Sp+Con.Den. The R-squared value and the adjusted R-squared value for the regression were 0.687 and 0.517, respectively. The p-value from the F-test in the ANOVA table of the regression analysis was 0.022.

Predictors	Coef.(a)	Std. Error(b)	t (c)	p- value(d)
(constant)	−5.122	1.979	−2.589	0.025
BV/TV	−5.472	2.636	−2.076	0.062
BS/BV	0.158	0.071	2.218	0.049
Tb.Th	11.494	4.752	2.419	0.034
Tb.N	2.247	0.895	2.509	0.029
Tb.Sp	0.514	0.268	0.029	0.082
Con.Den	−0.162	0.094	0.113	0.113

^(a)The regression coefficient from the multiple regression model. The coefficient label constant in the table is the intercept of the regression model.

^(b)The standard error of the coefficients

^(c)The test statistic t was equal to the coefficient divided by the standard error.

^(d)The p-value was computed under the t test statistic.

4. Discussion

Eighteen human vertebrae with intact posterior elements were scanned by the densitometer in the posterior-anterior projection and by the Micro-CT scanner. The stochastic predictors were calculated using the experimental variogram of the BMD map from the DXA scans of human vertebrae. The microarchitecture parameters were obtained from 3D Micro-CT images of trabecular bone within the vertebral body. Our results supported the hypothesis that the sill variance, one of stochastic predictors from DXA scans, was significantly correlated with the microarchitecture parameters of trabecular bone.

The relationships between stochastic predictors and microarchitecture parameters observed in this study were independent of theoretical models fitted over the experimental variogram. Although the magnitudes of stochastic predictors from the hole-effect and exponential models were significantly different (Table 2), the sill variance from the hole-effect model was significantly correlated with that from the exponential model. Therefore, it is not unexpected that microarchitecture parameters of trabecular bone were significantly correlated with the sill variance not only from the hole-effect model, but also from the exponential model (Table 3). Nevertheless, the hole-effect model may better represent the trend of experimental variograms from DXA scans of human lumbar vertebrae in which the semi-variance of the BMD decreased from its maximum to a local minimum and then increased again (Fig.1c).

The significant relationships between the sill variance of DXA scans and microarchitecture parameters were consistent with our previous study of 2D projection images generated from 3D Micro-CT images of trabecular bone (Dong et al., 2013). In the previous study of 2D projection images generated from 3D Micro-CT images of trabecular bone, we have also observed that the sill variance was positively correlated with bone volume fraction, trabecular thickness, and trabecular number, and was negatively correlated with bone surface to volume ratio and bone separation (Dong et al., 2013). Therefore, we have demonstrated that the stochastic assessment of inhomogeneous bone mineral density can be extended from 2D projection images to DXA scans.

We have attempted to compare stochastic assessment of DXA scans of human lumbar vertebrae with the Trabecular Bone Score (TBS), a textural index evaluating pixel gray-level variations in the lumbar spine DXA image (Silva et al., 2014). In the earliest description of TBS (Pothuaud et al., 2008; Pothuaud et al., 2009), TBS was defined as the slope at the origin of the log-log representation of the experimental variogram of DXA images. In this study, we have calculated the slope of experimental variograms of the BMD map, a parameter similar to the earliest description of the TBS. No significant correlations were observed between the slope of experimental variograms and microarchitecture parameters (Table 3). Nevertheless, the signs of Pearson correlation coefficients in this study were in agreement with the study by Pothuaud and colleagues (Pothuaud et al., 2008). Both the slope of the experimental variogram in this study and the earliest version of TBS at the lumbar spine (Pothuaud et al., 2008) had negative correlation coefficients with the bone volume fracture (BV/TV) and trabecular number (Tb.N), and positive correlation coefficients with the trabecular thickness (Tb.Th) and trabecular separation (Tb.Sp).

The more recent versions of the TBS are a black box algorithm based on fractional Brownian motion (Hans et al., 2011; Winzenrieth et al., 2013). A commercialized software package (TBS iNsight Software, Med-Imaps, Pessac, France) can be used to compute the more recent versions of the TBS. The TBS was found to have significant relationships with microarchitecture parameters of trabecular bone (Hans et al., 2011; Roux et al., 2013; Winzenrieth et al., 2013). TBS had significant positive correlations with bone volume fraction, trabecular number and connectivity density, and negative correlations with trabecular separation and trabecular thickness (Hans et al., 2011; Winzenrieth et al., 2013).

The negative relationship between TBS and trabecular thickness is a concern because this seems to contradict what we know about trabecular microarchitecture and strength (Bousson et al., 2012). One possible explanation is that the relatively low resolution of Micro-CT (93 μm) images in these studies is insufficient for the evaluation of the microarchitecture of trabecular bone (Winzenrieth et al., 2013). In another study, negative Pearson correlation coefficient between TBS and trabecular thickness was still observed when Micro-CT images of human vertebrae were acquired with a resolution of 35 μm (Roux et al., 2013). This implies that resolution of Micro-CT images is not the cause for such negative correlation. It is noted that a weak and non-significant correlation (r²=0.032, p=0.345) was observed between the bone volume fraction and the trabecular thickness in the aforementioned study (Winzenrieth et al., 2013). On the other hand, we have observed a strong and significantly positive relationship (r=0.845, p=0.000) between bone volume fraction and trabecular thickness in this study. Consequently, the positive correlation between the sill variance and trabecular thickness in this study is consistent with the existing understanding that a structure with thick trabeculae is stronger than one with thin trabeculae.

It may not be surprising that significant relationships are observed between stochastic predictors of DXA scans and microarchitecture parameters of trabecular bone because both stochastic assessment and microarchitecture quantification share the same underlying principles. Microarchitecture parameters of trabecular bone, such as bone volume fraction, bone surface to volume fraction, trabecular thickness, trabecular separation and connectivity density, can be evaluated by traditional histomorphometry (Parfitt et al., 1987), which is based on stereological techniques (Odgaard, 2009). The underlying principles of stereological techniques come from stochastic geometry (Stoyan et al., 1995; Chiu et al., 2013). Meanwhile, the random field, a major part of stochastic geometry, is also the theoretical basis for the stochastic assessment of the BMD map from DXA scans (Dong et al., 2010; Dong et al., 2013). Therefore, it is expected that there are certain connections between stochastic assessment and microarchitecture quantification. Nevertheless, such connections need to be further explored in the future studies.

The sill variance from DXA scans, to some extent, represents the standard deviation of bone mineral density within human vertebrae, and characterizes the inhomogeneous distribution of bone mineral density. Such variation of bone mineral density has been found to be a good predictor of biomechanical properties of the human vertebral body (Cody et al., 1991). In that study, Cody et al. described the surprising result that the standard deviation of vertebral regional bone mineral density values provided nearly as good as a predictor of fracture load as the densities themselves (Cody et al., 1991). The authors concluded that local remodeling effects, causing point-to-point variations of bone mineral density in specific locations, may ultimately be helpful in predicting fracture risk in conjunction with local bone density analysis (Cody et al., 1991). Therefore, the sill variance observed in this study may reveal the point-to-point variations of bone mineral density due to local bone remodeling.

Our results indicate that the inhomogeneity is positively related to microstructure, implying that more homogeneous vertebra would be a weaker structure. However, there are conflicting results regarding the association between inhomogeneity and strength in bone (Yeh and Keaveny, 1999; Burr, 2003; Kim et al., 2007; Busse et al., 2009). For example, one computational study found that vertebral strength decreased with increasing coefficient of variation (COV) of Micro-CT based gray level density (Kim et al., 2007). Another computational study also found that the increase in the coefficient of variation in trabecular thickness resulted in a reduction in modulus for trabecular bone (Yeh and Keaveny, 1999). On the other hand, there are reports in the literature that a decrease in bone tissue inhomogeneity has resulted in a reduction in the toughness of bone (Burr, 2003; Abel and Ural, 2015).

It is noted that there are several limitations for this study. First, eighteen human vertebrae were obtained from five tissue donors. The number of the subjects is small. The influence of small number of tissue donors on the results of this study is available in the Appendix 2. The further analyses indicate that more subjects are needed in the future study.

Second, only DXA scans of human vertebrae in the PA projection were examined in this study. The rationale is that most of routine clinical scans are performed in the PA projection. Nevertheless, DXA scans in the lateral projection have been considered by some researchers as having more potential in predicting the biomechanical properties of human vertebrae (Ebbesen et al., 1999; Perilli et al., 2012). Therefore, stochastic assessment of inhomogeneous distribution of BMD from lateral DXA scans may be investigated in the future.

Third, the effect of the posterior elements on the assessment of inhomogeneity has not been investigated in the study. This may be an interesting topic for future research. Stochastic predictors can be compared for DXA scans of human vertebrae specimens with intact posterior elements and without posterior elements. In addition, the stochastic assessment can also applied to 2D projection images generated from 3D Micro-CT images of human vertebrae with and without posterior elements.

Additionally, the relationship between stochastic predictors and biomechanical properties of human vertebrae has not been examined in this study. Therefore, future studies will investigate the relationship between stochastic predictors and biomechanical properties of human vertebrae either from mechanical testing (Perilli et al., 2012) and/or large-scale finite element analysis of human vertebrae based on Micro-CT images (Kim et al., 2007; Nekkanty et al., 2010). We can thus address the question whether a combination of stochastic predictors from DXA scans and BMD predicts the strength of human vertebrae better than using BMD alone.

Finally, the stochastic predictors from DXA scans may be influenced by scanner resolution, scan mode, and noise. Furthermore, structural changes and artifacts (e.g., osteophytes and facet sclerosis) may also pose challenges on the calculation of stochastic predictors from DXA scans. Therefore, these issues need to be addressed before such technique can be applied to the clinical settings and provide useful information for patients.

5. Conclusion

This study demonstrates that the stochastic assessment of the inhomogeneous distribution of bone mineral density from DXA scans of human lumbar vertebrae can reveal microarchitecture information of trabecular bone. However, future studies are needed to examine the potential of stochastic predictors from routine clinical DXA scans in providing bone fragility information complementary to BMD.

Appendix

1. Stochastic assessment of inhomogeneity in the BMD map

The spatial variation of the BMD map from the DXA scans of human vertebrae was described by an experimental variogram. The concept of experimental variograms is briefly described here. A semi-variance, γ(h), is defined as the half of the expected squared differences of bone mineral density between any two data locations with a lag distance of h.

$$\gamma \left(\mathbf{h}\right)=\frac{1}{2}E\left[{\left\{Z\right(\mathbf{x})-Z(\mathbf{x}+\mathbf{h}\left)\right\}}^2\right]$$ (1)

where Z(x) is a function to describe the random field of bone mineral density; Both x and h are vectors; x is the spatial coordinates of the data location. Lag distance, h, represents the Euclidean distance and direction between any two data locations.

The experimental variogram is calculated as an average of semi-variance values at different locations that have the same value of lag distance (h).

$$\widehat{\gamma }\left(\mathbf{h}\right)=\frac{1}{2m\left(\mathbf{h}\right)}\sum _{i=1}^{m\left(h\right)}E\left[{\left\{Z\right({\mathbf{x}}_{\mathbf{i}})-Z({\mathbf{x}}_{\mathbf{i}}+\mathbf{h}\left)\right\}}^2\right]$$ (2)

where m(h) is the number of data pairs for the observations with a lag distance of h.

The stationarity of the BMD map as a random field was established by the wavelet-based test of stationarity for locally stationary random fields, which was available in the R software package (Eckley et al., 2010; Nunes et al., 2014). A stationary BMD map indicated that the constancy of mean, variance, and covariance independent of absolute positions (Webster and Oliver, 2001; Chiu et al., 2013). The anisotropy of the BMD map was examined by generating the experimental variograms in the directions of 0°, 30°, 60°, 90°, 120° and 150° and no significant differences were observed for the experimental variograms at various directions. Therefore, the isotropic assumption of the BMD map of human vertebrae as a random field was established.

The experimental variogram of the BMD map from human vertebrae decreased from its maximum to a local minimum and then increased again. A hole-effect model has been used to describe such trend in the experimental variogram in geostatistics (Ma and Jones, 2001; Webster and Oliver, 2001). Therefore, we used the hole-effect model to fit over the experimental variogram to characterize the inhomogeneity of the BMD map. Additionally, an exponential model was used in this study to compare with the hole-effect model. The exponential model can be used to characterize an experimental variogram with monotonic increasing trend and has been used in the previous studies (Dong et al., 2010; Dong et al., 2013; Dong et al., 2015).

The semi-variance (γ) with a hole-effect model and an exponential model can be represented by the following formulas, respectively:

$$\gamma \left(\mathrm{h}\right)=c_0+c[1-\frac{\sin (\pi h∕L)}{\pi h∕L}]$$ (3)

$$\gamma \left(\mathrm{h}\right)=c_0+c(1-e^{-\mathrm{h}∕L})$$ (4)

where γ(h) is the semi-variance of bone mineral density as a function of lag distance (h). L, correlation length, is a distance parameter defining the spatial extent of the model. Correlation length is an important parameter to describe the spatial variation of a random field. A large correlation length implies a smooth variation whereas a small correlation length corresponds to rapid changes in the property over the spatial domain. The c₀, nugget variance, is the positive intercept on the axis of semi-variance. Any apparent nugget variance usually arises from errors of measurement and spatial variation within the shortest sampling interval (Webster and Oliver, 2001). The c, sill variance, is a priori variance of the random field when the nugget variance is not present. The experimental variogram may reach its sill variance asymptotically. When the nugget variance is present, the sill variance becomes a partial sill. The sum of sill variance and nugget variance is the converging value of variance when the lag distance approached infinity (i.e. the global variance in the BMD map), which gives rise to a measure of magnitude of spatial variation of BMD map.

The stochastic assessment was implemented in a software package written in MATLAB (Mathoworks, Natick, MA). The software package is available for research use upon request (Dong et al., 2015). A plugin of stochastic predictors for ImageJ, a public domain program, is currently under development.

2. Correlation coefficients within subjects and between subjects

We performed additional statistical analyses to examine the impact of small number of tissue donors (i.e., subjects) on the results of this study. Specifically, we used the analysis of covariance (ANCOVA) and weighted correlation analysis to examine the Pearson correlation coefficients within subjects and between subjects (Bland and Altman, 1994; Bland and Altman, 1995a; Bland and Altman, 1995b). In the analysis of covariance (ANCOVA), the microarchitecture parameter was the dependent variable, the subject was the independent category variable, and the sill variance was the covariate. We were able to remove the effect between subjects, and only examine the correlation within subjects. We answered the question whether there were significant correlations within an individual. Our results indicated that weak and non-significant relationships (p>=0.128) between the sill variance and microarchitecture parameters were observed within subjects (Table 6).

Table 6.

Correlations of the sill variance and microarchitecture parameters within subjects and between subjects using analysis of covariance and weighted correlation analysis, respectively.

		BV/TV	BS/BV	Tb. Th	Tb. N	Tb. Sp	Con.Den
Within subjects	r (a)	−0.378	0.307	0	−0.320	0.408	−0.362
	p-value (b)	0.295	0.287	0.369	0.289	0.147	0.128
Between subjects	r (c)	0.912*	−0.875	0.850	0.844	−0.901*	0.740
	p-value (d)	0.031	0.052	0.068	0.073	0.037	0.153

^(a)Pearson correlation coefficients were computed from the analysis of covariance using the formula from the paper in the literature (Bland and Altman, 1995). The analysis of covariance was implemented with the General Linear Model in SPSS (Version 20, IBM, Armonk, NY).

^(b)The significance value (p-value) was obtained from the F test in the associated analysis of covariance table (Bland and Altman, 1995).

^(c)Weighted Pearson correlation coefficients were calculated with an open source software package: R.

^(d)The significance value (p-value) from the weighted Pearson correlation analysis.

^*Correlation is significant at the 0.05 level.

In the weighted correlation analysis, we averaged the sill variance and the microarchitecture parameters for all human vertebrae from the same tissue donor and used the number of human vertebrae specimens in each tissue donor as the weight. Strong correlations were observed between the sill variance and microarchitecture parameters between subjects (Table 6). Significant relationships of the sill variance were observed with the bone volume fraction (r=0.912, p=0.031) and bone separation (r=−0.901, p=0.037). Marginally significant correlations were observed between the sill variance and bone surface to volume ratio (r=−0.875, p=0.052), trabecular thickness (r=0.850, p=0.068) and trabecular number (r=0.844, p=0.073). The correlation between the sill variance and connectivity density was not significant (r=0.740, p=0.153).