Aquaporin-1 facilitates pressure-driven water flow across the aortic endothelium

Abstract

Aquaporin-1, a ubiquitous water channel membrane protein, is a major contributor to cell membrane osmotic water permeability. Arteries are the physiological system where hydrostatic dominates osmotic pressure differences. In the present study, we show that the walls of large conduit arteries constitute the first example where hydrostatic pressure drives aquaporin-1-mediated transcellular/transendothelial flow. We studied cultured aortic endothelial cell monolayers and excised whole aortas of male Sprague-Dawley rats with intact and inhibited aquaporin-1 activity and with normal and knocked down aquaporin-1 expression. We subjected these systems to transmural hydrostatic pressure differences at zero osmotic pressure differences. Impaired aquaporin-1 endothelia consistently showed reduced engineering flow metrics (transendothelial water flux and hydraulic conductivity). In vitro experiments with tracers that only cross the endothelium paracellularly showed that changes in junctional transport cannot explain these reductions. Percent reductions in whole aortic wall hydraulic conductivity with either chemical blocking or knockdown of aquaporin-1 differed at low and high transmural pressures. This observation highlights how aquaporin-1 expression likely directly influences aortic wall mechanics by changing the critical transmural pressure at which its sparse subendothelial intima compresses. Such compression increases transwall flow resistance. Our endothelial and historic erythrocyte membrane aquaporin density estimates were consistent. In conclusion, aquaporin-1 significantly contributes to hydrostatic pressure-driven water transport across aortic endothelial monolayers, both in culture and in whole rat aortas. This transport, and parallel junctional flow, can dilute solutes that entered the wall paracellularly or through endothelial monolayer disruptions. Lower atherogenic precursor solute concentrations may slow their intimal entrainment kinetics.

abundant aquaporin (AQP)1 is found in numerous mammalian tissues, including vascular endothelial cells (ECs) from human and rat coronary arteries (53), the cornea, lung capillaries, and small vessels, (25, 31, 44), and mouse aortas (52). Swelling studies on single cells (53) and reconstructed liposomes (72) have shown that AQP1 facilitates passive osmotically driven water flows that, unlike pumps, require no ATP. AQP1 allows the passage of certain dissolved gases, e.g., nitric oxide (33), ammonia (43), and CO₂ (22, 69). Membrane electrolyte transport induces passive water transport via AQP1. AQP1 suppression in ECs decreases Na⁺ channels and Na⁺-K⁺-ATPase Na⁺/K⁺ pump proteins(25). The CFTR, a Cl⁻ transporter, and AQP1 often have similar tissue distributions. By interacting with other channels, the CFTR facilitates salt secretion in tissues, which causes passive water transport through AQP1 (31).

There are at least three well-studied systems where AQP1 plays a dominant role in water transport across a cell layer: the kidney, choroid plexus, and peritoneum. In the kidney, AQP1 is abundant in ECs of the outer medullary descending vasa recta microvasculature and in apical and basolateral membranes of the thin descending limb of Henle and proximal tubule. In the proximal tubule, salt is pumped from the lumen, which creates an osmotic gradient that concentrates the urine by extracting water via AQP1. AQP1-null mice cannot concentrate urine as well as wild-type mice (30, 65), whereas spontaneously hypertensive rats (SHRs) have increased AQP1 and produce more concentrated urine than normotensive rats (39).

AQP1 is located in the choroid plexus epithelium cytoplasm and apical membrane. It allows the transfer of cerebrospinal fluid to the brain and plays a role in hydrocephalus. This epithelium has 1/5 the water permeability and half the cerebrospinal fluid pressure in AQP1-null versus wild-type mice; AQP1-null mice do not suffer hydrocephalus. In contrast, SHRs overexpress AQP1 and exhibit accelerated cerebrospinal fluid exchange (45, 64). AQP1 is present in peritoneal capillaries and postcapillary venules, the main barriers to small solute transport in peritoneal dialysis, which involves both diffusive and convective transport. Decreased/increased AQP1 yields decreased/increased water permeability, the latter without altering the osmotic gradient or small-molecule permeability (17). In these, as in other known systems, osmotic gradients are far larger than negligible or nonexistent hydrostatic pressure gradients; thus, osmotic gradients drive AQP1 water transport.

In contrast, in the present study, we investigated the role of AQP1 in hydraulic conductivity (L_p), the ratio of transendothelial water flux (J_v) to hydrostatic pressure difference (ΔP) (63), across cultured aortic endothelial monolayers and excised whole rat aortas with virtually no transmural osmotic differences. Here, we show that AQP1 facilitates water movement driven by large hydrostatic ΔPs found in conduit arteries. Such measurements are more indirect than osmotic cell swelling experiments since they involve EC layers that allow parallel paracellular water transport. To evaluate the contribution of AQP1 to J_v or L_p, we imposed identical ΔPs across whole aortic walls ex vivo or across pairs of identical confluent endothelial monolayers. We compared L_ps of endothelia having normal, functioning AQP1 channels with those whose AQP1 channels were chemically blocked or knocked down via small interfering (si)RNA. Tracer experiments demonstrated that the observed J_v differences were not due to changes in paracellular transport; thus, they derive from transcellular, AQP-mediated flow. Our measured L_p changes led to an estimate of EC AQP1 density consistent with erythrocyte AQP1 density from osmotic swelling experiments. Transendothelial flow may have important physiological consequences. In conduit arteries, hydrostatically mediated water flow can affect metabolic access to and paracrine communication between ECs and smooth muscle cells (SMCs). As the sole source of pure water influx, it likely influences transmural solute concentration, which may affect extracellular solute binding kinetics. Rapid AQP1 upregulation by the atheroprotective transcription factor Krüppel-like factor 2 (KLF2) (32) seems to highlight the importance of AQP1 for vascular health.

MATERIALS AND METHODS

In Vitro Experiments

Cell culture, monolayer L_p, and tracer permeability.

Cell culture, monolayer L_p, and tracer permeability were performed as previously described in Ref. 11. We prepared bovine aortic EC (BAEC; VEC Technologies, Rensselaer, NY) monolayers on fibronectin-coated Transwell membranes incubated for 10 min in PBS with or without 25 μM HgCl₂ and measured (15) L_p of matched monolayer pairs 4–6 days postplating. Luminal (top) and abluminal (bottom) compartments, with the latter connected via a horizontal precision-diameter borosilicate glass tube on a spectrophotometer to a fluid reservoir (15), all at physiological pH, sandwiched the monolayer. A 10-cmH₂O hydrostatic pressure differential across the monolayer induced transmural flow, as monitored by spectrophotometer tracking of an air bubble (15) in the glass tube. Match of a nonlinear model of flow-induced EC junction sealing (51) to bubble position versus time data yielded steady monolayer L_p. Leaky monolayers with holes (L_p > 13.3 cm·s⁻¹·mmHg⁻¹) were not considered.

The change in time (Δt) of abluminal fluorescence intensity [calibrated to concentration (ΔC_a)] tracked fluorescent solute (added lumenally at t = 0) transport in eight parallel chambers, two of which measured J_v as well (11). The differential 10-cmH₂O hydrostatic pressure applied across the monolayer for 2 h was followed by zero ΔP (diffusive) for 1 h. Solute permeability was calculated as follows:

$$\text{Pe}=\left[\left(\Delta {\text{C}}_{\text{a}}/\Delta t\right)\times {\text{V}}_{\text{a}}\right]/(A\times {\text{C}}_{\text{p}})$$

where V_a is the abluminal chamber fluid volume, A is the filter surface area, and C_p is the luminal chamber fluorophore concentration, assumed time independent and large relative to the abluminal value.

Test for mercury toxicity in monolayers.

HgCl₂ reversibly blocks AQP1 water pores (9, 23, 49, 66). To test for toxicity and titrate to a nontoxic HgCl₂ level, we exposed monolayers to HgCl₂ concentrations (5, 10, 25, 50, 100, and 1,000 μM) for 1 h, washed the samples, added propidium iodide in PBS (1 μg/ml; Invitrogen) to samples, which only penetrates the membranes of dead or dying cells, and viewed samples under a Nikon Eclipse TE2000-E inverted microscope with a ×10 objective.

AQP1 knockdown with siRNA.

Twelve-well filters (Corning 3460) pretreated with fibronectin for 1 h were plated (at 32,000 cells/cm², passages 4–7) with aortic ECs and cultured in an incubator for 3 days until confluent. We followed Michel's optimized BAEC transfection protocol (27) with either Lipofectamine 2000 (Dharmacon, Lafayette, CO) alone, Lipofectamine 2000 + nontargeting (NT) siRNA, or Lipofectamine 2000 + one or both targets. The optimized concentration per 1.5 × 10⁴ cells was 20 pM siRNA for BAECS and 10 pM siRNA for rat aortic ECs (RAECs) (5, 10, 20, 40, and 80 pM tested, 3 monolayers each). L_p was measured as previously described 2 days posttransfection. Targets (antisense) were as follows: BAEC (Dharmacon), target 1 (T1) 5′-UUCUUCUUGAACUCGCUGGUU-3′ and target 2 (T2) 5′-UACUCCUCCACCUGACCGCUU-3′; and RAEC, AQP1-RSS351945 (Invitrogen, Grand Island, NY), 5′-AAGAGCUUCUUCUUGAUUUCGCUGG-3′.

Western blot analysis.

BAECs or RAECs were grown to confluence, lysed with ice-cold RIPA buffer with protease inhibitor cocktails (Roche Diagnostics), and sonicated. Protein was deglycosylated and incubated in sample buffer for 10 min at 60°C to reduce multimer formation. Twenty micrograms of PNGase F-digested (New England Biolabs, Ipswich, MA) protein were loaded per well, separated on a 12% SDS-polyacrylamide gel, transferred to polyvinylidene difluoride membranes, blocked, immunoblotted, immunoreactivity visualized (enhanced chemoluminescence kit, Amersham, Arlington Heights, IL), and densitometry probed with ImageJ (National Institutes of Health). Membranes were reprobed with β-actin (42 kDa) antibody as a loading control. We report percent knockdown relative to control. AQP1 blocking peptides (AQP1-P, Alpha Diagnostics, San Antonio, TX), which disrupt antigen-antibody binding, served as an AQP1 antibody blocking control.

RT-PCR.

We extracted RAEC RNA in the presence of RNase inhibitor, synthesized cDNA, performed PCR, separated PCR products, and detected with ultraviolet light. Quantitative RT-PCR amplification was done on 25-μl mixtures of 2× SYBR green fluorescein mix (Thermo Fisher), 70 nM primers, and 250 ng cDNA templates. An initial 5-min 95°C denaturation preceded fifty 30-s cycles at 94, 55, and 78°C. A negative nontemplate control was used. A dissociation curve analysis assessed product amplification specificity after each PCR. Target gene/primer sequence pairs were as follows: AQP1 (18), NM-012778 [forward (125–144): 5′-CCCTCTTCGTCTTCATCAGC-3′ and reverse (543–562): 5′-CTGAGCCACCTAAGTCTCGG-3′]; von Willebrand factor, XM-342759 [forward (4296–4316): 5′-GCAGTCAGTTGGCCTCTACCA-3′ and reverse (4366–4346): 5′-ACGGTCAATTTTGCCAAAGATC-3′]; GAPDH, NM_017008 [forward (372–390): 5′-TCTTCACCACCATGGAGAA-3′ and reverse (603–585): 5′-ACTGTGGTCATGAGCCCTT-3′ (54)]; and smoothelin, NM_001013049.2 [forward: 5′-TCGGAGTGCTGGTGAATAC-3′ and reverse: 5′-CCCTGTTTCTCTTCCTCTGG-3′ (50)].

Ex Vivo L_p(ΔP) Measurements

All animal protocols were approved by the Institutional Animal Care and Use Committee.

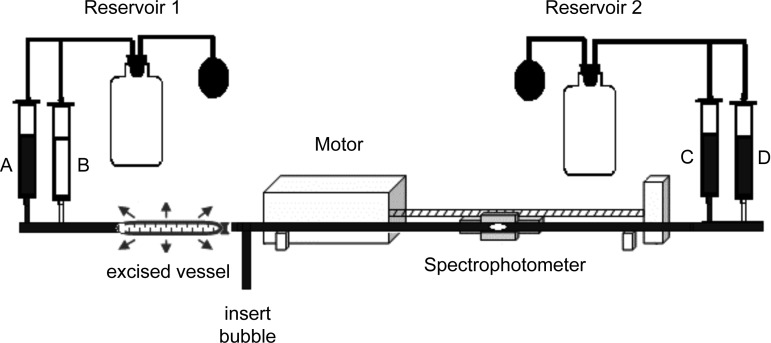
The aortas of male Sprague-Dawley (SD) rats (350–400 g) on a normal diet were removed under transmural ΔP, flushed with a perfusate solution [4% (wt/vol) BSA in PBS with 10⁻³ M NaNO₃ and 0.03% trypan blue (vital stain and leak reporter)], and submerged in a petri dish with the same solution minus trypan blue (which has a negligible effect on its osmotic pressure) as previously described in Ref. 55. The proximal end of the aorta was connected to reservoir 2 (Fig. 1; valves not shown) via a spectrophotometer bubble tracking system adapted from Ref. 15 that was identical to the in vitro L_p system described above. A distal cannulata connected it to a perfusate solution and pressure reservoirs whose pressure was adjusted by a mercury sphygmomanometer pump. Preconditioning (lowering and raising vessel ΔP to its minimal and maximal physiological ΔP three times, each for <1 min) reduced hysteresis.

Fig. 1.

Setup for hydraulic conductivity (L_p) measurements of the rat aorta ex vivo before and after administration of inhibitory agent (valves not shown). Setup is a modification of that in Ref. 55. Mercury sphygmomanometers control pressures in pressure reservoir bottles. Solution reservoirs A and D contain perfusate solution, including trypan blue. Reservoir C contains perfusate with the active agent HgCl₂ when used. Reservoir B is for fluid uptake. The text explains in detail how one measures L_p[pressure difference (ΔP)] before, then after a flush with HgCl₂, and again after endothelial denudation, all at the same three ΔPs and all on each vessel.

Transmural flux measurements.

After pumping reservoir D to the desired ΔP, we opened the proximal valve. The bubble tracking device measured the flow rate of fluid entering the vessel and exiting its walls. We only used data steady for >30 min. A mechanical caliper accurate to ±0.1 mm (55) measured vessel geometry before and 6 and 30 min after pressurization to track myogenic changes. We repeated this procedure for each ΔP. Next, to block AQP channels, a ∼5-mmHg ΔP drove the HgCl₂ solution from reservoir C through the vessel for 10 min. We flushed for 10 min and remeasured L_p(ΔP). To deendothelialize the vessel, we opened the proximal tie, inserted a 3- or 4-mm Foley catheter with a small Epon ball on its tip, advanced it to the distal end, and removed it with a slow rotation. After a 5-min flush at 10 mmHg from reservoir A, we retied the proximal cannula and remeasured L_p(ΔP). All three L_p(ΔP) sets were taken on every vessel.

Controls for technique, mercury toxicity, and effect on SMCs.

We measured L_p at three ΔPs, flushed with a blank solution, and remeasured L_p at the same ΔPs. A flush driven by a ≤5-mmHg ΔP left L_p unchanged at all ΔPs. To titrate for nontoxic HgCl₂ levels, we measured L_p at two ΔPs, tried an HgCl₂ exposure (concentration and time), remeasured L_p(ΔP), flushed with 2 μM 2-mercaptoethanol for 10 min to reduce the Cys-Hg²⁺ bond (23), and remeasured L_p(ΔP). Since Hg²⁺ blocks AQPs, it should either decrease L_p (if there is transcellular transport) or leave L_p unchanged; an L_p increase at any ΔP indicates cellular or junctional toxicity. We found a maximum HgCl₂ exposure that decreased L_p at all ΔPs. If 2-mercaptoethanol then returned L_p to baseline for all ΔPs, we concluded that Hg²⁺ caused no endothelial toxicity. To test if blockade of SMC AQPs affected medial L_p, we denuded samples, measured L_p(ΔP), exposed samples to Hg²⁺, and remeasured L_p(ΔP).

Electron microscopy.

Two male SD rats (8 rats total) were used for 50 and 100 mmHg with and without HgCl₂ treatment. A carotid artery cannulation connected the anesthetized, ventilated rat to a constant pressure reservoir. After the heart was stopped, a heparin-PBS rinse from the carotid artery to the femoral artery ran until the effluent was clear. Next came a 5 μM HgCl₂-PBS or pure PBS flush at ΔP for 10–15 min and glutaraldehyde-PBS at the same ΔP for 2 h (in situ fixation). The aorta was removed, placed in glutaraldehyde for 24–48 h with osmium tetroxide, embedded in resin, sectioned to 900Å (gold reflection) with a diamond knife in an LKB Ultramicrotome 4801A, stained with uranyl acetate and lead citrate, and viewed with a transmission electron microscope (Zeiss Electron Microscope 902).

Immunochemistry

Monolayers.

The monolayer protocol used was similar to that previously described in Ref. 68. Briefly, confluent BAEC monolayers grown on Transwell filters were fixed with PLP fixative, permeabilized with 0.075% saponin-PBS, and blocked with 15% goat serum, 0.3% Triton X-100, 20 mM sodium phosphate, and 0.9 mM NaCl. After exposure to rabbit anti-rat AQP1 primary antibody (Alpha Diagnostics; 1:250 dilution) in 15% goat serum, 0.2% BSA, and PBS and then to secondary antibody (Alexa 488-conjugated goat anti-rabbit IgG, Molecular Probes, Carlsbad, CA; 1:200) in 1% goat serum and PBS, samples were counterstained with 4′,6-diamidino-2-phenylindole (DAPI; 1:3,000), cut, mounted with Vectashield, and viewed under a Zeiss 510 confocal microscope with same laser intensity/exposure time for all samples.

Vessel sections.

Ventilated 250–300 g male SD rats were euthanized and perfused with 0.3 ml heparin (5,000 USP units/ml, China Chemical & Pharmaceutical, Taipei, China) in 60 ml PBS from the carotid cannula to the femoral artery until the effluent was clear followed by Accusan Bouin's fixative (Sigma Chemical, St. Louis, MO). The aorta was removed, further fixed in Bouin's fixative, and stripped of adventitia and connective tissue. The aorta was then cut into segments, washed in 70% alcohol plus several drops of NaOH, placed in 30% sucrose overnight at 4°C, and embedded in Tissue Tech OCT compound (Tissue-Tek, Sakura Finetek, Torrance, CA). Afterward, the aorta was cryostat (Microtome Cryostat Cryostar HM 560 MV) sectioned to 10 μm onto Superfrost Plus slides (Fisher Scientific, Pittsburgh, PA) and stained with hematoxylin (48) with or without Slow Fade Gold antifade with DAPI (Invitrogen, Carlsbad, CA). Pontamine Sky Blue 6BX (0.5%; Alpha Aesar, Haverhill, MA) restricted elastic's broad-spectrum autofluorescence to red (13). Immunochemistry was done as in culture except that 0.05% saponin was added to the blocker, the primary antiserum was in 3% goat serum, 0.2% BSA, and PBS (1:500) for 18–24 h, and secondary antibody was diluted to 1:50. Samples were mounted with Vectashield media (clear nail polish secured the coverslips) and viewed under a Leica TCS SP2 AOBS confocal microscope with Leica TCS SP/NT 2.5 version 2.51347d image-analysis software or a Zeiss LSM510 confocal microscope with LSM 3.5 SP 1.1 software.

Calculations

L_p was determined using the following equation:

$${\mathit{\text{L}}}_{\mathrm{p}}=\mathit{\text{vA}}/\left(\Delta \text{P}\times \hspace{0.17em}\pi \times \text{OD}\times \mathit{\text{L}}\right)$$

where v is the bubble front meniscus velocity, A is the tubing cross-sectional area, OD is the average outer diameter, and L is the length. π × OD × L is the vessel outer surface area.

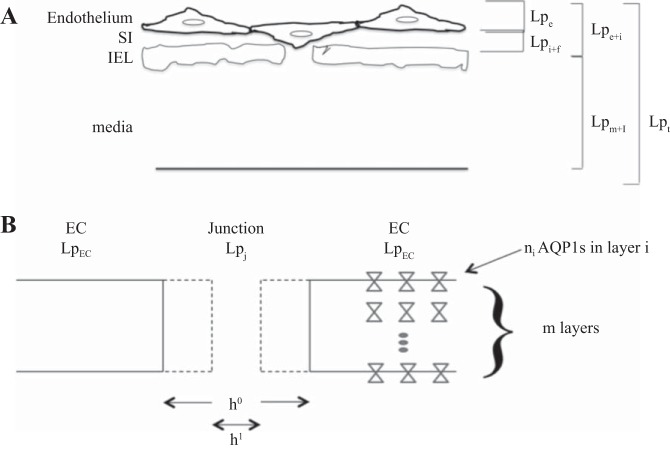
Osmotic gradients across large vessel walls are generally assumed negligible. Thus, L_p of the intact entire vessel wall (L_pt; Fig. 2A) can be related to that of the denuded vessel [media + internal elastic lamina (IEL); L_{pm + I}] and endothelium + subendothelial intima (SI) (L_{pe + i}) by the sum of specific resistances (1/L_p) (63) as follows:

$$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\text{p}}_{\text{t}}}$}\right.=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\text{p}}_{\text{e}+\text{i}}}$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\text{p}}_{\text{m}+1}}$}\right.$$ (1)

Vessel L_p experiments measured three sets of L_ps on each vessel (intact, after HgCl₂ AQP1 blocker, and denuded), each at the same three ΔPs. Equation 1 gives, for each vessel, the derived quantity, L_{pe + i}, without blocker [equal to (1/L_pt without blocker − 1/L_{pm + I} denuded)⁻¹] and with blocker [equal to (1/L_pt with blocker − 1/L_{pm + I} denuded)⁻¹] and their percent difference, with mean ± SE for all three.

Fig. 2.

A: breakdown of L_ps of artery wall layers. A: cartoon of the artery wall depicting the endothelium, subendothelial intima (SI), internal elastic laminar (IEL), and media. It shows a compressed SI with an endothelial cell (EC) blocking an IEL fenestra. Equation 1 breaks up the total wall resistance, 1/L_pt, into the sum of the resistances of its two sublayers, endothelium + SI (1/L_{pe + i}) and IEL + media (1/L_{pm + i}), in series. Equation 2 (appendix) breaks up 1/L_{pe + i} into endothelial (1/L_pe) plus SI + fenestrae (1/L_{pi + f}) resistances in series. SI flow resistance is due to the SI extracellular matrix. Fenestral resistance is due to flow alteration in the SI caused by EC blocking the fenestral entrance. B: model for possible change in junction width (h) with treatment. It is a detail of the junction in A, depicting two parallel pathways for transport, paracellular (junctional) and transcellular [via aquaporin (AQP)1 (hourglasses)]. We modeled a treatment that complicates junctions by a change in h of the narrow part of the junction open for transport from h⁰ (solid) to h¹ (dashed). Since the junction area ∼h × total junction length and since h ⪡ cell radius, the ratio of h¹/h⁰ of slit widths represents the post-to-pretreatment ratio of cross-sectional areas for transport. The right portion of B depicts the model (appendix) for junctional transport (L_pj) in parallel with AQP1-mediated transcellular transport (L_pEC). L_pEC results from AQP1 water channels in a series/parallel arrangement in the cell: n membrane layers in series; n_i AQP1s in parallel in membrane layer i (i = 1, . . ., m).

Statistics

Values are presented as means ± SE. We calculate P values from unpaired (paired¹) Student's t-tests for two columns of unpaired (paired) data and from ANOVA (with subsequent Tukey tests when appropriate) for multiple data columns. P values of <0.05 were considered significant. For more complex comparisons of two types of experiments that measured similar information, we used bootstrap (14, 21) nonparametric methods, which are detailed in the appendix.

RESULTS

Figure 3A shows a confocal section of immunocytochemically and DAPI-treated BAECs grown to confluence on a Transwell filter with xz and yz views; Fig. 3B shows the three-dimensional reconstruction. The isotype control (not shown) was nearly black. Blue (DAPI) stain indicates cell nuclei. Green (Alexa 488) stain indicates that BAECs avidly express AQP1 in some cultured cells, including around the nuclei and far from the perinuclear region. Fig. 3C shows a 200-nm confocal optical slice from a 10-μm transverse section of an SHR thoracic aorta. The result for a normotensive SD rat (not shown) was similar. Here, green again indicates AQP1, since we restricted tissue autofluorescence to red, as described above. The top red band is the IEL. DAPI (blue) labeled EC (SMC) nuclei above (below) the IEL, establishing AQP1 expression in both cell types in conduit arteries, as previously described for SMCs (53). To verify that all tissue autofluorescence was pushed into red, we performed the procedure without either antibody. To test for nonspecific primary antibody binding, we did a small peptide control to the primary antibody's AQP1-binding site (Fig. 3D). To test for nonspecific secondary antibody binding, we used secondary antibody but no primary antibody. All three controls showed red bands but no visible green fluorescence.

Fig. 3.

APQ1 expression in aortic ECs. A–C: Zeiss LSM510 (A–C) confocal images and three-dimensional reconstruction (B) of a confluent bovine aortic EC (BAEC) monolayer on a Transwell filter. Green (Alexa 488) staining indicates AQP1; blue [4′,6-diamidino-2-phenylindole (DAPI)] staining indicates the nucleus. AQP1 stains some cells more intensely than others. xz and yz views show AQP1 expressed around the nucleus as well as away from it. C: transverse 200-nm optical confocal section of a spontaneously hypertensive rat (SHR) thoracic aorta; the analogous image (not shown) for a normotensive Sprague-Dawley (SD) rat was similar. Black on top, lumen; top red line, IEL. ECs are between the lumen and IEL. Blue DAPI stained EC above the IEL and smooth muscle cell (SMC) nuclei below the IEL. Intense green staining of ECs and SMCs indicates AQP1. D: small peptide control (red and green channels) showed no visible green. Elastin autofluorescence was restricted to red. E: overlayed image of 50 serial 200-nm optical (Leica: D and E) confocal sections (no DAPI) from a 10-μm cryostat section on the black-and-white transmission image. A computer-generated outline tightly surrounds the region of intense green. The near coincidence of outline and EC border in the transmission image verifies that AQP1 is expressed in cell luminal and abluminal membranes and likely in its cytoplasm.

For a transcellular AQP water transport pathway, it is necessary (but not sufficient) that AQP1 be present both on the luminal and abluminal parts of the cell membrane. Fig. 3E shows the superposition of 50 serial, high-magnification 200-nm optical confocal slices through an EC from a 10-μm transverse section of an SHR [normotensive SD (not shown) similar] thoracic aorta. Our custom software creates a blue outline (tracing the maximum gradient in green intensity) to surround the region of intense, albeit uneven, green stain above the IEL. Superimposed on the confocal image is the black-and-white transmission image, blurry at high magnification. The near coincidence between the transmission image cell border and the blue outline of the green region indicates that AQP1 fluorescence extends to and includes both EC luminal and abluminal membranes. This bilateral distribution makes plausible transcellular trans-AQP1 water transport.

This plausibility motivated functional water transport experiments. We subjected matched (i.e., treated exactly the same) pairs of BAEC monolayers cultured on fibronectin-coated Transwell filters (15), one with and one without 25 μM HgCl₂, an AQP blocker (49), to a 10-cmH₂O hydrostatic ΔP and measured J_v across the monolayer versus time (15). This ΔP induces a J_v similar to that in large arteries in vivo. Hg²⁺ blocks AQP1 water transport by binding to Cys¹⁸⁹ at AQP1’s pore entrance (49) but can be cytotoxic above certain concentrations/exposure times. Propidium iodide staining, which only penetrates the membranes of dead/dying cells (i.e., toxicity), was only present at HgCl₂ concentrations above 50 μM; 25 μM yielded no evidence of toxicity. Human intestinal Caco-2 cells exposed to 100 μM Hg²⁺ showed no diminution in cell viability (1). Twenty-five micromolars is 1/40 the concentration used to block AQP1s in vascular SMCs (53) but is enough to block ∼90% of AQP1 in murine erythrocytes (70). In each matched pair of monolayers, L_p was significantly lower (22 ± 6%, n = 4 monolayer pairs, percent drops: 16.0%, 18.4%, 24.1%, and 29.9%, P = 0.0057; Table 1) in monolayers exposed to HgCl₂; toxicity would have caused it to rise.

Table 1.

HgCl₂ effects on BAEC L_p and TAMRA P₀

	Control		HgCl2
BAEC Parameter\Treatment	μ ± SE	n	μ ± SE	n	P Value (by t-Test)
Lp, ×107 cm·s−1·mmHg−1	7.75 ± 0.80	4	6.09 ± 0.71	4	0.0057, paired
TAMRA
P0, ×105 cm/s	1.47 ± 0.18	8	1.22 ± 0.17	8	0.69
Pc, ×105 cm/s	1.72 ± 0.42	8	1.52 ± 0.24	8	0.34
Dextran
P0, ×106 cm/s	2.01 ± 0.34	8	1.67 ± 0.43	8	0.77
Pc, × 106 cm/s	3.30 ± 0.46	8	3.60 ± 0.90	8	0.55
BAEC Statistical Test	Metric
Post-to-pre-HgCl2 treatment Lp ratios versus TAMRA P0 ratios	0.004 (P value by t-test)
Bootstrap distribution on derived statistic (where a negative mean indicates a significant difference) for TAMRA data (Fig. 7B)	99% probability that μ < −0.050

BAEC, bovine aortic endothelial cell; L_p, hydraulic conductivity; P₀, diffusive permeability; P_c, convective permeability.

To test if HgCl₂ treatment affected monolayer integrity, as reflected in paracellular transport, we performed 70-kDa dextran [∼7-nm radius (19)] solvent drag experiments. HgCl₂ altered neither its diffusive permeability (P₀) nor convective permeability (P_c) significantly (Table 1; note the large SE for P_c); thus, HgCl₂ did not harm monolayer barrier function. Since 70-kDa dextran only crosses the monolayer paracellularly, its nonsignificant P₀ change indicates that the observed L_p drop is not likely due to junctional (paracellular) changes. We also performed solvent drag experiments with TAMRA, a smaller tracer (0.8-nm radius) that also only crosses the monolayer paracellularly². As shown in Table 1, TAMRA P₀ = P_c, neither of which changed significantly with HgCl₂. P₀ = P_c means that the diffusive far exceeds the advective contribution to its transport, which implies (appendix) that the ratio of control-to-treated P₀s equals the ratio of control-to-treated junction pore widths. If all transport were paracellular (and Darcy; the appendix gives the Poiseuille alternative), this ratio of pore widths would also equal the ratio of control-to-treated L_ps (Fig. 2B). Since HgCl₂ caused a significant 22% drop in L_p with a statistically insignificant, yet ∼17%, change in P₀, we used statistical tests to see how unlikely the L_p drop is due to paracellular, i.e., pore width changes. A t-test showed that the sets of ratios³ of P₀s and L_ps were indeed different (P = 0.004; Table 1), i.e., arose from different distributions. A further check is that of nonparametric bootstrap (14, 21) statistic S (appendix), which is zero if all water transport is paracellular and negative if there is nonparacellular water transport that decreases upon HgCl₂ exposure. With 99% probability, S had mean < −0.05 (see Fig. 7B). Both tests indicated that HgCl₂-induced pore width (or P₀) changes are very unlikely to explain the drop in L_p with HgCl₂: thus, water transport is very unlikely purely paracellular. The siRNA results described below make an even stronger argument for the same conclusion.

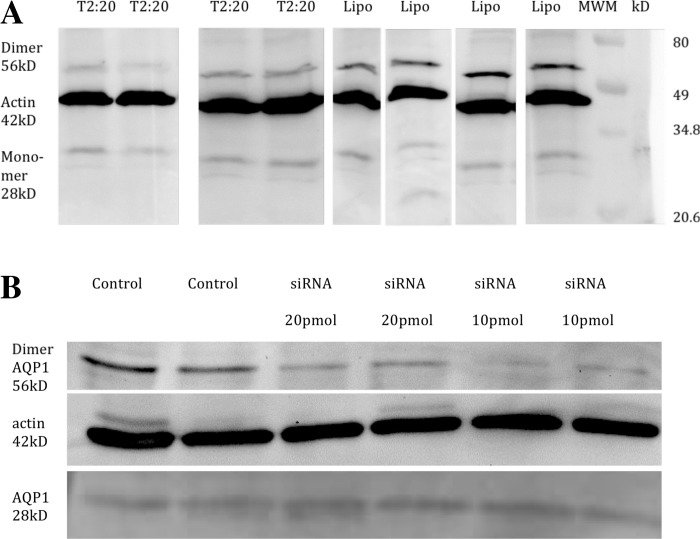
Since HgCl₂ blocking is nonspecific, we validated these results with siRNAs against bovine AQP1 mRNA on BAEC monolayers (27). Western blots (Fig. 4A) and densitometry demonstrated that T2 induced 70.3% (n = 4, P < 0.001) AQP1 (28 kDa + 56 kDa) knockdown relative to the 42-kDa β-actin control. L_ps for BAEC monolayers judged nonleaky showed a 53% (P = 0.04) drop in L_p (7.94 ± 1.90 vs. 3.73 ± 0.56, each × 10⁻⁷ cm·s⁻¹·mmHg⁻¹, n = 6) from scrambled NT siRNA in pooled data from T2 alone and 20 pM each of T1 + T2-treated monolayers; T1 had no effect on L_p. We repeated these experiments on RAECs to compare with rat aorta experiments.

Fig. 4.

Small interfering (si)RNA results. A: BAECs. Western blots (28-kDa monomer and 56-kDa dimer bands, n = 4) show knockdown versus control at optimized 20 nM siRNA2 relative to the vector β-actin (42 kDa) control. Relevant lanes were cut from a larger gel. Densitometry showed 70.3% knockdown (P < 0.0005) using ImageJ (National Institutes of Health). B: rat aortic ECs (RAECs). Western blots (56-kDa dimer band) with rat-specific AQP1 siRNA are shown. Lane 1, control without siRNA; lane 2, control with Lipofectamine 2000 but no siRNA; lanes 3 and 4, duplicates of 20 pmol siRNA; lanes 5 and 6, duplicates of 10 pmol siRNA. For 10 pmol, the AQP1 dimer band dropped 67.9% (P = 0.001) and the combined monomer + dimer bands dropped 59.2% (P = 0.00084), normalized by the β-actin control.

Analogous siRNA knockdown experiments for RAEC monolayers gave similar results. Western blots showed a 67.9% drop in the 56-kDa AQP1 dimer band (n = 2, P = 0.001; Fig. 4B) and a smaller change in the 28-kDa monomer band for a 59.2% drop (n = 2, P = 0.00084) in the 28-kDa + 56-kDa bands relative to the β-actin control. Higher multimer bands showed no significant change. Quantitative RT-PCR, given as 2^−ΔΔC_T (where C_T is threshold cycle), normalized to endogenous control (GAPDH) relative to untreated control, showed a 0.47 (+0.28/−0.18)⁴-fold change of AQP1 relative to control, i.e., a ∼53% siRNA-induced drop in AQP1 mRNA (n = 3). Treated and control groups showed no drop [2^−ΔΔC_T = 0.98 (+0.11/−0.10)] for von Willebrand factor (n = 3). Corresponding to AQP1 knockdown, we found a 56.4% (n = 7) reduction in mean monolayer L_p for this target siRNA (Table 2). L_p for no treatment, Lipofectamine 2000 alone, and Lipofectamine 2000 + NT siRNA (not shown) were nearly identical. Table 2 shows albumin (radius: 3.5 nm) and TAMRA solute drag results on control versus knocked down RAEC monolayers. The larger molecule, here albumin, had P₀ ≠ P_c⁵. As with HgCl₂/BAECs, P₀ (barrier function) was unaffected by siRNA (two-tailed t-test). The smaller molecule, TAMRA, had P_c ≈ P₀ for both treated and control monolayers, i.e., diffusive dominated advective TAMRA transport, with neither P_c nor P₀ affected by siRNA. Insignificant (−0.7%, 16.7%) solute tracer P₀ differences were far too small to explain the 56.4% siRNA-induced L_p drop. This indicates transcellular water flow. A t-test showed that post-to-pretreatment ratios of L_ps and TAMRA P₀s were different (P = 4.0 × 10⁻⁸; Table 2): they came from different distributions. The mean of the bootstrap statistic was less than −0.52 ⪡ 0 with 99% confidence (see Fig. 7A). Thus, with extremely high confidence, L_p has both paracellular and nonparacellular contributions and siRNA AQP1 knockdown reduced the latter significantly in RAEC monolayers.

Table 2.

si RNA inhibition of RAEC L_p and TAMRA P₀

	Control		siRNA
RAEC Parameter\Treatment	μ ± SE	n	μ ± SE	n	P Value (One Tail/Two Tails)
Lp, ×107 cm·s−1·mmHg−1	6.84 ± 0.27	8	2.98 ± 0.27	7	1.85 × 10−7
TAMRA
P0, ×105 cm/s	1.09 ± 0.11	8	1.17 ± 0.13	8	0.35
Pc, ×105 cm/s	1.39 ± 0.12	8	1.25 ± 0.07	8	0.65
Albumin
P0, ×106 cm/s	2.04 ± 0.40	13	1.70 ± 0.39	13	0.033/0.065
Pc, ×106 cm/s	3.74 ± 0.78	9	2.76 ± 0.73	9	0.0036/0.0072
RAEC Statistical Test	Metric
Post-to-pre-siRNA treatment ratios of Lp versus ratios of TAMRA P0	4.0 × 10−8 (P value by t-test)
Bootstrap distribution on derived statistic (where a negative value indicates a significant difference; Fig. 7A)	99% probability that μ < −0.52

RAEC, rat aortic endothelial cell; siRNA, small interfering RNA.

To assess AQP1’s contribution to whole vessel L_p, we measured L_p on each aorta at three ΔPs (as in Refs. 4 and 63) multiple times after various treatments. We first carried out controls to validate our technique and to assess toxicity. The results shown in Table 3 demonstrate that a flush driving ΔP of 5 mmHg left L_p unchanged. The results shown in Table 4 demonstrate that a 10-min flush of 5 μM HgCl₂ [which gives ∼40% osmotic permeability inhibition in erythrocytes (70)] followed by a 10-min wash to remove unbound Hg²⁺ lowered L_p at all ΔPs. 2-Mercaptoethanol returned L_p to baseline at all three ΔPs. [Note that the drop in L_p with HgCl₂ was larger at 60 mmHg (24%) and 45 mmHg (31% and 38%) than at 100 mmHg (7%, 18%, and 17%)]. Electron micrographs of control and HgCl₂-treated rat aortas fixed at 50 and 100 mmHg showed no EC morphological changes (Fig. 5). These L_p experiments and micrographs indicate that the 10-min 5 μM HgCl₂ exposure was not EC toxic.

Table 3.

Control L_p experiments for technique

Pressure, mmHg	Baseline Lp, ×108 cm·s−1·mmHg−1	Flushed Lp, ×108 cm·s−1·mmHg−1	Average Percent Change in Lp After Blockade
60	2.93 ± 0.21	2.99 ± 0.15	2.12% ± 2.11%
100	2.51 ± 0.44	2.50 ± 0.46	−0.68% ± 03.09%
140	2.88 ± 0.48	3.00 ± 0.49	3.95% ± 1.47%

n = 3. The control was a flush with blank solution.

Table 4.

Control L_p experiments for mercury toxicity

Pressure, mmHg	Baseline Lp, ×108 cm·s−1·mmHg−1	HgCl2 Flushed Lp, ×108 cm·s−1·mmHg−1	Lp After 2-Mercaptoethanol, ×108 cm·s−1·mmHg−1
Rat 1
60	2.67	2.02	2.48
100	2.47	2.30	2.40
Rat 2
45	1.98	1.37	2.07
100	1.76	1.44	1.89
Rat 3
45	2.03	1.26	1.98
100	1.76	1.48	1.68

The control was a flush with HgCl₂; Cys-Hg²⁺ was then reduced with 2-mercaptoethanol.

Fig. 5.

Electron micrographs of rat aortas fixed under pressure at 50 and 100 mmHg with and without HgCl₂ treatment. Images show that HgCl₂ treatment of rat aortas at dosages and times described in the text caused no visible morphological changes in RAECs in whole vessels. A and B: untreated (A) and treated (B) rat aortas fixed at 50 mmHg; C and D: untreated (C) and treated (D) rat aortas fixed at 100 mmHg.

The results shown in Fig. 3C confirm the well-known (53) fact that vascular SMCs express AQP1. To exclude the possibility that blockade of SMC AQPs caused the observed vessel wall L_pt changes, we denuded the aortic endothelium, measured baseline L_p(ΔP), flushed with HgCl₂, and remeasured L_p(ΔP). The results shown in Table 5 demonstrate that there were no significant L_p changes due to flushing a partially, fully (later with no modifier), or vigorously denuded (vigorous working of the catheter back and forth may affect the IEL) vessel with HgCl₂. Thus, blockade of SMC AQPs did not measurably decrease vessel wall L_pt. L_ps of denuded SD rat aortas (Fig. 6A) treated with HgCl₂ before denudation were similar to L_ps of denuded aortas both before and after HgCl₂ treatment (Table 5) and to L_ps of denuded Wistar-Kyoto rat aortas (n = 5, not shown) of the same age/weight not exposed to HgCl₂.

Table 5.

Control L_p experiments for smooth muscle cell AQP1 blockade on the whole rat aorta

Description	Pressure, mmHg	Baseline Denuded Lp, ×108 cm·s−1·mmHg−1	Denudation Followed by HgCl2 Flush Lp, ×108 cm·s−1·mmHg−1
Rat 1
Incomplete denudation	60	2.26	2.29
	100	2.62	2.70
Rat 2
Complete denudation	60	3.87	3.97
	100	3.73	3.40
	140	3.55	3.67
Rat 3
Vigorous denudation	60	4.93	5.34
	100	5.21	5.45

AQP1, aquaporin 1.

Fig. 6.

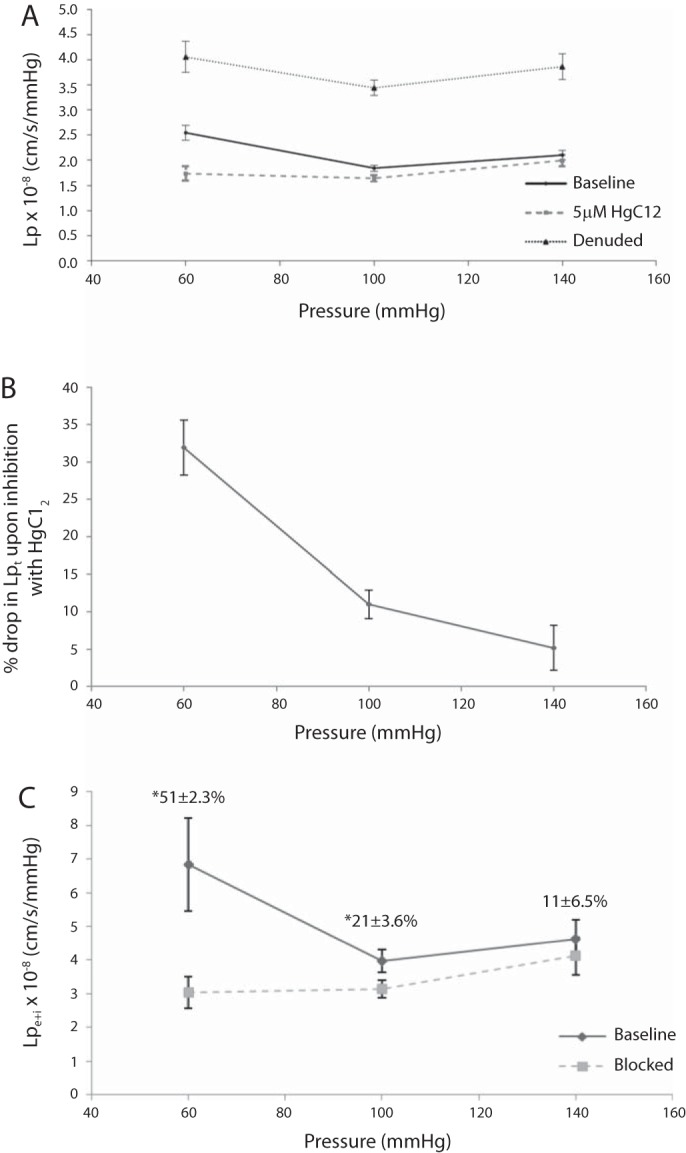
L_p of the rat aorta ex vivo. Figure 1 shows the experimental setup. A: L_p(ΔP) for an excised aorta from 300- to 350-g male SD rats, first without (bold solid) and then with (dashed) the AQP blocker HgCl₂, and then after endothelial denudation (thin solid), with all nine L_p values taken on each vessel. HgCl₂ reduced every vessel's L_p significantly at every pressure. B: replot of these data as means ± SE of the percent drop in L_pt with HgCl₂ versus ΔP. HgCl₂ reduced L_pt (32 ± 4%) at 60 mmHg and less [yet significantly different (P = 0.000026) and nonzero] at 100 (11 ± 2%) and 140 mmHg (5 ± 3%). C: since HgCl₂ does not change L_{pm + I} (Table 5), changes in L_pt reflect changes in endothelium + SI L_{pe + i} (points); numbers above the points are means ± SE of percent drops in L_{pe + i} with HgCl₂. These differences are distinguishable (P < 0.005) for 60 mmHg versus the other pressures only. (This figure and these statistics neglect the lone outlier that showed nearly no difference between L_pt and L_{pm + I}, and thus a huge L_{pe + i}, at 60mmHg only; the mean ± SE for the percent drop including this outlier at 60 mmHg was 56 ± 7.4%). L_{pe + i} dropped by more than half at 60 mmHg. n = 6.

Figure 6A shows L_pt at ΔP = 60, 100, and 140 mmHg at baseline and after HgCl₂ and L_{pm + I} after denudation, with all nine measurements taken on each vessel (n = 6). Each intact vessel L_pt dropped at every ΔP with HgCl₂. Figure 6B shows a plot of mean ± SE values of the percent L_pt drop of a vessel with HgCl₂ versus ΔP, which brings this out. At 60 mmHg, HgCl₂ decreases intact vessel L_pt by 32 ± 4% and less at ΔP ≥ 100 mmHg, as also seen in the controls in Table 4. Equation 1 (63) relates the apparent resistance, 1/L_{pe + i}, of the endothelium + SI to L_pt and L_{pm + I} (Fig. 6A). HgCl₂ increased the average endothelium + SI fraction, [(1/L_{pe + i})/(1/L_pt)], of the total wall resistance from 26 ± 8% to 56 ± 5% at 60 mmHg. Since HgCl₂ does not affect medial resistance, it increased this fraction by decreasing L_{pe + i} 51 ± 2.3% (average percent difference, not the percentage of average difference, since all measurements were done on each vessel) from 6.28 to 3.13 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ [n = 5; with one outlier (n = 6), the drop was 58 ± 2%] at 60 mmHg (Fig. 6C). If these percent changes simply represented a decrease in native endothelial L_pe, they would be ΔP independent. The data evinced smaller, yet significant (P < 0.05), percent drops in L_{pe + i} and L_pt at the higher ΔPs: 21 ± 4% and 11 ± 2% at 100 mmHg and 11 ± 7% and 5 ± 3% at 140 mmHg. ANOVA on the curves shown in Fig. 6, A and C, demonstrated that the flushed (A and C) and denuded (A) curves were flat, i.e., ΔP independent (P > 0.05), but that baseline L_{pe + i} (neglecting one outlier) and L_pt at 60 mmHg differed (P < 0.05 by ANOVA) from their (indistinguishable) values at 100 and 140 mmHg. L_pt (n = 2, not shown) with HgCl₂ showed that lowering ΔP from 60 to 20 mmHg raised L_pt by 17.4 ± 8.6%.

DISCUSSION

Immunochemistry demonstrated that cultured aortic ECs and RAECs in whole aortas express AQP1 (Fig. 3). Expression levels varied far more in culture than in vessels, likely due to the nonphysiological ΔP = 0 and high protein culture medium for growth to confluence. Quiescent cells likely also express differently from recently proliferative cells. The near coincidence of the transmission image's EC border and outline of the green (AQP1) region in the superposition of serial confocal sections (Fig. 3E) establishes AQP1 expression throughout whole aorta ECs, including luminal and abluminal membranes; thus, AQP1-mediated transcellular water flow is plausible.

In Vitro Experiments

L_p experiments on AQP1 knocked down BAEC and RAEC monolayers (Table 2), confirmed by Western blots and RT-PCR, and on BAEC monolayers with HgCl₂-blocked AQPs (Table 1) showed that reducing functioning EC AQP1 significantly reduced monolayer L_p.⁶ The reduction was larger for siRNA than for HgCl₂, likely because HgCl₂ concentrations used to avoid toxicity probably reduced AQP function less than siRNA.

HgCl₂ did not significantly affect monolayer 70-kDa dextran P₀; this verified monolayer integrity. Since 70-kDa dextran only crosses the endothelium paracellularly, the unchanged P₀ indicates unchanged junctional transport: the L_p drop was not due to junction strand changes or to junctional changes from cell swelling (5, 6), possibly secondary to Hg²⁺ blockade of AQPs (65). TAMRA is a tracer large enough to only pass through the large junction pores for water (28), yet small enough that, even with a 10-cmH₂O ΔP-driven flow across the monolayer, the diffusive far exceeds the advective contribution to its transport (P₀ ≈ P_c). Challenging matched pairs of control versus HgCl₂-blocked BAEC monolayers with TAMRA showed that changes in P₀ do not explain the observed L_p drops with HgCl₂. Similar tracer and L_p experiments on AQP1-knocked down RAEC monolayers confirmed this more strongly; they clearly indicated (>>99% confidence) that AQP1-mediated transcellular water transport represents a significant fraction of L_pe.

Gao et al. (25) added anti-AQP1 siRNA, transfection reagents, and 10-kDa dextran (radius: ∼3 nm, between TAMRA and 70-kDa dextran) together to cultured human pulmonary vasculature EC monolayers. They found that total tracer diffused across the layer doubled over the ensuing 24 h in the presence of reagents that affect EC membranes and junctions while knockdown and other dynamic changes occurred. Our study, on different cells, found a decrease in the instantaneous, i.e., 1 h, permeability of an already-knocked down, nonzero ΔP-adjusted monolayer in physiological media. It is impossible to compare these vastly different experiments.

Whole Vessel Experiments

We use rat, rather than the much smaller AQP1 knockout mouse, aortas because adequate L_p technique signal/noise requires a minimum endothelial area and transendothelial flow. The thin lubricating layer surrounding a tracked bubble that moves too slowly can break; the bubble then sticks to the tube wall (26, 46), which compromises the measurement.

The HgCl₂ concentration [which only negligibly inhibits ion transporters (37)] in our intact aorta study is lower than in our BAEC experiments, yet more effectively inhibits endothelial L_p. This is likely because, as noted, fewer ECs in culture express AQP1 as strongly as in vessels. Different conditions can yield different EC AQP1 functions and localization, e.g., AQP1 in rat choroid plexus epithelial cells mainly localizes in the apical cell membrane but shifts to the cytoplasm in cells of rats with increased choroid plexus pressure (hydrocephalus). A PKC mechanism (45) causes ΔP-induced AQP1 shuttling. Fluid shear at 1 dyn/cm² causes AQP2 translocation to the renal epithelial cell membrane (38), where it participates in transcellular flow (10). Doubling the perfusion rates in isolated renal microtubules for 15 min doubles AQP1 in the brush-border apical and basolateral membranes (47). Quiescent ECs exposed to large ΔP and shear, as in whole vessels but not in our monolayers, have tighter cadherin junctions and greater plasma membrane AQP1 content (42), i.e., lower junctional and higher transcellular flow: AQPs account for a larger share of transendothelial flow; thus, AQP blockade decreases L_p more in vessels than in culture.

HgCl₂ blockade of EC AQP1 reduces whole rat aortic wall L_pt ex vivo by 32 ± 4% at 60 mmHg. HgCl₂ exposures cause no significant cytotoxicity; no morphological changes appear, and removal of Hg²⁺ with 2ME returns L_pt to control values. HgCl₂ does not change denuded vessel L_{pm + I} (Table 5). Thus, L_{pm + I} represents the far less resistant route through the extracellular matrix around the SMCs (which lack tight junctions) rather than the parallel trans-SMC AQP1 path. Thus, the 32 ± 4% HgCl₂-induced L_pt reduction can only result from a reduction of its endothelium + SI conductivity (L_{pe + i}) by 51 ± 7% (Eq. 1). An estimate that half of the ΔP-driven transendothelial J_v is transcellular would be surprisingly high.

If this L_{pe + i} reduction were all in native endothelial L_pe, it would be ΔP independent. Yet, L_pt and L_{pe + i} drop far less at 100 and 140 mmHg. This suggests that structural changes, as previously demonstrated without HgCl₂ (4, 55, 63), may contribute. L_pt versus ΔP has a step shape: high at 60 mmHg, sharply reduced by 80–100 mmHg, and flat to >140 mmHg. L_{pm + I} (denuded endothelium) is ΔP independent at approximately twice intact vessel L_pt at high ΔP. Normal intact rat aorta SI (∼200 nm), composed of collagen and a loose extracellular matrix, is mostly void [∼93% sucrose space (35)]. A fenestrated IEL separates it from the >100-μm-thick and far denser media [∼42% sucrose space (62)]. We have proposed (35) that rising ΔP pushes ECs against the IEL and dense media. This decreases SI fiber spacing and causes ECs to obstruct IEL fenestrae (Fig. 2A), which substantially raises flow resistance/lowers L_pt. Firm, load-supporting SI collagen fibers limit compression/L_p drop. Denudation removes endothelial resistance and EC fenestra clogging; a higher, ΔP-independent L_{pm + I} results. Theory has predicted (35) a six- to sevenfold versus subsequently observed (34) fivefold SI compression. The study of Huang et al. (34) shows direct EC fenestral blockade.

Even though the percent drop in L_pt with HgCl₂ blockade is ΔP dependent (Fig. 6), the blocked L_pt values are approximately ΔP independent, particularly for 60–100 mmHg. This suggests that AQP1 blockade lowers the critical ΔP to compact the SI/block fenestral: it shifts the step in L_pt versus ΔP leftward to lower ΔP. Analogously, a weaker wind (ΔP) drives a sailboat with an intact sail (blocked AQPs) as fast as a stronger wind drives a boat with a sail with holes (functioning AQP1s). AQP1 blockade not only reduces intrinsic endothelial L_pe, but it also shifts part of the total ΔP = force/area from the media to the endothelium. This lowers the total ΔP needed to achieve the critical force/area on the endothelium for SI compression. At 60 mmHg, HgCl₂ exposure lowers L_pe and causes an uncompressed SI to compress; both effects lower L_{pe + i}. Thus, AQP1 represents <52% of L_pe, yet HgCl₂ still causes the large observed drop in L_{pe + i} and L_pt. At 100 and 140 mmHg, the SI is compressed without HgCl₂; thus, the drops in L_{pe + i} and L_pt with HgCl₂ are smaller.

The appendix estimates SI pressure and critical transendothelial pressure for SI compression. Table 6 shows the results. The results predict that HgCl₂ lowers ΔP for SI decompression from 60 to <46 mmHg and, with HgCl₂, that L_pt is ∼22% higher below 46 mmHg than at 60 mmHg. Measurements (n = 2) found that L_pt with HgCl₂ was 17.4 ± 8.6% higher at 20 mmHg than at 60 mmHg.

Table 6.

How AQP1 inhibition influences the state of the SI, endothelial L_p, and mean force/area felt by the endothelium: estimate of L_ps for different vessel wall layers at different pressures with or without HgCl₂ leading to an estimate of the critical ΔP to decompress SI with HgCl₂

	ΔP, mmHg
	<46	60	60	100
Treatment	HgCl2	No HgCl2	HgCl2	No HgCl2
SI state	Decompressed	Decompressed	Compressed	Compressed
Relations (appendix) amongst Lps	Lpe + i = Lpe	Lpe + i = Lpe	Lpi + f from 100 mmHg	SI + fenestrae: Lpi + f(Lpe + i, Lpe)
Lpt ×108 cm·s−1·mmHg−1	2.13	2.55	1.74	2.05/1.84**
Lpm + I ×108 cm·s−1·mmHg−1*	4.06*	4.06*	4.06*	4.06*
Lpe + i ×108 cm·s−1·mmHg−1	4.46	6.18	3.27	4.16
Lpe ×108 cm·s−1·mmHg−1	4.46	6.28	4.46	6.28
Lpi + f ×108 cm·s−1·mmHg−1	>>12.3	>>12.3	12.3	12.3
Estimated force/area (PL − Pi; in mmHg) on the endothelium	∼22	∼22	∼34	∼46

SI, subendothelial intima; ΔP, pressure difference; L_pt, L_p of the intact entire vessel wall; L_{pm + I}, L_p of the denuded vessel (media + internal elastic lamina); L_pe, L_p of the endothelium; L_{pe + i}, L_p of the endothelium + SI; L_{pi + f}, L_p of the SI + fenestrae; P_L, lumen pressure; P_i, SI pressure.

^*L_{pm + I} is ΔP and HgCl₂ independent (Fig. 6A, Table 5). We use L_{pm + I} at 60 mmHg, and no HgCl₂ for the entire estimate for consistency. The average experimental value at each condition differs insignificantly from it. Because of this difference, the resulting estimated value (2.05) for L_Pt differs (**) from the experimental value (1.84) at 100 mmHg, no HgCl₂. This L_Pt estimate plays no part in the estimation calculation; it is included for completeness.

From estimates of the portion of L_pe due to AQP1 in whole rat aortas and of l_p of a single AQP1 from an osmotic swelling study [∼1.3–2.6 × 10⁻¹⁹ cm³·s⁻¹·mmHg⁻¹·AQP⁻¹ (72)], one can estimate the EC membrane AQP1 density and compare it with literature values for red blood cell (RBC) membranes. The appendix constructs a series/parallel AQP1 and junctional flow scheme (Fig. 1B) that, with the data shown in Fig. 6, found ∼1.1–2.2 × 10¹¹ AQPs/cm² membrane in ECs (∼29–44% of L_pe). This compares well with 1.4–1.9 × 10¹¹ AQPs/cm² membrane in RBCs [2.0–2.7 × 10⁵ AQP1 channels/RBC (16, 57)]. The consistency of this trans-EC L_pe-derived EC AQP1 density and the osmotic swelling-derived RBC AQP1 densities corroborates/lends confidence to our finding of hydrostatic pressure-driven transendothelial flow in conduit arteries.

Summary and Significance

Osmotic differences (osmotic gradients) drive water across the well-studied family of AQPs. Large arteries are the physiological system where hydrostatic ΔP dominates osmotic gradients. Here, we show, for the first time, that ΔP drives water across arterial ECs via AQP1. AQP1s account for part of L_pe and L_pt, particularly under wall shear, as in vessels, which likely shifts AQP1 to the cell membrane (47). They set the critical transmural ΔP for the SI compression and the net force/area that ECs feel at a ΔP (Table 6). These all have potentially important effects on EC regulation, membrane and cytoskeletal structure, junctional integrity, and conduit artery mural and barrier function. By controlling L_pt, AQP1s may contribute to vessel wall health and pathology by regulating nutrient, catabolite, signal, and harmful solute advection and thus may be attractive drug targets.

The role of AQP1 in arterial endothelial L_pe and wall L_pt may be relevant to early atherogenesis. Low-density lipoprotein (LDL)-cholesterol (diameter: ∼23nm) transport from the blood into the arterial SI and its subsequent binding to the SI extracellular matrix are key early atherogenic events (56) believed to trigger lesion formation (59). LDLs do not appear to cross the endothelium uniformly but rather focally by ΔP-driven advection (61) around rare [∼1/(2,000–6,000) ECs in the rat aorta (40)], isolated ECs with temporarily loose junctions (36, 58, 67, 73). L_pt-controlled transmural flow can dilute SI LDL, thereby likely slowing its extracellular matrix binding kinetics (24, 71), and flush the SI of unbound LDL. Lower L_pt may impair dilution and clearance. This may be one reason that (pulmonary) hypertension is a strong risk factor for (pulmonary) atherosclerosis (20): chronic hypertension causes artery walls to remodel to a thicker and denser media and the SI to become cellular (29), which significantly lower L_pt versus normotension. Not only might medial thickening regulate L_pt over many months (29), but differential AQP1 expression might allow active, rapid L_pt regulation. At a mean physiological ΔP ∼ 100 mmHg, the SI is fully compressed but close to decompression ΔPs (3, 55). Figure 6 shows that SI compression decreases L_pt by ∼1/3; thus, SI decompression at normal or hypertensive ΔP can potentially raise L_pt by ∼50%. Coronary arteries experience ∼20% lower systole ΔP than the aorta when their blood flow is generally blocked (7). These vessels may be particularly susceptible to SI decompression, via naturally or pharmacologically increased EC AQP1 channels, to slow lipid transport and SI extracellular matrix binding. The next step is to observe disease progression in lipid-fed apolipoprotein E-deficient mice with normal and reduced AQP1. Unfortunately, the AQP1 knockout mouse suffers microcardia, reduced stroke volume, thin vessel walls, and hypotension (41). A model with reduced AQP1 only in conduit arteries but not elsewhere would be ideal.

EC-derived KLF2 facilitates atheroprotective EC and SMC phenotypes and induces exosomal transport of microRNAs from ECs to SMCs to produce a nonproliferative SMC phenotype (32). One of its earliest effects is AQP1 upregulation (8). Shear upregulates KLF2. KLF2 is expressed nonuniformly in arteries, with far lower expression at arterial branch points (2), the sites of low shear and high EC turnover, tracer permeability, and atherosclerosis proclivity (12). This is consistent with more solute, fewer AQP1 and less water transport. Since EC-derived nitric oxide exits ECs via AQP1 (7), ECs with fewer functioning AQP1s (at branches or via blockade or knockdown) likely transport less nitric oxide to medial SMCs. In contrast, in straight arterial regions, wall shear stress yields lower EC turnover and an endothelium less permeable to large solutes (25) and with lower inflammation (8). KLF2/AQP1 induction may reduce inflammation by slowing SI lipid entrainment that attracts monocytes that mature to macrophages.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant 1-R01-HL-067383 and National Science Foundation (NSF) Grants IOS-0922051 and CTS-0077520. T. Nguyen and S. Russell were partially supported by Levich Institute Soft Materials NSF-Integrative Graduate Education and Research Traineeship Grant DGE-0221589, S. Russel was partially supported by a Barbara Slifka City University of New York (CUNY) Dissertation-Year Fellowship, and J. Toussaint was partially supported by the Graduate School and University Center/CUNY Alliances for Graduate Education and the Professoriate program.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: T.N., J.D.T., Y.X., C.B.R., L.M.C., S.R., Y. Shou, Y. Sun, and R.Y. performed experiments; T.N., J.D.T., Y.X., C.B.R., L.M.C., S.R., Y. Shou, O.S., R.Y., and D.S.R. analyzed data; T.N., J.D.T., C.B.R., L.M.C., J.M.T., K.-M.J., and D.S.R. interpreted results of experiments; T.N., J.D.T., Y.X., C.B.R., and L.M.C. prepared figures; C.B.R., L.M.C., J.M.T., and D.S.R. edited and revised manuscript; J.M.T., K.-M.J., and D.S.R. approved final version of manuscript; K.-M.J. and D.S.R. conception and design of research; D.S.R. drafted manuscript.

Appendix: TECHNICAL ARGUMENTS

The Meaning of L_p Ratios and TAMRA Tracer Permeability P₀ Ratios

The results show that HgCl₂ (siRNA) treatment of BAECs (RAECs) reduces L_p significantly and does not change P₀. Rather than concluding from this qualitative argument that L_p represents paracellular and transcellular flow, we invoked two statistical tests with the following background. Diffusive transport under a fixed concentration gradient is proportional to the open junction cross-sectional area, which is, to a very good approximation, the total junction length (L) in the monolayer times the mean junction width (h). If L is the same for all monolayers of a given cell type (BAEC or RAEC), a lower diffusive transport indicates a smaller h. Liquid flow through a porous media obeys Darcy's law, and the Darcy flow rate through a slit (the junction) is proportional to h; thus, the Darcy flow across the monolayer is also proportional to h. If all transendothelial flow were paracellular, then both the post-to-pretreatment ratio of L_p and of P₀ would each reflect the post-to-pretreatment ratio of h (Fig. 2B) (assuming a Poiseuille junction flow means that the junctional portion of L_p goes ∼h³ rather than ∼h); measuring L_p and P₀ ratios would then sample the same distribution of post-to-pretreatment h ratios. Tables 1 and 2 show P values (4 × 10⁻³ for BAECs and 4 × 10^−8: for RAECs) comparing the sets of L_p and P₀ ratios; the results showed that they were different, i.e., they arose from different distributions. This means that L_p is not just paracellular flow.

Bootstrap Statistics

The bootstrap (14, 21) is a resampling method that allows testing of a statistical hypothesis based on the resampling of acquired data to get the distribution of a derived statistic. The key point of these methods is that after each sampling of this statistic, one returns the randomly selected datum to the pool from which the next sample is chosen. The distribution of the derived statistic results, from which one can determine confidence intervals for that statistic.

To construct a test statistic, let superscript 1 on L_p and P denote mean posttreatment and superscript 0 denote mean pretreatment (with the “0” in P₀ dropped for clarity). Define statistic S as the ratio of L_ps minus the ratio of TAMRA P₀s (or, for Poiseuille flow, of its cube). S has a mean zero for purely paracellular water transport. The following equation results:

$$S=\frac{L_{\text{p}}^1}{L_{\text{p}}^0}-{\left(\frac{{\text{P}}^1}{{\text{P}}^0}\right)}^j;j=\left\{\begin{array}{ll}1\hfill & \text{Darcy}\hfill \\ 3\hfill & \text{Poisseuillte}\hfill \end{array}\right\}$$

If part of the water transport is transcellular and treatment increases that portion, with the paracellular portion unchanged, then S is positive⁷. Let the null hypothesis be S ≥ 0: either transport is purely paracellular or treatment (BAECs: HgCl₂ exposure; RAECs: anti-AQP1 siRNA) increases or does not decrease transcellular transport fast enough. Figure 7 shows the distributions of S for RAEC (A) and BAEC (B) data for Darcy flow (j = 1). In both cases, nearly all of the distribution's mass is left of zero, with 99% confidence for BAECs that S is negative (less than −0.050) and 99% confidence that S for RAECs is (very) negative (less than −0.52). The confidence for RAECs is better because n is larger for the L_p experiments on RAECs than on BAECs and the variances of both L_p and solute drag experiments for siRNA on RAECs are tighter than for HgCl₂ on BAECs. Poiseuille junction flow (j = 3) gives (not shown) a similar confidence interval for RAEC data and >96% confidence that the test statistic is negative (less than −0.0035) for BAEC data. Thus, we reject the null hypothesis and conclude that L_p has both transcellular and paracellular contributions and that treatment decreases transcellular transport. Tables 1 and 2 show these statistical results for BAEC and RAEC data.

Fig. 7.

Bootstrap method resampled distribution of test statistic S (appendix), which represents the difference between the ratio of treated to untreated monolayer L_p minus the ratio of treated to untreated transendothelial TAMRA diffusive permeabilities. The appendix argues that this statistic tests the null hypothesis (S ≥ 0) that the drop in L_p upon treatment is due to changes in paracellular transport [i.e., treatment only affects mean inter-EC junction width (h)]. The resampled statistics reject the null hypothesis; thus the mean of S < 0 with [exceedingly (A)] high confidence for RAEC (A) and BAEC (B) data. We conclude that transcellular transport is significant and that the treatment in both cases inhibits transcellular water transport.

Details of the Estimate of the Pressure Needed to Decompress the SI in the Presence of HgCl₂ and of the Corresponding L_pt

Let P_L, P_i, and P_a be lumen, SI, and adventitial pressures, respectively, with ΔP = P_L − P_a. At steady state, J_v across the whole wall equals both that across the endothelium and that across the media. Each flux is the product of that layer's L_p and the ΔP across it: L_pt(P_L − P_a) = L_{pe + i}(P_L − P_i) = L_{pm + I}(P_i − P_a). Simple manipulation estimates the steady force/area, P_L − P_i=(L_pt/L_{pe + i})ΔP, on the endothelium. As shown in Fig. 6, HgCl₂ blockade at 60 mmHg raises this steady force/area 55% from (2.55/6.85)60≈22 to (1.74/3.06)60≈34 mmHg at ΔP = 60 mmHg. Raising ΔP from 60 to 100 mmHg, a ΔP where our theory predicts a compressed SI even without HgCl₂ and increases the force/area on the endothelium to [(1.84/3.97)100]≈46 mmHg. These numbers motivate the estimate below of the critical ΔP needed for SI decompression with HgCl₂. Table 6 shows the main relations and layer L_p and force/area estimates derived below.

As in Eq. 1, split the total specific resistance, 1/L_{pe + i}, of the endothelium + SI+ IEL fenestral entrance into the sum of endothelial, 1/L_pe, plus SI + fenestral, L_{pi + f}, resistances (Fig. 2A), as follows:

$$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\text{p}}_{\text{e}+1}}$}\right.=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\mathrm{p}}_{\mathrm{e}}}$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$L_{{\text{p}}_{\text{i}+\text{f}}}$}\right.$$ (2)

When the SI is decompressed, the resistance of the SI plus fenestrae is much smaller than that of the endothelium, or L_pe ∼ L_{pe + i}(60 mmHg, no HgCl₂) ∼ (6.28 ± 1.72) × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ (this number is the mean, neglecting one outlier, of the individual L_{pe + i} values calculated for each vessel using Eq. 1). Compression by increasing ΔP changes L_{pe + i} (mainly by fenestral blockage) but leaves L_pe unchanged. Thus, the change in L_{pe + i} allows one to estimate L_{pi + f}: if one uses the above L_pe value in Eq. 2 at 100 mmHg without blocker and uses the L_{pe + i} value (4.16 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹, again the average of the individual values calculated for each vessel using Eq. 1) for these conditions, one obtains L_{pi + f} of ∼(1/4.16 × 10⁻⁸ − 1/6.28 × 10⁻⁸)⁻¹ = 12.3 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ when the SI is fully compressed. If the SI at 60 mmHg with HgCl₂ is also fully compressed, then this L_{pi + f} should be the same there. One can calculate the drop in L_pe at 60 mmHg due to HgCl₂: Eq. 2 estimates that L_pe with HgCl₂ drops ∼29% to L_pe ∼ (1/3.27 × 10⁻⁸ − 1/12.3 × 10⁻⁸)⁻¹ = 4.46 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹. Since we seek a ΔP to decompress the SI with HgCl₂, which would require L_pe ∼ L_{pe + i}, inserting this value for L_{pe + i} and the denuded L_{pm + I} into Eq. 1 estimates the overall L_pt for the vessel wall at this unknown ΔP. Together with L_{pm + I} ∼ 4.06 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ at 60 mmHg (Fig. 6), this value and Eq. 1 give L_pt ∼ (1/4.46 × 10⁻⁸ + 1/4.06 × 10⁻⁸)⁻¹ = 2.13 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹, ∼22% higher than L_pt (1.74 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹) at 60 mmHg with HgCl₂. [By comparison, L_pt (2.55 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹) at 60 mmHg without HgCl₂ is 46% higher than with HgCl₂, since HgCl₂ lowers L_pe.] Fluid incompressibility and steady state mean that the flow across the endothelium and across the wall are equal, i.e., L_ptΔP = L_{pe + i}(P_L − P_i) ∼ 4.46 × 10⁻⁸(P_L − P_i) when the SI is decompressed in the presence of HgCl₂. For P_L − P_i ∼ 22 mmHg, a value established above as low enough to decompress the SI at 60 mmHg without blocker, and L_pt ∼ 2.13 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹, this equation predicts a value of ΔP ≤ 46 mmHg is adequate for SI decompression. Since the SI is decompressed and L_{pe + i} ∼ L_pe, L_pt is the same for any lower ΔP.

Estimation of AQP1 Expression in the EC Membrane

Recall that 1/L_{pe + i} = 1/L_pt − 1/L_{pm + I}. If AQP accounts for part of the intrinsic L_pe, then blockade of AQP1 will alter the effective parameter L_{pe + i.} Let L_pj be the junctional contribution to endothelial L_pe. The flows through inter-EC junctions and through the AQPs occur in parallel. The cell has more than one membrane that water must traverse in series (Fig. 2B). Since Starling's law is linear, in parallel, linear conductivities add and, in series, their inverses add. Suppose the cell has m layers in series, the ith of which has n_i AQPs per layer (i = 1, . . . ., m). The n_i AQPs in a layer operate in parallel. Thus, the total endothelial conductivity for this setup is L_pe ≈ L_pj + l_p [Σ_i(1/n_i)]⁻¹. If n_i = n is i independent, then:

$$L_{{\mathrm{p}}_{\mathrm{e}}}\approx L_{{\mathrm{p}}_{\mathrm{j}}}+n{l}_{\text{p}}/m$$ (3)

We now estimate L_pj. If HgCl₂ blocks all AQP, then L_pj is just L_pe with blocker. As above, if the SI is decompressed, then L_{pi + f} is far larger than L_pe; thus, L_{pe + i} ∼ L_pe. In the argument for decompressing the SI in the presence of HgCl₂ we found that the SI is decompressed at 20 mmHg with or without HgCl₂. Thus, L_pj ∼ L_{pe + i} (20 mmHg, HgCl₂). Similarly, without HgCl₂, L_pe ∼ L_{pe + i} (relaxed SI) ∼ L_{pe + i} (20 mmHg, no HgCl₂). With these estimates for L_pj and L_pe, Eq. 3 reduces to nl_p/m ∼ L_pe (20 mmHg, no HgCl₂) − L_{pe + i} (20 mmHg, HgCl₂). We have values for L_pt with [(1.90 ± 0.28) × 10⁻⁸ cm·s⁻¹·mmHg⁻¹] and without [(2.50 ± 0.12) × 10⁻⁸ cm·s⁻¹·mmHg⁻¹] blocker at 20 mmHg on the same vessel. If we use the 60-mmHg value for L_{pm + I} = 4.055 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ in Eq. 1, we can calculate L_{pe + i} at 20 mmHg for both conditions. We found nl_p/m ∼ 6.5 × 10⁻⁸ − 3.6 × 10⁻⁸ ∼ 2.9 × 10⁻⁸ cm·s⁻¹·mmHg⁻¹ and %(nl_p/m)/L_pe ∼ 44%. For l_p ∼ 1.3–2.6 × 10⁻¹⁹ cm³·s⁻¹·mmHg⁻¹·AQP⁻¹ (72), this equation gives n/m ∼ (1.1–2.2) × 10¹¹ AQP channels/cm² layer for an EC. A RBC [2.0–2.7 × 10⁵ AQP1 channels/RBC (16, 57), surface area: ∼140 μm², n = 2 layers (luminal, abluminal)] has 1.4–1.9 × 10¹¹ AQP channels/cm² layer. The consistency of the RBC estimate of AQP1 density derived from osmotic experiments and this L_p data-derived EC AQP1 density estimate derived from hydrostatic pressure experiments further supports AQP1-mediated transcellular flow.