Oscillatory dynamics coordinating human frontal networks in support of goal maintenance

Abstract

Humans have a capacity for hierarchical cognitive control—the ability to simultaneously control immediate actions while holding more abstract goals in mind. Neuropsychological and neuroimaging evidence suggests that hierarchical cognitive control emerges from a frontal architecture whereby prefrontal cortex coordinates neural activity in the motor cortices when abstract rules are needed to govern motor outcomes. Here we utilize the improved temporal resolution of human intracranial electrocorticography to investigate the mechanisms by which frontal cortical oscillatory networks communicate in support of hierarchical cognitive control. Responding according to progressively more abstract rules results in greater frontal network theta phase encoding (4-8 Hz) and increased prefrontal local neuronal population activity (high gamma amplitude, 80-150 Hz), which predicts trial-by-trial response times. Theta phase encoding couples with high gamma amplitude during interregional information encoding, suggesting that interregional phase encoding is a mechanism for the dynamic instantiation of complex cognitive functions by frontal cortical subnetworks.

Introduction

Humans have the ability to control immediate actions while maintaining more abstract overarching goals^1-5. The frontal lobes are crucial for goal-directed behavior⁶, including hierarchical control over action^7-9, and neuroimaging demonstrates that neural activity is greater in prefrontal cortex (PFC), compared to primary motor (M1) and premotor (PMC) cortices, as rules governing behavior become more abstract^2-4. This processing gradient may reflect a dynamic network architecture supporting hierarchical cognitive control whereby PFC interacts with M1/PMC during higher-order action selection^6,9-13. This control process is predicated on the capacity for the PFC to concurrently process information at multiple timescales and levels of abstraction. However, this fundamental problem in cognitive neuroscience—how groups of brain regions coordinate information transfer in a noisy neuronal environment to maintain multiple goals—has not been addressed neurophysiologically in the human brain. While fMRI, EEG, and lesion research has shown that the PFC is crucial for such complex cognitive processes^3,9,13-17, the temporal and spatial limitations of those techniques make it difficult to directly examine interregional interactions within frontal cortex.

Human intracranial electrocorticographic (ECoG) recordings allow for the reliable measurement of broadband gamma activity (∼80-150 Hz, hereafter “high gamma”), a physiological measure that is correlated with both the fMRI BOLD signal^18,19 and local neuronal population firing rates^18,20. High gamma activity provides a link between single unit physiology and mesoscale oscillatory dynamics^16,19-27. Recent phase/amplitude coupling (PAC) research has found that the phase of low frequency oscillations (e.g., theta; 4-8 Hz) is co-modulated with high gamma activity both at rest and in a behaviorally-relevant manner ^{16,21-23,25,26,28-31}, analogous to evidence that local neuronal spiking activity is biased according to local field potential oscillatory phase (spike/phase coupling)^32-35. In addition to the role that theta oscillations play in coordinating neuronal spiking activity, there is mounting empirical evidence for a privileged role for theta in coordinating neuronal ensembles during higher cognition, such as cognitive control³⁶. In particular, the modulation of midline frontal theta oscillations during the decision making process, but not during stimulus presentation, has been shown to predict individual differences in behaviour under response conflict³⁷. Moreover, a causal manipulation of hippocampal theta – specifically, theta phase-specific optogenetic stimulation in rats – has been shown to improve behavioral outcomes, perhaps by reducing task-irrelevant activity via phase-based information coordination. Thus, theta may coordinate endogenous spiking activity to facilitate information processing and/or transfer, but analytic methods that account for trial-by-trial behavior may be necessary to isolate these effects²⁹.

These observations suggest a possible mechanism by which spatially segregated neuronal assemblies might coordinate neuronal activity across brain networks²⁷. Specifically, we test a model wherein interregional theta phase encoding coordinates information transfer between frontal subregions during goal-directed behavior³⁶. Such phase encoding would link low frequency phase with high gamma amplitude in a task-dependent manner across phase encoding sites, permitting multiple behavioral goals to be simultaneously maintained³⁸. To evaluate this model, we adapted a task (used previously in fMRI in healthy subjects and in stroke patients with focal brain lesions^3,9) for ECoG wherein subjects executed stimulus-response mappings that increased in abstraction from zero-order (R1) through first- (R2), second- (D1), and third- (D2) order relationships (see Methods and Fig. 1A,B). As the level of abstraction increases, the task places increasing demands on hierarchical cognitive control and engages progressively more anterior regions of PFC^1,3,9. Moreover, prior work has demonstrated that demands specifically related to increases in rule abstraction drive the recruitment of more anterior frontal regions, as distinct from other types of general difficulty^3,6,39. However, the timing and physiological mechanisms of the interaction between these regions is unknown.

Figure 1.

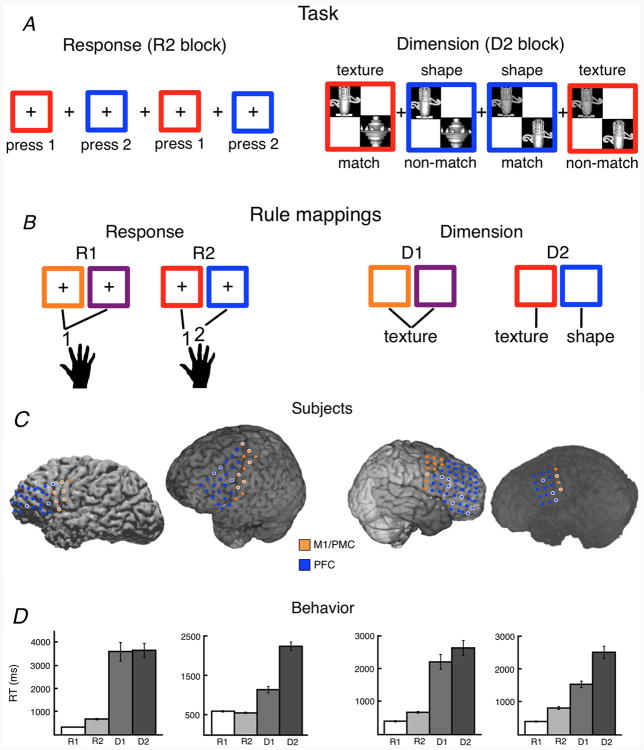
Task, subjects, and behavior. (A) Example trial events in the Response (R2 block) and Dimension (D2 block) sub-tasks. For the Response task, subjects responded according to 1st order mappings of colored squares to different button press responses; for the Dimension task subjects were cued by the colored square to make a 3rd order mapping – specifically, an object comparison based upon one of two object dimensions (texture or shape). Matching and non-matching examples are shown. (B) Example rule set mapping colors to key press responses across R1 (all colors map to the same response) and R2 (colors map to distinct responses) conditions of the Response task (left). Example mappings from colors to target dimensions across D1 (all colors map to the same dimension) and D2 (colors map to distinct dimensions) conditions of the Dimension task (right). (C) All artifact-free frontal electrodes were included in the analyses. All anterior electrodes are colored in blue and all posterior electrodes are colored in orange. Electrodes outlined in white showed significant task-dependent changes in high gamma amplitude. Of the 31 electrodes demonstrating a main effect of task on amplitude, 15 were located over M1/PMC and the remaining 16 were located over PFC. (D) Each subject showed a main effect of task on RTs such that RTs slowed as abstraction, and the corresponding cognitive control demands, increased. Subjects were fastest for zero-order stimulus-response mappings (R1, no conflict). RTs then increased parametrically for 1st order (R2), 2nd order (D1), and 3rd order response rules (D2). Error bars indicate SEM. (*) Significant regression of task condition on RT, p < 10^-20.

We hypothesized that, for lower order stimulus-response mappings, activity in posterior frontal regions (i.e., M1/PMC) would be sufficient to respond to the stimulus, whereas higher order cognitive control regions would be less active. In contrast, for more abstract tasks, high gamma activity would increase in anterior PFC. Furthermore, because increasingly anterior frontal regions become engaged during more abstract control processes, we further hypothesized that more abstract tasks would result in increased interregional frontal theta phase encoding. These phenomena would be reflected in regionally-specific task-related alterations in high gamma activity predictive of trial-by-trial behavioral outcomes. Finally, from a physiological perspective, if interregional theta phase encoding supports task-related information transfer, we predicted that increasing cognitive control would result in increased task-dependent interregional theta/high gamma activity as indexed by theta/high gamma PAC.

Results

Increased task abstraction results in slower response times

Each subject (Fig. 1C) showed a main effect of task abstraction on behavioral response time (RT) such that RT increases parametrically as a function of task (linear regression analyses; S1, n = 107: r = 0.77; S2, n = 128: r = 0.48; S3, n = 111: r = 0.82; S4, n = 98: r = 0.74; p < 10^-7 each; see Fig. 1D) with no significant effect of task condition on error rates (p > 0.05 each subject). Of the 140 total frontal electrodes examined across subjects, 31 electrodes showed task-dependent changes in baseline-adjusted high gamma analytic amplitude (hereafter, “amplitude”) in the two frontal regions of interest (ROIs): 15 in the M1/PMC and 16 in the PFC (Fig. 1C).

High gamma tracks task abstraction

Cortical high gamma amplitude provides high temporal resolution and a high signal-to-noise measure of trial-by-trial changes in local neuronal activity (Fig. 2A,B). The electrode selection criterion for the M1/PMC and PFC ROIs was such that only task-active electrodes—electrodes that showed a sustained encoding of task condition on high gamma amplitude (> 100 ms; p < 0.05)—were included in analyses. Note that this selection criterion is agnostic with regards to the direction and timing of high gamma encoding such that both task-related increases and decreases in high gamma activity were included in the ROI analyses and, thus, any significant directionality effects survived this classification procedure (see Methods).

Figure 2.

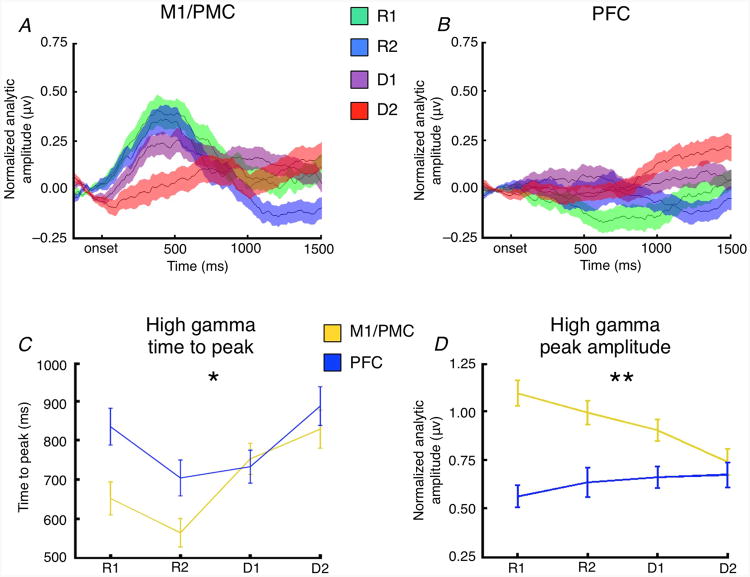
High gamma amplitude differentiates frontal responses. (A,B) Time-courses for the average event-related high gamma response across trials at the (A) 15 posterior (M1/PMC) and (B) 16 anterior (PFC) sites. (C) High gamma activity time to peak becomes increasingly delayed with increasing task abstraction in both M1/PMC (orange, p < 10^-5) and PFC (blue, p = 0.026) (* Significant interaction, p = 0.033; main effect of region, p = 0.00010; and main effect of task abstraction, p < 10^-4) (D) In contrast, peak high gamma amplitude decreases in M1/PMC (orange, p = 0.0023) as task abstraction increases, with no change in PFC amplitude (blue) (** Significant task-by-region interaction, p = 0.008; and main effect of region, p < 10^-9). Shaded regions and error bars indicate SEM.

Within these task selective electrodes, we observed a main effect of both frontal subregion (F_1,440 = 10.98, p = 0.00010) and abstraction (F_3,440 = 8.45, p < 10^-4) on trial-by-trial stimuluslocked event-related high gamma time-to-peak, as well as a significant interaction between frontal subregion and task abstraction (F_3,440 = 2.93, p = 0.033) (Fig. 2C). Post hoc analyses show that increasing abstraction is associated with an increase in high gamma time-to-peak in both M1/PMC (F_3,440 = 8.97, p < 10^-5) and PFC (F_3,440 = 3.12, p = 0.026), with pairwise t-tests suggesting that the interaction is driven by faster time-to-peak in M1/PMC for the R1 (p = 0.00048) and R2 (p = 0.0067) conditions, but not for D1 (p = 0.96) or D2 (p = 0.69). High gamma time-to-peak occurs later in the PFC than in M1/PMC for the R1 (214 ms later) and R2 (158 ms later) conditions, but not for the more abstract D1 and D2 conditions (R1: p = 0.00048; R2: p = 0.0067; D1: p = 0.96; D2: p = 0.69). Activity in both regions peaks before trial-by-trial RTs (paired t-test, M1/PMC: p < 10^-27; PFC: p < 10^-19).

With respect to high gamma amplitude, we observed a main effect of frontal subregion (F_1,440 = 39.23, p < 10^-9), along with a significant interaction between frontal subregion and abstraction (F_3,440 = 3.95, p = 0.008) (Fig. 2D). There was no main effect of abstraction on high gamma amplitude (F_3,440 = 1.28, p = 0.28), with the interaction being driven by a trial-by-trial decrease in amplitude with increasing abstraction in M1/PMC (F_3,440 = 4.92, p = 0.0023), but not in PFC (F_3,440 < 1.0). We emphasize that these effects observed for gamma time-to-peak and amplitude are present despite the fact that the electrode selection criterion was not based on any relationship between abstraction and gamma amplitude, and it was blind to the direction of the effect.

We next examined the relationship between trial-by-trial RT and the high gamma measures via linear regression analysis using time-to-peak and amplitude in both M1/PMC and PFC as regressors. We observed that these high gamma measures are predictive of trial-by-trial RT (full regression: R² = 0.075, p < 10^-6; M1/PMC amplitude p = 0.0012; M1/PMC peak time p < 10^-4; PFC amplitude p = 0.17; PFC peak time p = 0.045). This ability to predict trial-by-trial RT from frontal high gamma activity cannot be attributed to task difficulty (see Methods), as RT can still be predicted from high gamma activity even when removing the effects of task abstraction from trial-by-trial RT (R² = 0.024, p = 0.032). A significant proportion of the remaining variance in trial-by-trial RT—after controlling for the effects of task abstraction—is explained by delays in PFC high gamma time-to-peak (partial r = 0.13, p = 0.008) indicating that PFC timing delays drive slower RTs independent of task abstraction. Finally, even when removing trials in which gamma activity peaks within 100 ms of each trial's RT, both the regression models remain significant predictors of behavior (task abstraction: R² = 0.037, p = 0.014); trial-by-trial RT: R² = 0.053, p = 0.001).

Interregional theta phase encodes task information

We also examined the role that interregional theta phase encoding plays in coordinating frontal network communication during hierarchical cognitive control. As with the high gamma analyses, we first identified phase encoding pairs of electrodes within M1/PMC and PFC, as well as between M1/PMC and PFC, from the pairwise theta phase difference between electrodes (see Methods and model Fig. 3). An electrode pair was defined as task-encoding if the task condition explained a significant proportion (p < 0.05) of the circular variance of the pairwise theta difference for more than 100 consecutive ms (see Methods). Of 2533 total possible frontal electrode pairs across all subjects—141 within M1/PMC, 1457 within PFC, and 935 between M1/PMC and PFC—32 pairs (22.7%) were task-encoding within M1/PMC, 200 pairs (21.4%) were task-encoding between M1/PMC and PFC, and 319 pairs (21.9%) were task-encoding within PFC (no significant differences between proportions, χ²-test p > 0.7 all comparisons). As with the high gamma analyses, this selection method is blind with regard to the direction and timing of the encoding effect. In total this process results in 21.8% of the channels classified as phase encoding. We verified that this method did not result in an inflated number of false-positives by using a non-parametric resampling approach (see Methods). This permutation analysis resulted in significantly fewer phase encoding pairs, on average only 13.7% and at most 21.3%, fewer than the actual observed proportion of encoding pairs (21.8%). This means that the observed number of encoding pairs is greater than the maximum number of encoding pairs likely to be observed by chance alone, and is strong evidence that this approach is capturing taskdependent phase encoding.

Figure 3.

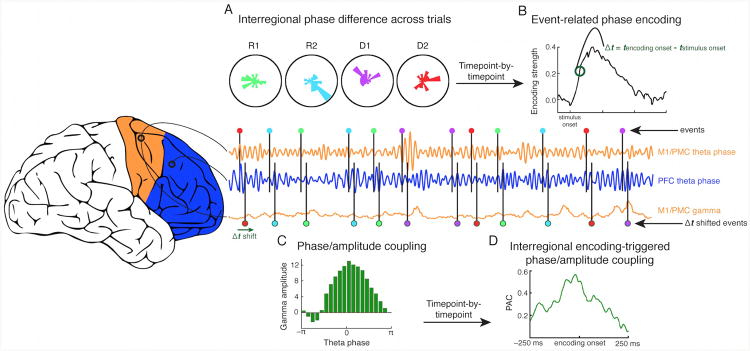
Frontal phase/amplitude communication model. (A) Example instantaneous theta phase encoding between PFC (blue) and M1/PMC (orange) (rose plots). Note that these plots are illustrative of significant, instantaneous phase-encoding at a single time point, but that these encoding values are dynamic and the encoding phases for each condition can change within a trial, across trials, and across channel pairs. (B) The onset of significant phase encoding relative to the stimulus onset (Δt) differs for each encoding electrode pair (see Methods). This relationship is shown for an example pair of M1/PMC and PFC electrodes, along with the corresponding gamma amplitudes in M1/PMC, across multiple trial events. (C) Following the onset of significant phase encoding, event-related theta phase/high gamma amplitude phase/amplitude coupling (PAC) can be evaluated. As seen in this example, PAC is statistically assessed as a non-uniformity in the distribution of high gamma amplitude relative to the theta phase difference between PFC and M1/PMC sites such that for an illustrative case, (D), interregional encoding-triggered PAC provides an index of frontal communication via temporally-specific high gamma increases during interregional theta phase encoding.

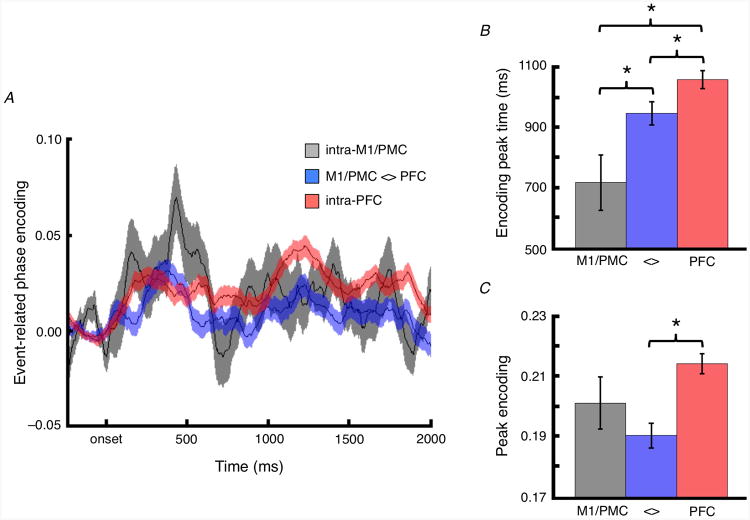
From this selection we calculated time-resolved event-related theta encoding between electrode pairs (Fig. 4A). Across these encoding pairs, the time-to-peak phase encoding is earliest for encoding pairs within M1/PMC, later for pairs between M1/PMC and PFC, and is latest for pairs within PFC (unpaired t-tests; intraregional M1/PMC versus interregional M1/PMC-with-PFC: t₂₃₀ = 2.25, p = 0.025; interregional M1/PMC-with-PFC versus intra-PFC: t₅₁₇ = 2.33, p = 0.020) (Fig. 4B). In contrast, peak event-related phase encoding is only different between M1/PMC-with-PFC and intraregional PFC (t₅₁₇ = 4.49, p < 10^-5) (Fig. 4C).

Figure 4.

Task- and region-dependent frontal theta phase encoding. (A) Time course of event-related interregional theta phase encoding between electrode pairs within M1/PMC (black), between M1/PMC and PFC (blue), and within PFC (red) for electrode pairs showing theta phase information transfer (phase encoding of the task). (B) Time-to-peak interregional theta phase encoding is earliest for electrode pairs within M1/PMC, peaks later for pairs between M1/PMC and PFC, and peaks latest for pairs within PFC (color scheme same as A). (C) Maximum event-related theta phase encoding is only different for pairs between M1/PMC and PFC compared to pairs within PFC. Note that the peak encoding and encoding times as inferred from the plots in A may differ from those found by averaging the trial-by-trial peaks shown in B and C due to the differences in findings peaks of averages (A) versus averaging peaks (B and C) (see Fig. S5 for an illustrative example). Shaded regions and error bars indicate SEM. (*) Significant t-test; p < 0.05. Horizontal bars indicate significant regression; p < 0.05 (uncorrected).

Because the ability to accurately estimate phase is dependant upon the oscillatory power within the band of interest, we looked at task-related changes in theta amplitude to see if such changes might contribute to the observed encoding and/or PAC results. We did not observe any effect of task abstraction on theta amplitude (no region-by-load interaction: F_3,438 = 1.29, p = 0.28; no main effect of task: F_3,438 < 1.0; no effect of task in either region: p > 0.10). We did observe a main effect of region such that M1/PFC theta amplitude was higher than PFC theta amplitude (F_1,438 = 14.6, p < 10^-3). However, we note that encoding was greatest for intraregional PFC, for which task-related theta amplitude was lowest. We also examined the effect of task abstraction on theta amplitude timing in the exact same manner as we used for gamma amplitude. We did not observe any effect of task abstraction on theta amplitude timing (no loadby-region interaction, no main effect of load, no effect of load in either region, and no effect of region; F < 1.0 for all).

These results suggest an important role for both theta phase encoding and high gamma activity in coordinating behavioral activity during cognitive control. However, they do not provide the critical physiological link needed to demonstrate that frontal theta networks coordinate interregional communication via phase dependent neural activity. To make this connection requires a method for analyzing the relationship between interregional communication and population activity, for which PAC is ideally suited.

Interregional theta phase coordinates transient communication networks

High gamma activity and frontal theta phase encoding independently tracked behavior, but it is unclear whether theta phase encoding dynamically establishes transient oscillatory networks for coordinating frontal communication. To examine whether theta phase encoding coordinates activity across spatially segregated neuronal assemblies in M1/PMC and PFC, we need to account for the endogenous temporal variability when these networks are established. To accomplish this, we restricted our analyses to the significant encoding electrode pairs from the theta phase analyses. For each encoding pair we identified the encoding onset time as the time when task abstraction explained a significant proportion of the variance in the theta phase difference between the electrode pair, across trials. These theta phase encoding onset times were then used as the new time-locking events for calculating event-related theta phase/high gamma amplitude PAC²⁸ (see Methods). Time locking to an endogenous event via encoding-triggered averaging accounts for any inherent variability in the timing of interregional communication (see model Fig. 3).

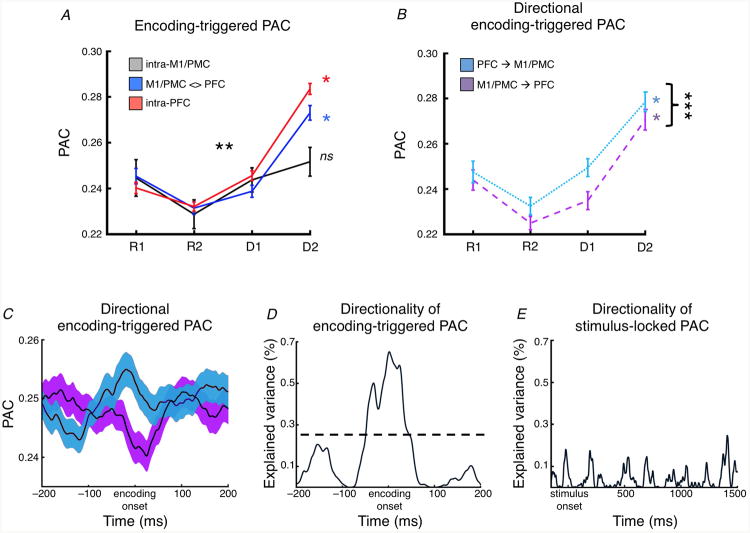
Theta/high gamma PAC increases with task demands such that the theta phase in an electrode provides task-dependent information about the gamma amplitude around the theta phase encoding time (Fig. 5A; main effect of task abstraction, F_3,1644 = 31.29, p < 10^-18). We also observe a task-by-region interaction (F_6,1644 = 3.04, p = 0.0058) such that encoding-triggered PAC increases as a function of task differentially depending on the location of the encoding pair. More specifically, encoding-triggered PAC increases as a function of task between encoding PFC electrode pairs (F_3,954 = 88.55, p < 10^-49) and for encoding pairs between M1/PMC and PFC (F_3,597 = 30.75, p < 10^-17), but less so for encoding pairs within M1/PMC (F_3,93 = 2.29, p = 0.084). These results were specific for the theta band (p > 0.24 each for 1-4 Hz delta; 8-12 Hz alpha; and 12-24 Hz beta interactions).

Figure 5.

Encoding-triggered PAC. (A) For electrode pairs showing theta phase encoding of the task, theta/gamma PAC around the encoding peak increases as a function of task demands (main effect of task abstraction, p < 10^-18). There was also a task-by-coupling region interaction (*** Significant task-by-region interaction, p = 0.0058) such that encoding-triggered PAC increases as a function of task between encoding PFC electrode pairs (p < 10^-49) and for encoding pairs between M1/PMC and PFC (p < 10^-17), but less so for encoding pairs within M1/PMC (p = 0.084). (B) There was also an effect of directionality on PAC between M1/PMC and PFC such that PFC theta phase was a stronger predictor of M1/PMC high gamma than M1/PFC theta phase was of PFC high gamma (*** Significant main effect of direction, p = 0.0021; main effect of load: p < 10^-23). (C) Time course of time-resolved PAC (averaged across task conditions, colors same as in B); and, (D) effect size of directional PAC relative to encoding onset, showing that the peak directional effect is near the theta phase encoding onset (dashed line shows maximum directional PAC effect size observed in stimulus-locked case). (E) At no point during the trial period does this directionality effect for stimulus-locked PAC reach the magnitude of the directional PAC effect observed in the encoding-triggered case. (*) Significant main effect of task, p < 10^-4. Error bars and shaded regions indicate SEM. (ns: not significant)

Critical to our model for interregional communication, there was also an effect of directionality on interregional encoding-triggered PAC between M1/PMC and PFC such that PFC theta phase was a stronger predictor of M1/PMC high gamma than M1/PFC theta phase was of PFC high gamma (Fig. 5B; main effect of direction, F_1,597 = 9.50, p = 0.0021). The time course of this effect of directionality of coupling peaks around encoding onset (Fig. 5C,D), and is only observed when accounting for temporal shifts in interregional theta phase encoding, as can be seen by the lack of a directional effect when directional PAC is calculated relative to stimulus onset (Fig. 5E).

Discussion

Here we provide evidence for a neurophysiological mechanism supporting frontal corticalcortical communication in cognitive control. The results demonstrate that high gamma amplitude changes differ between frontal cortical subregions, dependent on the degree of rule abstraction required to generate a response. The fact that the strength and timing of high gamma and interregional theta phase encoding predict performance on a trial-by-trial basis demonstrates the importance of large-scale frontal networks in coordinating behavior. We hypothesized that PFC modulates neural activity in the motor cortices when abstract rules are needed to govern motor outcomes. While the high gamma results show that the high gamma time-to-peak occurs later in the PFC than in M1/PMC, this is only true for the R1 and R2 conditions known to minimally recruit PFC. We observed that a significant proportion of the remaining variance in trial-by-trial RTs—after controlling for the effects of task abstraction—is explained by delays in PFC high gamma time-to-peak, suggesting that PFC timing delays drive slower RTs independent of task abstraction. Nevertheless, we argue that it may not strictly be the high gamma amplitude or timing, per se, that is the critical index of cognitive control, but rather its modulation by an oscillatory component. That is, we must account for the task-relevant modulation of population activity by a plausible communication mechanism.

Theta/high gamma PAC offers a possible mechanism by which the frontal cortex simultaneously maintains multiple behavioral modes²⁷. We find that multiple task demands are encoded by phase differences between frontal subregions such that theta phase encoding is strongest within electrodes in the PFC. As predicted by the PAC communication model, during times of task-relevant phase encoding theta phase dynamically and transiently organizes trial-bytrial gamma amplitudes in a task-dependent manner. Critically, PAC for intraregional PFC—and for interregional PFC-to-M1/PMC—increases as task abstraction increases. The PAC effect for encoding electrode pairs that span frontal cortex (PFC to M1/PMC) is stronger for the PFC to M1/PMC direction than it is for the reverse direction. That is, PFC theta phase predicts population activity more strongly in the M1/PMC only when accounting for the timing variability in endogenous oscillatory theta encoding. This finding suggests an anterior-to-posterior information flow, supporting a hierarchical cognitive control architecture.

These results lend strong support to the argument that PAC indexes task-relevant information transfer within the frontal cortex, and they are consistent with models that suggest that neural oscillations may serve to coordinate complex behaviors^16,28,40,41. While spike/phase encoding schemes have recently been found to play a role in coordinating behaviorally relevant neural activity in animals^42,43, to date there have been no studies that suggest that interregional phase amplitude coupling supports communication in support of higher cognition. These results address a fundamental issue regarding frontal lobe organization and function by showing that oscillatory phase encoding and temporally precise, dynamic spiking activity, manifested as cortical high gamma, may be the mechanism by which frontal subregions coordinate task-dependent neural processing.

Some caveats are worth addressing. ECoG recording restrictions resulted in sampling that was both sparse and spatially biased. This constraint required collapsing across broad cortical ROIs. Thus, though the present results are consistent with prior lesion and neuroimaging evidence regarding anterior-to-posterior frontal organization, they are unable to inform the multilevel anatomical specificity proposed by the most detailed versions of these models. In addition, the time limitations of the ECoG recording environment limited our ability to further manipulate rule abstraction across conditions without including additional controls for changes in task difficulty^3,9,13.

Our results contrast with invasive results from PFC recordings in macaques that show a critical role for other oscillatory frequencies, such as beta (12-24 Hz) in coordinating PFC ensembles. Most notably, these studies use penetrating intralaminar electrodes to record LFPs from macaques^44,45. This approach likely has an effect on the observable results since different cortical layers have different dominant frequencies. There is also increasing evidence that different frequencies may play different roles in routing information between brain regions⁴¹, that different regions have different preferred low coupling frequencies with high gamma¹⁶, and that low frequency oscillations may interact with, or be nested within, one another^46,47. Finally, it is likely that interregional coupling is mediated in part by subcortical structures including the basal ganglia^11,12,15 and/or thalamus^30,48, or other neocortical regions, such as parietal association cortex⁴⁹. In the context of preparatory cognitive control, for example, distinct cognitive control states have been shown to differentially activate theta-coherent frontoparietal sub-networks depending on task demands, an effect observed in both human⁵⁰ and non-human primate EEG⁴⁹. This finding is especially relevant given the broad role that oscillatory coherence plays in shaping ongoing, endogenous neural activity, as opposed to stimulus-locked effects³⁷.

In summary, our results address a major question in systems and cognitive neuroscience regarding how the frontal lobes coordinate information. Our results provide evidence that theta phase encoding dynamically coordinates local neuronal activity across frontal regions dependent on task demands. These data demonstrate how neural activity at different time scales might be used to coordinate information between anatomically distributed regions. Together, these findings suggest a mechanism for coordination of neural processing for complex cognitive functioning in the human frontal cortex.

Methods

Data collection

Data were collected from four subjects with intractable epilepsy who were implanted with chronic subdural grid electrodes as part of a pre-operative procedure to localize the epileptogenic focus. The surgeons determined electrode placement and treatment based solely on the clinical needs of each patient. Data were recorded at three hospitals: the University of California, San Francisco (UCSF) Hospital (subjects UC1 and UC2), the Johns Hopkins School of Medicine (subject JH1), and the Stanford School of Medicine (subject ST1). All subjects gave written informed consent to participate in the study in accordance with the University of California, Berkeley Institutional Review Board as well as the review board of the relevant hospital (i.e., the UCSF, Johns Hopkins Medicine, or Stanford Institutional Review Board).

ECoG data were acquired using a custom built Tucker Davis Technologies recording system (256 channel amplifier and Z-series digital signal processor board) at UCSF and Stanford, or via a clinical 128-channel Harmonie system (Stellate) recording system at Johns Hopkins. Data were sampled at 3052 Hz (UCSF and Stanford) or at 1000 Hz (Johns Hopkins). Signals were digitized for further analysis and, for subjects UC1, UC2, and S1, were resampled offline to 1000 Hz. ECoG data were individually referenced to the average potential of all electrodes.

Behavioral task

Hierarchical control demands were manipulated by parametrically increasing the order of abstraction of response selection rules across two manual response tasks shown in a previous fMRI study to recruit progressively more anterior portions of frontal cortex^3,18 (Fig. 1A,B). The Response task manipulated abstraction between zero and 1st order response rules, termed the R1 and R2 conditions, respectively. The Dimension experiment manipulated abstraction between 2nd and 3rd order rules, termed the D1 and D2 conditions respectively. All analyses assume a parametric relationship of increasing abstraction from R1 through D2, with D2 being the most abstract condition. Details of these tasks follow.

Response Task: On each trial, participants saw the outline of a coloured square. Based on the colour of the square, participants chose a key-press response on the keyboard. Trials were grouped into blocks. For each block, participants were given a previously trained rule set that mapped two coloured boxes to be seen over the course of the upcoming block to either one (R1) or two (R2) potential responses. Thus, during R1 blocks, there was no uncertainty about what response to make, so R1 provides a concrete motor baseline or a “zero-order abstraction condition”. By contrast, R2 involved selecting one of two responses contingent on colour, and so requires behaving according to a 1st order rule.

Trials began with the presentation of the coloured box. Upon presentation of the box, participants were instructed to respond as quickly but as accurately as possible. If participants had not responded within 15 s, the trial self-terminated and was not included in future analysis. Trials were separated by a 1000 ms ITI.

Dimension Task: Participants saw the outline of a coloured square surrounding two objects. On each trial, the two objects could be the same or different from each other in terms of their shape or their visual texture. The colour of the bounding square could also change on each trial and cued one of these two dimensions (shape or texture) as the target dimension for that trial. Using one of two keys on the keyboard, the participant indicated for each trial whether the two objects matched or not along the target dimension.

Trials were grouped into blocks. For each block, participants were given a rule set that mapped two coloured boxes to be seen over the course of the upcoming block to either one (D1) or two (D2) target dimensions. During D1 blocks, there is no uncertainty about which dimension is the target, as all the colours map to the same dimension. Thus, D1 only required choosing which of two responses to make based on the relationship between the two objects (a 2nd order rule). By contrast, D2 involved using the coloured box to select the appropriate dimension along which to relate the two objects. Thus, this condition required behaving according to a 3rd order rule.

Trials began with the presentation of the coloured box bounding the two objects. Upon presentation of the stimulus, participants were instructed to respond as quickly, but as accurately, as possible. If participants had not responded within 5 s, the trial self-terminated and was not included in future analysis. Trials were separated by a 200 ms ITI.

Prior to performing both types of task, participants went through a training phase to learn the rule sets for all conditions. For each rule set they were shown the relevant colour-to-response or colour-to-dimension mappings and then were verbally quizzed about each one. They then performed 12-16 trials of practice, during which timing was self-paced, followed by 12-16 practice trials using the same parameters as in the actual experiment. Following training, participants completed the task, consisting of 64 trials divided evenly between the R1 and R2 (or D1 and D2) conditions.

Electrophysiology pre-processing

All electrophysiological data were analyzed in MATLAB® using custom scripts. We analyzed data from electrodes over frontal cortex. Out of 142 frontal channels, 140 were artefact-free and included in subsequent analyses. Electrode classification into discrete PFC and M1/PMC regions of interest (ROIs) was based on surface anatomy. We included in the M1/PMC grouping any frontal electrodes on or posterior to the precentral sulcus. For all analyses, only data from correct trials were used. Data for each frontal channel were first filtered into separate theta (x_θ, 4-8 Hz) and high gamma (x_γ, 80-150 Hz) pass bands using a two-way, zero phase-lag, finite impulse response filter to prevent phase distortion (eegfilt.m function in EEGLAB toolbox^{16,22,23,26,51}). We then applied a Hilbert transform to each of these time series (hilbert.m function) to extract the analytic amplitude for both bands. The Hilbert transform gives a complex time series,

$$h_x[n]=a_x[n]e^{i{\varphi }_x[n]},$$ (1)

where a_x[n] represents the instantaneous analytic amplitude, and ϕ_x[n] is the instantaneous phase. This method is equivalent to sliding window FFT and wavelet decomposition approaches^18,19,21,52. For high gamma amplitude analyses, data were averaged for each region (PFC and M1/PMC) separately for each subject, and broken into event-related epochs using a 200 ms baseline to remove any pre-stimulus differences in baseline amplitude.

High gamma analyses

To identify task-selective high gamma channels we performed a sliding-window one-way ANOVA at each time point for each subject, channel, and band with a condition order of R1, R2, D1, D2. This approach permitted us to examine the amount of high gamma variance explained by the task, similar to methods used in single-unit electrophysiology experiments^{16,21-23,25,26,53}. Electrodes demonstrating a significant effect of task (p <= 0.05) for more than 100 consecutive ms were defined as task selective. This analysis is naïve with regards to electrode location or to whether task abstraction caused event-related high gamma amplitude increases or decreases. Trial-by-trial high gamma peaks and peak times were identified from the average high gamma analytic amplitude time series for each ROI. Subsequent high gamma amplitude and time-to-peak analyses (Fig. 2C,D) were performed using repeated measures ANOVA with task condition as the within-subjects factor and electrode location as the between-subjects factor.

Theta phase analyses

As noted from eq. 1, the Hilbert transform gives an estimate of amplitude (a_x[n]) and phase (ϕ_x[n]). The phase time series ϕ_X assumes values within (-π, π] radians with a cosine phase such that π radians corresponds to the trough and 0 radians to the peak. To calculate trial-by-trial interelectrode theta phase encoding, first ϕ_θ was estimated for each electrode and then, for each pair of frontal electrodes (i, j) the phase difference ϕ_θij was calculated at each time point, and this phase difference time series was then broken into individual trial epochs for future interregional phase encoding analysis.

$${\varphi }_{\theta ij}[n]={\varphi }_{\theta i}[n]-{\varphi }_{\theta j}[n],$$ (2)

To examine the behavioral role of interregional phase encoding we adopted a similar analysis protocol as used for the high gamma amplitude. First, encoding electrode pairs were identified using a sliding-window circular-linear correlation, which combines coefficients between a linear variable (task condition, C) and the linearized phase variable (ϕ_θij) by extracting the sin and cos components of ϕ_θij A single correlation coefficient, ρ, and its associated p value was then calculated where,

$${\rho }_{\varphi C}=\sqrt{\frac{r_{cC}^2+r_{sC}^2-2r_{cC}{r}_{sC}{r}_{cs}}{1-r_{cs}^2}},$$ (3)

with r_cC = c(cos ϕ_θij[n], C), r_sC = c(sin ϕ_θij[n], C), r_cs = c(sin ϕ_θij[n], cos ϕ_θij[n]), and c(x, y) equal to the Pearson correlation between x and y⁵⁴. Electrodes demonstrating a significant correlation (p <= 0.05) for more than 100 consecutive ms were defined as theta phase encoding. Encoding strength, ρ_ϕC, for encoding pairs was then averaged across possible ROI combinations: intraregional M1/PMC, intraregional PFC, or interregional PFC-with-M1/PMC, where the two encoding electrodes reside within the same ROI for the intraregional groupings, and cross ROIs for the interregional grouping. Trial-by-trial phase encoding was adjusted using a 200 ms prestimulus baseline to isolate behavioral changes. Note that this adjustment may result in taskrelated phase encoding that is lower than the baseline, and therefore ρ_ϕC, may be less than 0. For these analyses theta phase encoding was analysed using unpaired t-tests comparing encoding strength across regions.

This technique offers several benefits over, e.g., methods looking at coherence across time. First, just as with the high gamma amplitude analyses, this analysis is naïve with regards to electrode location and makes no a priori assumptions about the time window of interest. Specifically, because we are looking at the percent of interregional phase coupling variance explained by task condition across trials at every time point, 100 milliseconds of consecutive encoding (defined as 100 consecutive milliseconds of a significant relationship between interregional phase and task condition) is a conservative approach, as this procedure yields almost no encoding pairs is resampling methods are used (shuffling the relationship between phase difference and task condition). Second, it makes no strict assumptions about coherence, per se, and rather focuses on the task encoding aspect, specifically looking at how predictive of the task condition the moment-to-moment theta phase difference between the two electrodes is across trials. This is important because it reduces the probability of spurious coherence driven by, for example, equipment issues, electrode reference choice, or signal propagation and specifically requires there to be task-related changes. The downside is that because encoding is explicitly defined as the relationship between task and theta phase, it cannot be calculated separately for each task condition.

As a result, any given electrode could in theory participate in multiple theta encoding pairs at different times. By way of illustration, electrode i could show significant theta phase task encoding with electrode j from 1200-1600 ms, for example, while i could also show significant theta phase task encoding with electrode k from 400-550 ms. On the other hand, electrode j and k need not show any theta phase encoding and the null hypothesis would state that while two electrodes may show significant theta phase encoding of the task, theta phase need not have any predictive power for trial-by-trial variance in high gamma amplitude.

The primary phase-encoding analysis flow defines a channel pair as phase encoding if their phase differences significantly encode task parameters during the post-stimulus window for at least 100 ms using a sliding-window approach to estimate the relationship between theta phase difference and task on a timepoint-by-timepoint basis. This process results in 21.8% of the channels classified as phase encoding (as previously noted). To assess the likelihood that this process results in false positives, we performed permutation analyses. For this analysis, analyses were performed as normal, but trial condition identifiers were permuted in 100 surrogate runs. That is, for each subject the same number of trials were kept per condition, but their trial-by-trial condition mapping was randomly permuted. Using this surrogate trial remapping, the same sliding window analysis was performed as above and the number of channel pairs classified as phase encoding was stored. This was done 100 times for all channel pairs to get an estimate of the distribution of the proportion of false positives yielded by the primary method, keeping everything in place as before except for the trial encoding.

Phase/amplitude coupling analyses

For PAC analyses, for each theta phase encoding channel pair we examined the relationship between theta phase from electrode i and high gamma amplitude in that same electrode using the same circular-linear correlation method above, except with a_γ as the linear variable and ϕ_θi or ϕ_θj (instead of ϕ_θij) as the circular variable,

$${\rho }_{\varphi a}=\sqrt{\frac{r_{ca}^2+r_{sa}^2-2r_{ca}{r}_{sa}{r}_{cs}}{1-r_{cs}^2}},$$ (4)

Where r_ca = c(cos ϕ_θi[n], a_γi[n]), r_sa = c(sin ϕ_θi[n], a_γi[n]), and r_cs = c(sin ϕ_θi[n], cos ϕ_θi[n]). For directional analyses for M1/PMC with PFC pairs, ρ_ϕa was calculated as above but using theta phase from electrode i and the gamma amplitude from its theta-encoded pair, j. This slidingwindow approach was performed for stimulus-locked and encoding-triggered PAC, where “encoding-triggered” was identified from the onset time of significant theta phase encoding as calculated from the previous analysis (eq. 3). We hypothesized that PAC determined around the time of interelectrode communication would be significantly greater than PAC that did not account for this endogenous temporal variability.

PAC was calculated separately for each task condition and electrode pairing combination (intraregional M1/PMC, intraregional PFC, and interregional PFC-with-M1/PMC) as the average PAC value across a 100 ms window around encoding. Furthermore, for the interregional PFC-with-M1/PMC theta-encoding pairs, we could examine directionality effects to see if PFC theta modulates M1/PMC high gamma differently than M1/PMC theta modulates PFC high gamma. This approach allows us to assess the likelihood that task-dependent PAC effects are an epiphenomenon arising from task difficulty, or whether PAC is specifically conveying task-related information between frontal regions when those regions encode task parameters in their theta phases. For these analyses we performed a repeated measures ANOVA with task condition as the within-subjects factor and theta phase encoding region pair as the between-subjects factor.

Control analyses

An alternate explanation for the increased PFC high gamma activity and latency is that task difficulty by condition, rather than cognitive control per se, could give rise to the observed high gamma effects. While previous versions of this task were able to explicitly behaviorally control for task difficulty^3,9,13, the limitations of the ECoG recording environment prohibited longer behavioral experiments. However the improved signal-to-noise in trial-by-trial high gamma recordings relative to fMRI data allows for more careful quantitative approaches to comparing cognitive control versus task difficulty, which we outline here. In general each supplemental method requires removing the effects of RT differences between task conditions to equate difficulty. Two different methods were used that, given the linear nature of the analysis, are closely related though conceptually different:

1. Difficulty Correcting Method: The effects of task condition on RT can be held constant via linear regression, and the trial-by-trial relationship between high gamma activity and the residual variance can be examined. This method assumes that, if difficulty alone can explain gamma differences, then high gamma would have no explanatory power over the residual RT variance separate from task condition.

2. Difficulty Matching Method: Similarly, if difficulty alone explains high gamma activity differences across conditions, then across neighboring conditions (i.e., R1/R2, R2/D1, and D1/D2) for RT-matched trials, there should be no difference in high gamma given that the only difference is not in behavioral outcome but cognitive control.

Difficulty Correcting Method

For this method, a regression between task condition and RT was performed, from which the difference between the predicted RT and actual RT could be calculated (the residuals) given task condition alone. Next, high gamma activity (amplitude and time-to-peak) could then be regressed against these residuals to see if high gamma activity could explain any of the remaining trial-by-trial RT variance when task condition (here, conceptualized for hypothesis testing purposes as “difficulty”) was held constant. Even after removing the effects of task abstraction, trial-by-trial RT could be predicted from high gamma activity (R² = 0.026, p = 0.020).

Difficulty Matching Method

By matching trials by response time between neighboring task conditions, differences between behavioural variables are minimized, thereby emphasizing only differences in cognitive control. This paired analysis yielded 77 trial pairs within ±25 ms with no response time bias in either direction (p > 0.5). Such an analysis comparing PFC high gamma between any two randomly RT-matched trials should show that high gamma activity is greater for the more abstract condition compared to its RT-matched, but less-abstract, task condition pair. In keeping with the cognitive control hypothesis, PFC high gamma activity was significantly different between RT-matched trial pairs (p = 0.041). A resampling analysis of 10⁴ randomly selected groups of 85 between-condition trial pairs showed that PFC high gamma is, on average, 0.18 μV greater for the more abstract conditions (p = 0.047).

Statistical analysis

All analyses on RT and high gamma time to peak were done using the log₁₀ transformed times (in ms). This transformation was applied because the RT were skewed with a long right tail; the log transformation lead to a more normal distribution. Multiple linear regression models were constructed using the neural indexes (M1/PMC and PFC high gamma peak amplitude and time to first peak; stimulus-locked and peri-response frontal network theta phase encoding) as predictors of log₁₀ RT. Statistical tests performed are indicated next to reported p-values in the text. For parametric tests (regression, t-tests, and ANOVA), data were tested for normality, although for the relatively larger ns used for the analyses (performed on a trial-by-trial or channel-by-channel basis) this is not as much a concern as long as the data are not heavy-tailed (which these data are not)⁵⁵. In cases where normality was violated, specifically for RT, gamma peak time, and coherence peak time analyses, non-parametric equivalent statistics (e.g., Wilcoxon rank sum test) were used to confirm parametric results. In each such case, tests significant in the parametric case remained significant when a non-parametric equivalent was used. Trials for which RT or any of the neural measures included outliers (±4 standard deviations from the mean) were excluded from analyses. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those employed in ECoG studies. A methods checklist is available with the supplementary materials.