Abstract
Predicting RNA 3D structure from sequence is a major challenge in biophysics. An important sub-goal is accurately identifying recurrent 3D motifs from RNA internal and hairpin loop sequences extracted from secondary structure (2D) diagrams. We have developed and validated new probabilistic models for 3D motif sequences based on hybrid Stochastic Context-Free Grammars and Markov Random Fields (SCFG/MRF). The SCFG/MRF models are constructed using atomic-resolution RNA 3D structures. To parameterize each model, we use all instances of each motif found in the RNA 3D Motif Atlas and annotations of pairwise nucleotide interactions generated by the FR3D software. Isostericity relations between non-Watson–Crick basepairs are used in scoring sequence variants. SCFG techniques model nested pairs and insertions, while MRF ideas handle crossing interactions and base triples. We use test sets of randomly-generated sequences to set acceptance and rejection thresholds for each motif group and thus control the false positive rate. Validation was carried out by comparing results for four motif groups to RMDetect. The software developed for sequence scoring (JAR3D) is structured to automatically incorporate new motifs as they accumulate in the RNA 3D Motif Atlas when new structures are solved and is available free for download.
INTRODUCTION
RNA 3D motif structure, clustering and sequence alignments
Structured RNA molecules contain modular three-dimensional (3D) motifs that correspond to the hairpin loops (HL), internal loops (IL) and multi-helix junction loops (MHJ) one sees in RNA secondary structures. This paper focuses on 3D motifs in HL and IL, but the method can be generalized for MHJ loops. HL occur on the ends of Watson–Crick (WC) double helices and IL between two helices. Many 3D motifs formed by HL and IL are recurrent and found in a variety of non-homologous locations in diverse RNA molecules, including rRNAs, tRNAs, ribozymes and riboswitches. Some 3D motifs play architectural roles (e.g. kink-turns and C-loops), while others serve to anchor RNA tertiary interactions (e.g. GNRA HL and their receptors and T-loops), or provide binding sites for proteins or ligands (1). Such recurrent 3D motifs usually play similar roles in different RNAs. Other motifs such as Sarcin–Ricin (S/R) motifs have diverse functions in different contexts (2). Given that many HL and IL form defined 3D structures that are modular and recurrent, it is desirable to develop general methods to predict their presence in new RNA sequences.
Current tools make it possible to infer the secondary structures of new RNA molecules with reasonable accuracy and therefore to identify the locations and sequences of the HL and IL they contain (3–6). One can then try to exactly match these sequences to known instances of loops from RNA 3D structures (7). Unfortunately, exact sequence matches are rare, except for the smallest motifs, because the number of sequence variants found in 3D structures is still relatively limited.
RNA 3D motifs are structured by recurrent non-WC base-pairing, base-stacking and base-backbone interactions (1). It is the pattern of interactions and the overall motif geometry rather than the nucleotide sequence that is conserved across different instances of the same 3D motif. Moreover, some motifs admit variable-length insertions, which tend to occur at specific locations while conserving the core 3D structure (8). Thus, different sequences, potentially varying in length, can form the same 3D motif and perform similar functions.
To identify the best available structural data for each motif, we have established an automated pipeline that periodically extracts and clusters all HL and IL from a non-redundant (NR) set of high-quality RNA 3D structures from the PDB and NDB (9). Motifs are clustered according to conserved interactions and overall geometry, and not by sequence or overall length, so that the resulting motif groups in the RNA 3D Motif Atlas are meaningful for RNA structural analysis, comparison and modeling sequence variability consistent with the 3D structure (10). The Atlas is periodically updated with new structures, so it grows with the collection of new RNA 3D structures. Release 1.13 of the RNA 3D Motif Atlas contains 277 IL motif groups and 253 HL motif groups. Most of these groups are homogeneous in 3D structure, and thus matching and aligning a query sequence to a motif group amounts to a 3D structure prediction.
The goal of this paper is to identify the full range of sequences that can form a given RNA 3D motif, while minimizing false positive predictions. In previous work (11,12), we provided evidence that the actual sequence variability of basepaired nucleotides in structured RNA molecules follows the principle of isostericity (13): Base substitutions at corresponding paired positions in homologous instances of the same motif almost always conserve the basepair family as defined by Leontis and Westhof; moreover, within each basepair family, the most common base substitutions are isosteric, i.e. they preserve the geometry of the glycosidic bonds between the bases and the backbone. Isostericity thus provides the basis for scoring putative sequence variants for structured 3D motifs used here. In future work we will report on the ability of the models to match novel sequence variants to the correct motif group.
RNA multiple sequence alignments are sources of additional sequence variants for 3D motifs that can be used to build motif identification algorithms (14,15). These approaches work best when the alignment positions corresponding to a given 3D motif show good sequence conservation and sufficient but not excessive numbers of new sequence variants. However, in other cases, the number and variety of distinct sequences aligned to the same 3D motif suggests that either the alignment is wrong or the 3D motif is not conserved across all aligned sequences. Thus, to evaluate the quality of sequence alignments and to assess the likelihood that the same 3D motif is present at a particular location in an alignment, we need an independent model for the sequence variability that is consistent with the corresponding 3D structure. Producing such models is the main goal of the present paper. To avoid circularity of reasoning, we use 3D structures to build probabilistic models for sequence variability and use sequence variants from alignments to assess and validate the models. The models can also be used to assess and improve the sequence alignments themselves (16).
Review of relevant literature
The use of SCFGs to model RNA sequence variability was introduced in 1994 with the work of two groups (17,18). The covariance models of Eddy et al. are special types of SCFGs used to model the sequence variability among homologous RNA molecules that share a consensus RNA 2D structure. Their primary use to date has been to provide probabilistic models to assign new RNA sequences from genome projects to known families of homologous RNA molecules and to generate multiple sequence alignments. The program Infernal (19,20) has been used for several years with the Rfam database for this purpose (21,22). The parameters of each SCFG are set from hand-curated sequence alignments for each RNA family.
More recently, Theis et al. extend the work of Cruz and Westhof by extracting a large number of RNA internal and hairpin motifs and training Bayesian Network models on corresponding sequence alignments (14,15). These works are similar to the present paper in that they use probabilistic models capable of modeling nearly arbitrary interactions between nucleotides, but differ in that they train their parameters on sequence alignments and do not consider the false positive rate inherent in matching one sequence to multiple models.
Gardner and Eldai have used covariance models for RNA motifs (23). Their RMfam collection provides alignments and covariance models for 34 hand-curated motifs of varying types for curators and users of non-coding RNA (nc-RNA) alignments, with the goal of improving functional prediction of novel nc-RNAs and providing a resource for studying the evolution of RNA motifs. RMfam motifs are being annotated in Rfam as of release 12.0 (22).
Markov random fields are a well-studied extension of Markov chains to model arbitrary graphs (24). They are similar in modeling capability to Bayesian networks. MRF have been used for modeling sequence variability in protein–protein interactions (25).
MATERIALS AND METHODS
Distinguishing between core and non-core nucleotides
Many RNA 3D motifs have one or more ‘bulged’ or ‘looped out’ bases that do not interact with the other nucleotides of the motif, although they may interact with other parts of the RNA chain or other molecules. The simplest examples are IL consisting of a single nucleotide that bulges out of a helix without interrupting the stacking of the adjacent basepairs. In the construction of the RNA 3D Motif Atlas (10), we have taken care to distinguish between the ‘core’ and ‘non-core’ nucleotides of a motif, and to group instances based on the geometries and interactions of the core nucleotides. Structurally similar motifs that have bulged out nucleotides tend to have them at equivalent places in the structure, although the sequences and numbers of bulged bases can vary.
Components of the probabilistic models
Table 1 lists the different types of nodes (also known as SCFG rewrite rules) that we define to model RNA 3D motif sequence variation. Because Cluster and Hairpin nodes use Markov Random Fields (MRF) to model base triples and non-nested basepairs, we refer to these as hybrid SCFG/MRF models.
Table 1. Types of nodes implemented in the SCFG/MRF probabilistic models introduced in this paper.
| Node Name | For modeling: | Modeled with: | Examples: |
|---|---|---|---|
| Initial/Insertion (I) | Variable-length insertions | Length distribution, base distribution and independent bases | Allow for extraneous bases before the first flanking pair of a motif |
| Basepair (B) | Nested basepairs and adjacent variable-length insertions (bulged bases) | 4×4 probability score matrix for basepair; length and base distribution for insertions | All loops with nested basepairs |
| Cluster (C) | Base triples, crossing basepairs, basepairs on the same strand | Markov Random Field | S/R (base triple), C-loop (crossing basepairs) |
| Fixed (F) | Unpaired core nucleotides | 1×4 probability score vector for base | Conserved base stacked between basepairs |
| Hairpin (H) | Hairpin loops, which can contain base triples, non-nested basepairs and basepairs on the same strand | Markov Random Field | T-loop, GNRA loop, UNCG loop |
Building probabilistic models from multiple 3D motif instances
Here we provide details on the construction and parameterization of probabilistic models for motif groups having multiple instances, expanding on the description in the main text of the construction of models based on single instances. There are two challenges: determining interactions that are sufficiently well conserved across multiple instances and accounting for the sequence variability observed in those instances.
Identifying consensus basepairs to include in models
A basepair is included in the model when it occurs between corresponding nucleotides in a significant number of instances of the 3D motif group. We do not, however, require that all instances have the basepair to include it in the model. The motif groups in the Motif Atlas are constructed so that no two instances in the same motif group have two different FR3D-annotated basepairs (e.g. tSH and tWH) at the same position (29). In the best case, basepairs are conserved across all motif instances and are annotated consistently by FR3D either as full-fledged pairs or as ‘near’ pairs of the same kind (e.g. tSH or ntSH), which pose no problems. However, annotations do not always agree across all motif instances, due to variation in the quality of the underlying experimental data, 3D modeling, or inherent flexibility of the motif. Therefore, when clustering loop instances, the Motif Atlas makes allowance for a variety of near pairs at corresponding nucleotide positions (e.g. some ntSH and some ncWH), or even the complete lack of basepair annotations in some instances, if the instance is sufficiently similar in overall geometry to instances with annotations. The algorithm we have implemented for identifying basepairs takes account of this fact and deals generously with these cases: An annotated basepair is added to the list of consensus interactions of the probabilistic model if more than one third of instances have a full-fledged FR3D-annotated basepair. Near basepairs of the same type are allowed to compensate for lower numbers of full-fledged basepairs. For motif groups with many instances, a smaller percentage of annotated basepairs is allowed as long as more than 10 instances share the same interaction. In more detail, denoting the number of FR3D-annotated basepairs by T, the number of near and coplanar basepairs (26) of the same family by C, the number of near but non-coplanar basepairs by N and the number of instances in the motif group by L, we recognize a consensus basepair if and only if 3T + 2C + N > min(L, 30).
Determining consensus base-backbone interactions to include in models
Conserved base-phosphate (BPh) and base-ribose (BR) interactions are identified as follows: For each instance of the motif and each pair of interacting nucleotides i and j forming a base-backbone interaction we tally the base edges (Watson–Crick, Hoogsteen, or Sugar) of nucleotide i that form the full and near interaction with the phosphate (or ribose) of nucleotide j and designate by T and N the number of full and near interactions of the most commonly occurring edge. We recognize a consensus interaction if and only if 2T + N > L and 4T > = L. In particular, this recognizes a BPh interaction if more than half of the instances make a BPh interaction using the same edge.
Construction of basepair probability score matrices
Having identified a consensus basepair between positions i and j, we build the corresponding 4×4 probability score matrix (M) by averaging 4×4 matrices over the instances as follows: For each instance which makes the consensus conserved basepair or a near version of that basepair, we calculate the normalized 4×4 substitution matrix by scaling the IsoDiscrepancy Index (IDI) into a probability score, as described in Results, cf. Figure 2. When the base in position i (respectively j) makes a conserved base-backbone interaction, we modify row i (resp. column j) of the 4×4 matrix as described in the main text under ‘Base-backbone interactions.’ If bases i and j in the current instance do not make the conserved basepair (or near version of it), then we make a 4×4 matrix with 0.1 in the position corresponding to the bases in positions i and j and zeros elsewhere. This accounts for the observed base combination but does not predict any additional base combinations. After running through all instances, we sum and normalize the 4×4 matrices to produce the probability score matrix M for positions i and j.
Figure 2.

Empirically-based mapping of IDI to probability score for basepair substitutions. The function is piecewise linear between these (IDI,Score) points: (0,1), (1.8,0.8), (2.2,0.13), (3.1,0.07), (3.5,0.05), (7,0.03), (9,0.01), (10.0,0.01).
Treatment of large motif groups
When a 3D motif group has few instances, isostericity suggests additional plausible sequence variants. When a 3D motif group has many instances, their sequences alone represent the sequence variants that actually work in practice, so we weight the observed sequences more heavily, as follows. We calculate the 4×4 count matrix C to tally the number of observed base combinations (AA, AC, etc.) for given positions i and j. Letting L denote the number of instances and setting p = L/(L+100), the final 4×4 probability score matrix is (1-p)M + pC, which is a weighted average of the basepair probability score matrix M and the count matrix C. When L = 1, it is dominated by the matrix M, but as L increases, the contribution of M decreases and that of C increases, with equal contributions when L = 100. Thus, when a motif group has few instances, we score primarily by isostericity to remain open to new base combinations, but as the number of instances increases, we concentrate more of the score on the observed base combinations.
Treatment of non-basepaired fixed positions
Fixed nodes model positions that are conserved in all 3D instances of the motif and form some interaction within the motif, excepting basepairing, e.g. C7 in Figure 3(a). Cluster and Hairpin nodes can have such bases as well, as exemplified by U55, C56 and A57 in Figure 1(a) and U3 in Figure 4(a). We count the number of A, C, G and U in this position, add the counts to the vector [0.5 0.5 0.5 0.5] as a weak Dirichlet prior and normalize. For example, for the Fixed node in Figure 3(b) we assign the probabilities 1/12, 5/12, 1/12 and 5/12 for A, C, G and U, respectively, since two C's and two U's and zero A's or G's were observed in the four instances of this motif. When a fixed base makes a conserved BPh or BR interaction, the prior is weakened to increase the influence of the actual base counts.
Figure 3.
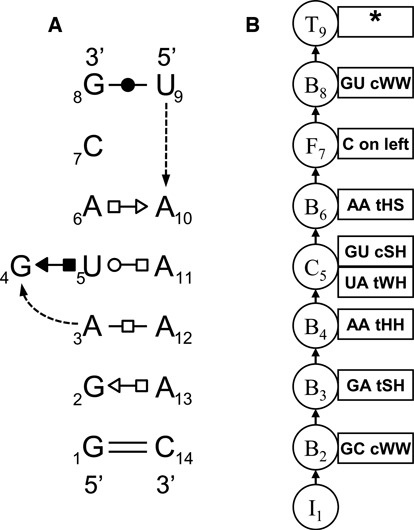
Panel (A) shows the annotation of instance IL_2AW7_041 of the S/R motif, numbered as in motif group IL_95652.3. Not shown are conserved base-phosphate interactions between the nucleotides 10 and 5, 4 and 11, 3 and 12, 14 and 13. Panel (B) shows the model tree consisting of an Insertion node (I), five Basepair nodes (B), one Cluster node (C), one Fixed node (F) and one Terminal node (T).
Figure 1.
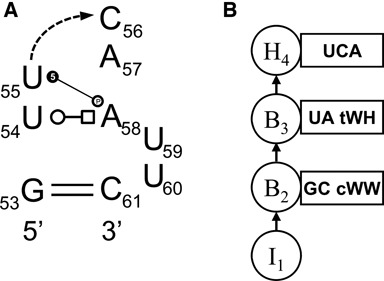
(A) Structure of the exemplar instance HL_3RG4_004 of motif group HL_72498.12, with annotations used to generate the SCFG/MRF model. The annotations include two basepairs, G53/C61 cWW U54/A58 tWH, bulged bases 59 and 60, and a 3-nucleotide hairpin with sequence UCA in which U55 makes a 5BPh base-phosphate interaction with A58. (B) Corresponding model tree of the SCFG/MRF model. The model tree consists of an Initial node (I1) to model nucleotides before G53 or after C61, basepair nodes (B2 and B3) to generate the paired nucleotides, and a hairpin node (H4). The nodes are labeled with information about the base combinations observed in the motif exemplar.
Figure 4.
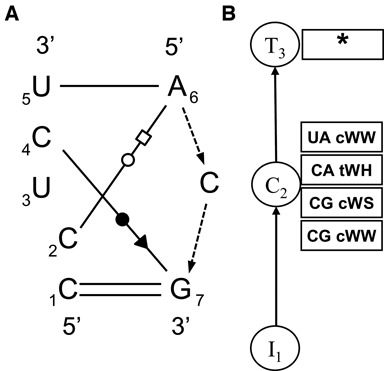
Panel (A) shows the annotation of instance IL_4JRC_003 of the C-loop motif, numbered as in motif group IL_73276.5; the unnumbered C between A6 and G7 is bulged out and not identified as a core nucleotide. Bases that are aligned vertically are stacked in the motif, in particular A6 and G7. Panel (B) shows the model tree consisting of an Initial node (I), Cluster node (C) and Terminal Node.
Treatment of bulged bases as variable-length insertions
As noted above, many motifs have one or more nucleotides with bases that bulge out and do not interact with the core motif nucleotides. Many such motifs can accommodate insertions of varying length without changing the overall structure of the motif. Moreover, length variations are observed between 3D instances and among aligned sequence variants. We model the number of insertions with a distribution over 0, 1, 2, etc. using observed insertion lengths from the 3D instances and assigning small non-zero probabilities to insertion lengths one less and one or two more than observed values, to broaden and smooth the length distribution. In detail, when there are L instances, we construct a vector of weights over 0, 1, 2, … insertions for each instance, sum these vectors and normalize to produce the smoothed length distribution. For an instance having 2 insertions the vector is [0, 1/(20L), 1, 1/(20L), 1/(400L), 0, 0, 0, …]. The letter distribution is set as it is for Fixed nodes, but without adjusting for BPh or BR interactions. For example, the T-loop instances in motif group HL_72498.12 usually have two bulged bases after the first basepair, but some have three. The inserted bases are most often U and A, but sometimes C and G. Referring to Figure 1, the insertions after the first basepair are modeled with probabilities 0.205, 0.112, 0.162 and 0.522 for A, C, G and U, respectively, and the length distribution is 0.0, 6.991×10−4, 0.9229, 0.07634, 9.225×10−5 and 2.865×10−6 for lengths 0, 1, 2, 3, 4 and 5, respectively.
We allow for variable length insertions on each strand after each basepair Node and after Fixed and Cluster nodes, even when no insertion is observed in any instance of the motif; when there is just one instance of the motif, the distribution is 0.9899, 0.0100, 0.0001 over lengths 0, 1 and 2, and as the number of instances with no insertion increases, the distribution is more concentrated on length 0.
Sequence variants from RNA multiple sequence alignments
To obtain additional sequence variants of RNA 3D motifs beyond what appears in 3D structures, alignments were downloaded from Silva on March 21, 2013 (27) and the Greengenes 2012 release (28). We obtained Silva alignments of the large ribosomal subunit for bacteria, archaea and eukaryotes, and of the small ribosomal subunit for eukaryotes. The Greengenes alignment covers the bacterial small subunit. Associations between alignments and 3D structures are listed in Supplementary Section H. To establish correspondences between nucleotides in a PDB file and the columns of the associated sequence alignment, Needleman-Wunsch with an affine gap penalty was used to find the best-matching sequence. All resolved nucleotides in eight 3D structures had exact correspondences in the multiple sequence alignments; one position in 1S72 and six positions in 3U5H did not have exact correspondences. These are listed in Supplementary Section H. For each motif instance from each of these structures, all columns of the alignments between and including the columns corresponding to the flanking WC pairs of the motif were extracted and gaps removed. For every alignment extract, we find that at least one sequence has an exact sequence match to at least one instance known from 3D data, evidence that we have located the correct columns of the alignment.
RESULTS
Overview
The SCFG/MRF models we construct are based on HL and IL motif groups from experimental RNA 3D structures collected in the RNA 3D Motif Atlas (10). Therefore, we begin with a brief overview of the construction of the Motif Atlas from HL and IL instances extracted from a non-redundant (NR) set of RNA-containing crystal structures deposited at PDB. Understanding how motifs are clustered into motif families is crucial for designing the corresponding probabilistic models.
Next, we describe the construction of hybrid stochastic context-free grammar (SCFG) and Markov random field (MRF) models for a single 3D instance of a loop. Under Materials and Methods section, we explain how to construct models for motif groups having multiple 3D instances. The models are based on FR3D annotations of nucleotide interactions in the 3D loop instance (29). Basepair isostericity is used to assign probability scores to sequence variants for each basepair. Base triples and crossing interactions are modeled using MRF production rules implemented in the SCFG. The insertions observed in 3D structures are used to set parameters for the distributions of variable-length insertions. The alignment score measures how well a sequence fits an SCFG/MRF model.
A central challenge in matching novel sequences to motif groups is the possibility of false positive matches. We gauge the false positive rate by scoring randomly-generated test sets of sequences against each motif group and defining acceptance and rejection regions for each group in terms of alignment score and edit distance. We then compare the performance of the acceptance/rejection regions to RMDetect.
Software for aligning sequences to SCFG/MRF models and scoring sequences against motif groups is provided. The software is named JAR3D, for Java-based Alignment of RNA using 3D structure information and is pronounced ‘jared.’
Internal and hairpin loops extracted from RNA 3D structures
We have developed and implemented a data pipeline to automatically extract and cluster RNA hairpin and internal loops from a non-redundant (NR) set of high quality 3D structures (9) and to cluster them into geometrically similar motif groups in a consistent way. To insure accessibility, the motif groups are available online through the RNA 3D Motif Atlas (10). The guiding principle of the clustering method is to group together instances having a common, core geometry and shared patterns of non-WC basepairs. Those motif nucleotides that interact with each other through non-covalent pairing, stacking or backbone interactions form the core of the motif, in contrast with bulged out nucleotides (see Materials and Methods section). Thus, motif instances assigned to the same group need not share the same number of nucleotides and may differ in the numbers and positions of bulged out nucleotides. The flanking WC pairs (i.e. cWW AU, GC and GU pairs) are included with each motif, one flanking pair for each hairpin loop and two for each internal loop. Flanking pairs are included because in a number of motif families, for example C-loops (cf. Figure 4(a)), they participate in base-specific interactions with other nucleotides and these interactions must be included to accurately model sequence variation in the motif. Please refer to the Discussion for an important point about the identification of flanking WC pairs in predicted secondary structures.
The RNA 3D Motif Atlas provides stable identifiers for individual loop instances and for motif groups. Loop IDs include the PDB file and position within that file, e.g. ‘HL_3RG5_004’ refers to the fourth hairpin loop in PDB file 3RG5 (see Figure 1(a)). This loop instance is assigned to the motif group with motif ID ‘HL_72498.12’ in release 1.13 of the RNA 3D Motif Atlas. The 5-digit motif ID code persists from release to release, while the version number provided after the period is incremented only when new instances are added to the group. Loop and motif IDs can be searched on the Motif Atlas website.
The RNA 3D Motif Atlas is updated periodically using PDB files from the most recent NR set, and so it grows as the RNA 3D structure database grows. The motif groups were reviewed manually to confirm the quality and stability of the clustering from release to release (10). In this paper, we refer to release 1.13 from March 29, 2014, which contains 278 internal loop groups and 253 hairpin loop groups. One motif group (IL_02957.1) was found to contain nested cWW pairs within the same strand and was not included in the present study as it is better modeled as a junction loop. The remaining 277 IL motif groups contain a total of 1581 loop instances, of which 127 form singleton groups composed of just one loop instance. The 253 HL motif groups contain 1025 instances, of which 127 form singleton groups. In addition, 54 IL groups and 110 HL groups contain no pairing or base-backbone interactions internal to the motif besides the closing WC basepair(s), although many show base stacking and have core nucleotides beyond the flanking basepairs. Many of these instances interact with RNA, protein, or small molecules and their 3D structures may be shaped in whole or in part by induced fit. Modeling sequence variation consistent with observed external interactions is beyond the scope of this paper. For loops that lack internal interactions, we make simple SCFG/MRF models and retain them in our diagnostics as distractors for motif identification.
Hybrid stochastic context-free grammar/Markov random field (SCFG/MRF) models
In the next sections, we outline how we build SCFG/MRF probabilistic models for the sequence variability of HL and IL motif groups starting with the 3D structures of known instances. We use SCFG probabilistic models to model the sequence variability of RNA 3D structures, with the following innovations: We use (i) 3D structure information to set the parameters of the probabilistic model, and (ii) Markov Random Fields (MRF) to model base triples, locally crossing interactions and same-strand basepairs. These innovations are needed to accurately model 3D motifs that include features such as the base triple in the S/R motif (Figure 3) and the crossing interactions in the C-loop (Figure 4).
While SCFGs are typically described using the formalism of ‘terminals,’ ‘nonterminals,’ ‘production rules’ and other specialized terminology (17), our modeling approach is more easily understood in terms of ‘guide trees,’ as described in Chapter 5 of the Infernal User Guide (19,30). Guide trees consist of a series of nodes each of which sequentially generates one or more nucleotides. Because the nodes of our guide trees differ from those used by Eddy and collaborators, we will refer to them as ‘model trees.’
Modeling hairpin loops with SCFG/MRF probabilistic models
We begin with a concrete example of a common structured hairpin loop, the T-loop, first identified in tRNA (31) and since observed in many other structured RNA molecules, including 16S and 23S rRNA (32). T-loops are of special interest because they mediate RNA–RNA interactions: Wherever they occur they provide intercalation sites for bulged bases from another RNA loop. Figure 1(a) shows the structural annotations of the exemplar instance HL_3RG5_004 of motif group HL_72498.12; the intercalated base, not shown, pairs with U55 and is stacked between A57 and A58. Comparison of the 3D instances of this motif group defines the conserved structural features of the motif, including both annotated basepairs, the position where the backbone changes direction (curved dotted arrow) and the bulged out bases, U59 and U60. Figure 1(b) shows the corresponding model tree for the SCFG/MRF, which consists of four nodes.
The model is most easily understood by examining how it generates sequence variants for T-loops, although in actual use, it is used to score putative hairpin loop sequences to determine which ones are most likely to form the characteristic T-loop 3D structure. Each node of the model tree successively generates letters corresponding to nucleotides, starting at the far left and far right of the eventual sequence and working toward the middle. Node I1 is an Initial node that generates unpaired letters with low probability, to model loop sequences having nucleotides that precede the closing WC basepair of the HL. Most of the time I1 generates no nucleotides. Next, the Basepair node B2 of the model tree generates paired letters to model the flanking WC basepair of the HL. With highest probability, B2 generates the base combinations GC, CG, AU and UA, which form canonical WC basepairs isosteric to the GC pair observed in the exemplar instance, but it can also generate, with lower probability, GU and UG, to reflect that these base combinations form cWW pairs that are only ‘near isosteric’ with GC. With yet lower probabilities B2 generates the remaining base combinations that form cWW pairs that are not isosteric with GC, reserving the lowest probability for GG, which cannot form a cWW basepair at all. Further details for calculating basepair substitution probabilities are given in the next section.
Node B3 models the U54/A58 tWH basepair characteristic of T-loops. Like B2, it generates with highest probability pairs of letters that form basepairs isosteric to UA tWH and with lower probabilities base combinations that form non-isosteric tWH pairs or lower yet, letters incapable of forming tWH basepairs. Node H4 is a Hairpin node that generates three letters for the hairpin turn that connects the left and right strands, using the observed sequence as a guide.
Unpaired bases occur between the two conserved basepairs in all T-loops. Rather than treat the bulged bases with separate Insertion nodes, we have chosen to generate them using the first or ‘outside’ Basepair node. Basepair nodes generate bulged bases independently in either strand, with a probability distribution parametrized for insertion length and letter distributions as described in Materials and Methods section. With highest probability, B2 generates zero letters on the left and two letters on the right, corresponding to the bulged bases shown in Figure 1(a). Finally, with low probability, node B2 can generate no letters at all, corresponding to the deletion of this basepair.
Putting this together, it should be clear that the output sequence 5′-A U UCG A AGCU-3′ should be generated with relatively high probability, for example by node I1 generating empty strings, node B2 generating an AU (cWW) basepair with inserted bases AGC on the right, node B3 the UA (tWH) basepair, and node H4 the hairpin sequence UCG. Conversely, the model should assign this sequence a relatively high alignment score.
Setting basepair probability scores from one instance of a motif
Isostericity of RNA basepairs accurately describes observed substitutions between corresponding positions in homologous RNA molecules. In previous work, we introduced the IsoDiscrepancy Index (IDI) to quantify isostericity or the geometric similarity of any two RNA basepairs (11). The IDI measures the local distortion of the sugar-phosphate backbone when one basepair substitutes for another. We calibrated the IDI to assign reasonable cutoffs for labeling basepairs as isosteric (IDI ≤ 2.0) and near isosteric (2.0 < IDI ≤ 3.3). We measured the IDI values for every pair of basepairs within each geometric base-pairing family, using exemplar structures of each basepair, i.e. representative instances (centroids by IDI) chosen by prioritizing basepairs from higher-resolution structures that have roughly co-planar bases (26). The basepair exemplars and mutual IDI values are available at http://ndbserver.rutgers.edu/ndbmodule/services/BPCatalog/bpCatalog.html.
To parameterize Basepair nodes, we need substitution probabilities for each basepair that occurs in the motif. As an example, the IDI values for the UA tWH basepair, which occurs in the T-loop (cf. Figure 1) and the S/R motif (cf. Figure 3), are collected in Table 2. The numbers in Table 2 are the IDI values between the exemplar UA tWH pair and the exemplars of each of the other base combinations in the tWH family. The smallest IDI values correspond to the tWH basepairs that are most similar to UA by IDI. While no basepair is isosteric to UA (IDI < 2.0), six are nearly isosteric, namely tWH CA, CC, CG, GG, UG and UU as they have IDI ≤ 3.3. The base combinations AC, AU, CU, GA, GC and UC do not make tWH basepairs, so the corresponding entries in Table 2 are indicated with ‘—.’
Table 2. IsoDiscrepancy Index (IDI) values calculated by comparing exemplars for all base combinations that form tWH basepairs to the UA tWH pair.
| A | C | G | U | |
|---|---|---|---|---|
| A | 4.0878 | — | 3.6083 | — |
| C | 2.6310 | 2.7488 | 3.1218 | — |
| G | — | — | 2.5703 | 4.2290 |
| U | 0.0000 | — | 2.5140 | 2.5829 |
To assign probability scores to base substitutions for each basepair, the IDI values are converted to scores using the piecewise linear function shown in Figure 2. This function models our observations that identical sequences or isosteric substitutions, with 0 ≤ IDI ≤ 2, occur in 88% of cWW pairs (and 95% of non-cWW pairs), near isosteric substitutions, with 2 < IDI ≤ 3.3, occur in 10% (respectively 2%), and non-isosteric substitutions in 2% (respectively 2%) of the cases (11). Base combinations not forming pairs are assigned the score 0.01. We make no claim that this is the optimal mapping of IDI to probability score, only that it reflects observations from conserved basepairs and, as shown below, works adequately.
Mapping the IDI values from Table 2 with the function in Figure 2 and then normalizing results in the probability scores in Table 3.
Table 3. Probability scores assigned to all base combinations, when UA tWH is observed in the 3D structure.
| A | C | G | U | |
|---|---|---|---|---|
| A | 0.0265 | 0.0056 | 0.0273 | 0.0056 |
| C | 0.0552 | 0.0461 | 0.0369 | 0.0056 |
| G | 0.0056 | 0.0056 | 0.0650 | 0.0259 |
| U | 0.5556 | 0.0056 | 0.0685 | 0.0597 |
Thus, having observed a UA tWH basepair in a motif, this is the 4×4 matrix of probability scores that we assign. While the scores are normalized to sum to 1 as probabilities must be, they are not meant to be strictly interpreted as the probabilities that each substitution will be observed. Actual substitutions will be limited by exogenous constraints imposed by the interactions the motif makes and endogenous constraints such as thermodynamic stability. Both are beyond the scope of this model. On the other hand, sequencing and alignment error and the quirks of biological systems make it possible to observe surprising sequence variants. Thus, the probability scores should simply be seen as a way of scoring possible substitutions for their ability to make the same interaction as seen in the 3D instance while being open to unusual variations.
Modeling internal loops
Next we illustrate the construction of an SCFG/MRF model for a recurrent and highly structured internal loop called S/R, using the instances in motif group IL_95652.3 (other variants of the S/R motif appear in other motif groups). Figure 3(a) shows the annotation of motif instance IL_2AW7_041 from this group, which contains five non-WC basepairs, two of which form a base triple with a common base, U5. This example illustrates the use of Markov Random Field (MRF) method for treating base triples and intra-strand basepairs. The model tree representing the SCFG/MRF is shown in Figure 3(b) with the nodes aligned to the structural features they represent. The sequences of internal loops are written with an asterisk, ‘*’, indicating where one strand of the motif ends and the second begins. The sequence of IL_2AW7_041 is written 5′-GGAGUACG*UAAAAC-3′ and the flanking WC pairs are G1/C14 and G8/U9. (Hairpin loops have no strand separator and multi-helix junctions have two or more strand separators, depending on the number of helices.) A Terminal node (T9 in Figure 3) is used to identify the break between strands. It generates, or ‘parses,’ the ‘*’ symbol.
The two basepairs that share base U5 form the base triple of the S/R motif and must be modeled as a unit because base changes in one pair may affect the other pair. Therefore, we model the base triple using a base Cluster node (C). Base Clusters implement Markov Random Fields by multiplying the probability scores of individual basepairs and dividing by a normalization constant chosen to make all probability scores sum to 1. The normalization constant only needs to be calculated once, when the model is being built. For example, to model the base triple in the S/R motif, we score each possible triple by multiplying the scores of the cSH base combination (from Table 4) and the tWH base combination (from Table 3) and then normalizing these products to sum to 1 by dividing by 0.3351645. The results of this calculation for the top 9 scoring three-nucleotide sequence variants are shown in the column labeled Score 1 in Table 5. Score 2 will be explained in the next section.
Table 4. Probability scores for all base combinations, when GU cSH is observed in the 3D structure.
| A | C | G | U | |
|---|---|---|---|---|
| A | 0.1105 | 0.1138 | 0.0062 | 0.0051 |
| C | 0.1069 | 0.1242 | 0.0013 | 0.1251 |
| G | 0.0108 | 0.0059 | 0.0121 | 0.1320 |
| U | 0.0095 | 0.1107 | 0.0013 | 0.1245 |
Table 5. Nine highest scoring sequence variants of the base triple in the S/R motif, together with their scores calculated using two scoring schemes.
| Variant | Score 1 | Score 2 |
|---|---|---|
| GUA | 0.2189 | 0.5718 |
| CUA | 0.2074 | 0.0774 |
| UUA | 0.2064 | 0.0770 |
| GUG | 0.0270 | 0.0705 |
| CUG | 0.0256 | 0.0096 |
| UUG | 0.0255 | 0.0095 |
| GUU | 0.0235 | 0.0614 |
| CUU | 0.0223 | 0.0083 |
| UUU | 0.0222 | 0.0083 |
Scoring scheme 1: Scores calculated using basepairs only. Scoring scheme 2: Scores calculated using basepairs and base-backbone interactions.
Figure 4 shows the annotation of an instance of the C-loop and the associated model tree, to further illustrate the use of Cluster nodes to model the non-nested, ‘crossing’ non-WC pairs C2/A6 and C4/G7. SCFGs model RNA sequence variability by ‘peeling off’ one basepair at a time, provided that the basepairs are nested within one another as in Figures 1 and 3. The Cluster node used to model the base triple in the S/R loop is a mild extension of the usual application of SCFG, as it generates three bases at once, but the triple is still nested within the other basepairs. The C-loop cannot be decomposed into nested basepairs, and so a Cluster node is used to model all of the bases between positions 1 and 7 simultaneously. Bases 1, 2, 4, 5, 6 and 7 make four basepairs, as indicated. Base 3 is stacked on Base 4 and so is considered to be a core nucleotide, even though it does not basepair; it is modeled as a fixed position in the Cluster. In the C-loop instance IL_4JRC_003 shown in Figure 4, the nucleotide between positions 6 and 7 is bulged out of the motif (as indicated by the dashed lines) and therefore is not a core nucleotide and is not numbered. Once bases 1–7 are generated, this additional base is generated as a variable-length insertion within the Cluster node. Indeed, other instances of the C-loop in motif group IL_73276.5 have 0, 1, or 2 nucleotides at this position, cf. Table 7.
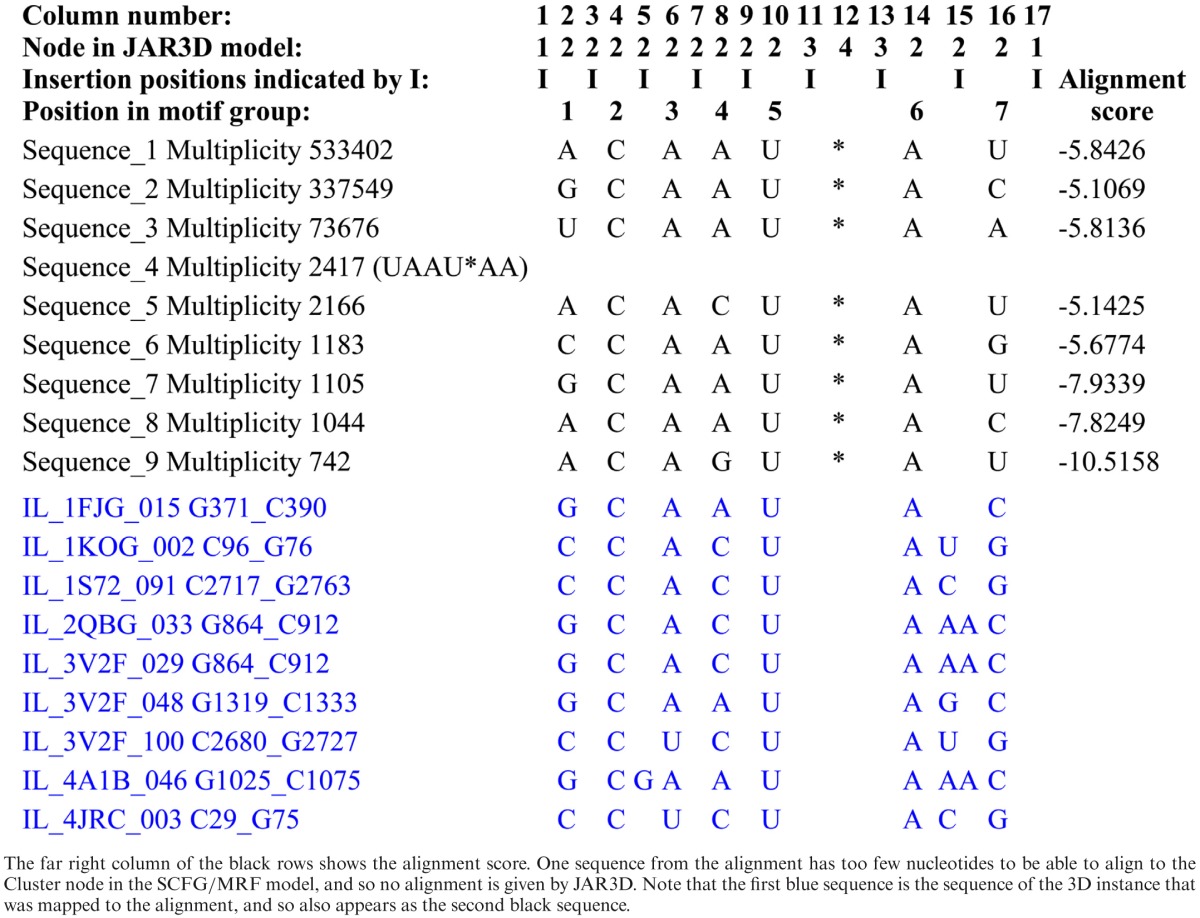
Table 7. Alignment of nine sequences from the Greengenes bacterial SSU rRNA alignment, corresponding to the C-loop motif instance IL_1FJG_015 from helix 15 of T. thermophilus 16S rRNA, to the SCFG/MRF model for motif group IL_73276.5 (shown in black) followed by the correspondences of selected 3D sequences from motif group IL_73276.5 to the SCFG/MRF model for that motif group (shown in blue).
|
Basepairs, crossing interactions and base triples can also occur in Hairpin nodes, and are treated as with Cluster nodes.
Finally, Figure 3 shows Fixed node F7, which is used to model a core nucleotide that plays an essential role in a motif but does not participate in a basepair. The node simply generates a base on the left strand with high probability and using the letter distribution explained in Materials and Methods section. The benefit of using a Fixed node for this purpose (instead of an Insertion node with substitution probabilities set to mimic the Fixed node) is that it makes sense to align a conserved, essential nucleotide to a specific feature in the model tree rather than to a node that is used to model variable-length insertions. Aligning a sequence to such a model then makes a specific inference about the role played by a particular nucleotide in the 3D structure.
Base-backbone interactions
Base-phosphate (BPh) interactions form between electropositive hydrogen-bond donor groups on RNA bases and negatively charged non-bridging phosphate oxygen atoms (12,33). The bases forming BPh interactions in 3D structures exhibit strong sequence conservation (typically >90%) in the corresponding columns of sequence alignments as documented in the cited work. Hydrogen bonds also form between RNA bases and the 2′ and 4′ oxygens of the ribose sugar, (‘base-ribose’ or ‘BR’ interactions). These interactions also show high conservation in sequence alignments of the base involved in the interaction, as explained in Section A of the Supplementary Material.
We model all base-backbone interactions except intra-nucleotide ‘Type 0’ interactions found in canonical RNA double helices. Probability scores are adjusted to favor the base that is observed to make each base-backbone interaction in the 3D structure. We illustrate the adjustment process for the base annotated G4 in Figure 3, which makes a base-phosphate interaction with the phosphate of A11. To reflect the 70% base conservation at position 4 in the S/R motif, the numbers in the third row of Table 4 are adjusted to favor G at this position by multiplying scores in that row by 7 and re-normalizing the matrix. The results are shown Table 6. A similar approach is applied to model conserved model BR interactions. Note that when the same two nucleotides making a base-backbone interaction simultaneously form a basepair, we do not make an adjustment for the base-backbone interaction, but rather rely solely on the probability scores for the observed basepair.
Table 6. Probability scores for all base combinations, when GU cSH is observed in the 3D structure and the G makes a base-phosphate interaction. These numbers can be compared to Table 4.
| A | C | G | U | |
|---|---|---|---|---|
| A | 0.0562 | 0.0579 | 0.0032 | 0.0026 |
| C | 0.0544 | 0.0632 | 0.0007 | 0.0637 |
| G | 0.0385 | 0.0210 | 0.0430 | 0.4704 |
| U | 0.0048 | 0.0564 | 0.0007 | 0.0634 |
Using the BPh weighted probability scores in Table 6 together with the scores for the UA tWH basepair given in Table 3 gives the second set of scores (‘Score 2’) in Table 5. Note that the triplet GUA now has by far the highest score. In fact, every instance of the S/R motif in 3D structures has this triplet in this position, and support for this triplet in sequence alignments is similarly strong.
Building probabilistic models from multiple instances of 3D motifs
Most motif groups in the RNA 3D Motif Atlas have more than one instance and some have dozens or more. These instances provide validated sequence variants of known structure for modeling sequence variation of recurrent 3D motifs. In the Materials and Methods section we describe in detail how we identify conserved pairwise interactions for each motif group and average 4×4 matrices of probability scores for basepairs over motif instances, how we adjust for base-backbone interactions, and how we set parameters for Fixed nodes and variable length insertions.
The text format for writing out SCFG/MRF models is explained in Section B of the Supplementary Material. The full model for T-loop group HL_72498.12 is provided in Supplementary Section C, the full model for S/R group IL_95652.3 is given in Supplementary Section D, and the full model for C-loop group IL_73276.5 is found in Supplementary Section E.
Scoring a sequence against a given model
Given a loop sequence and an SCFG/MRF model, we use the CYK (Cocke-Younger-Kasami) algorithm to determine the most likely way in which the model could generate the sequence and therefore the probability of the most likely ‘parse’ of the sequence. Note that Cluster nodes are a significant innovation. The parsing algorithm parses Cluster nodes by (i) looping through the various combinations of numbers of insertions that may have been made within the base cluster; (ii) identifying the letters that correspond to the interacting bases (there are three of these in the Cluster node in Figure 3 and seven in Figure 4); (iii) computing the probability that those letters form the indicated basepairs and/or occupy the fixed positions; (iv) calculating probability scores for variable-length insertions; (v) consulting the child node's maximal probability for generating the rest of the subsequence; and (vi) choosing the optimal combination.
The maximum-probability parse calculated by CYK infers which nodes generate which letters of the sequence, and thus leads to an alignment of the sequence to a given SCFG/MRF model. Alignments are discussed in the next section. For scoring purposes, the maximal probability itself quantifies how well the sequence matches the model. We call the natural logarithm of this maximal probability the alignment score. Typical values fall between −20 and −3. To infer the best parse for an IL, its sequence must be scored twice against the model, once for each ordering of the strands, because most SCFG/MRF models for IL are asymmetric and expect the motif to be presented in a particular ordering of the strands. For example, the sequence 5′-AACC*GUGU-3′ must also be scored as 5′-GUGU*AACC-3′. As autonomous motifs that connect two helices in the secondary structure, IL can occur in either orientation relative to the 5′-end of the molecule. However, the 5′ to 3′ ordering of the bases within each strand is not altered by 180° rotation of the motif.
Note that the current implementation of JAR3D only scores hairpin and internal loops, and does not fold the sequence to identify potential loops. Thus, users will need to predict the secondary structure and extract the sequences of these loops before submitting them to JAR3D. Please refer to the Discussion for an important point about the identification of flanking WC pairs in secondary structures. The upper limit on the length of an IL or HL sequence is 99 characters.
Aligning sequences to the SCFG/MRF model for a motif group
The JAR3D software can be used to align sequences to the probabilistic SCFG/MRF models. As an example we provide alignments and scores for C-loop sequences in Table 7, which shows the nine highest multiplicity sequences from the Greengenes SSU alignment, corresponding to instance IL_1FJG_015 from helix 15 of bacterial 16S rRNA (T. thermophilus), together with their alignment to the JAR3D model for the C-loop motif group IL_73276.5, as determined by the JAR3D alignment program (shown in black). At the far right of each line is the alignment score. One sequence has fewer than the seven nucleotides required for the Cluster node in the C-loop and so no alignment can be made. For comparison, Table 7 shows in blue the actual correspondences of nine sequences of 3D instances of the C-loop to the nodes of the SCFG/MRF model; these are the correspondences from the RNA 3D Motif Atlas that are used to define the SCFG/MRF model of sequence variability. The column headers show the correspondences between the seven core positions in the motif and the four nodes in the C-loop model (cf. Supplementary Section E). No alignment score is shown because these correspondences are not determined by running the JAR3D alignment program.
To demonstrate the ability of JAR3D to produce correct alignments, we aligned the sequences of all 3D instances from each of the 277 IL and 253 HL motif groups to the corresponding JAR3D models and juxtaposed the actual correspondence between each sequence position and the nodes in the SCFG/MRF models. For a handful of models, there are small mistakes in the JAR3D alignment, usually where two identical bases occur next to each other in the sequence, but for the vast majority of models, all sequences are aligned by JAR3D exactly as their 3D instances correspond to the motif group. These alignments are available for IL at the following URL and at a similar URL for HL:
http://rna.bgsu.edu/data/jar3d/diagnostics/IL/1.13/GroupToModelDiagnostic.html
Acceptance and rejection regions for each motif group
We can align a given sequence to a particular SCFG/MRF model and determine the alignment score, but how do we tell if the match is good enough to claim that the sequence forms the 3D structure of the associated 3D motif group? To address this question, we develop acceptance and rejection regions for each motif group in this section. We start by describing test sets of randomly-generated IL and HL sequences that serve as distractors, then use these to set cutoffs for each motif group. Then we address the related, multiple testing question: What percentage of the distractor sequences fall into the acceptance region of at least one motif group? Thus, a goal of this section is to assess and limit the global false positive rate when considering the match between a given sequence and all motif groups. The effort is complicated by the fact that we do not have sequences that are known to not fold into any of the 3D motifs in our collection.
Test sets of randomly-generated sequences
We begin by creating randomly-generated sets of IL and HL sequences, called IL_Rand and HL_Rand, respectively. The goal is to generate sequences that statistically resemble known loops but are less likely to form specific, low-energy 3D structures.
We construct the test sequences so that they have strand lengths observed in 3D instances or slightly longer, to be sure to cover the full range of sequences that could score well against the models. For IL, we examine all instances from 3D structures and record the length of both the shorter and longer strand. Each unique combination is recorded in the form (a,b), where a ≤ b, and for good measure we also include strand lengths (a,b+1), (a+1,b+1), and, if a < b, we include (a+1,b). This gives 93 unique combinations of strand lengths from (2,3) to (13,17). For HL, we consider all strand lengths from 3 to 22.
Given desired strand length(s) for a loop, we generate closing basepair(s) using the distribution over flanking pairs found over all known instances of 3D motifs. For IL this is: CG (0.2761), GC (0.3596), AU (0.1121), UA (0.1251), GU (0.0639), UG (0.0632). Next we generate the interior nucleotides of the strand(s) using a Markov chain whose parameters were trained by all interior nucleotides across all instances of known 3D motifs. For IL, the initial distribution for the first nucleotide 3′ to the flanking basepair is A (0.2653), C (0.1527), G (0.3227), U (0.2593) and the transition matrix is shown in Table 8.
Table 8. Transition probabilities for interior nucleotides in IL.
| A | C | G | U | |
|---|---|---|---|---|
| A | 0.4589 | 0.1240 | 0.2357 | 0.1814 |
| C | 0.4324 | 0.1905 | 0.2248 | 0.1524 |
| G | 0.5084 | 0.1200 | 0.1748 | 0.1968 |
| U | 0.4338 | 0.1392 | 0.2432 | 0.1838 |
Rows are labeled by the starting state, columns by the next state, and each row sums to 1.
For each unique combination of strand lengths, we generated 1000 test IL sequences and 1000 test HL sequences. The sets IL_Rand and HL_Rand thus have 93 000 and 20 000 sequences, respectively.
The sequences in IL_Rand and HL_Rand resemble known loops in that they have the correct distribution over base combinations in the flanking WC pairs, the correct distribution of the first interior nucleotide and the correct second-order statistics for interior nucleotides. However, there is no further dependence within each strand and no dependence between the interior nucleotides of the two strands in IL, and so no reason to suspect that the sequences will fold into structured 3D motifs. Nevertheless, as we will see below, the sequences are short enough that some of them happen to have the same interior sequence as known 3D instances, and others are close enough to known 3D instances that they can be expected to fold into known geometries. We simply do not have a source of sequences that are known to not fold into one specific 3D motif that is significantly more stable than alternative structures.
Cutoffs for each motif group
To find appropriate cutoffs between acceptance and rejection regions for alignment scores, we use 3D structures as the source of known 3D motif sequences and we use the randomly-generated sets IL_Rand and HL_Rand as a source of distractor sequences. As we mentioned above, however, some of the sequences in these sets can be expected to fold into known 3D motifs, so this is not a clear-cut case of binary classification.
We score each sequence from IL_Rand against all IL motif groups (and similarly with HL_Rand), recording the alignment score and the minimum interior edit distance (the Levenshtein distance between the non-flanking nucleotides on each strand) to known 3D instances. For each motif group, we prioritize those sequences having (1) interior edit distance ≤ 5 and (2) alignment score within 20 of the highest alignment score among 3D instances of that motif. The difference between the highest alignment score and the alignment score of the current sequence is called the alignment score deficit. The top panel of Figure 5 shows a scatterplot of these numerical features of sequences from IL_Rand (shown as red dots) scored against motif group IL_95652.3, an S/R motif with 14 core nucleotides and seven conserved basepairs, cf. Figure 3. Numerical values for known 3D instances are shown as blue X's and values for sequences from multiple sequence alignments (cf. Materials and Methods Section and Supplementary Section H) are shown as black dots. To aid in data visualization, the horizontal coordinates of each dot are shifted to the right by a uniformly distributed random number. The center panel of Figure 5 shows the plot for motif group IL_03282.1, which has ten core nucleotides and five conserved basepairs but does not have sequence alignment data. The bottom panel of Figure 5 shows the plot for motif group IL_86357.3 which has six core nucleotides and three conserved basepairs. The acceptance region for each motif group is shown in light gray.
Figure 5.
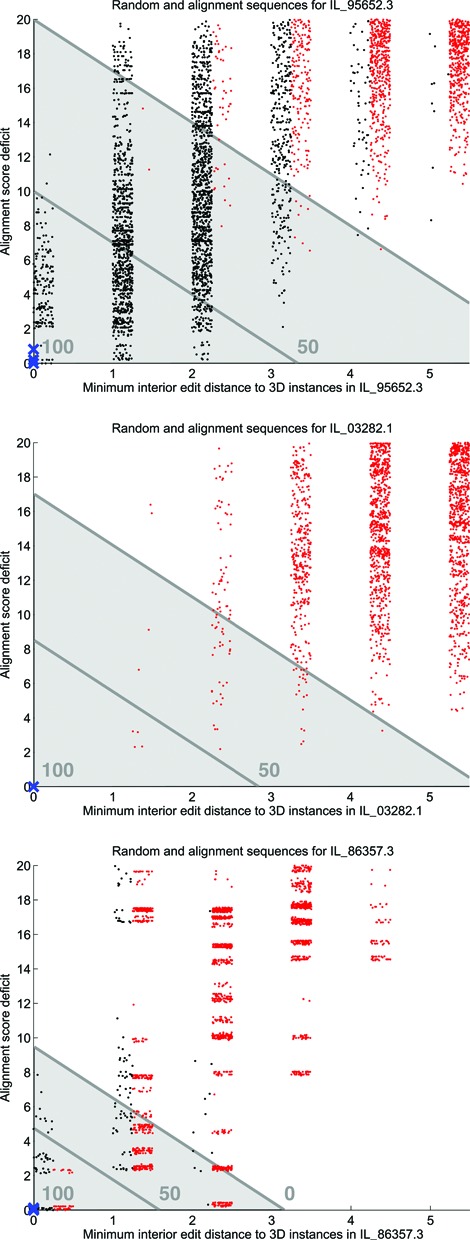
Scatterplots of alignment score deficit against interior edit distance for motif group IL_95652.3 (top), IL_03282.1 (center) and IL_86357.3 (bottom). Red dots are from IL_Rand, black dots are from multiple sequence alignments and large blue X's are from 3D instances. A uniformly distributed random number is added to the interior edit distance for each dot to aid in visualization. The acceptance region is shown in light gray, and Cutoff scores 0 and 50 are shown by the darker lines; Cutoff score 100 is at (0,0).
In Figure 5, The X's representing sequences from 3D structures appear in the lower left because they have interior edit distance 0 from known 3D instances and small alignment score deficits because the models are parameterized based on these instances. In the top and center panels of Figure 5, the sequences in IL_Rand (red dots) separate nicely from the 3D sequences (blue X's) and in the top panel the sequences from multiple sequence alignments (black dots) concentrate in the lower left of the graph. This makes it possible to mostly separate the sequences from IL_Rand from the others using the top dark lines shown in each panel; the lines are of the form Deficit + 3*EditDistance = k, where the constant k is specific to the motif group.
The bottom panel in Figure 5 concerns motif group IL_86357.3, which has interaction signature cWW-tWW-cWW. All five 3D instances have AC tWW as the non-WC basepair, but there are four different sequences of the flanking bases. A large number of sequences from IL_Rand have the same interior sequence. Thus, not all of the sequences in IL_Rand can be considered to be false positives for all groups. It is also not sensible to claim that all sequences from sequence alignments form the same motif as we see in 3D structures, as is apparent from the wide range of alignment score deficits even at interior edit distance 1 (black dots). Manual inspection of multiple sequence alignments confirms that many sequences differ in substantial ways from all known 3D instances, for example, by having multiple insertions or deletions. We use k = 9.5 as a compromise that accepts many of the sequences at edit distance 1 but accepts sequences with higher interior edit distances only when the alignment score deficits are low enough.
More generally, for each motif group we set k so that 4% of the sequences from IL_Rand (or HL_Rand) with interior edit distance ranging between 1 and 5 and alignment score deficit below 20 fall below the line Deficit + 3*EditDistance = k. We set a minimum value of k equal to 9.5 so that we do not make the acceptance region too small for small motifs. When the 4% cutoff gives k > 20, we redefine k so that just 2% of the sequences from the test set fall in the acceptance region, provided that this does not make k below 20. Finally, we set a maximum value of 25 to avoid enormous acceptance regions for large motifs. The top two panels in Figure 5 show values of k strictly between 9.5 and 25, and the bottom panel shows a case in which the minimum value of k is used. The coefficient 3 is chosen to accept sequences with rather large interior edit distance but small alignment score deficit, and to reject sequences with small edit distance but which do not fit the probabilistic model well. The distribution of points from IL_Rand in Figure 5 shows that alignment score deficit and interior edit distance together are more effective in separating points from IL_Rand from the other sequences than either one alone. Graphs analogous to Figure 5 are available for all IL motif groups at http://rna.bgsu.edu/data/jar3d/diagnostics/IL/1.13/ModelSpecificCutoffs.zip and at a similar URL for HL.
The acceptance region for a motif group with constant k is now defined to be all sequences with interior edit distance 0 or else having alignment score deficit less than or equal to 20, minimum interior edit distance less than or equal to 5, and Deficit + 3*EditDistance ≤ k. Other sequences are rejected as matches to the motif group. We find that when multiple sequence alignment data are available, sequences with interior edit distances greater than 5 are dominated by sequences from IL_Rand, even for large motifs, and thus matching such sequences to a motif group is not meaningful.
To quantify where in the acceptance region a sequence falls, we define a Cutoff score that has maximum value 100 at the point (0,0) and decreases linearly to 0 on the line between the acceptance and rejection regions. Figure 5 indicates Cutoff scores 0, 50 and 100. Negative values of Cutoff score tell how far outside the acceptance region a sequence lies. A small number of sequences have zero minimum interior edit distance to a 3D instance and yet negative Cutoff score, so we set the Cutoff score to 0 for these sequences. These surprising cases come from small motifs with many instances, and appear to be due to inhomogeneity in the motif groups. Resolving this will require refining the clustering procedures of the RNA 3D Motif Atlas. We anticipate that JAR3D models based on new releases of the Motif Atlas will show improvement.
Table 9 shows that sequences from 3D structures typically have high Cutoff scores. Note that just 0.57% of 3D sequences have Cutoff score equal to 0 (as discussed in the previous paragraph).
Table 9. Percentage of 1580 IL sequences from 3D structures which score above each indicated value of Cutoff score.
| Cutoff score | Percentage of 3D sequences scoring above the given Cutoff score |
|---|---|
| 99 | 31.33% |
| 95 | 45.00% |
| 90 | 53.73% |
| 80 | 71.33% |
| 50 | 92.91% |
| 0 | 99.43% |
Key features of the Cutoff score are (i) The maximum Cutoff score for all motifs is 100; (ii) Cutoff scores 0 and above are in the acceptance region; and (iii) Interpretation of the Cutoff score is uniform across motif groups.
Global acceptance rate
For most motif groups, the acceptance region is designed to accept just 4% of sequences in the set IL_Rand. However, each sequence in IL_Rand could be accepted by any of the 277 IL motif groups, so the global rate at which sequences from IL_Rand are accepted by at least one motif group will be higher than 4%. In fact, the overall acceptance rate is 22.7% for IL. For comparison, the percentage of sequences in IL_Rand with zero interior edit distance to a known 3D instance is 4.8% and the percentage with Cutoff score over 50 against at least one motif group is 7.4%. The overall acceptance rate for sequences in HL_Rand is 43.5%, the percentage with zero interior edit distance to a known 3D instance is 9.3%, and the percentage with Cutoff score over 50 is 19.3%. It is important to emphasize that these global acceptance rates are not the same as false positive rates and can be expected to be higher than the actual false positive rates, as will be explained in more detail below.
It is informative to break down the acceptance rate by strand length(s). Complete data are listed in Supplementary Section G for IL and HL, respectively. Table 10 shows part of Supplementary Table G.1, namely the 19 IL strand lengths having acceptance rates of at least 60%.
Table 10. Acceptance rates for sequences from IL_Rand, broken down by strand lengths.
| Row number | Shorter strand length | Longer strand length | % accepted by at least one model | % with cutoff score above 50 | % with zero interior edit distance | Groups with 3D sequence of these lengths |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 100 | 100 | 100 | 14 |
| 2 | 3 | 3 | 100 | 98.6 | 83.4 | 12 |
| 3 | 2 | 4 | 100 | 93.8 | 83.3 | 20 |
| 4 | 3 | 4 | 100 | 73.1 | 57.9 | 20 |
| 5 | 4 | 4 | 100 | 47.6 | 29.3 | 11 |
| 6 | 2 | 5 | 98.8 | 54.1 | 27.1 | 12 |
| 7 | 3 | 5 | 98.6 | 50.6 | 22.9 | 25 |
| 8 | 4 | 5 | 98.2 | 36.1 | 9.4 | 28 |
| 9 | 5 | 5 | 96.8 | 26.5 | 6.7 | 22 |
| 10 | 3 | 6 | 91.3 | 16 | 2.7 | 13 |
| 11 | 4 | 6 | 91 | 12.8 | 1.6 | 16 |
| 12 | 5 | 6 | 87.9 | 9.2 | 0.8 | 22 |
| 13 | 2 | 6 | 83.6 | 15.7 | 3.9 | 7 |
| 14 | 6 | 6 | 79.8 | 8.2 | 0.6 | 11 |
| 15 | 3 | 7 | 78.3 | 3.9 | 0.1 | 7 |
| 16 | 3 | 8 | 71.6 | 2.8 | 0.2 | 5 |
| 17 | 4 | 7 | 70.9 | 5.5 | 0.6 | 9 |
| 18 | 2 | 8 | 66.2 | 5.8 | 0.4 | 4 |
| 19 | 2 | 7 | 61.9 | 4.1 | 1.4 | 6 |
Column 4 indicates the percentage of the 1000 sequences of the given strand length from IL_Rand which are accepted by at least one IL model; the rows of the table are sorted by this column. Column 5 indicates the percentage of the sequences which have Cutoff score over 50 against at least one model. Column 6 indicates the percentage of the sequences which have interior edit distance 0 to at least one 3D instance. Column 7 indicates the number of 3D motif groups having at least one sequence with the given strand lengths.
The acceptance rates in Table 10 are surprisingly high, but this should not be interpreted to mean that the global false positive rate is higher than it should be. The very high acceptance rates in Rows 1 to 4 of Table 10 can be understood by the large percentage of these short sequences which have the same interior sequence as a known 3D loop instance, since these are guaranteed to be accepted by at least one motif group. Moreover, for Rows 1 to 12 of Table 10, many 3D motif groups have at least one sequence of the indicated length, giving many possibilities for the randomly-generated sequences to fall into at least one acceptance region by chance. In Rows 2, 5, 9 and 14, the two strand lengths are equal, so that these sequences can match motif groups using either strand order, effectively doubling the number of possibilities to be accepted by a motif group. For example, the sequence GCCCU*AUACU also needs to be considered as AUACU*GCCCU and thus has 44 opportunities to match a motif group having at least one sequence with strand lengths (5,5). This makes for a higher percentage accepted than would be expected based on total sequence length alone. In fact, many (5,5) sequences are accepted by multiple (5,5) motif groups, indicating that the acceptance regions of these motif groups overlap. Overlap of acceptance regions is a necessity, because some sequences are observed to form different geometries in different 3D structures. Additional research will be needed to understand the range of 3D structures that each sequence can form in different contexts. In addition, some (5,5) sequences are accepted by smaller motif groups, considering one base to be an insertion, or are accepted by larger motifs, with one deletion. Finally, in rows 10 to 20 of Table 10, the percentage of sequences from IL_Rand that have a Cutoff score over 50 against at least one model is fairly small, indicating that setting a stricter standard for matching can reduce the false positive rate of matching sequences to motif groups. JAR3D reports the Cutoff score, allowing the user to set stricter acceptance regions if desired. Of course a stricter acceptance criterion will result in a lower match rate, and the desired balance between the two will depend on the broader goals of the user of the software.
Comparison of JAR3D and RMDetect acceptance regions
Here we compare the acceptance regions of the JAR3D motif groups described above to the motif prediction program, RMDetect, that was designed to detect the presence of RNA IL in longer sequences in which they are flanked by WC basepairs (15). The RMDetect article includes models for four motifs, the G-bulge (which forms the core of the S/R motif), the kink turn, the C-loop and tandem GA basepairs. We compared the performance of RMDetect and JAR3D on sequences of these motifs taken from sequence alignments. Because the programs work differently, we submitted the sequences differently. For example, the S/R sequence CCUAGUAC*GGAACCG was scored as such by JAR3D, but for RMDetect we enclosed it with complementary sequence GCGC*GCGC and a stem and GNRA hairpin with sequence GCGAGAGC to form the sequence GCGCCCUAGUACGCGAGAGCGGAACCGGCGC (in which the S/R sequence is underlined). RMDetect was run with default parameters and JAR3D was run using the acceptance region described above for each motif group. For the G-bulge and the tandem GA, JAR3D and RMDetect agree on most sequences. To illustrate, Table 11 lists the number of agreements and disagreements between the two programs for 320 distinct sequences corresponding to instance IL_2QBG_011 (from Escherichia coli) of S/R motif group IL_85647.3, taken from the Silva bacterial LSU alignment. In this data set, JAR3D and RMDetect both accept 124 sequences, in the sense that these sequences fall into the JAR3D acceptance region for motif group IL_85647.3 and RMDetect accepts them as instances of the G-bulge motif. Of the other sequences, RMDetect accepts 6 that JAR3D does not, JAR3D accepts 57 that RMDetect does not, and both reject 133 sequences. In each of these four categories, Table 11 also shows the sequences with highest multiplicity in the alignment. Next to the sequences are the multiplicity, the minimum full edit distance to a known 3D instance, the minimum interior edit distance, and the JAR3D Cutoff score. Notice the high multiplicities and low edit distances of the sequences that JAR3D accepts but RMDetect does not. This is even more pronounced in some tandem GA instances from motif group IL_13959.4, cf. Supplementary Section H. This could be an artifact of the default cutoffs in RMDetect; if they were set to be more generous, there may be more sequences which both accept. Note also in Table 11 that the sequences with high multiplicities that are accepted by JAR3D all have Cutoff score above 40, indicating that they would survive a stricter standard for false positives.
Table 11. Comparison of 320 distinct sequences from Silva bacterial LSU alignment corresponding to the S/R motif in Helix 95 (motif group IL_85647.3) and 3D motif instance IL_2QBG_011 from E. coli.
| Multiplicity | Full edit | Interior edit | Cutoff score | |
|---|---|---|---|---|
| Both accept: 124 | ||||
| CUAAGUAC*GGAACUG | 7415 | 0 | 0 | 98.29 |
| CUAAGUAG*UGAACUG | 1951 | 2 | 0 | 86.50 |
| CUCAGUAC*GGAAGUG | 1488 | 1 | 1 | 60.89 |
| CUUAGUAG*CGAACUG | 1106 | 3 | 1 | 83.05 |
| CUCAGUAC*GGAACUG | 614 | 0 | 0 | 100.00 |
| RMDetect accepts, JAR3D does not: 6 | ||||
| ACAAGUAC*UGACCGA | 1 | 6 | 3 | −2.98 |
| CUAAGUAC*CUG | 1 | 4 | 4 | −292.51 |
| CUAAGUAC*GGAAACGUG | 1 | 2 | 2 | −3.63 |
| CUAAGUAC*GGAGUG | 1 | 2 | 2 | −25.21 |
| CUCAGUAC*CUG | 1 | 4 | 4 | −287.07 |
| JAR3D accepts, RMDetect does not: 57 | ||||
| CUAAGUAC*AGAACUG | 1129 | 1 | 0 | 85.56 |
| CUUAGUAC*AGAACUG | 617 | 2 | 1 | 71.34 |
| CUUAGUAA*CGAACUG | 138 | 3 | 1 | 71.14 |
| CUAAGUAA*AGAACUG | 47 | 2 | 0 | 81.77 |
| UUAAGUAU*GGAAUUG | 40 | 3 | 1 | 44.93 |
| Neither accepts: 133 | ||||
| CUUUUUCG*CAAAGUG | 9 | 8 | 4 | −20.18 |
| GGAAAAAC*UGGAUUG | 8 | 7 | 5 | −70.66 |
| UUAAUCGU*AGCCCG | 7 | 7 | 6 | −124.25 |
| CCAAAUAG*CAAACCG | 6 | 6 | 4 | −9.26 |
| UUCUCUAA*CGUUCC | 6 | 8 | 5 | −117.07 |
In each of the four categories, the five most frequent sequences are listed with their multiplicities, the minimum full edit distance to known 3D instances from IL_85647.3, the minimum interior edit distance, and the JAR3D Cutoff score
RMDetect accepts many kink turn sequences following a pattern similar to Table 11, but misses a large number of kink turn sequences from motif group IL_65553.8 that JAR3D accepts. These sequences come from helix 11 of 16S or 18S (SSU) rRNA and correspond to 3D motif instances with loop ids IL_3U5F_019, IL_4BPP_017 and IL_2AW7_014, from Saccharomyces cerevisiae, Tetrahymena thermophila and E. coli, respectively. These particular instances have the standard kink turn geometry except for an unusual nucleotide arrangement at the 5′-end of the shorter strand, which makes them stand out from the rest of motif group IL_65553.8 (in fact, in future releases of the RNA 3D Motif Atlas, they will be separated from this group to form a separate kink turn group). Nevertheless, JAR3D accepts these sequences as instances from this motif group, while RMDetect with the default parameters does not.
RMDetect fails to recognize most of the C-loop sequences, even ones that are exact sequence matches to those in 3D structures. Data from instance IL_1FJG_015 from Thermus thermophilus SSU and the corresponding columns of the Greengenes bacterial SSU alignment are summarized in Table 12. JAR3D accepts the most common sequences, which have sequences that were observed in 3D structures. The only instance in which RMDetect accepts a large number of C-loop sequences is instance IL_3V2F_100 from the Thermus thermophilus LSU, and then JAR3D and RMDetect agree with a pattern similar to Table 11, cf. Supplementary Section H.
Table 12. Comparison of sequences from the Greengenes bacterial SSU alignment corresponding to instance IL_1FJG_015 from Thermus thermophilus, which is in C-loop motif group IL_73276.5.
| Multiplicity | Full edit | Interior edit | Cutoff score | |
|---|---|---|---|---|
| Both accept: 0 | ||||
| RMDetect accepts, JAR3D does not: 1 | ||||
| UCCUAC*AGG | 1 | 3 | 2 | −96.47 |
| JAR3D accepts, RMDetect does not: 232 | ||||
| ACAAU*AU | 533646 | 0 | 0 | 86.35 |
| GCAAU*AC | 337751 | 0 | 0 | 93.99 |
| UCAAU*AA | 73701 | 2 | 0 | 86.66 |
| ACACU*AU | 2166 | 1 | 1 | 62.48 |
| CCAAU*AG | 1190 | 2 | 0 | 88.07 |
| Neither accepts: 388 | ||||
| UAAU*AA | 2423 | 3 | 1 | −999.00 |
| AAAU*AU | 786 | 1 | 1 | −999.00 |
| ACAA*AU | 143 | 1 | 1 | −999.00 |
| GACAAU*AC | 66 | 1 | 1 | −19.75 |
| CGCAU*AC | 65 | 2 | 2 | −90.95 |
There are 621 distinct sequence variants in this alignment. In each of the four categories, up to 5 sequences are listed followed by their multiplicity, the minimum full edit distance to known 3D instances from IL_73276.5, the minimum interior edit distance, and the JAR3D Cutoff score.
We have run the same comparison shown in Tables 11 and 12 on different motif instances from ribosomal structures for which alignment data were readily available; these are shown in Supplementary Section H. Generally speaking, JAR3D accepts more sequences than RMDetect, which could simply mean that JAR3D is more permissive. However, the sequences that JAR3D accepts but RMDetect does not accept are often ones with very high multiplicity and in complete accord with whatever sequence patterns one would expect for the motif, indicating that JAR3D is not overly permissive and may in fact be identifying more correct sequences than RMDetect.
DISCUSSION
While the structures of the SCFG/MRF models, which reflect the presence of particular basepairs, base triples, fixed bases and variable-length insertions, are determined by the consensus interactions in each motif group, the parameterization of the SCFG/MRF models is based largely on ad hoc choices of substitution probabilities, informed by isostericity, with adjustments for base-backbone interactions, plus ad hoc modeling of the distribution of variable-length insertions and the probability of deletion of basepairs and other features. The models are thus intermediate in computational complexity between RMDetect models, which use interactions from 3D structures but parameterize based on data from sequence alignments, and, for example, energy-based molecular dynamics modeling of new sequences threaded through known 3D structures. However, it would be time consuming to run molecular dynamics on each sequence against each possible 3D structure, and difficult to set up the initial 3D structures in an automated way. Probabilistic models such as RMDetect and JAR3D can be used to screen possible geometries before molecular dynamics studies.
When determining the consensus basepairs in an SCFG/MRF model, two errors can be made: including a basepair that does not belong, and omitting a basepair that should be modeled. The rules in Materials and Methods section for determining the presence of a consensus basepair are reasonably generous, especially when the number of 3D instances is large. If a basepair is included that does not belong, the sequence variation over the 3D instances and the scoring due to isostericity will tend to wash out any statistical dependence in the 4×4 interaction matrix for the basepair. However, when a basepair that should be modeled is omitted, the model is incapable of specifying the relevant covariation in other ways.
We investigated the possibility of using sequences from RNA multiple sequence alignments to inform the choice of cutoffs between acceptance and rejection regions for each motif group but chose not to do this for these reasons: First, this requires a very large number of 3D structures to be mapped to reliable multiple sequence alignments, and this was beyond the scope of the present work. Second, as the RNA 3D Motif Atlas grows, additional alignments would need to be added to keep pace. Third and most importantly, the quality of the alignments is of critical importance, but cannot be assured. Many of the sequences aligned to a given instance of a 3D motif can be seen by eye to be too long, too short, or too different to fold into the 3D structure observed in the one organism for which we have a 3D structure. It will be left to future work to ascertain why this is; it could be poor sequencing, poor alignment, unexpected sequences that make the same 3D structure or, most intriguingly, novel 3D structures that form in some of the organisms in the multiple sequence alignment.
The comparison to RMDetect reveals the major difficulty confronting developers of methods for inference of RNA 3D structure from sequence, even for small motifs: We simply do not know whether the sequences extracted from alignments that we are scoring actually form the 3D motif we have in mind. In the current study, we simply take sequence multiplicity in the alignment as a proxy indicator of the likelihood that the sequence forms the 3D structure known from one (or a small number) of homologs, and pay attention to how the methods score the sequences with the highest multiplicities. Better data will make it possible to make better evaluations of different methods of sequence identification.
During the course of this work, it became clear that improvements in the clustering of some loop instances in the RNA 3D Motif Atlas are needed. There are cases where loops with the same sequence and the same basic geometry are placed in different motif groups because of small differences in modeling, and other cases in which loops with different patterns of basepairing elude the screens that are meant to place them into different motif groups. An example of the latter was mentioned with kink turn group IL_65553.8. Improvements to the RNA 3D Motif Atlas will improve the performance of JAR3D by producing more homogeneous motif groups and thus tighter acceptance regions and better alignments of sequences to motif groups.
The techniques and diagnostics developed in this paper assume that the sequence of the IL or HL is known. Starting from an RNA sequence and secondary structure, one must correctly identify the end of a helix and the start of the loop. However, the sequences of 3D instances of loops in the RNA 3D Motif Atlas show that the bases next to the flanking WC basepair (as identified in the 3D structure) often have base combinations AU, GC, or GU; in fact, 17% of base combinations next to flanking WC pairs in IL have one of these base combinations, and 24% for HL. For example, many 3D instances of the UNCG HL in motif group HL_39895.6 have sequence CUUCGG. If this sequence were encountered at the end of a helix in a secondary structure, it could reasonably be deduced that the UG in the second and fifth position make a WC pair, and that the full sequence of the HL is in fact UUCG. Similarly, 3D instances of motif group IL_93424.4 have sequence CUAAG*CGAAG. In 3D, we see that the U in the second position does not make a WC pair with the A in the second to last position, but when this loop occurs in a secondary structure, it could be extracted as UAAG*CGAA, which JAR3D does not readily match to motif group IL_93424.4. Simply put, some AU, GC and GU base combinations are part of an IL or HL and not the last WC basepair of a helix, and so one additional pair of bases needs to be included in the sequence of the loop when extracting it from a secondary structure and scoring it against 3D motif groups. All six base combinations (AU, UA, GC, CG, GU and UG) occur, but, as in the examples above, UG is the most common in HL and UA is the most common in IL.
CONCLUSIONS
This paper presents a new methodology for building hybrid SCFG/MRF probabilistic models for sequence variability of RNA 3D motifs based on the motif groups in the RNA 3D Motif Atlas. JAR3D accurately aligns sequences from 3D to their corresponding motif group and can be used to align novel sequences to motif groups. For each motif group, acceptance/rejection regions and a cutoff score were developed to assess the quality of the fit between a sequence and the 3D motif group; this reduces the rate at which false positive matches are made and allows the user to decide how strict to make the cutoffs. The acceptance/rejection regions rely on both alignment score from the SCFG/MRF models and on interior edit distance, showing that both provide useful information to match sequences to possible 3D motifs. The motif instances used by JAR3D are drawn from the RNA 3D Motif Atlas, which is updated periodically to take advantage of new 3D structures as they are deposited in the PDB. Thus, the scope and accuracy of JAR3D should improve as the RNA 3D structure database grows.
AVAILABILITY
Supplementary Section F explains the different JAR3D program files and how to run them. The JAR3D executable files for scoring sequences against motif groups and for aligning sequences to a given motif group are available at http://rna.bgsu.edu/data/jar3d/models. The JAR3D model files for all releases of the RNA 3D Motif Atlas starting with release 1.0, along with the executable version of JAR3D, are also available at the same site. Executables, instructions, Matlab programs for generating probabilistic models, Java programs for scoring sequences against models, and Python programs for producing nicely formatted alignments are available as Release v1.0 on GitHub, see https://github.com/BGSU-RNA/JAR3D. Feedback, bug reports and code contributions can be directed to the authors via GitHub. The Matlab binary files from all releases of the RNA 3D Motif Atlas starting with release 1.0 are available at http://rna.bgsu.edu/data/jar3d/motifs/ These are necessary to build probabilistic models for Motif Atlas releases if one does not want to use the precomputed releases.
Supplementary Material
Acknowledgments
C.L.Z. oversaw the development of SCFG/MRF models and coding, wrote much of the Matlab code for model production and developed the acceptance regions and cutoff score. J.R. extended the modeling process to account for insertions and to average over multiple 3D instances, wrote code to generate random sequences, helped to refine the models and extended the Java code in a variety of ways. B.S. refactored the Java code and helped to debug it. A.I.P. developed the RNA 3D Motif Atlas with application to JAR3D in mind and advised on the development of JAR3D models. M.P. ported the SCFG/MRF alignment and scoring code from Matlab to Java. The project is based on manual analyses developed by N.B.L. and Eric Westhof for predicting RNA 3D motifs from sequence. N.B.L. obtained funding for the project, guided the overall project and writing of the manuscript.
In addition, we would like to acknowledge Michael Sarver, who developed the SCFG/MRF models used in JAR3D and Matlab code for alignment and also the contributions of Ali Mokdad and Jesse Stombaugh, who worked on RNA motifs and early versions of the motif identification project. Ivo Hofacker and Christian Höner von Siederdissen made several helpful suggestions, and Corinna Theis and Peter Kerpedjiev tested JAR3D. C.L.Z. would like to thank Ivo Hofacker and the TBI for hosting his visit in 2014–2015, when much of this work was done. Finally, we would like to thank three anonymous referees for their comments, which improved the paper.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
National Institutes of Health [GM085328 to N.B.L. and C.L.Z., GM055898 to N.B.L.]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Funding for open access charge: NIH grant R01GM085328.
Conflict of interest statement. None declared.
REFERENCES
- 1.Sweeney B.A., Roy P., Leontis N.B. An introduction to recurrent nucleotide interactions in RNA. Wiley Interdiscip. Rev. RNA. 2015;6:17–45. doi: 10.1002/wrna.1258. [DOI] [PubMed] [Google Scholar]
- 2.Leontis N.B., Stombaugh J., Westhof E. Motif prediction in ribosomal RNAs Lessons and prospects for automated motif prediction in homologous RNA molecules. Biochimie. 2002;84:961–973. doi: 10.1016/s0300-9084(02)01463-3. [DOI] [PubMed] [Google Scholar]
- 3.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Markham N.R., Zuker M. UNAFold: software for nucleic acid folding and hybridization. Methods Mol. Biol. 2008;453:3–31. doi: 10.1007/978-1-60327-429-6_1. [DOI] [PubMed] [Google Scholar]
- 5.Lorenz R., Bernhart S.H., Honer Zu Siederdissen C., Tafer H., Flamm C., Stadler P.F., Hofacker I.L. ViennaRNA Package 2.0. AMB. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Will S., Joshi T., Hofacker I.L., Stadler P.F., Backofen R. LocARNA-P: accurate boundary prediction and improved detection of structural RNAs. RNA. 2012;18:900–914. doi: 10.1261/rna.029041.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reinharz V., Major F., Waldispuhl J. Towards 3D structure prediction of large RNA molecules: an integer programming framework to insert local 3D motifs in RNA secondary structure. Bioinformatics. 2012;28:i207–i214. doi: 10.1093/bioinformatics/bts226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lescoute A., Leontis N.B., Massire C., Westhof E. Recurrent structural RNA motifs, Isostericity Matrices and sequence alignments. Nucleic Acids Res. 2005;33:2395–2409. doi: 10.1093/nar/gki535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zirbel C.L., Leontis N.B. Nonredundant 3D Structure Datasets for RNA Knowledge Extraction and Benchmarking. In: Leontis NB, Westhof E, editors. RNA 3D structure analysis and prediction. Vol. 27. Berlin; NY: Springer; 2012. pp. 281–298. [Google Scholar]
- 10.Petrov A.I., Zirbel C.L., Leontis N.B. Automated classification of RNA 3D motifs and the RNA 3D Motif Atlas. RNA. 2013;19:1327–1340. doi: 10.1261/rna.039438.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stombaugh J., Zirbel C.L., Westhof E., Leontis N.B. Frequency and isostericity of RNA base pairs. Nucleic Acids Res. 2009;37:2294–2312. doi: 10.1093/nar/gkp011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zirbel C.L., Sponer J.E., Sponer J., Stombaugh J., Leontis N.B. Classification and energetics of the base-phosphate interactions in RNA. Nucleic Acids Res. 2009;37:4898–4918. doi: 10.1093/nar/gkp468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Leontis N.B., Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Theis C., Honer Zu Siederdissen C., Hofacker I.L., Gorodkin J. Automated identification of RNA 3D modules with discriminative power in RNA structural alignments. Nucleic Acids Res. 2013;41:9999–10009. doi: 10.1093/nar/gkt795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cruz J.A., Westhof E. Sequence-based identification of 3D structural modules in RNA with RMDetect. Nat. Methods. 2011;8:513–521. doi: 10.1038/nmeth.1603. [DOI] [PubMed] [Google Scholar]
- 16.Sarver M. Structure-based multiple RNA sequence alignment and finding RNA motifs. 2006 OhioLINK Electronic Theses and Dissertations Center. [Google Scholar]
- 17.Eddy S.R., Durbin R. RNA sequence analysis using covariance models. Nucleic Acids Res. 1994;22:2079–2088. doi: 10.1093/nar/22.11.2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sakakibara Y., Brown M., Hughey R., Mian I.S., Sjolander K., Underwood R.C., Haussler D. Stochastic context-free grammars for tRNA modeling. Nucleic Acids Res. 1994;22:5112–5120. doi: 10.1093/nar/22.23.5112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nawrocki E.P., Kolbe D.L., Eddy S.R. Infernal 1.0: inference of RNA alignments. Bioinformatics. 2009;25:1335–1337. doi: 10.1093/bioinformatics/btp157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nawrocki E.P., Eddy S.R. Infernal 1.1: 100-fold faster RNA homology searches. Bioinformatics. 2013;29:2933–2935. doi: 10.1093/bioinformatics/btt509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burge S.W., Daub J., Eberhardt R., Tate J., Barquist L., Nawrocki E.P., Eddy S.R., Gardner P.P., Bateman A. Rfam 11.0: 10 years of RNA families. Nucleic Acids Res. 2013;41:D226–D232. doi: 10.1093/nar/gks1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nawrocki E.P., Burge S.W., Bateman A., Daub J., Eberhardt R.Y., Eddy S.R., Floden E.W., Gardner P.P., Jones T.A., Tate J., et al. Rfam 12.0: updates to the RNA families database. Nucleic Acids Res. 2014;43:D130–D137. doi: 10.1093/nar/gku1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gardner P.P., Eldai H. Annotating RNA motifs in sequences and alignments. Nucleic Acids Res. 2014;43:691–698. doi: 10.1093/nar/gku1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Winkler G. Image analysis, random fields and Markov chain Monte Carlo methods: a mathematical introduction. 2nd edn. Berlin; NY: Springer; 2003. [Google Scholar]
- 25.Kamisetty H., Ovchinnikov S., Baker D. Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. U.S.A. 2013;110:15674–15679. doi: 10.1073/pnas.1314045110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Abu Almakarem A.S., Petrov A.I., Stombaugh J., Zirbel C.L., Leontis N.B. Comprehensive survey and geometric classification of base triples in RNA structures. Nucleic Acids Res. 2012;40:1407–1423. doi: 10.1093/nar/gkr810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Quast C., Pruesse E., Yilmaz P., Gerken J., Schweer T., Yarza P., Peplies J., Glockner F.O. The SILVA ribosomal RNA gene database project: improved data processing and web-based tools. Nucleic Acids Res. 2013;41:D590–D596. doi: 10.1093/nar/gks1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.DeSantis T.Z., Hugenholtz P., Larsen N., Rojas M., Brodie E.L., Keller K., Huber T., Dalevi D., Hu P., Andersen G.L. Greengenes, a chimera-checked 16S rRNA gene database and workbench compatible with ARB. Appl. Environ. Microbiol. 2006;72:5069–5072. doi: 10.1128/AEM.03006-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sarver M., Zirbel C.L., Stombaugh J., Mokdad A., Leontis N.B. FR3D: finding local and composite recurrent structural motifs in RNA 3D structures. J. Math. Biol. 2008;56:215–252. doi: 10.1007/s00285-007-0110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dowell R.D., Eddy S.R. Evaluation of several lightweight stochastic context-free grammars for RNA secondary structure prediction. BMC Bioinformatics. 2004;5:71. doi: 10.1186/1471-2105-5-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rich A. The era of RNA awakening: structural biology of RNA in the early years. Q. Rev. Biophys. 2009;42:117–137. doi: 10.1017/S0033583509004776. [DOI] [PubMed] [Google Scholar]
- 32.Nagaswamy U., Fox G.E. Frequent occurrence of the T-loop RNA folding motif in ribosomal RNAs. RNA. 2002;8:1112–1119. doi: 10.1017/s135583820202006x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sponer J., Sponer J.E., Petrov A.I., Leontis N.B. Quantum chemical studies of nucleic acids: can we construct a bridge to the RNA structural biology and bioinformatics communities. J. Phys. Chem. B. 2010;114:15723–15741. doi: 10.1021/jp104361m. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


