Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data

Yang Wu; Binbin Shi; Xinqiang Ding; Tong Liu; Xihao Hu; Kevin Y Yip; Zheng Rong Yang; David H Mathews; Zhi John Lu

doi:10.1093/nar/gkv706

. 2015 Jul 13;43(15):7247–7259. doi: 10.1093/nar/gkv706

Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data

Yang Wu ^1,^†, Binbin Shi ^1,^†, Xinqiang Ding ¹, Tong Liu ¹, Xihao Hu ², Kevin Y Yip ², Zheng Rong Yang ³, David H Mathews ⁴, Zhi John Lu ^1,^*

PMCID: PMC4551937 PMID: 26170232

Abstract

Recently, several experimental techniques have emerged for probing RNA structures based on high-throughput sequencing. However, most secondary structure prediction tools that incorporate probing data are designed and optimized for particular types of experiments. For example, RNAstructure-Fold is optimized for SHAPE data, while SeqFold is optimized for PARS data. Here, we report a new RNA secondary structure prediction method, restrained MaxExpect (RME), which can incorporate multiple types of experimental probing data and is based on a free energy model and an MEA (maximizing expected accuracy) algorithm. We first demonstrated that RME substantially improved secondary structure prediction with perfect restraints (base pair information of known structures). Next, we collected structure-probing data from diverse experiments (e.g. SHAPE, PARS and DMS-seq) and transformed them into a unified set of pairing probabilities with a posterior probabilistic model. By using the probability scores as restraints in RME, we compared its secondary structure prediction performance with two other well-known tools, RNAstructure-Fold (based on a free energy minimization algorithm) and SeqFold (based on a sampling algorithm). For SHAPE data, RME and RNAstructure-Fold performed better than SeqFold, because they markedly altered the energy model with the experimental restraints. For high-throughput data (e.g. PARS and DMS-seq) with lower probing efficiency, the secondary structure prediction performances of the tested tools were comparable, with performance improvements for only a portion of the tested RNAs. However, when the effects of tertiary structure and protein interactions were removed, RME showed the highest prediction accuracy in the DMS-accessible regions by incorporating in vivo DMS-seq data.

INTRODUCTION

In addition to transferring genetic messages from DNA to protein, RNA contains a second layer of information that is embedded in the form of RNA structure. RNA structure affects nearly every step of the process of gene expression, and thus extensive efforts are focused on determining RNA structures experimentally (1). Classic techniques for probing the secondary structure of RNA use a variety of structure-sensitive chemicals or enzymes, giving rise to position-specific reactivity with RNA molecules (2). Among these classic techniques for probing secondary structure, SHAPE (selective 2′-hydroxyl acylation analyzed by primer extension) is one of the most accurate ones and its reagents can react with the vast majority of nucleotides found in RNA (3). Recently, high-throughput experimental techniques have emerged for probing the structure of multiple RNAs at the whole-genome level. For example, PARS (parallel analysis of RNA structure) has been applied to reveal the secondary structures of the yeast (4) and human (5) transcriptome. In PARS, RNAs are treated with structure-specific enzymes (RNase V1 for double-stranded nucleotides and S1 nuclease for unpaired nucleotides), followed by deep sequencing. Similarly, FragSeq, employing nuclease P1 to identify single-stranded nucleotides, was used to probe the mouse transcriptome (6). Another high-throughput technique, DMS-seq, has been utilized to detect the in vivo structural preferences for thousands of RNAs in Arabidopsis (7), mouse (8), yeast (9,10) and human (9). DMS-seq couples traditional DMS (dimethylsulfate, which rapidly penetrates cells (11)) methods with massively parallel sequencing. Experimental probing data generated using the methods described above can provide information about the structural state (single-stranded or paired) of each nucleotide with probing signals, but such data cannot specify the pairing relationship between bases (12). In other words, one-dimensional (1D) structure-probing data alone is insufficient for determination of two-dimensional (2D) secondary structure.

2D RNA secondary structure (involving canonical AU, GC and GU base pairs) is commonly predicted by computational methods based on a free energy model. Using this model, three major types of algorithms have been developed for determination of the secondary structure for a given RNA sequence using thermodynamics: minimizing free energy (MFE), maximizing expected accuracy (MEA) and sampling. MFE algorithms are used to search for a single structure with the lowest free energy change through dynamic programming (13). Representative examples of MFE algorithms include mfold (14), RNAstructure (15) and the ViennaRNA package (16). The prediction accuracy of MFE is limited due to factors such as errors from thermodynamic parameters, kinetic barriers, the existence of multiple structural conformations and protein interactions (17). In contrast, MEA and sampling algorithms consider all possible structures for an RNA sequence by calculating a partition function (18) (see ‘Materials and Methods’ section). Based on the partition function, some tools (e.g. MEA-based MaxExpect) predict a structure with a maximized expected accuracy (19–21). Other tools (e.g. sampling-based Sfold) sample statistically representative structures from the Boltzmann ensemble using the sampling algorithm (22). After clustering the sampled structures, the centroids can be selected as the predicted secondary structures (23). Although also suffering from errors in the thermodynamic parameters, the optimal structures predicted by MEA and sampling algorithms generally contain fewer prediction errors, as measured by positive predictive value (PPV), than those predicted by MFE algorithms (19,23).

There is a long history of using experimental probing data to restrain structure prediction (24,25). Recently, prediction tools were developed to incorporate certain types of experimental structure probing data as restraints to the free energy model of RNA secondary structure (12). Using data as restraints is more robust to errors in the experiments and to idiosyncrasies in the mapping techniques. In particular, several methods have been developed for SHAPE data (12). Fold of the RNAstructure package (called RNAstructure-Fold hereafter) incorporates SHAPE reactivity as an extra pseudoenergy term when minimizing the overall free energy change (MFE) (26). RNApbfold (27) and RNAsc (28) perturb the partition function with SHAPE restraints and use an MEA algorithm to predict RNA secondary structure. Sample-and-Select selects the structure with minimal distance to the SHAPE data from the sampling results (29). Among the tools described above, RNAstructure-Fold, which is based on an MFE strategy, shows the best performance for SHAPE and it has been extended to allow the use of DMS mapping data (7,30).

Despite the variety of secondary structure prediction algorithms, few of them are specifically designed for high-throughput probing data, which have different properties (e.g. discrete read counts and multiple layers of data) from SHAPE data. To our knowledge, only SeqFold (31), which is based on the sampling algorithm, has been specifically designed for PARS data. SeqFold first transforms two sets of read counts from RNase V1 and S1 nuclease into a structure preference profile based on a Fisher's exact test. Next, the structure centroid with minimal distance to the PARS data is selected from the sampling results. SeqFold is parameter free and shows more robustness for PARS data than RNAstructure-Fold and Sample-and-Select (31).

Here, we describe a new RNA secondary structure prediction tool, RME (restrained MaxExpect (19)), that can incorporate restraints derived from diverse types of experimental data. RME uses a posterior probabilistic model to transform various types of probing data into pairing probabilities, utilizes these probabilities to restrain the partition function and finally predicts RNA secondary structure with an MEA algorithm. We evaluate the prediction accuracy of RME and two other well-known tools for RNA secondary structure prediction, RNAstructure-Fold (MFE-based) and SeqFold (sampling-based), on different probing data. We demonstrate that RME substantially improves RNA secondary structure prediction with perfect restraints (base pair information from known structures). For real data, we collect structure-probing data from three typical kinds of experiments: SHAPE (low-throughput, in vitro), PARS (high-throughput, in vitro) and DMS-seq (high-throughput, in vivo). RME and RNAstructure-Fold perform better with SHAPE restraints. For high-throughput data (e.g. PARS and DMS-seq) with lower probing efficiency, the three methods are comparable, with some improvement on part of the test set. Overall, RME performs better when the probing data have higher discriminative power on paired bases in comparison with unpaired bases, because it markedly alters the free energy model with restraints. The performance of algorithms for RNA secondary structure prediction decreases when the experimental data are affected by factors other than secondary structure conformation. For example, the in vivo DMS-seq probing data are affected by tertiary structure and protein interactions. To illustrate the influence of such factors on secondary structure prediction, we demonstrate that, when these effects are removed, RME performs much better in the DMS-accessible regions by incorporating the in vivo DMS-seq data.

MATERIALS AND METHODS

RME is designed to improve RNA secondary structure prediction by incorporating restraints obtained from experimental data, and it is derived from an MEA method, MaxExpect (19). In this section we first briefly review MaxExpect. Next, we describe the framework of RME, as well as the posterior probabilistic model for transforming diverse types of experimental data into pairing probabilities. We train and test RME on three types of representative data, a low-throughput in vitro dataset (SHAPE), a high-throughput in vitro dataset (PARS) and a high-throughput in vivo dataset (DMS-seq). Finally, we describe the solvent accessibility calculation on an rRNA to test the influence of tertiary structure and protein interactions on the in vivo DMS-seq data and structure prediction performance.

Review of MaxExpect

For an RNA sequence, the probability of a specific secondary structure s with free energy ΔG_s is e^−ΔGs/RT/Q, where Q (the partition function) is the summation of Σ_s e^−ΔGs/RT over all possible structures (18), R is the gas constant and T is the absolute temperature (32). The pairing probability of any two bases i and j, P_bp(i, j), can be determined by adding the probabilities of all secondary structures that contain that pair, using the following equation (18):

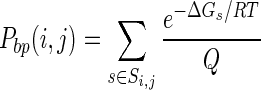(1)

where S_i,j is the set of possible RNA secondary structures in which the ith and jth nucleotides are paired. The pairing probabilities between every two bases constitute a matrix known as a base-pairing probability matrix (BPPM) (Figure 1, bottom-middle panel).

Based on the BPPM, MaxExpect predicts an RNA secondary structure with the maximum expected accuracy using dynamic programming (19) (Figure 1, bottom-right panel). The expected accuracy (EA) for a structure s is defined as the sum of the pairing probabilities (P_bp(i, j)) over all base pairs i-j (BP set), plus the sum of the single-stranded probabilities (P_ss(k)) over all nucleotides k that are single-stranded (SS set) in structure s, with the two parts weighted by a factor, γ, that is 1.0 by default (19):

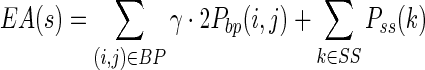(2)

Note that P_bp(i, j) is the (i, j) entry of the BPPM and P_ss(k) can be calculated conveniently from the BPPM (19):

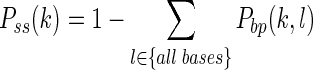(3)

The framework of RME

In this work, we extend MaxExpect to RME to incorporate information from structure probing data as restraints. As the prediction of MaxExpect is solely based on the BPPM, we restrain the BPPM using experimental data. As shown in the top panel of Figure 1, these alterations are applied both before and after the calculation of the partition function. To make full use of the experimental data, we modified the BPPM with two steps: RME-pre and RME-post.

Similar to RNAstructure-Fold (26), RME-pre adds a pseudoenergy term, ΔG(i), to base i's original energy term if the base is involved in base pair stacking. Instead of being used for minimizing the overall free energy, the modified free energy term for base i is used to calculate the partition function in RME-pre (Figure 1, top-left panel). For generalization to new types of data, we introduced a pseudoenergy term that takes the experimental pairing probabilities as inputs. We denote the experimental pairing probability for a base i by q(i), which can be inferred from the experimental data (see Equation 7). Motivated by the pseudoenergy terms derived from the log-likelihood ratio (30,33), we calculate an analogous term at nucleotide i based on the posterior odds, q(i)/[1-q(i)], as follows:

(4)

where a small value, ε, is added to ensure that the fraction inside the log function is valid when q(i) is 0 or 1 (in this study, ϵ was fixed at 0.01). A parameter, m, is introduced to adjust the relative contribution of the experimental restraints.

RME-pre adds the pseudo-free energy evenly to restrain the free energy parameter of each base pair, no matter if it agrees with the experimental data or not. A previous study suggested that the restraints could be differentially added, according to the discrepancies between energy parameters and probing signals for different nucleotides (12,27). After the BPPM is calculated with partition function based on RME-pre's energy model, we will be able to measure the discrepancy level between the pairing probability derived from the energy model (P_bp(i, j)) and the pairing probability derived from the probing data (q(i) × q(j)).

So, we introduce RME-post to modify the base pairing probability, P_bp(i, j), to a pairing propensity, P’_bp(i, j) (Figure 1, top-right panel). The difference between P_bp(i, j) and q(i) × q(j) is added as another restraint for each pair i and j:

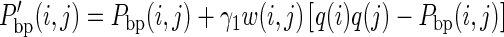(5)

where a factor γ₁ weights the contribution of the difference. Since the base pairs tend to stack together in known structures, the lengths of helices existing in the reference structures are longer than the lengths of other possible helices that could be formed by the same sequence (Supplementary Figure S1A). However, as the 1D structure probing data cannot reveal the pairing relationship between bases, the term q(i) × q(j) could still be large even when base i should be paired with nucleotide other than j (Supplementary Figure S1B). To penalize spurious pairs that are often involved in short helices, we add another weight, w(i,j), to a base pair, i-j, according to the maximum length of the helix in which it can be involved. Our current settings for w(i,j) are 0.25, 0.5, 0.75 and 1 for base pairs with a maximum helix length of 1, 2, 3 and 4 or more, respectively (Supplementary Figure S1C). And we show that adding the w(i, j) term indeed introduces additional performance gain for RME-post (Supplementary Figure S1D).

In the same way, we also modify the single-stranded probability for each nucleotide, P_ss(k), to a propensity, P’_ss(k). Because the sum of each row in the updated matrix of pairing propensities cannot be guaranteed to be <1, the calculation of P_ss(k) using Equation (3) is no longer feasible. Therefore, an independent update is applied to the single-stranded probability, P_ss(k), for each base k:

(6)

where the experimental restraint is represented as 1-q(k) and another weight factor, γ₂, is used to adjust the restraint strength.

Although RME-pre and RME-post can be used independently, combining two of them together is shown to be superior (Supplementary Figure S1D). In this study, we always use the combined one, RME. After RME-pre and RME-post, the pairing propensity (P′_bp(i, j)) and single-stranded propensity (P′_ss(k)) have been updated with restraints. To this end, the restrained expected accuracy (REA) is analogous to the EA in Equation (2). Our algorithm predicts the secondary structure with the maximum REA through dynamic programming using the same strategy used in MaxExpect (19). The performance improvements of RME are benchmarked on reference RNA structures in the ‘Results’ section.

Reference structures and structure-probing data

To test the effectiveness of RME, we first constructed a large database of RNA sequences with reference secondary structures derived from either crystallography or comparative analysis. The database includes 1673 RNAs and RNA domains (domains of long RNAs are counted separately) of diverse types (as used in our previous benchmark of MaxExpect (19,26,30,31)) from 424 species, including rRNAs, Group I/II introns, signal recognition particle RNAs, RNase P RNAs, tRNAs, telomerase and structured elements in mRNAs. Long rRNAs (23S and 16S for prokaryotic RNAs, and 25S and 18S for eukaryotic RNAs) were divided into domains using a previously described strategy (24,34) (Supplementary Figure S2). A summary of all RNAs is provided in Supplementary Table S1.

Structure probing data was collected from published studies. SHAPE reactivity for RNAs from multiple species was directly downloaded from relevant papers (26,35,36) and database (37), and SHAPE reactivity was mostly distributed between 0 and 2 (38). For high-throughput PARS and DMS-seq data from Saccharomyces cerevisiae, raw read counts were given along particular RNAs or along the genome (4,9). We aligned the RNA sequences with reference structures to the genome sequences and assigned the raw read counts to the aligned nucleotides. In total, we collected 42 RNAs and RNA domains that had both reference structures and structure probing data, of which 19 had SHAPE reactivity (5024 nt), 20 had PARS counts (5984 nt) and 14 had DMS-seq counts (5134 nt, 2463 of which were A or C bases). Detailed information about these RNAs is provided in Supplementary Tables S2 and S3.

Performance evaluation of different RNA secondary structure prediction methods

We compared the secondary structure prediction performance of RME (MEA-based) with two other well-known tools, RNAstructure-Fold (MFE-based) and SeqFold (sampling-based). Each of the methods was subjected to tests with and without experimental restraints, the latter of which were used as control tests. For SeqFold, we used the centroid of the largest structure cluster sampled from Sfold (23) as a control, which did not take the experimental restraints into account. To reduce the uncertainty of the structure sampling, SeqFold and SeqFold-control were each run 10 times (sampling 1000 structures each time) with default settings and the average performance scores from the 10 repetitions were used for comparison. We optimized the RME parameters for different input data type (i.e. Perfect, SHAPE, PARS and DMS-seq), respectively.

To avoid biased evaluation, we kept the training and test data strictly separate. For perfect restraints with large number of RNAs available for evaluation, we applied the five-fold cross validation. For SHAPE data, the Escherichia coli 23S rRNA was used for all training steps because it includes a large set of diverse and non-redundant RNA motifs (26). For PARS and DMS-seq data, the yeast 25S rRNA, which is the homolog of E. coli 23S rRNA, was used for training. Other RNAs that were not used in any of the training steps were left for independent performance tests (listed in Supplementary Tables S4–S6).

The RNA secondary structure prediction performance was evaluated using two statistical scores, sensitivity and PPV, based on the reference structures. Sensitivity is the fraction of the reference structures’ base pairs that are correctly predicted. PPV is the fraction of the predicted pairs that occur in the reference structures (39). We used the ‘scorer’ utility in the RNAstructure package to calculate sensitivity and PPV, where slipped base pairs are allowed (40). We also calculated the Matthews correlation coefficient (MCC), which summarizes both sensitivity and PPV, based on the method previously described for RNA secondary structure prediction (41). For comparing the structure prediction performances, a significance level of 5% was used for hypothesis tests.

Posterior probabilistic model for transforming experimental data

RME accepts experimental restraints in terms of pairing probabilities ranging from 0 to 1, which represent the probability that a base i is paired with another unknown base given its observed experimental signal P(S_i = 1 |D_i), where D is the experimental probing data and S is the structure class (S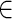 Inline graphic (1 = paired, 0 = single-stranded)). Similar to a previous study (42), according to the Bayes’ rule, P(S_i = 1 |D_i) can be calculated with a posterior probabilistic model (Posterior model):

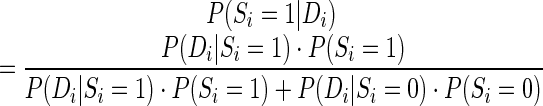(7)

where P(S) is the prior probability of a structure class (either paired or single-stranded). P(S) can be estimated as the fraction of paired bases or single-stranded bases in the reference structures. We estimate P(S) based on all reference structures (0.535 for P(S = 1) and 0.465 for P(S = 0)), and treat it as a constant in the following analysis to save computation time. Moreover, P(D|S) is the probability of observing a certain experimental value, D, given a structure class (paired or single-stranded) and it can be estimated from the probing data from the RNAs in the training sets, for which the secondary structures are known.

Processing of SHAPE data

We transformed the SHAPE data based on the Posterior model (Equation 7). As shown in a previous study (43), the SHAPE reactivity for each structure class follows a distinct parametric distribution. Thus, we estimated P(D|S = 1) and P(D|S = 0) through maximum likelihood fitting using SHAPE data from the training RNA (E. coli 23S rRNA). We first applied quantile normalization (44) to the SHAPE reactivity for the different RNAs, because the data were collected from different laboratories. Next, the normalized SHAPE dataset for the training RNA was divided into paired and unpaired datasets based on the reference structures. Similar to a previous study (43), we used a generalized extreme value distribution to fit the paired data. For the unpaired data, we used a gamma distribution, which showed better goodness-of-fit (passed the Kolmogorov–Smirnov test) than the exponential distribution (did not pass the Kolmogorov–Smirnov test) used in the previous study (43). We used two R packages, evir and MASS, for the fitting of the paired and unpaired data.

Processing of PARS data

Raw data generated by high-throughput probing experiments consists of counts of reads that begin at each RNA nucleotide. For PARS data, two read counts were obtained for each nucleotide: a V1 count from the RNA sample treated with RNase V1 (which preferentially cleaves double-stranded bases) and an S1 count from the RNA sample treated with S1 nuclease (which dominantly cleaves single-stranded bases). As the read count for each nucleotide is correlated with the expression level of the RNA to which it belongs, we first normalized the read counts to the RNA transcript abundance using a method adapted from a previous study (7):

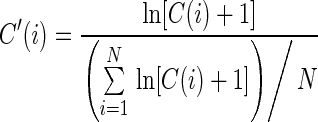(8)

where C(i) is the raw read count for nucleotide i and N is the length of the whole RNA transcript. A pseudocount of 1 is added to ensure the validity of the log-transformation for counts of 0. We normalized the V1 and S1 counts independently using Equation (8). Next, we subtracted the normalized V1 count C’_V1(i) from the normalized S1 count C’_S1(i) to obtain the PARS reactivity for nucleotide i (7).

As with the SHAPE data, the pairing probabilities for the PARS data were calculated according to the Posterior model (Equation 7), where the PARS reactivity (C′_S1–C′_V1) for the training RNA (yeast 25S rRNA) was used to fit a normal distribution for the paired bases and single-stranded bases, respectively (Supplementary Figure S3). Furthermore, we compared our Posterior model with two other published models for probability inference. The first model was the default setting for SeqFold and was based on the Fisher's exact test (Fisher model (31)). The second model was based on the mixture of Poisson linear model (MPL model (45)) and took into consideration both the expression levels of RNAs and local sequences. The performances of the three models are compared in the ‘Results’ section. Additionally, for RNAstructure-Fold, we transformed the PARS reactivity into a linear pseudoenergy change term (26), ΔG_PARS(i) = m × ln[PARS reactivity(i) + 1] + b, with two parameters, m and b, trained on yeast 25S rRNA.

Processing of DMS-seq data

DMS-seq experiments generate two sets of read counts: in vivo counts from the RNA sample treated with DMS under in vivo conditions, as well as control counts from the RNA sample that was first denatured by exposure to a high temperature and subsequently probed with DMS. We first normalized the in vivo and control counts independently using Equation (8). Next, we subtracted the normalized control count C′_control(i) from the normalized in vivo count C′_vivo(i) to obtain the DMS-seq reactivity for each nucleotide i (7). As the DMS chemistry is nucleotide-specific (reacting only with the adenine and cytosine residues (9)), only values of A/C bases were used for further analysis.

Subsequently, we fitted a normal distribution onto the DMS-seq reactivity (C′_v_ivo–C′_control) for paired bases (Supplementary Figure S4A). For single-stranded bases, we fitted a Gaussian mixture of two components using the R package mixtools, because the distribution of reactivity for the loops was shown to be a mixture (Supplementary Figure S4B). Next, the pairing probabilities were calculated using the Posterior model (Equation 7), where the likelihood for single-stranded bases, P(D_i|S_i = 0), was calculated from the mixture:

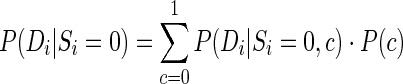(9)

where D_i is the DMS-seq reactivity, S_i is the structure class and c indicates one of the two Gaussian components. The yeast 25S rRNA was used as the training set for the distribution fitting. And we compared the Posterior model with the Fisher and MPL models in the ‘Results’ section. We also transformed the DMS-seq reactivity into a linear pseudoenergy change term for RNAstructure-Fold as for PARS data.

Solvent accessibility calculation on a yeast 18S rRNA complex

The bimodal distribution of the in vivo DMS-seq data on single-stranded bases is probably caused by tertiary structure and/or protein interactions. A previous study indicated that the probing efficiency of DMS is highly correlated with a nucleotide's solvent accessibility (9). Therefore, for the in vivo DMS-seq data, we compared the secondary structure prediction accuracy of RME for two groups, loops accessible by DMS and loops not accessible by DMS, which were defined on yeast 18S rRNA because its tertiary structure (with interacting proteins included) has been determined experimentally (46). As described previously (9), the solvent-accessible surface area was calculated using PyMOL, modeling DMS as a sphere of 3 Å in radius. Nucleotides with solvent accessibility area >2 Å² were defined as DMS-accessible (9).

RESULTS

RME significantly improves RNA secondary structure prediction with perfect restraints

To determine the best performance that can possibly be achieved for secondary structure prediction methods by incorporating restraints, we derived a set of perfect restraints from reference RNAs with known secondary structures. The pairing probability was considered to be 1 for a paired base and 0 for a single-stranded base. All 1673 RNAs (domains for long RNAs were counted separately) in the database were evaluated. We optimized the parameters for RME and RNAstructure-Fold using five-fold cross validation (Supplementary Figure S5). SeqFold required no training because it is parameter free.

The average performance scores for the RNA secondary structure predictions from the five-fold cross-validation are shown in Figure 2 (details in Supplementary Table S7). RME with perfect restraints significantly improved the accuracy of RNA secondary structure prediction in comparison with RME-control without restraints added. We compared the mean and standard deviation of the average MCC from five-fold cross validation. The average MCC was increased from (62.9 ± 0.6)% (sample size = 5) for RME-control to (93.7 ± 0.2)% (sample size = 5) for RME (P < 0.05, one-tailed Wilcoxon signed-rank test). RNAstructure-Fold also performed well with perfect restraints: the average MCC was increased from (62.0 ± 0.5)% (sample size = 5) to (93.4 ± 0.2)% (sample size = 5). Although the addition of perfect restraints to SeqFold (average MCC, (68.4 ± 0.7)%, sample size = 5) produced great improvement in comparison with SeqFold-control (average MCC, (61.6 ± 0.7)%, sample size = 5), SeqFold did not perform as well as RME or RNAstucture-Fold, because SeqFold cannot guarantee the correct structure is sampled, even when the restraint data is perfect.

The evaluation of perfect restraints reflects the best performance achievable by each algorithm by incorporating 1D structure information. The MEA and MFE algorithms were able to successfully resolve pairing relationships with the assistance of 1D restraints, demonstrating the effectiveness of altering the energy model when the restraint data quality is good. However, the perfect restraints were still incomplete data lacking information about the pairing relationship between two bases. Therefore, even perfect restraints could not always lead to perfect predictions. Besides, pseudo-knots were not predicted by any of our compared methods. When recalculating the structure prediction performances after pseudo-knots were removed, we observed increased sensitivities (∼3% for RME) and decreased PPVs (∼1% for RME) (Supplementary Figure S6). RME and RNAstructure-Fold were still substantially better than SeqFold no matter whether pseudo-knots were removed or not.

RME significantly improves RNA secondary structure prediction when supplemented with SHAPE data

We then tested the performance of RME on SHAPE data, which is low-throughput and in vitro data with high probing efficiency. First of all, we inferred the pairing probability for SHAPE data. We applied quantile normalization (44) to the SHAPE data (Supplementary Figure S7A-B) and then fitted distributions to normalized SHAPE reactivity for training RNA (E. coli 23S rRNA). The maximum likelihood probability density functions that were fit for paired bases and single-stranded bases are shown in Figure 3A and B (black line), respectively, which closely approximate the data histograms (gray bars). Finally, we transformed the normalized SHAPE reactivity into a pairing probability based on the Posterior model. Adapting a method previously introduced (12), we showed that the pairing probability generated by this model most closely approximated the empirical SHAPE data (Supplementary Figure S8A).

Figure 3. — RNA secondary structure prediction performance with SHAPE restraints. Distributions fitted onto the SHAPE data for (A) paired bases and (B) single-stranded bases are shown. Gray bars represent the histogram of normalized SHAPE reactivity and black lines show the maximum likelihood fitting to the data. The distribution functions and parameters trained on *Escherichia coli* 23S rRNA are shown in the box. (C) Sensitivity and (D) PPV for *RME, RNAstructure*-*Fold* and *SeqFol*d with restraints added (dark gray), as well as the results for the corresponding controls without restraints added (light gray), are shown. Error bars represent the standard errors across 13 tested RNAs.

Then we compared the RNA secondary structure prediction performance of RME, RNAstructure-Fold and SeqFold, with and without SHAPE restraints. E. coli 23S rRNA was used as the training set for parameter optimization (Supplementary Figure S9). All of the tested tools achieved better predictions in comparison with their corresponding controls on an independent test set (13 RNAs/domains) by incorporating SHAPE data (Figure 3C and D, Supplementary Table S4). We found that RME and RNAstructure-Fold that altered the energy model gave superior predictions with significantly higher sensitivity and PPV (P < 0.05, one-tailed Wilcoxon signed-rank test) using the SHAPE restraints. For RME, the average MCC was increased from 67.8 to 86.8%. For RNAstructure-Fold, the average MCC was increased from 68.3 to 85.8%. But the predictions of SeqFold were not significantly better than those of SeqFold-control (average MCC was increased from 69.0 to 73.4%, P > 0.05, one-tailed Wilcoxon signed-rank test). RME gave a slightly higher mean PPV than RNAstructure-Fold, but this difference was not statistically significant. Consistent with perfect restraints, RME and RNAstructure-Fold were better than SeqFold for SHAPE data (P < 0.05, two-tailed Wilcoxon signed-rank test).

Furthermore, the improvement of the RME predictions varied for individual RNAs (Supplementary Figure S10). RME with SHAPE restraints achieved large improvements for RNAs that were not well predicted using the free energy model (i.e. low accuracy for RME-control), but for RNAs with structures already predicted with high accuracy by RME-control, such as small RNAs like the adenine riboswitch, the improvement was smaller. The same trend was also observed for RNAstructure-Fold. Furthermore, the performance of RME was robust when tested with a leave-one-out jack-knife analysis in which parameters were trained using the entire dataset except one structure withheld for performance testing (Supplementary Table S8).

Improvement of secondary structure prediction is limited by incorporating PARS and DMS-seq data

We calculated the pairing probabilities for the PARS and DMS-seq data based on our Posterior model, which was shown to better distinguish paired and unpaired nucleotides than the Fisher and MPL models (Supplementary Figure S8 B and C). We then compared the RNA secondary structure prediction performance of RME, RNAstructure-Fold and SeqFold with and without restraints generated from PARS and DMS-seq (Supplementary Tables S5 and S6). For RME, we provided pairing probabilities based on the Posterior model. For RNAstructure-Fold, PARS reactivity (S1′-V1′) and DMS-seq reactivity (vivo′-control′) data were transformed to a pseudo-free energy change (see ‘Materials and Methods’ section). For SeqFold, the structure preference profiles generated by the Fisher model were used as the default profiles (31). The parameters for the fitted distributions (Supplementary Figures S3 and S4), RNAstructure-Fold and RME (Supplementary Tables S5 and S6) were trained on yeast 25S rRNA. The tested RNAs are listed in Supplementary Tables S5 and S6.

For the PARS data, the test set included eight snoRNAs, one yeast 5S rRNA and four domains of yeast 18S rRNA. The performance of RME, RNAstructure-Fold and SeqFold for all tested RNAs was shown in Supplementary Table S5. RME showed a trend for slightly increased PPV and slightly decreased sensitivity. We found that only some of the tested RNAs had structures that could be better predicted with the aid of PARS data, regardless of the method used (Figure 4A). Furthermore, we also showed that the RME and SeqFold structure prediction performance was similar with pairing probabilities from the Posterior, Fisher and MPL models (Supplementary Figure S11).

Figure 4. — RNA secondary structure prediction performance with (A) PARS and (B) DMS-seq restraints. The MCC for *RME*, *RNAstructure-Fold* and *SeqFold* with restraints added (solid lines) as well as the results for the corresponding control methods (dashed lines), are shown. (C) The discriminative power for separating paired bases from single-stranded bases is shown with ROC curves for SHAPE, PARS and DMS-seq reactivity. The ROC curves were drawn with different cut-offs for probing reactivity on reference RNAs with known structures. (D) The signal coverage on the RNAs (counted at the 1-nt level) for the three types of data are depicted using boxplots.

For the DMS-seq data, the test set included three mRNAs and a yeast 18S rRNA (four domains). Using this small test set, we tested RME, RNAstructure-Fold, SeqFold as well as their corresponding controls (Supplementary Table S6). With DMS-seq restraints, RME and RNAstructure-Fold showed slightly improved average sensitivity and PPV (not statistically significant) in comparison with the corresponding controls. RME gave better structure prediction with the aid of DMS-seq data for shorter RNAs (e.g. ASH1-E1, ASH1-E2A and the fourth domain of yeast 18S rRNAs) (Figure 4B). The RME and SeqFold structure prediction performance was similar with pairing probabilities from the Posterior, Fisher and MPL models (Supplementary Figure S12).

Limited structure prediction improvement is due to low probing efficiency on reference RNAs

To determine the reason that the incorporation of the PARS and DMS-seq data did not significantly improve the secondary structure prediction performance for the tested RNAs, we compared the probing efficiency of different types of experimental data. In total, we collected 42 RNAs/domains that had both reference structures and readily available structure probing data, of which 20 had PARS data, 14 had DMS-seq data (11 had both PARS and DMS-seq data) and 19 had SHAPE data (Supplementary Tables S2 and S3).

We first evaluated the discriminative power of structure probing data for the separation of paired nucleotides from single-stranded nucleotides using receiver operator characteristic (ROC) curves, generated by varying reactivity cutoffs (Figure 4C, Supplementary Figure S13). We used each cutoff to divide all nucleotides into reactive and unreactive groups and then calculated the agreement with the reference structures. True positives were defined as single-stranded bases with probing reactivity higher than the cutoff. True negatives were defined as paired bases with probing reactivity lower than the cutoff (Figure 4C). For the DMS-seq data, only A/C bases were considered. SHAPE (area under the ROC curve (AUC) = 0.80) was more discriminative than PARS (AUC = 0.67) and DMS-seq (AUC = 0.74), and the difference in AUC between SHAPE and the other tested high-throughput probing datasets was statistically significant (P < 0.001, Hanley and McNeil's test) (47). Because the distributions of probing data for paired and unpaired nucleotides are largely overlapped for high-throughput data, they would restrain the free energy model less than SHAPE, when predicting RNA secondary structure.

The probing efficiency of high-throughput data could be affected by many factors, such as sequencing bias and mapping error of raw reads. In addition, previous studies also suggested that enzymes with large molecular weight (e.g. RNase V1 and S1 nuclease, which are used in PARS) might be unable to access some nucleotides, depending on the structure of the target RNA (48). DMS is a chemical with smaller size than the enzymes used, which could partially explain the higher AUC score of the DMS-seq data in comparison with that of the PARS data. Moreover, DMS can achieve even better performance at low-throughput: a previous study showed that the probing accuracy of an in vitro DMS data on one single RNA at a time was even slightly better than in vitro SHAPE (30). However, DMS can probe only A/C bases. Thus its coverage (43% of bases had signals) was substantially lower than that of SHAPE (88%) or PARS (84%) (Figure 4D). In addition, the probing efficiency of DMS-seq data we used may have been affected by other factors such as protein binding, because the tested RNAs were probed under in vivo conditions.

RME performs best with in vivo DMS-seq data at solvent accessible regions

To study the effect of in vivo measurement conditions on DMS-seq data, we examined the probing efficiency of DMS for the yeast 18S rRNA complex, including its interacting proteins. We observed that the distribution of DMS-seq reactivity for single-stranded bases shows to be a mixture of two components (Supplementary Figure S4B). Inspired by previous clues (9,45), we hypothesized that the bimodal distribution of DMS-seq reactivity for single-stranded bases may be partially caused by the presence of two groups of RNA loops (unpaired bases) in vivo: a group accessible to DMS and a group embedded inside the tertiary RNA structure or bound by proteins.

To test this hypothesis, we first defined the DMS-accessible regions of the yeast 18S rRNA complex according to a previous study (9) on its crystal structure (46). We found that ∼38% of the bases with DMS reactivity around the peak on the right were accessible, while only 1.6% of the bases with DMS reactivity around the left peak were accessible (Figure 5A). We further tested the discriminative power of DMS-seq data for distinguishing paired bases from two groups of single-stranded bases (Figure 5B). We found an AUC of 0.97 for distinguishing paired bases with accessible loops, which was significantly higher than the AUC for distinguishing paired bases from inaccessible loops (0.68) (P < 0.001, Hanley and McNeil's test). This result indicates that the in vivo DMS-seq data may be highly affected by tertiary structures and/or protein interactions. Thus, the DMS-accessible loops of the yeast 18S rRNA represent only a small fraction of all of its single-stranded bases (51/383, 13%).

Figure 5. — *In vivo* effect of DMS-seq data on yeast 18S rRNA. (A) Histogram of DMS-seq reactivity on the single-stranded bases of yeast 18S rRNA, with two peaks shown in dashed lines. (B) ROC curves of the DMS-seq reactivity on yeast 18S rRNA for separating paired bases from all loops (dotted, gray), accessible loops (solid, orange) and inaccessible loops (dashed, blue). (C) Sensitivity and (D) PPV of the structure predictions are shown for the single-stranded nucleotides that are solvent accessible (orange), compared with the single-stranded nucleotides that are not solvent accessible (blue). Performances with restraints (restrained) and without restraints (control) are shown side by side.

Next, using the predicted structure of 18S rRNA (same as the one listed in Supplementary Table S6), we re-evaluated the structure prediction performance of RME, RNAstructure-Fold and SeqFold on the DMS-accessible and DMS-inaccessible regions. In our standard procedure, the sensitivity and PPV of a predicted structure were calculated based on the paired bases. However, most (51/54, 94%) of the DMS-accessible bases are single-stranded. Therefore, we re-calculated the sensitivity and PPV for predicting bases that are single-stranded. We found that RME performed dramatically better than RNAstructure-Fold and SeqFold in the DMS-accessible regions. The better performance was not caused by an effect of RME predicting slightly more bases as unpaired. We could clearly see that the accuracy of RME in the accessible loops was significantly better than its accuracy in the inaccessible loops: the sensitivity increased from 64 to 84%, while PPV increased from 66 to 98% (P < 0.05, Fisher's exact test) (Figure 5C and D). Furthermore, compared with RME-control, RME performed better, but did not predict more bases as unpaired. This further demonstrated that RME performed better when the restraints were well presented.

DISCUSSION

In this study, we reviewed three different types of structure probing data and extended the MEA-based method MaxExpect (19) into a new method called RME to predict restrained RNA secondary structures. RME is capable of incorporating various types of experimental restraints as a probabilistic score and its performance is dependent on the probing quality of the incorporated experimental restraints. Moreover, RME includes weighting parameters that can be adjusted if the probing quality of the restraints is low.

Based on the evaluation results for the reference structures, we found that the performance of the tested algorithms was dependent on the probing efficiency of the data. For high-quality restraints, such as perfect restraints, SHAPE data and DMS-seq data at accessible regions, the prediction performance was markedly enhanced when the free energy model was modified according to the data. Thus, RME and RNAstructure-Fold are expected to be superior. We also showed that SeqFold's prediction accuracy did not change much by trying larger sample sizes for structure sampling (Supplementary Figure S14). For SHAPE, we used data from the probing of a single RNA species at a time, but for DMS-seq and PARS, we are using high-throughput data. The high-throughput sequencing data usually has lower discriminative power for secondary structure because of many factors other than base pairing, such as sequencing bias and genome mapping errors. Furthermore, we tried to illustrate when PARS or DMS-seq data could better enhance the structure prediction. Based on RNA nucleotides with different probing data features (Supplementary Figure S15), we found that the prediction performance tended to be better enhanced by the experimental data when the data quality and coverage got higher (especially for DMS-seq). We also observed that DMS-seq better enhanced the prediction accuracy for the loop regions (base pairing probabilities derived from experimental data were low) when it disagreed with energy model (base pairing probabilities derived from energy model were high).

An interesting paradox also exists for structure probing experiments: on the one hand, we would like to probe structure in vivo because the RNAs do not exist alone in a cell; on the other hand, the protein binding would prevent the nucleotides being probed by chemicals or enzymes. Therefore, the information provided by these experiments may not exceed the quality of that provided by the thermodynamic model. For high-throughput sequencing data at regions with limited accessibility, the MEA, MFE and sampling algorithms showed very similar improvements and the difference among them was largely due to the inherent strength of the each strategy for optimal structure identification.

Although RME showed slightly better performance than RNAstructure-Fold for high efficiency probing data (i.e. perfect, SHAPE and especially DMS-seq restraints at accessible regions), the differences between the two approaches were often not statistically significant. One possible interpretation is that a limit may have been reached for achievable prediction accuracy gains from 1D probing data. Thus, the improvement may be largely due to the theoretically superior probabilistic treatment of restraints. And we also showed that the Bayesian approach based on curve fitting in this work is fairly robust to the noise in the area of sparse data (Supplementary Figure S16).

To ensure the validity of the Bayesian approach, it is important that the training and test data should be properly normalized. For SHAPE data collected from different labs, we use the quantile normalization method (44) to normalize the data across RNAs. It introduced a performance gain for RME in contrast to directly using downloaded SHAPE reactivity without additional normalization, or using a previously introduced normalization method for SHAPE (2/8% rule (31,38,49)) (Supplementary Figure S7C). For PARS and DMS-seq data, we normalize the effect of RNA transcript abundance caused by high-throughput sequencing (Equation 8) (7).

The relatively small set of reference RNAs with known structures has limited the estimation of parameter values for computational methods and the optimization of protocols used in probing experiments. In most cases, the computational parameters, as well as the probing experiment protocols, were optimized using ribosomal RNAs (7–10). For instance, the parameters of RME and RNAstructure-fold need to be optimized by data training on known RNA structures. Indeed, most of our conclusions were based on the limited set of reference RNA structures and three major types of probing data (mainly in E. coli and yeast): SHAPE (low-throughput, in vitro), PARS (high-throughput, in vitro) and DMS-seq (high-throughput, in vivo) (Supplementary Tables S2 and S3). Some other data and species (e.g. DMS-seq in plant (7), CIRS-seq in mouse (8) and in vitro DMS on single RNA (30)) were not tested, because we could not find enough well-confirmed reference structures for training and testing.

Furthermore, the novel long ncRNAs (lncRNAs), which are likely to be more flexible than rRNAs, may have distinct characteristics that limit the validity of rRNA-based parameter and protocol optimization. The prior probability of paired bases, P(S = 1), is treated as a constant (53.5%) in our calculations to save computation time. We also provide other options to calculate the base pair probability, P(S = 1), for each individual RNA (e.g. pre-calculate it by partition function). Subtle differences in sensitivity and PPV are observed for different P(S = 1) calculation methods (Supplementary Figure S17). However, in comparison with rRNA, the structural domains of lncRNAs might have fewer base pairs and be more flexible in terms of tertiary structure. On the other hand, some lncRNAs may act as ‘molecular sponges’ and interact intensively with proteins (50), making them hard to probe in vivo. To further understand the strengths and weaknesses of high-throughput structure probing data, more reference structures for various types of RNAs are critically needed.

Overall, our results using current reference structures demonstrate that RME, a new RNA secondary structure prediction tool that can incorporate restraints derived from diverse types of experimental data, has some advantages over RNAstructure-Fold and SeqFold, and represents a useful new method for researchers studying RNA secondary structure. We not only integrate a Bayesian approach into a thermodynamic folding algorithm, but also provide a platform that works for multiple data sources. Based on this platform, we highlight their differences in assisting RNA secondary structure prediction.

AVAILABILITY

RME is part of the RNAstructure package (15). The RME source code and processing scripts for experimental data can be downloaded from GitHub (https://github.com/lulab/RME).

Supplementary Material

SUPPLEMENTARY DATA

supp_43_15_7247__index.html^{(989B, html)}

Acknowledgments

We thank Yuchuan Wang for processing the data and Shenjie Wu for downloading and processing the raw data. We thank Chao Ye, Haowen Zhang, Long Hu, Yucheng Yang, Yang Yang, Jiapei Yuan, Yang Li and Mengrong Liu for helpful discussions. We thank Silvi Rouskin for sharing the solvent accessibility information with us.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Key Basic Research Program of China [2012CB316503]; National High-Tech Research and Development Program of China [2014AA021103]; National Natural Science Foundation of China [31271402]; Tsinghua University Initiative Scientific Research Program [2014z21045]; Hong Kong Research Grants Council Early Career Scheme [419612 to K.Y.]; National Science Foundation [1339282 to D.H.M.]; Computing Platform of the National Protein Facilities (Tsinghua University). Funding for open access charge: National Natural Science Foundation of China [31271402].

Conflict of interest statement. None declared.

REFERENCES

1.Wan Y., Kertesz M., Spitale R.C., Segal E., Chang H.Y. Understanding the transcriptome through RNA structure. Nat. Rev. Genet. 2011;12:641–655. doi: 10.1038/nrg3049. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Weeks K.M. Advances in RNA structure analysis by chemical probing. Curr. Opin. Struct. Biol. 2010;20:295–304. doi: 10.1016/j.sbi.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Wilkinson K.A., Merino E.J., Weeks K.M. Selective 2‘-hydroxyl acylation analyzed by primer extension (SHAPE): quantitative RNA structure analysis at single nucleotide resolution. Nat. Protoc. 2006;1:1610–1616. doi: 10.1038/nprot.2006.249. [DOI] [PubMed] [Google Scholar]
4.Kertesz M., Wan Y., Mazor E., Rinn J.L., Nutter R.C., Chang H.Y., Segal E. Genome-wide measurement of RNA secondary structure in yeast. Nature. 2010;467:103–107. doi: 10.1038/nature09322. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Wan Y., Qu K., Zhang Q.C., Flynn R.A., Manor O., Ouyang Z., Zhang J., Spitale R.C., Snyder M.P., Segal E., et al. Landscape and variation of RNA secondary structure across the human transcriptome. Nature. 2014;505:706–709. doi: 10.1038/nature12946. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Underwood J.G., Uzilov A.V., Katzman S., Onodera C.S., Mainzer J.E., Mathews D.H., Lowe T.M., Salama S.R., Haussler D. FragSeq: transcriptome-wide RNA structure probing using high-throughput sequencing. Nat. Methods. 2010;7:995–1001. doi: 10.1038/nmeth.1529. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Ding Y., Tang Y., Kwok C.K., Zhang Y., Bevilacqua P.C., Assmann S.M. In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature. 2014;505:696–700. doi: 10.1038/nature12756. [DOI] [PubMed] [Google Scholar]
8.Incarnato D., Neri F., Anselmi F., Oliviero S. Genome-wide profiling of mouse RNA secondary structures reveals key features of the mammalian transcriptome. Genome Biol. 2014;15:491. doi: 10.1186/s13059-014-0491-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Rouskin S., Zubradt M., Washietl S., Kellis M., Weissman J.S. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature. 2014;505:701–705. doi: 10.1038/nature12894. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Talkish J., May G., Lin Y., Woolford J.L., McManus C.J. Mod-seq: high-throughput sequencing for chemical probing of RNA structure. RNA. 2014;20:713–720. doi: 10.1261/rna.042218.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Wells S.E., Hughes J.M., Igel A.H., Ares M.J. Use of dimethyl sulfate to probe RNA structure in vivo. Methods Enzymol. 2000;318:479–493. doi: 10.1016/s0076-6879(00)18071-1. [DOI] [PubMed] [Google Scholar]
12.Eddy S.R. Computational analysis of conserved RNA secondary structure in transcriptomes and genomes. Annu. Rev. Biophys. 2014;43:433–456. doi: 10.1146/annurev-biophys-051013-022950. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Rivas E. The four ingredients of single-sequence RNA secondary structure prediction: A unifying perspective. RNA Biol. 2013;10:1185–1196. doi: 10.4161/rna.24971. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Bellaousov S., Reuter J.S., Seetin M.G., Mathews D.H. RNAstructure: web servers for RNA secondary structure prediction and analysis. Nucleic Acids Res. 2013;41:W471–W474. doi: 10.1093/nar/gkt290. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Lorenz R., Bernhart S.H., Höner Zu Siederdissen C., Tafer H., Flamm C., Stadler P.F., Hofacker I.L. ViennaRNA Package 2.0. Algorithms. Mol. Biol. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Doshi K.J., Cannone J.J., Cobaugh C.W., Gutell R.R. Evaluation of the suitability of free-energy minimization using nearest-neighbor energy parameters for RNA secondary structure prediction. BMC Bioinformatics. 2004;5:105. doi: 10.1186/1471-2105-5-105. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.McCaskill J.S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
19.Lu Z.J., Gloor J.W., Mathews D.H. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA. 2009;15:1805–1813. doi: 10.1261/rna.1643609. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Knudsen B., Hein J. Pfold: RNA secondary structure prediction using stochastic context-free grammars. Nucleic Acids Res. 2003;31:3423–3428. doi: 10.1093/nar/gkg614. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Do C.B., Woods D.A., Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90–e98. doi: 10.1093/bioinformatics/btl246. [DOI] [PubMed] [Google Scholar]
22.Ding Y., Lawrence C.E. A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res. 2003;31:7280–7301. doi: 10.1093/nar/gkg938. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Ding Y., Chan C.Y., Lawrence C.E. RNA secondary structure prediction by centroids in a Boltzmann weighted ensemble. RNA. 2005;11:1157–1166. doi: 10.1261/rna.2500605. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Mathews D.H., Sabina J., Zuker M., Turner D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
25.Mathews D.H., Disney M.D., Childs J.L., Schroeder S.J., Zuker M., Turner D.H. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Deigan K.E., Li T.W., Mathews D.H., Weeks K.M. Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. U.S.A. 2009;106:97–102. doi: 10.1073/pnas.0806929106. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Washietl S., Hofacker I.L., Stadler P.F., Kellis M. RNA folding with soft constraints: reconciliation of probing data and thermodynamic secondary structure prediction. Nucleic Acids Res. 2012;40:4261–4272. doi: 10.1093/nar/gks009. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Zarringhalam K., Meyer M.M., Dotu I., Chuang J.H., Clote P. Integrating chemical footprinting data into RNA secondary structure prediction. PLoS One. 2012;7:e45160. doi: 10.1371/journal.pone.0045160. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Quarrier S., Martin J.S., Davis-Neulander L., Beauregard A., Laederach A. Evaluation of the information content of RNA structure mapping data for secondary structure prediction. RNA. 2010;16:1108–1117. doi: 10.1261/rna.1988510. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Cordero P., Kladwang W., VanLang C.C., Das R. Quantitative dimethyl sulfate mapping for automated RNA secondary structure inference. Biochemistry. 2012;51:7037–7039. doi: 10.1021/bi3008802. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Ouyang Z., Snyder M.P., Chang H.Y. SeqFold: Genome-scale reconstruction of RNA secondary structure integrating high-throughput sequencing data. Genome Res. 2013;23:377–387. doi: 10.1101/gr.138545.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Mathews D.H. Revolutions in RNA secondary structure prediction. J. Mol. Biol. 2006;359:526–532. doi: 10.1016/j.jmb.2006.01.067. [DOI] [PubMed] [Google Scholar]
33.Rice G.M., Leonard C.W., Weeks K.M. RNA secondary structure modeling at consistent high accuracy using differential SHAPE. RNA. 2014;20:846–854. doi: 10.1261/rna.043323.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Jaeger J.A., Turner D.H., Zuker M. Improved predictions of secondary structures for RNA. Proc. Natl. Acad. Sci. U.S.A. 1989;86:7706–7710. doi: 10.1073/pnas.86.20.7706. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Duncan C.D., Weeks K.M. SHAPE analysis of long-range interactions reveals extensive and thermodynamically preferred misfolding in a fragile group I intron RNA. Biochemistry. 2008;47:8504–8513. doi: 10.1021/bi800207b. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Wilkinson K.A., Merino E.J., Weeks K.M. RNA SHAPE chemistry reveals nonhierarchical interactions dominate equilibrium structural transitions in tRNA(Asp) transcripts. J. Am. Chem. Soc. 2005;127:4659–4667. doi: 10.1021/ja0436749. [DOI] [PubMed] [Google Scholar]
37.Cordero P., Lucks J.B., Das R. An RNA Mapping DataBase for curating RNA structure mapping experiments. Bioinformatics. 2012;28:3006–3008. doi: 10.1093/bioinformatics/bts554. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Low J.T., Weeks K.M. SHAPE-directed RNA secondary structure prediction. Methods. 2010;52:150–158. doi: 10.1016/j.ymeth.2010.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Xu Z., Almudevar A., Mathews D.H. Statistical evaluation of improvement in RNA secondary structure prediction. Nucleic Acids Res. 2012;40:e26. doi: 10.1093/nar/gkr1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Fu Y., Sharma G., Mathews D.H. Dynalign II: common secondary structure prediction for RNA homologs with domain insertions. Nucleic Acids Res. 2014;42:13939–13948. doi: 10.1093/nar/gku1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Gorodkin J., Stricklin S.L., Stormo G.D. Discovering common stem–loop motifs in unaligned RNA sequences. Nucleic Acids Res. 2001;29:2135–2144. doi: 10.1093/nar/29.10.2135. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Bindewald E., Wendeler M., Legiewicz M., Bona M.K., Wang Y., Pritt M.J., Grice S.F.J.L., Shapiro B.A. Correlating SHAPE signatures with three-dimensional RNA structures. RNA. 2011;17:1688–1696. doi: 10.1261/rna.2640111. [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Sükösd Z., Swenson M.S., Kjems J., Heitsch C.E. Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res. 2013;41:2807–2816. doi: 10.1093/nar/gks1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Bolstad B.M., Irizarry R.A., Åstrand M., Speed T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
45.Hu X., Wong T.K.F., Lu Z.J., Chan T.F., Lau T.C.K., Yiu S.M., Yip K.Y. Computational identification of protein binding sites on RNAs using high-throughput RNA structure-probing data. Bioinformatics. 2014;30:1049–1055. doi: 10.1093/bioinformatics/btt757. [DOI] [PubMed] [Google Scholar]
46.Ben-Shem A., Garreau de Loubresse N., Melnikov S., Jenner L., Yusupova G., Yusupov M. The structure of the eukaryotic ribosome at 3.0 A resolution. Science. 2011;334:1524–1529. doi: 10.1126/science.1212642. [DOI] [PubMed] [Google Scholar]
47.Hanley J.A., McNeil B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
48.Novikova I.V., Hennelly S.P., Sanbonmatsu K.Y. Tackling structures of long noncoding RNAs. Int. J. Mol. Sci. 2013;14:23672–23684. doi: 10.3390/ijms141223672. [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Lucks J.B., Mortimer S.A., Trapnell C., Luo S., Aviran S., Schroth G.P., Pachter L., Doudna J.A., Arkin A.P. Multiplexed RNA structure characterization with selective 2‘-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq) Proc. Natl. Acad. Sci. U.S.A. 2011;108:11063–11068. doi: 10.1073/pnas.1106501108. [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Tripathi V., Ellis J.D., Shen Z., Song D.Y., Pan Q., Watt A.T., Freier S.M., Bennett C.F., Sharma A., Bubulya P.A., et al. The nuclear-retained noncoding RNA MALAT1 regulates alternative splicing by modulating SR splicing factor phosphorylation. Mol. Cell. 2010;39:925–938. doi: 10.1016/j.molcel.2010.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SUPPLEMENTARY DATA

supp_43_15_7247__index.html^{(989B, html)}

supp_gkv706_nar-00334-z-2015-File003.pdf^{(3.6MB, pdf)}

[B1] 1.Wan Y., Kertesz M., Spitale R.C., Segal E., Chang H.Y. Understanding the transcriptome through RNA structure. Nat. Rev. Genet. 2011;12:641–655. doi: 10.1038/nrg3049. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] 2.Weeks K.M. Advances in RNA structure analysis by chemical probing. Curr. Opin. Struct. Biol. 2010;20:295–304. doi: 10.1016/j.sbi.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] 3.Wilkinson K.A., Merino E.J., Weeks K.M. Selective 2‘-hydroxyl acylation analyzed by primer extension (SHAPE): quantitative RNA structure analysis at single nucleotide resolution. Nat. Protoc. 2006;1:1610–1616. doi: 10.1038/nprot.2006.249. [DOI] [PubMed] [Google Scholar]

[B4] 4.Kertesz M., Wan Y., Mazor E., Rinn J.L., Nutter R.C., Chang H.Y., Segal E. Genome-wide measurement of RNA secondary structure in yeast. Nature. 2010;467:103–107. doi: 10.1038/nature09322. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5.Wan Y., Qu K., Zhang Q.C., Flynn R.A., Manor O., Ouyang Z., Zhang J., Spitale R.C., Snyder M.P., Segal E., et al. Landscape and variation of RNA secondary structure across the human transcriptome. Nature. 2014;505:706–709. doi: 10.1038/nature12946. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] 6.Underwood J.G., Uzilov A.V., Katzman S., Onodera C.S., Mainzer J.E., Mathews D.H., Lowe T.M., Salama S.R., Haussler D. FragSeq: transcriptome-wide RNA structure probing using high-throughput sequencing. Nat. Methods. 2010;7:995–1001. doi: 10.1038/nmeth.1529. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B7] 7.Ding Y., Tang Y., Kwok C.K., Zhang Y., Bevilacqua P.C., Assmann S.M. In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature. 2014;505:696–700. doi: 10.1038/nature12756. [DOI] [PubMed] [Google Scholar]

[B8] 8.Incarnato D., Neri F., Anselmi F., Oliviero S. Genome-wide profiling of mouse RNA secondary structures reveals key features of the mammalian transcriptome. Genome Biol. 2014;15:491. doi: 10.1186/s13059-014-0491-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B9] 9.Rouskin S., Zubradt M., Washietl S., Kellis M., Weissman J.S. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature. 2014;505:701–705. doi: 10.1038/nature12894. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B10] 10.Talkish J., May G., Lin Y., Woolford J.L., McManus C.J. Mod-seq: high-throughput sequencing for chemical probing of RNA structure. RNA. 2014;20:713–720. doi: 10.1261/rna.042218.113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11.Wells S.E., Hughes J.M., Igel A.H., Ares M.J. Use of dimethyl sulfate to probe RNA structure in vivo. Methods Enzymol. 2000;318:479–493. doi: 10.1016/s0076-6879(00)18071-1. [DOI] [PubMed] [Google Scholar]

[B12] 12.Eddy S.R. Computational analysis of conserved RNA secondary structure in transcriptomes and genomes. Annu. Rev. Biophys. 2014;43:433–456. doi: 10.1146/annurev-biophys-051013-022950. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13.Rivas E. The four ingredients of single-sequence RNA secondary structure prediction: A unifying perspective. RNA Biol. 2013;10:1185–1196. doi: 10.4161/rna.24971. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B14] 14.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15.Bellaousov S., Reuter J.S., Seetin M.G., Mathews D.H. RNAstructure: web servers for RNA secondary structure prediction and analysis. Nucleic Acids Res. 2013;41:W471–W474. doi: 10.1093/nar/gkt290. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] 16.Lorenz R., Bernhart S.H., Höner Zu Siederdissen C., Tafer H., Flamm C., Stadler P.F., Hofacker I.L. ViennaRNA Package 2.0. Algorithms. Mol. Biol. 2011;6:26. doi: 10.1186/1748-7188-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17.Doshi K.J., Cannone J.J., Cobaugh C.W., Gutell R.R. Evaluation of the suitability of free-energy minimization using nearest-neighbor energy parameters for RNA secondary structure prediction. BMC Bioinformatics. 2004;5:105. doi: 10.1186/1471-2105-5-105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] 18.McCaskill J.S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]

[B19] 19.Lu Z.J., Gloor J.W., Mathews D.H. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA. 2009;15:1805–1813. doi: 10.1261/rna.1643609. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B20] 20.Knudsen B., Hein J. Pfold: RNA secondary structure prediction using stochastic context-free grammars. Nucleic Acids Res. 2003;31:3423–3428. doi: 10.1093/nar/gkg614. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B21] 21.Do C.B., Woods D.A., Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90–e98. doi: 10.1093/bioinformatics/btl246. [DOI] [PubMed] [Google Scholar]

[B22] 22.Ding Y., Lawrence C.E. A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res. 2003;31:7280–7301. doi: 10.1093/nar/gkg938. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B23] 23.Ding Y., Chan C.Y., Lawrence C.E. RNA secondary structure prediction by centroids in a Boltzmann weighted ensemble. RNA. 2005;11:1157–1166. doi: 10.1261/rna.2500605. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] 24.Mathews D.H., Sabina J., Zuker M., Turner D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]

[B25] 25.Mathews D.H., Disney M.D., Childs J.L., Schroeder S.J., Zuker M., Turner D.H. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] 26.Deigan K.E., Li T.W., Mathews D.H., Weeks K.M. Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. U.S.A. 2009;106:97–102. doi: 10.1073/pnas.0806929106. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B27] 27.Washietl S., Hofacker I.L., Stadler P.F., Kellis M. RNA folding with soft constraints: reconciliation of probing data and thermodynamic secondary structure prediction. Nucleic Acids Res. 2012;40:4261–4272. doi: 10.1093/nar/gks009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B28] 28.Zarringhalam K., Meyer M.M., Dotu I., Chuang J.H., Clote P. Integrating chemical footprinting data into RNA secondary structure prediction. PLoS One. 2012;7:e45160. doi: 10.1371/journal.pone.0045160. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B29] 29.Quarrier S., Martin J.S., Davis-Neulander L., Beauregard A., Laederach A. Evaluation of the information content of RNA structure mapping data for secondary structure prediction. RNA. 2010;16:1108–1117. doi: 10.1261/rna.1988510. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] 30.Cordero P., Kladwang W., VanLang C.C., Das R. Quantitative dimethyl sulfate mapping for automated RNA secondary structure inference. Biochemistry. 2012;51:7037–7039. doi: 10.1021/bi3008802. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B31] 31.Ouyang Z., Snyder M.P., Chang H.Y. SeqFold: Genome-scale reconstruction of RNA secondary structure integrating high-throughput sequencing data. Genome Res. 2013;23:377–387. doi: 10.1101/gr.138545.112. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B32] 32.Mathews D.H. Revolutions in RNA secondary structure prediction. J. Mol. Biol. 2006;359:526–532. doi: 10.1016/j.jmb.2006.01.067. [DOI] [PubMed] [Google Scholar]

[B33] 33.Rice G.M., Leonard C.W., Weeks K.M. RNA secondary structure modeling at consistent high accuracy using differential SHAPE. RNA. 2014;20:846–854. doi: 10.1261/rna.043323.113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] 34.Jaeger J.A., Turner D.H., Zuker M. Improved predictions of secondary structures for RNA. Proc. Natl. Acad. Sci. U.S.A. 1989;86:7706–7710. doi: 10.1073/pnas.86.20.7706. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B35] 35.Duncan C.D., Weeks K.M. SHAPE analysis of long-range interactions reveals extensive and thermodynamically preferred misfolding in a fragile group I intron RNA. Biochemistry. 2008;47:8504–8513. doi: 10.1021/bi800207b. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] 36.Wilkinson K.A., Merino E.J., Weeks K.M. RNA SHAPE chemistry reveals nonhierarchical interactions dominate equilibrium structural transitions in tRNA(Asp) transcripts. J. Am. Chem. Soc. 2005;127:4659–4667. doi: 10.1021/ja0436749. [DOI] [PubMed] [Google Scholar]

[B37] 37.Cordero P., Lucks J.B., Das R. An RNA Mapping DataBase for curating RNA structure mapping experiments. Bioinformatics. 2012;28:3006–3008. doi: 10.1093/bioinformatics/bts554. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B38] 38.Low J.T., Weeks K.M. SHAPE-directed RNA secondary structure prediction. Methods. 2010;52:150–158. doi: 10.1016/j.ymeth.2010.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B39] 39.Xu Z., Almudevar A., Mathews D.H. Statistical evaluation of improvement in RNA secondary structure prediction. Nucleic Acids Res. 2012;40:e26. doi: 10.1093/nar/gkr1081. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B40] 40.Fu Y., Sharma G., Mathews D.H. Dynalign II: common secondary structure prediction for RNA homologs with domain insertions. Nucleic Acids Res. 2014;42:13939–13948. doi: 10.1093/nar/gku1172. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B41] 41.Gorodkin J., Stricklin S.L., Stormo G.D. Discovering common stem–loop motifs in unaligned RNA sequences. Nucleic Acids Res. 2001;29:2135–2144. doi: 10.1093/nar/29.10.2135. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B42] 42.Bindewald E., Wendeler M., Legiewicz M., Bona M.K., Wang Y., Pritt M.J., Grice S.F.J.L., Shapiro B.A. Correlating SHAPE signatures with three-dimensional RNA structures. RNA. 2011;17:1688–1696. doi: 10.1261/rna.2640111. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B43] 43.Sükösd Z., Swenson M.S., Kjems J., Heitsch C.E. Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res. 2013;41:2807–2816. doi: 10.1093/nar/gks1283. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B44] 44.Bolstad B.M., Irizarry R.A., Åstrand M., Speed T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]

[B45] 45.Hu X., Wong T.K.F., Lu Z.J., Chan T.F., Lau T.C.K., Yiu S.M., Yip K.Y. Computational identification of protein binding sites on RNAs using high-throughput RNA structure-probing data. Bioinformatics. 2014;30:1049–1055. doi: 10.1093/bioinformatics/btt757. [DOI] [PubMed] [Google Scholar]

[B46] 46.Ben-Shem A., Garreau de Loubresse N., Melnikov S., Jenner L., Yusupova G., Yusupov M. The structure of the eukaryotic ribosome at 3.0 A resolution. Science. 2011;334:1524–1529. doi: 10.1126/science.1212642. [DOI] [PubMed] [Google Scholar]

[B47] 47.Hanley J.A., McNeil B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]

[B48] 48.Novikova I.V., Hennelly S.P., Sanbonmatsu K.Y. Tackling structures of long noncoding RNAs. Int. J. Mol. Sci. 2013;14:23672–23684. doi: 10.3390/ijms141223672. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B49] 49.Lucks J.B., Mortimer S.A., Trapnell C., Luo S., Aviran S., Schroth G.P., Pachter L., Doudna J.A., Arkin A.P. Multiplexed RNA structure characterization with selective 2‘-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq) Proc. Natl. Acad. Sci. U.S.A. 2011;108:11063–11068. doi: 10.1073/pnas.1106501108. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B50] 50.Tripathi V., Ellis J.D., Shen Z., Song D.Y., Pan Q., Watt A.T., Freier S.M., Bennett C.F., Sharma A., Bubulya P.A., et al. The nuclear-retained noncoding RNA MALAT1 regulates alternative splicing by modulating SR splicing factor phosphorylation. Mol. Cell. 2010;39:925–938. doi: 10.1016/j.molcel.2010.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data

Yang Wu

Binbin Shi

Xinqiang Ding

Tong Liu

Xihao Hu

Kevin Y Yip

Zheng Rong Yang

David H Mathews

Zhi John Lu

Abstract

INTRODUCTION

MATERIALS AND METHODS

Review of MaxExpect

Figure 1.

The framework of RME

Reference structures and structure-probing data

Performance evaluation of different RNA secondary structure prediction methods

Posterior probabilistic model for transforming experimental data

Processing of SHAPE data

Processing of PARS data

Processing of DMS-seq data

Solvent accessibility calculation on a yeast 18S rRNA complex

RESULTS

RME significantly improves RNA secondary structure prediction with perfect restraints

Figure 2.

RME significantly improves RNA secondary structure prediction when supplemented with SHAPE data

Figure 3.

Improvement of secondary structure prediction is limited by incorporating PARS and DMS-seq data

Figure 4.

Limited structure prediction improvement is due to low probing efficiency on reference RNAs

RME performs best with in vivo DMS-seq data at solvent accessible regions

Figure 5.

DISCUSSION

AVAILABILITY

Supplementary Material

Acknowledgments

SUPPLEMENTARY DATA

FUNDING

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases