Abstract
The dielectric properties of Z-type hexaferrite Sr3Co2Fe24O41 (SCFO) have been investigated as a function of temperature from 153 to 503 K between 1 and 2 GHz. The dielectric responses of SCFO are found to be frequency dependent and thermally activated. The relaxation-type dielectric behavior is observed to be dominating in the low frequency region and resonance-type dielectric behavior is found to be dominating above 108 Hz. This frequency dependence of dielectric behavior is explained by the damped harmonic oscillator model with temperature dependent coefficients. The imaginary part of impedance (Z″) and modulus (M″) spectra show that there is a distribution of relaxation times. The scaling behaviors of Z″ and M″ spectra further suggest that the distribution of relaxation times is temperature independent at low frequencies. The dielectric loss spectra at different temperatures have not shown a scaling behavior above 108 Hz. A comparison between the Z″ and the M″ spectra indicates that the short-range charges motion dominates at low temperatures and the long-range charges motion dominates at high temperatures. The above results indicate that the dielectric dispersion mechanism in SCFO is temperature independent at low frequencies and temperature dependent at high frequencies due to the domination of resonance behavior.
Hexaferrites are iron oxides with hexagonal structures and have long been used in technological applications such as permanent magnets and microwave devices1. The Z-type hexaferrites (Ba,Sr)3Me2Fe24O41 (Me is a divalent transition metal ion) are one of the families of hexagonal ferrites. The crystal structure of Z-type hexaferrite can be described as alternating stacking of the basic blocks RSTSR*S*T*S* (the asterisk corresponds to an 180° block turning around the hexagonal c-axis) where S is (Ba,Sr)Fe2O4, R is [(Ba,Sr)Fe6O11]2− and T is (Ba,Sr)2Fe8O14. Recently, it was reported that the polycrystalline Z-type ferrite Sr3Co2Fe24O41 could exhibit low-field magnetoelectric effects at room temperature2,3,4. The magnetic field tuning of electric polarization in Sr3Co2Fe24O41 was found to be induced by its transverse conical spin structure through the inverse Dzyaloshinskii-Moriya mechanism3. It was further revealed that the single crystalline Sr2.48Ba0.52Co2Fe24O41 Z-type ferrite exhibits a magnetoelectric susceptibility of 3200 ps/m which was much higher than other room temperature single phase multiferroic materials, for example BiFeO3 (55 ps/m)5,6. The findings of the room temperature magnetoelectric effects in Z-type hexaferrites will enable this material to be applied in the novel low-power magnetoelectronic devices7,8.
For the magnetoelectronic devices operating in the microwave region or under an alternative electric field, both electrical and magnetic properties of the device materials are important for the devices’ performance. Although the magnetic and magnetoelectric properties of the Z-type hexaferrites have been intensively studied in the recent years2,3,4,5,7,8,9,10,11, only few works have been reported on the dielectric properties of Z-type hexaferrites. The composition dependent dielectric properties of Z-type hexaferrite Ba3Co2Fe24O41 have been reported12,13,14. But the dielectric properties of substituted Ba3Co2Fe24O41 were investigated only at room temperature above 107 Hz. In addition, the impedance properties of Ba3Co2Fe24O41 have not been discussed. A recent work reported the observation of a large negative magnetodielectric effect of Sr3Co2Fe24O41 (SCFO) hexaferrite below 105 Hz9. However, the dielectric properties of SCFO have not been detailed discussed in this work. In addition, a systematical investigation on the temperature dependence of dielectric properties of SCFO has not been reported up to now2,3,4,5,7,8,9. The above works show that the reported studies on the dielectric properties of Z-type hexaferrites are still very limited. The dielectric dispersion mechanism and the microstructure-electrical property relationship in the Z-type hexaferrites, which is both physically interesting and technically important, have not been well understood until now. In this work, the dielectric permittivity, impedance and modulus of SCFO have been investigated as a function of the frequency (1–2 G Hz) and temperature (153 K–503 K). Both the relaxation-type and resonance-type dielectric behaviors in SCFO are observed. A damped harmonic oscillator model is used to explain the frequency dependence of dielectric behaviors at different temperatures. In addition, the scaling behaviors of imaginary impedance and modulus spectra are observed at low frequencies.
Results
Characterization of SCFO polycrystalline sample
Figure 1 is the X-ray diffraction θ–2θ spectrum of the sample. The peaks have been indexed according to the calculated Z-type SCFO spectra in the references2,15. Figure 1 shows that the majority phase of the sample is Z-type SCFO. However, a small amount of impurity U-type hexaferrite (Sr4Co2Fe36O60) exists in the sample. It has been shown that preparation of the pure Z-type phase is extremely difficult because other hexaferrite phases usually coexist with the Z-type during the synthesis process2,3,5,7,9. It can be expected that the electrical responses of the Z-type and U-type (sequence RSR*S*T*S*) phases are similar because they have the same stacking blocks and very close stacking sequences. Therefore, the dielectric properties of the polycrystalline sample in this work can’t be substantially changed by the existence of the U-type impurity2. The grain structure of SCFO was measured with Scanning Electron Microscope as shown in the inset of Fig. 1. It can be seen that the SCFO sample has plate-like grains which stack on each other.
Figure 1. XRD pattern of the SCFO sample taken at room temperature, the Z type phase has been indexed according to the calculated spectrum.
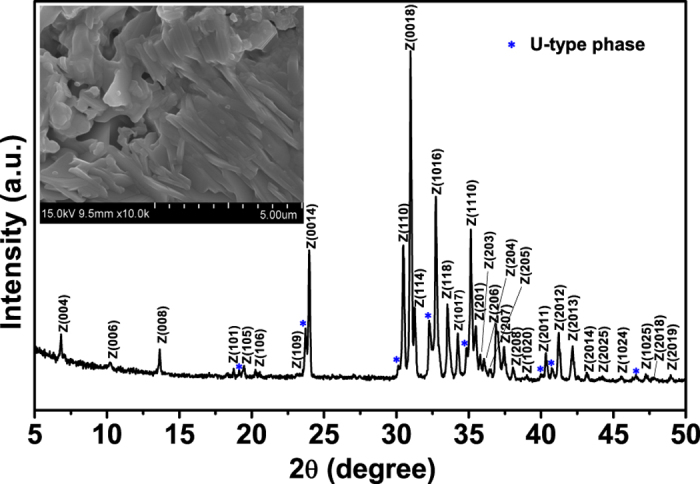
The inset is the SEM image of the sample.
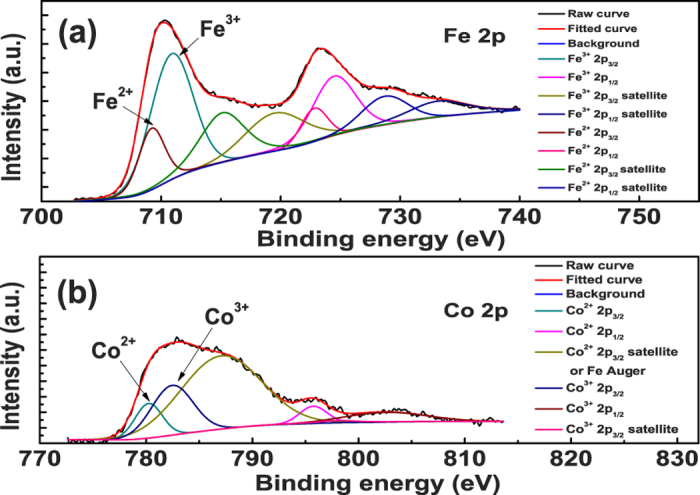
Figure 2 shows the X-ray photoelectron spectroscopy (XPS) spectra of the magnetic ions of the SCFO sample. Figure 2 shows that both divalent ions (Fe2+ and Co2+) and trivalent ions (Fe3+ and Co3+) exist in the sample. The electronic exchange between Fe2+ and Fe3+ produces n-type carriers and also the hole exchange between Co3+ and Co2+ gives rise to p-type carriers12,13,16. The formation of both types of charge carriers arises from the loss of oxygen during the high temperature sintering process. For charge compensation, a part of Fe3+ transforms to Fe2+ and a part of Co2+ transforms to Co3+. All the carriers involved in the sample will affect the dielectric dispersion behavior. However, it can be expected that the electron exchange between Fe3+ and Fe2+ will be dominating in SCFO due to the large atomic ratio of Fe in SCFO12,13.
Figure 2. XPS patterns of (a) the Fe ions and (b) Co ions in SCFO at room temperature.
Dielectric permittivity analysis
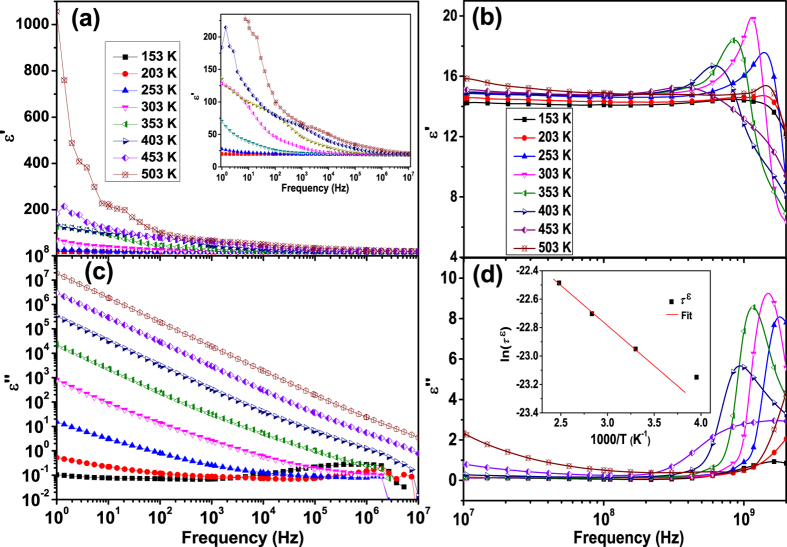
Figure 3 shows the frequency dependent dielectric constant ε′ and dielectric loss ε″ at different temperatures. Figure 3 shows that when the temperature is lower than 203 K, both ε′ and ε″ are rather small and have very weak dependences on the frequency below 1 GHz. This phenomenon has been referred as the “nearly constant loss” (NCL) behavior17,18. The NCL is generally regarded as resulting from relaxations of the charges moving in the asymmetric double-well potentials19. Such relaxation involves highly localized motions rather than the dominating hopping processes which usually occur in the ferrites at high temperatures12,13,16,20,21,22. When the temperature is increased above 253 K and the frequency is lower than 108 Hz, both ε′ and ε″ decrease with increasing frequency and increase with increasing temperature generally. The above frequency and temperature dependent ε′ and ε″ can be explained by Koop’s theory which takes the dielectric structure as an inhomogeneous medium composed of two Maxwell-Wagner type layers23,24,25. In this model, the dielectric structure is imagined to consist of fairly well-conducting ferrite grains separated by poorly conducting grain boundaries. The electrons reach the grain boundaries through hopping and if the resistance of grain boundaries is high enough, electrons pile up at the grain boundaries and produce polarization. However, as the frequency of the applied field is increased, the electrons reverse their direction of motion more often. This decreases the probability of electrons reaching the grain boundary and as a result, polarization decreases. Therefore, both ε′ and ε″ decrease with an increase in frequency. The decrease of ε″ is due to the decreased conductive process in the sample. The previous XPS results in Fig. 2 show that there are both iron and cobalt ion defects in SCFO which produce n-type and p-type carriers respectively. The electrons contribute to polarization by local displacement in the direction opposite to the electric field while the holes contribute to polarization by local displacement in the direction of the external electric field. The collective contribution of both types gives the dielectric response. With an increase in temperature, the electron hopping between Fe2+ and Fe3+ and hole hopping between Co3+ and Co2+ are thermal activated. This increases the probability of electrons reaching the grain boundary and as a result, polarization increases. Therefore, both ε′ and ε″ increase with increasing temperature.
Figure 3. Temperature dependent dielectric constant ε′ spectra (a) below 107 Hz and (b) above 107 Hz, dielectric loss ε″ spectra (c) below 107 Hz and (d) above 107 Hz, the inset of plot (d) is the temperature dependent relaxation times obtained from the peak frequencies of ε″spectra between 253 K and 403 K.
When the frequency is higher than 108 Hz, strong peaks are observed in both ε′ and ε″ spectra above 0.5 GHz between 203 K and 453 K. Both the ε′ peaks and ε″ peaks shift toward lower frequencies with increasing temperature. With an increase in temperature, the peak intensity increases firstly with a maximum value at 303 K and then decreases. In addition, the peak broadens with an increased asymmetry as the temperature increases. This shows again that the dielectric response at high frequency is temperature dependent. Moreover, the simultaneous appearance of ε′ and ε″ peaks with a slightly higher ε″ peak position has been referred as “anomalous dispersion” phenomenon26. In this case, the dielectric response is dominated by the resonance behavior instead of the relaxation behavior which usually occurs in the low frequency regions26,27,28.
The frequency dependence of complex dielectric constant can be described by a damped harmonic oscillator model with the expression26,27,28,29
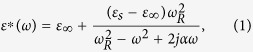 |
Then, the real and imaginary parts of the complex dielectric constant can be written as
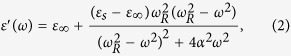 |
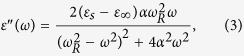 |
where εs and ε∞ are the static- and high-frequency limits of the dielectric constant, respectively, ω = 2πf is the angular frequency, ωR is the temperature dependent natural frequency of oscillation of the harmonic oscillator in the absence of damping, and α is the temperature dependent damping coefficient of the dielectric response. The parameter k =2α/ωR is an essential parameter for identifying the dielectric response mechanism. When k is zero, only resonance-type dielectric response takes place in the dielectric system in which the charge moving is dominated only by the inertial effects26. In this case, the dielectric loss is a delta function with an infinitely large value. When k is larger than zero, relaxation-type dielectric response comes into play. With an increase in k, the dielectric response of the system will pass from a resonance-dominated behavior (k < 1) to a relaxation-dominated behavior gradually and finally, to the Debye-type behavior which corresponds to a pure relaxation-type dielectric behavior with infinitely strong damping. In addition, the dielectric loss peak will broaden with increasing k26.
The high frequency dielectric loss peaks in Fig. 3(d) are fitted with Eq. (3) with α and Δε = εs − ε∞ as the fitting parameters. ωR has been calculated with the relation 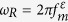 where
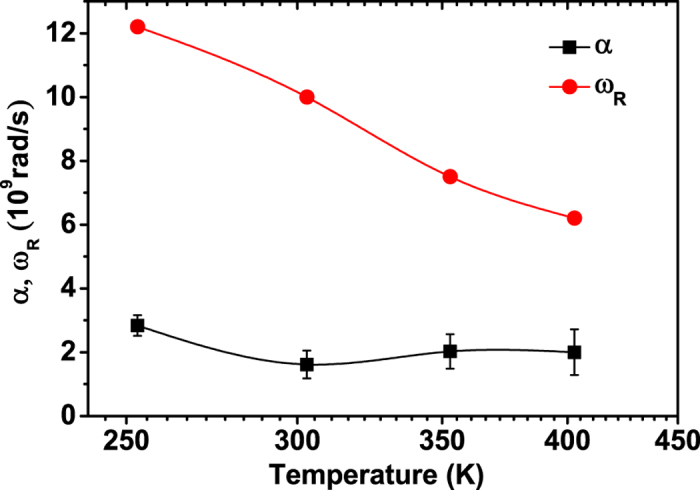
where 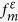 is peak frequency of ε″. The fitting results of α and ωR at different temperatures are shown in Fig. 4. Figure 4 shows that α is much smaller than ωR (k = 2α/ωR < 0.65) at all temperatures, indicating that the electrical damping in SCFO is small. This agrees with the appearance of resonance peaks in the permittivity spectra. In addition, with an increase in temperature, the fitting standard error increases due to the increased asymmetry of the peaks. It must be mentioned that Eq. (1) is derived from the damped motions of many identical non-interacting dipole oscillators. In the real sample, the dipole interactions are inevitable. In addition, it has been shown in Fig. 2 that there are both n-type and p-type carriers and hence different dipole oscillators which may have different temperature dependences in the SCFO sample. The above two factors and the electrical non-uniformities in the polycrystalline sample may lead to an increased peak width and asymmetry of the loss peak. An increase in temperature may lead to a variation of both charge carrier densities and dipole interactions28. Therefore, the deviation of the experimental data from the ideal damped harmonic oscillator model increases with increasing temperature. However, we can still see clearly from Fig. 4 that the ratio between α and ωR (k = 2α/ωR) increases with increasing temperature despite of the increase in fitting deviations. This indicates that increasing temperature leads to an increased damping motion of the dipoles and thus increased dielectric relaxation behaviors of the sample. This can be further evidenced by the decreased peak intensities on both ε′ and ε″ spectra with increasing temperature as shown in Fig. 3(b,d). The above results show that the high frequency dielectric response of the sample is firstly thermal activated with increasing temperature and then damped with a further increase in temperature.
is peak frequency of ε″. The fitting results of α and ωR at different temperatures are shown in Fig. 4. Figure 4 shows that α is much smaller than ωR (k = 2α/ωR < 0.65) at all temperatures, indicating that the electrical damping in SCFO is small. This agrees with the appearance of resonance peaks in the permittivity spectra. In addition, with an increase in temperature, the fitting standard error increases due to the increased asymmetry of the peaks. It must be mentioned that Eq. (1) is derived from the damped motions of many identical non-interacting dipole oscillators. In the real sample, the dipole interactions are inevitable. In addition, it has been shown in Fig. 2 that there are both n-type and p-type carriers and hence different dipole oscillators which may have different temperature dependences in the SCFO sample. The above two factors and the electrical non-uniformities in the polycrystalline sample may lead to an increased peak width and asymmetry of the loss peak. An increase in temperature may lead to a variation of both charge carrier densities and dipole interactions28. Therefore, the deviation of the experimental data from the ideal damped harmonic oscillator model increases with increasing temperature. However, we can still see clearly from Fig. 4 that the ratio between α and ωR (k = 2α/ωR) increases with increasing temperature despite of the increase in fitting deviations. This indicates that increasing temperature leads to an increased damping motion of the dipoles and thus increased dielectric relaxation behaviors of the sample. This can be further evidenced by the decreased peak intensities on both ε′ and ε″ spectra with increasing temperature as shown in Fig. 3(b,d). The above results show that the high frequency dielectric response of the sample is firstly thermal activated with increasing temperature and then damped with a further increase in temperature.
Figure 4. Temperature dependence of the damping coefficient α and peak frequency ωR of the dielectric loss, the α is obtained from the least-square fitting of dielectric loss ε″ spectra above 0.2 GHz to the Eq. (3), the error bar is the fitting standard error.
The most probable dielectric relaxation time τε of the sample is calculated using the relation 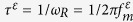 . The τε as a function of temperature is shown in the inset of Fig. 3(d). Result shows that τε increases with increasing the temperature, which agrees with the increase in the damping strength in the previous discussions. In addition, the τε above 303 K can be well fitted with the Arrhenius relation
. The τε as a function of temperature is shown in the inset of Fig. 3(d). Result shows that τε increases with increasing the temperature, which agrees with the increase in the damping strength in the previous discussions. In addition, the τε above 303 K can be well fitted with the Arrhenius relation 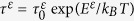 , where
, where 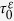 is the pre-exponential factor of the relaxation time, T is the temperature, and kB is the Boltzmann constant. The activation energy
is the pre-exponential factor of the relaxation time, T is the temperature, and kB is the Boltzmann constant. The activation energy 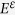 determined from the slope of the linear fit in the Arrhenius plot is 0.05 eV which is much lower than the values obtained from the dielectric relaxation peaks at low frequencies for many ferrites22,30,31,32. This agrees with the small damping dielectric behavior above 0.5 GHz in the SCFO sample.
determined from the slope of the linear fit in the Arrhenius plot is 0.05 eV which is much lower than the values obtained from the dielectric relaxation peaks at low frequencies for many ferrites22,30,31,32. This agrees with the small damping dielectric behavior above 0.5 GHz in the SCFO sample.
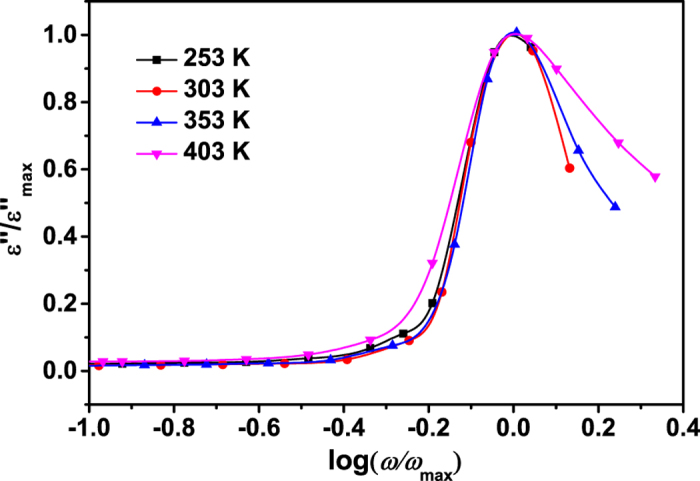
The above permittivity spectra shows that the dielectric response is non-Debye type and temperature dependent in the high frequency region. In order to confirm whether the distribution of relaxation times is temperature dependent or not, we plotted the ε″ in scaled coordinates for the spectra above 108 Hz, i.e., 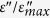 versus log(ω/ωmax), where
versus log(ω/ωmax), where 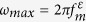 is the loss peak frequency. If all the permittivity loss profiles are collapsed into one master curve, it suggests that the distribution of relaxation times is temperature independent33. Figure 5 shows that for the permittivity spectra at temperature below 353 K, the peaks are nearly overlapped in relatively low frequency region. With a further increase in frequency or an increase in temperature to 403 K, the dispersion of the spectra occurs. The above results indicate that the distribution of the relaxation times is temperature dependent in the frequency region above 108 Hz.
is the loss peak frequency. If all the permittivity loss profiles are collapsed into one master curve, it suggests that the distribution of relaxation times is temperature independent33. Figure 5 shows that for the permittivity spectra at temperature below 353 K, the peaks are nearly overlapped in relatively low frequency region. With a further increase in frequency or an increase in temperature to 403 K, the dispersion of the spectra occurs. The above results indicate that the distribution of the relaxation times is temperature dependent in the frequency region above 108 Hz.
Figure 5. The dielectric loss ε″ spectra plotted with scaled coordinates above 108 Hz at different temperatures.
Complex impedance analysis
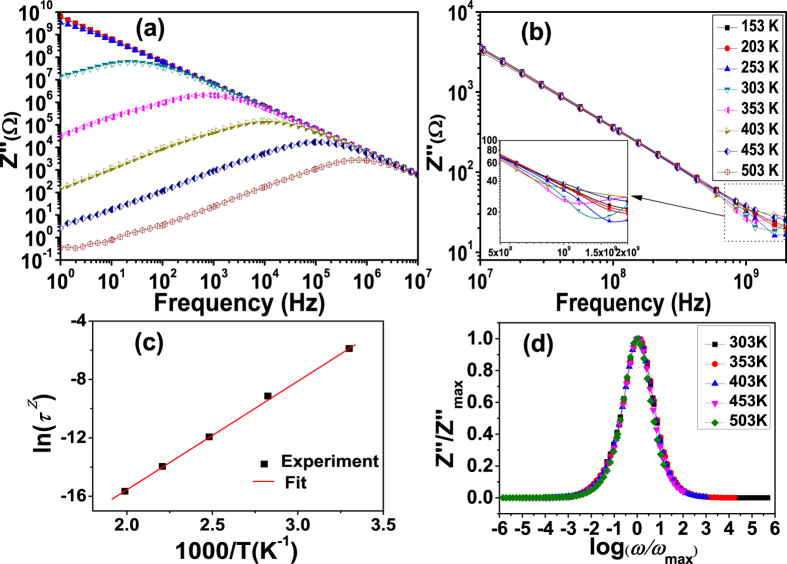
In order to get better understanding on the dielectric relaxation behaviors of SCFO, the impedance and modulus spectra of the sample have been studied. Figure 6 shows the frequency dependence of imaginary part (Z″) of the impedance Z* = Z′ − iZ″at different temperatures. Figure 6(a,b) show that at temperatures below 303 K, Z″decreases monotonically with increasing frequency and merges together at a very low value when frequency exceeds 100 Hz. On the other hand, the magnitudes of Z″ decrease with increasing temperature. The monotonic decrease of Z″ with increasing frequency indicates that at low temperatures, the relaxation is very weak. This should be due to the freezing of dipoles at low temperatures as indicated by the small values of dielectric constant and dielectric loss at low temperatures in Fig. 3. When the temperature is increased above 303 K, a strong impedance loss peak appears in the measured frequency range. The loss peak moves to higher frequency with a fall in intensity as the temperature increases. This implies that electrical responses are thermally activated. This is possibly due to the presence of space charge at the grain boundaries12,13,14. The shifting of peak position to higher frequency with increasing temperature indicates an increase in the relaxation rate. The dielectric relaxation time τZ is calculated using the relation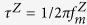 , where
, where 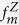 is peak frequency of Z″. This relaxation time as a function of temperature is shown in Fig. 6(c). As the temperature increases, the relaxation time decreases, which shows an opposite tendency of temperature dependence to that in Fig. 3(d). This should be attributed to the semiconductor-like conduction nature of the samples. It can be seen that the relaxation time τZ can be well fitted with the Arrhenius relation
is peak frequency of Z″. This relaxation time as a function of temperature is shown in Fig. 6(c). As the temperature increases, the relaxation time decreases, which shows an opposite tendency of temperature dependence to that in Fig. 3(d). This should be attributed to the semiconductor-like conduction nature of the samples. It can be seen that the relaxation time τZ can be well fitted with the Arrhenius relation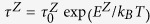 , where
, where 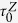 is the pre-exponential factor of the relaxation time. The activation energy EZ determined from the slope of the linear fit in the Arrhenius plot is 0.66 eV which is much higher than the value (0.05 eV) obtained from the ε″ spectra. This indicates again that the dielectric relaxation behavior undergoes a higher damping strength than the dielectric resonance behavior.
is the pre-exponential factor of the relaxation time. The activation energy EZ determined from the slope of the linear fit in the Arrhenius plot is 0.66 eV which is much higher than the value (0.05 eV) obtained from the ε″ spectra. This indicates again that the dielectric relaxation behavior undergoes a higher damping strength than the dielectric resonance behavior.
Figure 6. Temperature dependent imaginary part impedance Z″ spectra (a) below 107 Hz and (b) above 107 Hz, (c) the temperature dependence of the relaxation times obtained from the peak frequencies of Z″spectra above 303 K, (d) scaling behavior of the Z″ spectra in plot (a) at temperatures above 303 K.
Moreover, the full width at half maxima calculated from the impedance loss spectra (Z″ vs log f) are greater than 1.144 decades (ideal Debye relaxation), which indicates the deviation from Debye-type relaxation34. This deviation from ideal Debye relaxation might be due to an inherently nonexponential process, such as correlation between diffusive motion of the charge carriers, or nonuniformities in the material microstructure, leading in turn to a spatial distribution of local conductivities and electrical response times34,35,36. In addition, the Z″ curves at all temperatures merge together at high frequencies. The merge of the Z″ at higher frequency indicates a possible release of space charges at the grain boundaries and therefore, the high frequency dielectric response are dominated by the electrical response within the crystalline grains. Figure 6(b) show that when the frequency is increased above 0.5 GHz, dispersions of Z″spectra appear again. This should be due to the resonance-dominated dielectric behavior in the high frequency region as shown in Fig. 3.
The above impedance spectra shows a poly-dispersive nature for the dielectric relaxation at low frequencies. In order to confirm whether the distribution of relaxation times is temperature dependent or not, we plotted the Z″ in scaled coordinates, i.e., 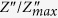 versus log(ω/ωmax), where
versus log(ω/ωmax), where 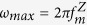 is the loss peak frequency. If all the impedance loss profiles are collapsed into one master curve, it suggests that the distribution of relaxation times is temperature independent34. Figure 6(d) shows that all peaks indeed overlap into one master curve at different temperatures above 303 K. It suggests that the dynamic processes of the charges occurring at different time scales exhibit the same activation energy and that the distribution of the relaxation times is temperature independent.
is the loss peak frequency. If all the impedance loss profiles are collapsed into one master curve, it suggests that the distribution of relaxation times is temperature independent34. Figure 6(d) shows that all peaks indeed overlap into one master curve at different temperatures above 303 K. It suggests that the dynamic processes of the charges occurring at different time scales exhibit the same activation energy and that the distribution of the relaxation times is temperature independent.
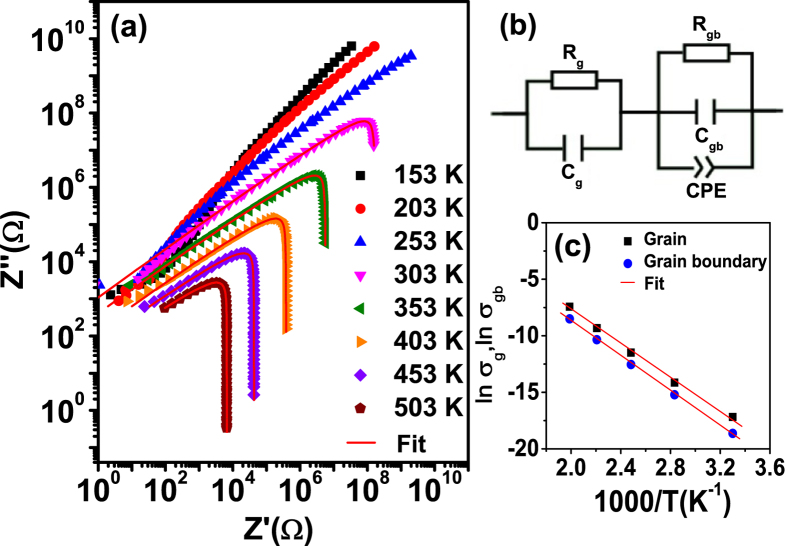
Figure 7 shows the complex impedance plane plots (Z′ vs Z″) and their fitting results. In order to compare the two responses with vastly different impedances in one plot, the log-log presentation of the complex impedance plots are presented. Although the semicircular arcs are distorted, logarithmic plot still offers significant advantages in several respects which have been discussed by Jonscher26. Figure 7(a) shows that there is only one arc appears in the right side of the curve which corresponds to the semicircular arc in the linear complex impedance plot. Furthermore, the arcs shift from right to left with reduced diameters as the temperature increases due to the associated decreases of the impedances.
Figure 7.
(a) Log-log plots of complex impedance (Z′ vs Z″) at different temperatures, (b) equivalent circuit based on the brick-layer model for the impedance spectra, (c) Arrhenius plots of the dc conductivities for grain and grain boundary obtained from the fitting results of equivalent circuit above 303 K.
In order to analyze the impedance data and establish a connection between microstructure and electrical properties, data are usually modeled by an ideal equivalent electrical circuit comprising of resistance (R) and capacitance (C). The polycrystalline materials generally show both grain and grain-boundary impedances. We find that the impedance data above 303 K in Fig. 7(a) can be best fitted with the equivalent circuit based on the brick-layer model as shown in Fig. 7(b)37. This circuit consists of a series array of two sub-circuits, one represents grain effects and the other represents grain boundaries. Let (Rg, Rgb) and (Cg, Cgb) represent the resistances and capacitances of grains and grain boundaries, respectively, and CPE denotes a constant phase element indicating the departure from ideal Debye-type model. The CPE admittance is YCPE = A0(jω)n, where A0 and n are parameters depending on temperature only, A0 confines the magnitude of the dispersion and 0 < n < 1. The parameter of n is equal to 1 for ideal capacitor and equal to 0 for ideal resistor37. Hence, the equation for the equivalent circuit in Fig. 7(b) can be represented by:
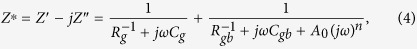 |
where,
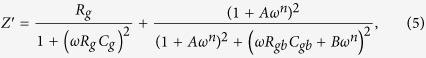 |
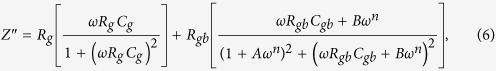 |
in which
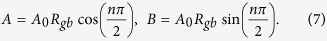 |
Our data were then fitted using software ZSIMPWIN version 2 by assuming the equivalent circuit discussed above. The impedance data below 303 K are not taken into the fitting because it is not a precise way to fit the low temperature data by extrapolating these straight lines to semicircular arcs. The fitted values of n of CPE at temperatures above 303 K are in the range of 0.47–0.63 and increase with increasing temperature. Figure 7(c) shows the fitted dc conductivities for grain σg(σg ∝1/Rg) and grain boundary σgb (σgb∝1/Rgb) plotted against the reciprocal temperature in the Arrhenius format. The fitting results indeed show that σgb is smaller than σg. This should be due to the lower concentration of oxygen vacancies and trapped electrons in grain boundaries during the cooling re-oxidation process37,38. The difference between σgand σgb will lead to the piling up of space charges at the grain boundaries and producing polarization (Maxwell-Wagner effect)16,22,31,32.
Figure 7(c) also shows that both σg and σgb obey the Arrhenius law σ = σ0 exp(EZ/kBT), where σ0 is the prefactor, EZ denotes the activation energy for the response, kB is Boltzman constant, and T is absolute temperature. From the slopes of the fitted straight lines we obtain an activation energy of 0.64 eV for σg and that of 0.66 eV for σgb. The comparable values of the activation energies of σg and σgb indicates that the relaxation and conduction process may be attributed to the same types of entities22.
Electric modulus analysis
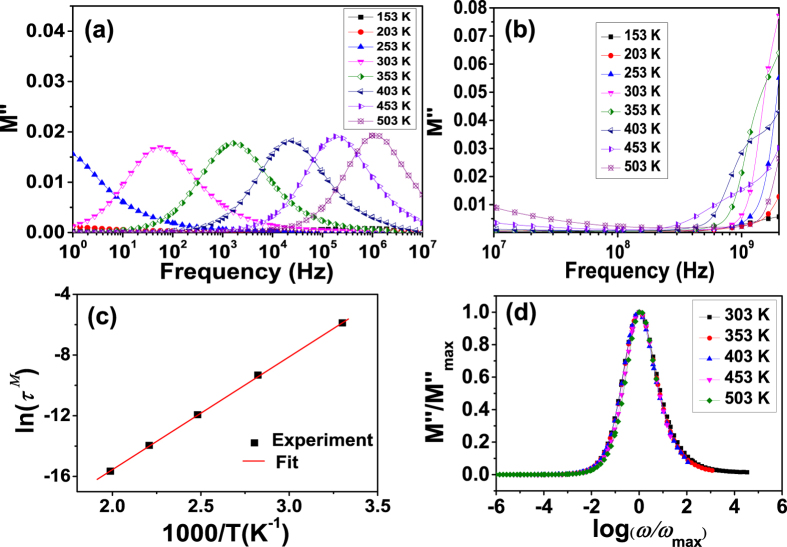
In the previous discussion, the dielectric relaxation has been analyzed in the formalisms of Z*. The modulus representation M* = M′ − iM″is often used together with the impedance formalisms to distinguish the microscopic processes responsible for localized dielectric relaxations and long-range conductions35. Figure 8 shows the frequency dependence of imaginary part (M″) of the modulus M* at different temperatures. Figure 8(a) shows that when the temperature is lower than 253 K, M″ is very small, indicating the freezing of dipoles in grain boundaries at low temperatures. When the temperature is increased above 303 K, a strong loss peak enters in the low frequency region with peak position shifting to higher frequency with increasing temperature. In the M″vs frequency spectra, the frequency region below the loss peak maximum determines the range in which charge carriers are mobile over long distances. At the frequency above peak maximum (high-frequency), the carriers are confined to potential wells, being mobile over short distances. The region where the peak occurs is indicative of the transition from long-range to short-range mobility with increase in frequency. This type of behavior of the modulus spectrum is suggestive of a temperature-dependent hopping type mechanism for electrical conduction (charge transport) in the system. The values of full-width-at-half-maxima calculated from the M″ loss spectra (M″ vs log f) are greater than 1.144 decades, indicating a non-Debye-type relaxation and a distribution of relaxation times34. The mean dielectric relaxation time τM is calculated using the relation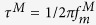 , where
, where 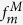 is peak frequency of M″. This relaxation time as a function of temperature is shown in the Fig. 8(c). It can be seen that the relaxation time τM can be well fitted with the Arrhenius relation
is peak frequency of M″. This relaxation time as a function of temperature is shown in the Fig. 8(c). It can be seen that the relaxation time τM can be well fitted with the Arrhenius relation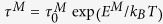 , where
, where 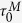 is the pre-exponential factor of the relaxation time. The activation energy EM determined from the slope of the linear fit in the Arrhenius plot is 0.64 eV. It is interesting to note that the activation energy EZ corresponding to Z″ spectra represent the localized conduction (i.e., dielectric relaxation) and that of M″ spectra represent nonlocalized conduction (i.e., long range conductivity)37. The comparable values of the activation energies of EZ and EM indicate that the relaxation and conduction processes may be attributed to the same types of charge carriers. This agree with the previous results in Fig. 7(d). Figure 8(b) shows that when the frequency is higher than 0.5 GHz, M″ increases greatly. This should be due to the resonance-dominated dielectric behavior at high frequencies as shown in Fig. 3. The M″ peaks are expected to appear above 2 GHz.
is the pre-exponential factor of the relaxation time. The activation energy EM determined from the slope of the linear fit in the Arrhenius plot is 0.64 eV. It is interesting to note that the activation energy EZ corresponding to Z″ spectra represent the localized conduction (i.e., dielectric relaxation) and that of M″ spectra represent nonlocalized conduction (i.e., long range conductivity)37. The comparable values of the activation energies of EZ and EM indicate that the relaxation and conduction processes may be attributed to the same types of charge carriers. This agree with the previous results in Fig. 7(d). Figure 8(b) shows that when the frequency is higher than 0.5 GHz, M″ increases greatly. This should be due to the resonance-dominated dielectric behavior at high frequencies as shown in Fig. 3. The M″ peaks are expected to appear above 2 GHz.
Figure 8. Temperature dependent imaginary part modulus M″ spectra (a) below 107 Hz and (b) above 107 Hz, (c) the temperature dependent relaxation times obtained from the peak frequencies of M″spectra above 303 K, (d) scaling behavior of the M″ spectra in plot (a) at temperatures above 303 K.
The above modulus spectra show that there is a distribution of relaxation times for dielectric relaxation at low frequencies. In order to confirm whether the distribution of relaxation time is temperature dependent or not, we plotted the M″ in scaled coordinates, i.e., 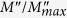 versus log(ω/ωmax), where ωmax the loss peak frequency. As shown in Fig. 8(d), all peaks collapse into one master curve at different temperatures ranging from 303 K up to 503 K. It indicates that the dynamical processes are nearly temperature independent in low frequency region.
versus log(ω/ωmax), where ωmax the loss peak frequency. As shown in Fig. 8(d), all peaks collapse into one master curve at different temperatures ranging from 303 K up to 503 K. It indicates that the dynamical processes are nearly temperature independent in low frequency region.
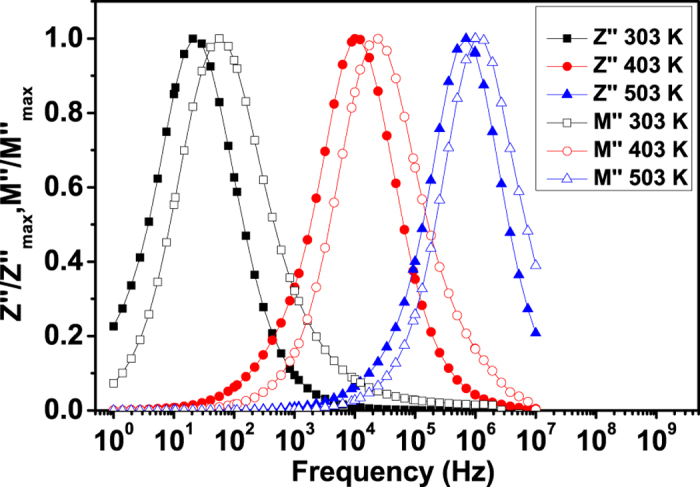
In the previous discussion, the dielectric relaxation has been analyzed in the formalisms of Z* and M* respectively. The combined plot of M* and Z* versus frequency is able to distinguish whether the short-range or long-range movement of charge carriers is dominant in a relaxation process37,38. The separation of peak frequencies between M*and Z* indicates that the relaxation process is dominated by the short-range movement of charge carriers and departs from an ideal Debye-type behavior, while the frequencies coincidence suggests that long range movement of charge carriers is dominant37. The normalized functions of 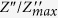 and
and 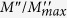 are shown in Fig. 9. The slight mismatch in the peak frequencies suggests a non-Debye-type behavior and coexisting of both long-range and localized relaxation. The mismatch between the Z″ and M″ becomes smaller with an increase in temperature, which indicates that the proportion of long-range charges movements increases with increasing temperature. This agrees with the previous results in Fig. 8 and the increase of both σg and σgb with increasing temperature as shown in Fig. 7. In order to mobilize the localized charge carriers, the aid of lattice oscillation is required. Under these circumstances, electrons are considered not to move by their own but by hopping motion activated by lattice oscillation39. Therefore, the increase of temperature can facilitate the long-range hopping movement of the charge carriers.
are shown in Fig. 9. The slight mismatch in the peak frequencies suggests a non-Debye-type behavior and coexisting of both long-range and localized relaxation. The mismatch between the Z″ and M″ becomes smaller with an increase in temperature, which indicates that the proportion of long-range charges movements increases with increasing temperature. This agrees with the previous results in Fig. 8 and the increase of both σg and σgb with increasing temperature as shown in Fig. 7. In order to mobilize the localized charge carriers, the aid of lattice oscillation is required. Under these circumstances, electrons are considered not to move by their own but by hopping motion activated by lattice oscillation39. Therefore, the increase of temperature can facilitate the long-range hopping movement of the charge carriers.
Figure 9. Normalized imaginary parts of electric modulus 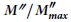 and impedance
and impedance 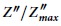 as functions of frequency at different temperatures for SCFO.
as functions of frequency at different temperatures for SCFO.
Discussion
In summary, the dielectric properties of SCFO have been investigated as a function of temperature from 153 to 503 K between 1 and 2 GHz. The dielectric responses of SCFO are found to be frequency dependent and thermal activated. The relaxation-type dielectric behavior is observed to be dominating in the low frequency region and resonance-type dielectric behavior is found to be dominating above 108 Hz. This frequency dependence of dielectric response is explained by the damped harmonic oscillator model with temperature dependent coefficients. The complex impedance plots show that the dielectric response of SCFO originates from both the grain and grain-boundary. The dielectric relaxation time decreases with increasing temperature in low frequency region and increases with increasing temperature above 108 Hz. The imaginary part of impedance (Z″) and modulus (M″) spectra show that there is a distribution of relaxation times. The scaling behaviors of Z″ and M″ spectra further suggest that the distribution of relaxation times is temperature independent at low frequencies. The dielectric loss spectra at different temperatures have not shown a scaling behavior above 108 Hz. A comparison between the Z″ and the M″ spectra indicates there are both short-range and long range motions of charge carriers with short-range motion dominating at low temperatures and long-range motion dominating at high temperatures. The above results indicate that the dielectric dispersion mechanism in SCFO is temperature independent at low frequencies and temperature dependent at high frequencies owing to the domination of resonance behavior.
Methods
Polycrystalline SCFO hexaferrites were prepared with the solid state reaction method and an annealing procedure same as that in the previous work9. The starting high purity (>99.9%) powder Fe2O3, SrCO3, Co3O4 were weighed to prescribed proportion, mixed, ground and then annealed in air at 1000 °C for 16 h. The resulting powder was ground again, pressed into pellet, and then annealed in air at 1200 °C for 16 h (cooling down at a rate of 1 °C/min). Air annealing was used because it has been widely adopted by industry and the reported works to prepare the polycrystalline hexaferrites1,3,9,12,13,14,20,21,22. The phase of SCFO was checked by X-ray diffraction (XRD) on a Rigaku DMax 2000PC XRD diffractometer with Cu-Kа radiation at room temperature. The grain structure of SCFO was measured from the broken interface of the sample with Scanning Electron Microscope (SEM, Hitachi, SU8010). The X-ray photoelectron spectroscopy characterization of SCFO was carried out on the PHI 5000 VersaProbe spectrometer with monochromatic Al Ka radiation. The dielectric properties of SCFO were measured using a NOVOCONTROL high resolution dielectric analyzer (Concept 80) in the temperature range 153–503 K and the frequency range between 1 and 2 G Hz. Silver paint was used on the polished surfaces as electrodes. The complex impedance Z* of the sample was obtained in the usual way, i.e., Z* = V*/I*, where V* and I* are the applied voltage and the resulting current, respectively. The dielectric permittivity ε* and modulus M* spectra were obtained from the impedance spectra by using the relations below:
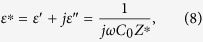 |
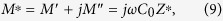 |
where ω is the angular frequency ω = 2πf and 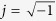 . C0 = ε0S/d is the empty cell capacitance, where S is the sample area and d the sample thickness.
. C0 = ε0S/d is the empty cell capacitance, where S is the sample area and d the sample thickness.
Additional Information
How to cite this article: Tang, R. et al. Dielectric relaxation, resonance and scaling behaviors in Sr3Co2Fe24O41 hexaferrite. Sci. Rep. 5, 13645; doi: 10.1038/srep13645 (2015).
Acknowledgments
The authors thank the discussions with Prof. Yonggang Zhao from Tsinghua University and Dr. Wenlong You from Soochow University. This work was financially supported by the National Natural Science Foundation of China (Grant No. 51202153, 11274237, 51228201, 11004145, and 11174130), the Research Fund for Doctoral Program of Higher Education of MOE of China (Grant No. 20123201120028), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). The work at Texas A&M University is funded by the U.S. National Science Foundation (DMR-1401266)
Footnotes
Author Contributions R.J.T. designed the experiments and wrote the paper; C.J. prepared the sample; C.J., X.Z., W.Q. and J.J. performed the measurements; R.J.T., H.Y.W. and H.Y. analyzed the data. All authors reviewed the manuscript.
References
- Smit J. & Wijn H. P. J. Ferrites. (Phillips Technical Library, 1959). [Google Scholar]
- Kitagawa Y. et al. Low-field magnetoelectric effect at room temperature. Nature Mater. 9, 797–802 (2010). [DOI] [PubMed] [Google Scholar]
- Soda M. et al. Magnetic ordering in relation to the room-temperature magnetoelectric effect of Sr3Co2Fe24O41. Phys. Rev. Lett. 106, 087201 (2011). [DOI] [PubMed] [Google Scholar]
- Kimura T. Magnetoelectric Hexaferrites. Annu. Rev. Condens. Matter. Phys. 3, 93–110 (2012). [Google Scholar]
- Chun S. H. et al. Electric field control of nonvolatile four-state magnetization at room temperature. Phys. Rev. Lett. 108, 177201 (2012). [DOI] [PubMed] [Google Scholar]
- Tokunaga M., Azuma M. & Shimakawa Y. High-field study of strong magnetoelectric coupling in single-domain crystals of BiFeO3. J. Phys. Soc. Jap. 79, 064713 (2010). [Google Scholar]
- Chen Y. et al. Electronic tuning of magnetic permeability in Co2Z hexaferrite toward high frequency electromagnetic device miniaturization. Appl. Phys. Lett. 98, 202502 (2011). [Google Scholar]
- Ebnabbasi K., Vittoria C. & Widom A. Converse magnetoelectric experiments on a room-temperature spirally ordered hexaferrite. Phys. Rev. B 86, 024430 (2012). [Google Scholar]
- Zhang X. et al. Magnetodielectric effect in Z-type hexaferrite. Appl. Phys. Lett. 100, 032901 (2012). [Google Scholar]
- Wu J. T. et al. Synthesis and room temperature four-state memory prototype of Sr3Co2Fe24O41 multiferroics. Appl. Phys. Lett. 101, 122903 (2012). [Google Scholar]
- Wang X. et al. Giant magnetoresistance due to magnetoelectric currents in Sr3Co2Fe24O41 hexaferrites. Appl. Phys. Lett. 105, 112408 (2014). [Google Scholar]
- Bao J. N. et al. Dielectric behavior of Mn-substituted Co2Z hexaferrites. J. Magn. Magn. Mater. 250, 131–137 (2002). [Google Scholar]
- Zhang H. G. et al. Dielectric characteristics of novel Z-type planar hexaferrite with Cu modification. Mater. Lett. 55, 351–355 (2002). [Google Scholar]
- Rashad M. M. et al. Magnetic and dielectric properties of polycrystalline La doped barium Z-type hexaferrite for hyper-frequency applications. J. Mater Sci: Mater. Electron 24, 282–289 (2013). [Google Scholar]
- Kikuchi T. et al. Synthesis of single-phase Sr3Co2Fe24O41 Z-type ferrite by polymerizable complex method. Mater. Res. Bull. 46, 1085–1087 (2011). [Google Scholar]
- Ali I. et al. Effect of Eu–Ni substitution on electrical and dielectric properties of Co–Sr–Y-type hexagonal ferrite. Mater. Res. Bull. 49, 338–344 (2014). [Google Scholar]
- Lee W. K., Liu J. F. & Nowick A. S. Limiting behavior of ac conductivity in ionically conducting crystals and glasses: A new universality. Phys. Rev. Lett. 67, 1559 (1991). [DOI] [PubMed] [Google Scholar]
- Nowick A. S., Vaysleyb A. V. & Kuskovsky I. Universal dielectric response of variously doped CeO2 ionically conducting ceramics. Phys. Rev. B 58, 8398 (1998). [Google Scholar]
- Estalji S. et al. Uncommon nuclear-spin relaxation in fluorozirconate glasses at low temperatures. Phys. Rev. B 43, 7481 (1991). [DOI] [PubMed] [Google Scholar]
- Almeida R. M. et al. Impedance spectroscopy analysis of BaFe12O19 M-type hexaferrite obtained by ceramic method, Ceram. Int. 35, 2443–2447 (2009). [Google Scholar]
- Kamba S. et al. Dielectric, magnetic, and lattice dynamics properties of Y-type hexaferrite Ba0.5Sr1.5Zn2Fe12O22: Comparison of ceramics and single crystals. J. Appl. Phys. 107, 104109 (2010). [Google Scholar]
- Costa M. M. et al. Impedance and modulus studies of magnetic ceramic oxide Ba2Co2Fe12O22 (Co2Y) doped with Bi2O3. J. Appl. Phys. 110, 034107 (2011). [Google Scholar]
- Koops C. On the Dispersion of resistivity and dielectric constant of some semiconductors at audio frequencies. Phys. Rev. 83, 121 (1951). [Google Scholar]
- Maxwell J. Electricity and Magnetism, Vol. 1 (Section 328). (Oxford University Press, London, 1873). [Google Scholar]
- Wagner K. Zur theorie der unvollkommenen dielectrica. Ann. Phys. 40, 817 (1913). [Google Scholar]
- Jonscher A. K. Dielectric Relaxation in Solids. (Chelsea Dielectric Press, London, 1983). [Google Scholar]
- McNeal M. P., Jang, S. J. & Newnham R. E. The effect of grain and particle size on the microwave properties of barium titanate (BaTiO3). J. Appl. Phys. 83, 3288 (1998). [Google Scholar]
- Guerra J., de. Los. S. & Eiras J. A. Mechanical and electrical driving field induced high-frequency dielectric anomalies in ferroelectric systems. J. Phys.: Condens. Matter 19, 386217 (2007). [Google Scholar]
- Hippel A. v. Dielectrics and Waves. (John Wiley & Sons Inc., New York 1959). [Google Scholar]
- Zheng H. et al. Colossal Permittivity and Variable-Range-Hopping Conduction of Polarons in Ni0.5Zn0.5Fe2O4 Ceramic. J. Phys. Chem. C 117, 12966–12972 (2013). [Google Scholar]
- Ali I. et al. Effect of Tb-Mn substitution on DC and AC conductivity of Y-type hexagonal ferrite. J. Alloy. Comp. 579, 576–582 (2013). [Google Scholar]
- Irfan M. et al. Effect of Y2O3 doping on the electrical transport properties of Sr2MnNiFe12O22 Y-type hexaferrite. Curr. Appl. Phys. 14, 112–117 (2014). [Google Scholar]
- Saha S. & Sinha T. P. Low-temperature scaling behavior of BaFe0.5Nb0.5O3. Phys. Rev. B 65, 134103 (2002). [Google Scholar]
- Ortega N. et al. Impedance spectroscopy of multiferroic PbZrxTi1 − xO3/CoFe2O4 layered thin films. Phys. Rev. B 77, 014111 (2008). [Google Scholar]
- Liu J. J. et al. Large dielectric constant and Maxwell-Wagner relaxation in Bi2/3Cu3Ti4O12. Phys. Rev. B 70, 144106 (2004). [Google Scholar]
- Moynihan C. T. Description and analysis of electrical relaxation data for ionically conducting glasses and melts. Solid State Ion. 105, 175 (1998). [Google Scholar]
- Raymond O. et al. Frequency-temperature response of ferroelectromagnetic Pb(Fe12Nb12)O3 ceramics obtained by different precursors. Part II. Impedance spectroscopy characterization. J. Appl. Phys. 97, 084108 (2005). [Google Scholar]
- Ke Q. Q., Lou X. J., Wang Y. & Wang J. Oxygen-vacancy-related relaxation and scaling behaviors of Bi0.9La0.1Fe0.98Mg0.02O3 ferroelectric thin films. Phys. Rev. B 82, 024102 (2010). [Google Scholar]
- Jaćimović J. et al. Pressure dependence of the large-polaron transport in anatase TiO2 single crystals. EPL. 99, 57005(2012). [Google Scholar]