Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Aug 28;5:13581. doi: 10.1038/srep13581

Enhancing Tabletop X-Ray Phase Contrast Imaging with Nano-Fabrication

Houxun Miao 1,*, Andrew A Gomella 1,*, Katherine J Harmon 1, Eric E Bennett 1, Nicholas Chedid 1, Sami Znati 1, Alireza Panna 1, Barbara A Foster 2, Priya Bhandarkar 2, Han Wen 1,a
PMCID: PMC4551996  PMID: 26315891

Abstract

X-ray phase-contrast imaging is a promising approach for improving soft-tissue contrast and lowering radiation dose in biomedical applications. While current tabletop imaging systems adapt to common x-ray tubes and large-area detectors by employing absorptive elements such as absorption gratings or monolithic crystals to filter the beam, we developed nanometric phase gratings which enable tabletop x-ray far-field interferometry with only phase-shifting elements, leading to a substantial enhancement in the performance of phase contrast imaging. In a general sense the method transfers the demands on the spatial coherence of the x-ray source and the detector resolution to the feature size of x-ray phase masks. We demonstrate its capabilities in hard x-ray imaging experiments at a fraction of clinical dose levels and present comparisons with the existing Talbot-Lau interferometer and with conventional digital radiography.

While conventional x-ray images indicate the amount of radiation energy deposited in materials according to the density distribution, phase contrast techniques are sensitive to the variation of the refractive index in the sample similar to the phase contrast mode of a light microscope. Refractive index variations lead to the bending and scattering of the x-ray wavefront which are detected by these techniques without depositing substantial energy in the sample1. Some of the first x-ray phase contrast images were diffraction enhanced images using Bragg analyzer crystals2,3 and free space propagation of spatially coherent beams4,5. At the same time monolithic crystal interferometers6 were extended to obtain high-contrast images of soft tissue samples1. Subsequently, x-ray grating interferometers were proposed and then realized7,8,9,10 for phase contrast imaging. Diffraction of a coherent beam by random phase objects and sharp edges also lead to speckle-based techniques11,12,13.

Common x-ray tubes are the choice for table-top systems, but their low spatial and temporal coherence has required additional filtering by absorptive elements such as single crystals that select a narrow incident angle for a given photon energy2, absorption masks14 or absorption gratings7,10 that improve lateral coherence. Additionally, polychromatic techniques often sense wavefront distortion from micron-scale intensity fringes, which requires high enough resolution on the part of the detector to resolve them. For conventional area detectors with typical resolutions of 50 μm or above this is solved by using an analyzer filter7,10,14. Thus just a fraction of the photon flux reaches the detector.

We show that it is possible to overcome this limitation and at the same time substantially elevate the sensitivity of tabletop systems with phase-shifting elements whose features are comparable in size to the lateral coherence of the x-ray source. The method is a polychromatic far-field interferometer (PFI) consisting of three phase gratings (Fig. 1). A phase grating imprints a periodic phase pattern on the x-ray wavefront. Recent progress in nano-fabrication provided hard x-ray phase gratings with periods down to 200 nm15, which approaches the lateral coherence of x-ray tube sources. Such gratings enabled the method to be realized in a table-top system. We demonstrate its capabilities in imaging experiments of biological specimens and a standard breast-mimicking phantom. We compare its performance with the existing Talbot-Lau interferometer for compact sources and with a state-of-the-art digital mammography scanner. To introduce its physical mechanism we describe a theoretical model with closed-form expressions for the key parameters of the system, which we verify experimentally.

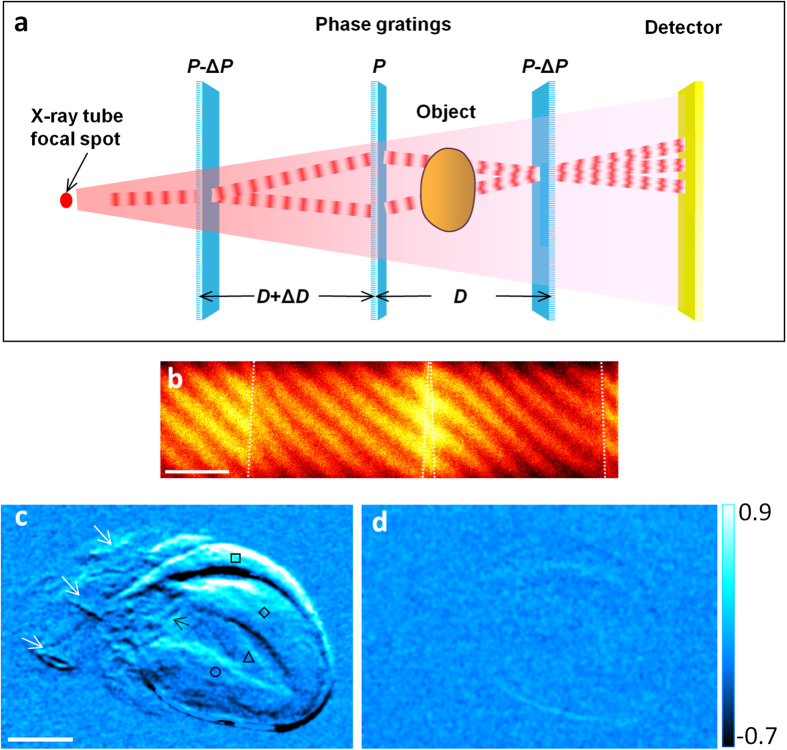
Figure 1. Schematic illustration of the hard x-ray polychromatic far-field interferometer.

Figure 1

Open in a new tab

(a) The imaging system consists of an x-ray tube emitting a polychromatic cone beam, three phase gratings and an area detector. The grating period P of 200 nm is comparable to the lateral coherence length of the x-ray tube at the first grating. A virtual narrow fan beam within the cone beam forms a polychromatic interferometer through grating diffraction as illustrated by the red waves. (b) Interferogram from the entire cone beam. Fringe distortion indicates the refractive index of water-filled Teflon tubes placed in the beam. The borders of the two tube segments are indicated by the dashed lines. The fringe contrast is optimized by adjusting the effective periods of the first and third gratings through tilting (ΔP) and adjusting the difference in the inter-grating spacings (ΔD). Scale bar is 5 mm. (c) A single-projection differential phase image of an unstained mouse heart specimen immersed in water taken with the PFI at 1.08 mGray entrance surface dose. The visible structures are the right ventricular wall (square), the septum (diamond), a papillary muscle column (triangle), the left ventricular wall (circle), the mitral valve (black arrow), and blood vessels (white arrows). Scale bar is 2 mm. (d) Differential phase image from a Talbot-Lau interferometer at 2.16 mGray entrance surface dose. Differential phase image is the phase shift of the interference fringes and proportional to the slope of the x-ray wave front after it undergoes refractive bending through the sample. The color scale unit is radians.

Results

The interferometer consists of three phase gratings arranged along the x-ray beam with approximately equal spacing (Fig. 1a). Their period ratios are approximately 1:1:1 or 2:1:2. The divergent beam from an area source can be viewed as a continuous array of narrow fan beams radiating out from the source. A single fan beam forms a Mach-Zehnder type polychromatic interferometer illustrated in Fig. 1a16. The interferograms from the array of fan beams overlap. By the appropriate tuning of the system they are brought into phase to contribute to a single interferogram (Fig. 1b). The tuning includes a small mismatch ΔD of the spacing D between the gratings and a small difference ΔP among the periods of the three gratings, for instance by tilting the first and third gratings. A sample placed in the x-ray field causes differential phase shifts and variable loss of mutual coherence between the interfering light paths, resulting in visible distortions of the interferogram (Fig. 1b). Theoretical modeling of the interferometer and experimental verification are described in the Methods section.

A key requirement of this method is that the period of the central phase grating be less than 2.5 times the lateral coherence of the source at the first grating. Thus, the demand on the coherence of the source is transferred to the phase gratings. For our hard x-ray imaging system the maximum limit on the grating period was 0.4 μm (source size of 60 μm, source-to-first grating distance of 28 cm, central wavelength of 0.41 Å at 40 kVp of tube voltage). Similarly, the demand on detector resolution is also transferred to the phase grating as the interference fringe period scales with 1/(grating period). In our system with 200 nm period gratings the fringe period of the interferogram was 0.50 mm. The effective periods of the first and third gratings were tuned by tilting at an angle θ, which gave a cosθ factor. For 200 nm gratings a 0.026 radian θ reduced the periods by 0.068 nanometers. The grating material and fabrication are detailed in the reference15 and summarized in the Methods section. The total distance from the source to the detector was 1.73 m. Other system parameters, the imaging protocol and image reconstruction are also described in the Methods section.

The combination of small grating periods and transparency of the optical elements provide sensitive detection of perturbations of the x-ray wavefront at low radiation dose levels. From a set of raw interferograms, an adaptive algorithm is used to retrieve the phase shift of the interference fringes called a differential phase image17 and an image of the de-coherence or scattering of the wavefront18,19,20. The differential phase image is the slope of the phase distribution of the wavefront after it passes through the object, multiplied with an instrumentation factor. It relates to the refraction angle of the x-rays as 2π*(refraction angle)*(sample-to-third-grating distance)/(middle grating period). Figure 1c is an example of a single projection differential phase image of an unstained mouse heart specimen immersed in water, showing the internal anatomy of the heart. When compared to the same image taken with a Talbot-Lau interferometer at twice the radiation dose (entrance surface dose of 1.08 mGray vs. 2.16 mGray) (Fig. 1d), internal anatomical structures become visible owing to an order of magnitude increase in phase contrast. The visible structures include the left and right ventricular walls and the septum, a papillary muscle within the left ventricle, the mitral valve and major blood vessels connected to the heart chambers. The Talbot-Lau grating interferometer is widely used for x-ray tube sources7,10. It employs absorption gratings of micron-sized slits to filter the source and to resolve a dense interferogram. The level of soft tissue contrast we obtained with the Talbot-Lau system in a single projection is consistent with published results, which used 3D tomography at substantially higher doses to visualize soft tissues21,22,23. More information on the experiment that compared the two systems and quantitative results are presented in the Methods section.

In another example, an unstained mouse pup specimen was imaged in sagittal projection view. A phase contrast image combining the integrated phase shift and the linear intensity attenuation is shown in Fig. 2a24,25, with details of the combination described in the Methods section. The phase contrast scan accumulated approximately 1/3 the radiation dose compared with the conventional radiography image (ESD 1.08 mGray vs. 3.08 mGray) (Fig. 2b). In the magnified view of the head region (Fig. 2c), phase contrast showed soft-tissue structures in the brain, the eyes, the nasal cavity and the mouth. The magnified view of the abdomen (Fig. 2d) also revealed detailed structures that are absent in the attenuation contrast image.

Figure 2. Single-projection phase contrast and attenuation contrast images of a mouse pup specimen suspended in a water-filled chamber.

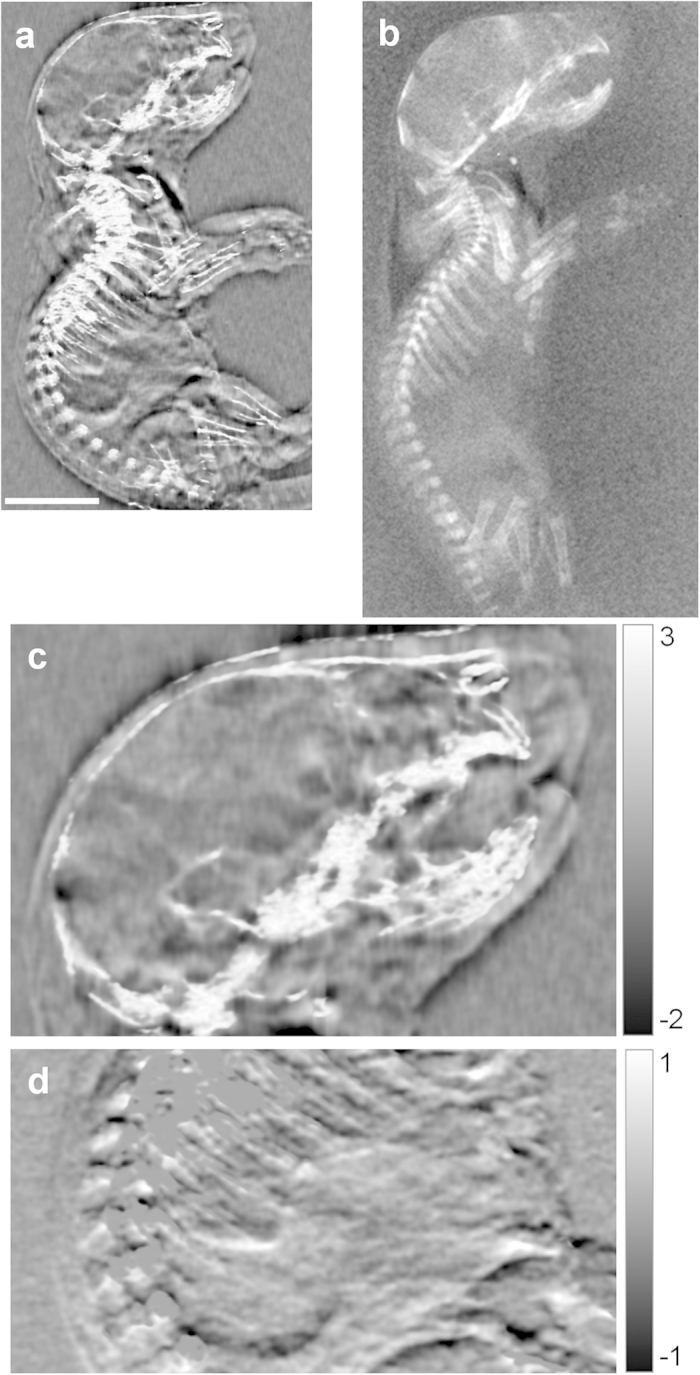
Figure 2

Open in a new tab

(a) Phase contrast image from the PFI at 1.08 mGray entrance surface radiation dose. The phase contrast image is a fused image of the phase shift of the wavefront and the linear intensity attenuation (see Methods section for description). The scale bar is 5.0 mm. (b) Attenuation contrast image from a digital flat panel detector at 3.08 mGray dose. (c) Magnified view of the head in the fused phase contrast image. Grayscale unit is radians. (d) Differential phase data of the abdomen area. Grayscale unit is radians. The highly scattering bones are removed by thresholding the scatter signal.

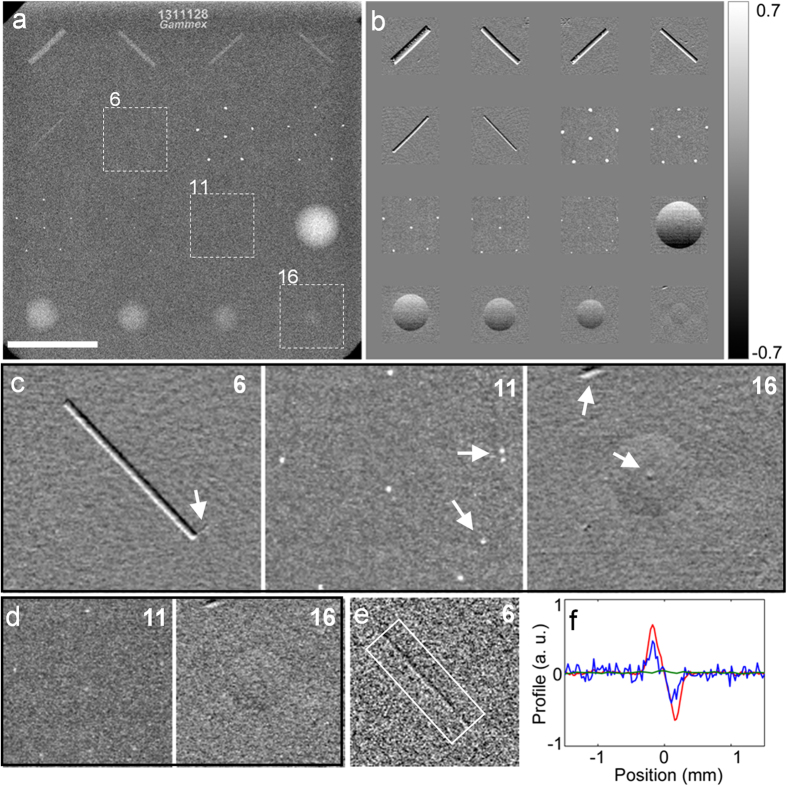
To evaluate the potential benefit for human imaging, we imaged a standard phantom used for quality assurance of mammography scanners (Fig. 3). The phantom has three groups of embedded structures that simulate fibrous tissue, micro calcification and tumor masses in the breast, down to 0.16 mm size. We used a high-performance digital mammography scanner as a reference26. In a standard clinical protocol on the digital mammography scanner, the smallest fiber (0.4 mm diameter, box 6 in Fig. 3a) and mass (circular lens-shaped feature of 0.25 mm thickness, box 16 in Fig. 3a) were at the detection threshold, while the smallest calcification specks (0.16 mm, box 11 in Fig. 3a) could not be detected. In comparison, the PFI resolved all of the smallest features with additional details and manufacturing defects in the phantom at 78% of the radiation dose (Fig. 3b and magnified in Fig. 3c). At 26% dose level it detected the smallest calcification and mass features (Fig. 3d). The calcification specks were visible in the de-coherence image, indicating that they disrupt the lateral coherence of the wavefront. The smallest fiber feature is still visible at 8.1% the dose level (white box in Fig. 3e). The measured noise floor of the differential phase signal inside the phantom corresponded to a 5.7 nano-radian bending of the x-ray wavefront. Figure 3f shows the differential phase profiles across the smallest fiber at 78% (red) and 8.1% (blue) dose levels, and the conventional attenuation profile (green) at full dose.

Figure 3. Comparison of images and radiation doses between the interferometer and a digital mammography scanner.

Figure 3

Open in a new tab

A standard mammographic accreditation phantom was studied. (a) The digital mammography scanner marginally detected the smallest filament (box 6) and mass (box 16) in the phantom but not the smallest calcification specks (box 11). Scale bar is 2.0 cm. (b) A montage of images from the PFI at 78% dose level of the mammography scanner. All features are visible. Grayscale unit is radians. (c) Magnified phase contrast views of the smallest features show additional details and defects indicated by arrows. (d) At 26% dose level the smallest calcification and mass features are visible with the interferometer. (e) The smallest filament seen at 8.1% the dose level. (f) Signal profiles across the smallest filament averaged over its length. The red and blue traces are from the interferometer at 78% and 8.1% of the clinical dose level, respectively. The green trace is from the image of the mammography scanner.

Discussion

Today despite significant progress in developing monochromatic or spatially coherent compact sources27,28,29, the Roentgen vacuum tube is the predominant source in compact imaging systems. In pursuit of better soft tissue detection with x-ray phase contrast techniques we developed an interferometry method using x-ray tube sources and phase gratings only, which also addresses the conflicting demands of detector efficiency versus resolution. The results from the first imaging tests suggest that the interferometer has the potential to detect soft-tissue pathologies at much lower doses than current clinical exams.

Nanometric phase gratings are challenging for current fabrication technology, but the difficulty is tempered by the much shorter path lengths required for phase modulation than intensity modulation. This is due to the fact that in heavy metal elements such as gold, the phase shift of hard x-rays is many times the intensity attenuation. Current gratings have an area of 1.0 mm by 7 cm. Therefore the sample needs to be scanned vertically and the multiple fields of view are stitched together into a full image. As fabrication techniques improve15,30,31, larger area phase masks with better phase profiles can lead to further advances with this method.

Methods

All animal experiments were performed in accordance with relevant guidelines and regulations, under a protocol approved by the Animal Care and Use Committee of the National Heart, Lung and Blood Institute, National Institutes of Health. A fresh heart specimen was excised from a euthanized adult mouse, fixed in 10% buffered formalin and then immersed in de-ionized water in a 15 mm thick chamber for imaging. A mouse pup was euthanized and prepared in the same procedure for imaging.

PFI specifications

The interferometer consisted of a tungsten-anode x-ray tube operating at 40 kVp/1.0 mA (Source-Ray Inc., NY, US), three phase-mask gratings of 1:1:1 or 2:1:2 pitch ratios with the central grating pitch of 200 nm, an x-ray detector consisting of a GdOS phosphor screen and a digital camera with a wide-aperture lens32 (Nikon D800 SLR, Japan). The grating lines were oriented horizontally. To counter focal-spot drift within the x-ray tube during exposure, a 60 μm-wide tungsten aperture was placed on the tube window. The detector matrix was 1237 × 820 with a pixel size of 52 μm. The detector was tilted to increase the resolution in the direction perpendicular to the grating lines. The inter-grating distance was 46 cm. The distance from the source to the first grating was 28 cm and from the third grating to the detector was 53 cm.

The gratings had an area of 1.0 mm by 7 cm, which set the field of view of a single image. The sample was scanned vertically in 0.6 mm steps and the multiple fields of view were stitched together into full images. The gratings were all rotated about the vertical axis by 60° to increase their effective depths to approximately 7 μm for sufficient phase modulation of the x-ray wave.

The tuning of the system involved adjusting the tilt of the first and third gratings by up to 1° to change their effective periods and adjusting the longitudinal position of the third grating in the range of a few millimeters, which was about 1% of the inter-grating spacing. The interference fringe contrast, defined as ΔIN = (Imax − Imin)/Iaverage, was optimized in this process. The measured and theoretically calculated peak fringe contrasts were 0.281 ± 0.003 and 0.290, respectively. Theoretical modeling predicts a fringe contrast of 0.73 with optimized phase profiles of the gratings. This serves as a guide for grating fabrication development.

Theoretical model of the PFI and experimental verification

Following the physics model described in the main text we developed a theoretical model called the sum-of-coherent-paths model. Referring to Fig. 1a, A closed-form expression of the interference fringe contrast for a system of central grating period P is

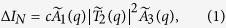graphic file with name srep13581-m1.jpg

where c is a known normalization factor, “∼” represents Fourier transformation, q is the Fourier space variable of 2π/P, Tj is the complex transmission function of the jth grating, and Aj is the shifted auto-product of the jth grating (Ãj being the conjugate of the Wigner distribution)

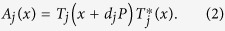graphic file with name srep13581-m2.jpg

The normalized shifts dj of the auto-products are determined by the asymmetry in the interferometer, including the deviation ΔP of the grating periods and the difference ΔD in inter-grating spacings. On the detector, the interference fringe spacing in the direction perpendicular to the grating lines is given by

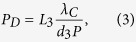graphic file with name srep13581-m3.jpg

where L3 is the distance between the third grating and the detector and λC is the central wavelength of the x-ray spectrum. In accord with the reciprocal symmetry of electromagnetic wave propagation, the phase of the interferogram at a given location on the detector has a cyclic dependence on the vertical location of the source, with the period of the cycle being

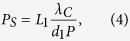graphic file with name srep13581-m4.jpg

where L1 is the distance between the source and the first grating. Therefore, for an extended source of size S, the grating period should meet the requirement PS > 2S, leading to an upper limit of the grating period

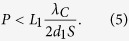graphic file with name srep13581-m5.jpg

The interference fringe contrast ΔIN was calculated for the hardware specifications of our system. The calculated ΔIN versus ΔD curves for two tilt angles of the first and third gratings were plotted in supplementary information Fig. 1 together with measured values. They were in good agreement. The calculated interferogram fringe spacing perpendicular to the grating lines was 0.51 mm at the condition of peak fringe contrast, which matched the measured spacing of 0.50 ± 0.03 mm. The maximum allowed grating period from equation (5) was 0.4 μm for our system, which is greater than the actual grating pitch of 0.2 μm.

Fabrication of hard x-ray phase gratings

The fabrication protocol is described in detail in a previous publication15. To briefly summarize, electron beam lithography was used to pattern a master template (Eulitha AG, Switzerland) for nano-imprint lithography on a silicon wafer, from which trenches were etched down to approximately 4 μm via cryogenic reactive ion etching. A conformal layer of platinum was deposited via atomic layer deposition (ALD) followed by conformal electroplating of gold to fill the trenches. Scanning electron micrographs of the cross section of a 200 nm-pitch grating before and after electroplating are shown in supplementary information Fig. 2. In this first iteration the grating area was limited by the length of the electron beam lithography step to 1.0 mm width and 7 cm length. The silicon substrate of each grating was backside-thinned to 170 to 200 μm thickness. Taking into account the 60° rotation of the gratings about the vertical axis, the x-ray path length through the substrate was between 340 and 400 μm.

X-ray phase-contrast imaging procedure

In the PFI, phase contrast information at each detector pixel was measured by the phase stepping process9,33. The third grating was stepped in increments of 60 nm. A phase stepping data set included 4 to 12 images of 5 to 20 second exposures, depending on the total radiation dose level. The reported doses are the sum of all exposures. All dose values were measured with an x-ray exposure meter (Rad-Check Plus, Fluke Biomedical, Cleveland, OH). The mouse heart and mouse pup specimens were imaged with a total entrance surface dose (ESD) of 1.08 mGray. The mammographic phantom was the American College of Radiology mammographic accreditation phantom model 156. It was imaged at ESDs of 2.16 to 0.23 mGray, and corresponding average glandular dose (AGD) of 0.96 to 0.10 mGray. The number of images and the exposure time per image were optimized for each dose level. The factors that influenced the choices included mechanical fluctuations in the phase stepping process favoring more images in a phase stepping set to reduce the random chance of under-sampling (degenerate sampling) of the intensity oscillation curve; mechanical drift during long exposures that degraded the interference fringes; the detector dark noise (x-ray off) which was exposure time dependent. For the PFI, 5 images of 5 second exposure each was found to be optimal at the lowest dose level, while 12 images at 20 second exposure to be optimal at the highest dose level. For the Talbot-Lau interferometer, 19 images of 4 second exposure each was found to be optimal at the ESD of 2.16 mGray, while less images of longer exposures did not improve the SNR of the result.

An adaptive image processing method was used to deal with mechanical instability in the interferometer25,34. It provided images of differential phase, de-coherence and conventional intensity attenuation. The differential phase and the attenuation images were sometimes combined into a phase contrast image. If we define A0 and Φ as the linear attenuation and the phase shift of the x-ray wavefront after propagation through the sample, A0 is then the absolute value of the natural logarithm of the transmission, and 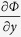Inline graphic is the differential phase (DP) measurement with the appropriate multiplier, where Y is the direction perpendicular to the grating lines. The first step is to incorporate the derivative of the linear attenuation 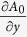Inline graphic into the DP measurement in a weighted sum of 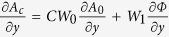Inline graphic, where C is the scaling factor between the real and imaginary parts of the refractive index, and the weights W0 and W1 are determined locally according to the amplitude of the interference fringes A1 and the noise level N1 in the fringe amplitudes. Once the combined differential image 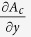Inline graphicis determined, it is integrated in the Y direction to retrieve a phase shift image which represents the phase distribution of the wavefront in units of radians. Since the initial differential phase measurement from the interferometer is a derivative measurement and lacks low spatial frequency information, the integration process generates smooth varying baseline noise in the Y direction. To counter this problem a high-pass filter in the Y direction is applied.

Comparison of the PFI with the existing Talbot-Lau interferometer

A Talbot-Lau interferometer was built with the same x-ray source as the PFI. Its source filter and detector analyzer filters were gold absorption gratings of 4.8 μm pitch and 60 μm nominal depths (Microworks GmbH, Germany). The middle phase grating was a silicon π/2 phase-shift grating of 2.4 μm pitch. All gratings were rotated by 30° about the vertical axis for an optimal fringe contrast of 0.40 at 40 kVp. The inter-grating spacing was 39 cm (the third-order Talbot distance for 28 keV). The PaxScan digital flat panel detector was used for image capture. The total length of the system was 1.02 m. A phase stepping set included 19 images of 4-second-exposure each. For quantitative comparison, we measured the differential phase signal in the mammographic phantom with both systems at the same ESD of 2.16 mGray. Images of the largest fiber feature and signal profiles are shown in supplementary information Fig. 3. The level of phase contrast increased by a factor of 15 from the Talbot-Lau system to the PFI. A more detailed description of our Talbot-Lau interferometer and comparison with attenuation radiography is presented in the reference35.

Attenuation contrast radiography

Attenuation contrast radiography of the mammographic phantom was performed with a digital mammography scanner (GE Senographe Essential model). The scanner operated in a standard clinical protocol, at 29 kVp tube voltage and 56 mA*sec in a Rh target/Rh filter configuration, at ESD/AGD of 4.98/1.23 mGray. Its digital flat panel detector has a pixel size of 100 μm. Attenuation contrast radiography of the mouse samples were carried out with a tungsten anode x-ray tube operating at 40 kVp/1.0 mA and a digital flat panel detector (Varian PaxScan 3024M) of 83 μm pixel size. All specimen chambers were placed directly on the surface of the detector to minimize scattering-induced blurring. The ESD was 3.08 mGray.

Additional Information

How to cite this article: Miao, H. et al. Enhancing Tabletop X-Ray Phase Contrast Imaging with Nano-Fabrication. Sci. Rep. 5, 13581; doi: 10.1038/srep13581 (2015).

Supplementary Material

Supplementary Information
srep13581-s1.pdf (666KB, pdf)

Acknowledgments

Micro fabrication was performed at the Nanofab Facility of the Center for Nano Science and Technology, National Institute of Standard and Technology. We are indebted to Dr. Leah Zadrozny for specimen preparation, to Mr. Gary Melvin and Dr. Dumitru Mazilu for mechanical design and machining, to Dr. Mark Rivers, Department of Geophysical Sciences and Center for Advanced Radiation Sources, University of Chicago, for his help with the instrument control software.

Footnotes

Author Contributions H.M., A.A.G., N.C. and S.Z. fabricated the diffraction gratings. A.A.G., E.E.B., H.M., H.W., K.J.H. and A.P. constructed the imaging systems. H.M., K.J.H., A.A.G., B.A.F., P.B. and H.W. performed the experiments. H.W. and H.M. wrote the manuscript with input from all authors. H.W. organized the study and did the theoretical calculation.

References

  1. Momose A. & Fukuda A. Phase-contrast radiographs of nonstained rat cerebellar specimen. Med Phys 22(4), 375 (1995). [DOI] [PubMed] [Google Scholar]
  2. Davis T. J., Gao D., Gureyev T. E., Stevenson A. W. & Wilkins S. W. Phase-contrast imaging of weakly absorbing materials using hard x-rays. Nature 373(6515), 595 (1995). [Google Scholar]
  3. Chapman D. et al. Diffraction enhanced x-ray imaging. Phys Med Biol 42(11), 2015 (1997). [DOI] [PubMed] [Google Scholar]
  4. Snigirev A., Snigireva I., Kohn V., Kuznetsov S. & Schelokov I. On the possibilities of x-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev Sci Instrum 66(12), 5486 (1995). [Google Scholar]
  5. Wilkins S. W., Gureyev T. E., Gao D., Pogany A. & Stevenson A. W. Phase-contrast imaging using polychromatic hard X-rays. Nature 384(6607), 335 (1996). [Google Scholar]
  6. Bonse U. & Hart M. An X-Ray Interferometer. Appl Phys Lett 6(8), 155 (1965). [Google Scholar]
  7. Clauser J. F. inventor; Clauser, JF, assignee. Ultrahigh resolution interferometric x-ray imaging. United States patent US 5,812,629. 1998 Sept 22.
  8. David C., Nohammer B., Solak H. H. & Ziegler E. Differential x-ray phase contrast imaging using a shearing interferometer. Appl Phys Lett 81(17), 3287 (2002). [Google Scholar]
  9. Momose A. et al. Demonstration of X-Ray Talbot interferometry. Jpn J Appl Phys 2 42(7B), L866–L868 (2003). [Google Scholar]
  10. Pfeiffer F., Weitkamp T., Bunk O. & David C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat Phys 2(4), 258 (2006). [Google Scholar]
  11. Morgan K. S., Paganin D. M. & Siu K. K. X-ray phase imaging with a paper analyzer. Appl Phys Lett 100(12), 124102 (2012). [Google Scholar]
  12. Berujon S., Wang H. C. & Sawhney K. X-ray multimodal imaging using a random-phase object. Phys Rev A 86(6), 063813 (2012). [Google Scholar]
  13. Zanette I. et al. Speckle-Based X-Ray Phase-Contrast and Dark-Field Imaging with a Laboratory Source. Phys Rev Lett 112(25), 25390 (2014). [DOI] [PubMed] [Google Scholar]
  14. Olivo A. & Speller R. A coded-aperture technique allowing x-ray phase contrast imaging with conventional sources. Appl Phys Lett 91(7), 074106 (2007). [Google Scholar]
  15. Miao H., Gomella A. A., Chedid N., Chen L. & Wen H. Fabrication of 200 nm Period Hard X-ray Phase Gratings. Nano Lett 14(6), 3453 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Wen H. et al. Subnanoradian X-ray phase-contrast imaging using a far-field interferometer of nanometric phase gratings. Nat Commun 4, 2659 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Shack R. V. & Platt B. C. Production and Use of A Lenticular Hartmann Screen. J Opt Soc Am 61(5), 656 (1971). [Google Scholar]
  18. Wen H., Bennett E. E., Hegedus M. M. & Carroll S. C. Spatial harmonic imaging of x-ray scattering - initial results. IEEE Trans Med Imaging 27(8), 997 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Pfeiffer F. et al. Hard-X-ray dark-field imaging using a grating interferometer. Nat Mater 7(2), 134 (2008). [DOI] [PubMed] [Google Scholar]
  20. Yashiro W., Terui Y., Kawabata K. & Momose A. On the origin of visibility contrast in x-ray Talbot interferometry. Opt Express 18(16), 16890 (2010). [DOI] [PubMed] [Google Scholar]
  21. Bech M. et al. Soft-tissue phase-contrast tomography with an x-ray tube source. Phys Med Biol 54(9), 2747 (2009). [DOI] [PubMed] [Google Scholar]
  22. Tapfer A. et al. Three-dimensional imaging of whole mouse models: comparing nondestructive X-ray phase-contrast micro-CT with cryotome-based planar epi-illumination imaging. Journal of Microscopy 253(1), 24 (2014). [DOI] [PubMed] [Google Scholar]
  23. Hoshino M., Uesugi K. & Yagi N. Phase-contrast x-ray microtomography of mouse fetus. Biology Open 1, 269 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Roessl E. et al. Image fusion algorithm for differential phase contrast imaging. Proceedings of SPIE 8313, 831354–6 (2012). [Google Scholar]
  25. Miao H. et al. Motionless phase stepping in X-ray phase contrast imaging with a compact source. P Natl Acad Sci USA 110(48), 19268 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Yaffe M. J. et al. Comparative performance of modern digital mammography systems in a large breast screening program. Med Phys 40(12), 121915 (2013). [DOI] [PubMed] [Google Scholar]
  27. Albert F. et al. Laser wakefield accelerator based light sources: potential applications and requirements. Plasma Physics and Controlled Fusion 56(8), 084015 (2014). [Google Scholar]
  28. Larsson D. H. et al. First application of liquid-metal-jet sources for small-animal imaging: High-resolution CT and phase-contrast tumor demarcation. Med Phys 40(2), 021909 (2013). [DOI] [PubMed] [Google Scholar]
  29. Ruth R. D. & Huang Z. inventors; The Board Of Trustees of the Leland Stanford Junior University, assignee. Compton backscattered collimated x-ray source. United States patent US 5,825,847 A. 1998 Oct 20.
  30. Lynch S. K. et al. Fabrication of 200 nm period centimeter area hard x-ray absorption gratings by multilayer deposition. J Micromech Microeng 22(10), 105007 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Chang C. & Sakdinawat A. Ultra-high aspect ratio high-resolution nanofabrication for hard X-ray diffractive optics. Nat Commun 5, 4243 (2014). [DOI] [PubMed] [Google Scholar]
  32. Panna A. et al. Performance of low-cost X-ray area detectors with consumer digital cameras. Journal of Instrumentation 10(05), T05005 (2015). [Google Scholar]
  33. Bruning J. H. et al. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Appl Opt 13(11), 2693 (1974). [DOI] [PubMed] [Google Scholar]
  34. Wen H., Miao H., Bennett E. E., Adamo N. M. & Chen L. Flexible retrospective phase stepping in x-ray scatter correction and phase contrast imaging using structured illumination. Plos One 8(10), e78276 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Harmon K. J. et al. Motionless electromagnetic phase stepping versus mechanical phase stepping in X-ray phase-contrast imaging with a compact source. Phys Med Biol 60(8), 3031 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep13581-s1.pdf (666KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES