Abstract
Quantum entanglement provides an essential resource for quantum computation, quantum communication, and quantum network. How to conveniently and efficiently produce entanglement between bright light beams presents a challenging task to build realistic quantum information processing networks. Here, we present an efficient and convenient way to realize a novel quantum phenomenon, named electromagnetically induced entanglement, in the conventional Λ-type three-level atomic system driven by a strong pump field and a relatively weak probe field. Nearly perfect entanglement between the two fields can be achieved with a low coherence decay rate between the two lower levels, high pump-field intensity, and large optical depth of the atomic ensemble. The physical origin is quantum coherence between the lower doublet produced by the pump and probe fields, similar to the well-known electromagnetically induced transparency. This method would greatly facilitate the generation of nondegenerate narrow-band continuous-variable entanglement between bright light beams by using only coherent laser fields, and may find potential and broad applications in realistic quantum information processing.
The strong interactions between material media and laser fields may lead to many special effects, such as coherent population trapping (CPT)1,2,3, electromagnetically induced transparency (EIT)4,5,6,7, rapid adiabatic population transfer8,9,10,11, enhancement of nonlinear optical processes12,13,14, and quantum correlation and entanglement15,16,17,18,19,20,21,22,23,24. The common physical mechanism underlying these peculiar effects is the laser-induced quantum coherence established in the media. Though the above-mentioned effects have been extensively examined in the Λ- or multi-Λ-type atomic systems driven by two or more laser fields, where at least one of the fields is generally treated classically, only a few studies have been performed on the quantum correlated properties of the pump and probe fields in the simplest and widely-employed Λ-type three-level atomic system25,26,27,28,29. The phase and amplitude correlations between the two laser fields in the Λ-type three-level atomic system have been investigated in refs. 25, 26, 27; it was pointed out by Nussenzveig et al.28,29 that there exist intrinsic quantum correlation and entanglement between the pump and probe fields in this simple EIT scheme. However, in refs. 28,29, they used the interaction between two fields and atoms in a ring cavity to approximately simulate the interaction of atoms with two propagating fields.
In this study, we directly consider the interaction of an ensemble of atoms with the propagating pump and probe fields on the basis of Heisenberg-Langevin equations, and demonstrate the novel effect, named electromagnetically induced entanglement (EIE), in the Λ-type three-level atomic system. It is shown that, in the traditional EIT regime, nearly perfectly correlated and entangled pump and probe fields can be achieved at high pump-field intensity, high optical depth of the atomic medium, and a relatively low coherence decay rate between the two lower levels (as compared to the spontaneous decay rate of the excited state). This method provides an efficient and convenient way to generate bright nondegenerate narrow-band entangled fields by using only coherent light fields, which may hold great promise for practical applications in quantum communication and quantum networks.
Results
Mechanism of excitations
The considered Λ-type three-level atomic system driven by a strong pump field (Ec) and a relatively weak probe field (Ep), as shown in Fig. 1a, is based on the D1 transitions in 85Rb atom used in the experiment30. Levels  ,
,  , and
, and  correspond, respectively, to the ground-state hyperfine levels 5S1/2 (F = 2), 5S1/2 (F = 3) and the excited state 5P1/2 in D1 line of 85Rb atom. The coherent probe field with frequency ωp and pump field with frequency ωc couple transitions
correspond, respectively, to the ground-state hyperfine levels 5S1/2 (F = 2), 5S1/2 (F = 3) and the excited state 5P1/2 in D1 line of 85Rb atom. The coherent probe field with frequency ωp and pump field with frequency ωc couple transitions  to
to  and
and  to
to  with the frequency detunings given by Δ1 = ωp − ω31 and Δ2 = ωc − ω32, respectively, where ωij (i ≠ j) is the atomic resonant frequency between levels i and j. We denote γ1 and γ2 as the population decay rates from level 3 to levels 1 and 2, respectively, and γ12 as the dephasing rate between levels 1 and 2 due to atomic collisions and/or finite interaction time between atoms and light fields. In what follows, we take into account the quantum features of both the pump and probe fields by using the Heisenberg-Langevin method, and show how EIE in this Λ-type three-level atomic system can be established via the atomic coherence between the lower doublet created by the two fields.
with the frequency detunings given by Δ1 = ωp − ω31 and Δ2 = ωc − ω32, respectively, where ωij (i ≠ j) is the atomic resonant frequency between levels i and j. We denote γ1 and γ2 as the population decay rates from level 3 to levels 1 and 2, respectively, and γ12 as the dephasing rate between levels 1 and 2 due to atomic collisions and/or finite interaction time between atoms and light fields. In what follows, we take into account the quantum features of both the pump and probe fields by using the Heisenberg-Langevin method, and show how EIE in this Λ-type three-level atomic system can be established via the atomic coherence between the lower doublet created by the two fields.
Figure 1.

(a) The Λ-type three-level system of the D1 transitions in 85Rb atom coupled by a strong pump field (Ec) and a relatively weak probe field (Ep). (b) The equivalent configuration of (a) for the light-atom interaction resulting in EIT and EIE.
The quantum operators of the probe and pump fields are denoted as a1(z, t) and a2(z, t), and the collective atomic operators as σij(z, t) (i, j = 1, 2, and 3), respectively. The interaction Hamiltonian in the rotating-wave approximation has the form25,31,32
 |
where  is the atom-field coupling constant with μ13(23) being the dipole moment for the 1–3 (2–3) transition and
is the atom-field coupling constant with μ13(23) being the dipole moment for the 1–3 (2–3) transition and  being the electric field of a single probe (pump) photon; ε0 is the free space permittivity and V is the interaction volume with length L and beam radius r; and N is the total number of atoms in the interaction volume. The Heisenberg-Langevin equations for describing the evolutions of the atomic operators can be written as
being the electric field of a single probe (pump) photon; ε0 is the free space permittivity and V is the interaction volume with length L and beam radius r; and N is the total number of atoms in the interaction volume. The Heisenberg-Langevin equations for describing the evolutions of the atomic operators can be written as
 |
 |
 |
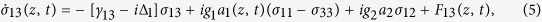 |
 |
where  , and Fij(z, t) are the collective atomic δ-correlated Langevin noise operators. The noise correlation functions for the noise operators Fij(z, t) can be expressed as
, and Fij(z, t) are the collective atomic δ-correlated Langevin noise operators. The noise correlation functions for the noise operators Fij(z, t) can be expressed as  , where
, where  is the Langevin diffusion coefficient and can be calculated by using the generalized dissipation-fluctuation theorem25. Under the assumption that the uniformly-distributed pencil-shaped atomic sample is optically thin in the transverse direction, the evolutions of the annihilation operators a1 and a2 can be described by the coupled propagation equations,
is the Langevin diffusion coefficient and can be calculated by using the generalized dissipation-fluctuation theorem25. Under the assumption that the uniformly-distributed pencil-shaped atomic sample is optically thin in the transverse direction, the evolutions of the annihilation operators a1 and a2 can be described by the coupled propagation equations,
 |
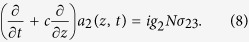 |
We use the similar analysis as in ref. 33 by writing each atomic or field operator as the sum of its mean value and a quantum fluctuation term (i.e.,  and
and  ) to treat the interaction between the atoms and the fields. We assume that
) to treat the interaction between the atoms and the fields. We assume that  and
and  (corresponding to the Rabi frequency of the pump field in semiclassical treatment) is much larger than
(corresponding to the Rabi frequency of the pump field in semiclassical treatment) is much larger than  (i.e., in the EIT regime), so the depletions of the pump and probe fields can be safely neglected. Under these conditions, the steady-state mean values of the atomic operators can be obtained by setting the time derivatives equal to zero and neglecting the noise operators. To get the quantum fluctuations of the atomic operators, we substitute the mean values of the atomic and field operators into the Fourier-transformed Heisenberg-Langevin equations for the quantum fluctuations of the atomic operators. By substituting δσ13(z, ω) and δσ23(z, ω) and their Hermitian conjugates into the Fourier-transformed coupled propagation equations of Eqs. (7) and (8) and their conjugates, the quantum fluctuations of the output field operators
(i.e., in the EIT regime), so the depletions of the pump and probe fields can be safely neglected. Under these conditions, the steady-state mean values of the atomic operators can be obtained by setting the time derivatives equal to zero and neglecting the noise operators. To get the quantum fluctuations of the atomic operators, we substitute the mean values of the atomic and field operators into the Fourier-transformed Heisenberg-Langevin equations for the quantum fluctuations of the atomic operators. By substituting δσ13(z, ω) and δσ23(z, ω) and their Hermitian conjugates into the Fourier-transformed coupled propagation equations of Eqs. (7) and (8) and their conjugates, the quantum fluctuations of the output field operators 
 and
and 
 with respect to the Fourier frequency ω can be attained, which are linear combinations of the quantum fluctuations of the input field operators
with respect to the Fourier frequency ω can be attained, which are linear combinations of the quantum fluctuations of the input field operators  (
( ) and
) and  (
( ) and Langevin noise terms. To test the entanglement feature between the output pump and probe fields, we use the entanglement criterion
) and Langevin noise terms. To test the entanglement feature between the output pump and probe fields, we use the entanglement criterion  , as proposed in ref. 34, where
, as proposed in ref. 34, where  and
and  with
with  and
and  being the amplitude and phase quadrature fluctuation components of the quantum field operator ai. Satisfying the above inequality is a sufficient demonstration for the generation of bipartite entanglement, and the smaller the correlation V12 is, the stronger the degree of the bipartite entanglement becomes. We assume the probe and pump fields to be initially in the coherent states
being the amplitude and phase quadrature fluctuation components of the quantum field operator ai. Satisfying the above inequality is a sufficient demonstration for the generation of bipartite entanglement, and the smaller the correlation V12 is, the stronger the degree of the bipartite entanglement becomes. We assume the probe and pump fields to be initially in the coherent states  and
and  , so the mean values of the field amplitudes are equal to
, so the mean values of the field amplitudes are equal to  and
and  , respectively. In the following, the relevant parameters are scaled with m and MHz, or m−1 and MHz−1, and set according to the realistic experimental conditions used in ref. 30 with the atomic density n = 1 × 1019, r = 2 × 10−4, L = 0.06, and γ1 = γ2 = 3.
, respectively. In the following, the relevant parameters are scaled with m and MHz, or m−1 and MHz−1, and set according to the realistic experimental conditions used in ref. 30 with the atomic density n = 1 × 1019, r = 2 × 10−4, L = 0.06, and γ1 = γ2 = 3.
Electromagnetically induced entanglement
Figure 2a gives the main result of this study, where the evolution of the correlation V12 at zero Fourier frequency as a function of the pump-field intensity  is depicted. Obviously, when the intensity of the pump field is very weak, V12 is much larger than 4, so no entanglement exists between the probe and pump fields. With the increase of pump field intensity, V12 decreases rapidly and becomes less than 4, which sufficiently demonstrates the generation of genuine bipartite entanglement between the two fields. When the pump field intensity is strong enough so that
is depicted. Obviously, when the intensity of the pump field is very weak, V12 is much larger than 4, so no entanglement exists between the probe and pump fields. With the increase of pump field intensity, V12 decreases rapidly and becomes less than 4, which sufficiently demonstrates the generation of genuine bipartite entanglement between the two fields. When the pump field intensity is strong enough so that  , V12 becomes nearly equal to zero, which indicates that perfectly quantum-correlated and entangled probe and pump fields can be obtained. For comparison, the absorption coefficient α of the probe field at zero Fourier frequency (
, V12 becomes nearly equal to zero, which indicates that perfectly quantum-correlated and entangled probe and pump fields can be obtained. For comparison, the absorption coefficient α of the probe field at zero Fourier frequency ( with
with  being the imaginary part of
being the imaginary part of  ) as a function of the pump field intensity is shown in Fig. 2b. It is clear that EIT is exhibited with the increase of pump field intensity. Note that in the above calculations, in order to keep the mean values of atomic operators and the intensity absorption rates of the pump and probe fields nearly stable so as to compare the degrees of entanglement under different pump field intensities, according to the results in ref. 25, the ratios of α2/α1, γ12/α2, and n/α2 should be kept fixed under the conditions of
) as a function of the pump field intensity is shown in Fig. 2b. It is clear that EIT is exhibited with the increase of pump field intensity. Note that in the above calculations, in order to keep the mean values of atomic operators and the intensity absorption rates of the pump and probe fields nearly stable so as to compare the degrees of entanglement under different pump field intensities, according to the results in ref. 25, the ratios of α2/α1, γ12/α2, and n/α2 should be kept fixed under the conditions of  and
and  , and in our calculations we set the α1 = α2/20, n =n0α1 and
, and in our calculations we set the α1 = α2/20, n =n0α1 and 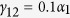 .
.
Figure 2.

(a) The evolution of the correlation V12 at zero Fourier frequency as a function of the pump field intensity  with
with  , L = 0.06,
, L = 0.06,  ,
,  ,
,  ,
,  , and
, and  in corresponding units of m and MHz, or m−1 and MHz−1. (b) The corresponding absorption coefficient α of the probe field exhibiting EIT.
in corresponding units of m and MHz, or m−1 and MHz−1. (b) The corresponding absorption coefficient α of the probe field exhibiting EIT.
The optical depth of the atomic ensemble plays a key role in the generation of entanglement, as seen from the dependence of the correlation V12 at zero Fourier frequency on the atomic density n shown in Fig. 3. Clearly, V12, with the initial value of 4, decreases rapidly with the increase of the atomic density, indicating the established bipartite entanglement between the pump and probe fields. When n0 is about larger than 7 × 1018/m3, V12 becomes nearly zero, and the two fields get perfectly entangled. Similar evolution of V12 with respect to the interaction length L is also observed. This indicates that the coherent pump and probe beams evolve from initially uncorrelated into nearly perfectly entangled beams as they propagate through the dense atomic medium, accompanying the building up of the atomic coherence between the two lower levels 1 and 2. The requirement of using large optical depth has also been extensively examined for generating entanglement between the Stokes and anti-Stokes fields in the double- and multiple-Λ-type atomic systems15,16,17,18,19,20,21,22,23,24.
Figure 3. The dependence of the correlation V12 at zero Fourier frequency on the atomic density n with α2 = 20α1 = 20, γ12 = 0.1, and the other parameters are the same as those in Fig. 2.

The physical mechanism underlying EIE resides in the quantum coherence established between the two lower levels, similar to EIT. This can be seen clearly from Eqs. (2, 3, 4, 5, 6, 7, 8). Due to the atomic coherence σ12 self-produced by the pump and probe fields, the quantum fluctuation of each output field operator comes from a linear combination of the input field operators  ,
,  ,
,  , and
, and 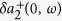 , as well as the Langevin noise terms; therefore, the fluctuations of the pump and probe fields are coupled together and subsequent correlation and entanglement between the two fields can be established as they propagate through the atomic medium. If there were no atomic coherence σ12, there wouldn’t be mutual coupling between the probe and pump fields, and therefore no entanglement would be established between the two fields.
, as well as the Langevin noise terms; therefore, the fluctuations of the pump and probe fields are coupled together and subsequent correlation and entanglement between the two fields can be established as they propagate through the atomic medium. If there were no atomic coherence σ12, there wouldn’t be mutual coupling between the probe and pump fields, and therefore no entanglement would be established between the two fields.
The generated bipartite entanglement between the probe and pump fields can also be well understood in terms of the quantum interference between two  –
– transition pathways as shown in Fig. 1b, which is the physical origin of EIT as well. One pathway for the
transition pathways as shown in Fig. 1b, which is the physical origin of EIT as well. One pathway for the  –
– transition is induced by absorbing one probe photon, and another one is induced by absorbing one probe photon and one pump photon and emitting one pump photon. The destructive quantum interference between these two
transition is induced by absorbing one probe photon, and another one is induced by absorbing one probe photon and one pump photon and emitting one pump photon. The destructive quantum interference between these two  –
– transition pathways results in EIT4,5,6,7. As a matter of fact, the second pathway for the
transition pathways results in EIT4,5,6,7. As a matter of fact, the second pathway for the  –
– transition can be regarded as the result of absorbing one photon from the four-wave-mixing (FWM) field produced by the pump and probe fields; consequently, the interaction between the two
transition can be regarded as the result of absorbing one photon from the four-wave-mixing (FWM) field produced by the pump and probe fields; consequently, the interaction between the two  –
– transition processes can be equivalently thought to be a closed-loop light-atom interaction of a FWM process. As the photon of the FWM field is identical to the probe field and every generated FWM photon is always accompanied by the depletion of one probe photon and one pump photon, as well as the generation of one pump photon, after this closed-loop light-atom interaction, there are no net losses of energy from both the pump and probe fields, and subsequently both EIT and EIE can be attained in the system. In fact, FWM has already been identified as an efficient process to produce entanglement, and the generations of entangled Stokes and anti-Stokes photons by using FWM processes have been extensively studied in the double- and multi-Λ-type atomic systems15,16,17,18,19,20,21,22,23,24. As the pump field intensity and the optical depth of the atomic ensemble are increased, the FWM process is strengthened, and therefore the degree of entanglement between the pump and probe fields would be greatly enhanced.
transition processes can be equivalently thought to be a closed-loop light-atom interaction of a FWM process. As the photon of the FWM field is identical to the probe field and every generated FWM photon is always accompanied by the depletion of one probe photon and one pump photon, as well as the generation of one pump photon, after this closed-loop light-atom interaction, there are no net losses of energy from both the pump and probe fields, and subsequently both EIT and EIE can be attained in the system. In fact, FWM has already been identified as an efficient process to produce entanglement, and the generations of entangled Stokes and anti-Stokes photons by using FWM processes have been extensively studied in the double- and multi-Λ-type atomic systems15,16,17,18,19,20,21,22,23,24. As the pump field intensity and the optical depth of the atomic ensemble are increased, the FWM process is strengthened, and therefore the degree of entanglement between the pump and probe fields would be greatly enhanced.
As is well known, EIT critically depends on the dephasing rate γ12 between the two lower levels, and would deteriorate with the increase of γ12. This is not the case for EIE under the realistic experimental conditions of  and
and  . Figure 4 displays the dependence of the correlation V12 at zero Fourier frequency on γ12. It can be seen that when there is no dephasing between the two lower levels, V equals 4, and no entanglement would exist between the pump and probe fields. With the increase of γ12, the bipartite entanglement is strengthened dramatically, and nearly perfect entangled pump-probe fields can be achieved. This is due to the fact that when the dephasing γ12 equals zero, not only
. Figure 4 displays the dependence of the correlation V12 at zero Fourier frequency on γ12. It can be seen that when there is no dephasing between the two lower levels, V equals 4, and no entanglement would exist between the pump and probe fields. With the increase of γ12, the bipartite entanglement is strengthened dramatically, and nearly perfect entangled pump-probe fields can be achieved. This is due to the fact that when the dephasing γ12 equals zero, not only  but also
but also  and
and  will become zero, that is, the atoms will always stay in the dark state and the medium is completely transparent to both the pump and probe fields, so no entanglement can be established between the two fields. Under conditions of
will become zero, that is, the atoms will always stay in the dark state and the medium is completely transparent to both the pump and probe fields, so no entanglement can be established between the two fields. Under conditions of 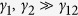 ,
,  and
and  , as
, as  and
and  increase linearly with γ1225, so the probability to leave the dark state will increase with increasing γ12 and the bipartite entanglement would be strengthened. However, when the dephasing rate γ12 becomes comparable to or larger than the decay rate γ1(γ2) of the excited state, the dissipation process becomes dominant, and the entanglement would be weakened and eventually disappear (Note that when the dephasing rate γ12 becomes relatively large, the approximation of neglecting the depletions of the pump and probe fields would break down). Similar behavior has been observed for generating pump-probe intensity correlation27 and nonclassical (e.g., squeezed) states of light35 with respect to the dephasing rate γ12 in the Λ-type CPT configuration.
increase linearly with γ1225, so the probability to leave the dark state will increase with increasing γ12 and the bipartite entanglement would be strengthened. However, when the dephasing rate γ12 becomes comparable to or larger than the decay rate γ1(γ2) of the excited state, the dissipation process becomes dominant, and the entanglement would be weakened and eventually disappear (Note that when the dephasing rate γ12 becomes relatively large, the approximation of neglecting the depletions of the pump and probe fields would break down). Similar behavior has been observed for generating pump-probe intensity correlation27 and nonclassical (e.g., squeezed) states of light35 with respect to the dephasing rate γ12 in the Λ-type CPT configuration.
Figure 4. The dependence of the correlation V12 at zero Fourier frequency on the dephasing rate γ12 with n = 1 × 1019, α2 = 20α1 = 20, and the other parameters are the same as those in Fig. 2.

Discussion
It is interesting to emphasize that entanglement between two weak light fields (even in the single-photon level) has been predicted in a coherently-prepared atomic medium by using two relatively strong driving laser fields with nearly equal intensity36, where the two driving fields for creating the atomic coherence are generally treated classically. However, here we show that the two laser fields for pre-establishing atomic coherence in EIT regime are intrinsically entangled themselves under certain conditions. The present result, together with our previous one22,23,24, clearly indicate that arbitrary number of entangled fields including the strong pump and probe fields traditionally-treated classically for preparing atomic coherence can be achieved via multiple FWM processes in the multi-Λ-type atomic systems.
In conclusion, we have demonstrated electromagnetically induced entanglement in the conventional Λ-type three-level atomic system driven by a strong pump field and a relatively weak probe field, which also holds for the ladder- or V-type three-level system. Moreover, this scenario is quite general and may be applied to other systems, such as in solid-state media. The underlying physical mechanism is the quantum coherence between the two lower levels self-produced by the pump and probe fields, similar to the well-known electromagnetically induced transparency. This technique provides a convenient and efficient way to generate nondegenerate narrow-band continuous-variable entanglement between two bright light beams with only coherent laser fields, which may bring great facility in realistic quantum information processing protocols.
Additional Information
How to cite this article: Yang, X. and Xiao, M. Electromagnetically Induced Entanglement. Sci. Rep. 5, 13609; doi: 10.1038/srep13609 (2015).
Acknowledgments
This work is supported by NBRPC (No. 2012CB921804), National Natural Science Foundation of China (Nos. 11274225 and 11321063), Key Basic Research Program of Shanghai Municipal Science and Technology Commission (No. 14JC1402100), and Shanghai Natural Science Foundation (14ZR1415400).
Footnotes
Author Contributions X.Y. and M.X. conceived the idea for this project. X.Y. performed the calculations and prepared figs 1–4. X.Y. and M.X. wrote the main manuscript text. All authors reviewed the manuscript.
References
- Alzetta G., Gozzini A., Moi L. & Orriols G. An experimental method for the observation of RF transition and laser beam resonances in oriented Na vapor. Nuovo Cimento B 36, 5–20 (1976). [Google Scholar]
- Gray H. R., Whitley R. M. & Stroud C. R. Jr. Coherent trapping of atomic populations. Opt. Lett. 3, 218–220 (1978). [DOI] [PubMed] [Google Scholar]
- Arimondo E. Coherent population trapping in laser spectroscopy. Prog. Opt. 35, 257–354 (1996). [Google Scholar]
- Boller K. J., Imamoglu A. & Harris S. E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66, 2593–2596 (1991). [DOI] [PubMed] [Google Scholar]
- Xiao M., Li Y. Q., Jin S. Z. & Gea-Banacloche J. Measurement of dispersive properties of electromagnetically induced transparency in rubidium atoms. Phys. Rev. Lett. 74, 666–669 (1995). [DOI] [PubMed] [Google Scholar]
- Harris S. E. Electromagnetically induced transparency. Phys. Today 50, 36–42 (1997). [Google Scholar]
- Fleischhauer M., Imamoglu A. & Marangos J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005). [Google Scholar]
- Bergmann K., Theuer H. & Shore B. W., Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003–1025 (1998). [Google Scholar]
- Vitanov N. V., Halfmann T., Shore B. W. & Bergmann K. Laser induced population transfer by adiabatic passage techniques. Annu. Rev. Phys. Chem. 52, 763–809 (2001). [DOI] [PubMed] [Google Scholar]
- Vitanov N. V., Fleischhauer M., Shore B. W. & Bergmann K. Coherent manipulation of atoms and molecules by sequential laser pulses. Adv. At. Mol. Opt. Phys. 46, 55–190 (2001). [Google Scholar]
- Kral P., Thanopulos I. & Shapiro M. Colloquium: Coherently controlled adiabatic passage. Rev. Mod. Phys. 79, 53–77 (2007). [Google Scholar]
- Jain M., Xia H., Yin G. Y., Merriam A. J. & Harris S. E. Efficient nonlinear frequency conversion with maximal atomic coherence. Phys. Rev. Lett. 77, 4326–4329 (1996). [DOI] [PubMed] [Google Scholar]
- Li Y. Q. & Xiao M. Enhancement of Non-Degenerate Four-Wave Mixing Using Electromagnetically Induced Transparency in Rubidium Atoms. Opt. Lett. 21, 1064–1066 (1996). [DOI] [PubMed] [Google Scholar]
- Lu B. L., Burkett W. H. & Xiao M. Nondegenerate Four-Wave Mixing in a Double-L System under the Influence of Coherent Population Trapping. Opt. Lett. 23, 804–806 (1998). [DOI] [PubMed] [Google Scholar]
- Duan L. M., Lukin M. D., Cirac J. I. & Zoller P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001). [DOI] [PubMed] [Google Scholar]
- van der Wal C. H., Eisaman M. D., André A., Walsworth R. L., Phillips D. F., Zibrov A. S. & Lukin M. D. Atomic memory for correlated photon states. Science 301, 196–200 (2003). [DOI] [PubMed] [Google Scholar]
- Kuzmich A., Bowen W. P., Boozer A. D., Boca A., Chou C. W., Duan L. M. & Kimble H. J. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003). [DOI] [PubMed] [Google Scholar]
- Lukin M. D., Hemmer P. R. & Scully M. O. Resonant nonlinear optics in phase-coherent media. Adv. At. Mol. Opt. Phys. 42, 347–386 (2000). [Google Scholar]
- Balic V., Braje D. A., Kolchin P., Yin G. Y. & Harris S. E. Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 94, 183601 (2005). [DOI] [PubMed] [Google Scholar]
- Boyer V., Marino A. M., Pooser R. C. & Lett P. D. Entangled images from four-wave mixing. Science 321, 544–547 (2008). [DOI] [PubMed] [Google Scholar]
- Marino A. M., Pooser R. C., Boyer V. & Lett P. D. Tunable delay of Einstein-Podolsky-Rosen entanglement. Nature 457, 859–862 (2009). [DOI] [PubMed] [Google Scholar]
- Yang X. H., Zhou Y. Y. & Xiao M. Generation of multipartite continuous- variable entanglement via atomic spin wave. Phys. Rev. A 85, 052307 (2012). [DOI] [PubMed] [Google Scholar]
- Yang X. H., Zhou Y. Y. & Xiao M. Entangler via electromagnetically induced transparency with an atomic ensemble. Sci. Rep. 3, 3479 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X. H., Xue B. L., Zhang J. X. & Zhu S. Y. A universal quantum information processor for scalable quantum communication and networks. Sci. Rep. 4, 6629 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleischhauer M. Correlation of high-frequency phase fluctuations in electromagnetically induced transparency. Phys. Rev. Lett. 72, 989–992 (1994). [DOI] [PubMed] [Google Scholar]
- Fleischhauer M. & Richter T. Pulse matching and correlation of phase fluctuations in Λ systems. Phys. Rev. A 51, 2430–2442 (1995). [DOI] [PubMed] [Google Scholar]
- Barberis-Blostein P. & Zagury N. Field correlations in electromagnetically induced transparency. Phys. Rev. A 70, 053827 (2004). [Google Scholar]
- Garrido-Alzar C. L., Cruz L. S., Aguirre Gómez J. G., França Santos M. & Nussenzveig P. Super-Poissonian intensity fluctuations and correlations between pump and probe fields in Electromagnetically Induced Transparency. Europhys. Lett. 61, 485–491 (2003). [Google Scholar]
- Garrido-Alzar C. L., Franca Santos M. & Nussenzveig P. Entanglement between two macroscopic fields by coherent atom-mediated exchange of photons. arXiv: quant-ph/0205119 (2002). [Google Scholar]
- Yang X. H., Sheng J. T., Khadka U. & Xiao M. Generation of correlated and anticorrelated multiple fields via atomic spin coherence. Phys. Rev. A 85, 013824 (2012). [Google Scholar]
- Kolchin P. Electromagnetically-induced-transparency-based paired photon generation. Phys. Rev. A 75, 033814 (2007). [Google Scholar]
- Glorieux Q., Dubessy R., Guibal S., Guidoni L., Likforman J. P., Coudreau T. & Arimondo E. Double-Λ microscopic model for entangled light generation by four-wave mixing. Phys. Rev. A 82, 033819 (2010). [Google Scholar]
- Davidovich L. Sub-Poissonian processes in quantum optics. Rev. Mod. Phys. 68, 127–173 (1996). [Google Scholar]
- Duan L. M., Giedke G., Cirac J. I. & Zoller P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000). [DOI] [PubMed] [Google Scholar]
- de Oliveira F. A. M., Dalton B. J. & Knight P. L. Squeezing and trapping in three-level atoms. J. Opt. Soc. Am. B 4, 1558 (1987). [Google Scholar]
- Lukin M. D. & Imamoglu A. Nonlinear Optics and Quantum Entanglement of Ultraslow Single Photons. Phys. Rev. Lett. 84, 1419–1422 (2000). [DOI] [PubMed] [Google Scholar]


