Abstract
Nonlamellar lipid membranes are frequently induced by proteins that fuse, bend, and cut membranes. Understanding the mechanism of action of these proteins requires the elucidation of the membrane morphologies that they induce. While hexagonal phases and lamellar phases are readily identified by their characteristic solid-state NMR lineshapes, bicontinuous lipid cubic phases are more difficult to discern, since the static NMR spectra of cubic-phase lipids consist of an isotropic 31P or 2H peak, indistinguishable from the spectra of isotropic membrane morphologies such as micelles and small vesicles. To date, small-angle X-ray scattering is the only method to identify bicontinuous lipid cubic phases. To explore unique NMR signatures of lipid cubic phases, we first describe the orientation distribution of lipid molecules in cubic phases and simulate the static 31P chemical shift lineshapes of oriented cubic-phase membranes in the limit of slow lateral diffusion. We then show that 31P T2 relaxation times differ significantly between isotropic micelles and cubic-phase membranes: the latter exhibit two-orders-of magnitude shorter T2 relaxation times. These differences are explained by the different timescales of lipid lateral diffusion on the cubic-phase surface versus the timescales of micelle tumbling. Using this relaxation NMR approach, we investigated a DOPE membrane containing the transmembrane domain (TMD) of a viral fusion protein. The static 31P spectrum of DOPE shows an isotropic peak, whose T2 relaxation times correspond to that of a cubic phase. Thus, the viral fusion protein TMD induces negative Gaussian curvature, which is an intrinsic characteristic of cubic phases, to the DOPE membrane. This curvature induction has important implications to the mechanism of virus-cell fusion. This study establishes a simple NMR diagnostic probe of lipid cubic phases, which is expected to be useful for studying many protein-induced membrane remodeling phenomena in biology.
Keywords: membrane curvature, detergent micelles, chemical shift anisotropy, T2 relaxation, motional correlation times
Introduction
Nonlamellar lipid membranes with high curvature are generated during many protein-mediated biological processes such as virus-cell fusion, virus budding, endocytosis, and pore formation by lytic and antimicrobial peptides1–5. Characterizing the type of membrane curvatures is important for understanding the mechanism of action of these proteins. Because lipid membranes are inherently non-crystalline and dynamic, solid-state NMR (SSNMR) spectroscopy is a natural technique for their characterization.
Liquid-crystalline phases formed by surfactants and lipids have been well studied by a variety of techniques (see, e.g. ref.6). The lamellar phase and the hexagonal phases give rise to characteristic static 31P NMR spectral lineshapes that allow these phases to be identified readily. However, among nonlamellar membrane morphologies, several types give rise to an isotropic peak in the static NMR spectra. These morphologies include micelles, small unilamellar vesicles, and cubic phases7–8. Bicontinuous lipid cubic phases have received increasing attention in recent years because of the importance of this class of topological structures for membrane fusion, membrane scission, virus budding and pore formation. Bicontinuous cubic phases are periodic repeats of minimal surfaces on which every point has negative Gaussian curvature and zero mean curvature9–11. The Gaussian curvature is the product of two principal curvatures at a point, while the mean curvature is the average. Thus, every point on the surface of bicontinuous cubic phases has equal magnitudes of positive and negative principal curvatures. Based on crystallographic space groups and symmetries, three bicontinuous lipid cubic phases can be distinguished: Pn3m (also called double diamond or D surface), Ia3d (gyroid or G surface) and Im3m (primitive or P surface)12–13. A lipid bilayer drapes onto the minimal surface, the two sides of which lie a continuous region of water. Bicontinuous cubic phases separate water into two non-intersecting channels. For the Im3m (P), Pn3m (D), and Ia3d (G) phases, water channels meet at 6-way (90°), 4-way (109.5°), and 3-way (120°) junctions, respectively (Fig. 1).
Figure 1.
Geometries of three common bicontinuous cubic phases and the calculated quasi-static 31P NMR lineshape for an oriented cubic-phase membrane. Red and green colors denote the two surfaces of the bilayer. (a) The primitive Im3m phase. (b) The double diamond Pn3m phase. For clarity, an extended view containing 8 unit cells are shown on the right at a different angle. (c) The gyroid Ia3d phase. Due to symmetry, a saddle area is shown in grey in (a) and (c) to indicate the minimum surface used for calculating the 31P NMR lineshape. (d) Simulated 31P CSA lineshape of the three cubic phases, assuming an oriented cubic-phase membrane whose z-axis of the unit cell is parallel to the magnetic field. All three cubic phases give the same spectrum.
Bicontinuous lipid cubic phases commonly exhibit unit-cell dimensions of 10–20 nm, which are not much larger than the dimensions of micelles. Thus, lipid lateral diffusion on cubic-phase surfaces causes fast molecular reorientation. Due to the symmetry of these phases, this fast reorientation averages second-rank nuclear-spin interaction tensors to their isotropic values7. Thus, although bicontinuous cubic phases are structurally non-isotropic, their static solid-state NMR spectra exhibit an “isotropic” peak, indistinguishable from the spectra of truly isotropic membrane morphologies such as micelles and small vesicles. Here the term “isotropic peak” refers to a peak at the isotropic NMR frequency, while “isotropic” morphologies refer to the three-dimensional structures of micelles and small vesicles.
Although isotropic phases and cubic phases cannot be distinguished by static NMR lineshapes, they may be resolved by NMR relaxation times. In contrast to NMR lineshapes, whose averaging depends only on the lower bound of motional rates, relaxation times are sensitive to motions on a range of timescales. In lipid membranes, many molecular motions exist to drive nuclear-spin relaxation. These include segmental torsional motions, whole-body uniaxial rotational diffusion around the long molecular axis, wobble of the molecular axis in a cone, tumbling of vesicles or micelles, and lipid lateral diffusion on the membrane surface14–15. The torsional motions, uniaxial rotation and wobble typically occur on the picosecond to nanosecond timescales for hydrated membranes16–17. Tumbling of nanometer-sized vesicles and micelles occurs on the microsecond timescale. Lateral diffusion depends on the radius of curvature and the diffusion coefficient. For nanometer-sized vesicles or micelles, lateral diffusion occurs on the tens of microsecond timescale, whereas for ~100 nm or larger vesicles, lateral diffusion occurs on the millisecond timescale. Thus, tumbling and lateral diffusion are much slower than torsional motions and rotational diffusion.
While a large body of literature exists on using 31P, 2H, 13C, and 14N relaxation NMR to investigate lipid motions in lamellar membranes (see, e.g. ref.18–19), the application of relaxation NMR for studying nonlamellar membrane morphologies is more scarce. 2H and 14N relaxation NMR has been used to study surfactant motions in various liquid-crystalline phases20–22. 13C T2 relaxation has been used to measure lateral diffusion coefficients of lipids in sonicated and extruded small vesicles23. 31P and 2H relaxation NMR has been used to compare the curvatures of hexagonal and lamellar phases24 and motions in spherical supported vesicles versus multilamellar vesicles25. Halle and coworkers presented a theory of nuclear-spin relaxation in bicontinuous cubic-phase liquid crystals that suggested the possibility of extracting time correlation functions for different cubic phases26. However, to our knowledge, no experimental demonstration of relaxation NMR for distinguishing cubic phases from isotropic phases has been reported.
In this work, we show that 31P T2 relaxation times readily distinguish lipid isotropic phases and bicontinuous cubic phases. We use LMPC as a representative micelle and monoolein/POPC as a representative cubic-phase membrane. From their 31P T1 and T2 relaxation times, we extract correlation times of fast and slow motions, and compare them between the micelle and the cubic-phase samples. Based on these model-compound data, we investigate the 31P relaxation times of a DOPE membrane containing the transmembrane domain (TMD) of a viral fusion protein. This viral fusion TMD causes an isotropic 31P peak to the DOPE membrane. We show that the 31P T2 relaxation times of this TMD-bound DOPE membrane are diagnostic of a cubic phase, which has significant implications to the mechanism of virus-cell fusion. We also examine the temperature dependences of the 31P relaxation times for all three membranes to obtain activation energies of fast and slow motions. In addition, we provide a mathematical description of the orientation distribution of lipids in cubic phases and show that, in the limit of slow lateral diffusion, an oriented cubic-phase membrane has unique NMR lineshapes.
Materials and Methods
Membrane sample preparation
Three membrane samples were prepared: 1-myristoyl-2-hydroxy-sn-glycero-3-phosphocholine (LMPC), 1-monoolein (MO)/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) (17: 3), and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) membrane containing the TMD of the parainfluenza virus 5 (PIV5) F protein. The peptide : lipid molar ratio of the TMD/DOPE sample is 1 : 15. LMPC was dissolved in water to a concentration of 400 mM and transferred into a 4 mm magic-angle-spinning (MAS) rotor. MO and POPC were codissolved in chloroform, while the PIV5 TMD and DOPE were dissolved in TFE and chloroform, respectively. The organic solvents were removed by nitrogen gas and the mixtures were lyophilized. The dry powders were suspended in 4 mL pH 7.5 HEPES buffer (10 mM HEPES-NaOH, 1 mM EDTA, and 1 mM NaN3). The MO/POPC mixture was incubated at 4°C overnight, while the TMD/DOPE mixture was dialyzed against 1 L buffer for one day. The samples were centrifuged at 4°C and 55,000 rpm for 3 hours to obtain membrane pellets, which were equilibrated to ~55% hydration for MO/POPC and ~30% for TMD/DOPE before transfer into MAS rotors.
Solid-state NMR experiments
Static 31P NMR experiments were carried out on a Bruker DSX-400 MHz (9.4 T) spectrometer operating at Larmor frequencies of 400.49 MHz for 1H and 162.12 MHz for 31P. 31P T2 relaxation times were measured between 273 K and 295 K using a Hahn echo sequence (90° - τ – 180° - τ) under 30 kHz 1H decoupling and echo delays (τ) of 50 µs - 30 ms. To extract T2 values, echo intensities as a function of 2τ were fit to a single-exponential function A·e−2τ/T2, where A is close to 1. 31P T1 relaxation times were measured using the inversion recovery sequence (180° - τ − 90°). The intensities was fit to a single-exponential function B·(1 − C·e−τ/T1), where B = 1 and C = 2 in the ideal case but are slightly adjustable in the fitting.
Results
Anisotropic NMR lineshapes of cubic-phase membranes
In static solid-state NMR spectra, cubic-phase membranes exhibit a narrow peak at the isotropic frequency because of fast lateral diffusion over the highly curved surface of the membrane. This isotropic spectrum is identical to that of micelles and small vesicles, even though the molecular orientational distribution in the cubic phase is non-isotropic. To elucidate this orientation distribution, we simulate the quasi-static 31P NMR lineshapes of oriented cubic-phase membranes in the absence of lateral diffusion. If the cubic phases are randomly oriented, then the NMR lineshape reverts to the powder lineshape of unoriented bilayers.
In liquid-crystalline lipid membranes, the three principal values of the rigid-limit 31P chemical shielding tensor, σxx, σyy and σzz, are averaged by the uniaxial rotation of the phospholipids to two components, σ‖ and σ⊥, where σ‖ is the component parallel to the uniaxial rotational axis, which is the local bilayer normal, while σ⊥ is the component perpendicular to it. The asymmetry parameter of the chemical shielding tensor, η ≡ (σyy − σxx)/(σzz − σiso), is averaged to 0, η̅ = 0, while the averaged anisotropy parameter, , is ~30 ppm for most phospholipids.
The angle β between the magnetic field B0 and the local bilayer normal gives the orientation-dependent 31P chemical shift frequency:
| (1) |
where ωiso is the trace of the chemical shift tensor. The Euler rotations that relate the laboratory frame to the bilayer frame are most conveniently considered through a coordinate system fixed to the cubic-phase crystal frame. When B0 is coincident with the z-axis of this crystal frame (Fig. 1a–c), β is simply the polar angle of the local bilayer normal in the crystal frame. Thus, based on the distribution of β on the cubic-phase surface, we can calculate the 31P spectral lineshape. The lineshapes of other B0 orientations relative to the crystal frame can be similarly calculated, as we show in the Supporting Information.
We constructed the geometries of the three bicontinuous cubic phases (Fig. 1a–c) following the mathematical protocols of Klinowski27–29 and Finch30–31. Detailed equations are given in the Supporting Information. For symmetry reasons, only 1/8 of the unit cells of the primitive (Im3m) and gyroid (Ia3d) surfaces need to be sampled to obtain the lineshapes of the full unit cell (Fig. S1–S3). The CSA spectrum for B0 along the z-axis of the unit cell is a superposition of an isotropic peak with an η̅ = 0 powder lineshape, and is identical for the three cubic phases (Fig. 1d). Thus, the cubic-phase spectrum differs from the lamellar bilayer spectrum at the isotropic frequency. Since this isotropic frequency corresponds to bilayer normals that are oriented at the magic angle, 54.7°, from the magnetic field, to show the high population of this magic-angle orientation, we plot the β distribution for the three cubic phases (Fig. 2). Indeed, the surface area at 54.7° and 125.3° dominates that of any other angles, and the distribution function can be approximated by the sum of sinβ and additional intensity at the magic angle. The CSA lineshape when B0 points along the x- and y-axes of the crystal frame is identical with Fig. 1d (simulation not shown), but other B0 orientations have distinct lineshapes, some of which are given in the Supporting Information (Fig. S4).
Figure 2.
Distribution of the angle β between the bilayer normal and the z-axis of the cubic-phase unit cell. (a) One saddle of the primitive surface Im3m. (b) One unit of the double diamond surface Pn3m. (c) One saddle of the gyroid surface Ia3d. Green, magenta and blue areas denote β angles of 90°, 0° or 180°, and 54.7° or 125.3°, respectively. (d) Normalized surface area as a function of the β angle. The smallest surface areas occur at β = 0° and 180°, while β = 54.7° and 125.3° exhibit the largest surface area.
While these simulated static 31P CSA lineshapes are interesting, in practice it is challenging to suppress lipid lateral diffusion and produce oriented cubic-phase membranes. Thus, we next explore 31P relaxation NMR to identify cubic phases under the realistic situation of random orientation and in the presence of fast lateral diffusion.
31P relaxation times of micelles versus cubic-phase membranes
The static 31P spectra of LMPC, MO/POPC, and TMD/DOPE membranes are shown in Fig. 3a. All three samples exhibit a single 31P isotropic peak at ambient temperature. The full widths at half maximum, Δ*, are ~90 Hz for LMPC and MO/POPC and increase to ~485 Hz for DOPE. In contrast, the 31P T2 relaxation decays of the three membranes, plotted on a logarithmic timescale (Fig. 3b), show a two-orders-of-magnitude difference among the three samples: the LMPC micelle has T2 values of more than 100 ms between 275 and 295 K, while the TMD/DOPE membrane shows 31P T2’s of 0.3–1.3 ms (Table 1). POPC in the cubic-phase MO/POPC membrane has intermediate T2’s of several milliseconds. All three samples exhibit increasing T2 with temperature. These T2 values translate to homogeneous linewidths, Δ' ≡ 1/πT2, of 1.5 Hz for LMPC, 30 Hz for MO/POPC, and 245 Hz for TMD/DOPE at ambient temperature. Simulated Lorentzian lineshapes for these homogeneous linewidths are shown in Fig. 3a to compare with the observed apparent linewidths. It can be seen that although the LMPC sample has the narrowest apparent linewidth, it is more inhomogeneously broadened (i.e. large Δ*/Δ’) than MO/POPC and TMD/DOPE, suggesting that the micelles have a large distribution of sizes, while the TMD/DOPE spectrum is the most homogeneously broadened.
Figure 3.
31P T2 relaxation times of LMPC, MO/POPC, and TMD-bound DOPE membranes. (a) Static 31P spectra of the three samples at 295 K. The measured spectra with apparent linewidths Δ* are shown in black whereas simulated Lorentzian lineshapes with homogeneous linewidths Δ’ based on the 31P T2 are shown in red. (b) 31P spin-echo intensities as a function of echo delay from 273 K to 303 K. LMPC micelles have 31P T2 values of 104 – 207 ms, MO/POPC shows T2’s of 3.7 – 10.7 ms, while the TMD/DOPE sample shows the shortest 31P T2 values of 0.38 – 1.3 ms.
Table 1.
31P T2 relaxation times (ms) of LMPC, MO/POPC and TMD/DOPE membranes.
| Membrane | 273 K | 278 K | 285 K | 290 K | 295 K |
|---|---|---|---|---|---|
| LMPC | 104 ± 4 | 117 ± 7 | 150 ± 18 | 207 ± 11 | |
| MO/POPC | 3.7 ± 0.5 | 6.1 ± 0.2 | 8.2 ± 0.6 | 10.7 ± 0.5 | |
| TMD/DOPE | 0.38 ± 0.02 | 0.50 ± 0.03 | 0.77 ± 0.04 | 1.3 ± 0.05 |
Compared to T2, 31P T1 relaxation times are more uniform among the three samples, about 1 s at ambient temperature (Table 2 and Fig. 4). However, LMPC and MO/POPC show decreasing T1 with decreasing temperature while TMD/DOPE manifests the opposite trend. Thus, the nanosecond motions in the TMD/DOPE membrane occur on the slow side of the T1 minimum while those in the MO/POPC and LMPC membranes occur on the fast side (see below).
Table 2.
31P T1 relaxation times (s) of LMPC, MO/POPC and TMD/DOPE membranes.
| Membrane | 273 K | 278 K | 285 K | 290 K | 295 K |
|---|---|---|---|---|---|
| LMPC | 0.81±0.01 | 0.82±0.01 | 0.88±0.01 | 1.06 ±0.03 | |
| MO/POPC | 0.74 ± 0.02 | 0.81 ± 0.02 | 0.88±0.03 | 0.95±0.03 | |
| TMD/DOPE | 1.13±0.02 | 1.09 ± 0.03 | 1.01 ± 0.02 | 0.99 ± 0.02 |
Figure 4.
31P T1 relaxation times of LMPC, MO/POPC and TMD/DOPE membranes as a function of temperature. The T1 values increase with temperature for LMPC and MO/POPC and decrease with temperature for TMD/DOPE.
We now consider the mechanisms of 31P T1 and T2 relaxations in lipid membranes in order to extract motional correlation times for the three membranes. The nuclear-spin interactions relevant for 31P relaxation are the 31P CSA and 31P-1H dipole coupling. At the magnetic field of 9.4 Tesla used here, the CSA mechanism dominates, and the T1 and T2 relaxation rates can be expressed as32–33
| (2) |
| (3) |
where ωP is the 31P Larmor frequency, is the rigid-limit chemical shift anisotropy, and J(ω) is the spectral density at frequency ω and is the Fourier transform of the correlation function of motion. If the motion is Markovian (e.g. diffusive or jump-like), then the correlation function is exponential with a time constant τc and J(ω) is Lorentzian34:
| (4) |
To simplify analysis, we separate lipid motions into two types: fast motions with a correlation time τf and slow overall motions with a correlation times τs. With this approximation, the spectral density function becomes35–36
| (5) |
where S is the order parameter of the fast motion.
The rigid-limit 31P CSA (σ) is about 160 ppm, η is about 0.5716, 37, and the Larmor frequency in our experiments is ωp = 2π × 162 × 106 rad/s. The order parameters of the glycerol backbone and the beginning of the headgroup are ~0.2 based on measured C-H dipolar couplings and 31P and 13C CSAs in liquid-crystalline phosphocholine38–39. Thus, from the measured T1 and T2 values, we can extract the two unknowns, τf and τs, by solving the simultaneous equations (2) and (3). In principle, from these quadratic equations more than one solution of τf and τs are possible. However, by removing unphysical values and using the fact that τf and τs should decrease with increasing temperature, we can obtain a unique set of correlation times at each temperature.
Tables 3 lists the measured fast and slow correlation times for the three membranes at various temperatures. We found τf values of 0.27–0.43 ns for LMPC and MO/POPC but a 10-fold longer τf value of 3–4 ns for the TMD/DOPE sample. Thus, phosphocholines in the micelle and the cubic-phase monoolein undergo faster motions than DOPE lipids in complex with the fusion protein TMD. The longer correlation time of DOPE may result from intermolecular hydrogen bonding between phosphoethanolamine headgroups and from DOPE – TMD interactions.
Table 3.
Fast and slow correlation times of three membranes at different temperatures.
| Membrane | 273 K | 278 K | 285 K | 290 K | 295 K | |
|---|---|---|---|---|---|---|
| LMPC | τf (ns) | 0.38 | 0.37 | 0.34 | - | 0.27 |
| τs (µs) | 0.077 | 0.067 | 0.050 | - | 0.035 | |
| MO/POPC | τf (ns) | - | 0.43 | 0.38 | 0.34 | 0.31 |
| τs (µs) | - | 2.5 | 1.5 | 1.2 | 0.89 | |
| TMD/DOPE | τf (ns) | 3.9 | 3.7 | 3.4 | - | 3.3 |
| τs (µs) | 25 | 19 | 12 | - | 7.3 | |
For slow motions, the τs values differ by two orders of magnitude among the three membranes (Table 3). LMPC has τs values of 0.04–0.08 µs over the temperature range studied, while POPC in cubic-phase MO/POPC exhibits τs values of 0.9–2.5 µs. TMD-bound DOPE has the longest τs of 7.3–25 µs.
To understand the origin of these very different τs values, we estimate the correlation times of various slow motions in lipid membranes. Two main sources of slow motions are whole-body tumbling and lipid lateral diffusion, whose correlation times can be calculated as40
| (6) |
where is the correlation time for lipid lateral diffusion, is the correlation time for tumbling, DL is the lateral diffusion coefficient, rL is the radius of curvature for lateral diffusion, rt is the radius of the tumbling vesicle, T is the absolute temperature, k is the Boltzmann constant, and ηW is the viscosity of the aqueous solution. For lipid cubic phases, rL ≪ rt because of the extended nature of the cubic-phase assembly, thus is much shorter than , making lateral diffusion the determining factor for the overall τs. Using a typical DL value of 10−8 cm2/s and a radius of 10 nm, we estimate a τs value of ~ 17 µs when lateral diffusion dominates the slow motion. For micelles, rL = rt. Using an ηW of 0.891·10−3 kg/m·s, a radius of 5 nm, and T of 295 K, we estimate a tumbling correlation time of 0.13 µs, which is much shorter than and thus dominates τs. Thus, micelles should have two-orders-of-magnitude shorter τs than lipid cubic phases, consistent with the measured τs differences between LMPC and MO/POPC. Therefore, the fact that TMD/DOPE exhibits even longer τs assigns this membrane to the cubic phase.
We can extract the activation energies Ea of the fast and slow motions from the measured temperature dependence of the correlation times. Assuming Arrhenius behavior, the correlation time depends on T as
| (7) |
where R is the ideal gas constant. Fig. 5 plots ln(τ) as a function of 1000/T, the slope of which gives the activation energies. For fast motions, we found similar activation energies of 13–14 kJ/mol for LMPC and MO/POPC, while the TMD/DOPE membrane has a 3-fold lower activation energy of 5.2 kJ/mol. For slow motions, activation energies of 26–41 kJ/mol were found, with LMPC giving the smallest value while MO/POPC and TMD/DOPE exhibit larger and similar activation energies.
Figure 5.
Activation energies of slow and fast motions in the three lipid membranes, extracted from the slope of the correlation times with respect to inverse temperature. (a) ln(τf) as a function of temperature. The activation energies range from 5.2 to 14 kJ/mol. (b) τs as a function of temperature. The activation energies range from 26 to 41 kJ/mol.
Discussion
These 31P relaxation data reveal that cubic-phase membranes can be distinguished from isotropic micelles by their different T2 relaxation times or homogeneous linewidths. Although LMPC and MO/POPC have the same apparent 31P linewidths (Fig. 3a), the underlying homogeneous linewidths are dramatically different. The narrower homogeneous linewidth of the LMPC micelle is empirically consistent with the fluid nature of the micelle sample. The estimated correlation times for whole-body tumbling and lateral diffusion over a radius of 5–10 nm provide insights into the different orders of magnitudes of T2 relaxation times. To understand τs and τf’s contribution to 31P T2 and T1 relaxation times, we consider the dependences of the spectral density function on correlation times. Setting τf to 0.1 – 10 ns and τs to 10 ns – 100 µs, the spectral density at the Larmor frequency, J(ωp; τs, τf), depends on τs and τf as
| (8) |
| (9) |
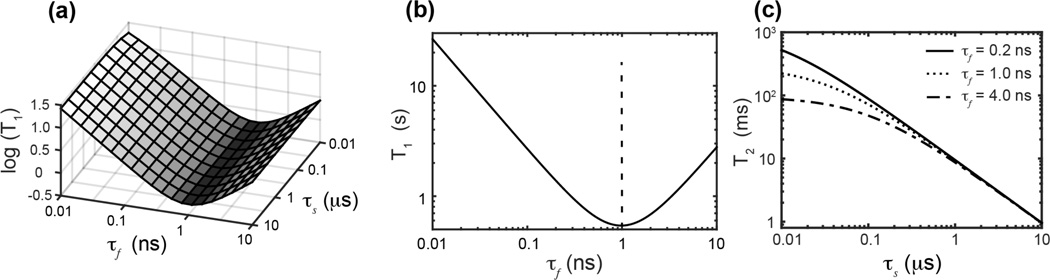
The approximation in eqn. (8) results from the fact that (ωPτs)2 ≫ 1. Since S is ~0.2, J(ωp; τs, τf) has negligible dependence on τs, indicating that slow motion has little impact on T1. In contrast, since ωPτf ~ 1, τf has a significant effect on J(ωp; τs, τf). These dependences of J(ωp; τs, τf) are plotted in Fig. 6a. Around the T1 minimum τf = 1/ωP, T1 decreases with increasing τf when τf <1/ωP but increases with increasing τf when τf >1/ωP (Fig. 6b).
Figure 6.
Dependences of 31P T1 and T2 relaxation times on fast and slow correlation times τf and τs. (a) log(T1) versus τf and τs. In the range of 10 ns < τs <10 µs, T1 is insensitive to τs. (b) 31P T1 relaxation time as a function of τf when τs = 1 µs. Under our experimental condition T1 has a minimum of ~0.54 s, which is achieved when τf = 1/ωP ≈ 1 ns. (c) 31P T2 relaxation time as a function of τs while τf is 0.2, 1 and 4 ns. T2 decreases with increasing τs and τf. The dependence of T2 on τf diminishes with increasing τs. When τs > 1 µs, T2 is independent of τf, and the relationship between T2 and τs is approximately linear.
T2 relaxation times depend on spectral densities at both the Larmor frequency and ω = 0. From Eqn. (5), J(0) = S2τs + (1 − S2)τf, indicating that J(0) is proportional to both τf and τs. Fig. 6c plots the calculated T2 values as a function of τs for several τf values. When τs > 1 µs, T2 is dominated by τs and mostly independent of τf. In this regime, R2 can be simplified as
| (10) |
indicating that the T2 relaxation time is dominated by and inversely proportional to τs (Fig. 6c). As a result, tumbling micelles with shorter τs values (< 0.1 µs) have longer T2 relaxation times than cubic-phase membranes with longer τs values (1–30 µs) due to lateral diffusion. These significant τs differences between LMPC micelles and the MO/POPC cubic phase are not manifested in the 31P spectral lineshapes because both motions are faster than the averaged 31P CSA of ~5 kHz. However, at larger magnetic field strengths, the 31P CSA may become sufficiently large such that the cubic-phase 31P spectrum may no longer be averaged to an isotropic frequency. Higher magnetic fields may also facilitate alignment of the cubic-phase membrane, if the magnetic susceptibility anisotropy of the cubic-phase membrane can be made sufficiently large using dopants such as lanthanide ions, so that the calculated 31P lineshapes may become observable.
The measured activation energies give useful insights into the nature of various lipid motions. For slow motions, TMD/DOPE and MO/POPC exhibit an activation energy of ~40 kJ/mol whereas the LMPC micelle has a much smaller activation energy of 26 kJ/mol. Pulsed-field gradient NMR data have yielded the activation energies of lipid lateral diffusion in various membranes. For example, hydrated POPC41 and MO in cubic-phase MO/water mixtures42 were reported to have activation energies of ~30 kJ/mol. The good agreement between these literature values and our data for TMD/DOPE and MO/POPC supports the assignment of the slow motion in these samples to lateral diffusion. For fast motions, the activation energies are smaller: LMPC and MO/POPC gave a value of 13–14 kJ/mol while TMD/DOPE showed the smallest activation energy of 5.2 kJ/mol. The former is in excellent agreement with the values obtained from previous field-dependent 31P T1 relaxation data, which indicated that most phospholipids have an activation energy of 13.2 ± 1.9 kJ/mol in the liquid-crystalline phase43–44. This energy barrier was assigned to diffusive motions in a spatially rough potential energy landscape44, and is associated with motions with correlation times of several nanoseconds. We found τf values of less than 1 ns for the LMPC micelle, which suggests that other motional processes may also be present. Single-field 31P relaxation times as measured here are not sufficient to separate multiple fast motions such as torsional motion, headgroup rotation, and lipid uniaxial rotation45; however, such a detailed separation of motional mechanisms is not the focus of this study. Even with our simplifying assumption of only one fast motion, the good agreement between our activation energies for LMPC and MO/POPC and literature values suggests that the fast motion can be reasonably assigned to rotational diffusion combined with wobble of the molecular axis.
The 31P T2 relaxation data indicate that the TMD of the fusion protein F of the parainfluenza virus 5 converts the DOPE membrane to a cubic phase. This is consistent with small-angle X-ray scattering (SAXS) data that showed the formation of an Ia3d cubic phase (unpublished data). Thus, the TMD of this viral fusion protein induces negative Gaussian curvature to the DOPE membrane, the type of curvature that is present in hemifusion intermediates and fusion pores4. The active participation of the TMD to viral fusion may not be restricted to the PIV5 fusion protein, but may occur in other viral fusion proteins as well. In addition to fusion proteins, the influenza M2 protein has also been shown to induce an isotropic peak in the 31P NMR spectra46 and cubic phases in the SAXS spectra47, and this curvature-inducing ability has been correlated with the membrane-scission function of the M2 protein48. The current 31P relaxation NMR approach should be useful for further characterization of M2-induced membrane restructuring as well as for de novo determination of the membrane morphologies with an associated isotropic 31P peak as generated by other proteins.
In conclusion, the lipid membrane morphology can be identified by first measuring the static 31P NMR lineshapes. Lamellar and hexagonal phases exhibit unique anisotropic powder patterns while micelles and cubic phase exhibit an isotropic peak. If the latter is found, then non-spinning 31P T2 relaxation times should be measured. If the T2 is longer than ~100 ms at room temperature, then the membrane is in an isotropic phase, while T2’s of less than ~10 ms indicate that the membrane is in a bicontinuous cubic phase. Temperature-dependent T1 and T2 relaxation times can be further measured to obtain more detailed information about the correlation times of lipid motion. The slow correlation time is especially distinct between the cubic phases (microseconds) and the micellar phase (10 – 100 ns).
Supplementary Material
Acknowledgement
This work is supported by NIH grant GM066976 to M. H.
Footnotes
Supporting Information
Detailed mathematical modeling, Tables and figures of the three bicontinuous cubic phases are provided. This information is available free of charge via the internet at http://pubs.acs.org.
References
- 1.Harrison SC. Viral membrane fusion. Nature Struc. Mol. Biol. 2008;15:690–698. doi: 10.1038/nsmb.1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 3.Schmidt N, Mishra A, Lai GH, Wong GC. Arginine-rich cell-penetrating peptides. FEBS Lett. 2010;584:1806–1813. doi: 10.1016/j.febslet.2009.11.046. [DOI] [PubMed] [Google Scholar]
- 4.Siegel DP. The modified stalk mechanism of lamellar/inverted phase transitions and its implications for membrane fusion. Biophys.. J. 1999;76:291–313. doi: 10.1016/S0006-3495(99)77197-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chernomordik LV, Kozlov MM. Protein-lipid interplay in fusion and fission of biological membranes. Annual review of biochemistry. 2003;72:175–207. doi: 10.1146/annurev.biochem.72.121801.161504. [DOI] [PubMed] [Google Scholar]
- 6.De Kruijff B, Cullis PR, Verkleij AJ, Hope MJ, Van Echteld CJA, Taraschi TF. The Enzymes of Biological Membranes. Springer; 1985. Lipid polymorphism and membrane function; pp. 131–204. [Google Scholar]
- 7.Lindblom G, Rilfors L. Cubic phases and isotropic structures formed by membranes lipids - possible biological relevance. Biochim. Biophys. Acta. 1989;988:221–256. [Google Scholar]
- 8.Seddon JM, Robins J, Gulik-Krzywicki T, Delacroix H. Inverse micellar phases of phospholipids and glycolipids. Phys. Chem. Chem. Phys. 2000;2:4485–4493. [Google Scholar]
- 9.Anderson DM, Gruner SM, Leibler S. Geometrical aspects of the frustration in the cubic phases of lyotropic liquid crystals. Proc. Natl. Acad. Sci. U. S. A. 1988;85:5364–5368. doi: 10.1073/pnas.85.15.5364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Luzzati V, Spegt PA. Polymorphism of lipids. Nature. 1967;215:701–704. [Google Scholar]
- 11.Scriven LE. Equilibrium bicontinuous structure. Nature. 1976;263:123–125. [Google Scholar]
- 12.Almsherqi ZA, Landh T, Kohlwein SD, Deng Y. Cubic membranes: the missing dimension of cell membrane organization. Int. Rev. Cell Mol. Biol. 2009;274:275–342. doi: 10.1016/S1937-6448(08)02006-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Almsherqi ZA, Margadant F, Deng Y. The Cubic “Faces” of Biomembranes. In: AIglic A, editor. Advances in Planar Lipid Bilayers and Liposomes. Vol. 12. Academic Press; 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Smith ICP, Ekiel IH. Phosphorus-31 NMR: Principles and applications. Academic Press; 1984. Phosphorus-31 NMR of phospholipids in membranes; pp. 447–474. [Google Scholar]
- 15.Yeagle PL. The membranes of cells. 2nd ed. San Diego: Academic Press; 1993. [Google Scholar]
- 16.Roberts MF, Redfield AG. High-resolution 31P field cycling NMR as a probe of phospholipid dynamics. J. Am. Chem. Soc. 2004;126:13765–13777. doi: 10.1021/ja046658k. [DOI] [PubMed] [Google Scholar]
- 17.Leftin A, Brown MF. An NMR database for simulations of membrane dynamics. Biochim. Biophys. Acta. 2011;1808:818–839. doi: 10.1016/j.bbamem.2010.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Blume A, Rice DM, Wittebort RJ, Griffin RG. Molecular dynamics and conformation in gel & LC phases of PE bilayers. Biochemistry. 1982;21:6220–6230. doi: 10.1021/bi00267a030. [DOI] [PubMed] [Google Scholar]
- 19.Skarjune R, Oldfield E. Physical studies of cell surface and cell membrane structure determination of phospholipid head group organization by deuterium and phosphorus nuclear magnetic resonance spectroscopy. Biochemistry. 1979;18:5903–5909. doi: 10.1021/bi00593a022. [DOI] [PubMed] [Google Scholar]
- 20.Eriksson PO, Khan A, Lindblom G. Nuclear magnetic resonance studies of motion and structure of cubic liquid crystalline phases. J. Phys. Chem. 1982;86:387–393. [Google Scholar]
- 21.Söderman O, Walderhaug H, Henriksson U, Stilbs P. NMR relaxation in isotropic surfactant systems. A 2H, 13C, and 14N NMR study of the micellar (L1) and cubic (I1) phases in the dodecyltrimethylammonium chloride/water system. J. Phys. Chem. 1985;89:3693–3701. [Google Scholar]
- 22.Söderman O, Olsson U, Wong TC. An x-ray and NMR study of the cubic phase at low water contents in the dodecyltrimethylammonium chloride/water system. J. Phys. Chem. 1989;93:7474–7478. [Google Scholar]
- 23.Ellena JF, Lepore LS, Cafiso DS. Estimating lipid lateral diffusion in phospholipid vesicles from carbon-13 spin-spin relaxation. J. Phys. Chem. 1993;97:2952–2957. [Google Scholar]
- 24.Thurmond RL, Lindblom G, Brown MF. Curvature, order, and dynamics of lipid hexagonal phases studied by deuterium NMR spectroscopy. Biochemistry. 1993;32:5394–5410. doi: 10.1021/bi00071a015. [DOI] [PubMed] [Google Scholar]
- 25.Dolainsky C, Möps A, Bayerl TM. Transverse relaxation in supported and nonsupported phospholipid model membranes and the influence of ultraslow motions: A 31P - NMR study. J. Chem. Phys. 1993;98:1712–1720. [Google Scholar]
- 26.Halle B, Ljunggren S, Lidin S. Theory of spin relaxation in bicontinuous cubic liquid crystals. J. Chem. Phys. 1992;97:1401–1415. [Google Scholar]
- 27.Gandy PJF, Cvijović D, Mackay AL, Klinowski J. Exact computation of the triply periodic D (diamond') minimal surface. Chem. Phys. Lett. 1999;314:543–551. [Google Scholar]
- 28.Gandy PJF, Klinowski J. Exact computation of the triply periodic G (Gyroid') minimal surface. Chem. Phys. Lett. 2000;321:363–371. [Google Scholar]
- 29.Gandy PJF, Klinowski J. Exact computation of the triply periodic Schwarz<i>P</i>minimal surface. Chem. Phys. Lett. 2000;322:579–586. [Google Scholar]
- 30.Finch SR. Computer algebra and elliptic functions. 2013 http://www.people.fas.harvard.edu/~sfinch/csolve/MinSrf.pdf. [Google Scholar]
- 31.Finch SR. Partitioning problem. 2013 http://www.people.fas.harvard.edu/~sfinch/csolve/ge2.pdf. [Google Scholar]
- 32.Abragam A. The Principles of Nuclear Magnetism. Clarendon, UK: Oxford; 1961. [Google Scholar]
- 33.Chang SL, Tjandra N. Temperature dependence of protein backbone motion from carbonyl 13C and amide 15N NMR relaxation. J. Magn. Reson. 2005;174:43–53. doi: 10.1016/j.jmr.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 34.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 35.Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studied by nitrogen-15 inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 36.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational diffusion anisotropy of human ubiquitin from 15N NMR relaxation. J. Am. Chem. Soc. 1995;117:12562–12566. [Google Scholar]
- 37.Herzfeld J, Griffin RG, Haberkorn RA. 31P chemical-shift tensors in barium diethyl phosphate and urea-phosphoric acid: model compounds for phospholipid head-group studies. Biochemistry. 1978;17:2711–2718. doi: 10.1021/bi00607a003. [DOI] [PubMed] [Google Scholar]
- 38.Hong M, Schmidt-Rohr K, Nanz D. Study of phospholipid structure by 1H, 13C, and 31P dipolar couplings from 2D NMR. Biophys. J. 1995;69:1939–1950. doi: 10.1016/S0006-3495(95)80064-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hong M, Schmidt-Rohr K, Pines A. NMR Measurement of Signs and Magnitudes of C-H Dipolar Couplings in Lecithin. J. Am. Chem. Soc. 1995;117:3310–3311. [Google Scholar]
- 40.Marasinghe PAB, Buffy JJ, Schmidt-Rohr K, Hong M. Membrane curvature change induced by an antimicrobial peptide detected by 31P exchange NMR. J. Phys. Chem. B. 2005;109:22036–22044. doi: 10.1021/jp054396i. [DOI] [PubMed] [Google Scholar]
- 41.Gaede HC, Gawrisch K. Lateral diffusion rates of lipid, water, and a hydrophobic drug in a multilamellar liposome. Biophys. J. 2003;85:1734–1740. doi: 10.1016/S0006-3495(03)74603-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Geil B, Feiweier T, Pospiech EM, Eisenblätter J, Fujara F, Winter R. Relating structure and translational dynamics in aqueous dispersions of monoolein. Chem. Phys. Lipids. 2000;106:115–126. doi: 10.1016/s0009-3084(00)00136-5. [DOI] [PubMed] [Google Scholar]
- 43.Ghosh R. Phosphorus-31 and deuterium NMR studies of structure and motion in bilayers of phosphatidylcholine and phosphatidylethanolamine. Biochemistry. 1988;27:7750–7758. doi: 10.1021/bi00420a025. [DOI] [PubMed] [Google Scholar]
- 44.Roberts MF, Redfield AG, Mohanty U. Phospholipid reorientation at the lipid/water interface measured by high resolution 31P field cycling NMR spectroscopy. Biophys. J. 2009;97:132–141. doi: 10.1016/j.bpj.2009.03.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dufourc EJ, Mayer C, Stohrer J, Althoff G, Kothe G. Dynamics of phosphate head groups in biomembranes. Comprehensive analysis using phosphorus-31 nuclear magnetic resonance lineshape and relaxation time measurements. Biophys. J. 1992;61:42–57. doi: 10.1016/S0006-3495(92)81814-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang T, Cady SD, Hong M. NMR Determination of Protein Partitioning into Membrane Domains with Different Curvatures and Application to the Influenza M2 Peptide. Biophys. J. 2012;102:787–794. doi: 10.1016/j.bpj.2012.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schmidt NW, Mishra A, Wang J, DeGrado WF, Wong GC. Influenza virus A M2 protein generates negative Gaussian membrane curvature necessary for budding and scission. J. Am. Chem. Soc. 2013;135:13710–13719. doi: 10.1021/ja400146z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rossman JS, Jing X, Leser GP, Lamb RA. Influenza virus M2 protein mediates ESCRT-independent membrane scission. Cell. 2010;142:902–913. doi: 10.1016/j.cell.2010.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.