Widespread non-additive and interaction effects within HLA loci modulate the risk of autoimmune diseases

Abstract

Human leukocyte antigen (HLA) genes confer strong risk for autoimmune diseases on a log-additive scale. Here we speculated that differences in autoantigen binding repertoires between a heterozygote’s two expressed HLA variants may result in additional non-additive risk effects. We tested non-additive disease contributions of classical HLA alleles in patients and matched controls for five common autoimmune diseases: rheumatoid arthritis (RA, N_cases=5,337), type 1 diabetes (T1D, N_cases=5,567), psoriasis vulgaris (N_cases=3,089), idiopathic achalasia (N_cases=727), and celiac disease (N_cases=11,115). In four out of five diseases, we observed highly significant non-additive dominance effects (RA: P=2.5×10¹²; T1D: P=2.4×10⁻¹⁰; psoriasis: P=5.9×10⁻⁶; celiac disease: P=1.2×10⁻⁸⁷). In three of these diseases, the dominance effects were explained by interactions between specific classical HLA alleles (RA: P=1.8×10⁻³; T1D: P=8.6×10²⁷; celiac disease: P=6.0×10⁻¹⁰⁰). These interactions generally increased disease risk and explained moderate but significant fractions of phenotypic variance (RA: 1.4%, T1D: 4.0%, and celiac disease: 4.1%, beyond a simple additive model).

Genetic variation in HLA genes, within the major histocompatibility complex (MHC) locus, is associated with many autoimmune diseases^1–3. For most of these diseases, the MHC explains more disease risk than any other locus. Previous research has shown non-additive effects (disease contributions beyond the cumulative effect of individual alleles) at classical MHC genes in resistance to infectious diseases^4–7, and researchers have proposed that non-additive effects may also occur in autoimmunity^8–12. Indeed, some studies have reported synergistic interactions between specific HLA haplotypes^13–15, but non-additive effects and interactions have not been systematically characterized in large population cohorts and across multiple diseases.

In an additive model, disease effects of two alleles are independent and combine linearly (on the log-odds scale); i.e. the presence of the first and second copy of an allele multiplicatively increases risk by the same amount. Non-additive effects describe deviations from this linear relationship and may arise from interactions between two alleles, or from intrinsic effects of individual alleles (e.g. haploinsufficiency)^16,17. Since both alleles at a given HLA locus are expressed, heterozygous genotypes might confer expanded antigen-binding properties and elevated autoantigen presentation, depending on the degree of complementarity between the two alleles¹⁸.

In order to test for the presence of non-additive effects, we used SNP2HLA¹⁹ to impute HLA alleles from dense ImmunoChip-based SNP genotype data in five autoimmune diseases: seropositive rheumatoid arthritis (RA, N_{cases/controls}=5,337/11,049)^20,21, type 1 diabetes (T1D, N=5,567/6,265)²², psoriasis vulgaris (N=3,089/5,964)²³, idiopathic achalasia (N=727/2,911)²⁴, and celiac disease (N=11,115/9,042)²⁵ (Supplementary Table 1). We demonstrated accurate HLA imputation elsewhere¹⁹ using the ImmunoChip platform and the same reference panel (T1D Genetics Consortium, N=5,225)²⁶.

For each of these five diseases, we focused our analyses on the HLA loci with the strongest effects (RA: HLA-DRB1^20,21, T1D: HLA-DRB1-DQA1-DQB1²², psoriasis: HLA-C²³, achalasia: HLA-DQA1-DQB1²⁴, celiac disease: HLA-DQA1-DQB1²⁵). We focused on four-digit classical alleles, which distinguish HLA gene variants at the amino acid sequence level²⁷. Since T1D, achalasia, and celiac disease have independent associations to multiple, linked HLA genes^22,24,25, we combined phased four-digit classical alleles from separate genes into multi-locus haplotypes for these diseases. For our primary test, we restricted our analysis to common alleles at each locus (reference panel allele frequency > 5%; Supplementary Table 2) and to individuals carrying only these common alleles (“common allele dataset”, Supplementary Table 1). This approach ensured the highest imputation accuracy and increased the statistical power to estimate the true additive component of each haplotype by providing a sufficient number of homozygote events. As a secondary test, we analyzed both rare and common haplotypes that were present in at least 10 homozygous individuals (“full dataset”, Supplementary Table 1).

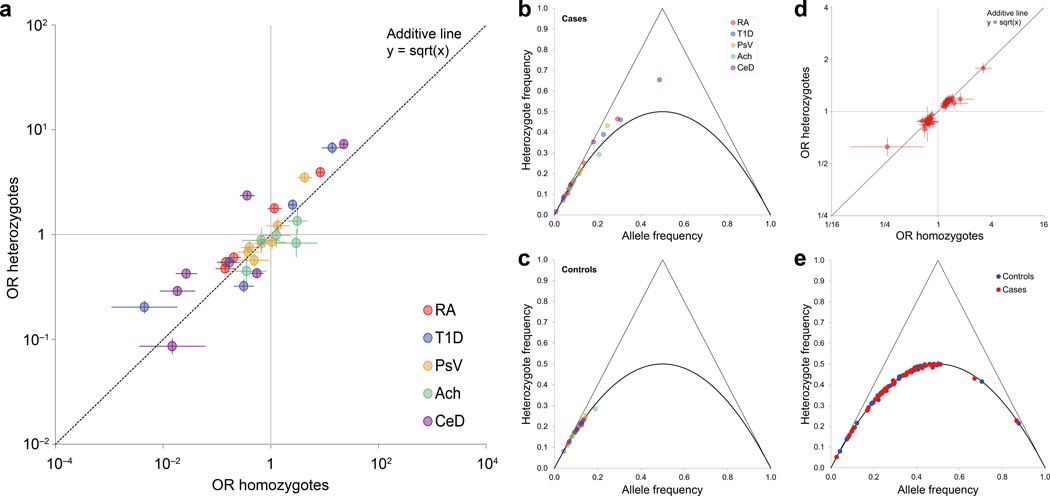
To assess for non-additive associations, we first examined disease risk of homozygotes and heterozygotes for each haplotype. Under additivity, for a given allele, the log-odds of heterozygotes compared to non-carriers of the allele should be half that of homozygotes. However, we found that many haplotypes deviated from this linear relationship (Fig. 1a, Supplementary Table 3). We also observed an excess of heterozygous genotypes deviating from Hardy-Weinberg equilibrium in cases (Fig. 1b, Supplementary Table 4), but not controls (Fig. 1c, Supplementary Table 4). In contrast, 43 RA-associated non-MHC SNPs²⁸ followed an additive relationship perfectly (Fig. 1d, Supplementary Table 5) and also followed Hardy-Weinberg equilibrium (Fig. 1e, Supplementary Table 6). We note that the lower effect sizes of non-MHC variants may limit our ability to detect non-additive effects.

Figure 1. Disease associations of HLA and non-HLA variants.

(a) Disease associations of HLA haplotypes with rheumatoid arthritis (RA), type 1 diabetes (T1D), psoriasis vulgaris (PsV), idiopathic achalasia (Ach), and celiac disease (CeD). For each common haplotype, the odds ratio (OR) for heterozygotes (vs. non-carriers) is plotted against the OR for homozygotes (vs. non-carriers). The dashed line represents a purely log-additive relationship, in which heterozygotes have exactly half the risk of homozygotes (on a log-odds scale). Data points above the dashed line represent haplotypes with a positive dominance component, and below the line haplotypes with a negative dominance component. Error bars represent 95% confidence intervals. (b,c) De Finetti diagram of the proportion of heterozygotes in relation to the frequency of each HLA haplotype (grouped across all diseases), shown separately for (b) cases and (c) controls. The solid line represents the expected proportion of heterozygotes under Hardy-Weinberg-Equilibrium. (d) Disease association of 43 known genome-wide RA-associated SNPs located outside the MHC region, using the same plotting scheme as for panel a. No single SNP shows a significant deviation from the dashed line (representing a purely additive disease contribution). (e) De Finetti diagram of heterozygote frequency for the same 43 non-MHC SNPs as in panel d, given separately for controls and cases.

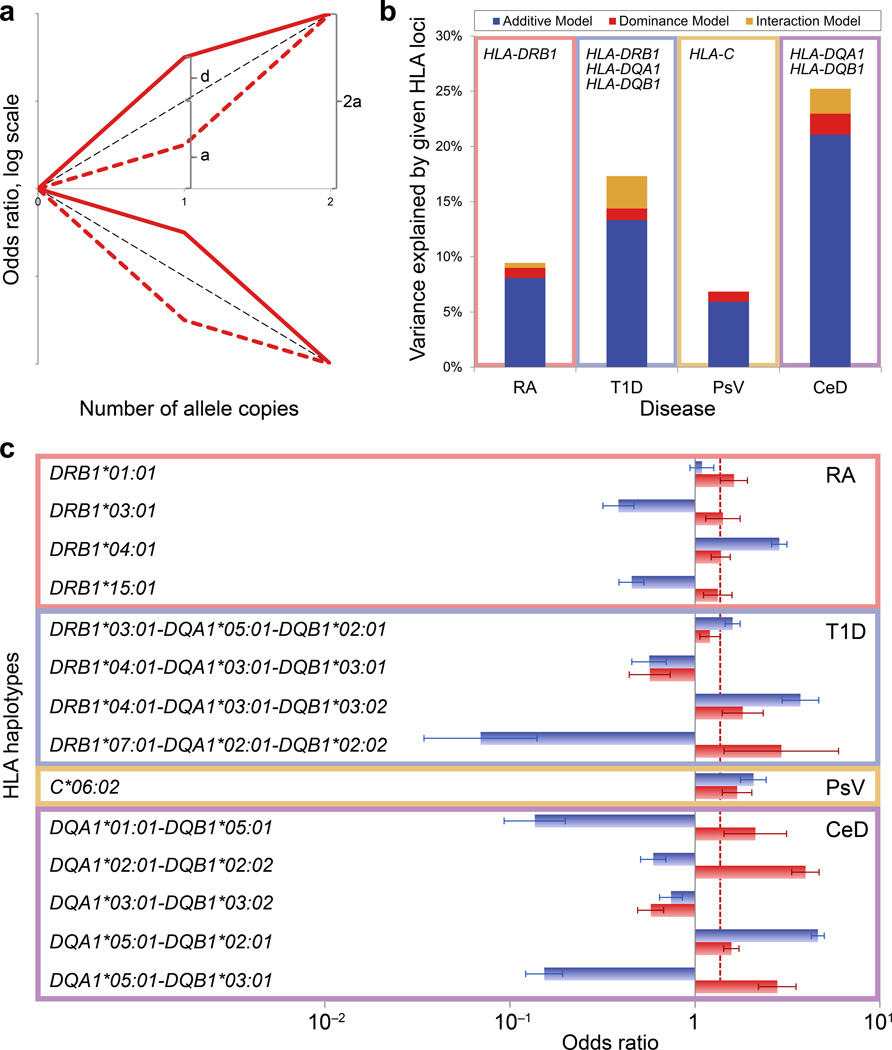
To test for the general presence of non-additive effects, we constructed one global logistic regression model for each disease that included additive and dominance terms for all common haplotypes simultaneously (Fig. 2a). The additive term captures the dosage effect (zero, one, or two copies) of a given haplotype, while the dominance term captures any deviations from the additive scenario²⁹. Strikingly, for four of the five diseases, the inclusion of dominance terms improved the fit of the models (RA: P_df=5=2.5×10⁻¹²; T1D: P_df=5=2.4×10⁻¹⁰, psoriasis: P_df=7=5.9×10⁻⁶; celiac disease: P_df=6=1.2×10⁻⁸⁷). In the achalasia dataset we observed a non-significant trend (P_df=5=0.066); power may have been limited due to the relatively small sample size of this dataset. These results were consistent in the full datasets, including a larger set of common and rare alleles (Supplementary Table 7), and also when using regression on a probit scale³⁰ instead of logistic regression (Supplementary Table 8). In a purely additive model, common HLA haplotypes explained 8.1% of phenotypic variance for RA, 13.3% for T1D, 5.9% for psoriasis, and 21.1% for celiac disease. The addition of dominance terms explained an additional 0.9%, 1.1%, 0.9%, and 1.9% of phenotypic variance, respectively (Fig. 2b). These values are comparable to the effect of the largest known non-MHC RA risk effect; the rs2476601 PTPN22 risk allele explains 0.8% of the total phenotypic variance in RA³¹.

Figure 2. Non-additive contribution of the HLA to autoimmune disease risk.

(a) Schematic overview of possible non-additive scenarios. The log-odds for heterozygote genotypes can be divided into an additive effect a and a dominance component d, which represents the departure from additivity. Depending on the signs of a and d, there are four possible scenarios, represented by red lines. Dashed black lines represent the expected log-odds under a purely additive model (d = 0). As an example, the values of a and d are indicated for the solid red line (risk variant with positive dominance component). (b) Phenotypic variance explained by additive, dominant, and interaction effects of HLA haplotypes, respectively, for each disease with a significant non-additive HLA contribution: rheumatoid arthritis (RA), type 1 diabetes (T1D), psoriasis vulgaris (PsV), celiac disease (CeD). (c) For each common HLA haplotype with significant non-additive effect in RA, T1D, PsV, and CeD, we calculated the additive (blue bars) and dominance (red bars) components of the log-odds for heterozygotes. The dashed line indicates the median of the dominance components depicted in the figure. Error bars represent 95% confidence intervals.

When we examined non-additive effects of individual HLA haplotypes separately, we observed that most haplotypes showed significant non-additive contributions in RA, T1D, and celiac disease (Table 1, Supplementary Table 3). In contrast, of 7 common haplotypes tested in psoriasis, only HLA-C*06:02 showed a non-additive effect. Across all four diseases, 14 of 23 HLA haplotypes showed non-additivity, and 12 had a positive dominance component; thus, for most alleles, heterozygosity confers a higher risk of autoimmunity than expected from homozygote disease risk (Fig. 2c, Supplementary Table 9).

Table 1. Effect sizes of common HLA haplotypes with significant non-additive effects.

Additive and non-additive effect sizes are shown for all haplotypes with significant non-additive disease contribution in rheumatoid arthritis (RA: HLA-DRB1), type 1 diabetes (T1D: HLA-DRB1-DQA1-DQB1), psoriasis vulgaris (PsV: HLA-C), and celiac disease (CeD: HLA-DQA1-DQB1). For diseases associated with multiple HLA loci, linked classical alleles across those loci were analyzed as haplotypes. P-values indicate the significance of improvement in fit of separate haplotype-specific models after sequentially including the additive and the non-additive term for a given haplotype. Odds ratios (OR) and 95% confidence intervals (CI) are given for a purely additive scenario (equivalent to a in Fig. 2a) and for a non-additive scenario, in which heterozygotes and homozygotes have separate effects (equivalent to a+d and 2a in Fig. 2a, respectively). Haplotypes are ordered by significance of the non-additive effect within each dataset.

Disease	Loci				Additive model			Non-additive model (add. + non-add. component)
	HLA-C	HLA-DRB1	HLA-DQA1	HLA-DQB1	P	OR	95% CI	P	Heterozygote effect		Homozygote effect
									OR	95% CI	OR	95% CI
RA		01:01			1.6×10−22	1.54	(1.41–1.68)	1.3×10−8	1.77	(1.61–1.96)	1.17	(0.87–1.58)
		04:01			2.0×10−206	3.31	(3.05–3.59)	1.4×10−7	3.93	(3.54–4.36)	8.34	(6.87–10.12)
		03:01			1.2×10−51	0.50	(0.45–0.55)	8.6×10−4	0.54	(0.49–0.61)	0.15	(0.10–0.22)
		15:01			7.7×10−43	0.55	(0.51–0.60)	1.2×10−3	0.60	(0.54–0.67)	0.21	(0.15–0.28)
T1D		07:01	02:01	02:02	4.2 ×10−50	0.38	(0.33–0.43)	1.9×10−5	0.32	(0.28–0.37)	0.31	(0.20–0.48)
		04:01	03:01	03:01	2.2×10−167	0.18	(0.16–0.21)	3.4×10−5	0.20	(0.18–0.23)	0.005	(0.001–0.018)
		04:01	03:01	03:02	5.4×10−224	6.09	(5.38–6.90)	3.5×10−5	6.72	(5.88–7.68)	13.86	(8.79–21.86)
		03:01	05:01	02:01	5.2×10−35	1.70	(1.56–1.85)	3.5×10−3	1.92	(1.71–2.16)	2.55	(2.12–3.08)
PsV	06:02				1.5×10−92	2.94	(2.65–3.28)	4.9×10−8	3.49	(3.09–3.95)	4.28	(3.11–5.87)
CeD			02:01	02:02	1.3 ×10−67	1.86	(1.73–1.99)	6.7×10−62	2.36	(2.18–2.55)	0.36	(0.27–0.50)
			05:01	03:01	5.3×10−156	0.35	(0.32–0.38)	3.0×10−25	0.42	(0.39–0.46)	0.03	(0.02–0.04)
			05:01	02:01	4.3×10−675	5.78	(5.38–6.20)	4.7×10−19	7.28	(6.67–7.95)	22.80	(19.43–26.75)
			03:01	03:02	8.5×10−67	0.50	(0.46–0.54)	3.5×10−11	0.43	(0.39–0.47)	0.55	(0.42–0.73)
			01:01	05:01	4.0×10−216	0.27	(0.25–0.29)	3.2×10−6	0.29	(0.26–0.32)	0.02	(0.01–0.04)

We considered that these non-additive effects might originate from imputation artifacts. To ensure high quality imputation, we only used samples genotyped on ImmunoChip, containing dense SNP coverage (>5,000 SNPs within the MHC)¹⁹. Additionally, our primary analyses focused on common alleles that were well represented in the reference panel and had high imputation confidence (INFO) scores³² (>0.973, median 1.003, Supplementary Table 2). Also, significance of non-additive effects were unrelated to INFO scores (Kendall’s tau=−0.08, P=0.56; Supplementary Fig. 1, Supplementary Table 10). Finally, we conducted a stringent permutation analysis where we reassigned case-control status, based on an additive risk model for HLA haplotypes; this approach conserved the additive effect of each haplotype (Supplementary Fig. 2) and simultaneously maintained any imputation inaccuracies within the dataset. In celiac disease, psoriasis, T1D, and RA, the significance of non-additive effects in 10,000 trials never exceeded that of the actual data (Supplementary Fig. 3). These results argue that our findings cannot be explained by imputation artifacts.

In RA, T1D, and achalasia, the strongest additive disease associations point to individual amino acids (rather than four-digit classical alleles)^20,22,24 and we found indeed non-additive disease associations also at the amino acid level (Supplementary Fig. 4, Supplementary Table 11). We did observe residual non-additive haplotype effects after adjusting for the amino acid residue with the most significant non-additive effect (Supplementary Note 1). In most cases we did not have sufficient power to differentiate non-additive interaction effects of key amino acid positions from those of classical alleles.

We then investigated whether interactions between specific haplotypes might explain the observed dominance effects. If disease risk of a specific genotype combination of two alleles deviates from the disease risk expected from both alleles alone, then there is an interaction between the two alleles. Importantly, such interactions may give rise to apparent dominance effects at individual alleles. For each disease, we defined a global logistic regression model that simultaneously included interaction terms between all common haplotypes within a given locus. For three diseases (RA, T1D, and celiac disease), including additive and interaction terms showed a significant improvement in fit, compared to a model with additive and dominance terms (RA: P_df=5=1.8×10⁻³, T1D: P_df=5=8.6×10⁻²⁷; celiac disease: P_df=9=6.0×10⁻¹⁰⁰). Hence, the observed non-additive effects for RA, T1D, and celiac disease are at least partially explained by interactions between HLA haplotypes. The models with additive and interaction terms explained 9.5%, 17.3%, and 25.2% of phenotypic variance for RA, T1D, and celiac disease, respectively; interactions yielded an additional 0.5%, 2.9%, and 2.3% of phenotypic variance over a model with additive and dominance terms (Fig. 2b).

In contrast, psoriasis showed no evidence of interactions (P_df=14=0.92). In order to further identify interactions, we imputed an additional 5,294 psoriasis cases and 10,295 controls genotyped on platforms other than ImmunoChip (Supplementary Table 1c). While this increased our sample size dramatically, we still observed no evidence of interactions (P_df=14=0.87; Supplementary Table 12). The contrast between psoriasis and other diseases may be related to recent suggestions that the psoriasis association with HLA-C*06:02 is caused by variation in an enhancer element³³, rather than antigenic binding properties. Achalasia showed no evidence for interaction effects in our primary analysis (P_df=5=0.15), and only nominal evidence when testing the full dataset. All other diseases yielded qualitatively identical results when we tested the full datasets with both rare and common haplotypes (Supplementary Table 7). Again, probit regression analysis showed qualitatively identical results (Supplementary Table 8).

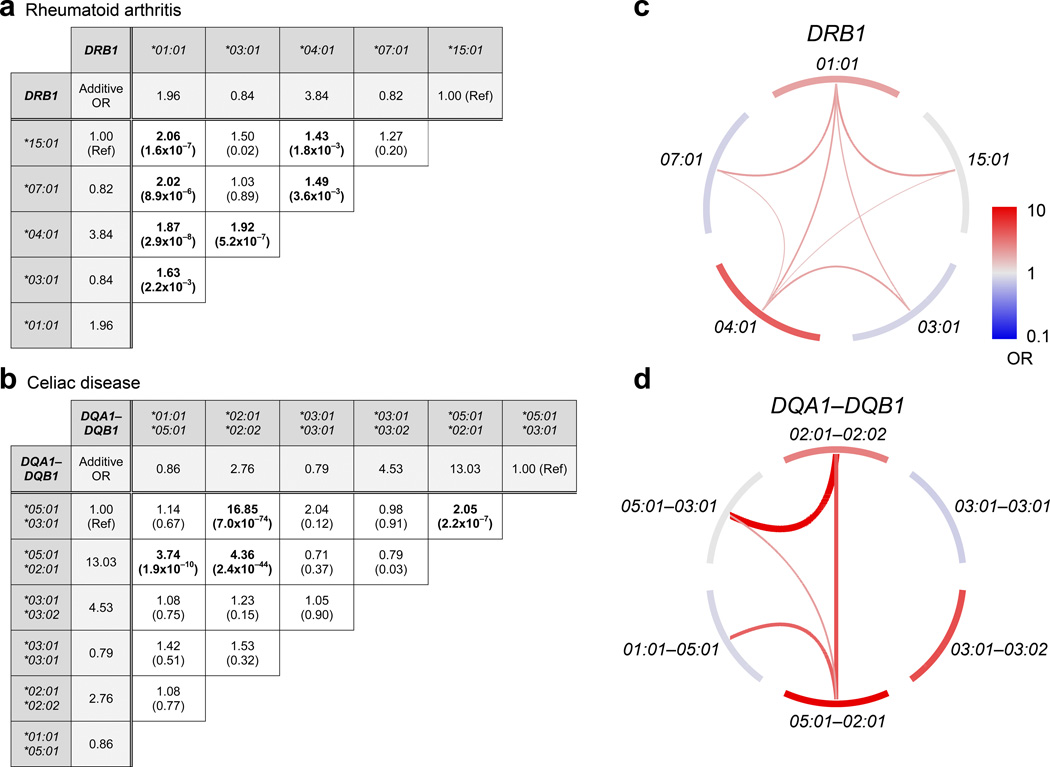
We then identified the specific HLA haplotypes contributing to interaction effects in RA, T1D, and celiac disease. For RA, 7 of the 10 possible interactions were significant (P<0.005=0.05/10), all of which increased disease risk beyond the separate additive contribution of each haplotype (Fig. 3a/c). For T1D, 7 of 10 interactions were significant (P<0.005=0.05/10), with five increasing risk and two reducing risk (Supplementary Fig. 5); these interactions are detailed elsewhere²². For celiac disease, among the 15 possible haplotype pairs, there were four significant pairwise interactions (P<0.003=0.05/15), each increasing risk (Fig. 3b/d). The identified interactions refined our previous findings of non-additive disease contributions. For instance, in celiac disease, DQA1*05:01-DQB1*02:01 had a significant non-additive component (P=4.7×10¹⁹) with d>0, indicating an elevated disease risk in heterozygotes. This elevated disease risk is explained by the interaction model, in which we observed significant risk-increasing interactions between DQA1*05:01-DQB1*02:01 and three other alleles (Fig. 3d).

Figure 3. Interaction effects among HLA haplotypes.

Pairs of common haplotypes with significant interaction effects (beyond the combined additive effect) are shown. For (a) rheumatoid arthritis (HLA-DRB1) and (b) celiac disease (HLA-DQA1-DQB1) we ran a global regression model that included additive terms for each haplotype and interaction terms between each pair of haplotypes. The fold change in odds ratio (OR) due to the inclusion of interaction effects is displayed for each haplotype pair, and the P-value associated with each interaction OR is shown in parentheses. Additive ORs are also displayed for each haplotype, shaded in light gray. The total OR of a haplotype pair is the product of two haplotypic additive ORs and one interaction OR. “Ref” indicates the reference haplotype for each regression model. Bolded values indicate interactions that are significant after multiple test correction (P < 0.05/10 = 0.005 for rheumatoid arthritis, P < 0.05/15 = 0.003 for celiac disease). Significant interactions are visualized for (c) HLA-DRB1 (rheumatoid arthritis) and (d) HLA-DQA1-DQB1 (celiac disease). Outer node segments represent haplotypes with the color indicating their additive disease contribution, while internal arches represent significant interaction effects. For both nodes and arches, red color indicates disease risk and blue indicates protection, with effect sizes following the scale in panel c. The effect sizes of the interactions are also represented by the width of the arches.

Our results build on previous studies that proposed specific non-additive associations in different autoimmune diseases. While previous studies of heterozygote risk in RA highlighted haplotypes with a common 'shared epitope' (SE) at positions DRβ1#70-74^34,35, we discovered significant interactions between SE haplotypes and non-SE haplotypes. There was no evidence for a previously reported interaction between DRB1*04:01 and DRB1*04:04³⁶ (Supplementary Note 2, Supplementary Table 13). Some specific interactions in T1D have been described previously, such as an elevated disease risk for HLA-DRB1*03:01-DQB1*02:01/DRB1*04:01-DQB1*03:02 genotypes¹⁵. Our recent comprehensive investigation of T1D also confirmed this interaction and revealed additional interactions with both increasing and decreasing risk effects²².

In celiac disease, the DQ2.5 haplotype, composed of HLA-DQA1*05:01 and HLA-DQB1*02:01, is the primary contributor to disease susceptibility^37,38. Here, we confirmed that DQA1*05:01-DQB1*02:01 has the strongest association in an additive model (P=4.3×10⁻⁶⁷⁵), and we also found significant interactions between DQA1*05:01-DQB1*02:01 and other haplotypes. Some of these combinations contained DQA1*05:01 and DQB1*02:01 in trans, but we also observed haplotype combinations that have not previously been implicated (e.g. DQA1*05:01-DQB1*02:01/DQA1*01:01-DQB1*05:01; interaction OR=3.74, P=1.9×10⁻¹⁰). Interestingly, the interaction with the strongest risk effect in our data (DQA1*02:01-DQB1*02:02/DQA1*05:01-DQB1*03:01; interaction OR=16.85, P=7.0×10⁻⁷⁴), identified in previous studies³⁹, contained the protective haplotype DQ7 (coded by DQA1*05:01-DQB1*03:01; homozygote OR=0.03), highlighting the complexity of interactions in the HLA.

Some previously reported interacting variants on the same haplotype have been disputed for only tagging hidden causal variants⁴⁰. However, here we show interactions between homologous haplotypes, which are unaffected by any linked variation. Interestingly, there was little overlap between diseases in the interacting pairs of haplotypes, suggesting that the precise interactions are disease specific. These interactions may depend on the exact autoantigens driving disease susceptibility². Such a scenario would be consistent with previous observations, e.g. in RA, where immune reactions against different citrullinated autoantigens seem to be restricted by specific HLA-DR variants^41,42. Additional complexity may arise from parent-of-origin effects in T1D (and potentially other diseases)^43,44,45. One possible mechanistic explanation for the interactions between HLA class II haplotypes is the formation of αβ-heterodimers in trans. In celiac disease, where the major disease antigen is known, expression of the gliadin peptide-presenting HLA-DQ2.5 molecule is the primary determinant of disease risk. Genotypes carrying HLA-DQA1*05:01 and HLA-DQB1*02:01 in trans can form this heterodimer, explaining the observed interaction effect between these haplotypes³⁸. Differential intrinsic stability of certain trans-heterodimers may also affect disease risk, as suggested for HLA-DQ in T1D⁴⁶. Further independent replication, for instance in other ethnicities, and experimental investigations of causal mechanisms are needed to generalize the findings and precisely understand how interacting alleles confer genetic predisposition for these complex diseases.

METHODS

Samples

We analyzed genotype data from previously published studies of HLA association in anti-citrullinated protein antibody positive (ACPA⁺) rheumatoid arthritis (RA, N = 16,386)²¹, type 1 diabetes (T1D, N = 11,832)²², psoriasis vulgaris (N = 9,053)²³, idiopathic achalasia (N = 3,638)²⁴, and celiac disease (N = 20,157)²⁵. Each dataset contained samples from multiple case-control GWAS cohorts, and all individuals had European ancestry (Supplementary Table 1). Each genotype dataset has undergone stringent quality control for the original studies above; here only post-QC data was used. Similarly, case-control matching was done as in the original studies. Generally, cases and controls were from the same patient collection and matched for country or region of origin. In most (but not all) of the studies, principal components were additionally used to adjust for any residual stratification. For data availability and specific quality control see Supplementary Table 14. All samples were collected from individuals after consent.

HLA genotypes and imputation quality

The SNP genotype data for the MHC region, obtained from previous disease-specific studies (see above), was generated by the Illumina ImmunoChip platform⁴⁷. Following previous studies, we defined the MHC region as the region on chromosome 6 from 29Mb to 34Mb. We imputed four-digit classical HLA alleles with SNP2HLA¹⁹, using dense SNP data across the MHC region for each disease dataset (number of SNPs used for imputation for RA: 4,499; for T1D: 4,604; psoriasis: 4,030; for achalasia: 3,773; and for celiac disease: 3,249) and a reference panel of 5,225 individuals of European ancestry from the Type 1 Diabetes Genetics Consortium (T1DGC)²⁶. Cases and controls were imputed together, to ensure consistent imputation quality across all samples. We have separately demonstrated high imputation accuracy using genotype data from the ImmunoChip platform¹⁹. Furthermore we found no evidence for a potential bias in imputation accuracy due to using a disease-specific reference panel (Supplementary Table 15).

For each allele, the INFO score was calculated from the ratio of the observed variance in dosage to the expected variance under Hardy-Weinberg equilibrium³²:

$$INFO=\frac{\mathit{\text{var}}(x)}{2(p)(1-p)}$$ (Equation 1)

where x is the imputed dosage and p is the frequency of the allele. An INFO score close to 0 indicates poor imputation quality, while a score closer to 1 indicates higher quality; a value greater than 1 is also possible. Due to the presence of non-additive effects that inflated the disease risk in heterozygotes, the allele distribution in disease cases deviated from Hardy-Weinberg equilibrium. Therefore, we calculated INFO scores using the variance and allele frequency in controls only (Supplementary Table 2). However, because the imputation algorithm does not take case/control status into account, we expected that imputation quality should be similar in cases and controls. For RA, we also calculated INFO scores within each cohort to test whether lower INFO scores (i.e. lower quality of imputed genotypes) were associated with a higher likelihood to detect non-additive effects, which could suggest that non-additive effects are an artifact of imputation errors.

Selection of genes for analysis

For each disease, we selected the HLA genes that were most significantly associated with disease risk in previous studies (RA: HLA-DRB1²¹; T1D: HLA-DRB1, HLA-DQA1, HLA-DQB1²²; psoriasis: HLA-C²³; achalasia: HLA-DQA1, HLA-DQB1²⁴; celiac disease: HLA-DQA1, HLA-DQB1²⁵). For diseases in which more than one HLA gene was implicated to confer major independent risk contribution, we defined haplotypes according to unique combinations of four-digit classical alleles at each relevant gene. We used phased best guess genotypes from SNP2HLA to ensure that each haplotype contained classical alleles on the same chromosome.

For RA and psoriasis, we repeated the analysis using imputed dosages (which range on a continuous scale from 0–2) rather than best guess genotypes (which are restricted to the integer values 0, 1, or 2; see Supplementary Table 16). Because imputed dosages do not contain phasing information, we did not perform this analysis for the diseases involving multiple genes.

Selection of alleles for analysis

We performed all association tests with two datasets: the common allele dataset and the full dataset. In the common allele dataset, we restricted our analysis to classical alleles with a frequency greater than or equal to 5% in the T1DGC reference panel, or haplotypes comprising these classical alleles (RA: m = 5; T1D: m = 5; psoriasis: m = 7; achalasia: m = 5; celiac disease: m = 6; where m indicates the number of included HLA alleles/haplotypes). This cutoff ensured a very high imputation quality, and INFO scores for all alleles in the common allele subset exceeded 0.97 (Supplementary Table 2). We also ensured that all haplotypes in the common subset had at least 10 homozygous individuals. (If fewer than 10 homozygotes are present, the additive and non-additive terms are statistically indistinguishable.) In the full dataset, we included all m variants (four-digit classical alleles or haplotypes) with at least 10 homozygous individuals (RA: m = 11; T1D: m = 11; psoriasis: m = 13; achalasia: m = 9; celiac disease: m = 10).

We ensured complete data in both datasets by excluding all individuals who lacked exactly two best-guess alleles at a given locus. For analyses that used imputed dosages, we excluded all individuals whose total dosage across the relevant alleles was less than 1.95 or greater than 2.05.

Statistical framework for association testing

To analyze the effects of HLA haplotypes on disease risk, we used a logistic regression framework (probit regressions yielded qualitatively identical results, Supplementary Table 4). We began by presenting a baseline model, consistent with the models used to fine-map HLA effects in previous recent publications for RA²¹, T1D²², psoriasis²³, achalasia²⁴, and celiac disease²⁵. These models assume a purely additive contribution from each haplotype. To control for cohort-specific effects and population stratification, we included an indicator variable for each cohort, the first L principal components (for RA, psoriasis, and achalasia), and a gender term (for T1D and celiac disease) as covariates. This resulted in the following logistic regression model:

$$\text{log}({\mathit{\text{odds}}}_i)=\theta +{\sum }_{j=1}^{m-1}{a}_j{x}_{i,j}+{\sum }_{k=1}^K{\delta }_{i,k}({\lambda }_k+{\sum }_{l=1}^L{\pi }_{k,l}{p}_{i,k,l})+\gamma g_i$$ (Equation 2)

where θ is the logistic regression intercept, a_j is the additive effect of allele j, and x_i,j is the allelic dosage (using best guess genotype or imputed dosage) of allele j in individual i. For a multi-allelic locus with m possible alleles, we included m − 1 a parameters, and we set the final a parameter to 0 to denote the reference allele. We arbitrarily selected the most common allele in the controls as the reference allele. The parameter δ_i,k is a binary indicator variable that equals 1 if and only if individual i is in cohort k, and λ_k is the effect for the k^th cohort. Among a total of K cohorts, we arbitrarily selected the largest cohort as the reference cohort and set its λ parameter to 0.

For RA, psoriasis, and achalasia, we also included the first L principal components, where p_i,k,l is the value of principal component l in cohort k for individual i, and π_k,l is the corresponding effect size. To be consistent with HLA fine mapping studies on other diseases, we used L = 10 for RA²¹ and psoriasis²³, L = 5 for achalasia²⁴, and no principal components for T1D²² or for celiac disease²⁵.

We included an additional covariate to account for gender differences in T1D and celiac disease, once again to conform to previous HLA fine-mapping analyses^22,25; however, the gender covariate had no significant effect on our results (Supplementary Table 17). Here, γ is the effect of gender, and g_i is a binary indicator variable that equals 1 if and only if individual i is female. We did not include the g_i parameter for RA, psoriasis, or achalasia, following refs.²¹,²³, and²⁴, respectively.

We tested significance in fit for each model by calculating the change in deviance (defined as −2 × the difference in log likelihood) from the original model to the revised model. This value follows a χ² distribution with n degrees of freedom, where n is the number of new parameters introduced in the revised model. For the additive model, n is 1 less than the total number of tested haplotypes (to account for a reference haplotype).

Analysis of dominance and interaction effects

For each disease, we tested for non-additive effects by including a dominance term d_j for each represented haplotype in the relevant dataset (the common allele subset or the full dataset):

$$\text{log}({\mathit{\text{odds}}}_i)=\theta +{\sum }_{j=1}^{m-1}{a}_j{x}_{i,j}+{\sum }_{j=1}^m{d}_j{\delta }_{x_{i,j}}+{\sum }_{k=1}^K{\delta }_{i,k}({\lambda }_k+{\sum }_{l=1}^L{\pi }_{k,l}{p}_{i,k,l})+\gamma g_i$$ (Equation 3)

where d_j represents the dominance effect of allele j, and δ_xi,j denotes that individual i is heterozygous for haplotype j. For analyses involving best guess genotypes, δ_xi,j if and only if x_i,j = 1. For dosage-based analyses, we used the formula δ_xi,j = 1 − abs(1 − x_i,j). We assessed the change in deviance between the additive model and the dominance model, which follows a χ² distribution with m degrees of freedom (1 for each haplotype). To determine the relative non-additive effect of a specific haplotype, we constructed a separate model for each haplotype by repeating the model in equation 3 for a single value of j (1 degree of freedom). For the single-haplotype models, we used a significance threshold of P < 0.05/m to correct for multiple tests.

We also constructed an interaction model, which contains an additive term for each haplotype and an interaction term between each pair of haplotypes:

$$\text{log}({\mathit{\text{odds}}}_i)=\theta +{\sum }_{j=1}^{m-1}{a}_j{x}_{i,j}+{\sum }_{j=1}^m{\sum }_{h=j+1}^m{\varnothing }_{j,h}{x}_{i,j}{x}_{i,h}+{\sum }_{k=1}^K{\delta }_{i,k}({\lambda }_k+{\sum }_{l=1}^L{\pi }_{k,l}{p}_{i,k,l})+\gamma g_i$$ (Equation 4)

where ϕ_j,h is effect size of the interaction between alleles j and h. We did not include dominance terms in this model, due to partial redundancy between dominance and interaction terms. The interaction model contains an additional m(m − 1)/2 degrees of freedom (1 for each pairwise interaction), compared to the additive model. We assessed the change in deviance between the dominance model and the interaction model, which follows a χ² distribution with m(m − 1)/2 − m degrees of freedom. To determine the relative significance of individual interaction terms, we compared the P-values associated with each ϕ parameter, and we used a significance threshold of P < 0.05 / [m (m − 1)/2].

To compare the disease risk in homozygotes and heterozygotes, we constructed additive models after excluding all homozygous individuals (to estimate the heterozygous effect size) or excluding all heterozygous individuals (to estimate the homozygous effect size). This separation of genotype groups was necessary to estimate the true additive component for each HLA haplotype’s disease risk (from homozygotes only) and subsequently allow for the calculation of the dominance component (based on heterozygotes only). For dosage-based analyses, we defined heterozygous individuals as those with a dosage greater than 0.95 and less than or equal to 1.05, while homozygous individuals were those with a dosage greater than 1.05.

Calculation of phenotypic variance explained

We calculated the proportion of phenotypic variance explained by a given locus using the liability threshold model^48,49. We assumed that disease risk is the consequence of an underlying liability score. Each individual with a score above a pre-specified threshold gets disease⁵⁰. Each genotype has the same threshold, but the distribution of liability can differ among genotypes. The variance between the genotype-specific liability functions is a measure of the variance explained by the locus. For a more detailed description, including equations, see Supplementary Note 3.

Analysis of amino acid-level non-additive effects

For RA, we also analyzed non-additive effects of individual amino acid positions within specific HLA genes. We used imputed amino acid genotypes at positions 13, 71, and 74 of HLA-DRB1, and we analyzed all residues at these positions with a frequency greater than or equal to 5% in the T1DGC reference panel. We used the previously described allele-level models (Equations 2 and 3) to assess the non-additive effects of amino acid variants.

Because residues at amino acid positions within a given locus are in strong linkage disequilibrium, we used a stepwise conditioning approach to test the effects at successive positions on RA risk, following refs.^20,51. We analyzed positions in the order of significance of additive contribution to disease risk. First, we analyzed non-additive effects in DRβ1#13. Then, we analyzed DRβ1#71 while conditioning on DRβ1#13, and we analyzed DRβ1#74 while conditioning on DRβ1#13 and DRβ1#71. To condition on a specific amino acid position, we included all possible amino acid variants at that position as covariates, but we excluded any variant that had strong correlations to other variants in the dataset (R² > 0.97)²³.

Permutation of imputed HLA genotypes

To verify that the observed non-additive effects were not a subtle artifact of imputation inaccuracies, we permuted SNP-imputed HLA genotypes across cases and controls, based on the case probability predicted by a purely additive model (Equation 2). This approach conserves allele frequencies (which confer additive disease associations) within cases and controls and also conserves individual genotypes. However, it randomizes the distribution of homozygote and heterozygote genotypes among cases and controls. We performed 10,000 permutations, and for each permutation we recorded the deviance of a non-additive model with dominance terms for all relevant HLA haplotypes (Equation 3). To validate the permuted cohorts, we also compared the distribution of additive effects for each relevant HLA haplotype with the observed values in the actual dataset (Supplementary Fig. 2).