Theory of bi-molecular association dynamics in 2D for accurate model and experimental parameterization of binding rates

Abstract

The dynamics of association between diffusing and reacting molecular species are routinely quantified using simple rate-equation kinetics that assume both well-mixed concentrations of species and a single rate constant for parameterizing the binding rate. In two-dimensions (2D), however, even when systems are well-mixed, the assumption of a single characteristic rate constant for describing association is not generally accurate, due to the properties of diffusional searching in dimensions d ≤ 2. Establishing rigorous bounds for discriminating between 2D reactive systems that will be accurately described by rate equations with a single rate constant, and those that will not, is critical for both modeling and experimentally parameterizing binding reactions restricted to surfaces such as cellular membranes. We show here that in regimes of intrinsic reaction rate (k_a) and diffusion (D) parameters k_a/D > 0.05, a single rate constant cannot be fit to the dynamics of concentrations of associating species independently of the initial conditions. Instead, a more sophisticated multi-parametric description than rate-equations is necessary to robustly characterize bimolecular reactions from experiment. Our quantitative bounds derive from our new analysis of 2D rate-behavior predicted from Smoluchowski theory. Using a recently developed single particle reaction-diffusion algorithm we extend here to 2D, we are able to test and validate the predictions of Smoluchowski theory and several other theories of reversible reaction dynamics in 2D for the first time. Finally, our results also mean that simulations of reactive systems in 2D using rate equations must be undertaken with caution when reactions have k_a/D > 0.05, regardless of the simulation volume. We introduce here a simple formula for an adaptive concentration dependent rate constant for these chemical kinetics simulations which improves on existing formulas to better capture non-equilibrium reaction dynamics from dilute to dense systems.

I. INTRODUCTION

Proteins bind together to form complexes that can then function in a variety of processes in the cell, including signal transduction, regulation of DNA transcription, and the assembly of larger and newly functional macromolecular complexes. A significant fraction of these binding events do not occur freely within solution but are influenced by or restricted to the two-dimensional (2D) surface of the plasma or internal membranes, such as that occurs in receptor binding events and in multiple stages of vesicle trafficking in the cell. Modeling the dynamics of such systems of reactive species almost always requires computer simulation, as analytical treatments are only available for the simplest types of reactions, where even solving A + B⇄C requires approximation. Probably, the simplest and most efficient approach to simulating reaction dynamics is via systems of rate equations that track the time-dependent concentrations of all species. Spatial resolution can also be built in by splitting the full volume into sub-volumes, but ultimately, the reactions between species are parameterized by single rate constants for each binding, unbinding, or other type of reaction. A more detailed approach to modeling reaction dynamics is to track the positions of each single particle as they obey diffusional dynamics and undergo association reactions upon collisions with their assigned binding partners. Smoluchowski theory (ST)¹ uses this single-particle model to describe the simplest diffusion influenced reactions parameterized by a diffusion constant D, a binding distance σ, and an intrinsic rate constant k_a that controls the probability of complex formation once binding partners have collided to an encounter complex. While more complex models of bimolecular association incorporate additional physical details driving the interactions,² the essential physics sufficient to study the effects of diffusion and barrier activated complex formation upon collisions is captured in the Smoluchowski framework.

A major focus of this paper is in characterizing when the dynamics of the bimolecular association process (A + B → C) can be accurately approximated by a simple rate-equation with a single characteristic rate constant in 2D. Such reactions could then be safely simulated or experimentally parameterized via the simpler chemical kinetics methods, without explicitly accounting for diffusion. Otherwise, extra care in both simulation and experiment must be taken to correctly treat these 2D reactions. We derive here such bounds on the reaction parameters by analyzing the rate behavior derived from Smoluchowski theory and deriving novel analytical results that allow us to quantify, via a rigorous theoretical analysis, how the reaction dynamics will vary based on the reaction parameters k_a and D, and independently of the size of the experimental system or simulation volume. This analysis follows in Secs. II C and III A and is summarized in Table I. The results are also of theoretical interest, as they highlight the practical irrelevance of known universal asymptotic behavior in 2D that cannot be observed over any measurable (including evolutionary) time-scale. The conclusions apply to any complex system of coupled reversible reactions, but we focus most of the analysis on irreversible association between binding partners, as this is the source of the breakdown in the single rate constant approximation.

TABLE I.

Regimes of parameters defining rate-limiting through to diffusion controlled reactions.

	Bounds on reaction parameters	% decrease of k(t1day) from k(t = 0)	Single rate fit to data
Rate limited	ka/D < 0.05	δ < 10%	kfit ∼ ka
Weakly diffusion influenced	0.05 < ka/D < 0.5	10% < δ < 50%	0.5ka < kfit < ka
Diffusion influenced	20 > ka/D > 0.5	50% < δ < 95%	0.05ka < kfit < ka
Strongly influenced/Diffusion controlled	ka/D > 20	<3% different from ka = ∞ for all t > 1 s	kfit < < ka

One motivation for establishing regimes of rate-behavior in 2D is because of the advantages of using rate-equations and simple chemical kinetics to describe reaction dynamics in simulation and experiment. In most experiments to measure binding kinetics between a pair of reactants, the default approach is to extract a single rate constant for the on and off reaction, independently of any knowledge of the diffusion constants or the container dimensions, via chemical kinetics. Only species concentrations need to be specified. As we detail below, this approach will result in rates that vary as the initial concentrations vary, for reactions where k_a/D > 0.05, and most noticeably when k_a/D > 0.5. Such rates then fail to provide a robust and transferrable characterization of the binding pair, as they are sensitive to the experimental setup. For simulations, rate equations are desirable because they have fewer degrees of freedom, they are routinely available in software packages,^3,4 and they are generally simpler to implement, more efficient, and more straightforward to maintain accuracy in the solutions.^5,6 These approaches can incorporate spatial resolution by partitioning the volume into sub-volumes⁷ and can also be combined with more detailed spatially resolved methods to create efficient multi-scale techniques that maintain high resolution only when necessary.⁸ Their limitations are that they provide no information on spatial distributions or fluctuations of particle positions, they cannot incorporate molecular structural details, reactant species are assumed well-mixed in each volume, and as we emphasize here, they do not correctly describe the dynamics of many 2D reactions. Numerical simulation methods that will always be able to correctly describe the dynamics are single-particle reaction diffusion methods. While less efficient than rate-equations, they require fewer assumptions, and very accurate methods for solving many-body systems include brute-force Brownian dynamics,⁹ and more efficient methods such as Green’s Function Reaction Diffusion (GFRD),¹⁰ the small-voxel tracking algorithm,¹¹ and the free propagator reweighting (FPR)¹² algorithm used here.

The reason that simple chemical kinetics is not generally an accurate description of 2D association dynamics is because it requires the assumption of a single phenomenological rate constant, k_on, that emerges from the microscopic searching and association of reactants. It is this assumption that is not generally applicable in 2D systems, and we note that this additional assumption is required even if one can also assume the reactant species are well-mixed. The origin of the breakdown in the expectation of a fixed single rate is due to the properties of the diffusional search or random walk that controls encounters between species in 2D versus 3D. In dimensions d ≤ 2, diffusional dynamics are re-entrant, such that, given enough time, all particles will eventually find one another. In 3D, particles beyond a finite separation will instead approach a vanishing probability of encountering one another in a diffusional search. The consequence of this fundamental property of diffusional searching in 2D is that complex formation is sensitive to the separations between reactant particles throughout the many-body association process, even for well-mixed initial conditions (ICs). Theoretically, this means that rate equations do not ever provide the correct description of time-dependent complex formation for self (A + A → 0) or distinct partners (A + B → 0) in 2D. Over short and long time scales, the rate of complex formation is always changing as the reaction proceeds and does not ever reach a limiting constant value like in 3D, because as t → ∞, the rate always decays to zero. However, much of the existing analysis on 2D RD association dynamics focuses on the universal time-dependent decay that becomes independent of the intrinsic rate k_a¹³ or focuses on diffusion controlled reactions (k_a = ∞),^14,15 or pseudo-first order reactions.¹⁶ Here, we highlight the practical differences that emerge for association dynamics as the barrier to complex formation grows (rate-limited regime as k_a → 0), regardless of whether the 2D system domain is infinite or bounded.

In 3D, because one is above the critical d = 2 dimension for two-particle reactions due to the properties of random walks, one instead observes association dynamics where the reaction rate is not sensitive to density fluctuations,⁴ and rate equations therefore work quite accurately beyond short times. In fact, it has been shown theoretically that in 3D, the long-time asymptotics of irreversible association of self (A + A → 0) or distinct partners (A + B → 0) in RD systems is governed by a single rate constant with a time dependence correctly described by rate equations^17,18 (with the exception of systems with approximately equal starting concentrations of A and B where the final relaxation follows a t^−d/4 decay¹⁹). The time-dependence of the rate therefore only alters association dynamics at short times. How short these ranges are before the single rate constant behavior is reached depends on the specific reaction parameters and diffusion constants but in 3D still encompasses measurable time scales for even the slowest diffusing proteins, which contrasts with 2D, as discussed below. The single rate constant in 3D accounts for both the time for (1) complexes to diffuse and encounter and (2) the rate that encountering reactants bind to form product. These association dynamics have been characterized via Smoluchowski theory¹⁵ and field theoretic renormalization group techniques (see, e.g., Refs. 13 and 18).

A major conclusion of this work is that in 2D, there exist regimes of the parameters describing reaction rates and diffusion where the effects of diffusion on the short, intermediate, or the long-time decay over any measurable time scale are increasingly small as to render simple rate-based kinetics a very accurate description of association with a single, nearly steady-state rate constant, just as in 3D. Our work makes it possible to know, a priori, from knowledge of the reaction parameters, when this behavior can be expected, as summarized in Table I. Importantly, our results do not require one to enforce an arbitrary size of the system in order to extract an estimated rate-constant, as previous approaches to estimating single rate constants in 2D require.^14,20 Instead, our results are built off (1) the fundamental distinction between 2D and 3D dynamics, that diffusion is re-entrant in 2D, and (2) the fact that this fundamental property in 2D becomes negligible for all practical measurement or simulation times when the ratio of k_a/D is small. This is because while the rate of complex formation will eventually decay to zero, we show here in Sec. II C that it does so with a power law time-dependence with a very small exponent, leaving the rate effectively unchanged over time scales observed for experimental molecular systems. The 2D system is now, similar to all 3D systems, effectively insensitive to density fluctuations as the reaction proceeds to completion. The time required for the rate to drop to zero will be much longer than the age of the universe.

The expectation of a single rate constant in fully characterizing a bimolecular reaction is highly non-trivial, both for simulation and experiment. It means that this same rate will apply for general non-uniform initial conditions, which is relevant for any complex system where reactants may participate in multiple binding interactions with multiple species. It also means the same rate will apply for all reactions proceeding out of equilibrium, which is common in most cellular reaction systems. In the opposite regime, where k_a/D grows larger than 0.05, simple chemical kinetics will fail to describe relaxation over all time scales, even for uniform initial conditions. In the regime where no single rate exists, it instead becomes necessary to use a multiple parametric description for experiment and simulation that in the simplest cases captures diffusion and the rate of encounter complex binding. We provide MATLAB code for fitting time-dependent concentration data to the multi-parameter Smoluchowski model to extract a transferable set of reaction parameters k_a, D, and the molecular length scale σ (see the supplementary material).²¹

Another focus of this paper considers how, despite the lack of a single characteristic rate constant in the regimes of diffusion influenced 2D reactive systems, one can still attempt to describe an adaptive rate constant for use in simple rate-equation based simulations. Our definition here in Sec. II D of a novel adaptive, density dependent rate constant builds directly off earlier approaches for estimating a mean rate of complex formation given the parameters of D, k_a, and the system volume, or area.^14,20,22,23 These characteristic rates²⁰ can be used to define reaction rates for use in deterministic and stochastic kinetic models, or the spatially partitioned reaction-diffusion master equation (RDME) methods.²⁴ The spatial resolution of RDME simulations depends on the lattice size, and as it is decreased, these mesoscopic rates will better describe the microscopic dynamics of single-particle Smoluchowski models, as long as the mesh size stays above a lower limit.^25,26 However, because these characteristic rates of complex formation have been derived for a single reactive pair in the defined volume (or area), they will underestimate the rate of complex formation when multiple mobile reactive species are present in the volume. Here, we extend the previous approach^24,25 to correct for the presence of multiple reaction partners within the system volume as simply as possible, by defining the maximum length scale bounding the reactant pairs to be dependent on the concentrations of reactive species. This adaptive rate can then capture the dependence of the rate of complex formation as it varies from dilute to dense systems, regardless of the initial conditions. It can therefore better reproduce the full time-dependence of the microscopic reaction-diffusion process, even for large simulation volumes.

Our analysis of the rate behavior of irreversible association between reactants applies equally to reversible systems, where the formed complex can also undergo dissociation. The off-rate is conceptually much simpler than the rate of association, because it only describes a temporal frequency of an event occurring, generally modeled as a Poisson process. It acquires a system or time dependence, however, when the macroscopic dissociation constant must account for the intrinsic unbinding reaction rate (k_b) as well as diffusion apart. This is analogous to the macroscopic on-rate and allows the reaction to maintain detailed balance as the reaction proceeds, such that K_D = k_b/k_a = k_off(t)/k_on(t). Because the macroscopic dissociation constant can be defined through this equation once the association rate behavior is determined, we focus the analysis on diffusion coupling to irreversible association reactions that can then be applied to reversible processes.

The final objective of our paper is to provide the first numerical tests of previously untested reaction dynamics in 2D compared to Smoluchowski theory and several additional theoretical approaches applied to reversible reactions.^27–30 We are able to do so via our implementation here in 2D of a recently developed single-particle algorithm for simulating reaction-diffusion systems both accurately and efficiently in 3D.¹² Theoretical treatments of nearly all many-body problems, particularly for reversible reactions, are ultimately restricted in their ability to fully describe the time dependence of the process, and require approximations and/or are limited to specific temporal limits. For irreversible reactions, renormalization group calculations on field theory formulated reaction-diffusion equations can predict the exact asymptotic behavior (reviewed in Ref. 18), and derivations of binary non-Markovian kinetic equations when accounting for many-body correlations provide a general framework for quantifying sources of deviations from simple chemical kinetics,^31,32 for example. Most treatments of 3D reaction dynamics have already been tested via numerical simulation,^12,33–36 and some predictions in 2D,^19,37 and here, we provide new simulations that highlight the effectiveness of specific theoretical approximations in describing 2D reaction dynamics.

In summary, we first review existing results from Smoluchowski theory describing the rate of complex formation for uniformly distributed systems of reactants in Secs. II A and II B. Then, by analyzing the asymptotic behavior of the time-dependent rate, we derive the regimes of diffusion and reaction parameters in 2D that differentiate rate-controlled through to diffusion-controlled reactions in Secs. II C and III A, summarized in Table I. We show in Eq. (16) that with small intrinsic rate constants, the time-dependent rate constant has a power law dependence on time, with a very small exponent, implying that the rate is nearly constant over measurable time scales. This result also means that for many-body processes in this regime, the long-time asymptotics will also be governed by power-law decay, never reaching, over any feasible time scales, the known universal log(t)/t decay.^13,38 This power law behavior occurs due to the presence of a significant and dominant prefactor to the time dependent logarithmic term. We describe the extension of a previously developed FPR algorithm¹² to the dynamics of RD systems in 2D and use the numerical simulations to study the behavior of irreversible and reversible RD systems relative to the approximate rate-based kinetics and theoretical treatments. Last, we compare options, including our adaptive density dependent rate defined in Sec. II D, for describing a single phenomenological rate constant for approximating the description of complex formation in equilibrium or non-equilibrium systems using rate equations.

II. THEORY

A. Background on Smoluchowski theory and many-body association

By explicitly accounting for the diffusion of particles to contact before reactive complexes can form, Smoluchowski theory¹ provides one of the simplest improvements relative to the rate equations of chemical kinetics for determining the time-dependence of complex formation. Smoluchowski theory, unlike chemical kinetics, captures correlations between independent pairs of reactants and is an exact description of dynamics only for a single immobile target surrounded by an initially uniform distribution of reactant partners.^18,39 When applied to many-body association such as A + A → 0 or A + B → 0 (illustrated in Figure 1), as described further below, it is no longer exact, but it is quite accurate in predicting the time-dependence of the association process.¹⁸ The theory solves for the density of particles ρ(r, t)^39,40 obeying the spherically symmetric diffusion equation

$${\displaystyle \frac{\partial \rho \left(r,t\right)}{\partial t}=D\frac{1}{r^{d-1}}\frac{\partial }{\partial r}\left(r^{d-1}\frac{\partial \rho (r,t)}{\partial r}\right)}$$ (1)

(where d is the dimensionality) in the presence of a reactive boundary at r = σ modeled via the radiation boundary condition (RBC),

$${\displaystyle D{\left.\frac{\partial \rho (r,t)}{\partial r}\right|}_{r=\sigma }=\kappa \rho (\sigma ,t),}$$ (2)

In 2D, κ = k_a/2πσ and in 3D, κ = k_a/4πσ². In its initial formulation, all collisions were assumed reactive (κ = ∞), but this partially absorbing boundary due to Collins and Kimball⁴¹ provides the flexibility to mimic barrier activated complex formations, such that some collisions are non-reactive. IC of the particle distribution is uniform, $\rho \left(r,0\right)=1$. Another way of solving for the density is by starting with the Green’s function (GF) solution to Eq. (1) with the same BC, with a delta function IC, and the solution given as p(r, t|r₀, 0).⁴² The density ρ(r₀, t) solution of Smoluchowski theory is then simply the integral over the GF solution with ρ(r, 0) = 1, and it is more conventionally defined as the survival probability, S(t|r₀) = ρ(r₀, t).^43,44 We explicitly define the 2D GF and survival probability (or density ρ(r₀, t)) in Sec. IV.

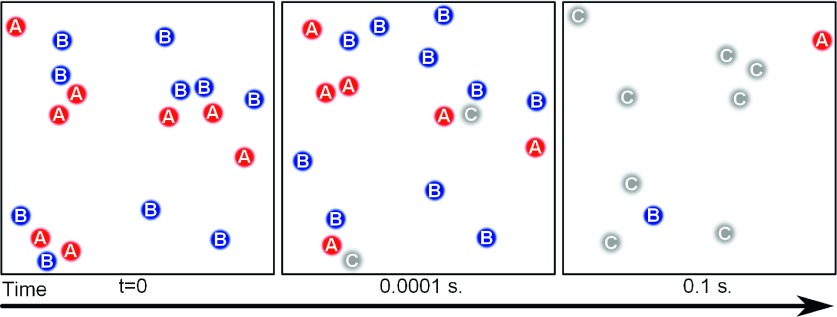
FIG. 1.

Complex formation, A + B → C, in 2D. To model the dynamics of complex formation using simple chemical kinetics, one must first assume the reactant species are well-mixed, which we can enforce here, and second, one must assume the rate of complex formation is a constant throughout the many-body reaction process. This second assumption does not generally apply in 2D, which represents a critical dimension where the rate of complex formation is always sensitive to the spatial distribution of reactants, and continuously decreases as the reaction proceeds and remaining reactants are farther and farther apart. The images represent snapshots of a 2D-FPR simulation with D_AB = 2 nm² μs⁻¹, k_a = 100 nm² μs⁻¹, σ_AB = 1 nm, and Δt = 0.1 μs.

The flux of particles across the reactive surface at r = σ defines the irreversible time-dependent rate of complex formation,^39,41

$${\displaystyle k\left(t\right)=2\pi \sigma D\frac{\partial }{\partial r_0}S\left(t|r_0\right){|}_{r_0=\sigma }.}$$ (3a)

For the RBC, it is also true that^43,45

$${\displaystyle k\left(t\right)={\left.k_{a}S\left(t|r_0\right)\right|}_{r_0=\sigma }.}$$ (3b)

This rate of complex formation therefore varies with time and represents a more detailed predictor of the rate of bimolecular complex formation from uniform initial particle distributions. This monotonic rate function k(t) captures rapid early complex formation due to short range particle pairs followed by slower complex formation from the remaining pairs present at increasingly larger separations.

Using this time-dependent rate in the ordinary-differential equation (ODE) for the well-mixed many-body association problem, for concentration dependent relaxation of self interactions A + A → 0,

$${\displaystyle \frac{dA\left(t\right)}{dt}=-k\left(t\right)A{\left(t\right)}^2,}$$ (4)

produces a quite accurate description of time-dependent association, despite ignoring correlations between many non-independent reactant pairs and any spatial inhomogeneities in the particle distribution throughout the full time evolution.^18,32 The application of Smoluchowski theory for many-body association assumes that the reaction between an immobile reactive center and a radially symmetric solution of reactive partners is not influenced by the presence of other reactive sources. In reality, the radial distribution of partners around any reactive center is influenced by other reactive events in solution, and all particles are mobile.

The solution to the ODE in Eq. (4) requires the integral ${\int }_0^{t}k\left(\tau \right)d\tau$, such that in the case of self interactions,

$${\displaystyle A\left(t\right)=A_0/(1+A_0{\int }_0^{t}k\left(\tau \right)d\tau ),}$$ (5)

or for distinct reactants,

$${\displaystyle A\left(t\right)=A_0(B_0-A_0)/\left[B_{0}exp(+(B_0-A_0){\int }_0^{t}k\left(\tau \right)d\tau )-A_0\right]}$$ (6)

for A₀ < B₀ where A₀ and B₀ are initial concentrations. The behavior of k(t) and its integral can be analyzed to predict the ultimate relaxation of the concentrations of complexes and reactive species in 2D.

The exact functional form of the rate in 2D we reproduce here. The solutions were initially printed in Sec. 13.5 of Ref. 42 of the density/survival probability which appears in the rate definitions, Eq. (3). In the case of partially reactive particles, where k_a < ∞, the rate is given by^42,46

$${\displaystyle k\left(t\right)=k_a+\frac{8D{k}_a^2}{\pi }{\int }_0^{\infty }\frac{du}{u}\frac{\left(e^{-D{u}^{2}t}-1\right)}{\left({\left[2\pi \sigma Du{Y}_1\left(\sigma u\right)+k_a{Y}_0\left(\sigma u\right)\right]}^2+{\left[2\pi \sigma Du{J}_1\left(\sigma u\right)+k_a{J}_0\left(\sigma u\right)\right]}^2\right)}.}$$ (7)

When k_a is infinity (absorbing BC), the rate is given by^42,46

$${\displaystyle k\left(t|k_a=\infty \right)=\frac{8D}{\pi }{\int }_0^{\infty }\frac{e^{-D{u}^{2}t}}{u\left({\left[Y_0\left(\sigma u\right)\right]}^2+{\left[J_0\left(\sigma u\right)\right]}^2\right)}du.}$$ (8)

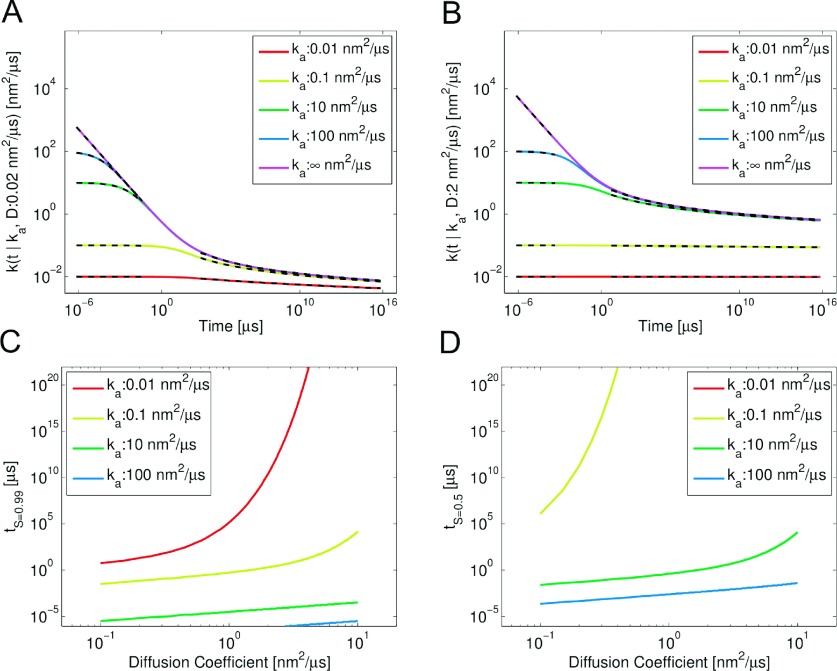
In Figures 2(a) and 2(b), we plot the time dependence of this rate for a range of k_a values and two diffusion constants. While the decrease is very apparent for large k_a, the rate starts to look flat for smaller and smaller values. In Figures 2(c) and 2(d), we plot the time it takes for the rate to decrease by 1% from its initial value and 50%, respectively. It is clear that for small k_a, it takes increasingly longer to see any change in the observed rate of complex formation.

FIG. 2.

(a) and (b): Behavior of time-dependent reaction rate $k\left(t\right)$ of reactions in 2D for varying intrinsic reaction rate k_a for different color curves and diffusion constants (a) D = 0.02 nm²/μs. (b) D = 2 nm²/μs. Black dashed curves are the asymptotes for t < 10⁻³σ²/D and t > 10 σ²/D from Eqs. (10), (11), (13), and (14). (c) and (b): The time passed before the rate has decreased by (c) 1% of its initial value, and (d) 50% of its initial value, plotted vs the diffusion constant. The curve for k_a = 0.01 nm²/μs is not visible in (d) as it takes longer than 10²⁰ μs for the rate to drop by 50%.

These 2D rates do not reach any long-time steady-state values but rather decay to zero as t → ∞, indicating no single characteristic rate. In contrast, in 3D, the time-dependent Smoluchowski rate reaches a well-known limiting long-time value³⁹ that is an obvious choice for use in the simple rate-equations of chemical kinetics, defined by

$${\displaystyle k_{\mathit{on}}^{3D}={\left(\frac{1}{k_a^{3D}}+\frac{1}{4\pi D\sigma }\right)}^{-1}.}$$ (9)

Because the long-time decay is then governed by this single rate constant, this means that the predictions of concentration dependent relaxation from rate equations will also be correct, and therefore, the impact of time-dependence in the 3D rate function is relevant only for short time scales.

An important note on the use of the Smoluchowski time-dependent rate function is that it only applies to simple reaction systems (A + B⇆C is the most complex) with uniform initial conditions, and it is therefore not a useful approach for modeling coupled systems of reactants. The time dependence of the rate evolves depending on the history of previous binding events (i.e., it is non-Markovian). The uniform density approximation is worse as the system relaxes, and therefore there is no unique mapping from the time-dependent rate to a rate at a corresponding bulk density of particles. In Sec. II D below, we develop a rate constant that is dependent on the bulk density of the particles and therefore varies as the reaction evolves, despite these considerations, as it nevertheless provides a means for modeling coupled systems of reactions using simple rate equations in 2D.

B. Time-dependent rate asymptotics

1. Long-time asymptotics

The 2D rate functions defined above are not readily analyzed in their integral form, and the behavior for both short (t < < σ²/D) and long time (t > > σ²/D) asymptotics can be usefully simplified.⁴² These expansions in powers of t not only provide much simpler closed form expressions of the time-dependent rate for our analysis in Sec. II C below but they also make it easier to evaluate, plot, and compare the decay as a function of varying parameters.

By expanding the solutions for k(t) in Laplace space and inverting term by term, the long time absorbing BC is given by (Sec. 13.5 of Ref. 42)

$${\displaystyle k\left(t\gg \frac{{\sigma }^2}{D}\right)=4\pi D\left(\frac{1}{log\left(4Dt/{\sigma }^2\right)-2\gamma }\right.-\left.\frac{\gamma }{{\left(log\left(4Dt/{\sigma }^2\right)-2\gamma \right)}^2}+\vartheta (log{\left(t\right)}^{-3})\right),}$$ (10)

where γ is Euler’s constant, 0.577216.

The long-time asymptotic behavior for RBC was derived in Ref. 47 and results in the form

$${\displaystyle k\left(t\gg \frac{{\sigma }^2}{D}\right)=4\pi D\left(\frac{1}{log\left(4Dt/{\sigma }^2\right)-2\gamma +4\pi D/k_a}-\frac{\gamma }{{\left(log\left(4Dt/{\sigma }^2\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^2}-\frac{1.311}{{\left(log\left(4Dt/{\sigma }^2\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^3}\right.+\left.\frac{0.25}{{\left(log\left(4Dt/{\sigma }^2\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^4}+\vartheta (t^{-1}log{\left(t\right)}^{-2})\right)}$$ (11)

which was also shown previously in this same functional format to lower order.⁴⁸ It is clear from these equations that as k_a → ∞, the asymptotics agree with the absorbing BC solution from Eq. (10). Both these asymptotics are plotted in black dashed lines atop the full k(t) in Figures 2(a) and 2(b), with excellent agreement.

To describe the long-time relaxation of the reactant species A(t), the integral over the rate is required for Eqs. (5) and (6). Integrating Eq. (11) above with RBC, this functional form becomes

$${\displaystyle {\int }_0^{t}k\left(\tau \right)d\tau =4\pi {\sigma }^2\left(Dt/{\sigma }^2\left(\frac{1}{log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}}+\frac{1}{{\left(log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^2}+\frac{2}{{\left(log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^3}+\cdots \right)\right.-\gamma Dt/{\sigma }^2\left(\frac{1}{{\left(log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^2}+\frac{2}{{\left(log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^3}+\cdots \right)-\left.\frac{1.331}{2}Dt/{\sigma }^2\left(\frac{2}{{\left(log\left(\frac{4Dt}{{\sigma }^2}\right)-2\gamma +\frac{4\pi D}{k_a}\right)}^3}+\cdots \right)+\vartheta \left(t\mathit{log}{\left(t\right)}^{-4}\right)\right)}$$ (12)

and we have used the series expansion of the Exponential integral for large arguments and included only terms in each series to order t/log(t).³

2. Short-time asymptotics

The short time asymptotics are also accessible from expansions of Bessel functions in Laplace space for large s (small t) (Sec. 13.3 of Ref. 42). For absorbing BC, it is given as⁴²

$${\displaystyle k\left(t\ll \frac{{\sigma }^2}{D}\right)=2\pi D\left(\frac{1}{\sqrt{\pi Dt/{\sigma }^2}}+\frac{1}{2}-\frac{1}{4}\sqrt{\frac{Dt/{\sigma }^2}{\pi }}+\frac{1}{8}Dt/{\sigma }^2-\frac{100}{384}Dt/{\sigma }^2\sqrt{\frac{Dt/{\sigma }^2}{\pi }}+\vartheta \left(t^2\right)\right)}$$ (13)

and for the RBC as

$${\displaystyle k\left(t\ll \frac{{\sigma }^2}{D}\right)=2\pi D\left(\frac{1}{2}-\frac{k_a}{2\pi D}\sqrt{\frac{Dt/{\sigma }^2}{\pi }}-\frac{k_a}{4\pi D}Dt/{\sigma }^2\sqrt{\frac{Dt/{\sigma }^2}{\pi }}+\frac{k_a}{2\pi D}exp\left(Dt/{\sigma }^2{\left(\frac{k_a}{2\pi D}\right)}^2\right)\mathit{erfc}\left(\frac{k_a}{2\pi D}\sqrt{Dt/{\sigma }^2}\right)\right.\left.\left(1-\frac{\pi D}{k_a}+\frac{k_a}{2\pi D}Dt/{\sigma }^2+\frac{k_a^2}{2{\left(2\pi D\right)}^2}{\left(\frac{Dt}{{\sigma }^2}\right)}^2\right)+\vartheta \left(t^2\right)\right),}$$ (14)

also previously derived with fewer terms.⁴⁸ These exhibit the correct behavior at t = 0, where k(t = 0) = k_a. This behavior is also plotted atop the full k(t) in Figures 2(a) and 2(b).

3. Convenient simple form of rate function

While these asymptotic forms are relatively simple over their specified time domains, we also determined a simplified and quite accurate functional form of k(t) for RBC using curve fitting from Eureqa⁴⁹ for a wide time range. Existing examples of simple fit functions for the rate with absorbing BCs are quite accurate over all time scales,^50,51 for the long-time survival probabilities with RBC,⁵² and for fluorescence quenching data with RBC.⁵³ We found, using ranges in σ : 1 − 20 nm, D : 0.005 − 20 μm² s⁻¹, k_a : 10⁻³ − 10³ μm² s⁻¹, and t : 10⁻³ − 8.6410⁴ s, an accurate approximation of k(t) given by

$${\displaystyle k_{\mathit{apprx}}\left(\sigma ,D,k_a,t\right)=\frac{k_{a}D}{D+p_1{k}_{a}log\left(p_2+\frac{p_{3}Dt}{{\sigma }^2}+\sqrt{\frac{p_{4}D{k}_{a}t}{{\sigma }^2\left(k_a+p_{5}D\right)}}\right)},}$$ (15)

where p₁ = 0.0791183, p₂ = 0.935916, p₃ = 2.62231, p₄ = 12.9791, and p₅ = 8.70808. The R² goodness of fit is 0.99998929 and the average absolute percent error is less than 1%. This equation provides a convenient and simple way to visualize the rate function as a function of the reaction parameters, and also highlights the weak dependence on time for small values of k_a. One can use this function in lieu of the much more complicated and difficult to work with Eq. (7) to fit the dynamics of association reactions to the Smoluchowski model.

C. Theory of time-dependent rate for small intrinsic rates, k_a

1. Asymptotic behavior of k(t)

For small ratios of k_a/D where multiple collisions are necessary to activate complex formation, we show here that the long-time rate behavior in 2D (Eq. (11)) can be well approximated by a power-law decay. This power-law decay will actually correctly describe the time-dependence of the rate over all measurable (including evolutionary) time scales, such that the known universal decay to zero with the log(t)/t dependence of the rate will never be observed. This is one of the primary results of our analysis that we can use to identify critical changes in the time-dependent decrease of the rate function k(t), and the corresponding regimes of parameters that control these differing types of rate behavior. Figure 2 suggests that there is a change in the time-dependence of the rate for small k_a, and here we make that rigorous. The long-time asymptotic expressions in Sec. II B above are accurate starting from t ≈ 10σ²/D, which for many membrane bound proteins will be on the order of ∼10⁻⁵ s. These asymptotic functions can therefore be used to describe much of the dominant rate behavior in 2D.

The power law decay for small k_a/D comes from re-writing the denominator of Eq. (11) in the form log(z) + 1. For log(z) < 0.1, the approximation that log(z) + 1 ≈ z is correct to less than 5%. This approximation results in the rate function

$${\displaystyle k\left(t\gg \frac{{\sigma }^2}{D}\right)=4\pi D\left(k_a/\left(4\pi D\right){\left(\frac{4Dt/{\sigma }^2}{e^{2\gamma }}\right)}^{-k_a/\left(4\pi D\right)}-\gamma {\left(k_a/\left(4\pi D\right)\right)}^2{\left(\frac{4Dt/{\sigma }^2}{e^{2\gamma }}\right)}^{-2k_a/\left(4\pi D\right)}\right.-\left.1.311{\left(k_a/\left(4\pi D\right)\right)}^3{\left(\frac{4Dt/{\sigma }^2}{e^{2\gamma }}\right)}^{-3k_a/\left(4\pi D\right)}+\vartheta \left(t^{-4k_a/4\pi D}\right)\right),}$$ (16)

with a power law rather than an apparently logarithmic dependence on time. To achieve this <5% deviation from the description of k(t) from Eq. (11), the constraint on the long-times t for a given set of reaction parameters (D, σ, k_a) is given by

$${\displaystyle \frac{k_a}{4\pi D}log\left(\frac{4Dt}{{\sigma }^2{e}^{2\gamma }}\right)<0.1,}$$ (17)

where t is also beyond the short time limit of 10σ²/D and γ is Euler’s constant.

The significance of these new relations is that they can be used to quantify straightforwardly how much the rate of complex formation will decrease with time from its maximum value of k_a, and correspondingly, whether its change with time will be negligible. For large ratios of k_a/D, Eq. (16) does not apply over any time scale, but for increasing smaller ratios of k_a/D, it extends to very large time scales. For these cases, the rate slows with the average power law dependence of Eq. (16) that has a very small exponent in time given by −k_a/4πD.

From Eq. (17), the effects of diffusion D and the length scale σ on changing the rate are also easier to interpret, with faster D contributing to more rate-limiting behavior and same for larger σ, although the impact of σ is significantly less due to its functional appearance only logarithmically. This is the same trend observed in the 3D case, where the steady state rate becomes more rate-limiting for larger D and larger σ, as is clear from Eq. (9).

2. Asymptotic many-body relaxation

We can apply this same analysis to characterize A(t) and the time-dependent complex formation for many-body systems described by Eqs. (5) and (6) which require the integral in Eq. (12). For smaller values of k_a/D the asymptotic expansion is strongly dominated by the first term and converges more slowly as you approach the absorbing limit, k_a = ∞. The leading order term of ${\int }_0^{t}d\tau k\left(\tau \right)$ is given by $\frac{k_{a}t}{\frac{k_a}{4\pi \text{D}}log\left(\frac{4Dt}{{\sigma }^2{e}^{2\gamma }}\right)+1}$ but using the same approximation as above for small enough values of k_a/D this is accurately described as ${\int }_0^{t}d\tau k\left(\tau \right)\approx k_{a}t{\left(\frac{4Dt}{{\sigma }^2{e}^{2\gamma }}\right)}^{-k_a/\left(4\pi D\right)}$, even for the longest times measurable. This behavior is similar to the behavior in 3D, where ${\int }_0^{t}d\tau k\left(\tau \right)\to k_{\mathit{on}}^{3D}t$ for all parameters at long times ($k_{\mathit{on}}^{3D}$ is defined in Eq. (9)). The additional time-dependent factor in 2D above will cause, for small k_a/D, a very slow drop in the scale factor of t, such that

$${\displaystyle k_{\mathit{on}}^{\mathit{eff}}\left(t\right)=k_a{\left(\frac{4Dt}{{\sigma }^2{e}^{2\gamma }}\right)}^{-k_a/\left(4\pi D\right)}}$$ (18)

is a very slowly decreasing function of time. The important implication of this behavior is that the near steady-state rate of complex formation implies that the rate equations will provide an accurate description of time-dependent complex formation in 2D, with the fixed rate close to the barrier activated value k_a. In Sec. III A below, we use these results to define regimes of rate-limited to diffusion controlled dynamics in 2D.

D. Concentration dependent adaptive rate constants for chemical kinetics

Approaches to solving coupled systems of reactions using deterministic or stochastic kinetic schemes^3,4,54 rather than single-particle RD methods are widespread due to their relative simplicity and efficiency. Recent work^24,25 has determined methods for defining the necessary fixed rate constants in 2D as a function of the system (or subsystem) area and the reaction parameters. Here, we build off this previous work to define an adaptive concentration dependent rate constant for use in such rate equation based methods which improves the agreement of their dynamics with true RD dynamics, without being more difficult to implement.

The average rate of complex formation or mean first passage time can be derived for a pair of particles in a fixed circular area, when one assumes one of the particles fixed centrally at the origin with an excluded volume of πσ², and the other particle is initially uniformly sampling the circle of radius b in the area π(b² − σ²).^14,42 The average time for complexes to form between the two particles given all initial separations σ < r < b has been shown elsewhere to be given by a relatively simple formula for $〈\mathrm{\tau }〉$ in all dimensions,²⁰ with the resulting average rate then given by $〈k_{\mathit{on}}〉={\left[\frac{〈\tau 〉}{\pi (b^2-{\sigma }^2)}\right]}^{-1}$, which approaches the contact limit k_on = k_a as b → σ. The characteristic rate is derived in application to the specific circular geometry with one fixed reactant and a single binding partner. Hence, it provides a theoretically sound choice for approximating the rate of complex formation, although it is not optimized in any sense to produce the correct many-body relaxation. This result has been used in previous definitions of the rate constant for RDME approaches,²⁴ where b is defined to encompass the full area of the system or voxel.

We consider here instead a value of b further constrained not only by the voxel area but also by the presence of multiple reactive partners within the volume. This is because, for a many-body system of reactant particles in some volume, there are generally multiple reactive partners present at any time, and the average distance between them is therefore constrained much more by the distance to the closest reactive partner than by the full volume. In this way, the length scale b controlling encounters between pairs will be dependent on the total density of reactive partners, and will therefore change as the reaction proceeds.

To define a concentration dependent rate constant, we therefore determine the average area per reactant, limited by whichever reactant has the higher density. As the density of targets increases, the distance to travel similarly decreases. This rate depends only on bulk density, and as a result cannot be expected to recover the more detailed RD dynamics sensitive to the full distribution of particle positions.

The value of b is determined by $\frac{\mathit{Area}}{max\left(N_A,N_B\right)}=\pi \left(b^2-{\sigma }^2\right)$, where the Area value is the full system or subsystem. Since, in general reversible reactions, all of the particles are assumed mobile and, in the theoretical setup, the particle is fixed at the center, a better result is to us

$${\displaystyle b\left(\rho \right)=2\sqrt{\frac{\mathit{Area}}{\pi max\left(N_A,N_B\right)}+{\sigma }^2}.}$$ (19)

The factor of two is introduced because the particles can both move in the volume, such that the maximum separation is on the order of twice the radius used in the theory. Values of σ cannot exceed the value of b as this is unphysical, hence if b < σ, the calculated rate should default to the fastest possible rate of k_a. For reversible reactions, the off-rate must be defined so as to preserve detailed balance via the density-dependent on-rate and the equilibrium constant, such that k(ρ)_off = K_Dk(ρ)_on, and

$${\displaystyle k{\left(\rho \right)}_{\mathit{on}}=\left[\frac{1}{k_a}+\frac{1}{8\pi D}\left(\frac{4log\left(\frac{b\left(\rho \right)}{\sigma }\right)}{{(1-{\sigma }^2/b{\left(\rho \right)}^2)}^2}\right.\right.-{\left.\left.\frac{2}{(1-{\sigma }^2/b{\left(\rho \right)}^2)}-1\right)\right]}^{-1},}$$ (20)

where we used the previously derived formula from Ref. 20 for $〈\mathrm{\tau }〉$ and replaced b with b(ρ) defined in Eq. (19).

III. RESULTS

A. 2D regimes of rate-limited to diffusion-controlled reactions

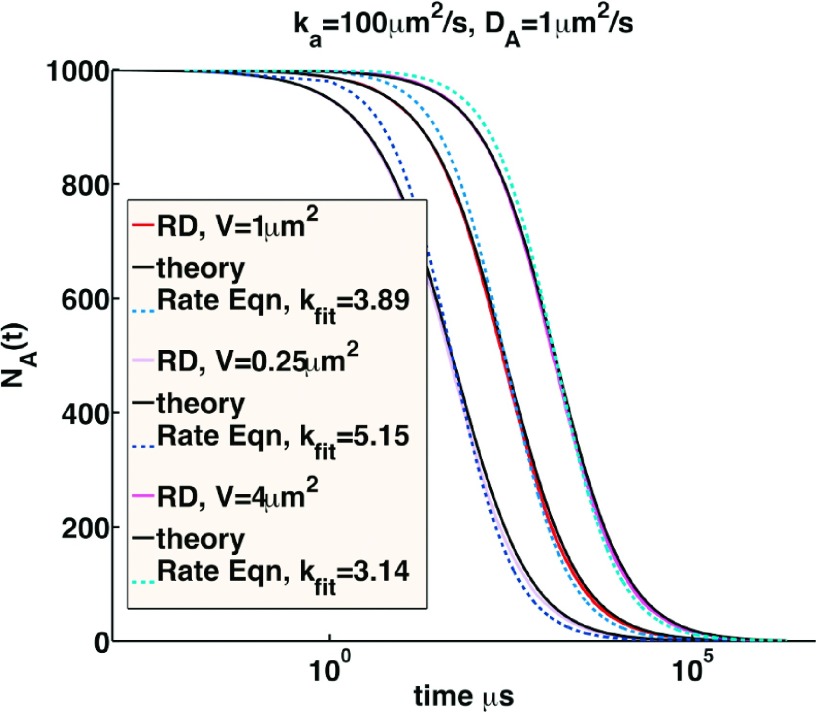
From the analysis we performed above in Sec. II C on the rate behavior derived from Smoluchowski theory, it is possible to determine the domains where reaction rates change so slowly that they are well described by a single rate constant, $k_{\mathit{on}}^{\mathit{eff}}\approx k_a$, over all measurable time scales. Conversely, we define where it will not be possible to define a $k_{\mathit{on}}^{\mathit{eff}}$ value, as any comparison to either simulated or experimental data will produce best-fit k_on values that vary with concentration and/or initial conditions. This latter behavior is illustrated in Figure 3, where the same reaction rate parameters are simulated with full single particle RD dynamics using the FPR algorithm¹² for varying initial concentrations. It is clear that the rate-based approximation to the relaxation is inaccurate over all time scales, and the rate-constant that supplies the best fit to rate equations decreases as the concentration does.

FIG. 3.

Rate-equation relaxation vs RD relaxation for A + A → 0 with fixed reaction parameters and varying initial conditions. All systems have k_a = 100 μm²/s, D_tot = 2 μm²/s, σ = 1 nm, and N_A = 1000 particles. Black curves are Smoluchowski prediction from Eq. (4). Solid purple, red, and magenta curves are numerical solutions using FPR, repeated for 50 trajectories, as V changes from 0.25 μm², 1 μm², and 4 μm². Dashed lines are solutions that are best-fit to the rate equation using a fixed rate constant, where the best fit was defined such that A(t)/A₀ = 0.5. The time-dependence deviates from the RD behavior, and the best-fit rate decreases as the volume increases.

We use Eq. (17) above to define where the rate only decays with the very slow power law of Eq. (16) or (18) from its initial value k(t = 0) = k_a. Equation (17) is generally applicable for any parameters but to connect to biomolecular systems, we consider explicit ranges of physiologically relevant time and parameter ranges. To provide minimal constraints, we consider a long-time for molecular time scale as extending all the way out to 1 week. The logarithm term in Eq. (17) then varies from ∼10 to 35, for D ranging from 10⁻² to 10³ nm²/μs and σ values ranging down to 10⁻² nm.

We find that the criteria for Eq. (17) to hold over these times and wide ranges of parameters is given by k_a/D < 0.05 where the rate behavior will then be well described by a rate of $k_{\mathit{on}}^{\mathit{eff}}\approx k_a$. From the leading order term in Eq. (16), the percent change in the rate over time from k(t = 0) = k_a, such that k(t) = (1 − δ(t)) k_a, is given by $\delta \left(t\right)=1-{\left(\frac{4Dt}{{\sigma }^2{e}^{2\gamma }}\right)}^{-k_a/4\pi D}$, which is close to zero for small values of k_a/D even for very large times. The age of the universe (10¹⁷ s) represents an extreme time scale, and even at this time, the rate at the upper limit of this regime (k_a/D = 0.05) has still only dropped by ∼20%, such that k(t_universe) ≈ 0.8k_a. Because we are interested in characterizing molecular reactions, for concreteness, we will consider deviations of the rate at k_long = k(t_1day).

In Table I, we collect the results of rate-limiting to diffusion-controlled regimes via analysis of Eq. (16) and numerical calculations of the time-dependent rate from Eq. (11). For the rate-limited reactions, where k_a/D < 0.05, one can expect that a single rate constant of k_long ∼ k_a will accurately describe complex formation for all densities and measurable time scales, effectively independently of the specific diffusion constant. On the other extreme, the diffusion-controlled or nearly diffusion-controlled regime, the effective reaction rate will be dependent on the density distribution of the reactants, which will continuously change for any system not in equilibrium. At short times, where particles are closest together, the specific values of k_a, D, and σ determine the rate of complex formation with time. However, for times greater than 1 s, we define nearly diffusion-controlled reactions as k_a/D > 20 extending up to the purely diffusion controlled k_a = ∞. By comparing the asymptotic decay of the time-dependent rate for t > 1 s in this regime, the relaxation becomes nearly independent of k_a, as evidenced by the convergence of k(t) for large k_a in Figures 2(a) and 2(b).

Between these two limits, there are reactive systems that are weakly influenced by diffusion and therefore can be somewhat adequately described by a single rate constant, although not without visible deviations. In the regime where 0.05 < k_a/D < 0.5, the k_a values tend to be relatively small, rendering the deviations of k(t) from k_a potentially less than the error present in experimentally measured rate constants. Finally, when 0.5 < k_a/D < 20, the dynamics are sensitive to both specific values of k_a and D, and do not rapidly converge to diffusion-controlled dynamics. The relaxation will not be well fit to a single rate constant.

The length scale σ is another reaction parameter that influences the relaxation dynamics, but its presence in the logarithmic terms makes it a less significant factor influencing the parameterized rate behavior. For the diffusion controlled regime, one can vary σ by orders of magnitude, and the deviation from rate behavior predicted by using k_a = ∞ (with the same D value) is only increased by a few percent. Hence, while it is necessary to define a length scale to parameterize the reactions, over the relevant length scales of 0.01 nm–100 nm, the influence is not nearly as critical as D and k_a.

B. Accuracy in Smoluchowski theory for irreversible reactions in 2D

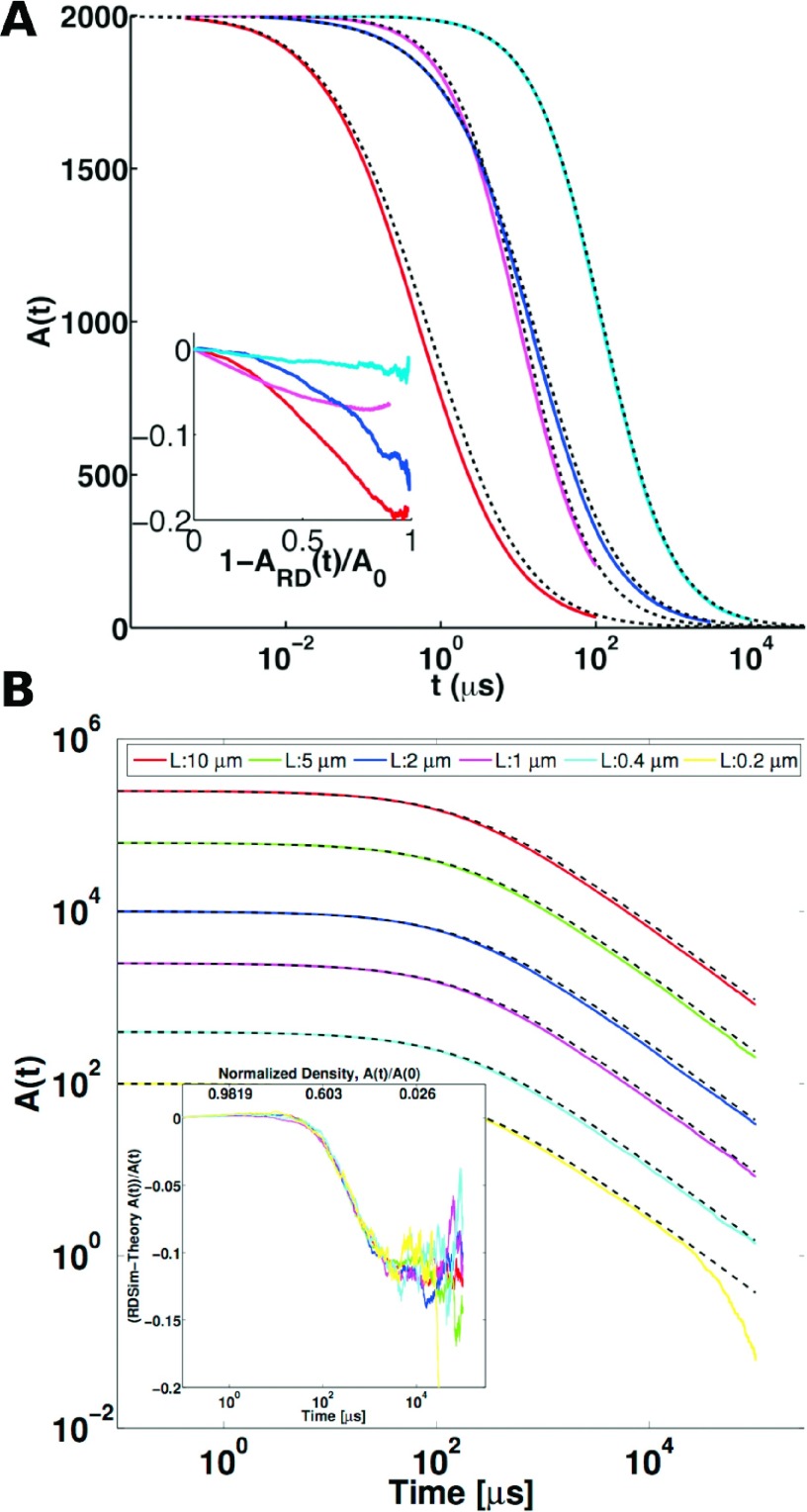
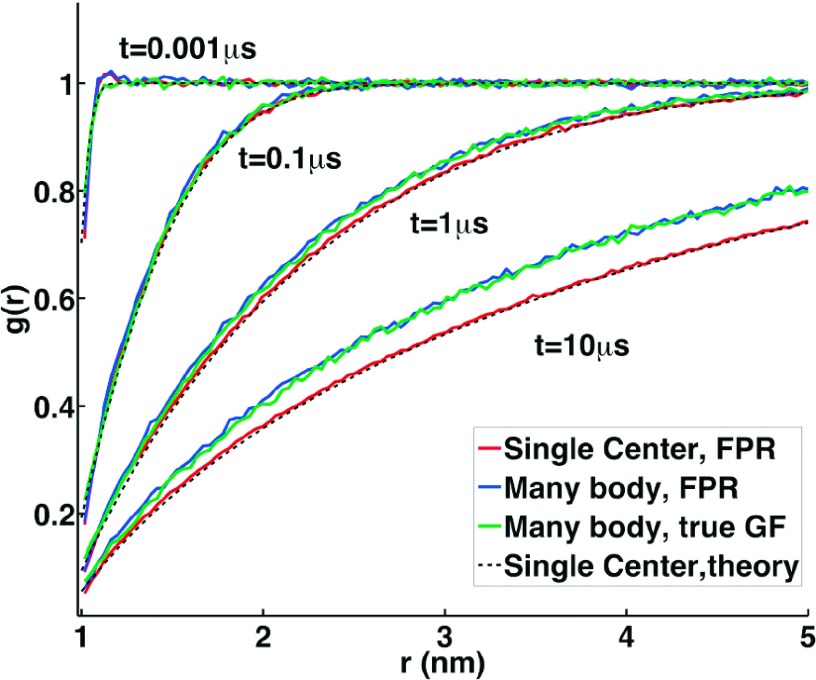
Here, we use numerical simulation to, for the first time in 2D, identify when Smoluchowski theory is most accurate at describing many-body complex formation in 2D. In 2D, it is known that the time-dependence of its predicted long-time decay agrees with field theory for irreversible A + A → 0 reactions,¹⁸ but not necessarily the prefactor of the decay or intermediate time scales. As discussed in the Introduction and Sec. II A, Smoluchowski theory is not an exact description of many-body dynamics, as it ignores correlations between multiple reactants. It is visible in Figure 4(a) that the true reaction dynamics of the many-body systems, simulated using the FPR algorithm adapted here to 2D, are somewhat faster at intermediate times relative to the Smoluchowski predictions coming via the solution in Eq. (5). Box size effects are not critical, as observed in Figure 4(b). Instead, errors in the predictions of Smoluchowski theory are due to the absence of multiple competing reactive centers in the theory that can influence both the short- and long-range density around other reactive centers. This density around particles is plotted in Figure 5, with comparison between RD simulation and the predictions of theory. The agreement is reasonable due to the important effect of complex formation at particle contact in decreasing the density as r → σ. However, in the simulations, reactions between other pairs influence the density around all centers, causing perturbations throughout the system.

FIG. 4.

(a) Irreversible A + A → 0 reaction, RD simulations with FPR compared with Smoluchowski theory predictions for varying k_a and volume (Eq. (4)). Red and magenta curves are FPR simulations at N/V = 0.1/nm², D_tot = 2 nm²/μs, with k_a = 100 and 1 nm²/μs, respectively. Blue and cyan curves are FPR simulations at lower density N/V = 0.01/nm², again for k_a = 100 and 1 nm²/μs. Time step used was 1 ns at V = 0.01, and 0.1 ns for V = 0.1. The inset shows the relative error of the Smoluchowski theory (ST) to the simulation [A_RD(t) − A_ST(t)]/A_ST(t), as a function of the reaction going to completion (A(t) → 0). Each RD simulation was repeated over 100-1000 trajectories. Error of the theory decreases with lower density and k_a. (b) Irreversible reaction A + A → 0 with changing box size for RD simulation vs Smoluchowski theory. The reaction parameters, D_A = 0.5 nm² μs⁻¹, k_a = 30 nm² μs⁻¹, and initial concentration of 2500 A particles per μm² are the same in all systems. Averaged trajectories of A(t) shown for square box edge L = 10 μm (red), 5 μm (green), 2 μm (blue), 1 μm (magenta), 0.4 μm (cyan), and 0.2 μm (yellow), simulated with Δt = 0.1 μs. The black dashed lines are the Smoluchowski theoretical results from the solution of Eq. (4). Inset shows the normalized error between theoretical and simulation results as a function of time and normalized density. The systems are clearly big enough that no effect of box size in controlling the spatial range and long-time behavior of these systems is occurring.

FIG. 5.

Comparison of the particle density, or radial distribution function, g(r), around each reactive particle calculated from theory and many-body simulation. Numerical simulations of the many-body A + A → 0 system are shown in blue (FPR simulations) and green curves, where green curve simulations sampled particle pair positions from simple BD updates but then rescaled to a separation defined by the true Green’s function. This comparison simply indicates the accuracy of the reweighting approach in reproducing the density of particles. The black dashed lines are the predictions of Smoluchowski theory assuming a single reactive center, and red curve is the same exact system as the theory defines, using the FPR approach for further validation of the simulations. N/V = 0.01/nm², k_a = 100 μm²/s, D_tot =2 μm²/s.

As a consequence, the true time-dependent complex formation proceeds at rates that are relatively accurately described by Smoluchowski theory, with largest deviations occurring for systems with higher densities and larger intrinsic rate constants k_a (Fig. 4, inset). With larger k_a, the coefficient of the asymptotic decay predicted by theory will be smaller than the true dynamics that evolves more rapidly, but the margin of difference is relatively small and diminishes as k_a decreases.

C. Accuracy of Smoluchowski theory of irreversible many-body simulations of A + B → 0

We perform the same comparison for the A + B → 0 reaction not previously done in 2D, where an additional factor influencing the dynamics of the true RD systems is the partitioning of the system into domains of A rich and B rich particles when A₀ ≈ B₀. This leads to a known slower t^−d/4 decay relative to the faster decay predicted by Smoluchowski theory.¹⁹ This behavior has been previously observed for numerical simulations where A₀ = B₀,^19,37 and here we instead compare the cases where Smoluchowski theory is better suited when A₀ < B₀, shown in Figure 6. The theory is again expected to do a reasonable but not exact job due to its approximation ignoring multiple reaction sites and spatial fluctuations, although we do enforce that A does not interact with other As and same for B. The agreement is best for systems with the largest disparities between the A₀ and B₀ initial concentrations, as expected, and which approach the pseudo-first-order decay. It is again better for small k_a systems. However, as the initial concentrations of A₀ and B₀ approach one another, the true RD decay is now slower than the predictions of Smoluchowski theory, which is the opposite of what is observed for the A + A → 0 reaction. The reason the A + B → 0 dynamics decay more slowly as their initial concentrations approach one another must be due to the inability of Smoluchowski theory to capture spatial partitioning of the reaction partners. This spatial partitioning is not an issue for the A + A → 0 reaction and is well-known to cause the aforementioned slower asymptotic decay when A₀ = B₀. Our simulations demonstrate that in 2D, this appears to be a source of deviations even when the initial concentrations of the reactants are not identical, as we see deviations emerging even for A₀ = 2B₀. This is perhaps not surprising given the sensitivity of 2D dynamics to spatial fluctuations for reactions with large k_a/D values, and accordingly, deviations are minimal for the smaller k_a simulations.

FIG. 6.

RD simulation vs theory for the many-body A + B → 0 systems, with initial particle numbers A₀ < B₀ and A₀/V = 0.001/nm². Accuracy of the Smoluchowski theoretical predictions shown in black dashed is expected to be best for larger ratios of B₀:A₀ (magenta and cyan), and for smaller values of k_a (cyan and green), as is clear from the comparison to our FPR simulations in the solid colored lines.

D. Pseudo-first-order reversible reactions in 2D

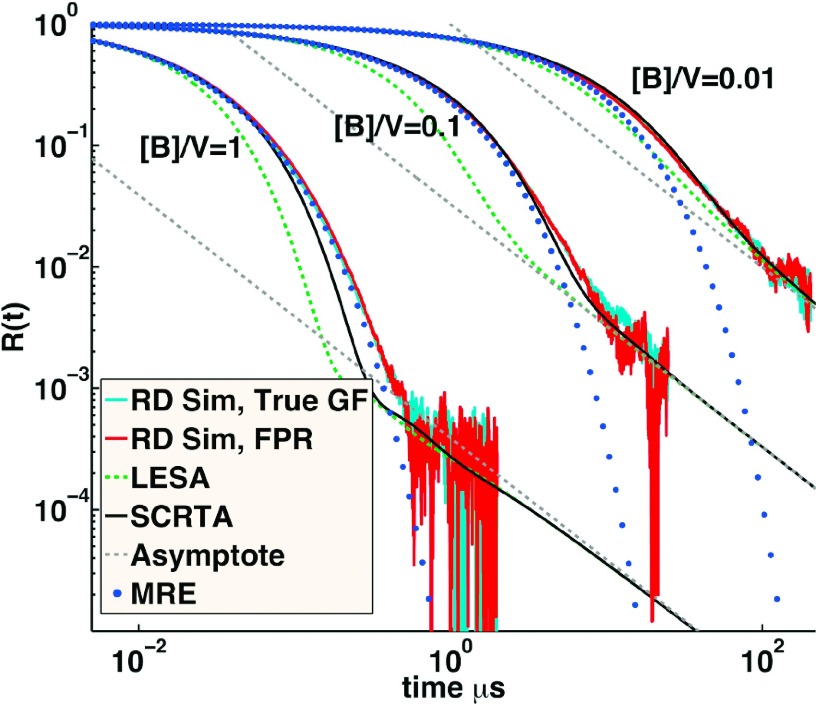
The FPR method applies equally well to reversible reactions, and we can use numerical simulation in 2D to similarly test various theoretical treatments of many-body systems undergoing reversible reactions. The simplest reversible system from a theoretical standpoint is the pseudo-first order reversible trap problem, A + B⇆C, where B₀ > > A₀ such that B is essentially constant with time, B(t) ∼ B₀. In Figure 7, we compare our simulations with the approximate theory from previous work^28,29 and the known asymptotic expressions.³⁰ Our numerical simulations represent unique tests of these theoretical results in 2D, because previous numerical tests were restricted to 3D and 1D.^33,35 For the self-consistent relaxation time approximation (SCRTA) method,²⁹ a pair of equations must be solved self-consistently, which cannot be done analytically in 2D, due to the lack of a steady state rate constant. Instead, we adapt the method from the original paper²⁹ to self-consistently solve the pair of equations where the second condition is resolved numerically rather than analytically. The linearized extended superposition approximation (LESA) approach is similar, but with a simpler definition of the effective rate constants used in the prediction of the relaxation.²⁸ We use systems with a quite fast off-rate (10⁶ s⁻¹) both because it equilibrates in less time and because it is easier to identify the effects of dissociation on the dynamics relative to simpler theories such as the modified rate equations²⁷ (MREs) defined below.

FIG. 7.

Relaxation of the pseudo-first order reversible reaction A + B⇆C with [B] ≫ [A] compared between numerical simulations and multiple theoretical predictions. R(t) = [A(t) − A_eq]/[A₀ − A_eq]. Cyan curves are solutions using RD with the correct GF used to select radial separations after collisions. Red curves are solutions using the FPR algorithm. The long time asymptotic power-law behavior is shown in dashed gray, and the increasingly accurate approximations from LESA²⁸ and SCRTA²⁹ are shown in green and black dashed, respectively. The MRE solution is shown in blue dots, which uses Smoluchowski theory and therefore cannot reproduce the power-law approach to equilibrium. For all cases, k_a = 100 μm²/s, k_b = 10⁶ s⁻¹, D_B = 2 μm²/s, and D_A = 0, σ = 1 nm and V is in nm².

E. General many-body reversible reactions in 2D

For reversible many-body RD systems with arbitrary initial concentrations, numerical solutions such as the FPR method used here provide the only way to solve the full time-dependent relaxation. Theoretical approaches to characterize the general A + B⇆C process and account for diffusion do exist but are highly non-trivial and still represent an approximation to the exact solution.^55,56 This is because additional spatial effects include the reappearance of reactants at close range upon dissociation. Only the immediate approach to equilibrium has relatively simple and correct closed form solutions,³⁰ resulting in a slower logarithmic relaxation to equilibrium than is described by rate equations.³⁰ This behavior, we note, is difficult to observe in experiment or simulation unless a weak binding interaction results from fast on and off rates (simulation examples in Refs. 12 and 33), as it directly precedes equilibration and is difficult to distinguish from measurement noise. In 3D, the dynamics can be in most cases be accurately compared with chemical kinetics, but for 2D, the issues raised above regarding the selection of the rate constant prevent this comparison from being generally applicable. Theoretical approaches more sophisticated than chemical kinetics and Smoluchowski theory have been used to derive closed systems of integro-differential equations that capture the effects of correlations between reactant pairs and spatial inhomogeneities in reversible reactions with arbitrary initial concentrations.⁵⁶ While these systems of equations would provide an appropriate comparison to our simulations, a much simpler comparison to theory can be made via the MRE, shown as the open circles in Figure 8. The MRE²⁷ is a simple extension of the Smoluchowski approach of Eq. (4) to reversible reactions,

$${\displaystyle \frac{dC\left(t\right)}{dt}=k\left(t\right)A\left(t\right)B\left(t\right)-K_{D}k\left(t\right)C\left(t\right),}$$ (21)

where detailed balance is used to define the off-rate via $k_{\mathrm{off}}\left(t\right)=K_D*k\left(t\right)$, K_D = k_b/k_a, and k_b which is the intrinsic off rate. We expect smaller deviations with smaller values of k_a, and less effect from dissociating complexes with slow (1 s⁻¹) off rates, and in Figure 8, we therefore observe good agreement.

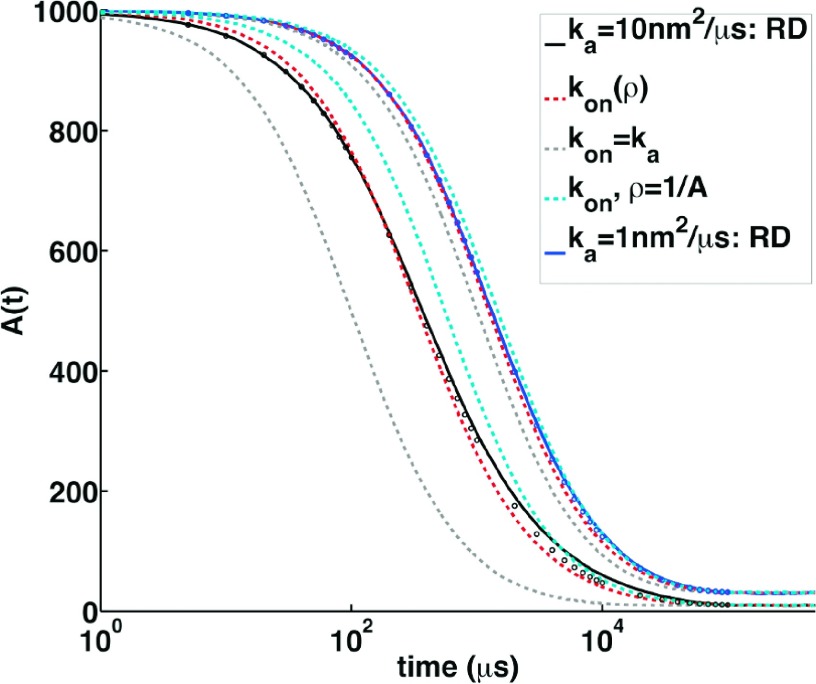
FIG. 8.

RD simulations versus rate-equation solutions for the reversible A + B ⇆ C reactions, where A₀/V = B₀/V = 0.001/nm². FPR simulations are shown in solid black and blue curves for k_a = 10 μm²/s and k_a = 1 μm²/s, respectively, and an intrinsic off rate of k_b = 1 s⁻¹. The dashed curves are all results from rate equations solved using the Gillespie algorithm. Gray dashed use a fixed rate of the maximum k_on = k_a. Cyan dashed use the rate derived by Fange et al.,²⁴ where k_on = 1.799 μm²/s and 0.6910 μm²/s. The red dashed curves use our adaptive concentration dependent rate defined in Eqs. (19) and (20). Neither system is in the rate limited regime, with ratios of k_a/D = 5 (black) and 0.5 (blue), hence the observed deviations between the rate-based approaches and RD. However, the adaptive rate reduces the deviations from the true RD dynamics as a function of time. For theoretical comparison, the MRE solution of Eq. (21) is shown in open circles.

F. Gillespie simulations with adaptive rate constant

In the regimes where k_a/D > 0.05, we have established that the association dynamics can only be approximated by rate equation kinetics with a fixed rate constant. We test the ability of our bulk-density dependent adaptive rate defined in Eqs. (19) and (20) to describe the true association dynamics by comparing it against the full RD simulations in Figure 8. We also include results using Gillespie simulations with alternate definitions of a fixed rate constant.²⁴ All in all, any constant rate approximation can be expected to deviate from the full single particle resolution RD dynamics for increasing k_a/D ratios, because the true rate of product formation depends on how far apart the particles are from one another. However, our adaptive rate can at least respond to changes in the particle separations arising from changes in the bulk density, unlike fixed rate constants. Compared to FPR simulations, the concentration dependent rate simulations do provide quite reasonable agreement with the true time-dependent complex formation. The adaptive rate simulations result in initial reactions that are too slow, and at longer times, this average rate is too fast, as the spatial distribution now is reduced to the particles at the farthest separations. This is not surprising, as the concentration dependent rate is an average over all separations, and for these non-equilibrium relaxation processes, the true RD dynamics proceed with the fastest reactions early, and increasingly slower reactions at the end. Nevertheless, our adaptive rate overall does a better job of reproducing the time evolution of the true RD dynamics compared to a single fixed rate constant, as it dynamically responds to changes in the bulk density of the system.

IV. METHODS

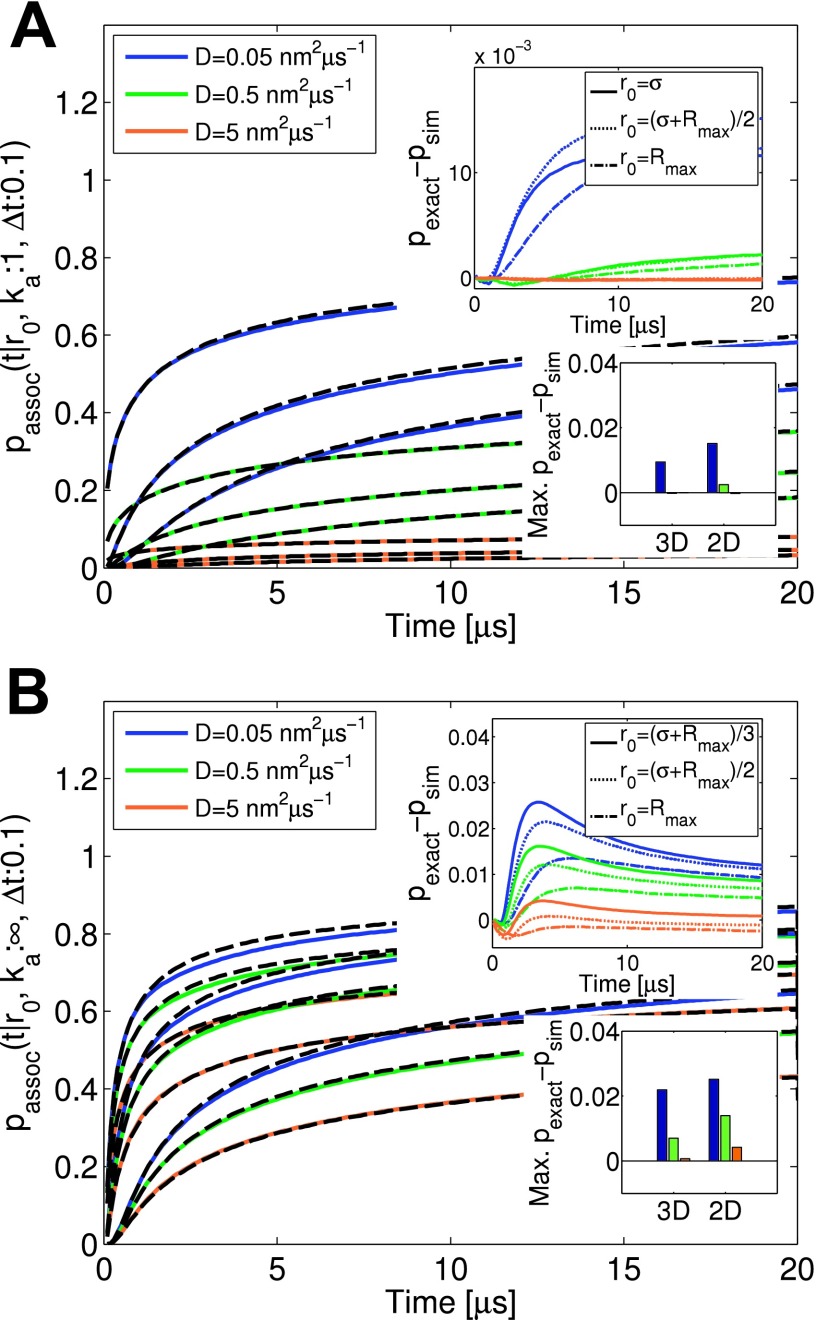
The FPR algorithm¹² is constructed to exactly reproduce the association probability between reactant pairs for all times and initial separations, hence ensuring the correct rates of association between reaction partners at all times. This is shown in Figure 9 for the 2D implementation we perform here. The method numerically solves for the positions of reacting species undergoing Brownian dynamics with reactive boundaries between binding partners by breaking the many-body problem into a series of one- or two-body problems. These one- or two-body problems can be either solved exactly or numerical tables of the solutions constructed, which is not true for any higher-body problems. The time step of numerical propagation is chosen to prevent or at least minimize the presence of any three-body or higher interactions at any time. The algorithm uses the GF propagator for reactive particles in combination with the free diffusion propagator. The free diffusion propagation of the particles is very simple to implement; however, when the inter-particle distances are comparable to the size of the particles, the particle dynamics are only approximate. This introduced error due to the free diffusion propagation is corrected by trajectory reweighting at each time step using the GF propagator for reactive particles. Originally FPR was presented for 3D systems.¹² Here, we provide necessary details of the implementation of FPR in 2D.

FIG. 9.

Probability of two particles having associated between times 0 and t, given they were separated by a distance r₀ initially. Results for the exact propagator are shown as black dashed lines (Eq. (27)). The binding radius is σ = 1 nm. The probabilities of association were gathered from 10⁶ simulation trajectories with Δt = 0.1 μs. Set of D values considered was 0.05,  0.5,  5 nm² μs⁻¹. (a) Results are shown for k_a = 1 nm² μs⁻¹ and three r₀ (σ, (σ + R_max)/2, R_max) choices. (b) Results are shown for the absorbing boundary condition (k_a = ∞) and three r₀ ((σ + R_max)/3, (σ + R_max)/2, R_max) choices. Large insets show the differences between results of Eq. (27) and simulations. Trajectory overlap issues can result in simulated association values slightly lower than exact, for reactions where D becomes very slow and k_a is large. Small insets compare the maximum error made for the same respective parameters used in 2D and 3D simulations within 20 μs.

A. GF solutions to the 2D RD equation

When the reactions between particle pairs depend only on the inter-particle separation, without any orientational constraints, the propagator for a single pair becomes effectively one-dimensional in space where now p(r, t|r₀) is the probability density of finding two particles at a separation r at time t, with an initial separation r₀. If we assume that there is no force field acting on the particles and neglect rotational diffusion, the same partial differential equation as Eq. (1) governs the spatio-temporal evolution of p(r, t|r₀) in 2D.

The Green’s function is probability density solved with delta function initial conditions, $p\left(r,0|r_0\right)=\frac{\delta (r-r_0)}{2\pi r}$. We reproduce here these previously derived functions for different boundary conditions below, as they are needed in our FPR algorithm. The algorithm requires the renormalized free propagator and the propagator solved with absorbing BC or RBC for the reweighting steps. The survival probability with absorbing BC or RBC is required to define the association probability.

When particles freely diffuse in an infinite medium without any reactions or interactions between them, the two boundary conditions are $\underset{r\to \infty }{lim}p\left(r,t|r_0\right)=0$ and ${\left.\frac{\partial }{\partial r}p\left(r,t|r_0\right)\right|}_{r=0}=0$. Then, the GF is (Eq. (14.8.1) of Ref. 42)

$${\displaystyle p_{\mathit{free}}\left(r,t|r_0\right)=\frac{1}{4\pi Dt}{e}^{-\frac{r^2+r_0^2}{4Dt}}{I}_0\left(\frac{r{r}_0}{2Dt}\right),r\ge 0,\hspace{0.17em}{r}_0\ge 0,}$$ (22)

where I₀ is the zeroth order modified Bessel function of the first kind.

In a system where particles not only diffuse but also react on collision with one another, the reactions are modeled via the radiation boundary condition defined in Eq. (2), where D is the sum of the translation diffusion coefficients of the two particles. The GF for the irreversible reaction $p_{\mathit{irr}}\left(r,t|r_0\right)$ is given by (Eqs. (14.8.12)-(13) of Ref. 42)

$${\displaystyle p_{\mathit{irr}}\left(r,t|r_0\right)=\frac{1}{2\pi }{\int }_0^{\infty }{e}^{-D{u}^{2}t}C\left(u,r\right)C\left(u,r_0\right)udu,}$$ (23)

where

$${\displaystyle C\left(u,r\right)=\frac{J_0\left(ur\right)\left[hu{Y}_1\left(\sigma u\right)+k_a{Y}_0\left(\sigma u\right)\right]-Y_0\left(ur\right)\left[hu{J}_1\left(\sigma u\right)+k_a{J}_0\left(\sigma u\right)\right]}{\sqrt{{\left[hu{Y}_1\left(\sigma u\right)+k_a{Y}_0\left(\sigma u\right)\right]}^2+{\left[hu{J}_1\left(\sigma u\right)+k_a{J}_0\left(\sigma u\right)\right]}^2}},}$$ (24)

where h = 2πσD, and J_n denotes order n Bessel function of the first kind and Y_n denotes order n Bessel function of the second kind. For a system where all particle collisions result in a reaction (k_a = ∞, absorbing boundary condition), Eq. (24) has a simpler form with⁴²

$${\displaystyle C\left(u,r\right)=\frac{Y_0\left(\sigma u\right)J_0\left(ur\right)-Y_0\left(ur\right)J_0\left(\sigma u\right)}{\sqrt{{\left[Y_0\left(\sigma u\right)\right]}^2+{\left[J_0\left(\sigma u\right)\right]}^2}}.}$$ (25)

The integral of the GF $p_{\mathit{irr}}\left(r,t|r_0\right)$ over the spatial domain defines the survival probability $S\left(t|r_0\right)$, previously described in Sec. II A that the two particles have survived until time t without reacting,

$${\displaystyle S\left(t|r_0\right)={\int }_{\sigma }^{\infty }{p}_{\mathit{irr}}\left(r,t|r_0\right)2\pi rdr.}$$ (26)

Then, the probability of association for the particles is

$${\displaystyle p_{\mathit{assoc}}\left(t|r_0\right)=1-S\left(t|r_0\right).}$$ (27)

The survival probabilities in 2D are given explicitly by (Sec. 13.5 of Ref. 42)

$${\displaystyle S\left(t|r_0\right)=1-\frac{2k_a}{\pi }{\int }_0^{\infty }\frac{1}{u}\frac{\left(e^{-D{u}^{2}t}-1\right)C\left(u,r_0\right)}{\sqrt{{\left[hu{Y}_1\left(\sigma u\right)+k_a{Y}_0\left(\sigma u\right)\right]}^2+{\left[hu{J}_1\left(\sigma u\right)+k_a{J}_0\left(\sigma u\right)\right]}^2}}du,}$$ (28)

when k_a < ∞, and

$${\displaystyle S\left(t|r_0\right)=\frac{2}{\pi }{\int }_0^{\infty }\frac{1}{u}\frac{e^{-D{u}^{2}t}\left(Y_0\left(u{r}_0\right)J_0\left(\sigma u\right)-Y_0\left(\sigma u\right)J_0\left(u{r}_0\right)\right)}{{\left[Y_0\left(\sigma u\right)\right]}^2+{\left[J_0\left(\sigma u\right)\right]}^2}du,}$$ (29)

when k_a = ∞. These survival probabilities directly simplify to the time-dependent Smoluchowski rate functions defined in Eqs. (7) and (8) via Eq. (3). The solution to the same diffusion problem with an explicit reversible boundary included at contact has been recently derived in Ref. 57. Here, we separate the irreversible binding from the unbinding, which is modeled as a Poisson process and which provides an excellent description of the full reversible dynamics, as demonstrated here and in previous work.^10,12

B. Trajectory reweighting in 2D

In FPR, the free diffusion trajectories of particle pairs are reweighted to recover the exact association probability of pairs obeying diffusion with reactive boundaries. The 2D treatment of reweighting is the same as the general treatment described in Ref. 12, but with the 2D functions defined above. We briefly review the method here, noting that a more detailed discussion is provided by the earlier work.¹²

For a system comprised of non-reacting particles, the free diffusion probability p_free (Eq. (22)) gives the correct distribution for the separation between each particle pair. However, for reactive particle pairs, as their separation approaches the boundary at r = σ, the exact separation distribution is $p_{\mathit{irr}}\left(r,t|r_0\right)$ (Eq. (23)). In the FPR algorithm, positional updates are sampled from the free diffusion propagator for efficiency, and reweighting of trajectories is applied to the association probabilities to correct this.

When sampling from the free diffusion propagator for positional updates, we note that, first, r cannot be less than σ, sum of the reactants’ radii, due to the boundary condition at this separation. Therefore, the GF is normalized as

$${\displaystyle p_{\mathit{free}}^{\mathit{norm}}\left(r,t|r_0\right)=\frac{p_{\mathit{free}}\left(r,t|r_0\right)}{{\int }_{\sigma }^{\infty }{p}_{\mathit{free}}\left(r,t|r_0\right)2\pi rdr}.}$$ (30)

Second, the proper radial distribution function should account for the missing particles that have already associated up to time t. To achieve this, the free diffusion separation distribution is rescaled simply by multiplying it with the current survival probability

$${\displaystyle p_{\mathit{free}}^{*}\left(r,t|r_0\right)=S\left(t|r_0\right)p_{\mathit{free}}^{\mathit{norm}}\left(r,t|r_0\right).}$$ (31)

This result is the pairwise separation distribution sampled by the FPR algorithm for particle pairs.

The association probability at time T + Δt that results from sampling from this distribution is given by

$${\displaystyle p_{\mathrm{assoc}}^{\mathit{approx}}\left(T+\mathrm{\Delta }t|r_0\right)={\int }_{\sigma }^{\infty }2\pi rdr{p}_{\mathit{free}}^{*}\left(r,T|r_0\right)p_{\mathrm{assoc}}\left(\mathrm{\Delta }t\right|r),}$$ (32)

where p_assoc(Δt|r_T) is defined by Eq. (27). This approximate solution differs from the exact solution, which is given by Eq. (32) where p_irr(r, t|r₀) replaces $p_{\mathit{free}}^{*}\left(r,T|r_0\right)$. However, by reweighting the value p_assoc(Δt|r) by the ratio of the free and exact trajectories,

$${\displaystyle w_{\text{ratio}}=p_{\text{irr}}(r,t|r_0)/p_{\text{free}}^{*}(r,t|r_0),}$$ (33)

in Eq. (32), one can recover the exact association rate, as is shown in Figure 9. The trajectories are Markovian, and therefore each GF can be constructed by the product of the single step propagators.

1. Trajectory overlap

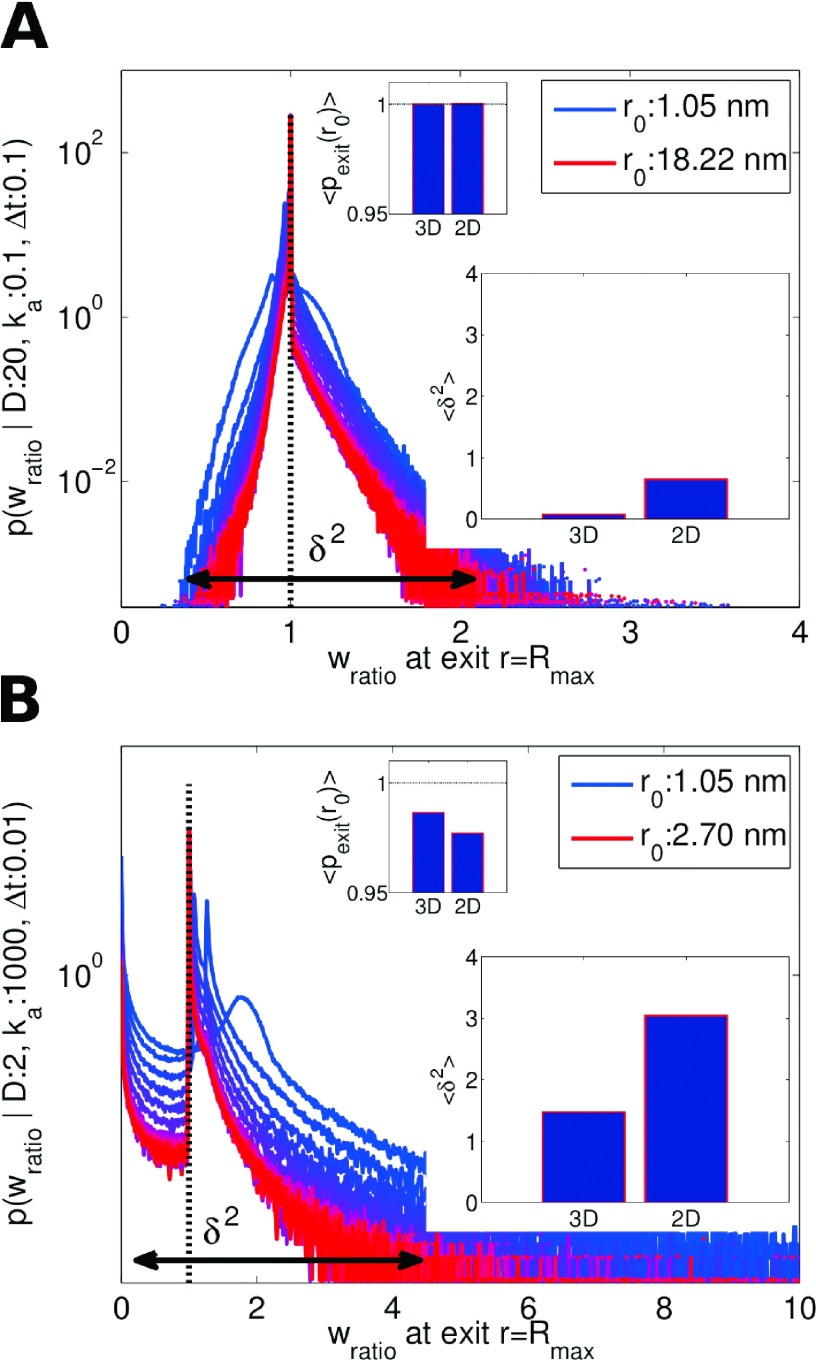
The distribution of reweighting ratios defined in Eq. (33) are plotted in Figure 10, along with the mean and spread of the distribution in the insets. The ratios are collected from simulation at the point when the particle separation exceeds the reaction zone (r > R_max), for particles started off at separations r₀, hence terming it the exit ratio. The average of the distribution of exit ratios is one by construction, ensuring correct association probabilities. As previously discussed in detail,¹² there is the possibility that trajectories of the free and exact propagator do not overlap, meaning the probability of a trajectory sampled with one propagator may be nonzero, but zero with the other propagator. In Figure 10(a), there is no overlap issue, but in Figure 10(b), this issue is reflected by sampling values of w_ratio = 0, in general giving rise to a wider distribution of trajectory ratio values. We denote this spread with ${\mathrm{\delta }}^2=\sum _{i}p\left(w_i\right){\left(w_i-1\right)}^2$ and present δ² values averaged over the different simulations of initial r₀ (Figure 10, large inset). The consequence is that the average trajectory ratio is not exactly one, but is slightly less, as is visible in Figure 10(b) (small inset). As a result, one observes association probabilities that are slightly less than the exact values (see error insets in Figure 9). Trajectory overlap only starts to become apparent when long trajectories are produced via very small time steps, slow diffusion, and high intrinsic rates. However, the effects, when present, are minor, as evidenced by Figure 9. We find that in 2D, overlap issues are slightly worse than in 3D, resulting in distributions of ratios that spread further around one (Figure 10, large inset), but nevertheless produce only minimal deviations from the expected $〈w_{\text{ratio}}〉=1$ (Figure 10, small inset). Hence, the many-body simulations will still be highly accurate.

FIG. 10.

The distribution of reweighting ratios w_ratio defined in Sec. IV A Eq. (33) upon exiting the reaction zone, given different initial starting particle separation r₀’s. These distributions reflect the degree of overlap between the exact and the simulated trajectories and give rise to an average ratio (small insets) of 1 when all trajectories overlap. Small insets compare this average ratio for the same respective parameters used in 2D and 3D simulations. There are slight deviations in 10B from the expected value of 1, with 2D being slightly worse than 3D. The large insets compare the spread of the exit ratio distributions around 1. (a) D = 20 nm² μs⁻¹, k_a = 0.1 nm² μs⁻¹, Δt = 0.1 μs and (b) D = 2 nm² μs⁻¹, k_a = 1000 nm² μs⁻¹, Δt = 0.01 μs, with each curve representing an increment in r₀. 10⁶ trajectories were sampled for each initial separation.

C. Numerical and simulation methods

1. Calculating GFs

Unlike the case in 3D, 2D solutions (Eqs. (23) and (30)) cannot be evaluated using closed functional forms and require numerical integration techniques. We generated 1D lookup tables for the normalization factor for the free diffusion probability (denominator of Eq. (30)) and the survival probability (Eq. (28)) because they both are functions of the current position r₀ only, with a fixed time step Δt. For the irreversible reaction GF (Eq. (23)), one needs a 2D lookup table, for both the variables r and r₀. For all the tables, we take equal number of spatial samples from the probability distributions with a step size $\mathrm{\Delta }\epsilon =\sqrt{D\mathrm{\Delta }t}/50$ over the domain $\left[\sigma ,R_{\mathit{max}}\right]$, where $R_{\mathit{max}}=\sigma +3\sqrt{4D\mathrm{\Delta }t}$. The probabilities of interest at specific r and r₀ were extracted from the tables using linear interpolation of the spatial samples. For the numerical integrations, we used GSL-1.16 qagiu routine which applies adaptive Gauss-Kronrod 21-point integration and domain mapping from [l_b ≥ 0, ∞) to (0, 1]. We note that with the integration to infinity in Eqs. (7), (8), (28), and (29), there are cases where the oscillations in the higher frequency Bessel functions prevent the integration from converging. To circumvent this, it is possible to truncate the integral at values lower than infinity. We performed truncation at the points beyond which the absolute value of the integrands is always smaller than ε = 10⁻¹⁶. For all integrations, we used a maximum value of 10⁻⁶ as a relative error tolerance. Smaller error levels were attempted and did not affect the results.

2. Many-body simulations

Many-body simulations were undertaken in boxes with periodic boundary conditions applied where particles undergo Brownian motion with a zero mean Gaussian random variable with variance 2DΔt. Time steps are chosen to minimize the many-body effects and protect the validity of the pairwise dynamics assumption. Therefore, in 2D for a system of A and B particles, we used time steps limited by $\mathrm{\Delta }{t}_{\mathit{max}}=D_{AB}^{-1}{\left(12\overline{\rho }\pi {\sigma }_{AB}\right)}^{-2}$, where $\overline{\rho }$ is the maximum of the average particle densities $\overline{{\rho }_A}$ and $\overline{{\rho }_B}$. For the reversible simulations, discrete time complex dissociations obey Poisson statistics and depend on the intrinsic dissociation rate k_b. A much more detailed description on the implementation of FPR for multiple particles is given in our previous work.¹²

3. Reversible trap simulations

In Figure 7, we simulated the reversible trap problem using the same approach as described for the 3D version in Ref. 12 and similar to the methods used in previous numerical studies in 1D and 3D.³³ A single A particle is placed at the center of the box, with multiple B particles uniformly distributed in the box at the densities N/V reported in Figure 7. The box length was chosen large enough that the box boundaries would not influence the particle interactions at the longest simulated time scales. The B particles cannot overlap A but do not interact with one another, and can therefore overlap each other. Each of the three systems was repeated for ∼300 000 trajectories. For the calculated R(t) = [A(t) − A_eq]/(A₀ − A_eq), we used the simulated A_eq value, such that R(t) correctly describes the approach of the simulation to its equilibrium value, which was very slightly higher than the theoretical A_eq = [1 + B₀/K_D]⁻¹ due to undersampling, as was observed in 3D as well¹² for the small time step (0.1-1 ns) used in these highly dense systems.

4. Gillespie simulations with adaptive rate

To perform stochastic simulations, or the Gillespie algorithm⁵ with an adaptive rate, only a single additional step is required. After each reaction is performed, the propensities for any reaction where the species number has changed must be updated in any implementation. The update is normally only due to changes in species number, but for the case of the adaptive rate, the update will also depend on the change in propensity due to the rate constant changing as a result of the new particle densities. Hence, the rates must be recalculated for these same sets of affected reactions, to reflect the change in density of the reactive species. This calculation will not affect the efficiency of the approach. There are also additional input parameters, because to calculate these adaptive rates, one must have an effective binding radius σ and diffusion constant D for each reaction in order to define the concentration-dependent rate defined in Eqs. (19) and (20).

V. DISCUSSION

A. Experimental measurements of reaction parameters:

This understanding of association dynamics in 2D is critical in both interpreting experimental results via a set of condition-independent physical constants, and in properly incorporating these values into models of the experimentally observed behavior. By simply assuming that the dynamics of reversible binding reactions can be fit by simple chemical kinetics approaches with single constant rates, the reported values of rate constants in 2D will only be descriptive of the conditions used in the specific experiment, which are not useful parameterizations of the process. Instead, it becomes necessary to define (1) a diffusion constant, (2) an intrinsic reaction rate, and (3) a length scale of molecular separations at contact, to be able to describe complex formation in any set of initial conditions for one reaction. The molecular length scale and diffusion constant can be reasonably estimated via knowledge of the reactants’ size and the Einstein-Stokes equation, respectively. The fit to the intrinsic rate constant k_a can be done using the modified rate equations of Eq. (21) that use the time-dependent k(t|D, σ, k_a) rather than fixed rate constants. Because k(t) is a difficult integral to work with, the much simpler and still accurate functional forms in Eqs. (11), (14), and (15) can be used with a nonlinear fitting routines to extract k_a. We provide MATLAB code for doing so online (see the supplementary material).²¹

B. Biological binding strengths for the reaction regimes

The regimes of biological reactions where this extra parameterization is necessary will be for k_a/D > 0.05, although even up to ratios of ∼0.5 a single rate constant would provide a reasonable fit to the data. Since k_a will not be known in advance, we estimate here which 3D solution binding strengths these 2D regimes would correspond with. Given a known reaction rate in 3D, $k_{on}^{3D}$, the intrinsic rate can be determined via Eq. (9), using D_3D and σ. The determination of the 2D values of k_a is a separate topic on its own, and so here we use the simple estimate from setting the κ values the same for the 2D and 3D reactive boundary that $k_a^{2D}\sim k_a^{3D}/2\sigma$. We estimate diffusion constants on the membrane on the order of ∼1 μm²/s, and reactant diameters of ∼1 nm, and we can now translate a $k_a^{3D}$ to a $k_a^{2D}/D$ region in 2D. This means that for $k_a^{3D}=3\times 10^4$ M⁻¹ s⁻¹ (and hence, $k_a^{2D}=0.0166$ μm²/s), the 2D binding is safely in the rate-limited regime where k_a/D < 0.05. For these weaker binders, experimental data will be accurately modeled via simple rate equation kinetics, with small fit values expected to give k_fit ∼ k_a. For stronger binders than this upper limit (i.e., for $k_a^{3D}=10^7$ M⁻¹ s⁻¹ and D = 2 μm²/s, the resulting $k_a^{2D}/D=8$), a single rate will do an increasingly poor job of describing relaxation and a full parameter description with k(t) should be used to extract the three reaction parameters.

VI. CONCLUSIONS

In this paper, we have shown that there are fundamental limitations on the ability of simple rate equation kinetics to describe the dynamics of association in 2D, because of the inability to assign a single rate constant to the process of complex formation. However, by analyzing the asymptotics of the time-dependent rates of complex formation from Smoluchowski theory, we derived quantitative bounds in Secs. II C and III A for discriminating which reaction types in 2D are, in fact, accurately defined by rate equations. For reaction parameters limited to k_a/D < 0.05, the rate of complex formation in 2D, while theoretically obeying the same asymptotic behavior as for larger k_a/D ratios, will decrease with such a slow power law time dependence as to be effectively constant. This importantly means that in 2D, rate equations will accurately describe relaxation for these systems and will grow more inaccurate as the ratio of reaction parameters increases, as summarized in Table I. This shift in behavior occurs because for small rates, complex formation is truly limited by the activation barrier and largely insensitive to the spatial distribution and particle separations, such that diffusion to contact provides a minimal contribution to the overall rate and k_on ≈ k_a.

The reaction dynamics in 2D for large k_a/D parameter sets contrasts significantly from in 3D, where in 3D, the kinetics of reversible association are generally still very well described by the use of a single phenomenological rate constant, thanks to the ultimate insensitivity of complex formation to spatial distributions beyond short time scales. In 2D, these diffusion influenced and diffusion controlled reaction types instead remain perpetually sensitive to spatial fluctuations.

We do not consider here the effects of interaction potentials^2,43,58 or hydrodynamics^9,59 on association, to provide the simplest improved description to rate-based kinetics of association. However, our analysis of rate behavior would occur even in the presence of interaction potentials, which would be added as a drift term in the diffusion equation. These additional details can also often be modeled by changing the specific reaction parameters to account for their effect on speeding or slowing down reactions. Adding more parameters to the model enhances its transferability but will ultimately require significantly more data for a unique parameterization from experiment.

Simulating coupled systems of reactions in 2D using rate equations may not provide an exact description of the true RD dynamics, but can still be relatively accurate when care is taken to define rate-constants for 2D reactions. A mean rate of complex formation can be derived for a pair of particles in a fixed 2D area,^14,20,24 and here we performed a simple extension to this approach to capture the additional effect of having multiple reaction partners within the system. Our adaptive concentration-dependent 2D rate constant from Sec. II D produces an improved description relative to fixed rate constants of the time-dependence of 2D reaction dynamics from dense to dilute systems (Figure 8). It therefore better describes non-equilibrium systems and is much less sensitive to the simulation volume or sub-volume. This method maintains equilibrium detailed balance, and applies to systems that include competing and coupled reactants and/or non-equilibrium driving forces. Because the density distribution is not tracked in these methods, only an average density, it will not be able to fully reproduce the time-dependent complex formation of RD processes in 2D. However, it is easy to implement in existing Gillespie routines, whether spatial or non-spatial, and is more efficient than full RD approaches when single particle resolution is not necessary.

Finally, we demonstrated in 2D the application of the FPR method to modeling detailed spatial and temporal dynamics of RD systems and provided novel tests of theoretical predictions of both irreversible and reversible 2D reaction dynamics. The advantage of such modeling is one need not assume well-mixed conditions, or a single rate, as diffusion and spatial fluctuations are explicitly captured. While less efficient, this approach is necessary for realistic biological systems where particles are localized, they can be restricted to spatial compartments or to membranes, they can form assemblies, and they have a finite volume that excludes other particles.