Local curvature analysis for classifying breast tumors: Preliminary analysis in dedicated breast CT

Abstract

Purpose:

The purpose of this study is to measure the effectiveness of local curvature measures as novel image features for classifying breast tumors.

Methods:

A total of 119 breast lesions from 104 noncontrast dedicated breast computed tomography images of women were used in this study. Volumetric segmentation was done using a seed-based segmentation algorithm and then a triangulated surface was extracted from the resulting segmentation. Total, mean, and Gaussian curvatures were then computed. Normalized curvatures were used as classification features. In addition, traditional image features were also extracted and a forward feature selection scheme was used to select the optimal feature set. Logistic regression was used as a classifier and leave-one-out cross-validation was utilized to evaluate the classification performances of the features. The area under the receiver operating characteristic curve (AUC, area under curve) was used as a figure of merit.

Results:

Among curvature measures, the normalized total curvature (C_T) showed the best classification performance (AUC of 0.74), while the others showed no classification power individually. Five traditional image features (two shape, two margin, and one texture descriptors) were selected via the feature selection scheme and its resulting classifier achieved an AUC of 0.83. Among those five features, the radial gradient index (RGI), which is a margin descriptor, showed the best classification performance (AUC of 0.73). A classifier combining RGI and C_T yielded an AUC of 0.81, which showed similar performance (i.e., no statistically significant difference) to the classifier with the above five traditional image features. Additional comparisons in AUC values between classifiers using different combinations of traditional image features and C_T were conducted. The results showed that C_T was able to replace the other four image features for the classification task.

Conclusions:

The normalized curvature measure contains useful information in classifying breast tumors. Using this, one can reduce the number of features in a classifier, which may result in more robust classifiers for different datasets.

1. INTRODUCTION

Mammography is a widely accepted screening methodology for breast cancer screening, which accounts for reducing the mortality rate by 30%–40%.¹ However, mammography has known limitations, such as low sensitivity for women with dense breast tissue^2,3 and a relatively high recall rate.⁴ In addition, traditional mammography projects three-dimensional (3D) breast tissue in a single image plane, which may result in obscuring a breast tumor behind complex breast tissue and thereby hindering detection.

To overcome this, 3D imaging modalities have been introduced. Dedicated breast computed tomography (bCT) is one such modality, where it allows us to access the full 3D breast morphology in detail. It has been shown via clinical studies that bCT can display a breast tumor with high contrast and improve visual conspicuity of tumors compared to mammography.^5,6

It could be possible to detect breast abnormalities earlier with improved imaging modalities. However, the emphasis on early detection can led radiologists to overcall breast abnormalities.⁷ This causes a high rate of unnecessary diagnostic imaging and ultimately unnecessary breast biopsies. In this respect, an accurate diagnosis is crucial to reduce overcalling. To achieve this, many computer-aided diagnosis (CADx) systems have been developed and it has been shown that they can improve both sensitivity and specificity of the diagnostic performance of radiologists.^8–12

As bCT is a recently introduced imaging modality, the development of a CADx scheme for bCT is in its infancy. To the best of our knowledge, there are only a few studies^13–16 that have been published for developing CADx schemes for bCT. For example, Ray et al.¹³ developed a preliminary CADx algorithm using eight morphological features and six texture features based on a gray-level co-occurrence matrix (GLCM) extracted from segmented lesions in bCT images. Those features were fed into artificial neural network (ANN) classifiers to determine the malignancy of the given breast lesion. In the receiver operating characteristic (ROC) curve analysis, their classifiers achieved an area under the ROC curve (AUC, area under curve) value of 0.7 and 0.8 for post- and precontrast image sets, respectively. In addition, Kuo et al.¹⁵ introduced a new 3D spiculation feature for classifying breast lesions in bCT images. After the segmentation of breast lesions, various morphological and texture features were extracted. They combined the 3D spiculation feature and other image features via stepwise feature selection and achieved an AUC value of 0.85 for a noncontrast bCT image set.

Although previous studies achieved a promising classification performance using various image features, they did not fully utilize the 3D information available in bCT images. In particular, none of the previous studies used the 3D surface information of the breast lesion, which may provide useful information for classifying a breast lesion. It has been known that malignant breast lesions frequently exhibit irregular borders, while typical benign breast lesions show smooth boundaries.¹⁷ This fact can be extracted further in detail when we consider the 3D surface of breast lesions; malignant breast lesions will show irregular variations in its lesion surface, while benign breast lesions will display smooth variations in its lesion surface. Although there exists a specific image feature measuring spiculation and irregularity of breast lesions,¹⁸ they are based on either the voxel or volume of the breast lesions, not the 3D surface. In addition, the 3D surface of a breast lesion may provide additional information other than the information from traditional image features.

In this paper, we introduce a novel-image feature that contains useful information available from the 3D surface of breast lesions. Specifically, this image feature represents the local variations in surface curvature of breast lesions extracted from bCT images. After segmentation of breast lesions, the curvatures of each vertex of the given breast lesion surface are computed. Logistic regression is used as a classifier to distinguish benign and malignant breast lesions. We then show the usefulness of the new image feature (local curvature) comparing the classification performance of existing image features.

2. METHODS

2.A. Dataset

The image dataset for this study included 137 biopsy proven breast lesions (90 malignant, 47 benign) in 122 noncontrast breast CT images of women aged 18 or older at the University of California, Davis. Under the approval of an institutional review board (IRB), patients’ breast CT images were acquired using the prototype dedicated breast CT system at the University of California, Davis.¹⁹ Coronal slice spacing ranged from 200 to 770 μm, and the voxel size in each coronal slice varied from 190  ×  190 to 430  ×  430 μm. Feldkamp–Davis–Kress (FDK) reconstruction²⁰ was used to reconstruct all bCT images. Table I summarizes the detailed characteristics of the image dataset used for this study.

TABLE I.

Characteristics of image dataset.

			All	Selected for study
Total number of lesions			137	119
Subject age (yr)	Mean [min,max]		55.6 [35,82]	55.2 [35,82]
Lesion diameter (mm)	Mean [min,max]		13.5 [2.3,35]	13.4 [2.3,35]
Breast density	1		16	14
	2		51	47
	3		51	43
	4		19	15
	Diagnosis	Malignant	IDC	61	50
IMC		13	13
ILC		8	7
DCIS		7	6
Lymphoma		1	1
Benign		FA	20	18
FC		7	6
FCC		4	4
PASH		2	2
CAPPS		2	2
Other benign lesions such as sclerosing adenosis and cyst		12	10

Note: IDC: Invasive ductal carcinoma, IMC: Invasive mammary carcinoma, ILC: Invasive lobular carcinoma, DCIS: Ductal carcinoma in situ, FA: Fibroadenoma, FC: Fibrocystic, FCC: Fibrocystic changes, PASH: Pseudoangiomatous stromal hyperplasia, CAPPS: Columnar alteration with prominent apical snouts and secretions.

2.B. Preprocessing

A semiautomated segmentation algorithm^21,22 was used to segment breast lesions. Briefly, this algorithm constructs multiple segmentation candidates via thresholding of a constrained region-of-interest centered on the lesion. Among candidates, the algorithm selects the one with the maximum radial gradient index (RGI) at its boundary. A research specialist, with over 15 yr of experience in mammography, marked the center of the lesion, which was used as a seed point for the algorithm. A previous study²² showed its effectiveness on segmenting breast lesions for dedicated bCT images.

Because of the large number of slices contained in each image volume, it is time consuming and cumbersome for the research specialist to segment all slices of a breast lesion in each image volume. Therefore, we asked the research specialist to segment the lesion in the three orthogonal cross-sectional (2D) views at the lesion center. Specifically, the research specialist outlined the lesion boundary on each cross-sectional view shown on a regular computer screen with a digital stylus. We treated them as the gold standard of lesion segmentation and used them for evaluating the quality of segmentation results.

We used the DICE coefficient²³ to evaluate segmentation results,

$${\displaystyle \text{DICE}=\frac{1}{3}\left(\frac{2\left|A_{xy}\cap B_{xy}\right|}{\left(\left|A_{xy}\right|+\left|B_{xy}\right|\right)}+\frac{2\left|A_{yz}\cap B_{yz}\right|}{\left(\left|A_{yz}\right|+\left|B_{yz}\right|\right)}+\frac{2\left|A_{xz}\cap B_{xz}\right|}{\left(\left|A_{xz}\right|+\left|B_{xz}\right|\right)}\right),}$$ (1)

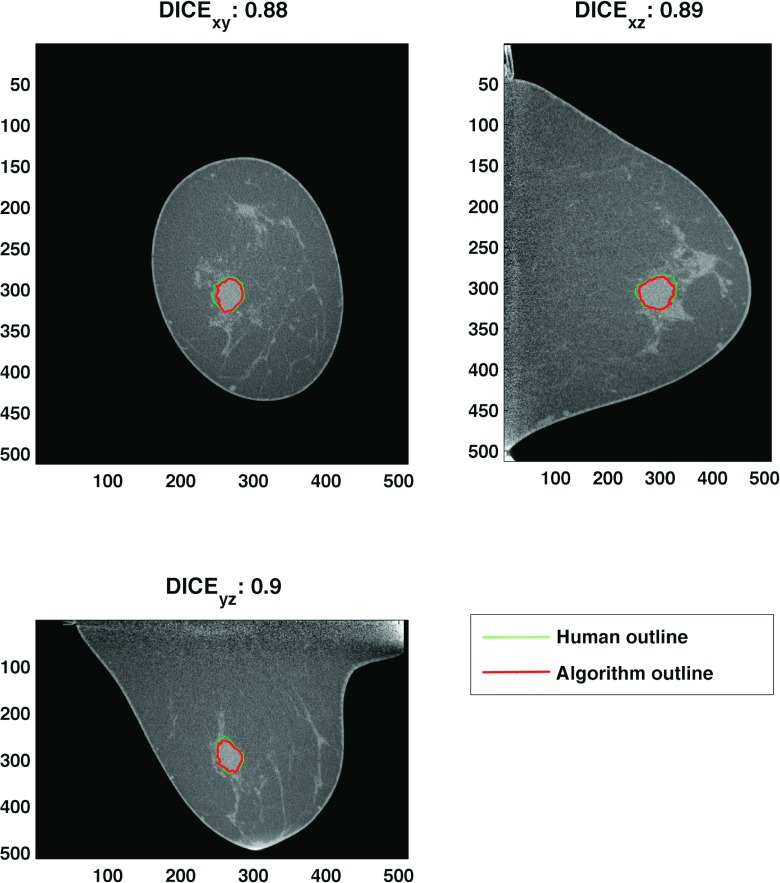
where A and B represent the segmented volume by the algorithm and the previously mentioned experienced research specialist, respectively. Subscripts xy, yz, and xz represent coronal, sagittal, and transverse cross sections at the lesion center, respectively. Figure 1 shows the DICE coefficient for one segmentation result. A previous study reported that segmentations with a DICE coefficient of 0.7 or higher show good quality.²⁴ Among 137 lesions, we removed a total of 18 lesions (17 bCT images) with poor segmentation outcome (DICE coefficient less than 0.7). Thus, this study used 119 breast lesions (77 malignant, 42 benign) of 104 bCT images (Table I).

FIG. 1.

This figure shows the DICE coefficient of one example segmentation result. The final DICE coefficient was computed by averaging DICE coefficients of each cross-sectional view. Any segmentation with a DICE value of less than 0.7 was removed from the study.

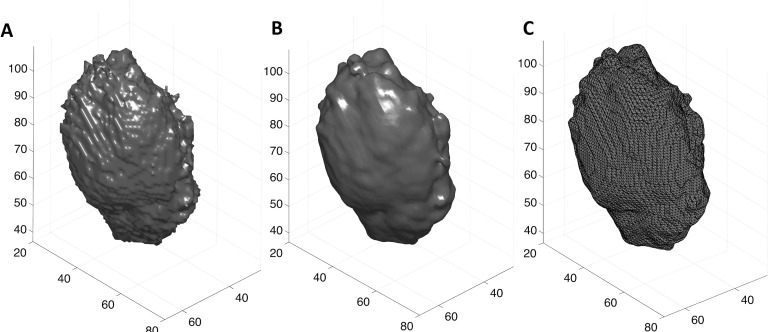
Then, we smoothed each volumetric segmentation using a cubic structure with a size of 3 × 3 × 3 voxels, to make it smooth enough to compute the surface curvature. We extracted a triangulated mesh from each volumetric segmentation using the isosurface function in matlab (v.8.3, Mathworks, Natick, MA). Figure 2 depicts a triangulated surface extracted from an example segmentation outcome.

FIG. 2.

(A) The volumetric segmentation obtained using the semiautomated segmentation algorithm. (B) and (C) display the smoothed version of the segmentation results and its triangulated surface representation [lines in (C) represent edges of triangulated surface], respectively. The smoothing operation retains the overall shape and detail of the breast lesion, while removing noise.

2.C. Surface curvature of breast lesion

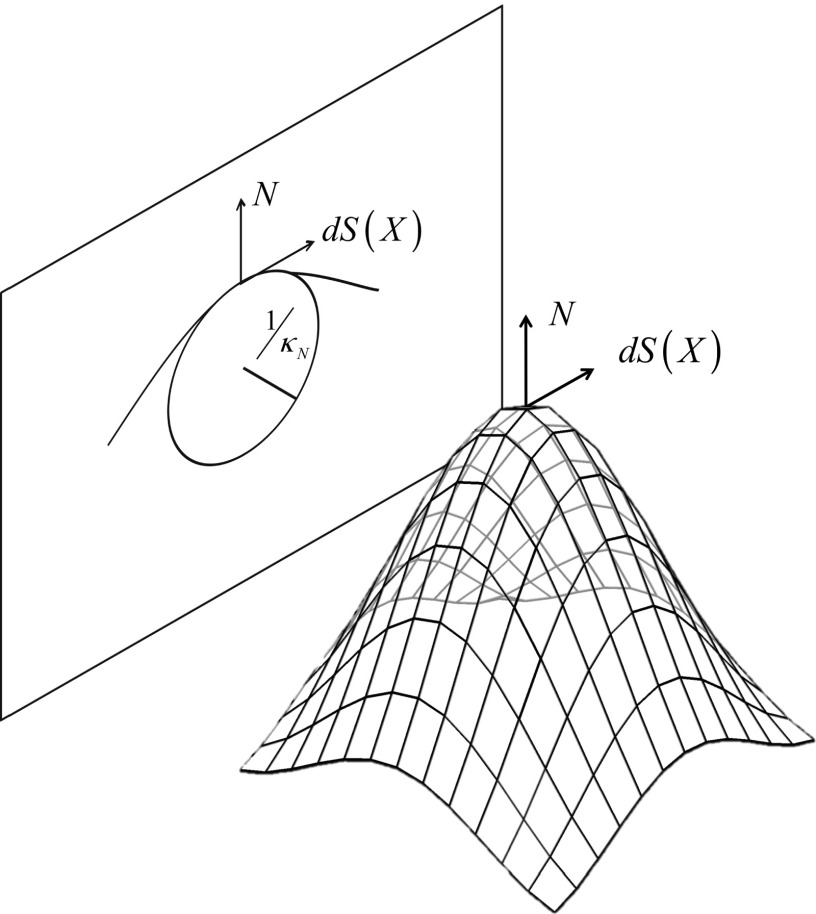
Let S be a function representing a surface of interest, where it maps a patch P in the Euclidean plane ℜ² to a surface $S\left(P\right)$ in the 3D space ℜ³ (i.e., S : P → ℜ³). The differential of S (i.e., dS) maps a vector X on the patch P to the tangent direction on the surface $dS\left(X\right)$. Also, let N a unit normal to $dS\left(X\right)$ and $dN\left(X\right)$ be its differential. Then, one can write the normal curvature in the direction of X²⁵ as

$${\displaystyle {\kappa }_N=\frac{-dS\left(X\right)\cdot dN\left(X\right)}{{\left|dS\left(X\right)\right|}^2}.}$$ (2)

As multiple tangent directions X exist at the vertex v on the surface, one can have multiple normal curvatures. One can obtain a maximum and a minimum among them, which are called principal curvatures κ_Max and κ_Min.

Principal curvatures were computed for the triangulated mesh of each smoothed segmentation. For this, we first computed curvatures for the edges of each triangulated mesh. Then curvatures at each vertex were obtained by integrating the curvatures of the neighboring edges around the vertex. Details about the algorithms for computing principal curvatures from a given surface can be found in the related papers.^26,27 Then, we computed the total, mean, and Gaussian curvatures at the vertex v of the surface S as follows:

$${\displaystyle T=\left|{\kappa }_{\text{Max}}\right|+\left|{\kappa }_{\text{Min}}\right|,}$$

$${\displaystyle H=\frac{{\kappa }_{\text{Max}}+{\kappa }_{\text{Min}}}{2},}$$

$${\displaystyle K={\kappa }_{\text{Max}}\cdot {\kappa }_{\text{Min}}.}$$ (3)

For each lesion, we calculated the above curvature measures at each vertex on the surface as well as their corresponding summary statistics (i.e., average and standard deviation).

Note that curvatures at a vertex are inversely proportional to the size (i.e., radius) of a circle fitted on the cross-sectional curve of a surface (Fig. 3). Thus, large breast lesions can have relatively smaller curvature values than smaller breast lesions. In addition, small breast lesions can show wider variations in curvature values than large breast lesions. This is because the number of vertices available for curvature calculation; small breast lesions have fewer vertices than large breast lesions. Figure 4 shows average and standard deviation across lesion surface for each of the three curvature measures, as a function of lesion diameter. As expected, a strong correlation with lesion diameter was found for average mean curvature, and moderate correlations were found between average total and Gaussian curvature and standard deviation of the total curvature measure, but not for the other two curvature measures.

FIG. 3.

An illustration of how the normal curvature at a vertex is related to the size of a circle fitted to the cross-sectional contour at the same vertex. The magnitude of the normal curvature has an inverse relationship with the radius of the circle.

FIG. 4.

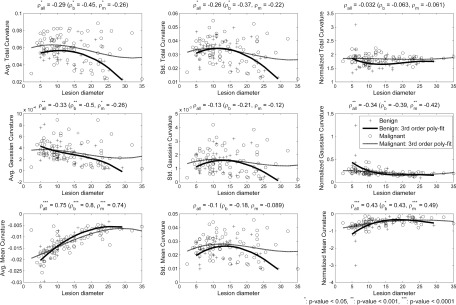
The first and second columns show the relationship of the average and standard deviation of each curvature measure with the lesion size. The last column shows the relationship between the normalized versions of the curvature measures and lesion size. Pearson’s correlation analysis was conducted on (1) all lesions, (2) benign lesions only, and (3) malignant lesions only. The normalization process successfully reduced each measure’s dependency on lesion size, especially for total curvature. To visualize the dependency between lesion size and each curvature measure, third order polynomial fits for benign lesions (solid line) and for malignant lesions (dashed line) are added on each plot. Fitted lines for normalized measures also show reduced dependency on lesion size compared to measures without normalization. Note that one benign lesion shows higher magnitude in normalized curvature values than the others. The correlation analysis after removing such lesion was similar to that of the original set; the correlation coefficient values for the normalized total, Gaussian, and mean curvature were 0.03 (p-value = 0.76), −0.44 (p-value < 0.0001), and 0.49 (p-value < 0.0001), respectively.

To remove the above dependency of curvature measures to the lesion size, we normalized the average of each curvature measure with its standard deviation,

$${\displaystyle C_T=\frac{\text{Avg}\left(T\right)}{\text{Std}\left(T\right)},C_H=\frac{\text{Avg}\left(H\right)}{\text{Std}\left(H\right)},C_K=\frac{\text{Avg}\left(K\right)}{\text{Std}\left(K\right)}.}$$ (4)

The last column of Fig. 4 shows the scatter plot between normalized curvature measures of breast lesions and their size. The normalized total curvature showed no correlation (statistically significant) between its value and the lesion diameter, while there still existed a linear correlation between the normalized measure value and the lesion size for the other two measures. However, the correlation was reduced (from ρ = 0.75 to ρ = 0.43) for the mean curvature and at least similar for the Gaussian curvature. Similar relationships were observed between the curvature measure values and the lesion diameter when considering benign and malignant lesions separately; the normalization process successfully reduced most of the curvature measure’s dependency on lesion diameters, except for the Gaussian curvature on malignant lesions.

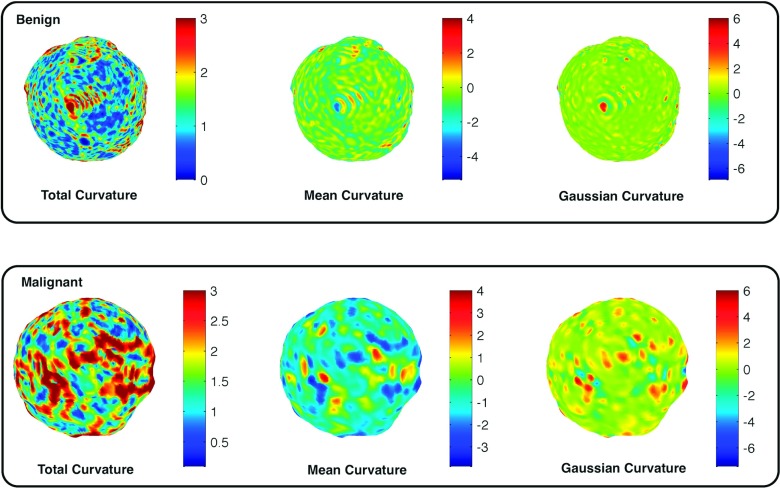
Note that one may normalize the above curvature measures using the number of vertices on a breast lesion, instead of its standard deviation. However, it was not able to remove the dependency of curvature measures on the lesion size; ρ-values for each curvature measure normalized by the number of vertices were −0.6, −0.45, and 0.49, which still shows strong dependency on the lesion size. Therefore, we used the curvature measures normalized by their standard deviations as our features for classification tasks in Sec. 2.E. Figure 5 shows how the normalized total, mean, and Gaussian curvature values differ for a malignant and a benign lesion. The malignant lesions tended to show more variation in curvature values than the benign lesions.

FIG. 5.

Illustrations of how the total, mean, and Gaussian curvature values vary on the lesion surface for malignant and benign lesions. Malignant lesions tended to show more variations in curvature values than benign lesions.

2.D. Additional image features for breast tumor classification

In addition to curvature measures, this study extracted a set of traditional image features that has been introduced by previous studies^13,14,18 from volumetric segmentations. The traditional image features selected for this study included three histogram based descriptors, seven shape descriptors, three margin descriptors, and two texture descriptors. A detailed description of each image feature, and how to extract it, is described in Table II. The operators $〈\cdot 〉$, | ⋅ |, and σ(⋅) represent the average, the norm of a vector, and the standard deviation, respectively. In addition, R, M, and d are the segmented region, its margin, and the distance from the margin voxel from the center, respectively. GV refers to image gray values and R_S represents the spherical region with the equal volume of R. Moreover, G, G_r, h are the image gradient vector, its radial component, and the semiaxes of an ellipsoid fit to R, respectively. GLCM in this paper refers to the 3D extension of 2D gray-level co-occurrence matrix, which represents the spatial relationship of neighboring pixels. Specifically, it shows how often pairs of voxels with specific gray values occurred in the specific spatial relationship. One may refer to the related paper²⁸ for more detail about our texture descriptors. These additional image features were used to compare the classification performance of the curvature measures introduced by this study.

TABLE II.

List of traditional image features.

Histogram descriptors		Definition
Average region gray value (HU)	H1	〈GV〉R
Region gray value variation (HU)	H2	σ(GV)R
Margin gray value variation (HU)	H3	σ(GV)M
Shape descriptors
Irregularity	S1	2.2∗R1/3/M1/2
Compactness	S2	(ΣR∩RS)/(ΣRS)
Ellipsoid axes min-to-max ratio	S3	min(h)/max(h)
Margin distance variation (mm)	S4	σ(|d|)M
Relative margin distance variation	S5	σ(|d|)M/〈|d|〉M
Average gradient direction	S6	〈cos(∠(G, r))〉M
Margin volume (mm3)	S7	ΣM
Margin descriptors
Average radial gradient (HU)	M1	〈Gr〉M
RGI	M2	〈Gr〉M/〈|G|〉M
Radial gradient variation	M3	σ(Gr)M
Texture descriptors
GLCM | energy	T1	Energy of 3D gray-level co-occurrence matrix
GLCM | contrast	T2	Contrast of 3D gray-level co-occurrence matrix

2.E. Classifier training and evaluation strategy

To evaluate the classification performance of curvature measures, we trained a logistic regression as our classifier. As the outcome variable for our problem is binary, i.e., whether the lesion is malignant or benign, we selected logistic regression as our classifier. One can use alternate methods, such as linear discrimination analysis (LDA); however, a previous study showed that LDA and logistic regression yield similar classification performance.²⁹ We labeled each breast lesion as benign or malignant following its biopsy result and treated them as dependent variables for the logistic regression. Each lesion’s normalized curvature measures in Eq. (4) were treated as independent variables.

For each curvature measure, a single feature classifier was created. Then, we used leave-one-out cross-validation (LOOCV) to evaluate the classification performance of each curvature measure. This study used the area under the ROC curve (AUC) as a figure of merit.

To show the usefulness of the curvature measures introduced by this study, we trained additional logistic regressions using the traditional image features described in Sec. 2.D. This study utilized the sequential feature selection scheme (the sequentialfs function with forward feature selection option) available in matlab to find a set of features optimized for classifying breast tumors. The classification performance of features that were most selected in the LOOCV loop was used to compare the classification performance of curvature measures.

As the above logistic regression models are based on the same dataset, their corresponding ROC curves are correlated to each other. To compare AUCs of those ROC curves, we therefore used the method described in the work of Delong et al.³⁰ The analysis was conducted using the statistical toolbox (v. 9.0) of matlab.

3. RESULTS

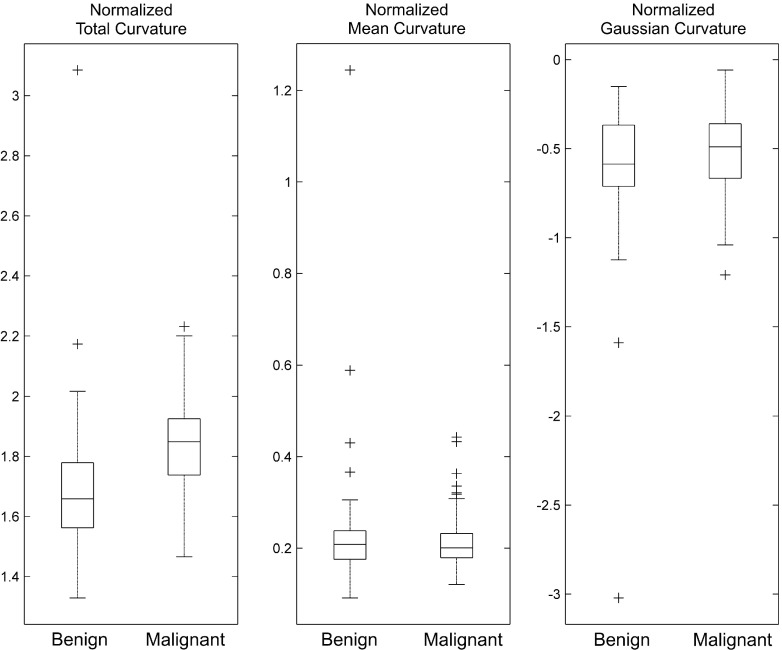
Figure 6 illustrates how the averaged values of the normalized total, mean, and Gaussian curvatures (C_T, C_H, and C_K) differ for the set of malignant and benign lesions. Malignant lesions tended to have higher total curvature values than benign lesions. However, there was no difference between malignant and benign lesions for the other two curvature measures. From this, we can expect that the normalized total curvature measure will have higher classification performance than the other two curvature measures, which is what we found (see Table III). The normalized total curvature measure, C_T, showed the best performance in both the training set (AUC of 0.76) and the test set (AUC of 0.74), while the other two measures showed similar performance (the cut-off AUC value of this decision was <0.6) of a chance classifier (i.e., AUC of 0.5) in the training set. Thus, their AUCs for the test set were not analyzed.

FIG. 6.

This box plot displays how the averaged normalized total, mean, and Gaussian curvature values differ for the set of malignant and benign lesions.

TABLE III.

Classification performance of curvature measures and traditional image features.

	AUC
Features	Training set (mean)	Test set
Curvature measures | individual model performance
CT: normalized total curvature	0.76	0.74
CM: normalized mean curvature	0.5	N/A
CG: normalized Gaussian curvature	0.54	N/A
Image features | individual model performance (selection frequency)
S3: ellipsoid axes min-to-max ratio (100%)	0.56	N/A
S6: average gradient direction (100%)	0.69	0.67
M2: RGI (100%)	0.74	0.73
T1: GLCM | energy (97%)	0.5	N/A
M3: radial gradient variation (96%)	0.65	0.6
Combined model performance via feature selection
Subset of features in Table II	0.87	0.78

Note: N/A: Not analyzed.

From the sequential feature selection, a total of five image features were frequently selected and their composite classification performance was 0.87 for the training set and 0.78 for the test set (Table III). We fitted a single feature classifier for each of the frequently selected features and found that most of the classification power was from M2 (the RGI: 0.74 in the training set, 0.73 in the test set), followed by S6 (the average gradient direction: 0.69 in the training set, 0.67 in the test set), and M3 (the radial gradient variation: 0.65 in the training set, 0.6 in the test set). The classification performance of C_T was higher than most of the individual image features and similar to M2 (C_T: 0.74, M2: 0.73 for test set).

To demonstrate the usefulness of the curvature measures, specifically the normalized total curvature measure, C_T, we conducted additional ROC analyses using logistic regression models with the following list of features: (1) the five mostly selected image features, (2) the five mostly selected image features + C_T, (3) M2 + C_T, and (4) different feature combinations in terms of its type (e.g., shape descriptors) as listed in Table IV. The classification performances of models (1), (2), and (3) were 0.83, 0.86, and 0.81, respectively. Although there was a 2%–3% increase in classification performance from model (3) to model (1) and from model (1) to model (2), the increment amount was not statistically significant (first–third rows in Table IV).

TABLE IV.

Classification performance comparison between different combinations of curvature and image features.

Performance comparison				Difference in AUC
Feature list	AUCL	Feature list	AUCR	AUCL − AUCR [95% CI]	p-value
[S3 S6 M2 T1 M3]	0.83	[S3 S6 M2 T1 M3] + [CT]	0.86	−0.029 [−0.071,0.012]	0.166
[M2] + [CT]	0.81	[S3 S6 M2 T1 M3]	0.83	−0.021 [−0.1,0.063]	0.627
		[S3 S6 M2 T1 M3] + [CT]	0.86	−0.05 [−0.12,0.018]	0.152
[M2]	0.73	[M2] + [M3]	0.74	−0.007 [−0.046,0.033]	0.746
				[M2] + [S3 S6]	0.78	−0.054 [−0.12,0.013]	0.115
				[M2] + [T1]	0.74	−0.007 [−0.05,0.031]	0.642
				[M2] + [CT]	0.81	−0.083 [−0.16,−0.005]	0.037a
		[CT]	0.74	[CT] + [S3 S6]	0.78	−0.039 [−0.14,0.066]	0.465
				[CT] + [T1]	0.73	0.007 [−0.024,0.038]	0.667
				[CT] + [M2 M3]	0.82	−0.079 [−0.17,0.008]	0.076
				[CT] + [T1 M2 M3]	0.83	−0.093 [−0.18,−0.004]	0.04a
				[CT] + [S3 S6 M2 M3]	0.83	−0.088 [−0.17,−0.005]	0.037a
				[CT] + [S3 S6 M2 M3 T1]	0.86	−0.12 [−0.22,−0.03]	0.009a

^aStatistically significant (p-value < 0.05).

It is important to note that there was no statistically significant difference between the performance of the minimal model (3) and that of (1) (second row in Table IV). This shows the effectiveness of the normalized total curvature, C_T, for classification tasks; C_T has useful information for classifying breast tumors, such that it can replace the other four image features for the task. In addition, M2 and C_T account for most of the classification power in model (2); M2 and C_T showed an AUC of 0.81, while model (2) showed an AUC of 0.86 for the test set. Each additional feature, other than M2 and C_T, improved the classifier by only 1%.

We then analyzed how C_T and M2 could achieve comparable performance of the full model (1). We found that the M2 needs the shape descriptors to achieve higher classification power (fifth row in Table IV); the difference between the AUC of the M2 only and the M2 with the shape descriptors (S3 and S6) approached statistical significance (p-value = 0.115), while the difference in the AUC for the combinations of other descriptors was clearly not statistically significant. Since the M2 and C_T achieved better classification power than the M2 only (seventh row in Table IV), we may conclude that the C_T contains the information of the lesion shape and it can be treated as one of the shape descriptors. This makes sense, as curvature measures have been used to describe the morphology of various objects of interest.^31–33

From additional performance comparisons between the C_T only and the C_T with other descriptors, we found that the C_T has complementary information to other existing features (last six rows in Table IV). Specifically, the shape descriptors (S3 and S6) contain additional information for classifying breast tumors, as it adds about a 0.04 increment in AUC, although it is not statistically significant. In addition, we found that the margin descriptors (M2 and M3) contain the best complementary information for classification tasks, while the texture (T1) does not; the difference in the AUC between C_T + M2 and M3 and C_T only is higher than that between C_T + T1 and C_T only (last fourth and fifth rows in Table IV). This analysis also confirms our findings above, that C_T is one of the shape descriptors.

In summary, only the normalized total curvature, C_T, has classification power for differentiating benign and malignant breast lesions. We can treat C_T as a type of shape descriptor that contains new information about breast tumors in classification tasks, where it can replace the traditional morphological image features.

As our results are based on the segmentation result using a semiautomated algorithm with a given seed point, it is important to check how variations in the location of the seed point affect the segmentation results and further the proposed curvature measure’s classification performance. To do so, we shifted the seed point from its original position for different amounts (the shifted amounts are summarized in the first column of Table V). We recomputed DICE coefficients in Eq. (1) for each error case. Then, to check the effect of annotation error on segmentation results, we conducted the paired t-test between DICE values from the original seed point and those from each error case. As we repeated the statistical test for each error case, we corrected the significance level using the Bonferroni correction; the resulting significance level was 0.05/9 = 0.0056.

TABLE V.

Effect of annotation errors in segmentation and classification performance.

	DICE		[M2] + [CT] vs. [S3 S6 M2 T1 M3]
Error (x, y, z) in voxel	Mean, Std [Min,Max]	No. < 0.7	AUCL	AUCR	AUCL − AUCR [95% CI]	p-value
+(0, 0, 0)	0.83, 0.058 [0.7,0.93]	0	0.81	0.86	−0.05 [−0.12,0.018]	0.152
+(1, 0, 0)	0.82, 0.078 [0.59,0.93]	9	0.81	0.84	0.028 [−0.05,0.11]	0.481
+(0, 1, 0)	0.82, 0.074 [0.59,0.94]	7	0.8	0.83	0.03 [−0.055,0.11]	0.494
+(0, 0, 1)	0.81, 0.102 [0.14,0.93]	10	0.81	0.82	0.0095 [−0.065,0.084]	0.803
+(2, 0, 0)	0.82, 0.089 [0.32,0.93]	9	0.81	0.84	0.033 [−0.04,0.11]	0.377
+(0, 2, 0)	0.82, 0.076 [0.59,0.93]	7	0.81	0.82	0.0098 [−0.069,0.089]	0.808
+(0, 0, 2)	0.81, 0.122 [0.14,0.93]	10	0.82	0.81	−0.0092 [−0.079,0.06]	0.796
+(5, 0, 0)	0.77,a 0.15 [0.02,0.93]	16	0.69	0.8	0.1 [0.025,0.18]	0.01
+(0, 5, 0)	0.78,a 0.171 [0.03,0.93]	12	0.8	0.76	−0.043 [−0.11,0.028]	0.234
+(0, 0, 5)	0.79, 0.143 [0.05,0.92]	11	0.83	0.81	−0.017 [-0.092,0.057]	0.645

^aDifference was statistically significant compared to the case without error (p-value < 0.0056).

For shifts up to 2 voxels, there was no statistical difference in segmentation performance. However, we found that shifts in seed points of 5 voxels (2 out of 3 cases with 5 voxel shifts) resulted in a statistically significant difference in segmentation performance and an increased number of cases with their DICE values below 0.7. Specifically, we observed that the number of cases with DICE values below 0.7 increased, as the shift increased from 2 to 5.

We further analyzed how degraded segmentation performance affects the classification performance of our normalized total curvature measure (i.e., C_T). For this, we compared the classification performance of the minimal model ([M2] + [C_T]) and that of the model with traditional features ([S3 S6 M2 T1 M3]) for each of the error cases. Note that we did not remove the cases with their DICE values <0.7 for this analysis, because we wanted to check the robustness of our measure to the segmentation error. Similar to the analysis on the segmentation results, we corrected the significance level using the Bonferroni correction.

For all cases, there were no statistically significant differences between above models (right half of Table V), which confirms our finding, i.e., C_T has useful information for classifying breast tumors and it can replace the other four image features for the classification task. Although it is not statistically significant, however, one error case did lower the classification performance of the minimal model (third row from the bottom of Table V) compared to other error cases. In fact, this is the case with the lowest segmentation performance; its mean DICE value is the lowest and the number of cases with DICE values <0.7 is higher than others. We found that this result is mainly due to the cases with very poor segmentation results (N = 3, with DICE values between 0.02 and 0.1). After removing these cases, the classification performance of the minimal model was improved (from 0.69 to 0.79). Thus, we can expect that C_T will maintain its classification performance as long as one includes cases with good segmentation results (i.e., DICE value >0.7). From these results, we can conclude that shifts up to 5 voxels will not change the overall performance of the classifier, but the accuracy of segmentation may decrease in some specific cases.

4. DISCUSSION

This paper introduced novel image features using 3D surface information from segmented breast lesions in bCT images. Our image features included total, mean, and Gaussian curvatures, and they can measure local variations in the curvature of the breast lesion surface. From ROC analysis for classifying breast tumors, we showed that the normalized total curvature is the best performing feature for the task. Combined with a traditional image feature (i.e., RGI, M2), the normalized total curvature achieved comparable classification performance of a classifier built from multiple traditional image features.

It has been known that we can interpret the shape of a volumetric object’s surface using mean and Gaussian curvature values.³⁴ In fact, mean and Gaussian curvatures have been extensively used in the computer vision field for various tasks, including the automatic detection of a point of interest of some object.^34–37 In medical imaging, mean and Gaussian curvatures have been used to analyze the morphology of the brain cortex (i.e., gyrification) for various brain related disorders, including Autism and Alzheimer’s disease.^31–33 In this respect, it is surprising that mean and Gaussian curvature values have no useful information for distinguishing malignant and benign breast lesions. It is possible that we lost useful information by simply averaging the mean and the Gaussian curvature values over the entire surface. Thus, we may need different ways to summarize the information available in the mean and the Gaussian curvatures. Finding such ways should be a good future follow-up study for this paper.

Our analysis showed that the normalized total curvature is one of the shape descriptors. This makes sense, as the curvature measure explains how much the shape of a breast lesion curves over its surface. In addition, we found that four out of five most selected traditional image features are directly related to the breast lesion morphology. This finding is similar to that of previous studies for bCT. Previous studies reported that classifiers with more morphological features yield higher classification performance than those of less morphological features.^13,14 This may suggest that future breast CAD systems (especially for bCT) should consider shape (or morphological) features for classification tasks. In fact, many recent breast CAD systems utilize morphological features for classifying breast tumors.^14,38 However, their usage is still limited to part of the full 3D breast lesion morphology. It is possible that we will eventually be able to extract more useful morphological information of breast lesions from its 3D surface representation.

It is worth noting that the normalized total curvature (C_T), with the RGI (M2), can achieve comparable performance of a classifier with five traditional image features. It is relatively easy to increase the classification performance by using many features for training a classifier. However, we cannot guarantee whether the resulting classifier will work on other independent datasets. This is where the limitation of previous studies arises; they utilized many features to train relatively small datasets. In the work of Ray et al.,¹³ a total of 14 image features were used to achieve an AUC of 0.8. In addition, Kuo et al.¹⁴ reported that five to seven image features were frequently selected to achieve an AUC of up to 0.78. Although various validation schemes were used, it is still possible that their classifiers might be overtrained. Because of this, many automated algorithms may only work in a specific dataset. To achieve robustness of the algorithm to other datasets, we need to minimize the number of features to be trained, at least until a large training set becomes available. Therefore, it is advantageous to replace 4–5 features with a single feature that can have comparable performance in classification tasks.

The limitations of our study include (1) the moderate size of the dataset and (2) the dependency of curvature measures on the segmentation result. The range in the 95% CI values ranged from 0.08 to 0.19, which is a fairly moderate range. We would like the range to be approximately 0.05, which is small enough to conclude that the difference is not important clinically, if the difference is statistically significant. Future research using a large dataset would be necessary. For the second limitation, we showed that poor segmentation results can affect our curvature measures. However, we can avoid this problem by including only lesions with good segmentation quality (e.g., DICE > 0.7), or we may utilize better segmentation algorithms that may become available in the future to ensure the quality of segmentation results. A previous study showed that better segmentation outcome results in higher classification performance for morphological image features.¹⁴ Thus, the curvature measures will show better classification performance than before if we use a better segmentation algorithm than the one used in this paper. Developing improved segmentation algorithms would be a good future study.

In conclusion, the normalized curvature measure is a new morphological image feature that contains useful information in classifying breast tumors. Using this feature, one can reduce the number of features in a classifier, which may result in a more robust classifier.