Objective classification system for sagittal craniosynostosis based on suture segmentation

Abstract

Purpose:

Spring-assisted surgery is an effective and minimally invasive treatment for sagittal craniosynostosis (CSO). The principal barrier to the advancement of spring-assisted surgery is the patient-specific spring selection. The selection of spring force depends on the suture involved, subtypes of sagittal CSO, and age of the infant, among other factors. Clinically, physicians manually judge the subtype of sagittal CSO patients based on their CT image data, which may cause bias from different clinicians. An objective system would be helpful to stratify the sagittal CSO patients and make spring choice less subjective.

Methods:

The authors developed a novel informatics system to automatically segment and characterize sutures and classify sagittal CSO. The proposed system is composed of three phases: preprocessing, sutures segmentation, and classification. First, the three-dimensional (3D) skull was extracted from the CT images and aligned with the symmetry of the cranial vault. Second, a “hemispherical projection” algorithm was developed to transform 3D surface of the skull to a polar two-dimensional plane. Through the transformation, an “effective” projected region can be obtained to enable easy segmentation of sutures. Then, the different types of sutures, such as coronal sutures, lambdoid sutures, sagittal suture, and metopic suture, obtained from the segmented sutures were further identified by a dual-projection technique of the midline of the sutures. Finally, 108 quantified features of sutures were extracted and selected by a proposed multiclass feature scoring system. The sagittal CSO patients were classified into four subtypes: anterior, central, posterior, and complex with the support vector machine approach. Fivefold cross validation (CV) was employed to evaluate the capability of selected features in discriminating the four subtypes in 33 sagittal CSO patients. Receiver operating characteristics (ROC) curves were used to assess the robustness of the developed system.

Results:

The segmentation results of the proposed method were clinically acceptable for the qualitative evaluation. For the quantitative evaluation, the fivefold CV accuracy of the classification for the four subtypes was 72.7%. This classification system was reliable with the area under curve (in ROC analysis) being greater than 0.8 for four two-class problems.

Conclusions:

The proposed hemispherical projection algorithm based on backtracking search can successfully segment sutures of the cranial vault. The classification system can also offer a desirable performance. As a result, the proposed segmentation and classification system is expected to bring insights into clinic research and the selection of the spring force to facilitate widespread application of this minimally invasive treatment.

1. INTRODUCTION

Craniosynostosis (CSO), the premature fusion of the cranial sutures,^1–3 is characterized by the abnormal morphology of the cranial vault, with the increment of the intracranial pressure. The incidence is about 1 in every 5000 births.^4,5 CSO, in terms of the prematurely fused suture, could be classified mainly into several types of isolated suture CSO, such as sagittal, coronal, metopic, and lambdoid. Among these types, sagittal CSO remains the most common type, accounting for 40%–60% of CSO.^6,7 Sagittal CSO results from the intramembranous ossification of the sagittal suture. For the treatment of sagittal CSO, Lauritzen in 1998 first introduced spring-assisted surgery.⁸ This treatment provides progressive change without the risks of cranial remodeling; it uses the force of a spring to reshape the skull in a slower manner that harnesses the growth of the skull to assist with shape change. Spring-assisted surgery has been considered as an effective and minimally invasive treatment regimen with promising clinic results.^8–14

Patient-specific spring selection is the principal barrier to the advancement of spring-assisted surgery for sagittal CSO because few surgeons have the experience to select personalized springs for each patient. The selection of the spring force is a crucial step in this surgical treatment, and it is dependent on the experience of the surgeon. To facilitate the widespread use of this minimally invasive treatment modality, the selection of the spring force, tailored to each patient, needs to be automated and reproducible. Important factors essential in the selection of the spring force include the suture involved and the subtypes of sagittal CSO.^15,16 For example, sagittal CSO with an elongated occiput needs a stronger posterior spring, while one with no predominant characteristics typically needs a midrange anterior and posterior spring.¹⁶ In order to optimize the selection of the spring force, an automated system for segmentation and characterization of sutures and further classification of the sagittal CSO, as a preliminary stage of the automated selection of the spring force, would be helpful.

In terms of the clinical classification of sagittal CSO, several forms have been proposed.^15,17,18 Taking into account the three rules of compensatory growth,¹⁹ Massimi et al.¹⁷ and Jane et al.¹⁸ classified sagittal CSO into three main variants: The anterior type shows evident frontal bossing. The posterior type is characterized by a narrowing of the posterior regions of the skull with protuberance of the occipital bones. The complete type is a combination of the two previous variants. The traditionally described characteristics, such as frontal bossing, biparietal narrowing, and occipital lengthening, however, are inconsistently present.¹⁵ David et al., based on the presence of a single dominant characteristic as seen on CT scans, stratified the sagittal synostosis into four subtypes: anterior (tight retrocoronal band), central (heaped-up sagittal ridge), posterior (prominent occiput), and complex (no specific dominant feature).¹⁵ In light of this classification system, David’s group modified the type, strength, and number of springs to improve the predictability of the clinical outcome of spring-assisted surgery.

Although sagittal CSO could be clinically classified by experienced surgeons, designing an automated classification system for sagittal CSO is a daunting task. To date, some studies have tried to coarsely classify CSO,^7,20–26 whereas limited literature about automated classification for sagittal CSO into subtypes exists. In 2006, Ruiz-Correa et al. introduced scaphocephaly severity indices, defined by the ratios of the head width to length from three selected planes, to predict and quantify the skull-shape deformity of isolated sagittal CSO.⁷ Then, symbolic shape descriptors were introduced to predicate sagittal and metopic CSO using the support vector machine (SVM),²² and a Bayesian methodology was adapted to the classification of CSO.²⁰ Yang et al. proposed a logistic regression to identify different types of CSO using a cranial image²² derived from the pairwise distance between evenly spaced points on the skull contours of selected multiple planes.^24,26 In order to classify the CSO into three types (sagittal, metopic, and unicoronal), Lam et al. developed a general platform upon which basic shape measures, both single-valued and vector-valued, were extracted from a single plane projection of a top view of the three-dimensional (3D) skull,²¹ and then three angle features and a width to length ratio are appended into the previous work to form a new algorithm.²³ Recently, a statistical shape model was proposed to label the sutures on infant cranial vault. The index of cranial suture fusion and curvature discrepancy was used to classify the CSO with promising performance.²⁵ Except for this study,²⁵ previous methods^7,20–24,26 considered mainly the shape of the cranial vault while paid little attention to the sutures. Overall, these methods^7,20–26 were used to develop automated classification system for CSO rather than sagittal CSO.

The clinic classification of sagittal CSO is based on the anatomical characterization, including the tight retrocoronal band, the heaped-up sagittal ridge, the prominent occiput, or no specific dominant feature.¹⁵ These anatomical structures are difficult to be fully described by feature descriptors. However, the abnormal deformations of infant cranial vault are mainly caused by fusion of the individual sutures,^27,28 suggesting attributes of sutures are essential and decisive for the classification of sagittal CSO.¹⁷ Therefore, the objectives of this work are to (1) perform a thorough segmentation and characterization of sutures to capture the essential information that describes sagittal CSO and (2) further classify sagittal CSO into four subtypes,¹⁵ as the preliminary stage of the automated selection of the spring force. In this work, we have to overcome three technical challenges: (1) the 3D surface segmentation of the sutures; (2) the features description for the 3D segmented sutures; and (3) the normalization of the cranial vault/segmented sutures, which should be done ahead of the classification stage, because of the significant difference between the cranial vaults of infants of different ages.^2,29 As far as we know, few approaches^25,30 have been proposed to segment sutures on infant cranial vault. Mendoza et al. labeled sutures using the multiatlas of normal anatomy²⁵ and Ghadimi et al. applied a coupled level set to segment sutures in each slice from newborn CT images.³⁰ Although these two methods can successfully segment sutures, it is still difficult to effectively normalize and comprehensively describe the 3D sutures for classification.

In order to deal with these challenges, we proposed a “hemispherical projection” algorithm based on backtracking search to transform a 3D surface of the cranial vault to a polar two-dimensional (2D) plane. Through this, the 3D information, such as two angles and distance in spherical coordinates, was preserved in the 2D projected matrix (two coordinates and intensity) without any information loss. An “effective” projected region from the transformation can facilitate easy segmentation and characterization of sutures. Meanwhile, the shape of the skull is normalized in the projected binary matrix because two coordinates describe the orientation of skull points in 3D space, and the physical distances information can be neglected. Based on the hemispherical projection technique, we proposed a segmentation and classification scheme with three phases. In the preprocessing stage, the 3D skull was extracted, using the imaging property of bone, and aligned based on the symmetry of the cranial vault. In the segmentation phase, the sutures were segmented by the hemispherical projection algorithm, and the different sutures (two coronal sutures, two lambdoid sutures, sagittal suture, and metopic suture) were identified using the dual-projection technique of the midline of sutures. In the classification phase, a total of 108 suture features were extracted, evaluated, and selected by extending our previously proposed feature scoring system^31,32 to the current multiclass problem. Then, sagittal CSO was stratified into four subtypes (anterior, central, posterior, and complex) using the established support vector machine tool LIBSVM.³³ Finally, we validated this classification system on 33 subjects with fivefold cross validated experiments and receiver operating characteristics (ROC) analysis.

Overall, the major contributions of the proposed approach can be summarized as follows. First, the hemispherical projection algorithm based on backtracking search can provide a projected matrix with designated resolutions, in which the segmentation, identification, and characterization of sutures are more feasible. Second, dual-projection technique of the midline of sutures can identify different types of sutures. Additionally, a multiclass feature scoring system is proposed to evaluate and select the features to avoid overfitting and to improve the classification accuracy. The clinical significance of our work can be summarized as (1) the segmentation and identification of sutures can offer a new perspective for clinical research of CSO, for example, quantitative research can potentially reveal the relationship between fusion conditions of sutures and cranial vault deformation and (2) the automatic segmentation and classification system can potentially be used to optimize the selection of spring force and be the foundation of automated selection of spring force.

2. METHOD

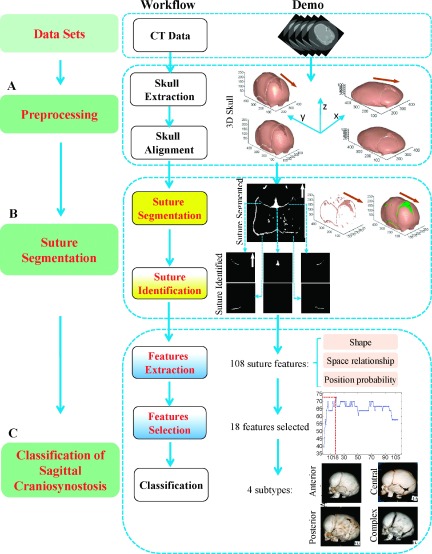
As shown in Fig. 1, the proposed segmentation and classification approach is comprised of three phases, i.e., a preprocessing phase (Sec. 2.A), a suture segmentation phase (Sec. 2.B), and a classification phase (Sec. 2.C). In the preprocessing phase, the skull is extracted from 3D CT data and aligned with the midsagittal line (MSL). In the suture segmentation phase, a “spherical projection” algorithm based on backtracking search projects the 3D skull to 2D plane (Sec. 2.B.1), in which the segmentation of the sutures could be readily obtained (Sec. 2.B.2), and the different types of sutures could be identified by the dual-projection technique of the midline of sutures (Sec. 2.B.3). In the last phase (Sec. 2.C), 108 features of the sutures are extracted (Sec. 2.C.1) and evaluated by a multiclass feature scoring system (Sec. 2.C.2). Then, the classification of sagittal CSO can be achieved using standard SVM (Sec. 2.C.3).

FIG. 1.

Schematic framework for the segmentation and classification of sagittal CSO. The arrows in the 2D projected images and 3D skull image denote the front of the skull.

2.A. Preprocessing

Suture segmentation is greatly facilitated by first extracting surrounding skull structures. Since CT intensities for bone tissues are consistently higher than brain tissues, the skull can be segmented quite robustly by simple thresholding. Given that the CT intensity for soft tissue is usually less than 60 Hounsfield units (HU) (for example, ventricle 1–12 HU, white matter 25–38 HU, and gray matter 35–60 HU) and 1000 HU for bones on average, we chose the threshold of 300 HU, such that pixels with intensity higher than the threshold are extracted as skull structure. This threshold is chosen to preserve the cranial tissue of the infant that is still in ossification and less dense than adult cranial tissues.

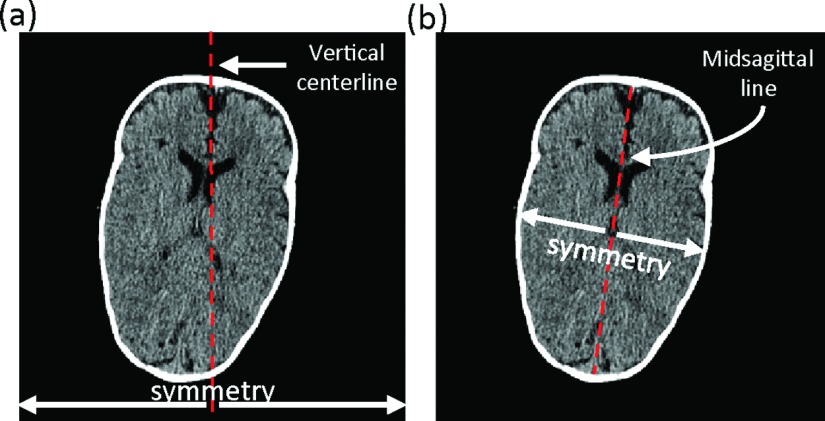
After extraction of the 3D skull, the inclination angle and position were corrected by aligning MSL with the vertical centerline of the image, as shown in Fig. 2(a). The brain can be roughly deemed as symmetric with the axis being the MSL, as shown in Fig. 2(b). Therefore, the determination of MSL of the brain was critical in this alignment. We used two steps to determine the MSL based on the symmetric property of brain, including (1) detection of candidate MSLs and (2) identification of final MSL.

FIG. 2.

(a) The vertical centerline of image and (b) midsagittal line.

First, a 2D mask was generated by projection of the 3D skull from the top view with holes in the mask filled by morphological operations (Fig. S1 of the supplementary material³⁶). For each point on the boundary of the 2D mask, we detected the longest line from this point to the other points on the boundary (Fig. S2 of the supplementary material³⁶). The lines with length ranked top 10% were selected as candidate MSLs. Here, the percentage was chosen empirically. Then, we flipped the mask along each candidate MSL and calculated the overlap between the original mask and the “mirror” mask. The final MSL was the candidate MSL with maximum overlap value.

Once the MSL was determined, we aligned the MSL with the vertical centerline of the image. More specially, the skull was translated by aligning the middle point of the MSL to that of the vertical centerline of the image, and rotated by the inclination angle between the MSL and vertical centerline of the image, as shown in Fig. 1(A) and Fig. S3 of the supplementary material.³⁶

2.B. Suture segmentation

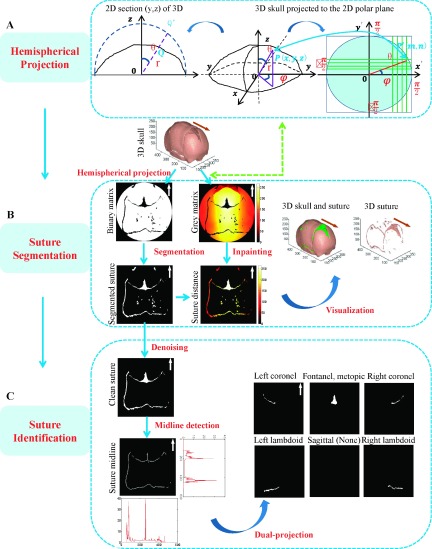
In this section, we will describe the details of the hemispherical projection algorithm based on backtracking search, which is the critical step in the proposed system. Then, the segmentation and identification of sutures is introduced, respectively, as shown in Fig. 3.

FIG. 3.

Suture segmentation and identification. The arrows in the 2D projected images and 3D skull image denote the front of the skull.

2.B.1. Hemispherical projection of the 3D skull

We assumed that the 3D skull surface was convex, which is reasonable because in CT images the skull almost always contain slices above the middle of the orbit. As shown in Fig. 3(A), only one point on the inner surface of skull along a ray from the central point in spherical polar coordinates (SPC) system was mapped to the minimum circumscribed hemisphere of the skull. Thus, the hemispherical projection from the 3D skull to the 2D plane can be considered as an isomorphic projection, confirming the rationality of the following work. The proposed hemispherical projection algorithm was mainly based on two considerations: (1) The hemispherical projection transforms a 3D skull surface to a definite polar 2D plane composed of the polar angle and azimuthal angle of SPC. (2) The projected matrix was practically yielded by the backtracking search method to ensure even distribution of the projected information.

Without loss of generality, we chose the center point of the bottom slice as the origin of the SPC. Using SPC, the ith voxel p_i on the segmented skull can be specified by a triplet, i.e., (r_i, θ_i, φ_i), where r_i, θ_i, and φ_i refer to radial distance, polar angle, and azimuthal angle, respectively, and θ_i, φ_i ∈ [ − π/2, π/2] by appropriately orienting the axes of SPC.

The SPC triplets were then partitioned to give two complementary matrix representations of the extracted 3D skull (voxel value equals 1, i.e., p = 1, if on the skull and 0 otherwise): binary matrix and gray matrix. For both matrices, the voxel p_i(r_i, θ_i, φ_i) was mapped to an element p′(m, n) according to

$${\displaystyle \left\{\begin{array}{l}m=\left[\frac{{\theta }_{i}cos\left({\phi }_i\right)}{\pi }N\right]+\frac{N}{2}\hfill \\ n=\left[\frac{{\theta }_{i}sin\left({\phi }_i\right)}{\pi }N\right]+\frac{N}{2}\hfill \end{array}\right.,}$$ (1)

where N is the number of rows/columns of the matrix. For binary matrix, the projected element p′ of pixel p_i was assigned a value of 1, while for the gray matrix, the value of r_i is assigned.

In practice, projected matrix (binary matrix and gray matrix) was yielded by the proposed backtracking search method. Let the projected element ${\tilde{p}}^{\prime }(\tilde{m},\tilde{n})$ correspond to a skull point ${\tilde{p}}_i$. The polar angle and azimuthal angle in SPC can be determined by the inverse transformation of Eq. (1) as follows:

$${\displaystyle \left\{\begin{array}{l}{\tilde{\phi }}_i=\sqrt{{\left(\frac{\tilde{m}}{N}-\frac{1}{2}\right)}^2+{\left(\frac{\tilde{m}}{N}-\frac{1}{2}\right)}^2}\cdot \pi \hfill \\ {\tilde{\theta }}_i={tan}^{-1}\left(\frac{\tilde{m}}{\tilde{n}}\right)\hfill \end{array}\right..}$$ (2)

We then searched whether a skull point existed along the direction of $({\tilde{\theta }}_i,{\tilde{\phi }}_i)$. In order to speed up the search, we used the radius ${\tilde{r}}_{\mathrm{in}}$ of the maximum inscribed hemisphere as the start point, and the radius ${\tilde{r}}_{\mathrm{ex}}$ of the minimum circumscribed hemisphere with certain minimum redundancy e_r as the end, so the search radius is ${\tilde{r}}_i^j\in [{\tilde{r}}_{\mathit{in}},{\tilde{r}}_{\mathit{ex}}+e_r]$, j = 1, …, T. T was the voxel number of the search range. In this work, the redundancy e_r was empirically selected as ten pixels, and the search step was set as a voxel. The $({\tilde{r}}_i^j,{\tilde{\theta }}_i,{\tilde{\phi }}_i)$ of SPC was transformed to Cartesian coordinates $\left({\tilde{x}}_i,{\tilde{y}}_i,{\tilde{z}}_i\right)$ by the following formula:

$${\displaystyle \left\{\begin{array}{l}{\tilde{x}}_i={\tilde{r}}_i^{j}sin{\tilde{\phi }}_{i}cos{\tilde{\theta }}_i\hfill \\ {\tilde{y}}_i={\tilde{r}}_i^{j}sin{\tilde{\phi }}_{i}sin{\tilde{\theta }}_i\hfill \\ {\tilde{z}}_i={\tilde{r}}_i^{j}cos{\tilde{\theta }}_i\hfill \end{array}\right..}$$ (3)

$\tilde{p}({\tilde{x}}_i,{\tilde{y}}_i,{\tilde{z}}_i)$ is a skull point, if $\tilde{p}({\tilde{x}}_i,{\tilde{y}}_i,{\tilde{z}}_i)$ is equal to 1. For binary matrix, the projected element ${\tilde{p}}^{\prime }=1$, while for the gray matrix, ${\tilde{p}}^{\prime }={\tilde{r}}_i$. If $\tilde{p}({\tilde{x}}_i,{\tilde{y}}_i,{\tilde{z}}_i)$ is always 0 in the whole search range, which means no skull point along this direction $\left({\tilde{\theta }}_i,{\tilde{\phi }}_i\right)$, hence ${\tilde{p}}^{\prime }=0$.

Actually, the matrix elements are defined only for θ_i ∈ [ − π/2, π/2]. This gives an effective circular region with radius π/2 that consists of pixel projections only from bone and nonbone structures. This effective circular region obtained from the transformation will play a vital role in the segmentation.

The coordinates (r_i, θ_i, φ_i) of 3D surface were all contained in the projected gray matrix. The coordinates in gray matrix describe the direction of the subject in 3D, and the intensity presents the distance. Thus, gray matrix can ultimately represent or used to reconstruct the 3D surface. In addition, the binary matrix is used to describe whether the skull point exists along an individual directional determined by the two coordinates. Besides, the binary matrix also can be considered as the normalized form for the 3D surface, because it contains the orientation information without distance, and the size of the 3D surface was manifested only by magnitudes of coordinates in 2D. This property of the binary matrix was essential to feature selection as well as the final classification.

In fact, the physical size of the projected matrix was fixed (i.e., π/2 × π/2) and N is the resolution. We empirically set the resolution N as 512, which can satisfy the requirement of this work.

2.B.2. Suture segmentation

Since cranial sutures are fibrous tissues connecting skull bones, the nonbone element (i.e., with value 0) within the effective circular region of the 2D skull projection matrix can be considered as the projection of 3D sutures. Thus, suture area can be easily obtained by excluding the skull area in the effective region, which was the significant contribution of the hemispherical projection. To visualize the segmented sutures, we then interpolated the suture area in the gray matrix, using a classic inpainting algorithm,³⁴ to obtain the radial distance for the segmented suture voxel in SPC. The 3D sutures can be reconstructed by Eq. (2), as shown in Fig. 3(B).

2.B.3. Suture identification

The cranial sutures are often classified into six categories, i.e., left and right coronal sutures, left and right lambdoid sutures, and sagittal and metopic sutures, which dominated the abnormal deformation of the cranial vault. Since there are some noise regions from the holes on the cranial vault of infants after the transformation, it was necessary to remove those noise spots, according to their position distribution and shape features. These noise regions are small and compact, and mainly lie between the coronal and lambdoid suture. Therefore, we proposed the following scheme to identify these noise regions. First, we assumed that Ω_i was the region in the segmented sutures, where i = 1, …, M, and M was the total number of regions. We then defined the compactness as

$${\displaystyle \text{Compactness}\left(i\right)=\frac{4\pi S_i}{L_i^2},}$$ (4)

where S_i and L_i is the area and perimeter of the region Ω_i, respectively. It means when the object is a circle, the compactness is equal to 1. A region of interest (ROI) from 300th to 400th row was empirically defined. $S_i^{\mathrm{roi}}$ is the area of the region Ω_i in the ROI. Finally, the noise regions can be determined by

$${\displaystyle \text{Noise}\_\text{region}=\left\{{\mathrm{\Omega }}_i|\text{Compactness}\left(i\right)>0.5\text{ or }\right.\left.S_i^{\text{roi}}/S_i>0.1\text{ and Compactness}\left(i\right)>0.3\right\}.}$$ (5)

We proposed a dual-projection technique for identification of sutures. First, midlines of sutures were detected by the morphological approach, in order to retain one pixel in one section of the suture, since the thickness varied across the segmented sutures due to the fusion condition and the bias possibly brought by the segmentation. We then projected midlines along the x-axis (column directional) and y-axis, respectively, and the pixel values were accumulated at each position of projected y- and x-axes. As a result, two histograms can be obtained, as shown in Fig. 3(C). Two peaks in the histogram of the projected y-axis were detected and further used to estimate ranges in y-axis for the coronal and lambdoid with the prior position knowledge of sutures. Analogously, peaks in the histogram of the projected x-axis can be estimated by the ranges in x-axis for the coronal, lambdoid, and fontanelle. By combining the different ranges in x-axis and y-axis, the different types of sutures can be identified. It should be noted that the anterior fontanelle is a junction of coronel sutures and metopic suture. In order to extract features efficiently, we technically considered the anterior fontanelle and metopic suture as one type in this algorithm.

2.C. Classification for sagittal CSO

2.C.1. Feature extraction

Our approach used for suture segmentation in 2D projected-space can simultaneously scale and normalize 3D cranial morphologies, which allow us to characterize sutures by their shapes and positions. The predominant trait for each subtype of sagittal CSO (Ref. 15) is mainly determined mainly by the fusion condition of the sagittal suture, and also directly related to the condition of other sutures, according to the three rules of compensatory growth.¹⁹ Therefore, we extracted 105 features from six individual suture sections (e.g., right lambdoid suture and right coronal area) and the whole structure of six sutures, and designed three distance relationships between different sutures. Overall, we designed 108 candidate features that were potentially useful in discriminating four subtypes of sagittal CSO. To our knowledge, it is the first time to systematically extract suture features for CSO classification. These attributes can be categorized into three groups: 98 features related to shape of sutures, 7 position probabilities of sutures, and 3 space relationships of sutures. A summary of these features is shown in Table S1 of the supplementary material.³⁶

2.C.1.a. Features related to shape of sutures.

We first determined the existence (1 or 0) for each suture, and calculated the average length and width, the suture area, and suture segments number in each suture area. Then, the suture segment with the largest area was selected as the primary segment, for which the area, perimeter, area of the bounding box, major axis length, minor axis length, orientation, eccentricity, sphericity, and compactness were calculated. We defined the sphericity as a ratio of the minimum distance to the maximum distance from the suture boundary to the central point and defined compactness by Eq. (4).

2.C.1.b. Position probabilities of sutures.

The suture position of the normal cranial vault was relatively fixed in the 2D projected plane, owing to the normalized property of the binary matrix in terms of the distance in 3D space. The accumulation of projected sutures in 2D plane, to some extent, represents the position distribution of sutures. Thus, a likelihood map could be created by accumulation and normalization of the certain amount of binary suture masks. Here, we applied 50 cases to form the likelihood map (Fig. S4 of the supplementary material³⁶). We then calculated the average probability for each suture in the likelihood image.

2.C.1.c. Space relationships of sutures.

The suture position of the abnormal cranial vault varies with samples. For example, the lambdoid suture position of a cranial vault with predominant occiput would probably move forward in the 2D projected plan. Thus, we defined three distances to describe the space relationship of sutures: the rear-distance from the lambdoid to the rear of the skull; the middle-distance from the lambdoid to the coronal suture; and the front-distance from the coronal suture to the front of the skull.

2.C.2. Feature selection

Feature selection is conducted to identify the most relevant features with a high degree of discrimination between different sample types. We previously proposed a feature selection scheme (based on DX score) and confirmed its effectiveness and efficiency in two-class problems of classification.³² Briefly, DX score assesses the degree of dissimilarity between positive and negative types for each feature, normalized by sum of variances in the respective sample types. The DX can be mathematically represented as

$${\displaystyle \text{DX}=\frac{{(m_1-m_0)}^2}{{d_1}^2+{d_0}^2}.}$$ (6)

In this formula, m₁ and d₁ are the mean value and standard deviation of the feature in the positive samples, while m₀ and d₀ are the corresponding statistics in the negative samples.

To deal with the current multiclass problem, we extended this method and modified it to the following DX-multiscore version:

$${\displaystyle {\text{DX}}_{\mathrm{multi}}=\sum _{i\ne j}\frac{{(m_i-m_j)}^2}{{d_i}^2+{d_j}^2+\delta },}$$ (7)

where m_i and d_i are mean and standard deviation for a selected feature in class i, respectively. Analogous to the two-class problem, we first separately evaluated the dissimilarity between any two different sample types i and j for each feature, and then summed up the combinatorial effects to a single score DX_multi. The small positive number δ is added to avoid zero divisors where both types have zero variances for a specific feature.

Machine learning methods are generally evaluated by fivefold cross validation (CV). In fivefold CV, our dataset was first randomly partitioned into five subsets of approximately equal size, with each subset containing roughly equal number of four types. Then, four subsets were used for training the classifier, and the remaining subset was retained as the validation data for testing this model. This procedure was repeated five times and each of the five subsets used exactly once as the validation data. The predication accuracy of fivefold CV is defined as the percentage of four types correctly classified in the test stage, averaging on five times of test.³²

Starting from the individual scores, we sequentially added each feature (with DX score from high to low) to form a feature set and test its prediction performance by fivefold cross validation. Thus, we obtained a curve of CV accuracy with number of top-ranked features. The optimized features with best accuracy will be used for late training and testing.

2.C.3. Classification using SVM

We chose the SVM algorithm³⁵ for classification. Specifically, we employed a well-established SVM tool LIBSVM (Ref. 33) as the classifier. The radial basis function (RBF) was used as the kernel function based on various trials. For each test group, we also performed a grid search on the RBF parameter γ and the trade-off coefficient C. In addition, ROC was conducted to evaluate the performance in accuracy and robustness of each classifier. The ROC curve is determined by the sensitivity and specificity, which can be calculated as $\text{sensitivity}=\text{TP}/\left(\text{TP}+\text{FN}\right)$ and $\text{specificity}=\text{TN}/\left(\text{FP}+\text{TN}\right)$, where TP, FP, FN, and TN refer to true positive, false positive, false negative, and true negative, respectively.

3. EXPERIMENTS AND RESULTS

3.A. Data sets

This study was approved by the Institutional Review Board of Wake Forest School of Medicine. Our dataset was collected at Wake Forest School of Medicine using CT scanners (Light Speed 16, GE Medical System) with an x-ray tube voltage of 100–120 kVp. The slice thickness is 0.625 or 1.25 mm. Each slice has a matrix size of 512 × 512 pixels, and the pixel size ranged from 0.43 to 0.41 mm, with a 16-bit gray level in HU.

Extending our previous work,¹⁵ the purpose of the current study is to objectively and automatically classify sagittal CSO into four subtypes, i.e., anterior, central, posterior, and complex. Five sets of reference standards of subtypes for 50 subjects were provided by four clinical experts from the Department of Plastic and Reconstructive Surgery and one medical physicist from the Department of Diagnostic Radiology, respectively. To ensure the reliability of the standard, the ground truth was chosen when least four out of the five experts agree on the classification. As a result, 33 subjects, including 13 anterior, 9 central, 4 posterior, and 7 complex subtypes, were used in this study of classification. The mean age of all patients at the time of diagnosis was 2.67 months, with a median of 2 months and a range of 12 days to 7 months.

3.B. Performance of segmentation for sutures

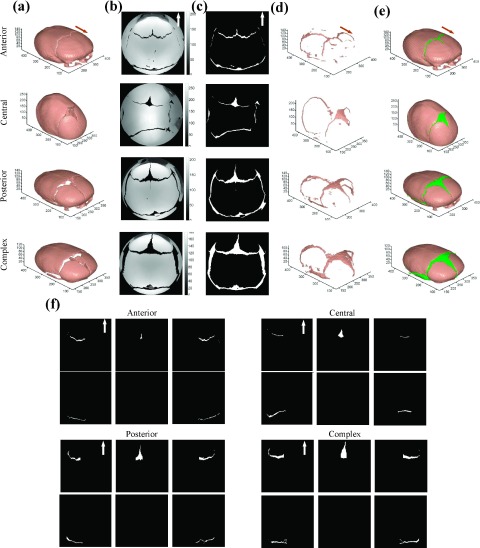
We applied the proposed segmentation and identification approach to our datasets. Figure 4 displays four representative samples of the anterior, central, posterior, and complex subtypes of sagittal CSO. (a) shows the preprocessing results of the skull extraction and alignment. In (b), gray projected matrices were from the hemispherical projection. We can see that in the effective circular region, there are only pixels projected from bone and nonbone sutures. Sutures can be easily obtained from this effective circular region, as shown in (c). (d) and (e) visualized the reconstructed sutures and skull in 3D. The identified different types of sutures are illustrated in subpanels of (f) correspondingly. We find that the segmented results are visually acceptable.

FIG. 4.

Illustration results of the segmentation and identification for sutures with four subtypes of sagittal CSO: (a) preprocessing results; (b) gray projected matrix from the hemispherical projection; (c) segmented sutures in 2D plane; (d) constructed 3D sutures; (e) constructed 3D skull and suture; and (f) identified different types of sutures.

3.C. Performance of the features in discrimination

Figure 5(a) shows the 108 features sorted by DX-multiscore from high to low. The x-axis and y-axis present the feature index and DX-multiscore, respectively. According to the definition of DX-multiscore, features with score possess stronger capability in discriminating different sample types. We then sequentially added ranked feature to form a feature set and to test prediction performance by fivefold CV, as shown in Fig. 5(b). Twenty-two top-ranked features, listed in Table I, were determined by the best accuracy, and will serve as the optimal feature set for later training and testing. This feature selection scheme could provide a reasonable performance in a feasible time $\left(O\left(n\right)\right)$ while the exhaustive searching takes too long to be practical $\left(O\left(2^n\right)\right)$.

FIG. 5.

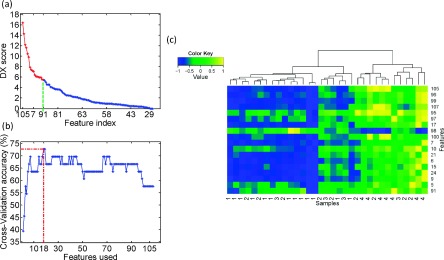
The performance of features in discrimination: (a) DX-multiscores of the 108 features. (b) Performance of fivefold CV by adding features sequentially. The highest prediction accuracy was achieved using the 18 top-ranked features with fivefold CV and RBF as kernel function. (c) Hierarchical clustering analysis for 18 features selected by (b) of each subtypes. The label value from 1 to 4 represents the subtypes of anterior, central, posterior, and complex, respectively.

TABLE I.

Eighteen selected features ranked by the DX-multiscore.

Rank	ID	Feature description	DX-multiscore
1	105	Eccentricity of the segment with largest area in the region of whole structure of six sutures	16.406
2	96	Area of whole structure of six sutures	14.304
3	99	Area of the segment with largest area in the region of whole structure of six sutures	12.227
4	107	Compactness of the segment with largest area in the region of whole structure of six sutures	11.641
5	95	Average length of whole structure of six sutures	10.481
6	97	Average width of whole structure of six sutures	9.860
7	17	Compactness of the segment with largest area in the region of the left coronal suture	7.893
8	98	Number of suture segments in the region of whole structure of six sutures	7.442
9	100	Perimeter of the segment with largest area in the region of whole structure of six sutures	7.266
10	7	Average width of the left coronal suture	7.127
11	10	Perimeter of the segment with largest area in the region of the left coronal suture	6.427
12	21	Area of the right coronal suture	6.113
13	6	Area of the left coronal suture	6.098
14	15	Eccentricity of the segment with largest area in the region of the left coronal suture	6.010
15	24	Area of the segment with largest area in the region of the right coronal suture	5.989
16	9	Area of the segment with largest area in the region of the left coronal suture	5.986
17	5	Average length of the left coronal suture	5.552
18	91	Sphericity of the segment with largest area in the region of metopic suture and anterior fontanelle	5.488

In order to further illustrate the performance of the selected 18 features in discriminating the four subtypes of the sagittal CSO, we performed hierarchical clustering analysis on them using the function heatmap.2 in R language with default settings. Figure 5(c) shows the effect of hierarchical clustering on 33 subjects, represented by the aforementioned 18 features. The label value from 1 to 4 represents the subtypes of anterior, central, posterior, and complex, respectively. The right patch mainly consists of the central and complex subtypes, while the left patch is dominated by anterior, central, and posterior subtypes. The anterior and complex subtypes are completely separated by the right and left patches, and in each patch the difference between subtypes is relatively noticeable. Thus, these features can be used to separate these four subtypes well. In addition, the discrimination of individual features is consistent with the DX-multiscore shown in Fig. 5(a). For example, the feature of index 96 with the second highest DX-multiscore can be used to distinguish the three subtypes of anterior, central, and complex. This feature refers to the area of whole structure of six sutures.

3.D. Performance of the classification system

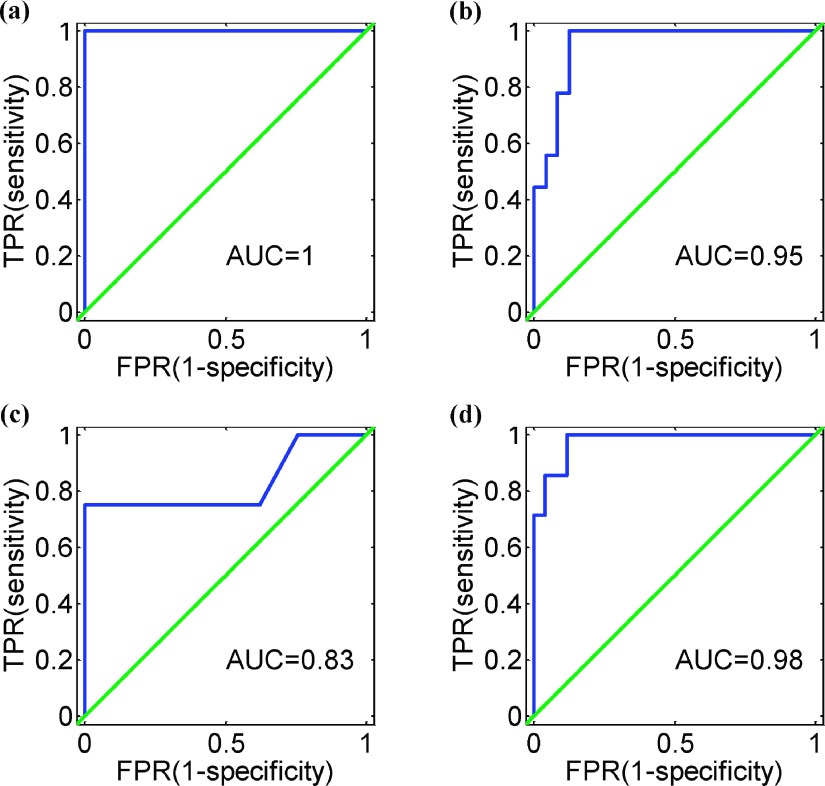
The fivefold experiments were performed on our data set for classification into four subtypes with 18 selected features, and the cross-validation accuracy was 72.7%. It demonstrates the promising prediction capability for our method. In order to assess the comprehensive performance in robustness of this classification system, we produced four ROC curves for the four two-class problems: anterior to the remain, central to the remain, posterior to the remain, and complex to the remain, as shown in Fig. 6. As expected, we got desirable performance with area under curve (AUC) greater than 0.8 for the four two-class issues. The best performance (AUC = 1) of this system is in the case of anterior against the rest [Fig. 6(a)], and for posterior against the rest yields the relatively “worst” performance with AUC = 0.83 [Fig. 6(c)].

FIG. 6.

Four ROC curves of the proposed classification system for the four two-class problems: (a) anterior to the remain, (b) central to the remain, (c) posterior to the remain, and (d) complex to the remain.

4. DISCUSSION

In this work, we have fulfilled two primary objectives: (1) the segmentation and characterization of sutures and (2) classification of sagittal CSO. The premature fusion of the cranial sutures is the root cause of sagittal CSO; thus, the segmentation and characterization of sutures are indispensable for classifying the sagittal CSO. A hemispherical projection algorithm was proposed to transform the 3D skull into 2D polar plane, in which we can effectively segment, identify, and characterize the sutures. In addition, we specifically developed an automated classification system for sagittal CSO. The segmentation and classification system for sagittal CSO is a very important step in the automated selection of spring force, which ultimately can advance spring-assisted surgery.

Clinically, physicians manually judge the subtype of sagittal CSO patients based on their CT image data, which easily causes bias from different clinicians. In our practice, the overlap of manual judgments from four clinical experts was only 30% of the whole samples, i.e., 15 out of the original 50 patient samples were consistently categorized by the four experts. This indicates that the classification of sagittal CSO is a challenging task and necessitates an objective and efficient system to make the classification less subjective. Our proposed classification system provides an encouraging fivefold CV accuracy (72.7%) of the multiclassification. It should be noted that the proposed segmentation and classification system can also be used for classifying the types of CSO besides the subtype classification of sagittal CSO addressed in the current work. In addition, this system can be further adapted to examine the relationship between the fusion conditions and the abnormal deformation, by taking other factors (e.g., thicknesses of sutures and age of the infant) into consideration.

We have overcome several technique issues to make the automated subtype classification feasible and reliable. Concretely, using the fact that the gap between cranial bones can be considered as suture, we propose a hemispherical projection algorithm based on backtracking search to transform the 3D skull surface into a 2D plane. From the transformation, an effective projected circle region, with a radius of π/2, simplifies the suture segmentation drastically. The effective projected circle area can serve as “prior knowledge” for the subsequent segmentation and as the primary contribution of the hemispherical projection algorithm. The segmentation performance of our approach was acceptable, although we did not evaluate the segmentation result quantitatively on account of the absence of the reference standard for the sutures in 3D.

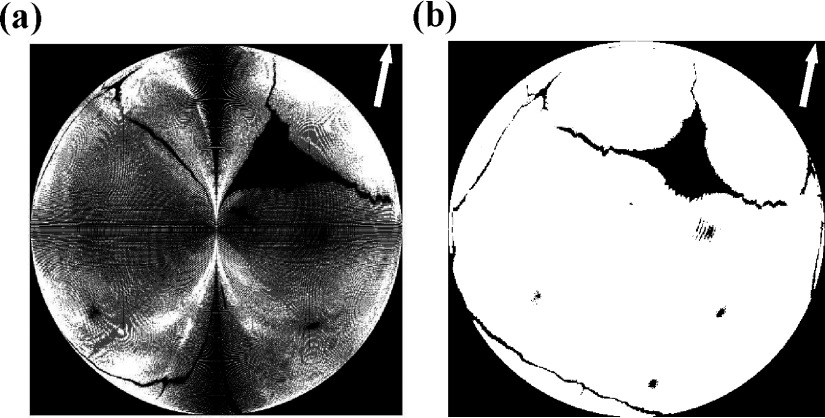
The advantage of the backtracking search scheme was its ability to generate the matrix with designated resolutions, such as 512 × 512 and 1024 × 1024. Conversely, the forward projection, directly from the skull point to the 2D plane, may offer an unacceptable projected matrix, as shown in Fig. 7(a). Though the physical size of the projected matrix is π/2 × π/2, the resolution was dependent on the surface size of the cranial vault and caused the uneven distribution of the projected pixel in the 2D plane.

FIG. 7.

The projected binary matrix from 3D surface of the skull: (a) by the forward projection and (b) by the backtracking search.

We extracted features from segmented sutures in 2D rather than reconstructed 3D sutures because there were two positive aspects. In 2D, two coordinates present the orientation of subjects in 3D, so the binary matrix of segmented sutures can be considered as the normalized form. It is required before the feature extraction since shapes between the cranial vaults of infants of different ages are significantly different. Additionally, it is highly difficult to describe the shapes of sutures in a 3D space while it is easy to achieve in 2D.

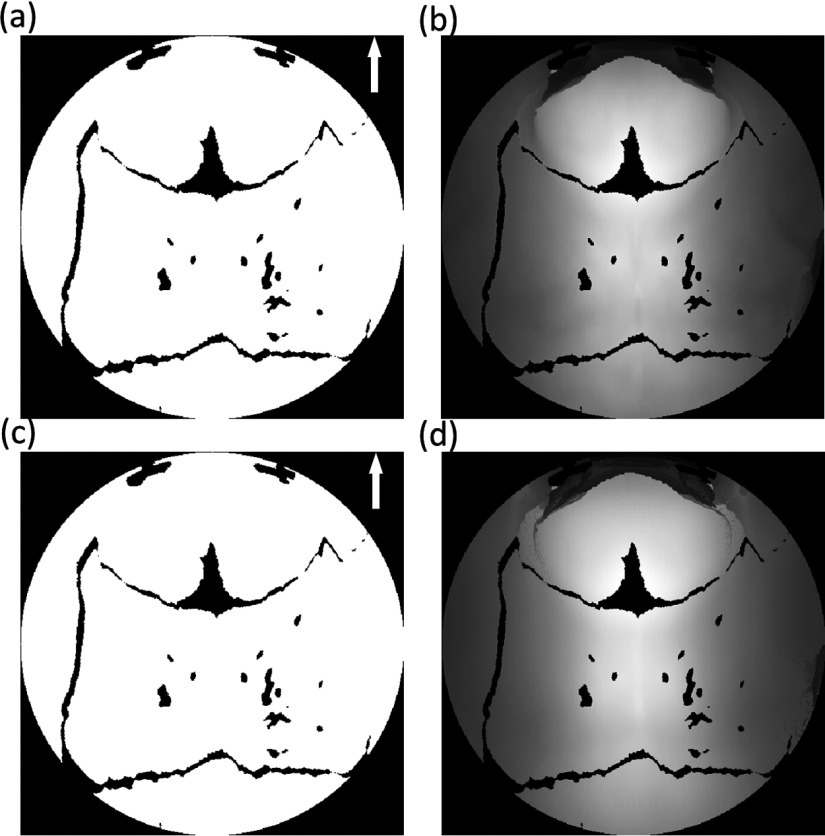
The 3D surface in the hemispherical projection algorithm is transformed into a 2D polar plane. In fact, the 3D surface can be the inner or external surface of the skull. In this work, we adopted the inner surface for transformation since we first identified the inner surface point along the ray from the center point and then identified the external surface point in the search step. We chose the inner surface for all the samples and made comparison across them; it is not essential whether the inner or external surface was considered. Obviously, the binary matrices from the inner surface and the external surface are identical [Figs. 8(a) and 8(c)], while the slight intensity difference between the gray matrices corresponds to the bone thickness [Figs. 8(b) and 8(d)]. Clinically, suture thickness is not used as a factor for stratifying the sagittal CSO; therefore, we did not take it into consideration in our study.

FIG. 8.

Projected matrixes: (a) and (c) are the binary matrices; (b) and (d) are the gray matrices. The first and second rows are transformed from the inner surface and the external surface, respectively.

In Sec. 2.A, we detected the longest line from each point on the boundary of 2D mask to the corresponding rest of boundary points, and then selected the lines with length ranked at top 10% as candidate MSLs. It is based on the fact that MSL should be one of the longest lines between the pairwise points on the boundary. Here, the percentage was chosen empirically, and the performances of subsequent alignments on 50 cases were acceptable. We also test the lines with length ranked top 20% and 50% as candidate MSLs, respectively, and ultimate performances of alignments exemplified negligible difference by vision, as shown in Fig. S5 of the supplementary material.³⁶

On the 18 top-ranked features (Table I), we can see that 44.44% features came from the whole structure of six sutures with 58.85% energy, and 50% features came from the coronal sutures with 37.55% energy, as shown in Table II. The whole structure of six sutures dominates the abnormal deformation of the cranial vault, and the coronal sutures also play a vital role in the classification of sagittal CSO. Specifically, ten top-ranked features were all extracted from the coronal suture and whole structure of six sutures. Since the sagittal sutures are fused in sagittal CSO, they cannot be segmented using our proposed automated segmentation and classification method. As a result, the conditions of the other sutures, especially the coronal sutures, are essential to the analysis of sagittal CSO.

TABLE II.

Contributions of the different sutures in the 18 top-ranked features. Energy is based on the DX-multiscore.

	Whole structure	Coronal	Metopic suture
	of six sutures	suture	and anterior fontanelles
No.	8	9	1
No. ratio (%)	44.44	50.00	5.56
Energy ratio (%)	58.85	37.55	3.60

Table III demonstrates the physical significance of different descriptors of the 18 top-ranked features. Among these descriptors, the area related features (33.30% energy) represent the most important characteristics. Simple descriptors including area, width, length, and perimeter of sutures take up 66.66% of the total features and 63.97% of the total energy. These simple descriptors are usually adopted by surgeons for the analysis of CSO analysis. Shape traits of eccentricity, compactness, and sphericity constitute 27.78% of the features and 31.15% of total energy. They are also very valuable for the classification of sagittal CSO. For the position probability of sutures, it is not in the 18 top-ranked features. Nonetheless, the performance of the position probability should be improved with increased sample size.

TABLE III.

Significance of different descriptors in the 18 top-ranked features. Energy is based on the DX-multiscore.

	Area	Width	Length	Perimeter	Eccentricity	Compactness	Sphericity	Number
No.	6	2	2	2	2	2	1	1
No. ratio (%)	33.33	11.11	11.11	11.11	11.11	11.11	5.56	5.56
Energy ratio (%)	33.30	11.15	10.53	8.99	14.72	12.83	3.60	4.89

5. CONCLUSIONS

In this study, we proposed an objective system for segmentation of sutures and classification of sagittal CSO. The suture segmentation benefited mainly from the hemispherical projection, and the features from segmented sutures further promoted the classification performance of sagittal CSO. The results demonstrated that the proposed system can be used to obtain reliable and accurate segmentation of sutures, and classification of the sagittal CSO. This system can be used for future research and can contribute to the automated selection of personalized springs in spring-assisted surgeries for corrections of CSO.