Force and number of myosin motors during muscle shortening and the coupling with the release of the ATP hydrolysis products

Abstract

The chemo-mechanical cycle of the myosin II–actin reaction in situ has been investigated in Ca²⁺-activated skinned fibres from rabbit psoas, by determining the number and strain (s) of myosin motors interacting during steady shortening at different velocities (V) and the effect of raising inorganic phosphate (P_i) concentration. It was found that in control conditions (no added P_i), shortening at V ≤ 350 nm s^–1 per half-sarcomere, corresponding to force (T) greater than half the isometric force (T₀), decreases the number of myosin motors in proportion to the reduction of T, so that s remains practically constant and similar to the T₀ value independent of V. At higher V the number of motors decreases less than in proportion to T, so that s progressively decreases. Raising P_i concentration by 10 mm, which reduces T₀ and the number of motors by 40–50%, does not influence the dependence on V of number and strain. A model simulation of the myosin–actin reaction in which the structural transitions responsible for the myosin working stroke and the release of the hydrolysis products are orthogonal explains the results assuming that P_i and then ADP are released with rates that increase as the motor progresses through the working stroke. The rate of ADP release from the conformation at the end of the working stroke is also strain-sensitive, further increasing by one order of magnitude within a few nanometres of negative strain. These results provide the molecular explanation of the relation between the rate of energy liberation and the load during muscle contraction.

Key points

• Muscle contraction is due to cyclical ATP-driven working strokes in the myosin motors while attached to the actin filament. Each working stroke is accompanied by the release of the hydrolysis products, orthophosphate and ADP. The rate of myosin–actin interactions increases with the increase in shortening velocity.

• We used fast half-sarcomere mechanics on skinned muscle fibres to determine the relation between shortening velocity and the number and strain of myosin motors and the effect of orthophosphate concentration.

• A model simulation of the myosin–actin reaction explains the results assuming that orthophosphate and then ADP are released with rates that increase as the motor progresses through the working stroke. The ADP release rate further increases by one order of magnitude with the rise of negative strain in the final motor conformation.

• These results provide the molecular explanation of the relation between the rate of energy liberation and shortening velocity during muscle contraction.

Introduction

Skeletal muscle is able to generate force and shortening for the cyclical interactions of the myosin motors (the heads of the myosin molecule extending from the thick filament) with the actin filament (Huxley, 1957; Huxley, 1969). During each interaction the myosin motor pulls the actin filament toward the centre of the sarcomere due to a structural working stroke powered by the free energy of the hydrolysis of one ATP molecule in its catalytic site (Huxley & Simmons, 1971; Lymn & Taylor, 1971). According to protein crystallography studies (Rayment et al. 1993; Geeves & Holmes, 2005), the working stroke consists of a 70 deg tilting of the light chain domain (LCD) of the myosin head about a fulcrum in the catalytic domain (CD), associated with the release of the hydrolysis products, first orthophosphate (P_i) and then ADP (White & Taylor, 1976; Nyitrai & Geeves, 2004). The lever arm action of the LCD amplifies to 11 nm the axial movement between the CD and the C-terminus of the LCD that connects the CD to the S2 rod and the thick filament backbone. In contrast to this all-or-none 11 nm working stroke, in situ mechanical–structural studies on single fibres from frog skeletal muscle indicate that the extent and the kinetics of the motor movement depend on the stress experienced by the actin-attached motors, supporting the view that the working stroke is partitioned in several structural transitions, which in physiological conditions only partly occur (Piazzesi et al. 2002, 2007, 2014; Reconditi et al. 2004; Decostre et al. 2005; Park-Holohan et al. 2012; Fusi et al. 2014). Under these conditions, how tight is the coupling between the structural–mechanical states and the biochemical states of the actin–myosin ATP hydrolysis cycle? How can the finding that the LCD tilting of myosin motors in isometric contraction is biased to the beginning of the working stroke be reconciled with the relatively high isometric rate of ATP hydrolysis (∼1/4 of the maximum rate observed during shortening; Woledge et al. 1985)?

Most of the details of the coupling between the relevant mechanical and biochemical steps in the actin attached myosin motor come from studies on demembranated muscle fibres, which allow the control of the chemical composition of the solution bathing the myofilaments (Brandt et al. 1982; Hibberd et al. 1985; Pate & Cooke, 1985, 1989a; Kawai et al. 1987; Brozovich et al. 1988; Cooke et al. 1988; Millar & Homsher, 1990; Dantzig et al. 1992; Martyn & Gordon, 1992; Walker et al. 1992; Regnier et al. 1995; Tesi et al. 2000, 2002). From these studies a mechanical–kinetic model of the actin–myosin interaction emerged (Caremani et al. 2013) with the following characteristics. 1 The force in the attached myosin heads is generated before P_i release for the transition between the weak binding state and the strong binding state (step 3), and thus in isometric contraction force-generating motors are in either the AM_i.ADP.P_i or the AM_i.ADP state (where i = 1,4) (Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992; Regnier et al. 1995; Tesi et al. 2000, 2002). 2 In isometric contraction myosin motors in the strong binding state can detach from actin at an early stage of their working stroke with the hydrolysis products (P_i and ADP) still bound to their catalytic site (step 6) and re-enter the cycle following rapid release of ligands and rebinding of ATP (step 7). 3 The working stroke kinetics is precisely defined by fitting phase 2 velocity transient following stepwise reduction in force. Phase 2 of the transient response to a step in either length or force is the mechanical manifestation of the working stroke; however only the velocity transient following a force step has direct information on the working stroke kinetics because it is not influenced by filament compliance (Piazzesi et al. 2014). The observed amplitude and rate of phase 2 velocity transient have been used to select the rate functions expressing the dependence of the transition between the structural states of the actin attached motor (M₁–M₄) and the relative position between the motor and the actin monomer. 4 During muscle shortening the execution of the working stroke and the release of hydrolysis products by the actin-attached motors are orthogonal events; namely P_i (step 4) and then ADP (step 5) can be released at any stage of the working stroke though the rate constants of product release increases with the progression in the working stroke. Actually the release of the ligand (either P_i or ADP) is a two-step process since the release itself, which is a diffusion limited process and as such very fast, must be preceded by the removal of the bonds blocking the exit of the ligand from the catalytic site. Our demonstration (Caremani et al. 2013) that the kinetics of the working stroke transitions is independent of that of product release (either step 4 or 5), while the kinetics of product release depends on the progression of motor through the working stroke, supports a picture in which the opening of the nucleotide binding pocket with the strain-dependent progression of the working stroke reduces the energy barrier for the breaking of the bonds and the actual release of the ligands. (5) The high power and efficiency of shortening muscle can be explained by assuming that a myosin motor with both ligands or only ADP in its catalytic site can slip (steps 8 and 9) from the original actin monomer to the next one farther from the centre of the sarcomere (Caremani et al. 2013).

A scheme in which P_i release and working stroke are orthogonal processes predicts that during steady shortening, as in isometric contraction, an increase in [P_i] does not affect per se the force and conformation distribution of the attached motors, but causes a reduction in the number of attachments because of the reduction of the apparent P_i dissociation constant (step 4), with rise in the AM.ADP.P_i fraction of the working motors. Moreover, during low load shortening, when the rate of P_i release becomes very fast as the motor progresses through the working stroke, the number and force of the myosin motors are determined by the rate of ADP release (k₅), giving information on the dependence of k₅ on motor conformation and strain.

In this study we determine the dependence of the force and fraction of the working motors on the shortening velocity and its modulation by [P_i]. The study involved the application of fast sarcomere-level mechanics to demembranated fibres of rabbit psoas (temperature 12°C; Linari et al. 2007) to measure half-sarcomere stiffness during steady shortening at different velocities (V) in control solution (no added P_i) and with 10 mm added P_i. The results are analysed in terms of a linear mechanical model of the half-sarcomere, composed of an array of myosin motors with a stiffness that is proportional to the half-sarcomere force, in series with the actin and myosin filaments with constant compliance (Brunello et al. 2006; Colombini et al. 2010; Fusi et al. 2010). The analysis allows the estimation of the stiffness (and thus the number) of the myosin motors working in each half-sarcomere during steady shortening (Piazzesi et al. 2007).

The results show that in 10 mm P_i, as in the control, for V up to 350 nm s⁻¹ per half-sarcomere (hs) the force of the ensemble of motors in the half-sarcomere is uniquely determined by the number of actin-attached motors, which can be modulated by either V or the concentration of P_i, while the strain and thus the force per motor remain constant. At higher V the strain in the motors drops with increase in V in roughly the same proportion in control as in 10 mm P_i. The dependence on V of the force and number of the motors provides a crucial test for the predictions of the model in Fig. 1, namely that the working stroke and the product release are orthogonal processes and that P_i and then ADP are released at rates that increase with the progression of the working stroke. During high-velocity (low-load) shortening the release of ADP mainly occurs from the conformation at the end of the working stroke with a rate constant of ∼150 s⁻¹, which further increases by one order of magnitude with the rise of negative strain.

Figure 1.

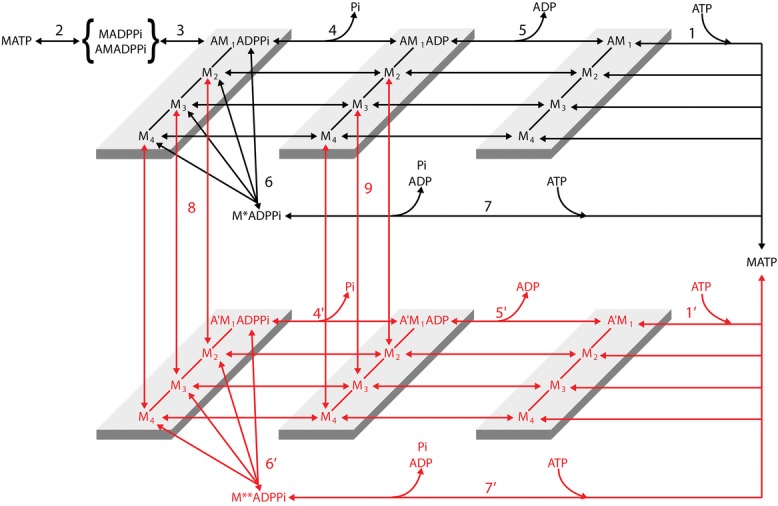
Chemo-mechanical cycle of the myosin motor

Transitions shown in black indicate the cycle undergone by myosin motors that interact with only one actin monomer (A). Transitions shown in red indicate the cycle undergone by myosin motors that slip to the next actin monomer 5.5 nm away from the centre of the sarcomere (A′). For simplicity this legend is mostly limited to black transitions. M₁–M₄ represent the structural states for a given biochemical state of the attached myosin motor. Binding of an ATP molecule to the catalytic site of the myosin head induces dissociation of the myosin motor from actin (step 1, 1′), which is followed by the recovery of the conformation of the motor at the beginning of the working stroke and the hydrolysis step (step 2). The M.ADP.P_i–AM.ADP.P_i state represents both the detached motor just after the hydrolysis step and the weakly actin-bound motor with the hydrolysis products still bound to the catalytic site. Strong binding of M to an actin monomer A (step 3) implies the formation of the first of four different force generating states, AM₁.ADP.P_i, which, without significant delay, undergoes the structural transition leading to the strained conformation responsible for the isometric force. The working stroke, in whichever of the biochemical states, AM.ADP.P_i, AM.ADP and AM, implies three subsequent force generating steps (M₁→M₂, M₂→M₃ and M₃→M₄) controlled by strain-dependent rate constants. Both biochemical events in the attached motor (release of P_i (step 4, 4′) and release of ADP (step 5, 5′)) can occur in any of the four structural states. The scheme retains the possibility of unconventional detachment of the myosin motor from actin at an early stage of the ATPase cycle, to generate a detached state with the hydrolysis products still bound to the catalytic site (step 6, leading to M*.ADP.P_i, and 6′ leading to M**.ADP.P_i), followed by fast release of products and binding of a new ATP (step 7, 7′).

Methods

Fibre mounting and mechanical apparatus

Experiments were done on glycerinated skinned fibre segments from the psoas muscle of adult male New Zealand White rabbit (4–5 kg). Rabbits were killed by injection of an overdose of sodium pentobarbitone (150 mg kg⁻¹) in the marginal ear vein, in accordance with the official regulations of the Community Council (Directive 86/609/EEC) and with Schedule 1 of the UK Animals (Scientific Procedures) Act 1986. The study was approved by the Ethical Committee for Animal Experiments of the University of Florence. Three rabbits were used in this work. Small bundles (70–150 fibres) were stored in skinning solution containing 50% glycerol at −20°C for 3–4 weeks and single fibres were prepared just before the experiment as already described (Goldman et al. 1984; Linari et al. 2007). A fibre segment 5–6 mm long was mounted between the lever arms of a loudspeaker motor and a capacitance force transducer as previously described (Linari et al. (2007) and references therein). Sarcomere length, width (w) and height (h) of the fibre were measured at 0.5 mm intervals in the 3–4 mm central segment of the relaxed fibre with a 40× dry objective (Zeiss, NA 0.60) and a 25× eyepiece. The fibre length (L₀) was adjusted to have a sarcomere length of 2.4–2.5 μm. The fibre cross-sectional area (CSA) was determined assuming the fibre cross-section to be elliptical (CSA = π/4wh) and its value ranged between 3600 and 6500 μm². Fibres were activated by temperature jump using a solution exchange system as previously described (Linari et al. 2007). The fibre was kept in activating solution at the test temperature (12°C in all experiments) for 2–3 s for the mechanical measurements (Fig. 2). A striation follower (Huxley et al. 1981) allowed nanometre–microsecond resolution recording of length changes in a selected population of sarcomeres (number range 500–1200) starting at the time the optic path was permitted through the glass window in the floor of the test temperature drop (Fig. 2A, vertical line in sarcomere length trace).

Figure 2.

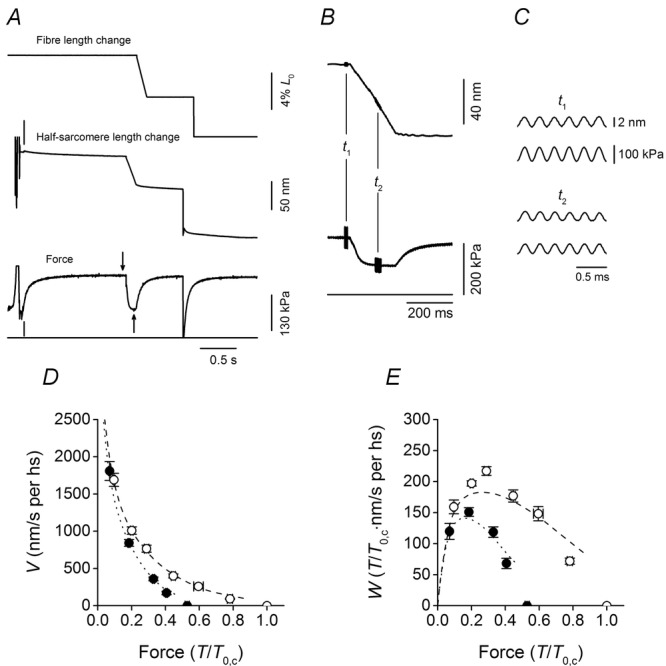
Experimental protocol, force–velocity and power–velocity relations

A, records of the force and sarcomere length change in response to a ramp shortening (amplitude 5% L₀, velocity 0.34 μm s⁻¹) imposed at 1.4 s after the fibre entered the test temperature solution. Following the force recovery at the end of the ramp, a stepwise shortening of 5% L₀ was imposed to drop the force to zero and have the baseline force in the test temperature solution. Upper trace, motor position; middle trace, half-sarcomere length change; lower trace, force; horizontal line, zero force. The vertical line on the half-sarcomere length trace marks the start of the striation follower recording. The vertical line on the force trace marks the time at which the fibre enters into the test temperature activating solution. The arrows mark the time of stiffness measurement at the isometric plateau (t₁, downward arrow) and during shortening (t₂, upward arrow). B, half-sarcomere length change (upper trace) and force (lower trace) on expanded time scales. Horizontal line, force baseline. Length oscillations of 4 kHz were imposed either at the isometric plateau (t₁) or during shortening (t₂). C, traces expanded further of half-sarcomere length change (upper) and force (lower) at t₁ (upper panel) and t₂ (lower panel). Fibre segment length, 5.4 mm; segment length under the striation follower, 1.1 mm; average sarcomere length, 2.47 μm; cross-sectional area, 6280 μm²; temperature, 11.8°C. D, force–velocity (T–V) relations in control (open circles) and in 10 mm P_i (filled circles). Force (T) is relative to the isometric plateau force in control (T_0,c). E, power–force (W–T) relations obtained from T–V relations in D. Data are means ± SEM. Lines in D and E are the relations simulated with the model in Fig. 1: dashed line, control; dotted line, 10 mm P_i.

Stiffness measurements during isometric contraction and steady shortening

The half-sarcomere stiffness was measured by imposing 4 kHz length oscillations (2 nm per hs peak to peak) at the isometric plateau and during the steady force response to shortening at velocities of 100–2000 nm s⁻¹ per hs (Fig. 2B and C). Elastic and in quadrature components were determined by Fourier analysis of force and sarcomere length signals sampled at 200 kHz. The amplitude of the viscous component was less than 3% of that of the elastic component for the whole range of shortening velocities used.

Solutions

Composition of the solutions was previously described (Caremani et al. (2008) and references therein). The starting P_i concentration was adjusted by adding KH₂PO₄ and reducing the concentration of disodium creatine phosphate (Na₂CP) and EGTA/CaEGTA to have the same ionic strength (190 mm) as in the control solution (no added P_i). The control solution without added P_i should contain about 1 mm P_i from two sources: P_i contamination in the experimental buffer and accumulation of P_i inside the fibre during contraction (Pate & Cooke, 1989a).

Data collection and analysis

Force, motor position and sarcomere length signals were recorded with a multifunction I/O board (PCI-6110E, National Instruments), and a dedicated program written in LabVIEW (National Instruments) was used for signal recording and analysis. Data are expressed as means ± SEM. The experiments were performed on 10 fibres in which the stiffness measurements with preservation of sarcomere signal could be completed both in control and in 10 mm P_i. Isometric force in control (T_0,0Pi) was 210 ± 10 kPa. Addition of 10 mm P_i reduced the isometric force to 0.53 ± 0.01 of the control value.

Model simulation

The mechanical–kinetic model used for the simulation is shown in Fig. 1. The scheme is similar to that described in Caremani et al. (2013), apart from two minor differences aimed at optimising the coherence of the scheme without any difference in the output. 1 We introduced the possibility for a myosin motor to detach with the ATP hydrolysis products still bound not only from the first actin (A, step 6) but also from the second actin (A′, step 6′) and form an M**.ADP.P_i state (different from the M*.ADP.P_i state generated by the early detachment from the first actin because its free energy is 27 zJ lower). The M**.ADP.P_i state, as the M*.ADP.P_i, undergoes the rapid completion of the working stroke and release of the hydrolysis products, followed by binding of another ATP (step 7′). This implementation ensures the same combination of pathways for a working myosin whichever is the actin to which it is attached. 2 We extended also to state M₄ the possibility for the AM_i.ADP.P_i and AM_i.ADP states to slip to the next actin farther from the centre of the sarcomere (steps 8 and 9). This was done for reasons of coherence, even if this has no practical consequences because for an AM₄.ADP motor the dominant path is the ADP release (step 5).

A specific aspect of the model, relevant for this paper, consists in the precise definition of the relation between V (and force (T)) and the number and average strain of the motors during steady shortening, which allows refinement of the rate functions concerning the kinetics of the product release and their dependence on the conformation and strain of the myosin motors. All the other rate functions are substantially the same as in Caremani et al. (2013). For reasons of clarity, all the equations expressing the rate constants for the forward transitions in the reaction scheme of Fig. 1 are listed in Appendix A, Table1. Moreover, in Appendix A, Fig. 7 are shown the rate functions for the forward and backward transitions which depend on x (the relative axial position between the myosin motor and the actin to which it is attached, with x = 0 for the position of the centre of distribution of the motors attached in the M₁ state in isometric condition and x < 0 for the shortening direction).

Table 1.

Equations expressing the rate constants of the forward transitions in the reaction scheme according to the direction of the reaction flow during steady shortening

k1,m, k1′,m (m−1 s−1)	= 4 × 105
k2 (s−1)	= 25
k3 (s−1)	= 30 exp(−0.1(x + x0 − 1.5)6)
k4,M1 (s−1), k4′,M1 (s−1)	= 60
k4,M2 (s−1), k4′,M2 (s−1)	= 100
k4,M3 (s−1), k4′,M3 (s−1)	= 1000
k4,M4 (s−1), k4′,M4 (s−1)	= 5000
k5,M1 (s−1), k5′,M1 (s−1)	= 0.5
k5,M2 (s−1), k5′,M2 (s−1)	= 10
k5,M3 (s−1), k5′,M3 (s−1)	= 15
k5,M4 (s−1)	= 150 + 1450exp((−3z(x + x0 + 3z + 4))/kBθ)/(1 + exp(−3z(x + x0 + 3z + 4)/kBθ))
k5′,M4 (s−1)	= 150 + 1450exp((−3z(x + x0 + 3z +9.5))/kBθ)/(1 + exp(−3z(x + x0 + 3z +9.5)/kBθ))
k6,M1 (s−1)	= 40 + 1460exp(−zε(x + x0 + 1.15)/kBθ)/(1 + exp(−zε(x + x0 + 1.15)/kBθ)
k6,M2 (s−1)	= 1500exp(−zε(x + x0 −1.5 + z)/kBθ)/(1 + exp(−zε(x + x0 −1.5 + z)/kBθ)
k6,M3 (s−1)	= 1500exp(−zε(x + x0 − 1 + 2z)/kBθ)/(1 + exp(−zε(x + x0 − 1 + 2z)/kBθ)
k6,M4 (s−1)	= 1500exp(−zε(x + x0 + 6 + 3z)/kBθ)/(1 + exp(−zε(x + x0 + 6 + 3z)/kBθ)
k6′,M1 (s−1)	= 40 + 1460exp(−zε(x + x0 +6.65)/kBθ)/(1 + exp(−zε(x + x0 + 6.65)/kBθ)
k6′,M2 (s−1)	= 1500exp(−zε(x + x0 + 4 + z)/kBθ)/(1 + exp(−zε(x + x0 + 4 + z)/kBθ)
k6′,M3 (s−1)	= 1500exp(−zε(x + x0 + 4.5 + 2z)/kBθ)/(1 + exp(−zε(x + x0 + 4.5 + 2z)/kBθ)
k6′,M4 (s−1)	= 1500exp(−zε(x + x0 + 11.5 + 3z)/kBθ)/(1 + exp(−zε(x + x0 + 11.5 + 3z)/kBθ)
k7 (s−1), k7′ (s−1)	= 2000
k8,M2 (s−1)	= 0.1exp(−zε(x + x0 + 0.5 + z)/kBθ)/(1 + exp(−zε(x + x0 + 0.5 + z)/kBθ)	x < −1
	= 0	x ≥ −1
k8,M3 (s−1)	= 60exp(−zε(x + x0 − 1 + 2z)/kBθ)/(1 + exp(−zε(x + x0 − 1 + 2z)/kBθ)	x < −1
	= 0	x ≥ −1
k8,M4 (s−1)	= 0.1exp(−zε(x + x0 − 1.3 + 3z)/kBθ)/(1 + exp(−zε(x + x0 − 1.3 + 3z)/kBθ)	x < −1
	= 0	x ≥ −1
k9,M2 (s−1)	= 1000exp(−zε(x + x0 + 0.5 + z)/kBθ)/(1 + exp(−zε(x + x0 + 0.5 + z)/kBθ)	x < −1
	= 0	x ≥ −1
k9,M3 (s−1)	= 1200exp(−zε(x + x0 − 1 + 2z)/kBθ)/(1 + exp(−zε(x + x0 − 1 + 2z)/kBθ)	x < −1
	= 0	x ≥ −1
k9,M4 (s−1)	= 10exp(−zε(x + x0 − 1.3 + 3z)/kBθ)/(1 + exp(−zε(x + x0 − 1.3 + 3z)/kBθ)	x < −1
	= 0	x ≥ −1
kw1 (s−1)	= 73500exp(−zε·(x + x0 + 0.5)/kBθ)/(1 + exp(−zε(x + x0 + 0.5)/kBθ)
kw2 (s−1)	= 49000exp(−zε(x + x0 + 0.5 + z)/kBθ)/(1 + exp(−zε(x + x0 + 0.5 + z)/kBθ)
kw3 (s−1)	= 24500exp(−zε(x + x0 + 0.5 + 2z)/kBθ)/(1 + exp(−zε(x + x0 + 0.5 + 2z)/kBθ)
kw1′ (s−1)	= 73500exp(−zε(x + x0 + 6)/kBθ)/(1 + exp(−zε(x + x0 + 6)/kBθ)
kw2′ (s−1)	= 49000exp(−zε(x + x0 + 6 + z)/kBθ)/(1 + exp(−zε(x + x0 + 6 + z)/kBθ)
kw3′ (s−1)	= 24500exp(−zε(x + x0 + 6 + 2z)/kBθ)/(1 + exp(−zε(x + x0 + 6 + 2z)/kBθ)

The rate constants of the transitions between different biochemical states or between different actin monomers are indicated as k_lm where l (from 1 to 9) identifies the transition according to the scheme of Fig. 1 and m (M₁→M₄) indicates the structural state involved in the transition. The rate constants of the structural transitions for the same biochemical state are indicated as k_w1, k_w2 and k_w3 for the transitions M₁→M₂, M₂→M₃ and M₃→M₄, respectively. These ‘structural’ rate constants have the same x-dependence for the different biochemical states but their values are multiplied by 0.01 for AM and A′M states. x₀ is the strain of the M₁ state at x = 0, which has been set to 1.15 nm. The prime symbol (′) is added to the subscript if the transition occurs on the second actin.

Results

The force–velocity and power–velocity relations

Figure 2D shows the force–velocity (T–V) relations determined in control (open circles) and in 10 mm P_i (filled circles). Data are means (and SEM) from 10 fibres. In these experiments increase in P_i concentration to 10 mm reduces the isometric force to 0.53 the control (T_0,c). In agreement with previous work (Cooke & Pate, 1985; Potma & Stienen, 1996; Homsher et al. 1997; Caremani et al. 2013), the inhibitory effect of P_i on force is larger in isometric contraction and progressively reduces with the increase in shortening velocity. The T–V relations are used to calculate the power (W = TV), as a function of the half-sarcomere force (Fig. 2E). The maximum power is attained at V = 750 nm s⁻¹ per hs (force 0.3T_0,c). As a consequence of the effect on the T–V relation, the power in 10 mm P_i (filled circles) is reduced with respect to that in control (open circles), especially at intermediate and low velocities.

Half-sarcomere stiffness and motor strain during steady shortening

The relation between half-sarcomere stiffness (k) and force (T), normalised for the isometric value in control (k_0,c and T_0,c) (Fig. 3A, open symbols), shows that the stiffness decreases less than in proportion to the reduction of T. This deviation from proportionality is expected for the presence of an element (the myofilaments) with constant stiffness in series with the attached myosin motors, but, at least in part, can also be due to the fact that the number of attached motors reduces less than T with the increase in shortening velocity (Piazzesi et al. 2007).

Figure 3.

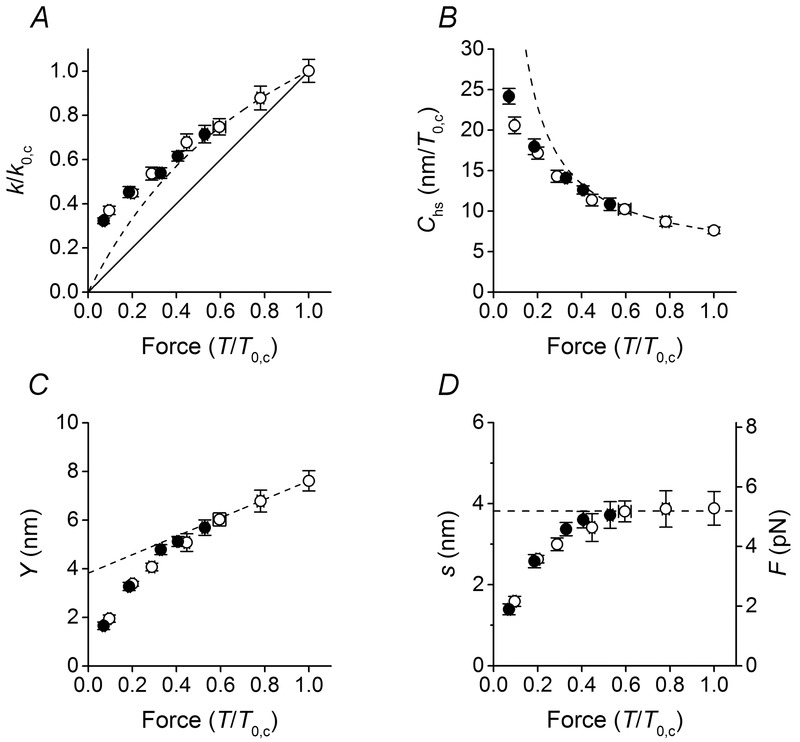
Half-sarcomere stiffness and derived parameters

A–C, dependence on force (T) of the half-sarcomere stiffness k (A), half-sarcomere compliance C_hs (B) and half-sarcomere strain Y (C). The continuous line in A is the direct proportionality line. The dashed lines in A–C describe the relations obtained under the assumption of a linear mechanical model of the half-sarcomere, as detailed in the text. Under this condition, in C the data for T > 0.5T_0,c can be fitted by a linear regression equation (eqn 2 in the text), where C_f = 3.72 ± 0.11 nm/T/T_0,c and s = 3.82 ± 0.92 nm. k and T are normalised for their respective isometric values in control (k_0,c and T_0,c). D, dependence on T of the average motor strain s (left ordinate) and of average motor force F (right ordinate) calculated as detailed in the text. The dashed line is the ordinate intercept of the linear fit in C. Data are means ± SEM.

The question is investigated by expressing the contributions of the myosin motors and myofilaments to the hs compliance C_hs (=1/k) in terms of equivalent series compliances (Ford et al. 1981):

1

where C_f is the compliance of the myofilaments and C_cb the compliance of the array of myosin motors. As shown in Fig. 3B, the C_hs–T relation (open circles) shows a hyperbolic-like dependence on force. Under the assumption that the activated half-sarcomere can be reduced to a linear mechanical model (Fusi et al. 2014), in which force increases in proportion to the number of myosin motors and the force per myosin motor (and thus the strain, s) is constant, the hs strain (Y) increases with force in proportion to the increase in the strain of the myofilaments with constant compliance (C_f) according to the first order equation:

2

Y at any force T can be calculated from C_hs as Y = C_hs × T (Fig. 3C, open circles). For forces >0.5T_0,c, the Y–T relation is linear, while it exhibits a downward deviation at lower forces. Fitting eqn 2 to Y–T values (open circles) >0.5T₀ (dashed line in Fig. 3C) gives C_f (the slope of the relation) = 3.72 ± 0.11 nm/T/T_0,c, or with T_0,c = 210 kPa, 17.7 ± 0.5 nm MPa⁻¹ and s (the ordinate intercept) = 3.82 ± 0.92 nm. Both the estimates of C_f and s do not differ significantly from the values reported in previous studies (Linari et al. 2007; Caremani et al. 2008) under the same conditions. In particular, the value of C_f found by Linari et al. (2007) by changing [Ca²⁺], and thus modulating the half-sarcomere force and the number of myosin cross-bridges in proportion, is 21.0 ± 3.3 nm MPa⁻¹.

It is worth noting that the swelling of the lattice caused by the fibre skinning produces an overestimate of C_f by a factor of 1.39 (Linari et al. 2007). After correction for this effect, C_f measured here decreases to (17.7/1.39 =) 12.7 ± 0.4 nm MPa⁻¹, in quite good agreement with the most accurate estimates from intact fibres of the frog in either mechanical experiments (12.8 ± 0.5 nm MPa⁻¹; Fusi et al. 2014) or X-ray diffraction experiments (13.1 ± 1.2 nm MPa⁻¹; Brunello et al. 2014).

The finding that the value of C_f estimated here is not significantly different from that estimated when the force is modulated by [Ca²⁺] is a demonstration that, in the region of T > 0.5T_0,c, also when the force is modulated with the shortening velocity, the slope of the Y–T relation is accounted for by the filament compliance and thus the half-sarcomere force changes in proportion to the number of motors. This in turn indicates that the average strain of the myosin motors (s) during shortening at high and intermediate loads (>0.5T_0,c) is the same as in isometric contraction and can be estimated by the ordinate intercept of the linear part of the Y–T relation.

The value of s at any value of T, estimated by subtracting the filament strain (C_fT) from Y is shown by open circles in Fig. 3D. For T > 0.5T_0,c, s is almost constant (∼3.8 nm) and corresponds to the ordinate intercept of the linear fit in Fig. 3C (dashed line). At lower force, s reduces progressively. The consequences of this effect on the k–T relation (Fig. 3A) and the C_hs–T relation (Fig. 3B) are shown by the deviation of the observed relations (open circles) from the relations expected on the basis of a linear mechanical model of the half-sarcomere, in which T changes in proportion to the number of motors (dashed lines calculated from the linear fit in Fig. 3C).

The fraction of myosin heads attached to actin in isometric contraction of skinned fibres from rabbit psoas activated by saturating [Ca²⁺] has been found to be 0.33 (Linari et al. 2007). With the number of myosin heads in each half-thick filament = 294, (294 × 0.33 =) 97 heads are attached to actin in the control isometric contraction. The corresponding isometric force per myosin motor (F₀) can be calculated from the macroscopic isometric force (210 kPa), considering the lattice dimensions (0.41 × 10¹⁵ thick filaments per m²; Brenner & Yu, 1991; Kawai et al. 1993; Park-Holohan et al. 2012). F₀ is (210 kPa/(0.41 × 10¹⁵ × 97) =) 5.28 pN. The force per motor at each sarcomere force during shortening (Fig. 3D, right ordinate), calculated from the motor strain, maintains the isometric value for shortening velocity <350 nm s⁻¹ per hs (T > 0.5T_0,c), while it decreases for higher shortening velocities.

The effects of rise in [P_i] on the motor strain

The same relations as in control (Fig. 3, open symbols) have been determined in the presence of 10 mm P_i (filled symbols). The force (T) and the stiffness (k) for 10 mm P_i are normalised for their respective values in isometric contraction without added P_i (T_0,c, k_0,c). Addition of 10 mm P_i reduces the isometric force to 0.53 the control value in these experiments, which is close to the steady force recorded during shortening at 350 nm s⁻¹ per hs in control (0.59T_0,c, compare in Fig. 2D the filled circle on the abscissa with the open circle at 350 nm s⁻¹ per hs). As shown in Fig. 3A, the stiffness is reduced less than in proportion to force in either case by roughly the same amount: the filled circle at 0.53T_0,c (the isometric point in 10 mm P_i) and the open circle at 0.59T_0,c (the control point at V = 350 nm s⁻¹ per hs) have a similar relative stiffness (∼0.71k_0,c) within the experimental error. The stiffness–force points determined in 10 mm P_i during shortening at low velocities (the first two points lower than the isometric point) lie close to the dashed line and deviate upward like the control points at higher velocities. Correspondingly, the hs compliance–force relation (Fig. 3B) shows that the 10 mm P_i points at low velocity lie close to the dashed line and at higher velocity are shifted downward like the control points. Concerning the half-sarcomere strain–force relation (Fig. 3C), a small but clear difference emerges between 10 mm P_i data at low velocity and control data at the same relative force. In fact in the force region 0.5–0.3T_0,c, filled circles lie closer to the dashed line, while open circles are progressively shifted downward. For lower relative forces filled circles deviate downward to superimpose on the open circles. The consequence for the motor strain in 10 mm P_i (Fig. 3D) is that the low velocity values (filled circles for T > 0.3T_0,c) lie closer to the horizontal line interpolated on the low velocity points in control, indicating that in this range of relative forces the motor strain in 10 mm P_i remains closer to the isometric value.

Comparisons in Fig. 3 suggest that during shortening the ability of the array of myosin motors to maintain the isometric strain (and force) by adapting the number of motors to the sarcomere force (Piazzesi et al. 2007) is defined by the shortening velocity. The rise in [P_i] per se reduces the sarcomere force by reducing the number of motors and thus does not affect the motor strain (and force) (see also Caremani et al. 2008). For V < 350 nm s⁻¹ per hs, the motor strain (and force) remains similar to the isometric value and the hs strain–force points follow the same relation whichever is the factor modulating the force, either the [P_i] or the shortening velocity. This conclusion is emphasised in Fig. 4, where the difference (Δs) between s for a T–V point and the isometric s is plotted versus either V (log scale, Fig. 4A) or the sarcomere force (Fig. 4B). In Fig. 4A both open (control) and filled symbols (10 mm P_i) lie along the same relation, showing that the strain remains similar to that in isometric contraction (Δs is nearly zero) for V < 350 nm s⁻¹ per hs (triangles) and progressively decreases with V for V > 350 nm s⁻¹ per hs (circles). When Δs is plotted versus the sarcomere force, open and filled symbols no longer superimpose: open symbols (control) start to decrease below zero at T < 0.59T_0,c (V > 350 nm s⁻¹ per hs) and filled symbols (10 mm P_i) start to decrease at T < 0.3T_0,c, that is again for V > 350 nm s⁻¹ per hs (see Fig. 2D).

Figure 4.

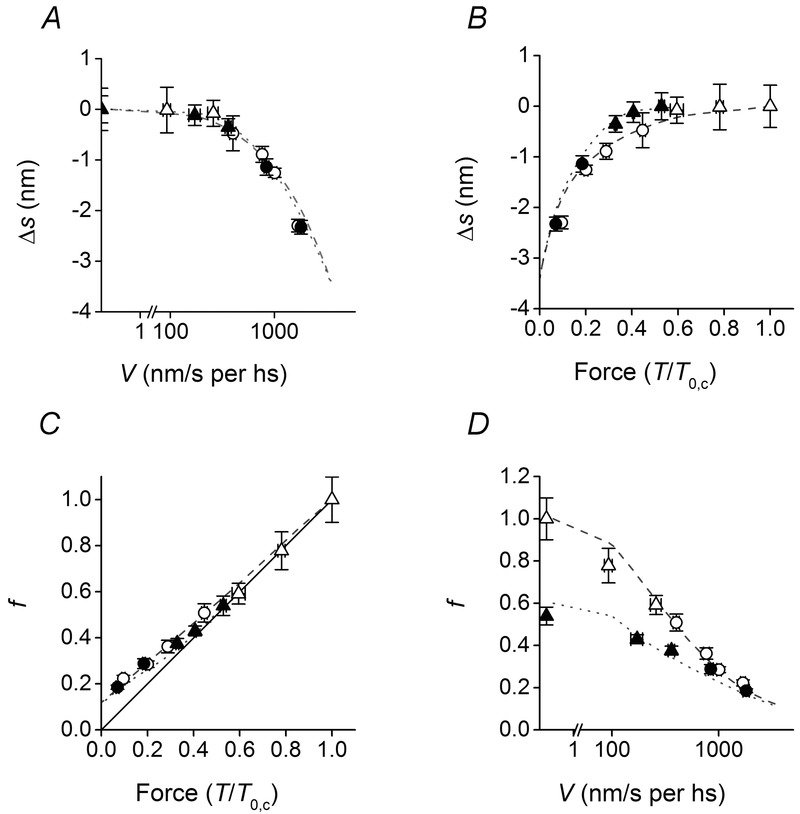
Strain and number of myosin motors

A and B, relation between Δs (the difference between s at any V and the isometric s) and either V (log scale, A) or T (B). C and D, relation between the number of myosin motors relative to the isometric control value (f) and either V (log scale, C) or T (D). Open symbols, control; filled symbols, 10 mm P_i. Different symbols indicate different velocity ranges: triangles, V ≤ 350 nm s⁻¹; circles, V > 350 nm s⁻¹. Lines, simulated relations: dashed, control; dotted, 10 mm P_i. The continuous line in C is the direct proportionality line. Data are means ± SEM.

The effect of shortening velocity and [P_i] on the number of motors

Using C_f estimated with the linear fit of Fig. 3C (3.72 nm/T_0,c) and the hs compliance–force relations of Fig. 3B, the compliance of the array of cross-bridges (C_cb) at any sarcomere force (T/T_0,c) can be calculated with eqn 1. The reciprocal of C_cb is the stiffness of the motor array in each half-sarcomere, eβ, where e is the stiffness when all heads are attached to actin and β is the fraction of attached heads. This fraction is 0.33 in control conditions (Linari et al. 2007). During steady shortening this fraction reduces in proportion to reduction in sarcomere force (Fig. 4C, where f expresses the fraction relative to the isometric control value) up to 0.5T_0,c (V ∼350 nm s⁻¹ per hs), as shown by the fact that the open triangles lie along the direct proportionality line (the continuous line). For smaller forces (V > 350 nm s⁻¹ per hs, open circles), f deviates upward showing that the number of motors reduces less than in proportion to force. The same analysis is done on data obtained in 10 mm P_i (filled symbols in Fig. 4C), when the fraction of motors attached to actin in isometric contraction is 0.53 relative to that in control. Also in this case, for the low velocity data (V < 350 nm s⁻¹ per hs, T > 0.3 T_0,c, filled triangles), f remains closer to the direct proportionality line than for higher velocities (T < 0.3T_0,c, filled circles), when it progressively deviates upward indicating that the number of motors decreases less than in proportion to force. Therefore, whatever the P_i concentration, for V > 350 nm s⁻¹ per hs, the number of motors decreases less than in proportion to sarcomere force. This implies that their average strain and thus the force per motor decreases with increase of V, indicating that the attached myosin motors attain a position for which they start to exert no force or negative forces. In conclusion, independent of [P_i], at velocities higher than ∼350 nm s⁻¹ per hs, detachment of motors becomes a relatively slow process.

Another effect that emerges from the comparison of the data in control and 10 mm P_i in the high velocity range is that the fraction of actin-attached motors, the parameter that mainly marks the difference between control and 10 mm P_i in isometric contraction and at high load, converges to the same value at low load. The effect is more explicit when the fraction of attached motors is plotted versus the sliding velocity (Fig. 4D).

Model simulation

The effects of shortening velocity and [P_i] on the number and force of actin attached motors

The kinetic model in Fig. 1, able to explain the isotonic velocity transients (Caremani et al. 2013) and the steady state relation between force, shortening velocity and power (Caremani et al. (2013) and see Fig. 2D and E, dashed lines control, dotted lines 10 mm P_i), is tested here for the ability to predict the new results summarised in Fig. 4. The average strain of the motors (s) is calculated by dividing the average force (obtained from the simulation described in Caremani et al. (2013)) by the motor stiffness (1.2 pN nm⁻¹; Linari et al. 2007). The dependence of the motor strain on the velocity of shortening and half-sarcomere force are satisfactorily reproduced by the model. In control solution the strain of the attached motors remains similar to that in isometric contraction up to V ≤ 350 nm s⁻¹ per hs and drops with V at higher velocities (dashed line in Fig. 4A). Addition of 10 mm P_i to the solution does not change significantly the Δs–V relation (dotted line in Fig. 4A). Conversely, when the change in strain is plotted versus the half-sarcomere force (Fig. 4B), the model predicts, as observed, that the relation in 10 mm P_i (dotted line) is shifted upward with respect to that in control solution (dashed line) and that the two relations converge at very low load.

The simulated relations between the fraction of attached myosin motors f and either sarcomere force or velocity of shortening are also in satisfactory agreement with the data (Fig. 4C and D).

The effect of conformation and strain of the myosin motor on the kinetics of product release

Under the assumption that ATP binding and detachment from actin are rapid events following the release of ADP from the catalytic site, the ADP release is the relevant process that defines the strain distribution of the attached heads just before detachment, and thus their average strain and number, in relation to shortening velocity. The relation in Fig. 4B provides powerful constraints for the dependence of the ADP release on the conformation and strain of the AM.ADP state. The assumption that the rate of ADP release increases only with the progression of the working stroke, that is in a conformation-dependent manner (Fig. 5C: M₁ dot-dashed line, M₂ dotted line, M₃ dashed line, M₄ continuous line) fails to simulate the data at low loads by predicting a larger than observed strain (Fig. 5A, green dashed line) and a smaller than observed number of myosin motors (Fig. 5B green). The reason is that a unique value of k₅ for the conformation at the end of the working stroke (M₄) implies that, once k₅ is selected to fit the T–V relation at very low loads (500 s⁻¹), it appears too high for x > −11 nm, reducing too much the population of attached motors and biasing their strain toward high forces (green dashed line in Fig. 5A and B). Both the relations in Fig. 5A and B and the T–V relation at very low load in Fig. 2D can be fitted satisfactorily (black dashed lines) only assuming that k₅ for the M₄ state changes also with x, further increasing when the motor at the end of the working stroke experiences a negative strain. As shown in Fig. 5D, the best fit for all conditions is obtained if k₅ for the M₄ state is 150 s⁻¹ for x > −11 nm and increases by one order of magnitude within a few nanometres when M₄ becomes negatively strained, attaining a value of 1600 s⁻¹ for x < −14 nm. The question whether k₅ can be strain sensitive also for the AM.ADP states (M₁–M₃) with a conformation preceding that at the end of the working stroke is not relevant because during low-load shortening the flux through the ADP release step is provided almost completely by the AM.ADP in the M₄ state, which is the dominant attached state (Fig. 5E and F).

Figure 5.

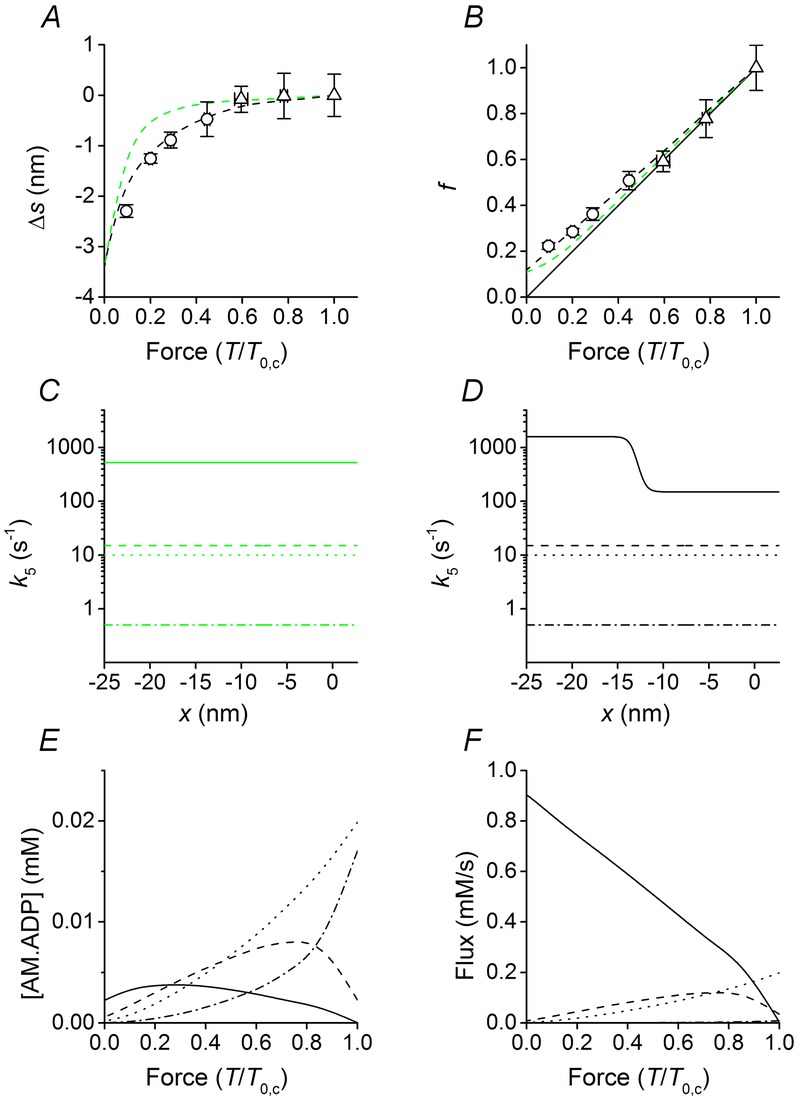
Model predictions in relation to the strain dependence and load dependence of ADP release

A–B, dependence on force of Δs and f in control. Δs is the difference between s during shortening and the isometric s; f is the fraction of attached motors relative to the isometric control value. Symbols, data from Fig. 4B and C, respectively. Dashed lines, model predictions; different colours indicate different assumptions on the forward rate constants for ADP release (k₅) from the four (M₁–M₄) structural states of AM.ADP: green, only conformation dependence for all structural states; black, the M₄ state is also strain dependent. Continuous line in B is the direct proportionality line. C–D, x-dependence of k₅ for M₁–M₄ states, identified by the line style: M₁, dot-dashed line; M₂, dotted line; M₃, dashed line and M₄, continuous line. E, load dependence of the concentrations of the four structural states of AM.ADP motors, identified by the same line code as in D. The total concentration of myosin motors is assumed to be 0.15 mm (He et al. 1997; Tikunov et al. 2001). F, load dependence of the flux through the four structural states of AM.ADP motors, identified by the same line code as in D.

Discussion

Using fast sarcomere-level mechanics in Ca²⁺-activated skinned fibres from rabbit psoas we define the number and strain (s) of myosin motors interacting during steady muscle shortening at different velocities and how these parameters are modulated by change in [P_i].

It is found that in control conditions (no added P_i) shortening at low velocity (V ≤ 350 nm s⁻¹ per hs, corresponding to forces >0.5 the isometric force, T_0,c) decreases the number of myosin motors in proportion to reduction of T, so that s remains practically constant and similar to the isometric value independently of V. At higher V the number of motors decreases less than in proportion to T, so that s progressively decreases.

Raising [P_i] by 10 mm, which reduces the force and the number of motors in isometric contraction by 40–50% of the control values without significant changes of s, does not influence the dependence on V of the motor number and strain, so that for shortening at V ≤ 350 nm s⁻¹ per hs, corresponding to forces T > 0.3T_0,c, the number of motors decreases in proportion to reduction of T and s remains constant, while at higher V the number of motors decreases less than in proportion to T and s progressively decreases. For V > 1000 nm s⁻¹ per hs (T < 0.2T_0,c) the number of motors and their average strain converge to a minimum value independent of [P_i].

A chemo-mechanical model of the myosin–actin ATPase reaction (Caremani et al. 2013), in which the state transitions responsible for the myosin working stroke and the release of the hydrolysis products are orthogonal processes, explains the results assuming that P_i and then ADP are released with rates that increase as the motor progresses through the working stroke, that is, in terms of the crystallographic model of the myosin motor (Rayment et al. 1993; Geeves & Holmes, 2005), with the progressive tilting of the lever arm about the catalytic domain and opening of the nucleotide binding pocket.

During low-load (high-velocity) shortening the execution of the working stroke becomes relatively faster than the product release, so that the release of ADP from the attached motors occurs mostly from the conformation at the end of the working stroke (M₄, see Fig 5E). For this state the rate of ADP release further increases by one order of magnitude within few nanometres of negative strain, due to the rise of compressive force on the motors that accelerates the ADP release by reducing the energy barrier for bond breaking. This mechanism implies a linear elastic behaviour of the myosin motor across the zero force and therefore that there is no substantial buckling of the S2 rod connecting the actin-attached motor to the myosin filament backbone. In this respect it must be noted that buckling of the S2 rod, reported in in vitro experiments (Kaya & Higuchi, 2010), is not supported by any evidence in the preserved sarcomere, either mechanical (Ford et al. 1977; Fusi et al. 2010) or structural (Brunello et al. 2014).

The finding in this work that during steady shortening against loads ≥0.5T_0,c the average strain and force in the myosin motors remain similar to those in isometric contraction agrees with the conclusions from combined mechanical and X-ray diffraction studies on intact fibres from frog muscle (Piazzesi et al. 2007). The underlying mechanism, confirmed by model simulation in this work, is that, with the increase in shortening velocity, the number of attached motors decreases in proportion to the decrease in half-sarcomere force, while each motor maintains the isometric force progressing through the working stroke. In the present model, developed to predict both the transient and steady state responses to a stepwise drop in force imposed on Ca²⁺-activated skinned mammalian fibres (Fig. 1 and Appendix A; see also Caremani et al. 2013), the working stroke consists of three transitions separated by 3.1 nm steps.

In a purely mechanical model put forward to explain the kinetics of the early phases of the response to step changes in length or force imposed on intact fibres from frog muscle, myosin motors are distributed between five sub-states, separated by four 2.75 nm steps (Linari et al. 2009; Piazzesi et al. 2014). As discussed in Park-Holohan et al. (2012), the smaller step size and the larger number of transitions in the model derived from frog intact-fibre studies are due to the evidence in frog fibre experiments of a larger stiffness of the motor (2.7 pN nm⁻¹; Brunello et al. 2014; Fusi et al. 2014), with respect to mammalian skinned-fibre experiments (1.7 pN nm⁻¹ (Linari et al. 2007) in the presence of the osmotic agent that recovers the lattice dimension of the intact fibre). In either case the motor stiffness is large enough to support the view that the isometric force is generated by a relatively narrow distribution of lever arm tilting biased towards the beginning of the working stroke, in agreement with the conclusions from X-ray diffraction experiments (Reconditi et al. 2004; Huxley et al. 2006; Piazzesi et al. 2007). According to those experiments, larger degrees of lever arm tilting, accounting for ∼6 nm working stroke, occur during steady shortening at high and moderate loads (Piazzesi et al. 2007), while the full 70 deg tilt (corresponding to the 11 nm working stroke) predicted by crystallographic models is observed only during the early rapid shortening following a stepwise drop in force to near zero. Under these conditions the relatively high isometric rate of ATP splitting (∼1/4 of the maximum rate observed during shortening; Woledge et al. (1985) and references therein) appears to be inconsistent with the idea that completion of the ATP hydrolysis cycle is tightly coupled to the 70 deg tilting of the lever arm. In an attempt to solve this contradiction it has been postulated (Smith, 2014) that in isometric contraction an increase in P_i, which biases the population of attached motors toward the beginning of the working stroke, raises the probability of buckling of the S2 portion of these motors, which then can undergo an unloaded working stroke and so account for ATP consumption. However both mechanical (Ford et al. 1977; Fusi et al. 2010) and structural evidence (Brunello et al. 2014) in intact frog fibres excludes any significant S2 buckling in a system with preserved filament lattice.

The different responses of isometric force and ATP hydrolysis rate to the increase in [P_i] can be explained if, as in the model of Fig. 1, the biochemical and mechanical cycles are not tightly coupled. The model assumes that 1 in isometric contraction the hydrolysis products can be released from the catalytic site of the myosin head following early detachment of the force generating motors, providing an alternative way to terminate the ATPase cycle that is favoured by the rise in P_i (Caremani et al. 2008; Linari et al. 2010), and 2 during shortening the release of hydrolysis products and the termination of the ATPase cycle can occur at any stage of the working stroke (Caremani et al. 2013). In fact, as shown in Fig. 5E, in isometric contraction the attached motors with the ligands bound are mostly only in the first two conformations, M₁ (dot-dashed line) and M₂ (dotted line), and the flux through the ADP release step is mainly due to the AM.ADP in the M₂ state (Fig. 5F). During shortening also the conformations ahead in the working stroke, M₃ (dashed line) and M₄ (continuous line), become populated at the expense of the first two and the M₄ state becomes that responsible for most of the flux through the ADP release step. Under unloaded shortening conditions almost 100% of ADP release occurs from the AM.ADP in the conformation at the end of the working stroke.

Conformation-dependence versus strain-dependence of biochemical steps

The model in Fig. 1 is unique in providing a detailed description of the relations between biochemical, structural and mechanical features of the energy conversion by the myosin motor during its interaction with the actin. In fact, models in which there is only one conformation for a given biochemical state (Pate & Cooke, 1989b; Dantzig et al. 1992; Homsher et al. 1997) and models in which the biochemical steps are in series with the working stroke (Smith, 2014) suffer from the limitation that the kinetics of biochemical steps in the attached motor is modulated by its strain, as detailed below.

According to the model in Fig. 1, the rate of P_i release is conformation dependent and increases by two orders of magnitudes with the progression of the working stroke (Appendix A; see also Caremani et al. 2013). At the same time the forward rate constant of the structural transitions representing the working stroke is strain dependent, that is, for any given structural state it increases with the decrease of x (the relative position between the myosin motor and the actin to which it is attached, as defined in Methods) (Huxley & Simmons, 1971; Piazzesi et al. 2002; Reconditi et al. 2004). Consequently, with the increase in shortening velocity the rate of the working stroke and the rate of P_i release increase in parallel, so that both the AM.ADP.P_i and the AM.ADP states are significantly populated throughout the working stroke and the change in their proportion depends on the balance between strain dependence of the working stroke rate and conformation dependence of the P_i release rate. This is a quite important feature that is missing in previous models (Pate & Cooke, 1989b; Dantzig et al. 1992; Homsher et al. 1997), in which for each biochemical state of the actin-attached motor there is only a free energy parabola and the kinetics of the biochemical step can be modulated only by changing its rate in relation to the position along the parabola. The same limits are shown by models in which the biochemical steps are in series with the working stroke (see for instance Smith (2014), where P_i release precedes the working stroke). In all these models the AM.ADP.P_i state during shortening is irreversibly depleted in favour of the AM.ADP state. The limits of these models emerge when they are used to simulate the force response to a stepwise increase in [P_i] by photogeneration from caged P_i (P_i transient) elicited either during isometric contraction or during steady shortening at constant velocity (isovelocity contraction) (Dantzig et al. 1992; Walker et al. 1992; Homsher et al. 1997). The step in [P_i] elicits a drop in force the rate of which increases with the final level of [P_i] in both isometric and isovelocity contractions. Models in which there is only one conformation per biochemical state and models in which the P_i release is in series with the working stroke are able to fit the rate–[P_i] relation in isometric contraction but not during isovelocity shortening (Homsher et al. 1997).

Notwithstanding the complexity and multiplicity of the paths that lead to the release of ADP from the pocket and the conclusion of the ATP hydrolysis cycle in the model of Fig. 1, the apparent rate constant for ADP release from attached motors (k_−ADP,app), calculated by dividing the sum of the fluxes through steps 5 and 5′ by the sum of all the concentrations of the AM.ADP state (Fig. 6A, dotted line), has the classical almost linear dependence on the shortening velocity found in previous work for the apparent detachment rate constant g (see for instance Piazzesi et al. 2007). Taking into account also the fraction of motors releasing the hydrolysis products following early detachment (step 7 and 7′), the relation of k_−ADP,app versus the shortening velocity exhibits a larger slope (Fig. 6A, dashed line) going from a minimum of ∼9 s⁻¹ in isometric contraction to 370 s⁻¹ during shortening at the maximum velocity (V₀). To compare this result with the conclusions from intact fibre experiments in which the estimated parameter is the detachment rate constant g (Piazzesi et al. 2007), the total flux must be divided by the sum of the concentrations of all attached states (continuous line in Fig. 6A). g in this work (skinned fibres from rabbit psoas at 12°C) rises from the isometric value of ∼8 s⁻¹ to the V₀ value of 240 s⁻¹, in quite good agreement with what has been found in frog muscle fibres at 4°C (Piazzesi et al. 2007). In Fig. 6B the same parameters as in A (k_−ADP,app and g) are plotted versus the sarcomere force, showing the expected hyperbolic relation.

Figure 6.

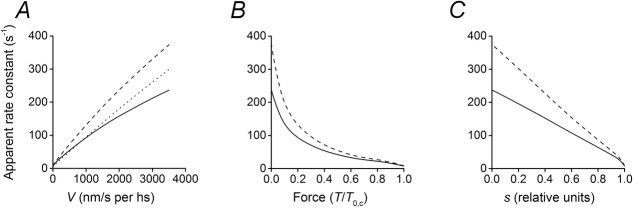
Dependence of the apparent rate constant of ADP release (k_−ADP,app) and the apparent detachment rate (g) on the velocity (A), the sarcomere force (B) and the average strain in the myosin motors (C)

k_−ADP,app is calculated either considering only the concentrations of the attached AM.ADP states (dotted line) or also the concentration of the early detached states (dashed line). g (continuous line) is calculated by dividing the total flux by the sum of the concentrations of all attached states.

Single molecule mechanical assays make it possible to directly relate the kinetic steps of the actomyosin interaction to the actual load on the myosin motor. Recently it has been shown, using optical trapping on single β-cardiac myosin, that g increases by about 5 times, reducing the load from 7 to 0 pN, attaining a maximum of 70 s⁻¹ under unloaded conditions (Greenberg et al. 2014). Our sarcomere level mechanics allows in situ measurements of the average strain (and thus the force) in the attached myosin motor and its relation to mechanical conditions (Figs 3 and 4). Consequently the dependence of k_−ADP,app and g on the strain (force) of the motor can be determined (Fig. 6C). g increases almost linearly by 30 times with the reduction of the strain, s, going from 8 s⁻¹ when s has the maximum isometric value to 240 s⁻¹ at s = 0. Thus g of the unloaded fast myosin isoform of our preparation is 3.5 time larger than that found in in vitro experiments for β-cardiac myosin. Beyond the limits in single molecule measurements, due to the frequency response of the system and the relatively large compliance of the transducers, it seems likely that a significant part of the difference is attributable to the intrinsic kinetic properties of the two isoforms. A direct test of this conclusion would by possible by extending our study to skinned fibres from soleus muscle, the slow mammalian muscle that contains the same β-cardiac myosin isoform as the cardiac muscle (Seebohm et al. (2009) and references therein).

The equilibrium constant for motor attachment/force generation and P_i release

Fundamental issues of the chemo-mechanical coupling of muscle myosin, which have been elusive for more than 30 years despite the bulk of experimental and modelling work, find a detailed explanation by using our model. The combined equilibrium constant of the isomerisation of the AM.ADP.P_i state, responsible for the formation of the strong force-generating myosin–actin bond (step 3 in Fig. 1), and of the following P_i release (step 4) changes by 10⁴ times between isometric contraction and the unloaded condition (or solution kinetic studies). The detailed explanation of this phenomenon according to the model in Fig. 1 is the following. Let us consider for simplicity a myosin motor that in isometric contraction is in the M₁ state and under unloaded conditions undergoes all the working stroke transitions. In isometric contraction the combined equilibrium constant K_c is (K₃K₄ = 0.12 × 12.5 × 10⁻³ m =) 1.5 × 10⁻³ m (see Appendix B), so that in control solution (1 mm P_i) the apparent equilibrium constant for step 4 (K_4,app) is 12.5 and the combined equilibrium constant is 1.5, close to unity (that is, the two-step process is reversible; Geeves & Holmes, 2005). Under unloaded conditions the change in free energy of the reactions under consideration (ΔG_c) implies also the change in free energy associated with the working stroke (ΔG_w) (Caremani et al. 2013; but see also White & Taylor, 1976). In detail, K_c can be calculated from the Gibbs equation:

3

where k_B is the Boltzmann constant (1.381 × 10⁻²³ J K⁻¹), Θ the temperature in K (285) and ΔG_c is given by the sum of the free energies of step 3 (ΔG₃), step 4 (ΔG₄) and the working stroke (ΔG_w). ΔG_w is the free energy change that accounts for the increase in the combined equilibrium constant during filament sliding elicited under loads <T_0. This is represented in our model by the three structural transitions M₁→M₂, M₂→M₃ and M₃→M₄, each accompanied by a 12 zJ drop between the minima of two consecutive free energy parabolas (see Fig. 8A in Appendix A). Thus for a myosin motor that progresses through the whole working stroke, ΔG_w is −36 zJ. According to the values for ΔG₃ and ΔG₄ reported in Table2 in Appendix B, under unloaded conditions ΔG_c is −37.5 zJ. In this case, from eqn 3, K_c = 13,800, that is 10⁴ times larger than the value in isometric contraction.

Table 2.

Free energy change and equilibrium constant

	Free energy (zJ)				Equilibrium constant
Condition	ΔGw	ΔG3	ΔG4	ΔGc	K3	K4,app	Kc
Isometric	—	8.4	−9.94	−1.54	0.12	12.5	1.48
Unloaded	−36	8.4	−9.94	−37.54	0.12	12.5	1.38⋅104

Free energy change and equilibrium constant for step 3 (ΔG₃, K₃), for step 4 (ΔG₄, K_4,app), for the whole working stroke (ΔG_w) and for the combined transitions (ΔG_c, K_c) in isometric and unloaded conditions.

The release of P_i from whichever of the four AM.ADP.P_i states implies the same free energy change (ΔG₄), −9.94 zJ in control. In Fig. 8B in Appendix A this is shown by the difference between the free energy minima of AM.ADP (black medium thickness line) and AM.ADP.P_i (black thinnest line). The free energy change reduces to −0.5 zJ in 10 mm P_i (the difference between the free energy minima of AM.ADP (green medium thickness line) and AM.ADP.P_i (black thinnest line, Fig. 8B in Appendix A). In conclusion the strain dependence of the rate constants for state transition determines the equilibrium constant of the structural steps, while for the P_i release step, the rate constant (but not the equilibrium constant) is determined by the conformation, increasing by 10² times from M₁ to M₄.

A similar argument is qualitatively valid for the ADP release step (step 5). k₅ increases by two orders of magnitude from M₁ to M₄. In this case, however, the precise definition of the relations between V (and T) and the number and strain of the myosin motors (Figs 4 and 5) indicates that ADP release from the state at the end of the working stroke (M₄) is also strain sensitive, further increasing by one order of magnitude with the rise in negative strain.

The molecular basis of the effect of P_i on the power output

Addition of 10 mm P_i to the solution implies a reduction in power output especially at low shortening velocity (high relative force, Fig. 2E). This effect is explained mainly by the depressant effect of P_i on the number of motors without change in force per motor (Figs 3D and 4). However, energetic considerations support the idea that also the work per motor must be reduced by increasing [P_i]. In fact, the free energy of the ATP hydrolysis per mole (ΔG^ATP) can be expressed as:

4

where ΔG₀ is the standard free energy (−30 kJ mol⁻¹), and R the gas constant (8.314 J K⁻¹ mol⁻¹). With the values for [ATP], [ADP] and [P_i] in our preparation of 5 mm, 30 μm and 1 mm, respectively, ΔG^ATP is −58.5 kJ mol⁻¹. The efficiency of energy conversion by mammalian muscle in the range of low shortening velocities, in which the efficiency is maximum, is about 0.32 (Barclay et al. 2010). Thus the corresponding work done by a myosin motor is (0.32 × 58.5 kJ mol⁻¹/6.022 × 10²³ =) 31.1 zJ. With a force per motor of 5.3 pN (Fig. 3D), the average sliding distance (L_w) per ATP hydrolysed is (31.1 zJ/5.3 pN =) 5.9 nm.

Addition of 10 mm P_i (i.e. raising the concentration of P_i from 1 mm to 11 mm) will lower ΔG^ATP to −52.8 kJ mol⁻¹. Assuming that the efficiency of energy conversion in elevated P_i is the same as in control, this reduction in free energy will account for a reduction in the work per motor to 28.1 zJ. Following the experimental evidences that force per motor is the same as in control (5.3 pN, Fig. 3D), the reduction in the work should imply a reduction of the average sliding distance to (28.1 zJ/5.3 pN =) 5.3 nm, that is, about 0.6 nm less than in control.

Conclusions

During shortening of active muscle against intermediate and high loads (corresponding to shortening velocities V ≤ 350 nm s⁻¹ per hs), the number of myosin motors reduces in proportion to the external load and their average force remains similar to that in isometric contraction due to the working stroke transitions; during shortening against lower loads (V > 350 nm s⁻¹ per hs) the number of motors decreases less than in proportion to the load, so that the force per motor progressively decreases.

The rise in [P_i] by 10 mm, which reduces by 40–50% the isometric force generated by the muscle by proportional reduction in the number of motors, does not influence the dependence on V of the motor number and strain. For V > 1000 nm s⁻¹ per hs (T < 0.2T_0,c) the number of motors and their average force converge to a minimum value independent of [P_i].

A chemo-mechanical model of myosin–actin ATPase reaction, in which the structural transitions responsible for the working stroke in the myosin motor and the release of the hydrolysis products are orthogonal processes, explains the results assuming that P_i and then ADP are released with rates that increase as the motor progresses through the working stroke. For the motors that attain the conformation at the end of the working stroke in the AM.ADP state, the rate of ADP release further increases by one order of magnitude within a few nanometres of negative strain.

This is the first model providing a detailed description of the relations between biochemical, structural and mechanical features of the energy conversion by the myosin motor during muscle shortening.

Glossary

A

actin monomer to which a myosin motor attaches

A′

actin monomer next to A, 5.5 nm away from the centre of the sarcomere

CD

catalytic domain

CSA

fibre cross-sectional area

hs

half-sarcomere

LCD

light chain domain

M

myosin motor

f

fraction of actin-attached motors relative to the number attached in isometric contraction in control conditions

P_i

inorganic phosphate

Appendix A Details of the model simulation, rate functions and free energy profiles

The mechanical–kinetic model used for the simulation, shown in Fig. 1, is similar to that described in Caremani et al. (2013). A minor difference is the introduction of the possibility for a myosin motor to detach, with the ATP hydrolysis products still bound, not only from the first actin (A, step 6) but also from the second actin (A′, step 6′), and form an M**.ADP.P_i state (different from the M*.ADP.P_i state generated by the early detachment from the first actin because its free energy is 27 zJ lower). The M**.ADP.P_i state, as the M*.ADP.P_i, undergoes the rapid completion of the working stroke and release of the hydrolysis products, followed by binding of another ATP (step 7′). This implementation ensures the same combination of pathways for a working myosin whichever is the actin to which it is attached. The features of the model that are relevant for this paper originate from the precise definition of the relation between V (and T) and the number and average strain (force) of the motors during steady shortening. As shown in detail in Figs 4 and 5, these results provide stringent constraints for the rate functions concerning the kinetics of the product release and their dependence on the conformation and strain of the myosin motors. All the other rate functions are substantially the same as in Caremani et al. (2013). For reasons of clarity, the relevant assumptions and parameter definitions are briefly summarised in the following section and the equations expressing all the rate constants of the forward transitions in the reaction scheme of Fig. 1 are listed in Table1. The plots of the forward and backward rate functions that are x-dependent are shown in Fig. 7.

Figure 7.

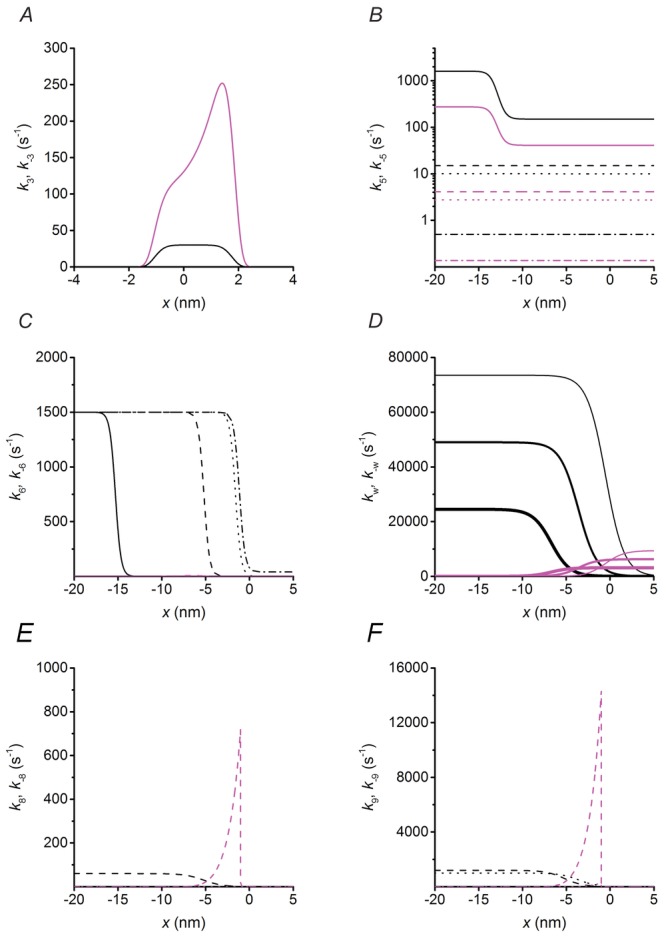
Strain dependence of the rate constants

Plots showing the dependence on x of the rate constants which are sensitive to strain: forward transitions, black; backward transitions, magenta. For simplicity the transitions considered are those concerning the myosin motor while attached to the first actin monomer A (A–D) and the slip to the next actin monomer A′, 5.5 nm away from the sarcomere centre (E–F). The transitions concerning the myosin motor while attached to A′ can be deduced by shifting the rate functions for A leftward by 5.5 nm. A, step 3: formation of the strong actin bond by the motor in M₁ state. B, step 5: ADP release. Line style refers to different structural states: M₁, dot-dashed line; M₂, dotted line; M₃, dashed line and M₄, continuous line. The same line code is used in panels C, E and F. C, early detachment with the hydrolysis products bound to the catalytic site. D, working stroke transitions. The thickness of the line identifies the progression of the state transitions from the first step, M₁→M₂, thinnest line, to the third step, M₃→M4, thickest line. E and F, slipping to the next actin monomer A′ by the motor in the M.ADP.P_i state (step 8, E), and in the M.ADP state (step 9, F).

Definitions

M.ATP, M.ADP.P_i-AM.ADP.P_i, M*.ADP.P_i and M**.ADP.P_i are detached states, AMi.ADP.P_i, AMi.ADP and AMi are states attached to an actin monomer (A) and A′Mi.ADP.P_i, A′Mi.ADP and A′Mi are states attached to the next actin monomer (A′) on the same strand, shifted by 5.5 nm farther from the centre of the sarcomere, with i varying from 1 to m according to the number of structural states assumed during the working stroke. Attachment to the actin monomer A occurs for a range of x from −2.75 nm to 2.75 nm, where x is the relative axial position between the motor and A, and is zero for the position of the centre of distribution of attachments of the motors in M₁ state. The structural change underlying the working stroke is represented by (m − 1) stepwise transitions each responsible for an axial movement z (Brunello et al. 2007). As detailed in previous work (Piazzesi & Lombardi, 1995; Woledge et al. 2009; Caremani et al. 2013), the value of z is constrained by the stiffness of the myosin motor. Under the conditions of this work, the average motor stiffness ε is 1.2 pN nm⁻¹ and z is chosen as 3.1 nm (Linari et al. 2007; Caremani et al. 2013). Three steps of 3.1 nm are necessary to fit both the kinetic requirements necessary to simulate force and velocity transients following length and force steps, respectively (Piazzesi et al. 2002; Woledge et al. 2009; Caremani et al. 2013). Thus there are four structural states of the attached motor (M₁, M₂, M₃ and M₄) and three transitions (M₁→M₂, M₂→M₃, M₃→M₄).

Details of x-dependence of the probability of a motor to attach to an actin monomer in isometric conditions, of the boundary conditions and of the possibility to slip on the next actin during shortening are given in Caremani et al. (2013). For any steady state mechanical condition (isometric contraction or steady shortening), the total flux of energy can be calculated from the flux between the states M.ATP and M.ADP.P_i–AM.ADP.P_i (step 2) or M.ADP.P_i–AM.ADP.P_i and AM1.ADP.P_i (step 3) in the cycle. The free energy of hydrolysis of one molecule of MgATP (ΔG^ATP) can be expressed as:

where k_B (= 1.381 × 10⁻²³ J K⁻¹) is the Boltzmann constant, Θ (= 285 K) is the absolute temperature and ΔG₀ is the standard free energy. ΔG^ATP is assumed to be 100 zJ in the control condition (MgATP, 5 mm; free ADP, 30 μm and free P_i, 1 mm; Barclay et al. (2010) and references therein) and it reduces with rising [P_i]: addition of 10 mm P_i will lower the free energy by about 10 zJ (see Fig. 8B).

Figure 8.

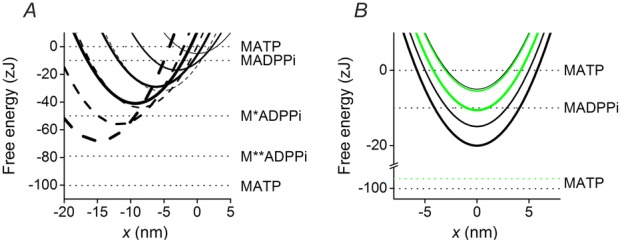
Free energy diagrams of the structural and biochemical states

A, free energy diagrams of the four structural states of the myosin motor in the AM.ADP.P_i state, attached to the actin monomer either, A (continuous lines) or A′ (dashed lines). The thickness of the line identifies the progression of the state transitions, from M₁, thinnest line, to M₄, thickest line. x is zero in correspondence of the free energy minimum of a myosin motor attached to A in the M₁ state. Horizontal lines show the free energy of the detached states. B, free energy diagrams of the myosin motor attached to the actin monomer A in the different biochemical states (AM.ADP.P_i, thinnest line; AM.ADP, medium thickness line; and AM, thickest line). Of the four structural states only M₁ is shown for clarity. The black lines are in control solution (no added P_i) and the horizontal lines show the free energy of the detached states. The green lines show the effect of the addition of 10 mm P_i on the free energy level of the AM.ADP, AM and M.ATP states (the upward shift accounting for the reduction in ΔG).

The equations expressing the reaction rate functions for the forward transitions are reported in Table1. The plots of the forward and backward rate functions that are x-dependent are shown in Fig. 7.

The distribution of myosin heads at any given time is calculated by numerical integration of the differential equations (Caremani et al. 2013).

The free energy profile (G(x), Fig. 8A) of the various states are related to the forward ki(x) and reverse k₋i(x) rate constants of the transition between neighbouring states p and q through the Gibbs equation:

One rate constant of the pair is calculated from the above equation after choosing the appropriate value for the other.

The free energy profiles of the attached states are parabolic according to the assumption that the motor stiffness ε, the second order derivative of the energy, is constant. Two consecutive structural states of the motor attached to actin A in the same biochemical state have the free energy parabolas shifted on x by the step size (3.1 nm) and the difference in their free energy minima is 12 zJ independent of the biochemical state. Thus the total energy change associated with the three structural transitions (M₁→M₂, M₂→M₃ and M₃→M₄) while the motor is attached to the same actin monomer A is 36 zJ (Fig. 8A).

The biochemical step in the attached states consists in a downward shift of free energy parabolas for each given structural state: the drop in the free energy minima induced by P_i release is 9.94 zJ in control solution (no added P_i) and 0.5 zJ in 10 mm P_i; the difference in the free energy minima induced by release of ADP is 5.1 zJ. The diagrams of the free energy profiles for the different biochemical states of the same structural state (M₁) without (black) and with 10 mm added P_i (green), are shown in Fig. 8B.

B Appendix Effect of mechanical conditions on the equilibrium constant for motor attachment/force generation and P_i release

The model is able to predict the change in the combined equilibrium constant of isomerisation of the AM.ADP.P_i state and of the following P_i release. The equilibrium constants (K_c) for the above steps (step 3 and step 4 in the cycle) and for the working stroke are calculated in Table2 together with the corresponding free energy change ΔG_c (which is related to K_c through the equation K_c = exp(−ΔG_c/k_BΘ)). For a motor that, under unloaded conditions, executes the whole working stroke, the change in free energy of the reactions implies the change in free energy associated to the three transitions leading from M₁ to M₄ (ΔG_w, 36 zJ) (White & Taylor, 1976; Caremani et al. 2013). The combined equilibrium constant (K_c) is in this case 13,800, about 10⁴ times that of a motor undergoing steps 3 and 4 in the M₁ state, which is assumed to occur in the isometric contraction (Table2).

Additional information

Competing interests

The authors have no competing interests.

Author contributions

M.C. and L.M. contributed equally to the paper: they carried out the experiments, participated in the design of the study and in data analysis, model simulation and interpretation of data. M.D. developed the model simulation; V.L. participated in the design of the study, interpretation of data and drafting the article and revising it critically; M.L. designed the study and participated in the model simulation, interpretation of data and drafting the article. All authors gave final approval for publication.

Funding

This work was supported by MIUR-PRIN project 2010R8JK2X (Italy), Ente Cassa di Risparmio di Firenze project 2012.0611 (Italy) and Telethon project GGP12282 (Italy).

Author’s present address

L. Melli: NHLBI, Cell Biology and Physiology Center, 50 South Drive, Bethesda, MD 20814, USA.