Dynamics of the sensory response to urethral flow over multiple time scales in rat

Abstract

The pudendal nerve carries sensory information from the urethra that controls spinal reflexes necessary to maintain continence and achieve efficient micturition. Despite the key role urethral sensory feedback plays in regulation of the lower urinary tract, there is little information about the characteristics of urethral sensory responses to physiological stimuli, and the quantitative relationship between physiological stimuli and the evoked sensory activation is unknown. Such a relation is critical to understanding the neural control of the lower urinary tract and how dysfunction arises in disease states. We systematically quantified pudendal afferent responses to fluid flow in the urethra in vivo in the rat. We characterized the sensory response across a range of stimuli, and describe a previously unreported long-term neural accommodation phenomenon. We developed and validated a compact mechanistic mathematical model capable of reproducing the pudendal sensory activity in response to arbitrary profiles of urethral flows. These results describe the properties and function of urethral afferents that are necessary to understand how sensory disruption manifests in lower urinary tract pathophysiology.

Key points

• Sensory information from the urethra is essential to maintain continence and to achieve efficient micturition and when compromised by disease or injury can lead to substantial loss of function.

• Despite the key role urethral sensory information plays in the lower urinary tract, the relationship between physiological urethral stimuli, such as fluid flow, and the neural sensory response is poorly understood.

• This work systematically quantifies pudendal afferent responses to a range of fluid flows in the urethra in vivo and describes a previously unknown long-term neural accommodation phenomenon in these afferents. We present a compact mechanistic mathematical model that reproduces the pudendal sensory activity in response to urethral flow.

• These results have implications for understanding urinary tract dysfunction caused by neuropathy or nerve damage, such as urinary retention or incontinence, as well as for the development of strategies to mitigate the symptoms of these conditions.

Introduction

Maintaining continence and efficiently expelling urine requires coordination of the bladder detrusor muscle and the urethral sphincters, a process that is regulated by contributions from the parasympathetic (pelvic nerve), sympathetic (hypogastric nerve), and somatic (pudendal nerve) nervous systems (Fowler et al. 2008). Disruption of afferent signals, particularly in the pelvic and pudendal nerves, caused by conditions including multiple sclerosis, diabetes mellitus, surgical injury, or age-related neuropathy (Giannantoni et al. 1999; Lee et al. 2004; Kielb & Clemens, 2005; Smith, 2010) or experimental transection of the nerves in animal studies (Elliott, 1907; Barrington, 1914, 1931; Sasaki, 1998), compromises function of the lower urinary tract (LUT). Despite the pivotal role of urethral afferents in normal LUT function, little is known about the response characteristics of flow-sensitive urethral afferents. The objective of the present study was to quantify the dynamic responses of pudendal afferents to urethral flow and pressure.

Pudendal afferent activity regulates reflexes that modulate detrusor contractility and tone in the urethral sphincters as required for continence and efficient voiding (Barrington, 1914; Bradley & Teague, 1972). This urethral sensory information predominantly travels through the sensory branch of the pudendal nerve (Garry & Garven, 1957; McKenna & Nadelhaft, 1986). Pudendal afferents appear to respond transiently when flow in the urethra is initiated or changed (Todd, 1964) and exhibit flow rate dependent firing rates (le Feber et al. 1998; Snellings & Grill, 2012). Pudendal afferents also respond to urethral pressure generated without flow, but it remains unclear if this stimulus is less effective (Talaat, 1937) or equally effective (le Feber et al. 1998) as equivalent pressures generated with flow. Previous studies investigating multi-unit urethral afferent activity recorded from fine nerve branches running along the proximal urethra (Talaat, 1937; le Feber et al. 1998), and may have included contributions from the pelvic nerve or pudendal efferents that do not reflect urethral sensory information.

A quantitative description of the dynamics of primary afferent response to physiological stimuli is required to understand the neural control of micturition as well as to identify aetiologies of LUT dysfunction. We quantified the response of afferents in the sensory branch of the pudendal nerve to flow in the urethra; we describe an initial transient onset response, a steady state sustained response, and for the first time performed a systematic investigation of primary afferent accommodation to repeated stimuli over long time scales. We developed a concise mathematical model of pudendal afferent activity as a function of the urethral pressure, its time derivative, and past afferent activity. The model accounts for all features of the observed electrophysiological data and predicted sensory activity generated in response to important test cases.

Methods

Animal preparation

All animal care and procedures were reviewed and approved by the Institutional Animal Care and Use Committee at Duke University. Female Sprague–Dawley rats (0.275 ± 0.027 kg, mean ± SD, n = 56) were initially anaesthetized with isoflurane gas, followed by two subcutaneous injections of urethane totalling 1.2 g kg⁻¹ (dissolved as 0.2 mg ml⁻¹ in 0.9% saline solution). One hour after injections the animal’s reflexes were tested via foot pinch, and supplemental 0.1 g kg⁻¹ doses of urethane were given as needed until the foot withdrawal reflex abated. The animal lay on a heated water blanket to maintain body temperature, and heart rate and blood oxygenation were monitored with a pulse oximeter (Nonin, Plymouth, MN, USA) on the hindpaw. Following the protocol the animal was killed with an i.p. injection of 500 mg of Euthasol.

The bladder was exposed via an abdominal incision and a polyethylene catheter with a heat-flared tip was passed through a small incision in the dome of the bladder and into the proximal opening of the urethra. Suture was tied around the proximal urethra without occluding the ureters to fix the catheter in place, and the abdomen was sutured closed. The bladder incision was left open so that the bladder remained empty throughout the experiment. With the rat lying prone an incision was made approximately 1 cm lateral to the spine. This allowed the blunt dissection of the gluteofemoralis muscle and ischiorectal fossa to expose the pudendal nerve. The sensory branch was carefully isolated from the compound nerve and surrounding blood vessels. Following gentle dissection with forceps to remove the connective tissue from around the nerve, a bipolar silicone cuff electrode (custom made with Teflon insulated, braided stainless steel wire stripped at the tip with contact spacing of approximately 3 mm) was placed around the sensory branch of the pudendal nerve (McKenna & Nadelhaft, 1986; Pacheco et al. 1989). In three experiments the surgical procedure was repeated on the contralateral side to the recording site and a cuff electrode was placed around the motor branch of the pudendal nerve that was used for stimulation (Fig.4). Removing the connective tissue improved recording quality, and in all experiments but one where single unit activity could be distinguished this process was used, though not all experiments using this process yielded single units.

Figure 4.

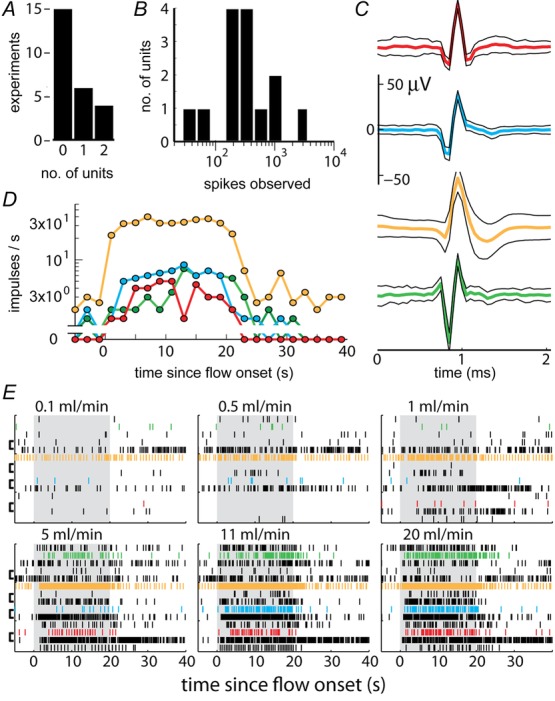
Individual pudendal afferents exhibited heterogeneous responses to urethral flow

A, the number of individual units that could be identified across experiments. B, histogram of the number of individual impulses observed during all flow rate trials across all identified units showed a broad distribution of spiking activity. C, example waveforms of identified units. The average waveform across all aligned time windows in which the unit was present is the thick centre trace and the surrounding black traces are one standard deviation. D, average firing rates of the four example units in C aligned to the onset of an 11 ml min⁻¹ flow rate trial, which is terminated 20 s later. E, raster plot indicating spike events of all identified units (vertical axis) across all experiments, separated by flow rate trials (panels), and aligned to the onset of flow (grey patches). The coloured units correspond to examples in C and D. The brackets on the left of the panels denote which units were observed in the same experiment.

A syringe pump was connected to the catheter in series with a pressure transducer and used to pass a solution of room temperature 0.9% NaCl through the urethra at controlled flow rates. Recordings from the pudendal sensory nerve were amplified at a gain of 10⁴, band pass filtered from 10² to 10⁴ Hz (SR560, Stanford Research Systems, Sunnyvale, CA, USA), and sampled at 20 kHz (PowerLab 8/35, ADInstruments, Colorado Springs, CO). Pressure signals were recorded unfiltered, amplified at a gain of 10 (ETH-255, CB Sciences Inc., Milford, MA, USA), and sampled at 100 Hz. The experimental setup is displayed in Fig.1.

Figure 1.

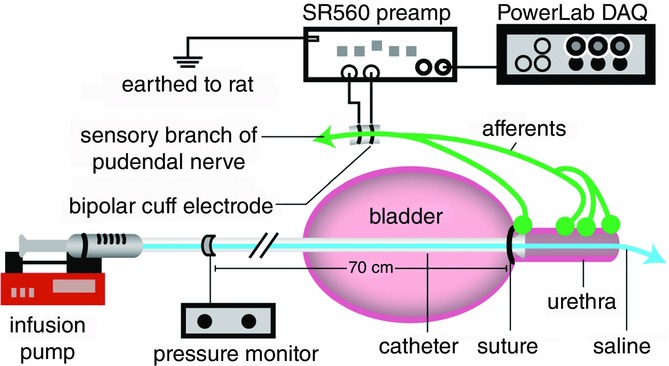
Experimental setup

Urethral pressure and electrical activity in the sensory branch of the pudendal nerve were recorded while physiological saline was passed through the urethra. Flow rate in the urethra was controlled directly by the infusion pump.

If the neural response to stroking of the meatus with a cotton swab did not generate a signal-to-noise ratio of approximately 2.5 or greater (Fig.10G) the experiment was not continued. The surgical procedure was performed on 56 rats in total, 11 of which failed due to surgical complications and 15 of which did not meet the signal-to-noise requirements. Most of the surgical failures occurred during the initial experiments when the protocol was being developed, and typically resulted from accidentally piercing the sensory branch itself or the adjacent internal pudendal blood vessel with forceps during the isolation of the sensory branch from surrounding tissue. Obtaining the requisite signal-to-noise ratio was more challenging; assiduous insulation of the nerve cuff electrode from surrounding tissue and moisture with silicone or Vaseline increased yield; however, even during the final 16 experiments, when the surgery was well practised, 3 failed to meet the signal fidelity requirements. A study recording electroneurogram (ENG) in small urethral nerve bundles reported an overall success rate of 15 in 36 (le Feber et al. 1998).

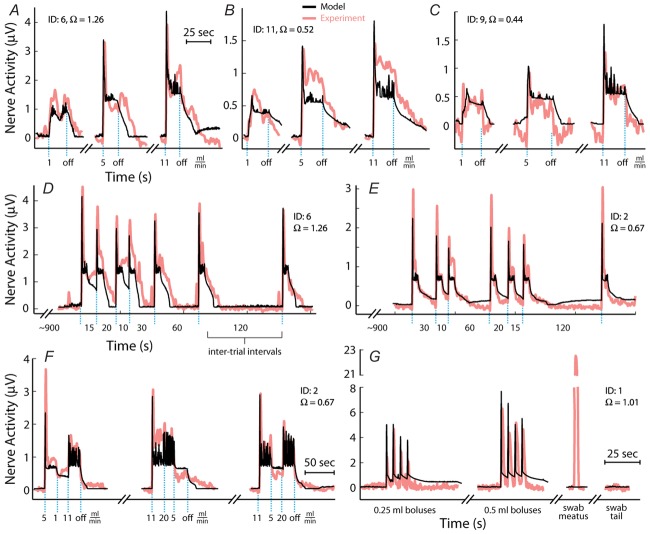
Figure 10.

Time series model predictions (black) of sensory nerve activity generated by urethral flow matched experimental measurements (pink) across a range of conditions

A–C, trials at three constant flow rates from three experiments. The position of blue dashed vertical lines indicates when flow began and ended for each trial and flow rate is listed under each line. Breaks in the abscissa denote data omitted for clarity during periods between trials where no flow was present. Data are plotted in order of increasing flow rate for clarity, but were randomized during the experiment along with other flow rates that are not shown. D and E, trials of variable inter-trial delays in two experiments. The position of blue dashed vertical lines indicates when flow began for each trial, and all flow rates were 5 ml min⁻¹ lasting for 10 s. The numbers between lines denote the time between flow termination of the previous trial and the start of flow in the subsequent trial. F, trials of a sequence of three flow rates without stopping the infusion pump. The changes to different flow rates are marked by the blue lines and the rate is listed below the line. Of note is the transient peak at the start of each trial, which was always larger than peaks caused by switching to high flow rates later in the trial. G, the two leftmost traces are of trials where a series of fluid boluses (0.25 or 0.5 ml) were pushed through the urethra in quick succession for testing the response to pressure derivative without a steady state component. The third trial was a light cutaneous swab of the genital region that generated large afferent response without a rise in urethral pressure. The fourth trial was a control where a region near the tail midpoint was lightly swabbed. The scale bar in F applies to D–F and the scale bar in A applies to A–C. The experiment ID and estimated coupling factor, Ω, are displayed in each panel for reference.

The flow rates were chosen to cover the range of plausible flows that a rat experiences under physiological conditions, although the flows were maintained for longer than natural periods in order to obtain steady state behaviour of the afferents. During voiding in rats the external urethral sphincter may phasically contract, and this behaviour has been quantified (Peng et al. 2006). The average flow rate was calculated from the reported parameters as the average volume voided over the average duration of the voiding period, 0.41 ml/3.85 s = 6.4 ml min⁻¹. Instead, if we assume that fluid is only allowed through the urethra during times in the voiding period where the urethral sphincter is silent (i.e. not during a phasic sphincter contraction) there is only 23.93 sp/void × 98.1 ms/sp = 2.35 s/void in which fluid is actually flowing (‘sp’ refers to silent periods of the urethral sphincter). This increases the average flow rate during a void to 0.41 ml/2.35 s = 10.4 ml min⁻¹. Low flow rates, such as 0.1 ml min⁻¹, represent a slow leak in cases of incontinence and the zero flow rate trials served as a control.

Adjustments to preparation when using neuromuscular blocking agents

In four experiments neuromuscular blocking agents were administered to study the contributions of urethral musculature to the observed neural accommodation to urethral flow, and this required additional preparation. Following anaesthesia (as above) the animals were intubated and placed on artificial ventilation with oxygen (PhysioSuite, Kent Scientific, Torrington, CT, USA). Insulated silver wire electrodes were inserted into the external urethral sphincter (EUS) for electromyographic recordings (EMG). An additional cuff electrode (as described above) was placed on the motor branch of the pudendal nerve. Low amplitude (50–150 μA) bipolar stimulation through this second cuff electrode was used to verify that the nerve branch was motor by visual confirmation of an evoked anal sphincter contraction, as well as accurate placement of the EUS EMG electrodes by observing a short latency evoked response to stimulation (Fig.8C). Following the main experiments (described above), the motor branch was stimulated at 0.5 Hz while pancuronium bromide (1.5 mg kg⁻¹) was administered i.v. Once evoked EUS EMG responses abated data were collected. Propranolol (1 mg kg⁻¹), a β-adrenergic receptor antagonist, and phentolamine (2 mg kg⁻¹), an α-adrenergic receptor antagonist, were then coadministered i.v., and following a period of 15 min data collection was repeated. Pancuronium bromide was administered first because striated muscle has a much larger impact on maintenance of urethral pressure than the urethral smooth muscle (Thind, 1995). Depth of anaesthesia was measured with a pulse oximeter on the hindpaw to track heart rate.

Figure 8.

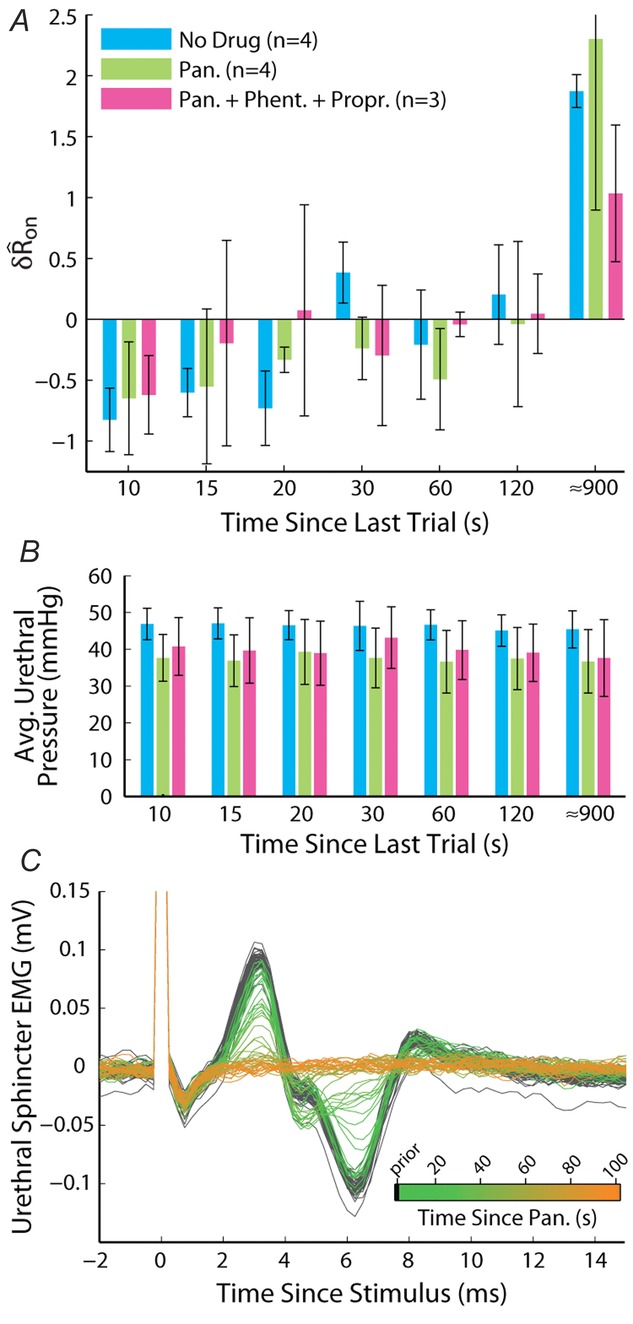
Block of urethral musculature did not prevent accommodation of the sensory response to urethral flow

A, variable delay trials were performed at a flow rate of 5 ml min⁻¹ in three conditions sequentially in the same animal. The first was under control conditions (No Drug) as in Fig.7, the second was after administration of pancuronium bromide (Pan., 1.5 mg kg⁻¹), and the third was after the additional co-administration of phentolamine (Phent., 2 mg kg⁻¹) and propranolol (Propr., 1 mg kg⁻¹). Bar heights are group means and error bars are one standard deviation. B, average urethral pressures showed a reduction following antagonists, but there was no difference between delays. Colours correspond to A. Bars are across-animal means, and error bars are one standard deviation. C, verification of skeletal muscle blockade following administration of pancuronium bromide from external urethral sphincter EMG. Each trace is a time series of the evoked EMG aligned to a current pulse delivered to the motor branch of the pudendal nerve at 0.5 Hz (stimulation artifact extends off vertical axis scale). The traces are overlaid and coloured by the time at which they occurred relative to administration of pancuronium bromide, as indicated in the colour bar inset.

Data analysis

Before analysing the data, ENG signals were digitally rectified and filtered (100–3000 Hz), and a moving average filter with a 200 ms sliding window was applied to smooth the neural response. A 200 ms window was centred at each point in the time series, an unweighted average of the window was taken, and this average became the value located at the centre of the window in the filtered time series. The filter resulting from this procedure was a −3 dB attenuation at 2.2 Hz and a roll off of −17.2 dB decade⁻¹.

To quantify trends of the pudendal afferent ENG across flow rates and trials, and to perform statistical analyses, we developed a scalar measure of the initial transient peak in response to flow onset, 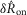, and the steady state response to flow, 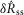. We quantified 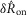by subtracting the baseline activity prior to the trial from the activity during the onset response, which is illustrated in Fig.2A for a typical trial. The shaded regions indicate the length of time, d, used to calculate this measure, and was set at 2 s for all analysis, which was heuristically found to capture the transient response. A similar procedure was used for 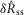, where baseline activity was subtracted from the steady state ENG response. Formally, the calculation is

1

2

where s is the nerve activity, 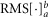is the root mean square of the argument from time a to time b, t₀ is the time at which the pump is turned on, and δ is inserted to emphasize that this measure is a difference from baseline (see the example in Fig.2A). The variable t_x is the time after flow onset when the ENG activity first exceeded the RMS value of the activity across the entire duration of the flow and t_f is the time that flow was turned off. The RMS calculation window could not be started immediately (or at a fixed latency) after turning on the infusion pump because each flow rate required a different amount of time to overcome urethral opening pressure, and pudendal afferents were not activated until the urethra opened and flow through the urethra began (examples in Fig.3B and C). If the ENG never exceeded baseline levels following flow onset, which occurred often in 0 ml min⁻¹ control trials and rarely in 0.1 ml min⁻¹ trials, t_x was set to t₀. The second term subtracts the baseline activity to account for different levels of noise and changes in spontaneous activity between experiments and trials.

Figure 2.

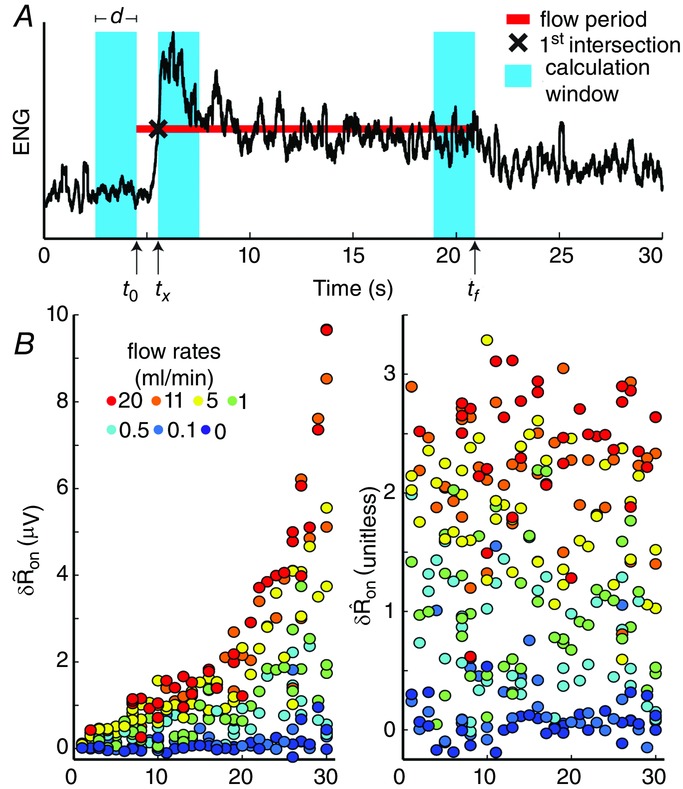
Scalar measure of pudendal sensory nerve activity in response to urethral flow

A, baseline RMS activity was subtracted from the RMS of the initial transient response. The window for the transient response began once the ENG activity crossed the value of RMS activity across the entire trial duration. The length of the red line indicates when the infusion pump was on, and the vertical position of the line corresponds to the RMS value of the ENG during the entire period when the pump was on (eqns 1 and 2). This example is from a trial with a flow rate of 11 ml min⁻¹. B, the unscaled (left) and normalized (right) measure of pudendal sensory nerve activity, with experiments ordered by within-experiment data variability. The subscript ‘on’ denotes that the measure was calculated following flow onset.

Figure 3.

Examples of ENG recorded from the sensory branch of the pudendal nerve in response to flow in the urethra

A, raw ENG at a flow rate of 5 ml min⁻¹ (also shown in B). Arrows indicate the onset and termination of flow. Low levels of spontaneous activity persisted after flow was terminated. B, rectified and smoothed nerve activity following subtraction of baseline activity. Activity reached a peak that depended on flow rate at the onset of flow and decayed to a steady state level that persisted throughout flow. The activity slowly decayed to baseline after flow was terminated. C, pressure in the proximal urethra corresponding to ENG traces in B. D, ENG (orange) and urethral pressure (blue) processed as in B and C, aligned in time to 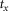(eqn 1), the ENG is scaled by the electric coupling factor (Ω), separated by flow rate, and averaged across all animals. Shaded bands are one standard deviation about the mean.

Normalization was required to allow comparisons between animals, 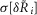in eqns 1 and 2, because the overall magnitude and signal-to-noise ratio of the ENG varied across experiments. The differences in signal amplitude across experiments arose, at least in part, from differences in the electrical coupling between the electrodes and the nerve, which differed across preparations. Therefore, to facilitate inter-experiment comparisons the normalization procedure must account for this difference. If we assume that differences in recording sensitivity caused by electrical coupling can be represented as a scale factor we may write

3

where 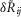is the scalar measure of observed ENG in response to the jth trial in the ith experiment, δR_ij is the ‘actual’ ENG that cannot in principle be obtained, and Ω_i is the coupling factor of the ith experiment representing the recording sensitivity. We then normalize the measurements j from the ith experiment by the standard deviation of measurements from that experiment such that 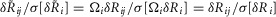, where 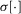is the standard deviation of the input. Normalizing the data in this way removes the scaling effects of different recording sensitivities without having to determine explicitly their magnitudes, and all data are scaled to unit variance. Therefore, we define the normalized measure as

4

The results of the normalization procedure are shown in Fig.2B. A simple scale factor was used rather than a frequency dependent function of electrode impedance, as the use of a high input impedance differential amplifier eliminates any signal frequency dependent effects of the electrode impedance on the recorded signal.

In the few cases where experiments had missing data the standard deviation of that experiment was multiplied by a corrective factor, 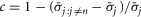. Here 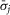is the average standard deviation across all experiments with all observations, j, included, and 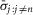is the average standard deviation across all experiments calculated without using observations at the flow rate n, which is the flow rate for which data is missing in the given experiment. Therefore, the correction is 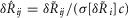, where c adjusts the standard deviation of the experiment with missing data by the amount that removing that same flow rate observation from all the experiments changes the average standard deviation across all experiments. The 20 ml min⁻¹ flow rate was not tested in the first five experiments, and is treated as missing data for those experiments, and transient increases in noise from unidentified external sources required us to exclude one 0.1 ml min⁻¹ and one 0.5 ml min⁻¹ trial from two different experiments.

In trials where neural accommodation was measured by varying the inter-trial time intervals (Fig.7) an offset that differed across experiments remained after normalizing 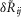. This is because there was no control trial that generated a fixed value (the 0 ml min⁻¹ trial produced a 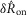near zero for the data shown in Fig.5 across all experiments). To correct for this, the mean of the data in each experiment was subtracted. The baseline activity level immediately before the first trial of the set of delay trials was used for all calculations in a single experiment. This was done because for some short latency delay trials the urethral pressure and neural activity had not yet returned to resting levels before the next trial began.

Figure 7.

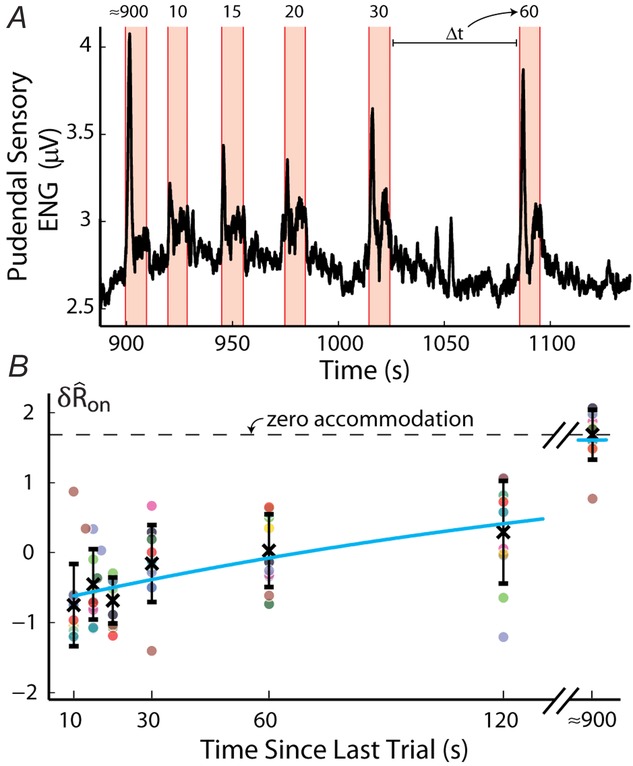
Long-term accommodation of the sensory response to urethral flow

A, pudendal sensory nerve activity during repeated applications of a 5 ml min⁻¹ flow rate in a single experiment illustrates the diminished initial transient peak in response to shorter inter-trial intervals. Periods when flow is on are marked by orange regions and time between flows in seconds, 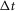, are listed above each flow period. B, the magnitude of the transient sensory response to flow, 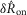, as a function of the inter-trial delay across all experiments at a flow rate of 5 ml min⁻¹. The pudendal sensory response to flow exhibited an exponential recovery time lasting longer than 2 min. The trials at 900 s delays (note the break in the abscissa) were not tightly controlled and varied by approximately 3 min; however, it appeared that neural recovery was complete by that time. The 900 s delay trial was always run first, and the other inter-trial intervals were presented in randomized order. The horizontal dashed line passes through the mean value for the 900 s delay trials for purposes of comparison to other data, and denotes the level of afferent activity in the absence of accommodation (i.e. zero accommodation). The blue curve is an exponential fit to the data (eqn 6). Error bars indicate standard deviation of the data and x’s are the mean at each delay. Each dot is an individual observation and all dots from the same experiment share the same colour, N = 11.

Figure 5.

Response of the sensory branch of the pudendal nerve to urethral flow rate during the initial transient peak following onset of flow (left, 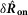) and at steady state (right, 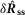) after 20 s of flow (n = 25)

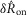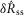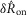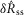was calculated from the ENG by subtracting the pre-trial root mean squared (RMS) baseline from the RMS during the transient peak, and was calculated by subtracting the RMS baseline from the RMS just prior to turning off the flow (eqns 1 and 2, Fig.2). Both and were normalized for each animal to account for differences in recording sensitivity across experimental preparations, and are therefore unitless (eqns 1, 2, and 4). Observations outside the central 99.3% of the data are marked as outliers.

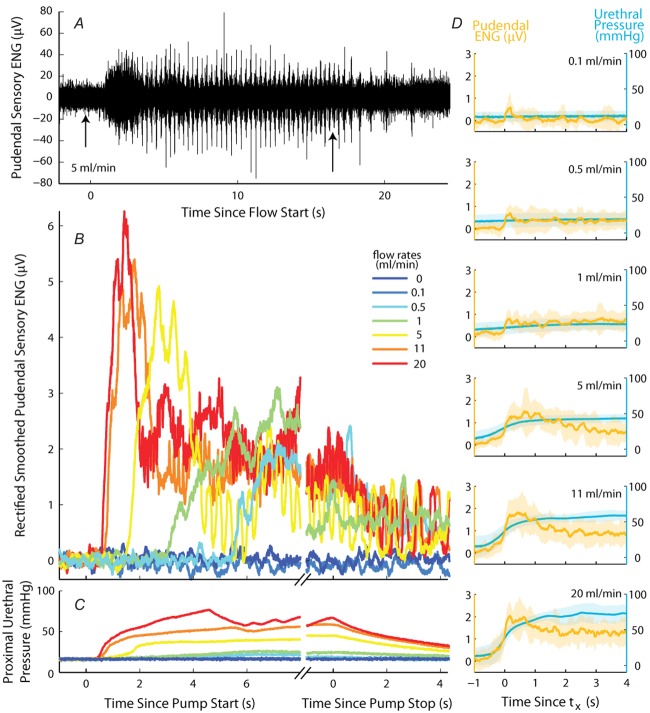
In a small subset of experiments, the saline exiting the urethra would pool in droplets on the meatus, rather than continuously flowing away from the animal; the droplets falling away from the meatus were discrete events that evoked cutaneous afferent responses. The frequency at which these droplets fell, and the corresponding evoked activity, was approximately periodic and proportional to the urethral flow rate, which can be seen in the traces in Fig.3B. Across-animal analyses (i.e. Fig.5) were not substantially affected by removing the experiments where these oscillations were present, and so no correction for this phenomenon was implemented. When it was recognized during an experiment that this phenomenon was occurring, we placed a piece of gauze beneath the meatus (in a position that did not increase the urethral outlet resistance), waited for the cutaneous response to subside, then resumed the trials. This procedure eliminated droplet formation and the associated cutaneous activation. Typical examples without these oscillations are shown in Figs2A, 6B and 4A, and examples from Fig.10A–C.

Figure 6.

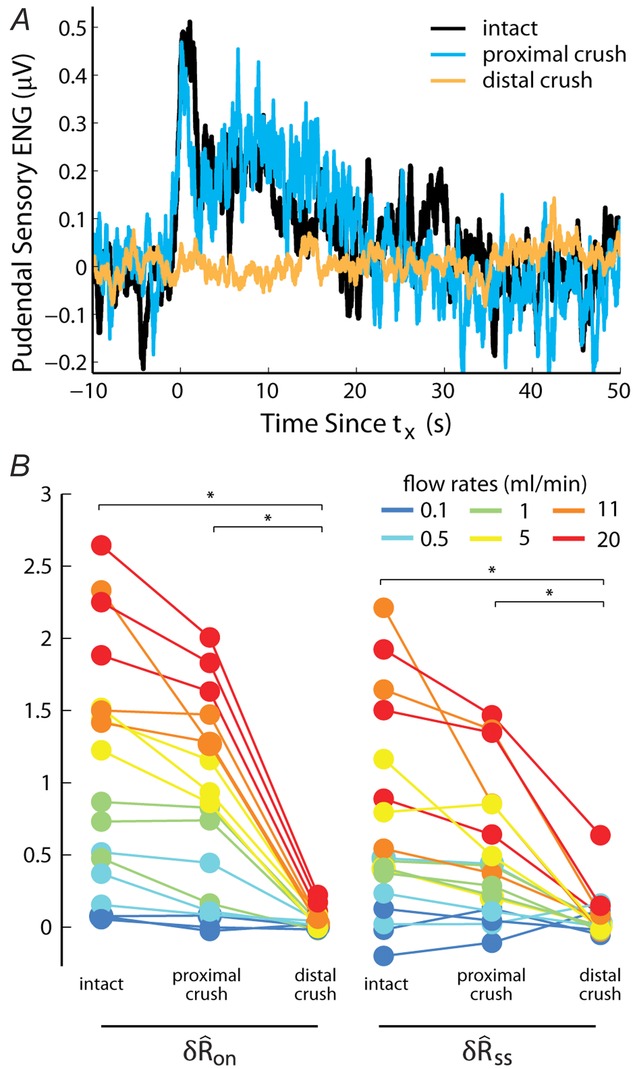
Blocking efferent transmission in the sensory branch of the pudendal nerve via crush did not significantly alter the response to urethral flow, indicating the response was predominantly afferent (n = 3)

A, example trials from each category illustrate that the response persisted following proximal crush, and activity was eliminated following subsequent distal crush. Trials are aligned in time to the onset of the neural response (eqn 1). B, the initial transient (left) and steady state (right) response to varied urethral flow rates. The categories are presented in the order in which they were performed during the experiment. Asterisks indicate which comparisons reached statistical significance with the Wilcoxon rank sum test. The intact trials used as controls were performed at the end of the experiment immediately before crushing the nerve.

The pressure transducer was in series with the catheter upstream of the urethra, and therefore, we accounted for the pressure drop from the proximal urethra to the transducer (a similar procedure was used in le Feber et al. 1998). In five experiments, following the data collection procedures, the abdomen was re-opened and a second transducer was placed in series with the catheter directly adjacent to the proximal urethra. Pressure was then recorded from both transducers at 14 flow rates ranging from 0.1 to 30 ml min⁻¹. A function was derived to map the values of the upstream transducer to the second transducer,

5

where P is the pressure measured at the upstream transducer and P_urethra is the estimated pressure at the proximal urethra. The results were highly repeatable, and parameters were estimated with a non-linear least squares algorithm as x₁ = 2.28, x₂ = 0.02, and x₃ = 31.86. This solution results in a nearly linear function for measured pressures greater than 15 mmHg. The prediction of eqn 5 yielded an average R² coefficient of determination of 0.97 and standard deviation 0.01 across the five experiments. All reported pressure measurements use this correction.

Identification of individual units from the ENG was done using an unsupervised wavelet and clustering procedure (Quiroga et al. 2004). Data were pre-processed for this analysis in a different way to Fig.2, and the corrective factor calculated in eqn 4 was not applied to the data prior to this analysis because binary spiking data does not require a scale correction for inter-animal comparisons. For each experiment, data from all constant flow rate trials were concatenated and digitally band-pass filtered from 400 to 6000 Hz before applying the algorithm. The general method was to express each potential spike as a point in a feature space determined by a wavelet decomposition, then iteratively regroup points among clusters (units) with a probability inversely proportional to their distance and proportional to a temperature parameter until the clusters reached a steady state. We then applied the following set of conservative criteria to the identified units to avoid false positives: the unit (1) must exhibit a response to flow, (2) cannot contain two spikes within 2 ms of one another, (3) must have a visually obvious multiphasic waveform, (4) must have a waveform peak at least 3.72σ above spike baseline (99.99% cumulative density of a Gaussian), (5) must have at least 20 observed spikes, and (6) must appear at a temperature parameter value below 0.15.

Model parameters and inputs

A model consisting of a system of two first order differential equations (eqns 12 and 13) was developed to predict pudendal afferent response from urethral pressure. The model was numerically integrated using MATLAB’s ode15s; however, all solvers produced similar results. The parameters reported in Table1 were determined using a simulated annealing algorithm to minimize the sum of squared error between the mean 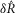of the model prediction and the observed results. The squared error was calculated for the means of 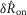in response to each flow rate, 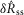in response to each flow rate, and 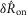for each inter-trial delay, weighted equally. All distributions used in the fitting procedure are plotted in Fig.9, and no other data besides the group means presented in Fig.9 were used to fit the model parameters. After the algorithm had settled in a local minimum the parameters were manually adjusted in that local region to qualitatively improve the fit.

Table 1.

Model parameters

Name	Value	Units
v	0.02	μV
w	0.06	s μV mmHg−1
k	23	s−1 μV−1
m1	0.0019	mmHg
m2	0.4	—
γ	3	μV
a	0.035	s−1
r	3	—

Figure 9.

Model predictions of sensory nerve activity matched experimental measurements of the initial transient response (A), steady state activity (B) and the accommodation of the initial transient response as a function of the time since the previous trial (C)

Observations outside the central 99.3% of the data are marked as outliers.

Before fitting the model to the pudendal nerve activity, both the pressure and ENG signals were pre-processed. The ENG was digitally rectified and filtered (100–3000 Hz) to focus on signal magnitude and to eliminate contamination of high frequency noise. A moving average filter with a 200 ms sliding window was then applied to smooth the neural response (filter described in the ‘Data analysis’ section). Finally, the baseline of the ENG, calculated as the RMS activity prior to presentation of the first stimulus of the experiment, was subtracted from all subsequent trials for each experiment (see Fig.10 for examples). The magnitude of the baseline ENG activity was caused primarily by noise and not relevant biological processes, and therefore it was not useful to fit this feature of the data with the model. However, baseline activity could be added to the model with the addition of a positive constant in eqn 12. The pressure data were also smoothed using the same 200 ms moving average and also had baseline subtracted. This smoothed pressure was then numerically differentiated and smoothed again with the 200 ms moving average filter to obtain the pressure derivative used in the model equations.

Statistics

All boxplots denote data quartiles, with the central bar being the median, and the whiskers extend to the largest non-outlier point. Outliers, identified as ±2.7σ (the central 99.3% of a normal distribution), are marked as crosses. Analysis of covariance (ANCOVA) tests, χ² tests, and Wilcoxon rank sum tests were performed with the MATLAB statistics toolbox (aoctool, chi2cdf and ranksum functions in version R2013a, respectively). Significance of the slope coefficient in linear fits was determined via an F test between the linear model error and the error produced using the mean as an estimate.

Results

Pudendal sensory response to urethral flow

Pudendal sensory nerve activity and pressure in the proximal urethra were recorded in response to different urethral flow rates (Fig.3). These data showed a large transient initial response to the onset of flow followed by a relaxation to steady state activity. Once flow was terminated, the ENG decayed back to baseline. Varying flow rate (and correspondingly, urethral pressure) modulated the initial transient to a greater extent than the steady state neural activity (also see summary data in Fig.5). The onset of neural activity with respect to the start of the infusion pump occurred sooner for high flow rates, which is very probably due to the time required to develop sufficient pressure in the catheter to overcome the urethral opening resistance (Bates et al. 1975). Qualitatively, the neural activity appeared to track the evolution of urethral pressure once the initial overshoot subsided.

The relation between urethral pressure and pudendal ENG is shown across animals in Fig.3D, where both pressure and ENG are averaged across animals and overlaid. The peak of the initial transient slightly lags the steepest region of urethral pressure. The variability in urethral pressure across animals generates variability in the timing and width of the initial transient, therefore the average peaks are somewhat broader and smaller than is typical in an individual experiment. There is a non-linear relationship between the constant urethral pressure and steady state ENG; the steady state ENG is very sensitive to low pressures but begins to saturate at the higher pressures generated by large flow rate trials. The shaded bands surrounding the mean also highlight the substantial inter-animal variability in both pressure and ENG. Because the onset of ENG activity following initiation of the pump was variable across trials and animals, each trace is aligned in time to t_x, the time at which ENG first exceeds the trial average (eqn 1, Fig.2A), prior to averaging across animals. Due to differences in electrical coupling between experiments, the ENG was normalized by the coupling factor, Ω (eqn 3), prior to averaging.

The raw ENG trace in Fig.3A shows an example where activity of a single unit stood out from the aggregate neural activity, which was observed by inspection at high flow rates in some experiments. For illustrative purposes an example trial with a large, slowly firing (2.5 Hz) unit is displayed where the individual spikes can easily be identified. The single unit activity, which was of very short duration (Fig.3C), was not visibly identifiable in the ENG traces after applying the smoothing filter to the data.

The activity of single flow-responsive units was identified in the ENG in 10 experiments (Fig.4A). The activity of pudendal afferents was heterogeneous (Fig.4B–E): units were observed with both high and low tonic firing rates, variable delays at which they responded to the flow stimulus, widely varying maximum firing rates, variability in their response to increasing flows, and differences in the duration of decline in firing rate after flow was terminated. Thus, while the aggregate ENG (Fig.3B) tracked the flow stimulus with high fidelity and exhibited a stereotyped initial peak and decay to steady state, individual afferent units were less predictable. The substantial increase in general nerve activity during the initial transient response to flow onset makes the likelihood of spikes being distorted by other units higher than during the steady state response. Because spike sorting algorithms group similarly shaped spikes into clusters to determine individual units, those units that fire predominantly during the high-activity period following flow onset will be more difficult to detect. This is an inherent limitation to detecting single units from whole nerve recordings and, along with a small sample size of units, may contribute to the fact that few units could be identified with high initial firing rates that decayed to lower steady state levels that behaved qualitatively similar to the aggregate ENG.

We quantified features of the ENG time series using normalized scalar values (eqns 1, 2 and 4, Fig.2A) to compare the afferent response to flow rate across animals and trials. The magnitude of the initial transient peak in response to the initiation of flow, , and the steady state response once the initial peak had subsided, , both varied as a function of the urethral flow rate (Fig.5). The initial transient was most sensitive to flows in the range between 0.5 and 11 ml min⁻¹. The peak response began to saturate at the 20 ml min⁻¹ flow rate and showed little response at 0.1 ml min⁻¹. The steady state response was less sensitive to flow rate increases, and exhibited strong signal dependent variability, while the initial transient did not. Linear fits to 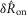and 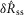as a function of flow rate were both significant (P < 0.001).

To determine any potential efferent contribution to the pudendal sensory branch activity, we recorded the response to urethral flow after crushing the nerve proximal to the recording electrode and again after crushing the nerve distal to the electrode in three animals. An example trial (5 ml min⁻¹) for all three conditions is displayed in Fig.6A, illustrating that the gross features of the neural response remained intact following proximal crush, but that the response was abolished following distal crush. 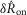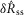The similarities in and distributions between the intact nerve response and the proximal crush indicate that only a small portion of the signal was generated by efferents, and the lack of response following distal crush emphasizes that the great majority of activity in the sensory branch of the pudendal nerve was afferent in origin (Fig.6B). The Wilcoxon rank sum test failed to reject the null hypothesis that the intact and proximal crush responses for 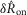and 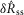were drawn from populations with equal medians at P = 0.48 and P = 0.52, respectively, but rejected the null hypothesis for intact and proximal crush compared to distal crush for both 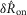and 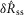(all at P < 0.005). This confirms that both the initial transient and steady state responses to urethral flow in the sensory branch of the pudendal nerve are predominantly derived from sensory activation, and not efferent commands. This analysis does not preclude the existence of motor fibres in the sensory branch, which have been shown to exist in male rats (Pastelin et al. 2008), rather, it demonstrates that these fibres are either not active during the variable flow trials or represent a very small portion of the aggregate electrical signal.

Neural accommodation

In addition to the within-trial adaptation to a constant flow rate, we observed a previously undescribed longer term accommodation or desensitization of the pudendal afferent response to flow. After an initial trial passing fluid through the urethra and measuring the afferent response, the response to the same flow rate on the subsequent trial was attenuated. This attenuation was measured systematically in 11 animals by first passing fluid through the urethra for 10 s at 5 ml min⁻¹, and then delivering a second equivalent flow stimulus at different controlled delays. An example of this long-term accommodation of the sensory response to flow is shown in Fig.7A, where it is evident that the peak height is a function of the inter-trial interval. The afferent response recovered as an exponential function of the time since the last trial and was fitted with the expression

6

where 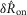is a function of the time elapsed since the end of the previous trial, 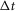, and x₀, x₁ and τ were fitted parameters with values 1.70, 2.43 and 191.5 s, respectively (Fig.7B). The return to the unaccommodated state was quite slow, as indicated by the 191.5 s time constant, suggesting that afferents require approximately 9.5 min between trials to recover 95% of their unaccommodated response for these trials. A linear fit to the response over inter-trial delays had a significant slope (P < 0.001, R² = 0.61), indicating an effect of time since the last trial on 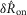. In Figs7B and 8A the mean value of all observations are subtracted (see Methods) such that the zero line represents the average neural response across all inter-trial delays, and the greater the spread about zero, the greater the accommodation effect. Therefore, the maximum value of 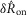(indicated with a dashed line in Fig.7B) is the unaccommodated response, and had there been no accommodation, or essentially an instantaneous recovery, values of 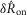would be equal across all delays. No such accommodation was detected in the steady state nerve activity, with a linear fit estimating a slope of 6 × 10⁻⁴ 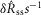, P = 0.05 and R² = 0.05.

There are several potential causes of the accommodation of the sensory response to urethral flow. (1) Reflex mediated urethral relaxation in response to sustained fluid flow (Barrington, 1914; Karicheti et al. 2010) could reduce urethral pressure, and consequently reduce the resulting afferent response, and this effect could be more pronounced for short inter-trial delays than longer delays if the relaxation reflex is slow to subside. (2) A relaxation effect could be caused by hysteresis of passive muscle and tissue properties of the urethra (Lose, 1989), similarly reducing urethral pressure and the corresponding afferent response differentially across inter-trial delays. (3) The accommodation may be mediated by predominantly neural mechanisms, and be unrelated to the mechanical features of the system.

We conducted additional experiments to investigate the contribution of active muscle properties to the accommodation of the sensory response to urethral flow. Cholinergic, α-adrenergic, and β-adrenergic receptor antagonists were administered in 4 of the 11 experiments in which accommodation was quantified (Fig.8). Variable delay trials were repeated following administration of pancuronium bromide (Pan), a cholinergic antagonist. No difference in the magnitude of accommodation was found between control and Pan conditions (Fig.8A, ANCOVA, F_(1,51) = 0.01, P > 0.5), no interaction between drug and inter-trial delay was detected (P = 0.32), and the effect of inter-trial delay remained significant (P < 0.001). The α- and β-adrenergic antagonists, phentolamine and propranolol, were then co-administered to block the urethral smooth muscle, and trials were repeated. No difference in the rate of accommodation was observed.

The average urethral pressure during flow exhibited no difference across inter-trial delays in the control condition (Fig.8B). This indicates that passive muscle properties were not generating the neural accommodation by causing higher urethral pressures in longer latency trials. A one-way ANCOVA found a statistically significant difference between urethral pressure in the control and Pan groups (F_(1,51) = 30.17, P < 0.001), without a significant effect of inter-trial delay (P > 0.5) or an interaction between latency and group (P > 0.5). This reduction in pressure was expected because there was no active urethral striated muscle tone following the administration of pancuronium bromide. However, the drop in pressure did not coincide with a loss of accommodation of the sensory response to urethral flow. This indicates that pancuronium bromide is blocking a tonic component of urethral muscle because there is a similar reduction in pressure at all flow rates, rather than reflex-mediated muscle activation that depends on the magnitude of flow rate.

The absence of a dependence of urethral pressure on inter-trial delay times shows that passive structural properties of the urethra are not responsible for changes in pressure that could modulate afferent responses. Further, the fact that accommodation persisted following administration of cholinergic and adrenergic receptor antagonists demonstrates that change in muscle tone is not a necessary condition for long-term accommodation and indicates that a neurally mediated mechanism is responsible for accommodation across trials.

Model of the pudendal sensory response to flow

We developed a mathematical model that estimates the pudendal sensory response to arbitrary time-varying pressure profiles generated by fluid flow in the urethra. Such a model is critical for making quantitative predictions about the relationship between physical stimuli and evoked neural responses, which is necessary both to understand how pudendal afferents encode sensations in the urethra and to develop treatments that modulate afferent activity to restore normal function. The model accounts for the initial transient peaks, steady state responses, and neural accommodation that were quantified in the previous sections, and generates predictions of neural activity evoked by any profile of pressure. The stimulus used is urethral pressure rather than flow rate because previous studies have shown that static urethral pressure without fluid movement readily generates a urethral sensory response (le Feber et al. 1998), indicating that pressure is more likely to be the primary mode of activation for these afferents. It should be noted that neither this nor any previous study has determined definitively that urethral pressure, rather than distension, is the physical stimulus driving pudendal afferents because these quantities tightly covary over all tested conditions.

Based on the observation that neural activity tracks urethral pressure through time (leaving aside for now the initial transient) and that the rise and fall of the neural activity to baseline is approximately exponential (Fig.3), we begin with a modified logistic model:

7

where s is the rectified, smoothed neural activity, k is a constant parameter controlling the reaction time of the nerve to the stimulus, and t is time. The term 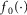is a transduction function that maps the time varying proximal urethral pressure, 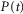, into the time rate of change of neural activity, and the term 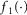is the contribution of the first derivative of 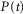to the time rate of change of neural activity. This form ensures that the neural activity tracks 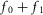through time and cannot be negative if 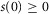, which is desirable because the goal is to estimate a rectified signal. Using the logistic model also ensures that transitions between different steady state levels of nerve activity are exponential, consistent with experimental observations.

At steady state urethral pressure 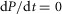, and the contribution of f₁ to neural activity vanishes. Therefore, f₀ accounts for all steady state neural activity and is related to a simple exponential function of urethral pressure,

8

where m₁, m₂ and v are constants determined empirically by the observed transduction of pressure into neural activity at steady state, 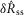(Fig.5).

The increase in urethral pressure from baseline to steady state caused by fluid flow followed a sigmoidal curve. The initial transient peak in neural activity was Gaussian and centred on the inflection point of the sigmoidal pressure profile (Fig.3), suggesting that the peak was a neural response to the derivative of pressure. The peak of this initial transient also declined as a function of time since the previous trial (Fig.7). Finally, we observed that urethral afferents responded selectively to the positive derivative of pressure, which can be seen in the example trials where the large pressure derivative caused by abruptly terminating flow did not cause an increase (or suppression) of afferent discharge. Therefore, we hypothesize that the neural activity during the initial transient response is proportional to the positive component of the derivative of urethral pressure and inversely proportional to the cumulative history of neural activity. Formally, the derivative term, f₁, has the form

9

where w is a constant scale factor determined by the transduction of the derivative of pressure into neural activity and γ is a constant that sets the sensitivity of f₁ to the cumulative history of s. The operator 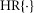is the half-wave rectifier, which sets all arguments less than zero to zero and does not affect arguments greater than or equal to zero. The functional Z_j(t, s) takes as its input the entire time-history of s, which it integrates to produce a scalar value representing the cumulative activation of s,

10

where r is a constant that uniformly scales the magnitude of the kernel, 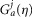, t is the current time, and j is a non-negative integer. The kernel is a gamma function and controls how each time point in the history of s is weighted in the integral, and is defined as

11

As indicated in eqn 9, the order, j, of Z_j(t, s) is taken to be zero for this model without loss of generality, which results in a kernel that monotonically devalues activity at times farther in the past. As the positive parameter a increases, the kernel density becomes concentrated at more recent times, thereby decreasing the impact that neural activity farther back in time has on accommodation. For all positive values of a, 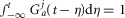, so that changes in j and a only affect the distribution of history weights but not overall scaling, which is controlled by the r parameter. The form of eqn 9 ensures that a complete absence of past neural activity results in scaling the pressure derivative by unity, and that increasing past activity results in a reduction of the contribution from f₁. The history functional and kernel have typically been used to describe oscillations in biological systems caused by negative feedback loops with intrinsic delays (Tyson, 2005).

Rather than leave the functional Z_j(t, s) in eqn 9, which would yield in an integro-differential equation, eqn 7 can be re-written using the ‘linear chain trick’ (MacDonald, 1989), made possible by the kernel property 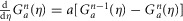. Therefore, the full model for the time rate of change of neural activity from eqn 7 can be stated as the system

12

13

where the variable z₀ now implicitly accounts for the history dependent dynamics described in eqns 10 and 11. The ratio of parameters v to w can be interpreted as the relative contribution to the total rate of change in sensory nerve activity of pressure and the derivative of pressure, respectively.

The eight model parameters (Table1) were fitted once to the normalized data displayed in Fig.9, and were not refitted across experiments or experimental conditions. Substituting in the measured proximal urethral pressure for P(t) and numerically integrating the model generates a prediction of aggregate pudendal sensory branch activity to within scaling. The solution is sufficient to predict the measures 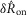and 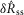(Fig.9) because the effects of electrical coupling, 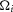, that differ across animals have been cancelled during normalization (eqns 1 and 2). To reproduce the non-normalized neural time series (Fig.10) 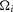must be estimated (eqn 3).

Model evaluation

The model was evaluated by comparing predictions of 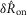and 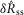in response to different flow rates and inter-trial delays to the experimental results from all experiments where urethral pressure was recorded (16 of 25). The model predictions were in remarkably close agreement with the measured neural activity, and their distributions are plotted in Fig.9 for the initial transient response to flow (Fig.9A), the steady state response to flow (Fig.9B), and the initial transient response to varied inter-trial delays (Fig.9C). The model reproduced the median of each distribution, and to a lesser extent, the variability. The model captured the natural variability in 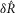at different flow rates insofar as the variability is manifested in the urethral pressure profile. However, variability across flow rates was larger for the observed data than for the model predictions, presumably due to unmodelled biological effects that stochastically influence nerve signalling.

Only the scalar measures of nerve activity (rather than the full ENG time series) shown in Fig.9 were used to fit the model parameters, meaning the 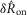and 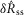values from the flow rate trials and the 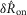values from the inter-trial delays. Therefore, Fig.9 demonstrates that the structure of the model can reproduce the data; time series test cases presented in Fig.10F and G that were not used to develop the model structure or fit parameters serve as validation of the model. A single fit was run over all these data to determine the model parameters, and the parameters were not refitted for each experiment and trial.

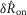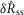The mean values of the and distributions at each flow rate for model predictions and data were treated as prediction–observation pairs for the χ² goodness of fit test. This resulted in P = 0.83 for the 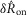measure 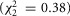and P = 0.77 for 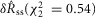, both failing to reject the null hypothesis that the model predictions and data are from the same distributions. The degrees of freedom parameter, 2, was determined as the number of categories, 7, less the number of parameters of the model that contribute to 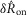and 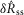, 5. Parameters γ, a and r only determine the model’s long-term accommodation, and therefore are not free parameters that contribute to fitting 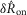and .

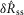Example traces for three constant flow rate trials in three experiments are shown in Fig.10A–C. The full time series predictions match all the slowly changing features of the observed data. Since the model parameters were fitted to the normalized population data, the model will have a small estimation bias for some individual experiments. This is shown in Fig.10B, where there is an underestimation bias of steady state activity, in Fig.10C where there is an overestimation bias, and in Fig.10E where there is an underestimation bias of the initial transient response.

Figure10D and E shows the model predictions for variable inter-trial delays from two experiments, illustrating the accommodation of the initial transient response, where the short delay trials have markedly reduced peaks. These examples also show that the model predicts accurately the decline of activity back to baseline over many conditions and that the magnitude of steady state neural activity is unaffected by accommodation.

An important aspect of this model is that it predicts neural activity in response to arbitrary pressure profiles, not just a response to a constant flow rate, which was not true in other models of pudendal activity (le Feber et al. 1998; Snellings et al. 2012). Predictions for non-constant flow rates are shown in Fig.10F and G. Figure10F shows a set of trials in which the flow rate was changed twice during each trial. The model predicts correctly both the initial transient response and the steady state responses. It is also important to note that, for example in the last trial in Fig.10F, the flow rate begins at 11 ml min⁻¹, where it exhibits a large initial transient, and is then reduced to 5 ml min⁻¹. When the flow is then increased to 20 ml min⁻¹ the transient is smaller than that following the initial 11 ml min⁻¹. This is consistent both with the observation of long-term accommodation and the transient being a function of the derivative of the pressure, and is captured by the model. This result also shows that the accommodation parameters fitted for the inter-trial delays at flow rates of 5 ml min⁻¹ generalized to other flow rates. These results serve as a critical validation for the model because these data were not incorporated into fitting the model parameters or building the model structure.

Figure10G shows a set of very different stimuli. The first two trials are the neural response to pushing fluid boluses through the urethra. The model predicts both the magnitude of the neural response to each bolus (with the exception of the first 0.25 ml bolus) and the decay following each consecutive bolus. The third trial shows the response to gently brushing the external meatus with a cotton swab (peak sensory activity evoked by 5 ml min⁻¹ trials across all experiments was 66 ± 22% smaller than swabbing). Note that the model fails to predict the evoked activity because the swab does not generate urethral pressure. Finally, a control trial is shown where the tail is brushed with a cotton swab, and no pudendal response is observed.

For the time series predictions to match non-normalized data from each experiment (unlike the normalized 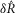measure) the coupling factor, 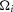, must be estimated separately for each experimental preparation to account for the differences in recording sensitivity (see eqn 3). Importantly, 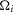is the only term that must be refitted for each experiment, and represents a scaling of the solutions of eqns 12 and 13 that is not a biologically relevant feature, but rather reflects differences in recording sensitivities between experimental preparations. 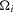was calculated analytically with a simple linear least squares procedure for each experiment using all data from the constant flow rate trials and the variable delay trials, and is listed in each panel in Fig.10.

To determine the domain over which the model predictions were most reliable we calculated the sum of the squared errors (SSE) between the model and many low-pass filtered versions of the experimental data for all variable flow rate trials. This allowed us to determine what frequency components of the neural response the model is best able to capture. Figure1A shows the normalized SSE as a function of the low-pass filter cutoff frequency used to filter the data. The model has low, stable error until the frequency content of the data exceeds 2 Hz, whereafter the error between the model predictions and the filtered data increases. The model is best suited to predict the slow features of the neural response because the dynamics are driven by urethral pressure, a signal which has its power predominantly localized in the low frequency range. A spectrogram of urethral pressure in a typical trial is given in Fig.1B, where the power is concentrated at frequencies below 6 Hz. The model is unable to reproduce responses with frequencies exceeding those contained in the pressure signal. The range of prediction errors varied across trials due to differences in signal to noise ratio (where fast dynamics due to noise are more prominent), differences in magnitude of urethral pressure either across experiments or across trials (where larger signals will cause larger SSE even if the percentage error is constant), and differences in the time required for pressure to relax to baseline. The z-score of SSE for each trial across cutoff frequencies (Fig.1A) represents how the model prediction error changes as a function of the cutoff frequency normalized to the amount of SSE in each trial.

Figure 11.

Model prediction performance across a range of frequencies

A, sum of squared errors (SSE), normalized for comparison (using the z-score, arbitrary units), between the model prediction and data for all variable flow rate trials as a function of frequency content in the data. Model errors are stable in the low frequency range, and exhibit a sharp rise beginning at 2 Hz, indicating the model is more accurate at low frequencies. Model predictions were generated as described above, and total SSE for each trial was calculated after passing the observed data through a low-pass filter with a cutoff frequency (−6 dB) indicated on the abscissa. The normalized SSEs for all trials were then averaged for each cutoff and plotted as the black line; the small grey band is one standard deviation. The inset is a histogram of raw SSEs for all trials without filtering. B, spectrogram (top) of urethral pressure from a 5 ml min⁻¹ trial (bottom), indicating that power in urethral pressure is contained predominantly below 8 Hz (spectrogram calculated with time-frequency bandwidth of 8, smoothed with 15 Slepian tapers, and a moving average window of 5 s).

A sensitivity analysis was conducted to assess the robustness of model predictions to changes in parameter values (Fig.2). This was done using the change-one-factor-at-a-time method where all parameters except one were fixed at their nominal values (Table1), and the differences between the model predictions and experimental measurements were calculated as the sum of squared differences between their population averages at each level of the independent variable. The sum of squared errors (SSE) for a given parameterization of the model was then expressed as a percentage of the SSE for the nominal parameter values,

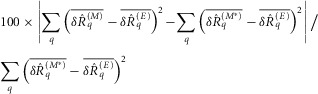14

where is the normalized scalar measure of nerve activity, the superscript M denotes the model prediction of 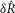at a given parameterization, 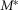denotes the model predictions for the nominal parameterization from Table1, and E denotes the experimental observations. All superscripts are in parentheses to emphasize that they are indices rather than exponents. The index q runs over each flow rate q = {0, 0.1, 0.5, 1, 5, 11, 20} or each inter-trial delay q = {10, 15, 20, 30, 60, 120, 900} as appropriate for the three measures. The overbar indicates that the quantity is an average of trials for the qth flow rate or latency across all experiments. Equation 14, therefore, represents the percentage change in SSE from the nominal parameterization over all conditions using any given parameterization, M. The results of the sensitivity analysis are shown in Fig.2 for each parameter (separated vertically), and for the three measures shown in Fig.9 (top, middle and bottom rows for each parameter).

Figure 12.

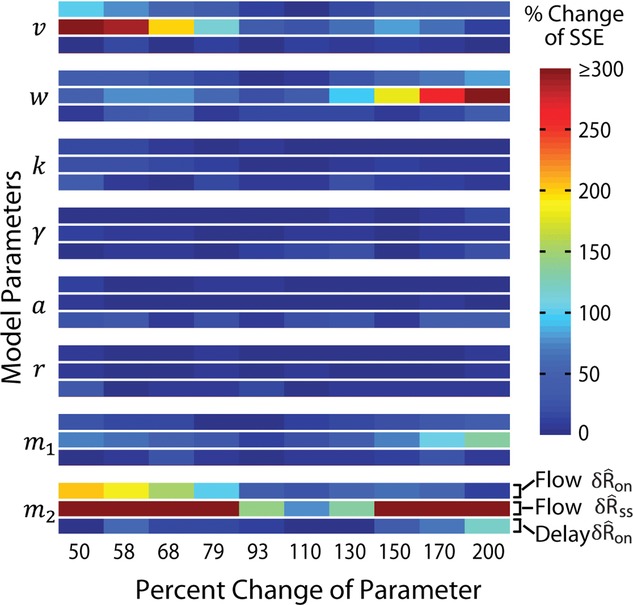
Sensitivity analysis of model parameters showed robust predictions using the change-one-factor-at-a-time method

A parameter was changed from its nominal value (Table1) by the percentage listed on the abscissa while leaving the remaining parameters unchanged. The percentage change in SSE of the tested parameterization with respect to the nominal parameterization for the three measures in Fig.9 (response to flow onset, steady state response, and accommodation to flow onset, from top to bottom) is plotted on the colour axis. The colour values of large SSE changes were clipped at 300% so that smaller changes would remain visually distinguishable.

The sensitivity analysis revealed that the model exhibited low sensitivity to most parameters 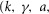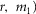, indicating that the model is robust to measurement uncertainty and errors in parameter estimation. The steady state activity was somewhat sensitive to parameters v and w, which control the relative contributions of pressure and derivative of pressure to afferent activity, respectively. To interpret the sensitivity analysis it is important to consider that all data were normalized by the standard deviation of across flow rates (eqn 4), which is why scaling w had little effect on SSE. However, when w was increased, causing the normalization factor to increase, the baseline activity was scaled down and caused underestimation of . The initial transient can grow indefinitely as w is increased, but reducing w cannot eliminate the initial portion of the neural response entirely because of the contribution by the f₀ term that is scaled by v, which explains why sensitivity to w is asymmetric. A similar effect occurred when increasing v, which increases the initial transient as well as baseline activity, thereby causing an increase in the normalization factor. The SSE was most sensitive to the m₂ parameter, which is the exponent of the urethral pressure in the term f₀(P(t)) in eqn 8, because small changes in the exponent substantially affect prediction. Because the model exhibits high sensitivity to only one parameter, the model parameterization is near a stable local error minimum in parameter space and small measurement noise or parameter estimation errors do not qualitatively affect the model structure.

Discussion

Pudendal afferents play a critical role in maintaining continence and producing efficient micturition through the regulation of reflexes in the lower urinary tract (LUT). Our experimental measurements quantitatively link pudendal afferent responses to flow stimuli in the urethra, including steady state responses, short-term accommodation, and long-term accommodation that has not previously been reported. Further, we developed a concise mathematical expression mapping physiological stimuli to afferent activity that reproduced all the features of the measured data and accurately predicted the response to validation cases. The aetiologies of many LUT diseases derive from disruption of afferent activity, and these results provide a framework to understand how changes in urethral flow impact the associated sensory signals.

Short-term accommodation of urethral afferent activity in response to persistent flow was described in past studies (Todd, 1964; le Feber et al. 1998; Snellings et al. 2012); however, longer-term accommodation across repeated instances of flow was not previously reported. Short-term (i.e. within trial) accommodation was quantified by considering the ratio of the initial transient response to the steady state response (Fig.3A). Within a trial, neural activity accommodated by nearly 50% for sufficiently large flow rates. Remarkably, the effect size of the long-term (i.e. across trial) accommodation (Fig.3A, grey region) was comparable to the differences in accommodation across flow rates. The difference in the accommodation ratio between trials with a delay of 900 s and 10 s was 1.04, while the difference in the accommodation ratio between the 11 ml min⁻¹ and 0.1 ml min⁻¹ flow rates was 1.10. This has significant implications for subsequent studies, because urethral reflexes will require long inter-trial intervals to recover fully when performing cystometric measurements or urethral perfusion. Further, if similar afferent properties exist in humans, clinical urodynamic measurements must also account for this effect. Finally, if neuropathy or insult can cause a significant increase in the recovery time of urethral afferents, then long-term accommodation could contribute to neurologically mediated urinary retention or incontinence.

Figure 13.

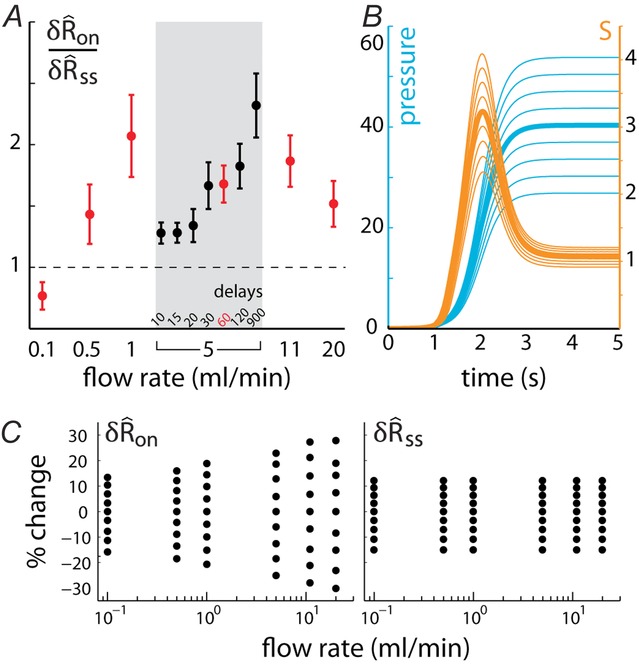
Pudendal afferent activity is affected by short-term accommodation, long-term accommodation, and urethral pressure variability

A, the ratios of the initial transient response to the steady response show that long-term accommodation is a large effect, in the same order as the differences in accommodation across different flow rates. Ratios are separated by flow rate, and trials with delays of 60 s are drawn in red. The shaded box marks flow rate trials at 5 ml min⁻¹ separated by inter-trial delays (see Fig.7). Error bars are ± one standard error about the mean. B, the model prediction of neural activity (orange, μV) in response to urethral pressure generated by a simulated 5 ml min⁻¹ constant flow rate trial (blue, mmHg). The thick centre pressure line represents a fit to the pressure data from 5 ml min⁻¹ constant flow rate trials (sigmoidal fit with rise 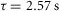and maximum value 40 mmHg, corresponding fits were performed for C). The thin surrounding pressure traces show the effects of scaling the maximum pressure by increments of 1/12 to ±1/3. Neural traces are the model outputs resulting from the corresponding pressure input. C, the example in B was repeated for all tested flow rates, 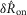and 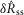were calculated, and the percentage change in these measures from their values in the unscaled cases (thick centre trace in B) were plotted for each pressure scaling.

Pudendal afferents were maximally sensitive to flow rates between 0.5 and 5 ml min⁻¹, which corresponds to physiological flow rates in rats (Peng et al. 2006), and the initial transient response was more sensitive to flow than the steady state response. To quantify this behaviour we fitted an increasing exponential decay model, 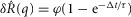, that yielded an asymptote, φ, of 2.17 and ‘flow rate’ decay constant, τ, of 1.34 ml min⁻¹ for (R² = 0.74), and 1.39 and 1.78 ml min⁻¹ for (R² = 0.47), respectively. The exponential fits indicate that steady state activity may continue to increase after the initial transient begins to saturate, and can be seen by the dip in the accommodation ratio in Fig.3A for 20 ml min⁻¹ trials. Further, the 0.1 ml min⁻¹ flow rate did not reliably evoke an initial transient response, which could indicate that a guarding reaction to leak in the urethra may require higher flow rates.

Developing a mechanistic model of urethral afferent responses to physical stimuli is challenging as it remains unclear what type of sensory organs transduce stimuli in the urethra (Gosling et al. 1981; Praud et al. 2003), and it is not known what the primary afferents actually respond to; candidates include distension, tension, pressure, turbulence and flow (Talaat, 1937; Todd, 1964; le Feber et al. 1998; Snellings et al. 2012). Studies that have attempted to model the afferent response to flow fit separate exponential functions to aggregate (le Feber et al. 1998) or single unit (Snellings et al. 2012) activity evoked by a series of constant flow rates. These approaches, however, have limited explanatory power because they are explicit functions of time, which they use as a surrogate variable for the actual stimulus driving afferent activation. This means that the time since flow onset does not itself cause afferent activity as previous models imply, rather it is the sustained flow, pressure, or distension in the urethra. As a result, these phenomenological models cannot generate predictions about any flow profile apart from the constant flow rates that were used to develop the models and they cannot be used to test hypotheses about the mechanisms generating afferent responses. Therefore, existing mathematical descriptions have not produced a mapping from general physical stimuli to sensory response in urethral afferents.

We developed a generalized model that predicts neural activity from actual urethral pressure. Our model made predictions across a wide range of conditions beyond constant flow rates (Fig.10A–C), including sequentially presented flows at varied delays (Fig.10D and E), abrupt changes of flow rates (Fig.10F), impulse responses (Fig.10G), low amplitude pressure oscillations (Fig.4A), and arbitrary simulated pressure profiles (Fig.3B). Further, the model predicted neural activity in response to the actual time-varying urethral pressure and, therefore, offers insight into the stimuli to which urethral afferents are most responsive as well as why urethral afferents accommodate. The model explains the short-term within-trial accommodation (Fig.3) and the long-term between-trial accommodation (Fig.7) using different neural mechanisms, which are likely to reflect differences in the adaptation rates of mechanosensitve afferents (Hao & Delmas, 2010). The short-term accommodation (the initial transient peak) may be caused by rapidly adapting receptors, or even dedicated pressure derivative receptors, while the longer across-trial accommodation could be caused by ultra-slowly adapting receptors. That the initial transients centre on the inflection point in the rise in pressure and subside early in the steady state pressure phase across many flow rates is a strong indication that at least some pudendal afferents detect changes in urethral pressure.

Figure 14.

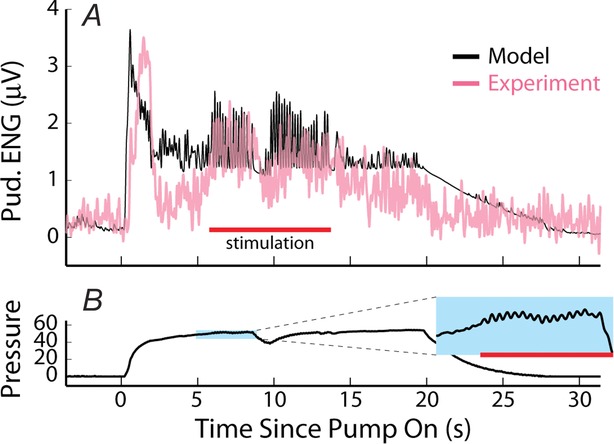
Stimulation of the contralateral motor branch of the pudendal nerve during flow mimics phasic bursting activity in rats, and enhances sensory activation evoked by fluid flow through the urethra

A, neural response, and model predictions for an 11 ml min⁻¹ flow rate trial with concomitant motor branch stimulation. B, the corresponding urethral pressure (mmHg) during the trial in A. The inset shows a zoomed-in region of the pressure oscillations caused by stimulation-evoked contraction of the external urethral sphincter (EUS) that increased the urethral resistance to flow. Red bar indicates stimulation.

Neurophysiological models have applications in understanding LUT function and pathophysiology. For example, pathological fluctuations in urethral pressure during voiding and filling (termed urethral instability, URI) have been linked to a number of LUT dysfunctions, including detrusor overactivity (Weil et al. 1986) and detrusor instability (McLennan et al. 2001). However, the causes and effects of URI remain unclear, and the debate over its uses as a clinical measure is ongoing (Groenendijk et al. 2009). Thresholds for determining URI vary in the literature (Groenendijk et al. 2009), but it has been found that 95% of control subjects do not exhibit fluctuations of urethral pressure exceeding 133% of baseline urethral pressure, and this level has been used as a diagnostic benchmark (Versi & Cardozo, 1986). By exposing our model to urethral pressure fluctuations of ±33% of steady state levels, we can assess the associated variability in the neural response in a condition similar to URI (example in Fig.3B). The effect of urethral pressure fluctuations has a much larger impact on the transient neural response than on the steady state response (Fig.3C), and pressure fluctuations around higher baseline pressures cause a larger percentage change in neural response than for lower baselines. These results show a potential mechanism by which URI could affect the bladder and contribute to the presentation of symptoms, namely that urethral pressure fluctuations could induce pathological urethral sensory responses that, in turn, activate voiding or guarding reflexes at inappropriate times. This result also indicates that it is important to normalize assessments of URI to baseline pressure because it is the change from baseline, or the fluctuation magnitude, rather than the absolute value of the urethral pressure that contributes most to neural activation.

Phasic activation of the EUS muscle is often observed during physiological voiding in rats, and transiently increases resistance to urethral flow and generates pressure oscillations in the bladder and urethra (Streng et al. 2004; Peng et al. 2006). During the variable flow rate trials the EUS did not exhibit this phasic behaviour. Therefore, to observe the system under more physiological conditions, in a subset of three animals the motor branch of the pudendal nerve contralateral to the recording site was stimulated with a train of charge balanced rectangular pulses to evoke contractions of the EUS while applying a constant flow rate through the urethra. A burst of three pulses was delivered with an intra-burst frequency of 40 Hz and an inter-burst frequency of 10 Hz (inspired by EUS motor unit activity during voiding in rats, D’Amico & Collins, 2012). An example of an 11 ml min⁻¹ flow rate trial is shown in Fig.4. The nerve activity increased in response to stimulation of the motor branch (stimulation artifacts were blanked). Our model of nerve activity was able to predict this increase due to the urethral pressure oscillations caused by EUS contractions (Fig.4B inset). Although the amplitudes of the pressure oscillations were small compared to the background urethral pressure during flow, sensory activity was still substantially enhanced as a result of the high sensitivity to changes in pressure. Pressure derivatives caused by the bursting, which can be large for even small amplitude changes, were sufficient to drive the increase of pudendal afferent activation. This suggests that phasic bursting of the EUS increases urethral sensory feedback by creating frequent changes in pressure, a signal to which the pudendal afferents are particularly sensitive. Such increased afferent activity may drive pudendal sensory mediated detrusor contraction (augmenting) reflexes to more efficiently empty the bladder during voiding (Barrington, 1931, 1941; Peng et al. 2008).

Glossary

ANCOVA

analysis of covariance

EMG

electromyogram

ENG

electroneurogram

EUS

external urethral sphincter

LUT

lower urinary tract

RMS

root mean square

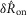
normalized integrated nerve activity following urethral flow onset

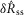
normalized integrated nerve activity at steady state urethral pressure

SSE

sum of squared error

URI

urethral instability

Additional information

Competing interests

The authors declare there are no competing interests.

Author contributions

Z.C.D. and W.M.G.: conception and design of the experiments. Z.C.D.: data collection and assembly and data analysis. Z.C.D. and W.M.G.: data and analysis interpretation. Z.C.D.: model development. Both authors were responsible for drafting the article, revising the article and responding to comments. It is hereby confirmed that both authors approved the final version of the manuscript, that both authors qualify for authorship, and that all those who qualify for authorship are listed as authors. All experiments were performed at Duke University.

Funding

This work was supported by the National Institute of Neurological Disorders and Stroke (NINDS; R01 NS050514 to W.M.G. and T32 051156 to Z.C.D.) and the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK; F32 DK098904 to Z.C.D.).