The Value of Interrupted Time-Series Experiments for Community Intervention Research

Abstract

Greater use of interrupted time-series experiments is advocated for community intervention research. Time-series designs enable the development of knowledge about the effects of community interventions and policies in circumstances in which randomized controlled trials are too expensive, premature, or simply impractical. The multiple baseline time-series design typically involves two or more communities that are repeatedly assessed, with the intervention introduced into one community at a time. It is particularly well suited to initial evaluations of community interventions and the refinement of those interventions. This paper describes the main features of multiple baseline designs and related repeated-measures time-series experiments, discusses the threats to internal validity in multiple baseline designs, and outlines techniques for statistical analyses of time-series data. Examples are given of the use of multiple baseline designs in evaluating community interventions and policy changes.

This paper advocates the use of time-series experiments for the development and evaluation of community interventions. Time-series experiments, particularly multiple baseline studies, have played a pivotal role in the development of interventions in clinical psychology (Barlow, et al., 1984), education (Kratochwill, 1978), and health promotion (Windsor, 1986), and have contributed greatly to the development of the principles and methods of the experimental analysis of behavior, especially to our understanding of reinforcement (Sidman, 1960). Analyses of interrupted time series are also playing an important role in research on the effects of public policy (e.g., Campbell, 1969; Chaloupka & Grossman, 1996; Cook & Campbell, 1979; Hingson et al., 1987 Wagenaar, 1983;). Despite the notable success of time-series methods in these areas, they are not widely used or well known in much of the behavioral sciences. Time-series experiments are as relevant for the community interventionist as they are for the behavior therapist or policy analyst. The present paper highlights one form of time-series experiment— the multiple baseline design—as a method of evaluating community interventions. Such a design is feasible whenever the process under study can be measured reliably on repeated occasions. The method makes possible the development and evaluation of community interventions using many fewer communities than are required to conduct a statistically powerful randomized controlled trial.

LIMITATIONS OF RANDOMIZED CONTROLLED TRIALS IN COMMUNITY INTERVENTION RESEARCH

Traditional randomized controlled trials are still the predominant approach to the experimental evaluation of community interventions. The primary limitations of this research method are (a) the high cost of research due to the number of communities needed in such studies, (b) the difficulty in developing generalizable theoretical principles about community change processes through randomized trials, (c) the obscuring of relationships that are unique to a subset of communities, and (d) the problem of diffusion of intervention activities from intervention to control communities. Because of these limitations, systematic research around factors that influence community-level change has progressed slowly. Policymakers and community organizations, however, continue to feel compelled to implement untested intervention strategies out of a desire to do something to address the targeted social concerns. Unfortunately, little scientific knowledge is gained under these conditions, and progress on the identification and implementation of effective community intervention methods is limited.

The High Cost of Randomized Controlled Trials

Conducting randomized controlled trials to develop and evaluate community interventions is a costly enterprise. The significant cost associated with rigorous research involving communities has resulted in relatively few such studies being undertaken. It is estimated that the National Cancer Institute’s experiment to evaluate community interventions to increase smoking cessation cost $45 million. The trial involved 11 pairs of communities throughout North America. The randomized controlled trial of a community intervention to prevent adolescent tobacco use that we have conducted (Project SixTeen) involved sixteen small communities. It has so far cost about $6 million, and we are still conducting follow-up assessments.

Three randomized community trials are also being conducted in Minnesota. Forster and colleagues (Forster et al., 1998) conducted a randomized controlled trial of a community intervention to reduce illegal sales of tobacco to young people in fourteen communities, at a cost of $1.29 million thus far (Forster, personal communication). Perry’s Project Northland (Perry et al., 1996), which evaluates a program to prevent adolescent alcohol use, is being conducted in 28 small rural communities and has thus far cost about $6 million (Perry, personal communication). Communities Mobilizing for Change on Alcohol (CMCA; Wagenaar et al., 1994), a randomized trial of a community intervention to reduce youth access to alcohol, cost $4.15 million.

We do not mean to imply that these expenditures are wasteful. The cost of the three just-cited Minnesota studies is only a fraction of the cost to our society of tobacco and alcohol use. Forster et al.’s study (1998) provides the public health community with an effective method of reducing illegal sales of tobacco to young people—a problem that is being tackled in every state in the nation. The CMCA project has demonstrated that randomly selected communities can be mobilized to action that significantly reduces youth access to alcohol (Wagenaar et al., in press). The benefit of these studies in contributing to reduced tobacco and alcohol use and their sequellae will far exceed their cost. If such experimental designs are what it takes to develop effective community interventions, the society will be well served to spend the money.

However, as community intervention research evolves, finding more efficient and cost-effective ways of developing and evaluating interventions would be of great benefit to the health and well-being of the nation. Indeed, additional lives will be saved if we learn how to develop community interventions more efficiently.

Randomized Controlled Trials Are Not a Good Vehicle for Identifying Principles about Variables that Influence Community Practices

A randomized controlled trial allows us to assess whether or not an intervention has an effect that is replicable across cases. Some would argue that this is the ultimate test of our community interventions. But, before we can develop interventions that have widely replicable effects, we need to establish a more fundamental understanding of how practices in a community are influenced. To see why this is so, we need to consider the nature of the practices in communities that one might be concerned with affecting.

A cultural practice can be conceptualized in terms of the incidence or prevalence of a behavior in a defined population, such as the number of 16 year olds in a community that begin smoking or smoked one or more cigarettes in the last week (Biglan 1995a). Or a practice can be conceptualized in terms of the actions of organizations. The actions of organizations can be dimensionalized in terms of the probability, frequency, incidence, or prevalence of an action. For example, we may be concerned with analyzing the probability that a city council will enact an ordinance regarding clean indoor air. We may be concerned with the frequency with which a human service agency does outreach to other organizations to affect families in need of parenting skills programs. An example of the incidence of the actions of organizations with which we might be concerned is the number of work organizations in a community during a year that adopt a policy allowing parental leave for school visits. An example of the prevalence of an action of organizations in a community is the number of tobacco outlets that sold tobacco to minors on two or more occasions in a year.

Prevention science is not simply a matter of developing programs that work. We strive to identify principles regarding relationships between independent and dependent variables that have precision, scope, and depth (Biglan & Hayes, 1996). By precision we mean that a limited number of concepts are needed to analyze a given phenomenon. By scope we mean that a small number of concepts can be used to analyze a wide range of phenomena. By depth we mean that analytic concepts relevant to one level of analysis cohere with others at other levels (e.g., psychological vs. anthropological level, sociological vs. anthropological level).

For example, although it is gratifying to bring about a reduction in the prevalence of smoking in one or more communities, scientific research strives to identify empirically based theoretical principles that would guide further interventions. We would argue that those principles are necessarily about contextual influences on either the practices of community organizations or the incidence or prevalence of behaviors (Biglan, 1995a). It is only by specifying replicable principles that we can assist other communities in achieving similar effects. But more importantly, such principles may prove to be much more broadly applicable than for the particular situation in which they were derived. For example, a principle about variables that influence a health care system to give advice to smokers to quit may be relevant to changing many other practices of health care organizations.

A randomized controlled trial is a good vehicle for testing the replicability of such principles, but it is a poor one for arriving at them. This is because the principles are necessarily about the relationships between practices or behaviors in a single community and the contextual variables that influence them (Biglan, 1995a). At this stage of our knowledge we know very little about the factors that influence most practices in communities. For example, we are far from being able to specify the factors that would influence human service organizations to adopt empirically-based programs for families (Biglan, et al., in press).

Thus, research is needed to tease out the manipulable variables that influence practices that we would want to influence in communities. For example, we need to identify variables that influence: (a) the media to cover an issue (e.g., COMMIT Research Group, 1995a), (b) schools to adopt programs or reforms (e.g, Trickett, 1991), (c) governments to adopt ordinances (Forster et al., 1998), or (d) community groups to organize to address a community concern (Fawcett et al., 1988, 1995). In most cases, however, we have developed very little knowledge about variables that influence the practices of organizations.

The COMMIT trial presents an example of the limitations of randomized controlled trials for developing empirically based theoretical principles that could guide community interventions. The study compared a comprehensive community intervention with no intervention in 11 pairs of communities. The effects of the intervention have proven to be modest (COMMIT Research Group, 1995a,b). The problem may have been that the intervention was not sufficiently developed before it was subjected to testing in such a trial; not enough was known about how to influence smoking control practices in individual communities. For example, a key component of the intervention was an effort to get health care providers to advise their patients who smoked to stop smoking. The component was predicated on substantial evidence that such advice increases the likelihood that smokers will quit (Ockene, 1987), especially when it is supplemented with very brief counseling (Hollis et al., 1993). However, we know little about the contextual factors that influence physicians to give such advice and even less about how to get an entire health care system to begin doing so. What was needed was the systematic manipulation of contextual influences on the advice giving practices of health care organizations.

Suppose that COMMIT investigators had begun by testing—in one community—an intervention that was believed to affect health care providers’ advice giving? It might have included advocacy for advice giving, organizing the medical society to adopt a standard, providing materials to facilitate brief advice-giving (e.g., Hollis et al., 1993), and training health care providers in giving advice. The dependent variables in this community would have been the proportion of physicians giving quit-smoking advice and the proportion of smoking patients getting such advice. Failure to affect these dependent variables might have been followed by the testing of additional interventions—for example, media urging smokers to ask their physicians for advice, or organizing health insurers and employers to request or require such advice giving. The success of any of these interventions could then have been followed by replication of the intervention in a second community, using a revised version of the intervention that was informed by all of the false starts and failures in the first implementation. Over three or four communities, what might have emerged was a much clearer understanding of the specific independent variables that affect health care providers’ advice giving. The development of intervention components through such contextual analyses might have produced a more powerful intervention than the one that was implemented when a group of investigators came together and were forced to begin a community-wide intervention with so little prior research or experience. And, it might have produced generalizable knowledge about the factors that influence the practices of health care organizations.

The work of Fawcett and colleagues (Fawcett et al., 1995) is noteworthy in this regard. They have been developing strategies for assisting individual community organizations to take specific actions in furtherance of community development goals by carefully tracking the actions taken, feeding the record of those actions back to the organization, and helping the organization to obtain funding on the basis of the actions achieved. This work has pinpointed a set of contextual influences on the actions of community organizations that has implications for community interventions on diverse problems.

The current situation in community intervention research is similar to what happened in the development of knowledge about the behavior of individuals (Biglan, 1995a). Much of our knowledge of the contextual influences on human behavior came from experimental manipulations of environmental influences on the behavior of individuals. For example, our understanding of the role of reinforcement and of many teaching strategies arose out of careful examination of the environment-behavior relationships in individual cases. It was only when there were viable principles about influences on the behavior of individuals that we could begin to test their replicability across individuals.

In sum, community prevention research needs to develop greater understanding of the contextual influences on community organization practices and the incidence and prevalence of behavior. Once we have improved our understanding of these influences through time-series experiments in one or a few communities, we will be in a far better position to demonstrate the power of community interventions.

Randomized Controlled Trials May Obscure Important Relationships that Are Unique to a Subset of Communities

The mechanist assumption that nomothetic laws will necessarily be discovered has been increasingly criticized in recent years (Biglan, 1995a,b; Biglan & Hayes, 1996; Cronbach, 1986; Sarbin, 1977). Although there is certainly value to identifying relationships that have great generality, we need not assume that such relationships are there to be found (Hayes, 1993). Indeed, the assumption may hinder our discovery of important, though local, relationships. When we begin with control group designs, we necessarily also begin with the assumption that the relationship we are studying is generalizable (at least across all of the cases in the study). This assumption is especially questionable in community intervention research, both because there may be important relationships that are unique to one or a subset of communities, and because we currently know little about the factors that affect community processes. Certainly interventions that have a significant effect on their target across diverse communities are of greatest value. However, an intervention could have a significant (strong and reliable) impact in one community but not in another. For example, an intervention method might work well only in small communities or in communities of a particular ethnic make-up. Such a method might not produce a significant effect over all communities, and we would fail to identify it as a useful intervention using a randomized controlled trial.

The Problem of Preventing Diffusion of the Intervention into Control Communities

One lesson from a recently completed randomized trial by one of the authors (Communities Mobilizing for Change on Alcohol (CMCA project); Wagenaar et al., 1994, 1999, in press) is that it can be difficult in community intervention research to ensure that there is no diffusion of ideas, strategies, and materials from intervention communities to control communities. The CMCA project involved random assignment to treatment and control conditions of a pool of 15 communities spread across a circle in the upper Midwest with a diameter of 500 miles. All the communities were distinct, “green-belted” communities, separated from other communities by large areas of very-low-population-density agricultural land. Despite efforts to prevent dissemination of the intervention before the study was completed, considerable evidence emerged from control group data collection efforts that control communities had also implemented components of the intervention before all post-intervention data were in. The result for this pre/post randomized community trial was reduced statistical power to detect intervention effects. In the CMCA case, overall tests of intervention effectiveness were nonetheless statistically significant, despite the control group also showing some improvement from pre to post. However, statistical power to isolate effects of the intervention on a wide range of specific measures was substantially impeded by the diffusion of a portion of the intervention to the control group.

THE LOGIC OF REPEATED TIME-SERIES EXPERIMENTATION

This section describes the key elements in repeated time-series designs that are feasible in community intervention research.

Repeated Measurement of a Process

In any community or policy intervention, we are trying to find ways to affect ongoing processes that can be repeatedly measured. It is appropriate, therefore, to focus on changes in important behaviors, practices, or outcomes over time. Examples include the prevalence of tobacco use, the prevalence of child abuse, the prevalence of “adequate” parental monitoring, the availability of supervised recreation for youth, the incidence of juvenile crime, the enforcement of laws, the number of traffic fatalities, and the total amount of charitable giving in a community.

Such behaviors and practices can be repeatedly measured. The result is a “repeated time series” that enables investigation of the pattern of change over time. Parameters of such a time series include its mean level (the average of all time points), its slope, and numerous more complex, non-linear changes in the shape of the time-series.

Manipulation of an Independent Variable

Once there is a repeated measure of the process of interest, one can assess the effects of any independent variable in terms of its impact on the average level or the slope of the measured process. The judgment that the independent variable affects the process is based on how much change its introduction produces in either or both the level and slope of the measured process.

A key issue is the degree of variability over time in the measured process (Barlow et al., 1984). Figure 1 shows two results of the measurement of a process. In the left panel, the process of interest is highly variable; in the right panel, it is not. It is easier to detect an effect on the process measured in the right panel.

Fig. 1.

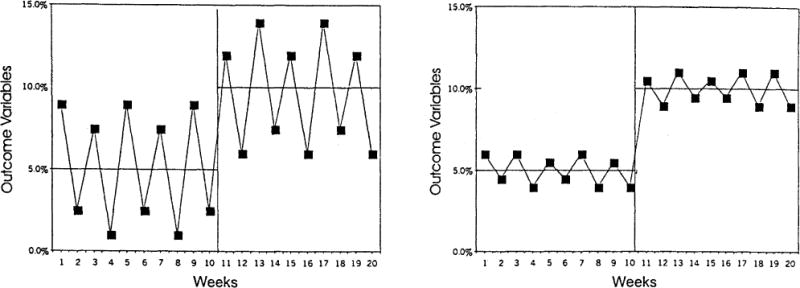
Measurement variability in two hypothetical interrupted time series. The first shows a highly variable series and the second a relatively stable series.

A–B Designs

By convention, in the behavioral literature, the phases of a repeated measures designs are labeled A, B, C, etc. The simplest repeated time-series design is an A–B design in which an independent variable is manipulated (that is, a new level of it introduced) after a series of baseline measurements in a single time series. Our ability to judge the effect of the independent variable is a function of the number of baseline data points, the number of intervention data points, the number of post-intervention data points, and the variability of the data.

This type of design has long been used to evaluate the effects of policies. For example, Fig. 2 presents an example of a simple A–B design from Wagenaar and Webster (1986) in which the effects of Michigan’s implementation of mandatory automobile safety seat use for children under age 4 was evaluated. The figure shows injuries to motor vehicle occupants 0 to 3 years of age. The law went into effect in April of 1982. As can be seen, there was an apparent reduction in the rate of children’s injuries. Similarly, Hingson et al. (1987) described the effects of changes in driving-under-the-influence legislation in Maine and Massachusetts. Warner (1977) evaluated cigarette consumption as a function of changes in policies about cigarette advertising and publicity about the harmful effects of cigarettes. The effects of tobacco taxes on consumption have been evaluated by examining the effect of changes in tax rates on annual consumption (US Department of Health & Human Services, 1994).

Fig. 2.

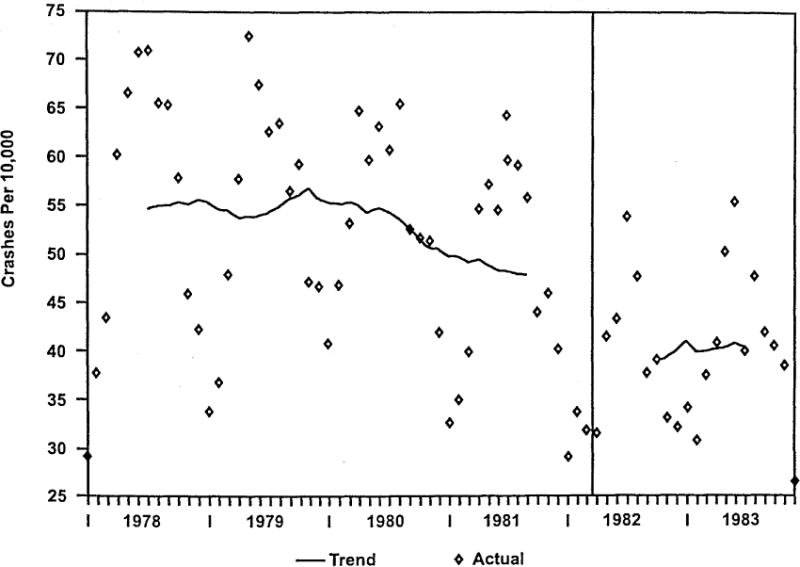
The effects of Michigan’s implementation of mandatory automobile safety seat on injuries to motor vehicle occupants 0 to 3 years of age.

One limitation of such a design is that a change in a time series could be due to numerous other factors that co-occur with the change in the independent variable. For example, a law regarding blood alcohol level may be introduced after a dramatic increase in the number of drunk driving deaths (Campbell, 1969). If the death rate subsequently drops, it could be due to the implementation of the law, but it also could be due to regression-to-the-mean, to the publicity about the high death rate before its enactment, or to other uncontrolled influences that would have led to a reduced rate even without legislative action. It could also be that it is not the law itself, but the publicity surrounding its enactment that influences people’s drinking and driving habits. If this were the case, one might see a decrease in the level of drunk driving deaths during legislative deliberation, but before enactment. And, one might find that there is a decrease in the level of drunk driving deaths at the point of enactment, but that the slope of the time series is significantly more positive following implementation (Ross, 1973). In other words the rate drops after the law is enacted, but it begins to climb back up as the publicity about the issue wanes.

Multiple Baseline Designs

One can have greater confidence that the manipulation of an independent variable was responsible for a change in the time series if there are multiple time series, each of which receives the manipulation or intervention at a different point in time. Designs in which the independent variable is manipulated at different points in time for time series are commonly called multiple baseline designs (Barlow et al., 1984; Barlow & Hersen, 1984).

There are two basic types of multiple baseline design. In a multiple baseline design across cases a phenomenon of interest is measured repeatedly in two or more cases and the manipulation of the independent variable occurs at different times for different cases. For example, Fig. 3 presents the example of a multiple baseline design across four communities that was used to evaluate a program to reduce illegal sales of tobacco to young people (Biglan et al., 1996b). The intervention involved merchant education, rewards to clerks who did not sell, and publicity for stores and clerks that did not sell. The dependent variable was the proportion of stores in each community that were willing to sell tobacco to minors. It was repeatedly assessed by having young people attempt to purchase tobacco in each store. The intervention was introduced into the first two communities, while a second pair of communities continued in baseline. Once there was a clear effect in the first two communities, the intervention was introduced in the second pair of communities. The procedure was evaluated in four other communities, also using a multiple baseline design across communities (Biglan et al., 1995); similar results were obtained. Averaging across all eight communities, the intervention produced a reduction in the percent of stores willing to sell tobacco from 57% at baseline to 22% during the intervention phase.

Fig. 3.

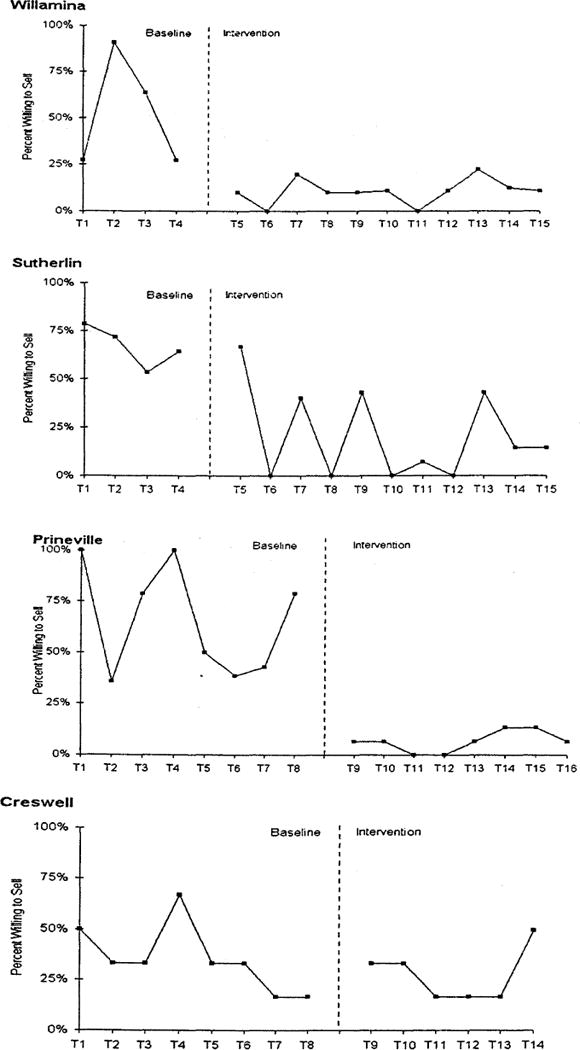
The proportion of tobacco outlets in each of four communities that were willing to sell to those under 18 before and after the implementation of a reward and reminder program.

The second type of multiple baseline design might be called a multiple baseline design within a case. Here two or more phenomena are measured repeatedly for a single case and the independent variable is applied to one of the phenomena at a time. For example, in evaluations of the effects of state policy changes in the 1970s and 1980s that raised the minimum age for drinking, effects on rates of single-vehicle, night-time traffic crashes were compared with effects on daytime and multi-vehicle crashes. Because we know most single-vehicle, night-time car crashes involve alcohol, and relatively few daytime multi-vehicle crashes do, if the higher legal drinking age reduced alcohol use by teens, we would expect to see reductions in teens’ involvement in single-vehicle night-time crashes but not in multi-vehicle daytime crashes (a result found in numerous states; O’Malley & Wagenaar, 1991; Wagenaar, 1983; 1986; 1993). Such time-series designs have been productively used for evaluation of numerous “natural experiments” involving changes in national, state, or local public policies.

One example of a multiple baseline design within a community would be an intervention to affect sales of tobacco and alcohol to minors, where the intervention initially targets tobacco sales and only later targets alcohol sales. Evidence that the intervention had an effect would be provided by an initial change in sales of tobacco that was not accompanied by a change in alcohol sales, followed by a change in alcohol sales when the intervention was applied to that problem.

One difficulty with such designs is that it is possible that the two or more phenomena that are being measured are inter-related in ways that cause all of them to change when the intervention is applied to one of them (Barlow & Hersen, 1984). For example, sales of alcohol to young people might change as a result of an intervention targeting sales of tobacco to young people. If this happens, one can have less confidence that the implementation of the independent variable brought about the change. In many instances, it will be necessary to accumulate evidence about whether two or more phenomena are interrelated in this way, before one can know whether such a design is feasible.

The strongest of multiple baseline designs combine multiple time series within geopolitical cases with time series across cases. For example, studies of the effects of the drinking age on alcohol related auto crashes compared time-series crash data within states. They looked at effects of drinking age on younger teens, older teens, and adults and they compared crashes that were likely to involve alcohol with those that were not—namely, night-time vs. daytime and single-vehicle vs. multi-vehicle crashes (Wagenaar, 1986). In addition, however, the studies compared the effects of changes in the drinking age in some states with other states in which the drinking age changed at a different time or did not change at all (O’Malley & Wagenaar, 1991; Wagenaar, 1993).

Barlow et al. (1984) have enumerated the comparisons that can be made in a multiple baseline design involving three time series to assess whether manipulation of the independent variable affects the dependent variable. First, within each time series one can examine whether the slope or level of the time-series changes when the independent variable is manipulated. Second, one can compare the change associated with manipulating the independent variable in the first time series with the change in the time series that did not receive a manipulation of the independent variable. When a change in the first series is coupled with the absence of change in the second two series, the inference that the independent variable brought about the change is strengthened. Third, in a three-series multiple baseline, the effect of the independent variable on the second series can be compared with the third time series. Replication of the effect in the second series, accompanied by no change in the unintervened third series, provides even stronger evidence of the effect of the independent variable.

Example of a Multiple Baseline Design across Communities

The Wagenaar team has initiated a new community trial using a multiple baseline design across communities. The design was motivated by the desire to address the problem of diffusion of the intervention into control communities that was described above. The Complying with the Minimum Drinking Age (CMDA) project is a multi-community time-series design. Intervention communities include a core city divided into 7 neighborhoods (by zip code), plus 10 suburbs (each an incorporated city). The comparison group consists of a similar core city with 10 neighborhoods, plus 7 suburbs. Rather than collection of two waves of data (pre/post) as is typically done in a conventional randomized community trial design, data are being collected biweekly in all the communities before, during, and after the 2-year intervention period. The resulting time-series measures will be correlated directly with the nature and intensity of intervention activities within each geographic unit in the trial. If intervention strategies diffuse from the intervention to comparison communities, they will likely be implemented in the comparison communities later than in the communities initially designated as intervention communities. The result is that in early phases of the project, intervention communities will have valid comparison communities by conventional standards, but later in the study, if comparison communities implement components of the intervention, they then can be treated as replications.

This design is employed because, despite researchers’ best efforts, we rarely can fully control community intervention implementation schedules. Therefore, assume community A implements in month 3, community B in month 9, community C in month 19, and community D in month 32, and community D turns out to have been initially labeled part of the “control” group. The time-series design allows each community to be treated as its own experiment, and its data to be compared with the other communities that had not implemented interventions during the same period. The fact that a subset or all of the “control” communities implement the intervention after it diffuses to them from the early successes in the intervention group does not threaten the validity of the design to the same degree as it would in a pre/post randomized trial. In short, in the CMDA trial, limited resources are allocated to obtaining hundreds of repeated measures over time, rather than allocated to collecting data and conducting the intervention in a set of communities widely dispersed around the country, in an attempt to obtain a “purer” control group. Moreover, in addition to knowing whether the intervention was successful or not (the typical result of a randomized trial), data on the differential effects of alternative forms of the intervention implemented in individual communities and implemented at different times will help advance knowledge on which components influence alcohol sales practices in communities.

ABA Designs

In these designs the intervention is introduced, withdrawn, and introduced again. If the level or slope of the dependent variable reliably changes in response to these manipulations, one can have increasing confidence that the changes are due to the manipulation of the independent variable. By convention, the A phase of the design is a baseline phase in which manipulation of the independent variable is not in force, while in the B phase it is. The design is also called a reversal design, because the influence of the independent variable is also tested by withdrawing it (the second A phase) and seeing if the effect of the independent variable is reversed. These designs have been used extensively in research on the effects of reinforcement on human behavior (e.g., Barlow et al., 1984).

The usefulness of ABA designs requires that it be possible to remove the effects of the independent variable and that such removal produce a reversal of the effect. For example, one might evaluate the effects of enforcement of access to tobacco laws by alternating periods of enforcement with periods in which they are not enforced. This might require a lengthy period of non-enforcement for the effect of enforcement to decay. Indeed, evidence about the time required for the effect to decay would be valuable.

Other Designs

There are a variety of other repeated time-series designs. All involve manipulation of an independent variable and observation of its effects on the time series. For example, in an ABAC design, the effects of different levels or different types of independent variables are evaluated. In an alternating treatments design, two different independent variables or two levels of an independent variable are alternated and the effects on the time series are examined. Barlow et al. (1984) provide detailed descriptions of the logic and procedures involved in these designs.

Systematic Replication in Interrupted Time-Series Experiments

It might be objected that in community intervention research, one is testing complex, multi-faceted interventions, often involving a series of efforts, and that it will be difficult to sort out which activities contributed to any changes that are observed. For example, to affect a practice in a community it may take 2 years of advocacy and numerous attempts to affect the targeted outcome. Practical experience suggests, however, that one emerges from the first effort with a good deal of clarity about how to streamline the intervention. Thus, in the second community, one can implement and test a more refined exemplar of the intervention. Moreover, once one has obtained evidence of an effect in one community, one can test the streamlined intervention (or the components presumed to be effective). For example, in the intervention to reduce illegal sales of tobacco to young people described above, we were fairly sure that merchant education in the absence of rewards to clerks and publicity for complying stores would not reduce sales, because in preliminary work we had tested the effects of merchant education alone and had observed no reduction in illegal sales. Thus, the addition of the rewards and publicity appeared to be critical.

This approach to teasing out the essential features of an independent variable is referred to as systematic replication (Sidman, 1960). As applied to community interventions, it involves systematically varying a component of a complex intervention to observe the effects of that component. In this way one can hone in on the minimum combination of activities that produce an effect.

Threats to Validity

Internal Validity

The essential purpose of any experimental design is to determine whether the independent variable of interest affects the dependent variable. Our confidence in the effect is a function of our ability to rule out other variables as contributors to the effect. This is a matter of the internal validity of the experiment. Cook and Campbell (1979) have delineated the most common extraneous variables that threaten internal validity. We will describe how the multiple baseline design in community intervention research controls for these threats.

History refers to events that co-occur with the intervention and might account for the observed change in the dependent variable. A multiple baseline design across communities only controls for historical events that occur across all communities. For example, statewide publicity about access or the modification of state law could affect all communities in the same state. Thus, if one community changes when the intervention is introduced while those remaining in the baseline phase do not, one can be confident that the change is not due to contemporaneous events that would affect the entire state. It is possible, however, that events could take place within a community that account for the effect in that community. For example, a prominent citizen dying of smoking-related cancer might make a special appeal to stop addicting young people. That might make the intervention far more powerful than it otherwise would be or might completely account for the effect. This possibility is addressed in the replication of the intervention in subsequent communities, since it would be extraordinary if such a confounding event occurred precisely at the point of intervention in every community.

Testing is a particular threat to validity in repeated time-series designs. Frequent assessment may, itself, have an effect on the measured process. For example, repeated assessment of public opinion in small communities might affect those opinions, independent of any influence of a community organizing or media campaign. The strongest evidence that repeated testing does not account for an effect comes from the demonstration of a clear change in level or slope of the measured process precisely at the point at which the independent variable is manipulated. If this change is accompanied by no change in the level or slope in other communities, it is likely the change is not due simply to repeated assessment. In addition, a long baseline that remains stable is evidence that testing does not account for changes, because if the level of the measure does not change with each additional assessment point, one becomes increasingly confident that the process of assessment is not affecting the measure.

Instrumentation refers to autonomous changes in the observers or changes in the measuring instrument over time. In the cited tobacco access study, for example, assessors might have been aware of the timing of the intervention. This might have influenced their expectations for more clerk refusals to sell tobacco, which could have subtly biased their interactions and brought that outcome about. Similarly, the social processes that lead to a change in law or policy in a community may also change how data about a behavior are taken. For example, publicity about the need for more youth activities, might prompt more organizations to characterize what they do as providing youth activities. Thus, it might appear that the change effort brought about an increase in youth activities, when it only increased the tendency of organization representatives to characterize their activities as targeting youth.

Instability refers to the variability in the repeated time series. To the extent that measures are highly variable, it is harder to detect the effects of an intervention. Much of the variability in a time series is systematic and predictable. Especially with an extended time series, the trends and cycles in a time series can be controlled statistically using methods such as Box-Jenkins modeling (Box & Jenkins, 1976). Nonetheless, uncontrolled variability is often a problem in time-series experiments. That variability could be due to unreliability of the measurements, but it may also reflect the fact that the process being studied is inherently unstable. In that case, it will be difficult to test the effects of an intervention until the sources of that instability are pinpointed and controlled.

Statistical regression refers to the tendency of extreme scores to regress toward the mean on subsequent measurement occasions. If a baseline measure is very high (or very low) we might conclude that a community intervention produced a change that was really due to regression toward the mean. Stable baseline data over repeated observations eliminates regression to the mean as a plausible explanation of change in the pattern of observed data. With a long time series, regression-to-the-mean effects can be modeled and estimated separately from the intervention effect.

Selection effects traditionally refer to preexisting differences between cases assigned to treatment and control conditions in group designs. They are a threat to internal validity, since they may account for what appear to be effects of experimental condition. Selection could be a threat in a time-series experiment if characteristics of the communities were somehow confounded with intervention. For example, it is possible that the difference that one observes between a community receiving the intervention and a community remaining in baseline is due to differences in the communities, not to the effect of the intervention. This is unlikely, however, if the control community baselines remain stable, while the intervention community time-series changes when the intervention is introduced. In addition, the subsequent replication of the effect of the intervention in the control communities provides further evidence.

An additional threat to the validity of interrupted time-series experiments concerns the control of the implementation of the independent variable. To the extent that the investigator cannot control when the intervention is implemented, it is harder to be sure that it was, in fact, that implementation that brought about observed change in the time series. For example, the control community might begin to adopt some or all of the intervention because of knowledge of its use in intervention communities or as a function of feedback or publicity about the level of the measured target variable. As a result the investigator might conclude that a change is underway anyway and that if they do not fully implement the intervention immediately, they will lose the opportunity to intervene at all. Studies of the effects of the implementation of policies such as changes in the drinking age (Wagenaar, 1986) are less than ideal for this reason; it is often hard to separate the effect of the political process and publicity that led to the law from the effects of the law.

The ideal time to implement the independent variable is when the baseline-time-series is stable (Barlow et al., 1984; Sidman, 1960), because it is more likely that any changes that follow implementation of the independent variable are due to the independent variable. However, this may often not be possible because the baseline is inherently unstable or because the time limited nature of the research project precludes long delays in intervention. Some might argue that the implementation of the independent variable should be determined at random. However, manipulating the independent variable at a randomly chosen point could lead to implementation at a point of instability in the time-series that could make it very difficult to discern whether the independent variable affected the dependent variable.

The primary concern with the analysis of internal validity is that one might conclude that an intervention or independent variable was responsible for the change in the measured time series, when the effect was, in fact, due to a confounding variable. However, these confounding variables can also obscure the effects of independent variables. For example, instability in a measure makes it harder to detect intervention effects.

External Validity

The external validity of an experiment is a matter of the extent to which observed effects can be generalized to other cases. This is a vital issue for building a science of general principles about the factors influencing community processes. The more generalizable the principles, the more they will be of assistance to other communities.

In keeping with the contextualist framework articulated, however, we should clarify that we are not saying that relationships between independent variables and dependent variables must be generalizable or that a relationship that can only be demonstrated in one or a few communities is not valid. Rather, we should take the failure to replicate a relationship in certain communities as a clue about the other variables—community characteristics—that moderate the relationships. For example, we might find that a relationship can be reliably demonstrated in small communities but not larger ones and proceed to study how community size affects the relationship.

The multiple baseline and other repeated time-series designs do not tell us a great deal about the generalizability of findings because the relationship is tested in only one or a few cases. The randomized controlled trial, on the other hand, directly tests the generalizability of the independent variable manipulation across the cases included in the design. Together the two methodologies provide a natural progression in the development and evaluation of independent variables. Multiple baseline designs can be employed to develop and sort through potentially effective intervention methods, followed by evaluation in randomized controlled trials both to test efficacy and to determine the extent of generalizability. As argued, the initial multiple baseline design studies can refine our understanding of the critical features of the independent variable and eliminate extraneous, ineffective components. Thus, these designs can help to develop strong interventions that can justify more extensive tests of their replicability using randomized controlled trials. If an intervention is found to produce an effect in the first community, but not the second, it will prompt further examination of the factors that moderate the relationship between the independent and dependent variables (Sidman, 1960). Thus, although the multiple baseline design allows one to test replicability only one community at a time, it may provide more information than a randomized controlled trial about the dimensions along which interventions can or cannot be generalized.

The Need to Distinguish Interrupted Time-Series Experiments from Quasi-Experimental Designs

Interrupted time-series experiments are often characterized as “quasi-experimental” designs (Cook & Campbell, 1979). This classification is unfortunate. To lump interrupted time-series experiments with designs such as one-shot case studies or simple pre-test–post-test only designs implies that time-series experiments provide far less valid evaluations of the effects of interventions than they actually do. This discourages the use of these designs.

As the review of an earlier version of this manuscript made clear, there are diverse opinions about how these designs should be characterized. Here, we offer several considerations.

First, there is a clear and strong tradition in behavioral approaches spanning animal behavior and clinical research to treat these designs as “experimental.” Indeed, the title of Barlow and Hersen’s book (1984) on the topic is Single Case Experimental Designs. It is certainly true that scientist who are not familiar with this tradition may reserve the term “experimental” for randomized trials, but if we brought biologists and physical scientists into the argument, those who view randomized trials as the only true experiment might be in the minority.

The underlying issue, of course, is the prestige associated with the term “experiment.” Within the scientific community, experiments are seen as preferable to “quasi-experiments.” And scientists have long wanted the public to give preference to policies and programs that have been experimentally evaluated. We cringe when policymakers adopt programs that have been evaluated (if at all) with quasi-experiments involving, for example, one-shot case studies. Thus, whether scientists call interrupted time-series designs experimental or quasi-experimental is quite consequential. It will affect the likelihood that they get funded and the likelihood that scientists, program planners, and policymakers will adopt programs and policies that are evaluated using such designs.

A fundamental question is whether evaluations involving repeated time-series experiments confer sufficient evidence about the effect of an intervention to warrant their adoption. In this regard, consider the decision of the APA task force on empirically supported clinical practices that equated evidence from interrupted time-series designs with evidence from randomized trials (see Chambless & Hollon, 1998). They concluded that a treatment program should be labeled “efficacious” if it is shown in at least two randomized trials, conducted by two different investigators, to be more efficacious than a control condition or if it was shown in two series of three interrupted time-series experiments, conducted by two different investigators to produce a significant effect on the target problem.

Finally, we would argue that to call these designs interrupted time-series experiments in no way confuses them with randomized controlled trials. We are not saying they are the same as randomized trials, only that they provide evidence about the effects of an independent variable that is superior to all other designs that have been labeled “quasi-experimental.”

Ironically, labeling these designs “quasi-experimental” may also undermine the movement toward selection of practices on the basis of sound empirical evidence (e.g., Chambless & Hollon, 1998). If interrupted time-series experiments are increasingly used to validate interventions, but they continue to be classed as quasi-experimental designs, it may encourage the belief that any quasi-experimental design provides sufficient evidence to validate an intervention.

STATISTICAL ANALYSES FOR TIME-SERIES EXPERIMENTS

Interrupted Time-Series Analysis

Statistical analyses of the effects of an independent variable on a time series are complicated by the dependencies that typically exist within the time series. Valid, ordinary, least-squares analysis is based on a number of assumptions regarding error residuals; they must be independent, normally distributed, random, and of constant variance (McCleary & Hay, 1980). It is the assumption of independence of residuals that is particularly problematic, because times-series data are typically autocorrelated. In other words the value of a measure at any given time t may be correlated with the value at time t-1, t-2, t-3, etc. Most such autocorrelations in community and policy research are positive (although negative autocorrelations are possible). For example, positive autocorrelations typically occur when measures are obtained on a monthly basis; if one month’s value is substantially above the mean, odds are that prior month’s value is also above the mean. Autocorrelations sometimes extend to relatively long lags. Staying with the example of monthly data, if this month’s value is substantially above the mean, odds are that the value for 12 months back is also above the mean, representing a significant positive lag-12 autocorrelation.

The typical consequence of positive autocorrelations is that estimated standard errors are biased low, leading to an overestimate of the statistical significance of an observed relationship or estimated intervention effect. For this reason, time-series analytic techniques have been developed for transforming the data to remove these dependencies before analyzing differences among conditions using the general linear model.

ARIMA Modeling

For long series, defined as approximately 50 or more repeated observations, statistical methods for transforming the data and estimating the effects of one or a few discrete interventions are well-developed. (See McCleary & Hay, 1980, for an accessible introduction and Glass et al., 1975 for a definitive account of ARIMA modeling in the analysis of time-series experiments.) The transformation of time-series data involves identifying a model of the dependencies among data points and then using that model to transform the data so that it eliminates the dependencies. The models are referred to as ARIMA models (Box & Jenkins, 1976), which stands for auto-regressive integrated moving average. The term “auto-regressive” refers to autocorrelation among time points. For example, a time series having two auto-regressive components would be one in which scores are predictable from the score one time-point before the score in question (a lag one autocorrelation) and from the score two time-points before the score in question (lag two). The moving average component involves each score in the time series being a function of the average of the error terms in a specified number of prior scores. Thus, an ARIMA model with an MA(2) component would be one in which the average of the error terms of the prior two scores predicted the scores in the time series.

The term “integrated” concerns the drift or trend that may be in the series (McCleary & Hay, 1980). In an ARIMA model one is seeking a residualized time-series that is stationary in the sense that it does not increase or decrease over time. Therefore, any trends and random drift (McCleary & Hay, 1980) in the series require transformation to meet this assumption. Trends or drift are typically removed through “differencing,” which transforms the values of a series (e.g., 1, 2, 3, 4) by taking the difference between each of the successive observations (e.g., 2-1, 3-2, 4-3). Typically, one such differencing procedure is adequate to remove trends in the data. It is possible, however, to difference the difference scores if a single differencing procedure does not remove the trend. It is also necessary that the residualized time series have the same variance across the entire series. Variance controlling transformations (e.g., log or exponential) can be used to decrease the extent to which variance varies across the time-series.

ARIMA models also often have parameters for seasonal effects. For example, monthly data on vehicle crashes or alcohol consumption typically has a peak in December. These seasonal effects are also modeled in terms of auto-regression, integrated, and moving average parameters.

Thus, the optimal ARIMA model may include auto-regressive terms, moving average terms, differencing operations, and log transformations that effectively yield small and nonsystematic residuals. Such models are referred to as ARIMA (p, d, q), (P, D, Q)_s, where p stands for the highest number of lags of the autoregressive parameter, d for the degree of differencing, q for the highest number of moving average components, and P, D, Q stand for the same parameters for any seasonal effect with a span of s, such as an effect from 12 months earlier in the time series.

The ARIMA approach to assessing the effects of an independent variable on the time series begins with building a model of the time series using only the baseline (i.e., pre-intervention) series. This model may involve autoregressive and/or moving average parameters, and it may involve differencing the series. The goal is to arrive at a model that accounts for all non-random trend or drift in the series. If the goal is met, the residuals will be entirely “white noise,” with no evidence of autocorrelation. Having identified a feasible model of the baseline data, that model is applied to the complete interrupted time series, and the intervention effect is added to the model, typically dummy-coded as 1 for the intervention phase and 0 for the baseline phase of the interrupted time series. A test for the difference between phases of the experiment can then be performed on these data using traditional statistics such as the t test.

This discussion has focused on the simple case of one time series with one dummy-coded intervention variable. However, the statistical methods directly generalize, permitting estimation of the effects of multiple intervention doses, multiple distinct types of interventions, while also controlling for the effects of multiple other time-varying covariates. With the increasing availability of several-hundred-observation-long time series, the potential knowledge gained from one complex model covering long time periods is immense.

Although the application of ARIMA modeling methods can be quite complex and painstaking, the resulting models are mathematically elegant and can provide a very satisfactory representation of the data. However, there is no guarantee that the model identified is necessarily the best model; there may be alternative models that can provide an adequate or feasible fit to the data. Many diagnostic tools are available to assess model quality.

Software for such models is now available in most standard statistical packages (such as SAS and BMDP) and is even easier with specialized time-series software such as SCA (Liu & Hudak, 1994). Simultaneous estimation of effects of many interventions while controlling for effects of many other continuous-variable covariates is an area of current methodological development. Vector ARIMA methods help address the issue of possible reciprocal causation (Enders, 1995), and hierarchical or multi-level analyses help address situations where many nonuniform replications of multiple interventions (policy changes across the 50 states, for example) provide the opportunity to systematically accumulate evidence regarding the underlying effect of each intervention.

Example of an ARIMA Analysis

The data in Fig. 2 were analyzed using ARIMA modeling (Wagenaar & Webster, 1986). It will be recalled that the data are for the rate of children 0 to 3 years old injured in car crashes in Michigan per 10,000 car crashes. The policy being evaluated was the requirement for child safety seats for children in this age range. The model which was found to fit the data was an ARIMA (0,0,5)(0,1,1)₁₂ as follows:

$$(1-B^{12})\mathrm{Ln}{Y}_t=(1+.359B+.334B^2+.305B^5)(1-.792B^{12})u_t-.208P_t-.314S_t,$$

where, B is a backshift operator (McCleary & Hay, 1980) such that B₁₂(Yt) = Yt_t-12, LnY_t is the natural logarithm of Y_t, u_t is a random error component, P_t is a pulse function representing the effect of publicity surrounding the enactment of the law that has a value of 1 for the 3 months preceding the law’s enactment and 0 otherwise, and S_t, is a step function with a value of 0 prior to implementation of the child restraint law and the value of 1 after the law took effect. The model was developed iteratively by repeatedly specifying a model, estimating it, and evaluating its adequacy, following Box and Jenkins’ (1976) criteria for model adequacy requiring that the model account for all significant autocorrelation patterns in the series. The dependent variable was log-transformed prior to estimating the parameters due to the variability in error variance across the series. A significant parameter for the step function indicated that the rate of injuries among children age 0 to 3 was significantly lower after the child safety seat requirement was introduced. The injury rate declined 27%.

Alternative Procedures

The primary limitations of the ARIMA approach are that it requires a lengthy series of observations to get estimates that approach stability, and the model identification procedures require considerable mathematical sophistication (Velicer & Harrop, 1983). As a result, a number of alternative methods of analyzing time series have been suggested.

Some methods that have been proposed for short series, such as the binomial approach and the C test (Tryon, 1982), are now known to be invalid, since they do not adequately control for autocorrelation and hence result in inflated type I error rates (Crosbie, 1993).

Another, more promising, alternative to the ARIMA models, the Interrupted Time-Series Experiment (ITSE) method, was developed by Gottman (1981). This approach evaluates differences in slope and intercept between the preintervention series data and the post-intervention series data, while including autocorrelation terms. The procedure produces an omnibus F test and subsequent t-tests for the effects on the slope and intercept. A Monte Carlo analysis of the procedure conducted by Crosbie (1993) showed that the procedure yields less biased results than the C test, but that the type I error rate is still inflated, owing to underestimation of positive autocorrelations.

Extending Gottman’s (1981) work, Crosbie (1993) developed a procedure for better estimating lag-1 autocorrelations for short series. A Monte Carlo study of his ITSACORR technique indicates that it does not produce inflated type I errors for short time-series. The approach appears promising for interrupted time-series studies of community intervention effects. Crosbie (1995) evaluated the power of the procedure to detect changes between phases of an experiment of 5 and 10 standard deviations. (An effect of five standard deviations is at the 25th percentile for applied behavior analysis journals and 10 standard deviations is at the median; Matyas & Greenwood, 1990). A Monte Carlo analysis of ITSACORR showed that regardless of the size of the autocorrelation, for N greater than or equal to 30, the power to detect an effect of five standard deviations is greater than .80. For a change of 10 standard deviations, the power is greater than .80 for a series having as few as 10 data points and any size autocorrelation (Crosbie, 1993).

A number of approaches to time-series analysis have been proposed that avoid the problem of model identification. Simonton (1977a) proposed simply assuming an ARIMA model in which there was a single autoregressive component. Harrop and Velicer (1985) found that the approach worked well in empirical evaluations of it.

Velicer and McDonald (1984) developed a general transformation approach in which the observed data points are transformed via the same transformation matrix for all cases. The numerical values of the elements of the transformation matrix are estimated for each problem. In most cases, no more than five non-zero weights are needed to adequately model the time series. Velicer and McDonald (1991) have shown that the approach can be generalized to the analysis of multiple cases. For example, the impact of an intervention across several communities could be analyzed simultaneously. A design matrix is specified that indicates the points in each time series at which an intervention effect is expected. It can also be used to specify tests for differences between communities in the size of the effect and can be used to specify particular patterns of post-intervention results for each community, such as decaying and sleeper effects.

Example of an Analysis Using ITSACORR

The data on illegal sales of tobacco to young people presented in Fig. 3 were analyzed using ITSACORR. Each data point represented the proportion of tobacco outlets willing to sell tobacco on that assessment occasion. For Willamina, the omnibus F test was significant, F(2,10) = 24.822, p = .000, as were the tests for change in intercept, t(10) = −7.389, p < .001, and slope, t(10) = 6.35, p < .001. The intercept was lower in the intervention phase, although the slope became more positive. For Sutherlin, the omnibus F test was not significant despite the fact that only one intervention data point was as high as any of the baseline data points. The variability in the intervention time-series undoubtedly was a factor in this outcome. For Prineville, the omnibus F test was significant, F(2,11) = 4.312, p = 0.041, and there was a significant reduction in the intercept, t(11) = −2.62, p = .024. The omnibus F for Creswell was not significant.

We also combined the data from all eight com munities to produce a single time-series of the average proportion of outlets willing to sell across the eight communities. An analysis using ITSACORR, indicated a significant omnibus F(2,12) = 3.904, p = .049 and a significant reduction in intercept, t(12) = −2.732, p = .018.

Aggregated Data within a Community

Often the data in a community intervention consist of aggregated data from numerous individuals or organizations. For example, one might have repeated reports of parents about their parenting practices both before and after the onset of a media campaign to affect parenting. Data on illegal sales of tobacco to young people described above consisted of the proportion of stores that sold at each time point. However, one could examine the willingness of each store to sell at each time point.

There are at least two statistical approaches that would appear appropriate for analyzing the data from individual cases within a community, rather than aggregating across cases. The approach of Velicer and McDonald (1991), described above, provides one approach to the problem. A design matrix can be created that specifies tests for the effect of the intervention for each case and tests for differences among cases in intervention effects.

Latent growth modeling (LGM) (McArdle, 1988; Meredith & Tisak, 1990) provides another useful method for analyzing intervention effects on individual cases. For example, suppose one has repeated assessments of young people’s reports of their parents’ parenting practices (e.g., Metzler, et al., 1998). LGM provides a means of analyzing the intercept and growth (linear, quadratic, etc.) of the measured variable for each case and assessing whether the introduction of an intervention was associated with changes in growth parameters. Moreover, the technique allows analysis of the correlates of growth parameters, including an analysis of individual differences in intervention effects. For example, one might find that gender, ethnicity, or initial level of problem behavior are predictors of changes in youth reports of parenting practices.

The question remains, however, as to when it is appropriate to analyze individual cases within the community. We suggest that it is appropriate whenever there is reason to believe that the intervention does not have a uniform effect across all cases. Kellam (1999) argues cogently that community intervention studies that fail to examine variation in development among cases are obscuring information that is vital to the refinement of intervention and the understanding of the factors that moderate the effects of our interventions.

Meta-Analysis

As the use of time-series data grows, there will be an increasing need to conduct meta-analyses of such studies. Impediments to doing so include the fact that many studies employing time-series data provide no statistical analysis at all (Busk & Serlin, 1992) and the fact that there is no agreed-upon metric for the effect size when statistical analyses are available (Allison & Gorman, 1993). The analytic method proposed by Velicer and McDonald (1984) would appear to provide a means of conducting meta-analyses for interrupted time-series experiments.

CONCLUSION

Interrupted time-series experimental designs have the potential to advance the science of community interventions. They provide valid tests of the effects of interventions much more cheaply than can be done in control group designs. They enable the refinement of interventions prior to their being tested on a wide scale. And they are ideally suited to the development of our theoretical understanding of the variables that influence processes in communities. Appropriate statistical methods for analyzing the results of interrupted time-series experiments are available. To the extent that the scientific community recognizes and accepts these designs, progress in community intervention research will accelerate. A critical step in the acceptance of these designs will rest with the newly reorganized behavioral science study sections of NIH. If the committees reviewing proposals for community interventions understand and appreciate the efficiency and validity of these designs, it will contribute greatly to the advancement of the science of community interventions.