Chemical Feasibility of the General Acid/Base Mechanism of glmS Ribozyme Self-Cleavage

Abstract

In numerous Gram-positive bacteria, the glmS ribozyme or catalytic riboswitch regulates the expression of glucosamine-6-phosphate (GlcN6P) synthase via site-specific cleavage of its sugar-phosphate backbone in response to GlcN6P ligand binding. Biochemical data have suggested a crucial catalytic role for an active site guanine (G40 in Thermoanaerobacter tengcongensis, G33 in Bacillus anthracis). We used hybrid quantum chemical/molecular mechanical (QM/MM) calculations to probe the mechanism where G40 is deprotonated and acts as a general base. The calculations suggest that the deprotonated guanine G40⁻ is sufficiently reactive to overcome the thermodynamic penalty arising from its rare protonation state, and thus is able to activate the A-1(2’-OH) group toward nucleophilic attack on the adjacent backbone. Furthermore, deprotonation of A-1(2’-OH) and nucleophilic attack are predicted to occur as separate steps, where activation of A-1(2’-OH) precedes nucleophilic attack. Conversely, the transition state associated with the rate-determining step corresponds to concurrent nucleophilic attack and protonation of the G1(O5’) leaving group by the ammonium moiety of the GlcN6P cofactor. Overall, our calculations help to explain the crucial roles of G40 (as a general base) and GlcN6P (as a general acid) during glmS ribozyme self-cleavage. In addition, we show that the QM/MM description of the glmS ribozyme self-cleavage reaction is significantly more sensitive to the size of the QM region and the quality of the QM-MM coupling than that of other small ribozymes.

INTRODUCTION

Riboswitches are RNA structural elements that typically occur in 5’-untranslated (5’-UTR) regions of mRNA in Gram-positive bacteria but are also found in other organisms representing all domains of life.¹ Their function is to regulate gene expression during transcription, translation, and splicing, usually in response to binding of a specific small molecule ligand.^2–10 Their mostly bacterial occurrence makes them attractive antibiotic targets.^11,12 The catalytic glmS riboswitch (henceforth referred to as a ribozyme) is located in a 5’-UTR of the mRNA coding glucosamine-6-phosphate synthase (glmS) in numerous Gram-positive bacteria. The expression of glmS, which catalyzes the conversion of glutamine and fructose-6-phoshate into glucosamine-6-phosphate (GlcN6P), is regulated by the glmS ribozyme upon binding of GlcN6P.^13–15 In contrast to other ribozymes, which typically undergo structural rearrangement upon ligand binding, resulting in either the formation of a terminator stem-loop to inhibit transcription or the sequestration of the ribosome binding site to inhibit translation, the glmS ribozyme does not undergo any detectable structural rearrangement upon GlcN6P binding.^14,16–18 Instead, GlcN6P binding activates site-specific self-cleavage of the ribozyme, which is followed by degradation of mRNA by RNase J1 and consequent down-regulation of glmS expression.^19,20 Thus, the glmS ribozyme is a unique model system, which acts both as a catalytic ribozyme and a riboswitch.²¹

Similar to other small self-cleaving ribozymes, the mechanism of glmS ribozyme self-cleavage involves nucleophilic attack of the A-1(2’-OH) hydroxyl group on the downstream phosphate of G1, which leads to formation of 2’,3’-cyclic phosphate and 5’-OH termini as products of the reaction.^22,23 During the reaction, the A-1(2’-OH) nucleophile is believed to be activated via deprotonation by a general base, possibly nucleotide G40, whereas the leaving group G1(O5’) is protonated by a general acid, possibly GlcN6P. GlcN6P is essential for the activation of glmS self-cleavage as it accelerates the cleavage rate constant by more than 10⁵-fold over ligand-free background decay.^14,19,24 Other ligands, e.g., glucosamine, serinol, L-serine, tris(hydroxymentyl)aminomethane, and ethanolamine, can also activate the self-cleavage reaction, albeit with diminished activity.¹⁹ By contrast, glucose-6-phosphate acts as a competitive inhibitor.¹⁹ These data strongly suggest that a primary amine with hydroxyl group in the vicinal position is required for glmS ribozyme activation. In addition, it has been shown that the cleavage rate depends on the pK_a of the ligand’s amino group. In fact, the pK_a of the GlcN6P amino group appears shifted toward neutrality in the context of the glmS ribozyme active site.^25–28 The apparent pK_as of both general acid and general base participating in the self-cleavage can in principle be elucidated from pH-rate profiles. In case of the glmS ribozyme, a sigmoidal (S-shaped) pH-rate profile was observed.²⁶ However, pH-rate profiles are notoriously ambiguous. Thus, while the most straightforward explanation of such a sigmoidal pH-rate profile is that the corresponding single apparent pK_a reports on the general base, it cannot be ruled out that the typical bell-shaped profile of a general acid/base mechanism appears sigmoidal since the pK_a of the general base lies beyond the measured pH range (in this particular case above pH ~9) so that the apparent pK_a in fact reports on the general acid.^{21,26,27,29,30}

Fedor et al. have suggested that the ascending part of the pH-rate profile with an apparent pK_a of 7.41±0.09 corresponds to the intrinsic acidity of the GlcN6P cofactor.²⁶ This ascending part of the pH-rate profile is less likely attributed to the deprotonation of G40 because the pK_a of an 8-azaG40 measured by pH-fluorescence profile equals 8.89±0.09, shifted up from its solution pK_a by ~0.7 units. Thus, the estimated pK_a of G40 is ~9.7.²⁹ Based on these observations, Fedor et al. concluded that G40 cannot act as the general base and rather participates in the reaction in its neutral form.²⁹ However, the ambiguity of pH-rate profiles allows for two interpretations of the experimental observations: (i) Either the pH-rate profile is indeed sigmoidal as G40 is not involved in any proton transfer (likely participating only in electrostatic stabilization of the transition state), so that the sigmoidal shape of the pH-rate profile attributes to the neutral amino group of GlcN6P acting as a general base; or (ii) the pH-rate profile is in fact bell-shaped (beyond the pH range measured), with a protonated GlcN6P and a deprotonated G40⁻ (or another general base with similar or higher pK_a) acting as general acid and base, respectively. Importantly, in crystal structures the amino/ammonium group of GlcN6P was found to be hydrogen bonded with the G1(O5') oxygen leaving group (see more details below). Taken together, these data support the view that GlcN6P acts as a general acid protonating the leaving G1(O5') group,²⁶ whereas a general base with a pK_a above ~9 activates the A-1(2-OH) nucleophile.

Analysis of the crystal structures of the glmS ribozyme from Thermoanaerobacter tengcongensis and Bacillus anthracis in the form of inhibited precursors (containing an inhibiting mutation, an active site occupied by a competitive inhibitor, or representing an apo-form), transition state analogs and products has revealed a rather rigid and structurally well-defined active site architecture.^31–34 Within this active site, G40 (according to T. tengcongensis numbering; G33 in B. anthracis) has been found to be within hydrogen bond distance of the A-1(2’-OH) nucleophile. In addition, the G40A mutation dramatically reduces the cleavage rate by five orders of magnitude, which is unlikely caused by any significant active site distortion because none is observed in the corresponding crystal structure.³¹ This implies an important catalytic role of guanine G40 in the self-cleavage reaction of the glmS ribozyme. It has been suggested that G40 may be deprotonated before the reaction to then act as a general base, accepting a proton from A-1(2’-OH) and activating the nucleophile.³⁵ Two alternative mechanisms were proposed wherein a canonical G40 is involved in electrostatic transition state stabilization, but does not directly participate in proton transfer. In particular, Ferre-D’Amare et al. suggested that the A-1(2’-OH) may be activated by two tightly bound water molecules shuttling the proton via the neutral amino group of the GlcN6P cofactor to the leaving G1(O5’) group.³¹ Alternatively, we noted that the non-bridging oxygens of the scissile phosphate may also act as general base to activate the 2’-OH since their pK_a is rapidly increasing upon nucleophilic attack on the phosphorous. The non-bridging oxygens may then either shuttle the proton directly to the leaving O5’ group and thus protonate it, or a different general acid may be involved in protonating the leaving group.³⁶

It is not always straightforward to analyze the catalytic pathways of ribozymes based on experimental structures. Precursor X-ray structures need to be inactivated and the reactive pre-cleavage states may utilize highly reactive but rarely accessed local conformations that are not captured by ground-state structures.³⁷ Our earlier classical molecular dynamics (MD) simulations of the glmS ribozyme suggested that the dominant protonation state under crystalline conditions contains the double-charged deprotonated phosphate moiety of GlcN6P, the protonated ammonium form of the GlcN6P amino group, and a canonical G40.³⁶ This was revealed by an analysis of differences between experimental structures and simulations testing different protonation states of the active site residues. The MD simulations thus supported a protonation state that at first sight did not appear to be consistent with catalysis. However, our results did not rule out participation of a deprotonated G40⁻ in catalysis. In principle, the catalytic mechanism could potentially proceed through a rare protonation state that is different from the ground state and is formed only transiently, provided that such a rare geometry is sufficiently reactive. The mechanism involving deprotonated G40⁻ would thus be chemically feasible if its reactivity compensates for the thermodynamic penalty arising from the rarity of the necessary protonation state of guanine at physiological pH and the associated instability of the active site arrangement.

In fact, our simulation results for the glmS ribozyme were reminiscent of the general base role of the deprotonated form of the active site guanine G8⁻ in the hairpin ribozyme. In the latter case, simulations suggested that a deprotonated G8⁻ is incompatible with the active site architecture observed in the crystal structures.³⁸ However, subsequent QM/MM calculations have indicated that the active site containing a deprotonated G8⁻ is sufficiently reactive to overcome the thermodynamic penalty arising from the rarity of the guanine protonation state, so that the mechanism involving G8⁻ can be considered a plausible reaction pathway for the hairpin ribozyme.³⁹ In other words, these mechanisms do not necessarily require a stable architecture of a rare active site ionization state that would be easily accessed by classical force field simulations. Instead, we propose that the reactions initiating these mechanisms may involve spontaneous but rare and transient (de)protonation of a specific active site moiety by solvent. Occasional formation of such an arrangement is then immediately followed by either a return of the system to the dominant protonation state, i.e., an unsuccessful reaction attempt, or the self-cleavage reaction. Alternatively, we also cannot rule out the possibility that the structures simulated with deprotonated guanines may be disfavored by the underlying force field approximations, such as inaccurate parameterization of van der Waals interactions or the neglect of polarization effects.⁴⁰ For an extensive discussion of force field approximations in molecular simulations of nucleic acids see, e.g., reviews in refs. ^41,42. The reliability of force field descriptions of protonated and deprotonated nucleobases in ribozyme active sites is a subject of our ongoing research.

In the present study, we focused on deriving a QM/MM description of the reaction mechanism of the self-cleavage reaction of the glmS ribozyme. Specifically, we tested whether the deprotonated active site guanine G40⁻ may promote activation of the 2’-OH nucleophile, and thus the self-cleavage reaction, with the ammonium group of the GlcN6P cofactor acting as the general acid.

METHODS

Molecular dynamics simulation

To identify the most plausible starting structures for subsequent QM/MM calculations, we performed explicit solvent MD simulation of the glmS ribozyme in its native form based on the available crystal structures (see ref. ³⁶ for details). In our earlier study of the glmS ribozyme, we identified the protonation state of the glmS ribozyme active site that is most consistent with the crystal structures. The active site was found to involve the canonical form of the catalytically important guanine G40 and ammonium form of GlcN6P with deprotonated double-charged phosphate moiety.³⁶ In the present study we performed new 100 ns long simulation of this dominant protonation state using the most recent all-atom ff99bsc0χ_OL3 RNA force field. This simulation was carried out using the GPU version of the AMBER 12 package.^43,44 The ff99bsc0χ_OL3 force field is based on the AMBER ff99^45,46 force field corrected by the Barcelona α/γ bsc0⁴⁷ and Olomouc χ_OL3^48,49 reparameterizations. Ff99bsc0χ_OL3 has been adopted as the standard AMBER RNA force field since 2010 and has been extensively tested.⁴² Note that this RNA force field is internally named ff10 in the AMBER code, which for RNA is also identical to the ff12 and ff14 internal AMBER force field abbreviations. As in the preceding study,³⁶ the starting structure for the present MD simulation was constructed by combining two crystal structures of the glmS ribozyme (PDB ID 2HO7; resolution 2.9 ų³ and PDB ID 2NZ4, resolution 2.5 ų⁴). We thus utilized the same protocol for the construction of the starting structure as used previously,³⁶ but employed a more recent force field and longer simulation time-scale.

A 100-ns MD simulation was carried out with the TIP3P explicit solvent model under Na⁺ net-neutral conditions (ion parameters: Na⁺ radius 1.369 Å and well depth 0.0874 kcal/mol⁵⁰). As in the earlier study, we included three structurally important Mg²⁺ ions (ion parameters: Mg²⁺ radius 0.793 Å and well depth 0.8947 kcal/mol).⁵¹ For these three ions, unequivocal experimental data have shown specific binding patterns.^33,34 Neutralization was then completed through the addition of monovalent ions. Note that divalent ions are generally poorly described by the approximate, non-polarizable force fields.⁵² Thus, in most cases their use in classical MD simulations should be avoided unless they play a significant structural role.^53,54 Hence, only the three abovementioned structural Mg²⁺ ions were included in the present simulation. The present simulation predicted a similar active site conformation of the glmS ribozyme as described in our previous work using the older force field version, and similarly showed only local conformational fluctuations within the active site that were significantly smaller compared to simulations of other ribozymes that we simulated in the past.³⁶ Subsequently, we selected five different representative snapshots with a high value for the catalytic in-line attack angle (O2’…P-O5’) as a set of starting structures for further QM/MM calculations. Since the simulation was carried out with the canonical form of the active site G40 according to the dominant protonation state, the guanine G40 was subsequently manually deprotonated and the systems were optimized in order to prepare the final starting structure for QM/MM calculations. The present study thus does not investigate the mechanism of G40 deprotonation. However, as the active site is accessible for solvent molecules, it can be assumed that the G40 can be deprotonated by solvent, either directly or by proton hopping through A-1(2’-OH) hydroxyl group.

QM/MM calculation setup

A two-layer ONIOM method⁵⁵ with electronic or mechanical embedding implemented in Gaussian09⁵⁶ was used for the QM/MM calculations. The MM region was treated by the ff99bsc0χ_OL3 force field. The QM region was described by density functional theory (DFT) methods.⁵⁷ The BLYP/6–31+G(d,p) level of theory was used for initial geometry optimizations and preliminary identification of the reaction coordinate. The more accurate hybrid-DFT MPW1K/6–31+G(d,p) functional (optimized for kinetics^58,59) was used for subsequent reoptimizations and calculation of the final energy profile (all energies henceforth correspond to MPW1K/6–31+G(d,p):AMBER(ff99bsc0χ_OL3) - referring to QM:MM levels of theory used within QM/MM description - with electronic embedding unless stated otherwise). Detailed information on the performance of these methods can be found in our recent article comparing different QM/MM methods for the description of RNA self-cleavage of the hairpin ribozyme.⁶⁰

As noted above, we studied the glmS self-cleavage using five different starting structures, mostly differing in the MM rather than the QM region. Initially, we fully explored the potential energy surface and identified the minimum reaction path based on one particular starting structure. Subsequently, we used the conformations of QM region for reactant and transition state obtained in this particular reaction path as initial guesses for subsequent reoptimizations for the remaining starting structures. Thus, we finally found five different reaction barriers that differed in the starting structure. We adopted the same QM/MM scheme that was applied in our recent studies of the HDV and hairpin ribozymes.⁴⁰

Size of the QM region

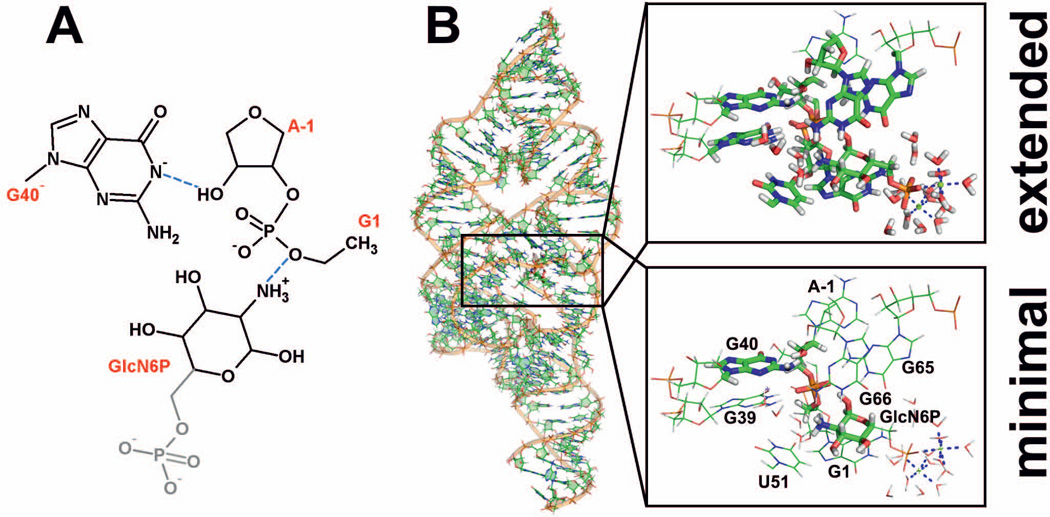
QM/MM calculations were performed using several variants of the QM region. Most of the calculations were carried out with a minimal QM region, which in this particular case comprised 65 atoms (Figure 1). It contained the deprotonated nucleobase G40⁻ capped by the C1’ methyl group, part of the GlcN6P cofactor without the methylphosphate group and part of the sugar-phosphate backbone ranging from the ribose of A-1 up to C4’ carbon of the G1 ribose. Hydrogen atoms were added to the dangling bonds at the interface between the QM and MM regions.

Figure 1.

(A) Schematic showing the minimal QM region used in most of our QM/MM calculations containing the C1’ methyl-capped deprotonated guanine G40⁻, part of the GlcN6P cofactor lacking its methylphosphate group (shown in gray), and part of the sugar-phosphate backbone ranging from the ribose of A-1 up to the G1(C4’) carbon. (B) Initial geometry used for the QM/MM calculations taken from our MD simulation with insets showing a magnified view of the minimal (bottom right) and extended (top right) QM regions represented as sticks.

To estimate the convergence of the calculations with respect to the completeness (size) of the QM region, we also performed large-scale QM/MM computations with an extended QM region, approaching the limits of contemporary computer facilities (see the Results and Discussion section for an analysis of the computational cost versus quality). More specifically, we calculated single-point energies using an extended QM region on the geometries optimized using the minimal QM region (for one starting structure only). This extended QM region included 248 atoms (Figure 1B, top) and involved the following additional segments and moieties: the complete GlcN6P cofactor, the 5’-terminus of A-1 forming a hydrogen bond with G40(O6), a C1’ methyl-capped G39 involved in type 4 base phosphate (4BPh) interaction⁶¹ with the scissile phosphate, an extension of the sugar phosphate backbone up to C2(O5’) including the complete G1 nucleotide (contributing to 4BPh interaction with the GlcN6P phosphate) and the C2 phosphate, a sodium ion bridging the C2 phosphate and G39(O6), a C1’ methyl-capped U51 forming a hydrogen bond with the ammonium group of the cofactor, a C1’ methyl-capped G65 hydrogen-bonding cofactor as well as the scissile phosphate, a G66 including its ribose moiety involved in interaction with G40⁻ and the A-1(2’-OH) nucleophile, two (solvated) Mg²⁺ ions located near the GlcN6P phosphate group, and additional 19 water molecules. In addition, we calculated corresponding single-point energies for two medium-sized QM regions between the minimal and extended ones to study the convergence of the barriers with increasing size of the QM region (see Supporting Information). Note that even for the second smallest QM region comprising 149 atoms, the SCF steps were too demanding so that we were not able to perform rigorous full QM/MM reoptimizations. However, we were able to complete partial reoptimizations (using loose convergence criteria) that allowed us to conclude that the geometries obtained using minimal QM regions were relevant for single-point calculations on larger QM regions since the observed geometrical changes during the partial reoptimization were rather small (see Figure S3 in Supporting Information).

In all QM/MM calculations, the ribozyme was immersed in a water droplet with an ~14 Å thick layer of water molecules surrounding the entire RNA molecule. The ~5 Å thick layer of water on the surface of the droplet and counter ions outside the droplet were kept fixed in space during all QM/MM calculations to prevent discontinuous changes in energy caused by hydrogen bond network reorganization at the water-vacuum interface. Note that using a fixed droplet surface, a sufficiently small step size in our potential energy surface scans, and careful optimization of each step are typically adequate to avoid the multiple-minima problem even with a relatively large portion of the system being optimized. The whole system contained ~33,000 atoms, of which ~15,700 were fixed.

Scanning of the potential energy surface

The reaction profile was explored by a set of flexible forward and reverse scans (lengthening and shortening of the A-1(O2’)…G1(P) and G1(P)…G1(O5’) distances, respectively) using 0.1 Å steps. All remaining degrees of freedom were fully relaxed at each point (except for the fixed water molecules at the surface of the water droplet, which were sufficiently far from the active site to prevent any structural bias). In addition, two-dimensional and three-dimensional scans across the potential energy surface were performed for accurate localization of the transition state as follows: i) a scan in the direction of nucleophilic attack of A-1(O2’) on the scissile phosphate and proton transfer from the A-1(2’-OH) hydroxyl to the deprotonated active site guanine G40⁻, and ii) a scan of both A-1(O2’)…G1(P) and G1(P)…G1(O5’) distances together with the second proton transfer from the ammonium group of the GlcN6P cofactor to the G1(O5’) leaving group. That is, we rigorously explored the potential energy surface through a few degrees of freedom of the active site conformation, while the remainder of the system was carefully relaxed.

Sampling in QM/MM scans versus QM/MM simulations

Carefully performed scans should typically provide a comparable level of sampling as more sophisticated QM/MM free energy simulations, except for the entropic contributions inherent to the few degrees of freedom that are biased (these contributions, however, are insignificant in this particular reaction; see discussion below). The explicit scan of key reaction coordinates provides complete information about the shape of the potential energy landscape in these coordinates, within the underlying structural context of the starting structure. By contrast, the perpendicular (orthogonal) degrees of freedom are sampled insufficiently in both QM/MM scans and QM/MM simulations. On the one hand, optimization scans do not sample these perpendicular degrees of freedoms. On the other hand, QM/MM simulations do in principle include such sampling, however, due to their enormous computational cost, the presently affordable QM/MM free energy simulations typically provide only a few picoseconds of unbiased dynamics of the perpendicular degrees of freedom. The accessible time-scale is too short to sample, e.g., other conformations of the ribozyme or ion positions distinct from those of the starting structure. Therefore, we posit that QM/MM scans should provide results that are not substantially inferior to those of short QM/MM free energy simulations, i.e., both methods are affected by the quality of the starting structures to a similar extent.

Limitations of entropy corrections

In our recent studies, we used an uncatalyzed reaction to estimate free energy corrections for QM/MM energies.^39,62,63 These terms are needed to correct the calculated (potential) energy reaction profile to yield the free energy profile, which includes the zero-point vibrational energy, the enthalpy correction to a finite temperature, and the entropy contribution derived from the standard harmonic oscillator approximation in the canonical ensemble.^39,62 The uncatalyzed reaction used in these studies utilized a small model of the sugar phosphate backbone outside the ribozyme but sharing the same mechanism as the pathway in the context of the full ribozyme. However, we found that, at least for the sugar-phosphate self-cleavage reaction, the corrections were rather negligible, typically contributing only 1–2 kcal/mol to the overall reaction barrier.^39,62 This observation was further confirmed by calculations on the hairpin ribozyme, where free energy landscapes obtained by semi-empirical QM/MM umbrella sampling simulations were similar to potential energy surfaces obtained by QM/MM optimizations (scans) using the same level of theory.⁶⁰ Thus, we propose that the entropic contribution to the barrier height originating from the QM region sampling is rather negligible and that energy barriers obtained by pure QM/MM optimization provide a reasonable estimate of the overall free energy barriers. In addition, we speculate that in this particular case the reliability of extrapolation of the free energy corrections from the uncatalyzed small model reaction may be rather limited because an estimation of the reaction energetics is significantly compromised by the inherent QM/MM inaccuracy caused by the electrostatic non-uniformity of the glmS ribozyme active site⁶⁴ (see also Results and Discussion). Thus, we decided to focus the major part of our efforts in the present work on optimizing the size of the QM region to improve the accuracy of the QM/MM energies.

Correction for the rare protonation states

As mentioned above, the total reaction barrier should include a penalty for the rare occurrence of the specific protonation state needed for a highly reactive active site. In our particular mechanism, we assumed that the active site guanine G40 is deprotonated prior to the reaction and that the amino group of the GlcN6P cofactor is protonated. The pK_a of the active site guanine and amino group of GlcN6P have been estimated as ~9.9²⁹ and 7.26,²⁵ respectively. The major protonation states under physiological conditions (pH~7) are therefore expected to be the canonical (neutral) form of G40 and an equilibrium of the ammonium and amino forms of GlcN6P, with the former protonated form slightly more populated. Thus, the energy of the precursor containing G40⁻ and the ammonium form of GlcN6P (which is the reference structure in our calculations), as well as all energies calculated along the entire QM/MM pathway (calculated with respect to this reference structure), had to be corrected for the presence of the minor equilibrium population of these protonation states (mostly due to the deprotonated G40⁻); then the state with zero Gibbs energy corresponds to the dominant rather than the rarely populated minor protonation state of the precursor. The corrections can be summarized as follows:

$$\mathrm{\Delta }{G}_{\mathrm{G}{40}^{-}}^{\text{corr}}=-RT\text{ln}10(\mathrm{p}\mathrm{H}-\mathrm{p}{K}_{\mathrm{a}}^{\mathrm{G}40})$$ (1)

$$\mathrm{\Delta }{G}_{\mathrm{G}\mathrm{l}\mathrm{c}\mathrm{N}6\mathrm{P}}^{\text{corr}}=-RT\text{ln}10(\mathrm{p}{K}_{\mathrm{a}}^{\mathrm{G}\mathrm{l}\mathrm{c}\mathrm{N}6\mathrm{P}}-\mathrm{p}\mathrm{H})$$ (2)

Hence, the total correction for the minor protonation states, where the dependance on pH cancels, can be written as:

$$\mathrm{\Delta }{G}^{\text{corr}}=-RT\text{ln}10(\mathrm{p}{K}_{\mathrm{a}}^{\mathrm{G}\mathrm{l}\mathrm{c}\mathrm{N}6\mathrm{p}}-\mathrm{p}{K}_{\mathrm{a}}^{\mathrm{G}40})$$ (3)

which is equivalent to 3.6 kcal/mol at 298 K.

RESULTS AND DISCUSSION

Energetics of self-cleavage: effects of the QM region size and the QM-MM coupling

In our QM/MM calculations investigating the self-cleavage of the glmS ribozyme, we focused on the possibility that the deprotonated active site guanine G40⁻ acts as a general base and activates the A-1(2’-OH) nucleophile, whereas the ammonium form of the GlcN6P cofactor acts as a general acid. We calculated the QM/MM energies along this pathway and derived the barrier height for five different conformations of the ribozyme and positions of counter ions to evaluate its energetic feasibility. The QM/MM approach is a well-established tool to map reaction paths of enzymes. Nevertheless, even sophisticated QM/MM methods are still based on numerous approximations, which make accurate evaluation of the energetics along the reaction path challenging. Since the glmS riboswitch contains a complex network of interactions contributing to catalysis, we used this system to perform several methodological tests. These tests also provide insight into the robustness of our results.

In our particular case, the main limitations of the QM/MM description of the reaction energy profile most likely stem from the description of the interactions between the QM and MM regions (see the comparison of different QM-MM coupling schemes below), and the sensitivity of the reaction barrier to the conformation of the MM region, mainly the arrangement of the entire ribozyme and positions of counter ions. Generally, two different schemes have been introduced for the description of the electrostatic interactions between the QM and MM regions: (i) electronic embedding (coupling, EE), in which the wavefunction of the QM region is polarized by the partial charges of atoms in the MM region, and thus the QM-MM electrostatic interactions are calculated at the QM level, and (ii) mechanical embedding (ME), in which QM-MM electrostatic interactions are described by classical Coulomb interactions between partial charges of the MM atoms and ESP charges (charges fitted to reproduce the electrostatic potential around the molecule) of the QM atoms.⁵³ The EE method is physically more justified as it explicitly includes polarization of the active site (QM region) by the entire ribozyme (as well as the solvent and co-solvent). However, in practice, the results may in some cases be seriously affected by over-polarization effects.⁶⁵ By contrast, the ME approach completely lacks inclusion of active site polarization, which may play an important role in the catalytic effect. Generally, the QM/MM energy profiles calculated by both approaches should converge with increasing size of the QM region. That is, the results obtained with electronic and mechanical embedding should converge to the same value once a sufficient fraction of the active site and its surroundings is explicitly included in the QM region.

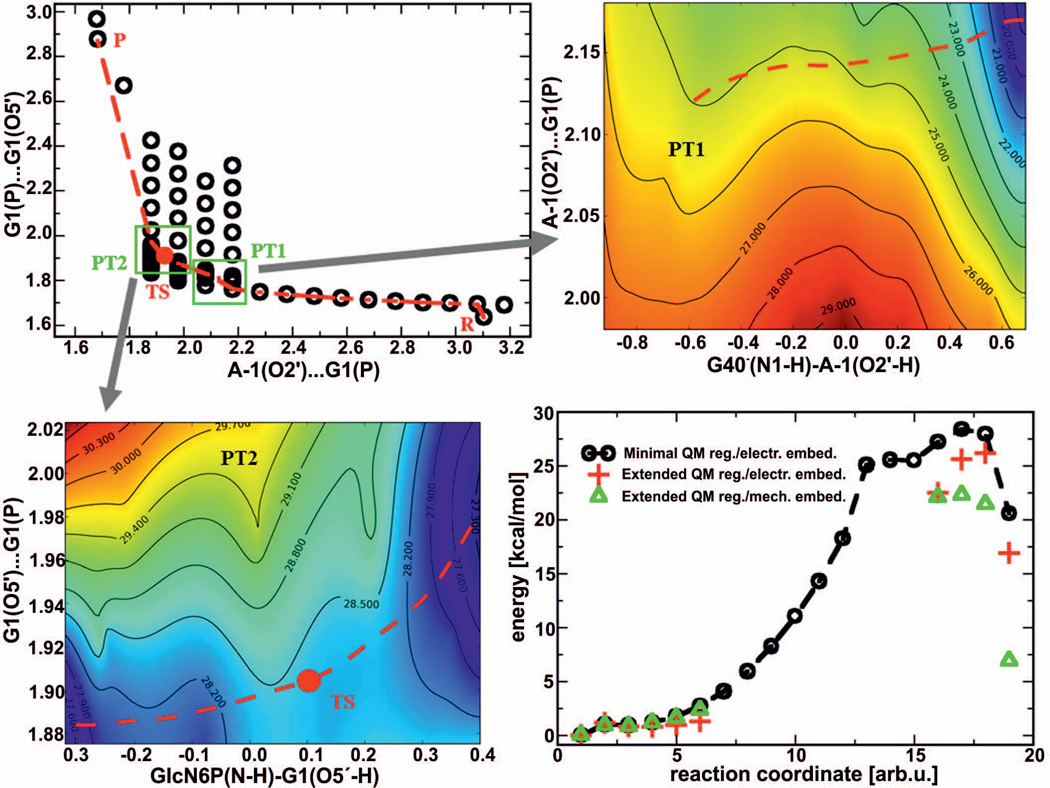
The effect of the QM-MM electrostatic coupling and the convergence of the energies with increasing size of QM region were tested on one particular starting structure. The QM/MM energies calculated for the smallest (minimal) and largest (extended) QM region (see Figure 1) with both embedding schemes are summarized in Table 1. For the minimal QM region, the EE and ME data are strikingly different. This suggests either the presence of significant polarization effects neglected by the ME description or a bias due to over-polarization when the EE is used. Most likely, both errors contribute to the difference and the correct energy values are expected to be in between those obtained by the two embedding schemes (likely closer to the value obtained by the more realistic EE).

Table 1.

QM/MM energies^a in kcal/mol, calculated using minimal (E_QM/MM,min) and extended (E_QM/MM,extend) QM regions with either electronic (EE) or mechanical embedding (ME).

State Embdedding	TS		P
	EE	ME	EE	ME
EQM/MM,min	32.0	11.2	24.2	−16.0
EQM/MM,extend	29.0	25.9	19.6	10.5

^aAll energies were corrected for the thermodynamic penalty of 3.6 kcal/mol due to the rare protonation form of the reactive state, i.e., the starting reactant (pre-cleavage) structure from which our scans were initiated was assigned an energy of 3.6 kcal/mol (see Methods).

The observed energy differences may be used as a rough estimate for the inaccuracies associated with the approximate nature of the QM-MM coupling. As mentioned above, the effect of the approximate description of the QM-MM coupling should decrease with the size of the QM region. Therefore, we progressively extended the size of the QM region and recalculated QM/MM single-point energies, using geometries along the reaction path obtained using the minimal QM region. In particular, we aimed to include all interactions that may significantly contribute to over-polarization and/or polarization of the QM region. Table 1 compares the data for the smallest and largest QM regions, while the remaining calculations can be found in Supporting Information. Notably, upon extending the size of the QM region the barrier height and relative energy of the post-cleavage state estimated by the EE decreased progressively, whereas the equivalent quantities calculated by the ME increased. In other words, the differences between the EE and ME descriptions were progressively reduced by increasing the size of the QM region. This was because the QM-MM interface was shifted further away from the area of the chemical reaction (see Table S1 and Figures S1–S2 in the Supporting Information). When the extended QM region had reached a size of 248 atoms, the gap between the EE and ME data had narrowed from the initial ~21 kcal/mol to ~3 kcal/mol for the barrier, and from ~40 kcal/mol to ~9 kcal/mol for the energy difference between the post-cleavage and pre-cleavage states. Thus, although we observed clear signs of convergence with increasing size of the QM region (see Figure S2), full convergence was not achieved even at the limit of our available high-performance computer cluster. We suggest that the remaining modest uncertainty between the EE and ME calculations of ~ ±1.5 kcal/mol for the TS obtained with the largest QM region can be used to estimate the inaccuracy caused by the remaining over-polarization and/or lack of QM region polarization in the EE and ME, respectively. In addition, the difference between the energy barriers obtained with the extended QM region (averaged EE and ME values, 27.4 kcal/mol) and the minimal QM region EE calculation (32 kcal/mol) may be used as an estimate of the systematic error due to the over-polarization when using EE calculations with the minimal QM region. In our particular case, this error equals −4.6 kcal/mol and we suggest to apply it as a correction to TS calculations executed using the minimal QM region with EE. Note that the likely least accurate ME calculation using the minimal QM region was excluded from this error estimation.

In order to also take into account the effect of the choice of starting structure on the barrier height, we calculated the reaction barriers using four additional, distinct starting structures (using minimal QM region and EE). The aim was to include sampling over different conformations of the MM region, particularly different conformations of the entire ribozyme and positions of the counter ions. As explained in Methods, such sampling cannot be captured even by common free energy QM/MM simulations using a single starting structure, because the unbiased MM region is sampled only negligibly in picosecond-scale simulation windows. Table 2 summarizes the reaction barrier and crucial distances averaged over these five independent QM/MM calculations, including an error estimation (we note that we reoptimized only the R and TS states in the calculations with additional starting structures). The reaction barrier shown in Table 2 includes the thermodynamic correction due to the rarely populated reactive state (3.6. kcal/mol, see Methods) and the correction for the systematic over-polarization of the minimal QM region (−4.6 kcal/mol, see the preceding paragraph) and is thus directly comparable to the experimental data (see Table 2).

Table 2.

QM/MM energies (kcal/mol) and key distances (Å) along the self-cleavage reaction path, i.e., for the pre-cleavage (R), transition (TS), and post-cleavage (P) states. The experimental reaction barrier is shown in the TS state column for comparison.

	R	TS	P
EQM/MMa	3.6	24.9±5.0	15.1±4.6
ΔG‡exp	-	17.2–22.6b	-
A-1(O2’)…G1(P)	3.1	2.0	1.7
G1(P)…G1(O5’)	1.6	1.9	2.9
A-1(O2’)…H	1.0	1.8	2.6
H…G40(N1)	1.8	1.0	1.0
GlcN6P(N)…H	1.0	1.3	1.8
H…G1(O5’)	1.8	1.2	1.0

^aThe energies of all states were corrected for the 3.6 kcal/mol thermodynamic penalty due to the rare protonation form of the reactive state. The TS energy was averaged over five calculations starting from different structures (see Table S2 in Supporting Information). The TS energy was further corrected by −4.6 kcal/mol to account for the inaccurate QM-MM coupling in the calculations using the minimal QM region. See Supporting Information for explanation of the error estimates.

^bThe range stands for the different rate constants reported for different conditions, namely in the presence of concentrations of 3 mM MgCl₂⁶⁶ and 30 mM MgCl₂²⁶.

Taking together all our QM/MM calculations, we estimate the barrier height to be 24.9 ± 5.0 kcal/mol. This includes the thermodynamics correction for the rare protonation states of G40 and GlcN6P, and a correction for the systematic error associated with the over-polarization in the minimal QM region with electronic embedding (see Methods, Table 2, Figure 2 and Supporting Information). This estimated range is higher than the barrier derived from the experimentally measured k_cat of ~93 min⁻¹ at 30 mM MgCl₂, corresponding to a free energy barrier of 17.3 kcal/mol at 298 K.²⁶ Notably, while our paper was under revision, another study reported a kinetic measurement at 3 mM MgCl₂ of a k_cat of 0.013 ± 0.003 min⁻¹, corresponding to a barrier of 22.6 ± 0.2 kcal/mol at 300 K.⁶⁶ Hammes-Schiffer et al. suggested in this study that 3 mM MgCl₂ is closer both to physiological conditions and to the concentration of divalents in the MD simulations. They thus suggested that the new experimental kinetic constant should be used for comparison with the theoretically calculated barriers.⁶⁶ However, such straightforward comparisons are not devoid of potential uncertainties. In particular, divalent ions do not directly participate in glmS ribozyme self-cleavage; they affect catalysis rather indirectly via facilitated GlcN6P binding and more compact RNA folding. Thus, the overall structure populated in MD, rather than a specific number of divalents, should be compared to the experimental conditions. Since glmS ribozyme MD simulations fluctuate around the starting structure, suggesting somewhat limited sampling, the snapshots derived by MD simulations and used in the QM/MM calculations may well reflect rather the ionic conditions used for crystallization, i.e., 30 mM MgCl₂ in this particular case. Thus, an unambiguous choice of experimental data to compare the theory with is not trivial.⁴² Taking into account all possible limitations of the theoretical calculations as discussed above, including the extraordinarily high sensitivity of the QM/MM energies to the QM-MM coupling and slow convergence of the energies with the size of QM region, there appears to be a reasonably good agreement between the experimentally measured kinetics and the calculated barrier. Due to the inherent limitations it is currently not realistic to achieve quantitative accuracy, yet we posit that the present calculations are sufficiently accurate to suggest that the reaction path of glmS ribozyme self-cleavage studied here is chemically feasible.

To understand the significance of the present work in the context of earlier studies, we note that our QM/MM calculations support the feasibility of a deprotonated active site guanine to play the role of general base in glmS ribozyme catalysis, consistent with our earlier work on the hairpin ribozyme.³⁹ However, in the present work we did not follow any other possible reaction scenario such as a monoanionic reaction path with the proton of A-1(2’-OH) shuttled via the non-bridging oxygen of the scissile phosphate to the leaving group 5’-oxygen.³⁹ Thus, our present work does not exclude alternative glmS ribozyme paths in which G40 acts in its canonical protonation form and stabilizes the catalytic geometry throughout the reaction. The nucleophile could then instead be activated, for example, by a solvent molecule (water or hydroxide ion since the A-1(2’-OH) is accessible to solvent), or by a non-bridging oxygen of a phosphorane intermediate/transition state arising during the nucleophilic attack. We also reiterate that, although the presently available computational methods allow for the identification of energetically feasible catalytic pathways, they are not sufficiently robust to compare different scenarios with quantitative accuracy. Coexistence of several competing micro-mechanisms therefore is a possibility that has been suggested for other ribozymes.³⁹

Sequential mechanism of nucleophile activation and nucleophilic attack

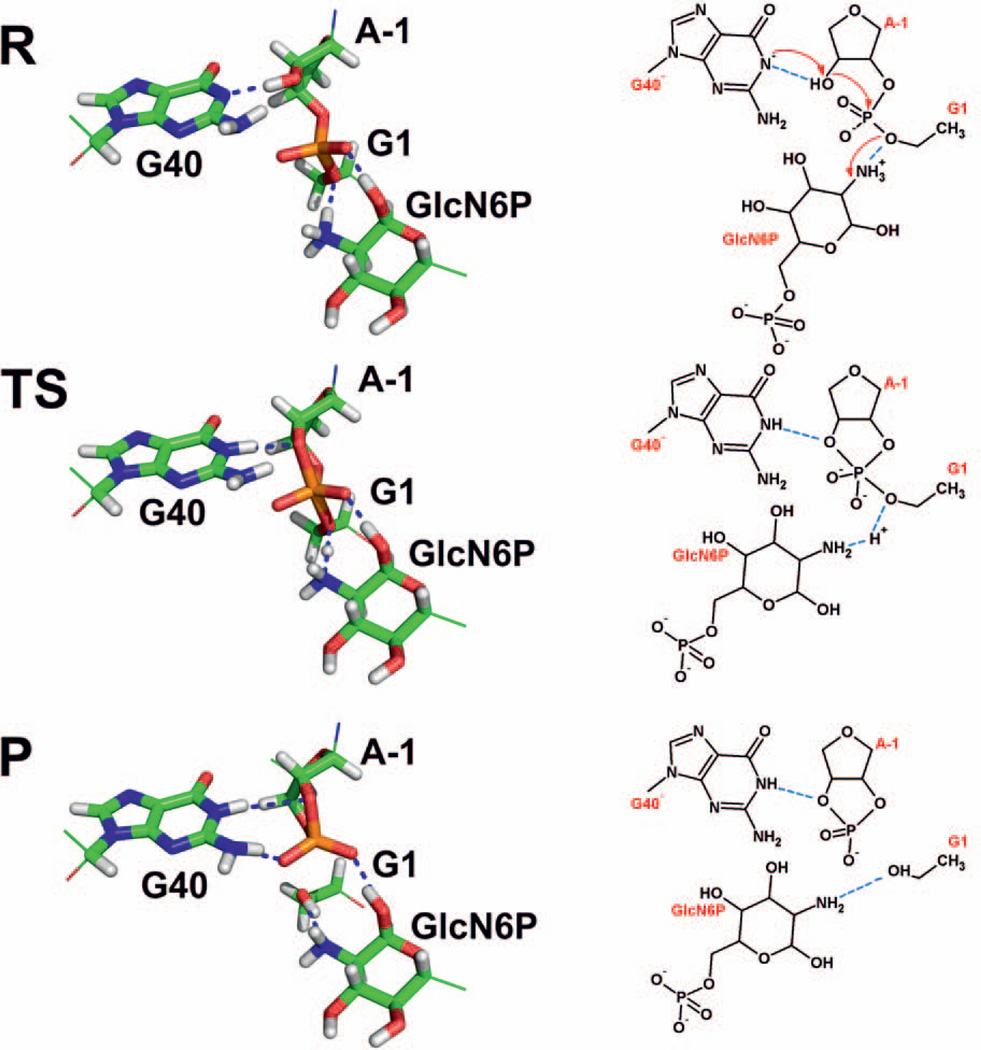
In the following, we discuss details of the reaction mechanism. In the initial part of the reaction, the pre-cleavage structure of the active site contains the deprotonated guanine G40⁻ and the ammonium form of the GlcN6P cofactor (structure R, Figure 3; see also Supporting Information for the structure of the QM/MM optimized pre-cleavage state). At the very beginning of the reaction, the deprotonated G40⁻ abstracts a proton from the A-1(2’-OH) nucleophile, and thus activates this group toward nucleophilic attack. Note that G40⁻ activates the 2’-OH at a G1(P)…A-1(O2’) distance of 2.15 Å (see Figure 2 top right). Thus, the 2’-OH group needs to be structurally shifted toward the scissile phosphate, presumably by thermal fluctuations, to overlap its orbitals with those of the scissile phosphate, which results in a decrease of its basicity. Although occurring at relatively short G1(P)…A-1(O2’) distance, the deprotonation of the A-1(2’-OH) nucleophile precedes the nucleophilic attack (Figure 2, top right and top left). Therefore, activation of the A-1(2’-OH) nucleophile and nucleophilic attack were identified as consecutive steps. A similar sequential mechanism of nucleophile activation followed by nucleophilic attack was found for the HDV ribozyme,⁶³ where deprotonation of the U-1(2’-OH) nucleophile was achieved via a hydroxide ion coordinated to an Mg²⁺ ion ([Mg(H₂O)₃.OH]⁺). It is worth noting that in both the HDV and glmS ribozymes, activation of the 2’-OH nucleophile was found not to be associated with the rate-determining step (with the highest barrier along the reaction path).⁶³ By contrast, a different mechanism was found to be energetically favored for the hairpin ribozyme, in which activation of the A-1(2’-OH) nucleophile via proton transfer to the deprotonated active site guanine G8⁻ and nucleophilic attack occur as simultaneous events and together represent the rate-determining step.^39,60

Figure 3.

Detailed QM region geometries (left) and corresponding schemes (right) obtained from QM/MM calculations for (i) the precursor state (R) containing deprotonated guanine G40⁻ and the ammonium form of GlcN6P, (ii) the transition state (TS) involving a canonical form of G40, i.e., the first proton transfer from A-1(2’-OH) to G40 is accomplished, whereas the second proton transfer from GlcN6P to G1(O5’) is under way, and (iii) the product (P) involving canonical guanine G40, the amino form of GlcN6P, and 2’,3’-cyclic phosphate and G1 5’-OH termini (see Supporting Information for the coordinates of all these three states). The red arrows in the R state scheme denote the flow of electron density during the reaction.

Figure 2.

Reaction pathway and the corresponding energetics (bottom right diagram) of the glmS ribozyme self-cleavage mechanism induced by the presence of the ammonium form of GlcN6P and activated by a deprotonated guanine G40⁻. The circles in the top left graph represent the sampling points on the potential energy surface along the path of nucleophilic attack, while the red line corresponds to the minimal energy path. The zoomed-in regions shown in the top right and bottom left plots correspond to proton transfers from the A-1(2’-OH) nucleophile to the deprotonated G40⁻ (PT1) and from the ammonium group of GlcN6P to the G1(O5’) leaving group (PT2), respectively. The contours in these graphs represent the uncorrected energies calculated with a minimal QM region with electronic embedding labeled in kcal/mol.

The rate-determining step relies on a general acid role of the GlcN6P cofactor

In contrast to the first proton transfer, i.e., the activation of the A-1(2’-OH) nucleophile, the second proton transfer, i.e., the protonation of the leaving G1(O5’) group by the ammonium group of the GlcN6P cofactor, was found to occur at A-1(O2’)…G1(P) and G1(P)…G1(O5’) distances of 2.0 and 1.9 Å, respectively (Figure 2 bottom left). This proton transfer thus appears to be concurrent with the nucleophilic attack (see Figure 2 top left, bottom left, and Figure 3). Notably, protonation of the G1(O5’) leaving group by the cofactor, which is simultaneous with the nucleophilic attack, corresponds to the maximum on the energy reaction profile and thus is associated with the transition state of the rate-determining step (Figures 2 and 3, and Table 1). That is, our calculations suggest that the cofactor is directly involved in the rate-determining step of the glmS ribozyme self-cleavage reaction as its presence or absence in the active site significantly influences the height of the highest reaction barrier, and thus the observed overall kinetics. The suggestion that the self-cleavage reaction may be directly induced by the presence of the cofactor is in accordance with the proposed mechanism of glmS ribozyme action, namely with the fact that the self-cleavage reaction ultimately relies on the presence or absence of the GlcN6P cofactor.^13–15 Importantly, this finding is consistent with the previously measured high value for the Brønsted coefficient of the reaction,²⁶ which indicates significant participation of the cofactor in proton transfer during the rate-determining transition state.

Electrostatic non-uniformity of the glmS ribozyme active site

The very large dependence of the results on the embedding scheme (Table 1) we observed here for the glmS ribozyme is quite unusual. No such sensitivity to the embedding or size of the QM region was found in our preceding studies of the reaction mechanisms in the HDV and hairpin ribozymes.^39,60,63 In particular, a detailed comparison of the EE and ME embedding for the hairpin ribozyme revealed almost identical potential energy surfaces for the self-cleavage reaction.⁶⁰ The present data, however, indicate that we in general cannot rely on such fast convergence of the results with the size of the QM core for all catalytic RNAs, and that the QM/MM description of the glmS ribozyme is especially challenging. We propose that that these observations are attributed to a more significant role of active site polarization in glmS ribozyme catalysis compared to the HDV and hairpin ribozymes.

We rationalize this large role of the QM-MM coupling for the glmS ribozyme compared to the HDV and hairpin ribozymes and the resulting difference in convergence of the QM/MM energies with the size of the QM region in the following way. The active site of the glmS ribozyme is electrostatically non-uniform. This non-uniformity appears due to the accumulation of several doubly charged moieties, such as the phosphate group of the GlcN6P cofactor and the adjacent two solvated Mg²⁺ ions in the active site (note that the HDV ribozyme contains only one Mg²⁺ ion in the active site and the active site of the hairpin ribozyme lacks divalent ions entirely). In addition, the GlcN6P, whose acidity critically affects the second proton transfer (and thus the barrier of the rate-determining step), contains a positively charged ammonium group on one side of the molecule and a doubly negatively charged phosphate on the other side, thus forming a sizable electric dipole. Therefore, it may act as an ‘antenna’ that is extraordinarily sensitive to the surrounding electrostatic field and consequently to the quality of description of this field in computations. This in turn may affect the acidity of GlcN6P and the reaction barrier height. Both of these proposed effects represent a challenge for a theoretical description since the catalyzed reaction may be significantly affected by long-range electrostatic interactions, accompanied by significant active site polarization effects. Our data suggest that the only way to accurately capture the polarization of the electronic structure of the active site without spurious over-polarization effects is to explicitly include a relatively large region surrounding the active site in the QM description, in our case 248 atoms. This makes computations very demanding, unless some computationally less expensive semi-empirical method is applied. Semi-empirical methods can, however, distort the potential energy landscape of the RNA backbone self-cleavage reaction and thus the computed reaction pathways.⁶⁰ Therefore, the description of the self-cleavage reaction of the glmS ribozyme remains computationally challenging and the energy profiles obtained should be regarded as likely less accurate than those of the HDV and hairpin ribozymes.

CONCLUSIONS

We report QM/MM calculations of the self-cleavage reaction of the glmS ribozyme, modeled as a general acid/base mechanism in which the active site guanine G40⁻ is deprotonated before the reaction. It then acts as a general base and the ammonium form of the GlcN6P cofactor acts as a general acid. The present calculations unambiguously support feasibility of this mechanism.

Our computations suggest that activation of the A-1(2’-OH) nucleophile via proton transfer from the 2’-OH hydroxyl to G40⁻ general base occurs when the A-1(2’-OH) group is already approaching the scissile phosphate, but still as a separate step that precedes the nucleophilic attack. In contrast, the nucleophilic attack occurs concurrently with the second proton transfer, i.e., protonation of the G1(O5’) leaving group by the ammonium group of the GlcN6P cofactor, and the concurrent transition state corresponds to the rate-determining step. Active participation of the cofactor in the rate-determining step is consistent with the Brønsted analysis published by Fedor et al.²⁶ In addition, our results imply that the presence of the GlcN6P cofactor in the active site of the glmS ribozyme is essential to facilitate the most critical step of cleavage, which helps explain the obligate ligand dependency of glmS ribozyme activity.

During the review process, an independent QM/MM study of glmS ribozyme self-cleavage has been published.⁶⁶ Both the reaction mechanism and the estimated barrier are consistent with our findings. Note that, although both QM/MM studies are based on similar DFT descriptions of the QM core, they differ methodologically in many significant aspects (see the discussion above) and use distinct starting structures. Thus, the convergence of the main results is encouraging for our ability to calculate reaction barriers of even challenging ribozyme reactions.

Our results also show that the glmS ribozyme differs (and appears to be more challenging) in its QM/MM description from the HDV and hairpin ribozymes, due to the electrostatic non-uniformity of its active site. This non-uniformity rationalizes the observed extraordinary sensitivity of the results to the QM-MM coupling method employed, as mechanical coupling likely neglects a significant portion of the active site polarization by the rest of the ribozyme, whereas electronic coupling tends to be distorted by an artificial over-polarization effect. Thus, QM/MM calculations of the glmS ribozyme require utilization of an unusually extended QM region, making the calculations computationally demanding. We have used calculations including 248 atoms in the QM core to obtain a correction for the data obtained with a smaller QM region of 65 atoms that was used for the basic analysis.

Finally, we emphasize that the present study explicitly investigates the feasibility of only one particular reaction scenario. Specifically, the computations start by assuming that G40 has already been deprotonated. The specific mechanism of its deprotonation is presently unclear and remains under further investigations. We also reiterate that classical MD simulations carried out so far indicate that the G40⁻ is not structurally stable in the active site. This, however, does not invalidate the G40⁻ general base mechanism for two reasons. First, the reaction can proceed via a rarely populated but highly reactive transient structure that may be very difficult to detect by classical simulations. Second, the non-polarizable simulation force field may be biased against binding of the G40⁻ in the catalytic center. However, since QM/MM data show that the activation of the A-1(2’-OH) nucleophile by G40⁻ is not directly involved in the rate-determining step, we cannot rule out other possibilities for the activation of the A-1(2’-OH) nucleophile.