Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2015 Aug 10;112(34):10651–10656. doi: 10.1073/pnas.1423035112

The collaborative roots of corruption

Ori Weisel a,1, Shaul Shalvi b,2
PMCID: PMC4553769  PMID: 26261341

Significance

Recent financial scandals highlight the devastating consequences of corruption. While much is known about individual immoral behavior, little is known about the collaborative roots of curruption. In a novel experimental paradigm, people could adhere to one of two competing moral norms: collaborate vs. be honest. Whereas collaborative settings may boost honesty due to increased observability, accountability, and reluctance to force others to become accomplices, we show that collaboration, particularly on equal terms, is inductive to the emergence of corruption. When partners' profits are not aligned, or when individuals complete a comparable task alone, corruption levels drop. These findings reveal a dark side of collaboration, suggesting that human cooperative tendencies, and not merely greed, take part in shaping corruption.

Keywords: cooperation, corruption, decision making, behavioral ethics, behavioral economics

Abstract

Cooperation is essential for completing tasks that individuals cannot accomplish alone. Whereas the benefits of cooperation are clear, little is known about its possible negative aspects. Introducing a novel sequential dyadic die-rolling paradigm, we show that collaborative settings provide fertile ground for the emergence of corruption. In the main experimental treatment the outcomes of the two players are perfectly aligned. Player A privately rolls a die, reports the result to player B, who then privately rolls and reports the result as well. Both players are paid the value of the reports if, and only if, they are identical (e.g., if both report 6, each earns €6). Because rolls are truly private, players can inflate their profit by misreporting the actual outcomes. Indeed, the proportion of reported doubles was 489% higher than the expected proportion assuming honesty, 48% higher than when individuals rolled and reported alone, and 96% higher than when lies only benefited the other player. Breaking the alignment in payoffs between player A and player B reduced the extent of brazen lying. Despite player B's central role in determining whether a double was reported, modifying the incentive structure of either player A or player B had nearly identical effects on the frequency of reported doubles. Our results highlight the role of collaboration—particularly on equal terms—in shaping corruption. These findings fit a functional perspective on morality. When facing opposing moral sentiments—to be honest vs. to join forces in collaboration—people often opt for engaging in corrupt collaboration.

Humans are an exceptionally cooperative species. We cooperate in groups that extend beyond the boundaries of genetic kinship even when reputational gains are unlikely. Such cooperative tendencies are at least partly driven by deeply ingrained moral sentiments reflected in a genuine concern for the well-being of others (1) and allow people to build meaningful relationships (2, 3), develop trust (4, 5), achieve mutually beneficial outcomes (6–8), and strengthen bonds with in-group members (9, 10). Furthermore, reciprocating others’ cooperative acts is essential for establishing long-term cooperation (11–13). Clearly, establishing sustainable cooperative relationships can set successful individuals and groups apart from less successful ones (1).

Whereas the benefits of cooperation are clear, little is known about its possible negative aspects (14). Our interest is in cases in which the collaborative effort of individuals working together necessarily and directly entails the violation of moral rules (here: lying), at a possible cost to the larger group, or the organization, to which they belong. In such cases there is a tension between two moral obligations: to tell the truth, and to collaborate. Are people prepared to accept the costs associated with violating moral rules (i.e., getting caught and punished, as well as the psychological costs associated with lying) to establish collaborative relations with others?

The answer is not trivial. On the one hand, as collaboration involves increased observability and accountability, reputational concerns may limit the willingness to violate moral rules. People may also shy away from lying in collaborative settings to avoid imposing undeserved, and potentially unwanted, profits on their partners, forcing them to become accomplices or “partners in crime.” On the other hand, a number of findings support the view that collaboration might have a liberating effect, freeing people to behave unethically. People lie more when it improves not only their own (14–16), but also others’ outcomes (17–21); when their lies benefit a cause or another person they care about (22); and group-serving dishonesty is modulated by oxytocin, a social bonding hormone (23). The idea that collaboration will increase dishonest behavior is in line with the functionalist approach to morality, which prescribes that people treat morality in a flexible manner, judging the same act as illegitimate or immoral in some cases, but legitimate or even moral in other cases, e.g., when it profits one's group members (24, 25).

Some collaborative settings may be more prone to corrupt behavior than others. In particular, corruption may emerge more readily when parties share profits equally. Indeed, equality is perhaps the most prevalent fairness norm (26–28); people are willing to pay a cost to restore it (29) and to punish others who violate it (30). Here, we conjecture that corrupt collaboration—the attainment of personal profits by joint immoral acts—would be (i) particularly prevalent when both interaction partners equally share the profits generated by dishonest acts, and (ii) more frequent than individual dishonest behavior in a comparable setting.

We experimentally examined corrupt collaboration using a novel sequential dyadic die-rolling paradigm. In seven treatments, participants (n = 280; 20 dyads per treatment; data collected in Germany) were paired and assigned to role A or B. In an additional individual treatment (n = 36) the same person acted in both roles (SI Appendix). As depicted in Fig. 1, each participant privately rolled a die and reported the outcome. Player A rolled a standard six-sided die first and reported the outcome by typing a number on the computer. Subsequently, player B was informed of A's reported number, and proceeded to roll a die and report the outcome as well. The information about B's reported outcome was then shared with A. The interaction was repeated for 20 trials.

Fig. 1.

Fig. 1.

Open in a new tab

Procedure for aligned outcomes (see SI Appendix for other treatments).

Die rolls were truly private, allowing participants to misreport the actual outcomes without any fear of being caught (31, 32). Such privacy is key to our design, as it reflects real-life situations in which cutting moral corners is difficult, if at all possible, to detect. Participants’ reported outcomes determined their payoff, according to rules that were explained in advance and varied between the treatments (Materials and Methods and SI Appendix).

In the main “aligned outcomes” treatment, participants earned money only if both A and B reported identical numbers (i.e., a “double”). In these cases each of them earned the reported numbers in euros (e.g., if both reported 4, each received €4). If the reports were not identical (i.e., not a double), neither A nor B earned any money. Reporting truthfully, the probability of rolling a double in a single trial is 1/6. The expected number of doubles reported by each pair in 20 trials is thus 3.33 (16.7%), and the mean report (of both A and B) is expected to be 3.5 ([1 + 2 + 3 + 4 + 5 + 6]/6). Fig. 2A shows a simulation of outcomes assuming such truthful behavior. As can be seen in Fig. 2B, however, reports in aligned outcomes were far from truthful (see SI Appendix, Fig. S10, for dyad-level figures). The 20 dyads reported 16.30 (81.5%) doubles on average, almost five times as much as the expected 3.33 assuming honesty (Wilcoxon signed rank: U = 210, P < 0.001; each dyad is a single observation). Corruption was not limited to inflation in the number of doubles. The mean reports of both A (5.02) and B (4.92) were significantly higher than the expected 3.5 (A: U = 208.5, P < 0.001; B: U = 171, P < 0.001), demonstrating that both parties—and not only player B—were dishonest.

Fig. 2.

Fig. 2.

Open in a new tab

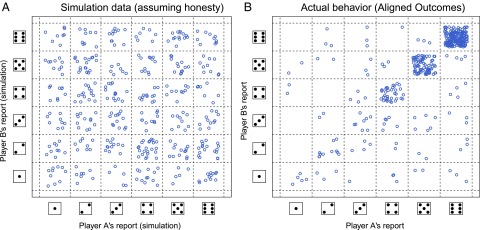
(A) Simulation of reported outcomes assuming honest reports. Each dot represents the reports of player A and player B in a single trial. The simulation assumes that each number (1 to 6) is reported with a probability of 1/6 in any given trial. The position of dots is jittered to allow visibility of identical outcomes. (B) The observed distribution of reported outcomes in aligned outcomes. Each dot represents the reports of player A and player B in a single trial. The position of dots is jittered to allow visibility of identical outcomes. High values on the diagonal—especially pairs of 6’s—which yield the highest payoffs, are overrepresented.

The organizational costs associated with lying are represented by the experimental budget, as common in experimental work studying dishonesty (31, 32). In the current setting the behavior of both players A and B affects these costs, but the situation is not symmetrical. Because player A can (only) “set the stage” by inflating his/her reports, but player B is the one who can “get the job done” by matching A’s report, the substantial organizational costs of corrupt behavior in this setting largely depend on player B. A dishonest player A can (only) increase the cost of reported doubles less than twofold, from an expected value of 3.5 (for a perfectly honest A) to a maximum of 6 (for a completely brazen A, consistently reporting 6’s). In contrast, when B lies in a totally brazen manner (i.e., always reports a double), the expected one-in-six likelihood of a double (assuming honesty) is shifted to a certain six-in-six (assuming full dishonesty), a sixfold increase. In aligned outcomes, 25% of A players and 50% of B players exhibited such brazen behavior (SI Appendix, Fig. S10).

To examine whether the degree to which incentives are aligned is related to the frequency of lying, we misaligned the incentives of A and B in a series of control treatments. Given B’s central role, we first focus on treatments that vary B’s incentives. A's incentives were kept as in aligned outcomes. Treatments B-high and B-low removed B's interest in the value of the double by having B earn a fixed amount—€6 or €1, respectively—if a double was reported, and nothing otherwise. Treatment B-fixed removed B's interest in reporting a double by having B earn a fixed amount of €1 regardless of whether a double was reported or not.

We expected that increasing B’s incentive to lie (B-high) will result in more reported doubles; decreasing B’s incentive to lie (B-low) will result in fewer reported doubles; and removing B’s incentive to lie altogether (B-fixed) will lower the number of reported doubles even more. Possibly due to the already high levels in aligned outcomes, the number of reported doubles in B-high (15.3 doubles per dyad) was a bit lower—but not significantly different—than in aligned outcomes (Mann–Whitney: U = 165.5, P = 0.34). As expected, the number of reported doubles was significantly reduced in B-low (12.2; U = 120, P = 0.028), and even more so in B-fixed (8.3; U = 64.5, P < 0.001; see Fig. 3).

Fig. 3.

Fig. 3.

Open in a new tab

Mean number of reported doubles and percentage of (totally) brazen B players per treatment. Mean number of reported doubles (Left vertical axis): the dotted line is the expected number of doubles assuming honesty (3.33); error bars are ±1 SE; mean and SD are at the Bottom of each bar; significance indicators: *P < 0.05. The number of doubles exceeded the honesty baseline in all treatments. Collaboration on equal terms (aligned outcomes) led to more reported doubles relative to individual behavior. Changes to the payoffs of either A or B had a very similar effect on the number of reported doubles. There were more brazen B players in aligned outcomes than in the other treatments (Right vertical axis).

The number of doubles in B-fixed was still more than twice the 3.33 that would be expected assuming honest behavior (U = 185, P = 0.003), demonstrating that B players are willing to lie even when only A players profit from it. Nevertheless, B-fixed is promising for an organization seeking to reduce corruption costs by providing an alternative to aligned outcomes as a way to compensate employees. In aligned outcomes, each player earned €4.28 per trial, for a total of €8.56 in organizational costs. Considering that the expected cost, assuming that both players A and B are honest, is €1.16 (1/6 × €3.5 = €0.58 for each player), this represents a “corruption excess” of €7.4. In B-fixed, B players earned exactly €1 per trial, and A players earned only €1.80 per trial (there were fewer doubles, and the average value of the doubles was lower), for a total of €2.80 in organizational costs, or a corruption excess of only €1.64, a 78% reduction relative to aligned outcomes. Clearly, B-fixed is superior to aligned outcomes from the organization’s perspective.

Given that B’s selfish incentive to report a double was removed in B-fixed, it is perhaps not surprising that the number of reported doubles was reduced relative to aligned outcomes. That reduction notwithstanding, B-fixed—at least at face value—is attractive from B’s perspective compared with the aligned outcomes setting. Consider a potential employee who is negotiating employment terms, and is given a choice between a self-reported performance-based salary, similar to aligned outcomes, and a fixed salary, similar to B-fixed. In this initial negotiation phase, the potential profits the employee may reap by engaging in corrupt behavior in aligned outcomes are not officially “on the table.” The only thing to consider is the expected value of the two settings assuming honest behavior; otherwise, the employee would be signaling an intention to behave dishonestly in the future, reasonably terminating the organization’s willingness to offer this person a job altogether. The expected payoff—assuming honesty—from a single trial under aligned outcomes is €0.58 (see above); a guaranteed €1 per trial is clearly a better deal, unless an employee has dishonest intentions and is willing to communicate those to the employer by rejecting a 72% payment increase (from €0.58 to €1). Offering B-fixed as an alternative compensation program to aligned outcomes not only reduces costs, but also provides the organization with a useful screening tool to detect people with dishonest intentions.

In some cases people work alone. Do people lie more when collaborating than when working alone? Additional participants (n = 36) played the role of both A and B (i.e., each participant rolled and reported twice). Individuals reported 11.0 doubles (55%) on average, significantly fewer than dyads in aligned outcomes (Mann–Whitney: U = 187, P = 0.003), showing that collaborative settings indeed liberate people to lie more than when they work alone. This finding suggests that organizations may be paying a (corruption) premium for having their employees team up and work together. The modest dishonesty estimates observed in past work (31–33) may have been conservative in comparison with settings in which people work in collaboration.

Player A’s incentive to report a double was varied in three additional control treatments—A-high, A-low, and A-fixed—that mirror the variations to B’s incentives in B-high, B-low, and B-fixed. B's incentives were kept constant as in aligned outcomes. Would these changes to A’s incentive structure affect the frequency of reported doubles to the same degree as (the same) changes to B’s incentives? Because B is the one determining whether a double is reported (or not), changes to A’s incentives should have a smaller impact—if any—on the amount of reported doubles. Surprisingly, however, the impact of changes in A’s incentives on the likelihood to report a double was nearly identical to that of changes in B's incentives (A-low vs. B-low: U = 176, P = 0.52; A-high vs. B-high: U = 197, P = 0.95; A-fixed vs. B-fixed: U = 160.5, P = 0.29; Fig. 3).

An important difference between the aligned outcomes setting and the other (control) treatments is the propensity of B players to behave in a brazen manner (i.e., to report a double in each and every trial). In many situations, people tend to avoid brazen immoral behavior, offsetting the psychological costs of immoral behavior by engaging in moral behavior as well (31, 33), a pattern observed in our control treatments. In aligned outcomes, however, the behavior of B players took a rather brazen form. Whereas the likelihood of honestly rolling a double in each and every one of the 20 trials is 2.7 × 10−16, this occurred in 10 of 20 cases in the aligned outcomes setting. Half of the B players in aligned outcomes behaved in a totally brazen manner, making no effort at all to even remotely suggest truthful reporting. See Fig. 4 for examples of such brazen behavior, which was more common in aligned outcomes compared with all other dyadic (15%; Fisher’s exact test: P = 0.001) and individual (19%; P = 0.03) settings (Fig. 3). Collaboration on equal terms, it seems, liberates people to turn corrupt by reducing the psychological costs associated with brazen lying.

Fig. 4.

Fig. 4.

Open in a new tab

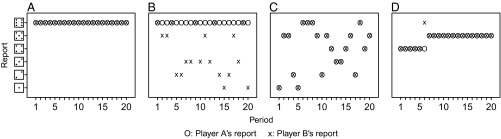
Four prototypical dyads. The horizontal axis represents the 20 trials; the vertical axis represents the die roll outcomes; an “O” represents player A’s report; and an “X” represents player B’s report. (A) A brazen dyad, reporting a “double 6” 20 times; (B) player A is brazen, player B appears honest; (C) player A appears honest, player B is brazen; (D) corrupt signaling. After mutual reports of 4 in the first five trials, A reported a 4 once more, but B replied with a 6, arguably to suggest to A that switching to higher numbers would be more profitable.

The finding that changes in A’s incentives affect the number of reported doubles suggests that B players are sensitive to the incentives, and possibly behavior, of A players. To test this notion, we classified each player as either brazen (i.e., A players reporting “6” 20 times; B players reporting 20 doubles) or not, and compared the proportion of brazen B players who were matched with brazen vs. nonbrazen A players. If players A and B have no effect on each other’s behavior, the likelihood of B being brazen should be independent of whether A is brazen or not. If however, players A and B do affect each other’s behavior, the likelihood of B being brazen should be higher when A is brazen as well. This is indeed what we found. In the aligned outcomes treatment, 100% of B’s were brazen when A was brazen as well (5 of 5 cases). When A was not brazen, the proportion of brazen B’s was only 33.33% [5 of 15 cases; χ2 (1) = 6.67, P < 0.01]. This pattern was attenuated in all other treatments where the proportion of brazen B’s when A was brazen as well was 36.36% (4 of 11 cases), compared with 12.84% (14 of 109 cases) when A was not brazen [χ2 (4) = 26.50, P < 0.001; the result holds also when excluding the A-fixed and B-fixed treatments].

The fact that B’s were more likely to turn brazen when A was brazen suggests that people perceive their counterpart’s brazen behavior as an “invitation to lie” (i.e., a signal) that justifies their own corrupt behavior. It is especially interesting that this association between the two party’s brazenness is stronger in aligned outcomes than in the other treatments. When incentives are perfectly aligned, one party’s brazen behavior is more likely to be picked up and serve as justification for the brazen behavior of the partner. More generally, this result suggests that (corrupt) signals are easier to interpret when outcomes are aligned.

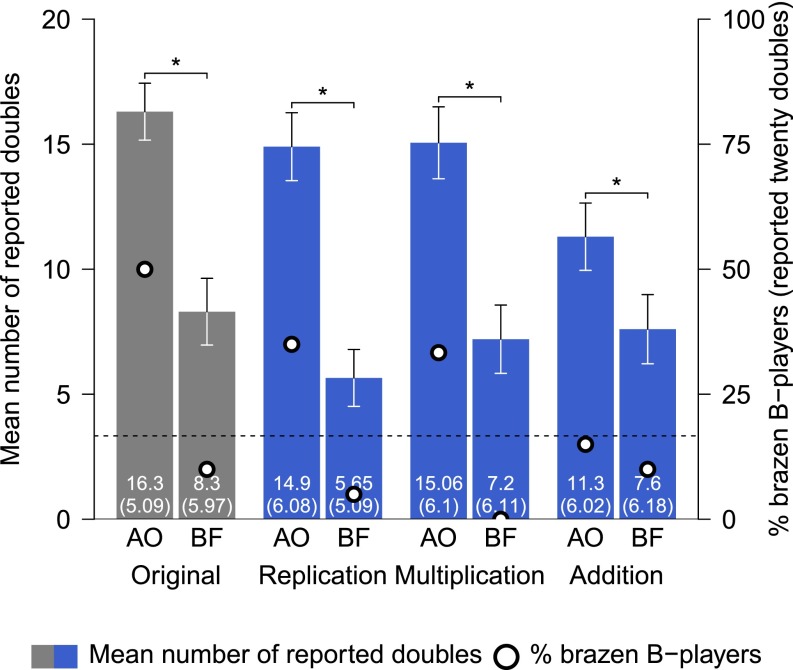
A possible concern is that our findings are idiosyncratic to particular characteristics of the experiment, namely the location and the stakes we used. To assess the robustness of our results, we conducted an additional experiment (n = 236) in the United Kingdom, with three variations of the original aligned outcomes and B-fixed treatments: replication, multiplication, and addition. The replication treatments (n = 80, 20 dyads per treatment) directly replicated the original aligned outcomes and B-fixed treatments (the only difference was using British pounds rather than euros). In the multiplication treatments, all payoffs were doubled (e.g., a double of 4’s yielded £8). In the addition treatments, £2 were added to all payoffs (e.g., the payoff for a double of 4’s was £6).

The results are displayed in Fig. 5. As in the original experiment, in all treatments (replication, multiplication, and addition) more doubles were reported in aligned outcomes than in B-fixed (P < 0.001, P < 0.001, P = 0.03, respectively). Despite the different subject pool, the absolute levels of dishonest behavior in the replication treatments were very similar to those in the original experiment (aligned outcomes: U = 167.5, P = 0.37; B-fixed: U = 145, P = 0.14). Furthermore, multiplying the payoffs by 2 did not affect the number of reported doubles (aligned outcomes: U = 178.5, P = 0.98; B-fixed: U = 177; P = 0.54; comparison between replication and multiplication). These results are consistent with past work in individual settings, which found that increasing the stakes does not affect lying rates (32, 33). The replication and multiplication settings are also similar in that in both, we observed more brazen behavior in aligned outcomes than in B-fixed (30% vs. 5% and 33% vs. 0%, respectively; both P < 0.05), again replicating the results obtained in the main experiment. Finally, further replicating the original results, in both the replication and multiplication versions of aligned outcomes there were more brazen B players when A was brazen (5 of 7; 71%), compared with when A was not brazen [7 of 33; 21%; χ2 (1) = 6.94, P = 0.008]. In B-fixed there was only one brazen A player, not allowing for a meaningful analysis of the way A's brazen behavior is related to B's brazen behavior.

Fig. 5.

Fig. 5.

Open in a new tab

Robustness treatments. Mean number of reported doubles and percentage of (totally) brazen B players per treatment. Mean number of reported doubles (Left vertical axis): the dotted line is the expected number of doubles assuming honesty (3.33); error bars are ±1 SE; mean and SD are at the Bottom of each bar; significance indicators: *P < 0.05.

In the addition setting, the pattern was somewhat different. Relative to the replication setting, there was less lying in aligned outcomes (the difference is marginally significant; U = 136, P = 0.08), but not in B-fixed (U = 157.5, P = 0.25). Further, aligned outcomes and B-fixed did not differ in the rates of brazen behavior (15% vs. 10%, P = 0.63). Because only one A player was brazen in the addition setting (aligned outcomes and B-fixed together), it was not possible to analyze whether A's brazen behavior was related to B's brazen behavior. The results from the addition setting suggest that even if the absolute incentive to lie and report a double remains unchanged, earning at least something rather than nothing, in case of failure to report a double, can reduce the likelihood of brazen lying and may limit the emergence of corrupt collaboration. From the point of view of an organization seeking to reduce corrupt behavior, assuring a decent base salary that does not depend on performance can reduce the likelihood that its employees engage in brazen lying.

The current work reveals a dark side of cooperation: corrupt collaboration. A collaborative setting led people to engage in excessive dishonest behavior. The highest levels of corrupt collaboration occurred when the profits of both parties were perfectly aligned, and were reduced when either player’s incentive to lie was decreased or removed. These results suggest that acts of collaboration, especially on equal terms, constitute “moral currencies” in themselves, which can offset the moral costs associated with lying. Paradoxically, the corrupt corporate culture and brazen immoral conduct at the roots of recent financial scandals (34) are possibly driven not only by greed, but also by cooperative tendencies and aligned incentives. In conclusion, when seeking to promote collaboration in our organizations and society, we should take note that in certain circumstances cooperation should be monitored, rather than encouraged unambiguously.

Materials and Methods

In the main experiment, 316 undergraduate students (56% females; Mage = 24.39, SDage = 4.84) were recruited using ORSEE (35), and took part in 11 experimental sessions, each consisting of between 20 and 32 participants, and lasting less than 1 h on average. The experiment was conducted in accordance with the ethics guidelines of the Max Planck Institute of Economics in Jena. All participants read and signed an informed consent before the experiment. We used a within-session design, meaning that all eight treatments (aligned outcomes, B-high, B-low, B-fixed, A-high, A-low, A-fixed, and individuals) took place simultaneously in the same session. Participants were given general instructions on paper, and treatment-specific instructions were presented on screen.

The general instructions, which were read out loud by an experimenter, informed participants that they will engage in a study composed of three stages. Each stage was explained separately once the previous stage was completed. Participants learned that they will earn money based on their performance in each of the three stages. In the first stage, participants learned that they will engage in a die-rolling task in which the amount of money they will earn depends on the results of two die rolls. Following the general instructions, participants received on-screen treatment-specific information about the rules determining their payoff (according to the treatment they are assigned to; see “treatments” below). To ensure proper understanding, participants were instructed to roll the die a couple of times and type in the results. They received feedback about the payoffs associated with these rolls, according to the relevant rules. After indicating they understood the rules, participants were paired (except those in the individual treatment), and played one period of the die-rolling task for actual payoffs. Upon completion of the first stage, participants were informed that in the second stage they will engage in up to 30 additional periods with a different partner, and that they will be paid according to the results of one of these periods, which will be randomly selected. In reality there were always 20 additional periods.

We varied participants' payoffs in eight between-subjects experimental treatments (n = 40 in each of the two-person treatments; n = 36 in the individual treatment). In the main aligned outcomes treatment, if both A and B reported the same number, each earned that number in euros (i.e., if both reported 1, each earns €1; if both reported 2, each earns €2; etc.). In the cases they reported different numbers, they earned nothing. In six control treatments the payoff of either A or B was varied. In treatment A-high (B-high) A (B) earned €6 if a double was reported (regardless of the value of the double), whereas B (A) earned the value of the double as in aligned outcomes. In treatment A-low, A (B) earned €1 if a double was reported (regardless of the value of the double), whereas B (A) earned the value of the double as in aligned outcomes. In treatment A-fixed (B-fixed), A (B) earned a fixed €1 in each period, regardless of whether a double was reported or not, whereas B (A) earned the value of the double as in aligned outcomes. In an individual treatment, the same person rolled and reported twice and earned the value of the double if a double was reported, nothing otherwise.

Finally, in the third stage, we assessed participants' social value orientation (SVO) using the SVO slider measure (SI Appendix, section ‎1.1.7). The measure assesses the magnitude of people's concern to others' outcomes. Each participant made a series of 15 choices between nine resource allocation options between self and another participant (i.e., in each choice there were nine available allocations to choose from). Payment for this part was based on one of these choices (randomly determined). The 15 choices were aggregated to determine a unique value for each participant, expressed as an angle on a self/other 2D space. The angle was used to classify participants as competitive, individualistic, prosocial, or altruistic. We followed ref. 36 to determine the borders between the four SVO types.

For the robustness experiment, 236 undergraduate students (65% females; Mage = 21.31, SDage = 3.16) were recruited using ORSEE (35) and took part in nine experimental sessions, each consisting of 24 or 28 participants, and lasting less than 1 h on average. The experiment was approved by the Research Ethics Committee of the School of Economics of the University of Nottingham. All participants read and signed an informed consent before the experiment. We used a within-session design, meaning that the aligned outcomes and B-fixed treatments within each setting (replication, multiplication, and addition) took place simultaneously in the same session. Participants were given general instructions on paper, and treatment-specific instructions were presented on screen. Payment in these sessions was given in British pounds sterling, as they were conducted at the University of Nottingham.

Each setting—replication, multiplication, and addition—included two treatments: aligned outcomes and B-fixed. In the replication setting, the payoffs were exactly as in the original experiment, except that they were given in £’s instead of €’s. In the multiplication setting, the payoffs were exactly double the amounts paid in the replication setting. In the addition setting, each player received an additional fixed amount of £2 per trial (relative to the replication), which was added to the earnings from the reported outcomes.

Supplementary Material

Supplementary File

Acknowledgments

We thank Abigail Barr, Benjamin Beranek, Simon Gächter, Georgia Michailidou, Lucas Molleman, Marieke Roskes, Jonathan Schultz, Rowan Thomas, Till Weber, the editor, and three anonymous reviewers for their helpful comments. The research was funded by the Max Planck Society, the European Research Council (ERC-AdG 295707 COOPERATION), and the European Union’s Seventh Framework Program (FP7/2007-2013; REA 333745).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1423035112/-/DCSupplemental.

References

  • 1.Bowles S, Gintis H. A Cooperative Species: Human Reciprocity and Its Evolution. Princeton Univ Press; Princeton: 2011. [Google Scholar]
  • 2.Baumeister RF, Leary MR. The need to belong: Desire for interpersonal attachments as a fundamental human motivation. Psychol Bull. 1995;117(3):497–529. [PubMed] [Google Scholar]
  • 3.Kameda T, Takezawa M, Hastie R. Where do social norms come from? The example of communal sharing. Curr Dir Psychol Sci. 2005;14(6):331–334. [Google Scholar]
  • 4.Kramer RM. Trust and distrust in organizations: Emerging perspectives, enduring questions. Annu Rev Psychol. 1999;50(1):569–598. doi: 10.1146/annurev.psych.50.1.569. [DOI] [PubMed] [Google Scholar]
  • 5.Rempel JK, Ross M, Holmes JG. Trust and communicated attributions in close relationships. J Pers Soc Psychol. 2001;81(1):57–64. [PubMed] [Google Scholar]
  • 6.Bazerman MH, Curhan JR, Moore DA, Valley KL. Negotiation. Annu Rev Psychol. 2000;51(1):279–314. doi: 10.1146/annurev.psych.51.1.279. [DOI] [PubMed] [Google Scholar]
  • 7.Murnighan JK. Bargaining Games: A New Approach to Strategic Thinking in Negotiations. HarperCollins; NY: 1992. [Google Scholar]
  • 8.Rusbult CE, Van Lange PA. Interdependence, interaction, and relationships. Annu Rev Psychol. 2003;54(1):351–375. doi: 10.1146/annurev.psych.54.101601.145059. [DOI] [PubMed] [Google Scholar]
  • 9.De Dreu CKW, et al. The neuropeptide oxytocin regulates parochial altruism in intergroup conflict among humans. Science. 2010;328(5984):1408–1411. doi: 10.1126/science.1189047. [DOI] [PubMed] [Google Scholar]
  • 10.Efferson C, Lalive R, Fehr E. The coevolution of cultural groups and ingroup favoritism. Science. 2008;321(5897):1844–1849. doi: 10.1126/science.1155805. [DOI] [PubMed] [Google Scholar]
  • 11.Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211(4489):1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
  • 12.Dawes RM. Social dilemmas. Annu Rev Psychol. 1980;31:169–193. [Google Scholar]
  • 13.Rand DG, Dreber A, Ellingsen T, Fudenberg D, Nowak MA. Positive interactions promote public cooperation. Science. 2009;325(5945):1272–1275. doi: 10.1126/science.1177418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Van Lange PA, Joireman JA. How we can promote behavior that serves all of us in the future. Soc Issues Policy Rev. 2008;2(1):127–157. [Google Scholar]
  • 15.Schweitzer ME, Ordóñez L, Douma B. Goal setting as a motivator of unethical behavior. Acad Manage J. 2004;47(3):422–432. [Google Scholar]
  • 16.Coricelli G, Joffily M, Montmarquette C, Villeval MC. Cheating, emotions, and rationality: An experiment on tax evasion. Exp Econ. 2010;13(2):226–247. [Google Scholar]
  • 17.Wiltermuth SS. Cheating more when the spoils are split. Organ Behav Hum Decis Process. 2011;115(2):157–168. [Google Scholar]
  • 18.Gino F, Ayal S, Ariely D. Self-serving altruism? The lure of unethical actions that benefit others. J Econ Behav Organ. 2013;93:285–292. doi: 10.1016/j.jebo.2013.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Conrads J, Irlenbusch B, Rilke RM, Walkowitz G. Lying and team incentives. J Econ Psychol. 2013;34:1–7. [Google Scholar]
  • 20.Cohen TR, Gunia BC, Kim-Jun SY, Murnighan JK. Do groups lie more than individuals? Honesty and deception as a function of strategic self-interest. J Exp Soc Psychol. 2009;45(6):1321–1324. [Google Scholar]
  • 21.Gneezy U. Deception: The role of consequences. Am Econ Rev. 2005;95(1):384–394. [Google Scholar]
  • 22.Lewis A, et al. Drawing the line somewhere: An experimental study of moral compromise. J Econ Psychol. 2012;33(4):718–725. [Google Scholar]
  • 23.Shalvi S, De Dreu CKW. Oxytocin promotes group-serving dishonesty. Proc Natl Acad Sci USA. 2014;111(15):5503–5507. doi: 10.1073/pnas.1400724111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Haidt J. The new synthesis in moral psychology. Science. 2007;316(5827):998–1002. doi: 10.1126/science.1137651. [DOI] [PubMed] [Google Scholar]
  • 25.Greene J. Moral Tribes: Emotion, Reason and the Gap Between Us and Them. Atlantic Books; Ocean City, NJ: 2014. [Google Scholar]
  • 26.Fehr E, Schmidt KM. A theory of fairness, competition, and cooperation. Q J Econ. 1999;114(3):817–868. [Google Scholar]
  • 27.Bolton GE, Ockenfels A. ERC: A theory of equity, reciprocity, and competition. Am Econ Rev. 2000;90(1):166–193. [Google Scholar]
  • 28.Andreoni J, Bernheim BD. Social image and the 50–50 norm: A theoretical and experimental analysis of audience effects. Econometrica. 2009;77(5):1607–1636. [Google Scholar]
  • 29.Dawes CT, Fowler JH, Johnson T, McElreath R, Smirnov O. Egalitarian motives in humans. Nature. 2007;446(7137):794–796. doi: 10.1038/nature05651. [DOI] [PubMed] [Google Scholar]
  • 30.Fehr E, Fischbacher U. Third-party punishment and social norms. Evol Hum Behav. 2004;25(2):63–87. [Google Scholar]
  • 31.Shalvi S, Dana J, Handgraaf MJ, De Dreu CKW. Justified ethicality: Observing desired counterfactuals modifies ethical perceptions and behavior. Organ Behav Hum Decis Process. 2011;115(2):181–190. [Google Scholar]
  • 32.Fischbacher U, Föllmi-Heusi F. Lies in disguise—an experimental study on cheating. J Eur Econ Assoc. 2013;11(3):525–547. [Google Scholar]
  • 33.Mazar N, Amir O, Ariely D. The dishonesty of honest people: A theory of self-concept maintenance. J Mark Res. 2008;45(6):633–644. [Google Scholar]
  • 34.Cohn A, Fehr E, Marechal MA. 2014. Business culture and dishonesty in the banking industry. Nature 516(7529):86–89.
  • 35.Greiner B. An online recruitment system for economic experiments. In: Kremer K, Macho V, editors. Forschung Und Wissenschaftliches Rechnen (GWDG Bericht 63) Gesellschaft für Wissenschaftliche Datenverarbeitung; Göttingen, Germany: 2004. pp. 79–93. [Google Scholar]
  • 36.Murphy RO, Ackermann KA, Handgraaf MJ. Measuring social value orientation. Judgm Decis Mak. 2011;6(8):771–781. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File
pnas.1423035112.sapp.pdf (2.7MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES