Significance
Advances in simulation and synthesis of nanoparticles and colloids are leading to a new class of active colloidal systems where self-propelled and self-rotated particles convert energy to motion. Such systems hold promise for the possibility of colloidal machines––integrated systems of colloids able to carry out functions. An important step in this direction is appropriately confining colloids within cells whose shape can be controlled and within which activity can be compartmentalized. This paper uses theory and computer simulation to propose active colloidal cells and investigates their behavior. Our findings provide motivation and design rules for the fabrication of primitive colloidal machines.
Keywords: active matter, emergent pattern, confinement, colloids
Abstract
Small autonomous machines like biological cells or soft robots can convert energy input into control of function and form. It is desired that this behavior emerges spontaneously and can be easily switched over time. For this purpose we introduce an active matter system that is loosely inspired by biology and which we term an active colloidal cell. The active colloidal cell consists of a boundary and a fluid interior, both of which are built from identical rotating spinners whose activity creates convective flows. Similarly to biological cell motility, which is driven by cytoskeletal components spread throughout the entire volume of the cell, active colloidal cells are characterized by highly distributed energy conversion. We demonstrate that we can control the shape of the active colloidal cell and drive compartmentalization by varying the details of the boundary (hard vs. flexible) and the character of the spinners (passive vs. active). We report buckling of the boundary controlled by the pattern of boundary activity, as well as formation of core–shell and inverted Janus phase-separated configurations within the active cell interior. As the cell size is increased, the inverted Janus configuration spontaneously breaks its mirror symmetry. The result is a bubble–crescent configuration, which alternates between two degenerate states over time and exhibits collective migration of the fluid along the boundary. Our results are obtained using microscopic, non–momentum-conserving Langevin dynamics simulations and verified via a phase-field continuum model coupled to a Navier–Stokes equation.
Active matter describes particulate systems with the characteristic that each “particle” (agent) converts energy into motion (1, 2). Active matter covers a range of length scales that include molecular motors in the cytoskeleton (3–5), swimming bacteria (6–8), driven colloids (9, 10), flocks of birds and fish (11–14), and people and vehicles in motion (15). Over the last decade, studies of active matter have demonstrated behavior not seen in equilibrium systems, including giant number fluctuations (16, 17), emergent attraction and superdiffusion (18–20), clustering (21, 22), swarming (23–27), and self-assembled motifs (28, 29). These systems provide interesting theoretical and engineering challenges as well as opportunities to explore and target novel behaviors that proceed outside of thermodynamic equilibrium.
Of particular interest are systems found in nature or inspired by natural phenomena. Biological systems usually operate in confined regions of space––think of intracellular space, interfaces and membranes, and the crowding of cells near surfaces. The role of hydrodynamics in confinement has been studied for biological swimmers, such as bacteria and sperm, showing accumulation at the walls (30–32) and upstream swimming along surfaces (33) or in a spiral vortex (34–36). Attraction to walls has also been reported in the absence of hydrodynamics for disks (37, 38), spheres (39), and dumbbell swimmers (40). But, whereas these examples study the behavior under the influence of hard boundaries, biological swimmers typically interact with soft boundaries, such as membranes and biofilms. Another design variable is the possibility that the boundary itself is active, as in the surface of a bacterium covered with flagellae or, as demonstrated recently, active nematic vesicles (41).
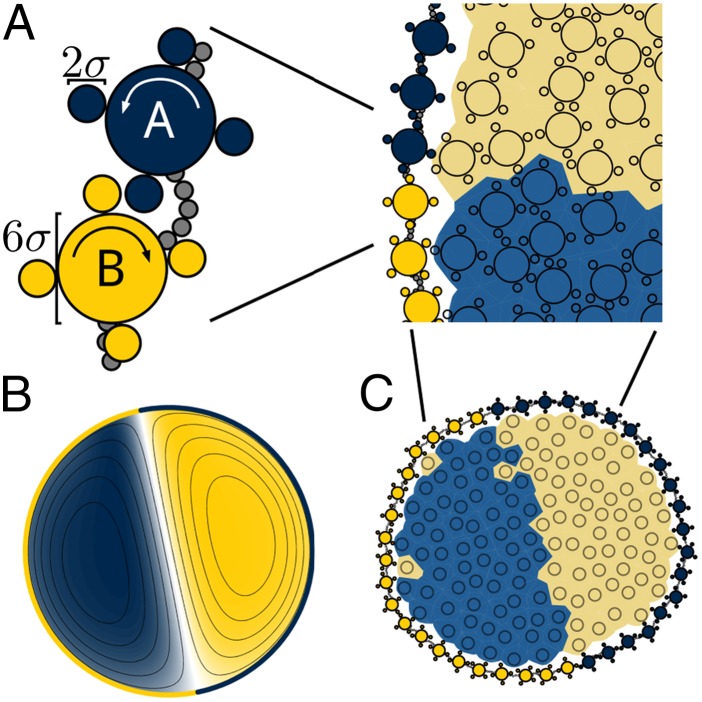
In this work, we propose and investigate an active matter system under flexible, active confinement. We call this system an active colloidal cell. Our realization of an active colloidal cell consists of independent particles, called spinners (42), that translate and rotate in two dimensions and are constrained within a finite area by a flexible boundary that is also built from spinners. Each spinner has a gear-like geometry, which consists of a large central disk and four smaller satellite disks (Fig. 1A). Similar gear-shaped rigid aggregates of self-propelled particles have been formed experimentally (43). Spinners are freely mobile in the cell interior. On the cellular boundary, spinners are connected to one another by a flexible chain of beads attached by finitely extensible springs. Both the interior and the boundary spinners can be subject to a clockwise or counterclockwise driving torque, which makes them active.
Fig. 1.
Schematic of the confined spinner models. (A) The active colloidal cell is made up of spinners driven counterclockwise (blue) or clockwise (yellow). Boundary spinners are connected by a flexible bead–spring chain (gray). We compare the behavior of a continuum model (B) to a microscopic model (C). The compartmentalization of interior spinners is visualized by coloring the Voronoi tessellation in the microscopic model.
Rotationally driven particles can synchronize and self-organize (44, 45) in the absence (42) and in the presence (46–48) of hydrodynamic interactions. Crystallization has recently been observed in rotating magnetic Janus colloids (49) and fast-moving bacteria (50). Spinners in the interior of the cell resemble molecular motors that push themselves forward on their neighbors and, thus, sustain convective dynamics. The effect of the boundary spinners is similar to that found in the cilia of living tissues, which stir nearby fluid. Our results demonstrate that a natural consequence of the activity present in the colloidal cell is control over both its external shape and internal structure. We report compartmentalization into regions of clockwise and counterclockwise spinners––a behavior which is affected by, and can be controlled via, properties of the enclosing boundary configuration as previously suggested (51). Transitions in the internal structure of the colloidal cell occur as its radius increases, and as the composition of the interior spinners and the patterning of the boundary are varied.
A previous study of spinners in bulk (42) showed phase separation into clockwise- and counterclockwise domains. Cates and collaborators (6, 52, 53) have suggested that phase separation is a generic consequence of local energy input in an otherwise equilibrium system. Here and in the study of bulk spinners we demonstrate phase separation due to local rotational, rather than translational, energy input. We obtain our results using a particulate, microscopic model (Fig. 1C) as well as a continuum model (Fig. 1B). This allows us to conclude that the phenomena we observe are robust with respect to details of the model.
In this study we use two models to study the behavior of an active colloidal cell, illustrated in Fig. 1. The microscopic model describes spinners as individual particles and simulates their motion using Langevin dynamics. It resolves the behavior of individual spinners but does not include hydrodynamic effects. In contrast, the continuum model describes the spinner system as a viscous binary fluid, which is governed by an incompressible Navier–Stokes equation coupled to a Cahn–Hilliard equation. Both models are described in detail in Materials and Methods below. Note that the microscopic model was introduced in earlier work using Brownian dynamics (42) and is extended here to include boundaries.
Results
Shape Control from Active Confinement.
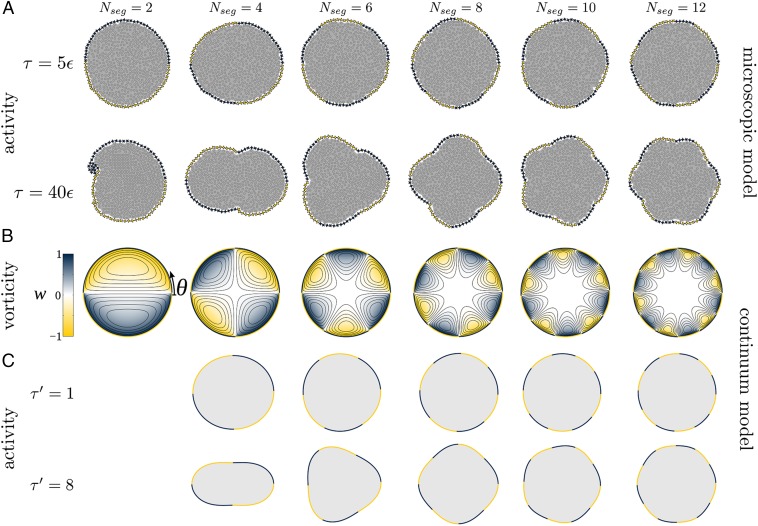
We first study the behavior of colloidal cells with passive (nondriven) spinners in the interior and active spinners on the boundary. We use the microscopic model while varying two parameters: the number of boundary segments n and the driving torque on the boundary τ. As shown in Fig. 2A and Movie S1, the effect of the active boundary is a deformation of the cell shape. The shape deformation follows the symmetry of the boundary pattern (horizontal axis in the figure) and becomes more prominent as the driving torque τ increases (vertical axis). Buckling occurs at places on the boundary where the direction of the driving torque switches. In particular, we observe inward buckling when two adjacent spinners on the boundary push interior spinners away from the space between them. Similarly, we find outward buckling when the boundary spinners pull interior spinners toward the space between them. Colloidal cells with active spinners in the interior display similar, but less well-pronounced behavior.
Fig. 2.
Cellular shape control for active boundaries with passive interior. (A) Simulations in the microscopic model with 512 interior spinners and 80 boundary spinners reveal a symmetric buckling of the colloidal cell. The buckling is suppressed for low driving torque τ (Top Row) but appears if the driving torque is sufficiently high (Bottom Row). We can control the symmetry by changing the number of alternately driven segments on the active boundary, varied horizontally. (B) Simulations in the continuum model with fixed boundaries reveal convective flows of the interior spinners, which we visualize via the vorticity field w. (C) Simulations in the continuum model with free boundaries confirm the shape changes observed in the microscopic model. Again, we show results for two different levels of activity for frictional damping and boundary tension in a cell of size . The case of exhibits a cusp-like singularity that cannot be captured by the perturbation analysis used to compute the cell shape (Materials and Methods).
To understand the deformation of the active colloidal cell, we analyze the velocity field of the passive spinners in the interior while fixing the geometry of the boundary. After reaching a steady state, we observe that the flow field has developed regions of counterclockwise and clockwise convection, which we visualize using the vorticity field w and the resulting streamlines in Fig. 2B. We apply the same color scheme for vorticity (blue for counterclockwise and yellow for clockwise) in the continuum model as for the rotation of individual spinners in the microscropic model. Note that counterclockwise (clockwise) flow is exclusively in contact with a clockwise (counterclockwise) rotating boundary.
We now use the continuum model to study the deformation of the colloidal cell. The active boundary drives convective flow along the cell wall. Because the passive interior spinners are transported fastest along the interface, they collect at places where they turn to flow inward (i.e., where the boundary changes from yellow to blue traveling counterclockwise), inducing a positive pressure on the boundary. The result is a higher pressure and outward buckling of the boundary. In contrast, at the other junction, passive spinners are transported away rapidly when they approach the boundary from the center of the cell. Thus, the boundary buckles inward at places where the boundary activity changes from blue to yellow traveling counterclockwise. The magnitude of the driving torque τ affects the strength of the pressure difference and thus the anisotropy of the cell shape.
To complete the comparison with the microscopic model, we release the boundary in the continuum model, adjusting its geometry based on the stresses acting on it from the interior fluid. We observe in Fig. 2C that the cell shape readily adjusts to a shape predicted by the microscopic simulations, confirming that the observed buckling is independent of using a microscopic (particulate) or a continuum model.
Compartmentalization.
We next consider what happens if active spinners are confined within active boundaries. It is known that without confinement, phase separation through a spinodal decomposition-like process eventually results in complete demixing of clockwise- and counterclockwise-driven spinners (42). As we will see, the presence of an active boundary still allows phase separation, but also induces a preference of oppositely driven interior and boundary spinners to be in contact near the boundary. We term this behavior compartmentalization. The presence of the active boundary can lead to more complex phase behavior than that found in the bulk system. The size of the colloidal cell also plays an important role for compartmentalization.
We systematically vary the two composition ratios, i.e., the fraction of clockwise- to counterclockwise-driven spinners in the interior (horizontal direction in Fig. 3) as well as the fraction on the boundary (vertical direction). We find perfect agreement between the microscopic model and the continuum model. The precise geometry of compartmentalization changes under variation of the composition ratios. We distinguish three cases:
-
i)
Core–shell. All boundary spinners are driven in the same direction and the domain interface forms a circle concentric to the boundary. We call this the core–shell configuration. The core–shell configuration maximizes the contact between interior spinners and boundary spinners of the same type.
-
ii)
Inverted Janus. For equal ratios of clockwise- to counterclockwise-driven spinners on the boundary and in the interior the domain interface is a straight line. We call this the inverted Janus configuration. The inverted Janus configuration maximizes the contact between unlike spinners at the cell boundary, as shown in Movie S2.
-
iii)
Bubble–crescent. Intermediate to the extreme cases of core–shell and inverted Janus is the bubble–crescent configuration. In the bubble–crescent configuration one of the spinner species attempts to minimize its area into a circular domain while simultaneously avoiding contact with the boundary.
Fig. 3.
Compartmentalization of a colloidal cell with active boundary and active interior. (A) A grid of representative snapshots of active colloidal cells with varying boundary (horizontal direction) and interior (vertical direction) composition in the microscopic model. A system of 128 interior spinners are enclosed by a boundary of 40 spinners. All spinners are active. We observe the core–shell and the inverted Janus configurations where the contact between like and unlike spinners, respectively, is maximized. The bubble–crescent configuration interpolates between these two extrema. (B) We confirm the steady-state behavior in the continuum model with and for cell of size with different patterns of boundary activity. The configurations in B correspond to the bottom row of A.
Compartmentalization can be understood as the result of competition between two effects. The observation of spinodal decomposition in the bulk system (42) suggests that like-driven spinners in the cell interior and boundary prefer to be in contact. We call this behavior the boundary preference. In addition, at an interface between clockwise- and counterclockwise-driven spinners, spinners develop a velocity profile flowing parallel to the interface. We call this behavior the interface preference.
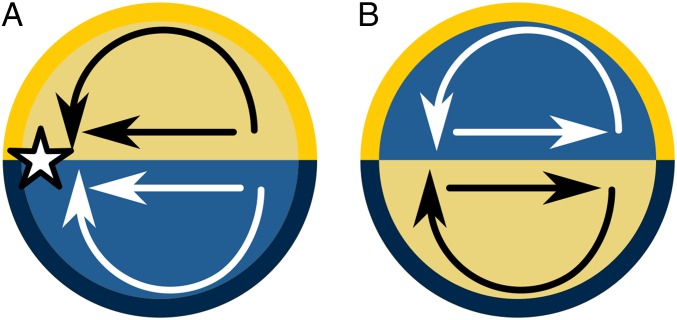
Both boundary preference and interface preference are satisfied for a single-component active boundary, which explains the geometry of the core–shell case. In the case of a Janus boundary, boundary preference and interface preference work against each other and result in competition. This can be understood from the schematic in Fig. 4. If the interior spinners were to phase separate into a regular Janus pattern (i.e., maximizing the contact between like spinners at the boundary), then the flows induced on the interior spinners by both the boundary and the interface between the two interior phases would converge to a single point, causing the entire colloidal cell to jam (Fig. 4A). In fact, if the boundary activity of an inverted Janus cell is instantaneously swapped to put the cell into a Janus configuration, the cell first jams and mixes before demixing into the inverted Janus configuration once more, as shown in Movie S3. By creating an inverted Janus configuration, the domain interface stabilizes a flow of spinners in the opposite direction of the pressure gradient imposed by the active boundaries, and the circular flow of the spinners in the interior can be maintained (Fig. 4B). This behavior is similar to the cell sorting model reported in ref. 37, where a mixture of self-propelled soft disks in confinement moves toward the walls of the container. Finally, the bubble–crescent configuration is an intermediate case. Spinners are slowed down when they enter a region of unlike boundary contact resulting in the formation of the crescent. The boundary preference causes a layer of whichever species is dominant to form a wetting layer in contact with the cell boundary of the same species. In the perfectly balanced inverted Janus case, neither species is dominant and the time-averaged width of the wetting layer approaches zero.
Fig. 4.
Explanation for the inverted Janus configuration. We compare the flows in the (nonobserved) Janus configuration (A) to the (observed) inverted Janus configuration (B). In the inverted Janus configuration the flow maintains two circular vortices, whereas in the noninverted Janus configuration the flow would converge to a singular point ().
Quantifying Intracellular Order and Finite-Size Effects.
To quantify the geometry of the domains and to distinguish the three types of colloidal cell compartmentalization, we construct a family of cellular order parameters for nonnegative integer n corresponding to observed symmetries within the cell. Each spinner is assigned a fictitious charge of or depending on whether it is being driven clockwise or counterclockwise. The order parameter is defined as
| [1] |
where ( is the position of the interior spinner j in polar coordinates with the origin at the center of mass of the colloidal cell, and a normalization factor.
The order parameter is designed to be maximal when one species moves to the outside of the cell, i.e., for the core–shell configuration. The order parameters , are maximal for systems that phase separate into radial sectors with n-fold symmetry, which is the case for the n-fold alternating boundary of Eq. 3. For example, measures radial asymmetry and measures dipolar order.
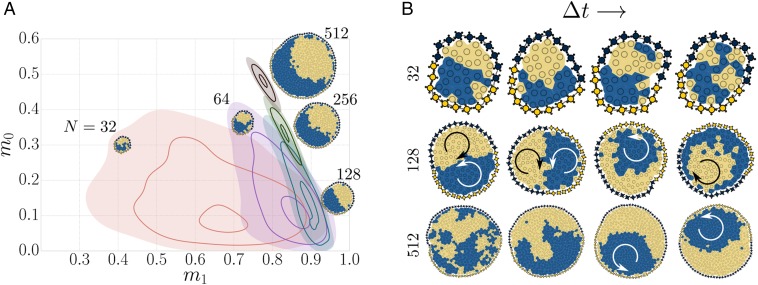
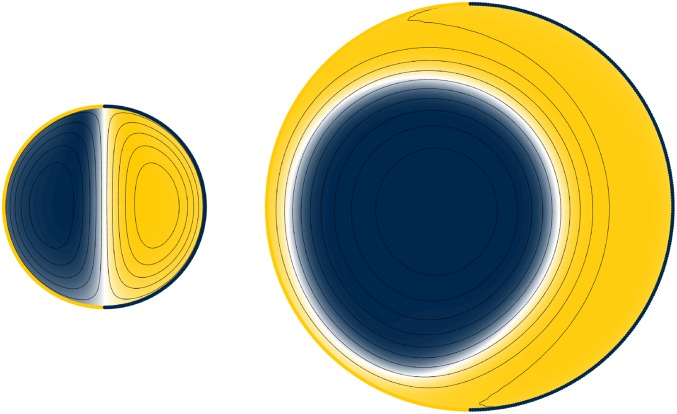
We find that the type of intracellular compartmentalization not only depends on the interior and boundary spinner compositions but also on the size of the colloidal cell (Movie S4). We simulate cells with an even composition of spinners at the boundary and in the interior. It is apparent from the order parameter histograms in Fig. 5A that small cells do not order well due to the stronger influence of noise. As the number of interior spinners increases to , the effect of noise decreases and the colloidal cell approaches the inverted Janus configuration. A further increase of N induces a transition of the Janus configuration into the bubble–crescent configuration by a spontaneous breaking of the mirror symmetry. Interestingly, the symmetry breaking is not persistent. As time progresses, the colloidal cell switches reversibly between a clockwise bubble and a counterclockwise bubble (Fig. 5B). We can explain the symmetry breaking as a kinetic effect. A colloidal cell can gain net rotation due to an imbalance in the number of interior spinners of each type touching the boundary of the same type. This behavior is self-reinforcing: once more clockwise-driven interior spinners are in contact with clockwise-driven boundary spinners, the cell boundary will begin to rotate clockwise, which brings it into contact with more clockwise-driven interior spinners. In small cells the boundary is able to switch rapidly between the two bubble–crescent configurations due to their size. As the cell size increases, however, fluctuations become less capable of inverting the bubble–crescent configuration and one species persists as the bubble. In the limit of infinite cell size, we expect the symmetry breaking to become irreversible. When the boundary spinners are pinned in place, the colloidal cell does not form the bubble–crescent pattern but remains in the inverted Janus configuration, as shown in Movie S5.
Fig. 5.
Order parameter histograms of common intracellular compartmentalizations. We use the cellular order parameters and to quantify core–shell and Janus behavior in simulations of the microscopic model. The order parameters are normalized such that and for the perfectly ordered configurations. (A) The interior composition and the boundary composition are kept even. As the size of the cell grows from 32 (salmon) to 64 (violet), 128 (teal), 256 (green), and 512 (brown) interior spinners, the cell configuration transitions from inverted Janus to bubble–crescent. For very small cells, thermal fluctuations smear out the histogram significantly. (B) Transient behavior in cells of 32 (top row), 128 (middle row), and 512 (lower row) interior spinners. Medium-sized cells exhibit periodic migrations where spinners of one type travel along the segment of the same type in the boundary. For large cells, this migration becomes self-reinforcing due to the boundary rotation it induces, causing a spontaneous symmetry-breaking.
The continuum model also captures the qualitative dependence on the cell size observed in the microscopic model. For a 50:50 mixture of active spinners confined within a 50:50 active boundary, we observe a destabilization of the inverted Janus configuration and the concomitant formation of the bubble–crescent configuration upon increasing the size of the cell from to (Fig. 6) in agreement with the result of the microscopic model. These results can be seen in Movies S6 and S7.
Fig. 6.
Active Interior, active boundary. Snapshots of the steady-state composition φ for two different cell sizes and . The cells contain 50:50 mixtures of clockwise- and counterclockwise-rotating spinners within an active boundary comprising two equally sized, counterrotating domains. Increasing the size of the cell results in the destabilization of the inverted Janus configuration and the formation of the bubble–crescent configuration. Here, the strength of active rotation is ; the strength of frictional damping is .
Discussion and Conclusion
We have introduced the active colloidal cell as a simple model for the study of an active matter system under confinement. The confinement is itself active and soft, allowing cells to be flexible in geometry. The main effect of the active boundary is the stirring of flow in the interior of the cell, which is observed in both a microscopic model without hydrodynamics and a continuum model. In both models, confinement results in a competition between complete phase separation with a straight interface, favored by spinners in the bulk (42), and deviating behavior imposed by the boundary conditions. There is an optimal size of the colloidal cell (in our model around ), which is large enough such that strong thermal fluctuations are suppressed, but not too large for the system to still be influenced by the activity of the boundary. A colloidal cell of this size conjures up the image of a soft, miniature robot that can change its shape, vary its internal patterning with two species of spinners, and even exhibit a bistable equilibrium that switches back and forth.
Although we have taken just an early first theoretical step on two simple model systems, it is tempting to consider the possibility of exploiting the behaviors we report in the development of colloidal machines––integrated systems of colloids able to carry out programmable functions. Recent experimental reports of functional bionic nanoparticle assemblies (54) and colloidal actuators (55) demonstrate prototypical functions of converting light into energy and converting energy into mechanical work, respectively––both functions critical for a colloidal machine. The behaviors of predictable compartmentalization, shape control, and switchability demonstrated in our model system of colloidal spinners provide additional, machine-like functionality. We expect such machines could be made from anisotropic colloids exhibiting, e.g., catalytically propelled or magnetic-field-induced motion (56).
Materials and Methods
Microscopic Model.
In the microscopic model, spinners are rigid bodies consisting of four peripheral disks of radius σ symmetrically arranged about a central disk of radius (Fig. 1A). The system is governed by the Langevin equation for translation,
| [2] |
where m is the mass and is the translational velocity of each of the disks comprising the ith spinner. If the spinner is active then its rigid body is driven by an external driving torque of constant magnitude, with positive sign for counterclockwise rotation (A, blue) and negative sign for clockwise rotation (B, yellow). In a real system, this torque could be due to the four peripheral disks being self-propelled particles, oriented symmetrically to impose a net torque but no net force on the spinner as a whole, much like the particles described in ref. 43. The torque on the particles would then be balanced by a torque on the stationary substrate. Spinners are hard particles that interact via a repulsive contact potential, resulting in internal forces . Translational and rotational kinetic energy is dissipated through the translational drag force applied to each constituent disk of a spinner. Noise is included via Gaussian random forces that model a heat bath at temperature T. Here are normalized zero-mean white-noise Gaussian processes, which ensure thermodynamic equilibrium in the absence of the externally applied torques. Note that in contrast with earlier work (42) we apply drag and random forces to each constituent disk of the spinner separately, which means we do not have to specify a separate Langevin equation for rotation. Because the random forces are not applied pairwise, the thermostat is non–momentum-conserving. Therefore, our microscopic model explicitly does not include hydrodynamics.
The boundary is modeled in two steps. First, we connect the ends of a linear chain of disks with radius that interact with their adjacent neighbors via a finitely extensible nonlinear elastic potential with spring constant k, divergence length , and separation distance r. Second, we rigidly attach a spinner to every 10th boundary disk, so that the boundary spinners can rotate freely without colliding if the boundary is sufficiently stretched. We can choose to make the boundary spinners active by driving them rotationally and vary the patterning of the boundary by constructing it from segments of equal driving torque. To describe the patterning we introduce the boundary activity function , where is an angle that describes the position at the boundary (if formed into a circle). indicates a counterclockwise driving torque whereas indicates a clockwise driving torque. Simple examples are the uniform boundary (all boundary spinners are driven counterclockwise), the Janus boundary (half counterclockwise and half clockwise), and the n-fold alternating boundary
| [3] |
where H is the Heaviside step function.
Langevin dynamics simulations are performed on graphic processing units with HOOMD-blue (57, 58) (codeblue.umich.edu/hoomd-blue) for colloidal cells with between 16 and 512 spinners in the interior. The contact between spinners is a Weeks–Chandler–Andersen potential (59) with parameter ε shifted to the surface of each disk such that its range is a small fraction of the disk diameter, thereby approximating hard shapes. Throughout the paper we report results for , , , and thermal noise using σ as the length unit and ε as the energy unit. These parameter choices correspond to the overdamped, diffusive limit. Active systems are often described by overdamped equations of motion where inertia is neglected (11, 17, 19). Although inertia is incorporated in our model, we confirmed that it is not crucial for any of the observed behavior. Additional studies of the role of convection in bulk systems of spinners are presented in ref. 60.
Continuum Model.
In the continuum model, the spinner dynamics is described by coupling the Cahn–Hilliard phase field equation to a Navier–Stokes equation with an active term representing the rotational driving torque. Previously, a continuum model was used to describe separation of translationally driven particles into high- and low-density phases, much like vapor–liquid or vapor–solid coexistence in single-component equilibrium systems (20, 61, 62). Here, instead, we model separation into clockwise- and counterclockwise-driven domains, analogous to equilibrium phase separation of a binary mixture of immiscible fluids as reported in ref. 42 for our microscopic model. Boundary effects are taken into account via the choice of boundary conditions for the equations. Depending on the presence or absence of activity at the boundary and in the interior we distinguish various cases. Here we first present the governing equations for the most general situation and refer to Governing Equations for details and derivations.
To describe the binary fluid of actively rotating spinners, we start with the Cahn–Hilliard equation for the fraction of clockwise- or counterclockwise-driven spinners within a fluid volume, φ. The Cahn–Hilliard equation can be written in nondimensional form as
| [4] |
The 2D fluid is modeled as a generalization of an incompressible, Newtonian fluid governed by the (nondimensional) Navier–Stokes equations (63, 64),
| [5] |
| [6] |
where is the fluid velocity, Re is a Reynolds number, Ca is a capillary number, is a translational drag coefficient present in the microscopic model, and measures the strength of the rotational driving torque. The form of the rotating driving implies that the torque density is proportional to the local composition φ (65). For simplicity, we neglect the effects of fluid inertia as well as that of capillary-like forces acting normal to the fluid–fluid interface (i.e., and ). These contributions are expected to be unimportant for the relatively small fluid domains described here. With these simplifications, convective flows are driven only by forces due to active rotation directed parallel to the interface separating the counterrotating domains, .
To solve for the 2D velocity field, it is convenient to introduce the stream function ψ where . As shown in Eqs. 12–14, the momentum equation (Eq. 5) can then be recast in terms of the stream function,
| [7] |
Importantly, the dimensionless coefficients and characterizing the strength of active rotation and frictional drag in the continuum model are directly analogous (in an order-of-magnitude sense) to the parameters τ and γ in the microscopic model. Together with an impermeable boundary with spatially varying stress, Eqs. 4 and 7 govern the dynamics of the composition φ and stream function ψ of the fluid. We integrate these continuum equations using COMSOL Multiphysics, Version 4.4.
The fluid is confined within an impermeable passive or active boundary, entering as boundary conditions for the continuum equations. The driving torques applied to the boundary spinners are equal to those driving the rotation of the interior spinners. This scenario can be approximated by the two boundary conditions and , where is the boundary activity. Furthermore, in the microscopic model, the active boundary is not fixed in place but is free to rotate relative to the stationary surroundings (e.g., an underlying substrate). To describe this effect in the continuum model, we fix the shape of the boundary to a circle of radius R but allow for its rotational motion with an angular velocity . In the low Reynolds number limit, the use of a rotating reference frame does not affect the equations of motion with the exception of the frictional damping term in the Navier–Stokes equation. Finally, the activity-induced flows create nonuniform stresses normal to the boundary that result in its deformation. To model shape changes of the active colloidal cell, we assume that the normal component of the stress at the boundary is balanced by a surface-tension–like force, which is proportional to the local curvature of the interface. After this short summary, we now derive the continuum model in detail.
Governing equations.
To describe the binary fluid of actively rotating spinners, we start with the convective Cahn–Hilliard equation for the compositional order parameter φ,
| [8] |
where is the fluid velocity, M is a mobility coefficient, and μ is the chemical potential. For simplicity, we assume the chemical potential is of the form
| [9] |
where r, λ, and K are positive coefficients. Physically, these coefficients determine the thickness of the interface separating two equilibrium phases with composition .
We further assume that the fluid is incompressible, Newtonian, and symmetric such that the bulk properties of the two phases are equal––in particular, the density ρ and viscosity η. The two components of the fluid are driven to rotate in opposite directions by a torque density , which is proportional to the order parameter φ and to a constant a that describes the magnitude of rotation. Under these conditions, conservation of mass and momentum implies that
| [10] |
| [11] |
where the additional terms in Eq. 11 describe (i) frictional drag against the stationary surroundings, , (ii) capillary-like forces acting normal to the fluid–fluid interface, , and (iii) forces due to active rotation directed parallel to the interface, .
Nondimensionalization.
At this point, it is convenient to nondimensionalize the governing equations using characteristic scales for the interfacial thickness , the time of demixing , and the equilibrium composition . In these dimensionless units, Eqs. 8 and 11 become
| [12] |
| [13] |
where is a Reynolds number, is a capillary number, and the dimensionless coefficients and characterize the strength of active rotation and frictional drag, respectively. Here, we focus exclusively on the low Reynolds number limit () and neglect capillary forces () such that fluid flow is driven solely by the active rotation of the particles. Systems with passive fluid interiors are described by setting .
To solve for the 2D velocity field, it is convenient to introduce the stream function ψ where such that Eq. 13 becomes
| [14] |
For such 2D flows, the fluid vorticity (in the z direction), , can be related to the stream function as . Together, Eqs. 12 and 14 govern the dynamics of the composition φ and the flow field.
Passive boundary.
In the microscopic model, a passive boundary refers to that formed by passive spinners that are otherwise free to rotate and translate subject to the constraints of their connectivity. In the continuum model, the passive boundary is described by a circle of radius R with no flow normal to the boundary and no stress tangent to the boundary
| [15] |
| [16] |
Here, and are the unit vectors normal and tangent to the boundary (with the convention ), and is the viscous stress tensor. In terms of the stream function and the vorticity, these conditions imply
| [17] |
| [18] |
everywhere along the circular boundary.
Similarly, for systems with active interiors, we require two boundary conditions to fully specify the composition field φ. First, there is no flux normal to the boundary
| [19] |
We also require a “wetting” condition that determines the effective contact angle between the counterrotating fluid phases and the bounding surface. For the symmetric fluids described here, this effective contact angle should be such that
| [20] |
Subject to these boundary conditions, Eqs. 12 and 14 are solved numerically using the commercial finite-element solver COMSOL.
Active boundary.
In the microscopic model, an active boundary refers to that formed by active spinners which are driven to rotate in either direction with a constant torque. These boundary spinners can induce stresses tangent to the boundary that drive flows of the interior fluid, which may be active or passive. In the continuum model, the active boundary is described by a circle of radius R with no flow normal to the boundary and a tangential stress related to the local composition φ and the boundary activity as
| [21] |
| [22] |
where , with for counterclockwise-rotating boundary spinners and for clockwise boundary spinners. Here, the driving torques applied to the boundary spinners are assumed equal to those driving the rotation of the interior spinners. Note that the vorticity w at the boundary (here equal to the tangent stress) depends on the difference between the spinner composition in the fluid interior and that at the boundary. An interface between like rotating particles results in no net stress (i.e., when ); the largest stresses occur at interfaces between counterrotating particles (i.e., when ). Systems with passive fluid interiors can be described by setting in Eq. 22.
To model the boundary activity used in the microscopic model, the function was chosen as
| [23] |
where n determines the number of domains on the boundary, and δ is a length characterizing the width of the transition from one domain to the next (here, ). The resulting flows for passive interiors with to are shown in Fig. 2B.
Finally, it is important to note that the active boundary is not fixed in place but is free to rotate relative to the stationary surroundings (e.g., an underlying substrate). To describe this effect in the continuum model, we fix the shape of the boundary to a circle of radius R but allow for its rotational motion with an angular velocity . We adopt a rotating frame of reference which is fixed to the boundary and participates in its motion. In the low Reynolds number limit, the use of a rotating reference frame does not affect the equations of motion with the exception of the frictional damping term in the Navier–Stokes equation, which describes the resistance to motion relative to the stationary surroundings. In the rotating reference frame, the stream function Eq. 14 becomes
| [24] |
It is further assumed that the net torque T acting on the surroundings is identically zero at all times (otherwise, the system would accelerate or decelerate its rotational motion). This condition implies that
| [25] |
where the integral is carried out over the entire fluid domain S. For a circular domain of radius R, the angular velocity is therefore
| [26] |
This integral constraint must be solved at each time step to describe the rotation of the cell. Note that such complications are necessary only in describing the most general case of actively rotating fluids confined by an active boundary.
Shape change.
The activity-induced flows create nonuniform stresses normal to the flexible boundary that can result in its deformation. To describe these deformations, we assume that the normal component of the stress at the boundary is balanced by a surface-tension–like force, which is proportional to the local curvature of the interface
| [27] |
where is the normal component of the viscous stress at the boundary, and κ is the surface tension of the boundary (in units of ). Provided that forces due to surface tension are large compared with those due to boundary activity (i.e., ), deformations in the shape of the boundary will be small. Under these conditions, we can use the stress computed for the circular boundary to approximate changes in cell shape , which is computed as
| [28] |
where is the local curvature specified by Eq. 27, and the subscripts denote differentiation with respect to θ.
Connecting the Continuum and Microscopic Models.
In the microscopic model, the key parameters such as the driving torque τ, the frictional drag γ, and the elasticity of the boundary κ are expressed using natural microscopic scales for length σ, time , and energy . Here, we connect these characteristic scales to those used in nondimensionalizing the continuum model. The characteristic length in the continuum model is taken to be the thickness of the interface separating the two counterrotating phases, ; this length should be comparable to the size of the particles such that . The characteristic time used in the continuum model is that of unmixing, , which should be comparable to the time required for a particle to diffuse one particle diameter––that is, . Finally, the characteristic energy scale used in the continuum model is taken to be . Approximating the fluid viscosity as (66) and applying the two relations above, this energy scale becomes .
To summarize, the characteristic scales used in the continuum model are––to within an order of magnitude––the same as those used in the microscopic model. Consequently, the parameter values used in each of the models––although not exactly equivalent––should be directly comparable to one another. This is reflected by the use of common notation, i.e., τ and for the driving torque in the microscopic model and the continuum model, respectively, as well as γ and for the frictional drag.
| Scale | Microscopic | Continuum |
| Length | σ | |
| Time | ||
| Energy | ε |
Summary of the characteristic scales used in the microscopic and continuum models.
Supplementary Material
Acknowledgments
This work was supported as part of the Center for Bio-Inspired Energy Science, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences under Award DE-SC0000989. Computational resources and services provided by Advanced Research Computing at the University of Michigan, Ann Arbor. M.S. was supported in part by a National Science Foundation Graduate Research Fellowship under Grant DGE 0903629. D.K. acknowledges FP7 Marie Curie Actions of the European Commission (PIOF-GA-2011-302490 Actsa). N.H.P.N. also acknowledges the Vietnam Education Foundation for prior support. S.C.G. was partially supported by a Simons Investigator Award from the Simons Foundation.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1513361112/-/DCSupplemental.
References
- 1.Vicsek T, Zafeiris A. Collective motion. Phys Rep. 2012;517(3-4):71–140. [Google Scholar]
- 2.Marchetti MC, et al. Hydrodynamics of soft active matter. Rev Mod Phys. 2013;85(3):1143–1189. [Google Scholar]
- 3.Khan SM, Ali R, Asi N, Molloy JE. Active actin gels. Commun Integr Biol. 2012;5(1):39–42. doi: 10.4161/cib.18286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang S, Wolynes PG. Active contractility in actomyosin networks. Proc Natl Acad Sci USA. 2012;109(17):6446–6451. doi: 10.1073/pnas.1204205109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao T, Blackwell R, Glaser MA, Betterton MD, Shelley MJ. Multiscale polar theory of microtubule and motor-protein assemblies. Phys Rev Lett. 2015;114(4):048101. doi: 10.1103/PhysRevLett.114.048101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tailleur J, Cates ME. Statistical mechanics of interacting run-and-tumble bacteria. Phys Rev Lett. 2008;100(21):218103. doi: 10.1103/PhysRevLett.100.218103. [DOI] [PubMed] [Google Scholar]
- 7.Darnton NC, Turner L, Rojevsky S, Berg HC. Dynamics of bacterial swarming. Biophys J. 2010;98(10):2082–2090. doi: 10.1016/j.bpj.2010.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wensink HH, et al. Meso-scale turbulence in living fluids. Proc Natl Acad Sci USA. 2012;109(36):14308–14313. doi: 10.1073/pnas.1202032109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howse JR, et al. Self-motile colloidal particles: From directed propulsion to random walk. Phys Rev Lett. 2007;99(4):048102. doi: 10.1103/PhysRevLett.99.048102. [DOI] [PubMed] [Google Scholar]
- 10.Palacci J, Sacanna S, Steinberg AP, Pine DJ, Chaikin PM. Living crystals of light-activated colloidal surfers. Science. 2013;339(6122):936–940. doi: 10.1126/science.1230020. [DOI] [PubMed] [Google Scholar]
- 11.Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel type of phase transition in a system of self-driven particles. Phys Rev Lett. 1995;75(6):1226–1229. doi: 10.1103/PhysRevLett.75.1226. [DOI] [PubMed] [Google Scholar]
- 12.Czirok A, Stanley HE, Vicsek T. Spontaneously ordered motion of self-propelled particles. J Phys Math Gen. 1997;30(5):1375–1385. [Google Scholar]
- 13.Czirok A, Vicsek M, Vicsek T. Collective motion of organisms in three dimensions. Phys A: Stat Mech Appl. 1999;264(1-2):299–304. [Google Scholar]
- 14.Cavagna A, Giardina I. Bird flocks as condensed matter. Annu Rev Condens Matter Phys. 2014;5(1):183–207. [Google Scholar]
- 15.Helbing D. Traffic and related self-driven many-particle systems. Rev Mod Phys. 2001;73(4):1067–1141. [Google Scholar]
- 16.Ramaswamy S, Simha RA, Toner J. Active nematics on a substrate: Giant number fluctuations and long-time tails. Europhys Lett. 2002;62(2):196–202. [Google Scholar]
- 17.Fily Y, Marchetti MC. Athermal phase separation of self-propelled particles with no alignment. Phys Rev Lett. 2012;108(23):235702. doi: 10.1103/PhysRevLett.108.235702. [DOI] [PubMed] [Google Scholar]
- 18.Bialké J, Speck T, Löwen H. Crystallization in a dense suspension of self-propelled particles. Phys Rev Lett. 2012;108(16):168301. doi: 10.1103/PhysRevLett.108.168301. [DOI] [PubMed] [Google Scholar]
- 19.Redner GS, Hagan MF, Baskaran A. Structure and dynamics of a phase-separating active colloidal fluid. Phys Rev Lett. 2013;110(5):055701. doi: 10.1103/PhysRevLett.110.055701. [DOI] [PubMed] [Google Scholar]
- 20.Stenhammar J, Tiribocchi A, Allen RJ, Marenduzzo D, Cates ME. Continuum theory of phase separation kinetics for active Brownian particles. Phys Rev Lett. 2013;111(14):145702. doi: 10.1103/PhysRevLett.111.145702. [DOI] [PubMed] [Google Scholar]
- 21.Peruani F, Deutsch A, Bär M. Nonequilibrium clustering of self-propelled rods. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(3 Pt 1):030904. doi: 10.1103/PhysRevE.74.030904. [DOI] [PubMed] [Google Scholar]
- 22.Buttinoni I, et al. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys Rev Lett. 2013;110(23):238301. doi: 10.1103/PhysRevLett.110.238301. [DOI] [PubMed] [Google Scholar]
- 23.D’Orsogna MR, Chuang YL, Bertozzi AL, Chayes LS. Self-propelled particles with soft-core interactions: Patterns, stability, and collapse. Phys Rev Lett. 2006;96(10):104302. doi: 10.1103/PhysRevLett.96.104302. [DOI] [PubMed] [Google Scholar]
- 24.Grossman D, Aranson IS, Ben Jacob E. Emergence of agent swarm migration and vortex formation through inelastic collisions. New J Phys. 2008;10(2):23036. [Google Scholar]
- 25.Nguyen NHP, Jankowski E, Glotzer SC. Thermal and athermal three-dimensional swarms of self-propelled particles. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;86(1 Pt 1):011136. doi: 10.1103/PhysRevE.86.011136. [DOI] [PubMed] [Google Scholar]
- 26.Cates ME, Tailleur J. When are active Brownian particles and run-and-tumble particles equivalent? Consequences for motility-induced phase separation. Europhys Lett. 2013;101(2):20010. [Google Scholar]
- 27.Cohen JA, Golestanian R. Emergent cometlike swarming of optically driven thermally active colloids. Phys Rev Lett. 2014;112(6):068302. doi: 10.1103/PhysRevLett.112.068302. [DOI] [PubMed] [Google Scholar]
- 28.Soto R, Golestanian R. Self-assembly of catalytically active colloidal molecules: Tailoring activity through surface chemistry. Phys Rev Lett. 2014;112(6):068301. doi: 10.1103/PhysRevLett.112.068301. [DOI] [PubMed] [Google Scholar]
- 29.Wensink HH, Kantsler V, Goldstein RE, Dunkel J. Controlling active self-assembly through broken particle-shape symmetry. Phys Rev E Stat Nonlin Soft Matter Phys. 2014;89(1):010302. doi: 10.1103/PhysRevE.89.010302. [DOI] [PubMed] [Google Scholar]
- 30.Maude AD. Non-random distribution of bull spermatozoa in a drop of sperm suspension. Nature. 1963;200(4886):381. doi: 10.1038/200381a0. [DOI] [PubMed] [Google Scholar]
- 31.Chilukuri S, Collins CH, Underhill PT. Impact of external flow on the dynamics of swimming microorganisms near surfaces. J Phys Condens Matter. 2014;26(11):115101. doi: 10.1088/0953-8984/26/11/115101. [DOI] [PubMed] [Google Scholar]
- 32.Elgeti J, Gompper G. Run-and-tumble dynamics of self-propelled particles in confinement. Europhys Lett. 2015;109(5):58003. [Google Scholar]
- 33.Hill J, Kalkanci O, McMurry JL, Koser H. Hydrodynamic surface interactions enable Escherichia coli to seek efficient routes to swim upstream. Phys Rev Lett. 2007;98(6):068101. doi: 10.1103/PhysRevLett.98.068101. [DOI] [PubMed] [Google Scholar]
- 34.Wioland H, Woodhouse FG, Dunkel J, Kessler JO, Goldstein RE. Confinement stabilizes a bacterial suspension into a spiral vortex. Phys Rev Lett. 2013;110(26):268102. doi: 10.1103/PhysRevLett.110.268102. [DOI] [PubMed] [Google Scholar]
- 35.Lushi E, Wioland H, Goldstein RE. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc Natl Acad Sci USA. 2014;111(27):9733–9738. doi: 10.1073/pnas.1405698111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tsang AC, Kanso E. Circularly confined microswimmers exhibit multiple global patterns. Phys Rev E Stat Nonlin Soft Matter Phys. 2015;91(4):043008. doi: 10.1103/PhysRevE.91.043008. [DOI] [PubMed] [Google Scholar]
- 37.Yang X, Manning ML, Marchetti MC. Aggregation and segregation of confined active particles. Soft Matter. 2014;10(34):6477–6484. doi: 10.1039/c4sm00927d. [DOI] [PubMed] [Google Scholar]
- 38.Fily Y, Baskaran A, Hagan MF. Dynamics of self-propelled particles under strong confinement. Soft Matter. 2014;10(30):5609–5617. doi: 10.1039/c4sm00975d. [DOI] [PubMed] [Google Scholar]
- 39.Elgeti J, Gompper G. Wall accumulation of self-propelled spheres. Europhys Lett. 2013;101(4):48003. [Google Scholar]
- 40.Hernandez-Ortiz JP, Stoltz CG, Graham MD. Transport and collective dynamics in suspensions of confined swimming particles. Phys Rev Lett. 2005;95(20):204501. doi: 10.1103/PhysRevLett.95.204501. [DOI] [PubMed] [Google Scholar]
- 41.Keber FC, et al. Topology and dynamics of active nematic vesicles. Science. 2014;345(6201):1135–1139. doi: 10.1126/science.1254784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nguyen NHP, Klotsa D, Engel M, Glotzer SC. Emergent collective phenomena in a mixture of hard shapes through active rotation. Phys Rev Lett. 2014;112(7):075701. doi: 10.1103/PhysRevLett.112.075701. [DOI] [PubMed] [Google Scholar]
- 43.Ebbens S, Jones RAL, Ryan AJ, Golestanian R, Howse JR. Self-assembled autonomous runners and tumblers. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(1 Pt 2):015304. doi: 10.1103/PhysRevE.82.015304. [DOI] [PubMed] [Google Scholar]
- 44.Grzybowski BA, Stone HA, Whitesides GM. Dynamic self-assembly of magnetized, millimetre-sized objects rotating at a liquid-air interface. Nature. 2000;405(6790):1033–1036. doi: 10.1038/35016528. [DOI] [PubMed] [Google Scholar]
- 45.Yan J, Bloom M, Bae SC, Luijten E, Granick S. Linking synchronization to self-assembly using magnetic Janus colloids. Nature. 2012;491(7425):578–581. doi: 10.1038/nature11619. [DOI] [PubMed] [Google Scholar]
- 46.Martin S, Reichert M, Stark H, Gisler T. Direct observation of hydrodynamic rotation-translation coupling between two colloidal spheres. Phys Rev Lett. 2006;97(24):248301. doi: 10.1103/PhysRevLett.97.248301. [DOI] [PubMed] [Google Scholar]
- 47.Uchida N, Golestanian R. Synchronization and collective dynamics in a carpet of microfluidic rotors. Phys Rev Lett. 2010;104(17):178103. doi: 10.1103/PhysRevLett.104.178103. [DOI] [PubMed] [Google Scholar]
- 48.Yeo K, Lushi E, Vlahovska PM. Collective dynamics in a binary mixture of hydrodynamically coupled microrotors. Phys Rev Lett. 2015;114(18):188301. doi: 10.1103/PhysRevLett.114.188301. [DOI] [PubMed] [Google Scholar]
- 49.Yan J, Bae SC, Granick S. Rotating crystals of magnetic Janus colloids. Soft Matter. 2015;11(1):147–153. doi: 10.1039/c4sm01962h. [DOI] [PubMed] [Google Scholar]
- 50.Petroff AP, Wu XL, Libchaber A. Fast-moving bacteria self-organize into active two-dimensional crystals of rotating cells. Phys Rev Lett. 2015;114(15):158102. doi: 10.1103/PhysRevLett.114.158102. [DOI] [PubMed] [Google Scholar]
- 51.Liu AJ, et al. Opportunities in theoretical and computational polymeric materials and soft matter. Soft Matter. 2015;11(12):2326–2332. doi: 10.1039/c4sm02344g. [DOI] [PubMed] [Google Scholar]
- 52.Cates ME, Marenduzzo D, Pagonabarraga I, Tailleur J. Arrested phase separation in reproducing bacteria creates a generic route to pattern formation. Proc Natl Acad Sci USA. 2010;107(26):11715–11720. doi: 10.1073/pnas.1001994107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cates ME. Diffusive transport without detailed balance in motile bacteria: Does microbiology need statistical physics? Rep Prog Phys. 2012;75(4):042601. doi: 10.1088/0034-4885/75/4/042601. [DOI] [PubMed] [Google Scholar]
- 54.Park JI, et al. Terminal supraparticle assemblies from similarly charged protein molecules and nanoparticles. Nat Commun. 2014;5(5):3593. doi: 10.1038/ncomms4593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Shah AA, Schultz B, Zhang W, Glotzer SC, Solomon MJ. Actuation of shape-memory colloidal fibres of Janus ellipsoids. Nat Mater. 2015;14(1):117–124. doi: 10.1038/nmat4111. [DOI] [PubMed] [Google Scholar]
- 56.Paxton WF, et al. Catalytic nanomotors: Autonomous movement of striped nanorods. J Am Chem Soc. 2004;126(41):13424–13431. doi: 10.1021/ja047697z. [DOI] [PubMed] [Google Scholar]
- 57.Anderson JA, Lorenz CD, Travesset A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J Comput Phys. 2008;227(10):5342–5359. [Google Scholar]
- 58.Nguyen TD, Phillips CL, Anderson JA, Glotzer SC. Rigid body constraints realized in massively-parallel molecular dynamics on graphics processing units. Comput Phys Commun. 2011;182(11):2307–2313. [Google Scholar]
- 59.Weeks J, Chandler D, Andersen HC. Role of repulsive force in determining the equilibrium structure of simple liquids. J Chem Phys. 1971;54(12):5237–5247. [Google Scholar]
- 60. Sabrina S, Spellings M, Glotzer SC, Bishop KJM (2015) Coarsening dynamics of binary liquids with active rotation. arXiv:1507.06715. [DOI] [PubMed]
- 61.Speck T, Bialké J, Menzel AM, Löwen H. Effective Cahn-Hilliard equation for the phase separation of active Brownian particles. Phys Rev Lett. 2014;112(21):218304. [Google Scholar]
- 62.Wittkowski R, et al. Scalar φ4 field theory for active-particle phase separation. Nat Commun. 2014;5:4351. doi: 10.1038/ncomms5351. [DOI] [PubMed] [Google Scholar]
- 63.Jasnow D, Vinals J. Coarse-grained description of thermo-capillary flow. Phys Fluids. 1996;8(3):660–669. [Google Scholar]
- 64.Anderson DM, McFadden GB, Wheeler AA. Diffuse-interface methods in fluid mechanics. Annu Rev Fluid Mech. 1998;30(1):139–165. [Google Scholar]
- 65.Rosensweig RE. Continuum equations for magnetic and dielectric fluids with internal rotations. J Chem Phys. 2004;121(3):1228–1242. doi: 10.1063/1.1755660. [DOI] [PubMed] [Google Scholar]
- 66.García-Rojo R, Luding S, Brey JJ. Transport coefficients for dense hard-disk systems. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(6 Pt 1):061305. doi: 10.1103/PhysRevE.74.061305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.