Rheological characteristics of inulin solution at low concentrations: Effect of temperature and solid content

Abstract

The rheological properties of inulin solution was investigated at different solid content (X_s) ranging from 1 to 12 % at wide range of temperatures ranging from 10 to 85 °C. The rheological parameter shear stress was measured upto a shear rate of 300 s⁻¹ using concentric cylinders attachment by controlled stress rheometer. The investigation showed that the inulin solution behaved like Newtonian liquid and viscosity (η) was in the range 2.0998 to 3.2439 mPa s depending upon the concentration and temperature studied. The temperature dependency of Newtonian viscosity of inulin solution was described by Arrhenius equation (r > 0.88, p < 0.05) and activation energy (E_a) for viscous flow was in the range 2.111 to 3.013 kJ/mol depending upon the solid content studied. The flow activation energy (E_a) of inulin solution was significantly (p < 0.05) affected by solid content and described by exponential type equation (r = 0.9646, rmse% = 1.07, p < 0.001). Effect of solid content on Newtonian viscosity was described by linear as well as power law models depending upon the temperature studied. The combined effect of temperature and solid content on Newtonian viscosity of inulin solution was described by power law type equation and represented as η = 0.8835* (X_s)^0.0731 *Exp(296.410/T), (r = 0.9538, p < 0.001, rmse% = 0.15) Where η is Newtonian viscosity in mPa s, X_s is solid content in % and T is temperature in Kelvin (K).

Introduction

Inulin is naturally occurring polysaccharides produced by many plants, which includes onion, banana, garlic, wheat, asparagus, Jerusalem artichoke and chicory. The Inulin belongs to a class of dietary fibers known as fructans and is a storage polysaccharide present in more than 30,000 species of plants. Inulin is used for reserving energy as well as regulating cold resistance found in roots and rhizomes in plants and is soluble in water. Plants can change the osmotic potential of cells by changing the degree of polymerization of inulin molecules by the process of hydrolysis. Due to change in osmotic potential without changing the total amount of carbohydrate, plants can withstand cold and drought during winter periods (Vijn and Smeekens 1999).

Inulin is a heterogeneous collection of fructose polymers. It is a fructan that is linked by β (2–1) glycosodic bonds and contains either a β-D-fructose or an α-D-glucose at terminal position. The degree of polymerization of standard inulin ranges from 2 to 60 with an average degree of polymerization is about 12. The fractions with a degree of polymerization lower than 10 referred as short-chained fructo-oligosaccharides and the long-chained molecules referred as inulin. Due to the β (2–1) linkages, inulin is not digested by enzymes in the human alimentary system, contributing to its functional properties: reduced calorie value, dietary fiber, texturizing agent, encapsulating agent, fat and sugar substitute and prebiotic effects. Inulin has attracted more attention in the food and pharmaceutical industry due its multi functional properties such as dietary fiber, prebiotic nature, modulation of microbial fermentation, reducing fat and pH reduction; these properties have a direct effect on reducing intestinal disturbances, constipation, hyperlipidaemia, hyperglycemia and intestinal cancer (Meyer et al. 2011; Pinto et al. 2012). Inulin exhibits a prebiotic function of stimulating the growth of Bifidobacterium sp., generally considered as health promoting and beneficial organism in large intestine increases the calcium absorption and reduces the cholesterol level (Liong and Shah 2005).

The rheological properties of fluid food are an important aspect in the field of food process engineering such as, in developing food processing techniques, design of processing equipments, structural understanding and quality evaluation of food and raw agricultural materials in the field of food science and technology. Addition of food additives such as gums, stabilizers, thickeners, gelling agents affects the textural and rheological properties of food systems. The rheological behavior of fluids is evaluated by the measurement of shear stress-shear rate data and representing the experimental data by rheograms and empirical equations as a function of concentration, temperature, particle size, processing conditions, the addition of additives etc. These properties are helpful in understanding the flow mechanism and structural understanding of complex fluid systems. The rheological properties of fluid foods are affected by temperature, concentration of solute, its molecular weight, pressure, suspended matter and level of additives (Bourne 2002). The relationship between shear stress and shear rate was described by Ostwald-De-Waele model or power law equation (Sanchez et al. 2009; Sogi et al. 2010)

$$\sigma =K{\gamma }^n$$ 1

where σ is shear stress (Pa), K is a consistency index (Pa sⁿ), γ is the shear rate (s⁻¹) and n is the flow behavior index (−). If the fluid is Newtonian in nature, n = 1 and hence K becomes viscosity η (Pa s) of the fluid. In general, liquid food such as fruit and vegetable juices behave like Newtonian fluids; so their flow behavior would be Newtonian in nature. Several investigators reported that clarified and depectinated juices and their concentrates exhibit Newtonian flow behavior. (Manjunatha and Raju 2013; Pranjal et al. 2013).

$$\sigma =\eta \gamma$$ 2

where σ is shear stress (Pa), η is coefficient of viscosity (Pa s) and γ is the shear rate (s⁻¹). Several authors have used Newtonian equation for describing rheological behavior of liquid food products like pomegranate juice (Altan and Maskan 2005; Kaya and Sozer 2005), Pekmez (Kaya and Belibagli 2002), lime juice (Manjunatha et al. 2012a), gooseberry juice (Manjunatha et al. 2012b), Tender coconut water (Manjunatha and Raju 2013), liquorice extract (Maskan 1999).

The rheological properties of aqueous solution of food additives effect of concentration, temperature and blending was investigated (Gomez-Diaz and Navaza 2003). Marcotte et al. (2001) studied the rheological properties of hydrocolloids such as carrageenan, pectin, gelatin, starch and xanthan as a function of concentration and temperature. Rheological behavior of syrups containing sugar substitutes such as sorbitol, maltodextrin, polydextrose and their combination were investigated (Chetana et al. 2004). The rheological characteristics of different gums namely gum ghatti, sodium alginate, Alyssum homolocarpum seed gum, carboxymethylcellulose, xanthan gum, gum Arabic were studied (Roopa and Bhattacharya 2009; Koocheki and Razavi 2009). The effect of inulin and pectin on rheological and thermal properties of potato starch paste and gel was investigated (Witczak et al. 2014). The rheological, textural and sensory properties kefir (fermented beverage) with inulin was investigated (Glibowski and Kowalska 2012). The effect of inulin on texture and clarity of gellan gels was investigated by large compression deformation and reported that increase in inulin concentration resulted in an increase in gel strength, which was greater for higher potassium concentration (Evageliou et al. 2010). Alvarez et al. (2011) studied the effect of inulin addition on viscoelastic properties of fresh and frozen/thawed mashed potatoes with and without added cryoprotectants and reported that inulin concentration marginally affected the rheological properties. The addition of inulin enhances the viscoelastic properties of glucono-δ-lactone (GDL)-coagulated silken tofu without increasing the protein concentration and effect in pH reduction (Tseng and Xiong 2009). The rheological and physico-chemical characteristics of prebiotic microfiltered fermented milk were investigated and was found that it had greater thixotropy and the hysteresis was lower with an increase in the temperature (Debon et al. 2010). The concentrated inulin solution behaved like pseudoplastic fluid, and the flow behavior was described by Herschel-Bulkley, Casson, cross and power law models (Toneli et al. 2008). Rheological characterization of inulin was investigated with combination of other gums such as xanthan, sodium alginate, calcium alginate, starch, cabroxymethylcellulose and microcrystalline cellulose. However, there is no information on rheological properties of inulin at low concentrations, which is very useful and important for the development of novel food products and understanding the behavior of inulin with other food component. The present investigation is undertaken to study the rheological behavior of inulin at low concentration in a wide range of temperature and modelling of these properties.

Material and methods

Raw material

Inulin powder “Fructafit® HD” having characteristic of dry matter 96.37 %, ash 0.2 % and negligible protein and fat were obtained from Adept Impex Pvt Lts, Agra, India

Solution preparation

The different concentrations of inulin solution were prepared by dissolving appropriate amount of inulin solids into an appropriate amount distilled water. The solutions were prepared with at a speed of 200 rotations per minute for 10 min using a magnetic stirrer (Model: D-55122 Mainz, Schoot instrument, Gmbh, Germany).

Rheological measurement

The rheological measurements were carried out using MCR100 controlled stress rheometer equipped with coaxial cylinders (CC 27) and the radii ratio of coaxial cylinders was 1.08477. The rheometer was equipped with an electric temperature controlled peltier system (TEZ-15P-C) to control the experimental temperature with an accuracy of 0.01 °C and a circulating water bath was used (Viscotherm VT-2). The rheological parameter, shear stress (Pa) was measured by increasing the shear rate linearly up to a maximum of 750 s⁻¹ for duration of 10 min. A total of 30 shear stress-shear rate data points were collected and analyzed using universal software US200. The rheological measurements were carried out at different temperatures ranging from 10 to 85 °C. All the measurements were carried out in triplicate and fresh sample was used in each measurement.

Statistical analysis

The experimental results and data analysis were carried out using statistical software (SYSTAT 12.0). The fitting and estimates were calculated at 5 % significance level (p < 0.05). The suitability of the models fitting was evaluated by determining the correlation coefficient (r) and root mean square error percent (rmse %) which was evaluated by the following equation:

$$\mathit{rmse}\%=100/n{\left[\sum {\left(W_{\mathit{exp}}-W_{\mathit{cal}}/W_{\mathit{exp}}\right)}^2\right]}^{1/2}$$ 3

where W_exp is the experimental value, W_cal is the calculated value and n is the number of data sets. The suitability of the model was decided based on higher correlation coefficient (r) and low percent root mean square error (rmse %) values and level of significance (p < 0.05).

Results and discussion

Flow behavior

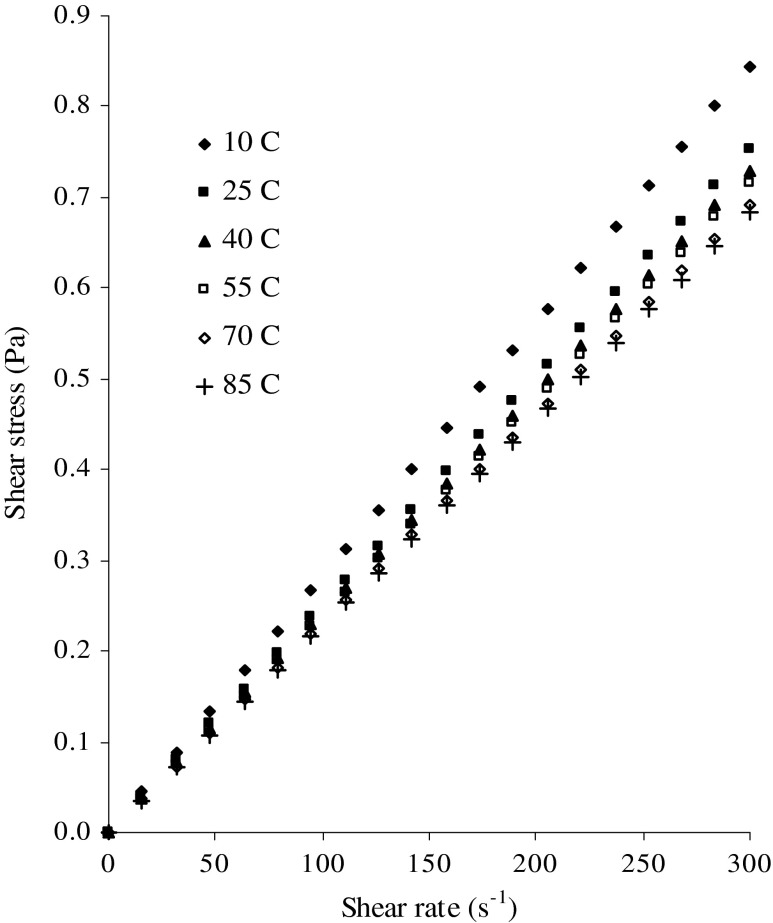
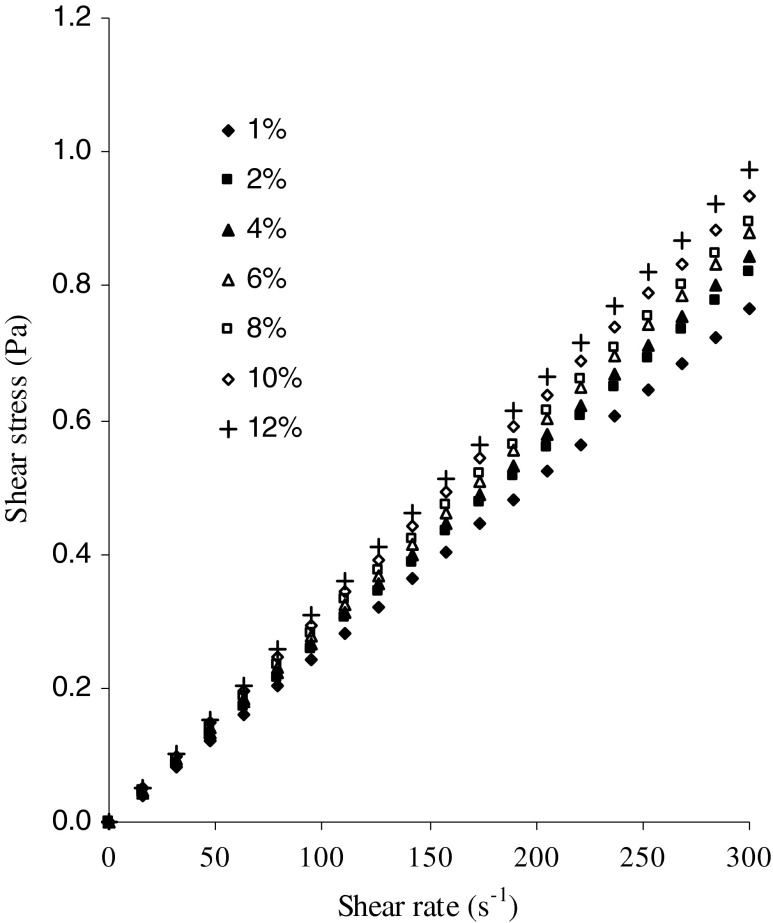
Figure 1 shows the relation between shear stress and shear rate of inulin solution at different temperatures at a concentration of 4 % solid content and Fig. 2 shows the relation between shear stress and shear rate of inulin solution at different solid content at a temperature of 10 °C. The flow behavior of inulin solution showed that there was a marked linear increasing shear stress with respect to increase in shear rate and flow curve passed through origin which indicating the flow behavior of inulin solution is Newtonian in nature. The Newtonian model was able to describe the relationship between shear stress and shear rate data. The Newtonian viscosity of inulin solution could be estimated using Newtonian model equation described by equation 2. The correlation coefficient values were greater than 0.99, (0.9902 ≤ r ≤ 0.9990, p < 0.001). The magnitude of viscosity of inulin solution was in the range 2.0998 to 3.2439 mPa s depending upon the solid content and temperature studied as reported in Table 1. The viscosity of inulin solution increased with increase in solid content and decreased with increase in temperature. The viscosity of fluid strongly dependent on inter-molecular forces between the molecules and solute-solvent interactions, which is due to inter-molecular spacings and strength of bonding between the molecules. The inter-molecular spacings and inter-molecular bondings are markedly affected by the concentration and temperature (Krokida et al. 2001; Rao 2007). The flow behavior of inulin solution behaved like a Newtonian fluid up to a concentration of 12 %. Bishay (1998) also reported that the flow behavior of inulin solution behaved like a Newtonian fluid up to a concentration of 15 % and even at 20 % solid content with low molecular weight, soluble inulin system behaved like Newtonian liquid, small amount of suspended inulin does not alter the Newtonian behavior. The viscosity of beetroot juice concentrates had a lower than concentrated fruit juice with same soluble solid content and at the same temperature studied. This deviation was attributed by its different levels of individual constituent sugars present in the juice (Juszczak et al. 2010). Chetana et al. (2004) reported that sugar and sorbital solutions behaved like Newtonian fluids while at other syrups such as polydextrose, maltodextrin and polydextrose combination behaved like shear thinning non-Newtonian flow behavior with yield stress. The results showed that the flow behavior of polydextrose and combination of maltodextrin + polydextrose syrups obeyed Hershel–Bulkley model. Sodium alginate dispersions exhibit shear-thinning characteristics and flow behavior was described by cross model.

Fig. 1.

Flow behavior of inulin solution at different temperatures at a constant concentration of 4 %

Fig. 2.

Flow behavior of inulin solution at different concentration at a constant temperature of 10 °C

Table 1.

Newtonian viscosity values of inulin solution at different solid content and temperatures

Solid content (%)	Temperature (°C)	Newtonian viscosity (mPa s)	r
1	10	2.5514 ± 0.0006	0.9939
	25	2.3562 ± 0.0004	0.9990
	40	2.2351 ± 0.0006	0.9988
	55	2.1970 ± 0.0001	0.9963
	70	2.1557 ± 0.0001	0.9990
	85	2.0998 ± 0.0003	0.9902
2	10	2.7360 ± 0.0042	0.9930
	25	2.4590 ± 0.0004	0.9955
	40	2,2907 ± 0.0005	0.9984
	55	2.2860 ± 0.0001	0.9985
	70	2.2621 ± 0.0001	0.9979
	85	2.2588 ± 0.0002	0.9959
4	10	2.8170 ± 0.0012	0.9944
	25	2.5104 ± 0.0008	0.9970
	40	2.4320 ± 0.0005	0.9978
	55	2.3865 ± 0.0001	0.9979
	70	2.3079 ± 0.0002	0.9977
	85	2.2758 ± 0.0001	0.9977
6	10	2.9285 ± 0.0008	0.9916
	25	2.5781 ± 0.0003	0.9938
	40	2.5324 ± 0.0002	0.9970
	55	2.4902 ± 0.0004	0.9963
	70	2.4017 ± 0.0003	0.9988
	85	2.3149 ± 0.0001	0.9902
8	10	2.9861 ± 0.0006	0.9953
	25	2.6644 ± 0.0004	0.9945
	40	2.5626 ± 0.0002	0.9942
	55	2.5960 ± 0.0001	0.9952
	70	2.4372 ± 0.0002	0.9979
	85	2.3294 ± 0.0003	0.9973
10	10	3.1138 ± 0.0003	0.9918
	25	2.7213 ± 0.0006	0.9942
	40	2.6579 ± 0.0004	0.9972
	55	2.6248 ± 0.0001	0.9945
	70	2.5320 ± 0.0003	0.9983
	85	2.3798 ± 0.0002	0.9973
12	10	3.2439 ± 0.0019	0.9920
	25	2.8283 ± 0.0002	0.9940
	40	2.6522 ± 0.0002	0.9953
	55	2.6486 ± 0.0003	0.9944
	70	2.5867 ± 0.0002	0.9985
	85	2.3961 ± 0.0002	0.9973

(n = 3), Mean ± S D

The thixotropic and time-dependent flow behavior parameters were sensitive to the concentration of alginate and temperature (Roopa and Bhattacharya 2009). Arabic gum aqueous solutions behaved like a non-Newtonian pseudoplastic fluid and power law model able to describe the rheological behavior of Arabic gum solution (Gomez-Diaz and Navaza 2003). The high intensity ultrasound affects the rheological properties of guar, xanthan and pectin dispersions. Sonication affected the consistency index (n), flow behavior index (k) and power law constants of complex viscosity and changes in the rheological properties of guar gum and pectin dispersions were significantly higher than that of xanthan gum dispersions (Tiwari et al. 2010). The addition of inulin markedly enhances the viscoelastic properties of glucono-δ-lactone (GDL)-coagulated silken tofu. This was attributed that heating could unfold the inulin native structure as result chain length is increased, which could be increased the physical interactions between protein molecules and unfolded long chain fructans (Tseng and Xiong 2009). The rheological properties of inulin solution depend on the nature of the solute and its molecular weight, molecular size and shape, solute-solvent interactions, processing conditions, state of hydration and presence of other molecules, pH, temperature etc. (Glibowski and Kowalska 2012; Evageliou et al. 2010; Alvarez et al. 2011; Juszczak et al. 2012; Tarrega et al. 2011; Glibowski 2010)

Effect of temperature

The temperature of a fluid had a major effect on the viscosity similar to the effect on the consistency coefficient for non-Newtonian fluids. The increase in temperature of fluid will enhances the mobility of the molecules and increase in inter-molecular spacing, which decreases the flow resistance of a fluid. The viscosity of inulin solution decreased with increase in temperature. The variation in viscosity of inulin solution with temperature was significantly higher at higher solid content. The effect of temperature on the viscosity of inulin solution with different solid content was described using the Arrhenius equation:

$$\eta ={\eta }_{\infty }Exp\left(E_a/RT\right)$$ 4

where η = Viscosity (Pa s), η_∞ = Material constant/ pre-exponential coefficient/frequency factor (Pa s), E_a = activation energy of viscous flow (J/mol), R = Gas constant (J/mol K) and T = absolute Temperature (K).

The parameters of Arrhenius model equation (eqn 4) which was determined by the method of least square approximation and is reported in Table 2. The correlation coefficient was greater than 0.88 and the activation energy for viscous flow was in the range 2.111 to 3.013 kJ/mol depending upon the solid content of inulin solution. The flow activation energy (E_a) was defined as minimum energy required for overcoming the energy barrier before the elementary flow can occur. The viscous flow occurs as a sequence of events which are shift of particles from one equilibrium position to another position by overcoming a potential energy barrier in the direction of shear force. The barrier height determines the free activation energy of viscous flow. The higher activation energy value indicates a greater influence of temperature on the viscosity, i.e. more rapid change in viscosity with temperature. The magnitude of energy of activation of viscous flow increased significantly (p < 0.05) with increase in solid content of the inulin solution, indicating that higher energy was required to overcome potential energy barrier at higher solids content, The frequency factor (η_∞) is markedly changed with increase in solid content and reported in Table 2. Therefore, the temperature had a greater effect on viscosity at higher solid contents. When the temperature increased, the thermal energy of the molecules and intermolecular spacing increased markedly, which tend to decrease in the magnitude of viscosity (Rao 2007). The magnitude of flow activation energy of inulin solution is low compared to that of other fluid foods at the same levels of solid content such as pineapple juice (Shamsudin et al.. 2007), orange juice (Ibraz et al. 2009), lime juice (Manjunatha et al. 2013a), gooseberry juice (Manjunatha et al. 2012b), Tender coconut water (Manjunatha and Raju 2013), sapota juice (Pranjal et al. 2013), blueberry puree (Nindo et al. 2007), ultraviolet-irradiated and thermally pasteurized pineapple juice (Shamsudin et al. 2013), liquorice (Glycyrrhiza glabra) extract (Maskan 1999), carbohydrate solutions, namely fructose, sucrose and glucose (Telis et al. 2007). The flow activation energy of these fluids was high because its viscosity is very sensitive to temperature due to increase in mobility of the molecules as well as an increase in inter-molecular spacing and also may be due to low molecular weight. The viscosity of inulin solution was decreased marginally at higher temperature due increase solubilisation due to the dissolution of high molecular weight compounds which leads to increase marginally in viscosity of inulin solution and increase in inter-molecular spacing the viscosity would be decreased, the net result will be marginal changes of viscosity of inulin solution and temperature as a dual role in the magnitude of viscosity values, this may be reason for marginal change in the magnitude of flow activation energy of inulin solution at low concentrations as reported (Toneli et al. 2008). The Arrhenius equation was satisfactorily described the temperature dependency of viscosity of model solutions such as sucrose, glucose, fructose and the flow activation energy was correlated with solute content by unique equation as a function of an effective volumetric fraction of solute (Telis et al. 2007). The activation energy for viscous flow was markedly affected by enzyme treatment of goldenberry juice (Sharoba and Ramadan 2011). The flow activation energy of concentrated orange juice was increased marginally with shear rate and a logarithmic model was reported for variation of flow activation energy with shear rate (Falguera and Ibarz 2010). The flow activation energy of pineapple juice was not affected by ultraviolet irradiation as well as thermal pasteurization treatment as compared to that of untreated juice (Shamsudin et al. 2013). The flow activation of fluids were depends on nature of solute, size, shape and molecular weight, solute-solvent interaction, state of hydration, temperature range studied.

Table 2.

Parameters of Arrhenius equation relating Newtonian viscosity of inulin solution with temperatures at different solid contents

Solid content (%)	η∞ (mPa s)	Flow activation energy (Ea) (k J/mol)	r
1	1.0188a ± 0.0007	2.111a ± 0.002	0.9678
2	1.0527b ± 0.0045	2.153b ± 0.013	0.8873
4	1.0237a ± 0.0008	2.307c ± 0.002	0.9477
6	1.0388c ± 0.0010	2.361d ± 0.003	0.9415
8	1.0189a ± 0.0006	2.467e ± 0.004	0.9479
10	0.9900d ± 0.0006	2.620f ± 0.002	0.9440
12	0.8698e ± 0.0019	3.013g ± 0.006	0.9440

(n = 3), Mean ± S D, Different superscripts in a column shows significantly different at p < 0.05

Effect of solid content on flow activation energy

The flow activation energy of inulin solution is increased significantly (p < 0.05) with increase in solid content. The variation of activation energy with concentration could be described by different empirical models, namely linear, power law and exponential type relations as described

$$\begin{array}{l}{E}_a=a+b{X}_s\hfill \\ E_a=a{\left(X_s\right)}^b\hfill \\ E_a=aExp\left(b{X}_s\right)\hfill \end{array}$$ 5

where E_a is the activation energy for viscous flow (kJ/mol), a is empirical constant (kJ/mol), X_s is solid content (%), b is empirical constants (%⁻¹). These models were fitted with activation energy values which were obtained by the Arrhenius equation at different solid content by least square approximation method at 5 % significance level (p < 0.05). The parameters of the three models, correlation coefficient (r) and root mean square error percent (rmse%) values were reported in Table 3. The investigation showed that the exponential model was better describe the variation of flow activation energy with solid content of inulin solution since the correlation is high and low root mean square error values compare to that of other models such as linear and power law models and described as

$$E_a=2.0092*Exp\left(0.0301*X_s\right),\left(r=0.9649,\mathit{rmse}\%=1.07,p<0.001\right)$$

Table 3.

Parameters of different models relating to flow activation energy to total solid content of inulin solution

Model	a (k J/mol)	b (%−1)	r	rmse %
Ea = a + b Xs	1.9900*** ± 0.0023	0.0721*** ± 0.0004	0.9550	1.20
Ea = a (Xs)b	1.9822*** ± 0.0028	0.1297* ± 0.0007	0.8732	2.00
Ea = a *Exp(b Xs)	2.0092*** ± 0.0019	0.0301*** ± 0.0001	0.9649	1.07

(n = 3), Mean ± S D, ^*** p < 0.001, ^** 0 < 0.01, ^* p < 0.05

Where E_a is flow activation energy in kJ/mol, Xs is solid content in %. This indicated that the flow activation energy increased exponentially with solid content and the variation of the coefficient of solid content is about 0.0301 %⁻¹. Similar types of results reported with a comparable magnitude of the coefficient of solid content for different fluid foods such as pomegranate juice (Altan and Maskan 2005; Kaya and Sozer 2005), lime juice (Manjunatha et al. 2012a), gooseberry juice (Manjunatha et al. 2012b), tender coconut water (Manjunatha and Raju 2013), sapota juice (Pranjal et al. 2013). It was reported that flow activation energy of liquorice (Glycyrrhiza glabra) extract is increased quadratically with soluble solid content, whereas it was increased significantly with square of total soluble solid content for blue berry and raspberry juices (Nindo et al. 2005). The flow activation energy was increased linearly with total dissolved solid content, in case of blueberry puree (Nindo et al. 2007). The deviation in models and model coefficient was due nature solute, molecular weight, size, shape, solute-solvent interactions, hydration state and range of temperature and solid content studied.

Effect of solid content

The concentration of the solids had a strong significant effect on the viscosity of the Newtonian fluids, where as consistency index and apparent viscosity of non-Newtonian fluids (Krokida et al. 2001). The viscosity of a fluid depends on the nature of solvent, nature of solute, their interaction, and amount of solid content in solution, solute shape, size, molecular weight and hydration state. The viscosity of inulin solution is increased significantly (p < 0.05) with increase in solid content. The variation in viscosity with solid content was due to variation in the degree of hydration of solute molecules, solute-solvent interactions and inter-molecular spacing. The variation of viscosity of with solid content was in very important in understanding the interaction between the molecules. The different empirical models, namely linear, power law and exponential model were used to investigate the variation in viscosity with solid content in different temperature studied. Different investigators were reported these models for establishing relation between rheological properties of fluid with solid contents and described as

$$\begin{array}{l}\mathrm{Linear}\mathrm{model}\mathrm{equation}:\eta =a+b{X}_s\hfill \\ \mathrm{Power}\mathrm{law}\mathrm{type}:\eta =a{\left(X_s\right)}^b\hfill \\ \mathrm{Exponential}\mathrm{type};\mathrm{First}\mathrm{order}:\eta =aExp\left(b{X}_s\right)\hfill \end{array}$$ 6

where η is the Newtonian viscosity in mPa s, a is empirical constant in mPa s, b is constant in %⁻¹ and X_s is solid content in %. The parameters of the above three model equations were estimated by the method of least square approximation at 95 % confidence level (p < 0.05). The parameters of variation in viscosity of inulin solution with solid content of three models, namely linear, power law and exponential model with a correlation coefficient (r) and root mean square error percent (rmse%) at different temperatures were reported in Tables 4, 5 and 6 respectively. The correlation coefficients were 0.8937 ≤ r ≤ 0.9919, 0.9594 ≤ r ≤ 0.9889 and 0.8899 ≤ r ≤ 0.9915 for linear, power law and exponential models respectively and root mean square error percentage values were 0.37 ≤ rmse% ≤ 0.72, 0.37 ≤ rmse% ≤ 0.62 and 0.30 ≤ rmse% ≤ 0.73 for linear, power law and exponential models respectively. The linear model equation is better to explain the variation of viscosity with solid content at 10 °C, 25 °C and 70 °C temperatures, whereas power law relation is better to describe the viscosity of inulin solution at 40 °C, 55 °C and 85 °C. This was due high correlation coefficient and lower root mean square error values. These deviations may be attributed by solubilisation of inulin at different temperatures. The inulin undergo some transformational changes in dilute solution and temperature marked affected structural arrangement in aqueous phase/

Table 4.

Parameters of linear model relating to Newtonian viscosity with solid content of inulin solution at different temperatures

Temperature (°C)	a (mPa s)	b (%−1)	r	rmse%
10	2.5671a ± 0.0008	0.0560a ± 0.0001	0.9834	0.55
25	2.3472b ± 0.0002	0.0392b ± 0.0001	0.9919	0.29
40	2.2376c ± 0.0005	0.0395c ± 0.0001	0.9658	0.61
55	2.1979d ± 0.0012	0.0425d ± 0.0001	0.9719	0.59
70	2.1582e ± 0.0002	0.0367e ± 0.0001	0.9876	0.37
85	2.1610f ± 0.0002	0.0216f ± 0.0000	0.8937	0.72

(n = 3), Mean ± S D, Different superscripts in a column shows significantly different at p < 0.05

Table 5.

Parameters of power law model relating to Newtonian viscosity with solid content of inulin solution at different temperatures

Temperature (°C)	a (mPa s)	b (%−1)	r	rmse%
10	2.5340a ± 0.0008	0.0886a ± 0.0002	0.9734	0.62
25	2.3275b ± 0.0003	0.0681b ± 0.0001	0.9628	0.58
40	2.2049c ± 0.0005	0.0754c ± 0.0001	0.9886	0.37
55	2.1648d ± 0.0012	0.0816d ± 0.0002	0.9889	0.39
70	2.1361e ± 0.0001	0.0703e ± 0.0001	0.9748	0.49
85	2.1353e ± 0.0002	0.0461f ± 0.0001	0.9594	0.44

(n = 3), Mean ± S D, Different superscripts in a column shows significantly different at p < 0.05

Table 6.

Parameters of exponential model relating to Newtonian viscosity with solid content of inulin solution at different temperatures

Temperature (°C)	a (mPa s)	b (%−1)	r	rmse%
10	2.5823a ± 0.0006	0.0191a ± 0.0000	0.9815	0.59
25	2.3534b ± 0.0030	0.0151b ± 0.0001	0.9915	0.30
40	2.2487c ± 0.0004	0.0157c ± 0.0001	0.9598	0.67
55	2.2107d ± 0.0011	0.0170d ± 0.0002	0.9654	0.66
70	2.1664e ± 0.0002	0.0153e ± 0.0001	0.9857	0.40
85	2.1657e ± 0.0001	0.0099f ± 0.0001	0.8899	0.73

(n = 3), Mean ± S D, Different superscripts in a column shows significantly different at p < 0.05

Combined effect of temperature and solid content

It is very important to know the combined effect of temperature and solid content on viscosity of inulin solution for understanding behavior of at different temperature and concentration for development of novel products for different applications. It is important to obtain a single equation which describes both temperature and solid content on viscosity inulin solution. Several authors have used different equations to describe the combined effect of temperature and solid content on the viscosity of the fluids (Altan and Maskan 2005; Kaya and Sozer 2005; Manjunatha et al. 2012a, b; Manjunatha and Raju 2013; Pranjal et al. 2013; Juszczak et al. 2010)

$$\begin{array}{l}\mathrm{Linear}\mathrm{equation}:\eta =a*\left(c{X}_s+d\right)*Exp\left(E_a/RT\right)\hfill \\ \mathrm{Power}\mathrm{law}\mathrm{equation}:\eta =a{\left(X_s\right)}^{c*}Exp\left(E_a/RT\right)\hfill \\ \mathrm{Exponential}\mathrm{equation}:\eta =a^{*}Exp\left(E_a/RT+c{X}_s\right)\hfill \end{array}$$ 7

Where η is viscosity in mPa s, X_s is solid content in %, Ea is flow activation energy J/mol, R is universal gas constant in J/mol K, T is absolute temperature in Kelvin (K) and a, b. c. d are empirical constants.

The parameters of the three models were estimated by multiple regression analysis by the method of least square approximation at a significance level of 5 % (p < 0.05). The suitability of the model was decided based on correlation coefficient (r) and percent root mean square error (rmse%) values and the level of significance. The parameters of the models, correlation coefficient (r) and root mean square percent (rmse%) are reported in Table 7. The correlation coefficient (r) is 0.9528, 0.9538 and 0.9515 for linear, power law and exponential models respectively and root mean square error percent (rmse%) is 0.19, 0.15 and 0.20 for linear, power law and exponential models respectively. The power law model equation is better to describe the combined effect of temperature and solid content on viscosity of inulin solution at different temperature and concentration due high correlation coefficient and lower root mean square error value. The combined equation represented as

$$\eta =0.8835*{\left({\mathrm{X}}_{\mathrm{s}}\right)}^{0.0731}*\mathrm{E}\mathrm{x}\mathrm{p}\left(296.410/\mathrm{T}\right),\left(\mathrm{r}=0.9538,\mathrm{p}<0.001,\mathrm{rmse}\%=0.15\right)$$

Table 7.

Parameters of different models relating to combined effect of solid content and temperature on Newtonian viscosity of inulin solution

Model	a (mPa s)	b = Ea/R (K)	c (%−1)	d (−)	r	rmse %
Linear equation: η = a*(c Xs + d)*Exp(Ea/RT)	0.2674** ± 0.0100	296.514*** ± 0.002	0.0584** ± 0.0023	3.346* ± 0.127	0.9528	0.19
Power law equation: η = a (Xs)c *Exp(Ea/RT)	0.8835*** ± 0.0005	296.410*** ± 0.173	0.0731*** ± 0.0001	–	0.9538	0.15
Exponential type equation: η = a *Exp(Ea/RT + c Xs)	0.8976*** ± 0.0004	296.614*** ± 0.176	0.0156*** ± 0.0001	–	0.9515	0.20

(n = 3), Mean ± S D, ^*** p < 0.001, ^** p < 0.01, ^* p < 0.05

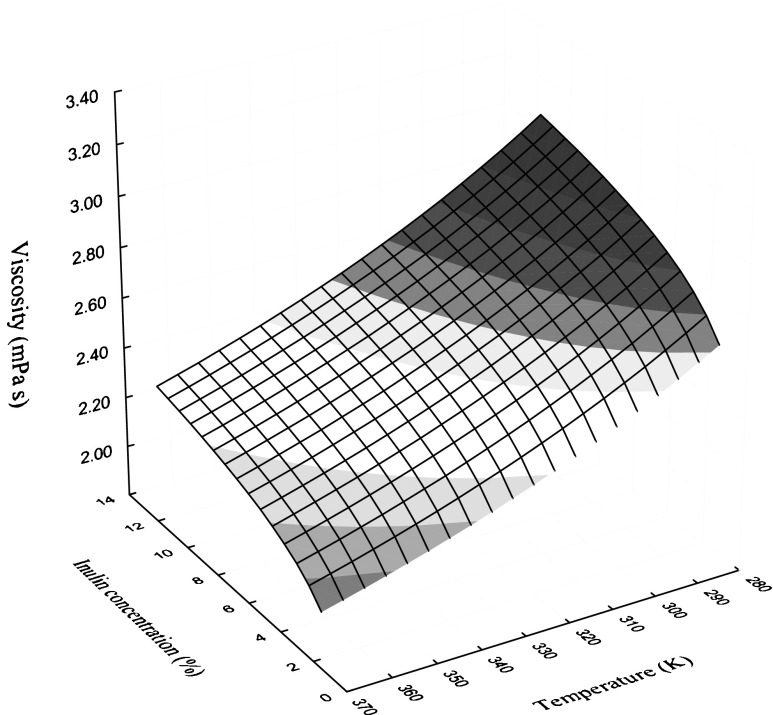
where η is viscosity in mPa s, T is temperature in Kelvin (K) and X_s is solid content in %. The viscosity of inulin solution was significantly (p < 0.001) affected by temperature and solid content. The surface plot that described the combined effect of temperature and total soluble solid content on viscosity of inulin solution at different temperatures and concentrations is shown in Fig. 3. The magnitude of viscosity depends on both temperature and solid content of inulin solution. At lower temperatures the magnitude of viscosity increased rapidly with solid content and increased marginally at higher temperatures, this was due to increase in thermal energy of the molecules and increase in intermolecular spacing at higher temperatures this strongly affected the viscosity. Similar type model was reported for rheological properties of clarified banana juice (Khalil et al. 1989). Pure and formulated chicory extract with hydrolyzed and modified starches exhibited non-Newtonian shear thinning flow behavior and flow behavior index for formulating chicory extracts are higher than those for pure extract. The apparent viscosity of suspension contained chicory extract formulated with two different starches namely hydrolyzed and modified are markedly influenced by a fraction and percentage of total starch in the system and temperature does not affect the apparent viscosity of the system (Nogueira et al. 2007). This investigation is very much useful for understanding of the rheological behavior of inulin at low concentration for other novel food and other applications.

Fig. 3.

Surface plot for combined effect of temperature and concentration on Newtonian viscosity of inulin solution

Conclusions

The inulin solution behaved like a Newtonian fluid at low concentration and Newtonian viscosity of inulin solution was in the range 2.0998 to 3.2439 mPa s depending upon temperature (10 to 85 °C) and solid content (1 to 12 %) studied. The viscosity of inulin solution was increased significantly (p < 0.05) with increase in solid content, whereas it decreased significantly (p < 0.05) with an increase in temperature. The temperature dependency on viscosity of inulin solution was described Arrhenius equation and flow activation energy was in the range from 2.111 to 3.013 k J/mol depending upon the solid content studied. The effect of solid content on flow activation energy followed exponential type relation. The effect of solid content on viscosity of inulin solution followed by linear and power law type relation depending upon the temperature studied. The combined effect of temperature and solid content on viscosity of inulin solution was described by power law equation described as η = 0.8835* (X_s)^0.0731 *Exp(296.410/T), (r = 0.9538, p < 0.001, rmse% = 0.15), where, η is the viscosity in mPas, X_s is the solid content in % and T is absolute temperature in Kelvin (K)

Abbreviations

η

Newtonian viscosity in mPa s

X_s

solid content in %

T

temperature in Kelvin (K)

Σ

shear stress (Pa)

K

consistency index (Pa sⁿ)

γ

shear rate (s⁻¹)

η_∞

Material constant/ pre-exponential coefficient/frequency factor (Pa s)

E_a

activation energy of viscous flow (J/mol)

R

Gas constant (J/mol K)

a

b, c, d, empirical constants

n

flow behavior index (−)

W_exp

the experimental value

W_cal

the calculated value

n

number of data sets

rmse

root mean square error

r

correlation coefficient

CMC

Carboxymethylcellulose