Modelling solubility of phenolics of mango ginger extract in supercritical carbon dioxide using equation of state and empirical models

Abstract

Solubility of phenolics of mango ginger extract in supercritical carbon dioxide was studied at 40–60 °C and 100–350 bar. Critical temperature, critical pressure and critical volume of caffeic acid, the principal component of the extract were calculated using group contribution methods and compared with the values obtained by CHEMDRAW®. Vapor pressure of caffeic acid was predicted by Reidel method. Solubility prediction in supercritical carbon dioxide was studied using two different equation of states (EOS) models and eight empirical models. Peng-Robinson EOS predicted the solubility very well with average deviation of 0.68 % from the experimental solubility. Empirical equations based on the simple error minimization using non-linear regression method which do not require complex physiochemical properties was also found suitable to predict the solubility at different extraction conditions. Jouyban et al. model showed very less deviation (2.25 %) for predicted solubility values from the experiment.

Electronic supplementary material

The online version of this article (doi:10.1007/s13197-014-1667-1) contains supplementary material, which is available to authorized users.

Introduction

Curcuma amada Roxb popularly known as mango ginger belongs to the family Zingiberaceae. The plant is widely cultivated in India apart from Malaysia, China, Bangladesh, Myanmar, Thailand, Japan and Australia (Sasikumar 2005). It is a unique spice morphologically similar to ginger but imparts mango flavor (Policegoudra et al. 2011). They are widely used in the preparation of culinary items such as pickles, sauces etc. in Indian subcontinent because of its exotic aroma. Nearly, sixty-eight compounds were identified from the steam distilled volatile oil of the rhizome (Rao et al. 1989). In the Indian system medicine, Ayurveda, the plant is given importance as appetizer, alexiteric, antipyretic, aphrodisiac and laxative properties (CSIR Council of Scientific and Industrial Research 1950). The extract of rhizome exhibited antimicrobial, antifungal and anthelmintic activity against tape worms. It is also rich major components including starch, phenolic acids, volatile oils, curcuminoids and terpenoids like difurocumenonol, amadannulen and amadaldehyde (Policegoudra et al. 2011). Many aspects of processing like drying (Krishna Murthy and Manohar 2013a), grinding (Krishna Murthy and Manohar 2013b) and extraction (Krishna Murthy and Manohar 2014) of mango ginger have been studied by the authors. Extraction of mango ginger for its bioactives on a commercial scale is not in practice and such extraction shall result in value-added products.

Supercritical carbon dioxide (SC-CO₂) is a highly promising solvent due to its relatively low critical temperature and pressure, high solvent power, high diffusivity, low viscosity and low surface tension. SC-CO₂ has an added advantage of being non-toxic and non-flammable as compared to many organic solvents that are reported to be carcinogenic (Yeoh et al. 2013). SC-CO₂ can be removed and recovered from the extracts after processing by simple condensation at room temperature. The extraction efficiency and selectivity can be enhanced by tuning pressure and/or temperature (Hojjati et al. 2009; Jafari et al. 2010). It is necessary to know the thermodynamic critical properties of bioactive components for adequate design of reactors and separation equipment involved in supercritical fluid extraction (SCFE) and in enhancement of yield of the nutraceuticals. Properties like critical volume, critical pressure, critical temperature, melting point, boiling point, compressibility factor and acentric factor are of practical importance as they are the basis for the estimation of solubility of pure component or mixture in supercritical fluid (SCF) by equation of state (Henderson et al. 2004). Commercial feasibility of most of the SCFE extraction process depends on solubility of the desired component in the supercritical fluid. Solubility affects yield of extraction, cost of processing and also the particle size and morphology of the product obtained (Yeoh et al. 2013). Critical properties of pure and simple compounds such as CO₂, water etc., are available in literature (McHugh and Krukonis 1994). Due to complex nature and instability of bioactive components at or near the critical temperature, experimental measurements of their critical properties are extremely difficult, if not impossible. It is therefore very important that prediction methods that are reliable and having low probability in failure when extrapolated be followed (Li and Kiran 1990). Group Contribution methods use basic structural information of a chemical molecule like a list of simple functional groups, adds parameters to these functional groups, and calculates thermo-physical and transport properties as a function of the sum of group parameters. Since 1950s, numerous methods have been developed for the estimation of critical properties. In the absence of experimental data available, Group contribution method of predicting critical properties is the most reliable one. Various group contribution methods generally used are Lydersen, Ambrose, Klincewicz-Reid, Joback method (Poling et al. 2000). Van der Waals equation, two parameter Redlich-Kwong equation, Berthelot equation, Dieterici equation, 3-parameter Clausius equation, Peng and Robinson equation, Wohl equation, Beattie-Bridgeman and Benedict-Webb-Rubin are some of the equations of state models that represent real nature of gases particularly at high pressure conditions (Manohar 2010).

Empirical models often applied for modeling of solubility of solids in supercritical fluids are density based models. These models do not require physicochemical data like critical properties, accentric factor, vapor pressure etc. as in the case of equation of state models. (Škerget et al. 2011)). A recent review covers various aspects of solubility measurement and mathematical models explaining solubility relations (Yeoh et al. 2013).

The present investigation aims to a) estimate the critical properties of the mango ginger phenolics (mainly, caffeic acid) by various group contribution method b) estimate the vapor pressure of caffeic acid at various temperatures and c) predict the solubility of mango ginger extract in terms of caffeic acid phenolics using well known Equation of State and empirical models.

Materials and method

Mango ginger

Fresh and matured mango ginger rhizomes were purchased from local market, Mysore, India. The moisture content of fresh rhizome was estimated by toluene distillation method (ASTA American Spice Trade Association 1985).

Chemicals

Food grade CO₂ (99.99 % pure) for extraction was procured from Kiran Corporation, Mysore, Karnataka, India. Gallic acid, tannic acid, caffeic acid, protocatechuic acid, p- coumaric acid, cinnamic acid, ferulic acid, syringic acid were purchased from Sigma-Aldrich Fine Chemicals (St.Louis, MO, USA). HPLC grade water, methanol and acetic acid were from Merk, Mumbai, India. Folin-Ciocalteu reagent was purchased from LobaChemie (Mumbai, India). All other chemicals were analytical grade.

Powder preparation

The rhizomes were washed to remove adhered soil and a slicing machine (M/s Robot coupe, USA, Model: CL 50 Gourmet) was used to slice rhizomes. The slices were dried at 45 ± 2 °C in low temperature low humidity dryer. The dried rhizomes were ground in hammer mill (M/s Apex, USA).

Particle size measurement

About 0.5 g of powdered material was dispersed in 5 ml water and placed in glass cuvette of the computerized particle size analyzer (Model: CIS-100, M/s Galai Production Ltd., Israel) which measures particle size distribution based on the principle of laser obscuration time (also known as Time‐of‐Transition). The volume mean particle size was determined by the built-in software.

Supercritical carbon-dioxide extraction

For all extraction experiments, high-pressure equipment (NOVA Swiss WERKE AG, EX 1000–1.4–1.2 type, Switzerland) designed to work up to 1000 bar and temperature up to 100 °C was used. The mango ginger powder was loaded into the extraction vessel of 1.1 L capacity. Experiments were conducted at different pressures (100–350 bar), temperature (40–60 °C). After attaining the desired temperature, the CO₂ which had been compressed to the set pressure was allowed into the extractor. The average flow rate was maintained at 1.8–2.0 kg/h. A fraction of extract was collected from the separator at definite time intervals and the weight of the extract was recorded and samples taken for further analysis.

Phenolic acid analysis

Total phenolic content of extracts were measured according to Folin-Dennis method (Singleton and Rossi 1965). 200 μg of extract was dissolved in 500 μl of methanol and the sample was incubated with 2.5 ml of 10 % Folin and Ciocalteu’s phenol reagent for 2 min at room temperature. To this mixture 2 ml of 7.5 % (w/s) Na₂CO₃ was added and incubated for 1 h at room temperature. The absorbance was measured at 765 nm against a blank developed with 0.5 ml solvent using a UV-Visible spectrophotometer (model UV-160A, Shimadzu Corporation, Japan). Total phenolic content in the extract was expressed as gallic acid equivalents (GAE).

Measurement of experimental solubility

The solubility of mango ginger phenolics at each extraction condition of temperature and pressures were calculated from the initial slope of the linear sections of the extraction curves of phenolics (kg) vs CO₂ consumed (kg). Experimental solubility was calculated in kg phenolics/kg CO₂ and converted to mole fraction units as required in equation of state models (Manohar and Sankar 2011; Liang and Yeh 1991).

Estimation of critical properties by group contribution method

Critical temperature, pressure and volume

The critical temperature is an important parameter in determining the phase boundaries of any compound and is a required input parameter for most phase equilibrium thermal property or volumetric property calculations using analytic equations of state or the theorem of corresponding states. A recent review analyzed various aspects and types of group contribution methods available in literature (Kolska et al. 2012). Only well known Lydersen (Lydersen 1955), Ambrose (Ambrose 1978), Joback (Joback 1984) and Klincewicz-Reid (Klincewicz and Reid 1984) methods have been used for estimation of critical temperature, critical pressure and critical volume in the present study. Equations pertaining to all the four methods for predicting critical properties are given in Table. 1.

Table 1.

Group contribution methods for predicting critical properties

		Critical temperature*	Critical pressure$	Critical volume#
Group contribution method	Lydersen	${\mathrm{T}}_{\mathrm{c}}=\frac{{\mathrm{T}}_{\mathrm{B}}}{\left[0.567+{\displaystyle \sum }{\mathrm{T}}_{\mathrm{L}}-{\left({\displaystyle \sum }\Delta {\mathrm{T}}_{\mathrm{L}}\right)}^2\right]}$	$P_c=\frac{MW}{{\left(0.34+{\displaystyle \sum }\Delta P_L\right)}^2}$	Vc = 40 + ∑ΔVL
	Ambrose	${\mathrm{T}}_{\mathrm{c}}=\frac{{\mathrm{T}}_{\mathrm{B}}\left(1+1.242+{\displaystyle \sum }\Delta {\mathrm{T}}_{\mathrm{A}}\right)}{\left(1.241+{\displaystyle \sum }\Delta {\mathrm{T}}_{\mathrm{A}}\right)}$	$P_c=\frac{MW}{1.01325{\left(0.339+{\displaystyle \sum }\Delta P_A\right)}^2}$	Vc = 40 + ∑ΔVA
	Klincewicz-Reid(group contribution)	Tc = 45.4 − 0.77 MW + 1.55TB + ∑ΔTK	$P_c=\frac{MW}{1.01325{(0.348+0.0159MW+{\displaystyle \sum }\Delta P_K)}^2}$	Vc = 25.2 + 2.8 MW + ∑ΔVK
	Klincewicz-Reid (simple)	Tc = 50.2 − 0.16 MW + 1.41TB	$P_c=\frac{MW}{1.01325{\left(0.335+0.009MW+0.019n_A\right)}^2}$	V c = 20 + 0.088 MW + 13.4 n A
	Joback	$T_c=\frac{T_B}{\left[0.584+0.965{\displaystyle \sum }\Delta T_J-{\left({\displaystyle \sum }\Delta T_J\right)}^2\right]}$	${\mathrm{P}}_{\mathrm{c}}=\frac{\left[{\left(0.113+0.0032{\mathrm{n}}_{\mathrm{A}}-{\displaystyle \sum }\Delta {\mathrm{P}}_{\mathrm{J}}\right)}^{-2}\right]}{1.01325}$	Vc = 17.5 + ∑ΔVJ

*ΔT_L Group Contributions for temperature in Lydersen equation, ΔT_A Group Contributions for temperature in Ambrose equation, ΔT_K Group Contributions for temperature in Klincewicz-Reid equation, ΔT_J Group Contributions for temperature in Joback equation, MW molecular weight of the compound, T_B Normal Boiling temperature

^$n_A number of atoms in the compound. ΔP_L Group Contributions for pressure in Lydersen equation, ΔP_A Group Contributions for pressure in Ambrose equation, ΔP_K Group Contributions for pressure in Klincewicz-Reid equation, ΔP_J Group Contributions for pressure in Joback equation

^#ΔVL Group Contributions for volume in Lydersen equation, ΔV_A Group Contributions for volume in Ambrose equation, ΔV_K Group Contributions for volume in Klincewicz-Reid equation, ΔV_J Group Contributions in Joback equation

Normal boiling point (T_B)

Generally measurements of boiling points are made at lower pressures for compounds with extremely high boiling temperature or for compounds that decompose before they boil at atmospheric pressure. Joback (1984) developed a method for normal boiling point which depends on structure only. The Joback’s equation (Eq.1) is as below:

$${\mathrm{T}}_{\mathrm{B}}=198+{\displaystyle \sum }\Delta {\mathrm{T}}_{{\mathrm{B}}_{\mathrm{J}}}$$ 1

Where ΔT_BJ = Group Contributions for boiling point.

Vapor Pressure

Vapor pressure is a very useful property that determines the feasibility of separation of the components under separation processes such as distillation. The vapor pressure is the pressure exerted by a pure component at equilibrium at any temperature when both liquid and vapor phases exist and thus extends from a minimum at the triple point temperature to a maximum at the critical temperature, the critical pressure.

Among the various equations available for prediction of vapor pressure, the most important is the Riedel (Riedel 1954) method which is given below:

$$\mathit{log}{P}_r^s=-S_1\left(T_r\right)-\left(S_2-7\right)S_3\left(T_r\right)$$ 2

where correlation functions S₁(T_r), S₃(T_r) and S₄(T_r) are given by:

$${\mathrm{S}}_1\left({\mathrm{T}}_{\mathrm{r}}\right)=0.118{\mathrm{S}}_4\left({\mathrm{T}}_{\mathrm{r}}\right)-7{\mathrm{logT}}_{\mathrm{r}}$$ 3

$${\mathrm{S}}_3\left({\mathrm{T}}_{\mathrm{r}}\right)=0.036{\mathrm{S}}_4\left({\mathrm{T}}_{\mathrm{r}}\right)-{\mathrm{logT}}_{\mathrm{r}}$$ 4

$${\mathrm{S}}_4\left({\mathrm{T}}_{\mathrm{r}}\right)=\frac{36}{{\mathrm{T}}_{\mathrm{r}}}+96.7log{\mathrm{T}}_{\mathrm{r}}-35-{\mathrm{T}}_{\mathrm{r}}^6$$ 5

$${\mathrm{S}}_2=\frac{{\mathrm{S}}_{21}}{{\mathrm{S}}_{22}}$$ 6

Where

$${\mathrm{S}}_{21}=0.136{\mathrm{S}}_4\left({\mathrm{T}}_{\mathrm{r}\mathrm{b}}\right)+log{\mathrm{P}}_{\mathrm{c}}-5.01$$ 7

$${\mathrm{S}}_{22}=0.036{\mathrm{S}}_4\left({\mathrm{T}}_{\mathrm{r}\mathrm{b}}\right)-\left(log{\mathrm{T}}_{\mathrm{r}\mathrm{b}}\right)$$ 8

where T_r, reduced temperature (T/T_C); T, temperature of interest; T_rb = reduced temperature at normal boiling temperature (T_B/ T_C) and S₁, S₂, S₃, S₄, S₂₁, S₂₂ are constants as defined in equations above.

Mathematical modeling of solubility prediction

Equation of state (EOS)

Equations of state are used to describe the thermodynamic states through the relationship of state parameters such as temperature, pressure, and volume. In SCFE processing, EOS describes the behavior of solute being dissolved in supercritical fluids. The solubility of a substance (component 2) in a supercritical fluid (component 1) can be obtained from fluid–solid phase equilibria. The subscripts 1 and 2 in the following derivations denote components CO₂ and solute (caffeic acid in the present work). At equilibrium, the fugacities of the components in the solid and gas phases are equal, i.e.:

$${\mathrm{f}}_2^{\mathrm{s}}\left(\mathrm{P},\mathrm{T},{\mathrm{x}}_2\right)={\mathrm{f}}_2^{\mathrm{v}}\left(\mathrm{P},\mathrm{T},{\mathrm{y}}_2\right)$$ 9

where f^s₂ is the fugacity of solute in the solid phase; f^v₂ fugacity of solute in the gas phase; P is the pressure; T is the temperature; x and y are mole fractions.

If the gas component 1 is assumed to be insoluble in solid phase (true in most of the cases), then

$${\text{γ}}_2{\varphi }_2^{\mathrm{s}}\mathrm{P}={\mathrm{P}}_2^{\mathrm{s}\mathrm{a}\mathrm{t}}{\varphi }_2^{\mathrm{s}\mathrm{a}\mathrm{t}}\exp \underset{{\mathrm{P}}_2^{\mathrm{s}\mathrm{a}\mathrm{t}}}{\stackrel{\mathrm{P}}{\int }}\left({\mathrm{v}}_2^{\mathrm{s}}\frac{\mathrm{d}\mathrm{P}}{\mathrm{R}\mathrm{T}}\right)$$ 10

$${\mathrm{f}}_2^{\mathrm{v}}={\mathrm{P}\mathrm{y}}_2{\varphi }_2^{\mathrm{v}}$$ 11

where, ϕ is the fugacity coefficient; V molar volume; R is the universal gas constant; superscripts s and sat denote solid and saturated conditions respectively.

From above equations, one can obtain:

$$y_2=\left(\frac{P_2^{sat}}{P}\right)E$$ 12

$${\mathrm{y}}_2=\frac{{\mathrm{P}}_2^{\mathrm{s}\mathrm{a}\mathrm{t}}\exp \left({\mathrm{v}}_2^{\mathrm{s}}\frac{\mathrm{P}}{\mathrm{R}\mathrm{T}}\right)}{{\varphi }_2^{\mathrm{s}}\mathrm{P}}$$ 13

where E is the enhancement factor which is the ratio of the solubility of the solute in super critical fluid to the solubility in an ideal gas. i.e. $\mathrm{E}=\frac{{\mathrm{y}}_2}{{\mathrm{y}}_{\mathrm{ideal}}}$

Large enhancement factors of the order of 10⁵ to 10⁷ are frequently observed due to small values of φ^v₂. φ₂^sat has a value of approximately one. V₂^s can be easily calculated from the density of component 2. Thus, to calculate E, one requires the value of φ^v₂. From well-known equation of state (EOS) available such as Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) models, φ^v₂. can be calculated.

A general form of the Peng-Robinson equation is:

$$\mathrm{P}=\left(\frac{\mathrm{R}\mathrm{T}}{\mathrm{V}-\mathrm{b}}\right)-\left(\frac{\mathrm{a}}{{\mathrm{V}}^2+2\mathrm{b}\mathrm{V}-{\mathrm{b}}^2}\right)$$ 14

The above can be written as:

$${\mathrm{Z}}^3-\left(1-\mathrm{B}\right){\mathrm{Z}}^2+\left(\mathrm{A}-3{\mathrm{B}}^2\right)\mathrm{Z}-\left(\mathrm{AB}-{\mathrm{B}}^2-{\mathrm{B}}^3\right)=0$$ 15

The above equation leads to:

$$ln{\phi }_2^v=\frac{b_2\left(Z-1\right)}{b}-ln\left(Z-B\right)-\left[\left(\frac{A}{2\sqrt{2B}}\right).\left\{2\left(a_{22}{y}_2+\frac{a_{11}{y}_1}{a}\right)-\left(\frac{b_2}{b}\right)\right\}.ln\left\{\frac{\left(Z+2.414B\right)}{Z-2.414B}\right\}\right]$$ 16

Soave-Redlich-Kwong equation of state (SRK-EOS) is:

$$\mathrm{P}=\left(\frac{\mathrm{R}\mathrm{T}}{\mathrm{V}-\mathrm{b}}\right)-\left(\frac{\mathrm{a}}{{\mathrm{V}}^2+\mathrm{b}\mathrm{V}}\right)$$ 17

The above can also be written as:

$$Z^3-Z^2+\left(A-B-B^2\right)Z-\mathit{AB}=0$$ 18

The above equation leads to

$$ln{\phi }_2^v=\frac{b_2\left(Z-1\right)}{b}-ln\left(Z-B\right)-\left[\left(\frac{A}{B}\right)\left\{\frac{2\left(a_{22}{y}_2+a_{12}{y}_2\right)}{a}-\frac{b_2}{b}\right\}.ln\left(1+\frac{B}{Z}\right)\right]$$ 19

Where

$$Z=\frac{Pv}{RT}$$ 20

$$A=\frac{aP}{R^2{T}^2}$$ 21

$$B=\frac{bP}{RT}$$ 22

a is intermolecular attraction parameter and b is co volume parameter

When the equation is extended to mixtures, the following mixing rule is employed:

$$a={\displaystyle \sum }{\displaystyle \sum }{y}_i{y}_j{a}_{ij}$$ 23

$$b={\displaystyle \sum }{\displaystyle \sum }{y}_i{y}_j{b}_{ij}$$ 24

where a_ij and b_ij are calculated from combining rules:

$$a_{ij}={\left(a_{ii}{a}_{jj}\right)}^{0.5}\left(1-k_{ij}\right)$$ 26

$$b_{ij}={\left(b_{ii}{b}_{jj}\right)}^{0.5}\left(1-n_{ij}\right)$$ 27

where k_ij and n_ij are the adjustable binary interaction parameters. The adjustable parameters are determined by regressing phase equilibrium data and assumed to be independent of temperature, pressure and composition. It may be noted that these parameters can take negative values and accordingly, the software program should be allowed to adjust these values suitably. Many authors have used single binary interaction parameter k_ij in their works. However, a second adjustable mixture parameter n_ij is also used in the present study, since n_ij can account for the large size disparity between a heavy non-volatile solute and a light SCF solvent (Mchugh and Krukonis 1994). For pure components, “a” and “b” parameters are calculated from critical constants T_c, P_c and acentric factor, ω depending on the type of EOS.

For, PR-EOS,

$${\mathrm{a}}_{\mathrm{i}}=0.45724\left(\frac{{\mathrm{R}}^2{\mathrm{T}}_{\mathrm{C}}^2}{{\mathrm{P}}_{\mathrm{C}}}\right)\mathrm{\alpha }$$ 28

$$\text{α}={[1+\mathrm{K}(1-{\mathrm{T}}_{\mathrm{r}}^{0.5})]}^2$$ 29

$$K=0.37464+1.54226\omega -0.26992{\omega }^2$$ 30

$${\mathrm{b}}_{\mathrm{i}}=\frac{0.07780\mathrm{R}{\mathrm{T}}_{\mathrm{C}}}{{\mathrm{P}}_{\mathrm{C}}}$$ 31

For SRK-EOS,

$${\mathrm{a}}_{\mathrm{i}}=0.42748\left(\frac{{\mathrm{R}}^2{\mathrm{T}}_{\mathrm{C}}^2}{{\mathrm{P}}_{\mathrm{C}}}\right)\mathrm{\alpha }$$ 32

$$\text{α}={[1+\mathrm{K}(1-{\mathrm{T}}_{\mathrm{r}}^{0.5})]}^2$$ 33

$$\mathrm{K}=0.48+1.57\mathrm{\omega }-0.17{\mathrm{\omega }}^2$$ 34

$${\mathrm{b}}_{\mathrm{i}}=\frac{0.08664\mathrm{R}{\mathrm{T}}_{\mathrm{C}}}{{\mathrm{P}}_{\mathrm{C}}}$$ 35

The computer program obtains the optimum k_ij and n_ij value by simple optimization technique using the built-in Solver Add-in in Microsoft Excel-2003 which gives minimum average absolute relative deviation (AARD) between experimental and calculated values of solubility:

$$\mathrm{AARD},\%=\frac{100}{\mathrm{N}}{\displaystyle \sum }\frac{{\mathrm{y}}_{\text{exp}}-{\mathrm{y}}_{\mathrm{cal}}}{{\mathrm{y}}_{\text{exp}}}$$ 36

where N is the number of experiments, y_cal and y_exp are the calculated and experimental solubilities of solute components respectively.

When the extract is assumed as a single pseudo-component, T_C, P_C, ω, P^sat of the extract is considered to be sum of the property of the main components multiplied by mole fraction of main components.

The entire calculation procedure (Basalingappa et al. 2001) described above can be summarized as below:

1. The critical values T_c, P_c and acentric factor for each component are estimated by group contribution methods.

2. Pure component parameters of the PR-EOS and SRK-EOS are estimated.

3. k_ij and n_ij are assumed initial values. Then “a” and “b” for mixture are calculated based on mixing rules.

4. The cubic equation of state is solved for Z.

5. φ^v₂ is calculated.

6. y₂ is calculated.

7. Steps 2 to 6 repeated for each pressure and temperature. AARD is then calculated. If AARD is not within tolerance limit set by the program, the procedure is repeated so that one obtains the optimal k_ij and n_ij parameters.

A program is written in MS-Excel® incorporating the above steps to calculate the solubility with minimum deviation from experimental solubility data (Manohar and Sankar 2011; Manohar 2010).

Empirical models

The solubility (S) of the compound increases with increasing density (ρ) of CO₂ fluid shows a linear relationship:

$$lnS=pln\rho +q$$ 37

Chrastil model (Chrastil 1982) is one of the popular density based empirical equations to determine solute’s solubility in supercritical fluids:

$$S={\rho }^{k}exp\left(\frac{a}{T}+b\right)$$ 38

The above model correlated the solubility of a solute in SC-CO₂ to the density and temperature where k is an association number which represents the average number of CO₂ molecules in the solvated complex, the constant ‘a’ depends on vaporization and salvation enthalpies of solute and the constant ‘b’ depends upon molecular weight of solute and molecular weight of supercritical fluid (Jouyban et al. 2002; Hojjati et al. 2009). Eight empirical density based models which have been used by researchers in SCF were selected for predicting the solubility of mango ginger extract in SC-CO₂ and presented in Table 2. To provide a reliable accuracy criterion to compare the models, average absolute relative deviation (AARD) values were used, which is calculated by

$$\mathrm{AARD}=\frac{100}{\mathrm{N}}{\displaystyle \sum }\frac{\left|{\mathrm{Y}}_{\text{exp}}-{\mathrm{Y}}_{\mathrm{p}\mathrm{r}\mathrm{e}}\right|}{{\mathrm{Y}}_{\text{exp}}}$$ 39

Table 2.

Empirical models for solubility prediction

Model No.	Model Equation	Reference
1	$lnS=A_0+A_{1}ln\rho +\frac{A_2}{T}$	Chrastil (1982)
2	$lnS=B_0+\frac{B_1}{T}+B_{2}ln\rho +\frac{B_3}{T^2}$	Del Valle and Aguilera (1988)
3	y 2 = C 0 + C 1 P + C 2 P 2 + C 3 PT(1 − y 2) + C 4 T + C 5 T 2	Yu et al. (1994)
4	ln y 2 = D 0 + D 1 P + D 2 P 2 + D 3 PT + D 4 T + D 5 T 2	Gordilo et al. (1999)
5	$ln{y}_2=M_0+M_{1}P+M_2{P}^2+M_{3}PT+\frac{M_{4}T}{P}+M_{5}ln\rho$	Jouyban et al. (2002)
6	$ln{y}_2=K_0+K_1\rho +K_2{P}^2+K_{3}PT+\frac{K_{4}T}{P}+K_{5}ln\rho$	Jouyban et al. (2002)
7	ln y 2 = J 0 + J 1 P 2 + J 2 T 2 + J 3 ln ρ	Jafari et al. (2010))
8	ln y 2 = E 0 + E 1 P + E 2 T + E 3 P 2 + E 4 T 2 + E 5 PT	Garcia et al. (2000)

Where N is no of data points, Y_exp is experimental solubility and Y_pre is model predicted solubility.

Results and discussion

The initial moisture content fresh mango ginger was found to be 90 ± 0.5 % (wb) and the mean particle size of the powder was 480 ± 40 μm.

Critical properties of caffeic acid

Functional groups along with structure of caffeic acid are presented in Table 3. The values of group contributions for caffeic acid as per Lydersen, Ambrose, Klincewicz-Reid and Joback methods are presented in Table S1-S4. Values of critical properties of caffeic acid were obtained on substituting these values in suitable group contribution equations. The values of T_C, P_C, V_C were calculated from the four group contribution and simplified Klincewicz-Reid method. The values obtained so were compared with the CHEMDRAW® (www.chembridgesoft.com) values and presented in Table 4. Joback is the only group contribution method for calculating normal boiling point and melting point. The values of T_B and T_M obtained from Joback method agreed very well with the values obtained from CHEMDRAW® with deviations of only 0.026 % and 0.083 % respectively (Table 4). The T_C values of group contribution compared with the CHEMDRAW® showed deviation of 14 to 21 %. Klincewicz-Reid simplified method showed higher deviation of 21 % compared with CHEMDRAW values. Because this method does not require group contribution values of the compounds. The critical pressure calculated from the four group contribution and simplified Klincewicz-Reid method were also compared with the CHEMDRAW® values and showed 0.015 to 52 % deviation. Prediction by Joback method has only 0.015 % deviated from the CHEMDRAW® values. The V_C values predicted by the Group contribution method showed deviation of 1 to 47 % with the CHEMDRAW®. But V_C value estimated by Ambrose method deviated only 1.1 % from CHEMDRAW®. Hence one needs to be cautious in applying the property data to real systems as there could be a big difference between predicted and experimental value.

Table 3.

Structural information of caffeic acid

Molecular Structure	Compound	Functional Groups	Number of Functional Groups	Number of Carbon atoms	Number of Hydrogen atoms	Numberof Oxygen atoms	Total number of atoms
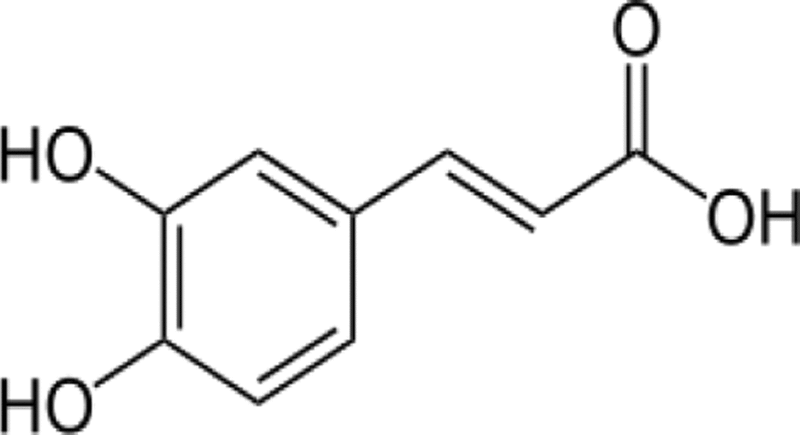
	C9H8O4	=CH-(ring)	3	3	3	0	21
		=-OH (phenol)	2	0	2	2
		=-COOH	1	1	1	2
	MW: 180.16 g/mol	=CH-	2	2	2	0
		=C< (ring)	3	3	0	0
		Total	11	9	8	4

Table 4.

Comparison of predicted critical properties of caffeic acid between different prediction methods

Properties	Notation	Units	Joback	Ambrose	Lydersen	Klincewiez-Reid(G)	Klincewiez-Reid(S)	ChemDraw
Normal boiling point	TB	K	742.91	–	–	–	–	743.11
Critical temperature	TC	K	993.05	999.79	999.13	951.40	1068.87	853.56
Critical pressure	PC	MPa	5.810	4.344	4.415	2.803	3.204	5.809
Critical volume	VC	cm3/mol	367.50	462.20	442.50	480.14	317.25	467.50
Melting point	TM	K	596.57	–	–	–	–	596.07

Vapor pressure- temperature relationship

Vapor pressure of caffeic acid predicted at different temperatures using the Riedel method (Eq.2) is shown in Fig. 1. The vapor pressure increased rapidly with temperature at high temperature regions. This behavior plays an important role in the determination of solubility of the phenolics in SC-CO₂ despite the low density of CO₂ at higher temperatures.

Fig. 1.

Predicted vapour pressure as a function of temperature for caffeic acid by Riedel method

Solubility prediction of mango ginger extract by EOS

Caffeic acid has been identified as a major phenolic acid present in mango ginger extract as reported in an earlier work by the authors (Krishna Murthy and Manohar 2014). The experimental solubilities (mole fraction) of phenolics acids in SC-CO₂ were in the range 9.77  ×  10⁻⁸ to 1.22  ×  10⁻⁵ depending on pressure and temperature of extraction. The experimental solubilities closely agreed with those predicted by PR equation of state (Fig. 2). The polar nature of phenolics makes it poorly soluble in SC-CO₂. In the present study, the total phenolics is assumed to consist of caffeic acid entirely in the prediction models such PR and SRK-EOS. Values of enhancement factors and interaction parameters for caffeic acid based on PR-EOS and SRK-EOS are in Table 5. An enhancement factor for caffeic acid was found to be high due to deviation from ideal gas behavior and indicates the non-ideal behavior. The binary interaction parameter k_ij is associated with the intermolecular interaction between a pair of unlike species. The values are positive for PR-EOS and negative for SRK-EOS. Negative value indicates the presence of specific chemical interactions such as hydrogen bonding (McHugh and Krukonis 1994). The AARD between experimental and predicted values for solubility of caffeic acid according to PR-EOS and SRK-EOS was 0.68 and 11.12 % respectively indicating that PR-EOS is the best in predicting the solubility.

Fig. 2.

Experimental and predicted solubility of mango ginger extract at different extraction conditions

Table 5.

Enhancement factors and interaction parameters for caffeic acid

Enhancement factor
Temperature (°C)	40			50			60
Pressure (bar)	100	225	350	100	225	350	100	225	350
PR-EOS	1.10E + 08	4.95E + 08	9.06E + 08	7.35E + 06	6.20E + 07	6.31E + 07	9.72E + 04	9.08E + 06	4.23E + 07
SRK-EOS	1.10E + 08	4.95E + 08	8.79E + 08	1.42E + 03	4.24E + 08	4.39E + 08	4.02E + 06	1.54E + 09	7.20E + 09
Interaction parameter
Temperature (°C)	40			50			60
Pressure (bar)	100	225	350	100	225	350	100	225	350
PR-EOS	0.071	0.250	0.309	0.185	0.313	0.384	0.367	0.371	0.395
SRK-EOS	−1.616	−0.913	−0.566	−0.617	−1.284	−0.506	−2.667	−1.445	−0.749

The results showed the solubility increased with increase in the pressure at constant temperature due to increase in the density of CO₂ and solvent power at each pressure increases. Similar behavior has been reported on solubility of phenolics (Chafer et al. 2007). With increased density the intermolecular distance is decreased, therefore the solute-solvent interactions are increased. As the temperature increased the solubility decreased significantly at lower pressures. The low values of solubilities of phenolics at lower pressures have been reported (Chafer et al. 2007). But this trend has been reversed at higher pressure and temperature. This happened due to increase in the solute vapour pressure at higher temperature even though density of CO₂ is less at higher temperature at a constant pressure. Solute vapor pressure dominates resulting in increased solubilities at higher pressure and temperature. The behavior known cross-over phenomena which is a result of mutual competition of the solvent density and solute vapor pressure effects in combination has been observed in the case of naphthalene-ethylene (McHugh and Krukonis 1994), phenolics-CO₂ (Murga et al. 2002), caffeine-CO₂ (Kim et al. 2008) and Resorcinol – CO₂ systems (Reddy and Madras 2011).

Solubility prediction of mango ginger extract by empirical models

Parameters of the selected empirical models obtained by the multiple regression using Data Analysis in Microsoft Excel® along with their AARD are provided in Table 6. All the models except Model 3 and Model 8 regressed very well with experimental data (AARD less than 10 %). Model 5 shows the least deviation from the experimental values. One can observe from Table 6 that merely increasing number of parameters of the models did not improve the quality of regression. Chrastil model (Model 1 in Table 6), a semi-empirical model, has theoretical backing and correlated well with experimental values (AARD, 8.40 %). The Chrastil model has been found to predict solubilities of 58 pure pharmaceutical compounds in SC-CO₂ well that includes caffeic acid also (Taberneroa et al. 2013). From the above models it is possible to calculate solute solubility at temperatures between 40 and 60 °C and pressure between 100 and 350 bar using an interpolation technique. These models could be employed in practice to simulate the solubility data in SC-CO₂. It is obvious that single empirical model cannot be appropriate in every case, which could be considered as one possible disadvantage of employing empirical models.

Table 6.

Model constants and AARD values for selected empirical models

Model*	Model coefficients						AARD, %
Chrastil (1982)	A0	A1	A2				8.40
	−31.23	−4.47	4.059
Del Valle and Aguilera (1988)	B0	B1	B2	B3			22.48
	−0.5492	1371.27	−2.65	−35154.1
Yu et al. (1994)	C0	C1	C2	C3	C4	C5	54.98
	6.77E-05	−5.1E-08	−2.8E-11	1.74E-09	−2.5E-06	2.14E-08
Gordilo et al. (1999)	D0	D1	D2	D3	D4	D5
	−3.93	−0.00773	−5.2E-05	0.000801	−0.29184	0.000633	2.80
Jouyban et al. (2002)-A	M0	M1	M2	M3	M4	M5
	28.16	−0.087	9.22E-05	0.000368	−32.44	−3.35	2.28
Jouyban et al. (2002)-B	K0	K1	K2	K3	K4	K5
	−11.59	−0.00126	−1.7E-05	6.65E-05	−7.78	0.062	3.93
Jafari et al. (2010)	J0	J1	J2	J3
	−35.39	−4.2E-06	8.19E-05	3.47			3.09
Garcia et al. (2000)	E0	E1	E2	E3	E4	E5
	6.77E-05	−5.1E-08	−2.5E-06	−2.8E-11	2.14E-08	1.74E-09	54.97

*Models described in Table 2

Conclusion

Based on the different group contribution method, critical properties of caffeic acid, the principal component of mango ginger extract was estimated. Experimental solubility of caffeic acid in SC-CO₂ was measured at temperatures 40–60 °C and pressures 100–350 bar. The experimental solubility of caffeic acid in the range 9.77  ×  10⁻⁸ to 1.22  ×  10⁻⁵ could be well predicted by the theoretical equation of state model PR-EOS with very less average deviation (0.68 %) from experimental solubility data. The enhancement factors are very high due to non-ideal behavior of caffeic acid. Solubility could also be predicted by the empirical equations proposed by previous researchers with AARD less than 2.28 %. Due to simplicity of empirical models over theoretical models in solubility prediction, empirical models could be employed to predict the solubility of mango ginger extract in the range of pressure and temperature employed.