Genetic GIScience: Toward a Place-Based Synthesis of the Genome, Exposome, and Behavome

Abstract

The exposome, defined as the totality of an individual’s exposures over the life course, is a seminal concept in the environmental health sciences. Although inherently geographic, the exposome as yet is unfamiliar to many geographers. This article proposes a place-based synthesis, genetic geographic information science (Genetic GISc) that is founded on the exposome, genome+ and behavome. It provides an improved understanding of human health in relation to biology (the genome+), environmental exposures (the exposome), and their social, societal and behavioral determinants (the behavome). Genetic GISc poses three key needs: First, a mathematical foundation for emergent theory; Second, process-based models that bridge biological and geographic scales; Third, biologically plausible estimates of space-time disease lags. Compartmental models are a possible solution; this article develops two models using pancreatic cancer as an exemplar. The first models carcinogenesis based on the cascade of mutations and cellular changes that lead to metastatic cancer. The second models cancer stages by diagnostic criteria. These provide empirical estimates of the distribution of latencies in cellular states and disease stages, and maps of the burden of yet to be diagnosed disease. This approach links our emerging knowledge of genomics to cancer progression at the cellular level, to individuals and their cancer stage at diagnosis, to geographic distributions of cancer in extant populations. These methodological developments and exemplar provide the basis for a new synthesis in health geography: genetic geographic information science.

Introduction

Environment, social and individual factors all play a role in an individual’s health and wellbeing. Linking social and health data to a particular location is important because where we live can and does influence our health (Tunstall, Shaw, and Dorling 2004). Health outcomes are related to an individuals’ physical and social environment, including factors such as water, soil and air content, exposure to hazardous materials, tobacco smoke, occupation, marital status, social support, and characteristics of the home, in addition to the composition of the local built environment (Marmot 2000; Pickle, Waller, and Lawson 2005).

Geographical epidemiology rests largely upon the assumption that the spatial incidence of diseases holds a key to their cause. However, high population mobility, long latent periods and environmental change complicate matters, distorting what might otherwise be a direct relationship between cause and effect (Jacquez 2004; Kwan 2009). This gives rise to what has been called the space-time lag (Dearwent, Jacobs, and Halbert 2001; Griffith and Paelinck 2009). From a geographical point of view, this means that the place or environment where the case is discovered and diagnosed is not necessarily the same place or environment where the exposure occurred (Picheral 1982; Sabel et al. 2003; Sabel et al. 2000).

Many studies examining associations between geographical patterns of health and disease and causal factors assume that current residence in an area can be equated with exposure to conditions that currently (and historically) pertain there (Bentham 1988). This is important, since the place of residence at the time of diagnosis or death is often adopted by epidemiologists and geographers as the location for further analysis of the disease in question. Yet people move, and hence previous exposure to pathogens will not be included in the study. The problems will be greater for diseases that have a long lag or latency period, allowing plenty of time for mobility of the population. By adopting only the current residential address, not only will an individual’s migration history be neglected, but additionally the daily “activity spaces” and associated uncertainties will be ignored (Jacquez 2004; Kwan 2012). For chronic diseases such as cancer we often use the place of residence at diagnosis or death to record the health event. But where people reside at time of diagnosis may be far removed from where they lived when causative exposures occurred. This disconnect is widely recognized (Wheeler, Ward, and Waller 2012), yet techniques for estimating appropriate sampling distributions for latencies for the geographic modeling of human diseases that are biologically reasonable, based on observable disease states, and that incorporate knowledge of disease progression are seldom available. This article attempts to address this need using the construct of Genetic GISc.

Space-Time Geovisualization and Modeling

There is a long and rich history of geographers investigating Space-Time interaction from Hägerstrand through Forer to the present (Forer 1978; Hägerstraand 1970; Richardson et al. 2013). Interest has focused on the Space-Time Cube. Space Time-Paths or geospatial life lines have largely been utilised to visualize (often neglecting modeling) individual mobilities through space, such as Forer’s work in Auckland visualising student lifestyles (Huisman and Forer 1998). Kwan (2000) has used the cube – she uses the term space-time aquarium - to study accessibilities differences among gender and different ethnic groups in Portland (Kwan 2000). Miller (1999) applied its principles in trying to establish accessibility measures in an urban environment (Miller 1999). For physical environmental exposures, Hedley (1999) created an application in a GIS environment for radiological hazard exposure (Hedley et al. 1999), and Gulliver and Briggs (2005) modeled space-time interactions to traffic derived air-pollution (Gulliver and Briggs 2005). Others have assessed similarity in geospatial lifelines and clustered them to quantify disease patterns for mobile populations (Jacquez et al. 2013; Sinha and Mark 2005). However, modeling latency between exposure and disease outcomes largely remains neglected.

Recent improved data gathering techniques, including the wider availability of GPS, cellphone and social media data have renewed interest in Time geography and the Space-Time-Cube. Dykes and Mountain (2003) discuss data collection techniques by mobile phone, GPS and location-based services and suggest a visual analytical method to deal with the data gathered (Dykes and Mountain 2003). Lam (2012) and Bian et al (2012) both discuss ongoing challenges to health risk assessment despite the wider availability of individual level data (Bian et al. 2012; Lam 2012).

The Exposome, Genome+ and Behavome

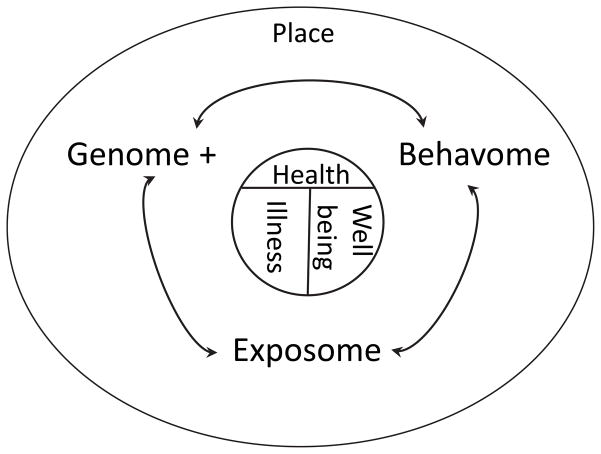
A new synthesis in health geography we are calling Genetic GISc seeks to document, quantify and model the relationships between place, the genome, exposome (Wild 2005b, 2012), and behavome that are the determinants of illness and wellness (Figure 1). This builds on and extends prior constructs in human biology and ecology, such as the nature-nurture debate and Meade’s Triangle of Human Ecology, which viewed health outcomes as the result of place and time specific interactions between populations, their environments and their behaviors (Meade 1977).

Figure 1.

Schematic representation of genetic geographic information science (Genetic GIS). The three primary determinants of health, both in terms of illness and well being, are (1) an individual’s biology which may quantified as their “Genome +”, comprised of their genome (genetic composition), regulome (which controls gene expression), proteome (their compliment of amino acids and proteins) and metabalome (the basis of metabolism and homeostasis). (2) The environments they experience, which may be quantified as the exposome, is defined as the totality of exposures over the life course (Wild 2005a). (3) The totality of an individual’s health behaviors over the life course, which may be quantified as the behavome, mediate the exposome and interactions between the exposome and the genome +. These determinants of human health act through place, defined as the geographic, environmental, social and societal milieus experienced over a person’s life course. This synthesis is referred to as genetic geographic science, or genetic GIS.

This paradigm requires an explicit understanding of how these determinants are related to space-time patterns of health outcomes in human populations. Because the genome, exposome and behavome are defined at the level of the individual, techniques for estimating disease latency – the time between the onset of disease and its diagnosis, are essential. A second key need is the ability to integrate and model the influence of the genome, exposome and behavome across biological scales and to then geographically map the results at local and regional scales. Finally, sound theory often requires a solid mathematical foundation, and one must be established for Genetic GISc. This article seeks to begin to mathematically formalize these requirements, and poses an example using one of the least understood cancers, pancreatic cancer.

Exposome

The term “exposome” was introduced by Wild (2005), to:

“… encompass life-course environmental exposures (including lifestyle factors), from the prenatal period onwards…the exposome is a highly variable entity that evolves throughout the lifetime of the individual.” (Wild, 2005, p 1848).

The exposome concept recognises three broad categories on non-genetic exposures: internal (e.g. metabolism), specific external (e.g. air pollution) and general external (e.g. socioeconomic factors)(Wild 2012). While a person’s genome is fixed at conception, internal and external sources of exposure cause the human’s internal chemical environment to vary throughout life (Rappaport 2011; Miller and Jones 2014). Essentially, an individual will have a particular profile of exposure at any given point in time which makes the characterisation of the exposome so challenging (Wild 2012). It is a concept to measure effects of a lifelong exposure to environmental influences on human health and therefore requires longitudinal sampling especially during foetal development, early childhood, puberty and the reproductive years (Rappaport 2011). These measures include external monitoring and modelling of media such as air and water but also biomonitoring (i.e. measurements) of biological markers of exposure through methods such as blood or urine sampling (Lioy and Rappaport 2011). Rappaport (2011) prioritises a top down approach applying biomonitoring to identify all important exposures, over a bottom up approach which is based on air, water or soils samples to identify all exogenous exposures.

Van Tongeren and Cherrie (2012), on the other hand, support the aim of developing an integrated concept of exposomics taking all sources of available exposure information into account (van Tongeren and Cherrie 2012). Internal and external exposure data, personal behaviour and environmental measurements could thus be used to determine the exposome. This requires the collaboration of researchers from a variety of disciplines to promote the concept and unravel complex relationships between social interactions, biological effects and the risk of diseases (Wild, 2012), an endeavor suited to but largely unexploited by geographers.

The exposome has a public health orientated objective and the aim of its application is to aggregate up from a group of individuals to a population, providing the basis for public health decisions (Wild, 2012).

Genome+

The “Genome +” is comprised of the individual’s genome (genetic composition), regulome (which controls gene expression), proteome (their compliment of amino acids and proteins) and metabalome (the basis of metabolism and homeostasis). Together, these constitute a good portion of an individual’s biological makeup. The last few years have seen major advances in our ability to quantify the Genome+. Technology improvements have dramatically reduced genome sequencing costs. In 2000 the Human Genome Project equenced the first whole human genome, at a cost over USD$2 billion (Davies 2010). In 2012 the 1000 genomes project released their phase 1 sequencing data (Pybus et al. 2014), documenting genetic variation in 1,000+ individuals from 25 populations from around the globe (The 1000 Genomes Project Consortium 2012). Genome sequencing costs continues to drop, and the USD$1,000 whole sequence genome is now available (Hayden 2014). In medical practice and research whole genome sequencing poses ethical challenges regarding information disclosure to the individual, especially given incomplete knowledge of the genetic basis of disease (Yu et al. 2013). Nonetheless, whole genome sequencing as a commodity will soon cost ~USD$100. Dramatic cost reductions are occurring in the exome, epigenome, and other genome+ constituents (Zentner and Henikoff 2012; Weinhold 2012; Meissner 2012; Mefford 2012). It is clear that measurements of the genome+ will soon be widely and inexpensively available, and will be incorporated into individual electronic health records, notwithstanding the informatics and ethical challenges posed by their integration (Kho et al. 2013; Flintoft 2014; Tarczy-Hornoch et al. 2013; Hazin et al. 2013)

As our understanding of the genetic bases of disease has grown, the need for a systems biology approach that integrate across genetic, cellular, organ, individual and population-level scales is increasingly recognized (Oreši 2014). How can we incorporate knowledge, for example, of the cascade of genetic mutations leading to pancreatic cancer into our understanding of cancer latency, and how might this impact estimates of the burden of cancer at the population level? How do changes manifested in pancreatic cells as a result of mutations translate into cancer progression, and can we construct models that capture biological nuance yet are suited to geographic information science? For geographers, how can systems biology approaches be integrated into space-time geographic disease models? This article addresses these needs by linking a model of carcinogenesis at the cellular level with a model of cancer stages at the individual and population level.

Behavome

The behavome is comprised of an individual’s health-related behaviors over their life course, and is the most inchoate of the Genetic GISc triad Genome+, exposome, and behavome. Recognition methods for assessing individual behaviors have been an important research topic for decades. With the advent of sensors in residences, health care facilities, and wearable on patients, the issue of multisensor data fusion for activity recognition has emerged. These technologies are already being deployed and assessed in nursing home and assisted living facilities, but as yet have little penetration in the geographic literature. Recent research has demonstrated these methods can identify risky behaviors with good accuracy and low deployment costs (Palumbo et al. 2013). The “internet of things” including smart homes, smart cars and smart workplaces, is in the early phase of what many predict to be explosive growth (Ashton 2009). In 2008 the number of devices on the Internet exceeded the number of people, and in 2020 will exceed 50 billion devices (Swan 2012). Information on when, where and how we use appliances, electronic devices, machinery and environmental controls in home and workplace settings, and while commuting, have yet to be used to quantify the behavome. The value of near real-time data on ambient temperatures and how often and when we use the refrigerator may have enormous value for quantifying, for example, personal energy budgets, a key problem in cancer etiology (Hursting 2014; Ballard-Barbash et al. 2013). A variety of different approaches for assessing health behaviors have been suggested using technologies such as inertial sensors, Global Positioning System, smart homes, Radio Frequency IDentification and others. Most promising is the sensor fusion approach that combines data from several sensors simultaneously (Lowe and ÓLaighin 2014). To our knowledge technologies such as Google Glass have yet to be used for capturing video images to chronicle dietary intake and other health-related activities. Other potential applications include quantification of personalized environmental metrics such as individual walkability (e.g. (Mayne et al. 2013)). Once health-related behaviors are known, the possibility of using gamification (Whitson 2013) and other approaches to encourage salubrious behaviors become possible (Schoech et al. 2013).

Contribution of this article

This article proposes a synthesis of the genome+, exposome and behavome that is place-based and offers a promising new landscape for research in health geography—Genetic GISc. The potential research contributions this synthesis offers geographers are manifold, including health geography, quantitative methods, behavioral geography, visualization, space-time modeling and social geography. The exposome and behavome are new concepts with many unsolved gaps of their own, several of which are addressed in this article. First, we demonstrate how disease latencies may be estimated using compartmental models and data available from systems biology. Disease latency estimation is a key problem for space-time lags in health geography. Second, space-time models that account for individual disease processes yet provide geographic estimates of disease burden are almost entirely lacking in health geography, a significant gap addressed by this article. Finally, as a motivating example we develop and apply a comprehensive modeling approach that estimates cancer latency, couples carcinogenesis and stage models, and that represents and links processes at the genomic level (e.g. mutation events, cascades of genetic changes that lead to cancer), cellular level (e.g. cell replication and death, DNA repair), organ level (e.g. carcinogenesis insitu and metastases to distant organs), individual level (e.g. cancer staging in the individual, progression of individuals through cancer stages), to the population level (e.g. predicted geographic distributions of undiagnosed cancers). While this by no means addresses all of the challenges and gaps posed by Genetic GISc, it hopefully illustrates the promise of this research direction and perhaps points the way forward.

It is important to note that the breadth of the concept and challenge represented in Figure 1 is substantial. This aim of this contribution is to communicate its scope, identify key research problems, and propose a way forward. The example of pancreatic cancer presented here deals primarily with the genome+. At the time of this writing, measurement of the exposome is at a nascent stage; and the term “behavome” is new. When data from the exposome and behavome become available they can be incorporated into the modeling framework through place- and person-specific effects on model flow parameters, for example, DNA mutation and repair rates. Opportunities for such adaptation and extension of the modeling framework are identified in the discussion.

We begin with an introduction to the approach for the modeling and analysis of dynamic geographic systems using process-based temporal lags. This is followed by a brief background on latency estimation approaches that motivate the use of residence times in compartmental systems. A primer on compartmental analysis is presented, followed by a simple three stage model of disease, and results for distribution of residence times. Next, the specific example of pancreatic cancer is considered, and a five state model of carninogenesis is developed along with its biological foundation. A second model of progression through cancer stages based on diagnostic criteria used by the American Cancer Association follows. These models are linked using knowledge of the mapping of stage of diagnosis with progression of tumor growth and metastatic capacity. This is applied to data from the Michigan cancer registry on stage at diagnosis for all incident pancreatic cancers in white males from 1985 to 2005 in the Detroit metropolitan area. Potential applications of this approach and next steps are then discussed.

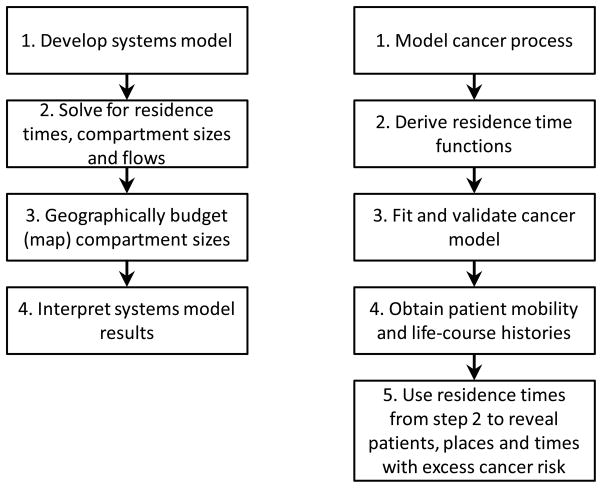
The generalized approach (Figure 2, left) applies to any geographic system amenable to a compartmental representation. Here the emphasis is on the development of a minimally sufficient but mechanistically reasonable systems model. An example application to a dynamic geographic systems model of cancer using residence times to estimate latency is shown in Figure 2, right.

Figure 2.

Steps in dynamic geographic systems analysis (left) and specific application to cancer using knowledge of residential history to budget excess risk (right).

Ideally, Genetic GISc will be based on model-based theory with several characteristics. First, models must be biologically reasonable and capture relevant aspects of disease etiology and natural history. Second, they must provide estimates of the distributions of disease latency.

Third, they must be estimable from empirical data, so we can derive latency distributions from observable measures and based on the current state of knowledge of the disease. Fourth, they must provide for geographically referenced data on individuals. The derivation of biologically-based estimates of disease latency is a difficult problem, and we next consider alternative approaches to latency estimation.

Disease latency estimation

Several techniques exist for modeling disease latency, including representations of cohort exposures, developmental stages of vulnerability, models of empirical induction periods, and compartmental models. We summarize these before focusing on residence times in compartmental systems.

Cohort exposures arise when a common exposure occurs for group of individuals, resulting in an overall increase in disease risk. Here the temporal lag between the causal event and health outcomes is directly observable. For example, Chernobyl released radioactive iodide over Belarus and led to an increase in pediatric thyroid cancers. The latent period for tumor development was 4–6 years (Nikiforov and Gnepp 1994).

Developmental stages of vulnerability arise when the timing and characteristics of biological stages of development are associated with increased risk of an adverse health event in later years. For example, genetic risk accounts for approximately 10–15 percent of breast cancer cases, and the windows of vulnerability occur before a woman’s first birth, and during the development of breast tissues (Colditz and Frazier 1995). Here an average latency and its distribution may be estimated as the time from the developmental stage to disease diagnosis.

The Empirical Induction Period (EIP) models latency as the sum of induction and latent periods defined as the periods between causal action and disease initiation (induction), and between disease initiation and detection (latent). The sum of the induction and latent periods is the empirical induction period. The induction period is not estimable except in relation to specific etiologic factors, since different exposures have different levels of effect on disease expression (Rothman 1981).

Residence times in compartmental models of disease may be obtained directly from the model itself. For a given compartmental model and parameter values the mean residence time and distribution of residence times in each compartment are known. This result holds for both deterministic and stochastic compartmental models, but has yet to be used in geographic models of human disease. When the compartments correspond to stages of disease, the compartmental residence times are estimates of disease latency. Compartmental models thus are best constructed so compartments correspond to known disease states (e.g. are biologically reasonable), and the coefficients governing transitions between compartments are formulated in terms of known biological and infection processes (e.g. the mechanics are process-based). Residence times from compartmental models thus convey the characteristics required at the beginning of this section; (1) they may be formulated in a biologically reasonable fashion. (2) They provide estimates of the distribution of latencies. (3) Whether a given model, and hence its residence times, is estimable is known once the model and observable measures are identified. The remainder of this article employs compartmental models. Refer to Appendix I for a Primer on compartmental models.

Residence times

Residence times are the time required for a particle to enter and then exit a compartment. Compartment residence times may be used in model validation by comparing residence times from the model to the observed residence times. For linear compartmental models the residence times are inverse exponential functions, and closed form solutions for calculating the probability density functions (pdf’s) are known (Jacquez 1996). In deterministic non-linear compartmental systems the distributions of residence times are functions of the state variables, and hence of the compartments sizes. The probability density functions of linear stochastic models are the same as for their deterministic analog. However, the probability density functions of residence times for non-linear stochastic systems differ from those of their non-linear deterministic counterpart (Jacquez 2002). This article presents residence times linear deterministic stage-based models of cancer, which also apply to their linear stochastic counterparts.

Simplicity versus complexity, and implications for residence times

There is a tension between simplicity, which makes models more easy to understand and mathematically tractable, and complexity, which seeks to incorporate the nuances and details of a complex reality. Simplicity may correspond to a representation with fewer compartments; an implicit combining of compartments that has implications for the modeling of residence times. When the residence times for a compartment in a model are too short, the creation of sub-compartments to represent that compartment can be used to obtain longer average residence times (Jacquez and Simon 2002). Correspondence of residence times to those observed in the system under scrutiny thus can be used as a diagnostic for model over-simplification and misspecification.

Modeling carcinogenesis – cancer in the individual

For the geographic modeling of disease we are interested in identifying places and sub-populations characterized by an excess of cancer for individuals in those states of carcinogenesis when exposures to mutagens might have been causal. That is, we are looking for the geographic signature of the actions of past environmental exposures that gave rise to cancers. To do this we require biologically reasonable models of carcinogenesis (e.g. the biological events that have cancer as their sequelae) and cancer stages (how cancers progress once they have started). We begin with carcinogenesis.

The initial biological event leading to cancer is damage to DNA. Such damage occurs on one DNA strand, and repair mechanisms can reverse that damage. Whether the damage is maintained among daughter cells depends on the timing of replication and repair. If replication occurs before repair then the damaged DNA strand is passed on to the daughter cells (a fixed mutation). Notice that only some of these mutations are deleterious and lead to cancers.

Carcinogenesis models usually treat irreversible steps in the chain of mutations leading to cancer as comprised of sub-states with reversible damage attributable to DNA repair mechanisms (Kopp-Schneider, Portier, and Rippman 1991; Jacquez 1999). The last few years have seen dramatic advances in our understanding of tumor genetics, and it now is possible to sequence the genomes sampled from cancer tumors to elucidate the sequence of mutations that lead to cancer. The specific mutations vary from one tumor to another and from one patient to another, but the steps of mutation, repair, and fixation of deleterious mutations via replication events are largely the same. The sub-states of a model of carcinogenesis thus should be constructed to correspond to the observed tumor morphological characteristics, with flows corresponding to state transitions from mutation, repair, and replication.

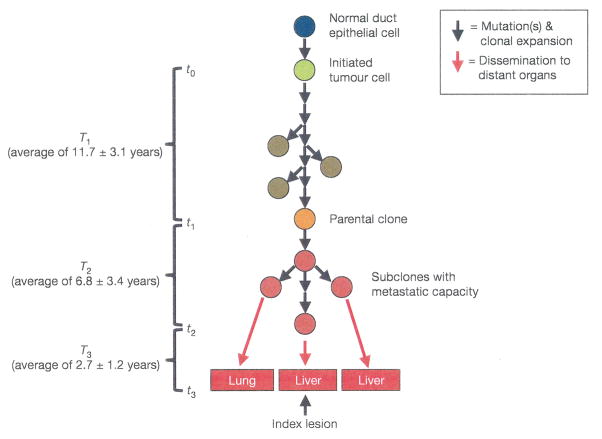
Consider pancreatic cancer (Figure 3) and its corresponding compartmental model (Figure 4). A cascade of specific mutation events lead to pancreatic cancer (Alian et al. 2014), although these differ from one patient to another (Maitra and Hruban 2008). These mutations include KRAS2, p16/CDKN2A, TP53, SMAD4/DPC4, and other genes, and result in genomic and transcriptomic alterations that lead to invasion, metastases, cell cycle deregulation, and enhanced cancer cell survival (Maitra and Hruban 2008). Precursor lesions include the mucinous cycstic neoplasm (MCN), the intraductal papillary mucinous neoplasm (IPMN) and the pancreatic intraepithelial neoplasia (PanIN). Here we consider the PanIN pathway, which is thought responsible for the majority of pancreatic cancers.

Figure 3.

Schematic of the evolution of pancreatic cancer. Normal pancreatic duct epithelial cells undergo mutation events to become an initiated tumor cell. Additional mutations and clonal expansions lead eventually to a founder cell of the index pancreatic cancer clone. These produce subclones with metastatic capacity, eventually leading to dissemination to distant organs such as the liver. Times shown are the empirical residence times in each system state. Adapted from Yachida, Jones et al. (2010).

Figure 4.

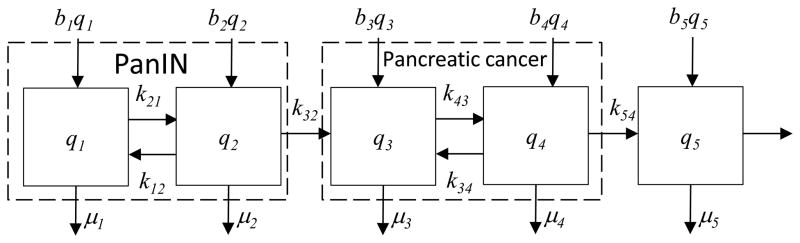
Model of pancreatic cancer carcinogenesis.

Carcinogenesis is initiated by a mutation in a normal cell that leads to accelerated cell proliferation. Waves of clonal expansion along with additional mutations progress to pancreatic intraepithelial neoplasia (PanIN) during time T₁ (Figure 3). This corresponds to the sub-states q₁ (normal cell) and q₂ (PanIN) in the model in Figure 4. One founder cell from a PanIN lesion will start the parental clone that will initiate an infiltrating carcinoma; this is indicated by the irreversible flow (k₃₂) from q₂ to q₃ in Figure 4. Here sub-state q₃ is the parental clone, and sub-state q₄ indicates sub clones with metastatic capacity. The flow k₃₂ to sub-state q₃ thus represents that replication that gives rise to the index pancreatic cancer lesion (the cells in q₃), along with the mutation events that confer metastatic capacity (resulting in the cells in q₄). The empirical residence time in sub-states q₃ and q₄ is T₂. The irreversible flow k₅₄ indicates a proliferation and spreading of cells with metastatic capacity, with metastases (state q₅₎ to other organs such as the liver occurring in time T₃. The observed average times in each model state are T1=11.7 years, T2=6.8 years, and T3=2.7 years (Campbell et al. 2010). These are the empirical residence times in those states describing pancreatic carcinogenesis, and were estimated from tumor histology and tumor genetics. This model is consistent with recent findings regarding mechanisms of pancreatic tumorigenesis. For example, inflammation and injury are implicated as a precursor event in some pancreatic cancers, leading to acinar-to-ductal metaplasia (ADM). ADM is reversible, but an oncogenic mutation in KRAS prevents this, and the injured cells enter the pathway to pancreatic intraepithelial neoplasia (PanIN). Additional mutation events then can result in pancreatic ductal adenocarcinoma (Seton-Rogers 2012), represented by the “pancreatic cancer” meta-compartment in Figure 4.

Details on model specification, system equations, parameter estimates and equilibrium conditions are in Appendix II.

Residence times

For an outflow connected system without inflow and comprised of n compartments (Figure 5), the compartment sizes and density function of residence times, given an input of 1 unit at t=0 into compartment 1, are (Jacquez 2002):

$$q_n=\frac{k^{n-1}{t}^{n-1}}{(n-1)!}{e}^{-kt}$$ Eqn 1

$$\theta (\rho ,t)=\frac{k^n{t}^{n-1}}{(n-1)!}{e}^{-kt}.$$ Eqn 2

Figure 5.

Outflow connected n compartment system useful for solving for the probability density function and cumulative distribution function of residence times.

Here ρ specifies the proportions of particles in the n compartments such that the first compartment has size 1, and the others have size 0. This means the initial conditions specify that all particles at time 0 are in compartment 1. These equations may be applied to solve for the density function of residence times in the compartmental model of pancreatic cancer (Figure 4) in the subsystems PanIN, pancreatic cancer, and metastatic pancreatic cancer, given certain simplifying assumptions.

Refer to Appendix III for the estimation of residence times in the compartmental model of pancreatic cancer.

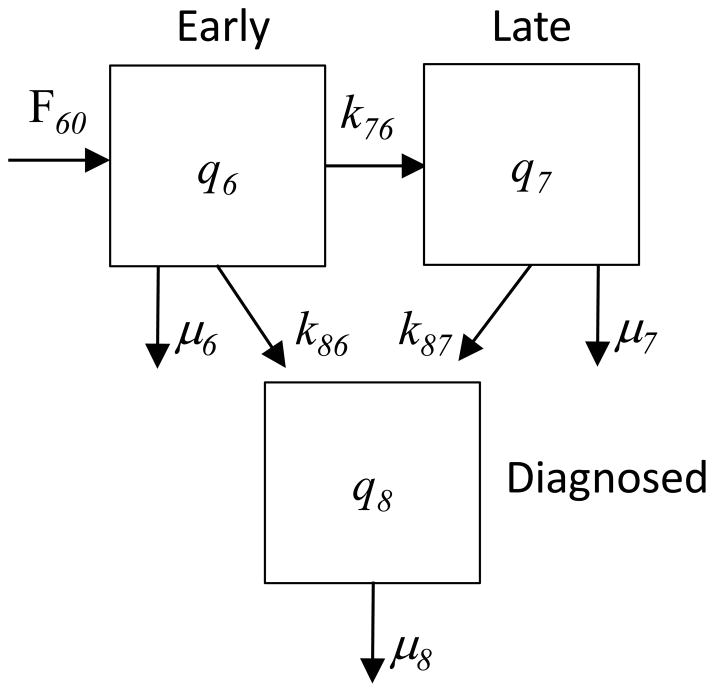
Modeling cancer stages – cancer in populations

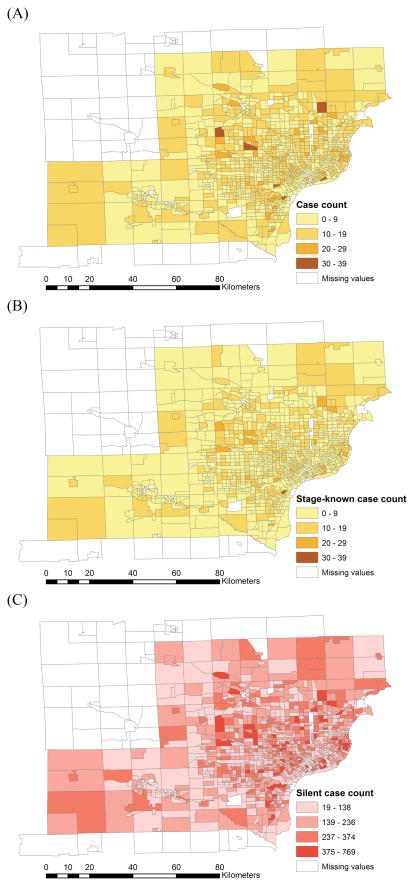
We now present a model of pancreatic cancer stages (Figure 6). Here, the unit of observation is the cancer patient, and we observe counts of patients in early and late stage pancreatic cancer, before and after diagnosis (Figure 7A and 7B). Counts of people in early and late stages prior to diagnosis are represented by q₆ and q₇. Compartment q₈ is comprised of patients who have been diagnosed, either in early or late stage cancer. The flow of the number of health individuals entering early stage cancer is F₆₀. The rate of progression from early to late stage cancer is k₇₆. Diagnosis events from early and late stage are given by the rates k₈₆ and k₈₇. Death from the compartments is represented by μ₆, μ₇, and μ₈.

Figure 6.

Stage-based model of pancreatic cancer. Here the compartment sizes are number of patients with early (q₆) and late stage cancers (q₇) prior to diagnosis, and the number diagnosed (q₈).

Figure 7.

Choropleth maps of pancreatic cancer cases in southeast Michigan, 1985–2005: (A) incident cases; (B) stage-known cases; (C) silent (yet to be diagnosed) cases.

System Equations

The system equations for this stage-based model of pancreatic cancer are

$$\begin{array}{l}\frac{{dq}_6}{dt}={\mathrm{F}}_{60}-q_6(k_{76}+k_{86}+{\mu }_6)\\ \frac{{dq}_7}{dt}=q_6{k}_{76}-q_7(k_{87}+{\mu }_7)\\ \frac{{dq}_8}{dt}=q_6{k}_{86}+q_7{k}_{87}-q_8{\mu }_8.\end{array}$$ Eqn 3

Equilibrium

Equilibrium occurs under the following conditions.

$$\begin{array}{l}0=\frac{{dq}_6}{dt}=\frac{{dq}_7}{dt}=\frac{{dq}_8}{dt}\\ q_6=\frac{{\mathrm{F}}_{60}}{(k_{76}+k_{86}+{\mu }_6)}\\ q_7=\frac{q_6{k}_{76}}{(k_{87}+{\mu }_7)}\\ q_8=\frac{q_6{k}_{86}+q_7{k}_{87}}{{\mu }_8}\end{array}$$ Eqn 4

Estimation

The number of incident early and late stage cancers (compartment q₈) are directly observable in most of the states comprising the United States from cancer registry data. The flows q₆k₈₆ and q₇k₈₇ are observable as the number in a defined time period of early and late stage diagnoses. The mortality rate q₈μ₈ is directly observable as the number of diagnosed pancreatic patients who die in a defined time period. The quantities q₆μ₆ and q₇μ₇ are the number of deaths of people with early and late stage, but undiagnosed, pancreatic cancer. The estimation of parameter values and the number of yet to be diagnosed cancer cases will be demonstrated below in the example of pancreatic cancer in Southeast Michigan.

Carcinogenesis and stage-based model of pancreatic cancer

The carcinogenesis model deals with pancreatic cancer cells in histological and genetic states as compartment members, whereas the stage-based model uses individuals and the stage of their pancreatic cancer to define compartment membership. The model of carcinogenesis informs the stage model through an equivalence of residence times and model states (Table 1, Table 2).

Table 1.

Equivalence of model states and residence times between carcinogenesis- and stage-based models, using diagnostic pancreatic cancer staging according to the American Cancer Society American Joint Committee on Cancer (Edge et al. 2010).

Stage model compartment	Carcinogenesis model compartment	Description	American Joint Committee on Cancer (AJCC) staging	Residence time
q6	q3, q4	Insitu, local, not diagnosed	Insitu: AJCC Tis, N0, M0 Local: AJCC IA, IB, N0, M0	T2 : 6.8±3.4 yrs
q7	q5	Regional, distant, not diagnosed	Regional: AJCC IIA, IIB Distant: AJCC IV	T3 : 2.7±1.2 yrs
q8	-	Diagnosed pancreatic cancer	May be in situ, local, regional, or distant; in most cases pancreatic cancer is diagnosed at an advanced stage	T4 : 0.5±0.25 yrs (2011 five-year survival rate < 6% and average life expectancy after diagnosis is 3 to 9 months.

Table 2.

Correspondence of modeled cancer stages to anatomic stages from the American Joint Committee on Cancer. Primary Tumor (T) coding is Tis: Carcinoma in situ; T1: Tumor limited to pancreas, 2cm or less in greatest dimension; T2: Tumor limited to pancreas, more than 2cm in greatest dimension; T3: Tumor extends beyond the pancreas but without involvement of the celiac axis or the superior mesenteric artery; T4: Tumor involves the celiac axis or the superior mesenteric artery (unresectable primary tumor). Regional lymph nodes (N) coding is N0: No regional lymph node metastasis; N1: Regional lymph node metastasis. Distant metastasis (M) coding is M0: No distant metastasis; M1: Distant metastasis.

Model stage	AJCC stage	Prognostic Groups			Diagnosed
Early (q6)	Stage 0	Tis	N0	M0	N
	Stage IA	T1	N0	M0	N
	Stage IB	T2	N0	M0	N
Late (q7)	Stage IIA	T3	N0	M0	N
	Stage IIB	T1–3	N1	M0	N
	Stage III	T4	Any N	M0	N
	Stage IV	Any T	Any N	M1	N
Diagnosed (q8)	Any stage	Any T	Any N	Any M	Y

Application: Pancreatic cancer in Southeast Michigan

To demonstrate the approach we apply the stage-based model to incident pancreatic cancer cases in southeastern Michigan. We employ the four steps illustrated in Figure 2, customized to this specific application.

• Step 1: Develop the minimally sufficient biologically reasonable systems model

• Step 2: Solve for residence times, compartment sizes and flows

• Step 3: Map the data to identify local populations with excess risk

• Step 4: Interpret the results

Background and Data

An analysis of pancreatic cancer mortality in white males in Michigan counties in two time periods from 1950–1970 and 1970–1995 found statistically significant clusters that persisted in Wayne county in both time periods and that expanded to include adjacent Macomb county in 1970–1995 (Jacquez 2009). This finding was confirmed using more recent incidence and mortality data from the Surveillance Epidemiology and End Results program, SEER (Ries et al. 2007). 17 registry/areas are included in the SEER program, including Atlanta, rural Georgia, California (Bay Area, San Francisco-Oakland, San Jose-Monterey, Los Angeles and Greater California), Connecticut, Hawaii, Iowa, Kentucky, Louisiana, New Jersey, New Mexico, Seattle-Puget Sound, Utah and Detroit. In 2000–2004 Detroit had the highest age-adjusted incidence rate for white males at 15.0 cases per 100,000 out of all of the 17 registry/areas, and the second highest mortality rate at 12.9 deaths per 100,000. In contrast, the SEER-wide averages for white males in this period were 12.8 incident cases and 12.0 deaths per 100,000. Notice the incidence is nearly equal to the deaths for the SEER-wide averages (12.8 vs 12.0), but the incident cases in Detroit exceed the mortality rate by a larger difference (15.0 vs. 12.9). This is consistent with the observation that pancreatic cancer incidence in Detroit is increasing, and that the Detroit system may not be in equilibrium. In terms of our compartmental model, it appears the flows in (F₀₆) exceed the flows out due to mortality (q₈μ₈). Notably, the Detroit registry pancreatic cancer mortality for white males in 2000–2004 increased on average 0.9 percent per year (Calculated by SEER*Stat from the National Vital Statistics System public use data file). The population covered by the Detroit registry in this period was 1,365,315 white males. The finding of excess pancreatic mortality with increasing incidence was thus independently confirmed by data from SEER and found to persist from 1950 through 2004 (Jacquez 2009).

As a follow-up to this study we obtained annual incidence data from the Michigan Cancer Surveillance Program (MCSP) for the period 1985–2005. The Michigan Cancer Registry is a gold-standard registry whose completeness and accuracy is certified on an annual basis, and MCSP compiles cancer records for the state. Funded in part by the National Program of Cancer Registries of the Centers for Disease Control, the MCSP is nationally certified by the North American Association of Central Cancer Registries. External audits have found a completeness percentage of 95 percent or higher on the population-based data collected by the MCSP.

Data cleaning and processing

As a follow-up to this study we obtained annual incidence data from the Michigan Cancer Surveillance Program (MCSP) for the period 1985–2005. A gold-standard registry whose completeness and accuracy is certified on an annual basis, the MCSP compiles cancer records for the state. Funded in part by the National Program of Cancer Registries of the Centers for Disease Control, the MCSP is nationally certified by the North American Association of Central Cancer Registries. External audits have found a completeness percentage of 95 percent or higher on the population-based data collected by the MCSP.

The geocoding budget and numbers of observations are as follows. A total of 11,068 pancreatic cancer cases were diagnosed between 1 January 1985 through 31 December 2005. Of these, 192 addresses of place of residence at diagnosis failed to geocode, leaving 10,876 cases with known places of residence at diagnosis. Stage at diagnosis (insitu, local, regional, distant and unknown) was recorded as unknown for 2,250 of these, leaving 8,826 cases with known place of residence and known stage at diagnosis. The head of pancreas and pancreas not otherwise specificed were the most frequent primary sites, with 4,496 and 1,621 respectively. Males accounted for 4,202 cases and females 4,424. By race, 6,356 cases were whites, 2,192 blacks, and the balance American Indian (8 cases), Asian (61) and other or unknown groups (9).

Analysis Steps

Step 1: Describe the model

We employ the model of pancreatic cancer stages in Figure 7A and 7B, system equations in Eqn 14.

Step 2: Estimate flows, compartment sizes and residence times

The quantities directly observable are the incident flows into compartment 8 from early and late stage but not diagnosed cancers. We use the data for all incident pancreatic cases, whether they geocoded or not, and whether the stage at diagnosis was known or unknown. Let o_e be the total number of cases from 1985 through 2005 observed in the early stage, o_L be the number late stage, and o_u be the number in unknown stage. Y is the number of years over which the observations accrued (21 years). We can then estimate the flows into compartment q₈ for early and late stage cancers as

$$\begin{array}{l}\widehat{q_6{k}_{86}}=\frac{(o_e+(\raisebox{1ex}{$o_e$}\!\left/ \!\raisebox{-1ex}{$(o_e+o_L)$}\right.)o_u)}{Y}=\frac{1246.8}{21}=59.37\\ \widehat{q_7{k}_{87}}=\frac{(o_L+(\raisebox{1ex}{$o_L$}\!\left/ \!\raisebox{-1ex}{$(o_e+o_L)$}\right.)o_u)}{Y}=\frac{1246.8}{21}=\mathrm{467.67.}\end{array}$$ (Eqn 5)

The units on these are number of cases in the given stage diagnosed per year. According to the American Cancer Society, for all stages of pancreatic cancer combined, the one-year relative survival rate is 20 percent, and the five-year rate is 4 percent. For μ₈ = 0.8 deaths/diagnosed case-year, and assuming the equilibrium condition in equation 15, we estimate the size of compartment q₈ as

$$\widehat{q_8}=\frac{q_6{k}_{86}+q_7{k}_{87}}{{\mu }_8}=\mathrm{658.81.}$$ (Eqn 6)

This is the average number of diagnosed and surviving (not yet deceased) pancreatic cancer cases. For the late stage but not diagnosed cases in compartment q₇ we note that at equilibrium

$$q_7(k_{87}+{\mu }_7)=q_6{k}_{76}.$$ (Eqn 7)

The rate μ₇ is deaths of late-stage but not diagnosed cases that are not diagnosed after the death event, and thus do not flow into compartment q₈ (they would have to be diagnosed to enter this compartment). We impose μ₇ = 0, under the assumption that all of the late-stage pancreatic cancer cases are diagnosed (this assumption can be relaxed but seems reasonable since late stage pancreatic cancers are by definition advanced and metastatic). Hence deaths for late stage but not yet diagnosed cases are diagnosed after they decease. This then yields

$$q_7{k}_{87}=q_6{k}_{76}=\mathrm{467.67.}$$ (Eqn 8)

Again, the units here are number of cases per year. Since q₇k₈₇ = q₆k₇₆ and q₆k₇₆ = 59.37,

$$\widehat{q_7}=59.37\frac{k_{76}}{(k_{86}+k_{87})}.$$ (Eqn 9)

The age-adjusted annual mortality rate from all causes in Michigan in 2010 was 764.2 deaths per 100,000 (Miniño and Murphy 2012), and has decreased from 1,027.10 deaths per 100,000 in 1985 (MDCH 2012). We therefore estimated the background mortality rate from 1985–2005 as the sum of the age-adjusted death rates for all races and sexes divided by the number of years being considered, yielding a 21 year average of 924.05 deaths per 100,000. We set person-specific annual death rate μ₆ = 0.00924 and using the equilibrium condition for compartment q₆ obtain

$$\begin{array}{c}{q}_6=\frac{{\mathrm{F}}_{60}}{(k_{76}+k_{86}+{\mu }_6)}\\ {\mathrm{F}}_{60}=q_6(k_{76}+k_{86}+{\mu }_6)\\ \widehat{F_{60}}=467.67+59.37+q_6{\mu }_6\\ \widehat{F_{60}}=467.67+59.37+\frac{59.37}{k_{86}}{\mu }_6=527.04+\frac{0.5486}{k_{86}},\text{and}\text{finally}\\ \widehat{q_6}=\frac{F_{60}-527.04}{0.009241}.\end{array}$$ (Eqn 10)

Earlier we demonstrated an equivalence between residence times in early and late stage cancer stages (q₆ and q₇) and residence times in the carcinogenetic model of PanIN and its sequelae. Then the residence time in q₆ is T₂, and in q₇ it is T₃. It still remains to solve for the residence time in q₈, T₄. Consider a pulse of newly diagnosed cases entering q₈ either from q₆ (diagnosed in early stage) or q₇ (diagnosed in late stage). Recall the median survival after diagnosis is 6 months, and that the one year survival rate is about 20 percent. Expressing time in days, we wish to fit the Erlang distribution such that CDF(182.5 days)=0.5, and CDF(365 days)=0.8. We solved this using the formulation for a one compartment system with μ₈ as the exit. At a daily mortality rate of μ₈ = 0.0038 we find CDF(182.5 days)=0.5002, and CDF(365 days)=0.7502.

Put another way, this states that for a pulse of cases diagnosed on the same day, about 50 percent will be alive after 182.5 days, and about 25 percent will be alive after 1 year. This indicates our fairly simple model of compartment q₈ is reasonably complete, at least in terms of its ability to represent observed 6 months and 1 year survival statistics.

Now that we have estimated μ₈ we use the relationship

$$q_8=\frac{\widehat{q_6{k}_{86}}+\widehat{q_6{k}_{86}}}{{\mu }_8}$$ (Eqn 11)

to solve for the size of compartment 8 yielding 379.98, $\widehat{q_8}=379.98$. This is the estimated average number of diagnosed but not deceased pancreatic cancer cases in the study area.

Earlier we solved for q₆ and q₇ using observed quantities such as incident early and late stage pancreatic cancer case diagnoses. It is interesting to note for q₆ that an alternative solution is to use the observed residence time in early stage, T₂, to then solve for q₆. This provides a validation of the estimate.

Define k′ to be the sum of the outflow coefficients from compartment q₆, k′ = k₇₆ + k₈₆ + μ₆. Notice we can now estimate k′ using the methods developed earlier for the residence time of the Erlang distribution. Specifically, solve for k′ for a 1 compartment system such that the mean residence time is T₂. This yields an estimate $\widehat{k^{\prime }}=0.00028$, which is the per case daily rate of exit from early stage but not-yet diagnosed pancreatic cancer, attributable to background mortality, progression to advanced cancer, and diagnosis. Multiplying by q₆ and using hat notation to indicate values we can estimate from the observed data yields

$$q_6\widehat{k^{\prime }}=\widehat{q_6{k}_{76}}+\widehat{q_6{k}_{86}}+q_6\widehat{{\mu }_6}.$$ (Eqn 12)

We now divide through by q₆, rearrange and have an estimator for q₆ as

$$\widehat{q_6}=\frac{\widehat{q_6{k}_{76}}+\widehat{q_6{k}_{86}}}{\widehat{k^{\prime }}-\widehat{{\mu }_6}}.$$ (Eqn 13)

Using the values obtained earlier yields (written using annual time orientation)

$$\widehat{q_6}=\frac{467.67+59.39}{0.1022-0.00924}=\mathrm{5669.75.}$$ (Eqn 14)

This is the estimated number of early stage cancers that are in the population but not yet diagnosed. We now use a similar approach to solve for the estimated number of undiagnosed advanced cancers, q₇. Recall at equilibrium the inflows into this compartment must equal the outflows, hence q₇k₈₇ = q₆k₇₆. This is estimated as the observed number of diagnosed advanced stage cancers, and for our system $\widehat{q_7{k}_{87}}=\widehat{q_6{k}_{76}}=467.67$, and $\widehat{q_7}=\frac{\widehat{q_6{k}_{76}}}{\widehat{k_{87}}}$. Again, we estimate $\widehat{k_{87}}$ using the Erlang distribution of residence times. Specifically, solve for $\widehat{k_{87}}$ for a 1 compartment system such that the mean residence time is T₃. This gives $\widehat{k_{87}}=0.000703$, which is the estimated daily diagnosis rate per person with advanced stage pancreatic cancer. Using annual values we now estimate

$$\widehat{q_7}=\frac{\widehat{q_6{k}_{76}}}{\widehat{k_{87}}}=\frac{467.67}{0.257}=1,\mathrm{822.6.}$$ (Eqn 15)

This is the number of individuals with undiagnosed advanced-stage pancreatic cancer.

Step 3: Map undiagnosed early and late stage pancreatic cancers; assess clustering of advanced stage cancers in age 55 and younger

We now estimated the numbers of undiagnosed cancers in total, and for both early and late stages. We define the estimated relative risks for total undiagnosed (TRR), early stage undiagnosed (ERR), and late stage undiagnosed (LRR) as the proportion of cases in each of these groups (total undiagnosed, early stage undiagnosed, late stage undiagnosed) relative to the total number of diagnosed cases,

$$\begin{array}{l}\widehat{\mathit{TRR}}=\frac{\widehat{q_6}+\widehat{q_7}}{\widehat{q_8}}=\frac{5,669.75+1,822.6}{379.6}=19.72\\ \widehat{\mathit{ERR}}=\frac{\widehat{q_6}}{\widehat{q_8}}=\frac{5,669.75}{379.6}=14.92\\ \widehat{\mathit{LRR}}=\frac{\widehat{q_7}}{\widehat{q_8}}=\frac{1,822.6}{379.6}=\mathrm{4.80.}\end{array}$$ (Eqn 16)

We find the total number of silent (yet to be diagnosed) case is more than 19 times the number diagnosed. Hence, for each case that is diagnosed we estimate there are 19 pancreatic cancer cases in the at-risk population that have yet to be diagnosed. Of these, almost 15 are in the early stages of pancreatic cancer, and nearly 5 are advanced. This means that application of a screen for early stage pancreatic cancer could dramatically reduce pancreatic cancer mortality, since such a large proportion of undiagnosed cases are in the early stages.

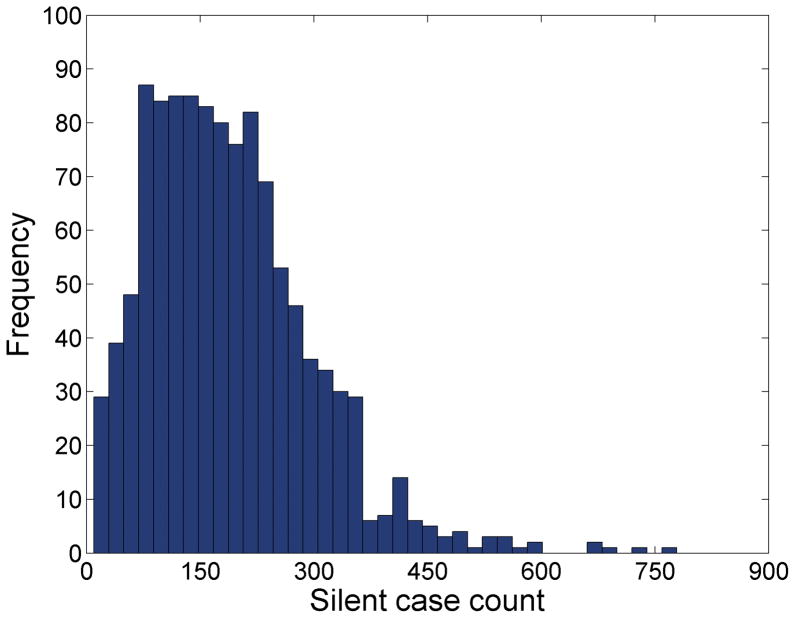
The choropleth maps of pancreatic cancer cases are shown in Figure 7A and 7B. The map and the frequency distribution of the estimated count of silent (yet to be diagnosed) cases are in Figure 7C and 8.

Figure 8.

Frequency histogram of silent (yet to be diagnosed) pancreatic cancer cases in the greater Detroit metropolitan area.

Step 4: Interpret results

This analysis of pancreatic cancer in Michigan demonstrated several important findings. First, the burden of undiagnosed pancreatic cancers in this population is large, approximately 19 times the number of diagnosed pancreatic cancer cases. This indicates a screening test for detecting early stage pancreatic cancer, coupled with appropriate surgical and chemotherapeutic intervention, has the potential for dramatically reducing pancreatic cancer mortality in this population. Second, we estimate there are 1,822.6 undiagnosed advanced stage pancreatic cancer cases in this population. Some of these will be diagnosed prior to death, others will be diagnosed post-mortem. The demand on treatment resources in the last months of advanced pancreatic cancer are substantial and this estimate can be used to predict the demand for health care resources and to predict care expenses. Third, there is some evidence that pancreatic cancer risk in this population is increasing. The SEER results place pancreatic cancer incidence and mortality among the highest in all SEER registries, and the change in the annual incidence rate is about 0.9 percent per year. We found a small but statistically significant relative risk of being 55 or younger and late stage at diagnosis when we consider years 1985–2005 combined. This suggests the possible action of a risk factor for pancreatic cancer that is impacting younger members of this population. However, demographic factors such as differential migration cannot be excluded without further analysis, and in any event the relative risk is not large. Finally, the map of silent (yet to be diagnosed pancreatic cancer cases) directly supports targeting of diagnostic services, planning for upcoming in-home health care needs, and the geographic allocation of future screening programs to local populations with high demand.

Discussion

This research addresses several important topics in the modeling of space-time systems, cancer biology, and cancer surveillance. It has developed, to our knowledge, the first comprehensive modeling approach that estimates cancer latency, couples carcinogenesis and stage models, and that represents and links processes at the genomic level (e.g. mutation events, cascades of genetic changes that lead to cancer), cellular level (e.g. cell replication and death, DNA repair), organ level (e.g. carcinogenesis insitu and metastases to distant organs), individual level (e.g. cancer staging in the individual, progression of individuals through cancer stages), to the population level (e.g. geographic distributions of local populations in cancer stages, estimates of the predicted geographic distributions of undiagnosed cancers). Specific benefits of the approach include.

1. The Genetic GISc construct makes place explicit in the emerging exposome-genome+-behavome synthesis, and demonstrates the vital contribution to be made by geography.

2. It is process-based, capturing the known biological characteristics and mechanics of the cancer process at multiple scales (e.g. genomic to population).

3. It provides estimates of cancer latency, based on the known genetic and histologic characteristics of the cancer.

4. The latency estimates are integrated into spatio-temporal models of cancer incidence, mortality and future cancer burden.

5. The impacts of cancer screening and diagnosis may be represented in the model by diagnosis events through which individuals progress from undiagnosed (silent) to diagnosed stages. This provides a ready mechanism for modeling improvements in pancreatic cancer screening.

6. It predicts the burden of silent cancer (yet to be diagnosed), and geographically allocates these silent cancers by cancer stages into local geographic populations. This provides the quantitative support necessary for forecasting the future cancer burden.

7. The model is readily updatable. As knowledge of cancer genomics becomes more detailed it may be incorporated into the carcinogenesis model by updating the cascade of events that underpin the flows and stages.

8. It provides a quantitative basis for evaluating alternative treatments and for predicting treatment efficacy, provided by the equations and conditions for cancer progression, metastasis and remission.

Several caveats apply

Assumptions implicit in compartmental models include the homogeneity assumption, which states the particles being modeled behave in an identical fashion. This means the pancreatic cancer cells in each compartment of the carcinogenesis model, and the cases in each compartment of the stage model, are assumed to behave in fashions identical to other particles in the compartment under consideration. This assumption is typical of all modeling approaches (since all models involve simplification and abstraction), and can be relaxed when needed by adding additional compartments to capture important aspects of heterogeneity. A second assumption of the compartmental approach is that of instantaneous and complete mixing. This assures that the kinetics (e.g. necessary for calculation of transit and residence times) of each particle may be calculated without consideration of when they entered the compartment or the order in which they entered. A final assumption is that the particles in the compartments (e.g. cells or cases) are sub-dividable, such that a flow of 0.3 cells is possible. This clearly is incorrect for cells and people, but in practice is not a bad assumption when the number of particles in any given compartment is large.

The parameter estimates for cell replication, cell death, DNA mutation rates, repair rates, metastases initiation, and cancer promotion and so on where extracted from the literature by the first author, who is not a trained oncologist or cell biologist. While the author believes the broad strokes are largely correct, the parameter estimates in this article are initial ones only, and the specific results may need to be revised. The overall mathematical and systems biology approach at this juncture appears sound, and it is their exposition that is the main contribution of this article (and not the initial parameter estimates).

There are several future directions for this research. First, knowledge of the exposome and its impacts on carcinogenesis may be incorporated by linking flows and coefficients related to specific exposures relevant to carcinogenetic events such as mutation, cell proliferation, replication and other biological mechanisms through which environmental exposures impact cancer initiation and progression. For example, nonmutational mechanisms (i.e. epigenetic events that turn genes on or off through methylation) can be incorporated into the model through those model coefficients that impact tumor initiation and progression. This requires knowledge or hypotheses regarding how the epigenetic event under consideration impacts carcinogenesis.

Second, the diversity of different pathways to cancer may be represented by fitting models for each pathway. For pancreatic cancers, precursor lesions include the mucinous cycstic neoplasm (MCN), the intraductal papillary mucinous neoplasm (IPMN) and the pancreatic intraepithelial neoplasia (PanIN). In this article we modeled the PanIN pathway, as it is the one responsible for the majority of pancreatic cancers. Pathway-specific models could be developed for cancers that are initiated by MCN and IPMN lesions.

Third, the carcinogensis model provides specific conditions for cancer progression, metastasis and remission. These could be used to predict treatment efficacy, and to evaluate alternative treatments by incorporating information on how specific treatments impact those model coefficients describing cancer cell proliferation, death, and progression to distant sites. Information on how combinations of agents that differentially impact cancer cell proliferation, death and metastatic capacity could be used in the model to evaluate novel multi-chemothearaputic agent treatment regimes.

Fourth, latency itself may be influenced by place-based exposure profiles. Cancer might appear earlier at higher exposures, and causative exposures might vary from one place to another. In the carcinogenesis model for the individual this would be treated by making the mutation coefficients (presented in this article as parameters) as functions based on location history. Similarly, the underlying population of undiagnosed individuals likely would have diverse exposure histories, and such heterogeneity would result in a distribution of expected times to diagnosis. The key methodology underpinning these (and other) elaborations is the ability to realistically model disease latencies, a major contribution of this article.

Finally, the technique is readily extensible to different cancers, and also to other chronic diseases.

A note on latency modeling in geographic and dynamical systems is warranted. A frequently used approach available in most dynamical system modeling software is the incorporation of specific time lags, in which the model incorporates explicit delays, in the flow from one compartment to another. Hence one could simply represent cancer latency by explicitly delaying (e.g. holding back) the entry of particles in the model to a destination compartment once they have exited the source compartment. This has two disadvantages. First, apriori knowledge of the time lag is required, and second the use of explicit time lags implies the model is incomplete. When the compartmental system is properly specified a distribution of residence times is observed that is Erlang distributed and that is representative of the empirical latency times.

A primary objective of this article has been to introduce the construct of genetic GISc (Figure 1) and to illustrate how it may be used to inform our understanding of geographic variation in human health by incorporating knowledge of the Genome +, exposome and behavome. Geographers are largely being by-passed in the fast moving exposome initiative. This article tries to correct this, but more needs to be done. Can Geographers for example incorporate the social dimension more explicitly into the exposome?

The example of pancreatic cancer was used to develop process-based approaches for estimating disease latency, a key problem that must be solved for effective disease mapping and surveillance. This relied heavily on the Genome + dimension of genetic GISc, and much work is needed to develop and exploit the exposome and behavome dimensions. The models developed can incorporate the exposome through their impact on mutation (e.g. through equation 29), although work is needed to make this more explicit and place-based. The use of wearable sensors at the human boundary layer should prove useful in this regard. The behavome, defined as behaviors over an individual’s life course that impact health, are not explicitly modeled in this article, and the quantification, representation and modeling of the behavome is expected to be a rich future research area at the interface of human, physical, medical and behavioral geography.

Figure 9.

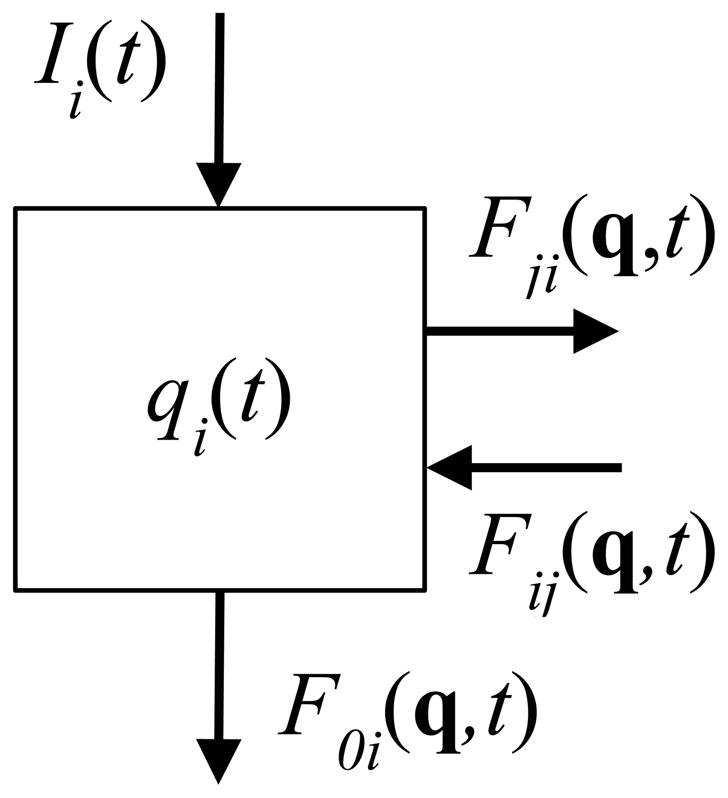
i^th compartment of a compartmental system with flows to (F_0i(q,t)) and from (I_i(t)) outside the system. Flows to and from other compartments are F_ji(q,t) and F_ij(q,t), respectively. The size of the i^th compartment at time t is q_i(t). Source: Jacquez (Jacquez 1996).

Figure 10.

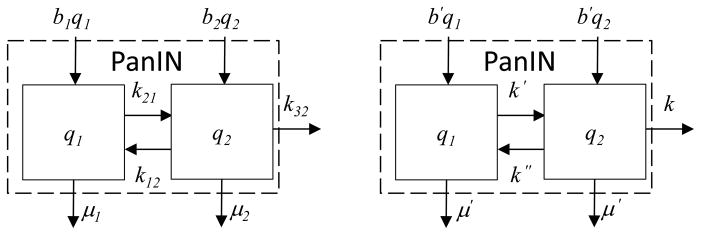
PanIN subsystem model for estimation of distributions of residence times. Original subsystem model (left); simplified model used for calculation of distributions of residence times (right).

Table 3.

Transfer coefficients and their biological mechanisms.

Coefficient	Biological Mechanism
k21	Initiating DNA damage of normal pancreatic cancer cell
k34, k12	DNA repair
k32	Promotion to pancreatic cancer cell, by additional mutation and/or gene expression
k43	Promotion to pancreatic cancer with metastatic capacity, by additional mutation and/or gene expression
k54	Formation of metastases; spread of primary cancer to distant sites

Table 4.

Model parameter estimates. Notes. #1: Cell death rate equals the birth rate in a normal pancreas. #2: For carcinogenesis the death rate of pancreatic cancer cells must be less than their death rate. As a point of departure we assume the death rate for cancerous cells is 0.75 the replication rate. #3: Using an assumed mutation rate per base pair per generation of 5 x 10⁻¹⁰, Yachida and Jones et al. (2010) estimated the mutation rate per cell generation to be 0.016. We require the mutation rate per cell per unit time, and hence estimate k′ to be 0.016 mutations / cell-replication * 1 cell-replication / 2.3 cell days. #4 We set the repair rate to be equal to 99 percent of the mutation rate per cell per unit time; k″=0.99 x 0.16/2.3.

Parameter	Description	Units	Estimate	Reference/note
b′	replication of cells in PanIN	Cell divisions per cell per unit time	1 replication / 2.3 cell days	(Yachida et al. 2010)
b″	replication of pancreatic cancer cells	Cell divisions per cell per unit time	1 replications / 2.3 days per cell division	(Yachida et al. 2010)
b5	Replication of metastatic cancer cells	Cell divisions per cell per unit time	1 replication / 56 days	(Yachida et al. 2010)
μ′	Normal cell death	Deaths per cell per unit time	1 death / 2.3 cell days	#1
μ″	Death of pancreatic cancer cells	Deaths per cell per unit time	μ″ < b″ – k54 ~0.75 * 1/2.3 deaths / cell day	#2
k′	Mutation/initiation to reversible pre-cancerous or cancerous condition	Mutations per cell per unit time	k′=6.957*10−3	#3
k″	DNA repair to normal or earlier cancer state	Repair to prior cell state per cell per unit time	k″=6.887*10−3	#4