Kindergarten Children’s Growth Trajectories in Reading and Mathematics: Who Falls Increasingly Behind?

Abstract

We used a large sample of children (N ≈ 7,400) participating in the Early Childhood Longitudinal Study – Kindergarten Cohort to estimate kindergarten children’s academic achievement growth trajectories in reading and mathematics. We were particularly interested in whether the growth trajectories of children with learning disabilities (LD) or speech language impairments (SLI)—as well as those of other groups of children—were consistent with a cumulative or compensatory developmental cycle. Both LD and SLI children displayed significantly lower levels of kindergarten reading achievement than non-disabled children. However, and over the subsequent five years of elementary school, only children with SLI lagged increasingly behind non-disabled peers in their reading skills growth. We observed a different pattern for mathematics achievement. Children with LD, but not SLI, lagged increasingly behind non-disabled children in their mathematics skills growth. We also observed some consistency in “poor-get-poorer” effects across reading and mathematic achievement for additional population subgroups. Those kindergarten children who were from lower socio-economic status (SES) families, who were African-American, and who more frequently displayed learning-related behaviors problems initially had lower levels of reading and mathematics achievement and also lagged increasingly behind in their acquisition of these skills over time. Some groups of children, including those with SLI, experience a cumulative rather than compensatory cycle of achievement growth.

Students with disabilities typically display low levels of proficiency in reading and mathematics. For instance, the National Center for Education Statistics (2007) reports that 65% and 66% of 8^th grade students with disabilities perform below “basic” (i.e., only partial mastery of the grade’s prerequisite knowledge and skills) levels of proficiency in reading and mathematics, respectively. In contrast, only 22% and 25% of students without disabilities perform below these basic levels. Large achievement gaps between students with and without disabilities are evident for each year that NCES reports such data (i.e., 1998, 2000, 2002, 2003, 2005, & 2007).

Federal legislation (i.e., No Child Left Behind Act, 2001) now targets the achievement gaps between advantaged and disadvantaged students, including those with disabilities. Students with disabilities are to be provided with increased access to high-quality instruction and educational programs, thereby “closing the achievement gap” with their non-disabled peers (Section 1001, No Child Left Behind Act, 2001). Increasing the academic proficiency of students with disabilities should in turn increase their educational and societal opportunities (e.g., Parsons & Bynner, 1997; Rivera-Batiz, 1992).

Yet surprisingly little is known about the growth trajectories that result in these achievement gaps. Those data analyzed by NCES are based on repeated cross-sectional samples, and so are not longitudinal. Some of the work that is longitudinal (e.g., Bast & Reitsma, 1998) has excluded those children who initially displayed very low levels of academic proficiency. Much of the remaining work investigating achievement gaps between advantaged and disadvantaged student groups have not separately identified the trajectories of children with disabilities (e.g., Kieffer, 2008; McCoach, O’Connel, Resi, & Levitt, 2006; Parrila et al., 2005). Those few studies that used samples of students with disabilities (i.e., Baker, Decker, & DeFries, 194; McKinney & Feagans, 1984; Scarborough & Parker, 2003; Skibbe et al., 2008) report inconsistent results. We further detail their findings below in the context of conflicting theoretical accounts of the processes that result in achievement gaps.

Contrasting Theoretical Accounts of Achievement Gaps

Theoretically, achievement gaps result from one of two developmental cycles. The first possibility is characterized as a Matthew effect or cumulative growth model (e.g., Bast & Reistma, 1998; Leppanen, Niemi, Aunola, & Nurmi, 2004; Onatsu-Arvilommi & Nurmi, 2000; Stanovich, 1986; Walsburg & Tsai, 1983). A Matthew effect is increasing advantage or disadvantage following initial advantage or disadvantage. For example, in reading, the Matthew effect would refer to a phenomenon where “over time, better readers get even better, and poorer readers become relatively poorer” (Bast & Reitsma, 1998, p. 1373). Thus, the “gap” between higher and lower skilled children should steadily increase. Those children who enter school as relatively less skilled should experience a negative Matthew effect, in that their academic achievement should lag increasingly behind their peers over time. This should occur in part because they respond less well from the reading or mathematics instruction typically offered by their elementary grade teachers (Skibbe et al., 2008).

A second possibility is a lag or compensatory growth model. Here, initially less skilled children acquire academic skills more rapidly than those who enter school as higher skilled. That is, lower-skilled children begin to “catch up” to their higher-skilled peers. This “narrowing of the gap” could occur as lower-skilled children begin to receive systematic instruction in school, thereby helping to overcome any learning disadvantages these children may have experienced prior to school entry (Leppanen, Niemi, Aunola, & Nurmi, 2004; Phillips, Norris, Osmond, & Maynard, 2002). Thus, and over time, the magnitude of the skills gap between lower- and higher-skilled children should decrease, rather than remain the same or increase (Aunola et al.; Jordan, Kaplan, Olah, & Locuniak, 2006).

Mixed and Limited Empirical Support for these Theoretical Accounts

To date, evidence for a cumulative or compensatory cycle is mixed (e.g., Bast & Reitsma, 1997, 1998; Leppanen et al., 2004; Parrila et al., 2005; Scarborough & Parker, 2003; Shaywitz et al., 1995). Empirical work consistently indicates that children’s relative skill levels are fairly stable (e.g., Anderson et al., 1988; Baker et al., 1984; Jordan, Kaplan, & Hanich, 2002; Juel, 1988; McGee, Williams, Share, Anderson, & Silva, 1986; Scarborough, 1998; Shaywitz et al.; but also see Phillips et al., 2002). That is, children who are poorly skilled in reading or mathematics tend to remain poorly skilled.

However, the empirical work is inconsistent on whether and to what extent the gap between lower- and higher-skilled children increases or decreases over time. For example, Bast and Reitsma (1998) reported that the gap in word recognition skills between good and poor readers gradually widened. Such a finding supports a cumulative cycle. Yet neither Aarnoutse and van Leeuwe (2000) nor Baker et al. (1984) nor McCoach et al. (2006), nor Rescoria and Rosenthal (2004) observed an increasing gap. Instead, poor readers have often been observed to narrow the reading or mathematics achievement gap (e.g., Aarnoutse & van Leeuwe; Catts, Hogan, & Fey, 2003; Jordan et al., 2002; Parrila et al., 2005; Phillips et al., 2002; Shaywitz et al., 1995). These findings support a compensatory cycle.

Which of these two developmental cycles do children with disabilities follow? Children with learning disabilities (LD) or speech or language impairments (SLI) should be especially likely to experience any “poor-get-poorer” effects. This is because most of these children have severe language- and literacy-related deficits (e.g., Lyon, 1995). For example, Snow, Burns, and Griffin (1998) estimated that about 80% of children with LD are poor readers. Catts et al. (2002) reported that 53% and 48% of kindergarten children with SLI met reading disability criteria in 2^nd and 4^th grade, respectively. Catts, Fey, Zhang, and Tomblin (1999) estimated that about 70% of poor readers had a history of early language deficits. The Matthew effect theory (Stanovich, 1986) is also a widely cited etiological account of children’s identification as LD (e.g., Roberts et al., 2008).

Yet children with LD and SLI also receive additional, specialized instruction from specially trained teachers, speech language pathologists, and other professionals. This additional instruction should have been individualized, so as to help mitigate the particular effects of each child’s disability and thereby allow the child to better access his or her school’s curriculum (Bateman & Linden, 2006). The receipt of such specialized instruction should make any compensatory effects more likely to occur.

Evidence regarding the growth trajectories of LD and SLI children also has theoretical and practical implications. Theoretically, such a study would help establish whether the growth trajectories of children with disabilities are best characterized by a cumulative or compensatory cycle. From the standpoint of practice, an increasing gap would indicate the need to increase the quality and intensity of instruction currently being provided to young children with disabilities. This is because currently delivered instruction may not be helping these children become as academically proficient as their non-disabled peers. In contrast, a decreasing gap would suggest that the instruction currently being provided is sufficient in helping children with disabilities attain academic proficiency.

Results from the few studies of whether achievement gaps between those with and without LD or SLI widen, lessen, or remain stable over time are inconsistent. McKinney and Feagans (1984) tracked a sample of children with LD over three years. Their results indicated that the gap in both word recognition and reading comprehension steadily increased between children with and without LD. These results are consistent with a cumulative cycle. The mathematics achievement gap, although substantial, remained mostly stable. In contrast, neither Baker et al. (1984) nor Scarborough & Parker (2003) found that the reading achievement gap between children with and without LD increased over time. Scarborough and Parker (2003)’s analyses instead yielded a correlation of -.77 between the children’s beginning reading scores and their reading growth. That is, the lower the initial reading skill of a child, the higher his or her rate of skills growth. The investigators concluded that the Matthew effect remains “elusive, despite the plausibility and wide-spread acceptance of that well-reasoned hypothesis (p. 65). Skibbe et al.’s (2008) analyses of a sample of children with and without criterion-identified language impairments also indicated little evidence of negative Matthew effects. Instead, the reading achievement gap gradually narrowed. Because the reading skills of children with language impairments grew relatively more rapidly, the reading achievement gap between the two groups of children decreased from 1 to less than .6 of a SD between preschool and 5^th grade. These findings support a compensatory cycle.

Confounds for a Matthew Effect in Children with LD or SLI

Rigorously investigating whether the growth trajectories of children with LD or SLI display a cumulative or compensatory cycle necessitates accounting for a number of potentially confounding factors. This is because children from other population sub-groups also may be at risk for experiencing a cumulative or compensatory cycle. Children from lower socio-economic status (SES) families, those who are minorities, those who were retained, and “garden variety” learners with low levels of skills proficiency are known to display growth trajectories consistent with either cycle (e.g., Hong & Raudenbush, 2005; McCoach et al., 2007; Morgan, Farkas, & Hibel, 2008). For instance, McCoach et al. (2006) recently reported that children from low-income families scored, on average, 6.2 point lower on a measure of reading proficiency than children from high-income families across their first two years of school.

Recent analyses by Kieffer (2008) indicate to what extent the failure to control for additional characteristics of the child, family, or school may bias estimates of the effects of a child’s disability status on his or her achievement growth trajectories. Kieffer contrasted the reading achievement of those children who entered school as English Language Learners (ELL) with initially limited English proficiency to that of children who were native English speakers. His initial effect size estimate of children’s ELL status on their 5^th grade reading achievement was -.83, or a large effect size. However, statistically controlling for variation in children’s socio-demographic and school characteristics substantially reduced this to a weighted average estimate to -.39, or a medium effect size. To date, however, the extant work investigating the growth trajectories of children with LD or SLI has not statistically controlled for variation that might instead be attributable to the child’s other socio-demographic characteristics (e.g., the child’s age, gender, or race/ethnicity), or his or her family’s or school’s characteristics (e.g., the family’s SES), or additional confounds (e.g., the frequency of the child’s learning-related behaviors). Doing so is important not only to better test for cumulative or compensatory effects among children with disabilities, but also to determine whether and to what extent other subgroups of children (e.g., those from lower SES families) are also at risk of experiencing such effects.

Study’s Purpose

We estimated children’s academic achievement growth trajectories in both reading and mathematics. We were particularly interested in whether the growth trajectories of children with LD or SLI were consistent with a cumulative or compensatory developmental cycle. Thus, we sought to establish whether the achievement gaps between those with and without LD or SLI increased, decreased, or remained stable across time. To better establish the extent to which either of these patterns were directly attributable to children’s disability status, we statistically controlled for effects that might be attributable to characteristics other than whether the children were disabled, such as whether they were being raised in a lower SES family, had been retained, or were frequently inattentive or otherwise displaying learning-related behavior problems.

We designed the study to be methodologically rigorous. We did so in three ways. First, we internally replicated our results. We tested for a cumulative or compensatory growth pattern using sub-samples of children with LD or SLI, as well as a large and more general sample of elementary schoolchildren. We did this for both reading and mathematics. Children with either type of disability should be especially likely to experience a negative Matthew effect in reading and, due to its phonological processing, listening comprehension, and vocabulary demands, in mathematics (e.g., Jordan et al., 2002; Miller & Mercer, 1997; Stanovich, 1986). Children who enter school identified as SLI frequently later display LD (e.g., Catts et al., 2002). Thus, young children with SLI might reasonably be considered at high risk for later LD identification. Including children with either type of disability should therefore result in a more sensitive analysis of the onset of a cumulative or compensatory cycle. Second, we constructed our analyses to be conservative. We statistically controlled for an increasingly wide range of potential confounds (e.g., children’s SES, their race/ethnicity) when evaluating whether the growth trajectories of children with LD or SLI could be characterized as displaying negative Matthew effects. Third, we tested for a cumulative or compensatory growth pattern over an especially long time period. We did so by using a longitudinal sample of children followed over the length of their elementary school years (i.e., kindergarten-5^th grade).

Method

Study’s Database and Analytical Sample

We used data from the Early Childhood Longitudinal Study—Kindergarten Cohort (ECLS-K). The ECLS-K is sponsored by the U.S. Department of Education, National Center for Educational Statistics (NCES). NCES selected a nationally representative sample of kindergarteners in the fall of 1998. Data from these children has now been collected through the spring of 2007, and the current study used data from kindergarten through elementary school (i.e., spring of 2004). The children attended both public and private kindergartens, offering full- and part-day programs, across about 3,500 classrooms in 1,280 schools. The NCES used sample freshening to help make the ECLS-K representative of all first graders in the fall of 1999. Data from the sampled children in this study were collected in fall 1998, spring 1999, spring 2000, spring 2002, and spring 2004. A small subsample of children also participated in the study in fall 1999.

We included those ECLS-K children in our analytical sample who were (a) identified as having LD or SLI, or (b) not on school record as having an IEP or disability diagnosis (see Disability Status below). The group of children without identified disabilities served as a reference group in our analytical sample. This analytical sample includes first time and retained kindergarteners, as well as children who changed or did not change schools between grades. We used NCES-constructed child-level sampling weights to account for the unequal sampling probabilities and non-response rates.

Measures

Disability Status

Information on a child’s disability status was obtained from the ECLS-K special education teacher questionnaire collected in the spring of 1999, when the children were in kindergarten. The questionnaire was administered to special education teachers of sampled children who had an IEP. This questionnaire surveys information on a particular child who has been receiving services from the special education teacher and whether the child is receiving special education services due to (a) a disability or (b) gifted/talented services.

The questionnaire includes questions on whether the child has a primary disability of (a) LD or (b) SLI. We used responses to these two questions in our analyses. Specifically, we used one dummy variable to indicate whether the special education teacher identified the child’s primary disability as LD. We used a second dummy variable to indicate whether the special education teacher identified the child’s primary disability as SLI. The remaining children in our defined sample belonged to the reference category of those kindergarteners with no record indicating either an IEP or a special education teacher-identified disability. We used these procedures to identify three groups of children: (a) those with identified LD; (b) those with identified SLI; and (c) those with no identified disabilities, and not receiving special education services.

Reading Achievement

We used scores from the ECLS-K Reading Test to estimate a child’s early reading achievement, as well as his or her rate of skills growth over time. In some regressions we also used the child’s spring of kindergarten Reading Test score as an autoregressor to more conservatively estimate the growth trajectories of children with LD or SLI, as well as the effects of the study’s other control factors.

The Reading Test seeks to measure children’s basic skills (e.g., print familiarity, letter recognition, decoding, sight word recognition), vocabulary (receptive vocabulary), and comprehension (i.e., making interpretations, using personal background knowledge). The Reading Test was constructed through a multi-stage panel review. Some items were borrowed or adapted from published tests (e.g., the Peabody Picture Vocabulary Test—Revised, the Woodcock Johnson Tests of Achievement—Revised). The Educational Testing Service, elementary school curriculum specialists, and practicing teachers supplied other items. All items were field-tested. Items were included in the Test’s final form if they displayed (a) acceptable item-level statistics, (b) good fit with maximum likelihood item response theory (IRT) parameters, and (c) no differential item functioning across gender or race (NCES, 2005).

NCES used IRT methods to generate adaptive tests that were administered one-to-one to each child, in an un-timed format. A child first took a brief routing test. A second test, which was matched based on a child’s scores on the routing test, was then administered. NCES considers use of the IRT scores as the most appropriate metric for growth modeling, as these scores can be compared across different test form administrations and across different grades (NCES, 2006). Reliabilities of the IRT scaled scores ranged from .91 to .96 across ECLS-K’s survey waves collected from children’s kindergarten years through 5^th grade (NCES, 2005). High correlations (i.e., 3^rd grade = .83, 5^th grade = .78) between the Reading Test’s IRT scores and children’s scores from the Woodcock-McGrew-Werder Mini-Battery of Achievement (Woodcock, McGrew, & Werder, 1994) support its construct validity.

Mathematics Achievement

We used scores from the ECLS-K Mathematics Test to estimate both a child’s early mathematics achievement and his or her rate of growth over time. We also used the child’s spring of kindergarten Mathematics Test score as an autoregressor. The Mathematics Test seeks to measure a range of age- and grade-appropriate mathematics skills (e.g., identify numbers and shapes, sequence, add or subtract or multiply or divide, use rates and measurements, use fractions, calculate area and volume). NCES used a multi-step panel review process to develop the ECLS-K’s Mathematics Test (NCES, 2005). This test was based on the NAEP’s specifications. A wide range of kindergarten, 1^st grade, 3^rd grade, and 5^th grade-level test items were used. As with the Reading Test, NCES used IRT methods to construct adaptive Mathematics Tests that were administered one-to-one to each child in an un-timed format. Reliabilities of the IRT scaled scores ranged from .89 to .94 across all ECLS-K’s survey waves used in this study (NCES, 2005). High correlations (i.e., 3^rd grade = .84, 5^th grade = .80) between the Mathematics Test’s IRT scores and children’s scores from the Woodcock-McGrew-Werder Mini-Battery of Achievement (Woodcock et al., 1994) indicate construct validity.

Learning-related Behaviors

In some regressions we predicted a child’s initial knowledge of reading or mathematics and skills growth over time using the frequency with which he or she displayed learning-related behaviors during the spring of kindergarten. The frequency of a child’s learning-related behaviors (e.g., attention, task persistence, organization) is consistently reported to predict his or her learning of reading or mathematics (e.g., Duncan et al., 2007; Morgan, Farkas, Tufis, & Sperling, 2008; Onatsu-Arvilommi & Nurmi, 2000; Nurmi & Aunola, 2005; Tach & Farkas, 2006). We measured a child’s learning-related behaviors using teacher ratings on the Approaches to Learning subscale from the modified Social Skills Rating System (SSRS; Grehsam & Elliott, 1990). NCES refers to the modified version of the SSRS as the Social Rating Scale (SRS). The SRS teacher ratings are intended to measure behaviors that likely impact the child’s ability to benefit from a classroom’s learning environment. The Approaches to Learning subscale’s items seek to measure a child’s attentiveness, task persistence, eagerness to learn, learning independence, adaptability to changes in routine, and organization. The spring kindergarten split half reliability for the subscale was .89 (NCES, 2006).

Age, Socioeconomic Status, Race, Gender, School Type and Kindergarten Retention

We analyzed to what extent a child’s age in kindergarten, socioeconomic status (SES), race, gender, school type or kindergarten grade retention predicted his or her initial skill level and rate of skills growth over time in both reading and mathematics. Data on these factors were collected during the fall or spring of kindergarten. The age variable indicated a child’s age in months at the start of kindergarten. The SES variable measured a household’s SES by the spring of kindergarten. NCES calculates a household’s SES using information about father’s (or male guardian’s) and mother’s (or female guardian’s) education, occupation, as well as the family’s household income. NCES estimates SES using both a continuous and a categorical scale. We used the continuous variable (i.e., WKSESL), which ranged from -4.75 to 2.75. The race variable indicated whether the child was parent-identified as in one of the following categories: (a) White, non-Hispanic; (b) Black/African-American, non-Hispanic; (c) Hispanic; and (d) Other. We also included in our analysis a dichotomous variable indicating whether the child repeated kindergarten or not. We did so to ensure that our estimate of the age effect was not confounded by whether the child was older only because he or she had repeated kindergarten. Doing so also enabled us to provide a separate estimate of retention’s effects on children’s reading and mathematics achievement. Information on school type was collected from school administrator questionnaire. The school administrator identified the school as public or private.

Missing Data

We excluded from subsequent analysis those children who had missing data on the child-level predictors measured during kindergarten (e.g., race, gender, retention, Reading or Mathematics Test score at the initial survey wave). Doing so resulted in an analytical sample of approximately 7,420 children. We used NCES-constructed sampling weights to help correct for missing data and for over-sampling of particular sub-groups of children. Table 1 displays descriptive information of the ECLS-K full and weighted analytical samples. Use of the sampling weights results in an analytical sample that closely approximates the nationally representative full sample in gender composition, percentage of African-American children, and in average SES. However, the samples are somewhat less comparable in their respective percentages of white children, those attending public and private school, and those of other racial/ethnic minority heritage. Subsequent to its initial capture, missing data occurred vary rarely for the analytical sample. Only 8%, 5%, and .04% of our analytical sub-samples of children with LD, SLI, and without disabilities, respectively, had missing Reading or Mathematics Test score data subsequent to our identification of these groups in kindergarten.

Table 1.

Socio-Demographic Characteristic for the ECLS-K’s Full and Analytical Samples

	Full Sample (N ≈ 17,080)	Weighted estimates for the analytical sample (N ≈ 7,400)
Gender
Male	50.59%	50.86%
Female	49.41%	49.14%
Race
White	56.21%	64.77%
Black or African American	14.27%	14.64%
Hispanic	17.52%	13.64%
Other	12.00%	6.95%
School Type
Public	76.92%	82.85%
Private	23.08%	17.15%
SESa	.03 (.80)	.05(.79)

Note. Standard deviations in parentheses;

^aUsing WKSESL, an NCES-constructed estimate of a family’s socioeconomic status using information self-reported by the child’s father and/or mother about his or her level of education, occupation, and income.

Analytical Strategy

We used growth curve modeling to estimate the effects of a child’s disability status, socio-demographic characteristics, grade retention, relative level of reading or mathematics achievement at school entry, and frequency of learning-related behaviors on the child’s spring of 1^st grade level and subsequent skills growth over time in reading and mathematics. We used four of available time points from ECLS-K (that is, spring of kindergarten, springs of 1^st, 3^rd, and 5^th grade for those children not retained). We used data collected by the spring of kindergarten to predict the intercept (i.e., spring of 1^st grade) and slope (i.e., spring of 1^st grade to spring of 5^th grade) terms when estimating children’s growth trajectories. We did not use the fall of 1^st grade data because NCES only collected such data from a small sub-sample of children during this survey wave.

Time

Because the study’s three estimated time points (i.e., springs of first, third, and fifth grades) are equally spaced, we set the value of our first time point at 0 (indicating the child’s relative level of mathematics knowledge at spring first grade) and then set values for the subsequent time points in relation to their relative distance from this first time point, with the addition of every 2 academic years associated with an increment of 1 in the time scale. This resulted in the values of 0, 1, and 2 for spring 2000, spring 2002, and spring 2004 test administrations, respectively.

We utilized Hierarchical Linear Modeling (HLM) to model the growth trajectories of children (Raudenbush & Bryk, 2002). HLM-type growth modeling treats the observations at varying time points as the 1^st level of data nested within an individual, which is at the 2^nd level. Models estimating these two levels are also called the repeated-observations model and the person-level model respectively in HLM. Use of HLM does not require data to be balanced within subjects (Raudenbush & Bryk). That is, HLM allowed us to use data from any available time point even when data from other time points was missing.

We estimated a two-level model with the repeated observations over time being the 1^st level and child the 2^nd level. Level 1’s equation specified the score at each time point as a function of time. We specified a quadratic growth model at Level 1. This equation is expressed as follows:

$$Y_{\mathit{ti}}={\pi }_{0i}+{\pi }_{1i}t+{\pi }_{2i}{t}^2+e_{\mathit{ti}}$$ (1)

for i=1, 2, 3, …, n subjects, where t is the time and π_0i is the initial status of the child at time 0, and π_1i is the linear slope, indicating the growth rate of person i from the initial time point and π_2i is the quadratic curvature and represents the acceleration in each growth trajectory. The growth rate of person i at any particular time point is the first derivative of the growth model at that point, which is equal to π_1i + 2π_2it. This indicates that if π_2i is positive, the person is growing at an accelerating rate. If π_2i is negative, the person is growing at a decelerating rate. e_ti is the measurement error at the 1^st level and is assumed to be normally distributed with a mean of 0 and constant variance.

In Level 2, the intercept and slope terms of the regression equation become the criterion variables and can be predicted by a set of child-level characteristics. The level 2 equations (for the study’s full set of predictors) for the reading initial status and growth rate parameters are as follows:

$$\begin{array}{l}{\pi }_{0i}={\beta }_{00}+{\beta }_{01}(\mathit{LD})+{\beta }_{02}(\mathit{SLI})+{\beta }_{03}(\mathit{Age})+{\beta }_{04}(\mathit{SES})+{\beta }_{05}(\mathit{Black})\\ +{\beta }_{06}(\mathit{Hispanic})+{\beta }_{07}(\mathit{other})+{\beta }_{08}(\mathit{Female})+{\beta }_{09}(\mathit{repeating}\_\mathit{kindergarten})\\ +{\beta }_{10}(\mathit{Public})+{\beta }_{011}(\mathit{Math})+{\beta }_{012}(\mathit{approaches})+r_{0i}\\ {\pi }_{1i}={\beta }_{10}+{\beta }_{11}(\mathit{LD})+{\beta }_{12}(\mathit{SLI})+{\beta }_{13}(\mathit{Age})+{\beta }_{14}(\mathit{SES})+{\beta }_{15}(\mathit{Black})\\ +{\beta }_{16}(\mathit{Hispanic})+{\beta }_{17}(\mathit{other})+{\beta }_{18}(\mathit{Female})+{\beta }_{19}(\mathit{repeating}\_\mathit{kindergarten})\\ +{\beta }_{110}(\mathit{Public})+{\beta }_{111}(\mathit{Math})+{\beta }_{112}(\mathit{approaches})+r_{1i}\\ {\pi }_{2i}={\beta }_{20}\end{array}$$ (2)

where a β estimates the effect of a predictor on a child’s initial status and growth rate, and r_0i and r_1i are random error. We specified the coefficient of the quadratic term as invariant. (Each growth model’s 3 time points did not provide us with sufficient degrees of freedom to estimate the random effects of the quadratic term). We left uncentered all categorical predictors. However, we grand-mean-centered the continuous predictors so that the intercept parameters.

Predictor Models

We estimated four models of the effects of a range of predictors on a child’s initial (i.e., spring of 1^st grade) and over time (i.e., spring of 1^st grade to spring of 5^th grade) reading and, separately, mathematics achievement. We entered the study’s predictors sequentially. Model 1 only includes the children’s status as being LD or SLI. These variables again indicate whether the child was (a) participating in special education and had a primary disability identification of LD or SLI or (b) was not participating in special education because he or she was not identified as having an IEP or a disability. Model 1 yields an initial estimate of the extent to which children with either disability display initially lower levels of reading or mathematics skill by the spring of 1^st grade and, subsequently, lower rates of reading or mathematics skills growth between the springs of 1^st-5^th grade than children without disabilities.

Model 2 adds the socio-demographic variables of age, SES, race, and gender as well as whether the child repeated kindergarten. Model 2 therefore evaluates to what extent a cumulative or compensatory cycle best characterizes the growth trajectories of children of different age, SES level, race/ethnicity, and gender. Model 2 also estimates whether children with disabilities display cumulative or compensatory growth trajectories after statistically controlling for these additional socio-demographic characteristics. Model 3 adds the child’s spring of kindergarten Reading or Mathematics IRT score and Approaches to Learning subscale score to the model. Model 3 therefore includes what we term the “domain-specific” autoregressor (i.e., earlier Reading Test score when predicting later Reading Test score; earlier Mathematics Test score when predicting later Mathematics Test score). Model 4 includes both the “domain-specific” and “domain-general” autoregressors (i.e., both Reading and Mathematics Test score when predicting later Reading Test score; both Mathematics and Reading Test score when predicting later Mathematics Test score). Model 3 and 4 therefore are especially conservative models. Model 4 uses the domain-general autoregressor because early skill level in reading or, separately, mathematics can be expected to strongly predict a child’s later skill level in either academic domain (Duncan et al., 2007). Model 3 and 4 statistically control for a child’s initial level of reading or mathematics “wealth” (e.g., whether he or she was ending kindergarten as a “rich” or “poor” reader), as well as the relative frequency of his or her task engagement in the classroom.

Estimating these models allowed us to investigate to what extent (a) children with LD or SLI display cumulative or compensatory growth trajectories in reading or mathematics and (b) other types of characteristics of the children (e.g., gender, race/ethnicity, the frequently in which they were inattentive), their families (i.e., SES), and schools (e.g., whether the school was public or private) mediated the effects otherwise attributable to the children’s disability status. Because our analyses statistically controlled for variation in a child’s socio-demographic characteristics, as well as additional, more educationally relevant factors (i.e., whether the child had attended a public or private school, whether the child had been retained, his or her relative proficiency in reading or mathematic while in kindergarten, the frequency of his or her learning-related behaviors), they should constitute an especially rigorous investigation into whether children with LD, or those highly at risk for LD due to their SLI, experience accumulating disadvantage or instead are able to compensate for initial disadvantage in either reading or mathematics during their elementary school years.

Results

We report two sets of statistical results. Tables 2-4 and Figures 1-4 display the first set. Here we report descriptive statistics of the samples of children with LD, SLI, and without disabilities. We identify general patterns in these data. Tables 5-6 display the second set of results. Here we report results on our increasingly conservative model estimation. Our initial model evaluates whether a cumulative or compensatory cycle characterizes the growth trajectories of children with LD or SLI. The subsequent models evaluate to what extent these trajectories are attributable to characteristics other than the child’s disability (e.g., the child’s gender, race/ethnicity, the family’s SES). We also report on the overall correlation between the general sample’s intercept and slopes. Prior investigations have used such a correlation as evidence for a Matthew effect if it is positive, and against such an effect if it is negative (e.g., Scarborough & Parker, 2003; Shaywitz et al., 1995).

Table 2.

Descriptive Statistics for the Analytical Samples of Children Entering Kindergarten with and without an IEP and a Primary Disability Diagnosis

	Children with LD***	Children with SLI***	Children with neither IEP nor Disability Diagnosis***
	Weighted Mean (SD)	Weighted Mean (SD)	Weighted Mean (SD)
	N ≈ 20	N ≈ 180	N ≈ 7,200
Age in month	71.49 (5.25)	67.55 (4.77)	66.09 (4.24)
SES	.17 (.60)	-.13 (.90)	.06 (.78)
White	.84 (.36)	.60 (.49)	.65 (.48)
Black	.12(.33)	.19(.39)	.15 (.35)
Hispanic	.04(.18)	.17(.38)	.14 (.34)
Other	.00	.04(.21)	.07(.26)
Female	.19 (.39)	.33 (.47)	.50 (.50)
Repeat K	.51 (.50)	.09 (.29)	.04(.19)
K Approaches score	2.68 (.56)	2.90 (.69)	3.14 (.68)
Attending public school	.84 (.37)	.95 (.22)	.82 (.38)

Note. IEP=Individualized Education Program. LD=Learning disability. SLI=Speech or language impairment. K=Kindergarten.

^***Each between-group contrast (i.e., LD vs. non-disabled; SLI vs. non-disabled; LD vs. SLI) for each variable was statistically significant at p<.001.

Table 4.

Kindergarten through 5^th Grade Mathematics Tests Scores for Children Entering Kindergarten with and without IEP and a Disability Diagnosis

	Children with LD***		Children with SLI***		Children with neither IEP nor Disability Diagnosis***
	N	Weighted Mean (SD)	N	Weighted Mean (SD)	N	Weighted Mean (SD)
Spring K	20	26.68 (6.11)	180	28.55 (10.24)	7,200	34.20 (11.66)
Spring 1st grade	20	52.05 (14.15)	180	47.86 (14.94)	7,200	59.20 (16.47)
Spring 3rd grade	20	81.93 (24.96)	180	79.01 (22.93)	7,200	93.76 (21.18)
Spring 5th grade	20	92.91 (21.91)	180	100.97 (24.61)	7,200	114.61 (20.99)

Note. IEP=Individualized Education Program. LD=Learning disability. SLI=Speech or language impairment. K=Kindergarten.

^***Each between-group contrast (i.e., LD vs. non-disabled; SLI vs. non-disabled; LD vs. SLI) for each variable was statistically significant at p<.001.

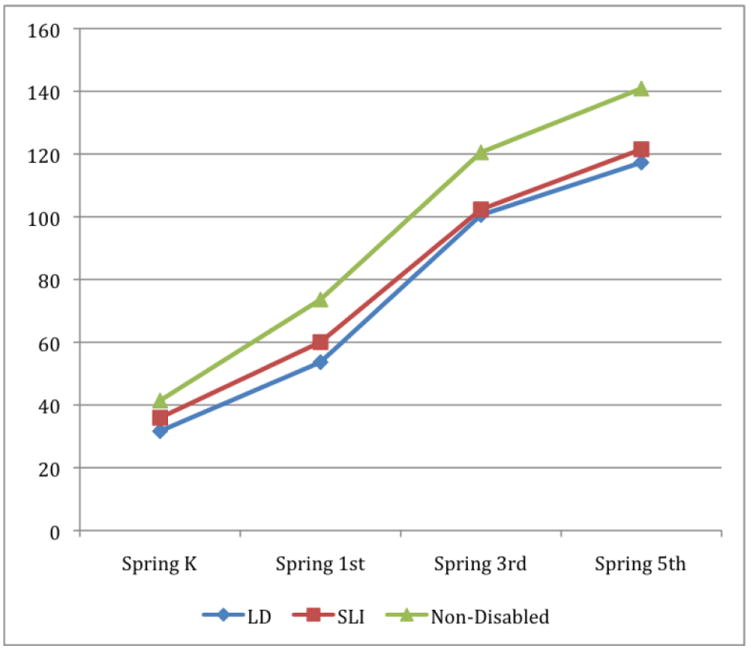
Figure 1. Mean Reading Test IRT Score for Children with LD, Children with SLI, and Children without Disabilities, K-5^th grade.

Note. LD=Learning Disability. SLI=Speech or language impairment.

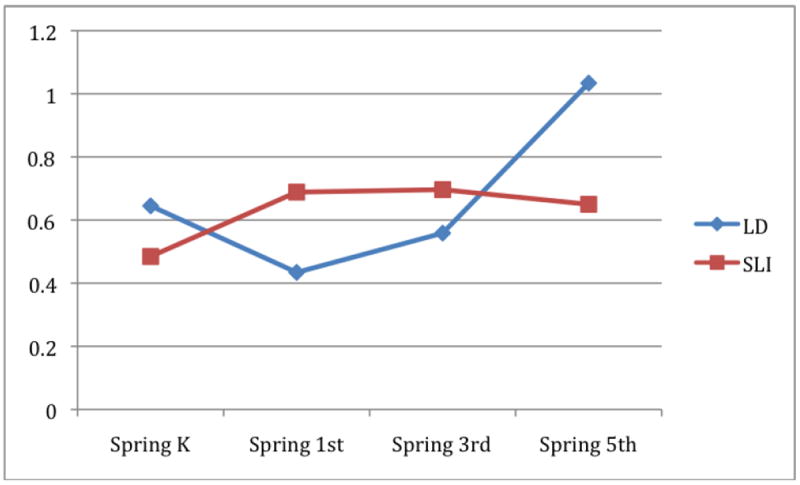
Figure 4. Standard Deviation Unit Differences in Mathematics Achievement between Children with LD or SLI and Children without Identified Disabilities.

Note. LD=Learning Disability. SLI=Speech or language impairment.

Table 5.

Reading Achievement Growth Models for Children Entering Kindergarten with and without IEP and a Disability Diagnosis

	Model 1			Model 2			Model 3			Model 4
	I	S	Q	I	S	Q	I	S	Q	I	S	Q
Intercept Disability status1	73.63*	59.70*	-13.06*	76.25*	60.38*	-13.06*	76.79*	61.03*	-13.05*	75.57*	60.69*	-13.05*
LD	-19.33*	-1.81		-20.33*	-1.75		-4.52	-4.26		-2.55	-3.69
SLI	-14.22*	-3.56*		-12.10*	-3.18*		-6.33*	-4.02*		-5.14*	-3.69*
Age in month			.96*	-.23*			.14	-.11*		-.02	-.16*
SES			9.85*	.75*			2.85*	1.90*		2.12*	1.70*
Race2
Black			-5.64*	-3.46*			-3.39*	-3.66*		-1.86	-3.23*
Hispanic			-2.52	-.31			-1.17	-.66		-.28	-.42
Other			-2.25	-.99			-1.51	-1.13		-.92	-.97
Female			3.37*	-.48			-.62	-.38		.68	-.01
Repeat K			-10.16	1.60			-7.76*	1.72		-7.32*	1.81
Public school			-1.92*	-.05			-.45	-.52		-.11	-.42
Spring of K Reading Test score							1.07*	-.23*		.87*	-.29*
Spring of K Mathematics Test score										.44*	.12*
Spring of K Approaches to Learning teacher rating							4.92*	1.30*		3.57*	.92*

Note. Estimates are weighted with the child-level weights. Level 1 units N = 22,150; Level 2 units N = 7,405. Age and SES are grand-mean centered; other predictors are uncentered.

^*p-value<.05.

¹Reference category is students with no disability.

²Reference category is the white students.

LD=Learning Disability. SLI=Speech or language impairment. K=Kindergarten. I=Intercept. S=Slope. Q=Quadratic.

Table 6.

Mathematics Achievement Growth Models for Children Entering Kindergarten with and without IEP and a Disability Diagnosis

	Model 1			Model 2			Model 3			Model 4
	I	S	Q	I	S	Q	I	S	Q	I	S	Q
Intercept Disability status1	59.23*	41.26*	-6.79*	63.90*	42.52*	-6.79	62.27*	42.85*	-6.78*	62.31*	42.86*	-6.79*
LD	-6.30	-7.24*		-12.14*	-5.70*		.83	-5.05*		1.06	-5.02*
SLI	-12.10*	-1.18		-11.84*	-.63		-5.88*	-.32		-5.86*	-.32
Age in month				.86*	-.28*		.02	-.33*		.02	-.33*
SES				7.51*	1.29*		2.14*	1.02*		2.01*	1.00*
Race2
Black				-8.63*	-3.04*		-3.69*	-2.81*		-3.82*	-2.83*
Hispanic				-3.54*	.55		-1.02	.54		-1.05	.54
Other				-3.91*	-.22		-2.23*	-.18		-2.27*	-.18
Female				-2.92*	-1.65*		-2.94*	-2.11*		-3.08*	-2.13*
Repeat K				-2.96	-1.49		.12	-1.06		.04	-1.07
Public school				-.36	.10		.83	.02		.88	.02
Spring of K Reading Test score										.06*	.01
Spring of K Mathematics Test score							1.00*	.01		.95*	.00
Spring of K Approaches to Learning teacher rating							2.87*	1.44*		2.74*	1.42*

Note: Estimates are weighted with the child level weights. Level 1 units N = 22,150; Level 2 units N = 7,405. Age and SES are grand-mean centered, other predictors are uncentered.

^*p-value<.05.

¹Reference category is students with no disability.

²Reference category is the white students.

LD=Learning Disability. SLI=Speech or language impairment. K=Kindergarten. I=Intercept. S=Slope. Q=Quadratic.

Descriptive Statistics

Table 2 displays descriptive statistics of the socio-demographic, kindergarten retention, learning-related behaviors, and additional characteristics for each of the three groups of children identified by their kindergarten disability diagnosis (or lack of such diagnosis). These three groups are (a) children with an IEP on record and a primary diagnosis of LD, (b) children with an IEP on record and a primary diagnosis of SLI, and (c) children having neither an IEP nor a disability diagnosis on record.

Kindergarten children diagnosed with LD varied substantially on a number of socio-demographic characteristics from their non-disabled peers. These children are more likely to be older, to be raised in higher-income households, and to be White and not Hispanic than either children diagnosed as SLI or those without a disability diagnosis. Children with LD are also more likely to be male, as well as to be more likely to repeat kindergarten. Children diagnosed with LD also display learning-related behaviors less frequently than children diagnosed as SLI or those without identified disabilities. Table 2 also indicates that children diagnosed with SLI are more likely to be raised in lower-income households than kindergarteners with LD or those without identified disabilities. Children with SLI in our analytical sample are also somewhat more likely to be African-American or Hispanic, and attend a public school. These children also engage in learning-related behaviors less frequently than kindergarten children without identified disabilities. Each of these between-group contrasts is statistically significant at the p<.001 level.

Table 3 displays descriptive statistics for the IRT scores on the Reading Test across the study’s survey waves for each of the three groups of children. The average scores for all three groups of children gain substantially over time. However, of these three groups, children with LD average the lowest scores at the end of kindergarten and then 5^th grade. This is followed in sequence by children diagnosed with SLI and then those children without a disability diagnosis. Children diagnosed with LD also display the lower Reading Test scores at each of the study’s four time points, followed by children diagnosed with SLI and then those without a disability diagnosis. Each of the aforementioned contrasts between children with LD, those with SLI, and those without identified disabilities is again statistically significant at p<.001.

Table 3.

Kindergarten through 5^th Grade Reading Tests Scores for Children Entering Kindergarten with and without IEP and a Disability Diagnosis

	Children with LD***		Children with SLI***		Children with neither IEP nor Disability Diagnosis***
	N	Weighted Mean (SD)	N	Weighted Mean (SD)	N	Weighted Mean (SD)
Spring K	20	31.68 (4.94)	180	35.94 (12.75)	7,200	41.42 (13.55)
Spring 1st grade	20	53.65 (15.63)	180	60.05 (19.77)	7,200	73.63 (22.34)
Spring 3rd grade	20	100.55 (30.02)	180	102.34 (26.90)	7,200	120.53 (24.43)
Spring 5th grade	20	117.29 (26.01)	180	121.51 (26.86)	7,200	140.89 (22.42)

Note. IEP=Individualized Education Program. LD=Learning disability. SLI=Speech or language impairment. K=Kindergarten.

^***Each between-group contrast (i.e., LD vs. non-disabled; SLI vs. non-disabled; LD vs. SLI) for each variable was statistically significant at p<.001.

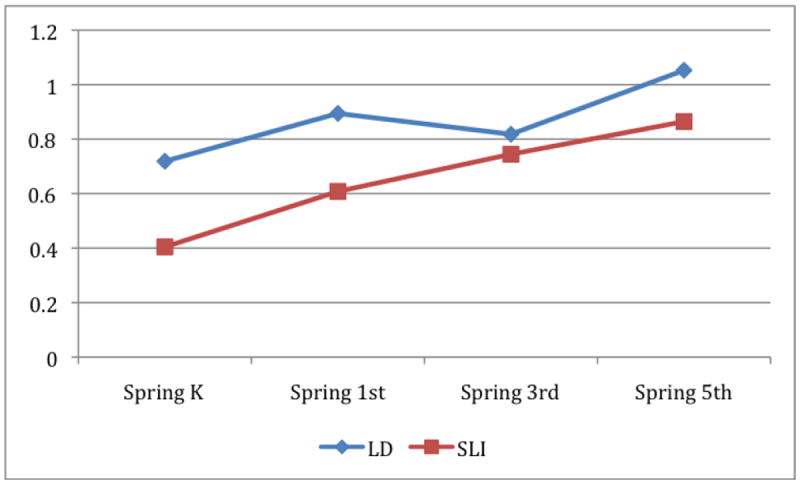
Table 3’s descriptive statistics indicate that children with LD and with SLI may experience negative (i.e., “poor-get-poorer”) Matthew effects. Figure 1 displays the children’s mean reading achievement growth trajectories. At the end of kindergarten, each group of children with disabilities initially displays lower reading achievement than their non-disabled peers. By the end of 5^th grade, these gaps have increased. For example, the average Reading Test score of children with LD at the end of 1^st and 5^th grade is 9.74 and 23.6 points below, respectively, the average Reading Test score of children without disabilities. Figure 2 plots in SD units differences in reading achievement between (a) those with LD or (b) those with SLI and (c) those without identified disabilities between the springs of kindergarten and 5^th grade. The gap in reading achievement between those without disabilities and either group of children with disabilities generally increases over time. This is especially evident for children with SLI. The gap in reading achievement between children with SLI and those without disabilities increases from .40 to .86 of a SD between the springs of kindergarten and 5^th grade. The gap between those with LD and those without disabilities increases from .72 to 1.05 of a SD.

Figure 2. Standard Deviation Unit Differences in Reading Achievement between Children with LD or SLI and Children without Identified Disabilities.

Note. LD=Learning Disability. SLI=Speech or language impairment.

Table 4 displays the same types of descriptive statistics for IRT scores on administrations of the Mathematics Test. A general data pattern is again evident. Specifically, children diagnosed with LD end their kindergarten year and then their 5^th grade year with the lowest average Mathematics Test scores, followed in sequence by children diagnosed as SLI and those without a disability diagnosis. Children with LD occasionally display higher average scores than children with SLI. However, by the end of their 5^th grade year, children identified by kindergarten as LD average Mathematics Test scores over a SD lower than those who had not been identified by kindergarten as disabled. Each of these between-group contrasts is statistically significant at p<.001.

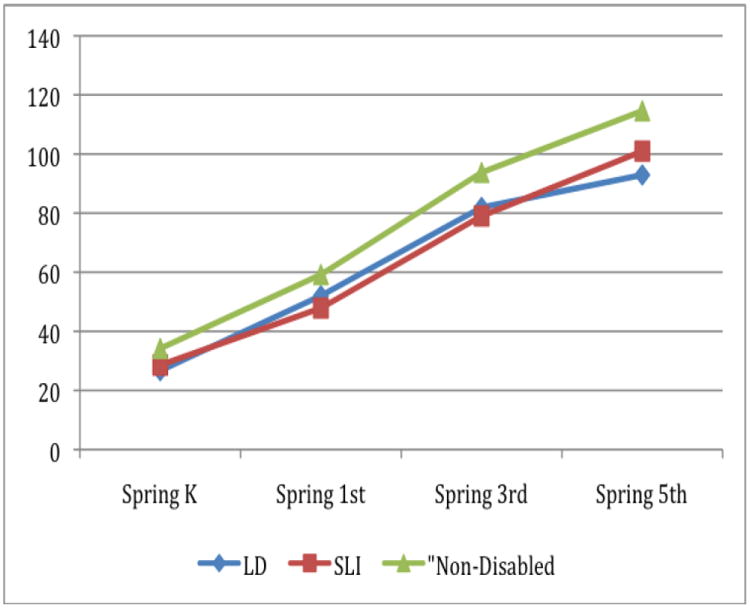
Figure 3 displays the children’s mathematics achievement growth trajectories. Figure 4 plots in SD units differences in mathematics achievement between (a) those without identified disabilities and (b) those with LD or (c) those with SLI from the spring of kindergarten to the spring of 5^th grade. Children with LD initially begin to narrow their achievement gap with children without disabilities. However, this compensatory effect does not maintain. Instead, the gap begins to increase. By the end of 5^th grade, the gap in mathematics achievement between children with LD and those without disabilities is over 1 SD. The gap in mathematics achievement between children with SLI and those without disabilities initially increases. However, it then remains fairly constant between 1^st and 5^th grade.

Figure 3. Mean Mathematics Test IRT Score for Children with LD, Children with SLI, and Children without Disabilities, K-5^th Grade.

Note. LD=Learning Disability. SLI=Speech or language impairment.

Study’s Growth Trajectories Estimates

Table 5 displays the estimated growth trajectory models for children’s reading achievement. Here the models are predicting both children’s spring of 1^st grade Reading Test scores (i.e., the intercept) and growth in their spring of 1^st grade to spring of 5^th grade scores (i.e., the slope). Model 1 uses the child’s disability status as LD or SLI as predictors. Model 2 adds the child’s socio-demographic characteristics, whether he or she was retained in kindergarten, and whether the child attended a public or private school as predictor into the equation. Model 3 adds to the equation the child’s spring of kindergarten Reading Test score (i.e., the domain-specific autoregressor) and his or her spring of kindergarten score on the Approaches to Learning subscale teacher. Model 4 then adds the child’s spring of kindergarten Mathematics Test score (i.e., the domain-general autoregressor) as a predictor. The statistical control used in these models allows for a more rigorous investigation on the extent to which the negative Matthew effects generally indicated in Table 3-4 and Figures 1-4 descriptive statistics are attributable to the children’s disability status or, instead, to other characteristics (e.g., the children’s gender, race/ethnicity, or age, their family’s SES, the type of school they attended, or the children’s relative level of academic proficiency in reading or mathematics).

We estimated the correlation between the general analytical sample’s intercepts and slopes for the unconditional model (i.e., the model using no predictors). This was -0.067 in reading. Children’s spring of 1^st grade reading achievement correlated very weakly with their spring of 1^st grade-spring of 5^th grade reading achievement growth. Thus, and for the general sample of elementary school children, our results provide little evidence for a Matthew effect in reading. We next examined whether children with LD or SLI, as particular population sub-groups of children, experience a negative Matthew effect. Model 1’s estimates indicates that children diagnosed with either LD or SLI by the end of kindergarten scored, on average and respectively, 19.33 and 14.22 points lower on the spring of 1^st grade administration of the Reading Test than those children not identified as disabled by the end of kindergarten. Children with SLI also averaged slower rates of growth in reading from the end of 1^st grade to the end of 5^th grade. Using this estimated model, students with LD had an average predicted reading score of 117.84 in the spring of 5^th grade; students with SLI had an average predicted score of 119.45; and students not identified as disabled had an average predicted score of 140.79. We then reanalyzed the data (using children with SLI as the reference group) to evaluate whether the difference in reading intercepts and slopes were statistically significant. Results indicated that neither the reading intercepts nor slopes were statistically significant between the groups of children with LD and SLI. We then estimated Models 2-4 to evaluate whether this Matthew effect was attributable to additional characteristics of the child, family, or school.

Model 2 adds the child’s (i.e., age, race/ethnicity, gender, and whether he or she was retained), family’s (i.e., SES), and school’s (i.e., public vs. private) characteristics as predictors of the intercept and slope terms. Older children initially display greater proficiency in reading by the end of 1^st grade, but then acquire reading skills at a slower rate between the end of 1^st grade and the end of 5^th grade. A family’s SES positively predicts a child’s initial skill level and over time growth in reading. In contrast, a child’s status as Black negatively predicts both initial and over time growth. A child’s female gender is a positive predictor of initial skill level but not of over time growth, as is a child’s enrollment in a private school. Statistically controlling for these socio-demographic factors does not substantially mediate the negative predictive effects of being identified as LD or SLI by the end of kindergarten.

Model 3 adds as predictors the child’s spring of kindergarten Reading Test score and Approaches to Learning teacher rating. Children displaying greater proficiency in reading at the end of kindergarten display relatively greater skill level by the end of 1^st grade, but then acquire reading skills at a slower rate between the end of 1^st grade and the end of 5^th grade. Children who are rated by their teachers as frequently engaging in learning-related behaviors average higher Reading Test scores by the end of 1^st grade, as well as higher rates of growth from 1^st to 5^th grade. Inclusion of these two factors reduces to statistical non-significance the positive effects of age and female gender on the intercept, and increases the negative effect of retention to statistical significance. Statistically controlling for these factors substantially mediates the negative predicted effects of the child’s disability status on his or her initial skill level. Specifically, the estimates for children’s disability status is reduced for those with LD and SLI from -19.33 and -14.22 (both p<.05), respectively, to 4.52 (p>.05) and -6.33 (p<.05), respectively. Children with SLI continue to display lower initial skill level and lower rates of growth in reading than children without disabilities.

Model 4 adds as a predictor the child’s spring of kindergarten Mathematics Test score. The child’s level of mathematics proficiency at school entry positively predicts his or her end of 1^st grade skill level and 1^st to 5^th grade skills growth. Inclusion of this factor does not substantially mediate the positive predicted effects of higher SES. However, it does mediate the negative predicted effect of being Black on the intercept term. Inclusion of the child’s spring of kindergarten Mathematics Test score further reduces the estimated effect of SLI on the intercept and slope terms, but does not reduce it to statistical non-significance. Thus, those kindergarten children identified as SLI but not LD display a negative Matthew effect in reading, in that they display both lower initial skill level and slower growth across time than their non-disabled peers. This cumulative effect is robust to statistical control of a wide range of potentially confounding factors, including even children’s initial skill level in reading and mathematics and the frequency of their learning-related behaviors.

Table 6 displays the estimated growth models of children’s mathematics achievement. Here the models are predicting both children’s spring of 1^st grade Mathematics Test scores and growth in their spring of 1^st grade to spring of 5^th grades scores. We first estimated the correlation between the general analytical sample’s intercepts and slopes for the unconditional model. This was .433. Thus, for the general sample of elementary school children, those who end 1^st grade as relatively more skilled in mathematics tend to display greater skills growth over the remainder of their elementary school years.

We then investigated to what extent children with LD or SLI followed a cumulative or compensatory growth trajectory. Model 1 indicates that a child’s diagnosis of LD negatively predicts his or her growth rate in mathematics, but not his or her initial level of skill. In contrast, a child’s diagnosis of SLI negatively predicts his or her initial level of skill, but not his or her growth rate. Using this estimated model, students with LD had an average predicted mathematics score of 93.81 in spring of 5^th grade; students with SLI had an average predicted score of 104.99; and students not identified as disabled had an average predicted score of 114.59. We further tested for statistically significant differences in the mathematics intercepts and slopes between those with LD and those with SLI (again using children with SLI as the reference group). Results indicated that the group of children with LD displayed statistically significantly lower slopes than the group of children with SLI. However, there were no statistically significant differences between the intercepts of the two groups. We then estimated Models 2-4 to evaluate to what extent the addition of statistical controls mediated this pattern.

Model 2 adds the aforementioned child’s, family’s and school’s characteristics. Some of the same effects seen in the Model 2 for reading are again observed in mathematics. Older children initially display greater proficiency in mathematics, but display less growth over time. A family’s SES positively predicts both the child’s initial level of skill and his or her rate of skills growth. A child’s status as Black negatively predicts both initial and over time skill level. Female gender negatively predicts both initial skill level and skills growth. Statistically controlling for a child’s socio-demographics characteristics does not substantially mediate the negative effects attributable to being diagnosed as LD or SLI.

Model 3 enters the more educational relevant factors. Being relatively more skilled in mathematics at kindergarten entry positively predicts mathematics skill level at the end of 1^st grade, but not 1^st to 5^th grade skills growth. More frequently engaging in learning-related behaviors at kindergarten entry positively predicts both end of kindergarten skill level and 1^st to 5^th grade skills growth. Adding these two factors substantially but not fully mediates the negative effect of being Black and the positive effect for SES. The negative effect of female gender is not mediated. Statistically controlling for these factors fully mediates the negative effect of LD status on these intercept but not slope terms. The coefficients are reduced from -12.14 and -5.70 (both p<.05), for the intercept and slope terms, respectively, to .83 (p>.05) and -5.05 (p<.05). The negative effect for SLI on the intercept is substantially reduced (i.e., -11.84 to -5.88, both p<.05).

Model 4 adds the child’s spring of kindergarten level of reading skill as an additional predictor. Being more skilled in reading at kindergarten entry positively (albeit weakly) predicts mathematics skills level at the spring of 1^st grade, but not spring of 1^st to spring of 5^th grade skills growth. This factor does not substantially mediate the effects of the other included factors. Thus, kindergarten children with LD display less skills growth in mathematics over time, despite these children beginning kindergarten not significantly less skilled than their non-disabled peers. (We note that the direction for the effect of LD on the mathematics intercept is negative in Model 1; the failure of this coefficient to achieve statistical significance may be due to the relatively small sample of LD children.) The negative direction of this growth rate estimate is counter to that expected for a compensatory cycle.

Kindergarten children with SLI initially display less proficiency in mathematics at the end of 1^st grade, but do not lag increasingly behind. However, neither group of children with disabilities experiences a negative Matthew effect in mathematics. Children who are low SES, black, female, or have poor learning-related behaviors in kindergarten instead experience these “poor-get-poorer” effects. The estimated effects for disability status, race, and gender are not fully mediated by the statistical control for a wide range of potentially confounding factors.

Discussion

We estimated children’s academic achievement growth trajectories in reading and mathematics. We were particularly interested in whether children with LD or SLI displayed cumulative or compensatory growth trajectories. Our investigation used internal replication and an increasingly conservative set of statistical modeling techniques. We sought to replicate our findings across two academic achievement domains (i.e., separate estimates for reading and mathematics). We also investigated these trajectories using samples of children formally identified with LD and SLI. Kindergarten children with SLI are highly at risk of later being identified as LD (e.g., Catts et al., 1999; Catts et al., 2001; Puranik, Petscher, Al Otaiba, Catts, & Lonigan, 2008).

Our analyses were increasingly conservative because we followed an initial examination of the study’s descriptive statistics with growth modeling that statically controlled for a range of factors that might be expected to be confounds. That is, the study’s growth modeling accounted for effects that might be attributable to characteristics other than whether the child was disabled, such as whether he or she was being raised in a low-income family, had been retained, was frequently inattentive or otherwise displaying learning-related behavior problem. Prior investigations of whether a Matthew effect characterizes children’s reading or mathematics achievement growth trajectories have not typically employed statistical control for socio-demographic factors. Such control provides for a more rigorous investigation of “who” experiences a Matthew effect (see Morgan et al., 2008 for an example). Additionally, the study’s models were also lagged or autoregressive. As such, they included controls for omitted variables that might be expected to have invariant effects on children’s academic achievement (Kessler & Greenburg, 1981).

Our analyses indicated that, for the sample as whole, children experienced a Matthew effect in mathematics but not in reading. This was indicated by the estimated correlations between children’s initial skill level and over time growth rates. Other investigators have also failed to find evidence for a Matthew effect in reading (e.g., Aunola, Leskinen, Onatsu-Arvilommi, & Nurmi, 2002; Shaywitz et al., 1995). Those few investigations of the Matthew effect in mathematics also have yielded null or negative findings (Jordan et al., 2002; Rescoria & Rosenthal, 2004). However, our study’s descriptive data repeatedly yielded evidence that children with LD and SLI experience “poor-get-poorer” effects. For both children with LD and those with SLI, and in both reading and mathematics, the achievement gap between their levels of academic proficiency and those of their non-disabled peers increased between the spring of kindergarten and 5^th grade. Any compensatory effects displayed by children with LD did not maintain.

Our growth modeling indicated that children with SLI continued to experience a “poor-get-poorer” effect in reading even after extensive statistical control for confounding factors, including the children’s initial level of proficiency in both reading and mathematics and their frequency of learning-related behaviors. Additionally, and although not statistically significant, the estimates for children with LD were directionally consistent with the estimates for those with SLI. Children with either type of disability were also likely to display lower levels of mathematics achievement. Those with LD displayed slower rates of skills growth than their non-disabled peers between the end of 1^st grade to the end of 5^th grade. Children with SLI averaged a lower level of mathematics achievement at the end of 1^st grade. These estimates were again robust to extensive statistical control.

Study’s Limitations

Our study has at least four limitations. First, the sub-sample of children with LD was relatively small. Analyses involving this sample were likely underpowered. This may explain the lack of statistically significant results for these children in our growth models. Second, our analyses did not include additional confounds (e.g., low birthweight, prematurity, less responsive parenting, family instability) that might further mediate the effects we report for children with LD or SLI. However, our analyses included both domain-specific and -general autogressors. Their inclusion should have accounted for the invariant effects of these omitted variables. Third, we estimated children’s elementary school growth trajectories. It is possible that the patterns we report here may not continue to be observed as children move onto the middle or high school grades. Fourth, we relied on school records and survey responses to identify groups of children with LD or SLI. Although school records are a frequently used indicator of disability status (e.g., Hollomon, Dobbins, & Scott, 1998; Hosp & Reschly, 2002), and both groups initially displayed low levels of achievement on the study’s reading and mathematics measures, we were unable to independently confirm the children’s status as disabled.

Study’s Contributions

Our study contributes to both theory and practice. Theoretically, our study indicates that the mechanics impacting children’s academic achievement may not have uniform effects in reading and mathematics, at least during children’s elementary school years. Here, the correlation between intercepts and growth rates for the sample as a whole were fairly consistent with a Matthew effect in mathematics, but not in reading. Stanovich (1986) hypothesized that children with LD should be especially likely to experience negative Matthew effects in reading. Yet our study’s results are not entirely consistent with this hypothesis. The study’s descriptive statistics yielded evidence for such an effect, yet the effect was not robust to statistically control for potential confounds. This null finding is consistent with that reported by Scarborough and Parker (2003). However, our analyses did indicate that children who, because of their SLI, might be considered as especially at risk for LD did experience “poor-get-poorer” effects in reading.

Our result that children with SLI follow a cumulative instead of a compensatory cycle in reading contrasts with that recently reported by Skibbe et al. (2008). These investigators reported that children with SLI (specifically, children identified as having language delays) displayed greater rates of growth than their typical peers, such that the reading achievement gap between these two groups of children narrowed over time. Methodological variation between the two studies may account for these contrasting findings. The Skibbe et al. study used a sample of children with criterion-identified SLI, as well as a set of measures in which only a more limited set of reading skills was measured across the study’s time points. Our study used a sample of children with school-identified SLI, as well as a measure that evaluated a wider range of reading skills at each time point. One explanation of the contrasting findings may be that the Skibbe et al. study’s estimates were more specific to growth in letter and word identification skill. It may be that the special education services provided to the children in the Skibbe et al. study specifically targeted the children’s word-level reading skills, resulting in the compensatory effect reported.

From the standpoint of practice, our study helps identify those particular groups of kindergarten children who are likely to experience “rich-get-richer” and “poor-get-poorer” effects. Some children are likely to leave kindergarten relatively more advantaged or “rich,” in that they are more likely to move through the elementary grades as increasingly higher skilled academically relative to their peers. In reading, these groups include: (a) children from high SES households; (b) children who are more proficient in mathematics by the end of kindergarten: and (c) those who more frequently engage in learning-related behaviors, such as attention, task persistence, and organization. In mathematics, these more advantaged groups include: (a) those from high-income households; (b) children who are boys; and (c) those who frequently engage in learning-related behaviors. Thus, our study suggests that kindergarten teachers who help their students become proficient in mathematics and, additionally, the behaviors necessary to meet an elementary school classroom’s learning demands, may in turn increase the likelihood that these students experience ever greater levels of academic achievement. (We caution that experimental evaluations that allow for unambiguous causal inferences are necessary to confirm this possibility). Our findings that SES, gender, early mathematics skill proficiency, and frequency of learning-related behaviors strongly relate to children’s academic skills growth is consistent with many other studies (e.g., Catts et al., 2001; Duncan et al., 2007; McCoach et al., 2006; McClelland, Morrison, & Holmes, 2000; Morgan et al., 2008).

Our study indicates that the frequency of a child’s learning-related behaviors may constitute an especially important target of intervention. The frequency of such behaviors was a consistently strong predictor of both children’s initial and over time academic skills growth. This was the case for both reading and mathematics achievement. Unlike children’s relative level of proficiency in mathematics or reading (i.e., the domain-specific and -general autogressors) at the end of kindergarten, the frequency of a child’s learning-related behaviors was a statistically significant predictor of children’s growth rates in mathematics.

Our study also identifies those who might be especially at risk of experiencing “poor-get-poorer” effects. In both reading and mathematics this group includes African-American and low SES children. In reading, this group includes children with SLI. In mathematics, this group includes children who are female. The finding that these groups are likely to experience negative Matthew effects is robust to statistical control of a range of confounds. Thus, these students may be more likely to spiral downward in a negative feedback cycle, in that they lag increasingly behind their peers academically, with the attending consequences of frustration, lowered expectation, and increasing task avoidance (Stanovich, 1983; Morgan et al., 2008). These children may therefore require additional and sustained support by their teachers if they are to become academically proficient.