On voxel-by-voxel accumulated dose for prostate radiation therapy using deformable image registration

Abstract

Since delivered dose is rarely the same with planned, we calculated the delivered total dose to ten prostate radiotherapy patients treated with rectal balloons using deformable dose accumulation (DDA) and compared it with the planned dose. The patients were treated with TomoTherapy using two rectal balloon designs: five patients had the Radiadyne balloon (balloon A), and five patients had the EZ-EM balloon (balloon B). Prostate and rectal wall contours were outlined on each pre-treatment MVCT for all patients. Delivered fractional doses were calculated using the MVCT taken immediately prior to delivery. Dose grids were accumulated to the last MVCT using DDA tools in Pinnacle^{3 ™} (v9.100, Philips Radiation Oncology Systems, Fitchburg, USA). Delivered total doses were compared with planned doses using prostate and rectal wall DVHs. The rectal NTCP was calculated based on total delivered and planned doses for all patients using the Lyman model. For 8/10 patients, the rectal wall NTCP calculated using the delivered total dose was less than planned, with seven patients showing a decrease of more than 5% in NTCP. For 2/10 patients studied, the rectal wall NTCP calculated using total delivered dose was 2% higher than planned. This study indicates that for patients receiving hypofractionated radiotherapy for prostate cancer with a rectal balloon, total delivered doses to prostate is similar with planned while delivered dose to rectal walls may be significantly different from planned doses. 8/10 patients show significant correlation between rectal balloon anterior-posterior positions and some V_D values.

Introduction

In external beam radiation therapy, the target dose is often limited by dose tolerance of the surrounding normal structures. With the increased use of image guided radiotherapy (IGRT) it is becoming evident that the delivered treatment dose is not necessarily what is planned. Thus, it is desirable to determine what dose is delivered during a treatment course (1,2). With knowledge of the delivered dose through image guidance techniques, one can monitor the achievable tumor control probability (TCP) while keeping the normal tissue complication probability (NTCP) within tolerance, a process termed ‘dose guidance’(3). Helical tomotherapy is one such image guided radiotherapy treatment system that incorporates a megavoltage fan beam CT (MVCT) scanner with fan-beam treatment delivery, allowing volumetric images of the anatomy to be obtained immediately prior to radiation delivery. As described in reference(3-5), dose guidance can only become a reality on tomotherapy when first, accurate calculation of delivered dose is achievable; secondly, one has the ability to reliably track four-dimensional target motion envelopes; and last, changes in the target can be reliably contoured and organ deformation can be quantified.

Several studies have discussed methods of calculating the delivered dose to the patient (6-12). It is necessary to have (i) repeated imaging of the patient (ii) methods to calculate the delivered dose for each fraction (iii) a tool to accumulate dose distribution to one reference image and (iv) consistent organ definition according to the patient’s planning image. The delivered dose can be calculated on multiple repeat images which are compared directly with the planned fractional dose, or can be summed using rigid and deformable methods to result in the total delivered dose to compare with the total planned dose.

In the present study, we explored the benefit of using total delivered dose calculated by deformable dose accumulation (DDA) workflow to estimate total absorbed dose by patient. We thus have calculated the delivered total dose to prostate cancer patients treated with helical tomotherapy with rectal balloons used as prostate immobilization devices. The delivered total dose was calculated using DDA of the dose calculated at multiple time points during treatment. The delivered total doses to the Planning Target Volume (PTV) and rectal wall were compared with the planned doses. In addition to dosimetric comparisons, the correlation between rectal balloon geometry and rectal dose was also investigated.

Materials and methods

Patient selection and Treatment Planning

Ten patients treated with rectal balloons were selected at random for dosimetric analysis from the database of our IRB approved prostate dose escalation study (RO-02803). Patients 1 to 5 were treated with the Radiadyne rectal balloon (Radiadyne, USA) hereafter referred to as balloon A, and Patients 6 to 10 were treated with the EZ-EM balloon (EZ-EM, USA), hereafter referred to as balloon B. Balloon B consists of a latex-free inflatable retention cuff enema tip connected to a 60 cc syringe. It was later replaced in clinical use in our department by the latex- free balloon A, which has a midline groove when inflated and is fixed over an end of a shaft. All patients had a planning kVCT taken with the rectal balloon in place for initial treatment planning purposes. The scan covered the whole abdomen and pelvic region. A 3 mm posterior margin and 5 mm margin in all other directions was applied to the prostate to obtain the PTV. Each patient received 12 fractions of 4.3 Gy to the PTV to a total dose of 51.6 Gy using the Hi-Art TomoTherapy delivery system (Accuray Inc., Sunnyvale, CA).

MVCT coverage

A MVCT was taken on Tomotherapy prior to delivery of each fraction for the purpose of daily patient setup verification. The scanned volume included several slices above and below the prostate. The MVCT image was rigidly registered to the planning kVCT using a combined soft tissue/bony anatomy algorithm employing four degrees of freedom (3 translational degrees of freedom AP, LAT, and VERT, and one rotational degree of freedom (gantry roll)) to the planning kVCT. The registration parameters were stored in the TomoTherapy database for later use.

Calculation of the delivered dose and planned dose

The Planned Adaptive TomoTherapy software (v 4.1.0.0) was used to calculate the delivered dose for each fraction. The registration shift parameters used for treatment setup were applied to the MVCT for registration with the planning kVCT such that the patient’s MVCT was representing the patient’s estimated position on the treatment couch. Once registration had been carried out, the slices in the kVCT covered by the MVCT scanning volume were replaced with the MVCT data to result in a merged image for each fraction. The dose was then calculated on the merged image using the ‘delivery’ sinogram data, which is the planned sinogram corrected for gantry roll for a given fraction. This resulted in a merged image for each fraction with that fraction’s calculated dose using the delivery sinogram.

There are two issues with dose calculation using the MVCT that need to be taken into account. The first is the possible change of image value-to-density table (IVDT) over the course of treatment (6,13). As reported by Langen et al., over a period of five months, a difference of 4.7% in the HU values was observed in high-density regions. In our study, we found that changes in the IVDT can cause up to 0.3 Gy difference in dose calculation between two consecutive fractions. Ideally, an IVDT should be measured for every fraction delivered for a given patient. As this is a retrospective study, IVDT data corresponding to each fraction was not available. Instead of using the daily measured IVDT, a bulk density override was performed using a step-IVDT applied to each MVCT and kVCT so that the patient body physical density was 1 g/cm³ and the rectal balloon contents (air) was 0 g/cm³. The second issue is that the field of view of the MVCT is 40cm, which is sometimes not large enough to cover the lateral and anterior abdomen surface of patients. The merged MVCT in the adaptive planning station thus uses the kVCT to fill in missing tissue around the patient’s external contour in the MVCT. The above two corrections were applied to allow consistent dose accumulation that is independent of the IVDT and the amount of replaced tissue.

Target and normal tissues contouring

In order to study inter-fraction motion, the prostate and rectal wall were contoured on the merged image by the same investigator. The contours were drawn only on slices common to all MVCT studies taken for a given patient. The prostate was outlined following a definition consistent with the planning prostate contours on the kVCT. The rectal wall Dose Volume Histogram (DVH) is regarded as a useful metric for prediction of rectal bleeding (14). The definition of rectal wall was a simple ring expansion of the inner rectal wall of 3 mm at the level of the balloon, and as a solid structure below the level of the balloon. Inter-observer contouring error was minimized for rectal wall, since we follow a three-step workflow: (a) using autocontour tool to delineate the inner rectal wall, which is identical with the rectal balloon; (b) generating a 3mm ring expansion of the inner rectal wall; (c) only keep the ring expansion contours on the image slices common to all MVCT studies taken for a given patient. This resulted in a set of prostate and rectal wall contours on each merged image with consistent superior-inferior spans. To facilitate comparison with the planned dose, the prostate and rectal wall were contoured on the planning kVCT only on the slices common with all MVCT data sets.

Deformable image registration (DIR) and Deformable Dose accumulation (DDA)

Whether DDA based on DIR benefits a patient group or not should be carefully explored in prospective clinical trials (4,15). Increasing and testing the voxel-by-voxel accuracy of DIR algorithm itself has been a field of active investigation (16-19). The methodology for DIR employed in this study and its clinical utility has been assessed and validated for the case of head and neck by expert physicians, who have rated the majority of the DIR-propagated organs at risk contours as requiring no or only minor modifications for clinical use (20). The interested reader is referred to Ref. [20] for a detailed description of the validation DIR workflow employed in this study. DIR and DDA hold great promise for improved prediction of normal tissue toxicity (4). Prostate cancer patients included in this study had rectal balloons placed yielding relatively consistent rectal wall volumes. For this reason we have decided to study only the dose to the rectal wall since the volumes of other normal tissues varied over the course of therapy calling into question the applicability of DIR and DDA. As a hollow organ, the surface is a reasonable approximation of the rectal shape; DIR-based propagation of the delineated rectal wall contours between the source and target MVCTs therefore provides a method to assess the accuracy of the DIR (21).

The DIR algorithms and contour propagation workflow used in this study have been implemented in a research version of the Pinnacle^{3 ™} treatment planning system (v9.100, Philips Radiation Oncology Systems, Fitchburg, WI, USA). The voxel-by-voxel DIR algorithm used was Fast Symmetric Demons DIR algorithm as implemented in the Insight Toolkit (22). The deformation vector field (DVF) from each merged MVCT to the 12^th fraction merged MVCT was qualitatively investigated by applying the DVF to the source image to result in a DIR-approximation of the 12^th faction merged image. The deformed image showed little difference when compared to the 12^th fraction merged MVCT (Figure 1(B)). We also used the DVF to non-rigidly propagate contours to check if propagated contours accurately outlined the anatomy of the target image (Figure 1(D)). Results show that for all of the ten patients, treated with either one of the balloons, DIR improved the registration accuracy over what could be achieved using rigid registration alone.

Figure 1.

(A): Fusion of source image (in inverse-grayscale) and target image (in grayscale) show differences between the two; (B): fusion of the deformed image (in inverse-grayscale) and target image (in grayscale) show reduced differences between the two; (C): Original contours for prostate and rectal wall (Red and Purple); (D): After propagation, the new contours (Blue and Green) delineate prostate and rectal wall on the right image with good agreement.

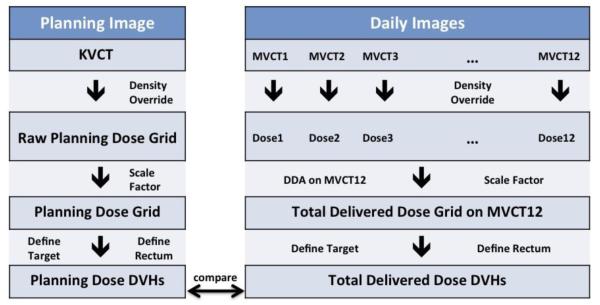
DDA was performed using adaptive tools in the planning system described above. The process used for DDA is described in Figure 2. In particular DDA was achieved by warping each merged image and its dose grid to the 12^th fraction’s merged MVCT image and summing the warped dose from each fraction to the dose of the 12^th fraction resulting in the total delivered dose from all 12 fractions on the 12^th merged MVCT image.

Figure 2.

Workflow of planning dose DVH calculation and total delivered dose DVH calculation.

The prostate and rectal wall DVHs were calculated for the planned dose on the planning kVCT, for each fraction’s dose on the corresponding merged MVCT and for the total delivered dose on the 12^th fraction merged MVCT. Since a step-IVDT was used to recalculate the planned doses, a scaling factor was applied to the recalculated planned dose prostate DVH and each fraction’s delivered DVH so that 50% of the prostate volume received a planned dose of 51.6 Gy or 4.3 Gy per fraction. Scaling was not applied to the total delivered doses on the 12^th fraction since this consists of the already scaled fractional doses (Figure 2). Scaling factors were typically 0.9 - 0.94. For each rectal wall DVH, the corresponding generalized equivalent uniform dose (gEUD) was calculated and used to determine the rectal wall NTCP for each patient. The Lyman Kutcher Burman (LKB) NTCP model (23,24) was used with the following parameters m=0.13, n=0.09 and TD₅₀=76.9 Gy that have been determined for the endpoint > Grade 2 late rectal bleeding as described in the QUANTEC Study (25). Since our ten patients received hypofractionated radiotherapy with a dose per fraction of 4.3 Gy, the prescription dose and DVHs were converted to equivalent dose in 2 Gy fractions (EQD₂) DVHs using an α/β-ratio of 3 Gy, that is, normalized to a prescription dose of 75.4 Gy (EQD₂=75.4Gy). Using these parameters our NTCP model takes the following form

$$\mathit{NTCP}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^t\exp \left(-u^2/2\right)\mathit{du}$$

where $t=\frac{g\mathrm{EUD}-{\mathit{TD}}_{50}}{m\cdot {\mathit{TD}}_{50}}$ and $\mathit{gEUD}={\left[{\sum }_{i=1}^M{v}_i{\left(D_i\right)}^{\frac{1}{n}}\right]}^n$.

D_i is the dose to relative volume ν_i in 2Gy per fraction equivalents, and the sum extends over all dose bins in the DVH.

Dosimetric effect of DDA error

The effect of errors in deformable dose accumulation and methods of how to mitigate them when employing the symmetric demon algorithm on the resulting dose volume histograms for target volumes and organs at risk have been described in Ref. (18,26-28). As pointed out in reference 18 even though DIR and DDA are not perfect and suffer from residual errors, estimates of toxicity or tumor control based on these methods are likely to be more representative of clinical reality, than estimates based on methods that ignore anatomical change and structure distortion through out treatment, and simply use the total planned dose to estimate expected normal tissue complications and local tumor control. The current study focuses on exploring the benefit of using the total delivered dose calculated employing the DDA workflow shown in Figure 2 to arrive at an estimate of total delivered dose to the patient. To this end we compare the total planned dose for prostate and rectal wall with the total delivered doses to these structures in terms of dose volume histograms, V_D and NTCP.

Errors that can impact the DDA workflow include inverse consistency and transitivity errors. When using DVFs that exhibit these types of errors, the total delivered dose to structures does depend on the image pathway taken during dose accumulation(18). In order to study how much the total delivered dose was affected by the DDA workflow, for each patient, we accumulated all of the 12 delivered fractional doses on each of the 12 daily images, and then calculated the NTCP for each of the total delivered doses resulting from each of the accumulation pathways taken to study the variation in NTCP.

Correlation study between balloon volume and delivered dose

The relationship between the updated delivered dose and the variation in the rectal balloon volume was investigated. The updated delivered dose was done by accumulating the delivered fractional doses to each MVCT, e.g. the first and second delivered fractional doses were accumulated to the second MVCT yielding a second updated delivered dose. The fractional volumes receiving high, intermediate and low doses - V₇₅, V₇₀, V₅₀, and V₃₀ - were studied. These were firstly converted from 2 Gy/fraction doses to our fractionation scheme using α/β = 3 Gy (V_51.37, V_47.95, V_34.25 and V_20.55) and then converted to updated delivered doses (e.g. for the second updated delivered dose, V_8.56, V_8.00, V_5.7 and V_3.42). The difference between the planned and updated delivered fractional volumes receiving these doses was then calculated using the planned and updated delivered rectal wall DVHs. The possible correlation between balloon volume and dose volumes was investigated using the Spearman’s rank correlation test. The Spearman’s rank correlation test is a non-parametric test that measures how well the relationship between two variables is described by a monotonic relationship.

Correlation of balloon position with delivered dose

It is also natural to ask if the positioning of the balloon affects the delivery of the planned dose. We delineated balloons on the same slices of MVCTs as we contoured prostates and rectal walls, and calculated the center of balloon for these balloon contours. The delivered dose used here were actually the updated delivered dose as mentioned in previous session. A correlation study between the changes of the 3D coordinates of the center of the balloon contours and the changes of V_D was performed.

Results

Inter-fractional dose variation

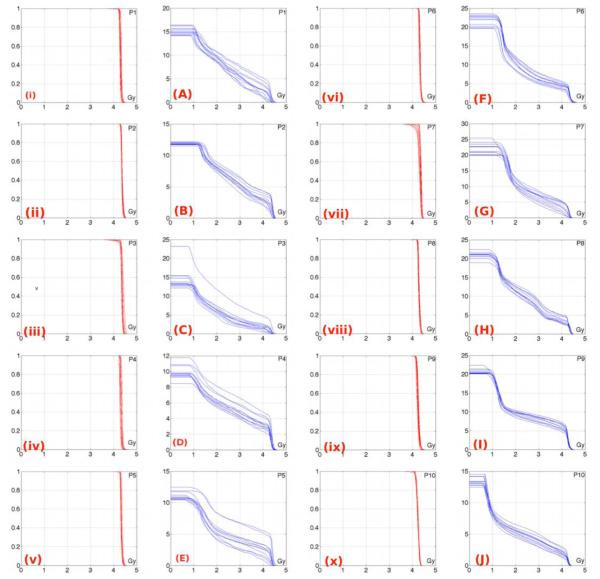
The delivered fractional dose prostate DVHs show consistency with the planned prostate DVH shape (Figure 3). With the exception of Patients 3 and 7, there is minimal inter-fraction variation of the delivered dose to prostate for each fraction, as expected since daily IGRT with target realignment to compensate for internal target motion was employed. Patient 3 and Patient 7 exhibit a loss of coverage of the prostate, seen by the more rounded shoulders of the prostate DVH curves. To facilitate comparison to other studies we have collected In Table I the minimum dose covering the prostate (D_min) and the dose covering 95% of prostate volume (D₉₅). There exists some inter-fraction variation in the delivered fractional dose rectal wall DVHs, however the overall shape is generally maintained (Figure 3(A, E) for patients treated with balloon A and Figure 3(F, J) for patients treated with balloon B). The volume of rectal wall (also, the volume of the rectal balloon) for each fraction has large effect on the volume receiving a given dose level over the course of therapy.

Figure 3.

The first column shows the normalized volume delivered fractional dose prostate DVH (red line) for patients treated with balloon A (P1 stands for patient 1). The second column shows the absolute volume delivered fractional dose rectum DVH (blue line) for patients treated with balloon A. The third column shows the normalized volume delivered fractional dose prostate DVH (red line) for patients treated with balloon B. The fourth column shows the absolute volume delivered fractional dose DVH (blue line) for patients treated with balloon B.

Table I.

Top: Balloon volume of the 10 patients as measured on the KVCT and MVCTs on the chosen slices. BL₁₂ is the balloon volume of the 12th fraction MVCT. BL_max, BL_min and BL_avg are the maximum, minimum and average balloon volume of all the 12 MVCT’s, respectively. Middle: Dose covering 95% of prostate (D₉₅) of the 10 patients as assessed from the 12 delivered fractional dose prostate DVHs. Bottom: Minimum dose to prostate (D_min) of the 10 patients as assessed from the 12 delivered fractional dose prostate DVHs. Mean, SD and 95% CI are the mean, standard deviation and 95% confidence interval width of D₉₅ and D_min.

Patient		1	2	3	4	5	6	7	8	9	10
kVCT (mL)		53.8	36.1	41.2	15.3	35.8	80.3	101.6	82.1	85.1	63.1
MV CT (mL)	BL12	50.0	51.6	45.6	26.3	30.0	85.1	107.4	84.5	78.6	74.8
	BLmin	42.5	43.5	37.9	18.8	30.0	80.4	106.2	80.3	77.0	54.4
	BLmax	59.6	55.8	95.6	36.6	51.5	99.8	139.5	102.8	110.2	77.1
	BLavg	51.6	49.8	51.9	28.3	34.9	89.5	119.0	93.5	88.0	66.5
	SD	5.3	3.3	15.7	5.0	6.3	6.2	12.7	7.2	8.6	8.2
D95 (Gy)	mean	4.25	4.31	4.30	4.28	4.29	4.28	4.24	4.22	4.16	4.13
	SD	0.02	0.01	0.02	0.03	0.02	0.02	0.08	0.01	0.02	0.01
	95% CI	0.01	0.01	0.01	0.02	0.01	0.01	0.05	0.01	0.01	0.01
Dmin (Gy)	mean	3.96	4.12	3.73	4.21	4.19	4.19	3.69	4.08	4.00	3.97
	SD	0.30	0.18	0.46	0.03	0.13	0.05	0.35	0.16	0.21	0.17
	95% CI	0.17	0.10	0.26	0.02	0.07	0.03	0.20	0.09	0.12	0.10

Total treatment dose variation

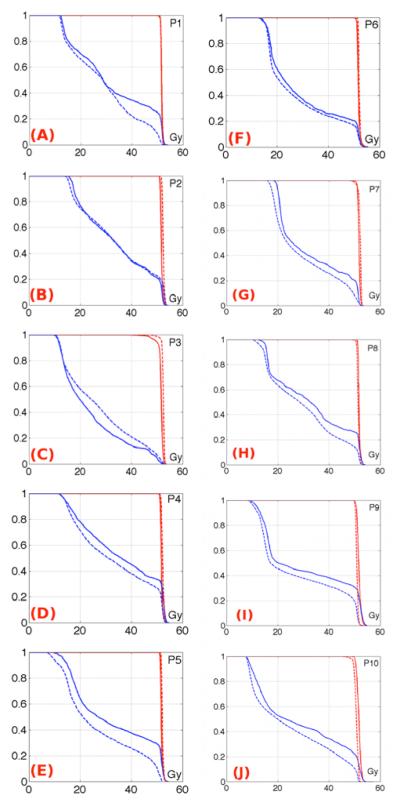
The normalized DVH curves show very little difference between the planned and total delivered prostate dose (Figure 4(A-E) for patients treated with balloon A, (F-J) for patients treated with balloon B). The total delivered dose D₅₀ was within ± 2% of the planned dose prostate D₅₀.

Figure 4.

The first column shows the normalized total delivered dose DVH (dashed line) compared to the planned dose DVH (solid line) for patients treated with balloon A (P1 stands for patient 1). The second column shows the normalized total delivered dose DVH (dashed line) compared to the planned dose DVH (solid line) for patients treated with balloon B. The prostate DVHs are in red and the rectal wall DVHs are in blue.

Figure 4 shows that the volumes receiving higher doses in the total delivered rectal wall DVHs were much lower than planned for 7/10 patients. The only two patients showing slightly more volume receiving high dose were treated with balloon A.

In order to quantify the setup consistency through out the treatment process, the balloon volumes for all fractions were measured on the slices that were in common for all image sets (Table I). Nine out of ten patients show minimal changes in volume over the course of the treatment, showing that consistent filling of the balloon was achieved in most cases. For one patient treated with balloon A (patient 3), the standard deviation (SD) of the balloon volume was above 15mL, and the maximum volume (V_max) is almost double of the average volume (V_avg).

The calculated rectal wall NTCPs for the planned and delivered doses are shown in Table II. For three out of ten patients (patient 2, 3 and 6), there were minimal differences in the rectal NTCP between the total delivered and planned dose. For the seven that had significant DVH differences, the NTCP calculated from the total delivered dose is less than that from the planned dose by 5 – 10%. Two patients show slightly increased delivered dose NTCP (patients 2 and 3) compared to their planned dose NTCP, which were also the only two patients not to exhibit a decrease in V₇₅ (Table II).

Table II.

Calculated rectal wall NTCPs for the planned and total delivered doses. A negative NTCP change means the NTCP calculated from the total delivered dose is less than that for the planned dose. NTCP Changes larger than +/−5% are shown in Bold. Changes of V₃₀, V₅₀, V₇₀ and V₇₅ between planned DVH and total delivered DVH are also shown. V_D changes larger than +/− 10% are shown in Bold.

Balloon	Patient	Planned NTCP	Delivered NTCP	NTCP change	Change of VD
					V30	V50	V70	V75
A	1	16.6%	7.3%	−9.4%	−5%	−4%	−14%	−16%
	2	15.5%	17.9%	2.4%	−2%	0	2%	3%
	3	4.4%	6.5%	2.1%	9%	8%	3%	2%
	4	24.0%	18.5%	−5.5%	−7%	−6%	−6%	−9%
	5	19.3%	8.8%	−10.6%	−11%	−11%	−15%	−20%
B	6	14.0%	11.8%	−2.3%	−6%	−2%	−4%	−5%
	7	13.4%	8.0%	−5.4%	−20%	−5%	−10%	−5%
	8	17.8%	10.6%	−7.2%	−4%	−8%	−11%	−12%
	9	21.7%	12.9%	−8.8%	−5%	−6%	−9%	−22%
	10	16.5%	8.4%	−8.1%	−3%	−9%	−11%	−13%

The difference in V₇₅, V₇₀, V₅₀ and V₃₀ between planned dose DVH and total delivered dose DVH were measured for each patient (Table II). Differences larger than 10% were found for Patient 1 for V₇₀ and V₇₅, Patient 5 for V₃₀, V₅₀, V₇₀ and V₇₅, Patient 7 for V₃₀ and V₇₀, Patient 8 for V₇₀ and V₇₅, Patient 9 for V₇₅ and Patient 10 for V₇₀ and V₇₅.

Error study for DDA

Results show the NTCP change caused by inverse consistency and transitivity uncertainties in the DDA process is 3.1- 6.1 % having 95% confidence interval widths from ±0.6-±1.1 % (Table III).

Table III.

Planned dose NTCP as calculated on the planning KVCT, average NTCP for total delivered doses on different daily MVCT’s, and the difference between maximum and minimum NTCP for total delivered doses on different daily MVCT’s. Standard deviations of NTCPs for total delivered doses on different daily MVCT’s and 95% confidence intervals of NTCPs for total delivered doses on different daily MVCT’s are also shown.

Patient	1	2	3	4	5	6	7	8	9	10
Planned NTCP	16.6%	15.5%	4.4%	24.0%	19.3%	14.0%	13.4%	17.8%	21.7%	16.5%
Average NTCP	7.1%	18.1%	7.5%	20.6%	9.5%	13.3%	8.3%	11.5%	15.2%	7.9%
MAX- MIN	6.1%	3.4%	5.9%	3.7%	4.1%	3.8%	3.1%	5.7%	5.0%	4.8%
SD	1.7%	1.1%	1.7%	1.2%	1.2%	1.2%	1.0%	1.9%	1.7%	1.4%
95% Confidence Interval width	±1.0%	±0.6%	±1.0%	±0.7%	±0.7%	±0.7%	±0.6%	±1.1%	±1.0%	±0.8%

Correlation study between rectal balloon volume and V_D

Table IV shows the correlation coefficients between each dose volume parameter and each balloon volume for all patients. For patients treated with balloon A, only for patient 5 did all four V_D values strongly correlate with balloon volumes. For 3 of the 5 patients treated with balloon B, some of the V_D values show strong correlation with balloon volume. For 3 out of 10 patients, statistically significant positive strong correlation between V₇₅ and balloon volume was found, meaning for these 3 patients as the volume of the balloon increased, so did the V₇₅. Although most correlations between balloon volume and dose were positive, meaning volumes receiving given doses increased with increasing balloon volume, there were some patients for whom a negative correlation between balloon volume and dose volume parameters was observed. These correlations however, were not statistically significant.

Table IV.

Spearman’s rank correlation test ρ value for each patient performed between balloon volume change and change of V₃₀, V₅₀, V₇₀ and V₇₅ (top). The Spearman rank correlation coefficients shown in Bold indicate a statistically significant correlation between balloon volume and the indicated dosimetric volume parameter at the p = 0.05 level.

	Correlation test between Balloon Volume change and VD
Patient	1	2	3	4	5	6	7	8	9	10
V30	0.54	0.1	0.5	0.17	0.90	0.34	0.2	0.5	0.52	0.85
V50	0.22	0.22	0.57	0.2	0.78	0.66	−0.12	0.38	0.73	0.85
V70	−0.06	0.38	0.33	0.15	0.75	0.8	0.39	0.45	0.85	0.8
V75	−0.42	0.29	0.4	0.05	0.68	0.83	0.36	0.38	0.66	0.38

Correlation study between center of balloon and V_D

Results show that for 8 of the 10 patients, the changes of the anterior-posterior direction coordinates of the center of rectal balloon are strongly correlation with some V_D values (Table V). For 4 of the 10 patients, the changes of the superior-inferior direction coordinates of the center of rectal balloon are strongly correlation with some V_D values. No strong correlation was found between the changes of the left-right direction coordinates of the center of rectal balloon and V_D values.

Table V.

Spearman’s rank correlation test results for each patient performed between balloon central position change and change of V₃₀, V₅₀, V₇₀ and V₇₅. The Spearman rank correlation coefficients shown in Bold indicate a statistically significant correlation between balloon volume and the indicated dosimetric volume parameter at the p = 0.05 level.

Patient		1	2	3	4	5	6	7	8	9	10
Left - Right	V30	−0.25	0.46	−0.55	0.56	−0.11	−0.29	−0.09	0.38	−0.14	−0.48
	V50	−0.08	0.43	−0.56	0.45	−0.2	−0.27	0.1	0.31	−0.26	−0.38
	V70	0.13	−0.07	−0.1	0.5	−0.13	0.00	0.09	0.12	−0.47	−0.49
	V75	0.44	−0.3	−0.18	0.49	−0.09	0.09	0.03	0.32	−0.53	−0.44
Ant - Post	V30	0.13	0.64	0.48	0.13	0.87	0.74	0.77	0.8	0.57	0.63
	V50	0.22	0.65	0.4	0.13	0.89	0.52	0.93	0.93	0.61	0.75
	V70	0.26	0.35	0.67	0.18	0.85	0.63	0.86	0.87	0.71	0.84
	V75	0.09	0.16	0.59	0.3	0.85	0.59	0.74	0.82	0.54	0.67
Superior - Inferior	V30	0.52	−0.01	0.52	0.44	0.91	0.10	−0.63	−0.25	0.8	−0.8
	V50	0.05	0.11	0.4	0.42	0.68	0.51	−0.6	0.05	0.68	−0.79
	V70	−0.25	0.38	−0.08	0.3	0.65	0.37	−0.81	0.17	0.43	−0.78
	V75	−0.57	0.39	−0.07	0.17	0.58	0.20	−0.8	−0.02	−0.04	−0.35

For patients 5 and 7, the changes of the anterior-posterior and superior-inferior direction coordinates of the center of rectal balloon are strongly correlated with all of the V_D values. The correlation coefficients in anterior-posterior part of Table V are all positive, which means as the balloon position shifts posteriorly, the V_D decreases. For patient 5, the correlation coefficients in superior-inferior part of Table V are all positive, which means as balloon position shifts superiorly, the V_D decreases. However, for patient 7, the correlation coefficients in superior-inferior part of Table V are all negatives, which means as balloon position shifts superiorly, the V_D increases.

Discussion

Comparison with published studies

The validity of using MVCT to calculate dose has been discussed by Langen et al. (6) in 2005. Kupelian et al. (11) studied the delivered dose from full courses of external beam radiotherapy for prostate patients using daily MVCT imaging. It was found that the prostate did receive the planned radiation dose, however, they also found significant daily variation in rectal and bladder doses without apparent pattern from patient to patient, or within individual patients. In 2010, Hatton et al. (8) assessed the 5-field conformal plan dose delivery using cone-beam CT (CBCT) taken twice a week. The initial plan was calculated on all CBCT scans to compare a group of delivered doses to the planned dose. It was found that planned doses to the prostate were not achieved for all patients, and that the rectal and bladder doses were higher than planned. In contrast to these studies, in the current retrospective study, we have investigated patients treated with rectal balloons. DIR was used to accumulate doses to a single image to compare the delivered dose to the planned dose. We found planned target doses were achieved for all of the patients studied, while total delivered dose to rectal wall were mostly lower than planned. Despite sophisticated image guidance and the use of rectal balloons, some variation in the delivered rectal wall dose was observed. The difference between delivered dose and planned dose for target and normal tissue depends on the institution’s setup and image guidance techniques as well as patient specific factors. In clinical scenario, it could be advantageous apply an adaptive protocol whereby the delivered dose (and calculated tumor control and normal tissue toxicity probability) is monitored during the treatment process, so that deviations from the plan can be corrected, or dose can be escalated safely.

The usage of rectal balloon during radiotherapy was to consistently localize the prostate and the rectal wall through the treatment delivery. For half of the patients, the V₇₅ and V₇₀ on total delivered dose DVHs were more than 10% lower than planned dose DVHs. In addition, for most of the patients studied, the total delivered dose NTCP was lower than planned dose NTCP by more than 5%, which meant that planned dose NTCP did not represent the total delivered NTCP. The planned dose rectal wall DVH does not represent the total delivered dose rectal wall DVH well. One possible reason could be that the rectal wall voxels in high dose regions were not always the same ones from fraction to fraction. This supports the findings of several published studies that have pointed out that normal tissues exhibit significant variation in position, shape, and volume during radiotherapy were prone to dose uncertainties(12,29-31).

Does DDA help to estimate delivered dose?

Numerical methods have been developed to quantitatively evaluate DIR algorithm, including use of contours and landmarks identified on both target and source images(16), use of phantoms with known physical deformation or phantoms with easily identifiable markers where motion can be accurately measured(32). There also exists method to analyze patterns of uncertainty in DVF measurements and their effect on dose mapping in image guided adaptive radiotherapy(19). In this study, the DIR algorithm worked well for prostate cancer patients treated with balloons in the aspects of prostate and rectal wall contour propagations, and the agreement of deformed images with target images. The 95% confidence interval of the total delivered dose NTCP is relatively small compared with the difference between total delivered dose and planned dose NTCPs. When DIR algorithms with small inverse consistency and transitivity errors are implemented in dose accumulation, the total delivered dose should vary little by the image pathway taken(18).

The implementation of DDA used in this study utilized trilinear interpolation to deform dose from one image to another. That is, the vector pointing from the target image voxel was used to determine the dose at the corresponding anatomical location in the source image, using trilinear interpolation to reduce the effects of the voxel correlation not being a true one-to-one correspondence. This method has been shown to introduce errors in DDA due to the possible rearrangement of the energy deposition per unit mass, which increases with dose and density gradients and voxel size(26,28). Proposed solutions require the use of monte carlo algorithms for dose calculation, so as to warp the energy deposition accordingly, which was not available in the current study. Thus, there will be some inherent uncertainty in the presented results due to this effect. This uncertainty however also reduces with voxel size(26,27); the voxel size used in this study (0.195 × 0.195 × 0.25 cm³), so we expect the errors in this study to be sufficiently lower than the errors one would observe without doing DDA.

Although it is shown in Figure 3 that one can observe deviations of the delivered dose from the planned dose on a fraction by fraction basis, DDA provides a single delivered dose distribution which has combined all delivered fractional doses up to that point. This is useful and arguably required when looking at an adaptive radiotherapy paradigm, where decisions on modification of the treatment plan based on the delivered dose need to be made using the most accurate information. This is of particular importance in heterogeneous dose distributions such as that seen by the rectum, so that any hot or cold spots seen by the organ in each fraction are summed appropriately in the context of hot and cold spots from other fractions. It is of lesser importance when highly homogenous dose distributions are seen by the organ, such as the prostate in the current study.

Conclusions

This retrospective study investigated the delivered doses to prostate cancer patients receiving hypofractionated radiotherapy with rectal balloons using dose calculated on daily MVCTs and accumulated on the final treatment fraction image. Delivered prostate doses were found to be close to planned doses for all patients and delivered rectal doses were lower than the planned rectal dose for eight out of ten patients. Additionally, seven patients showed significantly decreased delivered NTCP as compared to planned NTCP. Eight patients showed significant a correlation between the rectal balloon anterior-posterior position and some V_D values, i.e. as the balloon position moved posteriorly, the V_D decreased. DDA is not necessarily required for estimation of the delivered dose to the prostate, due to the highly homogenous dose distribution seen by the prostate. However, DDA is highly useful in comparing the total delivered dose with the planned dose in heterogeneous dose distributions such as that seen by the rectal wall, particularly in the context of plan adaptation during the course of radiotherapy.

Abbreviation

DIR

deformable image registration

DDA

deformable dose accumulation

gEUD

generalized equivalent uniform dose

NTCP

normal tissue complication probability

TCP

tumor control probability

IGRT

image guided radiotherapy

MVCT

megavoltage fan beam computerized tomography

DVH

dose volume histogram

PTV

planning target volume

IVDT

image value-to-density table

DVF

deformation vector field

EQD2

equivalent dose in 2 Gy fractions