Comparison of PCA approaches for very large group ICA

Abstract

Large data sets are becoming more common in fMRI and, with the advent of faster pulse sequences, memory efficient strategies for data reduction via principal component analysis (PCA) turn out to be extremely useful, especially for widely used approaches like group independent component analysis (ICA). In this commentary, we discuss results and limitations from a recent paper on the topic and attempt to provide a more complete perspective on available approaches as well as discussing various issues to consider related to large group PCA for group ICA. We also provide an analysis of computation time, memory use, and number of dataloads for a variety of approaches under multiple scenarios of small and extremely large data sets.

Introduction

A recent paper¹, presented some solutions for dealing with large group functional brain imaging studies that require data reduction with principal component analysis (PCA), most notably, as in group independent component analysis (GICA), which has become widely used in the analysis of functional magnetic resonance imaging (fMRI) data². This is an important topic, especially given the rapid increase in data sharing^3,4 as well as in the size of data sets being collected⁵. Current emphasis on projects such as the human connectome project (plus ongoing and future disease-related extensions) as well as the NIH focus on “big data” further motivate the need for approaches that can easily scale to extremely large numbers of subjects.

In the following sections, we found that there are a few points in the paper¹ that need clarification, ranging from subtle (perhaps unintentional) mischaracterization of standard approaches to shallow representation of the functionality of existing tools, notably the group ICA of fMRI toolbox (GIFT; http://mialab.mrn.org/software/gift). For example, the paper¹ claims improved accuracy over existing approaches and also claims that available PCA implementations are not scalable in memory (RAM) to large numbers of subject. However both of these points are slightly misleading. We present these points and others in four sections starting first with a discussion of a comparison of accuracy, then memory (RAM) use, followed by a Pareto front optimality analysis comparing ten different PCA strategies, and finally attempt to present the available methods in the context of their initial introduction to fMRI data. Finally, we present our conclusions and summarize the results.

Accuracy of Results

We start with the issue of accuracy. In the paper¹ there is an extensive amount of text and multiple figures devoted to comparing the accuracy of some existing and proposed PCA solutions. However, as we discuss, the performance comparisons and most figures in the paper are fairly unnecessary, and the highlighted differences with respect to GIFT due to the PCA decomposition are not accurate. The key issue is that the comparison is between subject-level whitening + PCA versus PCA directly on preprocessed data, although the pretext in the paper¹ is a comparison of different PCA approaches only. As it turns out, the ‘errors’ discussed therein are merely related to the degree to which the variance associated with the scaling of subject-level data is preserved during the whitening step. If one instead compares PCA approaches without subject-level whitening (easily done in GIFT), then one finds that all of the PCA approaches discussed are comparable in accuracy (see Table 1). This issue appears to stem from an implicit assumption that the optimal/ideal approach to group PCA revolves around evaluating it directly from raw (preprocessed) data, instead of initially whitening the subject-level data (i.e., not incorporating the eigenvalues in the matrix of subject-specific spatial eigenmaps).

Table 1.

Summary of various group ICA approaches (in chronological order): The computation times were obtained from resting state fMRI data⁹ containing s = 1600 subjects, v = 66745 in-brain voxels, t = 100 time points and extracting n = 75 group principal components. Here we opted not to whiten the subject-level data prior to group PCA in order to match the assumption in the original paper¹. Analyses were run on an 80-core Linux Centos OS release 6.4 with 512 GB and on an 8-core Windows Desktop with 4GB RAM. For Windows desktop, we report the computational times of only the PCA analyses that could be fit on 4GB RAM. For EM PCA2, MPOWIT and SMIG, the maximum number of iterations was set to 100 (on Linux server) and 40 (on Windows desktop) to limit the maximum number of dataloads per subject in each iteration. To compute the estimation error, we use L2-norm of the difference between the eigenvalues obtained from PCA methods and those from the temporal concatenation approach. Only errors greater than 1×10⁻⁶ are reported, and for iterative PCA methods like MPOWIT, EM PCA2, and SMIG we also report the number of iterations required to converge. Here the ranking is based on RAM use only. We also report the explained variance (EV) for each method using temporal concatenation as the reference.

Software (Name)	Date introduced	Average rank (based on least memory use only)	Compute time (min) (80-core Linux, 512 GB RAM; loading time irrelevant)	Compute time (min) (8-core Windows Desktop 4GB RAM; loading time dominates)
A. GIFT (EVD)	200118	9	60.15, EV = 100%	*
Original GIFT group ICA approach.
B. GIFT (3-step PCA, STP)	200412,23	3-5 (depending on blocksize)	27.96, error=0.05 EV – 99.9% ~2min loading data	67.97, error=0.05 EV = 99.9% ~39min loading data
A 3-step PCA method implemented early in the GIFT toolbox and similar to the MIGP approach. Subsampled Time PCA (STP)14 is a  more recent generalization which avoids whitening in the intermediate group PCA step during the group PCA space update. To  compute the memory required, we selected a value of 10 for the number of subjects in each group. The top 500 components were  retained in each intermediate group PCA.
C. MELODIC (Temporal Concat.)	200924	9	60.15	*
Original MELODIC group ICA approach after adoption of temporal concatenation as the default.
D. GIFT (EVD Full Storage)	2009 (GroupICAT v2.0c)	7	87.78, EV = 100%	*
Covariance is computed using two data-sets at a time (Time × Time) or one data-set at a time (voxels × voxels).
E. GIFT (EVD Packed Storage)	2009 (GroupICAT v2.0c)	6	915.32, EV = 100%	*
Only lower triangular portion of covariance matrix is stored. Covariance is computed in the same way as GIFT (Full Storage).
F. GIFT (EM PCA1)	2010 (GroupICAT v2.0d)8,9	8	152, iter=496 EV = 100%	*
Expectation maximization assuming all data is in memory.
G. GIFT (EM PCA2)	2010 (GroupICAT v2.0d)8,9	1	312.18, error=0.09 EV = 100%	2305, error=6.58 EV = 100%
Expectation maximization by loading one data-set at a time.
H. GIFT (MPOWIT)	201314,15	3	33.19, iter=7 EV = 100%	278.89, iter=7 EV = 100%
Multi power iteration method (MPOWIT) is an extension of subspace iteration. Typically we select a block multiplier which is 5 times  the number of components to be extracted from the data to speed up the convergence of desired eigenvectors. In Figure 1, we show the  memory required by MPOWIT when one dataset is loaded at a time.
I. MELODIC (SMIG)	20141	1	106.9, iter=32 EV = 100%	2310, iter=32 EV = 100%
MELODIC subspace iteration. Memory required will be the same as EM PCA2.
J. MELODIC (MIGP)	20141	4	48.48, error=1.87 EV = 100% ~2min loading data	47.51, error=1.58 EV = 100% ~39min loading data
MELODIC variation of 3-step PCA method in GIFT. Memory required is slightly higher compared to EM PCA2 and  SMIG. Here we used m = 2t – 1.

Ultimately whether this assumption is accurate depends on the problem at hand. Specifically, it comes down to how noise components should be handled and to what end principal components (PCs) will be used. For example, strong subject-specific noise components, highly explanatory of the variance across subjects, may be over-emphasized if their eigenvalues are carried forward to the group PCA estimation. This may also be the case if very weak noise components are whitened before proceeding to group PCA estimation, though the weakest components are typically discarded before whitening. If the ultimate goal is a group ICA estimation, then group PCs (i.e., the eigenmaps) are far less meaningful than the group ICs (consider an orthogonal transformation to the PC space which would produce an apparent “error” according to the paper¹ but would still lead to the same end ICA result). In addition, an ICA-oriented simulation (ideally one which fully controlled implicit linear and higher-order dependencies between sources) would be more meaningful than the source generation approach described in the paper¹, which has been previously criticized in ^6,7. Ultimately more research on this topic is needed. Of note, GIFT supports both approaches, using the expectation maximization (EM) PCA algorithm^8,9 and we report those estimates below (Figure 1).

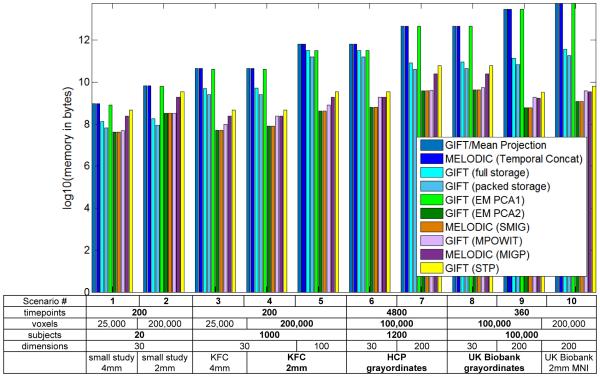
Figure 1.

Memory use of various approaches implemented in MELODIC and GIFT.

On another point related to accuracy, the paper¹ proposed a “3-step” MIGP (MELODIC's Incremental Group-PCA). However MIGP can be seen to be a slight variation of the familiar “3-step” PCA available in the GIFT toolbox since 2004^10-12. This is most evident from the second paragraph of the Conclusions section where the parallelization scheme described therein essentially outlines the steps in the original 3-step PCA. Unlike 3- step PCA, however, MIGP “propagates” the singular values of the current group-level estimate to the following iteration; 3-step PCA does not propagate the singular values of each group forward and, thus, yields group PCs that are different from those obtained by concatenating the entire data¹³. In other words, retaining the singular values of the current group PCs is key to approximate the group PCs from full concatenation; the singular values of the subject-level data, on the other hand, only relate to the “raw” versus whitened subject- level data debate mentioned above, not the approximation to full concatenation. A generalization of 3-step PCA (and MIGP) called subsampled time PCA (STP)^14,15 addresses the issue of preserving group-level singular values throughout and further improves flexibility between accuracy and execution speed. The accuracy of STP in our experiments was fairly comparable with other PCA methods and higher than MIGP (see Table 1).

Use of Memory (RAM)

Another key aspect is an emphasis on RAM efficient implementations of PCA. The paper¹ makes the claim that current solutions to this problem do not exist. However, this is not accurate as the GIFT software has implemented multiple memory efficient approaches since 2004 (see Table 1 for more details). The EM PCA implementation (which is as ‘good’ in minimizing RAM as the best solution presented in the paper¹) was announced on the GIFT listserv in early 2010, is included in the release notes (http://mialab.mrn.org/software/gift/version_history.html) and manual, and was also discussed in Allen et al.^8,9.

Furthermore, perhaps due to a lack of familiarity with GIFT, the memory estimates in Fig. 1 of the paper¹ for GIFT (either m = n or m = 2n) are incorrect since the GIFT toolbox implements the same “mathematically equivalent” approach mentioned for the full temporal concatenation (see Table 1). Specifically, instead of estimating the voxels × voxels covariance matrix of temporal correlations for each subject and then averaging over subjects, one can estimate the (subjects × timepoints) × (subjects × timepoints) covariance matrix of spatial correlations (note the GIFT toolbox covariance matrix is always computed along the smallest dimensions of the data by default). Of note, both GIFT and other tools contain many options and, while the default settings typically provide good guidance for the user, there are a number of available options that, depending on the problem, we anticipate would be explored by any user.

In order to provide a more complete and accurate picture of the current state of memory for the two software tools, we have made significant corrections to the original Fig. 1 in the paper¹. We have included four approaches (GIFT/Mean Projection, SMIG, MIGP, Temporal concatenation) from the original Fig. 1¹, two covariance computation strategies (full storage and packed storage), and three approaches that have been in GIFT for years (EM PCA1, EM PCA2 and 3-step PCA/STP) as well as the recently developed Multi power iteration (MPOWIT). Of note, Figure 1 includes the original GIFT approach (introduced in 2001) as well as the original MELODIC group ICA approach using temporal concatenation (introduced in 2009; tensor decomposition was used prior to that¹⁶).

Erhardt et al.¹⁷ provides extensive comparisons of multiple approaches for group ICA, including various group PCA approaches, and back-reconstruction methods (e.g. PCA-based, spatio-temporal (dual) regression). One of the important take-homes from ¹⁷ is that the subject-level PCA dimensionality should be higher than the group-level PCA dimensionality. This has been the GIFT default since 2010, despite the claim in the paper¹ that “typically” m =n.

Optimality Analysis

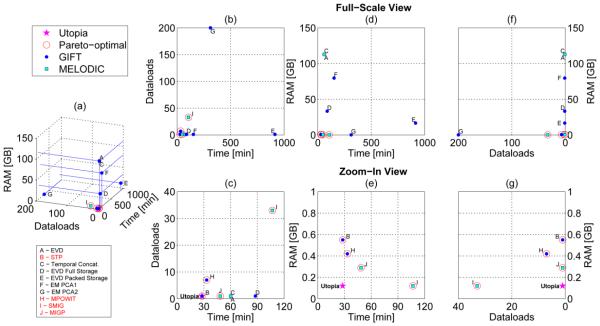
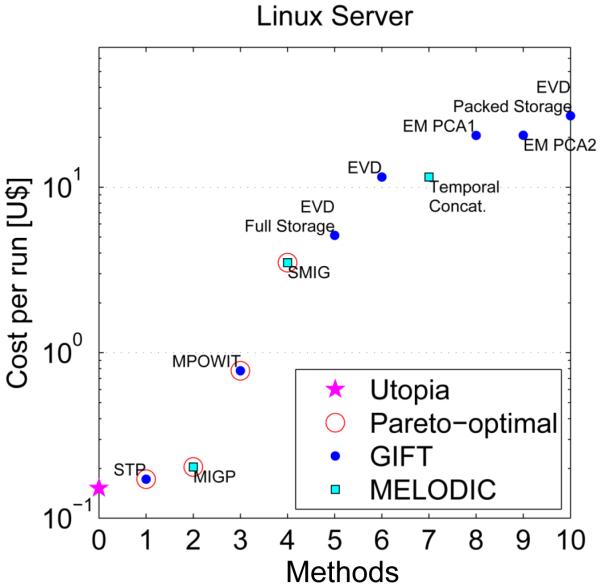
Here we study the optimality of the 10 PCA approaches presented in Table 1 (see the experimental setting description therein). We consider three different response measurements in our analysis: computation time in minutes, RAM memory used in GB, and number of dataloads. Since none of the three criteria alone suffices to establish preference of one method over the other, we considered all three simultaneously and determined the set of Pareto-optimal methods based on the set of non-dominated points in the three-dimensional space of response measurements (Figure 2, panel (a)). The non-dominated points are those that cannot be outperformed simultaneously in all criteria by any other point. These are called Pareto-optimal and are indicated with a red circle in Figures 2-3. The Pareto-optimal collection effectively outlines the trade-offs between each optimal method. Methods outside of the so-called Pareto-front are non-optimal since at least one method in the Pareto-front outperforms them in all criteria. In practice, a method from the Pareto-front should be selected as a result of constraints from the actual problem at hand. For didactical purposes, we then assigned the following fictitious costs in U$ for each response measurement: U$0.10 per GB of RAM per hour, U$0.10 per data-transfer from HD to RAM per 1600 subjects (i.e., per dataload in Figure 2), and U$0.10 per hour waiting for results to be obtained. The resulting fictitious costs are presented in Figure 3.

Figure 2.

Optimality analysis highlighting the set of Pareto-optimal methods on a Linux server. The utopia point combines the best performance measurements across all Pareto- optimal points.

Figure 3.

Fictitious cost analysis on a Linux server. Values obtained using fictitious costs in U$ for each response measurement: U$0.10 per GB of RAM per hour, U$0.10 per data- transfer from HD to RAM per 1600 subjects (i.e., per dataload in Figures 2), and U$0.10 per hour waiting for results to be obtained.

Figure 2 shows that STP, MPOWIT, SMIG and MIGP are Pareto-optimal. Panel (e) indicates that STP and MPOWIT can significantly improve execution time with respect to SMIG and MIGP at the cost of a small increase in RAM use. Note that accuracy (in terms of error with respect to the eigenvalues of full concatenation) was not included as a criterion in the optimality analysis. This was because all methods (except for MIGP and STP) attained very low L₂-norm error (< 1×10⁻⁶). The errors reported in Table 1 suggest STP makes a better approximation to the full concatenation than MIGP. Figure 3 suggests that STP and MIGP are both very cheap as compared to other techniques. Given the lower accuracy of STP and MIGP with respect to full concatenation, one recommendation is to use these approaches to initialize the more accurate iterative approaches (MPOWIT and SMIG), which should result in faster convergence. Note that these comparisons are meant to be descriptive and helpful, but it should be kept in mind that, though we tried to minimize other factors by using single-user workstations, for measures such as computation time there are many contributing factors and our results are not comprehensive in this regard. In addition, for the beginning user the number of PCA options can be a bit hard to sift through. In this case, we would recommend one of the Pareto-optimal approaches (e.g. STP, MIGP, MPOWIT, or SMIG) which can all handle large data sets and converge reasonably quickly.

Clarity and (Selective) History

In this section we respond to a few claims in the paper¹ which are either incomplete or not accurate. First, the statement “Current approaches…cannot be run using the computational facilities available to most researchers” is not accurate as we explained in the previous sections. In the paper¹ the sentence after this claim transitions to a discussion of the original group ICA paper from our group¹⁸ and claims “There can be a significant loss of accuracy…”, but fails to mention that this is not true if following the recommendations in ¹⁷ or using the default settings in the GIFT toolbox. The paper¹ also claims that “the amount of memory required is proportional to the number of subjects analyzed”, which is also untrue as described in the previous section. We have already addressed the “typically m=n” claim, and regarding “important information may be lost unless m is relatively large (which in general is not the case when using this approach)” is also not true (see ^17,19,20).

In addition, as a more minor point, the paper¹ refers (just prior to Equation 8) to the “power method” in the section on small memory iterative group PCA (SMIG). However, to clarify, power iteration methods estimate in deflationary mode (i.e., one component at a time) and, in contrast, the proposed approach estimates all components in parallel (i.e., symmetric mode) and, thus, it is more accurate to call the proposed approach a subspace iteration approach. Subspace iteration has been previously proposed^21,22, but was not cited in the paper¹. In contrast to subspace iteration, SMIG uses a normalization step that stems from the particular optimization problem proposed in the paper¹ instead of the typical QR factorization. Normalization is beneficial in subspace iteration to control the size of the eigenvalues of the covariance matrix powers and avoid ill-conditioned situations in the final SVD. The normalization in SMIG, however, does not allow a check for convergence, which is why the parameter “a” needs to be selected in advance. As an alternative, we have proposed in other work^14,15 a different normalization scheme, the MPOWIT algorithm, which enables us to efficiently check for convergence and stop iterating, thus limiting the number of dataloads, rather than just iterating a fixed amount of times.

Conclusions

In summary, we have attempted to provide some corrections and commentary on the important issue of memory efficient approaches for large group PCA that are needed for the widely used group ICA approach.

Highlights.

• Group ICA of fMRI on very large data sets is becoming more common

• GIFT (since 2009) and MELODIC (since 2014) enable analysis of thousands of subjects

• We compare ten available approaches including a Pareto optimal analysis

• We provide new analyses and comments on “Group-PCA for very large fMRI datasets”

Appendix

Group ICA on fMRI data is typically performed by doing subject-level PCA before stacking data-sets temporally across subjects¹⁸. We assume that 100% variance is retained in subject-level PCA for demonstration purposes. Let Z_i be the original data of subject i (having zero mean) and is of dimensions voxels by time points. PCA reduced data Y_i (Equation 3) is computed by performing eigen value decomposition on the covariance matrix C_i using the equations shown below (Equations 1 and 2) where ν is the number of voxels:

$$C_i=\frac{{Z_i}^T{Z}_i}{\nu -1}$$ (1)

$$C_i=F_i{\Lambda }_i{F_i}^T$$ (2)

$$Y_i=Z_i{F}_i{\Lambda }_i^{-1∕2}$$ (3)

Whitening normalizes the variances of components using the inverse square root of eigen values matrix Λ_i (Equation 3). Covariance matrix of Y_i is unitary or in other words eigen values of all components are 1. Therefore, group PCA space obtained by stacking whitened data across subjects Y is not comparable to group PCA space extracted from original data Z. However, if whitening is not used and only the eigen vectors F_i are used in projection (i.e., Y_i = Z_iF_i), eigen values information of each subject are propagated into the group PCA. We used a subset of 100 pre-processed fMRI subjects⁹ to compare the group PCA on original Z data and group PCA on stacked subject-level PCA with no whitening in the subject-level PCA. Table 1 shows the explained variance by each PCA method using the temporal concatenation on original data Z as the ground truth. It is evident that all PCA methods capture at least 99% explained variance.