Abstract
There is significant interest, both from basic and applied research perspectives, in understanding how structural/functional connectivity changes can explain behavioral symptoms and predict decline in neurodegenerative diseases such as Alzheimer's disease (AD). The first step in most such analyses is to encode the connectivity information as a graph; then, one may perform statistical inference on various ‘global’ graph theoretic summary measures (e.g., modularity, graph diameter) and/or at the level of individual edges (or connections). For AD in particular, clear differences in connectivity at the dementia stage of the disease (relative to healthy controls) have been identified. Despite such findings, AD-related connectivity changes in preclinical disease remain poorly characterized. Such preclinical datasets are typically smaller and group differences are weaker. In this paper, we propose a new multi-resolution method for performing statistical analysis of connectivity networks/graphs derived from neuroimaging data. At the high level, the method occupies the middle ground between the two contrasts — that is, to analyze global graph summary measures (global) or connectivity strengths or correlations for individual edges similar to voxel based analysis (local). Instead, our strategy derives a Wavelet representation at each primitive (connection edge) which captures the graph context at multiple resolutions. We provide extensive empirical evidence of how this framework offers improved statistical power by analyzing two distinct AD datasets. Here, connectivity is derived from diffusion tensor magnetic resonance images by running a tractography routine. We first present results showing significant connectivity differences between AD patients and controls that were not evident using standard approaches. Later, we show results on populations that are not diagnosed with AD but have a positive family history risk of AD where our algorithm helps in identifying potentially subtle differences between patient groups. We also give an easy to deploy open source implementation of the algorithm for use within studies of connectivity in AD and other neurodegenerative disorders.
Keywords: Brain connectivity, Non-Euclidean wavelets, Multi-resolution analysis, Graph wavelets, Diffusion tensor imaging (DTI), Family history, Alzheimer's disease (AD)
1. Introduction
Alzheimer's disease (AD) is a progressive neurodegenerative condition characterized by severe loss of cognitive function and ability to carry out activities of daily living (McKhann et al., 2011). Post-mortem diagnosis of the disease is determined by regional density of beta-amyloid plaques, and neurofibrillary tangles (Montine et al., 2012). The disease has a long course and significant pathology can accumulate prior to development of clinically relevant cognitive impairment (Perez-Nievas et al., 2013; Chételat et al., 2013).
While analyses of regional brain differences have come a long way toward informing upon the preclinical stages of AD, it has become increasingly clear that a better understanding of AD may not be possible based on characterizing regional pathology alone. AD poses a challenge given that the cognitive changes that define the disease do not manifest until significant brain pathology has accumulated, and because cognitive changes are poorly correlated with certain pathological features of the disease such as amyloid accumulation (Jack et al., 2013). A promising initiative then, is to derive a better understanding of the disease by characterizing changes in connectivity, taking into account the neural networks that comprise several affected regions. Functional connectivity changes are well-documented in the disease (Wang et al., 2007; Damoiseaux et al., 2012; Supekar et al., 2008), and promising studies suggest that connectivity changes can explain behavioral symptoms in AD and may predict conversion to AD (Filippi and Agosta, 2011; Li et al., 2002; Shao et al., 2012). Despite clear differences in connectivity at the dementia stage of the disease, AD-related connectivity changes in preclinical disease are not well-characterized.
In this study, we use a novel approach to probe connectivity differences in a cohort of late-middle-aged adults enriched for risk factors for AD, including parental family history and APOE ∈4 genotype. Our approach builds upon prior studies using graph-based network analysis to assess connectivity. Assume we are given a population of connectivity graphs, G = {Gi} where i ∈ {1,. . . ,n} indexes the study participants. Each graph Gi = {νi, εi} corresponds to a single subject, the vertex set νi is an anatomical starting point, and each edge in the set εi provides information about the relationship between these vertices. In this study, connectivity was based on the strength of white matter tract connections between template-defined anatomical locations, derived from diffusion tensor imaging (DTI).
In order to improve sensitivity, our study employed multi-resolution analysis using wavelets. Multi-resolution analysis exploits the “local context” of information to identify significant effects. That is, multi-resolution analysis takes into account the fact that information can be viewed at different resolutions (similar to zooming in and out of an image), which provides a mechanism to capture the ‘context’ of information when performing the downstream statistical analysis. To see why such an approach may be useful, observe that roughly speaking, the connectivity analysis literature may be broadly clustered in two categories. The first set of approaches take into account graph theoretic summaries of the entire graph (i.e., girth, diameter, modularity, small-worldness, degree distribution, etc.). Alternatively, we may go with more local approaches, i.e., a Voxel Based Analysis (VBA) type analysis applied to graph edges. To obtain disease specific behavior of specific edge connections, we see a need for a framework that lies in the continuum between the global and local methods. These requirements make wavelets a promising way to approach this problem. This approach is based on the concept that a signal can be represented by a set of localized wavelet coefficients, while noise in the signal is uniformly spread throughout the wavelet space (Ruttimann et al., 1998). Recent advances in multi-resolution wavelet analysis have facilitated the development of sensitive methods for image analysis, including the recent work on wavelet based morphometry (Canales-Rodríguez et al., 2013) in neuroimaging. The technique offers certain advantages in that it improves sensitivity and specificity relative to voxel based analysis, arguably due to the multi-resolution perspective of the data (Canales-Rodríguez et al., 2013). Tract based spatial statistics (TBSS) may also be considered a hybrid global/local approach (Smith et al., 2006). While not specifically based on wavelets, the general intuition of using a (structure dependent) parameterization of a set of related measurements for improving statistical power has been used in other disciplines such as statistical genomics. We provide a more detailed discussion of this issue later in Section 5 and relate it to the ideas developed here.
While multi-resolution wavelet analysis has been applied more extensively in classical image processing where images are signals sampled on a uniform lattice, connectivity graphs are not. The standard constructions are no longer applicable for non-Euclidean spaces. Based on recent work in harmonic analysis on spectral graph wavelets (Hammond et al., 2011) and using methods developed by our group to apply non-Euclidean wavelet based transformations to conduct shape analysis (Kim et al., 2012, 2014), we show how to perform multi-resolution wavelet analysis to connectivity graphs derived from DTI data. Multi-resolution wavelet analysis is ideal for improving sensitivity in both cases where sample sizes are low (often the case in patient-based studies), and where differences (effect sizes) may be small, often the case in studies of preclinical participants.
We evaluated preclinical alterations to structural connectivity in a late-middle-aged group of adults from the Wisconsin Registry for Alzheimer's Prevention (WRAP) study. In order to limit our analysis to white matter tracts that change in known disease, we first applied our approach to AD patients compared to age-matched controls from the Wisconsin Alzheimers Disease Research Center (ADRC). The starting point for tract connectivity was information derived from fractional anisotropy (FA), a summary measure of directional water diffusion that is highly sensitive to microstructural features including axonal density, diameter, myelination, and cytoskeletal features. We hypothesized that non-demented adults with increased risk for AD due to parental family history, would show differences in connectivity compared to controls. Further, given that our proposed approach is new, we compared it against standard methods of analysis, and hypothesized that we would find improved sensitivity using multi-resolution analysis.
The main contributions of this work are:
-
a)
We present an algorithm for performing multi-resolution statistical analysis of a population of brain connectivity graphs to identify group differences (at the level of edge weights).
-
b)
We present exhaustive experimental results showing how the machinery is able to characterize connectivity loss in preclinical AD by comparing asymptomatic individuals with and without risk factors for AD. The alternative (analysis for each edge) either fails to detect significant differences or yields p-values that are worse in comparison.
Of course, given the lack of ground truth data, one may suspect that the differences are merely an artifact of the framework and not a real disease (or risk) effect. We provide comparisons with prior findings (Racine et al., 2014; Adluru et al., 2014) showing that our final statistical results are consistent with and interpretable relative to current results.
2. Method
The algorithmic heart of the framework relies on going from an individual graph representing connectivity (i.e., weighted edges) to deriving a “descriptor” (a d-dimensional attribute) at each edge or node in the graph. The downstream statistical analysis will then be performed on a population of graphs with such multi-variate attributed edges, in a manner identical to current approaches. The method is transparent to the type of imaging modality used to derive connectivity; nonetheless, to make our presentation concrete, we will use connectivity derived from diffusion tensor imaging (DTI) as a running example throughout. Here, anatomical ROIs will denote the nodes of the graph and the strength of tracts provide the edge weights (more details shortly). Before we can apply a Wavelet transform on the graph, we will move to its so-called line-graph representation. Later, the wavelet coefficients will be derived which will enable hypothesis testing directly. This section describes these steps in the logical sequence.
2.1. Line Graphs of Connectivity Networks
In traditional graph theory, a graph G is defined by a vertex set ν, an edge set ε and corresponding edge weights ω. A dual representation of a given graph G is called the line graph L(G), also known as an edge graph or dual graph. We simply change the notion of nodes and edges; a node/vertex vi with two incident edges eij and eik is now thought of as connecting the two edges. After this transformation, these two edges become two distinct vertices in L(G), and they are connected by a binary edge (which corresponds to the common vertex vi in G).
Formally, a line graph L(G) = {νL, εL, ωL} is defined by a vertex set νL, an edge set εL, and a corresponding edge weights ωL, which is derived from the initial graph G. The vertex set νL and the edge set εL come from the edge set ε and the vertex set ν in G respectively, where as the edge weights ωL for the edges in εL are binary — the weight is 1 if there exists a common vertex between two edges, and 0 otherwise (Harary, 1969). It is easy to see that L(G) has NL vertices, same as the number of edges in G. One benefit of this transformation is that the original edge weights ω from G can now be treated as a function defined over the vertices νL in L(G). Consider the adjacency matrix AL of L(G), of size NL × NL, comprised of entries gij defined as,
| (1) |
where v is a vertex from ν and ei and ej are two different edges in ε. This means that when the ith edge ei and the jth edge ej are connected by a common vertex v, we assign 1 to gij, otherwise zero. Since AL gives the connectivity between edges through vertices, it is also known as the edge-adjacency matrix.
For obvious reasons, after this transformation, vertices in G with a single connected edge are neglected in L(G). When G is a connected graph, there is a path from any one vertex to another, the line graph transformation maps G to a unique L(G) with a single exception: a triangle shaped and ‘Y’ shaped graphs have similar line graphs. Moreover, if there is no isolated vertices in G, then G and L(G) have equal number of components. With this module, we transform a brain connectivity network to its corresponding line graph which will be utilized shortly.
The advantage of using line graph transform is that we can adopt edge weights in the original graph as a function defined on vertices in the line graph. Conventional expansions (wavelets or otherwise) are designed to analyze signals defined on the sampled vertices. Based on our connectivity analysis application, we have measurements at objects that relate such vertices, i.e., the edges. This makes the analysis/formulation inconvenient. However, we can observe that the notion of vertices or edges is artificial from the conceptual viewpoint, treating the edges as vertices and vertices as edges makes the machinery easily applicable yet does not affect the mathematical justification. Once the line graph is obtained from a graph, the edge weights in the original graph become a function that is defined on the vertices of the transformed line graph. We can then apply multi-resolution analysis using wavelets on the function defined on this line graph.
An illustrative example
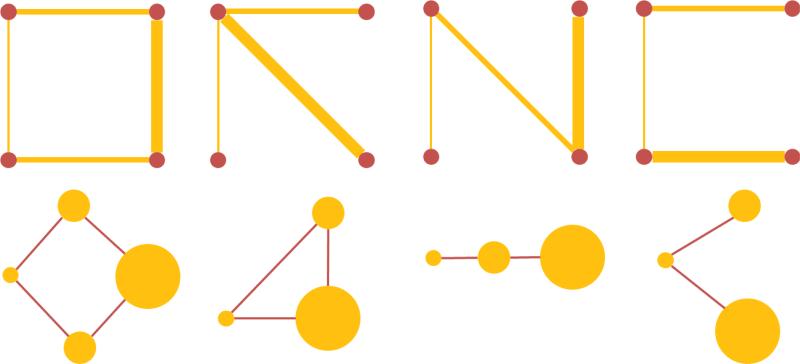
Four toy examples of this transformation are shown in Fig. 1. The top row shows the original graph G with four vertices and the bottom row shows the corresponding transformed line graphs L(G), which form a completely new non-Euclidean domain for analysis.
Figure 1.
Examples of simple graphs and the corresponding line graphs. Top: the original graphs are shown with the vertices in red and the edges in yellow, and the thickness of edges represents the edge weights. Bottom: Corresponding line graphs with yellow vertices and red edges. The vertex size is proportional to the signal defined on each vertex (i.e. the edge weight of the original graph).
2.2. Deriving a Wavelet based Descriptor at each node in L(G)
Wavelet are among the best known methods for processing a signal at multiple resolutions, and are heavily used for analyzing texture, shape, and other properties of the signal (Shen and Ip, 1999; Kim et al., 2013b). The traditional formulation of wavelets is defined for regular Euclidean spaces (Lowe, 1999; Witkin, 1984; Lindeberg, 1994, 1993); what is less widely known is that recent developments show how Wavelet theory is also applicable for non-Euclidean spaces such as graphs, if an appropriate basis can be defined (Hammond et al., 2011; Coifman and Maggioni, 2006). This enables one to perform band pass filtering in the frequency domain of the graph which is the key ingredient in deriving a local “contextual” descriptor at each graph node.
Recall that the wavelet transform starts by defining a mother wavelet ψs,a, which is a basis function with scale (s) and translation (a) properties. The wavelet transform is an analogue of the Fourier transform such that it decomposes a given function with bases functions and corresponding coefficients, but using ψ instead of sin() function. Wavelet bases ψ differ from Fourier bases in that they are compact and localized fluctuating functions. These properties essentially removes the ringing artifact (i.e., Gibbs phenomenon) common in Fourier analysis (because of the use of Fourier bases of infinite support). Formally, a wavelet transform is defined as the inner product of an original signal f and the wavelets ψ as,
| (2) |
yielding wavelet coefficients Wf(s, a).
Recent work in harmonics analysis enables defining the wavelet transform even in the non-Euclidean setting (Hammond et al., 2011; Coifman and Maggioni, 2006), which have been shown recently to be useful for statistical shape analysis (Kim et al., 2013a, 2014, 2012). If an implementation for non-Euclidean wavelet transform were available, we can collect the wavelet coefficients Wf(s, n) derived from the wavelet transform of a given signal f, defined at each vertex n of a given graph at multiple scales S = {s0, s1, . . . , s|S|−1}. When Wf(s, n) defined at each node of a line graph (without any soft/hard thresholding) is transformed to the original graph domain, it forms the Wavelet Connectivity Signature (WaCS), a descriptor on each edge of the original graph as
| (3) |
where e is a edge index from the original graph which corresponds to n, the node index in the line graph domain. Note that e and n are equivalent here. Since the line graph transformation maps the original connectivity graph to the dual representation where each vertex has an associated signal measurement, the wavelet coefficients (using a wavelet transform with a specifically constructed basis) will provide a multi-resolution view of the connectivity signal, as described next.
2.3. Multi-resolutional View of a Network
If one considers that the actual measurement is a combination of the true signal and a noise term, it is reasonable to assume that the true signal tends to change smoothly whereas noise varies rapidly (i.e., higher frequency terms). In signal processing, we decompose the signal in terms of its frequency components, and a low-pass filter helps identify and discard the high frequency parts. Using Wavelets, which are really a form of band-pass filters at multiple bandwidths, such smoothing can be efficiently performed by removing the finer scale components, where the finer scales corresponds to the high frequency components. Furthermore, each wavelet provides a view of the signal at multiple scales or resolutions. In particular, it is the inverse Wavelet transform, which provides the multi-resolution view once the noisier frequencies are taken care of. The inverse wavelet transform is defined as
| (4) |
which reconstructs the original signal f using wavelet coefficients and bases by summing over the entire scale s. The coarse scales will reconstruct the original signal at low resolution, which is a smooth approximation. Incrementally adding finer scales, the whole frequency spectrum contributes in the inverse transform, and finally recovers a perfect reconstruction. Using this approach, we can precisely assess what the signal looks like in a certain frequency band by selecting an optimal scale that is focused on that band. What this discussion has ignored so far is the precise specification of the actual Wavelet bases that will enable calculating the transform and its inverse.
Since a graph is an irregularly structured domain where each vertex has various number of neighbors with different connections, it is difficult to define the shape of the mother wavelet. The key idea in spectral graph wavelets (Hammond et al., 2011) to avoid this problem of defining wavelet transformation on graphs is to step into a dual domain (i.e., frequency domain) and then define band-pass filters there. Such a process still requires a set of orthonormal bases (e.g., Fourier bases) on graphs which enables us to transform a function to the dual domain. From spectral graph theory, a graph Laplacian is a simple positive semi-definite operator, and upon decomposition, gives the orthonormal bases we need. We use bases derived from the Laplacian of the line graph, L(G) and use the spectral graph wavelet transform described in (Hammond et al., 2011) in the forward direction to perform filtering on the graph, just as we would in traditional wavelet analysis. Then the inverse line graph transformation to the original graph domain yields the coefficients of interest.
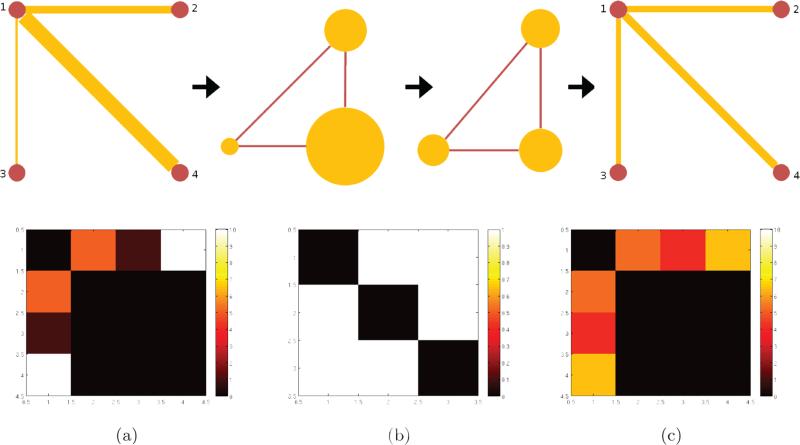
This process allows deriving a multi-resolution view of the brain connectivity graph. A simple example of the framework for the network filtering (smoothing) is given in Fig. 2 on a graph with three edges over four vertices. The top row of the figure shows the overall information flow. The original graph G consists of four vertices and three edges with corresponding edge weights (edge thickness) and is transformed into a line graph L(G); the edge weights become the measurements defined on each vertex of L(G). This signal is ‘filtered’ and then transformed back to the original space. In the final step, the signal becomes the filtered edge weights while respecting the original topology of G. In the bottom row, the corresponding adjacency matrices are shown. The first matrix shows the connectivity of each vertex in G and its edge weights. The second matrix shows the relation of each edge as L(G), and finally the third matrix shows the filtered edge weights maintaining the original connections in the first matrix.
Figure 2.
A toy example of graph structure filtering. The top row shows the graph filtering steps: (1) construction of the line graph, (2) smoothing(filtering) the signal on the line graph vertices, (3) reconstructing the filtered graph. The bottom row shows the corresponding adjacency matrices for each step.
2.4. Experiment Setup and Analysis Pipeline
There are a few additional parameters that need to be defined to fully specify our proposal. These parameters are mostly used for defining wavelet based descriptor via the functionality offered in SGWT toolbox Hammond et al. (2011). First, the mother wavelet function is realized using a piecewise spline function defined as
| (5) |
where s(x) = −5 + 11x − 6x2 + x3, α = β = 1, x1 = 1 and x2 = 2. The kernel function g() here is the default kernel function provided by the SGWT toolbox. It is designed to be monic power of x near the origin, and has power law decay far from the origin, therefore the mother wavelet achieves localization in the limit of fine scales. Here, we define 6 scales (5 scales from the mother wavelet and 1 scale using the scaling function) in the frequency domain, which are equally spaced in log scale in the range of 0 and the largest eigenvalue (150 in our case) of the graph Laplacian of the line graph of the original connectivity matrix.
For the experiment, a population of brain connectivity networks was given in the form of a 162 × 162 adjacency matrix and each element in the adjacency matrix was derived from the FA values between the ROIs, resulting in a total of 13041 brain connections for the analysis. First, line graph transform was applied to each adjacency matrix to obtain a dual representation for wavelet operations, and WaCS were obtained at each vertex in the line graph domain. Then, WaCS were transformed back to the original graph domain, resulting in multi-resolution descriptor at each graph edge. Since WaCS is a multivariate descriptor, we used a multivariate general linear model (MGLM) approach on WaCS to derive p-values controlling for covariates (i.e., age and sex), then corrected for false positives due to multiple comparisons. Those edges surviving the multiple comparisons correction procedures are considered as showing statistically significant group differences. As a baseline, we used a typical statistical approach by applying a general linear model (GLM) at each edge and correcting for multiple comparisons.
Throughout the analysis, we used scales of S = {0, 1, 2, 3, 4, 5} for the Wavelet transformation and used the set {0, 2, 4} for our multivariate analysis. To derive a WaCS with only a few degrees of freedom, we first used all scales together for the analysis, then checked by removing scales one by one if it made the results worse (i.e., the number of connections surviving multiple comparison correction). This helped determine the three scales for our analysis. There is a potential multiple testing issue here but it is fairly minor compared to the number of nodes and edges.
3. Dataset
For our analysis, we used two independent datasets obtained from 1) the Wisconsin Alzheimer's Disease Research Center (W-ADRC) and 2) the Wisconsin Registry for Alzheimer's Prevention (WRAP) study. The W-ADRC dataset is comprised of subjects diagnosed with AD as well as healthy controls (CN), while the WRAP dataset consists of healthy individuals only, but categorized by the presence or absence of certain AD risk factors. The demographics of the W-ADRC and the WRAP dataset are given in Tables 1 and 2, and the group-wise and sex-wise distributions of age from W-ADRC and WRAP dataset are given in Fig. 3. More details of each dataset are given in Section 3.1–3.2. The University of Wisconsin Institutional Review Board approved all study procedures and each participant provided signed informed consent before participation.
Table 1.
Demographics of W-ADRC dataset
| Category | AD(mean) | AD(s.d.) | CN(mean) | CN(s.d.) |
|---|---|---|---|---|
| Number of subjects | 44 | - | 58 | - |
| Age | 77.05 | 9.35 | 74.05 | 6.82 |
| Sex (M/F) | 31 / 13 | - | 33 / 25 | - |
| Global CDR | 0.74 | 0.37 | 0.06 | 0.16 |
| MMSE | 22.72 | 4.44 | 29.15 | 0.8543 |
| RAVLT total raw score | 20.52 | 8.07 | 43.76 | 8.49 |
| RAVLT long delay raw score | 0.66 | 1.46 | 8.41 | 3.12 |
CDR: Clinical Dementia Rating, MMSE: Mini Mental State Examination, RAVLT: Rey Auditory Verbal Learning Test
Table 2.
Demographics of WRAP dataset
| Category | FH+(mean) | FH+(s.d.) | FH-(mean) | FH-(s.d.) |
|---|---|---|---|---|
| Number of subjects | 93 | - | 250 | - |
| Age | 62.96 | 5.84 | 60.29 | 6.89 |
| Sex (M/F) | 64 / 29 | - | 166 / 84 | - |
| MMSE | 29 | 3.26 | 29.25 | 2.16 |
| RAVLT total raw score | 50.58 | 10.20 | 51.08 | 8.70 |
| RAVLT long delay raw score | 10.63 | 2.96 | 10.77 | 2.69 |
CDR: Clinical Dementia Rating, MMSE: Mini Mental State Examination, RAVLT: Rey Auditory Verbal Learning Test
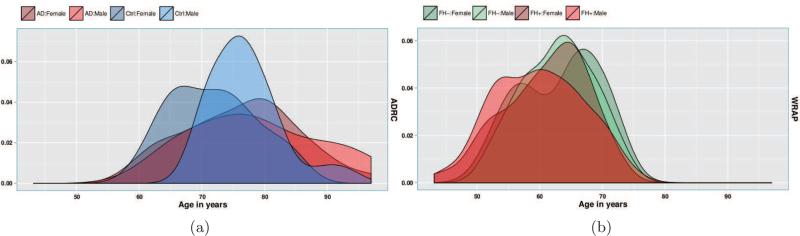
Figure 3.
Group and sex-wise age distributions of subjects in the a) ADRC study and b) WRAP study. Since the distributions have different means and variances affecting the group analysis, we include age and sex as covariates.
3.1. W-ADRC Dataset
The W-ADRC dataset included 102 subjects, labeled as AD (N = 44) and CN (N = 58). Participants were diagnostically characterized in the WADRC's multidisciplinary consensus conferences using standard procedures for the diagnosis of AD (McKhann et al., 1984, 2011). The demographics with respect to age are shown in Fig. 3 (a).
3.2. WRAP Dataset
In the WRAP dataset, 358 participants underwent brain imaging as part of studies on memory, aging, and risk for AD. WRAP is a registry of cognitively normal adults (at study entry) who are followed longitudinally and comprise a cohort whose members either have a biological parent who was diagnosed with AD (family history positive or FH+) of late onset AD or no first degree family history of diagonosed with AD (FH−) (Sager et al., 2005). A positive family history was defined as having one or both parents. Absence of family history of AD was verified through detailed medical history surveys and phone interview with the participants. Further, absence of family history of AD required that the father survive to at least age 70 and the mother to age 75 without incurring a formal diagnosis of dementia or exhibiting cognitive deterioration. Dividing the dataset into two groups, 250 participants were FH+ while 93 were FH−, and the demographics with respect to age are shown in Fig. 3 (b).
3.3. Image Processing
DTI acquisition
Participants were imaged on two identical General Electric 3.0 Tesla Discovery MR750 (Waukesha, WI) MRI systems fitted with an 8-channel head coil and using parallel imaging (ASSET). All participants in the W-ADRC dataset were imaged on one scanner, while all WRAP participants were imaged on a second, identical scanner. For both cohorts, DTI was acquired using a diffusion-weighted, spin-echo, single-shot, echo planar imaging (EPI) pulse sequence in 40 encoding directions at b = 1300s/mm2, with eight non-diffusion weighted (b = 0) reference images. The cerebrum was covered using contiguous 2.5 mm thick axial slices, FOV = 24 cm, TR = 8000 ms, TE = 67.8 ms, matrix = 96 × 96, resulting in isotropic 2.5 mm3 voxels. High order shimming was performed prior to the DTI acquisition to optimize the homogeneity of the magnetic field across the brain and to minimize EPI distortions.
Image analysis
We employed a robust processing pipeline, based on methods in (Zhang et al., 2007a) and reported in (Adluru et al., 2014). The processing stream is depicted in Fig. 4. For both datasets, head motion and image distortions (stretches and shears) due to eddy currents were corrected with affine transformation in the FSL (FMRIB Software Library) package (http://www.fmrib.ox.ac.uk/fsl/). Geometric distortion from the inhomogeneous magnetic field applied was corrected with the b = 0 field map, PRELUDE (phase region expanding labeler for unwrapping discrete estimates) and FUGUE (FMRIB's utility for geometrically unwrapping EPIs) from FSL, where field maps were available. All images were visually inspected at this stage to ensure that data with substantial artifact (loss of frontal or temporal lobe signal) or geometric distortions are not included in the final sample. Brain tissue was extracted using FSL's BET (Brain Extraction Tool). Tensor fitting was performed using a nonlinear least squares method in Camino (http://cmic.cs.ucl.ac.uk/camino/).
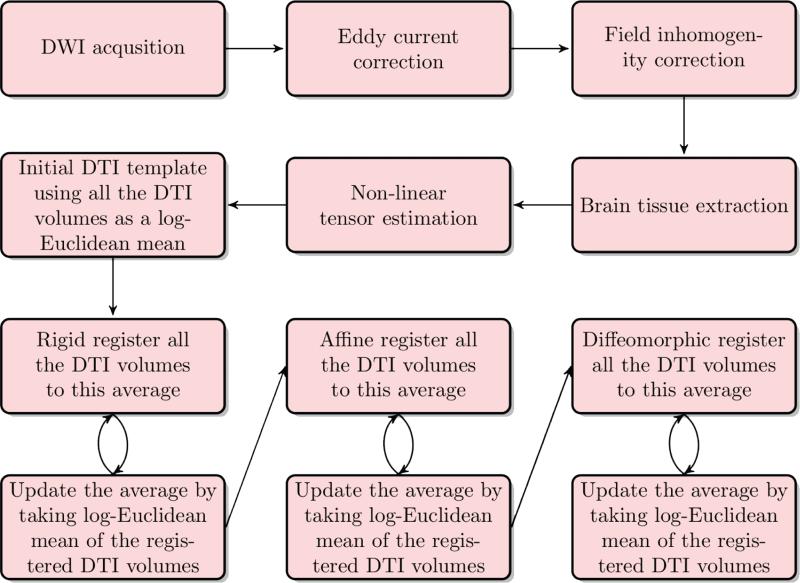
Figure 4.
The pipeline for generating the template: After the data are acquired, the DWI images are corrected for eddy current distortions and field inhomogeneity. Then, brain tissue is extracted from the images so further processing is done only on the relevant regions of the images. Tensors are estimated by non-linear optimization. An initial bootstrap template is then computed using the Log-Euclidean mean approach. Finally, the bootstrap template is iteratively improved using three layers: rigid registration, then affine registration and lastly by diffeomorphic registration.
Spatial normalization
For each of the dataset, we first created population specific templates using Diffusion Tensor Imaging ToolKit (DTI-TK, http://www.nitrc.org/projects/dtitk/) which is an optimized DTI spatial normalization and atlas construction tool (Zhang et al., 2006, 2007b) that has been shown to perform superior registration compared to scalar based registration methods (Adluru et al., 2012). The template is constructed in an unbiased way that captures both the average diffusion features (e.g., diffusivities and anisotropy) and the anatomical shape features (tract size) in the population (Zhang et al., 2007b). Individual maps were then registered to the study-specific templates using rigid, affine, and diffeomorphic alignments and finally interpolated to 2 × 2 × 2 mm2, voxel resolution before generating the network data. Note that we do not use an overall template representing both datasets since the node regions of interest provide us the correspondence across subjects and datasets.
Tractography based network estimation
Tractography was performed on the template using the following parameters for the track command implemented in Camino (Cook et al., 2006): curvature threshold of 45°, curve interval (i.e., the length of tract over which the curvature threshold is tested) of 10 mm. An Euler tracking algorithm with nearest neighbor interpolation based on probabilistic tensor deflection (TEND (Lazar et al., 2003)) was used to generate the tracks, and the step size for the Euler tracking was set to 0.1 mm. Bootstrapping (20 times) was performed (i.e., 20 tracts were generated per seed voxel where the seeds were defined as the entire brain mask.) The seed mask was obtained by binarizing the trace map of the population template where the lower and upper thresholds were 0.01 and 100 respectively. These thresholds are commonly used in DTI-TK (Zhang et al., 2006). The stopping criteria did not involve any thresholding for FA since the tracts were filtered to pass through the ROIs from the IIT atlas. Note that the bootstrap tractography procedure was used only to define the white matter region of interest which connects two separate nodes. Once the regions were defined from the tractography procedure, we took the mean FA values along the tracts, which is stable and is not affected by the number of bootstrap replications. The number of replications (20) was chosen based on our initial experiments to make sure we obtained reasonable white matter pathways between pairs of nodes and verified that changing the number of replications has no effect on the white matter region extracted. Then, a DTI white matter atlas (Varentsova et al., 2014) was registered to the population average FA map using Advanced Normalization Tools (ANTS) (Klein et al., 2009). In total, 164 regions were initially defined on a diffusion tensor template which has been made publicly available (Varentsova et al., 2014). Once we warped the FA of that template to the FA of the population template, we applied the warp to the 164 regions to align them onto the population template using nearest neighbor interpolation. In the end, two regions labeled unknown were excluded. Full brain tractography was then used with the conmat tool in Camino to obtain edge weights using the spatially normalized FA and MD measures giving us two 162 × 162 symmetric matrices per subject. A full index of the ROIs can be found in IIT3 atlas documentation at http://www.nitrc.org/projects/iit2.
Statistical analysis
The core comparisons for the statistical analysis are between (a) approach where statistical tests are performed on each edge weight individually (using a univariate general linear model) and (b) approach where statistical tests are performed on each edge using multi-scale wavelet-based connectivity descriptor (using a multivariate general linear model since the descriptors are vector valued). For both cases, age and sex are used as covariates.
4. Results
4.1. Brain Connectivity Differences between AD and Controls (W-ADRC Study)
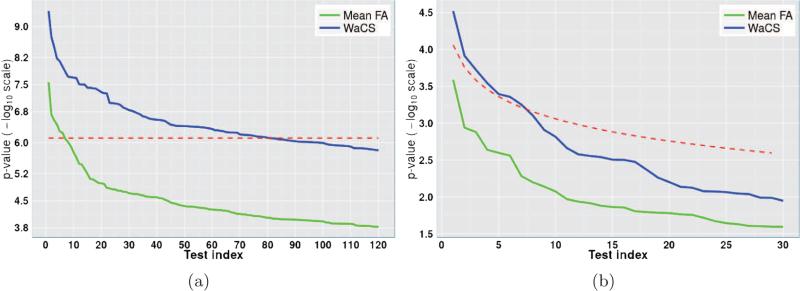
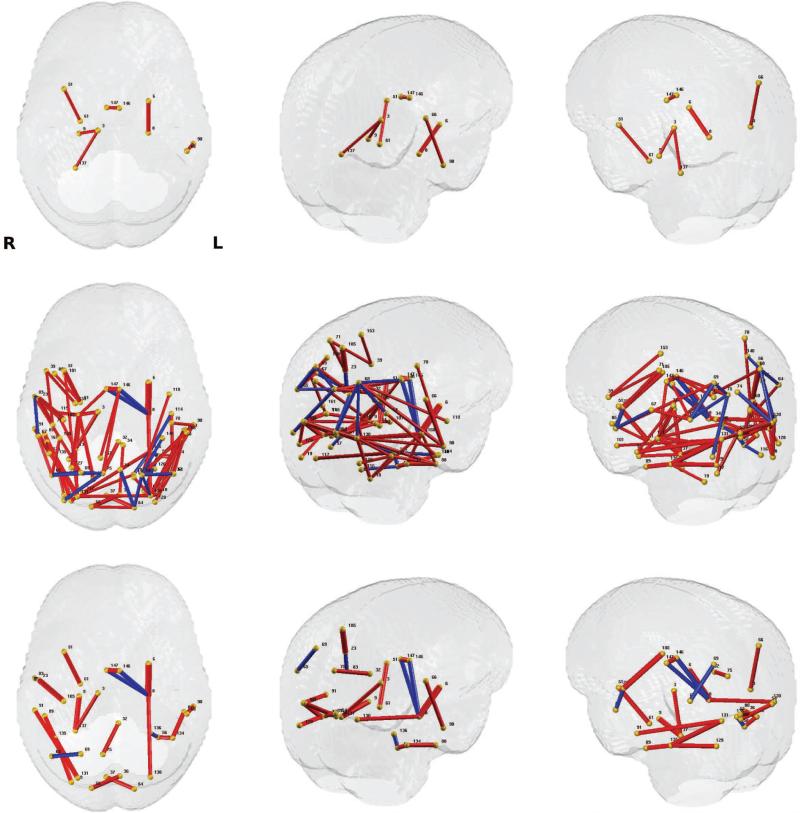
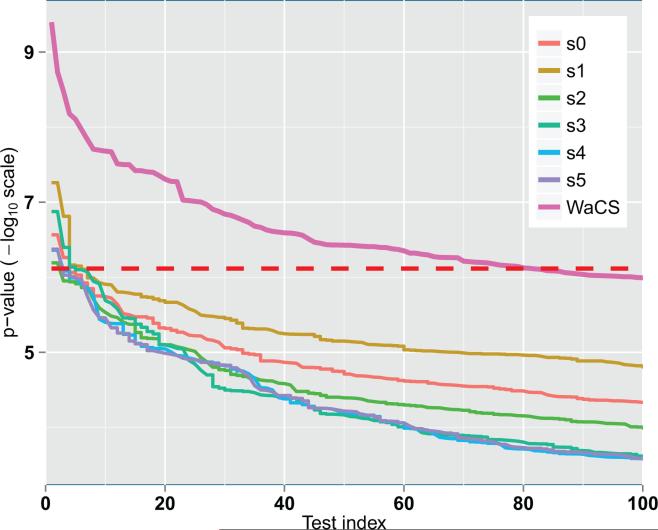
The baseline analysis using the FA weighted edges initially yielded 6 connections whereas when we performed the test on WaCS, we detected 81 out of 13041 brain connections spanning over 67 brain regions. To keep comparisons fair, both these analyses were performed at the Bonferroni correction threshold of α ≤ 0.01 controlling for age and gender. When using the baseline approach, the p-values were computed using a general linear model and a multivariate general linear model was used to obtain the p-values when using Wavelets (because the descriptor is multivariate). In both cases, age and gender were used as nuisance covariates. We show in Fig. 6 a) the p-value levels and Bonferroni thresholds in – log10 scale, comparing our result using Wavelets to the baseline outcome using raw FA values. We can observe that there are more edges that survive the Bonferroni threshold when using the proposed algorithm. Among the 81 connections identified with our framework, 19 of them showed higher FA in the AD group compared to control, while 62 connections showed a reverse phenomenon, i.e., higher FA values in the control group. The connections surviving the Bonferroni threshold are visualized in Fig. 7, the connections from baseline approach are shown in the top row and those from our framework are presented in the middle row. The bottom row presents more concise results with 22 significant connections with an even more conservative Bonferroni correction at α ≤ 0.001 to highlight some of the most significantly affected connections in the brain due to AD. The labels of the regions involved in these connections are given in Table. 3 which are difficult to identify with the traditional analysis.
Figure 6.
Comparison of sorted p-values using FA (green) and WaCS (blue) and multiple comparisons correction thresholds (red) in – log10 scale. a) p-values and Bonferroni threshold at α ≤ 0.01 from ADRC study (AD vs. CN), b) p-values and FDR threshold at 0.05 from WRAP study (FH+ vs FH−). The connections with – log10(p)-value above the threshold are considered as showing significant group differences. We can observe that the multi-resolution approach allows for detection of more connections affected by disease and risk compared to the baseline approach.
Figure 7.
Significant group differences (controlled for age and sex) from AD vs. control connection analysis using FA. Those connections with p-values that survive multiple comparisons correction are exhibited. The thickness of each connection represents the p-values in – log 10 scale (thicker connection corresponds to lower p-value), and the color of each connection represents the direction of the difference (red: stronger in controls group, blue: stronger in AD group). The region indices are given in Tab.3. Left column: top view, Middle column: upper-left view, Right column: upper-right view. Top row: result from GLM on raw FA values and Bonferroni thresholding at 0.01, Middle row: result from MGLM on WaCS and Bonferroni thresholding at 0.01, Bottom row: result from MGLM on WaCS and Bonferroni thresholding at 0.001. We can observe from the top two rows that the WaCS approach yields more sensitivity to significant connection.
Table 3.
Connections (between ROIs at each row) showing group difference (Bonferroni corrected at α ≤ 0.001) between AD and CN (controlled for age and sex). Direction −1/1 denotes to stronger FA value in AD / CN group respectively.
| Index | Region Label (Region Index) | Region Label (Region Index) | Direction |
|---|---|---|---|
| 1 | Left-Putamen (6) | Left-Hippocampus (8) | 1 |
| 2 | ctx_lh_G_pariet_inf-Supramar (66) | ctx_lh_G_temporal_middle (90) | 1 |
| 3 | Left-Hippocampus (8) | ctx_lh_S_oc_sup_and_transverse (90) | 1 |
| 4 | ctx_lh_G_oc-temp_lat-fusifor (56) | ctx_lh_S_oc-temp_lat (134) | 1 |
| 5 | ctx_lh_G_temporal_inf (88) | ctx_lh_S_oc-temp_lat (134) | 1 |
| 6 | ctx_lh_G_oc-temp_lat-fusifor (56) | ctx_lh_S_oc-temp_med_and_Lingual (136) | −1 |
| 7 | Left-Hippocampus (8) | ctx_lh_S_pericallosal (146) | −1 |
| 8 | ctx_lh_G_occipital_sup (54) | ctx_rh_G_cuneus (37) | 1 |
| 9 | ctx_lh_G_cuneus (36) | ctx_rh_G_occipital_sup (55) | 1 |
| 10 | ctx_rh_G_insular_short (51) | ctx_rh_G_oc-temp_med-Parahip (61) | 1 |
| 11 | ctx_rh_G_pariet_inf-Angular (65) | ctx_rh_G_parietal_sup (69) | −1 |
| 12 | ctx_lh_G_cingul-Post-dorsal (32) | ctx_rh_G_precuneus (75) | 1 |
| 13 | ctx_rh_G_and_S_subcentral (23) | ctx_rh_G_temp_sup-Lateral (83) | −1 |
| 14 | ctx_rh_G_and_S_subcentral (23) | ctx_rh_S_central (105) | 1 |
| 15 | ctx_rh_G_temporal_middle (91) | ctx _rh_S_oc_sup_and_transverse (131) | 1 |
| 16 | ctx_rh_G_temporal_inf (89) | ctx_rh_S_oc-temp_lat (135) | 1 |
| 17 | ctx_rh_S_oc_middle_and_Lunatus (129) | ctx_rh_S_oc-temp_lat (135) | 1 |
| 18 | ctx_rh_S_oc_sup_and_transverse (131) | ctx_rh_S_oc-temp_lat (135) | 1 |
| 19 | Right-Thalamus-Proper (3) | ctx_rh_S_oc-temp_med_and_Lingual (137) | 1 |
| 20 | Right-Hippocampus (9) | ctx_rh_S_oc-temp_med_and_Lingual (137) | 1 |
| 21 | Left-Hippocampus (8) | ctx_rh_S_pericallosal (147) | −1 |
| 22 | ctx_lh_S_pericallosal (146) | ctx_rh_S_pericallosal (147) | 1 |
ctx: cortex, rh: right hemisphere, lh: left hemisphere, G: gyrus, S: sulcal, inf: inferior, sup: superior, oc: occipital, temp: temporal, lat: lateral, med: medial
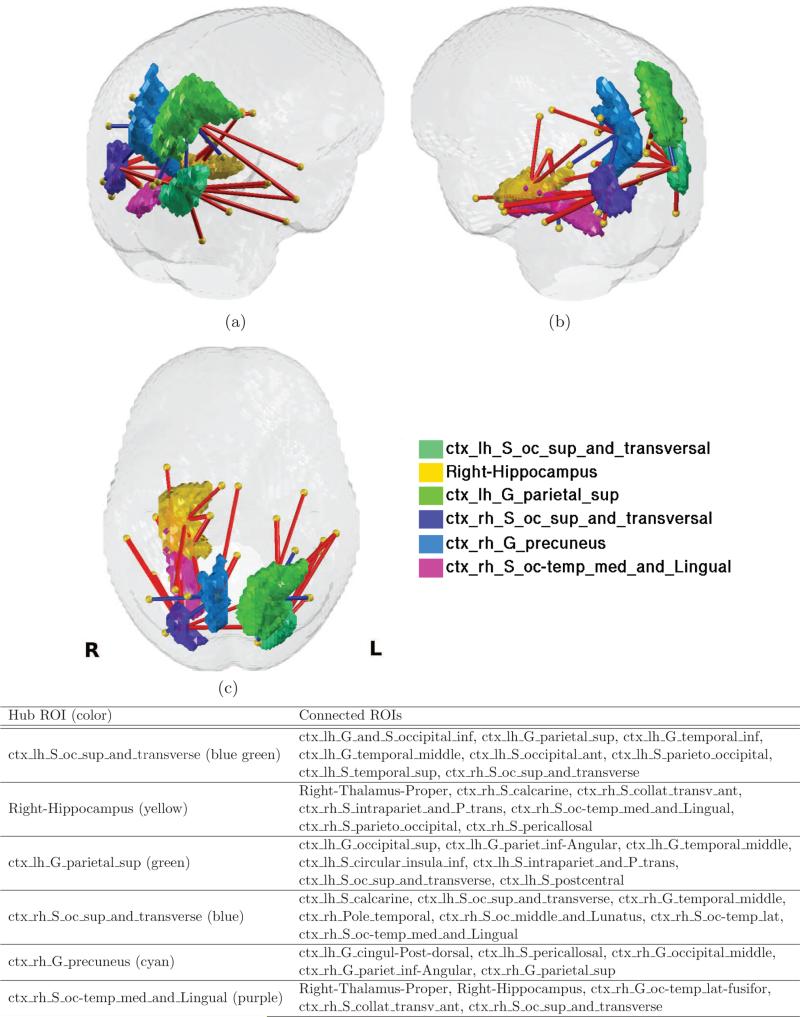
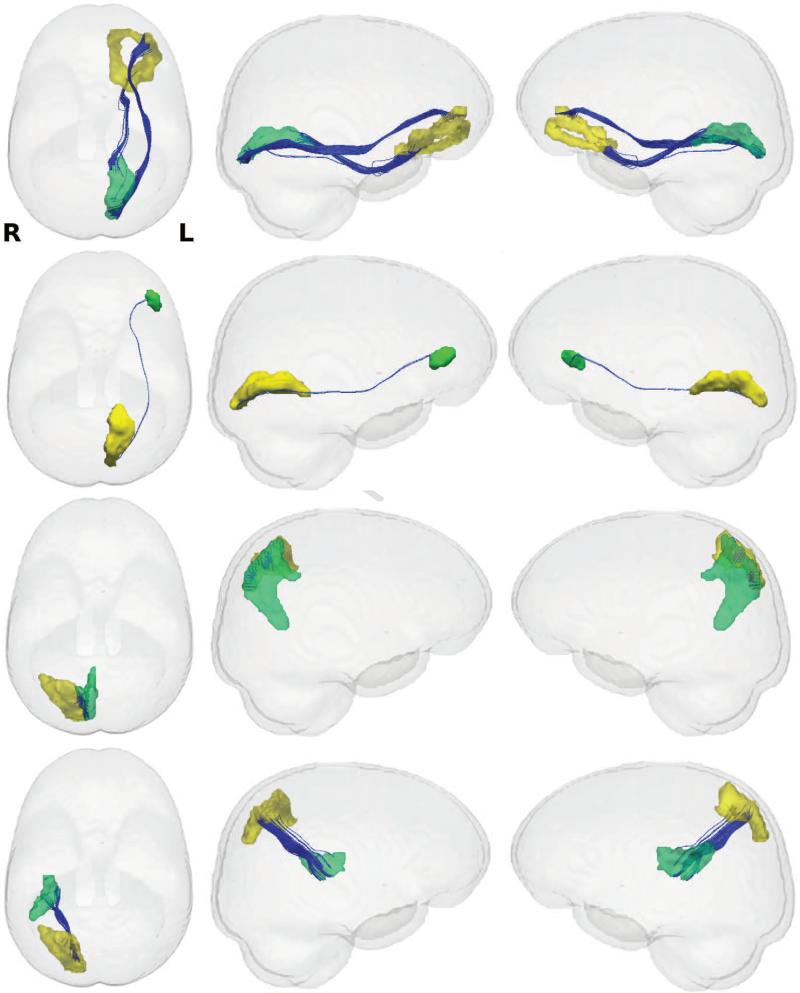
Of particular interest are ROIs with more than 5 connections, among the 81 significant connections, which can be considered as hub ROIs (the choice of the value 5 to define ”hubs” is arbitrary). These regions included the left superior and transverse occipital sulcus, right hippocampus, left superior parietal lobule, right transverse occipital sulcus, right precuneus, and right lingual component of the medial occipito-temporal gyrus. These hub ROIs and corresponding connections are shown in Fig. 8, and the number of connected ROIs are listed in Table. 4.
Figure 8.
Visualization of hub ROIs and the brain connections connected to the hub ROIs. a) upper-left view, b) upper-right view, c) top view. The hub ROIs are depicted in color, which are left occipital superior and transverse sulci (yellow), right hippocampus (green), left superior parietal lobule (light green), right occipital superior and transverse sulci (cyan), right precuneus (cyan), right medial occipital temporal lingual sulci (magenta), and the connections listed in the legend are presented by straight lines in red and blue denoted as in Fig. 7.
Table 4.
Hub ROIs with more than 5 connections and the degree (total number of connections) of each hub ROI.
| Region Index | Region Label | Degree |
|---|---|---|
| 130 | ctx_lh_S_oc_sup_and_transverse | 9 |
| 9 | Right-Hippocampus | 7 |
| 68 | ctx_lh_G_parietal_sup | 7 |
| 131 | ctx_rh_S_oc_sup_and_transverse | 7 |
| 75 | ctx_rh_G_precuneus | 5 |
| 137 | ctx_rh_S_oc-temp_med_and_Lingual | 5 |
4.2. Effects of Family History Risk on Brain Connectivity (WRAP Study)
The differences in healthy controls caused by a disease risk factor are expected to be subtle, making the task of finding group differences a more challenging task than comparing subjects with symptomatic disease to controls. We therefore selected connections of interest (COIs) based on the AD versus control analysis described above (section 4.1), and focus our analysis only on these pre-selected COIs. To obtain a large set of initial COIs (to reduce false negatives), we selected the connections in an AD vs. control comparison using our algorithm by applying false discovery rate (FDR) threshold of 0.001. This resulted in a total of 615 COIs out of 13041 connections which were then used to test for effects of family history (FH+ vs. FH−).
In Fig. 6 b), the resulting p-values from the baseline and our method are sorted and plotted in – log 10 scale along with the FDR threshold at 0.05 in Fig. 6 b), indicating that those p-values (blue) that are above the FDR threshold (red) survive the multiple comparison correction, whereas none from the baseline n) survives. Seven connections were identified to show significant group differences between FH+ and FH− groups, and those connections include 5 ROIs from the left hemisphere (orbital gray matter, calcarine sulcus, lateral orbital sulcus, postro ventral cingular gyrus and pericallosal sulcus) and 4 ROIs from the right hemisphere (precuneus, superior parietal lobule, posterior Sylvian fissure, calcarine sulcus, pericallosal sulcus).
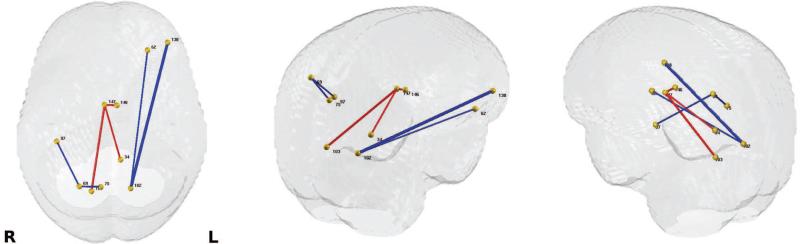
These connections are shown in Fig. 9, and each ROI and the connecting white matter pathways are visualized in Figs. 10 and 11, and the regions involved in these connections are listed in Table 5. Of note are two connections that were observed in both AD vs. control analysis and the FH+ vs. FH− comparison, which are shown in the second row of Fig. 10, the connection between left pericallosal (146) and right pericallosal region (147) and the third row of Fig. 11, the connection between right superior parietal lobule (69) and right precuneus (75). The baseline approach, applying statistical test on the raw FA data, did not reveal any significant connection differences between FH+ and FH−.
Figure 9.
Significant group differences (controlled for age and sex) from FH+ vs. FH− connection analysis using WaCS derived from FA. Those connections with p-values that survive FDR threshold at 0.05 are exhibited. Left: top view, Middle: upper-left view, Right: upper-right view. The thickness of each connection represents the p-values in – log10 scale, and the color of each connection represents the direction of the difference (red: higher in FH− group, blue: higher in FH+ group). The region labels and indices are given in Tab. 5
Figure 10.
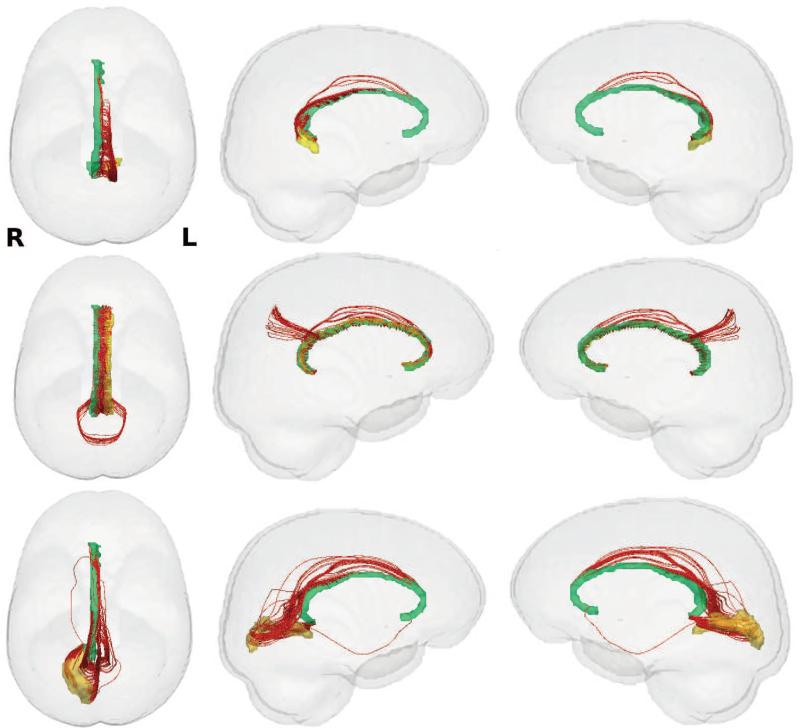
Visualization of the white matter tracks of connections (in red) with larger FA values in FH− group. Left column: top view, Middle column: left view, Right column: right view. First row: connection between left ventral posterior cingulate (yellow) and right pericallosal sulcus (green), Second row: connection between left pericallosal sulcus (yellow) and right pericallosal sulcus (green), Third row: connection between right calcarine sulcus (yellow) and right pericallosal sulcus (green). The connection between left pericallosal sulcus (146) and right pericallosal sulcus (147) in the second row is detected in both W-ADRC and WRAP studies.
Figure 11.
Visualization of the white matter tracks of connections (in blue) that have larger FA values in FH+ group. Left column: top view, Middle column: left view, Right column: right view. First row: connection between left orbital gyrus (yellow) and left calcarine sulcus (green), Second row: connection between left calcarine sulcus (yellow) and left lateral orbital sulcus (green), Third row: connection between right superior parietal lobule (yellow) and right precuneus (green), Fourth row: connection between right superior parietal lobule (yellow) and right posterior lateral fissure (green). The connection between right superior parietal lobule (69) and right precuneus (75) in the third row is detected in both W-ADRC and WRAP studies.
Table 5.
Identified connections (between left and right column) and corresponding ROIs showing group differences between FH+ and FH- (controlled for age and sex). Direction −1/1 denotes to higher FA value in FH+ / FH- group respectively.
| Index | Region Label (Region Index) | Region Label (Region Index) | Direction | p-value |
|---|---|---|---|---|
| 1 | ctx_lh_G_orbital (62) | ctx_lh_S_calcarine (102) | −1 | 2.997e-5 |
| 2 | ctx_lh_S_calcarine (102) | ctx_lh_S_orbital_lateral (138) | −1 | 1.218e-4 |
| 3 | ctx_rh_G_parietal_sup (69) | ctx_rh_G_precuneus (75) | −1 | 1.889e-4 |
| 4 | ctx_rh_G_parietal_sup (69) | ctx_rh_Lat_Fis-post (97) | −1 | 2.86e-4 |
| 5 | ctx_lh_G_cingul-Post-ventral (34) | ctx_rh_S_pericallosal (147) | 1 | 4.024e-4 |
| 6 | ctx_lh_S_pericallosal (146) | ctx_rh_S_pericallosal (147) | 1 | 4.396e-4 |
| 7 | ctx_rh_S_calcarine (103) | ctx_rh_S_pericallosal (147) | 1 | 5.598e-4 |
5. Discussion
We presented an algorithm for assessing brain connectivity changes in populations having Alzheimer's disease and in populations that are not diagnosed with AD but have a family history positive risk of AD. The technique, based on performing a Wavelet transform on non-Euclidean spaces such as graphs provides a method for identifying potentially subtle differences between patient groups, and is especially suited to detecting difference due to early, preclinical neurode-generation. Our study demonstrated extensive connectivity differences between AD patients and controls that were not evident using standard approaches. In addition, we identified connectivity differences due to increased risk for AD, differences that were not observed using a standard approach.
It is widely accepted that AD has a long preclinical phase during which the brain shows continued degeneration prior to the manifestation of cognitive symptoms. Substantial evidence suggests that the earliest pathology in AD involves abnormal processing of β-amyloid peptide, with the earliest evidence of the disease likely to manifest as alterations to amyloid-related bio-markers (Jack Jr et al., 2010). In addition to amyloid pathology, AD neuropathology is characterized by hyperphosphorylation of tau protein (the protein which stabilizes microtubules in neural cells), and extensive loss of synaptic connections. Increasing evidence suggests that the cognitive dysfunction found in AD may be due to disconnection between highly-interrelated brain regions (Delbeuck et al., 2003; Brier et al., 2014a). Of the characteristics which define AD, neuronal loss and synaptic pathology show the strongest relationship to dementia severity and cognitive deficits in AD (Gómez-Isla et al., 1997; Lassmann et al., 1993; DeKosky and Scheff, 1990; Perez-Nievas et al., 2013).
Among healthy individuals, neural connections underlie normal information processing, and constrain neural activity. Using statistical analysis to identify brain regions which show temporal coherence during fMRI, researchers have identified brain regions that show high-interconnectedness, for example, regions identified using resting-state or task-free fMRI that form the so-called Default Mode Network. Brain regions in this network include the medial prefrontal cortex, medial temporal lobe, and posterior cingulate cortex/retropslenial cortex. These brain regions are part of the episodic memory network (Xu et al., 2009; Johnson et al., 2006), in addition to being active during states of self-awareness (Craik et al., 1999; Gusnard et al., 2001; Fingelkurts et al., 2012; Johnson et al., 2007) and self-monitoring (Schmitz and Johnson, 2007). Interestingly, these brain regions are also those which show some of the highest levels of amyloid burden (Buckner et al., 2005) in AD. Perhaps not surprisingly then, several studies have found that AD patients show altered default mode network (DMN) activity which suggests a loss of connectivity. The finding of altered networks are robust in patients with AD or mild cognitive impairment (MCI) (Sorg et al., 2007; Greicius et al., 2004; Koch et al., 2014). More recently, fMRI based connectivity differences have also been observed in preclinical individuals at risk for the disease (Sperling et al., 2009; Brier et al., 2014b; Sheline et al., 2010).
In order to understand the structural basis for the connectivity loss observed in AD, recent studies have incorporated DTI-based information to determine the extent of loss of myelinated neuronal axons in the disease. In healthy adults, Grecius et al have shown that DMN regions are connected via major white matter tracts (Greicius et al., 2009). While this in itself is not highly surprising, it may suggest that even subtle damage to white matter tracts could potentially affect network efficacy. In support of this, Hahn et al have shown that disrupted white matter connectivity is associated with altered functional connectivity in MCI and AD (Hahn et al., 2013).
In the present study, we observed that AD affected no less than 81 white matter connections. The majority of the connectivity differences were centered on key brain regions, some of which are in the DMN, and that included portions of the lateral parietal lobe, precuneus, occipito-temporal brain regions, and hippocampus. Our analysis also revealed connectivity differences in tracts connecting to the occipital cortex, which while not a region of high amyloid burden, does show lower cerebral perfusion in MCI (Ding et al., 2014) and altered white matter in MCI patients who convert to AD. In individuals at risk for developing AD, we observed altered connectivity between similar brain regions to those observed in the AD comparison, including precuneus, lateral parietal lobe, and the gray matter of the pericallosal sulcus (which separates the cingulate from the corpus callosum). As with the AD comparison, individuals with family history of AD also showed altered occipital connections. No connectivity differences were detected using standard approaches.
Parental family history of AD is associated with altered connectivity even in asymptomatic adults. Parental family history of AD has in recent years been associated with several brain differences, including altered glucose metabolism (Mosconi et al., 2009), differences in BOLD signal during episodic memory (Xu et al., 2009), lower cerebral perfusion (Okonkwo et al., 2012), increased amyloid deposition, and lower gray matter volume (Mosconi et al., 2014), all in advance of any clinical symptoms of AD dementia. Resting-state connectivity differences have also been observed in individuals who harbor a combination of parental family history risk and APOE ∈4 carriage. Fleisher et al found differences in connectivity between posterior cingulate/retrosplenial cortex and several cortical regions in the DMN, including higher connectivity with prefrontal and temporal regions in high risk adults, and lower connectivity with precuneus (Fleisher et al., 2009). In addition to altered connectivity between several DMN regions observed in the AD versus control comparison, precuneus emerged as a hub region in the current study, and showed altered connectivity in the FH+ group. The findings also align with prior work from our group, suggesting that white matter changes are manifested in individuals with parental family history of AD (Adluru et al., 2014; Bendlin et al., 2010), including altered cingulum white matter, which carries fibers interconnecting precuneus (van den Heuvel et al., 2008) with other DMN regions. While the mechanism underlying increased vulnerability to AD based on family history is not known, both genetic and shared environmental factors may play a role (Huang et al., 2004).
It is worth noting that the direction of the connectivity differences between groups was not uniform. While the majority of the connections in the AD vs. control comparison revealed higher FA in healthy individuals, both the AD comparison, and the comparison by family history, revealed some connections where FA was higher in the AD, or the at risk group. While higher FA in a disease group is typically unexpected, accumulating studies suggest that selective axonal loss may result in higher FA in the disease group. A study comparing presymptomatic and symptomatic carriers of the presenilin 1 mutation that results in familial AD, has also found that patients in the asymptomatic disease stage exhibit higher regional FA compared to healthy controls(Ryan et al., 2013).
Limitations
A key limitation in this particular application is the physiologic interpretation of higher tract connectivity in AD and FH+. Whether this is due to actual increased connection strength of the tract or is an outgrowth of disease-related simplification / pruning / loss of crossing fibers allowing the tract to be visualized better in the disease group. Separate from this motivating application, we believe that the algorithm can be broadly applied to other types of brain connectivity analyses where the core advantages of higher sensitivity, due to a multi-resolutional perspective, should carry over with very few modifications in an analysis pipeline. Despite the various benefits of the algorithm, there are a few additional limitations that we must point out. First, note that the multi-resolution strategy and our framework involves a quadratic dependence of the number of connections on the number of regions. For example, the number of edges generated in a line graph from a node of degree d will be O(d2). Even for a fully connected graph, with N number of nodes in the original graph, the number of nodes in the line graph is upper bounded by the number of edges, O(N2). In our experiments, each network yields a sparse graph (due to a sparse adjacency matrix), so we did not encounter any scalability issues. Independent of computational issues, when the number of edges is large, the multiple comparisons correction will be fairly strict although our framework does provide means of detecting stronger differences that have a better chance of surviving the correction. A heuristic solution here is to use the multi-resolutional view to come up with a tessellation of the graph into smaller sub-graphs and perform the analysis on sub-graph summaries instead. The specifics will clearly depend on the needs of the application and are not investigated here. Second, as the number of regions p grows, so does the size of the matrix whose decomposition we must obtain. For the sizes used in this work, a Chebyshev polynomial approximation used in the spectral graph wavelet toolbox (Hammond et al., 2011) to approximate the wavelet transformation on graphs is sufficient. The paper will be accompanied by an open source library that will offer this functionality out of the box (http://pages.cs.wisc.edu/~wonhwa/project/mbca_toolbox.html). Finally, while the method can characterize signals that are scale dependent, when too many scales are defined over the eigen- value spectrum, the true signal may leak between different scales due to sampling. Choosing special types of wavelet such as ”Meyer” wavelet with a tight frame (instead of an overcomplete basis) may help in such cases, but was not needed in our experiments.
Is there a fundamental statistical reason why a multi-resolution view should improve power?
Notice that the goal of reducing Type 2 errors is also common in other areas of science (outside neuroimaging) such as statistical genomics. In particular, for analyzing differential gene expression Dahl and Newton proposed a very interesting idea (and accompanying statistical analysis) for improving power in microarray data analysis (Dahl and Newton, 2007). The rationale in that work is elegant yet simple. Consider a setting where the hypothesis tests are being performed on individual genes. Now, if one could define ‘true’ clusters of genes in terms of shared parameter values, one could improve the sensitivity of individual gene-level tests, because more data bearing on the same parameter values are available. In other words, if two genes were part of the same cluster, any degree of information sharing between them directly improves the power for hypothesis tests performed for each of them because in the most optimistic setting, we have twice as many measurements. The analysis in their work makes these arguments rigorous and develops ways of obtaining such a clustering based on non-parametric Bayesian methods. In the current work, we do not explicitly ‘cluster’ the edges of the graph. Nonetheless, interestingly, it is easy to think of a diffusion process on the graph (achieved by wavelets) as, in fact, serving a similar goal as clustering. By aggregating information at different/multiple resolutions (governed by the scaling and dilation parameters of the wavelet expansion), the framework described here offers improved sensitivity based on the same principles. That is, part of the reason why our proposed framework achieves better sensitivity is by considering multiple hypothesis testing and diffusion/wavelets jointly.
Highlights.
A novel multi-resolutional representation for brain connectivity graphs
Highly sensitive in identifying group differences in connectivity networks
Strong result detecting connectivity changes in the preclinical stage of AD
An open source implementation of the framework
Figure 5.
Orthogonal views and 3D surface rendering of the IIT3 gray matter atlas overlayed on the template FA map.
Acknowledgments
This research was supported by funding from NIH R01 AG040396, NIH R01 AG021155, NSF RI 1116584, NSF CAREER award 1252725, UW ADRC P50 (AG033514), the Wisconsin Partnership Program, UW ICTR (1UL1RR025011), NIH grants P30 AG010129, K01 AG030514, NIH R01 AG027161 and Waisman Core grant P30 HD003352-45.
Appendix A. Group Analysis on Individual WaCS Scales
Observe that occasionally, there may exist a single wavelet scale that returns the best result. If one could find such a scale, it is possible that it yields a better result than our multivariate analysis. To evaluate if this was true in the datasets we analyzed in this work, we performed further an additional group analysis on each individual WaCS scales used in our ADRC cohort (AD vs. CN), and compared them to the result using a combination of scales from the procedure described in section 2.4.
Figure A.12.
Comparison of sorted p-values (in – log10 scale) from individual scales of WaCS and combination of multiple scales of WaCS (bold pink). Red dashed line denotes to the Bonferroni threshold at 0.01. It shows that our individual scales We can observe that combining the multi-resolution approach allows for detection of more connections affected by disease and risk compared to the baseline approach.
Fig. A.12 shows sorted p-values in – log10 scale from group analysis using GLM at each individual scale of WaCS. We also plot sorted p-values in – log10 scale from MGLM using multiple scales that were used in our experiments. All tests controlled for age and sex. We see that multivariate analysis with the selected scales (scale 0, 2 and 4) made the method much more sensitive than using any of the single scale alone. Among those individual scales, scale 1 showed the best result, and scale 0, which is essentially smoothing with the scaling function, was the second best. All of them were sensitive enough to detect a few connections, but as seen in Fig. A.12, the number of identified edges were fewer than 10, while their combination yields 81 connections.
Note that the number of total scales in the transform as well as the number of selected scales for the analysis can be chosen by the user. But having a great deal of flexibility in the scales has a few disadvantages. First, each specific dataset may have an ideal number (and set of) scales which yields the best results. But sensitivity to group-wise differences is not monotonic as a function of the number of scales. Occasionally it may improve but also negatively affect the results, depending on which dataset we analyze. Trying out many different options, in the worst case, may give statistically spurious results. On a broad set of experiments on various datasets, we found that three scales were enough to obtain meaningful and robust results in general. Separately, choosing a large number/set of scales clearly increases the degrees of freedom of the descriptor. By itself, this is not a major issue. However, these descriptors now live in a much higher dimensional space (though the number of samples is fixed) where we are asking if the distributions across groups are different. Because of the high dimensionality, the distribution is sparse making it difficult to answer the main statistical question of interest, i.e., of group-level differences. It is possible that by suitably increasing the sample size, one can address this problem. Instead, our experiments suggest that working with a small number of scales is simpler and has fewer parameters to tune.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adluru N, Destiche DJ, Lu SY-, Doran ST, Birdsill AC, Melah KE, Okonkwo OC, Alexander AL, Dowling NM, Johnson SC, et al. White matter microstructure in late middle-age: Effects of apolipoprotein E4 and parental family history of Alzheimer's disease. NeuroImage: Clinical. 2014;4:730–742. doi: 10.1016/j.nicl.2014.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adluru N, Zhang H, Fox AS, Shelton SE, Ennis CM, Bartosic AM, Oler JA, Tromp DP, Zakszewski E, Gee JC, et al. A diffusion tensor brain template for rhesus macaques. Neuroimage. 2012;59(1):306–318. doi: 10.1016/j.neuroimage.2011.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendlin BB, Ries ML, Canu E, Sodhi A, Lazar M, Alexander AL, Carlsson CM, Sager MA, Asthana S, Johnson SC. White matter is altered with parental family history of Alzheimer's disease. Alzheimer's & dementia. 2010;6(5):394–403. doi: 10.1016/j.jalz.2009.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brier M, Thomas J, Ances B. Network dysfunction in alzheimers disease: Refining the disconnection hypothesis. Brain connectivity. 2014a;4(5):299–311. doi: 10.1089/brain.2014.0236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brier MR, Thomas JB, Fagan AM, Hassenstab J, Holtzman DM, Benzinger TL, Morris JC, Ances BM. Functional connectivity and graph theory in preclinical alzheimer's disease. Neurobiology of. 2014b;35(4):757–768. doi: 10.1016/j.neurobiolaging.2013.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Snyder AZ, Shannon BJ, LaRossa G, Sachs R, Fotenos AF, Sheline YI, Klunk WE, Mathis CA, Morris JC, et al. Molecular, structural, and functional characterization of alzheimer's disease: evidence for a relationship between default activity, amyloid, and memory. The Journal of Neuroscience. 2005;25(34):7709–7717. doi: 10.1523/JNEUROSCI.2177-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canales-Rodríguez EJ, Radua J, Pomarol-Clotet E, Sarró S, Alemán-Gómez Y, Iturria-Medina Y, Salvador R. Statistical analysis of brain tissue images in the wavelet domain: Wavelet-based morphometry. NeuroImage. 2013;72:214–226. doi: 10.1016/j.neuroimage.2013.01.058. [DOI] [PubMed] [Google Scholar]
- Chételat G, La Joie R, Villain N, Perrotin A, de La Sayette V, Eustache F, Vandenberghe R. Amyloid imaging in cognitively normal individuals, at-risk populations and preclinical Alzheimer's disease. NeuroImage: Clinical. 2013;2:356–365. doi: 10.1016/j.nicl.2013.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coifman R, Maggioni M. Diffusion wavelets. Applied and Computational Harmonic Analysis. 2006;21(1):53–94. [Google Scholar]
- Cook P, Bai Y, Nedjati-Gilani S, Seunarine K, Hall M, Parker G, Alexander D. Camino: open-source diffusion-MRI reconstruction and processing. 14th scientific meeting of the international society for magnetic resonance in medicine. 2006;2759 [Google Scholar]
- Craik FI, Moroz TM, Moscovitch M, Stuss DT, Winocur G, Tulving E, Kapur S. In search of the self: A positron emission tomography study. Psychological Science. 1999;10(1):26–34. [Google Scholar]
- Dahl DB, Newton MA. Multiple hypothesis testing by clustering treatment effects. Journal of the American Statistical Association. 2007;102(478):517–526. [Google Scholar]
- Damoiseaux JS, Prater KE, Miller BL, Greicius MD. Functional connectivity tracks clinical deterioration in alzheimer's disease. Neurobiology of aging. 2012;33(4):828–e19. doi: 10.1016/j.neurobiolaging.2011.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeKosky ST, Scheff SW. Synapse loss in frontal cortex biopsies in Alzheimer's disease: correlation with cognitive severity. Annals of neurology. 1990;27(5):457–464. doi: 10.1002/ana.410270502. [DOI] [PubMed] [Google Scholar]
- Delbeuck X, Van der Linden M, Collette F. Alzheimer's disease as a disconnection syndrome? Neuropsychology review. 2003;13(2):79–92. doi: 10.1023/a:1023832305702. [DOI] [PubMed] [Google Scholar]
- Ding B, Ling H.-w., Zhang Y, Huang J, Zhang H, Wang T, Yan FH. Pattern of cerebral hyperperfusion in alzheimers disease and amnestic mild cognitive impairment using voxel-based analysis of 3D arterial spin-labeling imaging: initial experience. Clinical interventions in aging. 2014;9:493. doi: 10.2147/CIA.S58879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filippi M, Agosta F. Structural and functional network connectivity breakdown in Alzheimer's disease studied with magnetic resonance imaging techniques. Journal of Alzheimer's Disease. 2011;24(3):455–474. doi: 10.3233/JAD-2011-101854. [DOI] [PubMed] [Google Scholar]
- Fingelkurts AA, Fingelkurts AA, Bagnato S, Boccagni C, Galardi G. Dmn operational synchrony relates to self-consciousness: evidence from patients in vegetative and minimally conscious states. The open neuroimaging journal. 2012;6:55. doi: 10.2174/1874440001206010055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleisher AS, Sherzai A, Taylor C, Langbaum JB, Chen K, Buxton RB. Resting-state bold networks versus task-associated functional mri for distinguishing alzheimer's disease risk groups. Neuroimage. 2009;47(4):1678–1690. doi: 10.1016/j.neuroimage.2009.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gómez-Isla T, Hollister R, West H, Mui S, Growdon JH, Petersen RC, Parisi JE, Hyman BT. Neuronal loss correlates with but exceeds neurofibrillary tangles in alzheimer's disease. Annals of neurology. 1997;41(1):17–24. doi: 10.1002/ana.410410106. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer's disease from healthy aging: evidence from functional mri. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(13):4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cerebral cortex. 2009;19(1):72–78. doi: 10.1093/cercor/bhn059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusnard DA, Akbudak E, Shulman GL, Raichle ME. Medial prefrontal cortex and self-referential mental activity: relation to a default mode of brain function. Proceedings of the National Academy of Sciences. 2001;98(7):4259–4264. doi: 10.1073/pnas.071043098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn K, Myers N, Prigarin S, Rodenacker K, Kurz A, Förstl H, Zimmer C, Wohlschläger AM, Sorg C. Selectively and progressively disrupted structural connectivity of functional brain networks in Alzheimer's diseaserevealed by a novel framework to analyze edge distributions of networks detecting disruptions with strong statistical evidence. NeuroImage. 2013;81:96–109. doi: 10.1016/j.neuroimage.2013.05.011. [DOI] [PubMed] [Google Scholar]
- Hammond D, Vandergheynst P, Gribonval R. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis. 2011;30(2):129–150. [Google Scholar]
- Harary F. Graph Theory. Addison-Wesley; Reading, MA.: 1969. [Google Scholar]
- Huang W, Qiu C, von Strauss E, Winblad B, Fratiglioni L. APOE genotype, family history of dementia, and Alzheimer disease risk: a 6-year follow-up study. Archives of neurology. 2004;61(12):1930–1934. doi: 10.1001/archneur.61.12.1930. [DOI] [PubMed] [Google Scholar]
- Jack CR, Knopman DS, Jagust WJ, Petersen RC, Weiner MW, Aisen PS, Shaw LM, Vemuri P, Wiste HJ, Weigand SD, et al. Update on hypothetical model of Alzheimers disease biomarkers. Lancet neurology. 2013;12(2):207. doi: 10.1016/S1474-4422(12)70291-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Jr, Knopman DS, Jagust WJ, Shaw LM, Aisen PS, Weiner MW, Petersen RC, Trojanowski JQ. Hypothetical model of dynamic biomarkers of the Alzheimer's pathological cascade. The Lancet Neurology. 2010;9(1):119–128. doi: 10.1016/S1474-4422(09)70299-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson S, Schmitz T, Moritz C, Meyerand M, Rowley H, Alexander A, Hansen K, Gleason C, Carlsson C, Ries M, et al. Activation of brain regions vulnerable to alzheimer's disease: the effect of mild cognitive impairment. Neurobiology of aging. 2006;27(11):1604–1612. doi: 10.1016/j.neurobiolaging.2005.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson SC, Ries ML, Hess TM, Carlsson CM, Gleason CE, Alexander AL, Rowley HA, Asthana S, Sager MA. Effect of Alzheimer disease risk on brain function during self-appraisal in healthy middle-aged adults. Archives of general psychiatry. 2007;64(10):1163–1171. doi: 10.1001/archpsyc.64.10.1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim WH, Adluru N, Chung MK, Charchut S, GadElkarim JJ, Altshuler L, Moody T, Kumar A, Singh V, Leow AD. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013. Springer; 2013a. Multi-resolutional brain network filtering and analysis via wavelets on non-euclidean space. pp. 643–651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim WH, Chung MK, Singh V. Multi-resolution shape analysis via non-euclidean wavelets: Applications to mesh segmentation and surface alignment problems. Computer Vision and Pattern Recognition (CVPR), 2013 IEEE Conference on. IEEE. 2013b:2139–2146. doi: 10.1109/CVPR.2013.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim WH, Pachauri D, Hatt C, Chung MK, Johnson S, Singh V. Wavelet based multi-scale shape features on arbitrary surfaces for cortical thickness discrimination. Advances in Neural Information Processing Systems. 2012;25:1250–1258. [PMC free article] [PubMed] [Google Scholar]
- Kim WH, Singh V, Chung MK, Hinrichs C, Pachauri D, Okonkwo OC, Johnson SC. Multi-resolutional shape features via non-euclidean wavelets: Applications to statistical analysis of cortical thickness. NeuroImage. Part. 2014;931(0):107–123. doi: 10.1016/j.neuroimage.2014.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang M-C, Christensen GE, Collins DL, Gee J, Hellier P, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain mri registration. Neuroimage. 2009;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch K, Myers NE, Göttler J, Pasquini L, Grimmer T, Förster S, Manoliu A, Neitzel J, Kurz A, Förstl H, et al. Disrupted intrinsic networks link amyloid-β pathology and impaired cognition in prodromal alzheimer's disease. Cerebral Cortex. 2014:bhu151. doi: 10.1093/cercor/bhu151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lassmann H, Fischer P, Jellinger K. Synaptic pathology of alzheimer's diseasea. Annals of the New York Academy of Sciences. 1993;695(1):59–64. doi: 10.1111/j.1749-6632.1993.tb23028.x. [DOI] [PubMed] [Google Scholar]
- Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley HA, Haughton V, Field A, et al. White matter tractography using diffusion tensor deflection. Human brain mapping. 2003;18(4):306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S-J, Li Z, Wu G, Zhang M-J, Franczak M, Antuono PG. Alzheimer disease: Evaluation of a functional mr imaging index as a marker 1. Radiology. 2002;225(1):253–259. doi: 10.1148/radiol.2251011301. [DOI] [PubMed] [Google Scholar]
- Lindeberg T. Scale-space theory in computer vision. Springer; 1993. [Google Scholar]
- Lindeberg T. Scale-space theory: A basic tool for analyzing structures at different scales. Journal of applied statistics. 1994;21(1-2):225–270. [Google Scholar]
- Lowe DG. Object recognition from local scale-invariant features. Computer Vision, 1999. The Proceedings of the Seventh IEEE International Conference on. Ieee. 1999;2:1150–1157. [Google Scholar]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM. Clinical diagnosis of Alzheimer's disease report of the nincds-adrda work group under the auspices of department of health and human services task force on Alzheimer's disease. Neurology. 1984;34(7):939–939. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]
- McKhann GM, Knopman DS, Chertkow H, Hyman BT, Jack CR, Jr, Kawas CH, Klunk WE, Koroshetz WJ, Manly JJ, Mayeux R, et al. The diagnosis of dementia due to Alzheimers disease: Recommendations from the national institute on aging-Alzheimers association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimer's & Dementia. 2011;7(3):263–269. doi: 10.1016/j.jalz.2011.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montine TJ, Phelps CH, Beach TG, Bigio EH, Cairns NJ, Dickson DW, Duyckaerts C, Frosch MP, Masliah E, Mirra SS, et al. National institute on aging–alzheimers association guidelines for the neuropathologic assessment of alzheimers disease: a practical approach. Acta neuropathologica. 2012;123(1):1–11. doi: 10.1007/s00401-011-0910-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosconi L, Mistur R, Switalski R, Brys M, Glodzik L, Rich K, Pirraglia E, Tsui W, De Santi S, De Leon M. Declining brain glucose metabolism in normal individuals with a maternal history of alzheimer disease. Neurology. 2009;72(6):513–520. doi: 10.1212/01.wnl.0000333247.51383.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosconi L, Murray J, Tsui WH, Li Y, Spector N, Goldowsky A, Williams S, Osorio R, McHugh P, Glodzik L, et al. Brain imaging of cognitively normal individuals with 2 parents affected by late-onset AD. Neurology. 2014;82(9):752–760. doi: 10.1212/WNL.0000000000000181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okonkwo OC, Xu G, Oh JM, Dowling NM, Carlsson CM, Gallagher CL, Birdsill AC, Palotti M, Wharton W, Hermann BP, et al. Cerebral blood flow is diminished in asymptomatic middle-aged adults with maternal history of alzheimer's disease. Cerebral Cortex. 2012:bhs381. doi: 10.1093/cercor/bhs381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Nievas BG, Stein TD, Tai H-C, Dols-Icardo O, Scotton TC, Barroeta-Espar I, Fernandez-Carballo L, de Munain EL, Perez J, Marquie M, et al. Dissecting phenotypic traits linked to human resilience to alzheimers pathology. Brain. 2013:awt171. doi: 10.1093/brain/awt171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Racine AM, Adluru N, Alexander AL, Christian BT, Okonkwo OC, Oh J, Cleary CA, Birdsill A, Hillmer AT, Murali D, et al. Associations between white matter microstructure and amyloid burden in preclinical Alzheimer's disease: A multimodal imaging investigation. NeuroImage: Clinical. 2014;4:604–614. doi: 10.1016/j.nicl.2014.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruttimann UE, Unser M, Rawlings RR, Rio D, Ramsey NF, Mattay VS, Hommer DW, Frank JA, Weinberger DR. Statistical analysis of functional MRI data in the wavelet domain. Medical Imaging, IEEE Transactions on. 1998;17(2):142–154. doi: 10.1109/42.700727. [DOI] [PubMed] [Google Scholar]
- Ryan NS, Keihaninejad S, Shakespeare TJ, Lehmann M, Crutch SJ, Malone IB, Thornton JS, Mancini L, Hyare H, Yousry T, et al. Magnetic resonance imaging evidence for presymptomatic change in thalamus and caudate in familial alzheimers disease. Brain. 2013;136(5):1399–1414. doi: 10.1093/brain/awt065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sager MA, Hermann B, La Rue A. Middle-aged children of persons with Alzheimers disease: Apoe genotypes and cognitive function in the wisconsin registry for Alzheimers prevention. Journal of geriatric psychiatry and neurology. 2005;18(4):245–249. doi: 10.1177/0891988705281882. [DOI] [PubMed] [Google Scholar]
- Schmitz TW, Johnson SC. Relevance to self: a brief review and framework of neural systems underlying appraisal. Neuroscience & Biobehavioral Reviews. 2007;31(4):585–596. doi: 10.1016/j.neubiorev.2006.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J, Myers N, Yang Q, Feng J, Plant C, Böhm C, Förstl H, Kurz A, Zimmer C, Meng C, et al. Prediction of alzheimer's disease using individual structural connectivity networks. Neurobiology of aging. 2012;33(12):2756–2765. doi: 10.1016/j.neurobiolaging.2012.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheline YI, Raichle ME, Snyder AZ, Morris JC, Head D, Wang S, Mintun MA. Amyloid plaques disrupt resting state default mode network connectivity in cognitively normal elderly. Biological psychiatry. 2010;67(6):584–587. doi: 10.1016/j.biopsych.2009.08.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen D, Ip HH. Discriminative wavelet shape descriptors for recognition of 2-d patterns. Pattern recognition. 1999;32(2):151–166. [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31(4):1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Sorg C, Riedl V, Mühlau M, Calhoun VD, Eichele T, Läer L, Drzezga A, Förstl H, Kurz A, Zimmer C, et al. Selective changes of resting-state networks in individuals at risk for alzheimer's disease. Proceedings of the National Academy of Sciences. 2007;104(47):18760–18765. doi: 10.1073/pnas.0708803104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling RA, LaViolette PS, O'Keefe K, O'Brien J, Rentz DM, Pihlajamaki M, Marshall G, Hyman BT, Selkoe DJ, Hedden T, et al. Amyloid deposition is associated with impaired default network function in older persons without dementia. Neuron. 2009;63(2):178–188. doi: 10.1016/j.neuron.2009.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Menon V, Rubin D, Musen M, Greicius MD. Network analysis of intrinsic functional brain connectivity in alzheimer's disease. PLoS computational biology. 2008;4(6):e1000100. doi: 10.1371/journal.pcbi.1000100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M, Mandl R, Luigjes J, Pol HH. Microstructural organization of the cingulum tract and the level of default mode functional connectivity. The Journal of neuroscience. 2008;28(43):10844–10851. doi: 10.1523/JNEUROSCI.2964-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varentsova A, Zhang S, Arfanakis K. Development of a high angular resolution diffusion imaging human brain template. NeuroImage. 2014;91:177–186. doi: 10.1016/j.neuroimage.2014.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Liang M, Wang L, Tian L, Zhang X, Li K, Jiang T. Altered functional connectivity in early alzheimer's disease: A resting-state fmri study. Human brain mapping. 2007;28(10):967–978. doi: 10.1002/hbm.20324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witkin A. Scale-space filtering: A new approach to multi-scale description. ICASSP. 1984;9:150–153. [Google Scholar]
- Xu G, Mclaren DG, Ries ML, Fitzgerald ME, Bendlin BB, Rowley HA, Sager MA, Atwood C, Asthana S, Johnson SC. The influence of parental history of Alzheimer's disease and apolipoprotein ε4 on the bold signal during recognition memory. Brain. 2009;132(2):383–391. doi: 10.1093/brain/awn254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Avants BB, Yushkevich PA, Woo JH, Wang S, McCluskey LF, Elman LB, Melhem ER, Gee JC. High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences: an example study using amyotrophic lateral sclerosis. Medical Imaging, IEEE Transactions on. 2007a;26(11):1585–1597. doi: 10.1109/TMI.2007.906784. [DOI] [PubMed] [Google Scholar]
- Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor mr images with explicit orientation optimization. Medical image analysis. 2006;10(5):764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]
- Zhang H, Yushkevich PA, Rueckert D, Gee JC. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2007. Springer; 2007b. Unbiased white matter atlas construction using diffusion tensor images. pp. 211–218. [DOI] [PubMed] [Google Scholar]