Transition state theory for enzyme kinetics

Abstract

This article is an essay that discusses the concepts underlying the application of modern transition state theory to reactions in enzymes. Issues covered include the potential of mean force, the quantization of vibrations, the free energy of activation, and transmission coefficients to account for nonequilibrium effect, recrossing, and tunneling.

1. Introduction

Enzyme catalysis occurs by a variety of mechanisms,¹ and enzyme kineticists use a variety of levels of theory to calculate reaction rates catalyzed by enzymes. Most of these methods, in one way or another, attempt to calculate the free energy of activation, a quantity whose meaning is defined by transition state theory. Attempts to go beyond transition state theory are often cast in terms of a transmission coefficient, which corrects for the breakdown of the assumption of a separable, classical reaction coordinate in transition state theory without a transmission coefficient. Thus a transmission coefficient in principle corrects for the breakdown of the fundamental reaction-coordinate-separability assumption of transition state theory,² but in practice it also incorporates quantum mechanics into the treatment of the reaction coordinate.³ Since there is universal agreement that the correct description of atomic motions is quantum mechanical rather than classical mechanical, the quantum mechanical aspect of transmission coefficient is considered as an intrinsic part of the theory, not as a correction for breakdown of the theory. The transmission coefficient is an intrinsic part of the theory in an even greater sense though because the factorization of a transmission coefficient out of the total rate expression is not unique; it depends on the way that the transition state dividing surface is defined. The present essay will try to make these issues and other aspects of modern transition state theory clearer, with an explicit focus on enzyme kinetics.

It is becoming increasingly possible to use simulations in which the motion of the substrate, enzyme, cofactors, if any, and an appreciable portion of the solvent are all represented explicitly. One can use transition state theory to extract rate constant predictions from such simulations, but this often requires going beyond textbook transition state theory and including new elements in the simulations. The present article is an essay that discusses the issues that arise in extending transition state theory to enzyme reactions.

Transition state theory was originally developed in the context of gas-phase reactions, but it was extended to condensed reactions shortly thereafter. The original formulation for condensed-phase reactions was in terms of quasithermodynamic concepts, in particular quasiequilibrium between the transition state and the reactants. I use the term quasiequilibrium for two reasons: (i) the transition state needs to be in equilibrium with the reactants, but the products states may be unpopulated; (ii) the transition state is missing one degree of freedom. For example, Evans and Polanyi⁴ defined the transition state as “an infinitesimally thin layer of phase space” extending to infinity in all directions except the reaction coordinate. Thus a transition state is a mathematical entity that is like a real molecule but is missing one degree of freedom, namely the reaction coordinate. In mathematical language, we would define the transition state with a delta function for the reaction coordinate. Real equilibrium constants are one-to-one functions of free energies of reaction, and the temperature dependence of the equilibrium constant can be used to separate the free energy into an enthalpy of reaction and a term involving the entropy of reaction. Since the transition state theory rate is proportional to a the quasiequilibrium constant between the transition state (sometimes called the activated complex), the transition state rate is interpreted in terms of a generalization of the concept of free energy of reaction, namely the free energy of activation, which is the difference in free energy between the mathematically defined transition state and the reactants, and the temperature dependence allows us to separate this into an enthalpy of activation and an term involving the entropy of activation. These functions are quasithermodynamic because they refer to a transition state rather than a real chemical species. This conceptual framework will be used in deriving transition state theory below.

An important distinction in discussing transition state theory is the difference between a potential energy surface (also called a potential energy function) and a free energy surface (also called a potential of mean force). In applying transition state theory to gas-phase reactions, the basic input (energies, vibrational frequencies, …) may be obtained from the Born-Oppenheimer potential energy surface, which is the electronic energy (including nuclear repulsion) of the ground electronic state as a function of nuclear coordinates. Potential energy surfaces for general gas-phase molecules with N atoms are functions of 3N - 6 coordinates, where 3N is the number of atomic Cartesian coordinates, and we subtract 6 because the electronic energy does not depend on translating the overall center of mass or rotating the whole system in space. Reactants and products are associated with local minima on the potential energy surface, and transition states were identified with saddle points on the potential energy surface. A saddle point is a local minimum of the potential energy surface in 3N - 7 degrees of freedom, where now we have omitted the reaction coordinate; but it corresponds to a local maximum along the reaction coordinate. Notation: A saddle point is often called a transition structure. Calculating a rate constant by transition state theory involves calculating certain free energy quantities from the potential energy surfaces, as discussed below.

Potential energy surfaces also underlie the theory for condensed phase systems, but N is a very large number for a liquid, and it may be tens of thousands or more for realistic models of liquid-phase enzymes, but the use of free energy quantities that depend on a smaller number of degrees of freedom (for example, the number of degrees of freedom of a solute or an active site) allows one manage the complexity. For this reason, free energy surfaces are more useful for condensed-phase reactions than for gas-phase ones – both for conceptual purposes and for calculations, and yet they are often not explained well in textbooks (and sometimes not even mentioned).

Extending conventional transition state theory to reactants in a condensed phase, for example in water, in the aqueous medium of a cell, or in an enzyme which itself is in a liquid-phase medium, is not as straightforward as many textbook treatments would lead one to believe. To see this, consider a solute with n atoms. Because it is surrounded by solvent, its electronic energy is not well defined; that is, there are questions about how to partition the solute–solvent interaction energy into energy of the solute and energy of the solvent. But suppose we come up with a scheme for that. We then find that the energy is not invariant to translation or rotation of the solute if the solvent is fixed at some instantaneous configuration. The free translations and free rotations have been converted to low-energy librations by interactions with solvent. We could try to ameliorate the problem by considering a “supersolute,” by which I mean a system consisting of the solute plus many nearby solvent molecules. Now we run into another problem. The solvent, being a liquid, has many local minima of nearly the same energy. Consider water. We could have many possible networks of hydrogen bonds, and rotation of a few water molecules from one hydrogen-bonding arrangement to another gives us another local minimum. Following Stillinger, one may call these local minima of the potential energy function "inherent structures." Stillinger proved that the number of distinguishable inherent structures of a liquid rises exponentially as a function of the number of molecules in the systems.⁵

For gas-phase systems, we can proceed theoretically by finding all the low-energy minima and low energy-saddle points.^6,7 We can then carry out a complete analysis of the nuclear motion and configurations by classical mechanics (for example, vibrations might be treated by the classical mechanical harmonic oscillator approximation) or, if the system is not too large, by quantum mechanics (for example, vibrations might be treated by the quantum mechanical harmonic oscillator approximation). Clearly that is impossible for a liquid or an enzyme in solution, where it is not practical to even think about all the structures, and we are forced to use statistical mechanical sampling rather than full enumeration of structures. Using statistical mechanics, we can make firm statements even without finding all the inherent structures. The present article will attempt to explain how we do this, using the least possible amount of mathematics, although the actual calculations involve a lot of mathematics.

In Section 2 we explain transition state theory in a classical mechanical world. By this we mean a world where nuclear motion follows the law of classical mechanics; as explained above, the potential energy surface that governs nuclear motion represents the electronic energy, and the electronic structure of atoms and molecules must always come from a quantum mechanical treatment (even though it might be represented by a molecular mechanics function that looks classical). The variational principle of variational transition state theory is rooted in classical mechanics and it is also explained in Section 2.

Classical mechanics describes many aspects of nuclear motion quite well, but for quantitative work one cannot neglect the quantum mechanical nature of nuclear motion, especially zero point energy and tunneling. Thus, in sections 3 and 4, we explain how quantum effects are included in transition state theory.

2. Transition state theory in a classical world

2.1. Basic concepts

To provide guidance for the statistical mechanical formulation of transition state theory for condensed-phase process, we return to gas-phase systems and reconsider the meaning of the quasithermodynamic functions. In pioneering work cited above, Polanyi, Evans, and Eyring arrived at the quasithermodynamic and statistical mechanical formulation of transition state theory by considering quasiequilibrium between reactants and transition states. Since, as already pointed out, transition states are not real species, this involved a somewhat intuitive generalization of the concept of equilibrium, which they combined with one-dimensional classical models for the reactive motion (motion along the reaction coordinate) that takes a system from one side of the transition state to the other. Although these derivations gave the correct result, there were not completely satisfactory, and even as late as the 1970s, people were arguing about factors of two in the derivation.⁸

A more solid foundation for transition state theory was provided by the work of Wigner. Before summarizing Wigner's results, I briefly explain the language to be used. Phase space is the 6N-dimensional space consisting of the 3N-dimensional coordinate space and the 3N-dimensional space of conjugate momenta. Points in phase space are called phase points; they are the “states” of a classical system. A region of phase space is said to be in local equilibrium if the relative population of states in that region satisfies a Boltzmann distribution. Note that since most phase points have nonzero momentum they are constantly moving from one position in phase space to another (from one state to another); the motion of a phase point in phase space is called a trajectory.

One more note on language: most chemical physicists use the words “surface” and "hypersurface" interchangeably; thus a surface is a geometrical structure with less degrees of freedom than the full space. A plane or the surface of a sphere is a two-dimensional surface in a three-dimensional space; a line (straight or curved) is a one-dimensional surface in a plane. We will discuss transition states as surfaces in this sense of the word, although a mathematician might prefer the word “hypersurface.” The word “surface” is also used as a synonym for “function;” this is the sense of the word that is used when we discuss potential energy surfaces and free energy surfaces.

Wigner's treatment of transition state theory (reviewed elsewhere⁹) leads to the following procedure for deriving transition state theory: (i) Assume all phase points are populated according to a Boltzmann distribution. (ii) Define a (6N - 1)-dimensional surface (to be called the dividing surface) that separates reactant regions of phase space from product regions. If reactants and products are well defined there will be a relatively sparsely populated region of phase space between them; the dividing surface should be in this region. Furthermore, since we usually define this surface to be independent of the 3N momentum components and the 6 overall translations and rotations, it has only (3N - 7) degrees of freedom. (iii) Calculate the one-way flux of phase points across the dividing surface. Note the net flux will be zero because the system is assumed to be at equilibrium, but the one-way flux is not zero. Because we are doing this calculation in a classical world, the one-way flux counts all trajectories passing through the transition state in the direction of products. In a classical world, systems with an energy below the lowest energy in the dividing surface cannot reach the transition state; if the dividing surface passes through the saddle point, the saddle point will be the lowest-energy point in the transition state. The difference between the saddle point energy and the equilibrium energy of reactants is called the classical barrier height.

When one calculates the one-way flux in step (iii), one finds that the one-way flux equals k_BT/h times exp(−ΔG_C,act/k_BT), where k_B is Boltzmann's constant, T is temperature, h is Planck's constant, and ΔG_C,act is a quantity that is exactly the same as one would get if one calculated the free energy of the dividing surface minus the free energy or reactants. The subscript C reminds us that we are in a classical world in this section. Because, as just mentioned and as introduced in the introduction, ΔG_C,act is a generalization of the free energy (because the dividing surface has one less degree of freedom than a thermodynamic species), it is reasonable to label it as some sort of free energy. It is not a real free energy because the dividing surface is not a real species (it is missing one degree of freedom, namely the reaction coordinate which is normal to the dividing surface), so it is called the free energy of activation.

For real thermodynamic functions, knowing the free energy is equivalent to knowing the system’s partition function, and therefore all other thermodynamic variables (e.g., enthalpy and entropy) can be calculated from the free energy as a function of the independent variables like temperature, pressure, and number of each kind of particles. These same relations are applied to the free energy of activation, and the resulting functions are called activation parameters (e.g., enthalpy of activation, entropy of activation, volume of activation, etc.); these activation parameters are also quasithermodynamic functions.

There are a few aspects of this derivation that deserve attention. First is that it is a purely classical derivation and yet the result involves h. This would never happen in real thermodynamics; it happens here because translating the partition function for the missing degree of freedom from quantum mechanics to classical mechanics involves h.

The second issue about the above derivation that deserves attention is: what does the one-way flux at equilibrium have to do with the usual rate constants of chemical kinetics? Here is where the physics comes into the mathematical derivation. First we posit a situation where the reactant region of phase space is populated at local thermal equilibrium, but there is no population of the products. Then we assume that any trajectory that crosses the dividing surface never crosses it again; this is the fundamental assumption of transition state theory. Under these assumptions, the one-way flux through the dividing surface toward products is the same as the one-way flux in the same direction for the original case where both reactants and product regions of phase space at equilibrium. Furthermore, under these assumptions, and if we equate one-way fluxes in phase space to one-way fluxes computed from rate constants, the rate constants are just equal to one-way fluxes divided by the reactant concentrations, or – stated another way – to the one-way fluxes when the concentrations are all unity. Therefore we have calculated the rate constants under the assumptions that reactants are in local equilibrium and trajectories do not recross the dividing surface. The expression we obtain, for a standard state of 1 mol/L is

$$k_{\mathrm{C}}={(\mathrm{L}/\text{mol})}^{m-1}(k_{\mathrm{B}}T/h)\text{exp}(-\mathrm{\Delta }{G}_{\mathrm{C},\text{act}}^{°}/N_A{k}_{\mathrm{B}}T)$$ (1)

where k_C is the rate constant in a classical world (as the subscript reminds us), m is the molecularity (1 for unimolecular reactions, 2 for bimolecular reactions), N_A is Avogadro’s number (included simply so that the free energy is in molar units), and now we have added the standard-state superscript to the free energy of activation because we got this result by assuming unit concentrations. (In the gas phase one usually wants to quote thermodynamic functions for a standard state of 1 bar rather than 1 mol/L; the conversion of standard states from 1 molar to 1 bar is just same as in real thermodynamics and involves straightforward formulas given elsewhere.¹⁰)

A note on “never crosses it again”: When I said that a trajectory does not recross the transition state I meant by molecular motions as part of single uninterrupted event. After moving to the product region, the product must eventually be thermalized, e.g., by nonreactive collisions with other molecules (including jostling with solvent, if present). After that, a given product molecule might indeed be activated again some time later and undergo reverse reaction, but that is a separate event that does not violate the no-recrossing assumption.

There are many subtle aspects of this derivation that could be discussed, but I will limit myself to one, namely the relation of rate constants to one-way flux coefficients. Naively it seems reasonable, when one has the reaction A − B and the rate equation

$$\text{Rate}=-d[\mathrm{A}]/dt=k_1[\mathrm{A}]-k_{-1}[\mathrm{B}]$$ (2)

to assume that the first term equals the one-way equilibrium flux from reactants to products, and the second term equals the reverse equilibrium flux. But this is not quite right.^11,12 In order to measure a rate constant that is independent of time, i.e., independent of the concentrations (that is why they are called rate constants), the system must have reached a steady state. At that point, for a noninfinitesimal rate, local equilibrium is perturbed, and k₁ and k₋₁ are not equal to equilibrium one-way fluxes. The rate constant calculated from the one-way flux at equilibrium is called the local-equilibrium rate constant. The deviation of the observable steady-state rate constant form the nonobservable local-equilibrium rate constant is a nonequilibrium effect, i.e., all the states (these would be phase points in a classical mechanical world) of A are not in local equilibrium with one another. Therefore there are two sources of possible error in transition state theory in a classical mechanical world: nonequilibrium effects and recrossing. Interestingly, nonequilibrium is unavoidable under circumstances where rates are measured (because the net rate is finite), but usually small in the condensed phase (or at least assumed to be so), whereas recrossing is avoidable but can be large if the transition state is not well optimized.

Nonequilibrium is unavoidable by definition when there is a noninfinitesimal net rate (rate constants can only be measured in a state of overall nonequilibrium – otherwise the net rate is zero). There are cases where nonequilibrium effects are very large, e.g., unimolecular and association reactions in the gas phase at low pressure and sometimes at moderate pressure;¹³ in fact the high-pressure limit is often unattainable for given experimental setup. But for bimolecular reactions in the gas-phase and for reactions in solution, nonequilibrium effects are usually assumed to be small. The kind of nonequilibrium effects being discussed here should not be confused with an effect confusingly called nonequilibrium solvation; they are not at all the same. Nonequilibrium solvation is discussed carefully elsewhere,^14,15 and it is discussed briefly below (it is really a breakdown of the no-recrossing assumption, not a breakdown of the local-equilibrium assumption).

Why is recrossing avoidable? That is the subject of the next section.

2.2. Variational transition state theory

Recrossing is avoidable in the following sense: In a classical mechanical world, there always exists a hypersurface in phase space that is not recrossed (note that if one restricts one’s search to dividing surfaces in coordinate space, existence is no longer guaranteed, as discussed recently¹⁶). However, for real-world applications it is too convoluted to find and use the exact dividing surface in phase space, and in fact we would have to abandon our convenient customary operating procedures of defining the transition state to depend only on internal coordinates (or, sometimes for gas-phase reactions, only on internal coordinates and the total energy), i.e., the dividing surface would have to depend on individual atomic momentum components. So as a practical matter, the dividing surface we define for practical work will be one that is recrossed. How do we minimize the recrossing? We use a variational principle that arises as follows: recrossing clearly lowers the net flux. Therefore, if we assume that nonequilibrium effects are negligible, then assuming no recrossing (which is the most basic assumption of transition state theory, as discussed above and also further below) always overestimates the rate. This leads to the variational principle: we should choose the dividing surface to minimize the calculated rate constant. Equation (1) shows that we may restate this as: we should choose the dividing surface to maximize the calculated standard-state free energy of activation. This is called variational transition state theory.¹⁷ A fixed-temperature system is sometimes called a canonical ensemble; as a consequence this is also called canonical variational theory or CVT. Note that the general prescription is to optimize the whole dividing surface, not just the value of a reaction coordinate. In practice, though, as discussed below, full optimization is not carried out and not required for a good approximation.

There is one point where Wigner's paper can easily be misinterpreted. When Wigner says that we have an upper bound on the rate constant, and when he says that choosing a complicated dividing surface to make the recrossing vanish will yield the exact rate constant, we must interpret this as an upper bound to the local-equilibrium rate constant and as yielding the exact local-equilibrium rate constant. Wigner did not mention that the local-equilibrium rate constant is different from the measurable steady-state rate constant, but – as mentioned above – they are often very similar, and, provided intermediates are treated as separate species, there is no evidence to suggest that nonequilibrium effects are important for enzyme-catalyzed reactions.

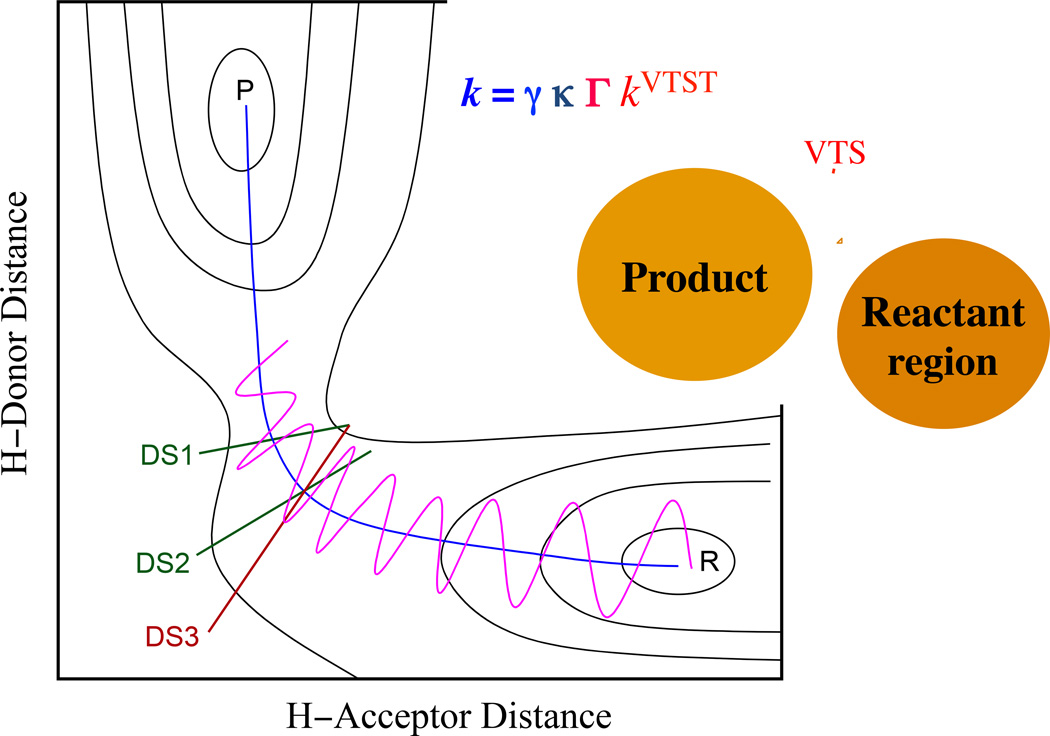
How do we find the dividing surface with the maximum free energy of activation? Before answering this we need a conceptual prologue. Consider a gas-phase molecule with n atoms. It has a potential energy function V(R), where R denotes the collection of all its 3n atomic Cartesian coordinates. (The fact the potential energy can also be written as function of only 3n − 6 coordinates, if one uses internal coordinates, is irrelevant here.) At any position R, the force on the nuclei is the negative gradient of the potential, i.e., −ΔV. Now consider a solute with n atoms that is equilibrated with a solvent at temperature T. The force on the atoms of the solute now depends on the instantaneous configuration of the solvent. We ask: is there a function W of R such that the mean force (where “mean” denotes an average over the finite-temperature ensemble) on the solute is −ΔW? The answer is yes, and this is called the potential of mean force (PMF). It is a function of 3n coordinates in the much larger coordinate space of solute plus solvent. Suppose that there are M atoms in the solvent; then the phase space has dimension 6N = 6n + 6M. One obtains the PMF by averaging an appropriate function over 6M solvent coordinates and momenta and 3n solute momenta. Actually one could average over other subsets of the dimensions. An important special case is to average over all the momenta and all but k of the coordinates; this produces what is called a PMF in k dimensions (where k is the number of coordinates not averaged over). We then think of these k degrees of freedom as being in a bath of the rest of the degrees of freedom (physicists sometimes describe this by saying these coordinates are “dressed” by a bath). The importance of the PMF in theoretical work was singled out in a recent perspective article.¹⁸ If one carries out the same average over all coordinates (k = 0) one obtains the system free energy, which is just a number (0-dimensional) for a give T, pressure or volume, and system composition. With this as a motivation, the PMF for k ≥ 2 is sometimes called a free energy surface¹⁹ (or free energy function), and a PMF with k = 1 is sometimes called a free energy profile. Free energy profiles are special cases of free energy surfaces. One can think of free energy surfaces as finite-temperature generalizations of potential energy surfaces, to which they reduce (in a classical mechanical world) as T → 0. They also reduce to potential energy surfaces as one strips away the solvent.

Early thinking on this subject of finding the transition state with maximum free energy was quite confused. There was discussion of finding a free energy surface (i.e., a free energy function of the coordinates– see above), but it was not clear how to do this. The first practical and general approach was based on free energy profiles in the gas phase.²⁰ Since the transition state is missing one degree of freedom (the reaction coordinate, which we usually define in coordinate space), a natural way to proceed is as follows. First define a path that leads from reactants to products in coordinate space (this will also lead from the reactants region of phase space to the products region of phase space); call this the reaction path. If there is a saddle point, the reaction path should ordinarily pass through the saddle point. Define a progress coordinate as the signed distance along this path from some reference point, e.g., from the saddle point. Then calculate a free energy profile along this path, where the unaveraged degree of freedom is locally the reaction coordinate, where the reaction coordinate is a coordinate normal to the dividing surface. The free energy of activation as a function of the progress variable is often a free energy profile, although a more technically correct name would be a generalized free energy of activation profile. The variational transition state is a surface that intersects the reaction path, is usually locally orthogonal to it, and has the minimum free energy of activation. The minimum here refers to a minimum from among all possible intersection points of the trial dividing surface with the reaction path. Since the reaction path is one-dimensional, finding the variational transition state reduces to a one-dimensional search, which is quite practical. Notes: (1) If the dividing surface intersects the reaction path orthogonal to it, then the reaction coordinate and the progress variable are locally the same, but not necessarily globally the same. (2) The progress variable is usually called the reaction coordinate, even though the above discussion shows that they are not quite the same thing. However, this usually causes no confusion.

The choice of reaction path and surface orthogonal to it usually based on making it practical and convenient to calculate the generalized free energy of activation. For example, the reaction path was originally taken as the path of steepest descent in isoinertial coordinates (i.e., coordinates scaled²¹ so they all have the same reduced mass) with the dividing surface orthogonal to it where they intersect. This makes the calculation of the free energy profile as straightforward as possible, and the gratifying empirical result is that this way of defining dividing surfaces does eliminate most of the recrossing. In advanced algorithms one sometimes uses other paths and/or one sometimes optimizes not just the location where the dividing surface intersects the reaction path but also the angle at which it intersects.

Note that optimizing the dividing surface is the same as optimizing the reaction coordinate since the reaction coordinate is the coordinate normal to the dividing surface.

The simplest generalization to liquid-phase reactions, including enzyme reactions, is as follows. First define a reaction coordinate; this can be very general, but a common choice in our work has been the internuclear distance of the bond being broken minus the internuclear distance of the bond being formed.²² This can be called a geometrical reaction coordinate; it increases as the reaction proceeds. One can then use any convenient algorithm to calculate the one-dimensional PMF along this coordinate; our own preferred method has been the WHAM method,²³ where WHAM stands for weighted histogram analysis method. (Other methods for calculating free energies are reviewed elsewhere.^24,25) The maximum of this profile gives us the classical variational free energy of activation, $\mathrm{\Delta }{G}_{\mathrm{C},\text{act}}^{\mathrm{C}\mathrm{V}\mathrm{T},°}$, and the rate constant is given by equation (2). However, this is the just the classical rate constant with no transmission coefficient, so we are not done.

We need to incorporate quantum effects and a transmission coefficient. These are discussed in Sections 3 and 4.

First though we comment on improving the reaction coordinate. One way to improve the reaction coordinate is to calculate a 2-D free energy surface (k = 2 in the notation above).^26,27 Rather than identify the dividing surface as orthogonal to a pre-chosen progress coordinate, one can then take it as normal to the steepest decent path from a saddle point in the 2-D function. Similarly the reaction coordinate is taken as the steepest-descent path at this saddle point.

More generally the reaction coordinate could involve the solvent or collective degrees of freedom of protein. For example, Hammes-Schiffer and coworkers use an energy gap coordinate defined as the difference in energy of a valence bond state representing the reactant one representing the product.²⁸ The use of this kind of coordinate has been compared to the use a geometrical reaction coordinate,²⁹ and it was concluded that the computed free energies of activation are expected to be similar from calculations employing the geometrical and energy-gap reaction coordinates.

Next we consider the case where one calculates a free energy surface as a function of two coordinates, with the first coordinate – call it x –being a geometrical coordinate based on solute bond lengths for a reaction in liquid-phase solution or based on substrate bond lengths for an enzyme-catalyzed reaction, and the second coordinate – call it y – being a solvent coordinate for a liquid phase or a protein or coenzyme relaxation coordinate for an enzyme-catalyzed reaction. Suppose that one finds a saddle point with an imaginary-frequency normal mode – call it z – that is not parallel to the x-axis. The classical motion is locally separable in normal mode coordinates so one expects no or little recrossing if the reaction coordinate is set equal to z. But if one takes the reaction coordinate to be x, there will be recrossing.³⁰ This is the effect that is called nonequilibrium solvation. It leads to a transmission coefficient less than unity for reactions in solution (in enzymes) when the reaction coordinate is assumed to be independent of solvent coordinates (protein or coenzyme coordinates). From another perspective this identical effect shows up as “solvent friction,” as in Grote-Hynes theory.³¹

When we want to stress the difference between placing the transition state in the original way of Eyring at a saddle point versus optimizing it, we use the following language: a conventional transition state is one that passes through a saddle pointed and is oriented perpendicular to the imaginary-frequency normal mode of that saddle point, and any other transition state is a generalized transition state. A generalized transition state that is optimized variationally is called a variational transition state. This kind of distinction has been useful for reactions in the gas phase. For reactions of complex molecules in the gas-phase, there are usually many transition states and a proper treatment involves a multi-faceted dividing surface that passes through them all.^6,7 If it passes through all the saddle points oriented normally to their imaginary-frequency normal modes, such a treatment is called multi-structural conventional transition state theory or multi-path conventional transition state theory (where the difference is in how the transmission coefficient is calculated). If the multi-faceted transition state is optimized, such a treatment is called multi-structural variational transition state theory or multi-path variational transition state theory (where the difference again is in how the transmission coefficient is calculated). However, as we already explained, for reactions in liquid-phase solutions or in liquid-phase enzymes, it is essentially impossible to find all the saddle points, and we use statistical methods to find the maximum of a free energy profile as a function of a pre-selected progress coordinate. In such a case conventional transition state theory is useless, and we are using only variational transition state theory. In many cases we just say “transition state theory” to refer to any or all of these kinds of treatment.

Finally, I want to comment on the fundamental assumption of transition state theory. As stated above, in conjunction with Wigner's derivation, the fundamental assumption is that no recrossing of the transition state occurs. Suppose that the reaction coordinate were globally separable. Then motion in the reaction coordinate would be uncoupled to other degrees of freedom, and the position of highest potential energy along the reaction coordinate would be independent of the values of the other coordinates. Defining the transition state at that value of the reaction coordinate would then eliminate recrossing. Thus, instead of saying that the fundamental assumption is no recrossing, one could say that the fundamental assumption is that the reaction coordinate is separable. Similarly, instead of saying that the transmission coefficient corrects for recrossing, one could say that it corrects for nonseparability. However, it is probably more constructive to think about it in terms of recrossing because even when the reaction coordinate is nonseparable, the assumption of no recrossing can be a good approximation, and it is the extent of recrossing that controls the error in transition state theory.

3. Quantum mechanical nuclear motion

Up to this point everything has been classical. We pointed out above that in a classical world, the zero-temperature limit of a free energy surface is the potential energy surface. Aside from considerations of degeneracy and symmetry, the zero-temperature limit in quantum mechanics is the sum of the potential energy plus the zero-point vibrational energy. Therefore we need to put in the effects of the quantization of bound vibrational modes, especially their zero point energy. We also need to correct for the fact that the reaction coordinate motion (which is locally an unbound vibration at the transition state) has been treated classically.

Before we proceed with practical matters, it is worthwhile to stop and address the following question: Is it really correct to quantize the vibrational energies when we stop to consider that the transition state is not stationary state. The answer is yes, but with broadening. The transition state is actually a metastable state. For example, in one dimension, a particle at the top of a parabolic barrier is metastable, as is a classical particle at a multidimensional saddle point of the potential energy surface. The quantum mechanical analogs of classical metastable states are called resonances^32,33 (one of the many uses of this overworked noun). The transition state analogs of quantized energy levels of equilibrium structures of molecules are resonance energy levels.^34,35 Resonances have complex energies; the real part of the energy is the analog of the quantized energy of a bound state. The imaginary part is written as ½Γ, where Γis called the width; it is associated with the lifetime by the Heisenberg uncertainty principle in time and energy. In particular, a large width corresponds to a broad resonance, which is associated with a short-lived resonance. A typical transition state resonance lifetime of a gas-phase atom-diatom reaction is ~30 fs, corresponding to a width of ~0.04 eV.³⁶ To a reasonable approximation, the real parts of transition state energy levels may be calculated by ignoring the unbound degree of freedom corresponding to the reaction coordinate.

How do we put in the effect of quantized vibrations for a condensed phase system? That is straightforward for gas-phase reactions because we calculate the free energy of activation from molecular partition functions, and so we simply replace the classical mechanical partition functions by quantum mechanical ones, while ignoring the unbound reaction coordinate at the transition state. For liquid-phase reactions and reactions in enzymes, we calculate the free energy of activation profile by liquid-phase simulation methods, which are typically based on classical molecular dynamics. There is no fully satisfactory way to add quantized vibrational modes to such calculations for general purposes, but for calculating a free energy profile, a scheme has been developed³⁷ and it seems to be satisfactory since it has yielded accurate kinetic isotope effects for several reactions,^38,39,40 and kinetic isotope effects are very sensitive to quantized vibrational energies.

After quantizing the vibrations, the maximum of the free energy profile is shifted. Placing the transition state at the maximum of the free energy profile without quantizing the vibrations yielded a result we called classical variational transition state theory or classical CVT. Placing the transition state dividing surface at the maximum of the quantized free energy profile is called quasiclassical ensemble-averaged variational transition state theory (QC-EA-VTST). It may be written:

$$k^{\mathrm{Q}\mathrm{C}-\mathrm{E}\mathrm{A}-\mathrm{V}\mathrm{T}\mathrm{S}\mathrm{T}}={(\mathrm{L}/\text{mol})}^{m-1}(k_{\mathrm{B}}T/h)\text{exp}(-\mathrm{\Delta }{G}^{\mathrm{Q}\mathrm{C}-\mathrm{E}\mathrm{A}-\mathrm{V}\mathrm{T}\mathrm{S}\mathrm{T},°}/RT)$$ (3)

where R is the gas constant, and ΔG^EA-VTST,° is the quasiclassical free energy of activation according to EA-VTST. The reason that EA is included in the name of this method is that for the free energy of activation is computed from a free energy simulation and is therefore ensemble averaged. The reason for the “quasi" here is that one important aspect of the treatment is still classical, even though the vibrations are now quantum mechanical. The missing aspect is the collection of quantum mechanical effects on the reaction coordinate at the transition state because the reaction coordinate is missing in the transition state and so it did not get quantized when we quantized the vibrations of the transition state. (The reaction coordinate did get quantized at reactants if it corresponds to a locally bound vibration there, as it does for unimolecular reactions.) Quantal effects on the reaction coordinate at the transition state are included in a transmission coefficient, as discussed in the next section.

4. Transmission coefficient

Adding tunneling to a gas-phase calculation involves replacing the classical reaction coordinate motion by a quantum mechanical motion. Classical reaction coordinate motion in classical transition state theory corresponds to zero probability of reaction at energies below the saddle point and a probability of reaction of one at higher energies. Classical reaction coordinate motion in quasiclassical transition state theory corresponds to zero probability of reaction at energies below the quantized transition state energy level and a probability of reaction of one at higher energies.

When one incorporates quantum effects on reaction coordinate motion, the transmission probability becomes nonzero below the barrier height and non-unity above it. The former is tunneling, and the latter is nonclassical reflection. Because the Boltzmann factors are larger at energies below the quasiclassical threshold than at energies above it, the tunneling effect is much large than the nonclassical effect. Therefore the factor in the transmission coefficient that accounts for quantum mechanical effects on the reaction-coordinate motion is usually called the tunneling transmission coefficient.

To calculate a quantum mechanical probability of reaction, we need to know more than the energy value at the transition state; rather we need a whole an effective potential energy along the whole reaction coordinate, and the tunneling the tunneling probability is greater if the effective barrier of this effective potential is thinner or if the reduced mass along the reaction coordinate is smaller. The effective potential should be consistent with transition state theory such that if we approximate the quantum probability of transmission through the barrier by the classical one (which is zero at energies below the maximum of the effective potential and one at higher energies), the transmission coefficient reduces to unity. The barrier that is consistent with transition state theory in this sense is obtained by adding the local quantized vibrational energy to the potential energy along the reaction path through the transition state.⁴¹

We typically make the ”ground-state approximation” which means that we define the tunneling transmission coefficient as the ratio of the thermally averaged quantum mechanical transmission probability for the ground-state effective potential to the thermally averaged classical mechanical transmission probability for the ground-state effective potential. The ground-state effective potential corresponds to adding the local zero-point vibrational energy to the potential energy. Calculating the transmission coefficient this way is called the zero-curvature tunneling approximation because the tunneling probability through the barrier is calculated as if the reaction coordinate were a single Cartesian coordinate. Notice that the zero-curvature tunneling approximation considers the changing vibrational energy in degrees of freedom transverse to the reaction path as well the motion parallel to the reaction path. For this reason we call it a multidimensional approximation.

The zero-curvature tunneling approximation is usually not very accurate. Actual dominant reaction paths and tunneling paths are not straight lines in Cartesian coordinates – just as internal coordinates like bond stretches and valence angle bends are nonlinear functions of atomic Cartesian coordinates. The dominant physical feature that they incorporate is corner cutting, i.e. the tendency for the optimal tunneling path to be shorter than the minimum-energy path. In the limit of large curvature of the reaction path, the optimum tunneling paths are straight lines⁴² (a straight line is the shortest distance between the two sides of the multidimensional effective potential barrier). Accurate multidimensional semiclassical methods for taking account of the curvature of the reaction coordinate have been developed, in particular the small-curvature tunneling (SCT) approximation,⁴³ the large-curvature tunneling (LCT) approximation,⁴⁴ the optimized multidimensional tunneling approximation,⁴⁵ and the least-action tunneling approximation.^46,47 These methods are reviewed elsewhere.^48,49

Notation: the word “semiclassical” here, as in most chemical physics literature, means that the tunneling is calculated by multidimensional generalizations⁵⁰ of the Wentzel-Kramers-Brillouin (WKB) method; in the kinetic isotope literature the word “semiclassical” is used for what I have called “quasiclassical”.

Adding tunneling to EA-VTST requires some extra considerations, because we have a free energy barrier, but tunneling occurs through potential energy barriers. One way to think about the problem is that we should thermally average the tunneling through the various potential barriers, not calculate the tunneling through a thermally averaged free energy barrier. However, one can justify using the free energy barrier for tunneling by an approximation called the zero-order canonical mean shape approximation.⁵¹

For a gas-phase case where one finds all the transition structures, there is a reaction path through each of them, and each reaction path has its own effective potential (in SCT) or effective potentials (in LCT, OMT, and LAT), and taking account of these yields multipath variational transition state theory.^6,7 In EA-VTST, though, we sample reaction paths^38,52 rather than consider them all, which would be impossible.

Now we write the final rate constant as

$$k=\gamma k^{\mathrm{E}\mathrm{A}-\mathrm{V}\mathrm{T}\mathrm{S}\mathrm{T}}$$ (4)

where k^EA-VTST is the quasiclassical rate constant of section 3, and

$$\mathrm{\gamma }=g\mathrm{\Gamma }\mathrm{\kappa }$$ (5)

and where g corrects for nonequilibrium effects, Γ corrects for recrossing, and κ is the tunneling transmission coefficient. (Notation: this Γ should not be confused with the Γ in section 3, but we want to use notation consistent with the rest of the literature, and Γ is used for both of these quantities.)

Nonequilibrium effects have already been discussed (we neglect them, i.e., we take g = 1).

If the reaction coordinate is sufficiently optimized, the recrossing can in principle be made small, but in practice the recrossing transmission coefficient is sometimes close to unity and sometimes significantly less.^{53,54,55,56,57,58,59,60,61,62,63,64}

Experimental kineticists often express experimental rate constants as

$$k={(\mathrm{L}/\text{mol})}^{m-1}(k_{\mathrm{B}}T/h)\text{exp}(-\mathrm{\Delta }{G}^{‡,°}/RT)$$ (6)

We can label the free energy in eq. (6) as the phenomenological free energy of activation. Comparing eq. (5) to eqs. (3) and (4) yields

$$\mathrm{\Delta }{G}^{‡,°}=\mathrm{\Delta }{G}^{\mathrm{Q}\mathrm{C}-\mathrm{E}\mathrm{A}-\mathrm{V}\mathrm{T}\mathrm{S}\mathrm{T},°}-RT\text{ln}g-RT\text{ln}\mathrm{\Gamma }-RT\text{ln}\mathrm{\kappa }$$ (7)

This is a convenient framework for interpreting experimental data, but it is not unique. If one had treated the dynamics quantum mechanically instead of semiclassically, one would not have been able to separate the contributions to the reactive flux into an overbarrier part and a tunneling part or into a variational transition state flux and a recrossing transmission coefficient.

Applications

Applications have been reviewed elsewhere, and hence we will simply refer to those reviews^{38,65,66,67,68,69,70,71}

Concluding remarks

In this article I have discussed some of the conceptual issues that underlie modern transition state theory as applied to condensed-phase reactions, using enzyme-catalyzed reactions as the example. Based on these kinds of ideas, ensemble-averaged variational transition state theory with multidimensional tunneling contributions has proved to be a powerful method for calculating rate constants for enzyme-catalyzed reactions. The leading errors are usually due more to the uncertainties in the potential energy functions than in the treatment of the dynamics per se.

Highlights.

• I discuss the foundations of transition state theory.

• The use of free energy surfaces is explained.

• I emphasize ensemble-averaged variational transition state theory for enzyme kinetics.

• Quantum effects – tunneling and zero point energy – have important effects on rates.