Real-Time Electrical Impedance Variations in Women With and Without Breast Cancer

Abstract

The chaotic vascular network surrounding malignant tumors leads to pulsatile blood flow patterns that differ from those in benign regions of the breast. This study aimed to determine if high-speed electrical impedance tomography (EIT) is able to detect conductivity changes associated with cyclic blood-volume changes and to gauge the potential of using these signatures to differentiate malignant from benign regions within the breast. EIT imaging of pulsating latex membranes submerged in saline baths provided initial validation of its use for tracking temporally varying conductivities. Nineteen women (10 with cancer, nine without) were imaged with EIT over the course of several heartbeats in synchrony with pulse-oximetry acquisition. Eight parameters (r_s, φ(r_t,max), r_t,max, P_low:full, P_high:full, P_low:high) relating the conductivity images and pulse-oximeter signatures were extracted and used as a means of comparing malignant and benign regions of the breast. Significant differences (p < 0.01) between malignant and benign regions of interest were noted in seven of the eight parameters. The maximum correlation between conductivity and pulse-oximeter signals, r_t,max, was observed to be the optimal discriminating parameter with a receiver operating characteristic area under the curve of 0.8 and a specificity of 81% at a sensitivity of 77%. Assessing the dynamic conductivity of breast may provide additional clinical utility to that of standard imaging modalities, but further investigation is necessary to better understand the biophysical mechanisms leading to the observed conductivity changes.

I. Introduction

The electrical impedance of breast is apparently different depending on whether it is benign or malignant [1]. In principle, the spatial distribution of its electrical properties can be imaged using electrical impedance tomography (EIT) to potentially identify the existence and location of various pathologies within the breast. In EIT, ac signals (voltages and/or currents) of specific excitation frequencies are applied and sensed at a number of electrodes placed on the surface of the breast. A numerical algorithm formulated around Laplace’s equation is used to estimate the internal electrical properties based on these peripheral measurements of voltage and current. A general overview of EIT instrumentation and image reconstruction algorithms can be found in [2].

Both single- and multi-frequency EIT systems have been developed to detect breast cancer [3]–[10]. For the single-frequency systems, image contrast is expected to stem directly from the electrical property differences between benign and malignant tissues when excited at a single frequency. Multi-frequency systems provide an opportunity to gauge how these properties change as a function of excitation frequency; benign and malignant breast tissues are expected to have different dispersion characteristics. Several of these multi-frequency instruments have been connected to planar arrays of electrodes pressed flat against the breast [7], [9], [11] while others have been used with circular electrode arrays placed around the tissue [4]. Comprehensive reviews of clinical studies of EIT for breast imaging are given in [12] and [13].

While current results continue to demonstrate some clinical potential [14]–[16], improvement in the sensitivity and specificity of detecting malignant formations within the breast with EIT is still needed. Static absolute imaging has been challenging because of the nonlinear, ill-posed, and ill-conditioned nature of image reconstruction. The relatively small number of measurements, significant noise contributions from both electronic and experimental sources, and the geometric and electrode contact related assumptions typically made to approximate the physical situation have all contributed to these difficulties. To mitigate some of these effects, research groups have advocated for the collection of multi-frequency measurements and have employed linearized algorithms to assess the changing conductivity as a function of frequency in an effort to image the dispersive properties of tissue [17]. Others have evaluated the dispersive relationships in order to identify cancerous lesions within the breast [18] instead of producing impedance images directly. These approaches have demonstrated promising initial results; however, larger patient series are needed to confirm the robustness of these methods.

An alternative to single- and multi-frequency EIT is dynamic, or time-difference, EIT which is employed to image time-varying impedance distributions. A number of clinical applications, aside from breast imaging, have been reported using dynamic EIT to evaluate cardiovascular dynamics [19], pulmonary dynamics [20], gastric emptying [21], [22], and evoked neural response [23]. Image reconstruction is linearized in these applications, which reduces errors associated with geometrical approximations, noise due to experimental conditions, and systematic electronic noise.

To date, dynamic EIT has not been considered for breast imaging largely due to the small temporal changes in impedance that are expected to occur in the breast. However, improved instrumentation over the last decade has produced EIT instruments with extremely high signal-to-noise ratios (SNR) approaching 100 dB [24]–[26] and may make it possible to detect these small changes. In this paper, we investigate whether it is possible to take advantage of low-noise, high-speed EIT to image dynamic impedance changes in the breast in order to detect and characterize breast abnormalities. A physiological rationale for pursuing this approach is presented followed by a discussion of the EIT system developed for this purpose, the image reconstruction algorithm used, and the signal processing and parameter extraction methodology developed to assess dynamic conductivity changes. The system’s ability to image dynamically changing environments is verified through phantom experiments. Finally, results obtained in a pilot imaging study of 19 women is presented and discussed.

II. Imaging Breast Tumor Hemodynamics

Increased effort to correlate dynamic signatures obtained from MR and Ultrasound (US) with hemodynamic histopathology in the breast is underway. The basis for these studies is the association of tumor angiogenesis with the progression of breast disease. For example, Wells et al. [27] have recently shown that the mean vessel density (MVD) in malignant breast tissue is 2.8 times greater than that of normal tissue and 1.57 times greater than that found in fibroadenomas.

Currently, the most robust method of performing breast MRI involves the acquisition and evaluation of time-intensity curves. These time-intensity curves are, however, dependent upon of a number of physiological parameters including blood flow, blood volume, capillary permeability, and surface area which can not be easily differentiated. New techniques in dynamic contrast-enhanced MR imaging (DCE MRI) have been used to isolate properties such as blood flow, blood volume, and capillary permeability [28]–[31]. A number of studies have attempted to directly correlate DCE MRI signatures with MVD and have found mixed results. For example, Stomper et al. [32] reported no correlation between MRI parameters and MVD, whereas both Ikeda et al. [33] and Tuncbilek et al. [34] have observed such a relationship. They, however, both suggest that the correlation between the rate of initial enhancement and microvessel density is more indicative of vascularization and not malignancy or benignity. The Wells report suggests MVD and malignancy are directly correlated, perhaps showing that these MRI studies are sensitive to multiple parameters as expressed in the observations made by Ikeda et al. and Tunbilek et al. Efforts have also been undertaken in US imaging to measure blood flow in tumors and relate US signatures with MVD. Ultrasound techniques based on color-coded Doppler have shown no evidence of correlation between the Doppler signature and microvessel density; however, they have found an association with the macrovasculature [35], [36]. More recent techniques utilizing power Doppler have shown better sensitivity to vascular detection than that of conventional Doppler imaging [37].

Neovasculature occurs primarily at a tumor’s periphery while its center tends to undergo necrosis. The physiological phenomena occurring within the microvasculature surrounding the tumor is complex, and studies have shown this network of vessels to be chaotically arranged, permeable capillaries [38]. Benign lesions are vascularized as well, but they are more well-defined and lack the chaotic structures of many malignant tumors.

As blood flows through the vasculature it experiences a periodic pulsatillity synchronized to the beating of the heart. The presence of the excessive chaotically arranged vasculature around a malignant tumor may present a different dynamic impedance signature than that obtained from normal and benign tissues within the breast. A high-speed, precise EIT system may be capable of imaging this periodic blood flow by recording measurements at various phases within the cardiovascular cycle. Further, collecting data at specific phases within the cardiac cycle, but over multiple cycles, will provide a multiplicity of data that can be averaged to increase noise suppression and improve image contrast. This would provide a new contrast mechanism, different from that available through static and multi-frequency EIT, which may prove more successful at differentiating breast tissues based on the dynamic characteristics of their blood flow instead. Previous work in impedance cardiography [49], rheoencephalography [50], and brain imaging [51] have compared cardiovascular pulse signals to impedance changes in clinical applications other than cancer imaging.

III. Eit Imaging and Analysis Overview

A. Image Synchronization

Dartmouth’s third generation breast EIT system is capable of collecting high frame rate data (>40 fps) as described previously [25], [39]. Briefly, it is a wide-bandwidth (10 kHz–10 MHz), 64 electrode, voltage-driven system specifically designed for use in breast imaging. In high-speed acquisition mode it collects bursts of 40 frames of data at a user specified frame rate (up to 180 fps); following acquisition the data is off-loaded from the system electronics to an interface computer for postprocessing and image reconstruction.

The system has been upgraded with a cardiovascular monitoring unit (CMU) to permit external triggering of data collection. Specifically, a USB-based analog signal capture device (PMD-1608FS, Measurement Computing, Norton, MA, USA) interfaced to the EIT system computer is used to record an external biophysical signal. The PMD-1608FS has eight single-ended analog inputs that are captured and converted to the digital domain with 16-bit ADCs. The EIT system software continuously scans a single analog input channel at a rate of 62.5 Hz and a software-based threshold detection scheme is used to trigger EIT data acquisition. Thresholds are manually selected based on the characteristics of the input signal. This provides the ability to trigger EIT data acquisition synchronously with the QRS complex of an ECG waveform or the peak in the absorbance signal sampled from a pulse-oximeter. Although either ECG or pulse-oximetry can be used, a finger-based pulse-oximeter (Nellcor N-395, Covidien, MA, USA) was used in this investigation because of the ease of deployment during patient imaging. The cardiovascular signal is recorded simultaneously while EIT data acquisition occurs. Following acquisition of a 40 frame burst of data, additional bursts of frames can be recorded. When an arbitrary number of bursts are collected, data acquisition is halted and the data is transferred for offline image reconstruction.

For the phantom experiments and patient series reported here, the system was configured to image a single plane, consisting of a circular ring of 16 electrodes. The 15 optimal trigonometric voltage patterns for a 16 electrode system as defined by Isaacson [40] were used as the driving patterns. Each acquisition frame consisted of 240 voltages measurements (15 patterns × 16 electrodes) which were arranged in the column vector V_i. Each 40-frame burst of recorded voltages defined a nonsquare matrix, V_n = [V₁ V₂ V₃ … V₄₀], where n represents the burst number when multiple bursts of image frames are collected. The corresponding biophysical signal sampled at 62.5 Hz defined a column vector y_n = [y₁ y₂ y₃ … y_Nc,samples]^T for each 40-frame burst, where n = 1, 2, 3, …, N_burst, and N_c,samples, the length of y_n, is based on the duration of the 40-frame EIT burst collection window. This length is a function of the EIT frame rate and for the data presented here is fixed at 17.3 fps.

B. Image Reconstruction

We used a finite element (FEM) based linear difference algorithm to estimate the changing conductivity distribution between frames. A 2-D circular mesh with 640 elements, 353 nodes and scalable diameter was generated to model the experimental geometry. The change in conductivity, Δσ_i at each of the mesh nodes is calculated from

$$\mathrm{\Delta }{\sigma }_i={(J^{T}J+\lambda L^{T}L)}^{-1}{J}^T\{V^{\text{ref}}-V_i\}i\in 1,2,3,\dots ,40$$ (1)

where J is a Jacobian matrix representing the sensitivity of changes in boundary voltages to changes in conductivity, L is a Laplacian regularization matrix, and λ is a regularization parameter used to stabilize the inversion. V^ref is a set of boundary voltages designated as a reference conductivity distribution, while V_i is the set of boundary voltages collected during each frame i. J is computed from the reference boundary voltages via the adjoint method [41] and is fixed for each Δσ_i calculation. The vector Δσ_i represents the 353 nodal change in conductivity values at each frame i and is computed using the change in measured boundary voltages with respect to the reference. V_ref is defined as the mean of all voltages recorded from a single burst of data

$$V^{\text{ref}}={\overline{\mathbf{V}}}_{\mathbf{n}}=\frac{1}{N}\sum _{i=1}^{40}{V}_i.$$

Taking the mean across all frames provides a less noisy reference from which to calculate conductivity changes. Δσ_i is calculated using (1) for each of the 40 frames recorded from a single acquisition burst. Empirical testing demonstrated that a λ of 0.001 provided a sufficient level of regularization to ensure stable inversion. Within each burst, Δσ_n = [Δσ₁ Δσ₂ Δσ₃, …, Δσ₄₀] represents the spatio-temporal sequence of changing conductivity estimates.

C. Data Processing

Following data acquisition and Δσ image reconstruction, the temporal data (Δσ images, Δσ_n, and biophysical signal, y_n) were analyzed in order to assess 1) the beat-to-beat correspondence between the cardiovascular and Δσ signatures and 2) the inter-beat statistics of these signals. The cardiovascular signal being sampled (either the ECG or pulse-oximetry waveform) provided a surrogate measure of blood flow through the breast and was the means of comparison to which the temporal conductivity changes were evaluated. Note that the pulse-oximetry signal used here provided only a relative reference for comparison since it is dependent on the location of the pulse-ox probe (i.e., finger-based versus carotid sampling). Sampling 40 frames/burst at 17.3 fps provided a 2.3-s sampling window. Resting heart rates typically ranged from 50–90 bpm (0.83–1.5 bps) resulting in 1.9–3.45 heart beats being sampled per burst during this 2.3-s window. Relatively large conductivity changes were present during phantom imaging (Section IV) and the signatures acquired from a single acquisition burst (40 frames) provided sufficient detail for identifying the temporal and spectral characteristics of the spatio-temporal conductivity variations induced. However, for dynamic breast imaging, the conductivity changes are much smaller and require additional processing over multiple acquisition bursts to characterize the signals. Specifically, a single heart beat was extracted from each acquisition burst to provide multiple cardiac events for processing. The specific procedures employed for each processing stage consisted of (Fig. 1).

Fig. 1.

Signal processing scheme employed for assessing dynamic breast imaging with EIT. PO denotes recorded pulse-oximetry signature, y.

1. Step 1: Input: The data collected during each burst consisted of the vector y_n (the cardiovascular signal being monitored at a sampling interval of T_c = 16 ms) and Δσ_n (the temporal change in conductivity sampled at T_σ = 57.8 ms).

2. Step 2: Resample Δσ_n: Because T_c ≠ T_σ, Δσ_n was resampled using cubic spline interpolation to match the sampling rate of y_n. This resampling was performed over each of the image nodes and ensured that the resampled signal, Δ̂σ_n and y_n were of the same length, with each sample occurring at equivalent instances in time. Each single acquisition burst was resampled in a similar fashion.

3. Step 3: Identify Single Beat: Following resampling, a single cardiac cycle was extracted from each burst. This was accomplished by determining successive peaks within the cardiovascular signal, y_n, and extracting the corresponding temporal points from within the resampled Δ̂σ_n sequence. Prior to peak detection, the cardiovascular signal, y_n, was demeaned and normalized. Identifying the peak of this demeaned and normalized signal, ŷ_n, depends on the signal characteristics and for the case of pulse-oximetry signatures, a derivative-based algorithm was employed as a simple, accurate and efficient mode of peak detection. To this end, the first-order difference, Δ_n, is calculated across the entire temporal sequence and normalized

   $${\mathrm{\Delta }}_{n,i}={\widehat{y}}_{n,i+1}-{\widehat{y}}_{n,i}i\in 1,2,3,\dots ,N_{c,\text{samples}}-1$$ (2)

   $${\widehat{\mathrm{\Delta }}}_{n,i}=\frac{{\mathrm{\Delta }}_{n,i}}{max({\mathrm{\Delta }}_n)}.$$ (3)
   A peak was defined at the sample, i, at which the maximum Δ̂ occurred within a predefined window beginning at the time point at which Δ̂ exceeded a specified threshold. The threshold, τ, was empirically determined by trial and error. The first peak, Γ₁, was defined as the maximum Δ̂ found within the window, ψ, following the first instance at which τ was exceeded

   $${\mathrm{\Gamma }}_1=max\left({\widehat{\mathrm{\Delta }}}_{i_{\tau }},{\widehat{\mathrm{\Delta }}}_{i_{\tau }+1},{\widehat{\mathrm{\Delta }}}_{i_{\tau }+2},\dots ,{\widehat{\mathrm{\Delta }}}_{i_{\tau }+\psi }\right).$$ (4)

   The burst number, n, is omitted from (4) to simplify the expression. For the pulse-oximetry signals acquired here, a τ of 0.35 and ψ of 20 proved robust in detecting the first peak in the pulse-oximeter signal from each of the acquired bursts. The second peak, Γ₂, was similarly found by providing the detection algorithm the cardiovascular signature ranging from the end of the first peak window, i_τ + ψ, to the sequence end.

4. Step 4: Extract Single Beat: A single cardiovascular period ranging from the sample points, γ₁ and γ₂, corresponding to Γ₁ and Γ₂, respectively, was extracted from the demeaned and normalized pulse-oximeter signal, ŷ_n and the resampled conductivity signal, Δ̂σ_n

   $${\stackrel{\sim }{y}}_n={[{\widehat{y}}_{n,{\gamma }_1}{\widehat{y}}_{n,{\gamma }_1+1}{\widehat{y}}_{n,{\gamma }_1+2},\dots ,{\widehat{y}}_{n,{\gamma }_2}]}^T$$ (5)

   $$\stackrel{\sim }{\mathrm{\Delta }}{\sigma }_n=\left[\widehat{\mathrm{\Delta }}{\sigma }_{n,{\gamma }_1}\widehat{\mathrm{\Delta }}{\sigma }_{n,{\gamma }_1+1}\widehat{\mathrm{\Delta }}{\sigma }_{n,{\gamma }_1+2},\dots ,\widehat{\mathrm{\Delta }}{\sigma }_{n,{\gamma }_2}\right].$$ (6)

   Here γ₁ and γ₂ denote the time points associated with the first and second peak in the pulse-oximeter signal, respectively.

   The extracted data therefore represents a single cardiovascular beat and includes all ŷ_n and Δ̂σ_n samples between γ₁ and γ₂ (i.e., γ₁, γ₁ + 1, γ₁ + 2, …, γ₂).

5. Step 5: Resample Individual Beats: Heart-rate variability is a well-established phenomenon [42] that manifests itself in this application as the temporal length of ỹ_n and Δ̃σ_n for each burst being variable. In order to account for this variability, the extracted single-beat sequences were resampled using cubic spline interpolation with a fixed number of samples (=40) to occur over a temporal duration of 1 s, effectively enforcing a 1 bps heart rate. By enforcing a fixed number of samples occurring over the 1-s interval, the sequences extracted from each burst were easily compared.

6. Step 6: Concatenate Individual Beats: The resampled ỹ_n and Δ̃σ_n sequences extracted from each burst are concatenated into single multi-heart beat time sequences y(t) and Δσ(t) in order to lengthen the signal for more accurate analysis of temporal and spectral statistics.

D. Image Analysis

After concatenating final sequences of y(t) and Δσ(t), image analysis consisted of extracting the mean Δσ within a specified region-of-interest (ROI) from each frame. This extraction provided a temporal sequence of Δσ_ROI(t) corresponding to a specific region inside the imaging domain. The temporal signature of each sequence was filtered using an 81-tap Hamming window with a cutoff frequency of 8.65 Hz (1/2 of the 17.3 Hz sampling frequency) and padded with zeroes prior to taking the 512-point Fast Fourier Transform (FFT). The power spectra, ΔΣ(f) and Y(f), were estimated as the square of the individual frequency components extracted from the FFT (i.e., ΔΣ(f) = |FFT(Δσ(t))|²). In a phantom imaging configuration with relatively large changes in conductivity, the temporal and power spectral signatures provided adequate information for characterizing the changing conductivity, while in patients no clear indications from these sequences were typically observed. To better evaluate these signatures in patients, several spectral and temporal measures were used to parameterize the waveforms. These parameters included.

1. Spectral Correlation Coefficient, r_s: Correlation coefficient between the pulse-oximeter signal spectra, Y(f) and the ΔΣ(f) spectra. The correlation was obtained for frequencies ranging from 1 to 8.65 Hz. DC to 1-Hz signals were not included because the shortest frequencies able to be gauged were 1 Hz due to the resampling procedure.

2. Maximum Temporal Correlation Coefficient, r_t,max: Maximum correlation coefficient occurring between the pulse-oximeter signal and a phase-shifted Δσ signal. The Δσ signal was phase shifted from 0° to 360°. The correlation coefficient was computed at each degree of phase shift and r_t,max denotes the maximum correlation coefficient obtained through the entire phase-shifting procedure.

3. Phase Shift at r_t,max, φ(r_t,max): The phase shift leading to the maximum correlation coefficient (r_t,max) between the pulse-oximeter signal and Δσ signal. This represents the phase shift required to produce the maximum correlation coefficient.

4. Spectral Power Ratio, P_x:y: The ratio of total spectral power within one frequency band in reference to a second frequency band as defined by

   $$P_{x:y}=\frac{\underset{f_1}{\overset{f_2}{\int }}\mid \mathrm{\Delta }\mathrm{\sum }(f)\mid df}{\underset{f_3}{\overset{f_4}{\int }}\mid \mathrm{\Delta }\mathrm{\sum }(f)\mid df}.$$ (7)
   Three spectral power ratio’s for each Δσ spectra were computed

   $$\begin{array}{ll}\hfill {\mathbf{P}}_{\text{low}:\text{full}}:{\mathrm{f}}_1& =1\text{Hz},{\mathrm{f}}_2=4.325\text{Hz},{\mathrm{f}}_3=1\text{Hz},{\mathrm{f}}_4=8.65\text{Hz}\hfill \\ \hfill {\mathbf{P}}_{\text{high}:\text{full}}:{\mathrm{f}}_1& =4.325\text{Hz},{\mathrm{f}}_2=8.65\text{Hz},{\mathrm{f}}_3=1\text{Hz},{\mathrm{f}}_4=8.65\text{Hz}\hfill \\ \hfill {\mathrm{P}}_{\text{low}:\text{high}}:{\mathrm{f}}_1& =1\text{Hz},{\mathrm{f}}_2=4.325\text{Hz},{\mathrm{f}}_3=4.325\text{Hz},{\mathrm{f}}_4=8.65\text{Hz}.\hfill \end{array}$$

IV. Phantom Imaging

A. Experimental Configuration

A series of phantom experiments were conducted in the same way that patient data was collected in order to evaluate system performance (Fig. 2). An 8-cm circular tank fitted with 1-cm stainless steel electrodes was positioned within the EIT system. A saline solution (σ = 0.113 S/m) was added to the tank to a height of 2 cm just covering the bottom layer of electrodes. A pulsating latex balloon positioned within the saline solution was used to simulate a dynamically varying low conductivity volume. A two-port Y-type connector interfaced to the balloon allowed fluid to flow in and out of the membrane. Flexible tubing extending from one of the ports was interfaced through a programmable COBE heart–lung precision blood pump (COBE Lakewood, CO, USA) to a second saline bath (σ = 0.014 S/m). This solution was pumped through the balloon, and a flexible tube connected to the second port acted to drain fluid from the balloon. An Agilent 33120A arbitrary waveform generator (Agilent Technologies, Santa Clara, CA, USA) was used to generate both sine and square waves of particular amplitudes and frequencies to drive the pump. The back V_emf signal of the pump was sensed by our cardiovascular monitoring unit and used to trigger EIT data acquisition.

Fig. 2.

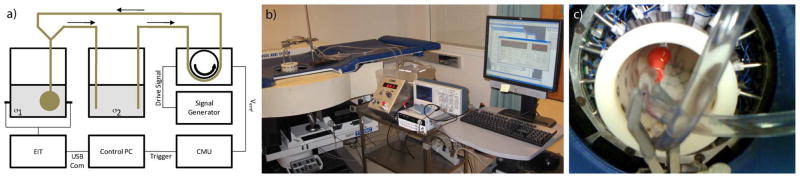
Phantom dynamic imaging experimental configuration. a) Schematic representation of interconnected electrical and fluid systems, b) physical configuration, c) balloon position within saline tank.

Eight different pumping schemes were imaged. Sine wave excitations at 1, 2, and 4 Hz were used, followed by square wave excitations at 1, 2, and 4 Hz. The drive amplitude for each of these waveforms was a constant 1 V_pp, which resulted in balloon diameter changes of 1–3 mm per cycle with the maximum balloon diameter extending to approximately 2 cm. Ten 40-frame acquisition bursts were collected at 17.3 frames per second for each driving configuration at 127 kHz.

B. Experimental Results

Fig. 3 displays a temporal sequence of Δσ images occurring over a single acquisition burst for sine wave excitation at 1, 2, and 4 Hz. The pulsing balloon was well-localized in each burst of frames for all excitation drive configurations. A 2-cm-diameter circular ROI was defined around the node having maximum change in conductivity over the course of the burst (x = 2.2 cm, y = 0.2 cm) and the mean Δσ within the ROI from each frame was extracted. The temporal sequences and power spectrum from each of the drive configurations demonstrates that the temporal changes in conductivity and its spectral signature correlated well with that of the recorded pump drive voltage, V_emf (Fig. 4). The phase shift noted between the temporal Δσ and V_emf traces is due to the phase introduced by the hydrodynamic coupling between the pump and fluid network. During sine wave excitation the principal spectral component for each drive configuration coincided with the programmed drive frequency at 1, 2, and 4 Hz. The additional peak in the 2 and 4 Hz configurations at ~1 Hz is due to rigid balloon translation and water displacement as the tubing moved during the pumping procedure. During square wave excitation, the pump was unable to generate a square wave at 4 Hz due to inertial damping within the motor. At 1 and 2 Hz, however, the pump was able to specify a square wave rotation (see square wave excitation of Fig. 4). As expected the hydrodynamic network interfacing the pump and reservoir to the balloon acted as a low pass filter. As a result, the Δσ images acquired during square wave excitation do not clearly display the sharper edges (high frequencies) present in the recorded pump V_emf. However, within the spectral domain, the Δσ signatures at 1 Hz show both the principal component at 1 Hz and the first odd harmonic at 3 Hz similarly to the V_emf spectrum. This harmonic was not present during sine wave excitation and demonstrates the system’s ability to sense multi-frequency components within a single temporal event. The odd harmonics were not found in the Δσ spectra for the 2-Hz square wave because the low-pass action of the hydrodynamic network acted to filter out these small harmonics. In addition, the first odd harmonic (12 Hz) for the 4-Hz excitation fell outside the bandwidth of EIT acquisition (8.65 Hz).

Fig. 3.

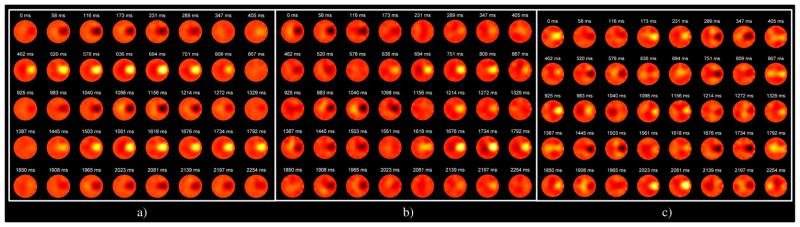
Representative 40-frame acquisition bursts of Δσ images recorded during dynamic balloon experiments for sine wave excitation at a) 1 Hz, b) 2 Hz, and c) 4 Hz. Note that the regions of low and high Δσ, corresponding to the inflating and deflating balloon, have a decreased temporal period as the excitation frequency increases. Color map represents Δσ and ranges from −8 mS/m to 8 mS/m.

Fig. 4.

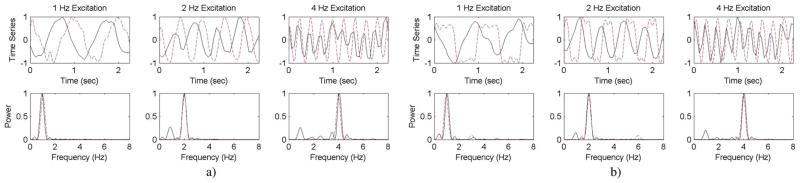
Assessment of dynamic balloon imaging for a) sine wave excitation and b) square wave excitation. Solid line denotes Δσ and dashed line denotes V_emf sensed by the EIT system for triggering. Note that in square wave variation, harmonics in Δσ occur at 1 Hz, which are absent in the higher frequencies because of the low pass filter effect of the long fluid paths within the system.

V. Breast Imaging

A. Breast Imaging Procedure

Women were recruited to be imaged with dynamic EIT as part of an Institutional Review Board approved study at the Dartmouth-Hitchcock Medical Center (Lebanon, NH, USA). The imaging procedure is described in detail in [25]. Briefly, each woman was positioned so that one breast hung pendant through an opening in the EIT examination table. The electrodes were actuated to come into contact with the breast and an effective contact impedance was gauged at each electrode to ensure that all were in contact with the skin. Conductive gel administered between the electrode and the skin reduced the level of this contact impedance. A finger-based pulse-oximetry sensor was placed on the index or middle finger of the patient and interfaced to an N-395 Pulse Oximeter System (Nellcor Pleasanton, CA, USA). The device had an analog output port that provided a filtered pulse-oximeter signal to the cardiovascular monitoring unit of the EIT system. This signal provided triggering for EIT image acquisition and was recorded during image acquisition so that post-acquisition correlation analysis between the cardiovascular and Δσ signals could be evaluated.

In the same way the balloon experiments were conducted, multiple acquisition bursts of EIT voltages were acquired at 17.3 fps and a signal frequency of 127 kHz. This signal frequency was chosen to achieve a relative conductivity contrast of approximately 3:1 between breast tissue and blood (~0.6 S/m blood [48] versus ~0.2 breast tissue [1], [25]). The individual bursts were triggered to begin when the pulse-oximetry signal reached a user-specified threshold selected to occur near the apex of pulse-oximeter signal during each heart beat. This threshold was specifically selected for each patient based on the characteristics of the measured signal which varied due to differences in sensor placement, finger thickness, and other factors. Triggering image acquisition to start precisely at the peak of the pulse-oximetry signal was not critical since a single full heartbeat event was extracted from each data-burst using the processing algorithm described in Section III (Fig. 1).

Following data acquisition (both EIT and pulse-oximetry voltages), Δσ images were reconstructed for each 40-frame burst, the signal processing scheme (Fig. 1) was implemented, and the correlative and spectral power parameters (r_s, φ(r_t,max), r_t,max, P_low:full, P_high:full, P_low:high) were extracted for a particular ROI (described below). The procedure was performed for both the left and right breast of each patient imaged in this study. The clinical evaluation of the cancer patients participating in this study, included MRI-based tumor identification and localization and biopsy-based pathological confirmation of disease. Clinical reports included the approximate tumor location (side and clock face) and tumor size. Because of the approximate nature of the description of tumor location and because there was not a one-to-one correspondence between MR and EIT imaging, the ROIs selected for analysis were assigned to be all nodes within a particular Δσ image quadrant. Quadrants designated as 1, 2, 3, and 4 corresponded to the area on a clock-face covered by 12:00–3:00, 3:00–6:00, 6:00–9:00, and 9:00–12:00, respectively. Based on the clinical tumor description, each quadrant was designated as either benign or malignant.

B. Breast Imaging Results

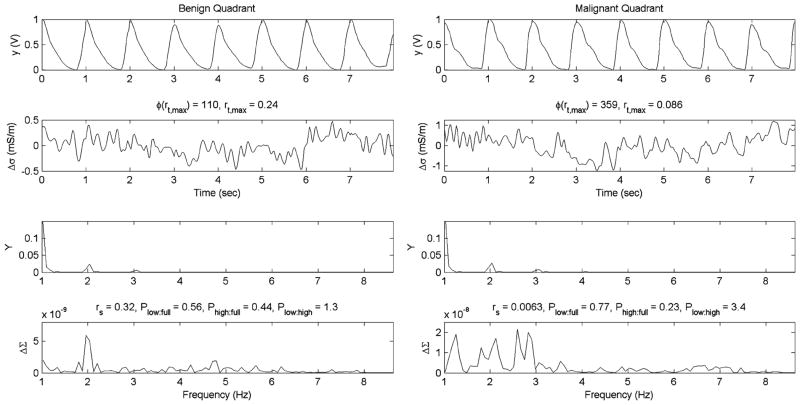
Nineteen (19) women were imaged following this protocol (10 with cancer, nine with no cancer). Among the 19 women imaged, there were 13 quadrants identified as malignant and 139 designated at benign (152 total quadrants = 19 women × 2 sides × 4 quadrants). Tumor characteristics for the cancer containing quadrants are shown in Table I. In three patients (2, 8, and 10), the lesions were identified at the 12:00 location and were therefore assigned to both quadrants 1 and 4. The temporal Δσ signatures observed in this patient cohort provided less obvious information than those obtained from the balloon experiments due to the much smaller changes in Δσ that occurred in vivo. As an example, no obviously differentiating features are noted between a control (normal) and cancer patient (Fig. 5). The temporal and spectral signatures extracted from example benign and malignant (patient 2, quadrant 4) quadrants (Fig. 6) demonstrate two features that were observed in multiple cases. First, the temporal and spectral correlations between Δσ and the pulse-oximeter signatures are quite low (r < 0.09) for the cancer quadrant, while the benign quadrant demonstrates a larger correlation (r > 0.24). Second, the spectral traces have more dispersive and dominant low frequency components in the cancer containing quadrant.

TABLE I.

Cancer Patient Characteristics

	Patient Characteristic							Correlative Measures			Power Spectral Ratios
	RD	Side	Quad	Size	Bx Path	Enhancement	Kinetics	rs	φ(rt,max)	rt,max	Plow:full	Phigh:Full	Plow:high
Patient
1	HD	L	3	33×22×33	IDC	Rim	Malignant (washout)	−0.035	55	−0.005	0.52	0.48	1.1
2	SC	R	1	42×27×35	IDC	Heterogeneous	Mixed progressive/plateau	0.515	82.8	0.082	0.65	0.35	1.8
			4					0.006	359	0.086	0.77	0.23	3.4
3	HD	L	2	19×18×15	IDC	Heterogeneous	Malignant (washout)	−0.025	359	0.104	0.80	0.21	3.9
4	HD	R	4	39×26×42	Inflammatory Ca	Heterogeneous	Mixed plateau/washout	0.810	359	0.159	0.57	0.43	1.3
5	ED	R	4	30×30×25	IDC	Heterogeneous	Mixed progressive/plateau	−0.030	83	0.094	0.69	0.31	2.2
6	SC	R	4	60×28×30	IDC/DCIS	Heterogeneous	Mixed plateau/washout	−0.015	239	0.096	0.60	0.40	1.5
7	HD	R	1	27×18×34	IDS/DCIS	Homogeneous	Mixed plateau/washout	0.110	138	0.262	0.65	0.35	1.8
8	ED	R	1	35×45×100	IDC	Heterogeneous	Malignant (washout)	0.060	359	0.118	0.76	0.24	3.1
			4					−0.005	331	0.070	0.85	0.15	5.7
9	HD	R	4	25	IDC	n/a*	n/a*	0.030	258	0.088	0.82	0.19	4.4
10	SC	R	1	42×27×35	IDC	Heterogeneous	Mixed progressive/plateau	−0.081	55.2	0.042	0.64	0.36	1.8
			4					−0.032	184	0.015	0.64	0.36	1.8

RD denotes Radiographic Density, Bx Path denotes biopsy based pathological findings, and Enhancement and Kinetics describe the washout dynamics of contrast-enhanced MR studies. ED = extremely dense, HD = heterogeneously dense, SC = scattered, DCIS = ductal carcinoma in situ, IDC = intraductal carcinoma.

^*no MRI obtained for this patient.

Fig. 5.

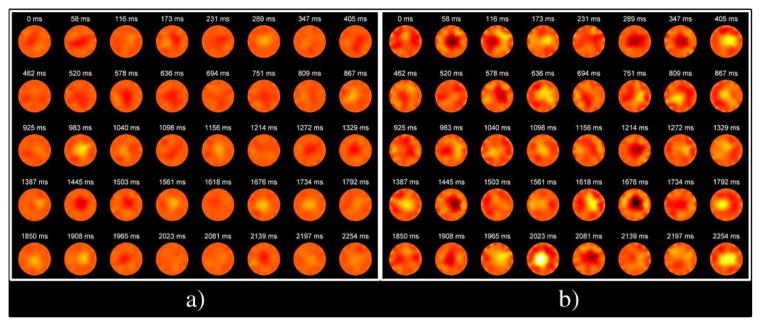
Representative 40-frame bursts of Δσ images acquired from a) normal and b) cancer patients. A 30 mm × 30 mm × 25 mm tumor was identified in MR in quadrant 4. Color map represents Δσ and ranges from −5 mS/m to 5 mS/m.

Fig. 6.

Example temporal and spectral signatures for benign and malignant quadrants. Oxygen-saturation (y) and change in conductivity (Δσ) are displayed as a function of time in the top two rows. The power spectrum for these signals, Y and ΔΣ are shown in the bottom two rows. Correlative and power spectral ratio parameters including r_s, P_low:full, P_high:full, and P_low:high are also displayed.

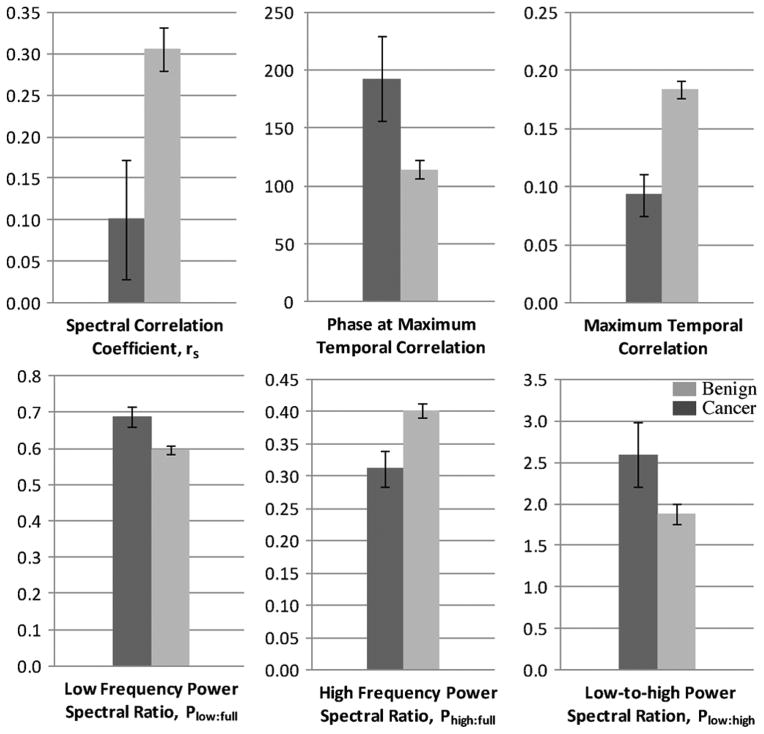
When the quadrants were divided amongst benign and malignant groups and compared, these two observations were consistent and significant (Fig. 7, Table II). All parameters were found to be significantly different (p < 0.05) when grouped as malignant and benign, and all but P_low:high reached significance levels of p < 0.01. In addition, no significant differences (p > 0.1) were noted between the spectral power ratios of the benign and malignant pulse-oximeter signals verifying the fact that the cardiovascular signals were similar in both patient cohorts.

Fig. 7.

Mean parameters for normal and cancer patients. Dark gray = cancer, Light gray = normal. Whiskers denote standard error.

TABLE II.

Statistics of Normal and Cancer Patients Obtained From Processing of Each Quadrant of Data

	Cancer						Benign
	Correlative Measures			Power Spectral Ratios			Correlative Measures			Power Spectral Ratios
	rs	φ(rt,max)	rt,max	Plow:full	Phigh:Full	Plow:high	rs	φ(rt,max)	rt,max	Plow:full	Phigh:Full	Plow:high
Range Stats
Minimum	−0.081	0	−0.005	0.52	0.15	1.07	−0.072	0	−0.011	0.23	0.10	0.30
25th Percentile	−0.030	83	0.070	0.64	0.23	1.75	0.047	64	0.128	0.51	0.32	1.02
Median	−0.005	184	0.088	0.65	0.35	1.84	0.220	83	0.183	0.60	0.40	1.48
75th Percentile	0.060	331	0.104	0.77	0.36	3.40	0.552	129	0.371	0.68	0.49	2.14
Maximum	0.810	359	0.262	0.85	0.48	5.69	0.978	359	0.460	0.90	0.77	9.35
Mean Stats
Mean	0.101	193	0.093	0.69	0.31	2.60	0.306	115	0.184	0.60	0.40	1.88
SD	0.261	133	0.066	0.10	0.10	1.39	0.300	96	0.087	0.13	0.13	1.40
SH	0.072	37	0.018	0.028	0.028	0.39	0.025	8	0.007	0.01	0.01	0.12
95% CI
Lower	−0.057	113	0.053	0.63	0.25	1.76	0.256	99	0.169	0.58	0.38	1.64
Upper	0.258	273	0.133	0.75	0.37	3.44	0.357	131	0.199	0.62	0.43	2.11

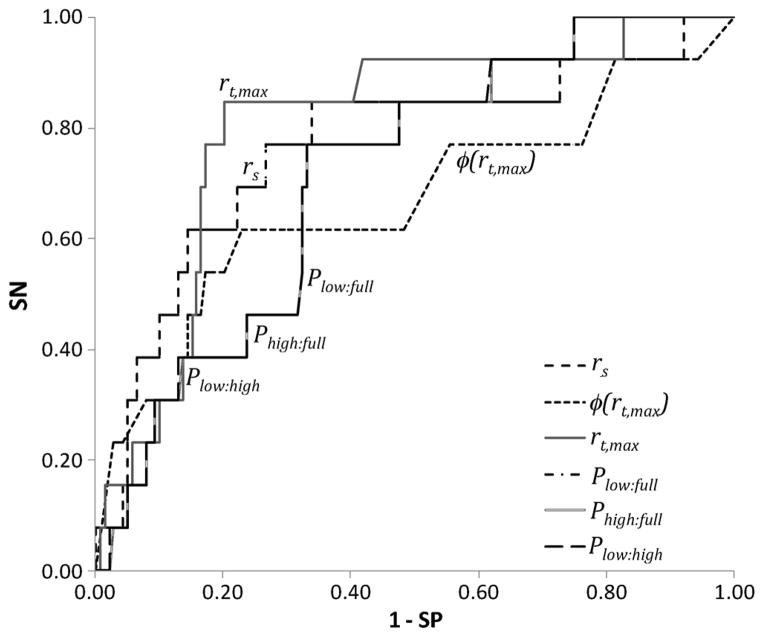
While the sample size is small, the potential clinical utility was evaluated by constructing receiver-operating characteristic curves and extracting the area under the curve (AUC) and other relevant clinical metrics including sensitivity (SN), specificity (SP), accuracy (ACC), positive predictive value (PPV), and negative predictive value (NPV) (Fig. 8, Table III). Specifically, the AUCs of all parameters were greater than 0.67 with r_t,max being the best discriminator with an AUC of 0.8, SN of 77%, and SP of 81%. The rather low PPV and high NPV are due to the large difference between benign and malignant sample sizes (139 quadrants versus 13 quadrants). The thresholds for obtaining these levels of SN and SP are also provided in the table.

Fig. 8.

Receiver operating characteristic (ROC) for the different correlative and spectral power parameters. Note that the spectral power parameters overlap in the ROC domain since they are linearly correlated. SN = sensitivity, SP = specificity.

TABLE III.

Clinical Metrics for Each of the Extracted Temporal and Spectral Power Parameters

	AUC	Threshold	SN	SP	ACC	PPV	NPV	p-value
Dynamic Parameters
rs	0.77	0.109	0.77	0.66	0.67	0.18	0.97	0.0091
φ(rt,max)	0.67	82.8	0.77	0.45	0.47	0.11	0.95	0.0040
rt,max	0.80	0.106	0.77	0.81	0.81	0.28	0.97	0.0002
Plow:full	0.71	0.637	0.77	0.67	0.68	0.18	0.97	0.0098
Phigh:Full	0.71	0.365	0.77	0.67	0.68	0.18	0.97	0.0098
Plow:high	0.71	1.75	0.77	0.67	0.68	0.18	0.97	0.0389

VI. Discussion

The normal breast is vascularized with a well-organized and regulated network of large feeding arteries and veins coupling into smaller arterioles, capillaries, and venules. The branching pattern is typically dichotomous as the network extends from the chest wall through the length of the breast. Around tumors, the vasculature environment is significantly different. Here, the vasculature is of irregular size, shape, and branching pattern and the network lacks normal hierarchy with haphazard branching patterns of trifurcated, uneven diameter vasculature junctions. Vessel density is higher around the tumor periphery with the mean vessel density at the tumor edge being 4–10 times higher than that inside the tumor [43]. In addition, the individual vessels are compromised, with larger inter-endothelial junctions, increased fenestrations, vesicles and vesicovascular channels and lack of normal basement membrane. These features result in lower perfusion rates (blood flow per volume), lower red blood cell velocity, heterogenous and chaotic blood flow around the tumor periphery, and a situation in which plasma oozes from the tumor periphery into the surrounding normal tissues [44]–[46]. These abnormalities in blood flow dynamics generate different temporally-varying conductivity environments than those associated with the benign breast.

While the Δσ images observed here (Fig. 5) do not display well-resolved blood flow and vasculature patterns, the average value within specific regions of interest do appear to provide signatures that are significantly different in benign versus malignant breast tissues. The lower correlative parameters (r_s and r_t,max) for malignant regions potentially arise from the heterogeneous blood flow around and within the tumor. In benign vasculature, the blood flow is more homogenous and more synchronized with the cardiovasculature signature which may explain the somewhat higher correlative parameters observed in these regions. For both malignant and benign tissues these correlative factors are only modest (mean r < 0.306); this is potentially due to the effect of averaging a full quadrant of data in the analysis. Smaller ROI’s will potentially provide areas with higher correlations; however, for the purpose of this study one-to-one correspondence between EIT and clinical MR images was not available and precluded a more refined ROI definition.

Both benign and malignant quadrants had the majority of the spectral energy concentrated in the low frequency band of 1–4.325 Hz, similarly to the pulse-oximeter (blood flow) signatures (Fig. 6). The malignant quadrants, however, had a larger proportion of the energy in this lower band as compared to the higher frequency band (2.6 versus 1.8, Table II). Leaky vasculature surrounding tumors provides low resistance pathway for blood to “ooze” into the interstitial spaces which may produce more low frequency blood flow signatures than those occurring in uncompromised, more rigid benign vasculature. Further, the low frequency energy appears to be more dispersive in the malignant quadrants than in the benign quadrants (e.g., see Fig. 6). This observation may arise from the extensive microvasculature around tumors which has been demonstrated to promote velocity fluctuations [47] that might explain the more dispersive spectral content of the blood flow signatures in the cancer quadrants. The hypotheses formulated from these observations require further experimentation to better understand the biophysical mechanisms producing the effects. Animal models explicitly evaluating the dynamically changing electrical properties associated with pulsatile blood flow through tumor vasculature may provide further insight.

Despite not having a definitive explanation for the significant differences observed between benign and malignant blood flow patterns as gauged by EIT, the clinical metrics computed suggest this modality has potential for differentiating benign from malignant tissues within the breast. The optimum discriminating parameter, r_t,max, provides a sense of how well the changing conductivity distribution within a region correlates with the periodic blood flow pattern. In benign tissues this parameter seems to have a higher correlation (~0.3) compared to malignant tissues where very little correlation (~0.09) appears, suggesting that in these regions the heterogeneous flow patterns associated with malignancy do not follow that of the cardiac-driven blood flow.

Several limitations in the current study are worth noting. First, one-to-one correspondence (registration) between the clinical MR and Δσ images was not available because the patient was not positioned in precisely the same orientation during each exam. The lack of correspondence made it necessary to use the average Δσ values over full quadrants instead of a more specific region-of-interest. This averaging procedure smoothed changes that might be present in smaller, more well-defined ROIs. Second, the sample size in the study was relatively modest, including only 19 women. A larger study, with a larger portion of malignant ROIs may provide a more accurate assessment of the clinical diagnostic performance achievable with the technique. Third, the EIT hardware employed here was limited to collecting 40-frame bursts of data which required additional signal processing and manipulation in order to generate long temporal sequences for analysis. High speed EIT systems with longer periods of sampling have been developed and should be employed to record longer more continuous temporal sequences which would enable improved temporal and spectral processing of these multi-wavelength signatures. Finally, the parameters chosen for evaluation were based on initial observations of the data and were rather simplistic. More complex processing schemes, including principal component or wavelet analysis, might be performed to extract different, potentially more sensitive and specific parameters. Despite these limitations, the different correlative and spectral power parameters found between malignant and benign regions in the breast were significant and suggestive of diagnostic clinical potential.

VII. Conclusion

Phantom studies demonstrated that EIT is able to track frequency variations and simultaneously extract multiple frequency components from within a single temporal event. The changing conductivity signatures obtained from clinical breast exams of women with and without cancer harbor correlative and spectral power parameters that can be extracted and used for differentiating malignant from benign regions within the breast. The optimal discriminating parameter, r_t,max, provided a specificity of 81% at a sensitivity of 77% when a threshold of 0.106 was used to differentiate benign from malignant regions. These diagnostic performance results are substantially superior to those we reported previously for static, absolute EIT imaging of the breast [14]. While further investigation is necessary to better understand the fundamental biophysical mechanisms responsible for the parameter differences observed here, the findings presented demonstrate the potential dynamic EIT may have for breast cancer imaging.