Tests of Calibration and Goodness of Fit in the Survival Setting

Summary

To access the calibration of a predictive model in a survival analysis setting, several authors have extended the Hosmer and Lemeshow goodness of fit test to survival data. Grønnesby and Borgan developed a test under the assumption of proportional hazards, and Nam and D'Agostino developed a nonparametric test that is applicable in a more general survival setting for data with limited censoring. We analyze the performance of the two tests and show that the Grønnesby-Borgan test attains appropriate size in a variety of settings, whereas the D'Agostino-Nam method has a higher than nominal Type 1 error when there is more than trivial censoring. Both tests are sensitive to small cell sizes. We develop a modification of the D'Agostino-Nam test to allow for higher censoring rates. We show that this modified D'Agostino-Nam test has appropriate control of Type 1 error and comparable power to the Grønnesby-Borgan test, and is applicable to settings other than proportional hazards. We also discuss the application to small cell sizes.

1. Introduction

Risk prediction models are a centerpiece for clinical decision making and prediction. Models such as Gail's model for 10 year risk of breast cancer [1] or Framingham 10-year CHD risk model [2-4] are used clinically for treatment decisions. It is critically important to have valid and objective means of evaluating performance of risk prediction models.

Calibration is one of the most important model performance characteristics because a miscalibrated model produces invalid risk estimates [5] and can introduce errors into decision-making. The Hosmer-Lemeshow goodness-of-fit test is often used as a test of calibration [6][7]. Originally developed for the logistic regression model, it was extended for survival data by Nam and D'Agostino [7] (ND test) and Grønnesby and Borgan [8](GB test). The latter group used martingale theory to develop a goodness of fit test for the proportional hazard regression model. While both tests perform well in their proposed settings, recent reports [9] [10] suggest that Nam-D'Agostino has incorrect size for moderate to high censoring rates (above 15%), May and Hosmer [11] showed that the GB test has incorrect size in other settings.

In this paper we show that the GB test achieves the target size in a wide range of simulations in the model-development setting. We demonstrate in our practical example, however, that the GB test can be insensitive to miscalibration when applied in the out-of-sample calibration context. Therefore the GB test can be viewed as a pure goodness-of-fit test only in the model development setting, and cannot be used as a test for external calibration. We propose a new calibration test based on the Nam-D'Agostino approach that is applicable in a more general setting than the GB test and which is not affected by the limitations of the ND test.

2. Model Formulation

For all individuals we record time when an outcome (for example a 10-year CHD event) has occurred or the time of censoring, which is the end of study/lost to follow up time. Denote the end of study time as T, i.e. for 10-year CHD outcome T=10. In addition to the time variable and the censored/event indicator, for each person we collect information on fixed covariates x₁,…,x_p measured at baseline. For this paper we assume that event times are right-censored. To model this kind of data we can use any technique developed for survival right-censored data. For example when the proportionality of hazards assumption is true one can use the Cox proportional hazards (PH) regression model, otherwise use a parametric or non-parametric regression model for censored survival data. For each person we calculate the predicted probability of an event. For cross-sectional data (no time of event) or data with a fixed time to event Hosmer-Lemeshow developed a goodness-of-fit test to evaluate model fit in 1964 using a binary regression model (logistic regression). Data is divided into subgroups based on the deciles or other groupings of predicted probabilities. The Hosmer-Lemeshow goodness-of-fit method tests whether the average of the predicted probabilities follows the observed event rate across the deciles. Grønnesby, Borgan and D'Agostino, Nam used two different approaches to extend this test for survival data. In all tests above and this article we assume that the model is a good fit for the data under the null.

2.1. Grønnesby and Borgan Test

Grønnesby and Borgan developed a goodness-of-fit test for the Cox PH regression model using a counting process approach. For t≤T define N_i(t) =number of observed events in our data for person i in [0,t]. Here we consider one event per person so that N_i(t) is just an event indicator for person i by time t. Using standard counting process notation [8] N_i(t) is generated by an intensity process λ_i(t)=Y_i(t)h_i(t), where h_i(t) is a hazard rate and Y_i(t) is at-risk indicator for person i. Under the assumptions of the Cox model h_i(t) is modeled as:

$$h_i(t)=h_0(t)exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta })$$

, where x_i is the vector of p covariates for person i. Therefore N_i(t) is generated by ${\lambda }_i(t)=h_0(t)exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta })Y_i(t)$

The sum of N_i(t) in group g is just the observed count of events in group g by time t.

$$\sum _{i\in g}{\mathrm{N}}_i(\mathrm{t})=\text{observed}(t)$$

The expected number of events can be calculated as a sum of cumulative intensities in group g up through time t,

$${\mathrm{\sum }}_{i\in g}{\int }_0^t{\lambda }_i(s)ds={\mathrm{\sum }}_{i\in g}{\int }_0^t{h}_0(s)exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta })Y_i(s)ds=\text{expexted}(t)$$ (1)

The difference between the number observed and expected in group g will tell us how close our model fits the data. H_g(t) = observed(t)-expected(t) =

$${\mathrm{\sum }}_{i\in g}{\mathrm{N}}_i(\mathrm{t})-{\mathrm{\sum }}_{i\in g}{\int }_0^t{h}_0(s)exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta })Y_i(s)={\mathrm{\sum }}_{i\in g}{M}_i(t)=H_g(t),$$ (2)

where $M_i(t)={\mathrm{N}}_i(t)-{\int }_0^t{h}_0(s)exp({\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta })Y_i(s)ds$ in formula (2) is a martingale residual. We will denote it as M̂_i(t) when we use estimates of β in M_i(t). Ĥ_g(t) is a group-wise sum of approximate martingale residuals. Using martingale theory Grønnesby and Borgan show how to calculateΣ̂(t), the variance –covariance matrix of (H₁(t), …, H_G‒1(t)) and prove that

$${\chi }_{GB}^2(t)=(H_1(t),\widehat{\dots ,H_{G-1}}(t)){\widehat{\mathrm{\sum }}}^{-1}(t){(H_1(t),\widehat{\dots ,H_{G-1}}(t))}^T~{\chi }_{G-1}^2.$$ (3)

May and Hosmer [12] proved that ${\chi }_{GB}^2(t)$ is algebraically equivalent to the well-known score test statistic which is available in most standard software packages. If the score test is not available, the likelihood ratio test statistics and Wald test are asymptotically equivalent to the score test [13]. Although May and Hosmer showed equivalency at time=∞, ${\chi }_{GB}^2(t)$ is equivalent to the score test for any fixed a priori time t<∞ as long as we do not use data beyond time t. Note that the test is inherently conditional on the censoring distribution in the observed data through the at-risk indicator Y_i(t). The martingales are based on the observed and expected numbers given the censoring times rather than at the end of a common time interval.

2.2. Nam-D'Agostino Test

Nam and D'Agostino [7] introduced a goodness-of-fit test for survival data. They suggested splitting the data into groups based on the risk scores (for example into deciles). To test how well the model fits the data in each decile, they define a test statistic:

$${\chi }_{\mathit{\text{ND}}}^2(t)={\sum }_{g=1}^G\frac{{[{\mathit{\text{KM}}}_g(t)-{\overline{p(t)}}_g]}^2{n}_g}{{\overline{p(t)}}_g(1-{\overline{p(t)}}_g)},$$ (4)

where KM_g(t) is the Kaplan-Meyer failure probability in the g-th decile at time t, $\overline{p{(t)}_g}$ is the mean predicted probability of failure for subjects in g-th decile using any survival modelling technique and n_g is number of observations in a group g. Under the null ${\chi }_{\mathit{\text{ND}}}^2(t)$ is distributed as a Chi-square random variable with G-1 degrees of freedom.

The ND test statistic in (1) can be rewritten in a more familiar “observed”-“expected” form:

$${\chi }_{\mathit{\text{ND}}}^2(t)={\sum }_{g=1}^G\frac{{[{\mathit{\text{KM}}}_g(t)-{\overline{p(t)}}_g]}^2{n}_g}{{\overline{p(t)}}_g(1-{\overline{p(t)}}_g)}={\sum }_{g=1}^G\frac{{[n_g{\mathit{\text{KM}}}_g(t)-n_g{\overline{p(t)}}_g]}^2}{n_g{\overline{p(t)}}_g(1-{\overline{p(t)}}_g)}={\sum }_{g=1}^G\frac{{[\mathit{\text{observed}}(t)-\mathit{\text{expected}}(t)]}^2}{n_g{\overline{p(t)}}_g(1-{\overline{p(t)}}_g)}$$ (5)

where n_g KM_g(t) is an estimator of the mean observed number of events by time t in n_g trials, had there been no censoring. The average number of events in each group is n_g KM_g(t) (=“observed”) and $n_g\overline{p_g}$ is an estimate of the “expected” number of events if the model is correct. The ND formula now has the familiar form of the Hosmer-Lemeshow statistic adapted for survival data. Note that the numerator differs from the sum of the martingales used in the GB statistic because the observed and expected events in the ND test are computed as if there were no censoring up to time t.

2.3. Comparison of Grønnesby-Borgan and D'Agostino-Nam Approaches

Time is one of the most fundamental features of survival analysis and is always present explicitly or implicitly in tests and procedures. For example Hosmer et al [13] point out that if the groups in the GB test are related to the probability of an event (i.e. top decile contains observations with the highest probability of the event) then proportionality of hazards allows forming the groups based on the risk score alone or equivalently on predicted probabilities estimated at time t, where t is common for all subjects. The same is true for the ND test if the expected number of events is calculated using the Cox PH model. However if predicted risk is not a monotonic function of a linear risk score, then groups should be formed explicitly on predicted probabilities at some common time t. Also note that it does not make sense to form deciles based on the survival probability estimated at different follow-up times for different subjects, because if the baseline hazard is non-constant, risk would be calculated over different periods in the same decile (see [13] section 6.5).

Additionally note that both tests themselves use time t in (3) and (4). The ND and GB tests can be estimated for t=T but can be evaluated at some t<T as well, if goodness of fit is of interest at some intermediate time t. In the GB test, to compare the observed and expected number of events by time t<T, individuals should be artificially censored at time t. This would ignore any events after t and potentially lose information in estimating the regression parameters of the Cox model. The ND test, however, could use later information to estimate the hazard ratios or other model form, but then estimate the predicted probabilities at time t. Note, however, that if T extends much further than t, such as estimating 10-year risk using 30 years of follow-up, then proportionality of hazards and other model assumptions may not hold and risk estimates may not be accurate.

Censoring is another fundamental feature of survival analysis. The two tests are conceptually different in their treatment of censoring. First, note that Σ_i∈gN_i(t) in GB formula (2) is the unadjusted raw observed count in group g. Second, n_g KM_g(t) is the observed count in the numerator of ND (5). KM_g(t) is a Kaplan Meier consistent estimator of survival probability which by definition is unaffected by censoring. Therefore the ND test is based on observed counts that are scaled up to compensate for censoring, whereas GB is using actual observed counts. The corresponding expected numbers used in the GB test are also as of the individual's follow-up time, while they are at time t in the ND test.

Finally, the GB test utilizes the powerful and efficient counting process theory. However it is limited to the Cox PH model. In contrast, the ND test does not make any specific modelling assumptions. Therefore, $\overline{p{(t)}_g}$ in (4) and (5) may be estimated by any survival modeling technique, including, for example, statistical learning methods [14].

3. Performance of the Nam D'Agostino Goodness of Fit Test

Paynter et al (for the ND test) and Guffey and May (for both tests) reported incorrect size for several settings. In this paper we demonstrate how the two goodness-of-fit tests perform in a typical cohort study. Cohort studies often estimate risk as of a specific follow-up time: i.e. 10-year risk of CHD, which can have in a population a low event rate such as .05. Censoring will further reduce the observed number of events. It is important to understand if and by how much the performance will deteriorate because of the small number of events and to find the best way to resolve problems with the performance.

3.1. Simulations Set Up

The goal of our simulations is to mimic a cohort study with a specific disease outcome (i.e. 10-year CHD event, or 5-year risk of breast cancer). Using population event rates of 5%, 10% or 40% we simulate data under the assumption of a proportional hazards Cox regression model with three baseline hazard functions: decreasing, constant and increasing. Event times follow the Weibull distribution

$$F(t)=exp(-t^{\alpha }\lambda exp({\beta }_1{x}_1+{\beta }_2{x}_2)).$$

In this paper x₁ is called “an old predictor”, x₂ “a new predictor”.

Parameters α, λ are calculated in such a way that 5%, 10%, or 40% of observations will have an event by year 10 in the absence of censoring. This event time distribution translates into the following form of baseline hazard:

$$h_0(t)=\alpha t^{\alpha -1}\lambda$$

where α is a shape parameter. We used α ∈{0.3, 1.0, 3.0}, corresponding to monotone decreasing, constant and increasing baseline hazard functions with respect to time t. λ is a scale parameter. It is calculated to ensure event rates of .05, .1 and .4 by year 10. β₁ is chosen so that HR(x₁) was 8.0 and β₂ correspond to a set of hazard ratios of x₂: {1,1.3,3.0,8.0,15.0}. Event times greater than 10 years are censored (administrative censoring). In addition, censoring due to lost to follow-up is implemented by generating uniformly distributed censoring times for all observations and ensuring that 25% (in one setting) or 50% (in another setting) of observations have censored times less than 10. A Sample size of N=5,000 was used to generate data in all presented simulations unless indicated otherwise.

3.2. Dealing With Sparse Deciles

Ideally a well- calibrated model performs well in a variety of divisions into groups. Asymptotic properties of all survival estimators (as KM_g(t) in formula (4)) rely on having a sufficiently large expected number of events in g-th decile. May and Hosmer [11] show that GB test becomes too liberal when there are too few events per decile. We observed similar behavior in our simulations. To ensure a sufficient number of events per decile May and Hosmer recommend either decreasing the number of groups or ignoring deciles with too few number of events. The latter strategy results in effectively discarding part of the data. We used a collapsing strategy instead. We started with 10 deciles, but collapsed small deciles with their closest neighbors, until all groups contained a predefined minimum number of events. This strategy always uses all the data, while ensuring convergence of the estimators. It will often lead to division into a sufficient number of groups which could also help encourage a chi-square distribution for our test statistic. We tested several collapsing rules: collapse if less than two, five and twenty events. Per our extensive simulations (Section 4.1) the collapse if less than 5 rule performs better than its two other alternatives, so we limit our results to that scenario.

3.3. Simulations Results

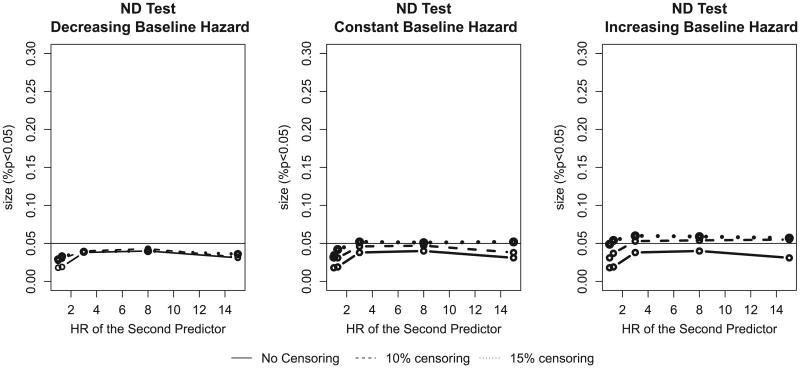
In their original paper Nam and D'Agostino [7] introduced their formula (4) for Framingham-type data – a cohort study with little censoring. Cook and Ridker [16] used a similar approach for the Women's Health Study (WHS) which also has low censoring rate: over eight years of follow-up only 1.87% of women were censored in WHS. Figure 1 demonstrates that the ND test has appropriate size for such low-censoring scenarios.

Figure 1.

The size of the Nam–D'Agostino (ND) test for a low censoring rate for decreasing, constant, and increasing baseline hazards. The population event incidence is 10%. HR, hazard ratio.

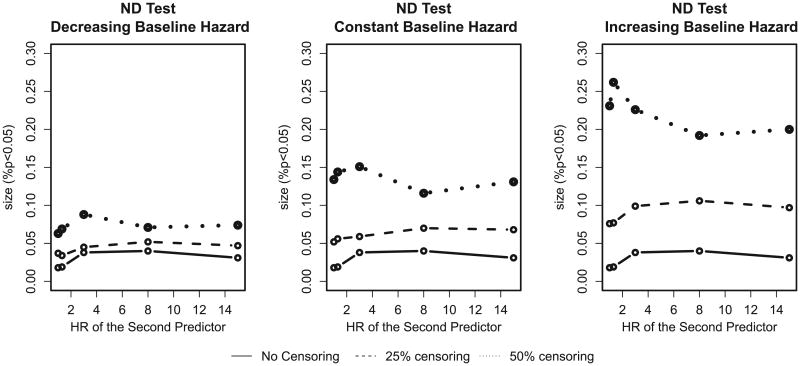
Oftentimes in practice higher censoring rates are observed in a study [17]. Crowson et al. [18] note that the ND test ignores censoring. In order to apply the ND test to a more general situation we first consider how it performs for higher censoring rates. Figure 2 demonstrates that at 50% censoring the test rejects the null hypothesis about 15% of the time which is much more often than we would have expected at a 5% significance level.

Figure 2.

The size of the Nam–D'Agostino (ND) test for a high censoring rate for decreasing, constant, and increasing baseline hazards. The population event incidence is 10%. HR, hazard ratio.

A possible explanation of this deterioration can be found by looking at the variance in the denominator of (4):

$$\frac{{[{\mathit{\text{KM}}}_g(t)-{\overline{p(t)}}_g]}^2{n}_g}{{\overline{p(t)}}_g(1-{\overline{p(t)}}_g)}$$

It is a variance of a binomial probability estimator in n_g trials (size of g-th decile). However in the numerator we have the estimator of 1-survival probability in the presence of censoring. So the more censoring there is the less stable the numerator will be. Also, varying event times should be taken into account. Therefore in the section below we suggest using the Greenwood estimator of the variance of the probability of failure in the denominator.

4. New Test Using the Greenwood Variance Formula

The denominator of the ND test statistic (4) can be interpreted as the squared standard error of the binary proportion estimator p̄_g. The binary proportion estimator was developed for binary data and does not account for censoring nor for time of event. It is appropriate to use it in the setting of a fixed event time, though even there the actual survival times are not taken into account. The Greenwood estimator is a consistent estimator of Var(KM_g(t)) in a survival analysis setting, and performed well in simulations [19]. We suggest using the Greenwood formula for the variance of failure probability KM_g(t) in the denominator of ND (2). The Greenwood variance estimator KM_g(t) can be written [19]:

$\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))={\mathit{\text{KM}}}_g{(t)}^2{\sum }_{i|t_i\le t}\frac{d_i}{n_i(n_i-d_i)}$, where d_i and n_i are the number of failures and number at risk at time t_i. The proposed Greenwood-Nam-D'Agostino (GND) statistic is

$${\chi }_{\mathit{\text{GND}}}^2(t)={\sum }_{j=1}^G\frac{{[{\mathit{\text{KM}}}_g(t)-\overline{p(t)}g]}^2}{\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))}~{\chi }_{G-1}$$ (6)

In the Appendix we prove that in the absence of censoring GND test can be written as ${\chi }_{\mathit{\text{GND}}}^2(t)={\sum }_{g=1}^G\frac{{[{\mathit{\text{observed}}}_g-{\mathit{\text{expected}}}_g]}^2}{n_g\widehat{p_g}(1-\widehat{p_g})}$, where $\widehat{p_g}=\frac{{\mathit{\text{observed}}}_g}{n_g}$. In this situation it is exactly equal to the ND test which is distributed as χ_G‒1 under the null. In the absence of censoring the GND test can be viewed as a variation of the Hosmer-Lemeshow test [20] (see Appendix).

5. Performance of Grønnesby-Borgan and Greenwood-Nam-D'Agostino Goodness-of-Fit Tests

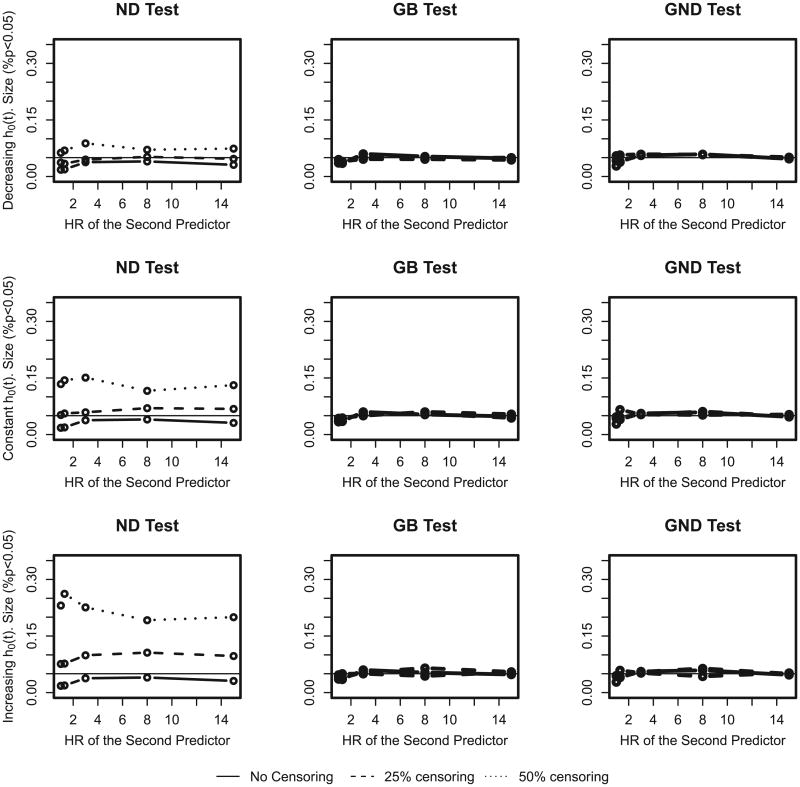
In this section we run extensive simulations of a variety of scenarios to evaluate the performance of goodness-of-fit tests for survival data. We focus on two tests: the GB, and the new GND tests. We include the GB test since it is one of the best tests to use in terms of performance [8] and ease of use [12] for proportional hazards survival data. The GND test is applicable in a wider variety of situations. In Figure 3 we plot the size of the tests: ND (4), GB(3) and GND(6) versus the hazard ratio of the second predictor variable x₂. One thousand simulations of sample size N=5000 were generated under the null: survival times were generated according to proportional hazards model with two normally distributed (N(0,0.5)) predictors (x₁ and x₂) and incidence rate of 0.1. In the top, middle and lower rows we present results for decreasing, constant and increasing baseline hazard functions. We used 0%, 25% and 50% censoring rates by generating uniform censoring times for 0, ¼, and ½ of the sample. Groups were defined by predicted probability deciles. Deciles with a small number of events were collapsed with the next decile, until each decile contained at least 5 events. We conclude that in these simulations the GB and the new GND test achieve the correct size under all three scenarios irrespective of censoring rate.

Figure 3.

The size of the Nam–D'Agostino (ND), Grønnesby and Borgan (GB) and proposed Greenwood–Nam–D'Agostino (GND) tests (testing deciles under the null) for decreasing (top row), constant (center), and increasing (bottom row) baseline hazards. The population event incidence rate is 10%. Deciles with less than five events were collapsed with the next neighbor. HR, hazard ratio.

The performance of the original ND (4) test depends on the censoring rate and on the form of baseline hazard, with the increasing baseline hazard and 50% censoring rate being the most problematic. An increasing baseline hazard affects the observed censoring rate, because the increasing form of baseline hazard results in later survival times, so observations have more time to be censored, whereas for decreasing hazard, more events are captured despite censoring. For example 50% censoring reduced the 10% event rate to 9.09% for the decreasing hazard, whereas for the increasing hazard the rate was only 6.42%. The censoring rate drives the performance of the ND (4) test.

Using a higher population event incidence (40%) resulted in similar plots. A new test for a lower incidence of 5% but with a doubled sample size also performed equally well.

5.1. Performance for Smaller Sample Size

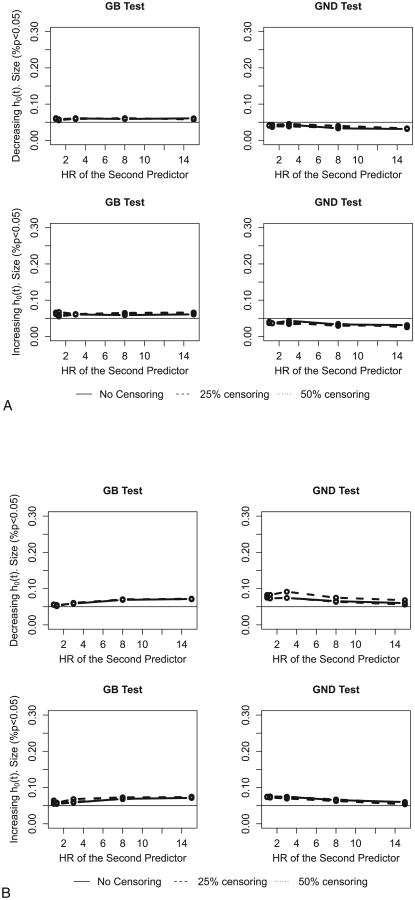
Figure 4A demonstrates the performance of the two tests in samples of size 1,000 with a 10% event rate. As in the previous analysis we collapse deciles with less than five events. With such a small number of events (roughly 100 events per sample) the size of the tests (especially GND) varies more from simulation to simulation. As can be seen from Figure 4A, the GB test has a slightly higher t size than the targeted .05 level, and the GND test's empirical size is a bit lower than 5%. So in this situation the GND test may be more useful than the GB test. When we use the “collapse if less than two” rule, both tests' performance noticeably deteriorates. We find that as long as there are enough events per group, GB performs well in our simulations. However as will be demonstrated in our practical example, there are other conditions when the GB test is less attractive (see Section 5).

Figure 4.

A. The size of Grønnesby and Borgan (GB) and proposed Greenwood–Nam–D'Agostino (GND) tests with smaller sample size (N = 1000, p = 0.1, and at least five events per decile for decreasing (top row) and increasing (bottom row) baseline hazards. HR, hazard ratio. B. The size of Grønnesby and Borgan (GB) tests and proposed Greenwood–Nam–D'Agostino (GND) with smaller sample size (N=1000, p=0.1, and at least two events per decile for decreasing (top row) and increasing (bottom row) baseline hazards. HR, hazard ratio.

5.2. Power for the GB and GND Tests Under Various Mis-Specified Models

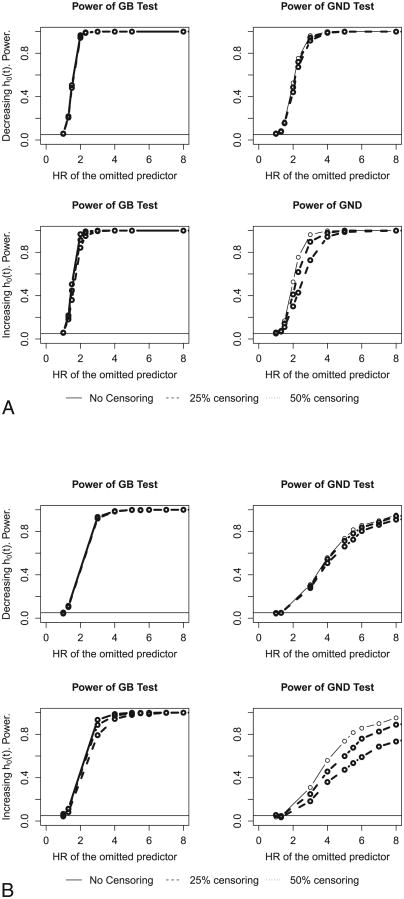
To examine the power of the two tests we have to see how the tests perform when the model is miscalibrated. We simulate data under the true model as described in Section 3 but we calculate predicted probabilities under various misspecified models. Ideally a good goodness-of-fit test, particularly when it is intended to test calibration, ought to have enough power to detect that the model does not fit the data well. We considered three scenarios: a) a missing quadratic term; b) a missing interaction; and c) a missing predictor.

First, In Figure 5A the data was generated under the following model

Figure 5.

A. Power of Grønnesby and Borgan (GB) and proposed Greenwood–Nam–D'Agostino (GND) tests when missing a quadratic term. N = 5000 and p = 0.1 for decreasing (top row) and increasing (bottom row) baseline hazards. (Models 7 and 7*). HR, hazard ratio. B. Power of Grønnesby and Borgan (GB) tests and proposed Greenwood–Nam–D'Agostino (GND) tests when missing an interaction term. N = 5000 and p = 0.1 for decreasing (top row) and increasing (bottom row) baseline hazards. (Models 8 and 8*). C. Power of Grønnesby and Borgan (GB) tests and proposed Greenwood–Nam–D'Agostino (GND) tests when missing an important predictor. N = 5000 and p = 0.1 for decreasing (top row) and increasing (bottom row) baseline hazards. (Models 9 and 9*). HR, hazard ratio. HR, hazard ratio.

$$F_{\mathit{\text{true}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1{x}_1+{\beta }_2{x}_1^2))$$ (7)

We fit Cox regression using the following misspecified model to generate predicted probabilities:

$$F_{\mathit{\text{fitted}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1^{\ast }{x}_1))$$ (7*)

We plot in Figure 5A the power of the GB and GND tests for various hazard ratios (e^β₂) for the omitted quadratic term in model (7). The power for the GB test is excellent; the GND test has lower power which is expected because it is less efficient due to its minimal usage of parametrics. For an increasing baseline hazard and 50% censoring rate the GND test has 55% power for HR=2.5 and 73% for HR=3.0 for the misspecified model (7*) (Figure 5A).

In Figure 5B we plot the power of the two tests for the true model:

$$F_{\mathit{\text{true}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_1{x}_2))$$ (8)

We omit the interaction term and fit the following misspecified Cox model:

$$F_{\mathit{\text{fitted}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1^{\ast }{x}_1+{\beta }_2^{\ast }{x}_2))$$ (8*)

The performance of GND deteriorates somewhat more for this situation. For example for increasing baseline hazard and 50% censoring rate, the GND test has only 18.3% power for HR=3.0 and 68.7% for HR=7.0 for the misspecified model (8*) (Figure 5B).

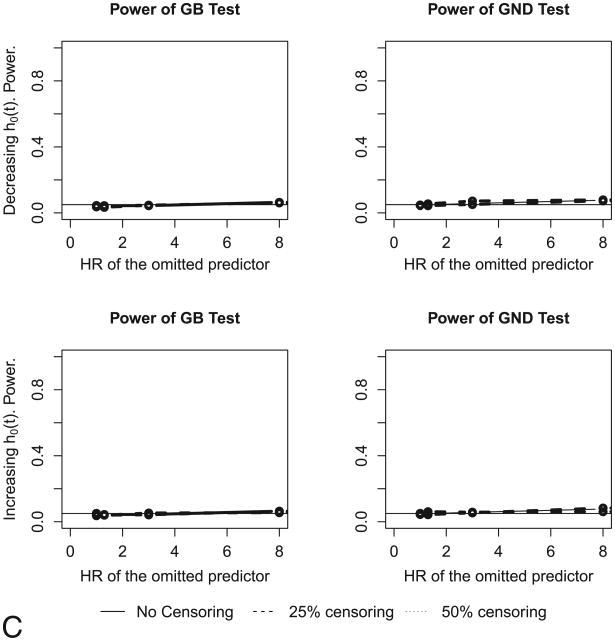
Lastly we omitted an important predictor. These data are generated under the model (9):

$$F_{\mathit{\text{true}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1{x}_1+{\beta }_2{x}_2))$$ (9)

But we used the following model to fit the data:

$$F_{\mathit{\text{true}}}(t)=exp(-t^{\alpha }\lambda exp({\beta }_1^{\ast }{x}_1))$$ (9*)

The power plot is shown in Figure 5C. We observe that both tests completely fail to detect a missing predictor, and the power plots in Figure 5C are similar to size plots. Unlike the power plots in Figures 5A and 5B, the GND and GB tests remain extremely low-powered (close to 5%) across the range of hazards ratios of the omitted predictor x₂, as has been seen previously[15][21].

We conclude that the two tests have enough power to detect an omitted term in situations when there is some information about the omitted term in the model: i.e. omitted quadratic term when the linear term is present, omitted interaction when main effects are present. However it is impossible to detect omitted, but completely unknown information.

6. Practical Example

We applied the GB and GND tests to Women's Health Study (WHS) data to illustrate the performance of the two tests in a real life situation. The WHS is a large-scale nationwide 10-year cohort study of women beginning in 1992. A full description of the WHS data can be found elsewhere [22]. To calculate the risk of 10-year hard CHD, including myocardial infarction and death from coronary heart disease, we use the published Framingham Adult Treatment Panel III (ATP III) model [23]. This model was developed for non-diabetic women, 30 to 79 years old without intermittent claudication at baseline. We removed from analysis observations for women who are diabetic, or 80+ years old leading to a sample size of N=26,865. The median follow-up was 10.2 years up through March 2004. A total of 213 women developed hard CHD by that time, and 36.6% of women were censored prior to year 10, most of censoring occurring after year 8.

ATPIII predictors [23] are four log transformed variables: age, total cholesterol, hdl cholesterol, systolic blood pressure; two categorical variables: current smoking status, treatment for hypertension (SBP>120); and two interaction terms: log-transformed total cholesterol with log-transformed age and smoking with log-transformed age. Published coefficients for the model are presented in [24] and are reproduced in Table 1.

Table 1. Published ATP III Model for Women: Cox regression Coefficients and estimated Means.

		Means
Independent Variable	Cox Parameter Coefficient	Framingham	WHS
Ln(AGE)	31.764001	3.92132	3.982996
Ln(TOTAL CHOL)	22.465206	5.362898	5.335407
Ln(HDL CHOL)	-1.187731	4.014637	3.951109
Ln(SBP)	2.552905	4.837649	4.809493
TRT for HTN (SBP > 120)	0.420251	0.142802	0.12172
CURRENT SMOKER	13.07543	0.32362	0.116397
Ln(AGE)*Ln(TOTAL CHOL)	-5.060998	21.05577	21.25574
Ln(AGE)*SMOKER	-2.996945	1.251988	0.462455
	Average 10 Year Survival	0.98767	0.991882

The ATPIII model was developed using Framingham data. The WHS data was collected at a different time with a different population. Indeed, the average 10-year failure probability in Framingham data is 1.5 times higher than in WHS (0.8% in WHS as compared to 1.2% in Framingham data). The smoking rate is lower in the WHS with 11.6% smoking in WHS versus 32.4% in Framingham's subset of women. In a different population one would expect to see some degree of miscalibration of the ATP III model. For instance, when we estimate the survival probability in WHS using the published ATPIII model, the expected counts in each decile are 2- to 6-fold larger than the observed counts (Table 2).

Table 2. Observed and Expected Counts in Each Decile for the ATP III Model Using WHS Data.

Decile**	Total n	Number censored	Number of Events	Observed Count*	Expected Count	Observed Failure Rate	Expected Failure Rate
				Kaplan Meier	ATP III Model	Kaplan Meier	ATP III Model
1-3	8060	3010	6	6.0	31.1	0.001	0.004
4	2686	956	7	7.0	20.2	0.003	0.008
5	2687	981	8	8.3	27.1	0.003	0.010
6	2686	935	14	14.5	36.8	0.005	0.014
7	2687	985	8	8.4	49.9	0.003	0.019
8	2686	932	25	26.1	69.9	0.010	0.026
9	2687	983	44	47.1	105.3	0.018	0.039
10	2686	1064	98	102.3	218.3	0.038	0.081

^*The observed count is adjusted for censoring. It is equal to the Kaplan-Meier estimate of the number of events had there been no censoring.

^**Deciles with less than 5 events were collapsed.

Therefore re-calibration is likely to improve the model fit. We ran the GB and GND tests for the ATP III model with four different recalibration strategies. For Run 1: we applied the published ATPIII model from the website. We calculated the survival probability using the following formula: survival probability S(t) for Cox model is estimated by the following formula:

$$S(t)=e^{(-{\int }_0^t\lambda (u)du)e^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}}}=e^{(-{\mathrm{\Lambda }}_0(t))e^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}}}=e^{(-{\mathrm{\Lambda }}_0(t))e^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}-{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}+{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}}}=e^{(-{\mathrm{\Lambda }}_0(t))e^{{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}}{e}^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}+{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}}}$$

We are interested in the survival probability at time 10, so we write: $S(t=10)={\left(e^{(-{\mathrm{\Lambda }}_0(10))e^{{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}}}\right)}^{e^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}-{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}}}=A^{(e^{{\mathit{\beta }}^{\mathbf{\prime }}\mathit{x}-{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}})}$. A can be approximated by using direct substitution: $\overline{S}(t=10)\cong A^{(e^{{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}-{\mathit{\beta }}^{\mathbf{\prime }}\overline{\mathit{x}}})}=A$. Therefore A can be approximated as an average survival probability at time 10. The formula for survival probability for Run 1 is thus:

$$S(t=10)={0.98767}^{(e^{{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}\mathit{x}-{\widehat{\mathit{\beta }}}^{\mathbf{\prime }}\overline{\mathit{x}}})},$$

Where β̂ (estimates of Cox regression coefficients) and x̄ (averages of the predictor variables) are from the published ATP III model [2] and are presented in the second and third columns of Table 1.

Run 2 also uses β̂ published for ATPIII model but we calibrate it in the large, so that the average of the estimated survival probabilities is equal to the observed 10-year survival estimated by Kaplan-Meier in the WHS (=0.991751). Calibration in the large is achieved by refitting the baseline hazard for the data. We implement this model by fixing the coefficients at the published values, but letting the Cox model estimate the baseline survival (the Cox PH model automatically refits the baseline hazard).

The results of Runs 1 and 2 are presented in the first two rows of Table 3. It is impossible to implement the GB test for the Run 1 because the GB test requires rerunning the Cox PH model which always calibrates in the large. This test thus cannot be considered a test of overall calibration. The GB test was calculated only for Run 2. The GND test is highly significant for both runs with p-values of <0.001 and 0.001 respectively indicating miscalibration. Yet the Grønnesby-Borgan test is non-significant. The two tests rarely produce contradicting results in our simulations, so we use the calibration slope approach [25] as an additional test of calibration. We fit the Cox survival model with z= β'^x as the only explanatory variable in the model. The regression coefficient of variable z is called the calibration slope. It is equal to 1.19 and is significantly different from 1.0 (95% confidence interval of [1.04; 1.33]), implying that Model 2 is miscalibrated. To remedy this problem we recalibrated the model using calibration slope of 1.19 as described by Janssen et al [26]. For Run 3 we use Cox regression coefficients which are equal to the product of the ATP III coefficients and the calibration slope of 1.19. The results for Run3 are also presented in Table 3. Both tests now agree (p-values of 0.3 and 0.2 for GND and GB respectively), implying sufficiently good fit (calibration).

Table 3.

WHS data. Results of Grønnesby and Borgan (GB) and proposed Greenwood-Nam-D'Agostino (GND) goodness-of-fit tests of four applications of the ATP III model with varying degrees of miscalibration.

	ATP III Model
Run	External	Calibrated in the large	Correct Functional Form	GB score statistic	GB p-value	GND statistic	GND p-value	Number of deciles
1	Yes	No	No	-	-	667.463	<0.001	8
2	Yes	Yes	No	7.064	0.422	23.582	0.001	8
3	Yes	Yes	Yes	8.291	0.308	10.301	0.172	8
4	No	Yes	Yes	9.628	0.211	10.055	0.185	8

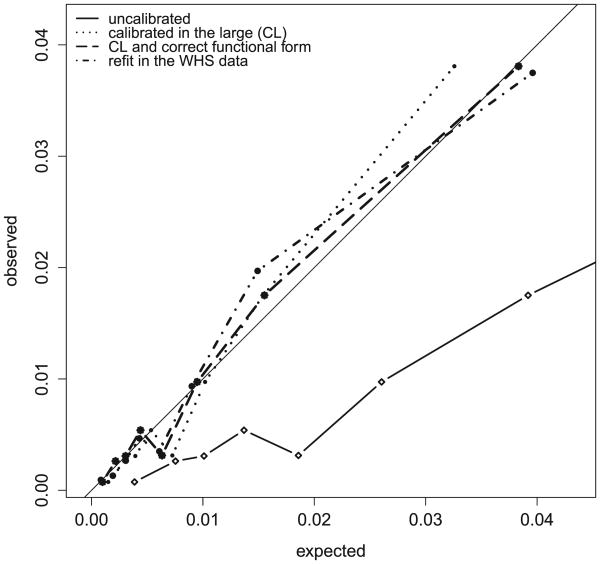
To illustrate the above findings we plotted the observed versus expected average failure probability in each decile for all models (Figure 6). If the model is well-calibrated we would expect the plot to be close to a 45 degree line. We added Run 4 in which the ATP III model is re-fit in the WHS data, which ought to be well-calibrated. Note that Run 1 is far off the 45 degree line. Run 2 – which is only calibrated in the large - also deviates from the 45 degree line confirming our guess that Run 2 is still miscalibrated. Of note, the lack of calibration in Run 2 in Figure 6 is driven mostly by the decile with the highest predicted event probability. Miscalibration of Run 2 was correctly picked up by GND test, but the GB test failed to detect the miscalibration. In further simulations using the WHS data we observed that when the calibration slope is small, then the Cox model is able to re-adjust the baseline survival so that the survival probability remains close to the true survival probability. The GB test calculated in this setting is not significant. However if we continue to distort β by increasing the value of the calibration slope, then adjustment of baseline hazard is not enough to compensate for this distortion. Distortion by a calibration slope of at least 1.8 was required to result in a significant GB test (and GND test) in this specific example. The GND test picks up the incorrect functional form for a calibration slope as low as 1.105. Looking at Figure 6, Run 3 is calibrated in the large and by the method of calibration slope and consequently closely matches the 45 degree line, illustrating that indeed with the second recalibration step [26] we achieve good calibration.

Figure 6.

Observed probability of failure versus expected in each decile by four different recalibration strategies. ATP III model applied to women's health study (WHS) data.

This practical example illustrates that the new GND method is robust whereas GB method has an important limitation: it re-estimates the baseline hazard, so it cannot be implemented for a situation when the baseline hazard and model coefficients are predetermined (i.e. come from an external model). We note that May and Hosmer did not suggest using the score test for externally estimated coefficients. In their two practical examples the beta coefficients were estimated internally. All of our simulations in which the beta coefficients were estimated internally demonstrated consistently good performance of the GB test.

7. Discussion

Recent movement toward improvement of reproducibility of research findings [27] puts calibration measures in the spotlight. Indeed as noted in [5] a miscalibrated model produces invalid risk estimates. In this paper we present simulations and a practical example that illustrate whether the ND and the GB goodness-of-fit tests can be used to assess calibration of the predictive model in the survival setting and propose a new test which is a modified version of the ND test. Our simulation results are applicable to specific, but commonly occurring, underlying parametric survival models, but should generalize to other types of models. Note also that results from all of these goodness-of-fit tests are affected by factors such as the number of groups chosen and the sample size. Such testing should be accompanied by graphical assessments of calibration.

Nam and D'Agostino developed their test specifically for the Framingham model, which has little or no censoring (with no administrative censoring, the Framingham dataset has a censoring rate of less than 5%). Our simulations confirmed that the ND test has appropriate size in this setting. In many settings the ND test will be adequate. But on the other hand existing models are routinely applied to new and sometimes heavily censored datasets. In order to apply the risk estimates to a new dataset we need to confirm that the model is calibrated well in the new data. Our computer simulations demonstrate that for censoring of 25% and higher the GB test performs quite well, but the ND test fails to achieve the .05 size even in the derivation dataset (see Figure 2).

To remedy this situation we developed a modified ND test (which we call the GND test). We investigated the performance of the three tests in a simulated and real-life cohort study. The proposed GND test has the correct size for a variety of settings: 25% and 50% censoring rate, .05, .1 and .4 event rate and decreasing/increasing/constant baseline hazard. Thus the GB and GND tests are better performing tests of fit. We focused on these two tests for the remaining analysis. Based on power plots in Figures 5A-C, we concluded that both methods can detect departures due to missing nonlinear or interaction terms, but neither can detect an omitted variable. This inability to detect an omitted covariate is common for all HL-style tests [28,29] and was noted for binary data by Cook and Paynter [15], who demonstrated through simulations that the power plot using logistic regression is similar to the 0.05 reference line.

Our practical example illustrates a subtle but important difference between a goodness-of-fit and a calibration test. In our practical example with WHS data Run 2 is miscalibrated (as shown by a calibration slope which is significantly different from 1.0). This miscalibration is correctly detected by GND test (p-value=0.001) but missed by the GB test (p-value=0.4), because in the process of running the GB test we re-estimate baseline hazard. Re-estimating the baseline hazard compensates for miscalibration, even when the regression coefficients are fixed in advance. Once we adjust the ATPIII coefficients by the calibration slope (Model 3), both tests are non-significant. This implies that the GB is a goodness-of-fit test of the selected variables but it is not a test of calibration.

Collapsing deciles worked quite well in our simulations: it helped to avoid small cells and guaranteed that the denominator in formula (5) is estimable. Several authors [11,29] addressed this problem by reducing the number of groups. This strategy does not guarantee non-zero events cells. Collapsing to achieve 5 events per cell showed greater stability of the estimates versus collapsing to achieve 2 events per cell.

To summarize, the GND test can be used to assess calibration as well as non-linearity in external validation sets and therefore it is more suitable for testing calibration. The GND test can be used for models for survival data other than the Cox model – for example, for nonparametric models in the machine-learning/data mining setting - and is therefore more general. Both tests share a common limitation of failure to detect an omitted variable. SAS[30] and R[31] code for GND test is added to the Appendix and is also available at http://ncook.bwh.harvard.edu.

Appendix

Notation

Greenwood-Nam-D'Agostino test statistic

$${\chi }_{\mathit{\text{GND}}}^2(t)={\sum }_{g=1}^G\frac{{[{\mathit{\text{KM}}}_g(t)-\overline{p{(t)}_g}]}^2}{\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))},$$ (1)

where

KM_g(t) = 1 − S_g(t)_KM is the Kaplan-Meyer failure probability in the g-th decile at time t, $\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))={(1-{\mathit{\text{KM}}}_g(t))}^2{\sum }_{i|t_i\le t}\frac{d_i}{n_i(n_i-d_i)}$, where d_i and n_i are the number of failures and number at risk at time t_i

Hosmer-Lemeshow test statistic

$${\chi }_{\mathit{\text{HL}}}^2={\sum }_{g=1}^G\frac{{[O_g-E_g]}^2}{n_g{\pi }_g(1-{\pi }_g)},$$ (2)

where

$${\pi }_g=\frac{E_g}{n_g}=\frac{\#\mathit{\text{expected events in group g}}}{\#\mathit{\text{observations in group g}}},$$

O_g = m_g = # observed events in group g

E_g = expected number of events in group g

Lemma

In the absence of censoring ${\chi }_{\mathit{\text{GND}}}^2(t)=\sum _{g=1}^G\frac{{[O_g-E_g]}^2}{n_g\widehat{p_g}(1-\widehat{p_g})}$.

Statement 1

In the absence of censoring ${\mathit{\text{KM}}}_g(t)=\frac{m_g}{n_g}=\text{observed proportion of events in the group g}$

Proof:

${\mathit{\text{KM}}}_g(t)=1-S_g{(t)}_{\mathit{\text{KM}}}=1-{\prod }_{t_i<t}\frac{n_i-d_i}{n_i}$, with n_i is the number in group g at risk by time t_i and d_i is number of events in group g at time t_i. In the absence of censoring we can simplify: ${\mathit{\text{KM}}}_g(t)=1-{\prod }_{t_i<t}\frac{n_i-d_i}{n_i}=1-\frac{n_g-1}{n_g}\times \frac{n_g-2}{n_g-1}\times \frac{n_g-3}{n_g-4}\times \dots \times \frac{n_g-D_g}{n_g-D_g+1}=1-\frac{n_g-m_g}{n_g}=\frac{m_g}{n_g}=\text{observed proportion of events in the group g}$.

q.e.d.

Now let's simplify Greenwood variance formula in the absence of censoring.

$$\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))={(1-{\mathit{\text{KM}}}_g(t))}^2{\sum }_{i|t_i\le t}\frac{d_i}{n_i(n_i-d_i)}=\mathit{\text{in the absence of censoring}}={\left(\frac{n_g-m_g}{n_g}\right)}^2(\frac{1}{n(n-1)}+\frac{1}{(n-1)(n-2)}+\cdots +\frac{1}{(n-m+1)(n-m)})$$ (3)

Lets consider the second term.

Statement 2

$$\frac{1}{n(n-1)}+\frac{1}{(n-1)(n-2)}+\cdots +\frac{1}{(n-m+1)(n-m)}=\frac{m}{n(n-m)}$$

Proof:

Left hand side contains m terms. We can write it as:

$$\#1+\#2+\#3+\dots +\#\mathrm{m}$$

Using this notation lets add terms one by one:

$$\#1+\#2=\frac{1}{n(n-1)}+\frac{1}{(n-1)(n-2)}=\frac{n-2}{n(n-1)(n-2)}+\frac{n}{n(n-1)(n-2)}=\frac{n-2+n}{n(n-1)(n-2)}=\frac{2n-2}{n(n-1)(n-2)}=\frac{2(n-1)}{n(n-1)(n-2)}=\frac{2}{n(n-2)}$$

$$\#1+\#2+\#3=\frac{2}{n(n-2)}+\frac{1}{(n-2)(n-3)}=\frac{2(n-3)}{n(n-2)(n-3)}+\frac{n}{n(n-2)(n-3)}=\frac{3n-6}{n(n-2)(n-3)}=\frac{3(n-2)}{n(n-2)(n-3)}=\frac{3}{n(n-3)}$$

Induction step: suppose $\#1+\mathrm{‥}+\#(\mathrm{i}-1)=\frac{i-1}{n(n-i+1)}$, lets prove that $\#1+\mathrm{‥}+\#\mathrm{i}=\frac{i}{n(n-i)}$.

Indeed: $\#1+\mathrm{‥}+\#\mathrm{i}=\frac{i-1}{n(n-i+1)}+\frac{1}{(n-i+1)(n-i)}=\frac{(i-1)(n-i)+n}{n(n-i+1)(n-i)}=\frac{in-i(i-1)}{n(n-i+1)(n-i)}=\frac{i}{n(n-i)}$

Therefore by induction

$$\#1+\#2+\#3+\cdots +\#m=\frac{m}{n(n-m)}$$

q.e.d.

Plugging statement 2 into formula (3) we obtain:

$$\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))={\left(\frac{n_g-m_g}{n_g}\right)}^2\left(\frac{m_g}{n_g(n_g-m_g)}\right)$$

Now we can simplify GND test statistic (1):

$${\chi }_{\mathit{\text{GND}}}^2(t)=\sum _{g=1}^G\frac{{[{\mathit{\text{KM}}}_g(t)-\overline{p{(t)}_g}]}^2}{\mathit{\text{Var}}({\mathit{\text{KM}}}_g(t))}=\sum _{g=1}^G\frac{{[\frac{m_g}{n_g}-\overline{p{(t)}_g}]}^2}{{\left(\frac{n_g-m_g}{n_g}\right)}^2\left(\frac{m_g}{n_g(n_g-m_g)}\right)}$$

Statement 3

$$\frac{{[\frac{m_g}{n_g}-\overline{p{(t)}_g}]}^2}{{\left(\frac{n_g-m_g}{n_g}\right)}^2\left(\frac{m_g}{n_g(n_g-m_g)}\right)}=\frac{{[O_g-E_g]}^2}{n_g\widehat{p_g}(1-\widehat{p_g})}$$

Proof:

$$\frac{{[\frac{m_g}{n_g}-\overline{p{(t)}_g}]}^2}{{\left(\frac{n_g-m_g}{n_g}\right)}^2\left(\frac{m_g}{n_g(n_g-m_g)}\right)}=\frac{{[\frac{m_g}{n_g}-\overline{p{(t)}_g}]}^2\times \frac{n_g^2}{n_g^2}}{\frac{(n_g-m_g)}{n_g^2}\frac{m_g}{n_g}}=\frac{{[\frac{n_g{m}_g}{n_g}-n_g\overline{p{(t)}_g}]}^2\times \frac{1}{n_g^2}}{\frac{(n_g-m_g)}{n_g^2}\frac{m_g}{n_g}}=\frac{{[m_g-n_g\overline{p{(t)}_g}]}^2}{(n_g-m_g)\frac{m_g}{n_g}}=\frac{{[m_g-n_g\overline{p{(t)}_g}]}^2}{n_g\frac{(n_g-m_g)}{n_g}\frac{m_g}{n_g}}=\frac{{[O_g-E_g]}^2}{n_g\widehat{p_g}(1-\widehat{p_g})}$$

where $\widehat{p_g}=\frac{m_g}{n_g}$.

q.e.d.

Therefore we showed that in the absence of censoring GND can be written as:

$${\chi }_{\mathit{\text{GND}}}^2(t)={\sum }_{g=1}^G\frac{{[O_g-E_g]}^2}{n_g\widehat{p_g}(1-\widehat{p_g})}.$$

Comparing it to the Hosmer-Lemeshow formula in (2) ${\chi }_{\mathit{\text{HL}}}^2={\sum }_{g=1}^G\frac{{[O_g-E_g]}^2}{n_g{\pi }_g(1-{\pi }_g)}$ we have proved that in the absence of censoring ${\chi }_{\mathit{\text{GND}}}^2(t)$ is very similar to ${\chi }_{\mathit{\text{HL}}}^2$. The only difference is how proportion of events is estimated in the denominator: as observed binomial proportion in GND or as expected proportion in HL.

CODE

#######################################################################

# R FUNCTION TO CALCULATE GREENWOOD-NAM-D'AGOSTINO CALIBRATION TEST FOR SURVIVAL MODEL

# Most up-to date version iof this code is available at 

http://ncook.bwh.harvard.edu/r-code.html

# FOR MORE DETAILS SEE Demler, Paynter, Cook “Tests of Calibration and Goodness of Fit

# in the Survival Setting” DOI: 10.1002/sim.6428

# TO RUN:

# GND.calib(pred,tvar,out,cens.t, groups, adm.cens)

# PARAMETERS:

# pred - PREDICTED PROBABILITIES OF AN EVENT CALCULATED FOR THE FIXED TIME WHICH IS THE SAME FOR ALL OBSERVATIONS (=adm.cens)

# out - OUTCOME 0/1 1=EVENT

# cens.t - CENSORED/NOT CENSORED INDICATOR 1=CENSORED

# groups - GROUPING ASSIGNMENT FOR EACH OBSERVATION

# adm.cens - END OF STUDY TIME

# REQUIRES AT LEAST 2 EVENTS PER GROUP, AT LEAST 5 EVENTS PER GROUP IS RECOMMENDED

# IF <2 EVENTS PER GROUP THEN QUITS

#######################################################################

kmdec=function(dec.num,dec.name, datain, adm.cens){

  stopped=0

  data.sub=datain[datain[,dec.name]==dec.num,]

  if (sum(data.sub$out)>1){

    avsurv=survfit(Surv(tvar,out) ∼ 1, data=datain[datain[,dec.name]==dec.num,], error=“g”)

avsurv.est=ifelse(min(avsurv$time)<=adm.cens,avsurv$surv[avsurv$time==max(avsurv$time[avsurv$time<=adm.cens])],1)

avsurv.stderr=ifelse(min(avsurv$time)<=adm.cens,avsurv$std.err[avsurv$time==max(avsurv$time[avsurv$time<=adm.cens])],0)

    avsurv.stderr=avsurv.stderr*avsurv.est

avsurv.num=ifelse(min(avsurv$time)<=adm.cens,avsurv$n.risk[avsurv$time==max(avsurv$time[avsurv$time<=adm.cens])],0)

  } else {

    return(c(0,0,0,stopped=-1))

  }

  if (sum(data.sub$out)<5) stopped=1

  c(avsurv.est, avsurv.stderr, avsurv.num, dec.num, stopped)

}#kmdec

GND.calib = function(pred,tvar,out,cens.t, groups, adm.cens){

  tvar.t=ifelse(tvar>adm.cens, adm.cens, tvar)

  out.t=ifelse(tvar>adm.cens, 0, out)

  datause=data.frame(pred=pred,tvar=tvar.t, out=out.t, count=1,cens.t=cens.t, dec=groups)

  numcat=length(unique(datause$dec))

  groups=sort(unique(datause$dec))

  kmtab=matrix(unlist(lapply(groups,kmdec,“dec”,datain=datause,adm.cens)),ncol=5, byrow=TRUE)

  if (any(kmtab[,5] == -1) stop(“Stopped because at least one of the groups contains <2 events. Consider collapsing some groups.”)

  else if (any(kmtab[,5] == 1)) warning(“At least one of the groups contains < 5 events. GND can become unstable.\

(see Demler, Paynter, Cook ‘Tests of Calibration and Goodness of Fit in the Survival Setting’ DOI: 10.1002/sim.6428) \

Consider collapsing some groups to avoid this problem.”)

  hltab=data.frame(group=kmtab[,4],

                   totaln=tapply(datause$count,datause$dec,sum),

                   censn=tapply(datause$cens.t,datause$dec,sum),

                   numevents=tapply(datause$out,datause$dec,sum),

                   expected=tapply(datause$pred,datause$dec,sum),

                   kmperc=1-kmtab[,1],

                   kmvar=kmtab[,2]ˆ2,

                   kmnrisk=kmtab[,3],

                   expectedperc=tapply(datause$pred,datause$dec,mean) )

  hltab$kmnum=hltab$kmperc*hltab$totaln

  hltab$GND_component=ifelse(hltab$kmvar==0, 0, (hltab$kmperc-hltab$expectedperc)ˆ2/(hltab$kmvar) )

  print(hltab[c(1,2,3,4,10,5,6,9,7,11)], digits=4)

  c(df=numcat-1, chi2gw=sum(hltab$GND_component),pvalgw=1-pchisq(sum(hltab$GND_component),numcat-1) )

}$GND.calib