Retention Projection Enables Accurate Calculation of Liquid Chromatographic Retention Times Across Labs and Methods

Abstract

Identification of small molecules by liquid chromatography-mass spectrometry (LC-MS) can be greatly improved if the chromatographic retention information is used along with mass spectral information to narrow down the lists of candidates. Linear retention indexing remains the standard for sharing retention data across labs, but it is unreliable because it cannot properly account for differences in the experimental conditions used by various labs, even when the differences are relatively small and unintentional. On the other hand, an approach called “retention projection” properly accounts for many intentional differences in experimental conditions, and when combined with a “back-calculation” methodology described recently, it also accounts for unintentional differences. In this study, the accuracy of this methodology is compared with linear retention indexing across eight different labs. When each lab ran a test mixture under a range of multi-segment gradients and flow rates they selected independently, retention projections averaged 22-fold more accurate for uncharged compounds because they properly accounted for these intentional differences, which were more pronounced in steep gradients. When each lab ran the test mixture under nominally the same conditions, which is the ideal situation to reproduce linear retention indices, retention projections still averaged 2-fold more accurate because they properly accounted for many unintentional differences between the LC systems. To the best of our knowledge, this is the most successful study to date aiming to calculate (or even just to reproduce) LC gradient retention across labs, and it is the only study in which retention was reliably calculated under various multi-segment gradients and flow rates chosen independently by labs.

1. Introduction

One of the major bottlenecks in fields such as metabolomics is our limited ability to identify small molecules, particularly in complex biological samples where easily thousands may be present [1-3]. LC-MS has evolved to become one of the primary analytical tools for this purpose. One advantage is that it provides both mass spectra and chromatographic retention, two pieces of information that are almost entirely unrelated and therefore highly complementary to one another [4-6]. In order to use them to narrow down the identity of a chromatographic feature, one would ideally have standards on hand in order to reject those candidates that do not yield the same mass spectrum or retention time. This approach is practical in some cases, but when the number of peaks to be identified and/or the number of potential identities is large (e.g., in a biological or environmental sample), such an approach becomes prohibitively expensive and time consuming. Instead of having standards on hand for each potential identity, it is more practical to use shared databases of MS and LC retention information. While MS databases have found relatively wide use for compound identification, LC retention databases have found little use, in large part because they are so irreproducible across labs.

In an attempt to improve reproducibility, LC retention databases usually store gradient retention as linear retention indices (LRIs) rather than as absolute retention times. LRIs describe the time a compound elutes relative to the nearest two bracketing standard compounds (from a series of homologues such as 1-nitroalkanes [7] or alkyl aryl ketones [8]) that are run at the same time [9]:

$${\mathit{LRI}}_x=100C_n+100\frac{t_{R\left(x\right)}-t_{R\left(n\right)}}{t_{R(n+1)}-t_{R\left(n\right)}}$$ (1)

where t_R(x) is the retention time of compound x, t_R(n) and t_R(n+1) are the retention times of the homologous standards eluting before and after compound x, and C_n is the number of carbon atoms in the standard eluting before compound x. The overarching assumption of linear retention indexing is that the relative retention of compounds always remains the same regardless of the experimental conditions. This is the same assumption made by peak alignment algorithms [10-12], where retention relative to other peaks arising from the sample is assumed to be the same.

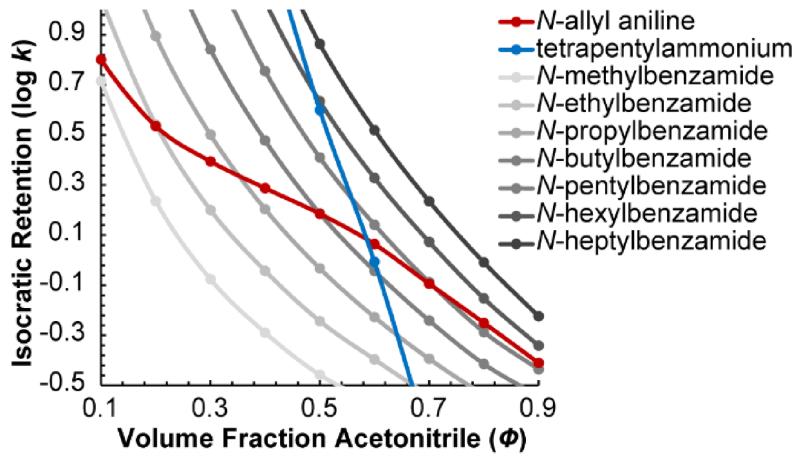
Unfortunately, the validity of this assumption is very rough—the peak patterns frequently change when the experimental conditions change. For example, Figure 1 shows isocratic retention as a function of solvent composition for a homologous series of seven benzamides, N-allyl aniline, and tetrapentylammonium. While the benzamides all show the same relative retention regardless of solvent composition, N-allyl aniline and tetrapentylammonium do not. In fact, tetrapentylammonium swaps elution order with five benzamides as the solvent composition changes from 45% to 65% acetonitrile. The peak pattern is even more strongly dependent on the experimental conditions in gradient elution, where it is altered not only by a change in the initial and final solvent compositions, but also by a change in the gradient slope, the column length, and the flow rate, among other factors. In fact, relatively small imperfections in the gradient produced by different HPLC instruments can change the peak pattern. Therefore, even when one attempts to strictly reproduce the original experimental conditions used by a different lab to measure an LRI, the LRI may be quite different.

Figure 1.

Isocratic retention (log k) vs. volume fraction acetonitrile (Φ) for a homologous series of seven N-alkyl benzamides, tetrapentylammonium, and N-allyl aniline. Relative retention often changes a lot when the solvent composition changes.

Other problems with LRI databases include the fact that they are measured under different experimental conditions—no standard experimental conditions have been widely adopted, nor are they likely to be, as they depend strongly on the research question. Additionally, no single set of retention index standards has been widely adopted. For example, some LRI libraries use alkane-2-ones [13] while others use alkyl aryl ketones [14-16] or 1-nitroalkanes [17]. Because of all this, LRIs are hardly ever used for compound identification by LC-MS.

1.1 “Retention Projection” Accounts for Intentional Differences in Experimental Conditions

A more general approach than retention indexing is to use each compound’s measured isocratic retention factor (k) vs. solvent composition (Φ) relationship, like those in Fig. 1, to calculate its retention time in a particular gradient. Gradient retention times are calculated numerically by treating the gradient as if it were the sum of a series of very short isocratic steps that closely approximate the true gradient. In this way, a retention time is projected by first finding the smallest n that makes the following inequality true [18-20]:

$${\Sigma }_{i=1}^n\frac{\delta t_c}{t_0,{\Phi }_i\left(1+k_{{\Phi }_i}\right)}\ge 1$$ (2)

where t_0,Φi is the dead time at the Φ of the isocratic step i, k_Φi is the retention factor of the compound at the Φ of the isocratic step i, and δt_c is the time that a solute is under the influence of a particular isocratic step of the gradient as it moves through the column:

$$\delta ,t-c.=\delta t+,\delta t-,k-,\Phi -i\dots$$ (3)

where δt is the length of time of each isocratic step (from a fixed point at the column inlet). Then the gradient retention time, t_R, may be calculated from:

$$t_R={\Sigma }_{i=1}^n\delta t_c=\delta t{\Sigma }_{i=1}^{n}1+\frac{1}{k_{{\Phi }_i}}$$ (4)

We call this approach “retention projection” because retention times are “projected” onto gradients from a library of k vs. Φ relationships. Unlike linear retention indexing, retention projection properly accounts for differences in the programmed gradient, the flow rate, the column length, and the column inner diameter because it is theoretically sound. (Of course, a more precise model could be made by taking into account distortion of the gradient from the column [21,22], pressure effects [23], and viscous frictional heating of the column [24], but here those relatively insignificant factors were ignored.)

1.2 Accounting for Unintentional Differences between HPLC Systems by Back-Calculation

Although retention projection is theoretically sound and thus affords more experimental flexibility than retention indexing, it is not very accurate unless the actual behavior of the LC system is measured very carefully and taken into account. Unintentional distortions of the gradient such as gradient delay, gradient dispersion, and solvent misproportioning can cause considerable error in projected retention times; in some cases by up to 25% [4]. These unintentional gradient distortions can be measured directly and then taken into account, but it is very difficult and time-consuming to make such measurements with the necessary level of precision [4,25]. Additionally, the gradient would have to be re-measured on a regular basis and any time the experimental conditions are changed.

Some of us recently reported an approach [25,26] that potentially solves this problem, making it relatively fast and simple to precisely measure the gradient produced by an HPLC system. First, a set of “instrument calibration standards” are spiked into a sample and the sample is run under gradient elution. Then the gradient retention times of these standards are entered into open-source and open-access software (www.retentionprediction.org/hplc). The software back-calculates the effective gradient that must have been delivered to the column (as well as the effective t₀ vs. Φ profile) in order to yield those retention times.

The gradient and t₀ vs. Φ profiles are back-calculated by an iterative algorithm [26]. It starts with the ideal (programmed) gradient profile and the expected t₀ vs. Φ profile. Then, in each of the following iterations, it makes a small change to each profile and re-projects the retention times of the instrument calibration standards. If the change improved the accuracy of the projected retention times, the change is kept, otherwise it is rejected. The iterations continue until the difference between the measured and projected retention times is minimized. At that point, the gradient and t₀ vs. Φ profiles are considered to be fully back-calculated.

Once the profiles are back-calculated, they can be used to project the retention times of other compounds for which their k vs. Φ relationships have been measured (presumably in a large database). A major advantage of the approach is that it requires no more experimental effort than retention indexing, but it is able to properly account for a range of experimental conditions – even those of which the operator is unaware – in a fundamentally sound (and thus, more accurate) way. From the user’s perspective, the methodology and software is simple to use even though the inner workings of the software are somewhat complicated.

This approach proved to be a practical and accurate way to calculate retention times under a wide range of gradients and flow rates, and on two different HPLC systems [26], but it was only tested in one lab and with the same operator. In this work, we test how well the methodology can account for both intentional and unintentional differences between HPLCs in eight different labs, each with different operators. First, we test its ability to account for unintentional differences between HPLC systems by projecting retention times when all experimental conditions are held nominally the same in each lab. Then we test its ability to account for intentional differences by projecting retention times under a variety of gradients and flow rates selected independently by each lab. In each case, we compare the accuracy of retention projections (RPs) to that of LRIs.

2. Experimental

2.1 Test mixture

A single test mixture was used throughout the study. It was composed of 20 “instrument calibration standards” that were used to back-calculate the gradient and t₀ vs. Φ profiles, and 19 chemically diverse “test compounds” whose retention times were then projected to test the accuracy of the methodology. The instrument calibration compounds were selected to elute over a wide range of retention times, to give a strong signal by both electrospray ionization-MS and UV absorption, and to be uncharged. N-methylacetamide (100 μM), N-ethylacetamide (100 μM), N,N-dimethylpropionamide (100 μM), and 16 N-alkyl benzamides (C1-C16) were selected (the concentration of N-methylbenzamide was 100 μM and the rest were 25 μM). N-propylbenzamide and all other benzamides of higher molecular weight were synthesized using an adaptation of the Schotten-Baumann method [25,27-29]. The more hydrophobic benzamides were insoluble in the test mixture unless the solution contained 50% acetonitrile or more. Lower fractions of acetonitrile produced an emulsion that also worked, but after a few weeks, the larger benzamides fell out of the emulsion and they became difficult to detect. All standards were detectable by electrospray ionization MS and by UV absorption [25].

The test compounds included N,N-diethylacetamide (75 μM), N-allyl aniline (100 μM), 1,3-naphthalenediol (400 μM), p-coumaric acid (200 μM), diphenylamine (75 μM), 7-amino-4-methylcoumarin (100 μM), naphthalene acetamide (100 μM), 2-phenylindole (500 μM), anilinoacetaldehyde diethylacetal (100 μM), tetrabutylammonium chloride (10 μM), dodecanophenone (300 μM), abscisic acid (400 μM), tetrapentylammonium bromide (10 μM), di-n-pentyl phthalate (100 μM), chlorogenic acid (300 μM), prednisone (100 μM), cortisone (100 μM), hydrocortisone (100 μM), and curcumin (200 μM). The test compounds were selected to represent the five types of interactions known to influence reversed-phase retention according to the Hydrophobic Subtraction Model [30,31]. Included in the mixture were compounds which interact by a combination of hydrophobicity (e.g., dodecanophenone, di-n-pentyl phthalate), hydrogen bond acidity (e.g., chlorogenic acid, abscisic acid), hydrogen bond basicity (e.g., cortisone, curcumin), charge (e.g., tetrabutylammonium, tetrapentylammonium), and show strong steric selectivity (e.g., prednisone, hydrocortisone). There were also three compounds with pK_as predicted to be near the mobile phase pH: N-allyl aniline, 4.5; 7-amino-4-methylcoumarin, 3.4; and chlorogenic acid, 3.3. These pK_as were predicted using Instant J-Chem from ChemAxon (Budapest, Hungary). The test compounds were also selected to elute over a wide range of retention times. The test mixture was dissolved in 2:1 water/acetonitrile. Those compounds that were not synthesized were purchased from Sigma-Aldrich (St. Louis, MO), Fisher Scientific (Pittsburg, PA), or Alfa Aesar (Ward Hill, MA).

2.2 HPLC columns

For all experiments, Agilent (Santa Clara, CA) Eclipse Plus C18 columns (100 mm long, 2.1 mm inner diameter, 3.5 μm particle diameter) were used. As a precaution, all columns contained stationary phase from the same batch, although so far we have observed little difference in selectivity between batches of the Eclipse Plus C18 stationary phase (data not shown). Upon receipt, each column was conditioned by running 50% acetonitrile with 0.1% formic acid through the column at 0.4 mL/min for 1 hr, after which the columns were capped and set aside for 24 hours. The columns were shipped to participating laboratories and stored containing the same solvent. One of the columns was used to measure the isocratic k vs. Φ relationships for each of the 39 compounds in the test mixture. Each lab received a different column.

2.3 Isocratic retention measurements

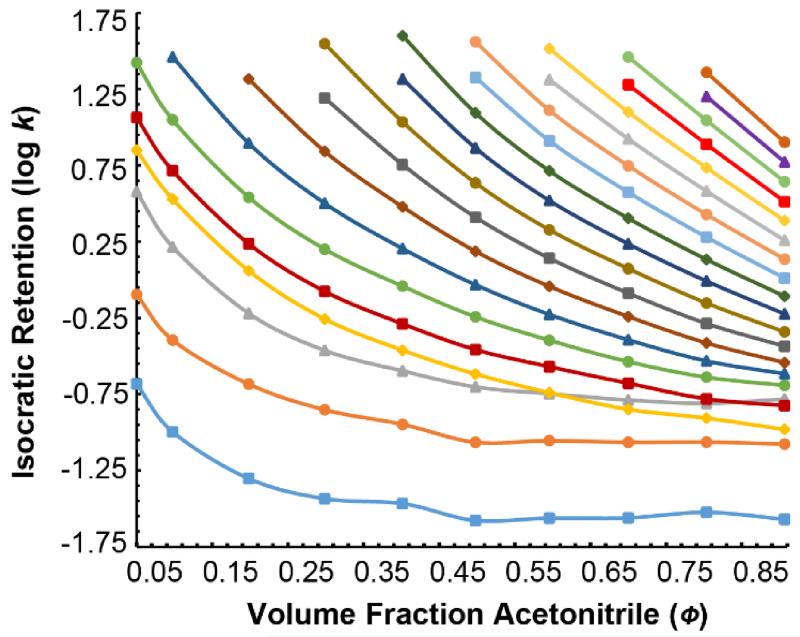
The “reference” lab (a lab separate from labs A-H) measured k as a function of Φ for each of the 39 compounds in the test mixture from a series of isocratic runs. Fig. 2 shows log k vs. Φ measured for the 20 instrument calibration standards and Fig. 3 shows the same for the 19 test compounds. The retention factors were measured at 10 different Φ from 5 to 90% B (5, 10, 20, 30, 40, 50, 60, 70, 80, and 90%, in that order) at 35.0 °C and 0.4 mL/min flow rate. Solvent A was 0.100% (v/v) formic acid in water and solvent B was 0.100% (v/v) formic acid in acetonitrile. Solvent A was prepared gravimetrically by adding 0.610 g formic acid to 498.00 g of water, while Solvent B was prepared by adding 0.610 g formic acid to 393.11 g of acetonitrile. (These ratios were calculated so that the volume fraction of formic acid would be precisely 0.100% at 20 °C using the densities for water, acetonitrile, and formic acid at 20 °C found in the 95^th edition of the CRC Handbook [32].) The column was held in a forced air oven, and the air temperature was determined to be within ±0.1 °C of the 35.0 °C set temperature by a secondary platinum reference standard temperature probe placed inside the oven on plastic standoffs. The column was equilibrated with 20 column volumes of eluent before each run. At the end of each run, compounds that did not elute were cleared out by running 95% B through the column for 10 min.

Figure 2.

Isocratic log k vs. solvent composition for the 20 instrument calibration standards. These include N-hexadecylbenzamide (), N-pentadecylbenzamide (), N-tetradecylbenzamide (), N-tridecylbenzamide (), N-dodecylbenzamide (), N-undecylbenzamide (), N-decylbenzamide (), N-nonylbenzamide (), N-octylbenzamide (), N-heptylbenzamide (), N-hexylbenzamide (), N-pentylbenzamide (), N-butylbenzamide (), N-propylbenzamide (), N-ethylbenzamide (), N-methylbenzamide (), benzamide (), N,N-dimethylpropionamide (), N-ethylacetamide (), and N-methylacetamide ().

Figure 3.

Isocratic log k vs. solvent composition for the 19 test compounds. These include N,N-diethylacetamide (), N-allyl aniline (), 1,3-naphthalenediol (), diphenylamine (), 7-amino-4-methylcoumarin (), naphthalene acetamide (), 2-phenylindole (), anilinoacetaldehyde diethyl acetal (), tetrabutylammonium (), abscisic acid (), tetrapentylammonium (), prednisone (), cortisone (), hydrocortisone (), curcumin (), chlorogenic acid (), p-coumaric acid (), dodecanophenone (), and di-n-pentyl phthalate (). Though the relationships are difficult to distinguish, one can see that they cover a wide range in retention and that the relationships do not generally run parallel to one another as is assumed in linear retention indexing.

Retention factors, k, were calculated using k = (t_R – t₀)/(t₀ – t_i) where t_R is the retention time (measured from the apex of each peak), t₀ is column dead time, and t_i is the instrument dead time (the time it takes for an injected solute to reach the detector when the column is bypassed). The data acquisition rate of the MS detector was not a major factor contributing to error as the acquisition rate was roughly 10 Hz (corresponding to a mass spectrum every 0.002 min). Thiourea was spiked into the test mixture and used as the dead time marker. Although it is slightly retained at lower acetonitrile concentrations, thereby biasing the retention factors, it does not bias the back-calculated gradient or the projected retention times because the t₀ used in the t₀ vs. Φ profiles that are used to project retention times is also a thiourea dead time, canceling any bias it might have otherwise caused. To measure the instrument dead time, the column was first removed and replaced with a zero dead volume connector. Then the test mixture was subjected to an isocratic run at 50% B and 0.4 mL/min flow rate and the tetrabutylammonium ion (242 m/z) was monitored, which is convenient because it gives an especially strong MS signal. The elution time of tetrabutylammonium was then used as the instrument dead time.

2.4 Instrumentation

Isocratic k vs. Φ relationships of the 39 compounds and LRIs were measured in the reference laboratory with a Thermo Scientific (Sunnyvale, CA) Ultimate 3000 RS LC coupled to an Ultimate TCC-3000RS column oven equipped with a 2 μL pre-column heater and a Bruker (Billerica, MA) Amazon SL ion trap.

Other laboratories that participated in the study used different instrumentation: Labs A and G used an Agilent 1290 Infinity HPLC coupled to an Agilent Q-TOF 6530 MS and an Infinity 1290 column oven with a built-in 3 μL pre-column eluent heater. Lab B used a Thermo Scientific Dionex Ultimate 3000 LC coupled to a Thermo Scientific Q Exactive MS and an Ultimate TCC-3000SD forced air oven with no pre-column eluent heater. Lab C used a Thermo Scientific (Sunnyvale, CA) Accela 600 LC coupled to a Thermo Scientific TSQ Vantage MS and an Accela 600 forced air oven with a built-in 3 μL pre-column eluent heater. Lab D used a Waters (Milford, MA) Acquity LC coupled to a Waters Xevo G2 TOF MS and an Acquity column oven with a built-in 3 μL pre-column eluent heater. Lab E used a Waters Acquity LC coupled to an MS and an Acquity adiabatic column oven with a built-in 3 μL pre-column heater. Lab F used an Agilent 1290 Infinity LC coupled to a Varian MS and an Infinity 1290 adiabatic column oven with a built-in 3 μL pre-column heater. Lab H used a Varian 212-LC pump coupled to a Varian 500-MS ion trap with an oven with no pre-column eluent heater.

2.5 Software

The HPLC retention projection software was compiled for compliance with the Java 1.6 (Oracle, Redwood Shores, CA) runtime environment. It includes the Java OpenGL (JOGL) binding library version 2.0-rc11 (JogAmp, http://jogamp.org), the Unidata netCDF library version 4.2 (Unidata®, Boulder, CO), the Savitzky-Golay filter library version 1.2 by Marcin Rzeźnicki (http://code.google.com/p/savitzky-golay-filter/), the jmzML library [33], and the jmzReader library [34]. The source code may be downloaded from http://www.retentionprediction.org/hplc/development.

2.6 Inter-laboratory study protocol

Each of eight laboratories received an Eclipse Plus C18 column (100 mm long, 2.1 mm i.d., 3.5 μm particle diameter), a test mixture (see Materials and Methods), and a protocol describing the experiments to perform. Before shipping the columns to labs A-H, the reference lab conditioned them according to the procedure described above and then tested to ensure that retention projections were equally accurate on each one.

Each laboratory was given a protocol with detailed instructions for preparing mobile phases A and B (0.100% formic acid in water and 0.100% in acetonitrile) gravimetrically to better than ±0.001% and how to measure their instrument dead time according to the procedure described above. It then instructed each lab to run a total of ten gradient methods (the column oven temperature was to be set to 35 °C for all experiments). The first four of these methods were fixed to be the same in each lab and were selected to cover a range of gradient slopes and flow rates. These four methods provided a way to test the ability of the methodology to account for unintentional differences between the HPLC systems since all of the controllable experimental conditions were held nominally the same in each lab. The last six methods were selected independently by each lab (see Supporting Information for descriptions of each method) to test the ability of the retention projection methodology to account for intentional differences in gradients and flow rates between labs. See Results and Discussion for details.

Certain commercial equipment, instruments, or materials are identified in this document. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products identified are necessarily the best available for the purpose.

3. Results/Discussion

3.1 Accounting for unintentional differences between labs

For the first part of the study, all eight laboratories ran nominally the same set of four methods so that any differences in the chromatograms obtained by each lab were the result of unintentional experimental differences that are not easily controlled. (Lab H was excluded from the following discussion for reasons described at the end of this section.)

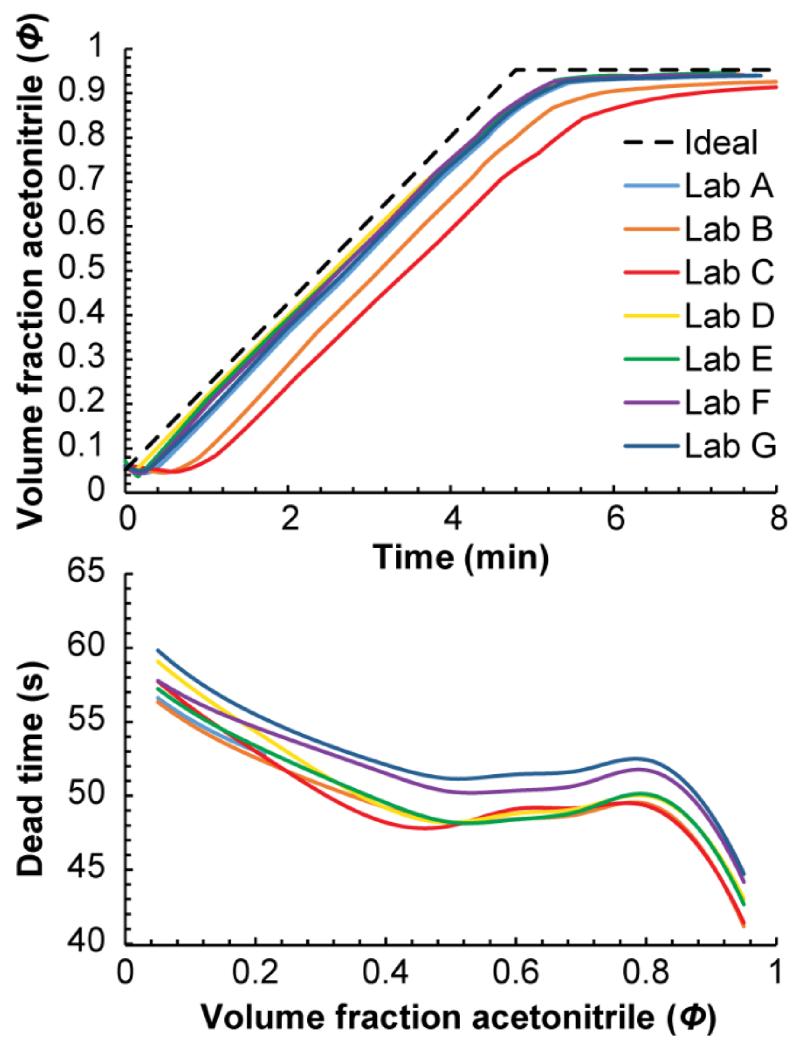
Such unintentional differences between the labs were important. Figure 4 shows the gradient and t₀ vs. Φ profiles back-calculated in seven of the labs from the retention times of the instrument calibration solutes in method 1 (a 5 min gradient from 5% to 95% B at 0.4 mL/min). The most important difference was the gradient delay, which spanned from ~10 s in lab F to more than 60 s in lab C. The amount of gradient dispersion, (i.e. rounding of the gradient) also varied significantly, with labs B and C showing a relatively large amount of dispersion compared to the other five; they did not even reach the final solvent composition by the end of the run. It also appears that solvent proportioning was different between the labs. For example, among labs A and D–G (the labs actually reached the final solvent composition before the end of the run), the effective final solvent compositions reached by the pumps varied by up to 0.6% B. The t₀ vs. Φ profiles also varied between labs, but to a lesser extent. These differences could reflect differences in the flow rates produced by the HPLC instruments combined with small differences between the columns’ dead volumes.

Figure 4.

Back-calculated gradient (top) and t₀ vs. Φ profiles (bottom) from method 1 for labs A-G in the study. There are significant differences in the profiles produced by each HPLC system even though the experimental conditions were nominally the same.

When interpreting the back-calculated profiles, it is important to keep in mind that although they are a good measure of the overall shape of gradients, small features/discontinuities should be ignored. Also, the shape of back-calculated profiles are affected when experimental factors that are not currently taken into account are significant, for example, if the column temperature is a bit inaccurate [25] or the column is slightly aged. Therefore, to a small extent, differences between the profiles may actually reflect differences in other experimental conditions. In addition, the back-calculated profiles are influenced by imperfections in the reference HPLC system used to measure the k vs. Φ relationships. In this case, it seems likely that the reference pump produced solvent compositions that were too high when it attempted to produce solvent compositions around 90-95% B, causing all the back-calculated gradients to appear to never quite reach the final solvent composition. Finally, it is important to understand that the “dead time” described by the t₀ vs. Φ profile is actually the thiourea retention time vs. Φ relationship (thiourea is slightly retained at low Φ). We use the thiourea retention time as the dead time because of the experimental simplicity of measuring it rather than measuring the true, kinetic dead time [35,36]. The slight retention of thiourea does not add significant error to retention projections, rather, it cancels out since all of the retention factors were calculated using thiourea as the dead time marker.

Table 1 shows an example of the accuracy of retention projections from just one of the labs (lab A) after taking into account the back-calculated profiles. For comparison, the accuracy of retention times calculated from LRIs are also shown. The LRIs were measured in the same method, but on an HPLC system in the reference lab (the reference lab is also the one that measured the k vs. Φ relationships used to calculate retention projections; it is not one of the Labs A-H), using the 20 instrument calibration standards in the test mixture as retention indexing standards. While LRIs were accurate to ±1.67 s overall, retention projections were almost three-fold more accurate, to ±0.62 s overall. This is remarkable considering that retention projections were calculated using data measured under very different conditions (i.e., they were calculated from a set of isocratic runs) while the LRIs were measured under nominally the same gradient, just on a different LC system. Even so, retention projections were more accurate than LRIs because they were able to properly account for unintentional differences between the HPLC systems. These differences caused the biggest errors in LRIs for N-allyl aniline, tetrapentylammonium, and chlorogenic acid because their k vs. Φ relationships were unusually steep or shallow compared to the standards bracketing them.

Table 1. Accuracy of Retention Projections and Linear Retention Indices in Method 1^a Run by Lab A.

Test compound	Measured retention time (s)	RP errorb (s)	LRI errorc (s)
N,N-diethylacetamide	124.69	0.17	−0.93
N-allyl aniline	162.73	0.52	4.76
1,3-naphthalenediol	N.D.d	--	--
p-coumaric acid	260.67	0.17	0.02
diphenylamine	280.42	0.19	−0.37
7-amino-4-methylcoumarin	160.20	0.62	−0.67
naphthalene acetamide	177.03	0.37	−0.31
2-phenylindole	285.58	0.17	−0.50
anilinoacetaldehyde diethylacetal	260.67	0.19	−0.44
tetrabutylammonium	199.19	1.40	0.41
dodecanophenone	N.D.d	--	--
abscisic acid	176.44	0.40	−0.56
tetrapentylammonium	243.91	0.81	1.30
di-n-pentyl phthalate	355.05	−0.62	−0.72
chlorogenic acid	107.66	0.93	−4.34
prednisone	177.20	0.81	−0.74
cortisone	180.50	0.43	−0.38
hydrocortisone	178.40	0.49	−0.28
curcumin	249.25	0.40	0.54
Overall error: e		±0.62	±1.67

^aMethod 1: 5% to 95% B in 5 min, then hold at 95% B for 5 min. The flow rate was 0.4 mL/min.

^bReported as the measured retention time minus the projected retention time. k vs. Φ relationships used to calculate the retention projections were measured in the reference lab.

^cReported as the measured retention time minus the retention time calculated from LRIs measured under the same method, but in the reference lab.

^dNot determined. The compound was not detected by this system.

^eOverall error is the root-mean-square (RMS) error of all compounds (i.e., the error at one standard deviation).

As an aside, it may be surprising that the retention of a compound like N-allyl aniline, which has a pKa close to the pH of the mobile phase, can be projected accurately even though its degree of protonation changes as a function of Φ. The reason is that its degree of protonation as a function of Φ is taken into account when the k vs. Φ relationships are measured. Indeed, this is likely the reason that N-allyl aniline’s k vs. Φ relationship has an unusual shape (Figure 1) compared to other compounds. During a gradient run, N-allyl aniline exhibits the same degree of protonation when it momentarily experiences a particular Φ as it does in an isocratic run at that same Φ, so the accuracy of retention projections are virtually the same as for other compounds.

Table 2 shows the overall errors in retention projections and in LRIs from the rest of the labs and methods. In each case, LRIs were measured from the same nominal method run in the reference lab. The table requires some additional explanation as it is split into two more subcategories: “charged test compounds” and “uncharged test compounds”. The charged test compound category includes just two compounds that are fully charged at the pH of the mobile phase: tetrabutylammonium and tetrapentylammonium. The uncharged test compound category includes all of the other 17 test compounds, though it must be noted that three of them (see section 2.1) have pK_as near the mobile phase pH and are partially charged. The data are split among charged and uncharged test compounds because retention projections and LRIs for charged compounds were significantly less accurate than uncharged compounds in some of the labs.

Table 2. Accuracy of Retention Projections and Linear Retention Indices in Methods 1–4 in Labs A–G.

		Uncharged test compoundsb		Charged test compoundsc
Methoda	Lab	RP error (s)d	LRI error (s)d	RP error (s)d	LRI error (s)d
1	A	±0.52	±1.74	±0.94	±0.97
	B	±0.62	±0.64	±0.64	±0.38
	C	±0.94	±0.99	±1.52	±0.40
	D	±0.99	±3.47	±1.34	±1.2
	E	±0.70	±2.30	±2.39	±3.37
	F	±0.61	±2.24	±4.06	±5.07
	G	±0.27	±3.30	±0.47	±1.06
Overall error:		±0.66	±2.1	±1.97	±1.78
2	A	±2.23	±2.96	±5.68	±7.55
	B	±2.01	±1.96	±2.57	±3.59
	C	±3.67	±4.35	±7.47	±9.65
	D	±4.07	±3.69	±5.20	±6.01
	E	N.P.e	N.P.e	N.P.e	N.P.e
	F	±1.96	±3.71	±20.71	±19.92
	G	±1.96	±2.62	±1.53	±2.68
Overall error:		±2.35	±3.21	±8.16	±8.23
3	A	±1.04	±3.98	±4.01	±4.31
	B	±0.78	±1.92	±2.47	±2.04
	C	±1.54	±1.47	±2.88	±0.47
	D	±1.55	±3.55	±3.36	±3.9
	E	±1.10	±4.87	±4.18	±5.25
	F	±1.02	±5.17	±7.94	±10.41
	G	±1.00	±4.9	±1.59	±3.11
Overall error:		±1.15	±3.69	±4.67	±4.21
4	A	±0.75	±1.42	±2.45	±2.58
	B	±1.35	±0.99	±1.79	±1.91
	C	±2.34	±2.57	±2.60	±2.98
	D	±1.05	±2.15	±2.59	±5.3
	E	±1.10	±1.6	±4.18	±2.79
	F	±0.74	±1.49	±5.47	±7.10
	G	±1.28	±0.85	±1.25	±1.22
Overall error:		±1.33	±1.58	±3.07	±3.41

^aAll methods were linear gradients from 5% B to 95% B, and were followed by a hold at 95% B for 5 min. Method 1 was a 5 min gradient, method 2, a 30 min gradient, and methods 3 and 4 were 10 min gradients. The flow rate in methods 1 and 2 was 0.4 mL/min, in method 3 it was 0.2 mL/min, and in method 4 it was 0.8 mL/min.

^bUncharged test compounds include all except tetrabutylammonium and tetrapentylammonium (a total of 17). N-allyl aniline was omitted from Lab D’s results as discussed in the main text.

^cThe charged test compounds are tetrabutylammonium and tetrapentylammonium.

^dError is reported as the root-mean-square (RMS) error of all compounds (i.e., the error at one standard deviation).

^eNo data provided for that run.

The lower accuracy for charged compounds was likely caused by a change in the selectivity of the columns over time. In some cases there was a delay of several months between initial equilibration of the columns and when the experiments were run. The change in column selectivity was confirmed by re-testing columns returned from labs D, F, and G to the reference lab. Though retention projections were initially accurate on these columns before shipping them to the labs, the accuracy was lower upon their return, matching the accuracy measured in the labs. For example, right after conditioning a new column, the error in the retention projection for the charged compound tetrapentylammonium was found to be 1.21 s (method 1) in the reference lab. The column was then sent to lab F where four months later the error was measured to be 5.88 s. Then the column was returned to the reference lab where the error was measured to be 5.23 s, nearly the same as that measured by lab F. These observations match those of others [37,38], where stationary phase degradation disproportionately affects charged compounds, likely because more silanols become exposed.

Looking at the uncharged compounds in Table 2, retention projections were more accurate than LRIs in 22 of the 27 runs, averaging 2-fold more accurate overall. Methods 1 and 3 showed the biggest difference, each being 3-fold more accurate than LRIs. This is because these two methods had the steepest gradients, causing differences in gradient delay and dispersion between labs to be more pronounced, factors which LRI cannot properly take into account. On the other hand, the difference in accuracy is less pronounced in the shallower gradients of methods 2 and 4 because the HPLC pumps were able to produce gradients with higher fidelity.

The accuracy of retention projections was also more consistent than LRIs. For example, the error in retention projections for each lab’s method 1 ranged from ±0.27 to ±0.99 s, while that for LRIs ranged from ±0.64 to ±3.47 s. Therefore, even when experimental conditions were nominally the same between labs, which is the best situation for linear retention indexing since differences in the experimental conditions of each lab will be as small as practically possible, the retention projection methodology was still more accurate because it properly accounted for the unintentional differences between the HPLC systems. Furthermore, most of the labs involved in this study had high-end HPLC systems with the lowest gradient delay and dispersion on the market. With a wider range of HPLC systems, these unintentional differences would be even more pronounced and the accuracy of LRIs would drop further while that of retention projections should be unaffected.

Among the eight labs involved in the study, a few experimental differences were encountered that neither retention projection nor LRI could properly take into account. For example, the first time lab G ran the test mixture, the accuracy of retention projections (and LRIs) were poor for all of the test compounds and particularly for N-allyl aniline, which in method 2, for example, eluted 28 s earlier than projected. We suspected that this was because the column temperature was too cool, so the effect of column temperature on the accuracy of retention projections was tested (see Supporting Information) and similar behavior was found: When the temperature was decreased from 35 °C to 30 °C, error in retention projections for the test compounds increased in magnitude from ±0.71 s to ±2.7 s and N-allyl aniline eluted 7 s earlier than projected. When the temperature was increased to 40 °C, error in retention projections for the test compounds increased in magnitude to ±3.3 s and N-allyl aniline eluted 10 s later than projected. The effect of temperature on the retention of N-allyl aniline is opposite that of most other compounds because its pK_a is near the pH of the mobile phase and its pK_a is strongly temperature-dependent [39]. At high T, more N-allyl aniline is in the neutral form (thus increasing its retention) and at low T, more of it is in the protonated form (thus decreasing retention). In this way, error in the retention projection for N-allyl aniline, combined with an increase in error for the rest of the test compounds, serves as an indicator that the column temperature is too high or too low. Lab G checked and confirmed that their column oven was not working properly. They solved the problem by using a different column oven.

Proper pre-column eluent heating was also found to be an important factor. Lab H was using an external, still air column oven without a pre-column eluent heater and all of their runs showed the same symptoms of low column temperature (i.e., N-allyl aniline eluted much earlier than projected and the other retention projections had systematically high error). Still air ovens are especially reliant on proper pre-column eluent heating because heat transfer to the column (and incoming eluent) from the surrounding air is so poor [24,40]. To bring up the incoming eluent temperature, they tried to create a makeshift pre-column heater by inserting a 30 cm coil of stainless steel tubing into the oven immediately before the column. It improved the accuracy of retention projections from ±2.9 s to ±1.7 s (method 4), but that error was still higher than the error from most other labs. When they then increased their oven’s set temperature to 40 °C, the accuracy improved further to ±0.8 s, suggesting that the improvised pre-column eluent heater was not totally effective. Since this lab could not properly control their column temperature, we excluded their data from the analysis.

Finally, one of the other labs (Lab D) showed consistently high error for N-allyl aniline. In that lab, N-allyl aniline eluted far earlier than projected (e.g., in methods 1 and 2, it was 11 s and 21 s early), but the accuracy of retention projections for the other test compounds were unchanged, which is inconsistent with a temperature-related problem. It is, however, consistent with mobile phases containing too little formic acid. When the reference lab decreased the formic acid concentration from 0.100% to 0.090%, a similar effect was observed: error in the N-allyl aniline retention projection increased two-fold (eluting much earlier than projected), but it had very little, if any, effect on the retention of the rest of the test compounds (see Supporting Information). Therefore, the N-allyl aniline retention projections and LRIs were omitted from Lab D’s results.

3.2 Accounting for intentional differences between labs

For the second part of the study, the accuracy of retention projections were compared with LRIs when the experimental conditions (i.e., the gradient program and flow rate) were purposefully changed. Each lab ran a set of six methods that they came up with independently: the first three were methods commonly used in their laboratories while the next three were methods that they thought might “stretch the retention projection methodology” (see Supporting Information). Certain constraints were placed on these methods (these constraints should not bias the results more favorably toward retention projections or LRIs): (a) the Eclipse Plus C18 column shipped to each lab had to be used, (b) the mobile phase solvents had to be prepared according to the protocol, (c) Φ had to be in the range of 5% to 95%, (d) the total gradient time had to be ≤60 min, (e) the MS had to scan faster than 2 Hz, (f) the injection volume had to be 1 μL, (g) the flow rate had to be between 0.2 and 0.8 mL/min, (h) the column oven temperature had to be 35 °C, and (i) the wash solvent had to be weaker than the test mixture solvent. No two labs chose the same method. A wide range of gradients, often multi-segment gradients, were chosen that covered the full range of allowed flow rates.

Table 3 shows the accuracy of retention projections and LRIs for the first two of these six methods in each lab (the other methods are listed in Supporting Information). Over all of the methods in all of the labs (including those not shown), retention projections for uncharged compounds were 22-fold more accurate than LRIs, being up to 60-fold more accurate in one method. Retention projections for charged compounds, though partially compromised by column selectivity changes in some labs, were still 10-fold more accurate than LRIs over all of the methods and up to 112-fold more accurate in one of the methods. While the accuracy of LRIs were strongly dependent on the gradients and flow rates chosen by each lab, retention projections were consistently accurate because they properly took the differences into account.

Table 3. Accuracy of Retention Projections and Linear Retention Indices in Methods 5 and 6 from Labs A–G.

		Uncharged test compounds		Charged test compounds
Lab	Methoda	RP error (s)	LRI error (s)	RP error (s)	LRI error (s)
A	5	±0.72	±26.91	±1.05	±62.32
A	6	±2.56	±36.22	±0.99	±111.31
B	5	±0.72	±2.88	±1.26	±6.08
B	6	±0.98	±23.6	±2.10	±39.88
C	5	±1.81	±11.79	±3.39	±23.62
C	6	±1.60	±18.0	±4.40	±7.43
D	5	±1.11	±8.49	±3.50	±14.95
D	6	±1.34	±18.28	±4.79	±29.35
E	5	±1.38	±44.3	±4.47	±97.25
E	6	±1.86	±48.94	±4.53	±103.86
F	5	±0.37	±55.43	±3.28	±10.92
F	6	±0.71	±2.70	±7.37	±3.20
G	5	±1.95	±29.63	±8.36	±58.32
G	6	±1.17	±3.76	±2.66	±3.57
Overall error: b		±1.90	±42.28	±5.42	±52.36

^aThe methods are each described in Supporting Information.

^bRMS error of all methods 5–10 in each of the seven labs (i.e., those not shown are also included).

4. Conclusions

The retention projection methodology provided a way to accurately and reliably predict LC retention times across labs using a single shared database of retention, even when the labs used a range of multi-segment gradients and flow rates. LC retention times were predicted in seven different labs with consistently higher accuracy than linear retention indexing, which until now has been the most reliable way to share LC gradient retention data across labs for over 50 years. Unintentional differences between the gradients and t₀ vs. Φ profiles produced by each lab were measured (and taken into account) using software that back-calculates the profiles from the retention times of a set of 20 standards. Therefore, even when each lab used nominally the same experimental conditions, which is the ideal case for retention indexing, retention projections still averaged 2-fold more accurate, with larger gains in steeper gradients where the gradients produced by the HPLC pumps were less ideal. Then, when each lab ran a range of multi-segment gradients and flow rates of their choosing, the retention projection methodology averaged 22-fold more accurate because it properly accounted for the intentional experimental differences. To the best of our knowledge, this is the most successful study to date aiming to calculate (or even just to reproduce) LC gradient retention across labs, and it is the only study in which retention was accurately calculated under a range of gradients and flow rates chosen independently by multiple labs.

Even so, some unintentional differences between the labs could not be taken into account by retention projection or linear retention indexing. Most importantly, the columns’ selectivity for charged compounds changed significantly over the course of several months. In the future, it will be important to either correct retention projections for this change in selectivity and/or to have column suitability checks built into the workflow to determine if a particular column is suitable for projections of charged compounds. An example of such a suitability check is described in the following, companion manuscript [41]. We also expect the accuracy of retention projections for all compounds (charged and uncharged) could be improved by taking into account distortion of the gradient from the column (“solvent demixing”) [21,22], pressure effects [23], and frictional (viscous) heating of the column [24].

The retention projection methodology shows potential as a tool to enable more labs to harness LC retention information for compound identification, but at this point a major drawback of the methodology is the effort required to measure k vs. Φ relationships. We are currently working to develop much faster and easier ways to measure the relationships so that it is more practical for individuals to measure their own data, perhaps with other stationary phases, temperatures, and mobile phases. In the meantime, we are building an open-access database of k vs. Φ relationships on the Eclipse Plus C18 phase, which is available in its current state at www.retentionprediction.org/hplc/database.