Abstract
The framing of decision scenarios in terms of potential gains versus losses has been shown to influence choice preferences between sure and risky options. Normative cognitive changes associated with aging have been known to affect decision-making, which has led to a number of studies investigating the influence of aging on the effect of framing. Mata, Josef, Samanez-Larkin, and Hertwig (2011) systematically reviewed the available literature using a meta-analytic approach, but did not include tests of homogeneity nor subsequent moderator variable analyses. The current review serves to extend the previous analysis to include such tests as well as update the pool of studies available for analysis. Results for both positively and negatively framed conditions were reviewed using two meta-analyses encompassing data collected from 3,232 subjects across 18 studies. Deviating from the previous results, the current analysis finds a tendency for younger adults to choose the risky option more often than older adults for positively framed items. Moderator variable analyses find this effect to likely be driven by the specific decision scenario, showing a significant effect with younger adults choosing the risky option more often in small-amount financial and large-amount mortality-based scenarios. For negatively framed items, the current review found no overall age difference in risky decision making, confirming the results from the prior meta-analysis. Moderator variable analyses conducted to address heterogeneity found younger adults to be more likely than older adults to choose the risky option for negatively framed high-amount mortality-based decision scenarios. Practical implications for older adults are discussed.
Keywords: aging, decision-making, framing
Introduction
Adults are often faced with the necessity of making decisions with personally important consequences, such as the selection of prescription drug plans, and the timing of retirement and collection of social security benefits. When facing complex choices, individuals often times employ decision making heuristics as a method of reducing cognitive demands to ensure that current processing does not exceed capacity (Payne, 1976). Compared to younger adults, older adults have been shown to more readily employ simpler, heuristic driven (or noncompensatory) strategies (Johnson, 1990; also see Peters, Finucane, MacGregor, & Slovic, 2000), effectively conserving cognitive resources (Hess, Rosenberg, & Waters, 2001) as a method of compensating for age-related cognitive decline. Specifically in the domain of risky decision-making, affective response to choice variables has been shown to influence how individuals assess risk and ultimately reach decisions (Slovic, Peters, Finucane, & MacGregor, 2005). These decision making biases can have tangible financial consequences for older adults by affecting the way they choose to optimize retirement benefits as well as address potential fraud and financial exploitation. Considering that older adults are more likely to be drawn to decision making heuristics, especially when faced with cognitively taxing decisions, it is important to understand how these heuristics influence decision making across the lifespan.
The Framing Effect
In the realm of decision-making, subtle changes in the wording of decision scenarios have been shown to influence choice preferences. A particularly reliable manipulation is the tendency of questions phrased in a manner that underscores the positive or negative aspects of a scenario to promote risk averse or risk seeking choices, respectively. Coined the “framing effect” by Tversky and Kahneman (1981), this manipulation is best demonstrated by their “Asian disease” problem:
Problem 1:
Imagine that the U.S. is preparing for the outbreak of an unusual Asian disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimate of the consequences of the programs are as follows:
If Program A is adopted, 200 people will be saved.
If Program B is adopted, there is a 1/3 probability that 600 people will be saved and 2/3 probability that no people will be saved.
Which of the two programs would you favor?
This positively framed pair of options can be contrasted with a negatively framed pair of logically identical options:
Problem 2:
If Program C is adopted, 400 people will die.
If Program D is adopted, there is a 1/3 probability that nobody will die and 2/3 probability that 600 people will die.
Which of the two programs would you favor?
In this example, the choices between Problem 1 and Problem 2 are logically equal. One can choose the option where 200 people will live and 400 people will die or the option with a 1/3 chance of all people living and 2/3 chance of all people dying. Still, a pattern emerges in the responses with the majority of respondents choosing the sure option (Program A) in Problem 1, where the options are phrased in a manner that highlights the positive aspects of the scenario, and the risky option (Program D) in Problem 2, where the negative aspects are highlighted. In a meta-analysis comprised of 230 effect sizes calculated from 136 separate studies, Kuhberger (1998) found that that the framing effect is a reliable phenomenon with a moderate mean effect size of d = .31 between conditions. While numerous models explain the framing effect (see Kuhberger, 1997), Kahneman and Tversky’s (1979) own prospect theory explains the framing effect as a result of individuals’ tendency to overvalue losses when compared to gains of the same magnitude.
Prospect Theory and the Framing Effect
Prospect theory, an extension of previous theories that posit that agents evaluate options as purely a function of their expected value (value weighted by probability) or expected utility (a function of expected value, risk aversion, and perceived utility; for an overview of expected utility theory see: Von Neumann & Morgenstern, 1947; Fishburn, 1970), describes a two-step decision-making process for an agent asked to indicate a preference between two probabilistic alternatives (Kahneman and Tversky, 1979). The first phase is composed of an editing process that, through the application of various heuristics, simplifies the decision-making scenario. In the second phase, the results of the editing process are evaluated and a decision is made. The value manipulation in the framing effect (describing scenarios in terms of either gains or losses) has influence in both steps of the decision-making process detailed in prospect theory.
Editing phase
Under prospect theory, subjective value is manipulated in the editing phase through a heuristic labeled “coding”. As opposed to considering outcomes by their final state, outcomes are perceived as gains and losses relative to a neutral reference point. Consider two choice scenarios described by Kahneman and Tversky (1979). In the first scenario, the agent is given $1,000 and then asked to choose between a sure increase of $500 and a 50% chance of gaining $1,000 (and a 50% chance of gaining $0). In the second scenario, the agent is given $2,000 and then asked to choose between a sure loss of $500 and a 50% chance of losing $1,000 (and a 50% chance of losing $0). Through the viewpoint of expected utility, these two scenarios are identical as a net positive outcome (both describe a scenario where the agent can choose between a sure increase of $1,500 or a risky choice where one has a 50% chance of gaining $1,000 and a 50% chance $2,000). Prospect theory, on the other hand, would predict that the agent would mentally edit the decision scenario before evaluation of the choices and ultimately reaching a decision. Through coding of the different descriptions provided in the scenarios, the agent would likely set their reference point after the initial gift of $1,000 or $2,000, resulting in the outcome choices being perceived as gains (in the first scenario) or losses (in the second scenario). Indeed, Kahneman and Tversky (1979) report experimental data showing a significant shift in preference between the sure (perceived gain scenario) and risky (perceived loss scenario) options that should not be apparent if individuals’ were appraising the choices in terms of their expected utility.
Evaluation phase
During the evaluation phase of the decision-making process, additional hypothetical weights are applied to both the values and probabilities associated with risky decisions, and our focus here is on the weighting of the value function, which directly influences the previously described framing effect.
The value function
Kahneman and Tversky (1979) propose that the value function is “S”-shaped, defined by a concave function above the reference point and a convex function below the reference point (see Figure 1). This function has several notable features. First the slope of the value function tapers off as the outcome value moves away from zero. Reminiscent of Weber’s law (size of just-noticeable difference threshold is proportional to the stimulus magnitude) for human perception, the difference between subjective values of gains or losses decreases as the outcome value increases (or decreases) further from zero. As an example, Tversky and Kahneman (1981) state that the difference between $10 and $20 is perceived as larger than between $110 and $120 in both gain and loss conditions. Second, losses are subjectively overvalued compared to gains, represented by a greater slope of the value function in the “losses” domain of the outcome value. In terms of money, this indicates that the subjective value of a loss would be perceived as larger than that of an objectively equivalent gain. As a simple example, Tversky and Kahneman (1981) point to individuals’ “reluctance to accept fair bets on a toss of a coin.” This difference in subjective evaluation influences individuals to embrace sure options in gain scenarios and risky options in loss scenarios. In the terms of the decision scenario described in the above section on the editing phase, the sure option is preferred in gain scenarios because the subjective value given to a sure gain of $500 is larger than 50% of the value given to a gain of $1,000. The risky option is preferred in loss scenarios because the subjective negative value given to a sure loss of $500 is smaller than 50% of the negative value given to a loss of $1,000.
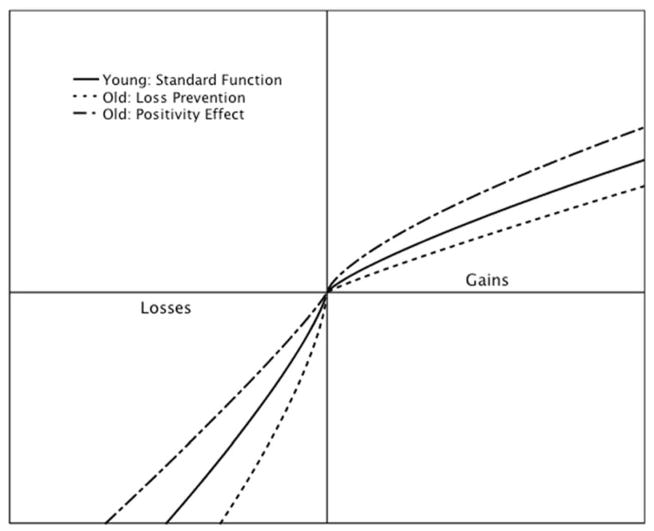
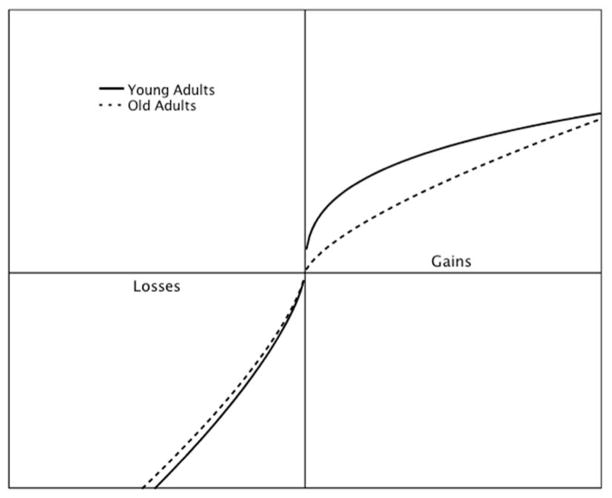
Figure 1.
Value functions for young adults (solid lines) and older adults as hypothesized by the “loss prevention” (short-dashed lines) and “positivity effect” (mixed-dashed lines) theories.
Aging and Framing
Normative aging is associated with numerous cognitive changes that affect decision-making across the lifespan. Contemporary theories provide affective based accounts to explain age differences in decision-making and the perceived values of gains and losses. Perhaps the most prevalent is the Socioemotional Selectivity Theory (Carstensen, Isaacowitz, & Charles, 1999), which posits that the decreasing future time perspective over the lifespan causes older adults to prefer to focus on positive aspects of their environment as a method of enhancing or maintaining their affective well-being. This trend results in a positivity effect, where older adults have been shown to display a higher preference towards diverting attention and memory resources towards positive material when compared to younger adults (Reed & Carstensen, 2012). An alternate goal orientation account theorizes that age-related changes in decision making are not driven by a preference for positive material (in this case, potential gains), but instead result from a lifespan trend where goal orientation shifts from growth and gains to maintenance and loss prevention as one ages (Ebner, Freund, & Baltes, 2006). Mata and Hertwig (2011) modeled these theories’ effects on the prospect theory’s value function, noting that the loss prevention account predicts a positive relationship between loss aversion and age (indicated by a steeper negative slope in perceived value in the loss domain) while the positivity effect account does not (Figure 1).
The loss prevention account effectively shifts the value function with age, predicting a larger prevalence of the framing effect in older adults in both gain and loss conditions (compare the solid and short-dashed lines in Figure 1). As goal orientation is shifted towards resource maintenance across the lifespan, older individuals will derive less utility from gains compared to their younger counterparts, leading to an increase in risk-averse choices in positively framed items. In the loss domain, older adult goals shift towards loss prevention, resulting in increased sensitivity to losses when compared to younger adults. For negatively framed items, this results in an increase in risk-seeking choices to potentially avoid losses. As interpreted by Mata and Hertwig (2011), the positivity effect predicts the reverse relationship, whereas younger adults are more likely to display the framing effect when compared to older adults (compare the solid and mixed-dashed lines in Figure 1). By focusing on the positive aspects of the decision scenarios, older adults are more sensitive to and derive more utility from positive outcomes (gains) than negative outcomes (losses). This would result in an increased likelihood for older adults to choose the risk-seeking option in gain scenarios and the risk-averse option in loss scenarios. These hypothesized relationships between framing and age were not supported in a recent meta-analysis (Mata, Josef, Samanez-Larkin, and Hertwig, 2011) and are reinvestigated in the current analysis.
In the earlier meta-analysis on the framing effect, Kuhberger (1998) made note of the fact that age was not coded for the analysis due to the lack of sufficient literature that systematically tested the effect of age on the framing effect. Researchers took note of this space in the framing literature and little more than a decade later enough studies were available to conduct a meta-analysis on the effect of age on the influence of framing (Mata el al., 2011). This later meta-analysis investigated age differences in risky choice in both gain and loss framing, but the article did not include tests of homogeneity or moderator variable analyses. Because these tests are necessary to complete and interpret meta-analytical results accurately, a second set of meta-analyses was conducted to re-investigate the effect of aging on the framing effect.
Method
Selection of Studies
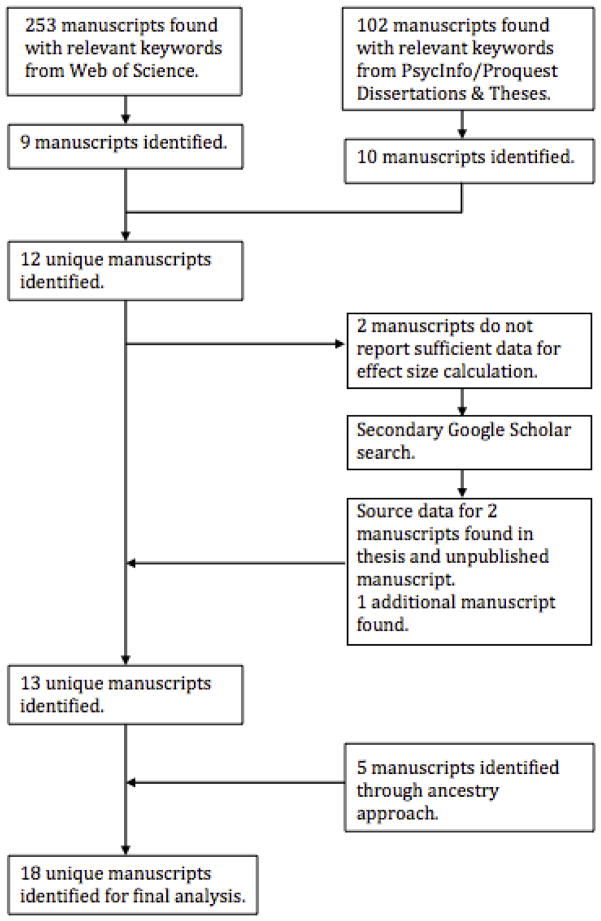
The current sample of studies was gathered through a two-step process illustrated in Figure 2. First, an initial online database search was conducted. The ProQuest (PsycINFO & Dissertations and Theses) and Web of Science databases were used to search for articles including the keywords “Aging OR older adults” AND “framing OR prospect theory” AND “decision making”. A total of 355 prospective articles were identified using this search method. Articles from the search pool were included in the final analysis if they conducted a risky-choice framing experiment with gain and/or loss framed conditions and had results reported for specific younger (e.g., 18–35 years old) and older adult populations (e.g., 60+ years old). Studies must have also provided sufficient data to compute an effect size comparing the two age groups. Fourteen potential abstracts, comprised of published articles and doctoral dissertations, were identified and subjected to further screening to ensure they met the inclusion criteria. Four of the published articles were excluded: two for not meeting the age group criteria and two for not reporting sufficient information to calculate an effect size (Woodhead, Lynch, & Edelstein, 2011; Tymula, Belmaker, Ruderman, Glimcher, & Levy, 2013), resulting in a pool of 10 studies.
Figure 2.
Search process.
Next, a secondary search was conducted by using Google Scholar with the same search terms described above. This search returned one new article as well as a thesis (Woodhead, 2006) and an unpublished manuscript (Tymula, 2012) that provided the source data for the two manuscripts rejected for reporting insufficient data to calculate an effect size. This secondary search was followed by an ancestry search of studies referencing and referenced by the set of 13 qualifying studies. The reference sections of each of the 13 articles were thoroughly scanned for relevant articles resulting in five additional published articles being identified. These five articles met the inclusion criteria and were combined with the articles found in the initial search to create a final pool of 18 studies for the meta-analysis.
The current analysis utilizes an expanded pool of studies compared to the Mata et al. (2011) analysis. Mata et al. calculated 21 effect sizes from 10 articles (11 in the positively framed condition and 10 in the negatively framed condition). The current analysis includes all 10 articles from the Mata et al. analysis, as well as three additional peer-reviewed journal articles and five doctoral dissertations and theses, a subset of papers often overlooked during meta-analysis literature searches. Ultimately, the current analysis utilized 51 effect sizes across the two conditions (27 in the positively framed condition and 24 in the negatively framed condition) calculated from 18 studies. In the current analysis, multiple effect sizes were calculated from multiple independent samples in five articles (Kim, Goldstein, Hasher, & Zacks, 2005; Mather et al., 2012; Ronnlund, Karlsson, Laggnas, Larsson, & Lindstrom, 2005; Thomas & Millar, 2012; Woodhead, 2006).
In the cases of Woodhead (2006, 2008) and Tymula (2012), effect sizes were calculated by retrieving data from unpublished manuscripts, theses, and dissertations that were the source material for later published peer-reviewed journal articles (Woodhead, Lynch, & Edelstein, 2011; Tymula et al., 2013) that did not include the information necessary for the calculation of effect sizes. The overall results and demographic data (sample size, age mean, age standard deviation) were compared between the published and unpublished documents to ensure that the data sets were identical.
Variables
A coding system was devised to draw relevant data from the final pool of studies. Ryan Best and Jacqueline Bartley independently coded the moderator variables for both the positive and negative frames from each of the studies (Kappa = .92 [Scenario]; .876 [Amount]). Coding differences were discussed until an agreement was made for the final coding value. All coding results can be seen in Table 1.
Table 1.
Effect Sizes by Study
| Source |
N
|
Task Characteristics
|
Effect Size (g)
|
|||
|---|---|---|---|---|---|---|
| Younger | Older | Scenario | Amount | Positive Frame | Negative Frame | |
| Bruine de Bruin et al. (2007) | 63 | 56 | Variable | Variable | 0.31 a | 0.04 a |
| “ (2007) | 63 | 56 | Mortality | Small | −0.03b | 0.03b |
| Holliday (1988) | 24 | 24 | Financial | Large | 0.11 | −0.21 |
| Karns (2013) | 119 | 106 | Mortality | Small | −0.69 | −1.26 |
| Kim et al. (2005) (1) | 53 | 53 | Mortality | Variable | 0.54a | 1.33a |
| “ (2005) (1) | 53 | 53 | Mortality | Small | 0.89b | 0.93b |
| Kim et al. (2005) (2) | 40 | 40 | Mortality | Variable | −.074a | 1.52a |
| “ (2005) (2) | 40 | 40 | Mortality | Small | −0.62b | 0.55b |
| Lauriola et al. (2001) | 26 | 23 | Financial | Large | −0.54 | 0.38 |
| Mather et al. (2012) (1) | 38 | 38 | Financial | Small | −0.80 | --- |
| Mather et al. (2012) (2) | 48 | 48 | Financial | Small | −0.86 | --- |
| Mather et al. (2012) (3) | 20 | 20 | Financial | Small | --- | 1.65 |
| Mather et al. (2012) (4) | 107 | 50 | Financial | Small | 0.06 | 0.36 |
| Mayhorn et al. (2002) | 58 | 58 | Variable | Variable | −0.59a | −.29a |
| “ (2002) | 58 | 58 | Financial | Large | −0.79b | 0.0b |
| McKee (2001) | 166 | 137 | Mortality | Small | 0.19 | 0.33 |
| Mikels et al. (2009) | 22 | 22 | Financial | Small | −0.03 | −0.70 |
| Ronnlund et al. (2005) (1) | 32 | 32 | Mortality | Large | −1.08 | −1.06 |
| Ronnlund et al. (2005) (2) | 32 | 32 | Financial | Large | 0.00 | −0.24 |
| Ronnlund et al. (2005) (3) | 32 | 32 | Financial | Large | 1.08 | 0.48 |
| Sproten et al. (2010) | 51 | 24 | Financial | Small | 0.05 | --- |
| Sproten (2012) | 36 | 18 | Financial | Small | −0.30 | --- |
| Thomas et al. (2012) (1) | 68 | 68 | Financial | Small | 0.12 | 0.07 |
| Thomas et al. (2012) (2) | 68 | 68 | Financial | Small | −0.15 | 0.04 |
| Thomas et al. (2012) (3) | 60 | 60 | Financial | Small | −0.04 | 0.75 |
| Thomas et al. (2012) (4) | 60 | 60 | Financial | Small | −0.08 | −0.04 |
| Tymula et al. (2012) | 34 | 36 | Financial | Small | −0.37 | −0.19 |
| Watanabe et al. (2010) (1) | 41 | 87 | Mortality | Variable | −1.13 a | --- |
| “ (2010) (1) | 41 | 87 | Mortality | Large | −0.89b | --- |
| Watanabe et al. (2010) (2) | 41 | 81 | Mortality | Variable | --- | −1.93 a |
| “ (2010) (2) | 41 | 81 | Mortality | Large | --- | −1.59b |
| Weller at al. (2011) | 358 | 61 | Financial | Small | −0.81 | −.10 |
| Woodhead (2006) (1) | 32 | 29 | Mortality | Small | −0.40 | 0.03 |
| Woodhead (2006) (2) | 31 | 29 | Mortality | Small | 0.80 | −0.44 |
| Woodhead (2008) | 40 | 40 | Mortality | Small | −1.25 | −.22 |
Indicates effect size used in meta-analysis, but excluded from moderator variable analyses when necessary to maintain assumptions of independence.
Indicates the effect size used in moderator variable analyses in lieu of a effect sizes when necessary to maintain assumptions of independence.
Numbers present after the source citation indicate separate effect sizes calculated from different sample populations reported within the same manuscript.
Dependent Variable
The results from each individual framed decision making scenario were coded as the numbers of sure and risky choices made for each age group in each of the framing conditions. For each choice scenario, the subject must make a binary choice indicating either the sure (risk-averse) or risky option. The number of sure and risky choices was recorded as either a mean (and standard deviation) of “sure/certain” choices made or as a proportion of the total sample size (n) for each age group. These values for both age groups were used to calculate a separate effect size for the positively and negatively framed versions of each question, resulting in two effect sizes for each decision scenario.
This coding system allows for the investigation of age differences in the influence of positive or negatively framed language on decision making by analyzing the standardized mean difference in the sure/certain choices between age groups. Unfortunately, this does not allow for the investigation of the “framing effect” which would require a within-subjects calculation of the standardized mean difference in the sure/certain choices between positive and negative frames. A within-subjects design of this nature would require the correlation of the response choices between frame conditions to be reported within each age group, but this information is not provided in the results of the current sample of studies. The underreporting of correlation data is a widespread issue and has been referenced as a common barrier to meta-analysis (Lipsey & Wilson, 2001; Cooper, Hedges, & Valentine, 2009).
Moderator Variables
Along with the dependent variable, data for moderator variables were coded when information was available from the article text. Moderator variable coding resulted in the ability to calculate multiple effect sizes in a single subject sample for six of the 18 studies. Due to the lack of reported correlation or covariance data between the effect sizes in these studies, these dependent effect sizes were unable to be utilized in a single meta-analysis without violating assumptions of independence of the data. Therefore, following the recommendation of Lispey and Wilson (2001), only one calculated effect size was selected to represent each of the six studies. The selection of effect size for each of these studies is discussed in a case-by-case basis after the descriptions of the moderator variables below.
Type of scenario
Various different decision scenarios were tested across the studies used in the current analysis. Across the pool of studies, decision scenarios almost exclusively described outcomes related to money or mortality. Studies were coded as “financial” when the decision scenarios used monetary or valuables (e.g. diamonds, paintings) rewards/losses. Only one of the scenarios (effect size: Ronnlund et al., 2005 “c”) coded as “financial” used valuables as the experimental variable. Scenarios that dealt with health or mortality (e.g. saving or losing lives) were coded as “mortality”. This moderator coding resulted in groups of 17 “financial” and 10 “mortality” effect sizes in the positive frame and 14 “financial” and 10 “mortality” effect sizes in the negative frame.
Amount
The decision-making scenarios used in the studies also varied in the amount of hypothetical gains and losses. After examining the experimental variable ranges in the studies, we decided to code the amount variable as either “small” or “large”, where an experimental value was coded as “small” when it was less than 100 and “large” when it was 101 or greater. The majority of the studies used in the analysis modeled their experimental items after the “Asian disease” problem (Tversky & Kahneman, 1981) and the “cancer treatment” problem (McNeil, Pauker, Sox, & Tversky, 1982) that use hypothetical outcome amounts ranging from 200–600 and 10–100, respectively. This coding fit the pool of studies well, resulting in 16 “small” and 11 “large” effect sizes in the positive frame and 13 “small” and 11 “large” effect sizes in the negative frame.
Combined
Lastly, in order to better parse out the influence of the type of scenario and variable amount, the first two moderator variables were combined into a third coding scheme. This resulted in four groups: small-amount financial, large-amount financial, small-amount mortality, large-amount mortality.
Addressing dependent effect sizes
Moderator variable coding resulted in 6 studies where multiple dependent effect sizes could be calculated. The decision scenarios in four of these studies could be coded as a single scenario variable, but as both amount variables. Watanabe and Shibutani (2010) included four independently reported mortality-based decision scenarios, three of which were coded as “large” and one coded as “small”. In an effort to retain the majority of the data, the effect size used in the moderator analyses for this study was calculated from the three “large” studies. Kim et al. (2005) included two independently reported mortality-based decision scenarios, one “large” and one “small”. The “small” scenario used an experimental variable ranging from 23–100 lives while the “large” scenario ranged from 2–6 billion lives. The “large” amount range in this study was considerably higher when compared to the rest of the studies (the next largest experimental amount was 600,000 lives) so we elected to calculate the effect size used in the moderator analyses for this study using the “small” amount. Holliday (1988) included monetary variables ranging from $6–$10,000, but the results were not independently reported. Due to the large range and the example scenario in the text using an experimental variable >$100, the effect size calculated from this study was coded as “large”. Lauriola and Levin (2001) used a logarithmic range of variables ($.50, $5, $50, $500, $5,000, and $50,000) that were not independently reported. Using the described coding scheme, half of the items would be coded as “small” and half “large”. Lacking any additional information, the effect size from this study was coded as “large” in an effort to balance the sample sizes between the two amount groups. Reversing the coding in this study was not found to change the results of the moderator analyses.
Two studies (Bruine de Bruin, Parker, & Fischhoff, 2007; Mayhorn, Fisk, & Whittle, 2002) used independent reported decision scenarios that could be coded as both options for each of the moderator variables. In each case, a single coding scheme allowed for the retention of more data than the other coding schemes. Ultimately, the effect size used in the moderator analyses from Bruine de Bruin, Parker, and Fischhoff (2007) was calculated from the “mortality” and “small” scenarios. The effect size from Mayhorn, Fisk, and Whittle (2002) was calculated from the “financial” and “large” scenarios.
Statistical Methods
The dependent variable in the current study was defined by binary choices (either the sure or risky option) made by two age groups (young and older adults). While this format lends itself to the calculation of an odds ratio, we instead calculated Hedge’s g in order to mirror the Mata et al. (2011) analysis. Following the procedure of the previous meta-analysis, we initially calculated Cohen’s d for each study by computing the difference of the younger adult mean and the older adult mean and dividing that difference by the pooled standard deviation (Borenstein, Hedges, Higgins, & Rothstein, 2009). In order to standardize the effect sizes for comparison, Cohen’s d was calculated such that a positive effect size was indicative of older adults’ making more risk-seeking choices compared to younger adults. Cohen’s d was then converted to Hedge’s g to correct for overestimation of effect sizes in studies with small sample sizes.
Due to some of the study designs, in some cases more than one effect size could be calculated from a single study using a within-subject design. In these cases, the values for the decision variables (choice [sure vs. risky] x age group [young vs. old]) were averaged to calculate a single effect size for that study. Studies that used between-subjects designs were represented by one effect size for each of the distinct populations tested. Some effect sizes were recalculated for the moderator analyses in studies that used within-subjects designs. This allowed for moderator variable coding while maintaining assumptions of independence in these analyses. These instances are described above in the moderator variable section.
Because the research findings on aging and framing are mixed, the meta-analysis was conducted using a mixed-effects model, allowing for moderator variables to be used in the analysis of heterogeneous samples. For each framing condition, the data were analyzed with the fixed-effects model to determine the presence of heterogeneity using the q statistic. Heterogeneity was further investigated by calculating an I2 and Birge’s ratio for each data set. If homogeneity was rejected, a moderator analysis was conducted using a weighted mixed effects analogue to analysis of variance (ANOVA) (Lipsey & Wilson, 2001). An ANOVA, as opposed to regression, model was used due to the categorical nature of the moderator variables. All meta-analytic results were calculated using SPSS macros developed by Wilson (2013).
Results
Positive Framing Condition
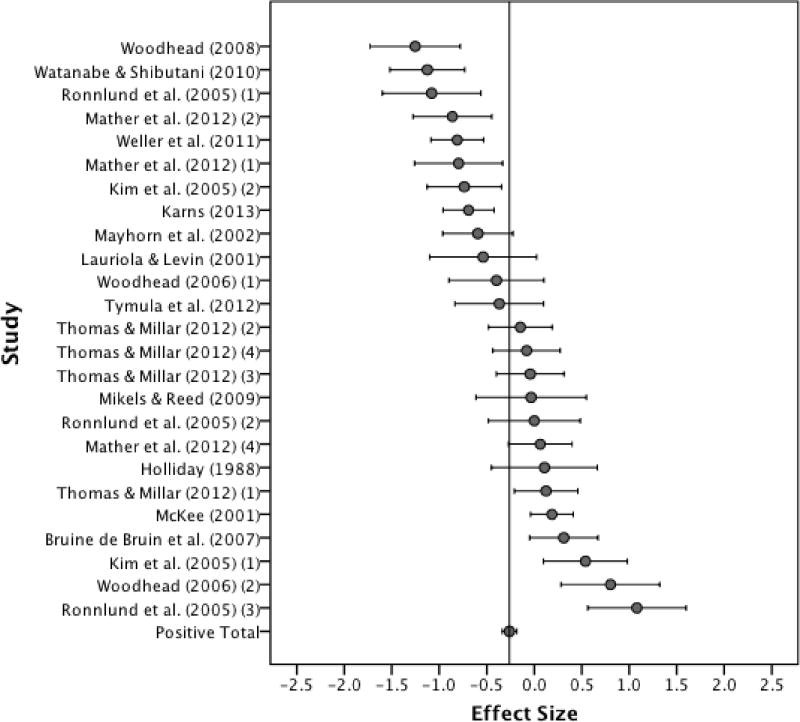
A meta-analysis was conducted on the effect sizes calculated from the positively framed items in each of the studies. The data was first fit to a fixed-effects model. In contrast to the results from Mata et al. (2011), an age effect was found within the gain domain (−0.25; 95% CI: −0.33, −0.18; p < .001) indicating a slightly higher likelihood of younger adults to choose the risky option in positively framed items. Tests of heterogeneity were also conducted on the data. As seen in the confidence interval plot in Figure 3, it was expected that the tests of heterogeneity would be significant. Using the fixed-effects model, this assumption was statistically confirmed. The Q test (Q(df=26) = 189.03, p < .001), was found to be significant in the positively framed condition. The group of effect sizes was further confirmed to be heterogeneous by the I2 (86.25%) and Birge’s ratio (7.27) values.
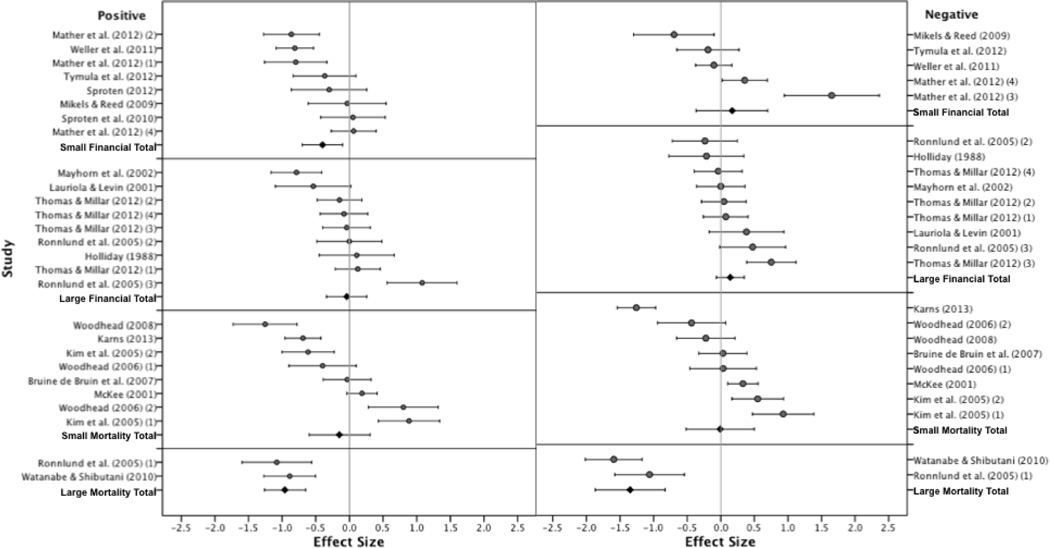
Figure 3.
Effect size by study: Positive frame. Numbers present after the source citation indicate separate effect sizes calculated from different sample populations reported within the same manuscript.
Due to the significant heterogeneity discovered when conducting the initial meta-analysis, the data was re-analyzed by including moderator variables in a meta-ANOVA analysis. As described in the methods, the effect size pool differs slightly in the moderator variable analyses. These differences had no effect on the results from the fixed-effects model (−0.26; 95% CI: −0.33, −0.18; p < .001). Three separate meta-ANOVAs were conducted, each including one of the moderator variables (Scenario, Amount, and Combined). Individually, the addition of the moderator variables “Scenario” (Qbetween[df=1] = 0.07; p = .79) and “Amount” (Qbetween[df=1] = 0.67; p = .41) did not explain a significant portion of the variance found between studies in the fixed effects model. The combination of the two moderator variables “Combined” (Qbetween[df=3] = 35.79; p < .001) did explain a significant portion of the variance found between the studies, but were still heterogeneous within each of the variable groups (Qwithin[df=23] = 150.56; p < .001) to differing degrees. Thus, a weighted mixed-model analysis was conducted by adding the separate between-studies variance estimates to the within study variances. The weighted meta-ANOVA shows that the there is a significant difference in age effect between positively framed items (Qbetween[df=3] = 19.13; p = <.001) using small-amount financial items and large-amount mortality items in the decision making tasks. No age effect was found in the studies using large-amount financial scenarios (−0.04; 95% CI: −0.34, 0.26; p = .78) and small-amount mortality scenarios (−0.15; 95% CI: −0.60, 0.31; p = .53). The mean was found to be moderately lower in small-amount financial scenarios (−0.40; 95% CI: −0.70, −0.10; p = .01), averaging roughly two-fifths of a standard deviation unit in size, with younger adults being more likely to make risky decisions. The mean was also found to be lower in high-amount mortality scenarios (−0.96; 95% CI: −1.26, −0.65; p = <.001), averaging roughly a standard deviation unit in size, with younger adults again being more likely to choose the risky option. The data was further tested for the presence of publication bias using the Egger’s test. The intercept and slope of the line were found not to be significantly different from zero (p = .89; p = .69), respectively), indicating that a publication bias favoring significant (or non-significant) results is not present in the gathered studies used in the current analysis.
Negative Framing Condition
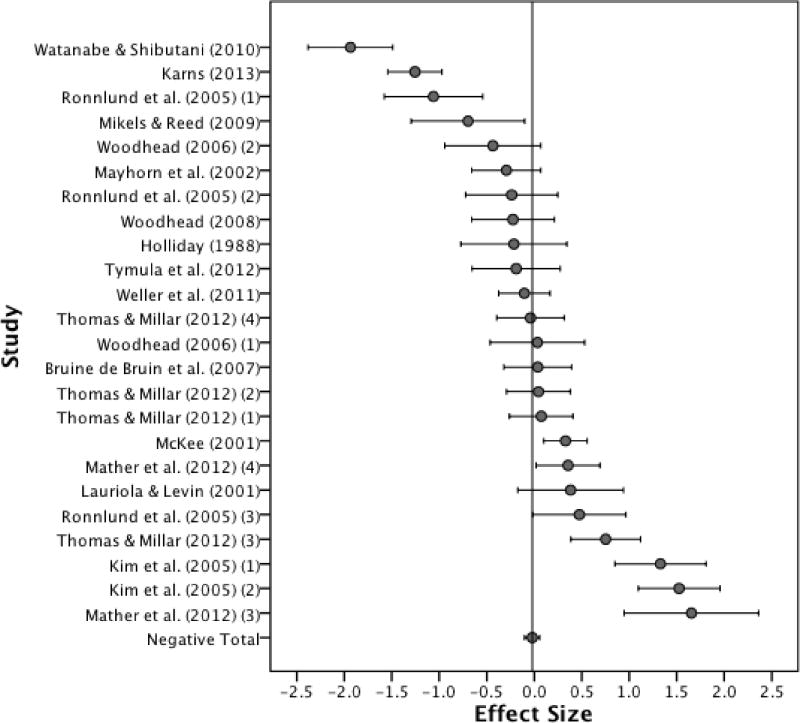
A separate meta-analysis was conducted on the effect sizes calculated from the negatively framed items from the same set of studies. As in the prior analysis, data was first fit to the fixed-effects model. No age effect was found for decisions made in the negatively framed conditions (−0.02; 95% CI: −0.10, 0.06; p = .59). Similar to the positive condition, an examination of the confidence interval plot seen in Figure 4 shows that heterogeneity is likely in the effect sizes calculated from the negatively framed conditions. Heterogeneity in the data was confirmed to be statistically significant (Q(df=23) = 309.78; p < .001). The I2 (92.58%) and Birge’s ratio (13.47) values further confirmed that moderate differences were present among the study results.
Figure 4.
Effect size by study: Negative frame. Numbers present after the source citation indicate separate effect sizes calculated from different sample populations reported within the same manuscript.
Due to the significant heterogeneity discovered when conducting the initial meta-analysis, the data was re-analyzed by including moderator variables in a meta-ANOVA analysis identical to that used for the positively framed effect sizes. Identical to the positive frame analysis, the effect size pool differs slightly in the negatively framed moderator variable analyses. Again, these differences had no effect on the results from the fixed-effects model (−0.04; 95% CI: −0.12, 0.04; p < .33). Three separate meta-ANOVAs were conducted, each including one of the moderator variables (Scenario, Amount, and Combined). The addition of the moderator variable “Amount” (Qbetween[df=1] = 0.63; p = .43) did not explain a significant portion of the variance found between studies in the fixed effects model. The addition of the moderator variable “Scenario” (Qbetween[df=1] = 17.23; p = <.001; Qwithin[df=22] = 217.32; p < .001) and “Combined” (Qbetween[df=3] = 72.65; p = <.001; Qwithin[df=20] = 161.90; p < .001) did explain a significant portion of the variance found between the studies in their respective analyses, but were still heterogeneous within each of the variable groups.
The mixed-model analyses were conducted by adding separate between-studies variance estimates to the within study variances in both of the moderator variable meta-ANOVA analyses. Using this model, the between group differences in age effect became non-significant for the “Scenario” (Qbetween[df=1] = 2.02; p = .16) moderator variable meta-ANOVA analyses. In the “Combined” moderator variable analysis, the weighted meta-ANOVA shows a significant difference in age effect between negatively framed items (Qbetween[df=3] = 27.66; p = <.001) using large-amount mortality items in the decision making tasks. The mean was found to be significantly lower in these scenarios (−1.35; 95% CI: −1.87, −0.83; p = <.001), averaging roughly one and one-third standard deviation units in size, with younger adults being more likely to make risky decisions. No age effect was found in the studies using small-amount financial scenarios (0.17; 95% CI: −0.37, 0.70; p = .54), large-amount financial scenarios (0.14; 95% CI: −0.07, 0.35; p = .19), and small-amount mortality scenarios (−0.01; 95% CI: −0.52, 0.50; p = .97). As with the positively framed items, the negatively framed data was tested for the presence of publication bias using the Egger’s test. The intercept and slope of the line were found to not be significantly different from zero (p = .65; p = .65, respectively), indicating that a publication bias favoring significant (or non-significant) results is not present in the gathered studies used in the current analysis.
Summary and Discussion
While a recent meta-analysis (Mata et al., 2011) investigated the general relationship between age and item framing on decision-making, tests of heterogeneity and models using moderator variables were not conducted. The general goal of the current analysis was to re-examine this relationship with an updated pool of studies and investigate any variables that may act as a moderator between age and framing. The current analysis achieved these goals by increasing the pool of studies from 10 to 18, resulting a pool of 51 effect sizes split between the positively and negatively framed conditions. Common design attributes between the studies allowed for the coding and analysis of two moderator variables related to the type of scenario (financial vs. mortality) and the amount of the experimental variable (small vs. large). These two moderator variables were also combined and coded for a third analysis. The increased pool of studies, recalculation of effect sizes, and moderator variable analyses produced a slightly different set of results.
The Mata et al. (2011) review found no overall age differences associated with question framing in positively worded scenarios. The current meta-analysis found the mean effect size to be significantly different than zero, with younger adults being approximately one-fourth of a standard deviation unit more likely to choose the risky option in a positively framed scenario. Homogeneity tests revealed significant variation between effects sizes. Moderator analyses were used to examine the predictive power of decision scenario type and experimental variable amount (both separately and combined) in explaining the age difference in risky decision-making in positively framed scenarios. The addition of the “combined” moderator variable into a weighted mixed-effects analogue to analysis of variance showed that younger adults were approximately two-fifths standard deviation units more likely to make risky decisions in small-amount financial scenarios and approximately one standard deviation unit more likely to make risky decisions large-amount mortality scenarios (Figure 5). No age difference was found in large-amount financial scenarios and small-amount mortality scenarios. Significant between-studies variation was apparent within each of the moderator subgroups, but the difference in the means was significant even after the inclusion of uncertainty due to the variation.
Figure 5.
Effect size by study, partitioned by “combined” moderator variable for both positive and negative frames. Numbers present after the source citation indicate separate effect sizes calculated from different sample populations reported within the same manuscript.
The 2011 analysis also determined that there was no age difference in the negatively framed condition. While this conclusion was supported in the fixed-effects model analysis in the current review, significant heterogeneity warranted further analysis of the negatively framed condition using moderator variables in a mixed-effects model. The same models used in the positively framed items analyses were used to investigate the negatively framed items. The addition of the “combined” moderator variable into a weighted mixed-effects analogue to analysis of variance again found an age difference in the large-amount mortality scenarios. Younger adults were found to be one and one-third standard deviation units more likely to make risky decisions when compared to older adults (Figure 5). No age difference was found in the other three groups. As in the positive frame analysis, significant between-studies variation was apparent within each of the moderator subgroups, but the difference in the large-amount mortality mean was significant even after the inclusion of uncertainty due to the variation.
To summarize, younger adults were found to be more likely to choose the risky option in small-amount financial and large-amount mortality-based scenarios when worded as a potential gain, and large-amount mortality scenarios when worded as a potential loss. It is important to note that the means for large-amount mortality-based scenarios, while significantly different than zero in both frames, are based on the results from only two effect sizes. This particular moderator subgroup was underrepresented in the available age comparison literature and highlights a topic that could benefit from further study.
The results from the current analysis partially support expectations based on previous research investigating the relationship between age and risk aversion in monetary domains. Numerous research findings show a significant increase in risk aversion associated with age using monetary gambling tasks where potential gains are wagered (Deakin, Aitken, Robbins, & Sahakian, 2004; Albert & Duffy, 2012; Tymula et al., 2013). While younger adults were found to choose the risky option more often than older adults in specific scenarios for both gain and loss frames, general risk aversion in the elderly does not explain the majority of the results from the current analysis where no age difference was present. Theoretical approaches related to ageing’s affect on the shape of the theoretical value function presented in prospect theory could also be used to interpret the findings from the current meta-analysis.
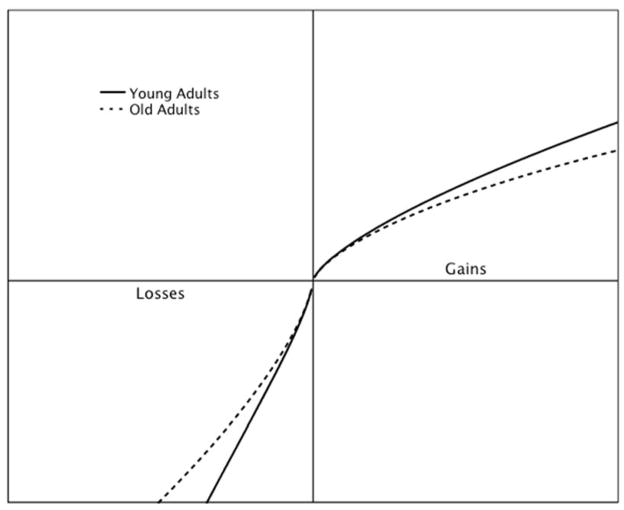
The loss prevention account (Ebner et al., 2006) predicts a larger framing effect in older adults for both gain and loss conditions (see Figure 1). This approach supports some of the findings from the current analysis. Older adults were found to choose the sure option more often than younger adults in positively framed items using small-amount financial and large-amount mortality scenarios. The value function in the gain frame is concave in nature, characterized by a decreasing slope as the amount increases from the reference point. Context dependent age differences in the variables of this function could account for the results of the meta-analysis. It is possible that for financial rewards, the subjective value attributed to gains by older adults rises with a more modest slope than younger adults, but eventually converges as the value increases (see Figure 6). This would account for younger adults over valuation of smaller rewards compared to older adults for small amounts and the lack of an age difference in risky decision-making for large-amount scenarios. For mortality-based scenarios, the subjective value for older and younger adults may increase at the same rate closer to the reference point, but the slope of older adult subjective values may begin to taper off before those of younger adults (see Figure 7). This could account for the lack of an age difference in the small-amount mortality scenarios, and the tendency for younger adults to choose the risky option in both positively and negatively framed large-amount mortality scenarios. While not predicted by the goal orientation framework, this context-specific loss aversion could explain younger adults tendency to choose the risky option more often than older adults in large-amount mortality scenarios.
Figure 6.
Hypothetical value functions as informed by the empirical effect-size pattern by age group for financial items.
Figure 7.
Hypothetical value functions as informed by the empirical effect-size pattern by age group for mortality items.
Socioemotional Selectivity Theory (Reed & Carstensen, 2012) predicts a larger framing effect in younger adults when compared to older adults due to the positivity effect (see Figure 1). This partially supports the results from the negatively framed condition in the current analysis, where younger adults were shown to be more likely to choose the risky option in large-amount mortality-based scenarios. This framing effect was not found to generalize to the identical positively framed scenario, where younger adults were again found to be more likely to choose the risky option. The tendency for younger adults to choose the risky option for large-amount mortality-based scenarios is therefore likely to not be driven by the positivity effect, as the results are homogeneous independent of the scenario framing. As this effect is context dependent to mortality-based scenarios, it is more likely that age differences in subjective evaluation and/or affective response to mortality are influencing decision-making. Survey results have shown that younger adults fear death more than older adults (Gesser, Wong, & Reker, 1987–1988). An increased affective sensitivity towards mortality may result in younger adults choosing the risky option in an attempt to maximize gain and minimize the loss of life in mortality-based scenarios.
These results have implications for those designing choice architecture for older adults. In a financial context when amounts are low, older adults are less likely than younger adults to incur risk as a method of maximizing utility and are more likely to be motivated to maintain their resources, though this age effect disappears when amounts are large and the stakes are more substantial. Financial or commodity based choices worded to emphasize the retention of current lifestyle or resources over time may be more attractive to older adults than choices worded to emphasize utility gains.
The limitations of this review allude to areas of the field that could potentially be improved. In general, the number of studies on the topic of age differences in the effect of message framing and risky decision-making could be increased. Only 18 studies were found to fit the inclusion criteria for the current meta-analysis, and two of those studies did not include a loss frame scenario. Also, many studies did not make a point to manipulate the amount of the gain/loss variable or use decision scenarios across domains (e.g. monetary, mortality). More pointedly, if studies collected data for a range of different amounts, they did not necessarily report the independent results for each amount (Holliday, 1988; Lauriola & Levin, 2001). Taking the results of the current meta-analysis into account, future studies investigating age differences in the effect of framing would be well served to collect data across a varying range of amounts and decision-making scenarios.
Acknowledgments
Research reported in this publication was completed while the authors were supported by a NIA grant under award number 3P01AG017211 (CREATE).
References
References offset by accents indicate studies included in the meta-analysis.
Proquest (PsycINFO & Dissertations and Theses) database: *
Web of Knowledge database:**
Both databases: ***
Google Scholar: ^
Ancestry: ~
Data found in separate, non-peer reviewed source: ŧ
- Albert SM, Duffy J. Differences in risk aversion between young and older adults. Neuroscience and Neuroeconomics. 2012;1:3–9. doi: 10.2147/NAN.S27184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to Meta-Analysis. New York, NY: Wiley; 2009. [Google Scholar]
- ~.Bruine de Bruin W, Parker AM, Fischhoff B. Individual differences in adult decision-making competence. Journal of Personality and Social Psychology. 2007;92:938–956. doi: 10.1037/0022-3514.92.5.938. [DOI] [PubMed] [Google Scholar]
- Carstensen LL, Isaacowitz D, Charles ST. Taking time seriously: A theory of socioemotional selectivity. American Psychologist. 1999;54:165–181. doi: 10.1037//0003-066x.54.3.165. [DOI] [PubMed] [Google Scholar]
- Cooper H, Hedges LV, Valentine JC. The handbook of research synthesis and meta-analysis. New York, NY: Russell Sage Foundation; 2009. [Google Scholar]
- Deakin J, Aitken M, Robbins T, Sahakian BJ. Risk taking during decision-making in normal volunteers changes with age. Journal of the International Neuropsychological Society. 2004;10:590–598. doi: 10.1017/S1355617704104104. [DOI] [PubMed] [Google Scholar]
- Ebner NC, Freund AM, Baltes PB. Developmental changes in personal goal orientation from young to late adulthood: From striving for gains to maintenance and prevention of losses. Psychology and Aging. 2006;21:664–678. doi: 10.1037/0882-7974.21.4.664. [DOI] [PubMed] [Google Scholar]
- Fishburn PC. Utility Theory for Decision Making. New York, NY: Wiley; 1970. [Google Scholar]
- Gesser G, Wong PTP, Reker GT. Death attitudes across the life-span: The development and validation of the Death Attitude Profile. Omega. 1987–1988;18:113–128. [Google Scholar]
- Hess TM, Rosenberg DC, Waters SJ. Motivation and representational processes in adulthood: The effects of social accountability and information relevance. Psychology and Aging. 2001;16:629–642. [PubMed] [Google Scholar]
- ~.Holliday SG. Risky-choice behavior: A life-span analysis. International Journal of Aging & Human Development. 1988;27:25–33. doi: 10.2190/139A-98AX-EL11-D120. [DOI] [PubMed] [Google Scholar]
- Johnson MMS. Age differences in decision making: A process methodology for examining strategic information processing. Journal of Gerontology. 1990;45:75–78. doi: 10.1093/geronj/45.2.p75. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk. Econometrica. 1979;47:263–291. [Google Scholar]
- *.Karns TE. Doctoral dissertation. Using a three-dimensional model to understand age differences in the framing effect. 2013. Retrieved from ProQuest Dissertations and Theses. [Google Scholar]
- ***.Kim S, Goldstein D, Hasher L, Zacks RT. Framing effects in younger and older adults. Journals of Gerontology Series B-Psychological Sciences and Social Sciences. 2005;60:215–218. doi: 10.1093/geronb/60.4.p215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühberger A. Theoretical conceptions of framing effects in risky decisions. In: Ranyard Rob, Ray Crozier W, Svenson Ola., editors. Decision Making: Cognitive Models and Explanations. London and New York: Routledge; 1997. [Google Scholar]
- Kuhberger A. The influence of framing on risky decisions: A meta-analysis. Organizational Behavior and Human Decision Processes. 1998;75:23–55. doi: 10.1006/obhd.1998.2781. [DOI] [PubMed] [Google Scholar]
- **.Lauriola M, Levin IP. Personality traits and risky decision-making in a controlled experimental task: An exploratory study. Personality and Individual Differences. 2001;31:215–226. [Google Scholar]
- Lipsey MW, Wilson DB. Practical Meta-Analysis. Thousand Oaks, CA: Sage; 2001. [Google Scholar]
- Mata R, Hertwig R. How to model age-related motivational reorientations in risky choice. Human Development. 2011;54:368–375. [Google Scholar]
- Mata R, Josef AK, Samanez-Larkin GR, Hertwig R. Age differences in risky choice: A meta-analysis. Annals of the New York Academy of Sciences. 2011;1235:18–29. doi: 10.1111/j.1749-6632.2011.06200.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ^.Mather M, Mazar N, Gorlick MA, Lighthall NR, Burgeno J, Schoeke A, Ariely D. Risk preferences and aging: The “certainty effect” in older adults’ decision making. Psychology and Aging. 2012;27:801–816. doi: 10.1037/a0030174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ***.Mayhorn CB, Fisk AD, Whittle JD. Decisions, decisions: Analysis of age, cohort, and time of testing on framing of risky decision option. Human Factors. 2002;44:515–521. doi: 10.1518/0018720024496935. [DOI] [PubMed] [Google Scholar]
- *.McKee DR. Doctoral dissertation. The effects of framing on younger and older adults’ medical decision making. 2001. Retrieved from ProQuest Dissertations and Theses. [Google Scholar]
- McNeil BJ, Pauker SG, Sox HC, Tversky A. On the elicitation of preferences for alternative therapies. The New England Journal of Medicine. 1982;306:1259–1262. doi: 10.1056/NEJM198205273062103. [DOI] [PubMed] [Google Scholar]
- ***.Mikels JA, Reed AE. Monetary losses do not loom large in later life: Age differences in the framing effect. Psychological Sciences. 2009;64:457–460. doi: 10.1093/geronb/gbp043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne JW. Task complexity and contingent processing in decision making: An information search and protocol analysis. Organizational Behavior and Human Performance. 1976;16:366–387. [Google Scholar]
- Peters E, Finucane ML, MacGregor DG, Slovic P. The bearable lightness of aging: Judgment and decision processes in older adults. In: Stern PC, Carstensen LL, editors. The aging mind: Opportunities in cognitive research. Washington, DC: National Academies Press; 2000. pp. 144–165. [PubMed] [Google Scholar]
- Reed AE, Carstensen LL. The theory behind the age-related positivity effect. Frontiers in Psychology. 2012;3:1–9. doi: 10.3389/fpsyg.2012.00339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ***.Ronnlund M, Karlsson E, Laggnas E, Larsson L, Lindstrom T. Risky decision making across three arenas of choice: Are younger and older adults differently susceptible to framing effects? The Journal of General Psychology. 2005;132:81–92. doi: 10.3200/GENP.132.1.81-93. [DOI] [PubMed] [Google Scholar]
- Slovic P, Peters E, Finucane ML, MacGregor DG. Affect, risk, and decision making. Health Psychology. 2005;24:35–40. doi: 10.1037/0278-6133.24.4.S35. [DOI] [PubMed] [Google Scholar]
- ~.Sproten A, Diener C, Fiebach C, Schwieren C. Working Papers University of Heidelberg. 2010. Aging and decision making: How aging affects decisions under uncertainty. [Google Scholar]
- Sproten A. Decision making and age: Factors influencing decision making under uncertainty. Developmental neuroeconomics: Lifespan changes in economic decision making (Doctoral Dissertation) 2012 Retrieved from http://archiv.ub.uni-heidelberg.de/volltextserver/14330/1/Doktorarbeit-SW.pdf#page=34.
- ***.Thomas AK, Millar PR. Reducing the framing effect in older and younger adults by encouraging analytic processing. Journals of Gerontology Series B-Psychological Sciences and Social Sciences. 2012;67:139–149. doi: 10.1093/geronb/gbr076. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science. 1981;211:453–458. doi: 10.1126/science.7455683. [DOI] [PubMed] [Google Scholar]
- ŧ **.Tymula A, Belmaker LAR, Ruderman L, Glimcher PW, Levy I. Like cognitive function, decision making across the life span shows profound age-related changes. Proceedings of the National Academy of Sciences. 2013;110:17143–17148. doi: 10.1073/pnas.1309909110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ^.Tymula A, Glimcher PW, Levy I, Belmaker LAR. Separating risk and ambiguity preferences across the life span: Novel findings and implications for policy. 2012. Unpublished manuscript. [Google Scholar]
- Von Neumann J, Morgenstern O. Theory of games and economic behavior. Princeton, NJ: Princeton University Press; 1944. [Google Scholar]
- ***.Watanabe S, Shibutani H. Aging and decision making: Differences in susceptibility to the risky-choice framing effect between older and younger adults in Japan. Japanese Psychological Research. 2010;52:163–174. [Google Scholar]
- ~.Weller JA, Levin IP, Denburg NL. Trajectory of risky decision making for potential gains and losses from ages 5 to 85. Journal of Behavioral Decision Making. 2011;24:331–344. [Google Scholar]
- Wilson DB. Meta-analysis macros for SAS, SPSS, and Stata. 2013 Retrieved, March 25, 2013, from http://mason.gmu.edu/~dwilsonb/ma.html.
- ^.Woodhead EL. Master’s Thesis. 2006. Debiasing the framing effect in younger and older adults’ medical decision making. Retrieved from ProQuest Dissertations and Theses. [Google Scholar]
- *.Woodhead EL. Doctoral dissertation. 2008. A process examination of the framing effect in younger and older adult medical decision making. Retrieved from ProQuest Dissertations and Theses. [Google Scholar]
- ŧ ***.Woodhead EL, Lunch EB, Edelstein BA. Decisional strategy determines whether frame influences treatment preferences for medical decisions. Psychology and Aging. 2011;26:285–294. doi: 10.1037/a0021608. [DOI] [PubMed] [Google Scholar]