Variable Density Incoherent Spatiotemporal Acquisition (VISTA) for Highly Accelerated Cardiac MRI

Abstract

Purpose

For the application of compressive sensing to parallel MRI, Poisson disk sampling (PDS) has been shown to generate superior results compared with random sampling methods. However, due to its limited flexibility to incorporate additional constraints, PDS is not readily extendible to dynamic applications. Here, we propose and validate a pseudo-random sampling technique that allows incorporating constraints specific to dynamic imaging.

Methods

The proposed sampling scheme, called variable density incoherent spatiotemporal acquisition (VISTA), is based on constrained minimization of Riesz energy on a spatiotemporal grid. Data from both a digital phantom and real-time cine were used to compare VISTA with uniform interleaved sampling (UIS) and variable density random sampling (VRS). The image quality was assessed qualitatively and quantitatively.

Results

VISTA improved the trade-off between noise and sharpness. Also, VISTA produced diagnostic quality images at an acceleration rate of 15, whereas UIS and VRS images degraded below the diagnostic threshold at lower acceleration rates.

Conclusions

VISTA generates spatiotemporal sampling patterns with high levels of uniformity and incoherence, while maintaining a constant temporal resolution. Using a small pilot study, VISTA was shown to produce diagnostic quality images at acceleration rates up to 15.

INTRODUCTION

Led by technological advances, the field of MRI has evolved considerably over the last two decades (1,2). In recent years, compressive sensing has attracted considerable attention in the scientific community and demonstrated notable impact on several biomedical imaging applications, including MRI (3,4). For cardiac MR (CMR), recent studies have demonstrated that the combination of compressive sensing and parallel MRI (pMRI) enables high temporal resolution imaging with sufficient image quality (5–7)—with the caveat of robustness issues using current sampling schemes, especially in dynamic imaging.

An effective application of compressive sensing, which exploits the underlying compressibility of the image, has three major requirements: the image is sparse in some transform domain, the undersampling artifact is incoherent (noise-like) in the sparsifying transform domain, and the image is recovered by a nonlinear method that enforces both image sparsity and data consistency (8). For MRI, the first requirement is generally met as most MRI images are compressible in an appropriate transform domain, e.g., discrete Wavelet domain (9,10). In recent years, significant strides have been made toward the third requirement by developing fast recovery algorithms for large imaging problems (11–14). For the second requirement, the high degree of incoherence is generally achieved by employing either Cartesian patterns with random or pseudo-random sampling or non-Cartesian patterns (8,15). Although non-Cartesian sampling methods allow far greater flexibility in designing low-coherence sampling patterns, such sampling schemes are highly sensitive to system imperfections and have found limited use in clinical practice (16,17). Therefore, in this study, we have focused exclusively on the Cartesian sampling, with fully sampled readout direction.

Although random sampling provides a high degree of incoherence (18), such sampling patterns can generate inconsistent results (10) due to excessively large gaps or clustering in the sampling pattern. The large gaps lead to high g-factor for pMRI—that is, ill conditioning of the underlying inverse problem (10)—and the clustering leads to high correlation among k-space data samples, degrading the acquisition efficiency. In contrast, pseudorandom sampling provides a high degree of incoherence while regulating the gaps between samples to a nearly uniform size. For pMRI, empirical evidence indicates that pseudo-random sampling methods based on Poisson disk sampling (PDS) tend to generate superior results compared with random sampling methods (10,19). For static applications, PDS with variable sampling density remains a popular pseudo-random sampling scheme (19,20). PDS, however, cannot be readily extended to k-t domain because it does not provide a mechanism to maintain a constant temporal resolution across frames. For PDS, enforcing a constant temporal resolution after the fact can destroy its uniformity. Therefore, most dynamic MRI applications resort to using random sampling (21), which can have the tendency to generate inconsistent results (22).

In this study, we propose a new k-t sampling method called variable density incoherent spatiotemporal acquisition (VISTA). Like PDS or other pseudo-random methods, VISTA allows 1) uniform coverage of the acquisition domain with regular gaps between samples, 2) incoherence, and 3) frequent sampling of the central region of k-space with high SNR. Importantly, the iterative nature of the VISTA design allows additional flexibility not offered by other pseudo-random sampling techniques. For example, VISTA possesses a unique ability to 1) maintain a constant temporal resolution by fixing the number of readouts per frame, 2) guarantee a fully-sampled, time-averaged k-space to facilitate GRAPPA or SPIRiT kernel estimation, 3) limit eddy currents by controlling the extent of jumps (in k-space) from one readout to the next, and (iv) allow distributing a precise, predefined number of samples. Here, we have validated VISTA using simulation as well as data from real-time, free-breathing cine. Although only applied to two-dimensional (2D) cine, VISTA can be extended to other applications and to higher dimensions.

THEORY

Here, we describe the distribution based on minimal Riesz energy (MinRE), an underlying concept for the proposed VISTA method. In addition, we provide implementation details for VISTA and SPIRiT-based image reconstruction (23).

MinRE

The problem of obtaining uniform distribution of samples using MinRE has been investigated extensively (24,25). In its original version, the problem consists of determining the position of N samples (or points) on an n-sphere in Euclidean (n + 1)-space such that a predefined measure of mutual distances among the samples is maximized. Practically, the distribution based on MinRE is obtained by minimizing a nonconvex cost function, U (26):

$$\widehat{\overrightarrow{v}}=\underset{\overrightarrow{v}}{\text{argmin }}U(\overrightarrow{v};s,c),$$

where

$$U(\overrightarrow{v};s,c)=\frac{1}{2}\sum _{i=1}^N\sum _{j\ne i}\frac{c^2}{{\Vert {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\Vert }^s},\text{with }s>0,$$ [1]

where c > 0 is a scaling constant, ${\overrightarrow{v}}_1,\dots ,{\overrightarrow{v}}_N$ represent N samples, with column vector ${\overrightarrow{v}}_j$ being the Cartesian coordinates in n + 1 spatial dimensions defining the location of the j^th sample on n sphere. Here, ${\Vert {\overrightarrow{v}}_i\Vert }^s={({\overrightarrow{v}}_i^T{\overrightarrow{v}}_i)}^{s/2}$. The minimizing set of samples $(\widehat{\overrightarrow{v}})$ is often referred to as “Fekete points.” For s = 1, U represents the electrostatic potential energy of N charged particles, each with charge c, on the sphere that repel each other according to the Coulomb’s law.

The value of U can be minimized iteratively using a gradient descent method. In each iteration, every sample is displaced in the direction of steepest descent: $-\overrightarrow{\nabla }U$. For the r^th iteration, the displacement of the i^th sample is given by

$${\overrightarrow{v}}_i^{(r)}={\overrightarrow{v}}_i^{(r-1)}-\lambda \overrightarrow{\nabla }{U}_i^{(r)},$$ [2]

where the constant λ controls the displacement step size, and $-\overrightarrow{\nabla }{U}_i^{(r)}$ represents the steepest descent direction for the i^th sample. After updating the location of the i^th sample (Eq. 2), it is projected back to the manifold (sampling domain), which, for a unit sphere, is equivalent to normalizing ${\overrightarrow{v}}_i^{(r)}$ to unit length. The process is repeated for all points, and it is iterated until convergence.

VISTA

For 2D dynamic CMR, we seek distribution based on MinRE on a k-t grid, which can be achieved by minimizing U over a 2D Cartesian grid under periodic boundary conditions. To create variable sampling density, we modify the original cost function by replacing c with $c(\overrightarrow{v})$, yielding

$$\widehat{\overrightarrow{v}}=\underset{\overrightarrow{v}}{\text{argmin }}U(\overrightarrow{v};s,c,W)\text{ subject to }\overrightarrow{v}\in 𝒞,$$

where

$$U(\overrightarrow{v};s,c,W)=\frac{1}{2}\sum _{i=1}^N\sum _{j\ne 1}\frac{c({\overrightarrow{v}}_i)c({\overrightarrow{v}}_j)}{{\Vert {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\Vert }_W^s},\text{ with }s>0,$$ [3]

Here, ${\overrightarrow{v}}_i\equiv {(k_i,t_i)}^T$ defines the Cartesian coordinates of the i^th sample on the k-t grid, 𝒞 represents user-defined constraints on the distribution of samples, and ${\Vert {\overrightarrow{v}}_i\Vert }_W^s={({\overrightarrow{v}}_i^{T}W{\overrightarrow{v}}_i)}^{s/2}$, with diagonal matrix W specifying the relative scaling of t and k dimensions of the k-t grid. The minimizing set of samples $(\widehat{\overrightarrow{v}})$ gives VISTA.

Unlike the traditional MinRE problem (Eq. 1), $c(\overrightarrow{v})$ in VISTA is not constant and varies with location on the k-t grid. In terms of the Coulomb’s law, this setup is analogous to introducing location-dependent changes in the magnitude of the electric charge on the samples. By reducing the magnitude of the charge near the center of k (phase encoding dimension), the sampling density toward the center can be increased. Although several parametric and nonparametric models can be used to represent $c(\overrightarrow{v})$ we have chosen it to be a Gaussian function,

$$c(\overrightarrow{v})=c(k,t)\equiv 1-\alpha \text{ exp }(-\frac{{(k-\frac{K}{2}-1)}^2}{2{\sigma }^2}),$$ [4]

where 1 ≤ k ≤ K is the phase encoding index, and the parameters 0 ≤ α ≤ 1 and σ > 0 control the sampling density profile. Note, $c(\overrightarrow{v})$ is only a function of k but not t, because no density variation is desired along time.

For a given choice of $c(\overrightarrow{v})$ the value of U in Equation 3 can be minimized iteratively using a gradient descent method in which every sample is displaced in the direction of steepest descent in each iteration. For the i^th sample, the negative of the steepest descent (displacement direction) is given by

$$\overrightarrow{\nabla }{U}_i=-\sum _{j\ne 1}(\frac{sc({\overrightarrow{v}}_i)c({\overrightarrow{v}}_j)W[{\overrightarrow{v}}_i-{\overrightarrow{v}}_j]}{{\Vert {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\Vert }_W^{s+2}}-\frac{c({\overrightarrow{v}}_j)\overrightarrow{\nabla }c({\overrightarrow{v}}_i)}{{\Vert {\overrightarrow{v}}_i-{\overrightarrow{v}}_j\Vert }_W^s}),$$ [5]

where $\overrightarrow{\nabla }c({\overrightarrow{v}}_i)$ is the gradient of $c(\overrightarrow{v})$ at location ${\overrightarrow{v}}_i$, and $W[{\overrightarrow{v}}_i-{\overrightarrow{v}}_j]$ represents matrix-vector multiplication.

The iterative implementation of VISTA is suitable for incorporating a variety of constraints in the distribution of the samples. In this study, we have enforced three constraints: constant temporal resolution, fully sampled, time averaged k-space (FTAK), and sampling on a Cartesian grid. To ensure constant temporal resolution, we started with an initialization such that the number of samples across frames is either fixed or differ at the most by one. Subsequently, the second component of the gradient $\overrightarrow{\nabla }{U}_i$ was set to zero in each iteration to prohibit displacement across frames. The FTAK and Cartesian constraints were enforced similarly using gradient projections (27). FTAK facilitates kernel estimation for GRAPPA or SPIRiT, thus eliminating the need to collect additional calibration data.

The steps involved in computing VISTA are as follows:

• Stage I (Optional)

• S1-a: For a given k-t grid size and net acceleration rate, R, initialize with a frame-invariant uniform sampling, with the sampling density given by $c(\overrightarrow{v})$.

• S1-b: In each frame, add a small random jitter (in the phase encoding direction) to the location of the samples.

• Stage II

• S2-a: Use the 2D sampling from the S1-b step as an initialization and minimize U (Eq. 3) by applying an iteration of gradient descent on all samples under periodic boundary conditions. Set the second component of the gradient, $\overrightarrow{\nabla }U$, to zero so that the samples do not drift along the temporal dimension.

• S2-b: At the end of every m^th iteration, use gradient projections to ensure FTAK and that the samples reside on a Cartesian grid.

• S2-c: Repeat Stage S2-a and S2-b until convergence.

For illustration, the sampling patterns after steps S1-a, S1-b, and S2-c are depicted in Figure 1.

FIG. 1.

Rate-8 VISTA distribution on a 64 × 64 grid at the various stages of implementation. Horizontal and vertical axes represent time and phase encoding directions, respectively. a: Distribution from S1-a step in Stage I. The spacing between the phase-encoding lines is determined by the profile c (Eq. 4). b: The distribution in panel a after adding a random frame-by-frame jitter (S1-b, Stage I). c: From the initialization given in panel b, the final pattern achieved by minimizing the cost function given in Equation 3 (S2-c, Stage II).

The S1-a step is intended to encourage in-frame uniformity. For a given $c(\overrightarrow{v})$ map, this step generates an identical distribution in each frame, with the distances between adjacent in-frame samples determined by the profile $c(\overrightarrow{v})$. The S1-b step is included to ensure that there is some frame-to-frame variation in the distribution and thus avoid convergence to bad local minima in Stage II. Because VISTA is sensitive to initialization, the inclusion of Stage I promotes in-frame uniformity and positively impacts the output of Stage II. The parameter W, in Stage II, provides additional control over the uniformity in the k-t domain versus the uniformity in individual frames.

The uniformity of the distribution based on MinRE has been studied extensively (28,29), but the incoherence of such sampling patterns has not been considered. We argue that VISTA, when initialized with random or perturbed patterns, results in incoherent sampling patterns in the ambient k-t domain. Figure 2 reports the 2D point spread function (PSF) of MinRE and VISTA patterns. The PSF was computed by taking the 2D Fourier transform of the sampling pattern in the k-t domain. Here, the side lobes of the PSF are used as a surrogate measure of incoherence. The PSF of the distribution based on MinRE has a visible annulus and strongly resembles the previously reported PSF of PDS (19). Compared with the distribution based on MinRE, VISTA has slightly stronger coherence, which reflects the structure introduced by additional constraints enforced in VISTA. Note, MinRE and VISTA exhibit incoherence in the ambient sampling domain, which may or may not fully translate to incoherence in a transform domain (4), but this limitation is not unique to VISTA and extends to almost all random or pseudorandom sampling patterns.

FIG. 2.

Comparison of PSFs for rate-8 random, MinRE, and VISTA distributions on a 64 × 64 grid. In the first set (a–d), no constraints were imposed on the distribution. In the second set (e–f), two constraints were imposed on the distribution: constant temporal resolution and variable density along the phase encoding direction. a: Random sampling. b: PSF of the sampling in panel a. c: The corresponding MinRE distribution. d: PSF of the sampling in panel c. e: Random sampling with constant temporal resolution and variable density. f: PSF of the sampling in panel e. g: The corresponding VISTA distribution with constant temporal resolution and variable density. h: PSF of the sampling in panel g. The peak side lobe in panel h is 26% stronger than the peak side lobe in panel d.

Advantages Over PDS

Dynamic pMRI, with two spatial and one temporal dimension, is not a true three-dimensional (3D) problem. Although the sparsity promoting regularization can be applied in the joint 3D spatiotemporal domain, the self-consistency constraint, which originates from employing multiple receiver coils, still applies to individual 2D frames and can benefit from the in-frame uniformity of the sampling. Therefore, uniformity of the distribution both in the k-t domain and in individual frames, along with the incoherence in the k-t domain, plays an important role in determining image quality. This is where VISTA offers a distinct advantage over random sampling and PDS. VISTA, by controlling the initialization (Stage I) and the diagonal entries of W in Equation 3, can manage uniformity in both 2D k-t domain and individual frames, while PDS has no mechanism to control in-frame uniformity of the sampling. Also, unlike PDS, VISTA can ensure FTAK, which facilitates kernel estimation for SPIRiT-type methods or coil sensitivity estimation for SENSE-type methods.

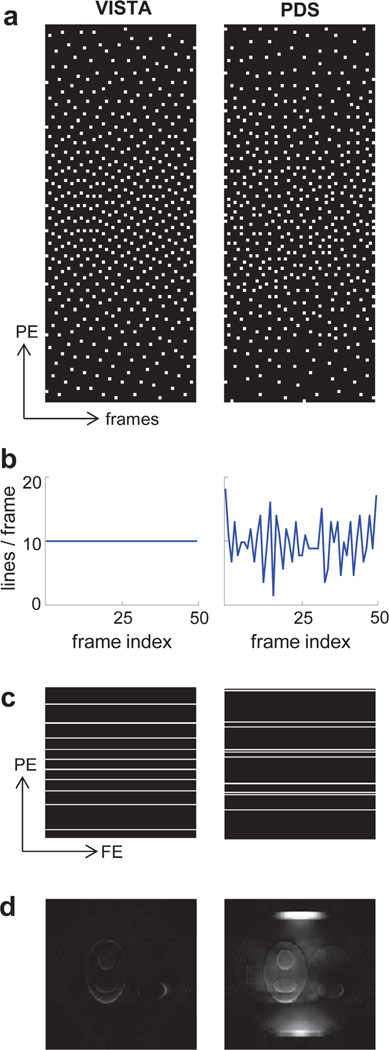
Figure 3 illustrates the relative merits of VISTA over PDS. The VISTA and PDS sampling patterns shown in Figure 3a were used to simulate data from a 120 × 120 dynamic phantom with 48 frames. (The phantom construction and the reconstruction process are described later.) Figure 3b displays the number of samples (i.e., readout lines) in each frame. In Figure 3c, the sampling patterns in the seventh frame are shown. From Figure 3c, it is clear that the uniformity provided by PDS in the k-t domain (Fig. 3a) did not translate to uniformity in individual frames. The sampling in individual frames of PDS was clustered and thus was not conducive to pMRI. Figure 3d shows error images (×5) for the seventh frame. Across all frames, the reconstruction from PDS had 76% higher root mean squared error (RMSE) compared with the reconstruction from VISTA.

FIG. 3.

Comparison of VISTA (left) and PDS (right). a: The two sampling patterns on a 120 × 48 k-t grid, with R = 12. Here, the horizontal axis represents time (frames), and the vertical axis represents the phase encoding direction. Each sample on the 2D grid represents a readout line along the third orthogonal direction (not shown). b: The number of samples (readout lines) in each column (frame) of the sampling grid. c: The sampling patterns in the seventh frame. Here, FE and PE denote frequency encoding and phase encoding directions, respectively. d: The error images (×5) corresponding to the seventh frame. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

More importantly, PDS sampling, in its current form, cannot ensure a constant temporal resolution. The varying number of samples in each frame (Fig. 3b) makes PDS unsuitable for dynamic applications, where constant temporal resolution is desired. There is no trivial way to enforce a constant temporal resolution in PDS while maintaining the uniformity of the distribution. On the other hand, VISTA generates a sampling pattern by maximizing the separation among the samples via a cost function minimization, and this framework allows enforcing constant temporal resolution while maintaining uniformity. Due to the aforementioned limitations of PDS for dynamic applications, it has been excluded from the rest of the study.

Image Recovery

The recently described SPIRiT (23,30)—an autocalibrating pMRI reconstruction method—offers a framework to incorporate sparsity-promoting spatiotemporal regularization into pMRI reconstruction and thus exploit both the sparsity of MRI signal and the incoherence of VISTA. Here, we have used a reconstruction framework (ℓ₁-SPIRiT) that combines SPIRiT with ℓ₁ -regularization in the joint spatiotemporal domain (23). If y represents the acquired noisy k-space data, x represents the desired fully sampled k-space data for all coils and all frames, S denotes the sampling pattern based on VISTA, and Gx represents frame-by-frame application of SPIRiT kernels, then x can be estimated by solving

$$\widehat{x}=\underset{x}{\text{argmin}}{\Vert Sx-y\Vert }_2^2+{\lambda }_1{\Vert Gx-x\Vert }_2^2+{\lambda }_2ℛ(\Psi Fx),$$ [6]

where F represents the frame-by-frame inverse 2D Fourier transform, ψ denotes the sparsifying transform for the spatiotemporal image Fx, operator 𝓡 represents a hybrid ℓ₂ – ℓ₁ norm (ℓ₂ norm across coils followed by ℓ₁ norm across the sparsifying domain), and λ₁ and λ₂ control the extent of data consistency (second term in Equation 6) and regularization (third term in Equation 6), respectively. Note that the application of VISTA is not tied to ℓ₁-SPIRiT, and other pMRI recovery methods can equally benefit from the proposed sampling technique.

METHODS

Generating Different Sampling Patterns

In this study, we compared image reconstruction using VISTA with image reconstruction using two commonly employed sampling methods: uniform interleaved sampling (UIS) and variable density random sampling (VRS). In VRS, each frame had an independent, random sampling pattern. For a fair comparison, the sampling density of VRS was adjusted such that it matched the sampling density of VISTA. Also, additional samples, if required, were added to the last frame of VRS to ensure FTAK.

2D VISTA was computed using two stages described in the previous section. The cost function, U, in Equation 3, was minimized using a gradient descent method under periodic boundary conditions. We chose the value of s to be 1.4. To vary sampling density, we chose α = 1/ 4 and σ = K/4. For the 2 × 2 diagonal matrix, W, we chose W(1,1) = 1 and W(2,2) = max(R/8, 1). A total of 120 iterations were used to minimize U. There was no difference in the parameter values or the implementation of VISTA used for simulation and in vivo studies except for the k-t grid size. For simulation, VISTA sampling patterns were generated on a 120 × 48 k-t grid, whereas for in vivo data, VISTA patterns were generated on a 144 × 48 k-t grid. Before acquisition, the samples in all odd frames were sorted in ascending order, while the samples in all even frames were sorted in descending order. This reordered zig-zagging through k-space minimizes gradient jumps from one readout line to the next and thus limits eddy currents associated with rapid gradient switching (31). The comparison among the three sampling methods was made across eleven different acceleration rates: R = 3–12, 15. Some of the sampling patterns used for in vivo data are shown in Figure 4. A MATLAB (MathWorks, Natick, Massachusetts, USA) code to implement VISTA can be downloaded from https://github.com/osu-cmr/vista.

FIG. 4.

Sampling patterns on a 144 × 48 grid used for in vivo acquisition. Here, the horizontal axis represents time (frames), and the vertical axis represents the phase encoding direction. Each sample on the 2D grid represents a readout line along the third orthogonal direction (not shown). a: Uniform interleaved sampling (UIS). b: Variable density random sampling (VRS). c: VISTA distribution. Only six (out of eleven) acceleration rates are displayed.

Implementation of ℓ₁ -SPIRiT

ℓ₁-SPIRiT was implemented by solving the optimization problem given in Equation 6 via nonlinear conjugate gradient (NLCG) with backtracking line-search. To compute the derivative of the last term in Equation 6, a smoothing technique was used that replaces the nonsmooth ℓ₁ norm with a smooth version by defining

$${\Vert x\Vert }_1^1=\sum _i\sqrt{x_i^{*}{x}_i+\epsilon ,}$$

where ε > 0 is a small positive real number (smoothing parameter) and x_i and $x_i^{*}$ are the i^th element of x and its complex conjugate, respectively.

To jointly exploit the structure across space and time, we applied the regularization in the joint 3D spatiotemporal domain. We used weighted 3D redundant Haar wavelet with single-level decomposition as the sparsifying transform, Ψ (32). The detail subbands along the third (time) dimension (LLH, LHH, HLH, and HHH) were weighted by R, the net acceleration rate. This weighting was intended to capture the higher temporal correlation expected at higher R as a result of increased frame rate. Because the edges in individual coil images appear at the same spatial position, wavelet coefficients exhibit similar sparsity patterns across coils. To exploit this structure across coils, a recently proposed joint sparsity model was used, which employs a hybrid ℓ₂ – ℓ₁ norm for the wavelet coefficients (19,33).

The SPIRiT kernels of size 7 × 7—which are used to construct the matrix G in Equation 6—were estimated from FTAK. For the VRS and VISTA datasets, we chose λ₁ = 1 × 10⁻², λ₂ = 5 × 10⁻⁶. For the UIS datasets, we chose λ₁ = 1 × 10⁻², λ₂ = 10 × 10⁻⁶. For all datasets, weighting of the detail subbands of the 3D redundant Haar wavelet along the time dimension was set equal to R. Before processing, the measured k-spaced data, y, was normalized by multiplying with $100\sqrt{N_c}/{\Vert y\Vert }_2$. These parameters were selected based on our experience with the simulated data. The same parameters were used for simulation and in vivo data.

A total of 30 NLCG iterations were used to perform the minimization in Equation 6. For the first 27 (90%) iterations, the estimated data were replaced with the measured noisy data, whereas for the last three (10%) iterations, the estimated data were allowed to evolve and were not replaced with the measured noisy data. We also observed that initialization had a significant impact on the number of iterations it takes for ℓ₁-SPIRiT reconstruction to converge. In this study, we used an initialization that employed view-sharing (34) across three adjacent frames followed by the application of GRAPPA with a 2 × 11 kernel size. This initialization led to faster convergence, well before 30 NLCG iterations. After the final iteration, the individual coil images were combined using the sum-of-squares method.

Performance Metrics

Variable density sampling patterns and regularized image recovery methods invariably offer a trade-off between image sharpness and SNR, much like the bias-variance trade-off encountered in the estimation theory. Therefore, it is important to measure both of these quantities. For the in vivo cine data, we used two quantitative performance metrics of noise and edge sharpness and one qualitative performance metric based on expert evaluation of overall image quality. The sharpness was quantified for the left ventricular boundary in short-axis orientation. To improve measurement accuracy, all frames were used collectively to measure the sharpness. For each sampling method, three expert readers—a physicist (O.P.S.) with over 20 years of CMR experience, a cardiologist (J.C.) with level III certification in CMR, and a radiologist with 5 years of CMR experience—evaluated the overall image quality using a Likert scale (where 1 is the worst and 5 is the best), with a score of 3 or more representing adequate diagnostic quality. For the simulation data, where the noiseless ground truth was available, we used three quantitative performance metrics: RMSE, noise, and edge sharpness.

The sharpness quantification method used in this study is based on parametric modeling of image edges, where the image intensity profiles across user-selected edges are modeled by a sigmoid function (35,36). There are no standard methods for measuring SNR or noise when spatiotemporal regularization is applied because it correlates noise across space and time. In this study, we extended the image difference-based method (37) such that the impact of correlation across neighboring frames is minimized. First, we selected image region or regions which are either static or have minimal signal, e.g., the peripheral air regions. Second, the data from these regions were organized into a 2D matrix, with the i^th column containing all the pixels from the selected regions in the i^th frame. Third, the ordering of the columns was randomized to minimize the impact of correlation across neighboring frames. Fourth, the forward difference was computed across columns by subtracting the i^th column from the (i + 1)^th column. Fifth, the resulting matrix, with i – 1 columns, was rearranged into a 1D vector. Finally, the standard deviation of the vector was defined as noise.

Simulation

To compare imaging results from UIS, VRS, and VISTA, a 120 × 120 dynamic digital phantom (38) with 48 temporal frames was created in MATLAB. The phantom consisted of both dynamic and static features. The dynamic ellipses had a periodic motion, with the frequency of the motion (number of cardiac cycles per frame) inversely proportional to the acceleration rate, R. To emulate experimental conditions, 12 uniformly spaced circular receive coils were simulated around the phantom using the Biot-Savart law. The image frames generated from the sum-of-squares of fully sampled, noiseless data were used as the ground truth; six such . frames are shown in Figure 5.

FIG. 5.

Representative frames from the 120 × 120 digital phantom used in simulation. The phantom contains both static (ellipses and a rectangle) and dynamic (ellipses) features. The frames were selected to capture the distinct phases of the cyclic motion of the dynamic features.

Real-Time Cine

Real-time cardiac cine data were acquired with UIS, VRS, and VISTA (3T Siemens, 32-channel cardiac array) at eleven different acceleration rates (R = 3—12, 15) from four healthy volunteers labeled A, B, C, and D. When the net acceleration rate was not an integer, the reported R represents the value after rounding the net acceleration rate to the nearest integer. The acquisition was performed under free-breathing conditions in both short and long-axis orientations. Other imaging parameters were as follows: 48 frames; matrix = 224 × 144; field of view = 360 × 288 mm² for volunteers A, B, and C and 400 × 320 mm² for volunteer D; slice thickness = 8 mm; SSFP sequence; TE of 1 ms, TR of 2.7 to 2.8 ms, receiver bandwidth = 1500 Hz/pixel; and flip angle = 60°. To collect data on the scanner, each sampling pattern was stored and retrieved as a lookup table. The acquisition order of the three patterns was randomized to minimize bias. For each volunteer, all 66 datasets (three sampling patterns, eleven acceleration rates, and two views) were collected back-to- back in one session. All aspects of the human study were approved by the local Institutional Review Board, and all subjects gave written consent for participation.

Computing Resources

All the data processing—including computation of VISTA and implementation of ℓ₁-SPIRiT—was performed off-line using a single workstation. The workstation was equipped with 64-bit MATLAB. It had an eight-core Intel Core i7-960 CPU running at 3.20 GHz with 24 GB system memory. For in vivo experiments, VISTA was computed in advance and the resulting sampling patterns were stored as lookup tables. During acquisition, the phase encoding indices were read directly from the tables. Once the data were collected, they were transferred to the dedicated workstation where they were processed and analyzed. For faster reconstruction, the frequency encoding direction was cropped in image space to approximately half of its original size, and the 32-channel data were compressed to generate 12 virtual channels (39).

RESULTS

Simulation

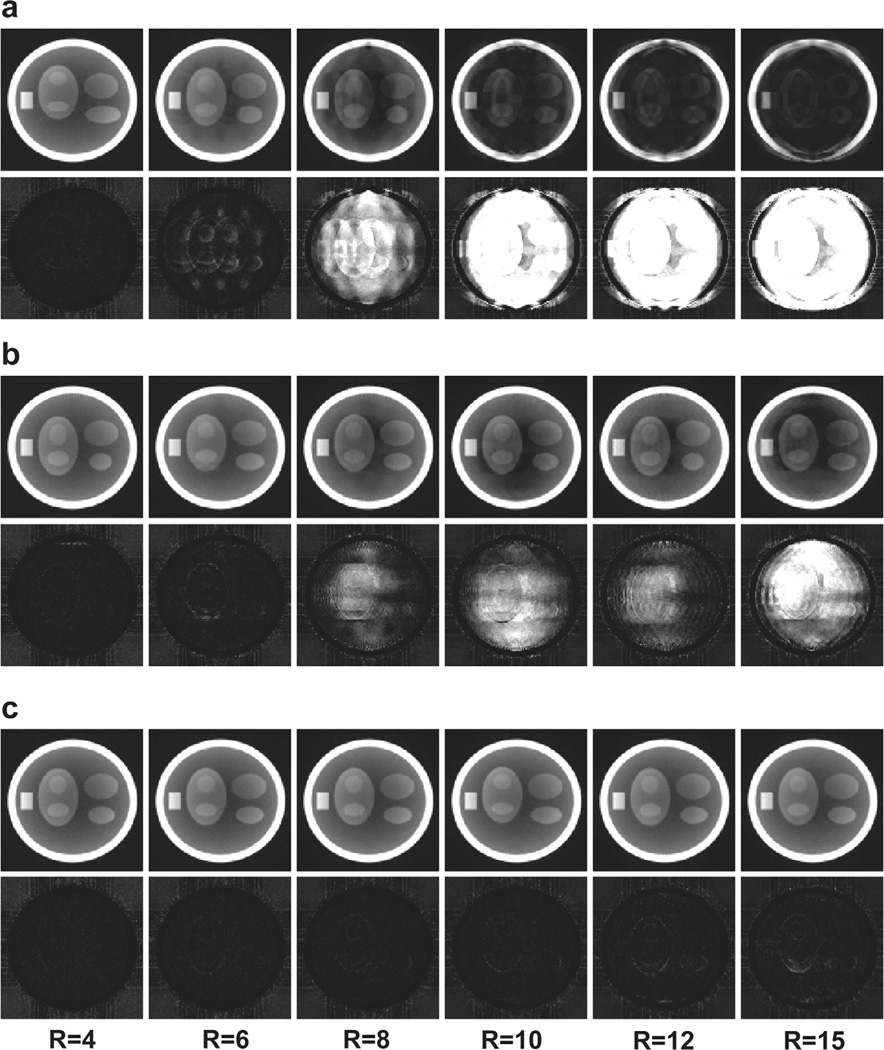
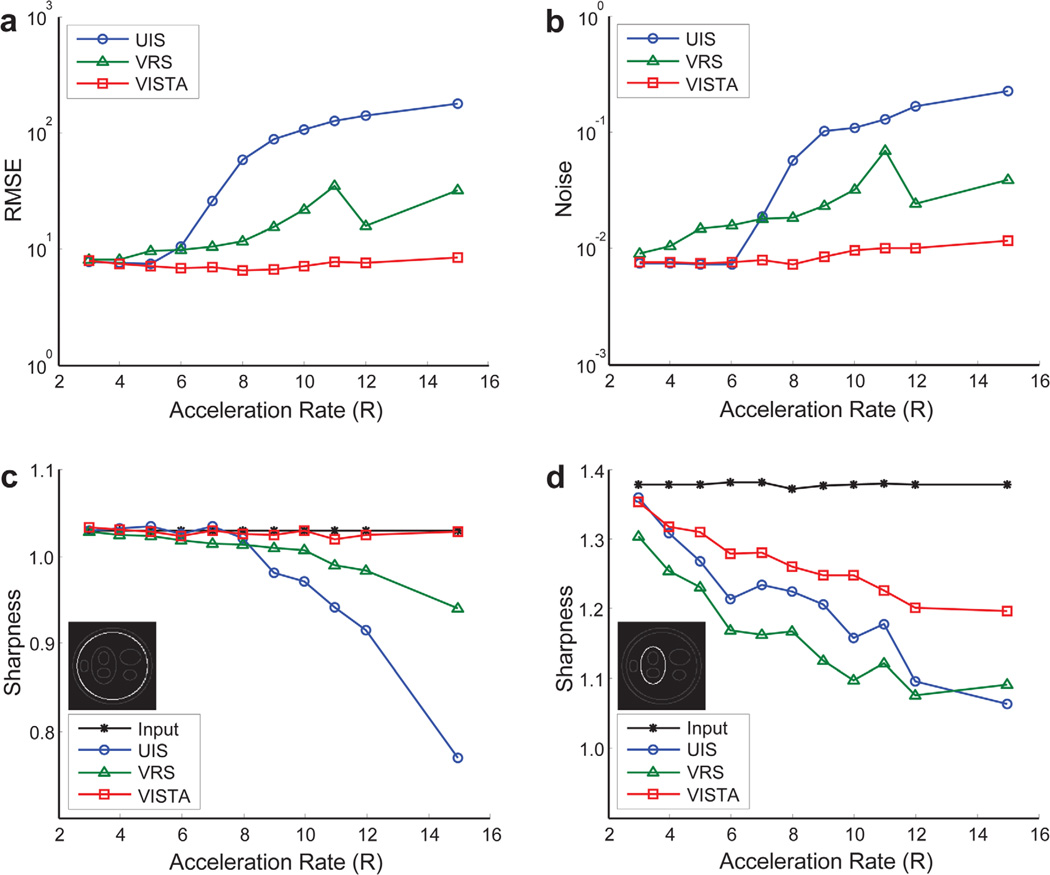
For the three sampling patterns considered in this study, Figure 6 shows the reconstruction results for six of the eleven acceleration rates. The difference images, after 5-fold amplification, are also shown. The frames shown here represent the worst-case scenario (i.e., out of the 48 frames available for each sampling method, we have displayed the frame with the highest RMSE for that method). Figure 7 shows the four quality metrics of the reconstructed images. Because temporal regularization affects static and dynamic edges differently, sharpness for a static and a dynamic edge is reported separately. The reconstruction time for each dataset was approximately 20 min.

FIG. 6.

Representative simulation results for six different acceleration rates. The worst (in terms of RMSE) frame from each dataset is presented. a: Results from the UIS distribution. b: Results from the VRS distribution. c: Results from the VISTA distribution. In each panel, the first row displays frames from the reconstructed images, and the second row represents the magnitude of the difference image after 5-fold amplification.

FIG. 7.

Quantification of simulation results. The comparison is made in terms of RMSE (a), noise (b), and image sharpness (c, d). For sharpness measurement, both static (c) and dynamic (d) features were considered. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Real-Time Cine

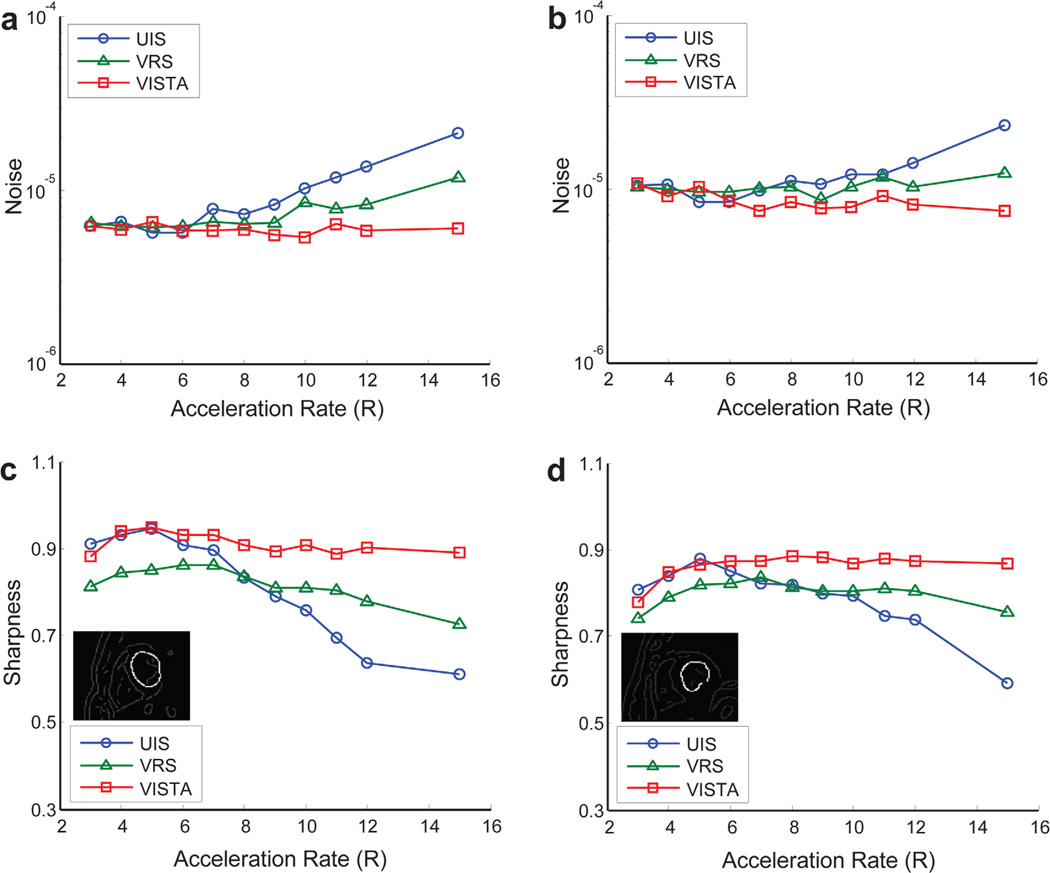
Figure 8 and Supporting Figure S1 show the reconstruction results for six of the eleven acceleration rates for UIS, VRS, and VISTA for volunteer A. Figure 8a shows frames for the short-axis view, and Figure 8b shows temporal profiles for pixels along the dashed line drawn on the top-left image in Figure 8a. The arrows in Figure 8b point to the visible artifacts in the reconstruction. Supporting Figure S1 is similar to Figure 8a but shows the long-axis view for volunteer A. The frames shown in Figures 8a and S1 represent the worst-case scenario (in terms of visible artifacts) for each of the selected datasets. If all frames in a reconstructed image series had the same quality, the frame was picked at random. The cine results for volunteer A are also captured in three movies for acceleration rates of 5 (Supporting Movie S1), 10 (Supporting Movie S2), and 15 (Supporting Movie S3). The frame rate of the movies was adjusted in accordance to the acceleration rate so that each movie displays the real-time dynamics of the heart. Figure 9 shows the image quality metrics. The edge sharpness was measured for the left ventricular boundary in the short-axis orientation for volunteers A and B. Both noise and edge sharpness were measured separately in all four volunteers but are reported for the first two volunteers only. The results from the other two volunteers were similar and are not shown. The results of overall image quality as assessed by three expert readers are reported in Table 1. The reconstruction time for each dataset was approximately 25 to 30 min.

FIG. 8.

Short-axis view of real-time, free-breathing cine from volunteer A. a: Individual frames from UIS, VRS, and VISTA with six different acceleration rates. From each image series, the worst (in terms of visible artifacts) frame is presented. b: Temporal profiles along the dashed line drawn on the top-left image in panel a. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

FIG. 9.

Quantification of real-time cine results from volunteer A (a and c) and volunteer B (b and d). The comparison is made in terms of noise and image sharpness. For the sharpness measurement, a left ventricular boundary (inset) is used. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 1.

Image Quality Scores Using a Likert Scale

	R
	3	4	5	6	7	8	9	10	11	12	15
UIS	3.92 ± 0.88	4.21 ± 0.78	4.21 ± 0.78	3.83 ± 0.87	2.92 ± 0.78	2.75 ± 0.68	2.25 ± 0.53	1.83 ± 0.70	1.54 ± 0.51	1.42 ± 0.50	1.13 ± 0.34
VRS	3.21 ± 0.66	3.58 ± 0.65	3.38 ± 0.71	3.17 ± 0.70	2.83 ± 0.70	2.92 ± 0.50	2.83 ± 0.64	2.08 ± 0.65	2.67 ± 0.70	2.38 ± 0.58	1.88 ± 0.68
VISTA	3.71 ± 0.81	4.13 ± 0.80	4.21 ± 0.72	4.08 ± 0.72	4.08 ± 0.65	3.83 ± 0.64	3.75 ± 0.61	3.63 ± 0.58	3.54 ± 0.72	3.54 ± 0.72	3.38 ± 0.58

In a Likert scale, 1 is worst and 5 is best. Values are presented as the mean score ± standard deviation for four volunteers, three expert readers, and two different views (n = 24).

DISCUSSION

The proposed VISTA sampling when coupled with joint spatiotemporal reconstruction results in high-fidelity images with minimal aliasing artifacts. As indicated by simulation and small in vivo study, the VISTA reconstruction exhibits lower RMSE, higher SNR, and higher edge sharpness compared with UIS and VRS. The evaluation by the experts also indicates that VISTA-based images retain adequate diagnostic quality at high acceleration rates. For rate 12, only one of the 24 scores assigned to VISTA-based reconstruction was below 3 (diagnostically unacceptable). Likewise, only one of the 24 scores assigned to VISTA-based reconstruction was below 3 for rate 15. In contrast, for UIS and VRS, 100% and 58% of the scores were below 3 at rate 12, respectively, and 100% and 83% of the scores were below 3 at rate 15, respectively.

The image quality for UIS and VISTA is similar at low acceleration rates (Table 1 and Figure 9), where the problem is well-conditioned and does not rely heavily on the regularization. At high acceleration rates, where the image recovery relies more on the regularization, VISTA consistently outperforms UIS. At high acceleration rates, UIS generates images with strong undersampling artifacts. Such artifacts are visible at R > 6 in both the simulation and the in vivo data. To suppress these excessive artifacts in UIS, we used slightly higher regularization (λ₂) compared with VISTA and VRS, but this higher value had a modest impact on the image quality. Further increase in λ₂ for UIS resulted in severe image blurring.

Compared with VISTA, the performance of VRS is consistently worse, even at low acceleration rates, where the poor g-factor associated with VRS is not adequately compensated by its incoherence. A frame-by-frame examination of the image series reveals that VRS does not generate consistent results across all frames. This fact is evident from Figure 6, which displays the worst-case scenario. This uncertainty in the performance of VRS is often mitigated by including a fully sampled region in the center of the k-space. Because each coil in the array has a different phase map, its center of k-space center is slightly shifted from the nominal position. To account for this variation, the fully sampled region is selected conservatively and often spans a nonnegligible fraction of the k-space to cover the high energy regions in all coils. The downside of this approach is that it limits the net acceleration that can be achieved using VRS. In addition, this approach reduces the sampling density for higher spatial frequency regions. We have experimentally observed (data not shown) that increasing the sampling density in the central regions of k-space progressively degrades image resolution. Therefore, although the uncertainty in VRS results can be reduced by densely sampling the center of k-space, this strategy may only further degrade the image sharpness.

For both the phantom and the in vivo data, VISTA offers a better sharpness–noise trade-off (i.e., it is simultaneously superior in both categories). Interestingly, the sharpness curves of dynamic boundaries in the digital phantom (Fig. 7d) decrease steeply with acceleration rate and do not match the sharpness curves from the cine results that exhibit an initial increase followed by a more gradual decrease in sharpness (Fig. 9c and 9d). The steeper decline in phantom sharpness can be attributed to higher initial sharpness of the digital phantom. For real-time cine results, the initial increase in measured sharpness, which is observed for all three sampling methods, reflects the impact of intraframe cardiac motion that is present in the cine data and not in the phantom data. For a given experimental setup, a lower acceleration rate equates to a lower temporal resolution for real-time cine. Therefore, the effect of the intraframe motion gets progressively worse with a decrease in acceleration rate, leading to sharpness loss at lower acceleration rates. This intraframe motion is also responsible for the relatively lower quality scores at rates 3 and 4 (Table 1).

VISTA offers a framework to generate pseudo-random, incoherent sampling patterns with parametrically controlled sampling density. More importantly, the iterative nature of VISTA allows flexibility that is not present in other pseudo-random sampling methods. For example, in VISTA, it is possible to ensure that the average-all data are fully sampled in k-space or that the number of readout lines in each frame is fixed. Also, VISTA has the potential of offering other advantages that have not been validated here. For example, by manipulating the matrix W in Equation 3, it is possible to generate sampling with anisotropic acceleration (19).

Our current MATLAB implementation of VISTA is significantly slower compared with other pseudo-random methods. For the data presented here, it took approximately 2 to 3 min to compute VISTA for the worst-case scenario (largest k-t grid, lowest acceleration). However, our current implementation of VISTA can be sped up by C++ implementation and parallel computing using graphical processing units. For a given CMR application, we anticipate that the number of tables required to cover a wide range of experimental conditions will only be in the hundreds. Therefore, look-up tables also provide a viable solution. Another limitation of VISTA is the possibility of converging to bad local minima. However, after including a random jitter (S1-b in Stage I) in the initialization, we did not observe such an occurrence.

The flexibility of VISTA inadvertently introduces free parameters. For the VISTA setup reported in this study, the user is responsible for selecting four parameters: s, α, σ, and second diagonal entry of W [i.e., W(2,2)]. We selected s = 14, but selecting a different value in the range of 1 ≤ s ≤ 1.5 did not have a significant impact on incoherence or image quality. The values of a and s control the sampling density and thus offer a trade-off between image sharpness and robustness. Densely sampling the center of k-space—at the expense of sampling in the peripheral regions—improves robustness but degrades image sharpness. Note, the problem of selecting an optimal sampling density is not unique to VISTA and is common to all random or pseudo-random sampling methods and requires further investigation. Based on our experience with the simulation data, we chose α = 1/4, σ = K/4, and W(2, 2) = max(R/8, 1). We anticipate that application-specific tuning of these parameters may be necessary for optimized performance.

CONCLUSIONS

In this study, we proposed a pseudo-random, incoherent sampling technique, VISTA, which is based on minimal Riesz energy problem. Compared with other pseudorandom methods (e.g., PDS), VISTA has the unique ability to incorporate a variety of problem-specific constraints. In this study, VISTA was applied to real-time CMR, where it not only provided an incoherent sampling with variable density but also ensured a constant temporal resolution and a fully sampled time-averaged data. VISTA was validated using simulation and in vivo data. Compared with other commonly employed sampling strategies, VISTA generates more consistent results with superior noise–sharpness trade-off, especially at high acceleration rates.