Mechanics of mouse ocular motor plant quantified by optogenetic techniques

Abstract

Rigorous descriptions of ocular motor mechanics are often needed for models of ocular motor circuits. The mouse has become an important tool for ocular motor studies, yet most mechanical data come from larger species. Recordings of mouse abducens neurons indicate the mouse mechanics share basic viscoelastic properties with larger species but have considerably longer time constants. Time constants can also be extracted from the rate at which the eye re-centers when released from an eccentric position. The displacement can be accomplished by electrically stimulating ocular motor nuclei, but electrical stimulation may also activate nearby ocular motor circuitry. We achieved specific activation of abducens motoneurons through photostimulation in transgenic mice expressing channelrhodopsin in cholinergic neurons. Histology confirmed strong channelrhodopsin expression in the abducens nucleus with relatively little expression in nearby ocular motor structures. Stimulation was delivered as 20- to 1,000-ms pulses and 40-Hz trains. Relaxations were modeled best by a two-element viscoelastic system. Time constants were sensitive to stimulus duration. Analysis of isometric relaxation of isolated mouse extraocular muscles suggest the dependence is attributable to noninstantaneous decay of active forces in non-twitch fibers following stimulus offset. Time constants were several times longer than those obtained in primates, confirming that the mouse ocular motor mechanics are relatively sluggish. Finally, we explored the effects of 0.1- to 20-Hz sinusoidal photostimuli and demonstrated their potential usefulness in characterizing ocular motor mechanics, although this application will require further data on the temporal relationship between photostimulation and neuronal firing in extraocular motoneurons.

the ocular motor plant, a term borrowed from control systems engineering, consists of the extraocular muscles, the globe, and other nonmuscular contents of the orbit. An understanding of its mechanical properties provides insight into the neurocomputational tasks that are accomplished by the eye movement control circuits, explains many manifestations of diseases affecting the ocular motor system, and is a prerequisite for building realistic computational models intended to explore both the normal condition and disease states (Anderson et al. 2009; Stahl and Thumser 2012). It has long been recognized that despite the ocular motor plant being far simpler than multijointed limbs, developing a realistic, detailed model is still challenging. The challenge stems from the number of properties that must be quantified and the technical difficulties of that quantitation. A classic modeling paper (Robinson 1981) outlined many of the defining properties: globe inertia, elasticity and viscosity of nonmuscular orbital tissues, elasticity and viscosity of noncontractile elements of the extraocular muscles, elasticity of the series-elastic component of the contractile element, and the length-tension-excitation and force-velocity relationships of the contractile elements.

Considerable progress has been made in quantifying some of the plant properties, particularly in humans and nonhuman primates (Anderson et al. 2009; Clark and Stark 1974a, 1974b; Fuchs et al. 1988; Gamlin and Miller 2012; Goldberg et al. 1998; Miller and Robins 1992; Quaia et al. 2009; Robinson 1964). With regard to the passive properties of the plant, a picture has emerged of a system dominated by a distributed viscosity and elasticity, with the mass of the eye being relatively inconsequential (Robinson 1964). The distributed viscous and elastic properties can be modeled as a cascade of discrete elements, each consisting of an elasticity (a spring) in parallel with a viscosity (a dashpot). These individual viscoelastic assemblies are termed “Voigt” elements. The response speeds of the Voigt elements (i.e., their time constants) are spread over a broad range of values (Sklavos et al. 2005, 2006). Whereas a model exactly replicating the eye and orbit would require an essentially infinite set of viscoelastic elements with continuously distributed time constants (Quaia et al. 2009; Tschoegl 1989), in practice much of the experimental data can be accommodated by models consisting of a small number of discrete elements (about 4) with time constants spanning 0.01–10 s.

Until recently, the majority of studies of ocular motor mechanics have focused on humans and nonhuman primates, although additional support for the distributed viscoelastic model derives from work in the rabbit (Stahl and Simpson 1995). Over the past decade, the laboratory mouse has emerged as an increasingly important model in the ocular motor field, yet knowledge of its plant mechanics is still rudimentary. Recordings of the relationship between abducens nucleus neuron firing and eye position have demonstrated that, as in the larger species, the mechanics can be modeled by a cascade of at least two viscoelastic elements with time constants spread about a decade apart (0.1, 0.9 s) (Stahl and Thumser 2012). The relatively long time constants suggested that the mouse ocular motor plant is “slower” than that of the primate. However, constraints imposed by the neuronal recordings on the range of stimulus frequencies that could be explored may have prevented detection of shorter time constants. In studies of primates and humans, very short time constants have been extracted from “duction-release” experiments; the eye is deflected from its rest position either by external traction or by electrically stimulating extraocular motoneurons, and the time constants are extracted from the time course with which the eye returns to the rest position following cessation of the perturbation (Anderson et al. 2009; Robinson 1964; Sklavos et al. 2006). External traction experiments have the disadvantage of needing to be performed under anesthesia, which likely alters motoneuron activity and with it, the mechanical state of the plant. Electrical stimulation can be performed in awake animals but has the potential to activate ocular motor circuits other than the motoneurons, particularly the brain stem velocity-to-position integrator circuit (Anderson et al. 2009).

Optogenetic techniques have created the opportunity to perform stimulus-based duction-release experiments in the mouse with potentially fewer complications than electrical stimulation. We activated abducens motoneurons by photostimulation in a transgenic mouse that expresses a channelrhodopsin specifically on cholinergic neurons, including brain stem extraocular motoneurons (Zhao et al. 2011). In addition to employing pulse stimuli along the lines used in the previous study of electrical stimulation in the primate (Anderson et al. 2009), we also explored the potential to use sinusoidal optogenetic stimuli to characterize ocular motor mechanics. Finally, we examined the degree to which a dependence of time constants on stimulus duration is a property of the muscles themselves, based on data from activation of isolated extraocular muscles in vitro generated for a previously published study (McMullen et al. 2004).

METHODS

Animals and animal preparation.

Experimental use of mice was approved by the Institutional Animal Care and Use Committees at the Louis Stokes Cleveland Department of Veterans Affairs Medical Center and Case Western Reserve University. Female transgenic mice expressing a mammalian-optimized (H134R) channelrhodopsin gene specifically within cholinergic neurons (Zhao et al. 2011) were obtained commercially [B6.Cg-Tg(Chat-COP4*H134R/EYFP,Slc18a3)6Gfng/J, catalog no. 014546; The Jackson Laboratory, Bar Harbor, ME]. Four of these “ChAT-ChR2” animals, ages 4–10 mo, were surgically prepared for video-oculography and extracellular recording of abducens nucleus neurons, as previously described (Oommen and Stahl 2008; Stahl and Thumser 2012). After the animals had recovered fully from the surgery, extracellular recordings were performed as the awake animals executed reflex eye movements, and the locations of the abducens nuclei were identified by their characteristic burst-tonic activity. The electrode was then replaced by a fiber optic probe (CFML12U; Thorlabs, Newton, NJ), which was advanced to place its tip in the fourth ventricle, ∼300 μm above the brain stem surface over the left abducens nucleus. Effective placement was confirmed by observing abduction of the left eye in response to 470-nm photostimuli delivered via the probe, and then dental acrylic was applied to fix the probe in place and close the recording craniotomy (with the exception of one animal described below, in which complete closure of the craniotomy was delayed to allow for further neuronal recording). The head fixation pedestal was painted black to minimize leakage of the photostimulation to the surround when recording eye movement responses in darkness.

Photostimulation and recording procedures.

Eye movements were recorded from awake, head-fixed mice using calibrated, 240 samples/s video-oculography as previously described (Stahl 2004; Stahl et al. 2000). Photostimuli were generated by a 470-nm LED source (M470F1; Thorlabs) in combination with a driver unit (DC2100; Thorlabs). This system was driven at its maximum output (2.53 mW) as either single pulses with durations of 20, 100, 250, 500, and 1,000 ms or trains of 40-Hz pulses, with each pulse lasting 20 ms and overall train durations of 120, 270, 520, and 1,020 ms. Command signals for the stimuli were generated by a digital pulse generator (model 2100; A-M Systems, Carlsborg, WA), with each stimulus initiated manually at a moment when the eye was motionless and within a few degrees of the central rest position, i.e., the position to which the eyes would gravitate when the animal was in darkness. Photostimuli were delivered in darkness so that visual feedback would not influence the time course of the evoked eye movements. Additional data were collected using sinusoidally modulated photostimuli. Command signals for the sinusoidal stimuli (frequencies 0.1, 0.2, 0.4, 0.8, 1.6, 2.5, 5, 10, 20 Hz) were generated by the data acquisition system (System 3; Tucker-Davis Technologies, Gainesville, FL). Command voltages were adjusted so that light intensity varied between zero and the system maximum (2.3 mW). Power values produced by the command voltages were assessed with a fiber optic power meter (PM20A; Thorlabs). Eye movement signals from the pupil tracker (ETL-200; ISCAN, Burlington, MA) and command signals to the LED driver were passed through four-pole Bessel low-pass filters (corner frequency 240 Hz) and then stored to computer via the digital acquisition system at a rate of 508.6 samples/s.

In one animal, single- and multiunit recordings were performed in the abducens nucleus during photostimulation, using 80-μm quartz-insulated platinum-tungsten fiber electrodes (Thomas Recording, Giessen, Germany). The abducens nucleus was approached at an oblique angle to avoid collision with the implanted fiber optic probe. Neuronal signals were conventionally amplified and stored at a rate of 48.8 kHz along with the stimulus and eye position data.

Data processing and analysis.

Position of the pupil in the video image was converted to horizontal eye angle with correction for changing pupil size, as previously detailed (Stahl 2004; Stahl et al. 2000). To extract time constants from pulse stimuli, we first identified all responses to a given set of step parameters that were initiated from a stationary eye position and proceeded without being interrupted by saccades or loss of the video-oculography signal. The selected responses were then aligned on stimulus onset and the responses were point-wise averaged. The relaxation phase of the averaged waveform was then fit with a sum of exponentials, e.g., E(t) = A₁e^−t/T₁ + A₂e^−t/T₂ + E₀, in the case of a two-element model. Fitting onset (t₀) was chosen as the moment of maximum eye velocity in the relaxation phase of the eye movement (although we also explored a later fit onset; see results). Curve fitting was performed using the “trust-region” nonlinear least-squares algorithm of the “cftool” function in MATLAB (The MathWorks, Natick, MA). Initial values of time constants were generally chosen with the shortest time constant equal to 0.01 s and successive time constants increasing by a factor of 10. All time constants and coefficients were constrained to realistic values, i.e., time constants were not allowed to become negative, and the offset term E₀ was not allowed to exceed 90°. Each session generated a set of average values (one for each stimulus condition). These were averaged across sessions to generate one set of values for each stimulus type per animal and then averaged across animals to generate the final multi-animal results.

The analysis of the responses to sinusoidal stimuli was limited to characterizing eye position amplitude and phase (with respect to stimulus intensity) as functions of stimulus frequency. Amplitude and phase extraction were performed in a manner similar to that employed to extract gains and phases of the vestibulo-ocular reflex (Stahl et al. 2000). Briefly, any saccades were detected and patched by linear interpolation from the surrounding eye movement data. Segments of data were excluded if necessitated by loss of tracking, excessive animal movement, or because the saccades were so numerous that the de-saccaded trace consisted of more “patch” regions than actual data. Cycles of stimulus and response were then point-wise averaged to generate a single averaged cycle of stimulus and response. Fourier analysis was performed to obtain the absolute amplitude and phase of the stimulus and eye position relative to a sine function. The eye movement absolute phase was then corrected to reflect the 12-ms processing delay within the ISCAN video-oculography system, a delay determined empirically on our system in consultation with the manufacturer. Absolute eye phase was then subtracted from stimulus phase to obtain the eye phase relative to the stimulus and plotted against stimulus frequency. Amplitude and phase vs. frequency curves drawn from multiple experimental sessions in one animal were averaged to yield a single curve per animal and then averaged across animals.

Analysis of neuronal activity data during photostimulation was limited to qualitative evaluations of peristimulus time histograms (PSTHs) generated from recordings of nondiscriminated multi-unit potentials (“hash”). Multi-unit data were processed by taking the absolute value of the recorded signal, filtering with a bandwidth of 0.1–20 kHz using fourth-order digital Butterworth filters implemented in MATLAB, and then downsampling (by averaging each successive 96 samples of the raw data) to match the 508.6-Hz acquisition rates of the eye movement and stimulus data. We inspected the traces, excluding any stimulus cycles that were interrupted by saccades or major instabilities in the neural recording, and point-wise averaged the remaining cycles to generate a PSTH.

Relaxation of isolated extraocular muscles in vitro.

Time constants from the relaxation of extraocular muscles activated in vitro were measured, drawing on data from a previously published study (McMullen et al. 2004). The muscle preparation and in vitro apparatus are detailed in that study. Briefly, whole medial rectus (n = 3) or superior rectus (n = 5) muscles were dissected from freshly euthanized 8-wk-old C57BL/6 mice of either sex and mounted at optimal length (the length that generated maximum tetanic force) between a force transducer and a rod fixed to a micrometer in a muscle chamber perfused with 25°C physiological salt solution containing d-tubocurarine. Isometric contractions were induced by field stimulation: 300-ms stimulus trains were delivered every 90 s with 0.5-ms pulses at rates escalating from 1 to 200 Hz. To minimize muscle run-down, a single train was delivered at each stimulus frequency. Note that at the 1-Hz interpulse interval, the 300-ms train parameters equate to the delivery of a single 0.5-ms pulse. For these analyses, we selected only the responses to the 1- and 200-Hz trains, because these should lead to muscle activation most comparable to our 20- and 250-ms single-pulse and 270-ms train optogenetic stimulations. Relaxation phases were fit with exponential curves in a manner identical to that described for the optogenetic data. Because the data were originally collected to study peak forces only, only the first 150 ms of the relaxation phase was captured and available for analysis.

Anatomic analysis.

At the end of the stimulation experiments, the mice were deeply anesthetized and then perfused transcardially with buffered saline followed by 4% paraformaldehyde in 0.1 M, pH 7.2 phosphate buffer (PB). The brains were cryoprotected in 30% sucrose PB and then cut transversely on a sliding microtome (American Optical) equipped with a freezing stage. Series of 50-μm sections were treated in one of the following ways: 1) To allow for visualization of neuronal cell bodies, sections were mounted on gelatinized slides, stained with cresyl violet, dehydrated in a graded series of ethanols, cleared in toluene, and coverslipped. 2) To allow visualization of the yellow fluorescent protein (YFP) product of the optogenetic transgene, sections were mounted on gelatinized slides, dehydrated in a graded series of ethanols, cleared in toluene, and coverslipped using nonfluorescing medium. 3) To allow comparison of YFP expression with anti-choline acetyltransferase (ChAT) staining, sections were rinsed three times in 0.3% Triton-X 100 in PB, blocked in 1% bovine serum albumin dissolved in 0.3% Triton-X 100 PB, rinsed again, and then incubated overnight at 4°C in primary antibody consisting of mouse anti-ChAT (Chemicon) diluted 1:500 in 0.3% Triton-X 100 PB. The antibody was then tagged using donkey anti-mouse IgG conjugated to Cy3 (Jackson Labs) diluted 1:200 in PB. Reacted sections were mounted onto gelatinized slides, dehydrated in a graded series of ethanols, cleared in toluene, and coverslipped using nonfluorescing medium containing DAPI to stain nuclei. All slides were examined using a Nikon Eclipse E600 fluorescence microscope and photographed with a Nikon DXM 1200F digital camera controlled using the Nikon Elements software. Images were adjusted for contrast, brightness, and color balance using Photoshop to most closely replicate in the printed image the view seen by eye.

RESULTS

Expression of transgene in abducens nucleus.

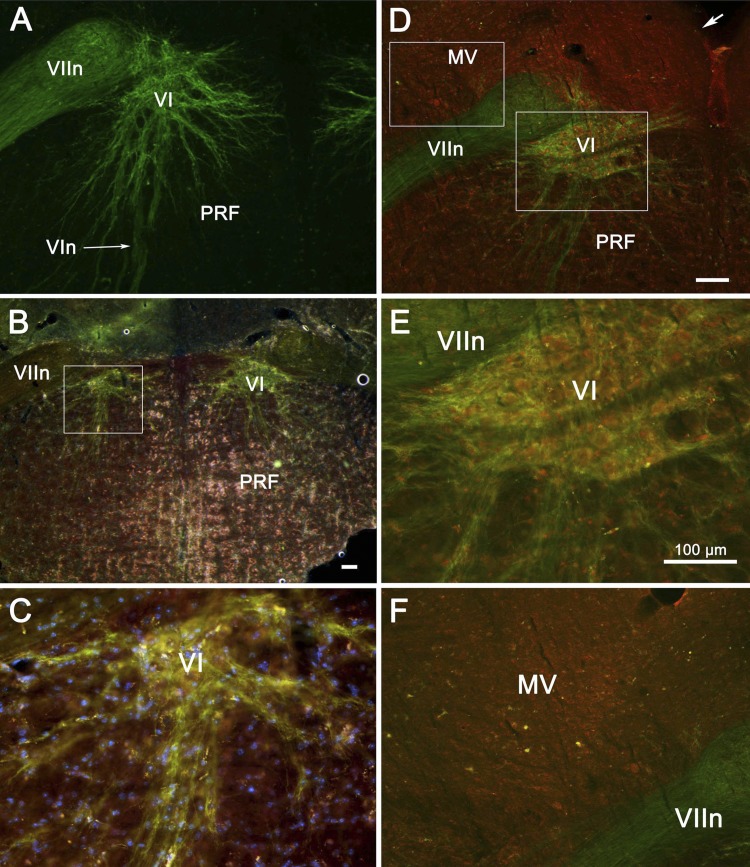
The originators of the ChAT-ChR2 transgenic noted that the optogenetic construct was expressed in “trochlear nucleus, facial nucleus, and various other brain stem motor nuclei” but provided no details regarding expression in the abducens nucleus (Zhao et al. 2011). As shown in Fig. 1A, abducens neurons were extensively labeled by the YFP marker of transgene expression. The nucleus is quite small and sits ventromedial to the genu of the facial nerve. In contrast, the labeled dendrites extended ventrally across the borders of the nucleus (VI), far into the pontine reticular formation. Some dendrites extended toward the midline, nearly meeting those of the opposite nucleus. Others (not shown) extended around the medial edge of the genu of the facial nerve (VIIn). In two other cases (Fig. 1, B and C, and D–F),we compared the expression of the YFP marker with the presence of ChAT. In these double-labeled sections, green labeling indicates the presence of channelrhodopsin, red label indicates ChAT, and their coincidence appears yellow. Abducens neurons presumed to be motoneurons exhibit yellow somata and green dendrites, indicating that the ChAT is localized to somata, whereas the channelrhodopsin is found in the membranes of both dendrites and somata. This is in contrast to the rare cholinergic neurons found scattered in the medial vestibular nucleus (MV in Fig. 1F) and the nucleus prepositus hypoglossi (not illustrated), where both ChAT and channelrhodopsin were expressed in somata but virtually no fluorescence of either type was observed in the dendrites. Clearly, far less channelrhodopsin was incorporated into the membranes of these nonmotoneurons. Thus photostimulation of these cells would likely be less effective, even if they were to receive as much light intensity as the neurons in the targeted abducens nucleus. Examination of the cresyl violet-stained sections (Nissl sections; not shown) indicated no obvious difference in size or numbers of neurons in the transgenic animals compared with C57BL/6 mice. Note that there was also no evidence that the fiber optic cannula had damaged the abducens nucleus in any of the four recorded animals.

Fig. 1.

Histochemical demonstration of channelrhodopsin expression in motoneurons of the abducens nucleus (VI) of ChAT-ChR2 mice used in the optogenetic stimulation experiments. VI may be seen in these transverse sections (A–F) lying ventromedial to the genu of the facial nerve (VIIn). Note in A the wide extent of the dendritic arbors. Low (B and C)- and high-magnification views (D–F) of double-labeled tissue from 2 additional animals are shown. Anti-choline acetyltransferase (ChAT) marker is red, channelrhodopsin marker is green, and their overlap appears as a yellow-orange color. Like abducens motoneurons, cholinergic medial vestibular (MV) neurons show coexpression of the ChAT and channelrhodopsin in their somata but lack the motoneurons' dendritic expression of channelrhodopsin. In B–F, nuclei fluoresce blue. Boxes in B and D indicate location of higher magnification views. Arrow in D indicates the ventricular surface. All scale bars are 100 μm; scale bar in D also represents A, and scale bar in E also represents C and F. MV, medial vestibular nucleus; PRF, pontine reticular formation; VIn, abducens nerve.

Qualitative features of response to pulse stimuli.

Both single-pulse and train stimuli generated a brisk abducting movement in the eye ipsilateral to the abducens nucleus that was “targeted” by the fiber optic probe. With increasing duration stimuli the eye tended to reach a maximum sustained deflection, which ranged 3–12° across the 4 animals. Most of this range reflected animal-to-animal variation, likely related to differences in how precisely the probe aligned with the target nucleus. Moment-to-moment variations in response amplitude may arise from variations in animal alertness and initial eye position, both of which would alter the contractile state of the extraocular muscles. However, these variations were far less than we observed when applying electrical stimulation through metal recording electrodes (unpublished observations) in a study of abducens nucleus physiology (Stahl and Thumser 2012). When averaged across animals within stimulus durations, peak eye velocity (the point from which quantitation of time constants began) was reached 18–24 ms after stimulus offset of single-pulse stimuli and 17–20 ms after offset of train stimuli.

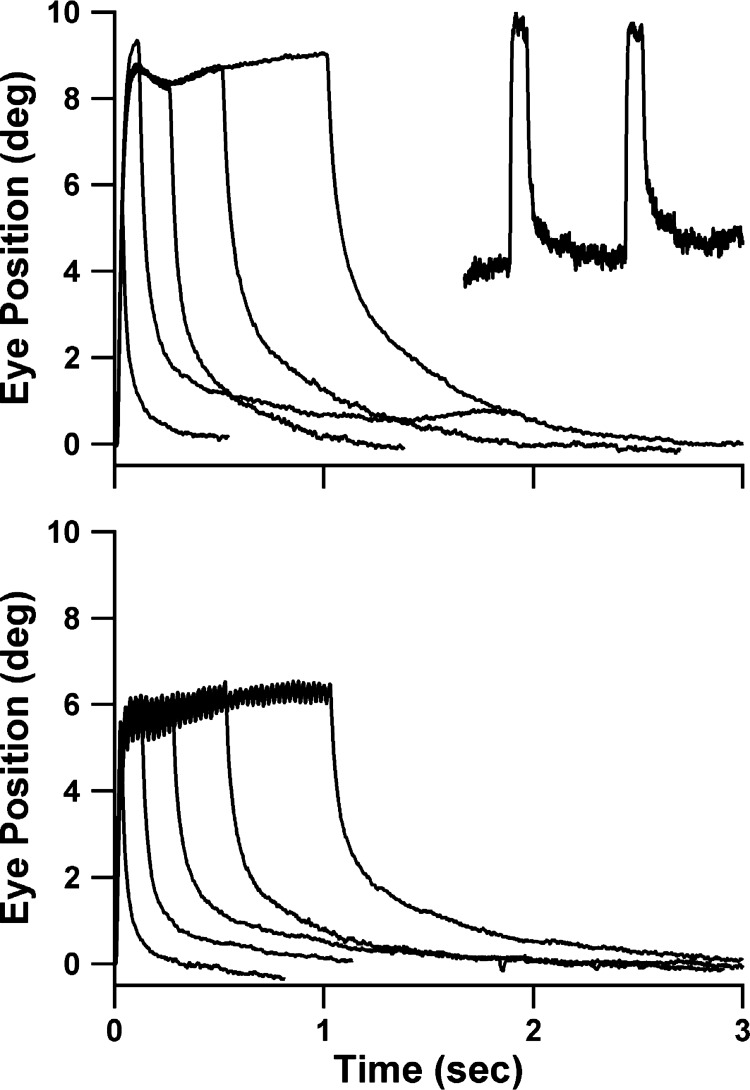
Examples of averaged responses to the single-pulse and train stimuli from single experimental sessions are shown in Fig. 2, top and bottom, respectively. Time constants for each experimental session were extracted from such averaged records. The inset trace shows typical examples of the individual (non-averaged) responses to the 250-ms single-pulse stimulus from which the accompanying averaged curve was derived. During train stimuli, individual twitches corresponding to each pulse were always visible in the non-averaged records up to pulse rates of ∼50 Hz. The maximum amplitude achieved tended to be smaller for the train compared with the single-pulse stimuli. Some of the difference likely relates to the 20% shorter total illumination time using the 80% duty-cycle pulsed stimuli: in one animal we compared the amplitude of responses to single-pulse stimuli, single-pulse stimuli reduced to 80% of their standard durations, and the 80% duty-cycle 40-Hz train stimuli. The reduced-duration single-pulse and train stimuli evoked responses of similar amplitudes. Specifically, averaging the three longest stimuli (250- to 1,000-ms single pulses and 270- to 1,020-ms trains), the average amplitudes for single-pulse, shortened single-pulse, and train stimuli were 8.1°, 6.5°, and 6.7°, respectively.

Fig. 2.

Examples of responses to single-pulse (top) and pulse-train (bottom) photostimuli of the 5 stimulus durations. Each trace is based on the average of all usable responses collected in a single experimental session of 1 animal; data in top and bottom panels were obtained from different animals. Inset shows 2 raw (non-averaged) responses that contributed to the depicted average response for 250-ms single-pulse stimuli.

Fine details of the configuration of the plateau phase of the response to the longest stimuli (500/520 and 1,000/1,020 ms) varied from animal-to-animal and sometimes session-to-session in any one animal. A slight decay followed by a gradual increase in eye position as shown in Fig. 2, top (a particularly robust example of the phenomena), were commonly seen. In other cases, either the initial sag or the delayed increase was missing. Notably absent were instances of long declines, suggesting development of depolarization blockade of the motoneurons, a phenomenon described in striatal cholinergic neurons by the developers of the ChAT-ChR2 strain (Zhao et al. 2011), is not a significant confound in this experiment.

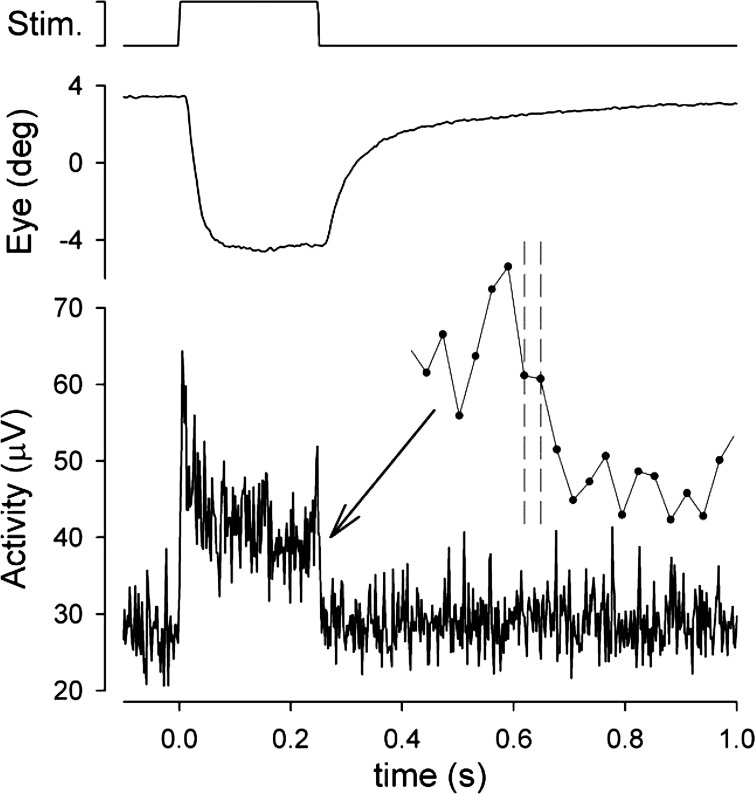
Figure 3 shows a typical PSTH of multi-unit neuronal (field) activity during the 250-ms single-pulse stimulation. The inset diagram shows the region around stimulus offset at greater temporal resolution. The neural response is notable for an initial phasic component that was manifest in varying degrees from recording site to recording site and may be responsible for the similarly variable overshoots in initial eye position exemplified in Fig. 2. The decline to a stable plateau of activity accords with the aforementioned impression from the eye movement responses that progressive depolarization blockade of the motoneurons is not a major factor in this preparation. Following stimulus offset, averaged neural activity declined to baseline within two to three samples (4–6 ms). Note that since the stimulus command signal is not synchronous with the bins of the PSTH, stimulus offset is distributed across two samples. The rapid return to baseline, which was the rule in all recorded examples, indicates that the neural activation underlying the eye position offset behavior accords closely with an ideal step change in innervation, with the further implication that the eye position decay is governed entirely by the inactivation properties of activated muscle and the passive mechanical properties of the ocular motor plant.

Fig. 3.

Peristimulus time histograms (PSTHs) of nondiscriminated multiunit field activity in the abducens nucleus during the 250-ms single-pulse stimulus. Record is average of 7 presentations of the stimulus. Inset shows the offset response at higher temporal resolution, with data points indicating the individual 1.97-ms samples. Dashed cursors indicate the 2 samples over which the stimulus offset is distributed.

Time constants from decay phase of pulse stimuli.

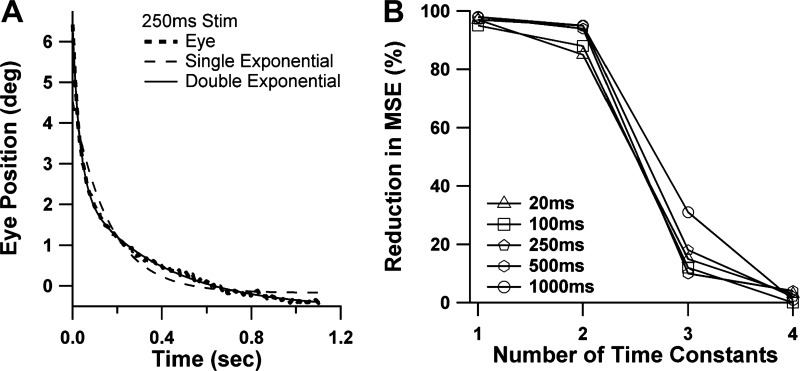
As described in methods, we fit the decay phases of the averaged responses to the pulse stimuli with sums ranging from one to four exponential terms. Figure 4A shows an example of fitting with both one- and two-term models. The fit is greatly improved by the addition of the second term. Figure 4B plots the percentage reduction of the residual mean squared error afforded by the addition of each exponential term, an approach to systems identification previously applied to similar data from the primate (Anderson et al. 2009). The graph in Fig. 4B is based on the responses to the single pulses only, and separate curves are shown for each stimulus duration. The curves drop off precipitously after the first two elements, indicating that the vast preponderance of the decay behavior could be explained by a cascade of just two viscoelastic elements, which would be modeled with a two-pole, one-zero (2P-1Z) transfer function.

Fig. 4.

Extraction of time constants from eye recoil following step stimuli. A: example of fitting single (dashed line)- and double (solid line)-exponential equations for an averaged response to the 250-ms single-pulse stimulus. B: determination of the optimum number of exponential terms across the entire data set for single-pulse stimuli of all durations. Percent reduction in mean square error (MSE) afforded by addition of each exponential term is plotted vs. total number of exponential terms.

Table 1 summarizes the results of the time constant analyses of the pulse data using the two-term model. Average coefficients of determination (r²) for the exponential fits were uniformly excellent. Note that the 100- to 1,000-ms single-pulse stimuli were introduced only for the last 2 of 4 animals. Despite the varying numbers of animals contributing to each set of results, the single-pulse and train stimuli generated comparable results for the time constant values. Scatter plots of time constants from the train vs. single-pulse data for the two animals in which both types of data were available (plots not shown) showed no consistent differences in T₁ or T₂ when all the different stimulus durations were taken into account. Accordingly, we then pooled the train and single-pulse results in Table 1. The data in Table 1 demonstrate that time constants were fairly stable over the range of stimulus durations from 100 ms and beyond, although there was a consistent pattern in which longer stimuli produced decays with slightly longer time constants. The trends for stimuli of 100- to 1,000-ms duration (120–1,020 ms for trains) are not likely to be a chance occurrence, since the much shorter, 20-ms stimulus resulted in markedly shorter time constant values.

Table 1.

Mean time constants and coefficients extracted from step stimuli

Duration, ms	Amplitude, °	T1, s	T2, s	A1, °	A2, °	r2	No. of Animals
Single pulse
20	3.36	0.018	0.239	1.65	1.28	0.9944	4
100	9.13	0.040	0.604	5.15	2.29	0.9964	2
250	8.50	0.038	0.471	4.23	2.91	0.9978	2
500	9.20	0.045	0.601	4.60	4.04	0.9972	2
1,000	9.74	0.057	0.817	4.61	4.16	0.9985	2
Train
120	4.60	0.035	0.495	2.69	1.65	0.9949	4
270	4.97	0.042	0.516	2.49	1.90	0.9955	4
520	4.75	0.042	0.540	2.14	2.25	0.9956	4
1,020	4.86	0.050	0.667	2.21	2.72	0.9955	4
Pooled
20	3.36	0.018	0.239	1.65	1.28	0.9944	4
100–120	5.03	0.032	0.444	2.82	1.67	0.9949	4
250–270	5.23	0.039	0.457	2.52	1.98	0.9955	4
500–520	5.17	0.040	0.510	2.30	2.45	0.9958	4
1,000–1,020	5.26	0.048	0.664	2.27	2.88	0.9961	4

T₁ and T₂, time constants; A₁ and A₂, response amplitudes; r², coefficient of determination for exponential fit.

Short-duration stimuli engender smaller deflections, which raises the possibility that the shorter time constants obtained with 20-ms stimuli reflect a dependence of time constants on deflection amplitude rather than stimulus duration. However, scatter plots (not shown) of T₁ and T₂ vs. peak response amplitude (one data point per session) for each of the stimulus durations of 100 ms and above revealed no patterns across the considerable ranges of response amplitudes (ranges of 3.4–4.8° for the 100- to 1,000-ms single-pulse stimuli and 6.1–7.2° for the 120- to 1,020-ms trains), nor was there any correlation between T₁ or T₂ time constants and the response amplitude for the 20-ms single-pulse stimulus alone (whose response amplitude ranged 1.4–6.5° across all sessions). The lack of a correlation between time constants and response amplitude is consistent with the ocular motor plant behaving in roughly linear fashion, in addition to indicating that the apparent relationship between time constants and duration in Table 1 is attributable to an effect of stimulus duration rather than response amplitude. One other pattern notable in Table 1 is that as stimulus duration grows, so does the contribution of the slower viscoelastic element (as evinced by A₂ and the A₁/A₂ quotient). The lower values of A₂ for the 20- and 100- to 120-ms stimuli are expected, since those stimuli are insufficiently long to fully stretch an element whose time constant exceeds 500 ms.

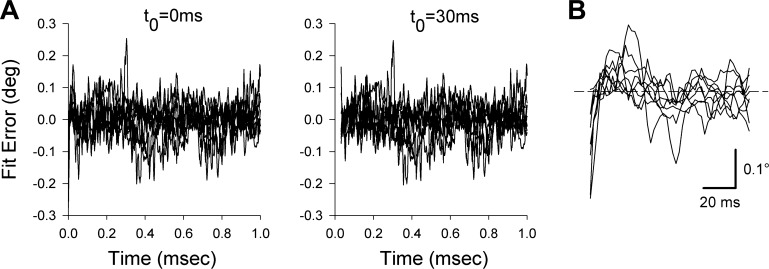
In the primate study in which time constants were obtained from responses to electrical stimulation of the abducens nucleus (Anderson et al. 2009), principle component analysis indicated that during the first 40 ms following stimulus offset (or ∼30 ms following their point of maximal recoil velocity), eye movements departed from ideal behavior of a linear viscoelastic system responding to a step decrement in force. It is likely that an important contribution to this non-ideal behavior was the non-instantaneous decrement in active muscle forces at stimulus offset. Because quantifying the passive mechanics from the earliest portion of the recoil would have been confounded by this non-ideal behavior, the authors based their time constant measurements on fits beginning 40 ms after stimulus offset. This approach removed a theoretical confound to extracting parameters of passive elements and reduced fitting errors. We repeated our own time constant analyses, shifting our fit onset (t₀) from 0 to 30 ms after peak recoil eye velocity. Time constants were uniformly somewhat longer with the 30-ms fit onset point. For instance, the value of T₁ for pooled single pulses and trains, averaged across the 4 longest stimulus durations, was 39.6 ms for nondelayed fitting and 67.2 ms for delayed fitting. T₂ was also lengthened (as well as becoming skewed by one spuriously long result), with median results of 0.483 and 0.641 s for nondelayed and delayed fitting, respectively. Delayed fitting produced less reliable results. The convergence of the delayed fits was more sensitive to the initial values of the parameters, and correspondingly, the confidence intervals on the parameters returned by the MATLAB fitting function were widened. For instance, for the pooled single-pulse and pulse-train data averaged across the different stimulus durations, the confidence interval expressed as a percentage of the average time constant value increased from 12 to 39% for T₁ and from 10 to 109% for T₂. In the monkey data, one powerful argument for delayed fitting was that it greatly attenuated systematic variations visible in the instantaneous fitting errors (see Fig. 3, C and D, in Anderson et al. 2009). Figure 5A displays the equivalent plots in the present mouse data, drawn from the first 1.0 s of the responses to the 520-ms trains, with error defined as actual minus fitted eye position. In sharp contrast to the monkey results, delayed fitting produced relatively little effect on the instantaneous errors. The comparisons of instantaneous and delayed fitting for the other stimulus conditions were similar to that shown in Fig. 5A.

Fig. 5.

A: comparison of instantaneous fit errors when a 2-term exponential fit to the 520-ms train data is initiated at the moment of maximal recoil eye velocity (t₀ = 0 ms) vs. 30 ms later (t₀ = 30 ms). The t₀ = 30 ms plot is shifted rightward 30 ms so that timing of the residuals in the 2 panels is comparable. In contrast to equivalent plots in the monkey, delaying the onset of fitting did not improve the instantaneous errors. B: the first 100 ms of the residuals of the t₀ = 0 ms plot from A, at an expanded scale. Horizontal cursor indicates 0 fitting error.

The error plots of the nondelayed fits do exhibit some consistent patterning in the first ∼30 ms. Figure 5B shows the first 100 ms of the nondelayed plot from Fig. 5A at an expanded timescale. The residuals are initially negative with a positive slope, indicating that the eye recoiled more slowly than the model, which is what would be expected if residual active force retarded the recoil. However, this period is quite brief, and again, its inclusion proved more beneficial than detrimental to fit stability.

Eye movement responses to sinusoidal photostimulation.

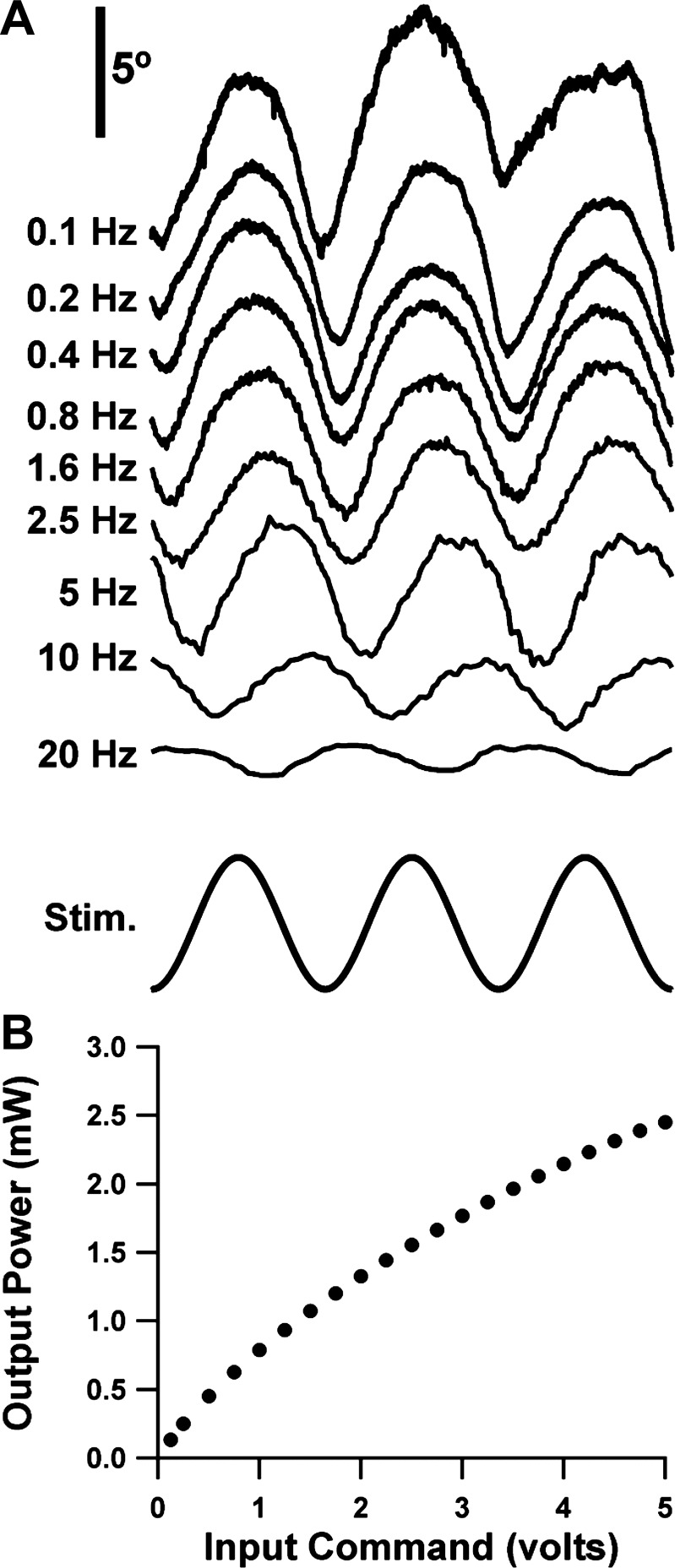
The literature on control systems analysis of vestibular and ocular motor physiology has focused extensively on the behavioral and neural responses to sinusoidal stimuli. Thus we felt it was important to test the feasibility of using sinusoidal photostimulation to activate extraocular motoneurons as a method of probing ocular motor mechanics. We were encouraged to attempt this because although optogenetic studies have customarily employed pulsed stimuli, recent work has shown that several channelrhodopsin varieties (including the H134R variety in our ChAT-ChR2 mice) can respond in graded fashion to sinusoidally modulated stimulus intensity (Tchumatchenko et al. 2013). We recorded the eye movement response while we drove the LED source with a sinusoidal command voltage. Figure 6A depicts examples of the resultant sinusoidal eye movement responses. The sinusoidal character was somewhat imperfect, since the peaks of the eye movement waveforms (corresponding to brightest stimulus and maximum abduction) were usually more broadly contoured than the troughs. Some of this asymmetry may simply reflect the voltage-to-power function of the M470F1 LED source (Fig. 6B), which flattens somewhat as voltage to the DC2100 driver approaches its 5-V maximum.

Fig. 6.

A: typical examples of the steady-state response to the sinusoidal photostimulus to each stimulus frequency. Abscissa is calibrated in number of cycle periods to facilitate comparison across stimulus frequencies. All traces share the same vertical scaling. Upward trace deflections correspond to abduction. B: luminous power of the Thorlabs M470F1 LED source (in mW) as a function of command voltage.

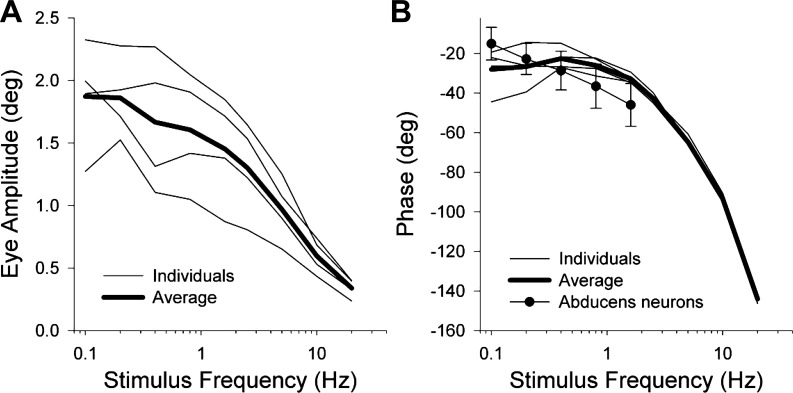
Figure 7 plots average eye amplitude vs. stimulus frequency (A) and eye phase lag with respect to LED intensity vs. frequency (B) for each of the four mice. Also included are the averages of the individual animal curves (heavy line). Animal-to-animal variability of the amplitude and phase tended to be greatest at the lowest stimulus frequencies. Some of the lesser variability of high-frequency responses stems from these responses being based on averages of larger numbers of cycles. Phase lag increased markedly as stimulus frequency increased, in a fashion characteristic for a system incorporating fixed delay elements (such as the delay introduced during conduction along the abducens nerve).

Fig. 7.

Eye movement amplitude (A) and phase with respect to photostimulus intensity (B) plotted vs. stimulus frequency during sinusoidal stimuli. Fine lines are curves for individual animals averaged over all sessions. Heavy line is the average across animals. Negative phases represent eye lagging stimulus. Graph in B includes our previously published plot of neuronal phase with respect to eye position [adapted from Stahl and Thumser (2012)] in which neuronal phase error bars are ±1SD.

Figure 7B includes the published curve depicting the phase lag of the eye with respect to firing rate of abducens nucleus neurons in the mouse (Stahl and Thumser 2012). The similarity between the two sets of data suggest that the photostimulation brings out mechanical properties comparable to natural activation and could be used in the future as a probe of ocular motor plant mechanics. Unfortunately, the present sinusoidal response data are insufficient to generate time constants of the ocular motor plant because the transformation between stimulus intensity and eye position reflects not only plant mechanics but also the dynamics mediating the transformation from light intensity to abducens motoneuron firing. Some of the mismatch between the optogenetic and neuronal recording curves may stem from the phase lags/leads introduced by that unknown transformation. The transformation reflects two processes: the transformation from light intensity to ChR2 currents, and the subsequent conversion from those currents to neuronal firing rate. A function for the first transformation has been published and indicates that it would contribute a sizable phase shift by the time stimulus frequency reaches 20 Hz (Tchumatchenko et al. 2013). To our knowledge there are no data in extraocular motoneurons that describe the subsequent transformation to neuronal firing.

Dynamics of relaxation, in vitro.

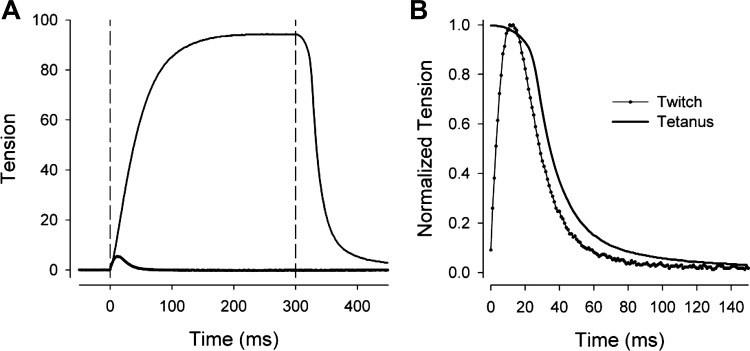
The results of the single-pulse and pulse-train stimuli indicate that the time constants were dependent on the duration of stimulation. To investigate whether the phenomenon is a property of the decay of active force of the contractile elements, we quantified the isometric relaxation of extraocular muscles activated electrically in vitro, using data of a previously published study (McMullen et al. 2004). Figure 8A shows a typical example of the isometric force curves of a medial rectus muscle responding to a single 0.5-ms pulse and a 300-ms train of 0.5-ms pulses delivered at 200 Hz (twitch and tetanus responses, respectively). Vertical cursors mark the onset and offset of the 300-ms train. Figure 8B shows the offset portion of the same response, at an expanded timescale and with all tensions normalized to their maximum values to facilitate comparisons of the twitch and tetanus. Time constants were fit from the time of peak relaxation rate using single- and double-exponential equations. The most robust fits (least sensitive to initial conditions, narrowest confidence intervals) were achieved with the single exponentials. The time constant T averaged 14.9 ± 5.1 and 18.0 ± 4.2 ms (means ± SD) for the twitch and tetanus, respectively. The associated fit r² values were excellent, averaging 0.9966 and 0.9990, respectively. The T results and other measures of the timing of the isometric tension response are summarized in Table 2. Although the longer stimulus was associated with a slightly larger average time constant, the difference was negligible compared with the more than doubling of T₁ that occurred in vivo as the photostimulus was increased from 20 to 250–270 ms. Thus the dependence of time constants on stimulus duration in vivo is unlikely to be a consequence of the decay of active forces elicited in this isolated muscle preparation.

Fig. 8.

Examples of isometric tension developed by an isolated medial rectus muscle responding to a 0.5-ms electrical pulse (twitch response) and a 300-ms-duration, 200-Hz pulse train (tetanus response). A: complete response. Tension calibrations are arbitrary, but twitch and tetanus responses share the same calibration. Vertical cursors indicate stimulus onset and the offset of the long stimulus. B: data are identical to A, but timescale is expanded and responses are normalized and time-shifted to facilitate comparison of the twitch and tetanus behaviors following stimulus offset.

Table 2.

Average dynamics measurements for isolated muscles

	Peak Tension Time From Onset, ms	Peak Rate Relaxation Time From Offset,ms	Half-Relaxation Time From Offset, ms	Half-Relaxation Time From Peak Tension, ms	Relaxation Time Constant, ms
Twitch	13.8 ± 3.9	25.8 ± 6.6	29.4 ± 8.0	16.2 ± 4.2	14.9 ± 5.1
Tetanus	300	27.5 ± 6.6	34.0 ± 7.9		18.0 ± 4.2
Twitch, Close and Luff (1974)	4.4 ± 0.4	—	8.9	4.8 ± 0.5	—

Values are means ± SD for 8 isolated muscles. No SD is given for the time of peak tension for tetanus because it is defined as the stimulus duration (300 ms). No SD is given for the Close and Luff half-relaxation time from offset because it is calculated from their mean time to peak, t_1/2 from peak, and stimulus duration (0.3 ms).

Table 2 includes the half-relaxation times, measured both from stimulus offset and from time of maximal tension. For the tetani, the maximum tension was present at stimulus offset, so those two time values are identical. In contrast, for the twitch responses, the tension continued to build for several milliseconds after stimulus offset, with the result that the relaxation times measured from peak tension are substantially shorter than those measured from stimulus offset. Note that because peak tension for tetanus was defined as the tension at stimulus offset, the time of peak tension measured from stimulus onset is simply the stimulus duration (300 ms). For comparison with the present data, Table 2 includes previously published results (Close and Luff 1974) on the twitch response in isolated rat inferior rectus muscles, recorded at 35°C. The twitch and relaxation times are approximately one-third of those measured from the present data. Some part of the difference likely reflects the measurements having been taken at different temperatures. Assuming no effect of the species difference, we can calculate the temperature effect Q₁₀ from our mouse data and Close and Luff's rat data in Table 2 as Q₁₀ = (R₂/R₁)^{10/(Temp₂ − Temp₁)}, where R values are the reciprocals of the twitch peak tension time or half-relaxation from peak tension time, and Temp_x are the corresponding temperatures. The calculations yield Q₁₀ values of 3.1 and 3.4 for peak tension and half-relaxation, respectively. These values are within the ranges reported for rodent skeletal muscle (Bennett 1984). There are no prior quantitative descriptions of the time course of relaxation following tetanic stimulation in rodent extraocular muscles for comparison with the present data.

DISCUSSION

This study is the first use of optogenetic techniques to measure the mechanics of the ocular motor system. The photostimulation was well tolerated by the animals and generated robust eye movements. Although the number of animals used was small (4 mice), the findings were very consistent. Compared with electrical stimulation of the abducens nucleus in the primate (Anderson et al. 2009), the photostimulation did not engender shifts in equilibrium eye position that were attributed to unintentional activation of the brain stem velocity-to-position neural integrator. Our limited recordings of single-unit and multiunit abducens nucleus activity provide further evidence against the photostimulation activating the neural integrator. In all cases the neuronal activity reverted to its prestimulation baseline in less than 10 ms. By contrast, the time constant of the neural integrator in mice is on the order of 5 s (Stahl et al. 2006). There was some potential for the neural integrator to be activated in this optogenetic model, since the circuit incorporates cholinergic neurons in the adjacent nucleus prepositus hypoglossi (Navarro-Lopez et al. 2004), which would express the channelrhodopsin. Apparently the illumination outside the targeted abducens nucleus was too weak, or the channelrhodopsin expression levels, which our histological results indicate are much lower outside than within the abducens nucleus, were too low to sensitize the integrator circuits to photostimulation. In contrast to electrical stimulation in the abducens nucleus, optogenetic stimulation is also not likely to activate abducens internuclear neurons, because these cells are not cholinergic (Carpenter et al. 1992; Nguyen and Spencer 1999).

A potential concern in approaching these experiments was the possibility that the relatively long stimulus durations required to energize appreciably any slow viscoelastic elements would lead to depolarization block of the motoneurons, as has been described in other neuronal cell types (Herman et al. 2014; Zhao et al. 2011). This concern was one motivation for our initial use of train rather than continuous photostimuli. However, experience proved that prolonged stimulation leads, if anything, to a gradual increase in the abduction amplitude, and the single-pulse stimuli actually evoked stronger abduction than did trains. Although there is often a brief spike in the initial eye movement and neuronal activation, followed by a decline toward final values, the time course of the spike and decline accords with the form of the channel currents themselves, which exhibit a spike-decay appearance attributed to a desensitization process whose time constant measures ∼25 ms in the H134R channelrhodopsin (Mattis et al. 2012). Because single pulses generated a stronger response than the comparable pulse trains and constitute a mathematically simpler driving function, we adopted single-pulse stimuli in all later experiments.

In addition to quantifying time constants from pulse and pulse-train photostimuli, we made a methodological exploration of the potential to characterize ocular motor dynamics using sinusoidal photostimuli. We demonstrated that the sinusoidal photostimulation could evoke sinusoidal eye movements with appreciable amplitudes and fidelity to frequencies as high as 20 Hz. At low frequencies, the phase relationship exhibited a relatively good match to the phase of neuronal firing with respect to eye position during sinusoidal eye movements evoked by natural stimulation, although this correspondence needs to be viewed with some caution because we lack knowledge of the exact phase relationship between photointensity and induced neural firing. The exact phase relationship must be determined from recordings of abducens neurons, in vivo, during optogenetic stimulation before these data can be used to extract plant time constants.

The ability of channelrhodopsins to respond in graded fashion to sinusoidal stimuli has been demonstrated (Laxpati et al. 2014; Tchumatchenko et al. 2013), but, to our knowledge, this is the first study to investigate the use of the property to probe the dynamics of neural circuitry. Linear control systems analyses and sinusoidal stimuli have played a critical role in explorations of ocular motor physiology, and the optogenetic techniques render it possible, in theory, to inject sinusoidal driving functions in specific neurons at various locations within the ocular motor circuitry of awake, behaving animals. The H134R channelrhodopsin current has been demonstrated to suffer a 50% attenuation at 37 Hz (Tchumatchenko et al. 2013). Since the spectrum of natural head frequencies in the mouse has been shown to extend no higher than 20 Hz and the vast majority of head movement power is below 5 Hz (Beraneck et al. 2008), the H134R channelrhodopsin is sufficiently “fast” to characterize vestibulo-ocular circuitry over the operating range relevant to natural head movements. The power spectrum of mouse saccades has not been described but likely extends beyond 60 Hz, since recordings of vestibular fast phases at sampling rates of 120 Hz (which would capture eye movement components up to only 60 Hz) have been demonstrated to underestimate peak eye velocities (Stahl et al. 2006). Thus a more rapid channel would be required to extend the characterization of the ocular motor circuit dynamics to the limit of their natural range.

Dependence of time constants on stimulus duration.

Both T₁ and T₂ exhibited a clear tendency to increase with stimulus duration, the phenomenon being exhibited most strongly over the increment from 20 to 100 ms in duration. This dependence should not occur in a linear viscoelastic system responding to an ideal step in excitation, with the caveat that the fitting model must contain a sufficient number of viscoelastic elements. If the model has an insufficient number of exponential terms, longer stimulus durations will recruit larger numbers of terms, and the fitting algorithm will report time constants that lengthen to capture some of the variance deriving from the more sluggish terms. However, since Fig. 4B suggests that a two-term viscoelastic model adequately captures the relaxation behavior, other explanations must be sought. Several possibilities arise from the fact that, contrary to the ideal scenario, the force profile following the offset of photostimulation does not decrement instantaneously in the manner of an ideal step function. The processes governing the decline of active force could be sensitive to the duration of the preceding stimulus. The rate of decline of sarcoplasmic calcium in limb muscles, for instance, exhibits such sensitivity (Carroll et al. 1997) and, with its time constant range of ∼25–60 ms, might have explained variations in T₁, and to a lesser extent in T₂. However, the relative absence of significant duration dependence in the isolated extraocular muscles argues against a role for calcium accumulation prolonging time constants in vivo.

A more promising explanation derives from consideration of the possible effects of multiply innervated muscle fibers (MIFs). The MIFs, also called “non-twitch” fibers, relax slowly and thus could slow the return movement of the eye. Since they are poorly activated by brief nerve stimuli (Shall and Goldberg 1992), they would likely be minimally activated by our 20-ms stimulus and progressively recruited as stimulus duration increased. MIFs do not appear to be activated by direct muscle stimulation (Close and Luff 1974), likely because of their insensitivity to brief stimuli, together with the fact that they do not conduct action potentials (Chiarandini and Stefani 1979). As such, their posited effects on tension relaxation would not have been observed in our in vitro preparation. Attributing to non-twitch fibers the slow component of relaxation following nerve stimulation (as opposed to direct muscle stimulation), Close and Luff (1974) noted that the non-twitch fibers “contributed very little to the total isometric tension.” However, this pronouncement should not lead to their being discounted as a factor in the decay to final eye position. MIFs compose 10% of the cross-sectional area of the global layer of extraocular muscles (Porter et al. 1995) and thus likely contribute in a meaningful way to the forces applied to the globe. Isometric forces engendered through specific activation of MIFs by succinylcholine reach as high as one-third of the levels generated by maximal tetanic nerve stimulation in cats and humans (Lennerstrand et al. 2010). Finally, the levels of force reflected by maximal isometric forces are only called into play during saccades, in which MIFs may play a limited role. MIFs are generally conjectured to be important when the muscle is operating at the lower force levels relevant to moving the eye at nonsaccadic velocities and maintaining steady eye positions, particularly near central orbital positions (Dean 1996). Those nonsaccadic conditions are more comparable to the relaxations following photostimulation, and as such MIFs may contribute significantly to the present data.

According to our MIF explanation of the stimulus duration dependence, the time constants measured following the 20-ms stimulus reflect a blend of passive viscoelastic properties and the relaxation of active forces in singly innervated (twitch) fibers, whereas time constant values following progressively longer stimuli would reflect an increasing contribution from the relaxation properties of the non-twitch MIFs. Furthermore, the results imply that the time constants of the active force decay and passive relaxations must be similar; otherwise, the analysis procedure would be able to extract them as discrete exponential terms. One difficulty with this scenario is that the relaxation of active force is likely to be rapid, on the order of a few tens of milliseconds, and thus would not explain the strong stimulus duration dependence of T₂. This conundrum underscores the need for more in vitro studies of the relaxation properties of extraocular muscles, with attention to conditions favoring either multiply or singly innervated muscle fibers, and with longer poststimulus recording times, which would allow for detection of any long time constants in the tension decay. As noted in results, the present data are the only available measurements of tension decay following tetanic stimulation, and the observation of the relaxation period was limited to just the first 150 ms.

Consequences of selection of fit initiation point.

In an ideal viscoelastic system composed of discrete mechanical elements, responding to a perfect step in innervation and recorded without the confound of biological or recording noise, the curve-fitting process should be capable of extracting all of the pole time constants and should be relatively insensitive to the point at which fitting is initiated. In reality, a number of factors deviate from the ideal conditions. First, if the true number of poles in the system exceeds the numbers of poles in the model, then the measured time constants will represent compromise values, and as the fit onset point is progressively delayed, the effects on that compromise of the shortest time constant will wane and the measured time constants will progressively increase. Although Fig. 4B indicates that our two-element model captured the bulk of the variance in our data, this approach to systems identification would likely overlook very short time constants, which, given our 240-Hz video-oculography sampling rate, would contribute very few data points to each decay. Theoretical considerations of the biomaterials of which the ocular motor plant is composed indicate there is a very large (possibly infinite) number of viscoelastic elements with a continuous distribution of time constants, including time constants shorter than the shortest value we obtained; i.e., T₁ = 18 ms for the response to the 20-ms stimulus (Sklavos et al. 2005). As such, any analytically tractable model is underspecified, and a rightward shift in the fit onset should result in increasing measured time constants. This phenomenon may underlie the prolongation of time constants we observed when we delayed fit onset by 30 ms.

A second important departure from the ideal relates to the certainty that active forces decay gradually, rather than instantaneously. The gradual decay can be modeled to a first approximation as a single pole cascaded with the 2-pole, 1-zero (2P-1Z) model of the passive plant, resulting in an overall 3P-1Z model. Its effect when the time constants are fit by a 2P-1Z model is to increase the apparent T₁ and T₂, with T₁ affected more strongly (so long as the active force time constant is of duration closer to T₁ than T₂). Moving the fit onset rightward will progressively escape the effects of the active force decay, causing the measured time constants to decrease toward their true values. Our in vitro data suggest that our in vivo time constants measured in the 20-ms stimulus condition may be relatively free of this effect. The isometric decay time constant was 15 ms, and this value would likely be closer to 5 ms at physiological temperatures. Our fits began at maximum recoil velocity, which occurred on average at about 20 ms after stimulus offset. As such, the decay of active force would likely be complete. The effect is presumably more relevant in the fitting responses to longer duration stimuli, particularly if we are correct that these long-duration stimuli activate the slowly relaxing MIFs. However, the fact that our delaying the fit onset by 30 ms tended to increase time constants suggests that the effect of bypassing the period of decaying active force was less important than the time constant-prolonging effects of rightward shifts in the fit onset point.

Our time constant results likely represent an upper bound on the true value of the short passive (mechanical) time constants, since both the decay of residual force and our delaying fit onset until the moment of peak recoil velocity would have the effect of prolonging the measured time constants. Our short time constant should also be viewed as describing combined active and passive/mechanical phenomena. The value we obtained is useful when one needs a descriptive model of the plant as part of a larger model of ocular motor circuitry. However, further study is required to disentangle the active and passive contributions to the earliest phases of the eye movement following stimulus offset.

Comparison of mouse and primate plants.

Our previous determination of oculomotor time constants in the mouse, based on analyses of the relationship of abducens nucleus firing to eye position during sinusoidal eye movements, yielded T₁ and T₂ on the orders of 100 and 900 ms, respectively (Stahl and Thumser 2012). The gradual sinusoidal stimuli used in that study (0.1–1.6 Hz) probably engender mechanical conditions most comparable to the long-duration stimuli of the present study, and thus those time constants should be compared with the present values of 48 and 664 ms. The differences between the time constants found in the two studies are sizable but not unreasonable given the major differences in the underlying methods. Furthermore, the mechanical states in the two experiments are not identical, because in one case the eye deviation was driven by optogenetic stimulation of the motoneurons of the lateral rectus alone, whereas in the other case the eye movements were driven by coordinated variations in the contractile states of both the lateral and medial recti. In the primate, the time constants for the first two viscoelastic elements were much shorter than in the mouse, measuring just 26 and 102 ms (Anderson et al. 2009). Thus the present data confirm the conclusion from our previous study of abducens nucleus firing that the mouse ocular motor plant is “slower” than that of the primate and bolster the idea that fast vs. slow ocular motor plants may correspond to presence vs. absence of a fovea or equivalent retinal structure (Stahl and Thumser 2012). As noted above, our estimates of time constants probably represent an upper bound on the true mechanical time constants, which might suggest that the present data exaggerate the interspecies differences. However, the primate time constants determined in electrical stimulation experiments are likely subject to the same time constant-inflating phenomena. Moreover, the interspecies contrast is strongest for T₂ (664 ms for the mouse vs. 102 ms for the rhesus), even though the effects of noninstantaneous decay in force and fit onset point are likely to inflate T₂ less severely than T₁.

On strict allometric grounds the mouse plant should be faster (i.e., possess shorter time constants), not slower, than that of the much larger rhesus macaque (Stahl and Thumser 2012). The saccades made by primates and other foveate mammals place significant demands on the ocular motor system; they need to be precise enough to place the fovea within fractions of a degree of the desired visual target, sufficiently identical in the two eyes to prevent diplopia, and must be initiated and completed as rapidly as possible so as to maximize the percentage of time in which gaze is held sufficiently steady for high-acuity vision. We have previously speculated that these demands underlie foveate mammals having “faster” ocular motor plants than afoveates (Stahl and Thumser 2012). How the faster mechanics are achieved remains unknown, although it may reflect some combination of differences in passive structures (e.g., nonmuscular and nonsarcomeric muscular structures), fiber subtype composition, myosin isoforms, and the innervation applied to the ocular motor plant, particularly the degree to which antagonist muscles are coactivated at any given eye position. This range of possibilities underscores the degree to which the determinants of ocular motor plant mechanics remain poorly understood and the potential for further cross-species studies to address this gap in ocular motor physiology.

Concluding comments.

In this study we limited our analysis to extracting pole (denominator) time constants from the relaxation phase of the response to the optogenetic stimuli. Values of the zero (numerator) time constants could be accomplished by fitting phase data from the responses to sinusoidal optogenetic stimuli, or the eye movement behavior during pulsatile optogenetic stimuli (as opposed to the relaxation following stimulus offset). Both approaches would require a precise knowledge of the time course of abducens nucleus firing during optogenetic stimuli. The present results have also pointed out the need for further information regarding the temporal course of active muscle forces, particularly under conditions (unlike those of the present in vitro experiments) that could be expected to activate MIFs. Recent studies of extraocular muscle forces in larger animals have benefited from advances in the technology of implanted force transducers (Gamlin and Miller 2012). However, adapting the force transducer technology to an animal the size of a mouse would be a formidable challenge. Thus the most likely avenue to obtaining these data in mice would be via anesthetized preparations implementing conventional armature-mounted force transducers or in vitro studies using nerve stimulation rather than the direct muscle stimulation used here.

As noted above, the mechanical conditions of the current preparation differ from the natural state in that the eye was moved by the contraction and relaxation of a single muscle, rather than coordinated changes in tension of agonist and antagonist muscles. Differences in the relationship of motoneuron firing to eye movement during different ocular motor behaviors have been described and attributed to behavior-specific mechanics arising from behavior-specific agonist-antagonist coordination (Miller et al. 2002; Sylvestre and Cullen 1999; Van Horn and Cullen 2009). It is unclear to what extent our measurements were affected by the unnatural coordination state. The effects may have been minimal in the case of the shortest duration stimuli, because active forces had probably returned to near baseline by the beginning of the portion of the response from which we measured the time constants. This question could be addressed through modeling, using time constants from our short-duration stimuli as a best guess of the passive properties of the ocular motor plant and empirical or theoretical decay profiles of active forces.

Addressing these lingering questions in the mouse is likely to be particularly rewarding because it will also provide data for comparisons to larger and foveate species, and such cross-species comparisons will help to understand how ocular motor mechanics are determined. Study of mouse mechanics is also important in its own right, since the mouse has become increasingly popular as an experimental model in ocular motor physiology, but it is now clear that quantitative data from the classic mechanics experiments in rabbit, cat, and rhesus have limited applicability to the mouse. Optogenetic tools, by providing a more precise and less invasive avenue for introducing signals into the ocular motor circuitry, can facilitate these further investigations.

GRANTS

This work was supported by the Department of Veterans Affairs (Veterans Health Administration, Office of Research and Development, Biomedical Laboratory Research and Development; application no. BX000278 to J. S. Stahl), National Eye Institute Grants EY014263 (to P. J. May) and EY12998, EY13724, and EY024347 (to F. H. Andrade), and United Kingdom Engineering and Physical Sciences Research Council Grant EP/1032533/1 (to P. Dean and S. R. Anderson).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.S.S., F.H.A., S.R.A., and P.D. conception and design of research; J.S.S., Z.C.T., P.J.M., and F.H.A. performed experiments; J.S.S. and Z.C.T. analyzed data; J.S.S., Z.C.T., P.J.M., F.H.A., S.R.A., and P.D. interpreted results of experiments; J.S.S., Z.C.T., and P.J.M. prepared figures; J.S.S. drafted manuscript; J.S.S. and P.J.M. edited and revised manuscript; J.S.S. approved final version of manuscript.