Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2015 Jun 23;6:7372. doi: 10.1038/ncomms8372

Interlayer orientation-dependent light absorption and emission in monolayer semiconductor stacks

Hoseok Heo 1,2,*, Ji Ho Sung 1,2,*, Soonyoung Cha 3, Bo-Gyu Jang 4, Joo-Youn Kim 3, Gangtae Jin 1, Donghun Lee 1, Ji-Hoon Ahn 1, Myoung-Jae Lee 1, Ji Hoon Shim 4, Hyunyong Choi 3, Moon-Ho Jo 1,2,5,a
PMCID: PMC4557351  PMID: 26099952

Abstract

Two-dimensional stacks of dissimilar hexagonal monolayers exhibit unusual electronic, photonic and photovoltaic responses that arise from substantial interlayer excitations. Interband excitation phenomena in individual hexagonal monolayer occur in states at band edges (valleys) in the hexagonal momentum space; therefore, low-energy interlayer excitation in the hexagonal monolayer stacks can be directed by the two-dimensional rotational degree of each monolayer crystal. However, this rotation-dependent excitation is largely unknown, due to lack in control over the relative monolayer rotations, thereby leading to momentum-mismatched interlayer excitations. Here, we report that light absorption and emission in MoS2/WS2 monolayer stacks can be tunable from indirect- to direct-gap transitions in both spectral and dynamic characteristics, when the constituent monolayer crystals are coherently stacked without in-plane rotation misfit. Our study suggests that the interlayer rotational attributes determine tunable interlayer excitation as a new set of basis for investigating optical phenomena in a two-dimensional hexagonal monolayer system.

Inline graphicSingle atomic layers of transition metal dichalcogenides have outstanding electrical and optical properties. Here, the authors show that light absorption and emission from stacks of different transition metal dichalcogenide monolayers can be tuned by rotating the crystals.

Hexagonal transition metal dichalcogenide monolayers (h-TMDCs MLs) form a new class of two-dimensional (2D) materials with extreme dimensional confinement effects1,2,3,4,5,6,7,8,9,10,11. In particular, large bandgap h-TMDC MLs such as MoS2, MoSe2, WS2 and WSe2 possess distinct singularities near the band edges, showing strong light–matter interactions in the visible range1,12,13,14,15,16. Artificial 2D superlattices, which are vertical stacks of dissimilar h-TMDCs MLs, are even more intriguing because upon light illumination, interlayer excitons can form across the constituent MLs at newly formed 2D electronic superstructures17,18,19; these excitons can recombine radiatively, thereby emitting light of different colours and intensities. This phenomenon strongly suggests that, upon inter-ML coupling, tunable light absorption and emission, as well as charge separation, can be achieved. Nevertheless, the relevant 2D band structure engineering has not been fully utilized20, mainly due to lack of control over the in-plane rotational misfit of hexagonal unit cells between the adjacent MLs21,22,23,24; this misfit may otherwise serve as an additional quantum index in defining the h-TMDC 2D superstructures25. For example, integration of discrete ML crystals into such 2D heterostructures usually entails mechanical exfoliation of individual MLs from bulk crystals, followed by manual transfer. By this method, the relative rotations of the individual hexagonal Brillouin zone in the stacks cannot be easily identified; consequently, the ‘interlayer' excitation cannot be immediately described13,23,26,27, although an example of a graphene/h-BN/graphene heterostructure has been described28. In h-TMDC ML stacks, the inter-ML bonding is inherently weak across van der Waals heterointerfaces, compared with the intra-ML bonding, so the ML stacking orientations of each hexagonal unit cell must sensitively determine the low-energy excitations.

In the following, we have investigated light absorption and emission at the heterointerfaces of ML stacks composed of MoS2 and WS2 MLs with and without inter-ML rotational misfit in both spectroscopic and time-resolved manners. We provide evidence that the interlayer excitation is intimately determined by the interlayer rotational degree of freedoms, which are tunable from direct- to indirect-gap transitions.

Results

Photocurrent spectra in MoS2/WS2 bilayer stacks

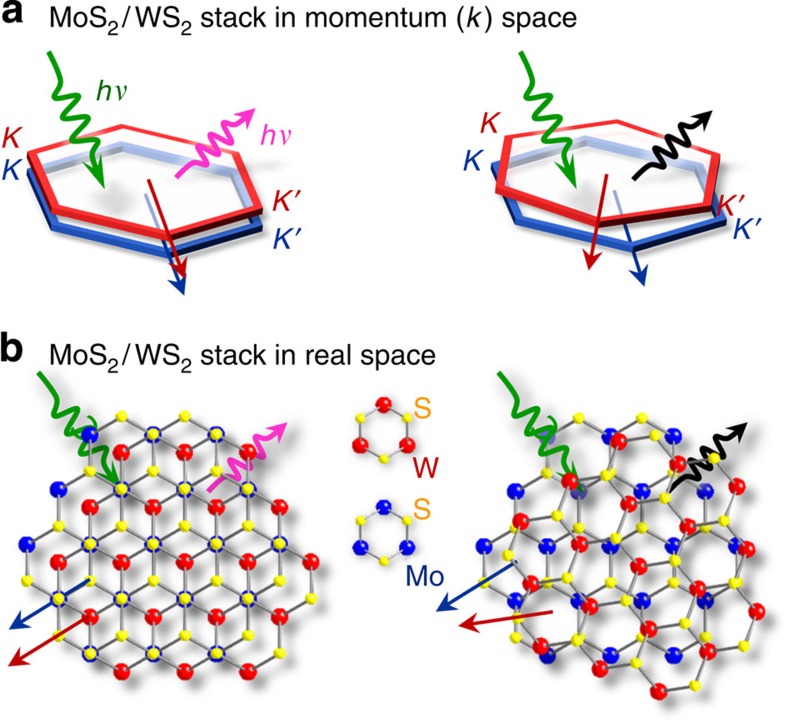
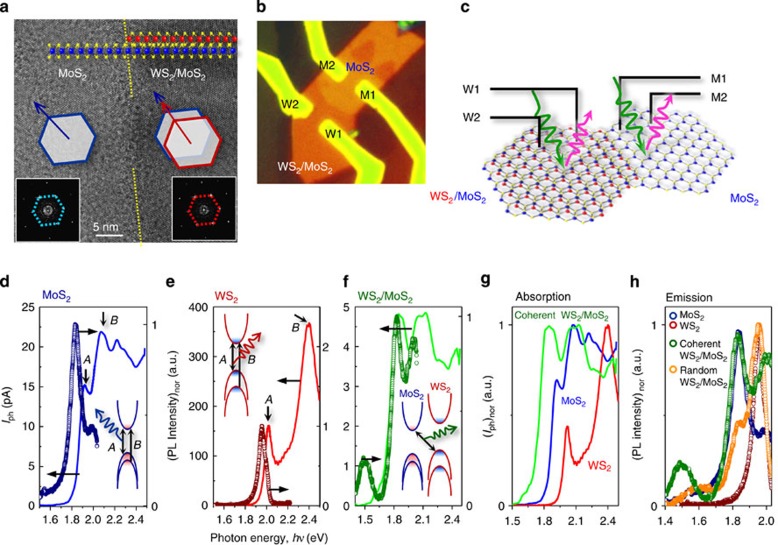
We designed an experiment (Fig. 1a) that uses spatially, spectrally and time-resolved optoelectronic probes. We first prepared two different kinds of MoS2/WS2 stacks (Fig. 1b). Coherent bilayer stacks with hexagon-on-hexagon unit-cell stacking of MoS2 and WS2 MLs without incommensurate interlayer rotations were achieved by vertical heteroepitaxial growth. Both ML crystals have the same hexagonal crystal symmetry and are of similar size (MoS2: a=3.150 Å; WS2: a=3.153 Å). Therefore, the individual atom positions and thus the crystallographic ML stacking orders can be thermodynamically stabilized without rotational misfit (Fig. 1b). Random bilayer stacks were fabricated by manual stacking of individual MoS2 and WS2 MLs; thus the rotation-misfit order is unknown. Heteroepitaxial stacking growth, in which the second WS2 ML grows over the first MoS2 and WS2 MLs, occurred by edge nucleation (the top inset of Fig. 2a). Fast Fourier transformation of transmission electron microscope images (the bottom insets of Fig. 2a) confirmed that the in-plane orientations of the h-unit cells are identical; thus the bilayer stack is rotationally coherent across the clean van der Waals interface. To investigate light absorption and emission arising from both intra- and inter-ML transitions, we fabricated bilayer devices from partially covered MoS2/WS2 stacks (Fig. 2b,c), in which multiple electrical contacts were made in such a way that we can collect photoexcited carriers (photocurrent, Iph) spectrally by scanning with a focused supercontinuum laser. Our diffraction-limited laser beam spot is small enough to spatially resolve each ML within the bilayer stacks29,30,31. Due to the small absorption volume of ML crystals, direct probing of optical absorption of individual MLs without ensemble averaging is technically difficult; instead, we use local light illumination to collect the Iph spectra, because this method can spectrally capture the local optical absorption and the subsequent photocarrier generation and transport. In the sense of the spectral responses, this measurement can be equivalent to optical absorption to a certain extent. For example, by locally illuminating only the bottom MoS2 ML, the collected Iph with the M1–M2 electrode pair can represent the MoS2 intralayer absorption. Such Iph spectra of MoS2 and WS2 MLs (Fig. 2d,e) are closely reminiscent of the equivalent absorption spectra, in that the spectral Iph onset and peak positions represent the absorption edges and excitonic transitions, so-called A and B excitons, respectively. By illuminating the MoS2/WS2 stack regions, the Iph arising from interlayer transitions can be selectively collected with the M1–W1 electrodes pair (Fig. 2f). This inter-ML Iph spectral onset shifts down to 1.5–1.6 eV, far below the fundamental energy gaps (Eg) of MoS2 MLs (Eg=1.87 eV) and WS2 MLs (Eg=1.96 eV) (Fig. 2g). Earlier theoretical calculations predict that the WS2/MoS2 junction forms a type-II band alignment with 1.58–1.60 eV interlayer Eg between the MoS2 valence band maxima (VBM) and the WS2 conduction band minima (CBM) (the inset of Fig. 2f)12,17,18,19; thus our observations of the photocurrent onset at 1.5–1.6 eV can be provisionally assigned to such an interlayer transition.

Figure 1. Schematics of this study for light absorption and emission by rotation of monolayer hexagonal semiconductors (MoS2 and WS2) in vertical stacks.

Figure 1

Open in a new tab

(a) The vertical stack of MoS2 and WS2 in momentum (k) space. (b) The vertical stack of MoS2 and WS2 in real space.

Figure 2. Rotational crystal structures of the MoS2/WS2 stacks and light absorption and emission characteristics.

Figure 2

Open in a new tab

(a) In-plane transmission electron microscopy images of the vertical stacking. The lower insets: fast Fourier transform diffraction patterns at each region, showing the invariable hexagonal unit-cell orientations in the stack. (b,c) Optical microscope image of the MoS2/WS2 stack device and schematics of local light absorption and emission. (d–f) Photocurrent (Iph) and photoluminescence (PL) spectra of MoS2 (blue), WS2 (red) and coherently stacked MoS2/WS2 bilayer (green) by local light illumination. Comparison of (g) Iph and (h) PL spectra.

Photoluminescence spectra in MoS2/WS2 bilayer stacks

Local light emission was investigated by measuring the photoluminescence (PL) spectra (Fig. 2d–f,h). Individual MLs of both MoS2 and WS2 typically exhibit a Stoke shift of ∼0.1 eV near the fundamental absorption edges, which indicates efficient radiative recombination from direct-bandgap transitions14. In addition, we observed substantial emission in the stack region at 1.5 eV with a Stoke shift >0.1 eV, which suggests the existence of another radiative recombination from inter-ML states. It is accompanied by a slight PL reduction at 1.8 eV, compared with the spectrum of individual MoS2 MLs. Provided that the oscillator-strength sum is conserved, this reduction can be understood to be due to split photoexcitation from the MoS2 VBM into the WS2 CBM and the MoS2 CBM. Another contribution from ultrafast charge separation into each ML before inter-ML recombination32 may also affect the relative spectral weight. By contrast, this low-energy emission is absent from the random stack (Fig. 2h), whereas it shows PL peaks from both MoS2 and WS2 at the higher excitation energy with pronounced PL suppression at 1.8 eV. This absence of the radiative recombination at 1.5 eV in the random stacks, together with their lower-energy photocurrent onset at 1.6–1.7 eV, confirms that the emission responsible is generated by the interlayer transition, which is effectively suppressed due to non-radiative recombinations by momentum mismatch or interfacial impurity centres in the random stacks.

Interlayer transition dynamics in MoS2/WS2 bilayer stacks

To further investigate the observed contrast in interlayer transitions between the coherent and random stacks, we used ultrafast time-resolved optical pump–probe spectroscopy to study the inter-ML transition dynamics. The stacks were excited using a 50-fs, 3.1-eV pump pulse, and the corresponding differential transmission data (ΔT/T0, where ΔT is the pump-induced transmission change, and T0 is the transmission without the pump) from 1.47 to 2.13 eV probe photon energy were measured as a function of pump–probe delay Δt33 (the inset of Fig. 3a; see also Supplementary Fig. 1). The two kinds of stacks were excited by the laser pump at a fluence of 24 μJ cm−2. Immediately after the pump, the signals for the interlayer exciton with 1.6 eV probe (both of coherent and random stacks) rapidly increase with ΔT/T0>0 (the upper panel of Fig. 3a). The positive ΔT/T0 originates from the reduced probe absorption by state-filling in the interlayer exciton states, that is, the Pauli-blocking effect. The kinetic origin of the increased interlayer transients is rapid charge separation into each ML; the photoexcited electrons and holes are immediately transferred into energetically favoured states in MoS2 and WS2, respectively33, as illustrated in the left and middle panels of Fig. 3d. This rapid charge transfer and resulting interlayer exciton population explain the measured PL intensity ratio (Fig. 2f,h); if the charge transfer is slow compared with the intralayer exciton lifetime of individual MLs, no interlayer PL can be expected. It also signifies that in the bilayer stacks, the charge-transfer dynamics determines the relative PL intensities between the inter- and intra-ML light emissions. In fact, the linear fluence dependence of the peak ΔT/T0 in Fig. 3b ensures that no higher-order nonlinear excitonic interactions are involved; that is, that first-order population dynamics primarily governs both the PL and the ΔT/T0 dynamics34. The spectrally resolved prominent ΔT/T0 peak at 1.6 eV measured at Δt≈0 ps (Fig. 3c) corroborates that the rapid charge separation leads to the interlayer population dynamics, rationalizing the interlayer excitonic PL in the coherent bilayer stacks. Although both stacks exhibit rapid charge separation, the corresponding decay dynamics show qualitatively different features, as indicated in bi-exponential function fits with fast (τ1) and slow (τ2) decay components. The initial decay was slower in the coherently stacked bilayer (τ1=5.3 ps) than in the randomly stacked bilayer (τ1=3.3 ps). This difference indicates that coherent stacks were less sensitive to defect-mediated recombination than were the random stacks, presumably because the coherent stacks have cleaner interfaces with fewer defects than the random stacks35. More importantly, for the slow decay component, τ2 was much faster in the coherent stacks (τ2=39 ps) than in the random ones (τ2=1.5 ns). This ultrafast timescale is comparable to direct-gap transitions in conventional III–V semiconductor superlattices36, and is qualitatively different from previous reports of random bilayer stacks of WSe2/MoS(Se)2 MLs, in which τ2 ranges from nanoseconds to microseconds, attributed to indirect-gap interlayer recombinations4,6. The substantially faster interlayer recombination dynamics of ∼39 ps in our coherent stacks is comparable to those typically observed in the intralayer direct-gap transitions in individual MoS2 MLs37,38. This similarity strongly suggests that our interlayer transitions may be like those of direct gaps. The slower transient character (nanoseconds) in the random stacks is consistent with the observed absence of the corresponding PL at 1.5 eV. This fast recombination dynamics of τ2 excludes a possibility that the excitons are recombined radiatively from defect states, by which the corresponding decay timescale would be very long in the range of nanoseconds39. Overall, the observed contrasts in interlayer transitions of the coherent and random stacks for both spectral and dynamic features suggest critical roles of the relative rotation misfit in the 2D hexagonal k-space of the bilayer stacks.

Figure 3. Ultrafast time-resolved exciton dynamics of coherently/randomly stacked bilayers.

Figure 3

Open in a new tab

(a) Top panel: comparison of transient dynamics of interlayer excitons in coherently stacked and randomly stacked bilayers. Both bilayers are pumped by the same laser fluence of 24 μJ cm−2, and measured at the same probe photon energy of 1.6 eV. Bottom panel: intralayer exciton dynamics of MoS2 (blue, 1.87 eV) and WS2 (red, 1.96 eV) measured in the coherently stacked bilayer with the same pump fluence of 24 μJ cm−2. (b) The pump-fluence-dependent maximum ΔT/T0 of the coherently stacked bilayer. (c) Spectrally resolved ΔT/T0 at the direct interlayer exciton state of ∼1.6 eV (the dashed line) is shown. The data are measured at Δt≈0 ps with a pump fluence of 32 μJ cm−2. (d) Schematic illustration of a pump-induced exciton transient as a function of pump–probe delay Δt (from left to right). Immediately after the 3.1-eV pump excitation (left), electrons are rapidly transferred in MoS2 and holes are rapidly transferred in WS2 (middle). Then the interlayer recombination is measured by setting the probe photon energy of 1.6 eV (right).

Interlayer band structure calculation

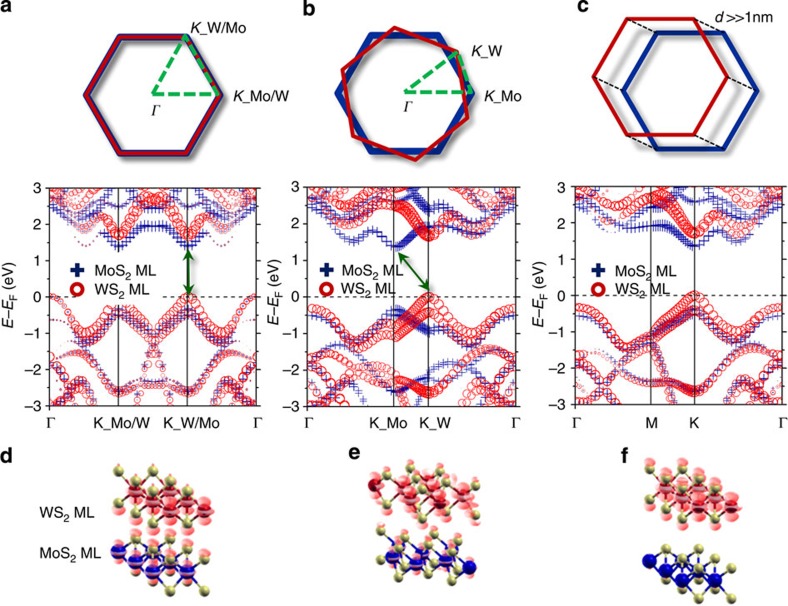
We performed band structure calculation of MoS2/WS2 bilayer for both coherent and random stacks (Fig. 4), in which two Brillouin zones of each ML are stacked atop each other. In principle, one must consider random displacements and rotations of the two hexagonal unit cells for the random stacks. However, we only considered the rotational symmetry (Fig. 4a,b; Supplementary Fig. 2), because the crystal momentum, and thus the consequent band dispersion is invariant and has a simple displacement between two MLs. The coherent stacking (Fig. 4a), shows a direct-bandgap feature at the K-point. At the K-point, the VBM mainly come from the WS2 ML and spin–orbit (SO) splitting of 0.42 eV is evident. The VB of the MoS2 ML, which has smaller SO splitting of 0.15 eV at the K-point, is well below the VBM. Thus, one can expect that the valley polarization in VB is induced mainly by the WS2 ML. At the CBM, the orbital character mainly comes from the MoS2 ML, and the SO splitting is almost negligible. Meanwhile, the random stacks show indirect-bandgap features, as exemplified for the 21.79°-rotated bilayer (Fig. 4b). The difference in the recombination time in our study may be due to this change in direct- and indirect-gap interlayer transitions. The random stacks also show a clear difference in the inter-ML orbital interactions from those of the coherent stacks. In the coherent stacks, the VBM is almost degenerate at the K and Γ points; notably, strong interlayer orbital mixing occurs at the Γ point, at which the main orbital contribution comes from S pz orbitals of both MoS2 and WS2 MLs. Thus, instead of the distinct direct-bandgap structure in each MoS2 or WS2 ML (Supplementary Fig. 3), the MoS2/WS2 bilayer displays both direct- and indirect-gap features. In the extremely strong interlayer interaction limit (effectively as in bulk crystals), this system shows clear indirect-bandgap features between K at CBM and Γ at VBM40. However, in the random stacks the Γ point is downshifted compared with the K-point, and the orbital mixing becomes much weaker; due to the rotational misfit in the random stacking, the orbital overlap between S pz orbitals from each ML becomes much smaller, and the VBM at the Γ point is mainly contributed from the WS2 ML. Such interlayer orbital interaction can be identified from the charge density plot of the orbitals at the Γ point (Fig. 4d,e). We attempted to correlate the interlayer interaction with the band structure and the associated charge recombination. Figure 4c shows the band structures of the well-separated MoS2/WS2 bilayer (thus inducing effectively small interlayer orbital interaction (Supplementary Fig. 3 for the inter-ML distance dependence) without rotational misfits. The Γ point energy of the VB decreases as the interlayer distance increases, forming the direct bandgap at the K-point (Supplementary Fig. 3). At the same time, the orbital of the VBM at the Γ point originates mostly from the WS2, with the interlayer orbital mixing being much smaller. The charge density plot (Fig. 4f) supports our hypothesis that interlayer orbital mixing was suppressed, as observed for the random stack. With strong interlayer interaction, recombination centres can form at the Γ point, thereby reducing the exciton lifetime, as observed in our experiments41. Because the photogenerated holes are distributed to the Γ point with the mixed orbital characters of both MLs, the recombination occurs in similar timescales in the inter-ML recombination. Nevertheless, if the interlayer interaction diminishes due to the interlayer distance or the rotation misfit, the orbital mixing between two MLs weakens and recombination lifetime lengthens, possibly with inelastic scattering processes. We find qualitatively the same conclusion from a calculated optical absorption of the MoS2/WS2 stack using the Bethe–Salpeter equation method, in which the absorption spectrum of the stack is significantly different from the sum of the spectra of the two MLs with a large absorption cross-section below the Eg of MoS2 and WS2 MLs, due to the interlayer transition12.

Figure 4. Band structures of coherent and random stacking MoS2/WS2 bilayers and partial charge density plot of MoS2/WS2 bilayers.

Figure 4

Open in a new tab

Band structures of (a) coherent and (b) random stacks. Here we consider random stacking with a rotation by 21.79° between two MLs. The upper figures represent the overlap view of the primitive cell Brillouin zones for each stacking type. Dashed lines on the Brillouin zone indicate the k path, which the band structures are calculated along. The coherent and random stacking bilayers show the direct- and indirect-bandgap features, respectively. Each contribution from MoS2 ML and WS2 ML is denoted by the size of the blue crosses and red circles, respectively. (c) The band structure of coherent stacking with large distance (d≫1 nm) between two layers. (d–f) The partial charge density plot of the structure used in a–c at the Γ point in the VB.

Discussion

We tested the hypothesis of interlayer charge separation and direct-gap recombination by further examining the timescale of individual A-exciton transients of MoS2 ML (1.87-eV probe) and WS2 ML (1.96-eV probe) as in the lower panel of Fig. 3a. Near Δt≈0, we observed photoinduced bleaching42 and absorption of the A excitons in MoS2 and WS2, respectively, that is, ΔT/T0>0 for MoS2 and ΔT/T0<0 for WS2 (refs 33, 43, 44). All ΔT/T0 signals decayed in ∼100 ps, except in the random stack, in which the intralayer A excitons of MoS2 ML and WS2 ML are well known to be direct-gap transitions. Thus, the faster decay of the ΔT/T0 in the coherent stacks than in the random stacks strongly supports the direct-gap recombination, in direct comparison with the indirect-gap recombination in the random stack, as they are also consistent with our model calculation. Our observations suggest that the h-TMDC ML stacking orientation is an additional quantum attribute in inter-ML exciton phenomena, and also demonstrate the achievability of tunable interlayer optical excitations for novel 2D photonics and photovoltaics based on h-TMDC MLs.

Methods

Spatially and spectrally resolved photocurrent spectroscopy

For the spectral photocurrent measurements, we used a broadband supercontinuum laser (450≤λ≤2,000 nm) combined with a monochromator to obtain high-resolution spectra. During the wavelength scanning, photocurrent was measured using a lock-in technique with a chopper frequency of 500 Hz and then normalized to the photon flux. The chopped laser beam was focused by a microscopic lens (numerical aperture=0.8) and illuminated the ML devices.

MoS2/WS2 bilayer band calculations

The band structure calculations were performed using the Vienna ab initio package (VASP)45. The projector-augumented wave method with the PBE-sol exchange-correlation functional46 was used for the density functional theory calculation. The plane-wave cutoff was set to 500 eV and a 10 × 10 × 2 k-mesh was used for the self-consistent calculation. SO coupling was considered in this calculation. To consider the bilayer effect, calculations assumed a vacuum thickness of ∼10 Å.

Additional information

How to cite this article: Heo, H. et al. Interlayer orientation-dependent light absorption and emission in monolayer semiconductor stacks. Nat. Commun. 6:7372 doi: 10.1038/ncomms8372 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-3 and Supplementary References

ncomms8372-s1.pdf (742.1KB, pdf)

Acknowledgments

This work was supported by the Institute for Basic Science (IBS), Korea, under the project code of IBS-R014-G1. S.C., J.-Y.K. and H.C. were supported by the National Research Foundation of Korea (NRF) through the government of Korea (MSIP) (Grants No. NRF-2011-0013255). J.H.S. was supported by Global Frontier Program through the Global Frontier Hybrid Interface Materials (2013M3A6B1078870).

Footnotes

Author contributions H.H., J.H.Sung and M.-H.J. conceived and designed the experiments. H.H., G.J. and J.-H.A. synthesized the WS2 and MoS2 monolayer crystals. J.H.Sung, D.L. and M.-J.L. performed photocurrent spectroscopy and analysed the data. B.-G.J. and J.H.Shim performed first-principle calculations. S.C., J.-Y.K. and H.C. performed time-resolved optical pump–probe spectroscopy.

References

  1. Britnell L. et al. Strong light-matter interactions in heterostructures of atomically thin films. Science 340, 1311–1314 (2013). [DOI] [PubMed] [Google Scholar]
  2. Yu W. et al. Highly efficient gate-tunable photocurrent generation in vertical heterostructures of layered materials. Nat. Nanotechnol. 8, 952–956 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Fang H. et al. Strong lnterlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Natl Acad. Sci. USA 111, 6198–6202 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lee C.-H. et al. Atomically thin p-n junctions with van der Waals heterointerfaces. Nat. Nanotechnol. 9, 676–681 (2014). [DOI] [PubMed] [Google Scholar]
  5. Furchi M. M., Pospischil A., Libisch F., Burgdörfer J. & Mueller T. Photovoltaic effect in an electrically tunable van der Waals heterojunction. Nano Lett. 14, 4785–4791 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rivera P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2-WSe2 heterostructures. Nat. Commun. 6, 6242 (2015). [DOI] [PubMed] [Google Scholar]
  7. Baugher B. W. H., Churchill H. O. H., Yang Y. & Jarillo-Herrero P. Optoelectronic devices based on electrically tunable p–n diodes in a monolayer dichalcogenide. Nat. Nanotechnol. 9, 262–267 (2014). [DOI] [PubMed] [Google Scholar]
  8. Hwang C. et al. Lateral heterojunctions with monolayer MoSe2-WSe2 semiconductors. Nat. Mater. 13, 1096–1101 (2014). [DOI] [PubMed] [Google Scholar]
  9. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2010). [DOI] [PubMed] [Google Scholar]
  10. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
  11. Lopez-Sanchez O., Lembke D., Kayci M., Radenovic A. & Kis A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013). [DOI] [PubMed] [Google Scholar]
  12. Bernardi M., Palummo M. & Grossman J. C. Extraordinary sunlight absorption and one nanometer thick photovoltaics using two-dimensional monolayer materials. Nano Lett. 13, 3664–3670 (2013). [DOI] [PubMed] [Google Scholar]
  13. Mak K. F., McGill K. L., Park J. & McEuen P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014). [DOI] [PubMed] [Google Scholar]
  14. Mak K. F., He K., Shan J. & Heinz T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498 (2012). [DOI] [PubMed] [Google Scholar]
  15. Zeng H., Dai J., Yao W., Xiao D. & Cui X. Valley polarization in MoS2 monolayer by optical pumping. Nat. Nanotechnol. 7, 490–493 (2012). [DOI] [PubMed] [Google Scholar]
  16. Wu S. et al. Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2. Nat. Phys. 9, 149–153 (2013). [Google Scholar]
  17. Komsa H. et al. Electronic structures and optical properties of realistic transition metal dichalcogenide heterostructures from first principles. Phys. Rev. B 88, 085318 (2013). [Google Scholar]
  18. Terrones H., López-Urías F. & Terrones M. Novel hetero-layered materials with tunable direct band gaps by sandwiching different metal disulfides and diselenides. Sci. Rep. 3, 1549 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kośmider K. & Fernández-Rossier J. Electronic properties of the MoS2-WS2 heterojunction. Phys. Rev. B 87, 075451 (2013). [Google Scholar]
  20. Mele E. J. Commensuration and interlayer coherence in twisted bilayer graphene. Phys. Rev. B 81, 161405 (2010). [Google Scholar]
  21. Dean C. R. et al. Hofstadter's butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013). [DOI] [PubMed] [Google Scholar]
  22. Ponomarenko L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013). [DOI] [PubMed] [Google Scholar]
  23. Hicks J. et al. Symmetry breaking in commensurate graphene rotational stacking: comparison of theory and experiment. Phys. Rev. B 83, 205403 (2011). [Google Scholar]
  24. Hunt B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructures. Science 340, 1427–1430 (2013). [DOI] [PubMed] [Google Scholar]
  25. Woods C. R. et al. Commensurate-incommensurate transition in graphene on hexagonal boron nitride. Nat. Phys. 10, 451–456 (2014). [Google Scholar]
  26. Wallbank J. R. et al. Moiré minibands in graphene heterostructures with almost commensurate Inline graphic hexagonal crystal. Phys. Rev. B 88, 155415 (2013). [Google Scholar]
  27. Righi A. et al. Graphene Moiré pattern observed by umklapp double resonance Raman scattering. Phys. Rev. B 84, 241409 (2011). [Google Scholar]
  28. Mishchenko A. et al. Twist-controlled resonant tunnelling in graphene/boron nitride/graphene heterostructures. Nat. Nanotechnol. 9, 808–813 (2014). [DOI] [PubMed] [Google Scholar]
  29. Kim C.-J., Lee H. S., Cho Y. J., Kang K. & Jo M. H. Diameter-dependent internal gain in ohmic Ge nanowire photodetectors. Nano Lett. 10, 2043–2048 (2010). [DOI] [PubMed] [Google Scholar]
  30. Kim C.-J. et al. On-nanowire band-graded Si:Ge photodetectors. Adv. Mater. 23, 1025–1029 (2011). [DOI] [PubMed] [Google Scholar]
  31. Sung J. H. et al. Atomic layer-by-layer thermoelectric conversion in topological lnsulator bismuth/antimony tellurides. Nano Lett. 14, 4030–4035 (2014). [DOI] [PubMed] [Google Scholar]
  32. Hong X. et al. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotechnol. 9, 682–686 (2014). [DOI] [PubMed] [Google Scholar]
  33. Sim S. et al. Exciton dynamics in atomically thin MoS2: interexcitonic interaction and broadening kinetics. Phys. Rev. B 88, 075434 (2014). [Google Scholar]
  34. Kumar N. et al. Exciton-exciton annihilation in MoSe2 monolayers. Phys. Rev. B 89, 125427 (2014). [Google Scholar]
  35. Wang H., Zhang C. & Rana F. Ultrafast dynamics of defect-assisted electron–hole recombination in monolayer MoS2. Nano Lett. 15, 339–345 (2015). [DOI] [PubMed] [Google Scholar]
  36. Capasso F. Band-gap engineering: from physics and materials to new semiconductor devices. Science 235, 172–176 (1987). [DOI] [PubMed] [Google Scholar]
  37. Cui Q., Ceballos F., Kumar N. & Zhao H. Transient absorption microscopy of monolayer and bulk WSe2. ACS Nano 8, 2970–2976 (2014). [DOI] [PubMed] [Google Scholar]
  38. Lui C. H. et al. Trion induced negative photoconductivity in monolayer MoS2. Phys. Rev. Lett. 113, 166801 (2014). [DOI] [PubMed] [Google Scholar]
  39. Lefebvre P. et al. Time-resolved photoluminescence as a probe of internal electric fields in GaN-(GaAl)N quantum wells. Phys. Rev. B 59, 15363–15367 (1999). [Google Scholar]
  40. Tongay S. et al. Tuning interlayer coupling in large-area heterostructures with CVD-grown MoS2 and WS2 monolayers. Nano Lett. 14, 3185–3190 (2014). [DOI] [PubMed] [Google Scholar]
  41. Mai C. et al. Many-body effects in valleytronics: direct mearsurement of valley lifetimes in single-layer MoS2. Nano Lett. 14, 202–206 (2014). [DOI] [PubMed] [Google Scholar]
  42. Wang Q. et al. Valley carrier dynamics in monolayer molybdenum disulfide from helicity-resolved ultrafast pump-probe spectroscopy. ACS Nano 7, 11087–11093 (2013). [DOI] [PubMed] [Google Scholar]
  43. Mai C. et al. Temperature dependent valley relaxation dynamics in single layer WS2 measured using ultrafast spectroscopy. Phys. Rev. B 90, 041414 (2014). [Google Scholar]
  44. Shi H. et al. Exciton dynamics in suspended monolayer and few-layer MoS2 2D crystals. ACS Nano 7, 1072–1080 (2013). [DOI] [PubMed] [Google Scholar]
  45. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. J. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
  46. Perdew J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-3 and Supplementary References

ncomms8372-s1.pdf (742.1KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES