Agent-based model of angiogenesis simulates capillary sprout initiation in multicellular networks

Abstract

Many biological processes are controlled by both deterministic and stochastic influences. However, efforts to model these systems often rely on either purely stochastic or purely rule-based methods. To better understand the balance between stochasticity and determinism in biological processes a computational approach that incorporates both influences may afford additional insight into underlying biological mechanisms that give rise to emergent system properties. We apply a combined approach to the simulation and study of angiogenesis, the growth of new blood vessels from existing networks. This complex multicellular process begins with selection of an initiating endothelial cell, or tip cell, which sprouts from the parent vessels in response to stimulation by exogenous cues. We have constructed an agent-based model of sprouting angiogenesis to evaluate endothelial cell sprout initiation frequency and location, and we have experimentally validated it using high-resolution time-lapse confocal microscopy. ABM simulations were then compared to a Monte Carlo model, revealing that purely stochastic simulations could not generate sprout locations as accurately as the rule-informed agent-based model. These findings support the use of rule-based approaches for modeling the complex mechanisms underlying sprouting angiogenesis over purely stochastic methods.

Introduction

To understand, harness, and modulate complex systems, science must go beyond a deterministic cause-and-effect view of the natural world. While some biological subsystems may be described using rule-based methods, many must be supplemented with probabilistic or stochastic techniques to understand, model, and predict the outcomes of biological processes^1–3. Randomness in model descriptions of a biological system can be included at three tiers: (1) the biology itself may include stochastic elements or events (e.g. gene expression) that are described in the model using stochastic methods^{2, 4}, (2) measurements of the biological system may introduce sampling errors that propagate random noise, which should be accounted for in a model to understand the underlying biological mechanism being sampled; or (3) underlying deterministic behavior can be modeled using validated stochastic approaches as a method to reduce model complexity and computational cost without loss of insight^{5, 6}. Further, stochastic behavior may represent a contextual phenotype – a system may normally exist with strict rule-based control but then transition to stochastic behavior when certain conditions are met (e.g. chemokine signaling or pathological pathway activation)⁷. Alternatively, a system may be stochastic at physiological conditions but converted to deterministic behavior when integrated into more robust signaling network, such as in bacterial colony formation^{8, 9}.

We sought to explore this balance of stochastic and rule-based behaviors in the setting of sprouting angiogenesis, a fundamental biological process underlying blood vessel network growth throughout development¹⁰. In the adult, sprouting angiogenesis has roles in both wound healing and endometrial vascularization. Additionally, pathologic sprouting angiogenesis is implicated in the expansion of solid tumors^11–14, growth of ectopic endometrial tissue in endometriosis^{15, 16}, and in neoangiogenesis of diabetic retinopathy^17–19. Sprouting angiogenesis can be approximated by five main stages: (1) tip cell selection, (2) endothelial stalk extension, (3) stalk guidance to neighboring or nearby vessels, (4) anastomosis with a neighboring vessel (success) or regression/collapse to the originating vessel (failure), and (5) maturation and lumenization of anastomosed vessels²⁰. Regardless of the final fate of the sprout, this process must begin with appropriate selection of a quiescent endothelial cell to undergo phenotype switching, becoming a tip cell with increased filopodial extension frequency. These cell behaviors, in aggregate and in conjunction with external signaling cues, have been presumed to dictate where new vessels initially form within a blood vessel network.

Regulation of endothelial phenotype switching is closely tied to several signaling pathways, including the well-studied Notch1/Delta-Like-Ligand 4 (DLL4) intercellular pathway^{10, 20–27}, which suppresses sprout initiation, and the vascular endothelial growth factor receptor (VEGFR) axis that signals to increase phenotype switching and sprout frequency^{10, 28, 29}. Disruption of either the suppressive pathway (Notch1/DLL4) or the activating pathway (VEGF/VEGFR) results in dramatic blood vessel phenotypes ranging from early embryonic lethality to significant vascular dysmorphogenesis (e.g. hypersprouting, hyperbranching phenotypes). Further, there are several isoform and dimerization states of VEGFRs allow for differential signaling^{21, 23, 28, 30, 31}. In this work, we explore the balance between pro-angiogenic VEGFR2 and VEGFR1, which can function as a decoy receptor for VEGF. As such, the balance between the DLL4 and VEGFR signaling axes is crucial to vascular patterning. However, endothelial cell behaviors leading to sprout initiations in the context of intercellular signaling and capillary network connectivity remain unclear.

Computational models offer unique insight into the study of biological systems, enabling us to query unmeasurable, unobservable, or inaccessible metrics pertinent to biomedical science^32–37. In assembling a model, the investigator is able to explicitly define methods for simulating each aspect of the biological processes they are modeling – either as stochastic or as rule-based. Comparisons between models that assume different relative contributions of stochastic and rule-based behaviors empower investigation of the underlying system properties by contrasting the accuracy of each technique. The relevant question then becomes: what do we learn from modeling a system using separate rule-based and stochastic techniques that both provide verifiable results?

Several other computational models have been developed using primarily rule-based methods to explore the process of sprouting angiogenesis with single-cell and subcellular resolution. These include ABMs of endothelial phenotype switching that focus on filopodial extension and intercellular Notch1 signaling²⁷. Bentley and colleagues have extended this model to bone regrowth as the multiscale model of osteogenesis and sprouting angiogenesis incorporating lateral inhibition of endothelial cells (MOSAIC)³⁸, and more recently used it to explore endothelial cell motility in the context of the extending sprout stalk with and without genetic mosaics³⁹. At the subcellular level, Hashambhoy et al. have used mass action kinetics models to explore VEGF diffusion, VEGFR dimerization, and surface signaling in simulated endothelial extensions⁴⁰. Finally, Kleinstreuer et al. used a Cellular Potts Model to study vasculogenesis of the fetal liver with subsequent endothelial sprout formation as a screening tool for high throughput toxicology analysis⁴¹. Though the specific approaches differ, these models all sufficiently capture and explore the possibility for a deterministic (or rule-informed) basis for cellular behaviors in sprouting angiogenesis at multiple resolutions. However, while these rule-based approaches are certainly valid, they do not compare their results to stochastic alternatives that may be similarly predictive of biological behavior.

Here, we describe a new agent based model (ABM) of angiogenic sprout initiation informed by high-resolution dynamic spatial and temporal data from the three-dimensional embryoid body (EB) model of embryogenesis⁴². Our ABM includes Notch1-DLL4 and VEGF signaling within and between cells to predict the frequency and location of endothelial sprout initiation events in image-based realistic multicellular networks and is validated against the data from the EB time-lapse movies. This is the first report of validating an ABM one-to-one with dynamic data of angiogenic sprouts. Further, we constructed a Monte Carlo simulation as a benchmark for asserting accuracy of sprout localization using purely stochastic methods. By comparing the rule-based ABM to the Monte Carlo we demonstrate that rule-based models more accurately simulate endothelial cell sprout initiation location. This combined approach supports the hypothesis that the location of sprout initiations in multicellular endothelial networks occur with in a rule-based manner, informed by underlying cell-signaling pathways.

Experimental

Embryoid body experiments

Maintenance and differentiation of mouse embryonic stem (ES) cells was described previously.⁴³ Stable expression of PECAM-eGFP in ES cell lines was previously reported.⁴⁴ Real-time imaging of day 7–8 differentiating ES cell cultures was conducted as follows: confocal images were acquired at 4–10 min intervals for 16–20 hr with an Olympus FluoView FV1000 or FV10i system (full environmental controls) using either a 10× or 20× objective. At each location, a z-stack of 6–8 images was acquired with 4–6 microns between focal planes. These images were compressed post-acquisition into a single frame for each time point.

Agent based model

Agent and time definitions

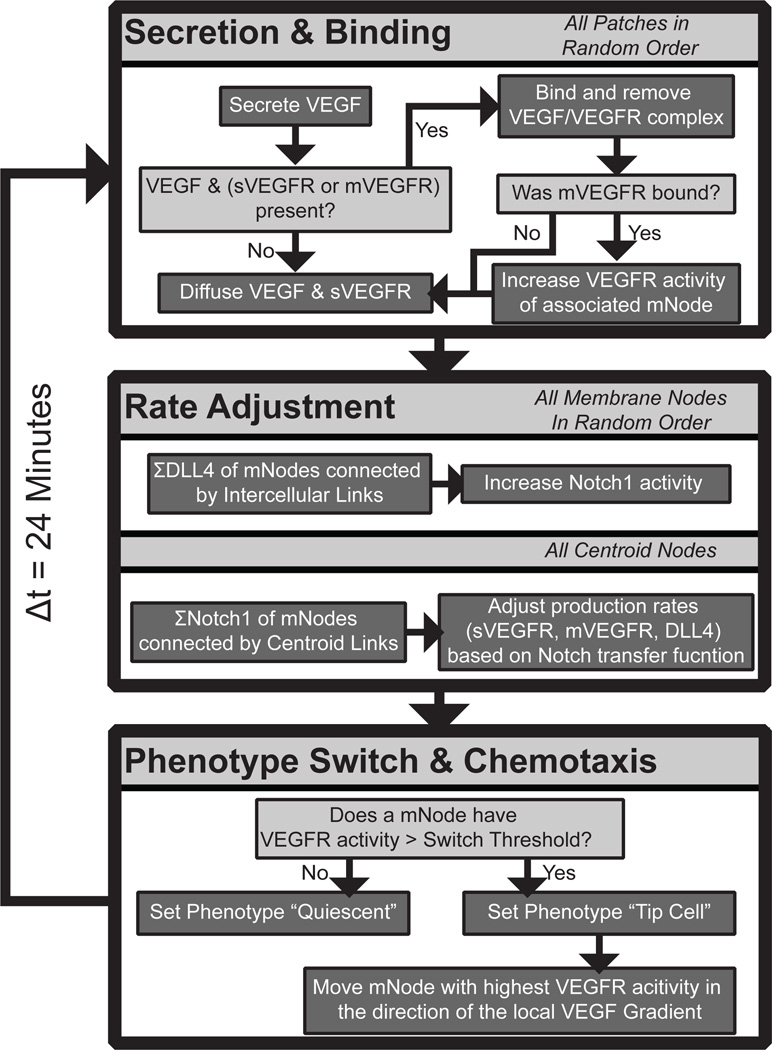
The ABM was built using Netlogo 5.0 and data were analyzed using MATLAB^{45, 46}. Each endothelial cell (EC) is spatially defined by eight membrane nodes (mNode) and a single centroid “nucleus” linked to each membrane node; the mNodes are connected to each other by membrane links (Figure 1A). The two-dimensional space occupied by cells is discretized into 10 µm × 10 µm pixels. During the course of the simulation the each cell adjusts its shape to approach an average endothelial cell surface area (EC_SA, Table 1); this is achieved by having links convey movement between their attached nodes – when a node is moved all linked nodes attempt to follow but may be hindered by other links. The time step of the simulation is 24 minutes, enough time to resolve micron-scale changes in cell position and still capture changes in protein levels⁴⁷ (Figure 2).

Figure 1.

Construction of ABM from experimental time-lapse movies. Each cell is comprised of multiple agents including mNodes, nuclei, inter-, and intra-cellular links as shown in the cartoon (A). The embryoid body movie’s initial frame is converted to an ABM representation to match EC locations. Simulation predictions of sprout initiations (circles) are then compared to observed sprout initiations from the EB movie (squares) and scored as true positive or false positive (B).

Table 1.

ABM Parameter Values

Parameter	Description	Value	Reference
ECSA	EC Surface Area	962E-8 cm2	59
dsVEGFR1	Initial sVEGFR1 Secretion Rate	2.8E-10 nmol cm−2 ·s−1	40
dmVEGFR1	Initial mVEGFR1 Insertion Rate	2.8E-10 nmol cm−2 ·s−1	40
dVEGFR2	Initial VEGFR2 Insertion Rate	8.4E-10 nmol cm−2 ·s−1	48
dVEGF	VEGF Production Rate	5.0E-10 nmol cm−2 ·s−1	40
dDLL4	Initial DLL4 Insertion Rate	0	Estimated
dNOTCH	Initial Notch Insertion Rate	0	Estimated
xmin	Minimum insertion rate	1.0E-12 nmol cm−2 ·s−1	Estimated
xmax	Maximum insertion rate	1.0E-8 nmol cm−2 ·s−1	Estimated
ECctx	Chemotactic Migration Rate	30 µm ·h−1	Estimated from47, 60, 61
α	Notch Transfer Coefficient	Model Specific	Parameter Fit
β	Tip Cell Activation Threshold	Model Specific	Estimated

Figure 2.

ABM workflow. Each of the main subroutines occur sequentially at every time step: section and binding, rate adjustment, and phenotype switching and chemotaxis.

Modeling molecular biology: VEGF and DLL4 signaling axes

Each pixel stores concentration values of soluble VEGFR1 (sVEGFR1) and VEGF. sVEGFR1 is secreted by endothelial cells and in this simulation are produced by the mNodes. VEGF is secreted by cells throughout the tissue and therefore is produced by the pixels in this model. Diffusion is included using a simple distribution command – 25% of each diffusible species in each pixel is equally distributed among its eight neighboring pixels (Moore neighborhood).

Receptor binding kinetics are assumed to be 1:1 interactions between dimerized VEGFRs and dimeric VEGF^{48, 49}– if a pixel contains VEGF and also includes either (1) an mNode with membrane-bound VEGFR1 (mVEGFR1), (2) an mNode with VEGFR2, or (3) sVEGFR1, then binding will occur until one of the pools (ligand or receptor) is completely depleted. For example, if there 10 molecules of VEGF and 100 available VEGFR2, the ABM will remove all VEGF from the pixel, while the local mNode reduces VEGFR2 to 90, and adds 10 phosphorylated VEGFR2 (pR2). When binding sVEGFR1 or mVEGFR1 there is no downstream function – receptor-ligand complexes are removed from the cell surface without further impact on signaling. These binding rules do not account for equilibria or mass action kinetics, favoring simpler, lower resolution molecular interactions at the multicellular scale. When VEGFR2 is converted to pR2 it increases the DLL4 production in that cell, following the formula:

$$\mathrm{D}\mathrm{L}\mathrm{L}{4}_{t+1}=\mathrm{D}\mathrm{L}\mathrm{L}{4}_t+(k\times \mathrm{p}\mathrm{R}2)-(k_{\text{deg}}\times \mathrm{D}\mathrm{L}\mathrm{L}{4}_{\mathrm{t}})$$ (1)

where DLL4_t+1 expression level is defined as the current amount of DLL4_t, increased by activation of pR2, and decreased at a constant degradation rate (Figure 2).

Based on what is known about the molecular biology of these families in endothelial cells, production rates of the VEGFRs are directly related to DLL4 expression on neighboring cells by the formula:

$${ẋ}_{\text{min}}=x_{\text{min}}+(x_{\text{max}}-x_{\text{min}})e^{-\alpha \mathrm{\Sigma }\mathrm{D}\mathrm{L}\mathrm{L}{4}_{\text{neighbors}}}$$ (2)

where ẋ is the production rate per time-step of receptor x, and x_min and x_max are the minimum and maximum production rates, respectively. The DLL4 content of each neighboring cell (defined as having an intercellular link between mNodes) is summed and then scaled by the Notch1 transfer coefficient α. When α is 0 there is no information transfer between neighboring cells. Notch1 signaling alters the transcriptional regulation of VEGFRs, increasing the production of both sVEGFR1 and mVEGFR1 and decreasing the production of VEGFR2 (Figure 2). VEGFR production rates are updated with each time-step.

Initial production rates for VEGF and VEGFRs are estimated based on literature-derived values (Table 1). In the case of Notch1 and DLL4, the initial values were set at 0 and instantiated based on Equation 2 and basal production rates. Minimum and maximum production rates (x_min and x_max, respectively) were estimated to be two orders of magnitude above and below the basal production rate.

Phenotype switch from quiescent to tip cell

When the pR2 levels on an endothelial cell in the model are above the tip cell activation threshold (β, Table 1) they undergo transition to the tip cell phenotype. Activated tip cells respond to VEGF signaling via chemotaxis towards the nearest source of VEGF. To calculate the direction of movement, the cell determines the mNode with highest pR2, and moves in the direction of the neighboring pixel with the highest VEGF concentration. This ability to sense VEGF concentrations at a distance of up to 10 µm accounts for the effects of filopodial extension without explicitly modeling individual filopodia in the ABM. Endothelial cells in the tip cell state that drop below the tip cell activation threshold return to a quiescent phenotype.

Rendering embryoid body data as ABM geometries

Projections of confocal image stacks were converted to 16-bit intensity maps and loaded into the ABM using a custom image processing program written in Netlogo (Figure 1B). Loaded images were then converted to starting ABM configurations by manually selecting cell locations and then allowing for membrane shape change to approach the average endothelial cell surface area, EC_SA. Using the EB image as a guide, each cell mNode could be manually edited to better match the geometric configuration of the fluorescence intensity data. The EB image was then cleared and the resulting vessel geometry file exported for use in simulations (Figure 1B).

Parameter estimation of Notch Transfer Coefficient

From each of three EB movies a quadrant was selected and used as training data to determine the Notch Transfer Coefficient (α, Equation 2) for subsequent simulations. Simulation of sprouting using these starting configurations was performed over a parameter range from 0 to 2 in increments of 0.2, yielding a total of 16 different parameter values, each evaluated in 20 replicate ABM simulation runs. The number of sprout initiations over the course of each simulation was compared to raw sprout initiation counts from the paired EB movie and the best fit Notch Transfer Coefficient value was determined.

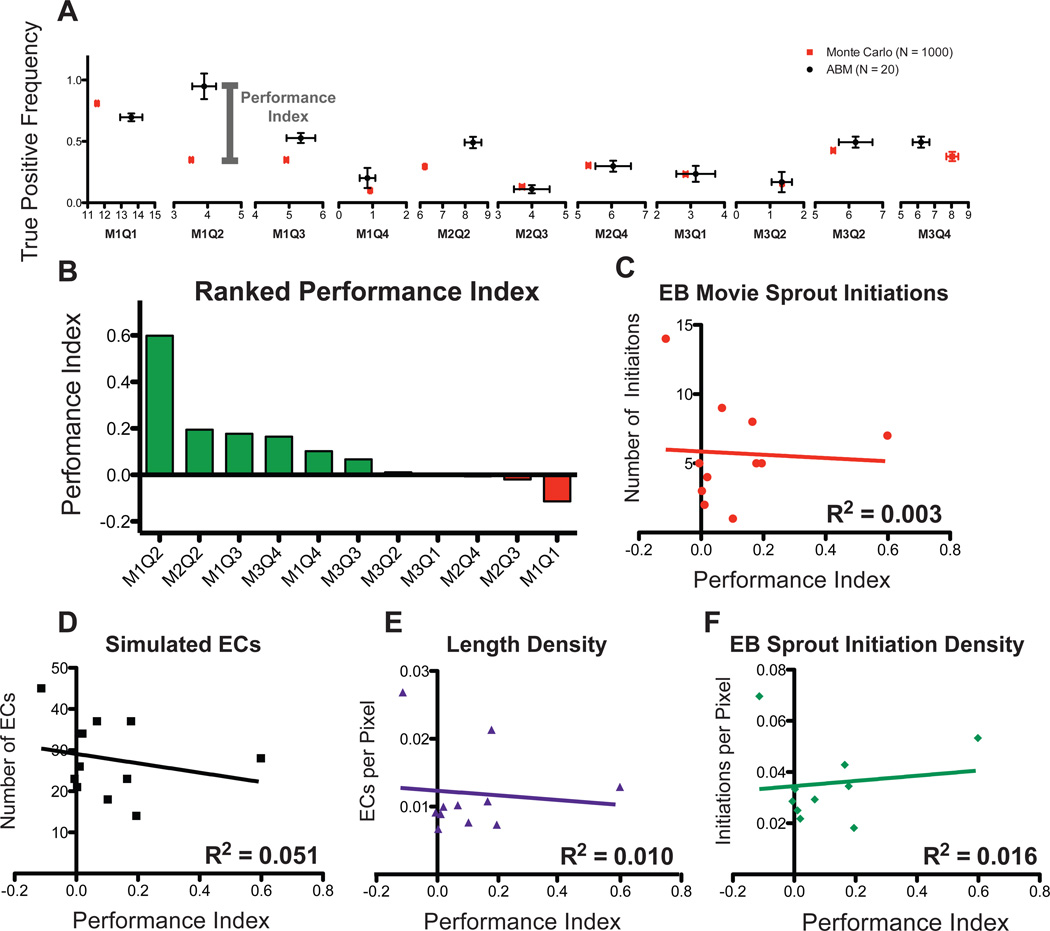
The Notch Transfer Coefficient value that generated the best fit from the parameterization was then validated in seven additional, independent EB Movie quadrants to confirm its accuracy and robustness across different initial network geometries. An example of true positive predictions as compared to false positives is shown in Figure 4B.

Figure 4.

Comparing ABM and Monte Carlo predictions of sprout initiation locations. For each movie, the Monte Carlo (red) and ABM (black) prediction of sprout initiations (x-axis) and true positive frequency (y-axis) were compared (SEM, A). A performance index, defined as the difference between ABM and Monte Carlo true positive frequency, was calculated. The ABM outperforms the Monte Carlo simulation in 7 out of 11 EB Movie simulations (Green Bars, B). C–F, Metrics of EC network structure from each EB Movie plotted as a function of the performance index; no correlation could be discerned.

Sensitivity analysis

A local approach was used to evaluate sensitivity to the ABM Notch Transfer Coefficient: all other variables were held constant while sampling the parameter space of the Notch Transfer Coefficient between 0 and 2.0 using a 0.2 step size. A total of 20 simulations were run at each parameter value for each of the eleven total starting geometries defined by EB Movie quadrants.

Monte Carlo analysis of stochastic sprouting without molecular control

For each EB movie quadrant, Monte Carlo simulations wer performed using Netlogo. Unlike the ABM, the Monte Carlo simulation randomly selects endothelial cells to undergo phenotype switch to tip cells (i.e. this method does not include the molecular mechanisms of VEGF and Notch1 signaling). The cells chosen were selected from a uniform distribution with replacement – this allowed the same cell to be chosen to be a tip cell more than once, as might occur in the ABM or EB model if a tip cell becomes quiescent and then reactivates at a later time point. The Monte Carlo simulations were not tasked with predicting the number of sprout initiation events; rather, the number of sprout initiation events (i.e. number of tip cell selection events) was drawn from a normal distribution with mean and standard deviation taken from ABM predictions. Each EB movie quadrant was evaluated over 1000 replicates.

The set of available sprout initiation locations available to the Monte Carlo simulation was bounded by the location of endothelial cells in the starting configurations of each EB movie quadrant. A performance index was defined as the difference between true positive frequencies in the ABM and Monte Carlo analyses – a positive value indicates better predictive performance of the ABM whereas a negative value indicates better predictive power of the Monte Carlo simulation.

Genetic algorithm

A genetic algorithm (GA) was applied to four parameters of the ABM (Notch Transfer Coefficient, tip cell activation threshold, sVEGFR1 production rate, and mVEGFR1 production rates) with the goal of maximizing the true positive frequency of the worst performing simulation, using the following objective function:

$$1-X_{TP}=ℱ(x_1,x_2,x_3,x_4)$$ (3)

where X_TP is the true positive rate achieved by the ABM using a set of parameter values x_n. Minimum values for each parameter (x_n in Equation 3) were set to zero while maximum values were set to 100× the initial parameter value (Table 1). The simulation was run for 190 generations with 20 ABM replicates at each generation to determine an average true positive frequency.

Statistical analysis

Confidence intervals, Pearson’s correlation, and partial least squares regression analysis were performed using GraphPad Prism version 5.0d for Mac OSX. Unless otherwise stated, significance was asserted at P ≤ 0.05.

Results

ABM Notch Transfer Coefficient parameter estimation

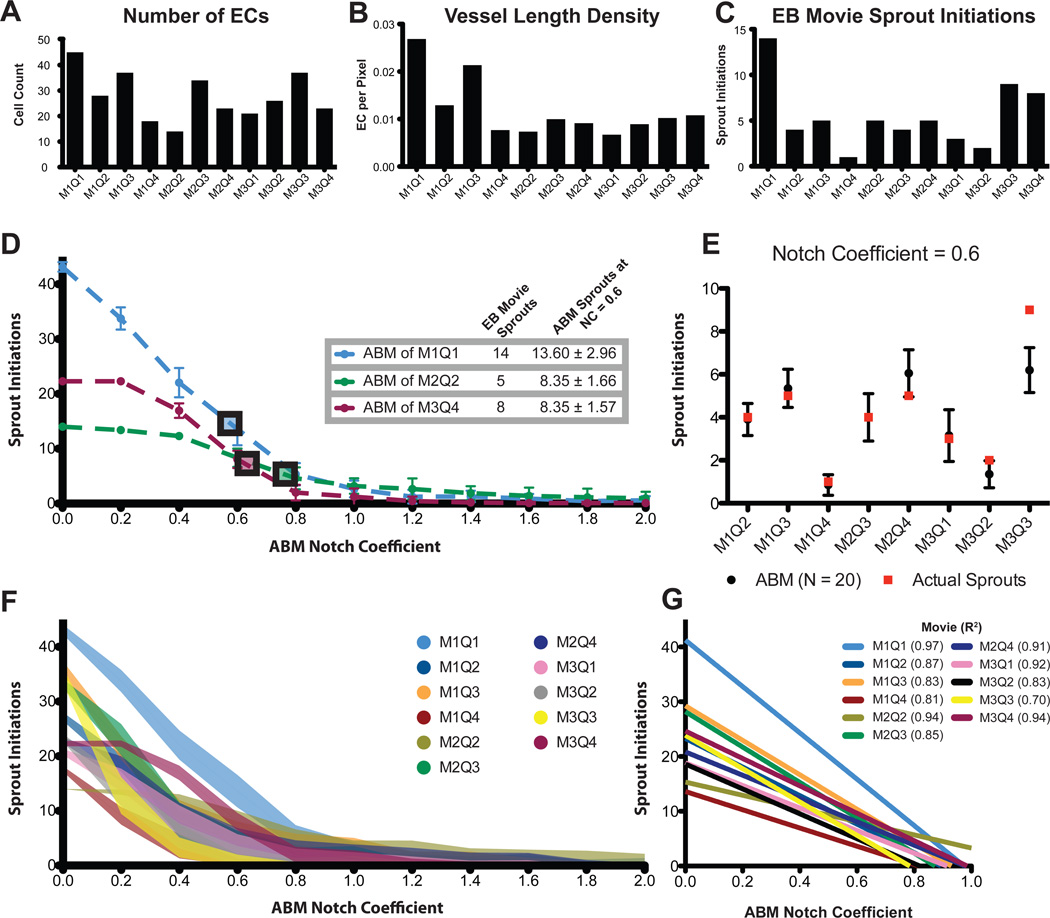
Lacking a literature-derived value for the Notch Transfer Coefficient (α, Equation 2), the key parameter governing the strength of Notch1 intercellular signaling, necessitated the use of parameter estimation. A single quadrant from each of three independent EB movies was evaluated over 16 different Notch Transfer Coefficient (α) parameter values (Figure 3D). As the strength of Notch lateral inhibition increases (increasing α), the number of sprout initiations occurring over the course of the simulations decreases, as would be expected. Above a value of α = 1.6 all three simulated movie quadrants converged to 0 sprout initiation events, effectively preventing any phenotype switching. Conversely, when the Notch Transfer Coefficient parameter was maintained at 0, no lateral inhibition was possible, and every cell in the simulation attempted to sprout. A Notch Transfer Coefficient parameter of approximately 0.6 resulted in agreement between the ABM predictions of sprout initiations and the observed sprout initiations in the three training quadrants (Figure 3D).

Figure 3.

Parameterization and validation of ABM based on a diverse population of EB Movies. The vessel network characteristics of each EB Movie are not uniform and represent a diverse sampling of possible EC network architectures (A–C). Using three EB Movies the ABM Notch Transfer Coefficient was parameterized to predict the number of sprout initiations (D). The Notch Transfer Coefficient value of 0.6 was then tested in all other EB Movies. The number of sprout initiations observed in the EB Movies (red squares) is shown to fall within the 95% confidence interval of ABM predictions (black circles and error bars, E). Perfoming the same sweep of the Notch Transfer Coefficient from 0.0 through 2.0 for all EB Movies demonstrates a similar trend, possessing a linear response region from 0.0 to 1.0 (shaded region is one standard deviation, F,G).

ABM simulates sprout initiation frequency

We sought to validate the Notch Transfer coefficient value of 0.6 established by parameter estimation with 3 training EB movie quadrants. To achieve this, 8 additional test EB movie quadrants were analyzed (Figure 3E). For all but one simulation (M3Q3), the observed number of sprout initiations in the corresponding EB movie quadrant fell within the ABM predicted 95% confidence interval of sprout initiations. This discrepancy for M3Q3 may be due to having a high number of sprout initiations occurring in close proximity in the EB movies – two sprout initiations that occur in close proximity may be underestimated by the ABM which predicts only one sprout initiation.

Sensitivity of ABM to Notch Transfer Coefficient parameter

All EB movie quadrants were evaluated for sensitivity to the Notch Transfer Coefficient. Across the range of tested parameter values (α = 0.0–2.0) all simulated vessel networks demonstrated a sprout initiation frequency that was inversely proportional to the Notch Transfer Coefficient (Figure 3F). Further, we performed a bidirectional sensitivity analysis for sprout initiation frequency, simultaneously varying both the Notch Transfer Coefficient (α) and the tip cell activation threshold (β). While the sensitivity to the Notch Transfer Coefficient is preserved across values of the tip cell activation threshold, the latter demonstrates less of an affect on the former (Figure S1). In all EB movies, the sprout initiation frequency was less sensitive to the tip cell activation threshold than the Notch Transfer Coefficient.

Despite variations in vessel network morphology such as number of endothelial cells and vessel length density (Figure 3A–C), all simulated movie responses could be estimated using linear functions within the parameter range from 0.0 to 1.0 (Figure 3G) with coefficients of determination greater than 0.80 for all simulations except one (M3Q3, R² = 0.70) and with non-zero slopes that were statistically significant (p < 0.05). These data demonstrate sensitivity to the Notch Transfer Coefficient across all tested EB movie vessel networks

Use of a Monte Carlo model to evaluate accuracy of ABM-simulated sprout initiation locations

The trued positive frequency of ABM sprout initiation locations was scored using the methods described in Figure 1B. A Monte Carlo analysis was performed to determine the likelihood of correctly predicting sprout initiation locations purely by random chance, given the mean and standard deviation of paired ABM simulation sprout initiation events as input. The frequency of true positive events (determined by comparison to the observed sprout initiations in the EB movies) as generated by Monte Carlo simulation was compared to that of the ABM in the range of sprout initiation frequency when the Notch Transfer Coefficient parameter is set to 0.6 (Figure 4A).

Using the difference in true positive frequency as a performance index we demonstrated that the ABM has higher spatial accuracy in 7 of 11 starting geometries (Figure 4B). There appeared to be no correlation between performance index and initial conditions of the EB movie networks, such as number of sprout initiations, number of starting endothelial cells, vessel length density, or sprout initiation density (Figure 4C–F).

Unsupervised parameter identification in ABM using GA

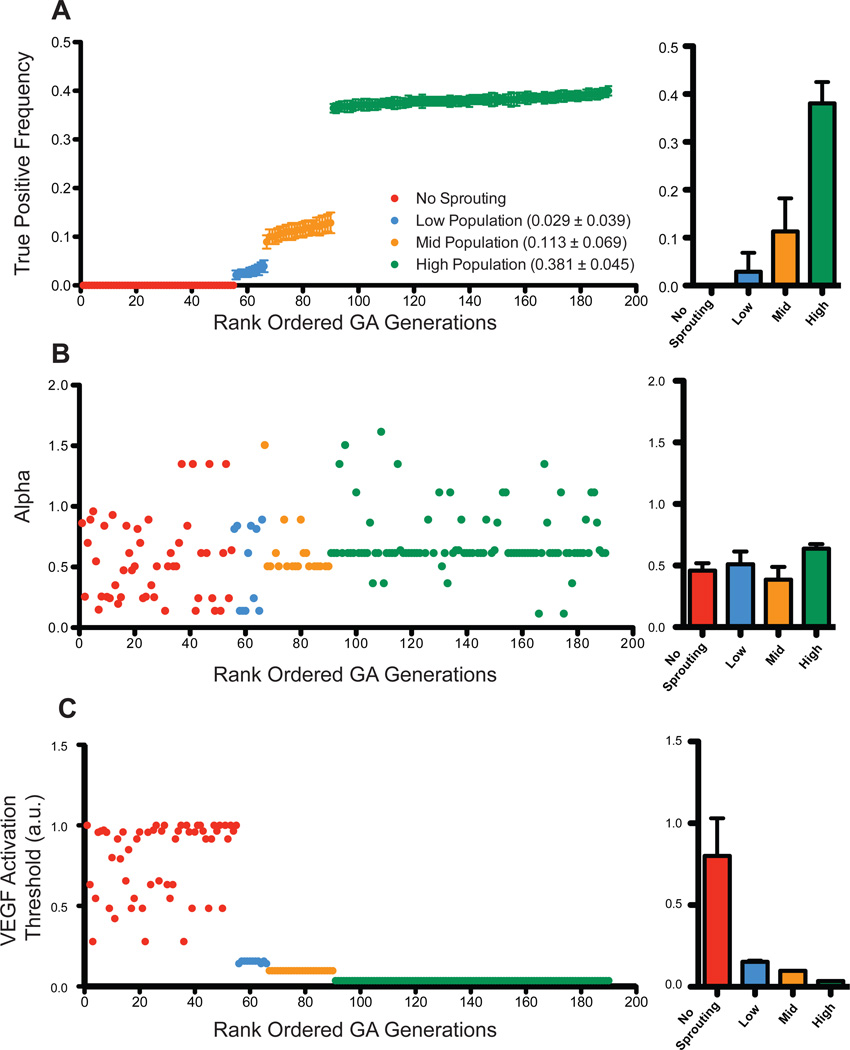
The parameter values used in the ABM simulations were literature-derived values (Table 1), with the exception of the Notch Transfer Coefficient, which was estimated (Figure 3). However, it is possible that a set of optimal parameters could improve the performance index of the ABM simulations. To explore this possibility, we used an unsupervised approach to search for a set of parameter values that could maximize the true positive frequency of the simulation with the worst performance index, M1Q1 (Figure 4B).

We used a GA to identify, in an unsupervised manner, the values of four key parameters (Notch Transfer Coefficient, tip cell activation threshold, sVEGFR1 production rate, VEGFR1 production rate, Equation 3) over the range from 0 to 100 times their original simulation values. As shown in Figure 5A the true positive frequency of the GA derived parameter values approach 40% accuracy. This rank ordering of all generations demonstrates four populations of outcomes: zero accuracy (no sprout initiations), low accuracy (less than 10%), medium accuracy (10%), and the highest accuracy (40%). Notably, these are all less than the original true positive frequency of the ABM (approximately 60%, Figure 4A).

Figure 5.

Parameter optimization using genetic algorithm to improve performance index. The true positive frequency for each generation was plotted in increasing rank order to highlight four distinct outcome populations: no sprouting, low-, medium-, and high-populations (mean ± SD, A). The Notch Transfer Coefficient (α) was plotted using the same rank-ordered generations and found to approach a value of 0.6 (B). To achieve improved true positive frequency the genetic algorithm attempted to minimize the tip cell activation threshold for phenotype switch from quiescent EC to tip cell (C).

Of interest, the GA obtained its best results when minimizing the tip cell activation threshold for phenotype switch from quiescent endothelium to tip cell. Conversely, reduced values of the Notch Transfer Coefficient (α) were associated with poorer performing populations (Figure 5C). Additionally, for the highest true positive frequency population (defined as >36%), the average value of α was 0.63 (Figure 5B), in agreement with the parameter estimation performed in Figure 3.

The GA derived production rates of mVEGFR1 and sVEGFR1 were both approximately six orders of magnitude higher than the values used in Table 1, with the ratio of soluble to membrane bound production being 1.6 (data not shown).

Conclusions

With the advent of innovations in intravital microscopy, such as light sheet microscopy, confocal, and multi-photon microscopy, imaging dynamic processes in living tissues and in ex vivo engineered tissue model systems has become more feasible^50–52. These approaches generate data-rich movies that capture the dynamic behaviors of cells as they migrate within tissues and form multicellular structures, such as blood vessels^53–55. Viewing movies of tissue morphogenesis prompts the observer to ask a number of questions about underlying mechanisms, such as: are these behaviors defined by rule-based pathways? Are they the result of stochastic biological noise? Or, perhaps, are they controlled by some combination of both rule-based and stochastic influences? By combining computational modeling with confocal imaging we have attempted to address these questions in the context of angiogenic sprouting. We compared two different modeling approaches: (1) an ABM in which endothelial cell behaviors are governed by a set of rules and (2) a Monte Carlo simulation with purely stochastic cell behaviors, uninformed by signaling pathways.

In developing our ABM, we had to make several simplifying assumptions. In particular, diffusion and binding kinetics play important roles in signaling through the VEGFR family, including homo- and heterodimerization states that were not included in the ABM. Furthermore, VEGF itself was modeled as a single diffusive isoform with properties similar to the VEGF₁₂₁ splice variant that lacks a heparin binding domain³¹. We feel these assumptions are valid in the context of simulating the locations and frequencies of sprout initiations; however, simulating subsequent steps in sprouting angiogenesis, such as extension of the sprout away from its parent blood vessel, would likely require more high-resolution simulation of these molecular pathways, incorporating the physics of particle diffusion and mass action kinetics^{40, 48, 49}. Furthermore, a similar irreversible binding kinetics model has been suggested for the related Epidermal Growth Factor (EGF) membrane-bound polypeptide signaling receptor complex⁵⁶. It is important to note that while the ABM simulations are driven by deterministic rules, diffusion of VEGF was modeled as a stochastic process, allowing for variation in receptor binding for each simulation.

Additionally, the ABM demonstrates sensitivity to the Notch Transfer Coefficient with a response region that can be approximated by a linear response with a non-zero slope. This permits tuning of the model to additional experimental conditions. For example, decreasing the Notch Transfer Coefficient parameter mimics inhibition of the Notch1-DLL4 pathway and produces increased sprout initiations as would be expected by small molecule inhibition (e.g. the gamma-secretase inhibitor DAPT)^{23, 57}.

The Monte Carlo simulation, with no molecular mechanisms included, was constructed to compare a purely stochastic method of modeling endothelial cell behavior against ruled-based ABM-generated sprout initiation locations. Whereas we could directly compare the number of sprout initiations simulated by the ABM to the number of sprout initiations observed in the EB movies, there was no gold standard for evaluating the accuracy of sprout initiation locations. The Monte Carlo provided a benchmark for assigning a performance index (Figure 4B) of ABM accuracy as compared to the accuracy of random chance.

We demonstrate that the ABM accounting for Notch1-DLL4 lateral inhibition under control of VEGFR regulation is capable of simulating the frequency of angiogenic sprout initiations within the EB (Figure 3E). Despite disparate initial endothelial cell network configurations from one EB movie to the next (Figure 3A–C), the ABM predicted the correct number of sprout initiation events in all but one of the EB movie quadrants. Further, the ABM outperforms the Monte Carlo simulation of endothelial sprout initiation location in 7 of 11 EB movies (Figure 4B), strongly suggesting that deterministic rules are necessary for accurately simulating sprout initiation locations.

Using a GA, we attempted to improve the performance of an ABM with the lowest performance index as defined by the Monte Carlo. Four key parameters were selected and systematically tested by the GA to maximize the ABM true positive accuracy for that movie quadrant (Equation 3). Despite the use of this optimization algorithm, there was no improvement in the ABM’s ability to accurately simulate sprout locations. Note that the objective function employed (Equation 3) does not penalize for false positive predictions – our primary use of the GA was to test for a parameter set that improved upon our literature-derived values for predicting sprout initiations. As an alternative, using an objective function that negatively weighted false positives would potentially provide a more constrained parameter set. Nevertheless, as compared to the values obtained in an unsupervised manner by the GA using a less conservative objective function, literature-derived parameter values are better approximations of the underlying biological processes that they describe.

Taken together, our use of a Monte Carlo simulation and a GA optimization algorithm to score ABM performance and attempt to improve upon that performance, respectively, lead us to conclude that inclusion of additional biological mechanisms in future iterations of the ABM may be necessary to improve its predictive capabilities. We speculate that the addition of new rules accounting for the presence of perivascular cells, for example, or that simulate VEGF molecular diffusion and receptor binding at the cell surface with higher spatial resolution, may extend the ABM’s capabilities.

Others have also begun to explore how accurately angiogenic sprouting can be modeled by purely stochastic methods. Silva et al. recently investigated the frequency of sprouting events in a fibrin bead assay by comparison to a theoretical Poisson distribution and demonstrated that this probabilistic approach consistently underestimated sprout frequency⁵⁸. They concluded that enrichment with “efficient” sprouting endothelial cells was responsible for the discrepancy – indeed, isolation of a population of endothelial cells expressing low levels of CD143 and subsequent analysis in bead sprouting assays demonstrated significant increase in sprout frequency over both control (mixed) and isolated “inefficient” sprouting cells. Thus, after demonstrating that a probabilistic model insufficiently captured the features of fibrin bead sprouting, a new hypothesis – the existence of populations of endothelial cells with differential sprouting capacity – was generated and tested. Including this new rule-based cellular behavior (efficient or inefficient sprouting) into the theoretical Poisson distribution generated sprout frequency predictions in agreement with experimentally observed results. Our present study is consistent with theirs, and suggests that probabilistic models that lack the inclusion of rule-based mechanisms may be insufficient for accurately simulating sprouting angiogenesis.

Our manuscript represents a first step towards greater understanding of sprouting angiogenesis through the integration of ex vivo, dynamic imaging techniques and computational simulations with both rule-based and stochastic methods. Our ABM uses a minimal set of rules to simulate, with considerable accuracy, the frequency and locations of endothelial sprout initiations in the EB during sprouting angiogenesis. By comparing ABM to Monte Carlo predictions, we were able to quantitate the spatial accuracy of the ABM and evaluate whether or not unsupervised parameter exploration improved its performance. Moreover, our simulations suggested that deterministic rules that account for key biological mechanisms are better able to recapitulate experimentally observed angiogenic sprout initiations than random chance, suggesting that rule-based influences predominate over stochastic influences in this setting of embryonic vascular development.

Table 2.

Summarized ABM Rules

Rules	Key Parameters	Reference
Endothelial cells migrate towards the highest concentration of VEGF, based on VEGFR2 activation	ECctx	10, 47, 60–62
Increased VEGFR2 activation increases DLL4 expression		57, 63, 64
DLL4 activates Notch1, resulting in decreased VEGFR2 expression	α	57, 63
mVEGFR1 and sVEGFR1 act as a decoy receptors to reduce local VEGF concentrations		30, 65
VEGFR2 activation induces a tip cell phenotype characterized by increased EC sprouting	β	10, 66